3.3 模拟高通滤波器设计-数字信号处理
模拟信号处理系统设计中的滤波器设计

模拟信号处理系统设计中的滤波器设计在模拟信号处理系统设计中,滤波器设计是非常重要的一部分。
滤波器的作用是根据信号的频率特性,将输入信号中的特定频率范围内的信号通过,而抑制其他频率范围内的信号,从而实现信号的滤波和增强。
在设计滤波器时,首先需要确定滤波器的类型,常见的有低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
每种类型的滤波器都有不同的频率响应特性,根据实际需求选择合适的类型进行设计。
其次,在滤波器设计中需要考虑的关键参数包括截止频率、通带波动、阻带衰减等。
截止频率是指滤波器的频率响应开始发生明显变化的频率点,在滤波器设计过程中需要根据实际应用需求合理确定截止频率。
通带波动是指在通带范围内允许的最大频率偏差,阻带衰减则是指在阻带范围内要抑制的最小频率衰减。
另外,在滤波器设计中还需要考虑滤波器的阶数。
滤波器的阶数越高,对信号的滤波效果越好,但同时也会增加系统的复杂度和成本。
因此在设计中需要权衡滤波器的阶数和性能要求,选择合适的阶数进行设计。
在实际的滤波器设计过程中,可以采用模拟滤波器或数字滤波器的方式。
模拟滤波器是基于模拟电路设计的,通常采用电容、电感和运算放大器等元件进行设计,具有较好的性能和稳定性。
数字滤波器则是通过数字信号处理算法实现的,能够实现更高级别的滤波和信号处理功能。
综上所述,在模拟信号处理系统设计中,滤波器设计是至关重要的一步。
通过合理选择滤波器类型、关键参数和阶数,可以实现对信号的滤波和增强,提高系统的性能和稳定性。
在实际设计过程中,需要根据实际需求和系统要求进行综合考虑,选择合适的设计方案进行实施。
只有在滤波器设计得当的情况下,整个信号处理系统才能发挥最佳效果。
数字信号处理实训论文——模拟带通滤波器和数字滤波器的仿真

摘要数字滤波在数字信号处理中,占有重要的地位。
数字滤波包括FIR和IIR 两种滤波方式,其中FIR滤波具有很多优点,可以在幅度特性随意设计的同时,保证精确、严格的线性相位,滤波稳定,不会出现递归型结构中的极限振荡等不稳定现象,且误差较小,可采用FFT算法实现,因此运算效率高。
设计FIR滤波器常用的方法有窗函数法与频率抽样法,但是这两种方法均不易精确控制通带与阻带的边界频率,所以在实际应用中有一定的局限性。
本次实训包含硬件跟软件两个部分。
硬件部分先通过mutime仿真软件仿真,得到差不多的中心频率,带宽,再画原理图,做电路板,做出的电路板通过调节相关的电位器,则比较容易调到所需的中心频率跟带宽。
软件部分做的是FIR 滤波器,通过matlab软件设计FIR滤波器,包含了高通,低通,带通,带阻,通过matlab软件输入不同的频率及选择相关函数设计FIR滤波器的窗函数。
关键字:数字滤波器;Matlab;FIR;Abstractcharacteristics random design at the same time, ensure accurate, strict linear phase, filter stability, won't appear recursive type structure of the extreme oscillation and unstable phenomenon, and less error, can use FFT algorithm, so the operation efficiency. Design FIR filters the commonly used method with a window function method and frequency sampling method, but the two methods are not easy precise control and stopband bandpass boundary frequency, so in practical application are subject to some limitations.The hardware and software training contains two parts. First mutime hardware part through simulation software simulation, get about of center freq, bandwidth, draw principle diagrams, make circuit boards, make by adjusting the circuit boards of related potentiometer, it is easier to adjust to the required center frequency with bandwidth. Part of the software to do is FIR filters, through the matlab software design FIR filters, contains a high, low pass, band-pass, with resistance, through the matlab software input different frequency and choose relevant function design of FIR filters window function.Key word: digital filter; Matlab; FIR目录引言 (4)1硬件部分 (4)1.1 带通滤波器的设计及参数计算 (4)1.2 电路板PCB图1.2及mutime仿真软件的电路仿真图1.3见附录 (5)1.3 硬件设计所需相关器件 (5)1.3.1芯片5532介绍 (5)1.4 硬件的调试与检测 (6)1.4.1检测硬件电路 (6)1.4.2模块调试检测 (6)1.4.3整体调试检测 (6)2 软件部分 (6)2.1 滤波器概述 (6)2.2 窗函数的介绍 (7)2.3 FIR数字滤波器 (7)2.3.1数字滤波器设计原理 (7)2.3.2FIR滤波器设计方法 (8)3 MATLAB GUI的简介 (8)4 基于Matlab GUI的数字滤波器设计 (9)4.1 GUI界面设计概述 (9)4.2 GUI页面设计 (10)4.3 “滤波器设计软件”回调函数编写 (12)4.4 软件运行和结果 (13)5 总结 (14)谢辞 (14)参考文献 (15)附录 (16)引言数字滤波器是一种用来过滤时间离散信号的数字系统,通过对抽样数据进行数学处理来达到频域滤波的目的。
模拟信号处理中的滤波器设计技巧

模拟信号处理中的滤波器设计技巧
在模拟信号处理中,滤波器设计是一项关键的技术,它可以帮助我们对信号进行处理和改善,使得我们可以更好地提取出有用的信息。
在设计滤波器时,有一些技巧是非常重要的,下面我将介绍一些常用的技巧和方法。
首先,我们需要了解滤波器的种类和特性。
常见的滤波器包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
每种滤波器都有其特定的频率响应和传递函数,我们需要根据信号的特点和需求选择合适的滤波器类型。
其次,我们需要考虑滤波器的设计参数。
在设计滤波器时,我们需要确定滤波器的截止频率、通带波纹、阻带衰减等参数。
这些参数将直接影响滤波器的性能和效果,因此需要进行合理的选择和调整。
另外,我们还需要考虑滤波器的设计方法。
常用的滤波器设计方法包括脉冲响应不变法、双线性变换法和频率变换法等。
每种方法都有其优缺点,我们需要根据具体的应用需求选择合适的方法。
此外,在设计滤波器时,我们还需要考虑滤波器的稳定性和实现方法。
滤波器的稳定性是一个重要的性能指标,我们需要确保滤波器在所有频率下都是稳定的。
同时,我们还需要考虑如何实现所设计的滤波器,可以选择模拟电路、数字电路或者混合电路进行实现。
总的来说,滤波器设计是模拟信号处理中的重要技术,通过合理选择滤波器类型、设计参数、方法和实现方式,我们可以实现对信号的有效处理和改善。
希望以上介绍的技巧和方法能够对您在滤波器设计中有所帮助。
如果您对滤波器设计还有其他问题或者需要更深入的了解,请随时联系我,我会尽力为您提供帮助和支持。
数字信号处理中的滤波器设计技术

数字信号处理中的滤波器设计技术滤波器是数字信号处理中广泛应用的重要技术之一。
它可以用于去除信号中的噪声、调整信号频率、改善信号质量等。
本文将介绍数字信号处理中常见的滤波器设计技术。
一、低通滤波器低通滤波器可以通过保留低频信号,滤除高频干扰信号。
在数字信号处理中,常见的低通滤波器设计技术有有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器。
FIR滤波器是一种线性相位滤波器,其特点是稳定性好、易于设计和实现。
在FIR滤波器的设计中,常用的方法有窗函数法、频率采样法和最小二乘法。
窗函数法主要用于设计线性相位FIR滤波器,可以通过选择不同的窗函数来调整滤波器的频率响应特性。
频率采样法则主要应用于非线性相位FIR滤波器的设计,通过采样输入输出信号的频谱来确定滤波器系数。
最小二乘法则是一种优化问题的求解方法,通过最小化期望输出与实际输出之间的误差来设计FIR滤波器。
IIR滤波器采用递归结构,其特点是具有较窄的转换带宽和较快的滚降特性。
IIR滤波器的设计一般基于模拟滤波器的原型设计,可以通过脉冲响应不变法、双线性变换法和频率变换法实现。
脉冲响应不变法是通过将模拟滤波器的脉冲响应与数字滤波器的单位采样响应相等来设计IIR滤波器。
双线性变换法是通过将模拟滤波器的传输函数与数字滤波器的传输函数进行线性映射来设计IIR滤波器。
频率变换法则通过对模拟滤波器的频率进行变换,再进行离散化得到IIR滤波器。
二、高通滤波器高通滤波器可以通过保留高频信号,滤除低频干扰信号。
常见的高通滤波器设计技术与低通滤波器设计类似,可以采用FIR滤波器和IIR 滤波器。
对于FIR滤波器,可以通过选择适当的窗函数和设计方法来实现高通滤波器的设计。
而对于IIR滤波器,可以采用类似的方法,将低通滤波器的设计进行变换得到高通滤波器。
三、带通滤波器带通滤波器主要用于保留一定频率范围内的信号。
在数字信号处理中,常见的带通滤波器设计技术有窗函数法、频率采样法和最小二乘法等。
第七章 模拟滤波器的设计(数字信号处理)

s
c
)
2N
10
a s / 10
(7.2.15)
由(7.2.14)和(7.2.15)式得到:
(
p
s
)
N
10 10
a p / 10 a s / 10
1 1
令
sp s / p , k sp
10 10
a p 10 as 10
1 1
,则N由下式表示:
N
1
1
1
1
0
fC a ) 低通
f
0
fC b ) 高通
f
0
fC1 c) 带通
fC2
f
0
fC1 d ) 带阻
fC2 f
7.1 理想滤波器
无过渡带且在通频带内满 足不失真测试条件的滤波 器称为理想滤波器。理想 滤波器的频率响应函数为:
|H(f)| A0
-fc
A e j 2 p ft 0 0 H(f) 0 f fc 其它
lg k sp lg sp
(7.2.16)
用上式求出的N可能有小数部分,应取大于等于N
的最小整数。关于3dB截止频率Ωc,如果技术指标中没 有 给 出 , 可 以 按 照 (7.2.14) 式 或 (7.2.15) 式 求 出 , 由
图7.2.2 低通滤波器的幅度特性
滤波器的技术指标给定后,需要设计一个传输函
数Ha(s),希望其幅度平方函数满足给定的指标αp和αs, 一般滤波器的单位冲激响应为实数,因此
H a ( j )
2
H a ( s )G ( s )
s j
H a ( j ) H a ( j )
数字信号处理课程设计--基于DSP 的 FIR 数字滤波器的设计

数字信号处理课程设计报告设计题目:基于DSP 的 FIR 数字滤波器的设计专业班级学号学生姓名指导教师教师评分目录一、摘要 (1)二、概述 (2)三、系统设计 (3)3.1 DSP 系统原理框图 (3)3.2 DSP 系统各部分分析 (4)四、硬件设计 (5)4.1 硬件整体电路及框图 (5)4.2 硬件各部分组成简介 (6)五、软件设计 (10)5.1 FIR 数字滤波器的基本网络结构 (10)5.2 FIR 数字滤波器的设计 (10)5.2.1 FIR 滤波器的主要特点 (10)5.2.2 FIR 滤波器设计方法 (10)5.2.3 窗函数法设计的基本思想 (11)5.2.4 用窗函数设计FIR滤波器的步骤 (12)5.3 FIR数字滤波器的MATLAB的实现 (13)5.3.1 Matlab软件介绍 (13)5.3.2 用Matlab实现FIR数字滤波器的几种方法 (13)5.4 FFT参数的计算 (17)5.5 DSP程序流程图 (17)六、实验结果 (19)七、个人总结 (21)八、参考文献 (22)附件: (23)数字信号处理课程设计一、摘要数字滤波器是数字信号处理中最重要的组成部分之一,数字滤波器是由数字乘法器、加法器和延时单元组成的一种算法或装置,可作为应用系统对信号的前期处理。
DSP芯片实现的数字滤波器具有稳定性好、精确度高、灵活性强及不受外界影响等特性。
因此基于DSP实现的数字滤波器广泛应用于语音图像处理、数字通信、频谱分析、模式识别、自动控制等领域,具有广阔的发展空间。
本文首先介绍了数字滤波器的概念及分类,以及数字滤波器的实现方法。
在理解FIR 滤波器的工作原理及其设计方法的基础上,在MATLAB环境下利用矩形窗设计实现FIR滤波器。
然后通过DSP结合CCS2.0软件进行编程,最终实现了基于DSP的FIR数字低通滤波器的设计。
仿真结果表明,基于DSP实现的滤波器具有稳定性好、精确度高、灵活性强等优点,并能实现对信号的实时滤波。
数字信号处理与滤波器设计考核试卷

D.冲激响应和系统函数没有直接关系
8.以下哪些方法可以用于数字滤波器的实现?()
A.递推算法
B.并行算法
C.快速傅里叶变换(FFT)
D. A、B和C
9.数字滤波器中的窗函数用于()
A.控制旁瓣水平
B.确定通带边缘
C.影响阻带衰减
D. A、B和C
10.在数字滤波器设计中,以下哪些因素会影响滤波器的性能?()
A.滤波器类型
B.滤波器阶数
C.采样频率
D. A、B和C
11.数字滤波器的幅频特性曲线可以用来分析()
A.滤波器的通带
B.滤波器的阻带
C.滤波器的群延迟
D. A和B
12.以下哪些条件可以导致数字滤波器不稳定?()
A.系统函数的极点不在单位圆内
B.系统函数的零点不在单位圆.无理函数
C.幂级数
D.微分方程
11.在FIR滤波器设计中,窗函数法的主要作用是()
A.产生理想滤波器的频率响应
B.限制滤波器的通带宽度
C.消除旁瓣
D.提高滤波器的阻带衰减
12.判断下列哪个选项是正确的关于数字滤波器的描述?()
A.数字滤波器只能实现模拟滤波器的设计指标
B.数字滤波器可以实现模拟滤波器无法实现的设计指标
2.详细说明FIR滤波器和IIR滤波器的区别,包括它们的设计复杂性、相位特性、稳定性和应用场景。
3.描述数字滤波器设计中的窗函数法,并解释窗函数的类型如何影响滤波器的频率响应。
4.讨论数字滤波器设计时需要考虑的实际问题,包括有限字长效应、硬件资源限制和实际应用中的性能评估。
标准答案
一、单项选择题
1. A
数字信号处理与滤波器设计考核试卷
《模拟滤波器设计》课件

滤波器的频率响应
幅度频率响应
群时延频率响应
描述滤波器对不同频率信号的幅度增 益或衰减。
描述滤波器对不同频率信号的群时延 变化。
相位频率响应
描述滤波器对不同频率信号的相位偏 移。
滤波器的传递函数
一阶滤波器:具有一个极点和零点的传递函数。 高阶滤波器:具有多个极点和零点的传递函数。
二阶滤波器:具有两个极点和两个零点的传递函数。
频率等参数,可以使用 MATLAB等工具进行辅助设
计。
巴特沃斯滤波器的应用广泛, 如音频信号处理、图像增强等
。
切比雪夫滤波器设计
切比雪夫滤波器是一种具有等波纹特性的滤波 器,其幅度特性在通带和阻带内都是等波纹的 。
设计切比雪夫滤波器时,需要确定滤波器的阶 数、通带和阻带的波纹幅度等参数,可以使用 MATLAB等工具进行辅助设计。
ERA
模拟滤波器设计的挑战与机遇
挑战
随着信号处理技术的发展,对模拟滤波器的性能要求越来越高,如何提高滤波器的性能、减小其体积 和成本是当前面临的主要挑战。
机遇
随着新材料、新工艺的不断涌现,为模拟滤波器的设计提供了更多的可能性,同时也为解决上述挑战 提供了新的思路和方法。
未来发展方向与趋势
发展方向
切比雪夫滤波器的应用也较广泛,如雷达信号 处理、通信系统等。
椭圆滤波器设计
1
椭圆滤波器是一种具有最小相位特性的滤波器, 其幅度特性和相位特性都是线性的。
2
设计椭圆滤波器时,需要确定滤波器的阶数和截 止频率等参数,可以使用MATLAB应用相对较少,主要在一些特殊领 域如控制系统、信号处理等领域中使用。
测试结果的评价与改进
结果评价
根据测试数据,对模拟滤波器的性能进行客观评价,与设计要求进行对比,找出性能不足之处。
数字信号处理实验报告--滤波器设计

大连理工大学实验报告学院(系): 专业: 班级:姓 名: 学号: 组: ___实验时间: 实验室: 实验台: 指导教师签字: 成绩:实验三 滤波器设计一、实验结果与分析IIR 部分:1.用buttord 和butter 函数,直接设计一个巴特沃兹高通滤波器,要求通带截止频率为0.6π,通带内衰减不大于1dB ,阻带起始频率为0.4π,阻带内衰减不小于15dB ,观察其频谱响应的特点: clc,clearwp=0.6*pi/pi; ws=0.4*pi/pi; ap=1,as=15;[N,wn]=buttord(wp,ws,ap,as); [bz,az]= butter(N,wn,'high'); [H,W]=freqz(bz,az);plot(W,20*log10(abs(H))); grid on;xlabel('频率/弧度') ;ylabel('对数幅频响应/dB') ; axis([0.2*pi pi -40 1]);1 1.522.53-40-35-30-25-20-15-10-50频率/弧度对数幅频响应/d B2. 给定带通滤波器的技术指标:通带上下截止频率为0.4,0.3ππ,通带内衰减不大于3dB ,阻带上下起始频率为0.5,0.2ππ,阻带内衰减不小于18dB 。
用buttord 和butter 函数,对比巴特沃兹和切比雪夫的效果: clc,clearwp=[0.3*pi/pi,0.4*pi/pi]; ws=[0.2*pi/pi,0.5*pi/pi]; ap=3,as=18;[N,wn]=buttord(wp,ws,ap,as); [bz,az]= butter(N,wn); [H,W]=freqz(bz,az);plot(W,20*log10(abs(H))); grid on;xlabel('频率/弧度') ;ylabel('对数幅频响应/dB') ; axis([0 pi -60 1]);00.511.52 2.53-60-50-40-30-20-10频率/弧度对数幅频响应/d B3.用双线性变换法的模拟滤波器原型设计一个巴特沃兹低通滤波器,给定技术指标是100p f Hz =300st f Hz =3p dB α=20s dB α=,抽样频率为1000sF Hz =:clc,clear;Rp=3; Rs=20;wp=0.2*pi; ws=0.3*pi; Fs=1000;wap=2*Fs*tan(wp/2);was=2*Fs*tan(ws/2);[N,Wn]=buttord(wap,was,Rp,Rs,'s'); [Z,P,K]=buttap(N);[Bap,Aap]=zp2tf(Z,P,K); [b,a]=lp2lp(Bap,Aap,Wn); [bz,az]=bilinear(b,a,Fs); %绘制频率响应曲线 [H,W]=freqz(bz,az);plot(W,20*log10(abs(H))); grid on;xlabel('频率/弧度')ylabel('对数幅频响应/dB') axis([0 0.5*pi -50 1])0.511.5-50-45-40-35-30-25-20-15-10-50频率/弧度对数幅频响应/d B4. 用双线性变换法的模拟滤波器原型和直接设计法(buttord 以及butter )两种方法,设计一个数字系统的抽样频率Fs=2000Hz ,试设计一个为此系统使用的带通数字滤波器。
有源模拟高通滤波器的设计与分析

摘要滤波器广泛应用于电信设备和各类控制系统中,对无用信号尽可能大的衰减,让有用信号尽可能无衰减的通过,从而纠正信号的波形畸变。
其设计优劣直接决定产品的优劣,所以,滤波器的研究和生产历来为各国所重视。
可以说,一个国家的滤波器技术代表着一个国家的电子设备制造水平。
本文通过对滤波器原理和其组成部分的研究,设计了一个压控型有源二阶和四阶高通模拟滤波器,完成了原理图设计,实现了滤波器的设计功能。
首先应用Multisim对设计出的原理图进行仿真,分析了滤波器的幅频和相频特性,验证了有源滤波器的特性。
其次通过对滤波器的传输函数进行复频域分析,运用Matlab 软件编程,仿真测试了幅频和相频特性,进一步验证了设计的正确性。
最后利用软件编程,分析了Q值改变时对滤波器特性的影响,并且测试滤波系统的稳定性能,从而实现电路的优化设计。
关键词:有源模拟高通滤波器,Multisim,Matlab,幅相频特性,Q值改变AbstractThe filters are widely used in telecommunications equipment and various types of control system, it can attenuate the unwanted signals as large as possible so that the useful signal without attenuation through as far as possible, thereby correcting the signal waveform distortion. Its design will directly determine the pros and cons of the product, so the research and production of the filter has always been attached much important for every country. It can be said that a country's filter technology represents a country's electronic equipment manufacturing level.Based on the filter theory and its component of the study, this paper designed an active second-order and forth-order high-pass analog filter. First, according to the use of Multisim,the dissertation simulated the circuit schematic diagram , and then analysised the design of the schematic diagram of frequency and phase frequency characteristic analysis, thus validate the characteristics of the active filter.Followed by the filter transfer functionanalysis of the complex frequency domain, the paper apply Matlab software programming to simulate and test the amplitude frequency and phase frequency characteristics, to further verify the design correctness. Finally,this paper simulated and tested Q value change on the filter properties, and test of filtering system performance and stability through MATLAB software programming to, thereby realizing the optimization design of circuit.Key words: active analog high-pass filter, Multisim, Matlab, amplitude and phase frequency characteristics, Q value change目录摘要Abstract1. 绪论1.1.选题依据及意义1.2.高通滤波器的发展概况1.3.设计思想2. 滤波器简介2.1.滤波器的基本原理2.2.滤波器的有关参数2.3.有源滤波和无源滤波2.3.1.简介2.3.2.优缺点3. 电路设计3.1.有源高通滤波器的原理图3.2.各部分电路设计3.2.1.滤波电路设计3.2.2.集成运放加反馈电路设计3.3.设计方案3.3.1.设计阶数3.3.2.二阶高通滤波器3.3.3.四阶高通滤波器3.3.4.方案论证4. 电路仿真与测试4.1.参数确定4.1.1.确定原则4.1.2.计算参数4.2.实际计算4.3.Multisim仿真分析4.3.1.性能仿真4.3.2.性能分析4.4.Matlab编程仿真测试4.4.1.不同Q值时的特性分析4.4.2.不同Q值时的仿真分析4.4.3.滤波器系统稳定性分析结论参考文献致谢1. 绪论1.1.选题依据及意义滤波器是减少或消除谐波对电力系统影响的电气部件,广泛应用于电力系统、通信发射机与接收机等电子设备中,它能减弱或消除谐波的危害,对无用信号尽可能大的衰减,让有用信号尽可能无衰减的通过,从而纠正信号波形畸变。
数字信号处理(方勇)第三章习题答案
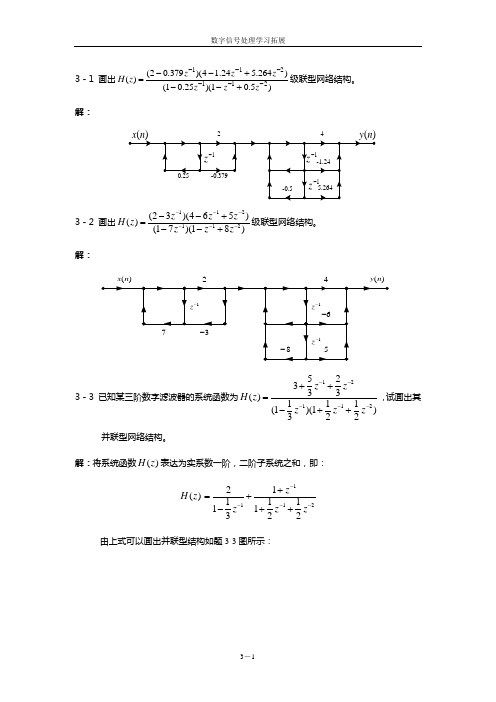
3-1 画出)5.01)(25.01()264.524.14)(379.02()(211211------+--+--=z zz zzzz H 级联型网络结构。
解:243-2 画出112112(23)(465)()(17)(18)z z zH z z zz--------+=--+级联型网络结构。
解:()x n ()y n 243-3 已知某三阶数字滤波器的系统函数为1211252333()111(1)(1)322zzH z z zz-----++=-++,试画出其并联型网络结构。
解:将系统函数()H z 表达为实系数一阶,二阶子系统之和,即:()H z 11122111111322z zzz----+=+-++由上式可以画出并联型结构如题3-3图所示:)题3-3图3-4 已知一FIR 滤波器的系统函数为121()(10.70.5)(12)H z z z z ---=-++,画出该FIR滤波器的线性相位结构。
解: 因为121123()(10.70.5)(12)1 1.30.9H z z z z z z z ------=-++=+-+,所以由第二类线性相位结构画出该滤波器的线性相位结构,如题3-4图所示:()x n 1-1-1z -题3-4图3-5 已知一个FIR 系统的转移函数为:12345()1 1.25 2.75 2.75 1.23H z zzzzz-----=+--++求用级联形式实现的结构流图并用MATLAB 画出其零点分布及其频率响应曲线。
解: 由转移函数可知,6=N ,且)(n h 偶对称,故为线性相位系统,共有5个零点,为5阶系统,因而必存在一个一阶系统,即1±=z 为系统的零点。
而最高阶5-z 的系数为+1,所以1-=z 为其零点。
)(z H 中包含11-+z 项。
所以:11()()(1)H z H z z -=+。
1()H z 为一四阶子系统,设12341()1H z bz cz bz z ----=++++,代入等式,两边相等求得12341()10.2530.25H z z z z z ----=+-++,得出系统全部零点,如图3-5(b )所示。
3.3 模拟高通滤波器设计-数字信号处理.ppt

例: 设计满足下列条件的模拟BW型高通滤波器
fp=5kHz, fs=1kHz, Ap1dB, As 40dB
Gain in dB
0 -10 -20 -30 -40 -50 -60 -70
0
1000
2000 3000 4000 Frequency in Hz
5000
6000
Ap= 40.0000 As= 0.1098
1)
④ 求高通滤波器的传递函数
H(s) = G(P) |P=p / s = G(P) |P=200π / s
例: 设计满足下列条件的模拟BW型高通滤波器
fp=5kHz, fs=1kHz, Ap1dB, As 40dB。
%高通滤波器的设计 wp=1/(2*pi*5000);ws=1/(2*pi*1000);Ap=1;As=40; [N,Wc]=buttord(wp,ws,Ap,As,'s'); [num,den] = butter(N,Wc,'s'); disp('LP 分子多项式'); fprintf('%.4e\n',num); disp('LP 分母多项式'); fprintf('%.4e\n',den); [numt,dent] = lp2hp(num,den,1); disp('HP 分子多项式'); fprintf('%.4e\n',numt); disp('HP 分母多项式'); fprintf(‘%.4e\n’,dent);
3.3 模拟高通滤波器设计
1.模拟高通滤波器的设计 由于滤波器的幅频特性都是频率的偶函数,
低通滤波器G(jλ)和高通滤波器的H(jη) 的幅频特性曲线为:
数字信号处理中的滤波器设计与实现研究

数字信号处理中的滤波器设计与实现研究数字信号处理(Digital Signal Processing,DSP)是指将模拟信号经过采样、量化等处理,转换为数字信号,并通过算法对数字信号进行处理和分析的技术领域。
而滤波器则是DSP中非常重要的一部分,它用于去除噪声、增强信号等。
本文将重点探讨数字信号处理中的滤波器设计与实现。
一、滤波器的基本原理滤波器是一种电子器件或数字算法,用于根据信号的频率特性选择性地去除或传递信号的不同频率组成部分。
滤波器根据其频率响应特性可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器等。
低通滤波器(Low-pass Filter,LPF)用于在一定频率以下传递信号,而抑制高于该频率的信号。
高通滤波器(High-pass Filter,HPF)则相反,用于传递高于一定频率的信号,并滤除低于该频率的部分。
带通滤波器(Band-pass Filter,BPF)用于在某一频段内保留信号,滤除其他频率的信号。
带阻滤波器(Band-stop Filter,BSF)则在某一频段内抑制信号。
滤波器的设计与实现通常按照以下步骤进行:1. 信号特性分析: 首先分析输入信号的频率特性和要求,确定所需滤波器的类型。
2. 滤波器设计: 根据信号特性,选择适当的滤波器设计方法,进行滤波器参数的计算。
3. 滤波器实现: 根据设计得到的滤波器参数,利用模拟电路、数字滤波器算法等实现滤波器。
4. 仿真与优化: 对实现的滤波器进行仿真分析,根据仿真结果进行优化调整。
5. 实验验证: 利用信号发生器、示波器等仪器对滤波器进行实验验证,检验设计与实现的效果。
二、经典滤波器设计方法1. IIR滤波器设计: 无限脉冲响应滤波器(Infinite Impulse Response,IIR)是一类具有无限脉冲响应的滤波器。
常用的IIR滤波器设计方法包括脉冲响应不变法、双线性变换法和频率响应匹配法等。
脉冲响应不变法将模拟滤波器的脉冲响应函数离散化,得到数字滤波器的差分方程,再使用数字滤波器的参数来设计并实现IIR滤波器。
模拟高通带通滤波器设计

电路设计
设计滤波器电路结构
根据滤波器类型和电路元件选择,设计出合适的电路结构。
计算元件参数
根据设计目标和电路元件选择,计算出各元件的具体参数值。
绘制电路图
使用电路设计软件绘制出高通带通滤波器的电路图。
仿真验证
建立仿真模型
在仿真软件中建立高通带通滤波器的电路模型,并设 置适当的仿真参数。
进行仿真实验
群时延特性分析
总结词
群时延是衡量滤波器对信号畸变影响的指标,它反映了信号通过滤波器后的时间 延迟。
详细描述
高通带通滤波器的群时延特性在通带内应保持相对稳定,以保证信号的完整性。 在通带边缘和阻带,群时延特性会出现较大的波动,这可能会影响信号的相位特 性。
插入损耗分析
总结词
插入损耗是指滤波器接入电路后,输入信号的功与输出信 号的功率之比。
椭圆函数逼近法
利用椭圆函数来逼近理想 滤波器的频率响应特性, 设计出具有特定性能的高 通带通滤波器。
高通带通滤波器的设计难点
如何平衡阻带抑制与通带平坦度
在设计中需要权衡阻带抑制和通带平坦度,以确保滤波器性能达到 要求。
如何减小群时延波动
群时延是衡量滤波器对信号时间延迟的参数,需要在设计中尽量减 小群时延波动。
定义。
品质因数
衡量滤波器性能的一个 重要参数,与滤波器的 带宽和截止频率有关。
群时延
衡量滤波器对信号时间 延迟的参数,要求在通
带内保持恒定。
滤波器设计方法
01
02
03
切比雪夫逼近法
通过逼近理想滤波器的频 率响应特性,设计出具有 特定性能的高通带通滤波 器。
巴特沃斯逼近法
通过逼近理想滤波器的频 率响应特性,设计出具有 平坦幅频特性的高通带通 滤波器。
数字信号处理中的滤波器设计与时域频域分析方法

数字信号处理中的滤波器设计与时域频域分析方法在数字信号处理中,滤波器设计和时域频域分析是非常重要的方法和技术。
滤波器是一种能够改变信号频谱特性的系统,它可以增强或者抑制信号的某些频率分量。
本文将从滤波器设计和时域频域分析两个方面介绍相关概念和方法。
一、滤波器设计滤波器设计是指根据特定的信号处理需求来设计合适的数字滤波器。
在数字信号处理中,常见的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
1.低通滤波器:低通滤波器可以通过抑制高频成分实现对信号进行平滑处理。
在滤波器的频率响应中,低通滤波器允许通过低频信号,而抑制高频信号。
2.高通滤波器:高通滤波器可以抑制低频成分,使得高频成分能够通过。
在滤波器的频率响应中,高通滤波器允许通过高频信号,而抑制低频信号。
3.带通滤波器:带通滤波器可以通过抑制频谱中的低频和高频成分,保留一个特定频率范围内的分量。
在滤波器的频率响应中,带通滤波器允许通过特定的频率范围内的信号,而抑制其他频率信号。
4.带阻滤波器:带阻滤波器可以抑制特定频率范围内的信号,保留其他频率分量。
在滤波器的频率响应中,带阻滤波器抑制一个特定频率范围内的信号,而允许其他频率信号通过。
滤波器设计的方法主要包括经验法、基于窗函数的设计法和基于优化算法的设计法。
经验法是基于经验和直觉设计滤波器,常用的方法包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。
窗函数法是通过选择适当的窗函数来设计滤波器,常用的方法包括海明窗、矩形窗和汉宁窗。
优化算法包括最小二乘法、进化算法和遗传算法,这些方法利用数学优化技术来自动选择滤波器参数。
二、时域频域分析方法时域和频域分析是对信号进行特性分析的两种常用方法。
1.时域分析:时域分析是将信号从时域(时间域)进行分析。
时域分析方法包括时域波形分析、自相关分析和互相关分析。
时域波形分析是通过绘制信号的波形图来观察信号的变化情况。
自相关分析是通过计算信号与其自身的相关性来研究信号的周期性和重复性。
数字信号处理-模拟高通、带通滤波器设计

模拟带通filter的设计方法 的设计方法 模拟带通 带通滤波器的指标要求
ηs1 = Ω s1 / B,ηs 2 = Ω s 2 / B ηl = Ωl / B,ηu = Ωu / B η02 = ηlηu
B = Ωu − Ωl
带通滤波器频率特性是正负对称的, 带通滤波器频率特性是正负对称的,故 这个变换必须是一对二的映射, 这个变换必须是一对二的映射,它应该 是 的二次函数
去归一化, 去归一化,将p=s/
2 Ωc G( s) = 2 2 s + 2Ω c s + Ω c
代入上式得到: c代入上式得到:
(5) 将模拟低通转换成模拟高通。将G(s) 将模拟低通转换成模拟高通。 的变量换成1/s,得到模拟高通 的变量换成 ,得到模拟高通Ha(s): :
H ( s) = G( p)
sB 2 s 2 +Ω0
p=
设计模拟带阻滤波器,其技术要求为: 例6.2.5 设计模拟带阻滤波器,其技术要求为: × l=2π×905rad/s,
s2=
× s1=2π×980rad/s, × u=2π×1105rad/s,
2π×1020rad/s, ×
αp=3dB,αs=25dB。试设计巴特沃斯带阻滤波器。 。试设计巴特沃斯带阻滤波器。 解 (1) 模拟带阻滤波器的技术要求: 模拟带阻滤波器的技术要求: × l=2π×905, × s1=2π×980,
1 = 0.163rad / s, α p = 3dB 6.155 1 Ωs = = 0.604rad / s, α s = 15dB 1.6s对3dB截止频率
c归一化,这里
c=
p
Ωs λ p = 1, λs = = 3.71 Ωp
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
④ 求高通滤波器的传递函数
H(s) = G(P) |P=p / s = G(P) |P=20 0π / s
例: 设计满足下列条件的模拟BW型高通滤波器 fp=5kHz, fs=1kHz, Ap1dB, As 40dB。
%高通滤波器的设计 wp=1/(2*pi*5000);ws=1/(2*pi*1000);Ap=1;As=40; [N,Wc]=buttord(wp,ws,Ap,As,'s'); [num,den] = butter(N,Wc,'s'); disp('LP 分子多项式'); fprintf('%.4e\n',num); disp('LP 分母多项式'); fprintf('%.4e\n',den); [numt,dent] = lp2hp(num,den,1); disp('HP 分子多项式'); fprintf('%.4e\n',numt); disp('HP 分母多项式'); fprintf(‘%.4e\n’,dent);
3.3
模拟高通滤波器设计
模拟高通、带通及带阻滤波器的设计方法都是 先将要设计的滤波器的技术指标(主要是Ω p, Ω s)通过某种频率转换关系转换成模拟低通滤 波器的技术指标,并依据这些技术指标设计出 低同滤波器的转移函数,然后再依据频率转换 关系变成所要设计的滤波器的转换函数。
3.3
模拟高通滤波器设计
例: 设计满足下列条件的模拟BW型高通滤波器 fp=5kHz, fs=1kHz, Ap1dB, As 40dB
0 -10 Gain in dB
-20
-30
-40
-50 -60
-70
0
1000
2000 3000 4000 Frequency in Hz
5000
6000
ቤተ መጻሕፍቲ ባይዱ
Ap= 40.0000 As= 0.1098
解: ① 先将频率归一化得η p=1,η s=0.5
② 作频率转换,得 λ p=1,λ s=2,仍 有α p=3dB,α s =30dB ③ 设计巴特沃思滤波器,由例1可知 C=1, N=5,因而归一化转移函数为
3.3
模拟高通滤波器设计
G ( P) 1 (P 1)(P 2 0.618P 1)(P 2 1.618P 1)
设计流程为
高通、 低通滤 带通和 频 率 转 波器的 带阻的 换 技术指 标 技术指 标 设 计 G 得到高 ( P )模 频 率 转 通 、 带 拟低通 换 通或带 滤波器 阻滤波 器H(s)
3.3
模拟高通滤波器设计
低通滤波器传递函数为G(s),G(jΩ ), 归一化频率λ ,P=jλ 高通、带通带阻滤波器传递函数为H(s), H(jΩ )归一化频率η ,q=jη 因此相应归一化的转移函数、频率特性分别为 H(q)及H(jη ),λ 与η 的关系λ =f(η ) 称为频率变换关系。
p
3.3 模拟高通滤波器设计
得 H(q)=G(P)|p=-1/q = G(-1/q)
考虑到 |G(jλ )| 的对称性,令q=1/p,即 H(q)=G(1/q) 又由于 所以, q=jη =jΩ /Ω p=s/Ω p H(s)=G(P)|p=Ω p / s
3.3
模拟高通滤波器设计
例 试用巴特沃思滤波器设计一高通模拟滤波器, 要求fp=100Hz, α p=3dB, fs=50Hz,α s =30dB
3.3
模拟高通滤波器设计
1.模拟高通滤波器的设计
由于滤波器的幅频特性都是频率的偶函数, 低通滤波器G(jλ )和高通滤波器的H(jη ) 的幅频特性曲线为:
3.3
模拟高通滤波器设计
| G(jλ)|
-λs′
λp′=-1
λ p=1
λs
λ
| H(jη )|
η s
η p=1
η
3.3
模拟高通滤波器设计
η和λ的对应关系
λ
λ′=-λ
η
η
∞ ηp=1 Ηs
0
λp′=-1 - λs′
∞
0
3.3
模拟高通滤波器设计
所以 λ ′η =-1 或λ η =1 (1) 通过(1)式可将高通滤波器的频率η 转换 成低通滤波器的频率λ ,通带与阻带衰减α p, α s保持不变,这样可设计模拟低通滤波器的转 换函数G(P) 1 1 q=jη = j
