模拟滤波器的设计(1)
第8章模拟滤波器的设计

h(t) F 1 H () 1 e jtD e jtD d
2
1
2
cos(t
tD)
j sin (t
tD )d
1
0
cos
(t
tD
)d
1
C 0
cos
(t
t
D
)d
C sin C (t tD ) C (t tD )
第15页/共65页
8.3.2 滤波器的理想特性与实际特性
(8-24)
H(
j)
2
A(2 )
1
1 C
2n
巴特沃思滤波器的MATLAB调用函数为:[Z,P,K]=buttap(n)
n:阶数
z,p,k: 滤波器零点、极点和增益。其幅度平方函数随Ω
变化的曲线如下图所示 :
第24页/共65页
8.4.2 模拟滤波器的设计
由上图可知,巴特沃思滤波器的幅度平方函数具有下列特点:
第17页/共65页
8.4 模拟滤波器的设计
8.4.1 模拟滤波器的一般设计方法 :
• 根据设计的技术指标即滤波器的幅频特性,确定滤波器的传递
•
函数H(S);
• 设计实际网络(通常为电网络)实现这一传递函数.
第18页/共65页
8.4 模拟滤波器的设计
幅度特性函数|H(Ω)|的确定:
由于
而 则 又 那么 从而
第8页/共65页
8.2 模拟和数字滤波器的基本概念
模拟滤波器的重要用途: 模拟滤波器是现代控制系统中的重要部件。最常见的应用例子,是传感器输出
信号中混有噪声干扰的情况,在传感器及测试电路中,可以在工艺上使布线尽量合理, 元件布局合理,并采用屏蔽技术等措施来防止噪声进入系统,但信号中仍可能含有不可 忽略的噪声,此时常采用模拟滤波器抑制这些噪声,使有用信号能通过而输出。
模拟信号滤波器设计

模拟信号滤波器设计模拟信号在现代电子技术中占据着重要的地位,然而在很多应用场合中,模拟信号常常受到各种噪声或干扰的影响,这时就需要使用模拟信号滤波器来对信号进行处理,从而达到降噪或抗干扰的目的。
本文将介绍模拟信号滤波器设计的一些基本知识和方法。
一、模拟信号滤波器的分类根据滤波器的传输特性,模拟信号滤波器可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器四种类型。
低通滤波器:可以让低于一定频率的信号通过,而对高于该频率的信号进行衰减,常用于滤除高频噪声或振荡。
高通滤波器:可以让高于一定频率的信号通过,而对低于该频率的信号进行衰减,常用于滤除低频噪声或直流分量。
带通滤波器:可以让一定范围内的频率信号通过,而对其他频率信号进行衰减,常用于保留一定频率范围内的信号。
带阻滤波器:可以让一定范围外的频率信号通过,而对该范围内的信号进行衰减,常用于滤除一定频率范围内的信号。
二、模拟信号滤波器的设计模拟信号滤波器的设计需要确定其传输特性和电路参数。
根据电路参数的不同,可以将模拟信号滤波器分为被动滤波器和有源滤波器。
被动滤波器指的是由电阻、电容和电感等被动元器件组成的滤波器,其缺点是带宽窄、增益小、稳定性差,适用于低频和中频信号的滤波。
有源滤波器指的是使用了运放等有源器件的滤波器,其优点是带宽宽、增益大、稳定性好,适用于高频信号的滤波。
有源滤波器的设计需要确定运放的电路结构和参数。
在具体的滤波器设计中,需要确定滤波器的截止频率、滤波器型号、电阻、电容、电感等电路元器件的值,以及电路的耦合方式和截止特性等。
还需要进行仿真和实验验证,以确保所设计的滤波器能够滤除目标噪声或干扰。
三、模拟信号滤波器的应用模拟信号滤波器在很多现代电子产品中都有广泛的应用,例如通信领域的信号处理、音频系统的去噪处理、传感器的信号处理等。
在工业自动化控制系统中,模拟信号滤波器也被广泛应用于模拟量的采集和处理中,以提高信号的稳定性和准确度。
模拟高通带通滤波器设计
①低通滤波器通带截止频率 p 1/ p ;
②低通滤波器阻带截止频率 s 1/ s ;
③通带最大衰减仍为 p ,阻带最小衰减仍为 s 。
(3)设计归一化低通滤波器G(p)。 (4)设计归一化高通滤波器G(q)。
p1 q
(5)求模拟高通的H(s)。 去归一化,将 q s 代入G(q)中
C
H (s) G( p) pc s
上式是直接由归一化低通转换成带阻的频率变换公式。
H(s) G( p)
p
s2
sB 02
下面总结设计带阻滤波器的步骤:
(1)确定模拟带阻滤波器的技术要求,即:
下通带截止频率 l ,上通带截止频率 u
阻带下限频率
,阻带上限频率
s1
s2
阻带中心频率 02 lu,阻带宽度 B u l
它们相应的归一化边界频率为
4.模拟滤波器的频率变换——模拟高通、带通、带阻滤波器的 设计
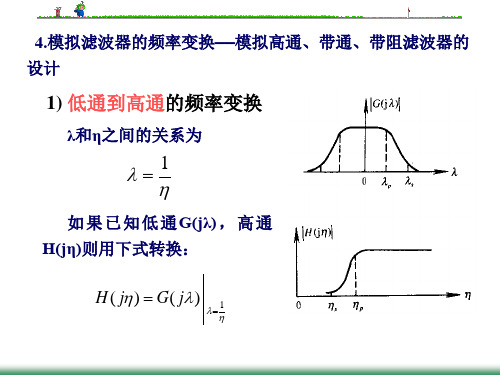
1) 低通到高通的频率变换
λ和η之间的关系为
1
如 果 已 知 低 通 G(jλ) , 高 通 H(jη)则用下式转换:
H ( j) G( j) 1
模拟高通filter的设计方法
H (s) G( p) pc s
转换关系
模拟高通滤波器指标
其中:num,den为低通原型的分子分母系数 OmegaZ,B 为带阻的中心频率Ωz和阻带宽度B numT,denT为带阻滤波器的分子分母系数
数字高通、带通和带阻滤波器的另一种设计
转换关 系
数字滤波器的指标 2 tan 1 T2
模拟滤波器指标 ALF的指标
数字低通H(Z) 双线性变换法
低通Ha(s)
p2 2p 1
去归一化,将p=s/Ωc代入上式得到:
实验四IIR数字滤波器的设计(1)(2)课案

实验四 IIR 数字滤波器的设计及网络结构一、实验目的1.了解IIR 数字滤波器的网络结构。
2.掌握模拟滤波器、IIR 数字滤波器的设计原理和步骤。
3.学习编写数字滤波器的设计程序的方法。
二、实验内容数字滤波器:是数字信号处理技术的重要内容。
它的主要功能是对数字信号进行处理,保留数字信号中的有用成分,去除信号中的无用成分。
1.数字滤波器的分类滤波器的种类很多,分类方法也不同。
(1)按处理的信号划分:模拟滤波器、数字滤波器 (2)按频域特性划分;低通、高通、带通、带阻。
(3)按时域特性划分:FIR 、IIR2.IIR 数字滤波器的传递函数及特点数字滤波器是具有一定传输特性的数字信号处理装置。
它的输入和输出均为离散的数字信号,借助数字器件或一定的数值计算方法,对输入信号进行处理,改变输入信号的波形或频谱,达到保留信号中有用成分去除无用成分的目的。
如果加上A/D 、D/A 转换,则可以用于处理模拟信号。
设IIR 滤波器的输入序列为x(n),则IIR 滤波器的输入序列x(n)与输出序列y(n)之间的关系可以用下面的方程式表示:1()()()M Ni j i j y n b x n i a y n j ===-+-∑∑(5-1)其中,j a 和i b 是滤波器的系数,其中j a 中至少有一个非零。
与之相对应的差分方程为:10111....()()()1....MM NN b b z b z Y z H Z X z a z a z ----++==++ (5-2)由传递函数可以发现无限长单位冲激响应滤波器有如下特点: (1) 单位冲激响应h(n)是无限长的。
(2) 系统传递函数H(z)在有限z 平面上有极点存在。
(3) 结构上存在着输出到输入的反馈,也就是结构上是递归型的。
3.IIR 滤波器的结构IIR 滤波器包括直接型、级联型和并联型三种结构:① 直接型:优点是简单、直观。
但由于系数bm 、a k 与零、极点对应关系不明显,一个bm 或a k 的改变会影响H(z)所有零点或极点的分布,所以一方面,bm 、a k 对滤波器性能的控制关系不直接,调整困难;另一方面,零、极点分布对系数变化的灵敏度高,对有限字长效应敏感,易引起不稳定现象和较大误差。
模拟信号处理中的滤波器设计技巧

模拟信号处理中的滤波器设计技巧
在模拟信号处理中,滤波器设计是一项关键的技术,它可以帮助我们对信号进行处理和改善,使得我们可以更好地提取出有用的信息。
在设计滤波器时,有一些技巧是非常重要的,下面我将介绍一些常用的技巧和方法。
首先,我们需要了解滤波器的种类和特性。
常见的滤波器包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
每种滤波器都有其特定的频率响应和传递函数,我们需要根据信号的特点和需求选择合适的滤波器类型。
其次,我们需要考虑滤波器的设计参数。
在设计滤波器时,我们需要确定滤波器的截止频率、通带波纹、阻带衰减等参数。
这些参数将直接影响滤波器的性能和效果,因此需要进行合理的选择和调整。
另外,我们还需要考虑滤波器的设计方法。
常用的滤波器设计方法包括脉冲响应不变法、双线性变换法和频率变换法等。
每种方法都有其优缺点,我们需要根据具体的应用需求选择合适的方法。
此外,在设计滤波器时,我们还需要考虑滤波器的稳定性和实现方法。
滤波器的稳定性是一个重要的性能指标,我们需要确保滤波器在所有频率下都是稳定的。
同时,我们还需要考虑如何实现所设计的滤波器,可以选择模拟电路、数字电路或者混合电路进行实现。
总的来说,滤波器设计是模拟信号处理中的重要技术,通过合理选择滤波器类型、设计参数、方法和实现方式,我们可以实现对信号的有效处理和改善。
希望以上介绍的技巧和方法能够对您在滤波器设计中有所帮助。
如果您对滤波器设计还有其他问题或者需要更深入的了解,请随时联系我,我会尽力为您提供帮助和支持。
第七章 模拟滤波器的设计(数字信号处理)

s
c
)
2N
10
a s / 10
(7.2.15)
由(7.2.14)和(7.2.15)式得到:
(
p
s
)
N
10 10
a p / 10 a s / 10
1 1
令
sp s / p , k sp
10 10
a p 10 as 10
1 1
,则N由下式表示:
N
1
1
1
1
0
fC a ) 低通
f
0
fC b ) 高通
f
0
fC1 c) 带通
fC2
f
0
fC1 d ) 带阻
fC2 f
7.1 理想滤波器
无过渡带且在通频带内满 足不失真测试条件的滤波 器称为理想滤波器。理想 滤波器的频率响应函数为:
|H(f)| A0
-fc
A e j 2 p ft 0 0 H(f) 0 f fc 其它
lg k sp lg sp
(7.2.16)
用上式求出的N可能有小数部分,应取大于等于N
的最小整数。关于3dB截止频率Ωc,如果技术指标中没 有 给 出 , 可 以 按 照 (7.2.14) 式 或 (7.2.15) 式 求 出 , 由
图7.2.2 低通滤波器的幅度特性
滤波器的技术指标给定后,需要设计一个传输函
数Ha(s),希望其幅度平方函数满足给定的指标αp和αs, 一般滤波器的单位冲激响应为实数,因此
H a ( j )
2
H a ( s )G ( s )
s j
H a ( j ) H a ( j )
滤波器设计仿真

同步技术原理与仿真通信系统有发送信号和接收信号的俄过程,其中接收信号是从噪声、干扰中提取有用信号,获取通信系统发送的信息。
提取信息是估计再生信号的某个或某些特征参数:载波频率、振幅、相位以及发送的时间等。
锁相环是一个频率与相位同步反馈控制系统。
模拟通信中载波抑制双边带(DSB-SC )、SSB 数字通信中:PSK 、DPSK 、MPSK 、MSK 、QAM 遥控遥测系统无线电定位导航系统模拟锁相环原理()()phoutt f t dff f phint f t lo lo lo in in in +=+=+=πθπθ22可以得到相位误差:()()()()()phoutphin dft phout t f phin t f t t t lo in lo in e -+=+-+=-=πππθθθ222输入信号()()()()()()()()()()()()()()()()()()()()()()()()()()()[]()()()()()()()()()[]()()()()()()[]()()()()()()()()[]()()t t t t n t t n t t t t n t t n t t t t t t t n t t t t t t t n t t t t n t t t t n t n t t n t t n t n t n t t V t x c s s c s c s c s c i θωθθθωθθθθωθθωθθωθθωθθωθθωωωθω+--++=+-+-+++=-+--+=⎩⎨⎧-=++=00000000000sin sin cos cos sin cos sin cos cos sin sin sin cos cos sin cos sin cos sin()()()()()()()()()()()()()()⎩⎨⎧-=+=t t n t t n t N t t n t t n t N c s s s c c θθθθsin cos sin cos 锁相环环路滤波器()s F 设计仿真一、1阶锁相环设计仿真1. 1阶锁相环()()1=s Ft1阶数字锁相环()n x算法流程()()()()()()13111212111312112sin w K n w w w w w T n x w w G n x n n out e out in e ⋅==+=⋅+==-=θθθθθ二、2阶锁相环设计仿真1. 1阶环路滤波器 积分器设计T zs 1111--⇒211111T zz s ---+⇒ 1阶环路模拟滤波器1阶环路数字滤波器21w1阶数字锁相环算法流程()()()()23212222212313222111121211130121122sin w K n w w w w w T w w w w w w w w T x w w G x n n out e out in e ⋅==+=⋅+==+=⋅⋅+==-=θωθθθθ2. 无源RC 积分滤波器()1/1111111+=+=+=sss s s s F ττττ微分方程()()()()()()()()()()()⎰⎰⎰⎰-=⇒+=⇒⎥⎦⎤⎢⎣⎡+=⇒=+=+=+=dt t y dt t x t y dt t y t y dt t x s s Y s s X s X s Y sss s s s F ττττττττττ1111/1111/1111111差分方程表达式1:算法流程()()()ττ//213121222221311111121211w w w w w n y T w w w n y w w n x T w w -==+⨯=+==⨯+=差分方程表达式2:算法流程()()()ττ/2//2/233121222221232221311311121211131211w w w w w w w w n y T w w w n y w w w w w n x T w w ==+=+⨯=+==+=⨯+=数字锁相环结构算法流程()()()()()()()()()43414242414342412331212222212322213113111212111312112//2/21sin w K n w w w w w T n y w w w w w w w w w T n y w w w w n y w w w w w Tn x w w G n x n n out e out in e ⋅==+=⋅+=-==+=⋅+=+==+=⋅⋅+=⋅=-=θττθθθθ微分方程()()()()()()()()()t y t x t y t y t y t x s X s Y s s F ''11τττ-=⇒+=⇒=+=3. 无源比例积分滤波器传递函数()()()()()()s X s Y ss s s s s s s s s s F 1222122122122122111/111111111111+=+-+=+-+=+-+=+-++=++=ττττττττττττττττ 令()⎩⎨⎧=-=222211/1/ττττa a可以得到()()()sa a s X s Y s F /112111+==微分方程()()()()()()()()()()()()t y a t x a t y s s Y a s X a s Y s s Y a s Y s X a sa a s X s Y s F '2121212111///11-=⇒-=⇒+=⇒+==微分方程结构框图滤波器结构框图积分方程()()()()()()()()()()()()dtt y a dt t x a a t y s Y a ss sX a a s Y s Y a s sY s sX a a s sa s a a s X s Y s F ⎰⎰-=⇒-=⇒+=⇒+=+==22111221112112121111/11积分方程结构框图滤波器结构框图数字滤波器数字锁相环结构w42算法流程:()()()()()()()()()()()()42414242414342411232312122222123221213113111121211*********122sin Kw n w w w w w w Tn y w n y n x n y w a w w w w w w w Tn y w w w n y w w w w w w Ta a n x w G n x n n out e out in e ==+=+⋅=+=-==+=+⋅=+==+=+⋅⋅==-=θθθθθ4. 有源比例积分滤波器()()()1211211τττττ+==+=s s X s Y s s s F 滤波器结构框图数字滤波器结构数字锁相环结构框图)22w算法流程()()()()()()()()()23212222212322211112121113121111312212sin w K n w w w w w w Tn y w w w w w w w T n x w w n x n y G n x n n out e out in e ⋅==+=+⋅==+=+⋅⋅=+⋅==-=θτττθθθθ5. 跟踪频率斜升信号的二阶环路滤波器 传递函数()22112211ss s s F ττττ++=滤波器结构框图6. GPS 导航二阶环路滤波器数字滤波器)算法流程22201ωωa G G ==()()()232122222123202221213201112121113121011102/2/w n y w w w w w T w w w G n x w w w w w w w w w w T G n x w ==+=⋅+=⋅+==+=+=⋅⋅=数字锁相环框架结构锁相滤波算法()()()()()2/2/2/sin 3331323231333231232122222123222021213201112121113121011110T w K n w w w w w w y w w y w w w w w w w w T G x w w w w w w w w w w T G x w G x n n out e out in e ⋅⋅==+=+===+=+=⋅⋅+==+=+=⋅⋅==-=θθθθθ三、3阶锁相环设计仿真()t数字锁相环框图)303ω=G 232ωa G = 031ωb G =算法流程()()()()()()3331323231333230311233021222221232022212132011121211131210113102/2/2/w n y w w w w w w w w T G n x w w w w w w w w w w T G n x w w w w w w w w w w T G n x w ==+=+=⋅⋅+==+=+=⋅⋅+==+=+=⋅⋅=数字锁相环框图结构33数字锁相环算法流程()()()()()()2/2/2/2/sin 4341424241434241333132323133323031123302122222123222021213201112111213121011310T K w n w w w w w w y w w y w w w w w w w w T x G w w w w w w w w w w T x G w w w w w w w w w w T G x w G x n n out e out in e ⋅⋅==+=+===+=+=⋅⋅+==+=+=⋅⋅+==+=+=⋅⋅==-=θθθθθ四、FLL+PLL数字环路滤波器f G 03ω=202p G ω=p a G 021ω=数字滤波算法流程()()()()()()23212222212322202111320111212111312101132102/2/w n y w w w w w w w w T G n x w w w w w w w w w w T G n x G n x w ==+=+=⋅⋅+==+=+=⋅⋅+⋅=数字FLL+PLL 结构框图FLL+PLL 锁频锁相算法流程()()()()()()()()()()()()()()()e ee e G x x m I m Q a dt d m I m Q a w m Q w w w w w T n m ix w w w m I w w w w w T n m ix w w n lo n sig input n m ix n lo n sig input n m ix θθθθsin tan tan 2/cos _2/sin _cos __cos _sin __sin _23212222212322211311121211131211==⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛===+=⋅+===+=⋅+=⋅=⋅=∑∑()()()()()()()n dt n f pi n lo n dt n f pi n lo w K n w w w w w T y w w w w y w w w w w w w w T w w G x w G x G x w out lo out lo out θθθ+⋅⋅⋅⋅=+⋅⋅⋅⋅=⋅==+=⋅+=+==+=+=⋅=⋅=⋅+⋅=2cos cos _2sin sin _2/2/53515252515352513342313232313332303141301422341二阶FLL+三阶PLL 环路结构数字滤波器框图205f G ω=f a G 024ω=303ω=G 232ωa G = 031ωb G =数字滤波算法流程()()()()()()()()()333132323133323031123302122222123222021421320111212111312101153102/2/2/w n y w w w w w w w w T G n x w w w w w w w w w w T G n x G n x w w w w w w w w w w T G n x G n x w ==+=+=⋅⋅+==+=+=⋅⋅+⋅+==+=+=⋅⋅+⋅=二阶FLL+三阶PLL 环路结构框图五、卡尔曼滤波 六、载波同步跟踪环平方环信Castos环路环路传递函数数字锁相框架1(costas+有源比例积分滤波器)算法流程()()()()()()()()()()()()()5251525251535251334231323132334332311414312414241231321222221232221111212111312112/2//1/2/cos _2/sin _cos __cos _sin __sin _w K n w w w w w T n y w w w w n y w w w w w T w w w w w w w n x G w w w n x w w w w w T n m ix w w w w w w w T n m ix w w n lo n sig input n m ix n lo n sig input n m ix out ⨯==+=⨯+=+==+=⨯+=⨯=⨯=⨯=⨯==+=⨯+==+=⨯+=⨯=⨯=θτττ数字锁相环框架2输入信号()phin ft A sig input +⋅=π2sin _。
常用模拟滤波器的设计方法

常用模拟滤波器的设计方法设计模拟滤波器常用的方法有很多种,如巴特沃斯滤波器、切比雪夫滤波器、脉冲响应滤波器等。
这些方法各有特点,适用于不同的滤波器设计需求。
下面将逐步介绍常用模拟滤波器的设计方法。
1. 巴特沃斯滤波器的设计方法巴特沃斯滤波器是一种最常用的模拟滤波器,其主要特点是通频带的频率响应是平坦的,也就是说在通过的频率范围内的信号不会被衰减或增强。
巴特沃斯滤波器的设计方法包括以下步骤:1.1 确定滤波器类型首先,根据滤波器的设计需求,确定滤波器的类型,包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
不同类型的滤波器在频率响应和陡度上有一些差异。
1.2 确定滤波器模型根据滤波器类型,选择相应的滤波器模型。
比如,低通滤波器通常选择Butterworth滤波器模型、Elliptic滤波器模型或者Chebyshev滤波器模型。
1.3 确定滤波器参数确定滤波器的相关参数,包括截止频率、阻带衰减和通带波纹等。
这些参数的选择需要根据特定的滤波器性能需求决定。
1.4 开始设计根据确定的滤波器模型和参数,开始进行滤波器的设计。
可以使用电路设计软件进行模拟,或者手动计算和画图设计。
1.5 仿真和优化设计完成后,对滤波器进行仿真,检查其频率响应和时域特性。
根据仿真结果,可以调整一些参数以优化滤波器的性能。
1.6 实际搭建和测试在电路板上搭建设计好的滤波器电路,并进行实际测试。
测试结果比较与设计要求进行评估和调整,最终得到满足要求的滤波器。
2. 切比雪夫滤波器的设计方法切比雪夫滤波器是一种在通频带内具有较窄的波纹和较快的过渡带的滤波器。
其设计方法如下:2.1 确定滤波器类型和阶数选择滤波器的类型和阶数,通常切比雪夫滤波器可以选择类型Ⅰ和类型Ⅱ。
阶数的选择取决于滤波器对波纹的要求和频率范围。
2.2 确定滤波器参数确定滤波器的相关参数,包括截止频率、阻带衰减、通带波纹和过渡带宽度等。
这些参数的选择需要根据特定的滤波器性能需求决定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模拟滤波器的理论和设计方法已发展得相当成熟,且 有若干典型的模拟滤波器供我们选择,这些滤波器都 有严格的设计公式、现成的曲线和图表供设计人员使 用。
典型的模拟滤波器 – 巴特沃斯 Butterworth 滤波器
为什么要借 助于模拟滤
幅频特性单调下降
波器设计数
– 切比雪夫 Chebyshev 滤波器
Butterworth低通滤波器的幅度函数只由阶数N控制
可整理ppt
12
2)幅度平方函数的极点分布:
Ha(
j)
2
Ha(
j)
H
a
(
j)
H ( j) H ( j) H (s)H (s) s j
1
2N
一 c 个全极点滤波器,其极点:
s k ( 1 ) 2 1 N j c c e j 1 2 2 2 k N 1 k 0 . 1 ,2 ,. . . ,2 N 1
Ha(s)
N 1
(
1 s
sk
)
k0 c c
式中,s/Ωc=jΩ/Ωc。
令 λ=Ω/Ωc , λ 称 为 归 一 化 频 率 ; 令 p=jλ,p称为归一化复变量,这样归一化巴特
p 10lg Ha( jp) 2 s 10lg Ha( js) 2
以上技术指标用图所示。图中Ωc称为3dB截止频 率,因
Ha( jc) 1/ 2 20lg Ha( jc) 3dB
可整理ppt
6
逼近方法—用频率响应的幅度平方函数逼近
滤波器的技术指标给定后,需要构造一个传
输函数Ha(s),希望其幅度平方函数满足给定 的指标αp和αs,一般滤波器的单位冲激响应 为实数,因此
可整理ppt
3
1.模拟低通滤波器的设计指标及逼近方法
模拟低通滤波器的设计指标 构造一个逼近设计指标的传输函数Ha(s)
Butterworth(巴特沃斯)低通逼近 Chebyshev(切比雪夫)低通逼近
可整理ppt
4
1.模拟低通滤波器的设计指标及逼近方法(续)
模拟低通滤波器的设计指标有αp, Ωp,αs和 Ωs。
字滤波器
幅频特性在通带或者在阻带有波动
– 贝塞尔 Bessel 滤波器
通带内有较好的线性相位持性 以这些数学函
– 椭圆 Ellipse 滤波器
数命名的滤波 器是低通滤波
可整理ppt
器的原型
1
模拟滤波器按幅度特性可分成低通、高通、带 通和带阻滤波器,它们的理想幅度特性如图所 示。
H a (jΩ)
H a (jΩ)
Ha(j)2 Ha(j)Ha(j) sj
Ha(s)Ha(s)
幅度平方函数在模拟滤波器的设计
中起很重要的作用,对于上面介绍
的典型滤波器,其幅度平方函数都
有自己的表达式,可以直接引用。
可整理ppt
7
(1)由幅度平方函数 Ha( j) 2 确定模拟滤波 器的系统函数 H a ( s )
H a (j )2 H a (j )H a * (j ) h(t)是实函数
通常只观察正 频部分
低通
高通
0
Ω0
Ω
H a (jΩ)
H a (jΩ)
带通
c
Ω0
带阻 Ω
可整理ppt
2
设计滤波器时,总是先设计低通滤波器,再通 过频率变换将低通滤波器转换成希望类型的滤 波器。
下面我们先介绍低通滤波器的技术指标和逼近 方法,然后分别介绍巴特沃斯滤波器和切比雪 夫滤波器的设计方法。
可整理ppt
9
2、Butterworth 低通的设计方法
幅度平方函数
1)幅度函数特点 2)幅度平方函数的极点分布 3)滤波器的系统函数 4)滤波器的设计步骤
可整理ppt
10
1)幅度平方函数
Ha( j) 2
1
2N
1
c
N为滤波器的阶数
c 为通带截止频率
当
Ha(j c)21/2时p
20lg Ha(j0) Ha(jc)
2N个极点等间隔分布在半径为 c 的圆上 (该圆称为巴特沃斯圆),间隔是π/N rad。
可整理ppt
13
• 极点在s平面呈象限对称,分布在Buttterworth圆上,共2N点
• 极点间的角度间隔为/Nrad
?
• 极点不落在虚轴上
• N为奇数,实轴上有极点,N为偶数,实轴上无极点
一半极点在 左半平面
Ωp;通带截止频率 Ωs:阻带截止频率 αp:通带中最大衰减系数 αs;阻带最小衰减系数
αp和αs一般用dB数表示。对于单调下降 的幅度特性,可表示成:
p10lg H a(j0)22
H a(j p)
s10lgH H aa ((j j0s ))22
可整理ppt
5
如果Ω=0处幅度已归一化到1,即|Ha(j0)|=1,αp和 αs表示为
H a (j )H a ( j ) H a(s)H a(s)sj
将左半平面的的极点归 H a ( s )
将以虚轴为对称轴的对称
零点的任一半作为H a ( s ) 的零点,虚轴上的零点一
半归 H a ( s )
可整理ppt
8
由 H a (j )2 确 定 H a (s ) 的 方 法
由幅度平方函数得象限对称的s平面函数 将Ha(s)Ha(s)因式分解,得到各零极点 对比Ha( j)和 H a ( s ) ,确定增益常数 由零极点及增益常数,得H a ( s )
j 2
s0 c e 3
j 2
s2 ce 3
s4 c
s1 c
j1
s3 c e 3
j 1
s5 c e 3
Ha(s)
3 a
j2
j2
(sc)(sc3 )(sc 3 )
可整理ppt
15
3)归一化系统函数
由于各滤波器的幅频特性不同,为使设计
统一,将所有的频率归一化。这里采用对3dB
截止频率Ωc归一化,归一化后的Ha(s)表示为
一半极点在 右半平面
可整理ppt
14
为形成稳定的滤波器,2N个极点中只取s平面左半平
面 的 N 个 极 点 构 成 Ha(s) , 而 右 半 平 面 的 N 个 极 点 构 成 Ha(-s)。 Ha(s)的表示式为
Ha(s)
N c
N 1
(s sk )
k 0
设N=3,极点有6个,它们分别为
3dB
称 c 为Butterworth低通滤波器的3分贝带宽
可整理ppt
11
2)幅度函数特点:
Ha( j) 2
1
2N
1
c
0 Ha(j )21
c H a (j )2 1 /2p 3 d B 3dB不变性
c 通带内有最大平坦的幅度特性,单调减小
c 过渡带及阻带内快速单调减小
