第11章卡方检验(李晓松版)
医疗统计学在临床的应用

医 学 统 计 学(第二版) 李晓松
16/129
随机化(Randomization)
❖ 随机抽样 ❖ 随机分配 ❖ 试验次序随机
二者区分与联络
医疗统计学在临床的应用
医 学 统 计 学(第二版) 李晓松
17/129
设置对照
❖ 是控制试验中其它非试验影响原因和偏倚不可缺乏主 要伎俩。
❖ 依据研究目标设置恰当对照,如: ➢抚慰剂对照 ➢空白对照 ➢试验对照 ➢标准对照 ➢本身对照
医疗统计学在临床的应用
医 学 统 计 学(第二版) 李晓松
6/129
第一节 医学统计学地位和作用
❖ 怎样描述这部分人高血压病患病情况? ❖ 怎样从这部分人推论到整个城市人群? ❖ 对于这种推论正确性抱有多大信心?
统计学将回答上述问题!
医疗统计学在临床的应用
医 学 统 计 学(第二版) 李晓松
7/129
医学统计学在临床医学中应用
医疗统计学在临床的应用
四川大学华西公共卫生学院
1/129
医学统计学地位和作用
医疗统计学在临床的应用
医 学 统 计 学(第二版) 李晓松
2/129
第一节 医学统计学地位和作用
❖ 当研发了一个治疗高血压病新药,应该怎样评价该 新药疗效?
❖ 患者
一组服用新药 一组服用对照药
然后分析该新药有效性和安全性
医疗统计学在临床的应用
医 学 统 计 学(第二版) 李晓松
29/129
表1. 两种方法检测12名妇女最大呼气率(L/min)结果
被检测者号 mini
wright
(1)
(2)
(3)
1
525
490
2
应用经济统计学(第二版) :卡方检验
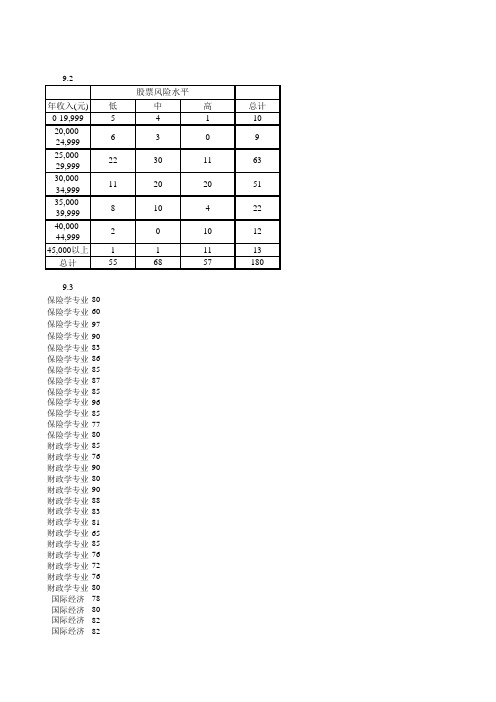
9.2股票风险水平年收入(元)低中高总计0-19,9995411020,000-6309 24,99925,000-22301163 29,99930,000-11202051 34,99935,000-810422 39,99940,000-201012 44,99945,000以上111113总计5568571809.3保险学专业80保险学专业60保险学专业97保险学专业90保险学专业83保险学专业86保险学专业85保险学专业87保险学专业85保险学专业96保险学专业85保险学专业77保险学专业80财政学专业85财政学专业76财政学专业90财政学专业80财政学专业90财政学专业88财政学专业83财政学专业81财政学专业65财政学专业85财政学专业76财政学专业72财政学专业76财政学专业80国际经济78国际经济80国际经济82国际经济82国际经济97国际经济76国际经济80国际经济73国际经济62国际经济81国际经济88国际经济73国际经济82国际经济80国际经济67国际经济80国际经济90金融学专业86金融学专业77金融学专业86金融学专业80金融学专业80金融学专业87金融学专业81金融学专业81金融学专业83金融学专业94金融学专业80金融学专业95金融学专业80金融学专业87金融学专业71金融学专业97金融学专业70金融学专业86金融学专业85金融学专业94经济学专业80经济学专业90经济学专业71经济学专业94经济学专业71经济学专业75经济学专业71经济学专业85经济学专业74经济学专业90经济学专业74经济学专业75经济学专业68经济学专业77经济学专业86经济学专业749.5家庭条件1=很好 2=一般 3=较差宿舍关系1=融洽 2=一般22 11 22 11 21 22 11 22 12 22 22 11 21 12 21 32 11 22 21 22 22 21 12 31 22 11 21 21 21 12 12 21 32 22 21 22 22 22 31 22 21 22 21 22 21 21 12 32 2132 12 32 22 11 12 21 22 31 21 21 22 22 22 12 22 22 21 32 21 32 11 21 32 22 21 21 22 21 22 22 22 31 12 22 21 12 21 21 21 11 31 22 22 31 22 11 21 11 11 22 1132 22 22 12 21 12 21 22 32 21 22 22 31 11 21 22 22 11 12 11 21 32 11 22 22 11 11 21 22 22 11 22 11 12 22 11 22 12 12 22 22 22 21 22 22 11 21 11 21 22 21 2211 21 21 11 22 11 32 22 22 12 31 22 12 22 31 22 21 21 22 12 22 22 12 22 12 22 21 22 22 22 11 21 31 22 22 12 21 22 21 21 21 21 22 22 31 21 21 21 22 21 31 2221 21 22 22 22 12 11 21 22 32 31 12 12 21 22 22 22 22 22 22 22 22 21 12 12 22 11 21 21 21 22 22 21 11 21 21 22 21 22 22 21 31 21 12 22 21 11 21 22 21 22 2211 31 21 31 21 11 21 22 32 21 22 22 22 22 11 21 21 21 22 21 12 21 21 31 21 12 21 22 21 32 12 22 11 12 21 11 22 21 22 21 21 22 21 21 12 22 11 22 22 32 22 2222 21 32 21 22 21 22 21 21 12 21 21 21 22 22 22 31 22 21 21 31 32 22 21 21 21 21 22 21 21 11 32 11 22 21 21 22 22 22 21 22 11 22 22 22 22 12 31 22 21 22 2121 22 12 12 21 22 21 32 11 22 22 21 32 21 12 21 11 21 22 22 22 11 11 22 12 32 11 22 21 22 12 11 22 22 21 22 21 21 21 21 21 21 21 21 22 21 11 21 22 21 32 2222 21 22 21 21 32 22 12 22 21 22 22 22 12 22 21 12 32 11 22 21 12 11 21 21 22 22 22 21 21 22 12 21 22 21 22 32 21 21 21 21 11 21 21 31 21 21 21 22 21 22 2222 21 31 21 32 22 21 22。
医学统计学(李晓松主编第2版高等教育提高出版社)附录思考与理解练习95%答案解析
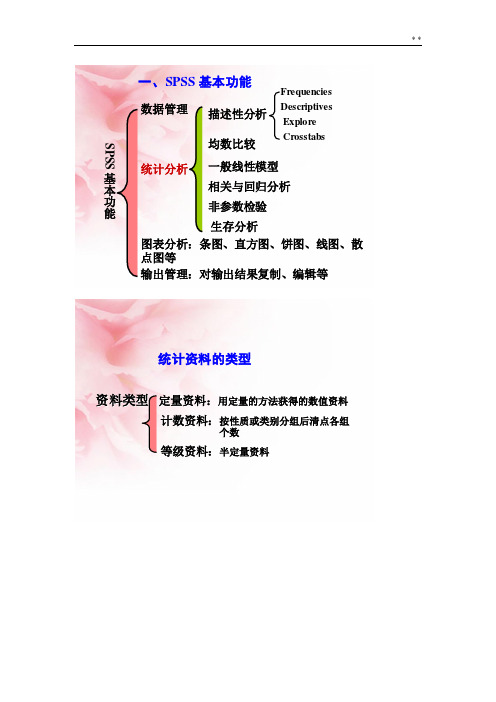
一、SPSS 基本功能SPSS基本功能数据管理统计分析图表分析:条图、直方图、饼图、线图、散点图等输出管理:对输出结果复制、编辑等描述性分析均数比较一般线性模型相关与回归分析非参数检验生存分析FrequenciesDescriptivesExploreCrosstabs 统计资料的类型资料类型定量资料:用定量的方法获得的数值资料计数资料:按性质或类别分组后清点各组个数等级资料:半定量资料定量资料的统计推断正态分布两组均数比较单样本设计t检验配对设计t检验成组设计t检验三组及以上均数比较完全随机设计方差分析随机区组设计方差分析重复测量方差分析析因设计方差分析偏态分布配对设计秩和检验单样本设计秩和检验成组设计秩和检验资料类型定量资料计数资料等级资料统计分析统计描述统计推断相对数总体率的估计假设检验u检验卡方检验4假设检验参数检验非参数检验正态分布等级资料偏态分布资料分布类型未知方差不齐,且不易变换达到齐性数据一端或两端不确定的资料1.参数检验:已知总体分布类型,对未知的总体参数做推断的假设检验方法。
故参数检验依赖于特定的分布类型,比较的是总体参数2.非参数检验:不依赖于总体分布类型、不针对总体参数的检验方法。
故非参数检验对总体的分布类型不做任何要求,不受总体参数的影响,比较的是分布或分布位置。
适用范围广,可适用于任何类型资料 参数检验➢ 优点:资料信息利用充分;检验效能较高 ➢ 缺点:对资料的要求高;适用范围有限 ➢ 优点:适用范围广,可适用于任何类型的资料 ➢ 缺点:检验效能低,易犯Ⅱ型错误 凡适合参数检验的资料,应首选参数检验对于符合参数检验条件者,采用非参数检验,其检验效能低,易犯Ⅱ型错误第一章绪论1.举例说明总体和样本的概念。
研究人员通常需要了解和研究某一类个体,这个类就是总体。
总体是根据研究目的所确定的所有同质观察单位某种观察值(即变量值)的集合,通常有无限总体和有限总体之分,前者指总体中的个体是无限的,如研究药物疗效,某病患者就是无限总体,后者指总体中的个体是有限的,它是指特定时间、空间中有限个研究个体。
卡方检验

表7-1 两种疗法疗效的比较的四格表(four-fold table)
分组
试验组 对照组 合计
疗效
有效 无效
99
5
75
21
174
26
合计
104 96 200
有效率
95.20% 78.13% 87.00%
πA = πB
pA ≠ pB
pA = pB?
πA ≠ πB ?
表7-1 两种疗法疗效的比较的四格表(four-fold table)
1+ 2-
4
-
+
3+
3+
…
…
…
…
…
n
-
+
n1 + n2 +
配对四格表的χ2检验(McNemar's test)
例7-3 分析目的:两法有无差别 假设(+,-)与(-,+)两格子理
论频数相等均为:
Q. McNemar 1900-1986 美国心理学家 统计学家
配对四格表的χ 2检验
HH01α: :=BB0.= ≠0C5C。或或两两种种方方法法检检出出率率不相同同 b+c≥40:
2. Scheffè可信区间法 3. Bonferroni法:调整检验水准
– k=R(R-1)/2,α’=α/k
– 例7-9: α’=0.05 / 3=0.0167 – 结果保守 4. SNK检验:参照定量资料的原理
χ2检验的其它应用
拟合优度检验(goodness of fit)
– 判断实际频数与理论频数的吻合程度 – 应用:
是否为小概率事件,以判断假设检验是否成 立。
χ2分布(chi-square distribution)
第二节 普通四格表χ 2检验与专用公式
卡方检验(李晓松版)

重点 四格表2检验 2×2列联表资料的2 检验
2
第一节 独立样本列联表的2检验
3
一、基本思想
✓ 应用范围 基本形式 基本思想
X2检验是以X2分布为理论依据,用途颇广的假设检验方法。常用于 ①推断两个或多个总体率或总体构成比之间有无差别; ②配对计数资料及两种属性或特征之间有无关联性; ③频数分布的拟合优度检验
=0.05
(二)、求检验统计量
两种疗法的心血管病病死率比较
疗法
盐酸 苯乙双胍 安慰剂
合计
死亡
26 (21.3)
2 ( 6.7)
28
生存
合计
178 (182.7)
62 ( 57.3)
240
204 64 268
本例:
● 基本公式计算结果为:
● χ四2格表(专2用6公式2计1.算3结)2果 为:(178182.7)2(26.7)2(6257.3)2
4
一、基本思想
应用范围 ✓ 基本形式 基本思想
组别
甲药 乙药 合计
甲乙两药治疗小儿上消化道出血的效果
有效
无效
合计
27
18
45
40
5
45
67
23
90
5
一、基本思想
应用范围 基本形式 ✓ 基本思想
以X2值的大小来反映理论频数与实际频数的吻合程度。在零假设H0 成立的条件下,实际频数与理论频数相差不应很大,即X2值不应 该很大;若实际计算出的X2值较大,超过了设定的检验水准所对 应的界值,则有理由怀疑H0的真实性,从而拒绝H0,接受H1
❖
单向有序列联表资料宜用秩和检验或Ridit分析。
❖
卡方检验1011ppt课件

多个样本率的比较
例11.3 某研究者欲比较A、B、C 三种方案治疗轻、中度高血压 的疗效,将年龄在50~70岁的240例轻、中度高血压患者随机等 分为3组,分别采用三种方案治疗。一个疗程后观察疗效,结果 见表11.4。问三种方案治疗轻、中度高血压的有效率有无差别?
表11.4 三种方案治疗轻、中度高血压的效果
编号
组别
编号
1
乙药
67
2
甲药
68
3
乙药
69
4
甲药
70
5
乙药
71
6
甲药
72
7
甲药
73
8
乙药
74
9
甲药
75
10
乙药
76
11
甲药
77
组别 甲药 乙药 乙药 甲药 乙药 甲药 甲药 甲药 乙药 乙药 甲药
患儿编号 1 2 3 4 5
.
.
Table. 结果记录表 处理 乙药 甲药 乙药 甲药 乙药
. .
疗效 有效 有效 无效 有效 无效
对子 2
C
随机
T
对子 3
C
配对设计
✓ 自身配对 a. 同一对象给予两种不同处理 b. 同一对象处理前后
例11.6 某研究者欲比较心电图和生化测定 诊断低钾血症的价值,分别采用两种方法 对79名临床确诊的低钾血症患者进行检查 ,结果见表11.9。问两种方法的检测结果是 否不同?
患者编号 1 2 3 4 5
表11.9 两种方法诊断低血钾的结果
心电图
+ - 合计
生化测定
+
-
45
25
4
5
49
生统计学第八版李晓松第十一章 直线相关与回归的推断

第十一章 直线相关与回归的推断
王 彤
山西医科大学
目录
01 第一节:直线相关系数的统计推断
02 05
第二节:直线回归的统计推断
重点难点
※ 总体相关系数的置信区间估计和相关系数的假设检验 ※ 总体回归系数的置信区间估计及回归方程的假设检验 ※ 回归中反应变量平均值的置信区间估计与个体值的预测区间估计 ※ 回归模型及其方差分析
在第二章骨关节炎评分OAP与粮食真菌DON含量的关系分析中,根据散
点图并结合专业上的考虑,可以依据一定的规则寻找一条潜在的直线来刻画两 变量之间的数量依存关系。简单直线回归模型假设y 的观测值服从一系列随解
释变量x而变化的正态分布,其连续变化的均值取决于x 值。
ei
第二节 直线回归的统计推断
(一)回归模型与参数解释
第一节 直线相关系数的统计推断
第一节 直线相关系数的统计推断
(一)总体相关系数的置信区间估计 1.总体相关系数 ρ
直线相关系数表示了两个变量之间直线关系的强度和方向,两变量无需区分 解释变量与反应变量。第二章我们基于样本数据介绍了样本相关系数,与之相对 应的参数即总体相关系数,用希腊字母ρ 表示。如ρ =0表示两变量间不存在直线 相关关系。在实际工作中,常用样本相关系数r估计总体相关系数 ρ。
2 2
10.0847 2.028 4.2524 = 1.4608, 18.7086
第二节 直线回归的统计推断
(四)反应变量个体值的预测区间
第二节 直线回归的统计推断
(五)应用条件
需满足:①反应变量与解释变量之间呈直线关系;②各观测值相互独立; ③解释变量固定时所对应反应变量服从条件正态分布;④不同解释变量取值下 反应变量的条件方差相等即方差齐。 统计模型是基于一系列假设条件下对客观现象的抽象化表示,独立、正态 分布、方差齐的若干解释变量的条件均数恰好在一条直线上就是直线回归模型 的基本假设。
卡方检验

浙江大学医学院流行病与卫生统计学教研室
沈毅
卡方检验基础
2值的计算:
( A E) E
供了完整的支持,此处只涉及两分类变量间关联程度的指
标,更系统的相关程度指标见相关与回归一章。
浙江大学医学院流行病与卫生统计学教研室
沈毅
两分类变量间关联程度的度量
相对危险度RR:是一个概率的比值,指试验组人群反应阳性概率 与对照组人群反应阳性概率的比值。数值为1,表明试验因素与
反应阳性无关联;小于1时,表明试验因素导致反应阳性的发生
小 结
3.Kappa一致性检验对两种方法结果的一致
程度进行评价;配对检验则用于分析两种
分类方法的分类结果是否有差异。
浙江大学医学院流行病与卫生统计学教研室
沈毅
小 结 4.分层卡方检验是把研究对象分解成不同层次,按 各层对象来进行行变量与列变量的独立性研究。可 在去除分层因素下更准确地对行列变量的独立性进
浙江大学医学院流行病与卫生统计学教研室 沈毅
小 结
2.关联程度的测量:卡方检验从定性的角度分析是否存在 相关,而各种关联指标从定量的角度分析相关的程度大小。 不同的指标适合不同类型的变量。 RR值是一个概率的比值,是指试验组人群反应阳性概率与 对照组人群反应概率的比值。用于反映试验因素与反应阳 性的关联程度。 OR值是比值的比。是反应阳性人群中试验因素有无的比例 与反应阴性人群中试验因素有无的比例之比。在下列两个 条件均满足时,可用于估计RR值:①所关注的事件发生概 率比较小(<0.1),②所设计的研究是病例对照研究。 浙江大学医学院流行病与卫生统计学教研室 沈毅
统计方法卡方检验

卡方检验用途:可以对两个率或构成比以及多个率或构成比间的差异做统计学检验第一节. 四格表资料的χ2检验例8.1 为了解铅中毒病人是否有尿棕色素增加现象,分别对病人组和对照组的尿液作尿棕色素定性检查,结果见表8.1,问铅中毒病人和对照人群的尿棕色素阳性率有无差别?表8.1 两组人群尿棕色素阳性率比较组别阳性数阴性数合计阳性率%病人29(18.74) 7(17.26) 36 80.56对照9(19.26)28(17.74) 37 24.32合计38 35 73 52.05卡方检验的基本思想表1中29、7、9、28是构成四格表资料的四个基本格子的数字,其余行合计和列合计以及总的合计都可以根据该四个数字推算出来,故该类资料被称为四格表资料四格表卡方检验的步骤以例8.1为例1.建立假设:H0:π1 = π2H1:π1≠π2α=0.05四格表的四格子里的数字是实际数,在表1中四个数字旁边括号中的四个数字为理论数,其含义是当无效假设成立的时候,理论上两组人群各有多少阳性和阴性的人数。
若H0:π1=π2成立→p1=p2=p即假设两组间阳性率无差别,阳性率都是等于合计的52.05%,那么铅中毒病人36人,则理论上有36 ╳52.05%=18.74人为阳性;对照组37人,则理论上有37 ╳52.05%=19.26人为阳性。
故每个实际数所对应的理论数算法是,该实际数对应的行和乘列和再除以总的N样本含量。
即TRC=nR nC / n2.计算理论数第1行1列: T11=36×38/73= 18.74依次类推T12 = 17.26T21 = 19.26T22 = 17.74四格表中理论数的两大特征:(1)理论频数表的构成相同,即不但各行构成比相同,而且各列构成比也相同;(2)各个基本格子实际数与理论数的差别(绝对值)相同。
一、卡方检验基本公式A: 实际数 T: 理论数卡方检验的基本思想是看理论数与实际数的吻合程度上述公式中卡方统计量的大小取决于实际数和理论数的相差大小情况,如果无效假设成立的话,那么实际数和理论数不应该相差过大,所以卡方统计量应该较小,而如果卡方统计量越大,则越有可能推翻无效假设而得出有统计差异的结论。
卡方检验.ppt

两种消毒方法对消毒效果的比较
方法 0.5%过氧乙酸
80%乙醇 合计
消除 35 27 62
未消除 27 46 73
合计 62 64 126
消除率 56.45 28.13 42.06
2019-6-26
谢谢你的观赏
6
R
C
C1
R1
a
R2
c
nR合计
a+c
C2
nC合计
率
b
a+b
a/(a+b)
d
c+d
c/(c+d)
一. 通用公式法
二.
专用公式法
三.
四格表χ2值的校正
四. 精确概率法
五.
配对资料的χ2检验
2019-6-26
谢谢你的观赏
4
一. 通用公式法
χ2=
A
T
T
2
其中为A实际频数,T为理论频数,,nR是行和,nC是列和,n是 四格数之和。
2019-6-26
谢谢你的观赏
5
例1 某护士为了解过氧乙酸和乙醇两种消毒方法对 HBV血清中HBsAg的消毒效果,做了两种方法的比较试 验,结果如下:
2019-6-26
谢谢你的观赏
1
二项分布中,我们应用正态近似法介绍了
两个率的u检验。但在观察例数不足够大或拟
对多个率进行比较时,u检验就不适宜了,因
为直接对多个样本率作两两间的u检验有可能
加大第一类误差( 如同直接对多个样本均数
作两两间的t检验)。X2 检验(chi-square test)可
解决此问题。
的皮肤炎患病率,结果如下:
防护服种类
第10章--卡方检验-(Chi-PPT课件

例题:某学校对学生的课外活动内容进行调查,结果 整理成下表:
-
18
应用举例一
女性 男性 总和
自我知觉
总和
过轻
过重
419
1995
2414
(786.78)(1627.22)
959
855
1814
(591.22)(1222.78)
1378
1995 1938.67
56.33 3173.41
1.37
5816 5816
0
2297.1 3
df=3-1=2 查表,0.05水平上临界值为5.99,故……
df=3-1=2 查表, 0.01水平上临界值为9.21
-
15
三、卡方独立性检验
(一)适用材料 主要用于两个或两个以上因素多项分类的计数资料
分析。如果要研究的两个自变量之间是否具有独 立性或有无关联或有无“交互作用”的存在,就 要应用卡方独立性检验。 如果两个子变量是独立的,无关联的,就意味着对 其中一个自变量来说,另一个自变量的多项分类 次数上的变化是在取样误差的范围之内。假如两 个因素是非独立,则称两变量有交互作用。
第十二章 非参数检验
-
1
一、参数与非参数检验
参数检验 用于等比/等距型数据 参数检验的前提:正态分布和方差同质
非参数检验 不用对参数进行假设 对分布较少有要求,也叫distributionfree tests 用于名义/顺序型数据
-
2
参数统计和非参数统计优缺点
• 参数统计 优点:
对资料的分析利用充分 统计分析的效率高
于等与临界值才显著),使用9或3均可 • 接受虚无假设
医学统计学课件卡方检验

队列研究中的卡方检验
总结词
在队列研究中,卡方检验用于比较不同暴露 水平或不同分组在某个分类变量上的分布差 异,以评估暴露因素与疾病发生之间的关系 。
详细描述
队列研究是一种前瞻性研究方法,按照暴露 因素的不同将参与者分为不同的组,追踪各 组的疾病发生情况。通过卡方检验,可以比 较不同暴露水平或不同分组在分类变量上的 分布差异,如分析不同饮食习惯的人群中患
卡方检验与相关性分析的区别
卡方检验主要用于比较实际观测频数与期望频数之间的差异,而相关性分析则用于研究 两个或多个变量之间的关联程度。
卡方检验与相关性分析的联系
在某些情况下,卡方检验的结果可以为相关性分析提供参考,帮助了解变量之间的关联 程度。
05
卡方检验的应用实例
病例对照研究中的卡方检验
总结词
02
公式
卡方检验的公式为 $chi^{2} = sum frac{(O_{ij} - E_{ij})^{2}}{E_{ij}}$,
其中 $O_{ij}$ 表示实际观测频数,$E_{ij}$ 表示期望频数。
03
适用范围
卡方检验适用于两个分类变量的比较,可以用于分析病例对照研究、队
列研究等类型的研究。
卡方检验的用途
如比较不同年龄组、性别组等人群中某种疾病的患病率。
卡方检验的基本假设
每个单元格中的期望 频数应该大于5。
卡方检验对于样本量 较小的情况可能不适 用。
观察频数与期望频数 应该服从相同的概率 分布。
02
卡方检验的步骤
收集数据
01
02
03
确定研究目的
在开始卡方检验之前,需 要明确研究的目的和假设 ,以便有针对性地收集数 据。
四格表卡方检验ppt课件

三、连续变量分布的吻合性检验
• 对于连续随机变量的计量数据,有时在实 际研究中预先不知道其总体分布,而是要 根据对样本的次数分布来判断是否服从某 种指定的具有明确表达式的理论次数分布。
• 关于分布的假设检验方法有很多,运用卡 方值所做的配合度检验是最常用的一种。
18
举例:正态分布吻合性检验
• 例题:p.336
– 独立性检验是对同一样本的若干变量关联情形的检验, 目的在于判明数据资料是相互关联还是彼此独立。
– 同质性检验是对两个样本同一变量的分布状况的检验, 是对几个样本数据是否同质作出统计决断。
31
一、单因素分类数据的同质性检验
• 步骤和例题(p.355)
32
二、列联表形式的同质性检验
• 方法与单因素的相同。 • 具体方法和例题(p.357)
21
六、卡方的连续性校正
• 当某一期望次数小于5时,应该利用校正公 式计算卡方值。
• 公式(p.340) • 例题:p.341
2 ( f0 fe 1/ 2)2
fe
• 如果三项分类或更多时,出现某一单元格 内的理论次数小于5的情况,则不需要进行 校正也能得到较为准确的结果。
22
主要内容
第一节 卡方检验的原理 第二节 配合度检验 第三节 独立性检验 第四节 同质性检验
19
四、比率或百分数的配合度检验
• 如果计数资料用百分数表示,最后计算出 来的卡方值要乘以100/N后,再与查表所得 的临界值进行比较。
• 例题:p.337
20
五、二项分类的配合度检验与比 率显著性检验的一致性
• 二者实质相同,只是表示方式不同。 • 相比较而言,配合度检验计算方法更为
简单。
(医统)卡方检验

2
观测值的自由度(vi>2),Si为第i组观测值的标 准差 2 • 拒绝原假设的条件为: 2 ,
F检验
• 检验两组观测值的方差的齐性 • 原假设: 2 2
1 2
• 检验统计量:
2 2 2 S1 F 2 2 ~ F( 1 , 2 ) 1 S2
• 拒绝条件: F F /2 (1, 2 )或F F1 /2 (1, 2 )
2.拟合优度检验
• B.表征实验分布,即用卡方统计量检验实验分布 是否服从某一理论分布(正态、二项等) • 步骤:1.将总体X的取值范围分成k个互不重迭的 小区间 • 2.计算落入第i个小区间的样本值的观测频数 • 3. 根据所假设的理论分布, 算出总体X的值落入每 个小区间的概率p,于是np就是落入该区间的样本 值的理论频数 • 4.计算卡方统计量 • 5.与临界值进行比较,进行决策
χ2 检验 数据资料 总体 检验对象
离散型资料 总体分布是未知的
连续型资料假设检验
连续型资料 正态分布 对总体参数或几个总体 参数之差
不是对总体参数的检 验,而是对总体分布 的假设检验
三、χ2 检验的用途
适合性检验
是指对样本的理论数先通过一定的理
论分布推算出来,然后用实际观测值与理论
数相比较,从而得出实际观测值与理论数之
理论值(E)
696.75 232.25 929
O-E
+8.25 -8.25 0
由于差数之和正负相消,并不能反映实 际观测值与理论值相差的大小。
为了避免正、负相抵消的问题,可将实际 观测值与理论值的差数平方后再相加,也就是 计算:
∑(O-E)2
O--实际观察的频数 E--无效假设下的期望频数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四格表2检验
2×2列联表资料的2 检验
第一节 独立样本列联表的2检验
一、基本思想
应用范围
基本形式
基本思想
X2检验是以X2分布为理论依据, 用途颇广的假设检验方法。常用于 ①推断两个或多个总体率或总体构 成比之间有无差别; ②配对计数资料及两种属性或特征 之间有无关联性; ③频数分布的拟合优度检验
功能性 3
2 6 2 13
恶性 1
2 5 4 12
良性 5
50 15 14 84
合计 9
54 26 20 109
≤50
51― 61― 71― 合计
表
三种疗法治疗慢性喉炎的结果
例 数
治疗方法 综合治疗
电子治疗仪 清音丸
治愈 显效 好转 无效 合计
186
32 22
72
24 14
26
16 22
24
20 20
本例:
●
基本公式计算结果为:
2 (178 182.7) 2 (2 6.7) 2 (62 57.3) 2 (26 21.3) χ2 21.3 182.7 6.7 57.3 1 1 1 1 2 4.7 ( ) 4.84 21.3 182.7 6.7 57.3
●
四格表专用公式计算结果为:
2 268 (26 62 178 2) 4.82 2 204 28 240 64
二者结果完全一致。自由度=(2-1)(2-1)=1
3、确定P值、下结论
查2界值表,由检验统计量2值确定P值, 自由度相同时,2值越大则P值越小。若 P≦则拒绝H0,接受H1;P>便接受H0 。 由χ 2界值表查得χ 20.05,1 =3.84,小于本 例所得χ 2值(无论是校正的或非校正的), 所以P<0.05,按α =0.05水准拒绝H0,接 受H1,用盐酸苯乙双胍治疗引致的心血管 病病死率高于安慰剂。
表 黑色素瘤患者随访术后三年生存情况
治疗组 三年生 存例数 77 89 99 90 355 三年死 亡例数 108 103 104 91 406 合计 三年生 存率 (%) 41.6 46.4 48.8 50.0 46.6
I II III IV 合计
185 192 203 181 761
H0:π1=π2=π3=π4
2 c ( 2 9 5 26 42 2) 2 42 28 14 7 35 3.62
查χ2界值表得P>0.05,按=0.05水准不拒绝H0,尚不能认 为两零售点沙门氏菌带菌率有显著性差异。 如果不校正
2 42 (2 9 5 26) 5.49 2 28 14 7 35
查χ2界值表(附表8)ν=3一行,得 0.5>P>0.25,以α=0.05水准不拒 绝H0,即尚不能认为四种不同疗法 的三年生存率有不同。
二、两个或多个构成比的比较
例 为研究两种口服洁肠剂的不良反 应,将 192 例接受洁肠处理的患者随 机分为两组,一组94例口服硫酸镁; 另一组98例口服甘露醇。服后的反应 见下表,试比较之。
2 值反映实际频数 A与理论频数 T 的吻合程度。
如果H0成立,则A与T之差一般不会太大,出现 大的2值的可能性很小。所以:
2值小A与T相差小接受H0
2值大 A与 T 相差太大 拒绝 H0, 接受H1 。
四格表
四格表:即2× 2表
基本形式
表 甲乙两药治疗小儿上消化道出血的效果
308
92 78
第二节 配对设计资料的2检验
资料类型:
配对计数资料又称两个相关样本率 资料,顾名思义,是采用配对设计 (见配对t检验一节),且结果是 “二分类”或“多分类”的计数资 料。
一、配对2×2列联表资料的 X2检验
T
(5 15)
连续性校正的四格表专用计算公式为
因连续性校正公式中的分子部分较非连续性校正公式减去了
一个常量,故所得χ2值必然较后者小,即必然有χ2>χ2c。这一 差别有时会导致相互矛盾的统计推断结果
表
两零售点猪肉表层沙门氏菌带菌情况检查结果
零售点 甲 乙
阳性
2(4.17) 5(2.33)
阴性
两种疗法的心血管病病死率比较
病死率 (%) 12.75 3.13 10.45
疗法
盐酸 苯乙双胍 安慰剂 合 计
死亡
26 2 28
生存
178 62 240
合计
204 64 268
*基本步骤 建立假设和确定检验水准
求检验统计量
确定P值、下结论
(一)、建立假设和确定检验水准
P值,下结论。
查χ2界值表(附表8)ν=4一行,因 χ2=81.66>χ20.005,4=14.86,所以,P<
0.005,以α=0.05水准拒绝H0,接受H1,
即两种洁肠剂的服后反应构成不同,
以甘露醇的不良反应较强。
多个构成比的比较
例5-12(P80) 对1135例绝经后出血的妇
女进行临床与病理分析,结果见表5-6,
查χ2界值表得P<0.025,结论为乙零售点沙门氏菌带菌率较 高,得出相反的结论。
三、行×列表资料的2检验
主要用于以下几方面: 两个率的比较 多个率的比较
两个构成比的比较
多个构成比的比较
检验统计量及自由度的计算公式:
=(行数-1)(列数-1)
(一)多个样本率的比较
例 将接受了切除术的761例皮肤黑色素瘤 患者随机分为4组,第I组185例,术后不接 受任何治疗;第II组192例,术后接受化疗; 第III组203例,术后接受免疫治疗;第IV组 181例,术后同时接受化疗和免疫治疗。 随访术后三年生存率,结果见下表,试比 较四种不同疗法的三年生存率有无差异。
表5-5 两种洁肠剂的服后反应
洁肠剂
无
恶心
呕吐
腹涨
其它
合计
硫酸镁
74
8
4
7
1
94
甘露醇 合计
14 88
21 29
17 21
43 50
3 4
98 192
H0:两处理组的总体构成相同; H1:两处理组的总体构成不相同;
=0.05
2 742 82 72 42 2 192( 94 88 94 29 94 21 94 50 2 2 17 2 432 14 21 1) 81.66 98 88 98 29 98 21 98 50 (2 1)(5 1) 4
计算公式
示例
组别 甲药
有效 27
无效 18
合计 45
乙药
40
67
5
23
45
90
应用条件
合计
四格表
基本形式
四格表:即2× 2表
表甲乙两药治疗小儿上消化道出血的效果 有效 无效
计算公式
示例 应用条件
27 (a) 40 (c) 67(a+c)
18 (b) 5 (d) 23(b+d)
45 (a+b) 45 (c+d) 90(n)
有效
无效
nR nC 45 67 T11 = 33.5 n 90
27 (a)
18 (b)
45 (a+b)
40 (c) 67(a+c)
5 (d) 23(b+d)
45 (c+d) 90(n)
T12=45-33.5=11.5 T21=67-33.5=33.5 T22=23-11.5=11.5
二、2×2列联表资料的2检验
2 2 2 60 16 43 1) 58.91 2 1135( 135 355 135 253 111 527 (4 1)(3 1) 6
查 χ2 界 值 表 ν=6 一 行 , 因 χ2=58.91 > χ20.005 , 6=14.86 ,所以, P < 0.005 ,以 α=0.05 水准拒绝 H0 ,接受 H1 ,即不同年 龄组妇女绝经后出血的病变类型构成不 同,随年龄的增大,恶性病变的比例呈 增大趋势。
前提条件
N≥40且T≥5时,直接使用2检验(Pearson Chi-Square)的基本公式或专用公式
N≥40且1≤T<5时,宜用校正2检验或确切概 率法 N<40或T<1时,宜用确切概率法 (Fisher’s exact test)
连续性校正的基本公式为
2 c
( AT 0.5) 2
理论频数
基本形式
计算公式
示例 应用条件
a 、 b 、 c 、 d 为四格表的基本数 据,称之为实际数据(A),实 际数据应为正整数; T 为理论频数 , 根据 X2 的假设检 验计算而得(P135-11.1)
TRC为R行C列的格子内的理论数,nR 为与理论数同行的合计数,nC为与理 论数同列的合计数
(π1=π2)
H1:两种疗法的心血管病总体病死率不相同
(π1π2) =0.05
(二)、求检验统计量
两种疗法的心血管病病死率比较
疗法 盐酸 苯乙双胍 安慰剂 合 计
死亡
生存
合计
26 178 (21.3) (182.7) 2 ( 6.7) 28 62 ( 57.3) 240
204
64 268
试分析病变类型是否与年龄有关?
表5-6 不同年龄妇女绝经后出血的病变类型
年龄组 (岁) ≤50 病变类型,例数(%) 功能性
60(44.4)
恶性
16(11.9)
良性
