第二章(一种聚类准则函数J的定义)
模式识别聚类分析

x1 ,
(
( x1
x2旳值。可用下列递推
k ) xi ) /( N1(k ) 1)
x(k 1) 2
(k)
x2
(k)
(x2
xi
)
/(
N
(k 2
)
1)
x1 (k ) , x2 (k )是第k步对分时两类均值,
x1(k 1) , x2(k 1)是下一次对分时把xi从G1(k )
划到G2(k)时的两类均值
所以x1 Z1(1)
再继续进行第二,第三次迭代… 计算出 E(2) , E(3) , …
次数 1 2 3 4 5 6 7 8 9
10 11
G1 G2
x21 x20 x18 x14 x15 x19
x11 x13 x12 x17 x16
E值 56.6 79.16 90.90 102.61 120.11 137.15 154.10 176.15 195.26 213.07 212.01
Ni为第i类的样本数.
离差平方和增量:设样本已提成ωp,ωq两类, 若把ωp,ωq合为ωr类,则定义离差平方:
Dp2q Sr (S p Sq )
其中S p , Sq分别为 p类于q类的离差平方和, S r为 r 类的离差平方和
增量愈小,合并愈合理。
聚类准则
Jw Min
类内距离越小越好 类间距离越大越好
体积与长,宽,高有关;比重与材料,纹理,颜 色有关。这里低、中、高三层特征都有了。
措施旳有效性
特征选用不当 特征过少 特征过多 量纲问题
主要聚类分析技术
谱系法(系统聚类,层次聚类法) 基于目旳函数旳聚类法(动态聚类) 图论聚类法 模糊聚类分析法
2.2模式相同度度量
模式识别第二章ppt课件

• 试探方法
凭直观感觉或经验,针对实际问题定义一种 相似性测度的阈值,然后按最近邻规则指定 某些模式样本属于某一个聚类类别。
– 例如对欧氏距离,它反映了样本间的近邻性,但 将一个样本分到不同类别中的哪一个时,还必须 规定一个距离测度的阈值作为聚类的判别准则。
精选ppt课件2021
• 特征选择的维数
在特征选择中往往会选择一些多余的特征,它增加了 维数,从而增加了聚类分析的复杂度,但对模式分类 却没有提供多少有用的信息。在这种情况下,需要去 掉相关程度过高的特征(进行降维处理)。
• 降维方法
– 结论:若rij->1,则表明第i维特征与第j维特征所反 映的特征规律接近,因此可以略去其中的一个特
– 距离阈值T对聚类结果的影响
精选ppt课件2021
17
2.3 基于试探的聚类搜索算法
2.3.2 最大最小距离算法
• 基本思想:以试探类间欧氏距离为最大 作为预选出聚类中心的条件。
• 病人的病程
– 名义尺度:指定性的指标,即特征度量时没有数量
关系,也没有明显的次序关系,如黑色和白色的关
系,男性和女性的关系等,都可将它们分别用“0”
和“1”来表示。
• 超过2个状态时,可精选用pp多t课个件2数021值表示。
8
2.2 模式相似性的测度和
聚类准则
2.2.1 相似Βιβλιοθήκη 测度• 目的:为了能将模式集划分成不同的类别,必须定义 一种相似性的测度,来度量同一类样本间的类似性和 不属于同一类样本间的差异性。
12
2.2 模式相似性的测度和
聚类准则
2.2.2 聚类准则
• 聚类准则函数法
– 依据:由于聚类是将样本进行分类以使类别间可 分离性为最大,因此聚类准则应是反映类别间相 似性或分离性的函数;
第二章距离分类器和聚类分析
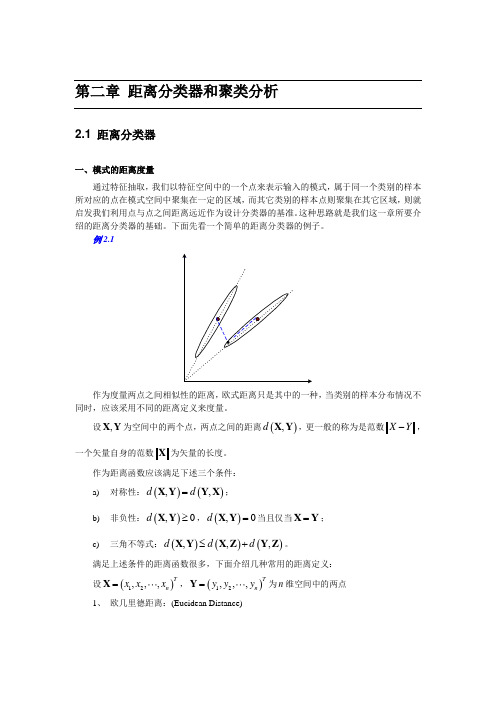
第二章 距离分类器和聚类分析2.1 距离分类器一、模式的距离度量通过特征抽取,我们以特征空间中的一个点来表示输入的模式,属于同一个类别的样本所对应的点在模式空间中聚集在一定的区域,而其它类别的样本点则聚集在其它区域,则就启发我们利用点与点之间距离远近作为设计分类器的基准。
这种思路就是我们这一章所要介绍的距离分类器的基础。
下面先看一个简单的距离分类器的例子。
例2.1作为度量两点之间相似性的距离,欧式距离只是其中的一种,当类别的样本分布情况不同时,应该采用不同的距离定义来度量。
设,X Y 为空间中的两个点,两点之间的距离(),d X Y ,更一般的称为是范数X Y -,一个矢量自身的范数X 为矢量的长度。
作为距离函数应该满足下述三个条件: a) 对称性:()(),,d d =X Y Y X ;b) 非负性:(),0d ≥X Y ,(),0d =X Y 当且仅当=X Y ; c) 三角不等式:()()(),,,d d d ≤+X Y X Z Y Z 。
满足上述条件的距离函数很多,下面介绍几种常用的距离定义: 设()12,,,Tn x x x =X ,()12,,,Tn y y y =Y 为n 维空间中的两点1、 欧几里德距离:(Eucidean Distance)()()1221,ni i i d x y =⎡⎤=-⎢⎥⎣⎦∑X Y2、 街市距离:(Manhattan Distance)()1,ni i i d x y ==-∑X Y3、 明氏距离:(Minkowski Distance)()11,mnm i i i d x y =⎡⎤=-⎢⎥⎣⎦∑X Y当2m =时为欧氏距离,当1m =时为街市距离。
4、 角度相似函数:(Angle Distance)(),T d ⋅=X YX Y X Y1nTi i i x y =⋅=∑X Y 为矢量X 和Y 之间的内积,(),d X Y 为矢量X 与Y 之间夹角的余弦。
一种基于遗传算法的Kmeans聚类算法

一种基于遗传算法的K-means聚类算法一种基于遗传算法的K-means聚类算法摘要:传统K-means算法对初始聚类中心的选取和样本的输入顺序非常敏感,容易陷入局部最优。
针对上述问题,提出了一种基于遗传算法的K-means聚类算法GKA,将K-means算法的局部寻优能力与遗传算法的全局寻优能力相结合,通过多次选择、交叉、变异的遗传操作,最终得到最优的聚类数和初始质心集,克服了传统K-means 算法的局部性和对初始聚类中心的敏感性。
关键词:遗传算法;K-means;聚类聚类分析是一个无监督的学习过程,是指按照事物的某些属性将其聚集成类,使得簇间相似性尽量小,簇内相似性尽量大,实现对数据的分类[1]。
聚类分析是数据挖掘技术的重要组成部分,它既可以作为独立的数据挖掘工具来获取数据库中数据的分布情况,也可以作为其他数据挖掘算法的预处理步骤。
聚类分析已成为数据挖掘主要的研究领域,目前已被广泛应用于模式识别、图像处理、数据分析和客户关系管理等领域中。
K-means算法是聚类分析中一种基本的划分方法,因其算法简单、理论可靠、收敛速度快、能有效处理较大数据而被广泛应用,但传统的K-means算法对初始聚类中心敏感,容易受初始选定的聚类中心的影响而过早地收敛于局部最优解,因此亟需一种能克服上述缺点的全局优化算法。
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化搜索算法。
在进化过程中进行的遗传操作包括编码、选择、交叉、变异和适者生存选择。
它以适应度函数为依据,通过对种群个体不断进行遗传操作实现种群个体一代代地优化并逐渐逼近最优解。
鉴于遗传算法的全局优化性,本文针对应用最为广泛的K-means方法的缺点,提出了一种基于遗传算法的K-means聚类算法GKA(Genetic K-means Algorithm),以克服传统K-means算法的局部性和对初始聚类中心的敏感性。
用遗传算法求解聚类问题,首先要解决三个问题:(1)如何将聚类问题的解编码到个体中;(2)如何构造适应度函数来度量每个个体对聚类问题的适应程度,即如果某个个体的编码代表良好的聚类结果,则其适应度就高;反之,其适应度就低。
聚类分析基本讲义

数据的粗聚类是两类,细聚类为4类
8
2.2 模式相似性测度
2.2.1 距 离 测 度
2.2.2 相 似 测 度 2.2.3 匹 配 测 度
9
•在聚类之前,要首先分析样品间的相似性,常
用距离来测度样品之间的相似程度。每个样品有
p个指标(变量)从不同方面描述其性质,形成 一个p维的向量。如果把n个样品看成p维空间中 的n个点,则两个样品间相似程度就可用p维空间 中的两点距离公式来度量。两点距离公式可以从 不同角度进行定义。
19
(3) 指数相关系数
2 ( x y ) 1 3 i i e( x , y ) exp[ ] 2 n i 1 4 i n
这里假设 x 和 y 的维数n相同、概率分布相同。
i2是第i个分量的方差。
性质:不受量纲变化的影响。
20
无论是夹角余弦还是相关系数,它们的绝对值都小 于1,作为变量近似性的度量工具,我们把它们统记 为cij。当∣cij∣= 1时,说明变量Xi与Xj完全相似; 当∣cij∣近似于1时,说明变量Xi与Xj非常密切;当 ∣cij∣ = 0时,说明变量Xi与Xj完全不一样;当 ∣cij∣近似于0时,说明变量Xi与Xj差别很大。据此, 我们把比较相似的变量聚为一类,把不太相似的变 量归到不同的类内。 在实际聚类过程中,为了计算方便,我们把变量间 相似性的度量公式作一个变换为 dij = 1 ∣cij∣ 或者 dij2 = 1 cij2 用表示变量间的距离远近,小则与先聚成一类, 这比较符合人们的一般思维习惯。
d ( x , y ) x y [ ( xi yi )2 ]1/ 2
i 1 n
, yn ) '
⑵ 绝对值距离(街坊距离或Manhattan距离)
遥感影像识别-第三章 聚类分析 Part Ⅰ

(2)马氏(Mahalanobis)距离
定义:马氏距离的平方
2 ( x )T 1 ( x )
马氏距离排除了不同特征之间相关性的影响, 其关键在于协方差矩阵的计算。当∑为对角阵时 ,各特征之间才完全独立;当∑为单位矩阵时, 马氏距离等于欧氏距离。 马氏距离 比较适用于对样本已有初步分类的 情况,做进一步考核、修正。
从上图看出,(b)、(c)特征空间划分是不同的。 (b)中 x1 , x2 为一类,x3 , x4 为另一类,(c) 中 x1, x3 为一类,x2 , x4 为另一类。
欧氏距离具有旋转不变的特性,但对于一般的线性变换 不是不变的,此时要对数据进行标准化(欧氏距离使用 时,注意量纲,量纲不同聚类结果不同,克服这一缺点 ,要使特征数据标准化使之与量纲无关)。 另外,使用欧氏距离度量时,还要注意模式样本测量值 的选取,应该是有效反映类别属性特征(各类属性的代 表应均衡)。但马氏距离可解决不均衡(一个多,一个 少)的问题。 例如,取5个样本,其中有4个反映对分类有意义的特征 A,只有1个对分类有意义的特征B,欧氏距离的计算结 果,则主要体现特征A。
当预先不知道类型数目,或者用参数估计和非 参数估计难以确定不同类型的类概率密度函数 时,为了确定分类器的性能,可以利用聚类分 析的方法。 聚类分析无训练过程,训练与识别混合在一起 。
§ 3-1 相似性准则
xn} 设有样本集 X {x1, x2 ,...., ,要求按某种相似性把 X 分类,怎样实现?
1
2
n
1
2
c
c
J c || xk m j ||2
j 1 k 1
c
数据挖掘算法_聚类数据挖掘

10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10
基于质心的 k-means聚类算法
坐标表示 5 个点{ X1,X2,X3,X4,X5}作为一个聚类分析的二维
样 本 : X1=(0,2),X2=(0,0),X3=(1.5,0),X4= (5,0),X5=(5,2)。假设要求的簇的数量k=2。
聚类分析的应用实独立变量 数目增加时, 发现簇的难 度开始增加
美陆军委托他人研究如何重新设计女兵服装,目 的在于减少不同尺码制服的库存数,但必须保证 每个士兵都有合体的制服。 选取了3000名女性,每人有100多个度量尺寸。
常见的聚类方法--划分聚类方法
典型的应用
作为一个独立的分析工具,用于了解数据的分布; 作为其它算法的一个数据预处理步骤;
应用聚类分析的例子
市场销售: 帮助市场人员发现客户中的不同群体, 然后用这些知识来开展一个目标明确的市场计划; 土地使用: 在一个陆地观察数据库中标识那些土地 使用相似的地区;
保险: 对购买了汽车保险的客户,标识那些有较高 平均赔偿成本的客户;
第1步:由样本的随机分布形成两个簇: C ={X1,X2,X4}和C2={X3,X5}。 这两个簇的质心M1和M2是:
1
1 2
M ={(0+0+5)/3,(2+0+0)/3}={1.66,0.66};
M ={(1.5+5)/2,(0+2)/2}={3.25,1.00};
基于质心的 k-means聚类算法
﹒.· .
﹒.┇ . .· · . . · · . · ﹒.﹒. ﹒.﹒.﹒.· ﹒. ﹒. ﹒. 类别3
聚类分析算法

第二章聚类分析2·4 聚类的算法2.4.1 聚类的技术方案⑴简单聚类根据相似性阈值和最小距离原则聚类∀x i∈Ω={ x1,x2,…,x n} = ω1⋃ω2⋃…⋃ωc;if D(xi ,mj)≤T, mj=(1/nj)∑xi(j),xi(j)∈ωj,nj是ωj中的样本个数,T是给定的阀值。
Then xi ∈ωi类心一旦确定将不会改变。
⑵谱系或层次聚类按最小距离原则不断进行两类合并类心不断地修正,但模式类别一旦指定后就不再改变。
⑶依据准则函数动态聚类影响聚类结果的主要因数:类心、类别个数、模式输入顺序。
所谓动态聚类,是指上述因数在聚类过程中是可变的。
规定一些分类的目标参数,定义一个能刻划聚类过程或结果优劣的准则函数,聚类过程就是使准则函数取极值的优化过程。
这类方法有—均值法、ISODATA法、近邻函数法以及运用图论理论的最小张树法。
2.4.2 简单聚类方法㈠根据相似性阈值和最小距离原则的简单聚类方法⒈条件及约定设待分类的模式为,选定类内距离门限。
⒉算法思想计算模式特征矢量到聚类中心的距离并和门限比较而决定归属该类或作为新的一类中心。
通常选择欧氏距离。
⒊算法原理步骤⑴取任意的一个模式特征矢量作为第一个聚类中心。
例如,令第一类的中心。
⑵计算下一个模式特征矢量到的距离。
若,则建立新的一类,其中心;若,则。
⑶假设已有聚类中心,计算尚未确定类别的模式特征矢量到各聚类中心的距离,如果,则作为新的一类的中心,;否则,如果( 2-4-1)则指判。
检查是否所有的模式都分划完类别,如都分划完了则结束;否则返到⑶。
⒋性能●计算简单。
●聚类结果很大程度上依赖于距离门限的选取、待分类特征矢量参与分类的次序和聚类中心的选取。
当有特征矢量分布的先验知识来指导门限及初始中心的选取时,可以获得较合理结果。
⒌改进通常采用试探法,选用不同的门限及模式输入次序来试分类,并对聚类结果。
例如,计算每一聚类中心与该类中最远样本点进行检验,即用聚类准则函数J1的距离,或计算类内及类间方差,用这些结果指导及的重选。
模式识别作业

第二章主要内容:几种常见的聚类算法已经所使用的准则函数。
作业1:对如下5个6维模式样本,用最小聚类准则进行系统聚类分析 已知样本如下:x1: 0, 1, 3, 1, 3, 4;x2: 3, 3, 3, 1, 2, 1;x3: 1, 0, 0, 0, 1, 1;x4: 2, 1, 0, 2, 2, 1;x5: 0, 0, 1, 0, 1, 0 第1步:将每一样本看成单独一类,得(0)(0)(0)112233(0)(0)4455{},{},{}{},{}G x G x G x Gx Gx =====计算各类之间的欧式距离,可得距离矩阵(0)D第2步:矩阵(0)D,它是(0)3G 和(0)5G 之间的距离,将他们合并为一类,得新的分类为(1)(0)(1)(0)(1)(0)(0)(1)(0)112233544{},{},{,},{}G G G G G G G G G ====计算聚类后的距离矩阵(1)D 第3步:由于(1)D 它是(1)3G 与(1)4G 之间的距离,于是合并(1)3G 和(1)4G ,得新的分类为(2)(1)(2)(2)(2)(1)(1)1122334{},{},{,}G G G G G G G ===同样,按最小距离准则计算距离矩阵(2)D,得第4步:同理得(3)(2)(3)(2)(2)11223{},{,}G G G G G == 满足聚类要求,如聚为2类,聚类完毕。
系统聚类算法介绍:第一步:设初始模式样本共有N 个,每个样本自成一类,即建立N 类。
G 1(0), G 2(0) , ……,G N (0)为计算各类之间的距离(初始时即为各样本间的距离),得到一个N*N 维的距离矩阵D(0)。
这里,标号(0)表示聚类开始运算前的状态。
第二步:假设前一步聚类运算中已求得距离矩阵D(n),n 为逐次聚类合并的次数,则求D(n)中的最小元素。
如果它是Gi(n)和Gj(n)两类之间的距离,则将Gi(n)和Gj(n)两类合并为一类G ij (n+1),由此建立新的分类:G 1(n+1), G 2(n+1)……第三步:计算合并后新类别之间的距离,得D(n+1)。
聚类分析(第4节_动态聚类法)

K- 均值法和系统聚类法一样,都是以距离的远近 或样品(或变量)的亲疏为标准进行聚类的,但是 两者的不同之处也是明显的:系统聚类对不同的类 数产生一系列的聚类结果,而 K- 均值法只能产生指 定类数的聚类结果。具体类数的确定,离不开实践 经验的积累;有时也可以借助系统聚类法以一部分 样品为对象进行聚类,其结果作为 K- 均值法确定类 数的参考。下面通过一个具体问题说明 K- 均值法的 计算过程。
第四节 动态聚类法
◆
●
逐步聚类法(动态聚类法) 按批修改法 ⑴ 按批修改法的具体步骤:
step1 选择一批凝聚点(个数为k个),并选定所采 用的距离定义(通常采用欧氏距离情形较为普遍); step2 将所有的样品按与其距离最近的凝聚点归类 (“就近归类原则”);
第四节 动态聚类法
step3 计算每一类的重心(即平均值),将重心作为新 的凝聚点,然后转到步骤2 。如果某一步骤所有的新凝聚 点与前一次的老凝聚点重合,则过程终止。有时并不绝 对要求这个过程收敛,而可以人为地规定这个修正过程 重复若干次后停止计算即可(有时确实无法收敛)。 ⑵ 分类准则函数。分类准则函数的定义方法很多,这 里介绍最直观的形式:设 X (i ) (i 1,2,, n)为n个样品点, 初始分类为k类: G1 , G2 ,, Gk , 它们的重心记为
两个正数必须取得适当。然后以每个样品为中心,
第四节 动态聚类法
d1 为半径,想象成一个圆,凡距离≤ d1 的样品数称
为该样品的密度。把每个样品的密度都求出后,按密 度大小依次考察各样品是否可作为凝聚点。以密度最 大的样品作为第一凝聚点;考察密度次大的样品,如 果它与第一凝聚点的距离大于d 2 ,就可作为第二凝聚 点,否则考察下一个密度次大的样品,直到找到第二 凝聚点。在考察下一个密度次大的样品,如果它与第 一、第二凝聚点的距离都大于 d 2 ,就可作为第三凝聚 点,直至所有的样品都考察一遍为止。
聚类 课件

基于网格的聚类算法
将数据空间划分为网格,然后在网格 上进行聚类,如STING算法、 CLIQUE算法等。
02
K-means聚类算法
K-means算法的原理
K-means算法是一种基于距离的聚 类算法,通过迭代过程将数据点划分 为K个聚类,使得每个数据点与其所 在聚类的中心点之间的距离之和最小 。
DBSCAN算法的步骤
01 扫描所有点,标记为核心点、边界点和噪 声点。
02 对于每个核心点,以其为起点,扩展与其 密度相连的区域。
03
将扩展的区域内的所有点标记为同一簇。
04
重复上述步骤,直到所有点都被处理。
DBSCAN算法的优缺点
01
优点
02
对异常值具有较强的鲁棒性。
能够发现任何形状的簇。
03
互信息
总结词
衡量聚类结果与真实类别之间相似度的指标,值越大表示聚 类效果越好。
详细描述
互信息是一种衡量聚类结果与真实类别之间相似度的指标, 其计算方法为聚类结果与真实类别之间的熵值之差。如果聚 类效果好,则聚类结果与真实类别之间的相似度会较高,熵 值之差会较小,因此互信息值会较大。
调整兰德指数
总结词
步骤2
重复以下步骤,直到满足终止条件
• 步骤2.1
将每个数据点与最近的簇中心点合并,形成新的 簇中心点。
• 步骤2.2
更新簇中心点为新合并的簇中所有点的平均值或中 心点。
• 步骤2.3
重复步骤2.1和步骤2.2,直到所有数据点都归入某 个簇或达到预设的簇数量。
输出聚类结果。
步骤3
层次聚类算法的优缺点
DBSCAN算法的优缺点
模式识别第2章 非监督学习方法

当特征只有两个状态(0,1)时,常用匹配测度。 0表示无此特征 1表示有此特征。故称之为二值特征。 对于给定的x和y中的某两个相应分量xi与yj 若xi=1,yj=1 ,则称 xi与yj是 (1-1)匹配; 若xi=1,yj=0 ,则称 xi与yj是 (1-0)匹配; 若xi=0,yj=1 ,则称 xi与yj是 (0-1)匹配; 若xi=0,yj=0 ,则称 xi与yj是 (0-0)匹配。
青蛙
无肺
有肺
14
特征选取不同对聚类结果的影响
(c) 按生活环境分
羊,狗,猫 蜥蜴,毒蛇 麻雀,海鸥
金鱼 绯鲵鲣
蓝鲨
青蛙
陆地
水里
两栖
15
特征选取不同对聚类结果的影响
(d) 按繁衍后代方式和肺是否存在分
蜥蜴,毒蛇 麻雀,海鸥
青蛙
金鱼 绯鲵鲣
非哺乳且有肺 非哺乳且无肺
羊,狗,猫
哺乳且有肺
蓝鲨
哺乳且无肺
p
q
最近距离法
1/2
1/2
0
-1/2
最远距离法
1/2
1/2
0
1/2
中间距离法 重心距离法 平均距离法 可变平均法 可变法 离差平方和法
1/2
np n p nq
np n p nq
(1 ) np np nq
1
2
nk n p nk nl
1/2
nq n p nq
nq n p nq (1 ) nq
48
2·3 类的定义与类间距离
49
2·3 类的定义与类间距离
w j 的类内离差阵定义为
S ( j) W
1 nj
nj
(
PD病症的综述

2.1 聚类分析的相关概念
• 特征选择的维数
在特征选择中往往会选择一些多余的特征,它增加了 维数,从而增加了聚类分析的复杂度,但对模式分类 却没有提供多少有用的信息。在这种情况下,需要去 掉相关程度过高的特征(进行降维处理)。
• 降维方法
– 结论:若rij->1,则表明第i维特征与第j维特征所反 映的特征规律接近,因此可以略去其中的一个特 征,或将它们合并为一个特征,从而使维数降低 一维。
模式识别的应用(举例)
• 生物学
– 自动细胞学、染色体特性研究、遗传研究
• 天文学
– 天文望远镜图像分析、自动光谱学
• 经济学
– 股票交易预测、企业行为分析
• 医学
– 心电图分析、脑电图分析、医学图像分析
模式识别的应用(举例)
• 工程
– 产品缺陷检测、特征识别、语音识别、自 动导航系统、污染分析
• 其他刊物
– Pattern Recognition (PR) – Pattern Recognition Letters (PRL) – Pattern Analysis and Application (PAA) – International Journal of Pattern Recognition and
2.2 模式相似性的测度和 聚类准则
2.2.2 聚类准则 • 聚类准则函数法
– 依据:由于聚类是将样本进行分类以使类别间可 分离性为最大,因此聚类准则应是反映类别间相 似性或分离性的函数;
– 由于类别是由一个个样本组成的,因此一般来说 类别的可分离性和样本的可分离性是直接相关的;
– 可以定义聚类准则函数为模式样本集{x}和模式类 别寻{找S准j, j则=1函,2,数…极,c}值的的函最数优,化从问而题使。聚类分析转化为
聚类分析

的类别中。
思路总结: 先找中心后分类;关键:怎样开新类,聚类中心如何定。
为使聚类中心更有代表性,可取各类的样本均值作为聚类中心。 20
例3 对图示模式样本用最大最小距离算法进行聚类分析。
x2
7 5
②距Z1最远,选为Z2。计算T。
集出现不同聚类结果的现象。
5
x2 (mm )
x2 (mm )
5
4 c(0.1,4)
3
2
1 a(0,1)
0
d(0.4,5)
b(0.5,0) 12
(b)
5 c(1,4)
4
d(4,5)
3
2
1 a(0,1)
b(5,0)
0
1
23 4
(a)
5 x1 (mm )
x2 (cm)
3 x1 (cm)
3 2 1 c(1,0.4)
对结果验算,类内各样
本点间距离方差之和太大
T1
T1
T2
减小T,修改中心Z。
图5 选取不同阈值和聚类中心时得到的不同 聚类结果
18
2 最大最小距离算法(小中取大距离算法 )
1) 问题已知N个待分类的模式 X1, X 2,, X N ,
分类到聚类中心 Z1, Z2,对应的类别中 。
2) 算法描述
j
相似性测度函数的共同点都涉及到把两个相比较的向量Xi,Xj 的分量值组合起来,但怎样组合并无普遍有效的方法,对具体的
模式分类,需视情况作适当选择。
11
2 聚类准则
聚类准则:根据相似性测度确定的,衡量模式之间是否相似的标 准。即把不同模式聚为一类还是归为不同类的准则。
07-聚类

例:如下图所示
G3 G1
• • • • • •
G2
G5
G4 G6
x
D(0)
ω3 ω4 ω5
1、设全部样本分为6类, 2、作距离矩阵D(0) 3、求最小元素: 4、把ω1,ω3合并ω7=(1,3) ω2 ω3 ω4,ω6合并ω8=(4,6) 5、作距离矩阵D(1) ω4
ω5 ω6
ω1 ω2 3 1 7 4 4
K-Means
优点
简单、快速 对处理大数据集,该算法保持可伸缩性和高效率 当结果簇是密集的,它的效果较好
缺点
– 对躁声和孤立点数据敏感 – 在簇的平均值被定义的情况下才能使用,可能不适用于某些 应用 – 必须事先给出k(要生成的簇的数目),而且对初值敏感, 对于不同的初始值,可能会导致不同结果。 – 不适合于发现非凸面形状的簇或者大小差别很大的簇 – 非常不适合分布均匀,数据界限不明晰的聚类
(7.67,7.33)T
10 9 8
X2
( 2) Z2
x19 x20
x16 x17 x18 x12 x13 x14 x15 x9
x10 x11
7 6
5
4
3
Z
( 2) 1
2
x3
1
x6 x7 x8 x4 x5
X1
0
1
2
3 4
x1
x2
5
6 7 8
9 10
• 第四步: 因Z j (3) Z j (2), j 1, 2, 转第二步 • 第二步: 重新计算x , x ,..., x 到Z (3), Z (3)的距离,
• 密度相连:对xi与xj,若存在xk使得xi与xj均 由xk密度可达,则称xi与xj密度相连.
K-均值聚类算法报告

K-均值聚类算法报告1.算法思想K-均值算法也称C-均值算法,是根据函数准则进行分类的聚类算法,基于使聚类准则函数最小化。
K-均值算法的主要思想是先在需要分类的数据中寻找K 组数据作为初始聚类中心,然后计算其他数据距离这三个聚类中心的距离,将数据归入与其距离最近的聚类中心,之后再对这K 个聚类的数据计算均值,作为新的聚类中心,继续以上步骤,直到新的聚类中心与上一次的聚类中心值相等时结束算法。
准则函数:聚类集中每一样本点到该类中心的距离平方和。
对于第j 个聚类集,准则函数定义为:S j :第j 个聚类集(域),聚类中心为Zj ;Nj :第j 个聚类集Sj 中所包含的样本个数。
对所有K 个模式类有:K-均值算法的聚类准则:聚类中心的选择应使准则函数J 极小,即使Jj 的值极小。
即有:可解得:上式表明,Sj 类的聚类中心应选为该类样本的均值。
2.算法描述(1)任选K 个初始聚类中心:Z 1(1), Z 2(1),…,ZK (1)括号内序号:迭代运算的次序号。
(2)按最小距离原则将其余样品分配到K 个聚类中心中的某一 个,即:则 (3)计算各个聚类中心的新向量值:Nj :第j 类的样本数。
(4)如果 则回到(2),将模式样本逐个重新分类,重复迭代计算。
ji j N i j i j S J ∈-=∑=X Z X ,||||12ji K j j N i j i S J ∈-=∑∑==X Z X 112,||||0)()(||||1T 12=--∂∂=-∂∂∑∑==j N i j i j i j j N i j i j Z Z X Z X Z X Z j i j N i i j j S N ∈=∑=X X Z ,11{})()(,,2,1,)(min k D k K i k j j i =-==-Z X Z X )(k S X j ∈K j k j ,,2,1)1( =+Z ()K j N k k j S X j j ,,2,11)1( ==+∑∈X Z K j k k j j ,,2,1)()1( =≠+Z Z如果 ,则算法收敛,计算完毕。
聚类算法简介-ppt

基于聚类的检测方法
• 主要由两大模块构成:
– 模型建立 – 模型评估
• 第一步:对训练集进行聚类; • 第二步:利用聚类结果得到分类模型; • 检测率:被正确检测的攻击记录数占整个攻击记录数的比例。 • 误报率:表示正常记录被检测为攻击的记录数占整个正常记录 数的比例。 • 未见攻击类型的检测率:表示测试集中出现而训练集中没有出 现的新类型攻击记录被正确检测的比例。
t ClassData; Class(t) f (t)
分类图示
训练数据 待分类数据
1 2
3
4
聚类与分类的区别
• 有类别标记和无类别标记; • 有监督与无监督; (有训练语料与无训练语料) • Train And Classification (分类); • No Train(聚类);
聚类的基本要素
什么是分类?
• 数据集合 Data ,类别标记集合 C
x Data, Class( x) C
• 数据集合: 训练数据 TrainData 待分类数据 ClassData • 已知 x TrainData; konwClass( x)&&Class( x) C • 问题:t ClassData; Class(t)? • 方法:根据训练数据获得类别划分标准 f ( x)
c个类别,待聚类数据x,mi为类别Ci的中心, mi
xCi
x
| Ci |
Je || x mi ||2
i 1 xCi
c
Je越小聚类结果越好
Je
衡量属于不同类别的数据与类别中心的的误差和;
• 最小方差:
1 Si 2 n
xCi x' Ci
