建筑制图 第三章--立体投影.ppt
合集下载
《建筑制图与识图》第3章

3.2.3 曲面立体表面上点的投影
1.利用曲面投影的积聚性
例3-2 如图(a)所示,已知圆柱体表面上一点A的V面投影。 求点A的H面、W面投影。
3.2.3 曲面立体表面上点的投影
分析与作图: 因圆柱的轴线垂直于H面,故圆柱的水平投影有积聚性,又 因a′可见,表明点A位于圆柱的前半个表面上,因此过a′向下投 影,在圆柱水平投影的前半圆周上得点A的水平投影a。由a,a′ 可求出a″,如图3-9(b)所示。因a′位于V投影对称轴的右侧, 故a″为不可见,A点在圆柱体上的位置如图3-9(c)所示。
3.3.1 截切体
因为立体的形状都不一样,截平面与立体表面的相对位置 也各不相同,由此产生的截交线形状也千差万别,但所有的截交 线都具有以下基本性质:
① 共有性。截交线是截平面与立体表面的共有线,既在截 平面上,又在立体表面上,是截平面与立体表面共有点的集合。
② 封闭性。由于立体表面是有范围的,所以截交线一般是 封闭的平面图形。
第3章 立体的投影
目录
3.1
平面立体
曲面立体
3.2
3.3
截切体和相贯体
组合体
3.4
3.1 平面立体
3.1.1 常见平面立体的投影图
平面立体
3.1.2 平面立体的投影图的绘制
3.1.3 平面立体表面上点和直线的投影
3.1.1 常见平面立体的投影
3.1.1 常见平面立体的投影
3.1.1 常见平面立体的投影
3.1.2 平面立体图的绘制
绘制平面立体的三面投影图,首先要按正确位置将 形体放入三面投影体系中,让形体的表面和棱线与投影 面尽量平行或垂直。
绘制平面体的投影图实际上就是绘制平面体底面和 侧表面的投影,一般先画出反映底面实形的正投影图, 然后再根据投影规律画出其他两个投影。
《建筑工程制图与识图》(第二版)课件 第3章

◦ 只要求出直角Δ AB0B的实形,即可求得AB对V面的倾角β 及其实长。 ◦ AB的正面投影a′b′已知,B、A两点到V面的距离之差, 可由其水平投影求得,由此即可作出直角Δ AB0B.的实形。
作法(1)
◦ 1)过a作OX轴的平行线与b′b交于b1,则bb1等于B、A两 点到V面的距离之差; ◦ 2)过b′作a′b′的垂线,在该垂线上截取b′B0 = bb1, 连接a′B0,则∠B0 a′b′即为AB对V面的倾角β ,a′B0 =AB(T.L)。
已知点A的三个投影,另一点B在点A上方8mm。左方 12mm,前方10mm,求点B的三面投影。
◦ (1)在a′左方12mm,上方8mm处确定b′。 ◦ (2)过b′作OX轴的垂线,在其延长线上a前10mm处确定b。 ◦ (3)根据三面投影关系求得b″。
重影点及其投影的可见性
◦ 若空间两点位于某一投影面的同一条投影线上,则它们 在该投影面上的投影必然重合,这两点投影称为该投影 的重影点(ghost image point)。 ◦ 水平投影重合的两个点,叫水平重影点; ◦ 正面投影重合的两个点,叫正面重影点; ◦ 侧面投影重合的两个点,叫侧面重影点。
点的单面投影 点的三面投影 点的投影规律 点的投影与坐标 两点的相对位置和重影点
点在某一投影面上的投影,实质上是过该点向投影 面所作垂线的垂足。因此,点的投影仍然是点。 过空间点A向投影面H作投影线,该投影线与投影面 的交点a,即为点A在投影面H上的投影。这个投影 是唯一确定的。 仅根据点的一个投影还不足以确定点在空间的位置。
在立体图中画出点A(20,12,15)的投影及其空 间位置。
◦ (1)画出H、V、W三投影面的立体图:将V面画成正离的 矩形,下边作为OX,右边作为OZ,;然后分别以OX和OZ为 一边,把H面和W面画成锐角为45ْ的两个相交平行四边形, 交线即OY。
作法(1)
◦ 1)过a作OX轴的平行线与b′b交于b1,则bb1等于B、A两 点到V面的距离之差; ◦ 2)过b′作a′b′的垂线,在该垂线上截取b′B0 = bb1, 连接a′B0,则∠B0 a′b′即为AB对V面的倾角β ,a′B0 =AB(T.L)。
已知点A的三个投影,另一点B在点A上方8mm。左方 12mm,前方10mm,求点B的三面投影。
◦ (1)在a′左方12mm,上方8mm处确定b′。 ◦ (2)过b′作OX轴的垂线,在其延长线上a前10mm处确定b。 ◦ (3)根据三面投影关系求得b″。
重影点及其投影的可见性
◦ 若空间两点位于某一投影面的同一条投影线上,则它们 在该投影面上的投影必然重合,这两点投影称为该投影 的重影点(ghost image point)。 ◦ 水平投影重合的两个点,叫水平重影点; ◦ 正面投影重合的两个点,叫正面重影点; ◦ 侧面投影重合的两个点,叫侧面重影点。
点的单面投影 点的三面投影 点的投影规律 点的投影与坐标 两点的相对位置和重影点
点在某一投影面上的投影,实质上是过该点向投影 面所作垂线的垂足。因此,点的投影仍然是点。 过空间点A向投影面H作投影线,该投影线与投影面 的交点a,即为点A在投影面H上的投影。这个投影 是唯一确定的。 仅根据点的一个投影还不足以确定点在空间的位置。
在立体图中画出点A(20,12,15)的投影及其空 间位置。
◦ (1)画出H、V、W三投影面的立体图:将V面画成正离的 矩形,下边作为OX,右边作为OZ,;然后分别以OX和OZ为 一边,把H面和W面画成锐角为45ْ的两个相交平行四边形, 交线即OY。
制图-立体的投影-三视图教材课件

制图-立体的投影-三视图教材课件
目录
• 立体投影与三视图概述 • 立体几何基础知识 • 正投影法与三视图形成原理 • 三视图绘制方法与步骤 • 三视图识读技巧与实例分析 • 计算机辅助设计软件在三视图应用 • 课程总结与拓展延伸
01 立体投影与三视图概述
立体投影基本概念
投影法
投影线
投影面
投影
用光线照射物体,在预 设的面上得到图形的方
轴测图表达复杂形体 轴测图的形成原理及种类 轴测图在表达复杂形体中的优势与局限性
拓展延伸:复杂形体表达方式探讨
01
透视图表达复杂形体
02
透视图的基本概念及种类
透视图在表达复杂形体中的效果与特点
03
拓展延伸:复杂形体表达方式探讨
01
02
03
计算机辅助设计(CAD) 在复杂形体表达中的应用
CAD技术的发展现状与 趋势
还培养了空间想象能力和分析问题、解决问题的能力。同时,我也意识 到自己在学习过程中存在一些不足,如缺乏主动性和创新性等。 • 改进措施:在今后的学习中,我将更加积极主动地参与课堂讨论和实践 活动,注重培养自己的创新意识和实践能力。同时,我也会加强与同学 之间的交流和合作,共同提高学习效果。
拓展延伸:复杂形体表达方式探讨
06 计算机辅助设计软件在三 视图应用
AutoCAD等CAD软件简介
AutoCAD
AutoCAD是一款广泛应用于各个 行业的计算机辅助设计软件,具 有强大的二维和三维设计功能, 支持多种文件格式,适用于 Windows和Mac操作系统。
SolidWorks
SolidWorks是一款专注于三维设 计的CAD软件,具有直观易用的 界面和强大的建模功能,广泛应 用于机械设计、工业设计等领域。
目录
• 立体投影与三视图概述 • 立体几何基础知识 • 正投影法与三视图形成原理 • 三视图绘制方法与步骤 • 三视图识读技巧与实例分析 • 计算机辅助设计软件在三视图应用 • 课程总结与拓展延伸
01 立体投影与三视图概述
立体投影基本概念
投影法
投影线
投影面
投影
用光线照射物体,在预 设的面上得到图形的方
轴测图表达复杂形体 轴测图的形成原理及种类 轴测图在表达复杂形体中的优势与局限性
拓展延伸:复杂形体表达方式探讨
01
透视图表达复杂形体
02
透视图的基本概念及种类
透视图在表达复杂形体中的效果与特点
03
拓展延伸:复杂形体表达方式探讨
01
02
03
计算机辅助设计(CAD) 在复杂形体表达中的应用
CAD技术的发展现状与 趋势
还培养了空间想象能力和分析问题、解决问题的能力。同时,我也意识 到自己在学习过程中存在一些不足,如缺乏主动性和创新性等。 • 改进措施:在今后的学习中,我将更加积极主动地参与课堂讨论和实践 活动,注重培养自己的创新意识和实践能力。同时,我也会加强与同学 之间的交流和合作,共同提高学习效果。
拓展延伸:复杂形体表达方式探讨
06 计算机辅助设计软件在三 视图应用
AutoCAD等CAD软件简介
AutoCAD
AutoCAD是一款广泛应用于各个 行业的计算机辅助设计软件,具 有强大的二维和三维设计功能, 支持多种文件格式,适用于 Windows和Mac操作系统。
SolidWorks
SolidWorks是一款专注于三维设 计的CAD软件,具有直观易用的 界面和强大的建模功能,广泛应 用于机械设计、工业设计等领域。
立体表面上点的投影PPT课件

平移
当立体表面沿某个方向移动时,其上的点也会相应地移动,导致投 影点的位置发生变化。
缩放
当立体表面按比例放大或缩小时,其上的点也会相应地放大或缩小 ,导致投影点的位置发生变化。
THANKS
感谢观看
投影的平移
总结词
平移是移动投影中心到新的位置,但不改变投影平面的方向。
详细描述
在投影变换中,平移是指将投影中心移动到新的位置,但不改变投影平面的方向。通过平移,可以改 变投影中心的位置,使得立体表面上的点在投影平面上呈现不同的位置。平移操作不会改变点在立体 表面上的位置和方向,只是改变了投影中心的位置。
05
CATALOGUE
立体表面上的点与投影的关系
点与投影的对应关系
投影线与投影面
每个点在立体表面上有且仅有一 条投影线,该线与投影面相交于 一点,该点即为该点在投影面上 的投影。
唯一性
一个点在投影面上的投影位置唯 一确定,反之亦然,即每个投影 点都对应立体表面上的一个点。
点与投影的度量关系
距离关系
04
详细描述
投影与原点连线与曲面相切,并且投 影与原点之间的连线与曲面内的任意 一条线段都垂直。
06
详细描述
投影与原点连线长度保持不变,即投影与原点 之间的距离等于原点到曲面的垂直距离。
点在多个面上的投影
总结词
确定点在多个面上的投影位 置
详细描述
当一个点位于多个平面的交 线上时,其投影将位于这些 平面的交线上,并且与原点
具有相同的距离。
总结词
投影与原点连线垂直于所有平面
详细描述
投影与原点连线垂直于所有相关平面,并 且投影与原点之间的连线与所有平面内的 任意一条线段都垂直。
当立体表面沿某个方向移动时,其上的点也会相应地移动,导致投 影点的位置发生变化。
缩放
当立体表面按比例放大或缩小时,其上的点也会相应地放大或缩小 ,导致投影点的位置发生变化。
THANKS
感谢观看
投影的平移
总结词
平移是移动投影中心到新的位置,但不改变投影平面的方向。
详细描述
在投影变换中,平移是指将投影中心移动到新的位置,但不改变投影平面的方向。通过平移,可以改 变投影中心的位置,使得立体表面上的点在投影平面上呈现不同的位置。平移操作不会改变点在立体 表面上的位置和方向,只是改变了投影中心的位置。
05
CATALOGUE
立体表面上的点与投影的关系
点与投影的对应关系
投影线与投影面
每个点在立体表面上有且仅有一 条投影线,该线与投影面相交于 一点,该点即为该点在投影面上 的投影。
唯一性
一个点在投影面上的投影位置唯 一确定,反之亦然,即每个投影 点都对应立体表面上的一个点。
点与投影的度量关系
距离关系
04
详细描述
投影与原点连线与曲面相切,并且投 影与原点之间的连线与曲面内的任意 一条线段都垂直。
06
详细描述
投影与原点连线长度保持不变,即投影与原点 之间的距离等于原点到曲面的垂直距离。
点在多个面上的投影
总结词
确定点在多个面上的投影位 置
详细描述
当一个点位于多个平面的交 线上时,其投影将位于这些 平面的交线上,并且与原点
具有相同的距离。
总结词
投影与原点连线垂直于所有平面
详细描述
投影与原点连线垂直于所有相关平面,并 且投影与原点之间的连线与所有平面内的 任意一条线段都垂直。
建筑制图与识图3立体的投影

3
3.3 切割体的投影
3.3.1 平面切割体的投影
(2)棱面法——面面交线法
将平面立体上参与相交的各棱面, 与截平面求交线,这些交线即围成所 求的平面立体截交线。
3.3 切割体的投影
3.3.1 平面切割体的投影
作图步骤:
1)空间分析及投影分析 a、截平面与立体的相对位置——确定截交线的形状 b、截平面,立体表面与投影面的相对位置——确定截交线的投影特性
PV2
6′ (7′) 7 ′′
例3-8:求作被截五棱柱的三面投影图
4′ (5′) 2′ ( 3′)
PV1
1′
5′′ 3 ′′
6′′
4′′ 2′′ 1′′
3 7(5)
1
2
6(4)
3.3 切割体的投影
3.3.2 曲面切割体的投影
截交线:一般为封闭的平面曲线,特殊情况为直线。 其形状取决于曲面立体的几何特征,以及截平面与曲面立体的相对位置。
c’ (2)绘出圆柱的顶面和底面。
(3)画出正面转向轮廓线和侧面转向轮廓线。
Z
a1’ c1’(d1’) d(d1)
a(a1) c(c1)
d1’
b1’
a1”(b1”) c1’’
c’d’ b’
V a’
D
A
d” B
a”b”
c”W
C
b(b1)
圆柱的投影
正面转向轮廓线 a1’
X
c1’d1’ A1 d(d1)
da11””(b1)”c1” C1b(b1)
曲面上可见与不可见的分界线称为回转面对该投影面的转向轮 廓线,在其他投影面不应画出。
圆柱体的投影
圆柱表面由圆柱面和上下两底面所组成。圆柱面是由一直母线绕与之 平行的轴线回转而成。圆柱上任意一条平行于轴线的直母线称之为素线。
3.3 切割体的投影
3.3.1 平面切割体的投影
(2)棱面法——面面交线法
将平面立体上参与相交的各棱面, 与截平面求交线,这些交线即围成所 求的平面立体截交线。
3.3 切割体的投影
3.3.1 平面切割体的投影
作图步骤:
1)空间分析及投影分析 a、截平面与立体的相对位置——确定截交线的形状 b、截平面,立体表面与投影面的相对位置——确定截交线的投影特性
PV2
6′ (7′) 7 ′′
例3-8:求作被截五棱柱的三面投影图
4′ (5′) 2′ ( 3′)
PV1
1′
5′′ 3 ′′
6′′
4′′ 2′′ 1′′
3 7(5)
1
2
6(4)
3.3 切割体的投影
3.3.2 曲面切割体的投影
截交线:一般为封闭的平面曲线,特殊情况为直线。 其形状取决于曲面立体的几何特征,以及截平面与曲面立体的相对位置。
c’ (2)绘出圆柱的顶面和底面。
(3)画出正面转向轮廓线和侧面转向轮廓线。
Z
a1’ c1’(d1’) d(d1)
a(a1) c(c1)
d1’
b1’
a1”(b1”) c1’’
c’d’ b’
V a’
D
A
d” B
a”b”
c”W
C
b(b1)
圆柱的投影
正面转向轮廓线 a1’
X
c1’d1’ A1 d(d1)
da11””(b1)”c1” C1b(b1)
曲面上可见与不可见的分界线称为回转面对该投影面的转向轮 廓线,在其他投影面不应画出。
圆柱体的投影
圆柱表面由圆柱面和上下两底面所组成。圆柱面是由一直母线绕与之 平行的轴线回转而成。圆柱上任意一条平行于轴线的直母线称之为素线。
第三章-立体的投影PPT课件

1″ 7″
9″
4(2)
6(8)
3(1) 5(7)
10(9)
可编辑课件PPT
35
可编辑课件PPT
36
可编辑课件PPT
37
可编辑课件PPT
38
3.3 曲面立体
曲面立体:所有表面都是由曲面或曲面和平面 所围成的立体称为曲面立体。它们通常被称为 回转体。
一动线绕一定线回转一周后形成的曲面称为回 转面。不动线称为回转轴,动线称为母线,母 线在回转面上的任意位置称为素线。
4(8) 3(7) 2(6)
1(5)
可编辑课件PPT
68
二、 平面与圆锥相交
1. 平面与圆锥相交所得截交线形状 2. 例题
可编辑课件PPT
69
1. 平面与圆锥相交所得截交线形状
圆
过锥顶的两直线
小小规定
可编辑课件PPT
5
一、 棱柱
1. 棱柱的组成
正面投影
由两个底面和几个侧 面组成。侧面与侧面 的交线叫侧棱,侧棱 相互平行。
2. 棱柱的投影
侧面投影
水平投影
可编辑课件PPT
在图示位置时,六棱 柱的两底面为水平面, 在水平投影中反映实 形。前后两侧面是正 平面,其余四个侧面 是铅垂面,它们的水 平投影都积聚成直线, 与六边形的边重合。
s
1
4 2 ●
●
●
解题步骤
1.空间分析:截平面与 四条侧棱均相交,因此 截交线是一个四边形。
3
● 3
2.投影分析:截平面为
正垂面,截交线的正面
投影已知,水平投影和
侧面投影未知;
4 ●
3
1
●
s●
2●
第三章 建筑制图-立体投影

A1 B1 C1
6
3
4
A
c
a c b
1
2
a1
3
4
b1 按两个贯穿点既位于一个立体的同一表面上、又位于另一立 体的同一表面上的条件依次连接。 23
5(6)
3.4.2 平面立体与曲面立体相交
1. 相贯线的形状 平面立体与曲面立体相交,一般情况下,相贯线是由 若干段平面曲线或平面曲线和直线围成。
例4
求切口圆柱的水平投影和侧面投影。
解题步骤 1 分析 截交线的水平投影为椭 圆,侧面投影为圆; 2 求出截交线上的特殊点; 3 求出若干个一般点; 4 光滑且顺次地连接各点,作 出截交线,并且判别可见性; 5 整理轮廓线。
Ⅱ Ⅰ Ⅳ
Ⅲ
例5
求截切圆柱的水平投影和侧面投影。
解题步骤 1 分析 截交线的水平投影 为圆的一部分,侧面投影 为矩形; 2 求出截交线上的特殊点Ⅰ 、Ⅱ、Ⅲ、Ⅳ; 3顺次地连接各点,作出截 交线并判别可见性; 4 整理轮廓线。
1.求相贯线的一般步骤
① 分析已知条件,读懂投影图,分析是全贯、互贯、有几个 贯穿点…… ②求贯穿点; ③连接贯穿点; ④判别可见性:相贯线的可见性、轮廓线重影 部分的可见性。
a1
2
a b
1
5
b1 c1 Ⅰ B C 可见性判断:相贯线的投影 c1 只有同时位于两个立体的可 见表面时才可见。 Ⅱ Ⅴ Ⅵ Ⅲ Ⅳ
3" 7" 2"
4 光滑且顺次地连接各点,作 出截交线,并且判别可见性; 5 整理轮廓线。
Ⅵ
Ⅰ
4
6 1
Ⅳ Ⅷ
Ⅴ
工程制图-立体的投影

•圆球的投影
三个视图均为与圆球的直径相等的圆,它 们分别是圆球三个方向轮廓素线的投影。
•圆球的投影特点 圆球的轮廓线的投影
•圆球可见性的判别
(3)圆球表面上的点
圆的半径?
采用辅助圆法求圆球面上的点
例: 圆球面上特殊点的求法
b a
(b) a
(c)
c
(c) b
a
A为一般点; B、C为特殊点。
(4)圆球面上的曲线
轮廓线的投 影是判断曲面 可见性的依据
(2)圆柱的视图
圆柱面的俯视 图积聚成一个圆, 在另两个视图上 分别以两个方向 的外形轮廓线的 投影表示。
其上下底圆为 水平面,在俯视图 上反映实形,在 另两个视图上分 别积聚成为一直 线。
•分析圆柱轮廓线的投影一
•分析圆柱轮廓线的投影二
•圆柱投影对V面可见性的判别mm点的可见性判别:
k
m k
k
若点所在的平
面的投影可见,
点的投影也可见;
若平面的投影积
聚成直线,点的
投影也可见。
用相对坐标,量取坐标差 的方法在表面取点。
(3)五棱柱的视图
2.棱锥
⑴ 棱锥的组成
由一个底 面和若干侧棱 面组成。侧棱 线交于有限远 的一点——锥 顶。
(2)棱锥的投影三视图
S
s
s
b’
➢第3章 立体的投影(一)
➢3.1 立体的三面投影 ➢3.2 基本立体的三视图 ➢3.3 平面与立体相交 ➢3.4 立体与立体相交
➢3.1 立体的三面投影
➢3.1.1 立体的投影 ➢3.1.2 三面投影与三视图 ➢3.1.3 三视图之间的对应关系
➢3.1.1 立体的投影
立体的投影,实质上是构成该立体的所有 表面的投影总和。
高校高等职业教育《建筑工程制图与识图》教学课件 第3章 基本体的投影

§3.3
3.3.1平面体的截交线
截割体的投影
由于平面体是由平面围成,所以平面体的截交线是封闭的平面折线, 即平面多边形。
求平面立体截交线的步骤:
(1)分析 截交线形状及投影形状; (2)求点 利用截平面的积聚性求棱线与截平面的交点; (3)连线 按一定顺序并根据可见性连线。
§3.3 截割体的投影
圆锥与各种平面立体的相贯线; ➢ 用辅助平面法可求: 圆球与各种平面立体的相贯线。
圆环与各种平面立体的相贯线。
§3.4 相贯体的投影
[例题15] 已知圆柱体与四棱柱相贯的俯视图,补全V、W面投影。
易多线 1’
2’
解题步骤:
1’’(2’’)
3’(5’)
4’(6’)
5’’(6’’)
3’’(4’’)
二、圆锥
投影分析和画法 圆锥的底圆平面为水平面,其
水平投影为圆,且反映实形; 正面投影和侧面投影均积聚为
直线段,长度等于底圆的直径。
投影特点: 一个视图为圆,另两个为三角形。
§3.2
二、圆锥
圆锥表面上取点:
回转体的投影
素线法取点
§3.2
二、圆锥
圆锥表面上取点:
回转体的投影
纬圆法取点
四、圆环
圆环的三视图:
回转体的投影
§3.2
四、圆环
圆环表面取点:
已知圆环面上的 点A、B 的一个 投影,求它们的 另一个投影
回转体的投影
§3.2
四、圆环
回转体的投影
圆环表面取曲线:
已知圆环面上的 曲线AD 水平投 影,求正面投影
§3.1 基本体的投影
[例题3] 补全属于基本回转体表面的点和线段的三面投影。
建筑制图和识图第3章 立体-PPT文档资料
1
建筑制图与识图
(ห้องสมุดไป่ตู้)投影
土木工程学院
①.安放位置:为简 便作图,一般将圆柱 体的轴线垂直于某一 投影面。将圆柱体的 轴线(OO1)垂直于H 面,则圆柱面垂直于H 面,上、下底圆平行 于H面。 ②. 投影分析 H面投影:为一个圆。 它是可见的上底圆 和不可见的下底圆 V面投影:为一矩形。 它是可见的前半圆 柱的不可见的后半 圆柱投影的重合。 W面投影: 为一矩 形。它是可见的左 半圆柱和不可见的 右半圆柱投影的重 合。
建筑制图与识图
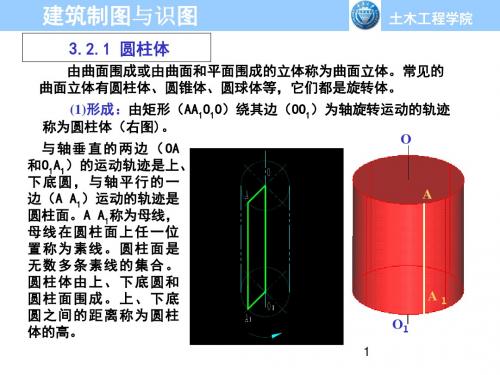
3.2.1 圆柱体
土木工程学院
由曲面围成或由曲面和平面围成的立体称为曲面立体。常见的 曲面立体有圆柱体、圆锥体、圆球体等,它们都是旋转体。
(1)形成:由矩形(AA1O1O)绕其边(OO1)为轴旋转运动的轨迹 称为圆柱体(右图)。 O 与 轴 垂 直 的 两 边 ( OA 和O1A1)的运动轨迹是上、 下 底 圆 , 与轴 平 行 的 一 A 边(A A1)运动的轨迹是 圆柱面。A A1称为母线, 母 线 在 圆 柱面 上 任 一 位 置 称 为 素 线。 圆 柱 面 是 无 数 多 条 素线 的 集 合 。 圆 柱 体 由 上、 下 底 圆 和 A1 圆 柱 面 围 成。 上 、 下 底 圆 之 间 的 距离 称 为 圆 柱 O1 体的高。
W面投影:底边
8
建筑制图与识图
土木工程学院 (4) 圆锥体表面上取点
【例6-3】已知圆锥上1点
的V面投影(可见),求 另二投影。
m" '
9
建筑制图与识图
3.2.3 圆球体
(1)形成
土木工程学院
半圆面绕其直经(OO1)为轴旋转运动的轨迹称为圆球体。半圆线旋转运 动的轨迹是球面,即圆球的表面。
建筑制图与识图
(ห้องสมุดไป่ตู้)投影
土木工程学院
①.安放位置:为简 便作图,一般将圆柱 体的轴线垂直于某一 投影面。将圆柱体的 轴线(OO1)垂直于H 面,则圆柱面垂直于H 面,上、下底圆平行 于H面。 ②. 投影分析 H面投影:为一个圆。 它是可见的上底圆 和不可见的下底圆 V面投影:为一矩形。 它是可见的前半圆 柱的不可见的后半 圆柱投影的重合。 W面投影: 为一矩 形。它是可见的左 半圆柱和不可见的 右半圆柱投影的重 合。
建筑制图与识图
3.2.1 圆柱体
土木工程学院
由曲面围成或由曲面和平面围成的立体称为曲面立体。常见的 曲面立体有圆柱体、圆锥体、圆球体等,它们都是旋转体。
(1)形成:由矩形(AA1O1O)绕其边(OO1)为轴旋转运动的轨迹 称为圆柱体(右图)。 O 与 轴 垂 直 的 两 边 ( OA 和O1A1)的运动轨迹是上、 下 底 圆 , 与轴 平 行 的 一 A 边(A A1)运动的轨迹是 圆柱面。A A1称为母线, 母 线 在 圆 柱面 上 任 一 位 置 称 为 素 线。 圆 柱 面 是 无 数 多 条 素线 的 集 合 。 圆 柱 体 由 上、 下 底 圆 和 A1 圆 柱 面 围 成。 上 、 下 底 圆 之 间 的 距离 称 为 圆 柱 O1 体的高。
W面投影:底边
8
建筑制图与识图
土木工程学院 (4) 圆锥体表面上取点
【例6-3】已知圆锥上1点
的V面投影(可见),求 另二投影。
m" '
9
建筑制图与识图
3.2.3 圆球体
(1)形成
土木工程学院
半圆面绕其直经(OO1)为轴旋转运动的轨迹称为圆球体。半圆线旋转运 动的轨迹是球面,即圆球的表面。
第三章-建筑制图-斜面体投影PPT课件

.
33
作图:
(1)交线的正立投影不能直接画出来,可根据“三等” 关系,从水平投影和侧投影找出A、B、C、D四点的 正投影,连接起来即成。DC在烟囱后面是不可见线,
所以d΄c΄应画成虚线。
.
34
(2)当没有侧投影时,可根据点在线上、线在面上的 原理,过ac画一辅助线 与屋面上二直线相交,求 出其正投影得a’、c’,过a’ 、 c’分别作两条水平线得b’、 d’,a’、b’为实线,c’d’为 虚线。
.
39
5、【例】已知屋檐的H投影及同坡屋顶的坡度为 30º,画出其三面投影。
作图 (1)先按投影规律画出屋顶的H投影。由于屋檐的水平夹 角都是90°,因此见角就画45°线。左端两斜脊相交于a点, 右下端两斜脊相交于b点(图a),过a、b两点分别作两屋檐的 平行线得两平脊,左边平脊与斜脊相较于c点、右下边平脊 与天沟相交于d点(图b)。连c、d为直线即为所求(图c)。
AH=a″b″=318
(c)
.
61
习题二(共4页)
.
62
习题二(3)
.
63
习题二(4)
.
64
第四节 任意斜面的投影
一、任意斜面的投影
在建筑工程中有时还会遇到倾斜于三个投影面的斜面——任 意斜面。
2b
.
65
比较一下两组图中同一物体的斜面, 因和投影面的关系 不同,其投影有什么不同?
.
66
第一组
.
15
从上述三例可以看出:
1、垂直于一个投影面的斜面,在该投影面上的投影积 聚为直线,并反映斜面与另两个投影面的倾斜角度, 此斜面的其余两个投影面形状缩小。
(1)
(2).
(3)
