2018年秋电子科技大学(高等数学)专科在线作业三及满分答案【最新版】
2018年高考理科数学全国卷3(含答案与解析)
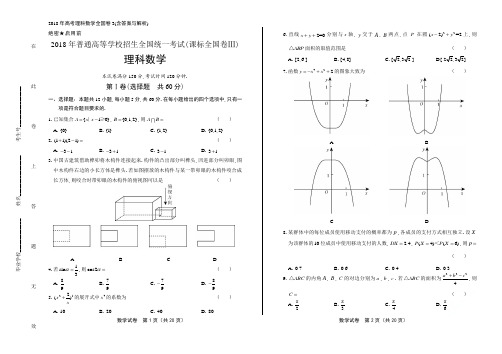
2018年高考理科数学全国卷3(含答案与解析) 数学试卷 第1页(共20页) 数学试卷 第2页(共20页)绝密★启用前2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理科数学本试卷满分150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{10}A x x =-∣≥,{0,1,2}B =,则A B = ( )A .{0}B .{1}C .{1,2}D .{0,1,2} 2.()(1i 2i)+-=( )A .3i --B .3i -+C .3i -D .3i +3.中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )ABC D 4.若1sin 3α=,则cos2α=( )A .89B .79C .79-D .89-5.252()x x+的展开式中4x 的系数为( )A .10B .20C .40D .806.直线2=0x y ++分别与x 轴,y 交于A ,B 两点,点P 在圆22(2)=2x y -+上,则ABP △面积的取值范围是( )A .[2,6 ]B .[4,8]C .[2,3 2 ]D [ 22,32] 7.函数422y x x =-++的图象大致为( )ABCD8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数, 2.4DX =,()6(4)P X P X ==<,则p =( )A .0.7B .0.6C .0.4D .0.39.ABC △的内角A ,B ,C 的对边分别为a ,b ,c .若ABC △的面积为2224,则C = ( )A .π2B .π3C .π4D .π6毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共20页) 数学试卷 第4页(共20页)10.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为( )A .123B .183C .243D .54311.设1F ,2F 是双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若1||6||PF OP =,则C 的离心率为 ( )A .5B .2C .3D .2 12.设0.2log 0.3a =,2log 0.3b =,则( )A .0a b ab +<<B .ab a b +<<0C .0a b ab +<<D .0ab a b +<<第Ⅱ卷(非选择题 共90分)二、填空题:本题共4小题,每小题5分,共20分.13.已知向量2)(1,=a ,)2(2,=-b ,),(1λ=c .若2()+∥c a b ,则=λ . 14.曲线)e (1xy ax =+在点(0,1)处的切线的斜率为2-,则a = .15函数π()cos(3)6f x x =+在[0,π]的零点个数为 .16.已知点1()1,M -和抛物线C :²4y x =,过C 的焦点且斜率为k 的直线与C 交于A ,B 两点.若90AMB ∠=,则k = .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.) (一)必考题:共60分. 17.(12分)等比数列{}n a 中,11a =,534a a =. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .18.(12分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min )绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高,并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过超过m不超过m第一种生产方式 第二种生产方式(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:22()(a b)(c d)(a c)(b d)n ad bc K -=++++,2()P K k ≥0.050 0.010 0.001k3.841 6.635 10.82819.(12分)-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------2018年高考理科数学全国卷3(含答案与解析)数学试卷 第5页(共20页) 数学试卷 第6页(共20页)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC -体积最大时,求面MAB 与面MCD 所成二面角的正弦值.20.(12分)已知斜率为k 的直线l 与椭圆C :22143x y +=交于A ,B 两点,线段AB 的中点为(1,)()M m m >0.(1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:FA ,FP ,FB成等差数列,并求该数列的公差. 21.(12分)已知函数22()()ln(1)2f x a x x x x +=-++.(1)若0a =,证明:当10x -<<时,()0f x <;当0x >时,()0f x >; (2)若=0x 是()f x 的极大值点,求a .(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4—4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,O 的参数方程为cos ,sin x y θθ=⎧⎨=⎩(θ为参数),过点(0,2)且倾斜角为α的直线l 与O 交于A ,B 两点. (1)求α的取值范围;(2)求AB 中点P 的轨迹的参数方程.23.[选修4—5:不等式选讲](10分) 设函数()211f x x x =++-. (1)画出() y f x =的图象;(2)当[ 0),x ∈+∞,()b x f ax +≤,求a b +的最小值.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共20页) 数学试卷 第8页(共20页)2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理科数学答案解析第Ⅰ卷一、选择题 1.【答案】C【解析】∵={1}A x x |≥,{0,1,2}B =,∴={1,2}A B ,故选C .2.【答案】D【解析】21i 2i)(2i 2i i 3i )(+-=-+-=+,故选D . 3.【答案】A【解析】两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件,易知俯视图可以为A .故选A . 4.【答案】B 【解析】由1sin 3α=,得22127cos212sin 12()=1=399αα=-=-⨯-.故选B .5.【答案】C【解析】252()x x+的展开式的通项251103155()(2)2r r r r r r r T C x x C x ---+==,令1034r -=,得2r =,所以4x 的系数为225240C ⨯=.故选C . 6.【答案】A【解析】由圆22(2)=2x y -+可得圆心坐标(2,0),半径r =ABP △的面积记为S ,点P 到直线AB 的距离记为d ,则有12S AB d =.易知AB =maxd ==min d =所以26S ≤≤,故选A .7.【答案】D【解析】∵42()2f x x x =-++,∴3()42f x x x '=-+,令()0f x '>,解得x <或x 0<此时,()f x 递增;令()0f x '<,解得x <0或x ,此时,()f x 递减.由此可得()f x 的大致图象.故选D . 8.【答案】B【解析】由题知~1()0,X B p ,则(101 2.4)DX p p =⨯⨯-=,解得0.4p =或0.6.又∵()6(4)P X P X ==<,即446664221010(1)(1)(1)0.5C P p C P p p p p --⇒-⇒<<>,∴0.6p =,故选B .9.【答案】C【解析】根据余弦定理得2222cos a b c ab C +-=,因为2224ABCa Sbc +-=△,所以c 42os ABC ab C S =△,又1sin 2ABC S ab C =△,所以tan 1C =,因为π()0,C ∈,所以4C π=.故选C .10.【答案】B【解析】设ABC △的边长为a ,则1sin60=932ABC S a a =△,解得6a =(负值舍去).ABC △的外接圆半径r 满足62sin60r=,得r =球心到平面ABC 的距离为2=.所以点D 到平面ABC 的最大距离为246+=,所以三棱锥DABC -体积的最大值为163⨯=故选B .11.【答案】C【解析】点2(,0)F c 到渐近线b y x a =的距离2(0)PF b b ==>,而2OF c =,所以在2Rt OPF △中,由勾股定理可得OP a ,所以1PF ==.在2Rt OPF △中,222cos PF b PF O OF c∠==,在12F F P△中,2222222121221246cos 22PF F F PF b c a PF O PF F F b c+-+-∠==⋅⋅2,所以222222463464b b c a b c a c bc +-=⇒=-,则有22223()46c a c a -=-值舍去),即e =.故选C .2018年高考理科数学全国卷3(含答案与解析)数学试卷 第9页(共20页) 数学试卷 第10页(共20页)12.【答案】B【解析】解法一:∵0.20.2log 0.3log 1=0a =>,22log 0.3log 1=0b =<,∴0ab <,排除C . ∵0.20.20log 0.3log 0.2=1<<,22log 0.3log 0.5=1-<,即01a <<,1b <-,∴0a b +<,排除D .∵220.2log 0.3lg0.2log 0.2log 0.3lg 2b a ===,∴2223log 0.3log 0.2log 12b b a -=-=<,∴1bb ab a b a+⇒+<<,排除A .故选B . 解法二:易知01a <<,1b -<,∴0ab <,0a b +<, ∵0.30.30.311log 0.2log 2log 0.41a b +=+=<, 即1a bab+<,∴a b ab +>, ∴0ab a b +<<.故选B .第Ⅱ卷二、填空题13.【答案】12【解析】由已知得2(4,2)+=a b .又,()1c λ=,2()+∥c a b ,所以42=0λ-,解得12λ=. 14.【答案】3-【解析】设(e ))1(x f x ax =+,则()()1e x f x ax a '=++,所以曲线在点(0,1)处的切线的斜率(0)12k f a '==+=-,解得3a =-. 15.【答案】3【解析】令()0f x =,得πcos(3)6x +,解得ππ+()39k x k =∈Z .当0k =时,π9x =;当1k =时,4π9x =;当2k =时,7π9x =,又[ 0,π]x ∈,所以满足要求的零点有3个.16.【答案】2【解析】解法一:由题意可知C 的焦点坐标为(1,0),所以过焦点(1,0),斜率为k 的直线方程为1y x k =+,设111,y A y k ⎛⎫+ ⎪⎝⎭,221,y B y k ⎛⎫+ ⎪⎝⎭,将直线方程与抛物线方程联立得21,4,y x k y x ⎧=+⎪⎨⎪=⎩整理得2440y y k --=,从而得124y y k +=,124y y =-.∵1()1,M -,90AMB ∠=,∴0MA MB =,即1212(2)(2)(1)(1)0y yy y k k+++--=,即2440k k -+=,解得2k =.解法二:设11A(,)x y ,22(),B x y ,则2112224,4,y x y x ⎧=⎨=⎩①②②-①得2221214()y y x x -=-,从而2121124y y x x k y y --+==.设AB 的中点为M ',连接MM '.∵直线AB 过抛物线24y x =的焦点,∴以线段AB 为直径的M '⊙与准线:1l x =-相切.∵1()1,M -,90AMB ∠=,∴点M 在准线:1l x =-上,同时在M '⊙上,∴准线l 是M '⊙的切线,切点M ,且MM l '⊥,即MM '与x 轴平行,∴点M '的纵坐标为1,即1212221y y y y =⇒++=,故124422y y k =+==. 故答案为:2. 三、解答题17.【答案】(1)解:设{}n a 的公比为q ,由题设得1n n a q -=.由已知得424q q =,解得0q =(舍去)或2q =-或2q =. 故1(2)n n a -=-或12n n a -=. (2)若1(2)n n a -=-,则1(2)3nn S --=.数学试卷 第11页(共20页) 数学试卷 第12页(共20页)由63m S =得(2)188m -=-.此方程没有正整数解.若12n n a -=,则21n n S =-.由63m S =得264m =,解得6m =. 综上,6m =.【解析】(1)解:设{}n a 的公比为q ,由题设得1n n a q-=.由已知得424q q =,解得0q =(舍去)或2q =-或2q =. 故1(2)n n a -=-或12n n a -=.(2)若1(2)n n a -=-,则1(2)3n n S --=.由63m S =得(2)188m -=-。
2018年普通高等学校招生全国统一考试数学试题 理(全国卷3,含解析)

2018年普通高等学校招生全国统一考试数学试题理(全国卷3)注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,,则A. B. C. D.【答案】C【解析】分析:由题意先解出集合A,进而得到结果。
详解:由集合A得,所以故答案选C.点睛:本题主要考查交集的运算,属于基础题。
2.A. B. C. D.【答案】D【解析】分析:由复数的乘法运算展开即可。
详解:故选D.点睛:本题主要考查复数的四则运算,属于基础题。
3. 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A. AB. BC. CD. D【答案】A【解析】分析:观察图形可得。
详解:观擦图形图可知,俯视图为故答案为A.点睛:本题主要考擦空间几何体的三视图,考查学生的空间想象能力,属于基础题。
4. 若,则A. B. C. D.【答案】B【解析】分析:由公式可得。
详解:故答案为B.点睛:本题主要考查二倍角公式,属于基础题。
5. 的展开式中的系数为A. 10B. 20C. 40D. 80【答案】C【解析】分析:写出,然后可得结果详解:由题可得令,则所以故选C.点睛:本题主要考查二项式定理,属于基础题。
6. 直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是A. B. C. D.【答案】A【解析】分析:先求出A,B两点坐标得到再计算圆心到直线距离,得到点P到直线距离范围,由面积公式计算即可详解:直线分别与轴,轴交于,两点,则点P在圆上圆心为(2,0),则圆心到直线距离故点P到直线的距离的范围为则故答案选A.点睛:本题主要考查直线与圆,考查了点到直线的距离公式,三角形的面积公式,属于中档题。
2018 年全国 III 卷数学(理)答案及解析

− x + x + 2 的图像大致为( 7.函数 y =
4 2
)
A.
B.
C.
D.பைடு நூலகம்
【答案】D 【考点】函数图像以及性质 【难易程度】基础题 【解析】当 x=1 时,函数值大于 0,排除 A、B;因为 F(x)=F(-x),函数为偶函数,图像关于 y 轴
−4 x 3 + 2 x =0 ,解得 x=0、 、 对称, 令F '( x) =
p ,各成员的支付方式相互独立。设 X 为该群
,
P( x = 4) < p( x = 6) ,则 p =(
D.0.3
)
C.0.4
DX = np(1 − p) =10 × p(1 − p) = 2.4 , 解 得
= p1 0.6 = , p2 0.4 .
因为 P(X=4)<P(X=6),即
4 6 C10 p 4 (1 − p )6 < C10 p 6 (1 − p ) 4 ,所以 p 取 0.6。故答案选 B.
2 7 = 9 9 ,故答案选 B.
2 ( x 2 + )5 x 的展开式中 5、
A.10 【答案】C 【考点】二项式定理 【难易程度】基础题 B.20
的系数为( D.80
)
C.40
2 ( x 2 + )5 x 的展开式中的第 r+1 项为 【解析】
,题目中需要求解 ,故答案选 C
的系
4 ,则 r = 2 ,∴ 数,需使 2 × (5 − r ) − r =
是带卯眼的木构件的俯视图可以是(
)
A.
B.
C. 【答案】A 【考点】三视图 【难易程度】基础题
2018广东省高职高考数学试题有答案
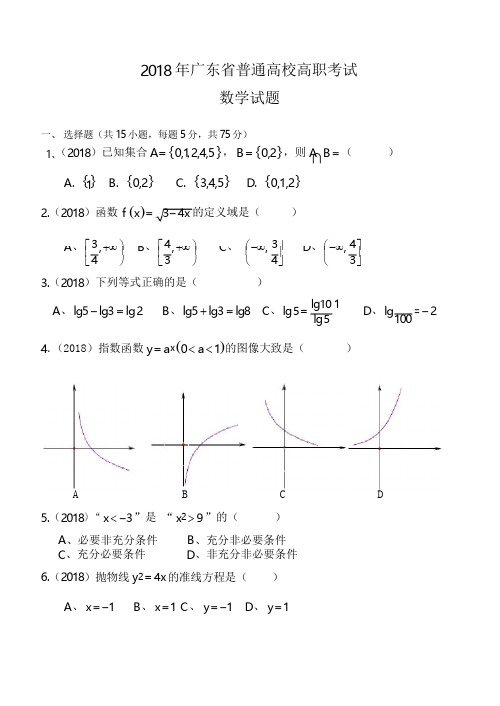
A、⎢,+∞⎪B、⎢,+∞⎪C、 -∞,⎥D、 -∞,⎥,13⎤D、lg=-22018年广东省普通高校高职考试数学试题一、选择题(共15小题,每题5分,共75分)1、(2018)已知集合A={0,12,4,5},B={0,2},则A B=()A.{}B.{0,2}C.{3,4,5}D.{0,1,2}2.(2018)函数f(x)=3-4x的定义域是()⎡3⎫⎡4⎫⎛⎛4⎤⎣4⎭⎣3⎭⎝4⎦⎝3⎦3.(2018)下列等式正确的是()A、lg5-lg3=lg2B、lg5+lg3=lg8C、lg5=lg101lg5100 4.(2018)指数函数y=a x(0<a<1)的图像大致是()A B C D5.(2018)“x<-3”是“x2>9”的()A、必要非充分条件B、充分非必要条件C、充分必要条件D、非充分非必要条件6.(2018)抛物线y2=4x的准线方程是()A、x=-1B、x=1C、y=-1D、y=18.(2018)1 + + 2 2 2 2+ 11.(2018) f (x ) = ⎨ A 、 B 、 C 、 D 、7.(2018)已知 ∆ABC , BC = 3, AC = 6, ∠C = 90︒ ,则()A 、 sin A =226B 、coA=C 、 tan A = 2D 、 cos( A + B) = 131 1 1 1+ + +234 1 2n -1= ( )A 、 2 ⨯ (1 - 2 -n )B 、 2 ⨯ (1 - 21 - n )C 、 2 ⨯ (1 - 2n -1 )D 、 2 ⨯ (1 - 2n )9.(2018)若向量 AB = (1,2 ), AC = (3,4 ),则 BC = ()A 、 (4,6 )B 、 (-2, -2)C 、 (1,3 )D 、 (2,2 )10.(2018)现有 3000 棵树,其中 400 棵松树,现在提取 150 做样本,其中抽取松树做样本的有( )棵A 、15B 、20C 、25D 、30⎧ x - 3 , x ≥ 0 ⎩ x 2 - 1, x < 0,则 f ( f (2))= ( )A 、1B 、0C 、 -1D 、 -212.(2018)一个硬币抛两次,至少一次是正面的概率是()1 12 33 2 34 13.(2018)已知点 A (-1,4 ), B (5,2 ) ,则 AB 的垂直平分线是()A 、 3x - y - 3 = 0B 、 3x + y - 9 = 0C 、 3x - y - 10 = 0D 、 3x + y - 8 = 014.(2018)已知数列 {a }为等比数列,前 n 项和 S = 3n +1 + a ,则 a = ()nnA 、 -6B 、 -3C 、0D 、315.(2018)设 f (x )是定义在 R 上的奇函数,且对于任意实数 x ,有 f (x + 4) = f (x ),若 f (-1) = 3 ,则 f (4)+ f (5) = ()A 、 -3B 、3C 、4D 、616、(2018)双曲线 - 3 4 a b二、 二、填空题(共 5 小题,每题 5 分,共 25 分)x 2 y 24 32= 1 的离心率 e = ; 17、(2018)已知向量 a = (4,), b = (x ,),若 a ⊥ b ,则 b =;18、(2018)已知数据10, x,11, y ,12, z 的平均数为 8,则 x, y , z 的平均数为 ;19、(2018)以两直线 x + y = 0 和 2 x - y - 3 = 0 的交点为圆心,且与直线 2 x - y + 2 = 0相切的圆的标准方程是;20 已知 ∆ABC 对应边分别为的内角 A ,B ,C 的对边分别为 a, b , c ,已知3b = 4a, B = 2 A ,则 cos A =;三、解答题(50 分)21、(2018)矩形周长为 10,面积为 A ,一边长为 x 。
最新2018高职高考数学模拟考试题和参考答案解析一教学内容

2017年高职高考数学模拟试题数 学本试卷共4页,24小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A)填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本大题共15小题,每小题5分,满分75分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知集合{1,1},{0,1,2},M N =-=则MN =( )A .{0 } B.{1 } C.{0,1,2 } D.{-1,0,1,2 } 2、函数y=的定义域为( ).(2,2).[2,2].(,2).(2,)A B C D ---∞-+∞3、设a ,b ,是任意实数,且a<b,则下列式子正确的是( )22..1.lg()0.22a b b A a b B C a b D a><-><4、()sin30︒-=( )11...22A B C D -5、=(2,4),=(4,3),+=a b a b 若向量则( ).(6,7).(2,1).(2,1).(7,6)A B C D --6、下列函数为奇函数的是( ) ..lg .sin .cos xA y eB y xC y xD y x ====7、设函数21,1()2,1x x f x x x⎧+≤⎪=⎨>⎪⎩,则f(f(—1))=( )A .-1B .-2C .1 D. 2 8、 “3x>”是“5x >”的( )A.充分非必要条件B.必要非充分条件C.充分必要条件D.非充分非必要条件 9、若向量a ,b 满足|a+b|=|a-b|,则必有( ).0.0.||||.0A a B b C a b D a b ====10、若直线l 过点(1, 4),且斜率k=3,则直线l 的方程为( ).310.310.10.10A x yB x yC x yD x y --=-+=--=-+=11、对任意x R ∈,下列式子恒成立的是( )22121.210.|1|0.10.log (1)02xA x xB xCD x ⎛⎫ ⎪⎝⎭⎛⎫-+>->+>+> ⎪⎝⎭12a +a =( ).2.4.24.24A B C D ---或或13、抛物线28yx =-的准线方程是( ).2.2.2.2A x B x C y D y ==-==-14、已知x 是1210,,,x x x 的平均值,1a 为123456,,,,,x x x x x x 的平均值,2a 为78910,,,x x x x 的平均值,则x =( )121212122332....552a a a a a a A B C a a D ++++15)( ).0.45.0.55.0.65.0.75A B C D二、填空题:本大题共5小题,每小题5分,满分25分.16、函数()3sin 4f x x =的最小正周期为__________17、不等式2280x x -->的解集为________18、若sin θ=35,tan θ< 0,则cos θ=_________ 19、已知等差数列{}n a 满足3285,30,a a a =+=则n a =_______20、设袋子内装有大小相同,颜色分别为红,白,黑的球共100个,其中红球35个,从袋子内任取1个球,若取出白球的概率为0.25,择取黑球的概率为____________三、解答题:本大题共4小题,第21~23题各12分,第24题14分,满分50分.解答须写出文字说明、证明过程和演算步骤. 21.(本小题满分12分),,,3(1)(2)cos B ABC a b c ABC C a π∆∆∠∠∠=∠=已知是中,A 、B 、C 的对边,b=1,c 求的值;求的值.22.(本小题满分12分){}{}(){}(){}21-12n n n =132n 6n+3(n=2,3,)b 1b 2b n S n n n n n n a a a a a =+-⋅⋅⋅已知数列的首项,数列的通项公式b =+n :证明数列是等比数列.求数列的前项和.23.(本小题满分12分)2212x=19A BAB C F(3,0)F(3,0)4DC DC D Cxoy y+=-在平面直角坐标系中,直线与圆x交于两点,,记以为直径的圆为,以点和为焦点,短半轴为的椭圆为。
电子科技大学 18秋《移动互联网技术》在线作业2满分答案

18秋《移动互联网技术》在线作业2
下列说法正确的是?()
A.每个进程都运行于自己的 java 虚拟机(VM)中
B.默认情况下,每个应用程序中均运行于自己的进程中,而且此进程不会被消毁
C.每个应用程序会被赋予一个唯一的 linux 用户 ID,从而使得该应用程序下的文件,其它用户也可以访问
D.一个应用程序数据,可以随意被其它应用程序所访问
正确答案:A
对于XML布局文件中的视图控件,layout_width属性的属性值不可以是什么?()
A.match_parent
B.fill_parent
C.wrap_content
D.match_content
正确答案:D
对一些资源以及状态的操作保存,最好是保存在Activity生命周期的哪个函数中进行?()
A.onStart( )
B.onPause( )
C.onCreate( )
D.onResume( )
正确答案:A
android 中文件操作模式中表示只能被本应用使用,写入文件会覆盖的是?()
A.MODE_APPEND
B.MODE_WORLD_READABLE
C.MODE_WORLD_WRITEABLE
D.MODE_PRIVATE
正确答案:D
在手机开发中常用的数据库是?()
A.SQLite
B.Oracle
C.Sql Server
D.MySQL。
电子科技大学 18秋《工程力学》在线作业1满分答案

18秋《工程力学》在线作业1
关于平面力系的主矢和主矩,以下表述中正确的是()。
A.主矢的大小、方向与简化中心无关
B.主矩的大小、转向一定与简化中心的选择有关
C.当平面力系对某点的主矩为零时,该力系向任何一点简化结果为一合力
D.当平面力系对某点的主矩不为零时,该力系向任一点简化的结果均不可能为一合力
正确答案:A
两根细长压杆的长度、横截面面积、约束状态及材料均相同,若a、b杆的横截面形状分别为正方形和圆形,则二压杆的临界压力Pa和Pb的关系为( )。
A.Pa<Pb
B.Pa>Pb
C.Pa=Pb
D.不可确定
正确答案:B
表示扭转变形程度的量( )。
A.是扭转角ψ,不是单位长度扭转角θ
B.是单位长度扭转角θ,不是扭转角ψ
C.是扭转角ψ和单位长度扭转角θ
正确答案:A
材料的塑性指标有( )。
A.σs和δ
B.σs和ψ
C.δ和ψ
D.σs、δ和ψ
正确答案:C
几何形状完全相同的两根梁,一根为钢材,一根为铝材。
若两根梁受力情况也相同,则它们的( )。
A.弯曲应力相同,轴线曲率不同
B.弯曲应力不同,轴线曲率相同
C.弯曲应力与轴线曲率均相同
D.弯曲应力与轴线曲率均不同。
电子科技大学20年秋季《高等数学(理科本科)》在线作业3附参考答案

{图}
A.A
B.B
C.C
D.D
答案:C
18.题面见图片
{图}
A.A
B.B
C.C
D.D
答案:D
19.题面见图片
{图}
A.A
B.B
C.C
D.D
答案:B
20.1{图}
A.A
B.B
C.C
D.D
答案:C
21.1{图}
A.A
B.B
C.C
D.D
答案:B
22.1{图}
A.A
B.B
C.C
D.D
答案:A
D.D
答案:A
5.题面见图片
{图}
A.A
B.B
C.C
D.D
答案:C
6.1{图}
A.A
B.B
C.C
D.D
答案:B
7.1{图}
A.A
B.B
C.C
D.D
答案:D
8.1{图}
A.A
B.B
C.C
D.D
答案:A
9.题面见图片
{图}
A.A
B.B
C.C
D.D
答案:B
10.题面见图片
{图}
A.A
B.B
C.C
D.D
答案:A
电子科技大学
试卷总分:100 得分:100
一、单选题 (共 25 道试题,共 100 分)
1.题面见图片
{图}
A.A
B.B
C.C
D.D
答案:B
2.1{图}
A.A
B.B
C.C
D.D
答案:A
更多加微boge30619
2018年湖北成人高考高起点数学辅导及答案(三).doc

2018年湖北成人高考高起点数学辅导及答案(三)温馨提示:下载整套试卷可直接点击附件!一、选择题:1~10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后的括号内.1.A.x3+3x-4B.x3+3x-3C.x3+3x-2D.x3+3x-12.A.2hB.α·2α-1C.2αln 2D.03.已知y=2x+x2+e2,则 yˊ等于( ).A.B.C.D.4.A.B.C.D.5.A.B.1/4C.1/2D.6.设F(x)的一个原函数为xln(x+1),则下列等式成立的是().A.B.C.D.7.A.B.C.D.8.A.B.C.D.9.A.B.C.D.10.若事件A与B为互斥事件,且P(A)=0.3,P(A+B)=0.8,则P(B)等于().A.0.3B.0.4C.0.5D.0.6二、填空题:11~20小题,每小题4分,共40分.把答案填在题中横线上.11.12.13.14.15.16.17.18.19.20.三、解答题:21~28小题,共70分.解答应写出推理、演算步骤.21.22.23.24.(本题满分8分)甲、乙二人单独译出某密码的概率分别为0.6和0.8,求此密码被破译的概率.25.26.(本题满分10分)设函数y=αx3+bx+c在点x=1处取得极小值一1,且点(0,1)为该函数曲线的拐点,试求常数a,b,c.27.(本题满分10分)设函数y=y(x)是由方程cos(xy)=x+y所确定的隐函数,求函数曲线y=y(x)过点(0,1)的切线方程.28.参考答案及解析一、选择题1.【答案】应选C.2.【答案】应选D.【提示】利用函数在一点可导的定义的结构式可知3.【答案】应选C.【提示】用基本初等函数的导数公式.4.【答案】应选B.【解析】本题考查的知识点是复合函数的概念及其求导计算.5.【答案】应选A.6.【答案】应选A.【解析】本题考查的知识点是原函数的概念.7.【答案】应选B.【解析】本题考查考生对微分、积分的基础知识和换元积分法的掌握情况.请考生注意:由于这种题考查的都是基本概念和基本方法,所以是历年“专升本”考试中常见的典型试题,熟练地掌握这类题的解法是十分重要的.8.【答案】应选B.【提示】本题考查的知识点是反常积分的求解.9.【答案】应选A.10.【答案】应选C.【解析】本题考查的知识点是互斥事件的概念和加法公式.二、填空题11.【答案】应填一2.【提示】利用重要极限Ⅱ的结构式:12.【答案】应填0.13.【答案】【提示】先求复合函数的导数,再求dy.14.【答案】应填0.【解析】本题考查的知识点是驻点的概念及求法.15.【答案】应填2.【解析】本题考查的知识点是二阶导数值的计算.16.【答案】应填XCOS x-sin x+C.17.【答案】应填π/4.18.【答案】应填1.【提示】被积函数的前一部分是奇函数,后一部分是偶函数,因此有解得α=1.19.【答案】应填0.20.【解析】本题考查的知识点是复合函数求偏导和全微分的计算公式.三、解答题21.方法计算.22.本题主要考查商的导数计算.23.本题考查的知识点是不定积分的积分公式及凑微分(即第一换元积分法)的积分方法.【解析】当被积函数的分母为一项而分子为两项或两项以上的和时,通常分为几个不定积分之和分别计算.如果被积函数的分子中有sin戈或COSx的奇次方项时,常用凑微分法将sin xdx写成一d(COS x),而cos xdx=d(sinx),换成对cosx或sinx的积分.24.本题考查的知识点是事件相互独立的概念和概率的加法公式.【解析】本题的关键是密码被破译这一事件是指密码被甲破译或被乙破译,如果理解成甲破译密码且乙破译密码就错了!另外要注意:甲、乙二人破译密码是相互独立的.解设A=“甲破译密码”,B=“乙破译密码”,C=“密码被破译”,则C=A+B,所以P(C)=P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)P(B)=0 6+0.8-0. 6×0.8=0. 9225.本题考查的知识点是定积分的分部积分法.【解析】将被积函数分成两项,分别用公式法和分部积分法计算.26.本题考查的知识点是可导函数在某一点取得极小值的必要条件以及拐点的概念.联立①②③,可解得α=1,b=-3,c=1.27.本题是一道典型的综合题,考查的知识点是隐函数的求导计算和切线方程的求法.【解析】本题的关键是由已知方程求出yˊ,此时的yˊ中通常含有戈和y,因此需由原方程求出当x=0时的y值,继而得到yˊ的值,再写出过点(0,1)的切线方程.计算由方程所确定的隐函数y(x)的导数,通常有三种方法:直接求导法(此时方程中的y是x的函数)、公式法(隐函数的求导公式)和微分法(等式两边求微分).解法l直接求导法.等式两边对x求导,得解法2解法3微分法.等式两边求微分,得28.本题考查的知识点是条件极值的计算.【解析】计算条件极值的关键是构造拉格朗日函数.在求驻点的过程中通常都将参数消去.。
(精校版)2018年全国卷Ⅲ理数高考试题文档版(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项: 1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1,2},则A1.已知集合A={x|x-1≥0},B={0,A.{0} 2.(1+i)(2-i)= A.-3-i B.-3+i B.{1} B=2} C.{1,1,2} D.{0,C.3-i D.3+i 3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是 14.若sinα=,则cos2α= 38A. 95 B.79 C.-7 9 D.-8 92⎫⎛5. x2+⎪的展开式中x4的系数为 x⎭⎝ A.10 B.20C.40 D.80 6.直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是 6] A.[2, 8] B.[4,⎤C.⎡⎣2,32⎦⎤D.⎡⎣22,32⎦ 7.函数y=-x4+x2+2的图像大致为 8.某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4)<P(X=6),则p= A.0.7 B.0.6 C.0.4 D.0.3 a2+b2-c29.△ABC的内角A,B,C的对边分别为a,b,c,若△ABC的面积为,则C= 4ππππA. B. C. D. 2346C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为93,则三棱10.设A,B,锥D-ABC体积的最大值为 A.123 B.183 C.243 D.543x2y2b>0)的左、右焦点,O是坐标原点.过F2作C的一条渐近11.设F1,F2是双曲线C:2-2=1(a>0,ab线的垂线,垂足为P.若PF1=6OP,则C的离心率为 A.5 B.2 C.3 D.2 12.设a=log0.20.3,b=log20.3,则A.a+b<ab<0 C.a+b<0<ab B.ab<a+b<0 D.ab<0<a+b 二、填空题:本题共4小题,每小题5分,共20分. 13.已知向量a=(1,2),b=(2,-2),c=(1,λ).若c∥(2a+b),则λ=________. 1)处的切线的斜率为-2,则a=________. 14.曲线y=(ax+1)ex在点(0,π⎫⎛π]的零点个数为________. 15.函数f(x)=cos 3x+⎪在[0,6⎝⎭1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若 16.已知点M(-1,∠AMB=90︒,则k=________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.学科.网(一)必考题:共60分. 17.(12分)a5=4a3.等比数列{an}中,a1=1,(1)求{an}的通项公式;(2)记Sn为{an}的前n项和.若Sm=63,求m. 18.(12分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:第一种生产方式第二种生产方式超过m 不超过m (3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:K=2n(ad-bc)2(a+b)(c+d)(a+c)(b+d), P(K2≥k) 0.050 0.010 k 3.841 0.0016.635 10.828 19.(12分)如图,边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD⊥平面BMC;(2)当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值. 20.(12分) x2y2m)(m>0).已知斜率为k的直线l与椭圆C:+=1交于A,B两点,线段AB的中点为M(1,431(1)证明:k<-; 2(2)设F为C的右焦点,P为C上一点,且FP+FA+FB=0.证明:FA,FP,FB成等差数列,并求该数列的公差. 21.(12分)已知函数f(x)=2+x+ax2ln(1+x)-2x.(1)若a=0,证明:当-1<x<0时,f(x)<0;当x>0时,f(x)>0;(2)若x=0是f(x)的极大值点,求a.(二)选考题:共10分,请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22.[选修4—4:坐标系与参数方程](10分)⎧x=cosθ,在平面直角坐标系xOy中,⊙O的参数方程为⎨(θ为参数),过点0,-2且倾斜角为y=sinθ⎩()()α的直线l与⊙O交于A,B两点.(1)求α的取值范围;学.科网(2)求AB中点P的轨迹的参数方程. 23.[选修4—5:不等式选讲](10分)设函数f(x)=2x+1+x-1.(1)画出y=f(x)的图像;+∞),f(x)≤ax+b,求a+b的最小值.(2)当x∈[0,参考答案: 1 C 13.2 D 3 A 4 B 5 C 6 A 7 D 8 B 9 C 10 B 11 C 12 B 1 14.-3 15.3 16.2 217.(12分) 解:(1)设{an}的公比为q,由题设得an=qn-1. 由已知得q4=4q2,解得q=0(舍去),q=-2或q=2. 故an=(-2)n-1或an=2n-1. (2)若an=(-2)n-11-(-2)n,则Sn=.由Sm=63得(-2)m=-188,此方程没有正整数解. 3m若an=2n-1,则Sn=2n-1.由Sm=63得2=64,解得m=6.综上,m=6. 18.(12分)解:(1)第二种生产方式的效率更高. 理由如下:(i)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高. (ii)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高. (iii)由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高. (iv)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.学科*网以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分. (2)由茎叶图知m=列联表如下:第一种生产方式第二种生产方式 279+81=80. 2超过m 15 5 不超过m 5 1540(15⨯15-5⨯5)2=10>6.635,(3)由于K=所以有99%的把握认为两种生产方式的效率有差异. 20⨯20⨯20⨯2019.(12分)解:(1)由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM. 因为M为CD上异于C,D的点,且DC为直径,所以DM⊥CM. 又 BCCM=C,所以DM⊥平面BMC. 而DM⊂平面AMD,故平面AMD⊥平面BMC. (2)以D为坐标原点,DA的方向为x轴正方向,建立如图所示的空间直角坐标系D−xyz. 当三棱锥M−ABC体积最大时,M为CD的中点. 由题设得D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),M(0,1,1),AM=(-2,1,1),AB=(0,2,0),DA=(2,0,0) 设n=(x,y,z)是平面MAB的法向量,则⎧⎪n⋅AM=0,⎧-2x+y+z=0,即⎨⎨⎪⎩n⋅AB=0.⎩2y=0.可取n=(1,0,2). DA是平面MCD的法向量,因此 cosn,DA=n⋅DA5,=|n||DA|525, 525. 5sinn,DA=所以面MAB与面MCD所成二面角的正弦值是20.(12分) x12y12x22y22+=1,+=1. 解:(1)设A(x1,y1),B(x2,y2),则4343两式相减,并由y1-y2=k得x1-x2x1+x2y1+y2+⋅k=0. 43由题设知x1+x2y+y2=1,1=m,于是 22k=-3.① 4m由题设得0<m<31,故k<-. 22(2)由题意得F(1,0),设P(x3,y3),则(x3-1,y3)+(x1-1,y1)+(x2-1,y2)=(0,0). 由(1)及题设得x3=3-(x1+x2)=1,y3=-(y1+y2)=-2m<0. 又点P在C上,所以m=于是 333,从而P(1,-),|FP|=. 422x12x|FA|=(x1-1)+y=(x1-1)+3(1-)=2-1. 422212同理|FB|=2-x2. 21(x1+x2)=3. 2所以|FA|+|FB|=4-故2|FP|=|FA|+|FB|,即|FA|,|FP|,|FB|成等差数列. 设该数列的公差为d,则 2|d|=||FB|-|FA||=将m=11|x1-x2|=(x1+x2)2-4x1x2.② 223代入①得k=-1. 4712所以l的方程为y=-x+,代入C的方程,并整理得7x-14x+=0. 44故x1+x2=2,x1x2=1321,代入②解得|d|=. 2828所以该数列的公差为21.(12分) 321321或-. 2828解:(1)当a=0时,f(x)=(2+x)ln(1+x)-2x,f'(x)=ln(1+x)-设函数g(x)=f'(x)=ln(1+x)-x. 1+xxx,则g'(x)=. 21+x(1+x)当-1<x<0时,g'(x)<0;当x>0时,g'(x)>0.故当x>-1时,g(x)≥g(0)=0,且仅当x=0时,g(x)=0,从而f'(x)≥0,且仅当x=0时,f'(x)=0. 所以f(x)在(-1,+∞)单调递增.学#科网又f(0)=0,故当-1<x<0时,f(x)<0;当x>0时,f(x)>0. (2)(i)若a≥0,由(1)知,当x>0时,f(x)≥(2+x)ln(1+x)-2x>0=f(0),这与x=0是f(x)的极大值点矛盾. (ii)若a<0,设函数h(x)=f(x)2x=ln(1+x)-.2+x+ax22+x+ax2由于当|x|<min{1,1}时,2+x+ax2>0,故h(x)与f(x)符号相同. |a|又h(0)=f(0)=0,故x=0是f(x)的极大值点当且仅当x=0是h(x)的极大值点. 12(2+x+ax2)-2x(1+2ax)x2(a2x2+4ax+6a+1).h'(x)=-=22221+x(2+x+ax)(x+1)(ax+x+2)如果6a+1>0,则当0<x<-6a+11,且|x|<min{1,}时,h'(x)>0,故x=0不是h(x)的极4a|a| 大值点. 如果6a+1<0,则ax+4ax+6a+1=0存在根x1<0,故当x∈(x1,0),且|x|<min{1,221}时,|a|h'(x)<0,所以x=0不是h(x)的极大值点. x3(x-24)如果6a+1=0,则h'(x)=.则当x∈(-1,0)时,h'(x)>0;当x∈(0,1)时,22(x+1)(x-6x-12)h'(x)<0.所以x=0是h(x)的极大值点,从而x=0是f(x)的极大值点综上,a=-1. 622.[选修4—4:坐标系与参数方程](10分)【解析】(1)O的直角坐标方程为x2+y2=1.当α=当α≠π时,l与O交于两点. 2π2|<1,解时,记tanα=k,则l 的方程为y=kx-2.l与O交于两点当且仅当|221+kπ3π). 24ππ42π3π综上,α的取值范围是(,). 44得k<-1或k>1,即α∈(,)或α∈(,⎧π3π⎪x=tcosα,(t为参数,<α<).(2)l的参数方程为⎨44⎪⎩y=-2+tsinα设A,B,P对应的参数分别为tA,tB,tP,则tP=tA+tB ,且tA,tB满足t2-22tsinα+1=0.2⎧⎪x=tPcosα, 于是tA+tB=22sinα,tP=2sinα.又点P的坐标(x,y)满足⎨y=-2+tsinα.⎪⎩P⎧2x=sin2α,⎪π3π⎪2(α为参数,<α<).所以点P的轨迹的参数方程是⎨44⎪y=-2-2cos2α⎪⎩2223.[选修4—5:不等式选讲](10分) 1⎧-3x,x<-,⎪2⎪1⎪【解析】(1)f(x)=⎨x+2,-≤x<1,y=f(x)的图像如图所示. 2⎪⎪3x,x≥1.⎪⎩(2)由(1)知,y=f(x)的图像与y轴交点的纵坐标为2,且各部分所在直线斜率的最大值为3,故当且仅当a≥3且b≥2时,f(x)≤ax+b在[0,+∞)成立,因此a+b的最小值为5.。
电子科技大学 18秋《物联网技术基础》在线作业满分答案

18秋《物联网技术基础》在线作业
车载网在智能交通中的应用不包括( )。
A.智能驾驶
B.车辆辅助驾驶
C.不停车加油
D.车载导航与娱乐
正确答案:C
预测到2020年,物联网上物与物互联的通信量和人与人的通信量相比将达到( )。
A.10:1
B.20:1
C.30:1
D.50:1
正确答案:C
以下不属于数据中心成本组成部分的是( )。
A.服务器成本
B.用户按流量计费成本
C.网络设备成本
D.能源成本
正确答案:B
物联网技术在健康监控中的应用案例不包括( )。
A.加利福尼亚大学基于无线传感器网络的人体健康监测平台CustMed
B.美国公司研制的救生衬衫和智能衬衫产品
C.医院门禁系统
D.美国公司研发的智能婴儿服
正确答案:C
以下关于VPN特点的描述中错误的是( )。
A.VPN是指在按IP协议组建的企业专用传输网络中建立虚拟的数据传输通道
B.“虚拟”表示通过“隧道”或“虚电路”的方式建立的一种逻辑网络
C.“专用”表示VPN可以为接入的网络与主机,提供保证安全与服务质量的传输服务
D.VPN技术可以在感知层与应用层之间建立安全的通信“隧道”
正确答案:A。
2018年全国(三卷)高考数学(理)试题及答案,推荐文档

绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}|10A x x =-≥,{}012B =,,,则A B = A .{}0B .{}1C .{}12,D .{}012,,2.()()1i 2i +-=A .3i--B .3i-+C .3i-D .3i+3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若1sin 3α=,则cos 2α=A .89B .79C .79-D .89-5.522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为A .10B .20C .40D .806.直线20x y ++=分别与x 轴,y 轴交于A ,B 两点,点P 在圆()2222x y -+=上,则ABP △面积的取值范围是A .[]26,B .[]48,C .D .⎡⎣7.函数422y x x =-++的图像大致为8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设X 为该群体的10位成员中使用移动支付的人数, 2.4DX =,()()46P X P X =<=,则p =A .0.7B .0.6C .0.4D .0.39.ABC △的内角A B C ,,的对边分别为a ,b ,c ,若ABC △的面积为2224a b c +-,则C =A .π2B .π3C .π4D .π610.设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为,则三棱锥D ABC -体积的最大值为A .B .C .D .11.设12F F ,是双曲线22221x y C a b-=:(00a b >>,)的左,右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若1PF =C 的离心率为A B .2C D12.设0.2log 0.3a =,2log 0.3b =,则A .0a b ab +<<B .0ab a b <+<C .0a b ab+<<D .0ab a b<<+二、填空题:本题共4小题,每小题5分,共20分。
2018年高考真题——理科数学(全国卷Ⅲ)+Word版含解析【KS5U+高考】

绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合,,则A. B. C. D.【答案】C【解析】分析:由题意先解出集合A,进而得到结果。
详解:由集合A得,所以故答案选C.点睛:本题主要考查交集的运算,属于基础题。
2.A. B. C. D.【答案】D【解析】分析:由复数的乘法运算展开即可。
详解:故选D.点睛:本题主要考查复数的四则运算,属于基础题。
3. 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A. AB. BC. CD. D【答案】A【解析】分析:观察图形可得。
详解:观擦图形图可知,俯视图为故答案为A.点睛:本题主要考擦空间几何体的三视图,考查学生的空间想象能力,属于基础题。
4. 若,则A. B. C. D.【答案】B【解析】分析:由公式可得。
详解:故答案为B.点睛:本题主要考查二倍角公式,属于基础题。
5. 的展开式中的系数为A. 10B. 20C. 40D. 80【答案】C【解析】分析:写出,然后可得结果详解:由题可得令,则所以故选C.点睛:本题主要考查二项式定理,属于基础题。
6. 直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是A. B. C. D.【答案】A【解析】分析:先求出A,B两点坐标得到再计算圆心到直线距离,得到点P到直线距离范围,由面积公式计算即可详解:直线分别与轴,轴交于,两点,则点P在圆上圆心为(2,0),则圆心到直线距离故点P到直线的距离的范围为则故答案选A.点睛:本题主要考查直线与圆,考查了点到直线的距离公式,三角形的面积公式,属于中档题。
2018年全国卷3理科数学试题及参考答案

绝密★启用前试题类型:新课标Ⅲ2018年普通高等学校招生全国统一考试理科数学参考答案注意事项:1. 答题前,考生先将自己的姓名、准考证号填写在答题卡上.2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如需改动,用橡皮擦干净后,再选涂其他答案标号. 回答非选择题时,将答案写在答题卡上. 写在本试卷上无效.3. 考试结束后,将本试卷和答题卡一并交回.一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|10A x x =-≥,{}0,1,2B =,则A B = ( ) A .{}0 B .{}1 C .{}1,2 D .{}0,1,2 【答案】C【解析】:1A x ≥,{}1,2A B ∴= 【考点】交集2.()()12i i +-=( )A .3i --B .3i -+C .3i -D .3i + 【答案】D【解析】()()21223i i i i i +-=+-=+【考点】复数的运算3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫做榫头,凹进部分叫做卯眼,图中的木构件右边的小长方体是榫头. 若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )【答案】A【解析】注意咬合,通俗点说就是小长方体要完全嵌入大长方体中,嵌入后最多只能看到小长方体的一个面,而B 答案能看见小长方体的上面和左面,C 答案至少能看见小长方体的左面和前面,D 答案本身就不对,外围轮廓不可能有缺失 【考点】三视图 4.若1sin 3α=,则cos 2α=( ) A .89 B .79 C .79- D .89- 【答案】B【解析】27cos 212sin 9αα=-= 【考点】余弦的二倍角公式5.522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为( )A .10B .20C .40D .80 【答案】C【解析】522x x ⎛⎫+ ⎪⎝⎭的第1r +项为:()521035522rr r r r r C x C x x --⎛⎫= ⎪⎝⎭,故令2r =,则10345240r r r C x x -=【考点】二项式定理俯视方向D.C. B.A.6.直线20x y ++=分别与x 轴、y 轴交于点,A B 两点,点P 在圆()2222x y -+=上,则ABP ∆面积的取值范围是( )A .[]2,6B .[]4,8 C. D.⎡⎣【答案】A【解析】()()2,0,0,2A B --,AB ∴=,可设()2,P θθ+,则4P ABd πθ-⎛⎫==+∈ ⎪⎝⎭[]12,62ABP P AB P AB S AB d ∆--∴=⋅=∈ 注:P AB d -的范围也可以这样求:设圆心为O ,则()2,0O,故P AB O AB O AB d d d ---⎡∈+⎣,而O AB d -==,P AB d -∴∈ 【考点】点到直线距离、圆上的点到直线距离最值模型(圆的参数方程、三角函数) 7.422y x x =-++的图像大致为( )【答案】DxxxxyyyyD.C.B.A.OO11OO111111【解析】()12f =,排除A 、B ;()32'42212y x x x x =-+=-,故函数在0,2⎛⎫⎪ ⎪⎝⎭单增,排除C【考点】函数图像辨识(按照奇偶性、特殊点函数值正负、趋势、单调性(导数)的顺序来考虑)8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设X 为该群体的10为成员中使用移动支付的人数, 2.4DX =,()()46P X P X =<=,则p =( )A .0.7B .0.6C .0.4D .0.3 【答案】B【解析】由题意得X 服从二项分布,即()~10,X p ,由二项分布性质可得()101 2.4DX p p =-=,故0.4p =或0.6,而()()()()64446610104161P x C p p P x C p p ==-<==-即()221p p -<,故0.5p >0.6p ∴=【考点】二项分布及其方差公式9.ABC ∆的内角,,A B C 的对边分别为,,a b c ,若ABC ∆的面积为2224a b c+-,则C =( )A .2πB .3πC .4πD .6π【答案】C 【解析】2221sin 24ABCa b c S ab C ∆+-==,而222cos 2a b c C ab+-= 故12cos 1sin cos 242ab C ab C ab C ==,4C π∴= 【考点】三角形面积公式、余弦定理10.设,,,A B C D 是同一个半径为4的球的球面上四点,ABC ∆为等边三角形且其面积为D ABC -的体积最大值为( )A .B .C .D .【答案】B【解析】如图,O为球心,F为等边ABC∆的重心,易知OF⊥底面ABC,当,,D O F三点共线,即DF⊥底面ABC时,三棱锥D ABC-的高最大,体积也最大. 此时:6ABCABCABS∆∆⎫⎪⇒==等边,在等边ABC∆中,233BF BE AB===,在Rt OFB∆中,易知2OF=,6DF∴=,故()max163D ABCV-=⨯=【考点】外接球、椎体体积最值11.设12,F F是双曲线()2222:10,0x yC a ba b-=>>的左,右焦点,O是坐标原点,过2F作C的一条渐近线的垂线,垂足为P.若1PF=,则C的离心率为( )AB.2CD【答案】C【解析】渐近线OP的方程为:by xa=,利用点到直线的距离公式可求得2PF b=,(此结论可作为二级结论来记忆),在Rt ABC∆中,易得OP a=,1PF∴=,在1POF∆中,由余弦定理可得:22216cos2a c aPOFac+-∠=,又2cosaPOFc∠= 22262a c a aac c+-∴+=,故cea==【考点】双曲线几何性质、余弦定理解三角形OF ECBAD12. 设0.2log 0.3a =,2log 0.3b =,则( )A .0a b ab +<<B .0ab a b <+<C .0a b ab +<<D .0ab a b <<+ 【答案】B【解析】首先由0.2log y x =单调递减可知0.20.20.20log 1log 0.3log 0.21a =<=<=,同理可知21b -<<-,0,0a b ab ∴+<<,排除C 、D 其次:利用作商法:0.30.30.311log 0.2log 2log 0.41a b ab a b+=+=+=<(注意到0ab <) a b ab ∴+>【考点】利用对数函数单调性确定对数范围、作商法比较大小 二、填空题:本大题共4小题,每小题5分,共20分13. 已知向量()1,2a = ,()2,2b =- ,()1,c λ=. 若()//2c a b + ,则_______.λ= 【答案】12【解析】()24,2a b +=,故24λ=【考点】向量平行的坐标运算14. 曲线()1xy ax e =+在点()0,1处的切线斜率为2-,则______.a =【答案】3-【解析】()'1x xy ae ax e =++,12k a ∴=+=-【考点】切线斜率的计算方法15.函数()cos 36f x x π⎛⎫=+ ⎪⎝⎭在[]0,π的零点个数为_________.【答案】3【解析】[]0,x π∈,3,3666t x ππππ⎡⎤=+∈+⎢⎥⎣⎦,由cos y t =图像可知,当35,,222t πππ=时cos 0t =,即()f x 有三个零点 或者:令362x k πππ+=+,则93k x ππ=+,当0,1,2k =时,[]0,x π∈,故3个零点【考点】换元法(整体法)、余弦函数的图像与性质16. 已知点()1,1M -和抛物线2:4C y x =,过C 的焦点且斜率为k 的直线与抛物线交于,A B 两点,若90AMB ∠= ,则_______.k =【答案】2 【解析】(1) 常规解法:设直线方程为1x my =+,联立214x my y x=+⎧⎨=⎩可求121244y y m y y +=⎧⎨=-⎩,由()()12121212110MB MA y y y y x x x x ⋅=-++++++= ,可得12m =,故2k =(2) 二级结论:以焦点弦为直径的圆与准线相切设AB 中点为N ,则由二级结论可知NM ⊥准线,1N M y y ∴==,故22A B N y y y +==,由点差法可得,42A B k y y ==+ 进一步可得二级结论:AB M k y p ⋅=【考点】直线与抛物线联立(二级结论、点差法)三.解答题:共70分. 解答应写出文字说明,证明过程或演算步骤.. 第17~21题为必考题,每个试题考生必须作答. 第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17. (12分)等比数列{}n a 中,1531,4a a a ==. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和. 若63m S =,求m . 【答案】(1)12n n a -=或()12n n a -=-;(2)6m =【解析】(1)25334a a a q ==,2q ∴=±,∴12n n a -=或()12n n a -=-(2) 当2q =时,()()112631mmS -==-,解得6m =当2q =-时,()()112633mm S --==,得()2188m-=-无解综上:6m =【考点】等比数列通项公式与前n 项和公式 18. (12分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式. 为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人. 第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:第一种生产方式第二种生产方式8655689 9 7 627012234 5 6 6 89 8 7 7 6 5 4 3 3281445 2 11 009(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过m 和不超过m 的工人数填入下面的列联表:超过m不超过m第一种生产方式 第二种生产方式(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:()()()()()22n ad bc K a b c d a c b d -=++++,()2P K k ≥ 0.0500.010 0.001k3.8416.63510.828【答案】(1)第二组生产方式效率更高;(2)见解析;(3)有;【解析】(1)第二组生产方式效率更高;从茎叶图观察可知,第二组数据集中在70min~80min 之间,而第一组数据集中在80min~90min 之间,故可估计第二组的数据平均值要小于第一组数据平均值,事实上168727677798283838485868787888990909191928420E +++++++++++++++++++==同理274.7E =,21E E < ,故第二组生产方式效率更高 (2)由茎叶图可知,中位数7981802m +==,且列联表为:超过m 不超过m第一种生产方式15 5 第二种生产方式515(3)由(2)可知()22224015510 6.63520202020K -==>⨯⨯⨯,故有99%的把握认为两种生产方式的效率有差异 【考点】茎叶图、均值及其意义、中位数、独立性检验 19.(12分)如图,边长为2的正方形ABCD 所在的平面与半圆弧 CD所在的平面垂直,M 是CD 上异于,C D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC -体积的最大时,求面MAB 与面MCD 所成二面角的正弦值.【答案】(1)见解析; 【解析】(1)ABCD CDM BC DCM BC DM DM BMC ADN BMC BC CD MC DM ⎫⊥⎫⇒⊥⇒⊥⎬⎪⇒⊥⇒⊥⊥⎬⎭⎪⊥⎭(这边只给出了证明的逻辑结构,方便大家阅读,考试还需要写一些具体的内容)(2)ABC S ∆ 恒定,故要使M ABC V -最大,则M ABC d -最大,结合图象可知M 为弧 CD中点时,M ABC V -最大. 此时取CD 的中点O ,则MO DC ⊥,故MO ⊥面ABCD ,故可建立如图所示空间直角坐标系 则:()0,0,1M ,()2,1,0A -,()2,1,0B ,()0,1,0C ,()0,1,0D -MBCDA()()0,2,0,2,1,1AB MA ==--,∴平面MAB 的法向量为()11,0,2n = ,易知平面MCD 的法向量为()21,0,0n =,故12cos ,5n n <>== , ∴面MAB 与面MCD【考点】面面垂直的判定、三棱锥体积最值、二面角的求法 20. (12分)已知斜率为k 的直线l 与椭圆22:143x y C +=交于,A B 两点,线段AB 的中点为()()1,0M m m >.(1)证明:12k <-; (2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=. 证明,,FA FP FB 成等差数列,并求该数列的公差. 【答案】(1)见解析;(2)28d =±【解析】(1) 点差法:设()()1122,,,A x y B x y ,则22112222143143x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩相减化简可得: 1212121234y y y y x x x x -+⋅=--+,34OM AB k k ⋅=-(此公式可以作为点差法的二级结论在选填题中直接用),34m k ∴=-,易知中点M 在椭圆内,21143m +<,代入可得12k <-或12k >,又0m >,0k ∴<,综上12k <-联立法:设直线方程为y kx n =+,且()()1122,,,A x y B x y ,联立22143x y y kx n⎧⎪+=⎨⎪=+⎩可得,()2224384120k x knx n +++-=,则122212284341243kn x x k n x x k -⎧+=⎪⎪+⎨-⎪=⎪+⎩,()121226243ny y k x x n k +=++=+224143343M M kn x k n y m k -⎧==⎪⎪+∴⎨⎪==⎪+⎩,两式相除可得34m k =-,后续过程和点差法一样(如果用∆算的话比较麻烦)(2) 0FP FA FB ++= ,20FP FM ∴+= ,即()1,2P m -,214143m ∴+=,()304m m ∴=>∴71,4k n m k =-=-=,由(1)得联立后方程为2171404x x -+=,1,2114x ∴=±, ()22121223c a c a cFA FB x x a x x a c a c a ⎛⎫⎛⎫∴+=-+-=-+= ⎪ ⎪⎝⎭⎝⎭(此处用了椭圆的第二定义,否则需要硬算,计算量太大)而32FP =2FA FB FP ∴+=故,,FA FP FB成等差数列.221212214c a c a c d FA FB x x x x a c a c a ⎛⎫⎛⎫=±-=±---=±-=± ⎪ ⎪⎝⎭⎝⎭28d ∴=±【考点】点差法、直线与椭圆联立求解、等差数列、椭圆的第二定义21. (12分)已知函数()()()22ln 12f x x ax x x =+++-.(1)若0a =,证明:当10x -<<时,()0f x <;当0x >,()0f x >; (2)若0x =是()f x 的极大值点,求a . 【答案】(1)见解析;(2)16a =-【解析】(1)常规方法:当0a =时,()()()()2ln 121f x x x x x =++->-,()()1'ln 111f x x x∴=++-+ ()()2''1xf x x ∴=+,当10x -<<时,()''0f x <;当0x >时,()''0f x >()'f x ∴在()1,0-上单调递减,在()0,+∞上单调递增,而()'00f =, ∴()'0f x ≥恒成立,()f x ∴单调递增,又()00f = ∴当10x -<<时,()0f x <;当0x >,()0f x >改进方法:若0a =,则()()()()()22ln 122ln 12x f x x x x x x x ⎡⎤=++-=++-⎢⎥+⎣⎦令()()2ln 12x g x x x =+-+,则()()()()22214'01212x g x x x x x =-=>++++ 所以()g x 在()0,+∞单增,又因为()00g = 故当10x -<<时,()()00g x g <=,即()0f x <; 当0x >时,()()00g x g >=,即()0f x >;方法对比:若直接求导,那么完全处理掉对数经常需要二次求导,而方法二提出()2x +之后对数单独存在,一次求导就可消掉对数(2) 方法一:极大值点的第二充要条件:已知函数y =()f x 在0x x =处各阶导数都存在且连续,0x x =是函数的极大值点的一个充要条件为前21n -阶导数等于0,第2n 阶导数小于0()()()22ln 12f x x ax x x =+++-()()()21'21ln 111ax f x ax x x +∴=+++-+,()'00f ∴=()()()2234''2ln 11ax ax xf x a x x ++∴=+++,()''00f ∴=()()232661'''1ax ax x a f x x +-++∴=+0x =是()f x 的极大值点,()'''0610f a ∴=+=,16a ∴=-,下证:当16a =-时,0x =是()f x 的极大值点,()()()3163'''1x x f x x -+=+,所以()''f x 在()1,0-单增,在()0,+∞单减 进而有()()''''00f x f ≤=,从而()'f x 在()1,-+∞单减,当()1,0x ∈-时,()()''00f x f >=,当()0,x ∈+∞时,()()''00f x f <= 从而()f x 在()1,0-单增,在()0,+∞单减,所以0x =是()f x 的极大值点.方法二: 0x =是()f x 的极大值点,所以存在0δ>,使得在()(),00,δδ- ,()()00f x f <=,即()()22ln 120x ax x x +++-<当()0,x δ∈时,()ln 10x +>,故()()()()2222ln 122ln 1ln 1xx x x x x a x x x +--+-++<=+,当(),0x δ∈-时,()ln 10x +<,故()()()222ln 1ln 1x x x a x x -++>+即()()()()()()()()()()()22000022ln 11ln 1limlimln 121ln 11ln 111lim lim 42642ln 144ln 141x x x x x x x x x x a x x x x x x x x x x x x x x →→→→-++-++==++++--++===-++++++++(洛必达法则,极限思想)【考点】导数的应用(二)选考题:共10分,请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.22. 选修44-:坐标系与参数方程(10分)在平面直角坐标系xOy 中,O 的参数方程为cos sin x y θθ=⎧⎨=⎩(θ为参数),过点(0,且倾斜角为α的直线l 与O 交于,A B 两点.(1) 求α的取值范围;(2) 求AB 中点P 的轨迹的参数方程.【答案】(1)3,44ππα⎛⎫∈ ⎪⎝⎭;(2)23,,44222x y αππαα⎧=⎛⎫⎪⎛⎫∈⎨ ⎪ ⎪⎝⎭⎝⎭=-⎪⎩【解析】(1)当2πα=时,直线:0l x =,符合题意;当2πα≠时,设直线:l y kx =-1d =<,即()(),11,k ∈-∞-+∞ ,又tan k α=,3,,4224ππππα⎛⎫⎛⎫∴∈ ⎪ ⎪⎝⎭⎝⎭综上,3,44ππα⎛⎫∈ ⎪⎝⎭(2)可设直线参数方程为cos 3,44sin x t y t αππαα=⎧⎛⎫⎪⎛⎫∈⎨ ⎪ ⎪=+⎝⎭⎪⎝⎭⎩,代入圆的方程可得:2sin 10t α-+=122P t t t α+∴==cos 3,44sin x y ααππααα⎧=⎛⎫⎪⎛⎫∈⎨ ⎪ ⎪⎝⎭⎝⎭=+⎪⎩即点P的轨迹的参数方程为23sin 2,,244x y ππααα⎧⎛⎫=⎪⎛⎫∈⎨⎪ ⎪⎝⎭⎝⎭⎪=⎩(也可以设直线的普通方程联立去做,但是要注意讨论斜率不存在的情况) 【考点】参数方程、直线的斜率,轨迹方程23. 选修45-:不等式选讲(10分)已知函数()211f x x x =++-. (1)画出()y f x =的图像;(2)当[)0,x ∈+∞时,()f x ax b ≤+,求a b +的最小值. 【答案】(1)见解析;(2)5【解析】(1)()13,212,123,1x x f x x x x x ⎧-<-⎪⎪⎪=+-≤≤⎨⎪>⎪⎪⎩,图象如下(2)由题意得,当0x ≥时,ax b +的图象始终在()f x 图象的上方,结合(1)中图象可知,3,2a b ≥≥,当3,2a b ==时,a b +最小,最小值为5, 【考点】零点分段求解析式、用函数图象解决恒成立问题xy21.531-0.5O。
电子科技大学 18秋《高等数学(文科专科)》在线作业2满分答案

枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:D
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:B
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:D
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:D
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:B
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
1
A.A
B.B
C.C
D.D
淏 湘偶:A
1
A.A
B.B
C.C
D.D
淏 湘偶:C
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:B
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:C
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
1
A.A
B.B
C.C
D.D
淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:C
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:B
枙醱獗芞
A.A
B.B
C.C
D.D
2018年高考理科数学全国卷3(含答案与解析)
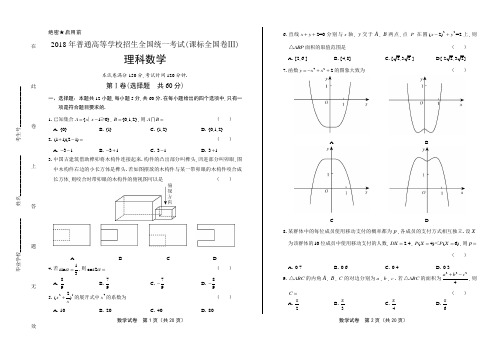
数学试卷 第1页(共20页) 数学试卷 第2页(共20页)绝密★启用前2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理科数学本试卷满分150分,考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{10}A x x =-∣≥,{0,1,2}B =,则A B = ( )A .{0}B .{1}C .{1,2}D .{0,1,2} 2.()(1i 2i)+-=( )A .3i --B .3i -+C .3i -D .3i +3.中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )ABC D 4.若1sin 3α=,则cos2α=( )A .89B .79C .79- D .89- 5.252()x x+的展开式中4x 的系数为( )A .10B .20C .40D .806.直线2=0x y ++分别与x 轴,y 交于A ,B 两点,点P 在圆22(2)=2x y -+上,则ABP △面积的取值范围是( )A .[2,6 ]B .[4,8]C .[2,3 2 ]D [ 22,32] 7.函数422y x x =-++的图象大致为( )ABCD8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数, 2.4DX =,()6(4)P X P X ==<,则p =( )A .0.7B .0.6C .0.4D .0.39.ABC △的内角A ,B ,C 的对边分别为a ,b ,c .若ABC △的面积为2224a b c +-,则C = ( )A .π2B .π3C .π4D .π6毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共20页) 数学试卷 第4页(共20页)10.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为( )A .123B .183C .243D .54311.设1F ,2F 是双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若1||6||PF OP =,则C 的离心率为 ( )A .5B .2C .3D .2 12.设0.2log 0.3a =,2log 0.3b =,则( )A .0a b ab +<<B .ab a b +<<0C .0a b ab +<<D .0ab a b +<<第Ⅱ卷(非选择题 共90分)二、填空题:本题共4小题,每小题5分,共20分.13.已知向量2)(1,=a ,)2(2,=-b ,),(1λ=c .若2()+∥c a b ,则=λ . 14.曲线)e (1xy ax =+在点(0,1)处的切线的斜率为2-,则a = .15函数π()cos(3)6f x x =+在[0,π]的零点个数为 .16.已知点1()1,M -和抛物线C :²4y x =,过C 的焦点且斜率为k 的直线与C 交于A ,B 两点.若90AMB ∠=,则k = .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.) (一)必考题:共60分. 17.(12分)等比数列{}n a 中,11a =,534a a =. (1)求{}n a 的通项公式;(2)记n S 为{}n a 的前n 项和.若63m S =,求m .18.(12分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min )绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高,并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过超过m不超过m第一种生产方式 第二种生产方式(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:22()(a b)(c d)(a c)(b d)n ad bc K -=++++,2()P K k ≥0.050 0.010 0.001k3.841 6.635 10.828数学试卷 第5页(共20页) 数学试卷 第6页(共20页)19.(12分)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)当三棱锥M ABC -体积最大时,求面MAB 与面MCD 所成二面角的正弦值.20.(12分)已知斜率为k 的直线l 与椭圆C :22143x y +=交于A ,B 两点,线段AB 的中点为(1,)()M m m >0.(1)证明:12k <-;(2)设F 为C 的右焦点,P 为C 上一点,且0FP FA FB ++=.证明:FA ,FP ,FB成等差数列,并求该数列的公差. 21.(12分)已知函数22()()ln(1)2f x a x x x x +=-++.(1)若0a =,证明:当10x -<<时,()0f x <;当0x >时,()0f x >; (2)若=0x 是()f x 的极大值点,求a .(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4—4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,O 的参数方程为cos ,sin x y θθ=⎧⎨=⎩(θ为参数),过点(0,2)且倾斜角为α的直线l 与O 交于A ,B 两点. (1)求α的取值范围;(2)求AB 中点P 的轨迹的参数方程.23.[选修4—5:不等式选讲](10分) 设函数()211f x x x =++-. (1)画出() y f x =的图象;(2)当[ 0),x ∈+∞,()b x f ax +≤,求a b +的最小值.-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共20页) 数学试卷 第8页(共20页)2018年普通高等学校招生全国统一考试(课标全国卷Ⅲ)理科数学答案解析第Ⅰ卷一、选择题 1.【答案】C【解析】∵={1}A x x |≥,{0,1,2}B =,∴={1,2}A B ,故选C .2.【答案】D【解析】21i 2i)(2i 2i i 3i )(+-=-+-=+,故选D . 3.【答案】A【解析】两个木构件咬合成长方体时,小长方体(榫头)完全嵌入带卯眼的木构件,易知俯视图可以为A .故选A . 4.【答案】B 【解析】由1sin 3α=,得22127cos212sin 12()=1=399αα=-=-⨯-.故选B .5.【答案】C【解析】252()x x+的展开式的通项251103155()(2)2r r r r r r r T C x x C x ---+==,令1034r -=,得2r =,所以4x 的系数为225240C ⨯=.故选C . 6.【答案】A【解析】由圆22(2)=2x y -+可得圆心坐标(2,0),半径r =ABP △的面积记为S ,点P 到直线AB 的距离记为d ,则有12S AB d =.易知AB =maxd ==min d =所以26S ≤≤,故选A .7.【答案】D【解析】∵42()2f x x x =-++,∴3()42f x x x '=-+,令()0f x '>,解得x <或x 0<此时,()f x 递增;令()0f x '<,解得x <0或x ,此时,()f x 递减.由此可得()f x 的大致图象.故选D . 8.【答案】B【解析】由题知~1()0,X B p ,则(101 2.4)DX p p =⨯⨯-=,解得0.4p =或0.6.又∵()6(4)P X P X ==<,即446664221010(1)(1)(1)0.5C P p C P p p p p --⇒-⇒<<>,∴0.6p =,故选B .9.【答案】C【解析】根据余弦定理得2222cos a b c ab C +-=,因为2224ABCa Sbc +-=△,所以c 42os ABC ab C S =△,又1sin 2ABC S ab C =△,所以tan 1C =,因为π()0,C ∈,所以4C π=.故选C .10.【答案】B【解析】设ABC △的边长为a ,则1sin60=932ABC S a a =△,解得6a =(负值舍去).ABC △的外接圆半径r 满足62sin60r=,得r =球心到平面ABC 的距离为2=.所以点D 到平面ABC 的最大距离为246+=,所以三棱锥DABC -体积的最大值为163⨯=故选B .11.【答案】C【解析】点2(,0)F c 到渐近线b y x a =的距离2(0)PF b b ==>,而2OF c =,所以在2Rt OPF △中,由勾股定理可得OP a ,所以1PF ==.在2Rt OPF △中,222cos PF b PF O OF c∠==,在12F F P△中,2222222121221246cos 22PF F F PF b c a PF O PF F F b c+-+-∠==⋅⋅2,所以222222463464b b c a b c a c bc +-=⇒=-,则有22223()46c a c a -=-,解得c a=负值舍去),即e =.故选C .数学试卷 第9页(共20页) 数学试卷 第10页(共20页)12.【答案】B【解析】解法一:∵0.20.2log 0.3log 1=0a =>,22log 0.3log 1=0b =<,∴0ab <,排除C . ∵0.20.20log 0.3log 0.2=1<<,22log 0.3log 0.5=1-<,即01a <<,1b <-,∴0a b +<,排除D .∵220.2log 0.3lg0.2log 0.2log 0.3lg 2b a ===,∴2223log 0.3log 0.2log 12b b a -=-=<,∴1bb ab a b a+⇒+<<,排除A .故选B . 解法二:易知01a <<,1b -<,∴0ab <,0a b +<,∵0.30.30.311log 0.2log 2log 0.41a b +=+=<, 即1a b ab+<,∴a b ab +>,∴0ab a b +<<.故选B .第Ⅱ卷二、填空题13.【答案】12【解析】由已知得2(4,2)+=a b .又,()1c λ=,2()+∥c a b ,所以42=0λ-,解得12λ=. 14.【答案】3-【解析】设(e ))1(xf x ax =+,则()()1e xf x ax a '=++,所以曲线在点(0,1)处的切线的斜率(0)12k f a '==+=-,解得3a =-. 15.【答案】3【解析】令()0f x =,得πcos(3)6x +,解得ππ+()39k x k =∈Z .当0k =时,π9x =;当1k =时,4π9x =;当2k =时,7π9x =,又[ 0,π]x ∈,所以满足要求的零点有3个.16.【答案】2【解析】解法一:由题意可知C 的焦点坐标为(1,0),所以过焦点(1,0),斜率为k 的直线方程为1y x k =+,设111,y A y k ⎛⎫+ ⎪⎝⎭,221,y B y k ⎛⎫+ ⎪⎝⎭,将直线方程与抛物线方程联立得21,4,y x k y x ⎧=+⎪⎨⎪=⎩整理得2440y y k --=,从而得124y y k +=,124y y =-.∵1()1,M -,90AMB ∠=,∴0MA MB =,即1212(2)(2)(1)(1)0y yy y k k+++--=,即2440k k -+=,解得2k =.解法二:设11A(,)x y ,22(),B x y ,则2112224,4,y x y x ⎧=⎨=⎩①②②-①得2221214()y y x x -=-,从而2121124y y x x k y y --+==.设AB 的中点为M ',连接MM '.∵直线AB 过抛物线24y x =的焦点,∴以线段AB 为直径的M '⊙与准线:1l x =-相切.∵1()1,M -,90AMB ∠=,∴点M 在准线:1l x =-上,同时在M '⊙上,∴准线l 是M '⊙的切线,切点M ,且MM l '⊥,即MM '与x 轴平行,∴点M '的纵坐标为1,即1212221y y y y =⇒++=,故124422y y k =+==. 故答案为:2. 三、解答题17.【答案】(1)解:设{}n a 的公比为q ,由题设得1n n a q -=.由已知得424q q =,解得0q =(舍去)或2q =-或2q =. 故1(2)n n a -=-或12n n a -=. (2)若1(2)n n a -=-,则1(2)3nn S --=.数学试卷 第11页(共20页) 数学试卷 第12页(共20页)由63m S =得(2)188m -=-.此方程没有正整数解.若12n n a -=,则21n n S =-.由63m S =得264m =,解得6m =. 综上,6m =.【解析】(1)解:设{}n a 的公比为q ,由题设得1n n a q-=.由已知得424q q =,解得0q =(舍去)或2q =-或2q =. 故1(2)n n a -=-或12n n a -=.(2)若1(2)n n a -=-,则1(2)3n n S --=.由63m S =得(2)188m -=-。
电子科技大学 18秋《高等数学(文科专科)》在线作业1满分答案

淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:C
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:B
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:D
A.A
B.B
C.C
D.D
淏 湘偶:D
1
A.A
B.B
C.C
D.D
淏 湘偶:C
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:C
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:D
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:D
1
A.A
B.B
C.C
D.D
淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:D
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:B
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
枙醱獗芞
A.A
B.B
C.C
D.D
淏 湘偶:A
1
A.A
B.B
C.C
D.D
淏 湘偶:B
1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业提交 3
1. 函数 (A) 的单调减少区间为( ) (B) (C) (D)
[参考答案:A] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
2. 函数 (A) -1 在区间[-2,2]上的最大值点是 (B) -2 (C) 2 ( ) (D) 1
[参考答案:D] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
3. 曲线 在点 (A) -4 的切线斜率 (B) 2 (C) 4 ( ) (D) -2
[参考答案:C] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
4. 函数 在 (A) 不单调 内是( ) (B) 不连续 (C) 单调增加 (D) 单调减少
[参考答案:D] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
5. 极限 ( )
(A) 1
(B) 3
(C) -3
(D) -1
[参考答案:B] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
6. 函数 (A) 单调增加 [参考答案:C] 分值:5 得分:
5
在区间 (B) 不连续
内是( ) (C) 不单调 (D) 单调减少
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
7. 函数 在 (A) 不单调 内是( ) (B) 单调减少 (C) 单调增加 (D) 不连续
[参考答案:B] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
8. 曲线 (A) 的拐点为( ) (B) (C) (D)
[参考答案:B] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
9. 函数 (A) 5 在 (B) 2 上最大值为( ) (C) -1 (D) 7
[参考答案:A] 分值:5
得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
10. 曲线 (A) 2 在点 (B) -1 处的切线斜率 (C) 1 ( ) (D) -2
[参考答案:D] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
11. 函数 (A) 0 在区间 (B) -1 上的最小值为 ( ) (C) 2 (D) 1
[参考答案:A] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
12. 曲值反映的是函数的( ) (A) 连续性质 [参考答案:D] 分值:5 得分:
5
(B) 凹凸性质
(C) 单调性质
(D) 局部性质
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
13. 设 (A) 单增且凸 [参考答案:B] 分值:5 得分:
5
,则曲线 (B) 单减且凹
在区间 (C) 单减且凸
内沿 x 轴正向( ) (D) 单增且凹
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
14. 函数 (A) 单调增加区间是( ) (B) (C) (D)
[参考答案:D] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
15. 函数 (A) 的单调减少区间为( ) (B) (C) (D)
[参考答案:D] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
16. 极线 (A) 不存在 的凹区间是( ) (B) (C) (D)
[参考答案:B] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
17. 函数 (A) 0 在区间 (B) -1 上的最小值点是 (C) 2 ( ) (D) 1
[参考答案:B] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
18. 曲线 (A) 在点 处切线方程为( ) (B) (C) (D)
[参考答案:A] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
19. 极限 (A) 1 ( ) (B) (C) (D) 2
[参考答案:D] 分值:5 得分:
5
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
20. 函数 (A) 单调增加 [参考答案:C] 分值:5 得分:
5
在
内是( ) (B) 不单调 (C) 单调减少 (D) 不连续
分
系统自动批改于 2017 年 6 月 13 日 11 点 33 分
。
