方差分析对应的非参检验
非参数检验课件

13.71
5
19.61
24.37
4.76
6
14.50
92.75
78.25
7
49.63
121.57
71.94
8
44.56
89.76
45.20
编秩次,求秩和 去掉d=0的对子,总的对子数也要相应减去; 用绝对值︱d︳编秩次,如果出现绝对值相等时(ties) ,则将它们的平均秩次值作为他们的秩次;
第二节 单样本资料的符号秩和检验
• 目的:推断样本中位数与已知总体中位数 (常为标准值或大量观察的稳定值)有无 差别,常用于不满足单样本t检验应用条 件的资料;其检验假设是M=M0.
• 例10-2 已知某地正常人尿氟含量的中位 数为2.15mmol/L.今在该地某厂随机抽取 12名工人,测得尿氟含量,结果见表2。 问该工厂的尿氟含量是否高于当地正常人 ?
参数检验方法
• t检验 两独立样本t检验要求:正态、方差相等、个体独立 配对t检验要求:差值正态、个体独立
• 方差分析 完全随机设计方差分析要求:正态、方差相等、个体独 立
参数检验方法
• 两组性别结构是否相同?
• 两组某种不良反应的发生率是否相同?
• 多组发生率是否相同? • 多组构成是否相同?
定性无序分 类资料
未解决的问题
• 疗效用痊愈、显效、有效、无效四级分类法进行 评价时,两组或多组如何比较?
• 对两组患者空腹胰岛素水平进行比较时,有的病 例测量结果为Ins<2.0 或Ins>300,如何处理?
未解决的问题
• 对应于多分类变量(有序) • 非正态分布 • 不完整数据:如,Ins<2.0 或Ins>300 • 正态分布但方差不相等时
多样本比较方差分析与非参数方法的公式整理

多样本比较方差分析与非参数方法的公式整理方差分析是一种常用的统计方法,用于比较多个样本之间的平均值差异。
在实际应用中,我们常常需要比较多个样本的方差,以确定它们之间是否存在显著的差异。
本文将介绍多样本比较方差分析的公式整理,并对非参数方法进行概述。
一、多样本比较方差分析多样本比较方差分析是一种常用的统计方法,用于比较多个样本的方差是否存在显著差异。
通常情况下,我们希望通过方差分析来确定样本所属的总体是否有明显的差异。
方差分析的基本假设是各组样本都来自于具有相同方差的总体,也就是说,样本之间的差异只是由于随机误差引起的。
我们可以使用方差分析来检验各组均值之间是否存在显著差异,进而判断它们所属的总体是否有明显不同。
多样本比较方差分析的公式如下所示:H0:各组均值之间没有显著差异H1:各组均值之间存在显著差异计算公式为:F = (SSB / (m-1)) / (SSE / (n-m))其中,SSB表示因组别引起的平方和,m表示组别的个数;SSE表示由于误差引起的平方和,n表示总样本数。
二、非参数方法除了上述介绍的多样本比较方差分析,还存在一种非参数方法,用于比较多个样本的位置参数差异。
与方差分析不同,非参数方法对于数据的分布不作要求,更加灵活。
下面列举一些常用的非参数方法:1. Mann-Whitney U检验Mann-Whitney U检验是一种用于比较两个独立样本的非参数方法。
它的基本思想是将两个样本的所有观测值进行合并,然后对合并后的观测值进行排序,并计算两个样本的秩和。
通过比较秩和的大小,可以得出两个样本的位置差异是否显著。
2. Kruskal-Wallis H检验Kruskal-Wallis H检验是一种用于比较多个独立样本的非参数方法。
它的基本思想是将所有样本的观测值进行合并,然后对合并后的观测值进行排序,并计算各组的秩和。
通过比较秩和的大小,可以得出各组样本的位置差异是否显著。
3. Friedman检验Friedman检验是一种用于比较多个相关样本的非参数方法。
ancova(协方差分析)非参数和随机方法

第7章ANCOV A(协方差分析):非参数和随机方法Peter S. PetraitisSteven J. BeaupreArthur E. Dunham7.1生态学问题生态学参数往往不能满足参数假定的要求。
当这种情况发生时,随机方法是更常用的参数方法,比如协方差分析(ANCOV A)和回归分析的一个很好的替代选择。
使用随机方法很简单,并且由于标准参数ANCOV A为生态学家所熟知,我们用它来激发对非参数和随机方法的优点和存在问题的讨论。
我们通过对检验随机和非参数方法分析性别和生境影响响尾蛇种群的个体大小来进行讨论,年龄在这里被作为一个混淆(confounding)因素考虑。
个体大小的变异常见于许多动物中(即, 无脊椎动物: Paine 1976; Lynch1977; Sebens 1982; Holomuzki 1989; 两栖动物: Nevo 1973; Berven1982;Bruce和Hairson 1990; 有鳞的爬行动物:Tinkle 1972;Dunham 1982; Schwaner 1985; Dunham等1989; 哺乳动物:Boyce 1978;Melton 1982; Ralls和Harvey 1985), 并且由于其与许多繁殖特征, 比如成熟年龄,子代个体的数量和大小,和亲代对子代的投入, 有协变关系,从而引起进化生态学家的极大兴趣,(Stearns 1992; Roff 180, 1992)。
对个体大小变异的解释包括资源的季节性,质量和可利用性(如,Case 1978; Palmer 1984; Schwaner和Sarre 1988), 基于个体大小的捕食性(Paine 1976), 种群密度(Sigurjonsdottir 1984), 特性替代(Huey和Pianka 1974; Huey 等1974)和生长速率的渐变变异(Roff 1980)。
然而个体大小的地理变异可能常由于个体大小决定的生长速率和种群年龄结构的相互作用所致。
ancova(协方差分析)非参数和随机方法

第7章ANCOV A(协方差分析):非参数和随机方法Peter S. PetraitisSteven J. BeaupreArthur E. Dunham7.1生态学问题生态学参数往往不能满足参数假定的要求。
当这种情况发生时,随机方法是更常用的参数方法,比如协方差分析(ANCOV A)和回归分析的一个很好的替代选择。
使用随机方法很简单,并且由于标准参数ANCOV A为生态学家所熟知,我们用它来激发对非参数和随机方法的优点和存在问题的讨论。
我们通过对检验随机和非参数方法分析性别和生境影响响尾蛇种群的个体大小来进行讨论,年龄在这里被作为一个混淆(confounding)因素考虑。
个体大小的变异常见于许多动物中(即, 无脊椎动物: Paine 1976; Lynch1977; Sebens 1982; Holomuzki 1989; 两栖动物: Nevo 1973; Berven1982;Bruce和Hairson 1990; 有鳞的爬行动物:Tinkle 1972;Dunham 1982; Schwaner 1985; Dunham等1989; 哺乳动物:Boyce 1978;Melton 1982; Ralls和Harvey 1985), 并且由于其与许多繁殖特征, 比如成熟年龄,子代个体的数量和大小,和亲代对子代的投入, 有协变关系,从而引起进化生态学家的极大兴趣,(Stearns 1992; Roff 180, 1992)。
对个体大小变异的解释包括资源的季节性,质量和可利用性(如,Case 1978; Palmer 1984; Schwaner和Sarre 1988), 基于个体大小的捕食性(Paine 1976), 种群密度(Sigurjonsdottir 1984), 特性替代(Huey和Pianka 1974; Huey 等1974)和生长速率的渐变变异(Roff 1980)。
然而个体大小的地理变异可能常由于个体大小决定的生长速率和种群年龄结构的相互作用所致。
非参数检验

非参数检验的概念
非参数检验又称为任意(不拘) 非参数检验又称为任意(不拘)分布检验 distributiontest), ),这类方法 (distribution-free test),这类方法并不依赖总
非 参 数 检 验
体分布的具体形式,应用时可以不考虑研究变量 体分布的具体形式, 为何种分布以及分布是否已知,进行的是分布之 为何种分布以及分布是否已知, 间而不是参数之间的检验,故又称非参数检验
参数检验的特点
分析目的:对总体参数(µ π)进行估计或检验。 进行估计或检验。 分析目的:对总体参数(
非 参 数 检 验
分布:要求总体分布已知, 分布:要求总体分布已知,如:
•连续性资料——正态分布 连续性资料——正态分布 •计 数 资 料——二项分布、POISSON分布等 ——二项分布 POISSON分布等 二项分布、
序号 (1) 1 2 3 4 5 6 7 8 9 10 11 12
数据 (2) 39 42 45 43 52 45 22 48 40 45 40 49
排秩 ( 3)
非 参 数 检 验
非 参 数 检 验
疗效
A组 (1 ) 15 11 20 8
B组 (2 ) 12 3 7 4
排秩
平均秩次
控制 显效 有效 近控
参数检验方法的局限
非 参 数 检 验
t检验 成组t 成组t检验要求:正态、方差相等、个体独立 配对t 配对t检验要求:差值正态、个体独立 方差分析 单因素多水平比较方差分析要求:正态、方差 相等、个体独立 多个分析因素时方差分析要求:分布、方差、 个体独立性
定性无序分类资料
非 参 数 检 验
两组性别结构是否相同? 两组某种不良反应的发生率是否相同? 多组发生率是否相同? 多组构成是否相同?
非参数检验的统计值符号

非参数检验的统计值符号
非参数检验是一种统计方法,用于在不假设数据来自特定分布的情况下,比较两组或多组数据的差异。
非参数检验通常包括秩和检验(如Mann-Whitney U检验和Wilcoxon符号秩检验)以及基于秩次的方差分析(如Kruskal-Wallis检验)。
在这些非参数检验中,通常不会计算像t检验或方差分析中的p值或F值这样的统计值。
相反,它们通常使用基于秩次的统计量,如U值、W值、H值等。
这些统计量通常用于查找临界值或计算p值,以判断观察到的效应是否显著。
以下是一些常见的非参数检验及其相关的统计量:
1. Mann-Whitney U检验:计算U值,该值表示在合并的两组数据中,一个组中的观察值在另一个组中的观察值之前的数量。
U值用于查找临界值或计算p值。
2. Wilcoxon符号秩检验:计算W值,该值表示在单个样本中,正秩和与负秩和的最小值。
W值用于查找临界值或计算p值。
3. Kruskal-Wallis检验:计算H值,该值是基于每个组秩和的平方和。
H值用于查找临界值或计算p值。
请注意,具体的统计值和符号可能因不同的统计软件或文献而略有不同。
因此,在解释非参数检验的结果时,重要的是查阅所使用的软件或方法的文档,以了解如何解释相关的统计值。
方差分析与非参数检验

北京建筑大学理学院信息与计算科学专业实验报告课程名称《数据分析》实验名称方差分析与非参数检验实验地点基C-423 日期2017.3.30(1)熟悉数据的基本统计与非参数检验分析方法;(2)熟悉撰写数据分析报告的方法;(3)熟悉常用的数据分析软件SPSS。
【实验要求】根据各个题目的具体要求,完成实验报告。
【实验内容】1、附件给出某年房屋价格的相关数据,请选用恰当的分析方法,对影响房屋价格的因素进行分析。
(注意数据要调整成标准的格式,变量值、组别(字符变量转换成数值变量))(单因素方差分析选择其中两个因素、双因素方差分析选择其中任一对因素即可)2、附件给出管理才能评分的相关数据,请选用恰当的分析方法,分析该评分数据是否服从正态分布。
3、附件给出了某体育比赛的两位裁判打分数据,请选用恰当的分析方法,检验该两组评分分布是否有显著差异。
(注意数据要调整成标准的格式,变量值、组别)4、附件给出了减肥茶数据,请选用恰当方法分析,检验该减肥茶是否对减肥有显著效果。
(注意数据要调整成标准的格式,变量值、组别)【分析报告】1、对影响房屋价格的因素进行分析。
(单因素方差分析选择其中两个因素、双因素方差分析选择其中任一对因素即可)。
表1-1(a)装修状况对均价影响的单因素方差分析结果均价平方和df 均方 F 显著性组间79.180 1 79.180 62.408 .000组内230.914 182 1.269总数310.094 183表1-1(b)所在区县对均价影响单因素方差分析结果均价平方和df 均方 F 显著性组间91.919 3 30.640 25.279 .000组内218.174 180 1.212总数310.094 183表1-1(a)是装修状况对均价影响的单因素方差分析结果。
可以看到:观测变量均价的离差平方总和为310.094;如果仅考虑装修状况单个因素的影响,则均价总变差中,不同装修状况可解释的变差为79.180,抽样误差引起的变差为230.914,它们的方差分别为79.180和1.269,相除所得的F统计量的观测值为62.408,对应的概率P-值近似为0.如果显著性水平α为0.05,由于概率P-值小于显著性水平α,应拒绝原假设,认为不同装修状况对均价的平均值产生了显著影响,不同装修状况对均价的影响效应不全为0。
方差分析与非参数检验

方差分析与非参数检验方差分析和非参数检验是两种常见的统计分析方法,用于比较不同组之间的差异或关联。
本文将详细介绍方差分析和非参数检验的原理、应用场景以及各自的优缺点。
方差分析(Analysis of Variance,ANOVA)是一种用于比较多个组之间均值差异的统计方法。
它基于总体均值与组内个体的个体值之间的差异,将总方差拆分为组内方差和组间方差,通过比较组间与组内方差的大小来判断组间均值是否显著不同。
方差分析一般分为单因素方差分析和多因素方差分析两种类型。
单因素方差分析适用于只有一个自变量(即因素)的情况,用于比较不同水平的因素是否对因变量(即观测值)有显著影响。
多因素方差分析适用于有多个自变量(即因素)的情况,用于比较各个因素及其交互作用对因变量的影响。
方差分析的优点主要有以下几点:1.可以同时比较多个组之间的差异,提供了一种全面且有效的统计方法。
2.可以通过比较组间与组内方差来判断差异是否显著,更加客观。
3.可以用于不同水平的因素对因变量的影响程度排名,帮助进一步探究因素的影响机制。
然而,方差分析也存在一些限制:1.方差分析对数据满足正态分布和方差齐性的要求比较严格,如果数据不满足这些要求,结果可能不准确。
2.方差分析只能对均值差异进行比较,不能揭示具体的分布差异。
3.方差分析本身不能进行推断和预测,只能判断差异是否显著。
非参数检验(Nonparametric Test)是一种不依赖于总体分布的统计方法,适用于数据不满足正态分布或方差齐性的情况。
与方差分析不同,非参数检验基于样本的秩次或次序,通过比较统计量来判断组间差异是否显著。
非参数检验包括了多种方法,如Wilcoxon秩和检验、Mann-WhitneyU检验、Kruskal-Wallis H检验等。
它们在样本较小或数据不满足正态分布的情况下具有较高的灵活性和鲁棒性。
非参数检验的优点有以下几点:1.不依赖于总体分布的参数,对数据的要求较低,尤其适用于数据不满足正态分布的情况。
第九章 非参数检验

第九章非参数检验(医学统计之星)上次更新日期:非参数统计是统计分析的重要组成部分。
可是与之很不相称的是它的理论发展远远不及参数检验完善,因而比较完善的可供使用的方法也不多。
在SAS中,非参数统计主要由UNIVARIATE过程、MEANS过程和NPAR1WAY过程来实现,前两者在前面的章节中已经介绍,它们可以进行配对设计差值的符号秩和检验(WILCOXON配对法);后者是一个单因素的非参数方差分析过程,可进行成组设计的两样本(WILCOXON法)或多样本比较(KRUSKAL-WALLIS法)的秩和检验。
本章将主要介绍NPAR1WAY过程。
由于在理论上还有争议,作为权威性的统计软件,SAS不提供非参检验两两比较的方法。
据我所知,其余统计软件里也只有PEMS提供这一功能(因为她是医统·医百的配套软件,而非参两两比较是写入了该书的)。
如果你需要这一结果,那么恐怕只有手算了。
9.0.1 语法格式NPAR1WAY过程不能处理按频数输入的资料。
这意味着如果你的数据是以频数方式输入的,那么除非你将资料想办法转换成按例记录的资料,否则SAS 无法处理。
有的同学将“NPAR1WAY”打成了“NPARLWAY”,可以这样来记:“NPAR”即“非参”的英文缩写,“WAY”是维数,更明确的说是因素的意思,而“1WAY”就代表一个因素,合起来“NPAR1WAY”说的是“单因素的非参数检验”。
怎么样,明白这个过程在做什么了吧!9.0.2 语法说明【过程选项】NPAR1WAY过程常用的选项有:∙MISSING 将缺失值也用于统计分析∙ANOV A 同时进行方差分析∙MEDIAN 要求进行中位数检验∙NOPRINT 禁止统计结果在OUTPUT视窗内输出∙SA V AGE 要求对样本进行SA V AGE得分分析∙WILCOXON 要求进行WILCOXON秩和检验我们常用的秩和检验就是WILCOXON秩和检验,对于其它方法,有兴趣的读者可参阅有关统计书籍。
非参数检验卡方检验讲解

行总和 பைடு நூலகம்1=100 R2=80 T=180
C1=120
( f oij f eij )2 f eij
(58 66.7)2 (42 33.3)2 (62 53.3)2 (18 26.7)2 7.61 66.7 33.3 53.3 26.7
2 0.05 (1) 3.84
独立性检验
配合度检验
• 例1:某大学二年级的公共体育课是球类 课,根据自己的爱好,学生只需在篮球、 足球和排球三种课程中选择一种。据以 往的统计,选择这三种课程的学生人数 是相等的。今年开课前对90名学生进行 抽样调查,选择篮球的有39人,选择足 球的28人,选择排球的23人,那么,今 年学生对三种课程选择的人数比例与以 往不同?
df (行数-1) (列数-1) 1
2 2 0.05 (1)
拒绝零假设,即男女对公共场所禁烟的态度有显著差异。
四格表的简易算法
赞成 男 女 A 58 C 62 A+C=120 不赞成 B 42 D 18 B+D=60 A+B=100 C+D=80 N=A+B+C+D=180
N ( AD BC ) 7.61 ( A B)(C D)( A C )( B D)
• • •
类别数据的处理形态: 次数与百分比 类别数据的呈现: 次数分布表与列联表 类别数据的分析: 卡方检验与其它关联性 分析法
卡方检验的主要内容
•
•
配合度检验
– – – – 某一个变量是否与某个理论分布或总体分布相符合 检验的内容仅涉及一个变量,是一种单因子检验 同时检测两个类别变量﹙X与Y﹚之间的关系时,其 目的在于检测从样本得到的两个变量的观察值,是 否具有特殊的关联。 检测同一个样本的两个变量的关联情形
非参数检验-秩和检验-研-精选文档

-4.5
T+=15.5 T-=29.5
11
方法步骤:
1、建立检验假设,确定检验水准 H0:患者治疗前后白细胞总数差值的总体中 位数Md=0 H1:……差值的总体中位数Md≠0
α=0.05
12
2、计算检验统计量T值
(1)求差值
(2)编秩次:
按绝对值大小差值为Βιβλιοθήκη 舍去不计秩次相等取平均秩次
(3)求秩和:T+ T- (T++T- =n(n+1)/2)
(4)确定检验统计量T:(任取T+或T- )
13
3、确定P值,作出推断结论
根据T值( T+=15.5 或 T-=29.5 )查T 界值表(P282) 原则:如果T位于检验界值区间内,P>, 不拒绝H0;如果T位于检验界值区间外,
P,拒绝H0,接收H1
14
正态近似法:
n>25时,T分布近似正态分布可用正
4
非参数检验适用于:
非正态分布的资料 方差不齐的资料 等级资料 一端或两端有不确定数值(如>10.0、 <0.1等)的资料 分布不明的资料
5
非参数检验的优缺点:
优点:
适用范围广 对数据要求不严 方法简便、易于理解和掌握
缺点:
损失信息、检验效能低
符合条件 不符合条件 首选参数检验 非参数检验
第七章
非参数检验
(Nonparametric test)
1
检验方法的选择及应用条件:
t检验: u检验: 方差分析:
2
参数: 统计量: 参数检验:若样本所来自的总体分布 已知(如正态分布),对其总体参数 进行假设检验,则称为参数检验。
方差方程的 levene 检验

方差方程的 levene 检验引言方差分析是一种用于比较两个或多个样本差异是否显著的统计方法。
它在实验设计和数据分析中被广泛应用,特别是在处理多组数据时。
然而,方差分析最基本的假设是各个样本的方差相等。
如果方差不相等,就会对分析结果产生影响,因此需要进行方差齐性检验。
Levene 检验是一种常用的方差齐性检验方法。
它是由 Howard Levene 在1960年提出的,用于检验各组之间方差是否相等。
Levene 检验是一种非参数检验方法,因此不对数据的分布做出假设。
本文将详细介绍方差方程的 Levene 检验的原理、应用和计算方法。
方差方程的基本原理方差方程是统计学中的一种重要概念,它描述了变量之间的差异程度。
在方差方程中,方差是一个重要的衡量指标,用于度量数据的离散程度。
方差等于每个数据点与平均值的差的平方和除以数据点的个数。
在方差分析中,我们希望比较多个样本的均值是否相等,因此需要比较各个样本的方差是否相等。
方差方程的基本原理是根据样本的方差来推断总体的方差,从而进行统计推断。
通常,我们假设各个样本的方差相等(方差齐性假设)。
Levene 检验的原理Levene 检验是一种用于检验方差齐性假设的方法。
它的基本思想是比较各个样本的观察值与各组的均值之间的偏差。
如果偏差越大,说明样本的方差越大,方差齐性假设越不成立。
Levene 检验的原假设是各组的方差相等,备择假设是各组的方差不等。
Levene 检验有许多不同的实现方法,其中最常用的是基于绝对偏差的 Levene 检验和基于平方偏差的 Levene 检验。
两种方法的原理相似,只是计算过程中使用的偏差计算方式不同。
Levene 检验的应用Levene 检验可以用于许多不同的应用场景。
最常见的应用是在方差分析中,用于检验各组的方差是否相等。
除了方差分析,Levene 检验还可以用于其他统计方法、回归分析等。
比如,假设我们想要比较不同药物对某种疾病的治疗效果。
参数检验和非参数检验

一.单因素方差分析(one-way ANOVA),用于完全随机设计的多个样本均数间的比较,其统计推断是推断各样本所代表的各总体均数是否相等。
完全随机设计(completely random design)不考虑个体差异的影响,仅涉及一个处理因素,但可以有两个或多个水平,所以亦称单因素实验设计。
在实验研究中按随机化原则将受试对象随机分配到一个处理因素的多个水平中去,然后观察各组的试验效应;在观察研究(调查)中按某个研究因素的不同水平分组,比较该因素的效应。
二.T检验,亦称student t检验(Student's t test),主要用于样本含量较小(例如n<30),总体标准差σ未知的正态分布资料。
t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。
它与Z检验、卡方检验并列。
t检验t检验分为单总体检验和双总体检验。
单总体t检验时检验一个样本平均数与一个已知的总体平均数的差异是否显著。
当总体分布是正态分布,如总体标准差未知且样本容量小于30,那么样本平均数与总体平均数的离差统计量呈t分布。
单总体t检验统计量为:双总体t检验是检验两个样本平均数与其各自所代表的总体的差异是否显著。
双总体t 检验又分为两种情况,一是独立样本t检验,一是配对样本t检验。
独立样本t检验统计量为:S1 和S2 为两样本方差;n1 和n2 为两样本容量。
(上面的公式是1/n1 + 1/n2 不是减!)配对样本t检验统计量为:t检验的适用条件(1) 已知一个总体均数;(2) 可得到一个样本均数及该样本标准差;(3) 样本来自正态或近似正态总体。
t检验步骤以单总体t检验为例说明:问题:难产儿出生体重n=35,X拔=3.42,S =0.40,一般婴儿出生体重μ0=3.30(大规模调查获得),问相同否?解:1.建立假设、确定检验水准αH0:μ = μ0 (无效假设,null hypothesis)H1:μ≠μ0(备择假设,alternative hypothesis,)双侧检验,检验水准:α=0.052.计算检验统计量3.查相应界值表,确定P值,下结论查附表1,t0.05 / 2.34 = 2.032,t < t0.05 / 2.34,P >0.05,按α=0.05水准,不拒绝H0,两者的差别无统计学意义例:某校二年级学生期中英语考试成绩,其平均分数为73分,标准差为17分,期末考试后,随机抽取20人的英语成绩,其平均分数为79.2分。
方差不齐用什么检验方法

方差不齐用什么检验方法
方差不齐是指不同组或样本的方差不相等,这种情况下,传统的方差分析方法
可能会导致结果不准确甚至错误。
因此,需要采用适当的检验方法来处理方差不齐的数据,以确保分析结果的可靠性和准确性。
一般来说,处理方差不齐的数据可以采用以下几种检验方法:
1. Welch检验,Welch检验是一种用于处理方差不齐的数据的方法,它可以有
效地解决方差不齐对方差分析结果的影响。
Welch检验不要求各组数据的方差相等,因此适用于方差不齐的情况。
2. Brown-Forsythe检验,Brown-Forsythe检验是另一种处理方差不齐的方法,
它可以在方差不齐的情况下进行方差分析。
与传统的方差分析方法相比,Brown-Forsythe检验对方差不齐的数据更为稳健,能够产生更加可靠的结果。
3. Kruskal-Wallis检验,Kruskal-Wallis检验是一种非参数检验方法,适用于处
理非正态分布和方差不齐的数据。
与传统的方差分析方法相比,Kruskal-Wallis检
验不要求数据满足正态分布和方差齐性的假设,因此更加灵活和适用于实际情况。
在选择合适的检验方法时,需要根据实际数据的特点和分析的要求来进行判断。
通常情况下,可以通过Levene检验或Bartlett检验来检验数据的方差齐性,然后根
据检验结果来选择合适的方法进行方差分析。
总之,方差不齐的数据会对方差分析结果产生影响,因此在进行数据分析时需
要选择适当的检验方法来处理方差不齐的情况,以确保分析结果的准确性和可靠性。
以上介绍的几种检验方法可以作为处理方差不齐数据的参考,希望对您有所帮助。
统计学非参数检验

非参数检验的弱点
可能会浪费一些信息 特别当数据可以使用参数模型
的时候 大样本手算相当费事 一些表不易得到
参数检验
〔parametric 总体分t布es类t〕型,对未知
➢ 在参数检验和非参数检验都可以使用的情况下, 非参数检验的成效〔power〕要低于参数检验方 法。
以下情况下应当首选非参数方法
➢ 参数检验中的假设条件不满足,从而无法应用。例 如总体分布为偏态或分布形式未知,且样本为小样 本时。
➢ 检验中涉及的数据为定类或定序数据。 ➢ 所涉及的问题中并不包含参数,如判断某样本是否
在非正态总体小样本的情况下,假如要对总体 分布的位置进展推断,由于t检验不适用,也 可使用符号检验的方法。
在数据呈偏态分布的情况下,我们可能对总体 的中位数更感兴趣,希望对总体的中位数作出 推断,这时可以使用符号检验的方法。
例6.3 在某地区随机调查了60个家庭的月收入。 〔数据文件:家庭月收入.sav〕。根据样本数 据能否认为总体中家庭月收入的中位数等于 5000元〔显著性程度a=0.05〕?
c2统计量的分布与自由度有关; c2统计量描绘了观察值与期望值的接近程度
拟合优度检验〔goodness of fit test〕
用c2统计量进展统计显著性检验的重要内容之 一;
根据总体分布状况,计算出分类变量中各类别 的期望频数,与分布的观察频数进展比照,判 断期望频数与观察频数是否有显著差异,从而 到达对分类变量进展分析的目的。
非参数统计的名字中的“非参数(nonparametric) 〞意味着其方法不涉及描绘总体分布的有关参 数;
非参数检验思路总结
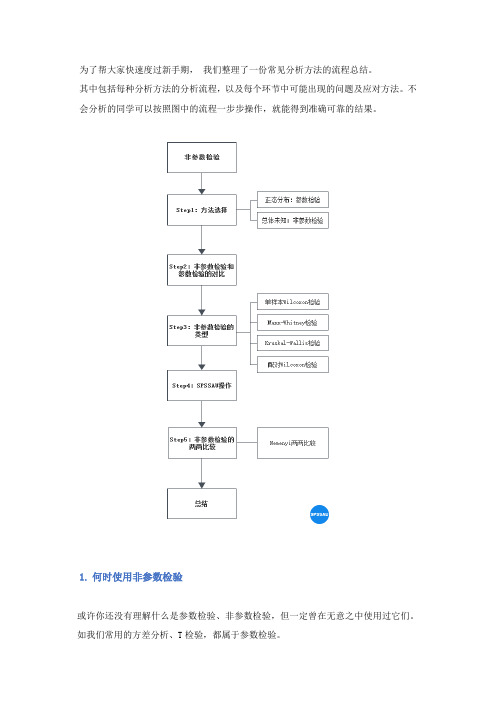
为了帮大家快速度过新手期,我们整理了一份常见分析方法的流程总结。
其中包括每种分析方法的分析流程,以及每个环节中可能出现的问题及应对方法。
不会分析的同学可以按照图中的流程一步步操作,就能得到准确可靠的结果。
1.何时使用非参数检验或许你还没有理解什么是参数检验、非参数检验,但一定曾在无意之中使用过它们。
如我们常用的方差分析、T检验,都属于参数检验。
参数检验,就是假定数据服从某种分布,通过样本信息对总体参数进行检验。
因而在分析前,先要检验数据是否符合该类型的分布,如果数据无法满足检验假设的情况不符合分布情况,则可以考虑选择使用非参数检验。
比如使用方差分析时,需要在分析前对数据的正态性和方差齐性进行判断,如果服从正态性、方差齐性,才可以使用方差分析。
反之,如果没有满足这些假设条件,则使用非参数检验。
2.非参数检验和参数检验的对比①适用范围正态分布分布未知②检验效能高低③描述指标平均值中位数④图形展示折线图箱线图①适用范围:非参数检验用作参数检验的替代方法,当数据不满足正态性时,将使用非参数检验。
因此,关键是要弄清楚是否具有正态分布。
如果数据大致呈现"钟型"分布,则可以使用参数检验。
②检验效能:如果数据满足参数分布,应该优先选择参数检验方法。
愿因在于参数检验的检验效能要高于非参数检验。
尤其是在样本数较大的情况下,参数检验结果较为稳健,所以即使不服从正态分布,也会选择参数检验。
③对比指标:参数检验一般用平均值反映数据的集中趋势;但由于数据不满足正态分布,在非参数检验中如果再使用平均值描述显然不太准确(比如常被吐槽的人均收入),此时中位数是更好的选择。
参数检验分析结果参数检验用平均值及标准差描述样本分布请况。
非参数检验分析结果非参数检验结果中使用的是中位数描述差异。
④图形展示除了使用以上指标进行分析,还可以通过图形直观展示数据情况。
参数检验常用图形有:折线图、条形图等,非参数检验可以使用箱线图查看。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一个式子表明,如果各个处理很不一样,和的 平方就会很大,结果就显著。 第二个公式是为了计算方便而导出的。它有近似 的(有k-1个自由度的)卡方分布。
土壤4
11
13
19
Friedman秩和检验
Friedman秩和检验是关于位置的,和KruskalWallis 检验类似,形式上,假定这些样本有连 续分布F1,…,Fk,零假设为H0:F1=…=Fk,备选 假设为 Ha : Fi(x)=F(x+qi) , i=1,…,k ,这里 F 为 某连续分布函数,而且这些参数qi并不相等。 由于区组的影响, 要首先在每一个区组中计算各 个处理的秩; 再把每一个处理在各区组中的秩相加. 如果Rij表示在j个区组中第i个处理的秩。则秩按 照处理而求得的和为 b
k
2 i
Kruskal Wallis 检验案例——house
为了调查三个地区的房价是否类似,在每个地区抽样,得 到三个样本量分别为20、30、25的房价样本。利用SPSS软 件容易得到下面的检验结果:
Test Statisticsb,c Chi-Square df Asymp. Sig. Monte Carlo Sig. PRICE 10.365 2 .006 .005a .003 .007
Friedman秩和检验案例——fert
这里有三种肥料作为第一个因子(肥料因子)的三个水平; 而四种土壤为第二个因子(土壤因子)的四个水平。感兴 趣于是否这三种肥料对于某作物的产量有区别。称肥料因 子为处理,而土壤因子为区组。(单位公斤)。 肥料种类 肥料A 土 壤 类 型 土壤1 土壤2 土壤3 22 25 18 肥料B 46 36 21 肥料C 68 48 20
Kruskal Wallis 检验
注意这里所说的位置参数是在下面意义上的qi; 由于它在分布函数Fi(x)中可以和变元x相加成 为F(x+qi)的样子,所以称qi为位置参数,即 Fi(x)=F(x+qi) 形式上,假定这些总体有连续分布F1,…,Fk,
零假设为H0:F1=…=Fk, 备选假设为Ha:F(x+qi),i=1,…,k,这些参数qi并 不相等
Jonckheere-Terpstra检验
Jonckheere-Terpstra检验先在每两个样本 所有观测值对之间比较,计算第i个样本观 测值中小于第j个样本观测值的对子数:
Uij #( X ik X jl , k 1,..., ni , l 1,..., nl )
J Uij
Friedman秩和检验案例——fert
Ranks A B C Mean Rank 1.00 2.25 2.75
Test Statistics a N Chi-Square df Asymp. Sig. Exact Sig. Point Probability a. Friedman Test 4 6.500 2 .039 .042 .037
a. Grouping Variable: GROUP
Jonckheere-Terpstra检验——SPSS
使用house.sav数据。 选项为Analyze-Nonparametric Tests-K Independent Samples。 把变量(这里是price)选入Test Variable List; 再把数据中用1、2、3来分类的变量group输入 Grouping Variable,在Define Groups输入1、2、 3。 在下面Test Type选中Jonckheere-Terpstra。 在点Exact时打开的对话框中可以选择精确方法 (Exact),Monte Carlo抽样方法(Monte Carlo) 或用于大样本的渐近方法(Asymptotic only)。 最后OK即可
Sig. 99% Confidence Interval
Lower Bound Upper Bound
a. Based on 10000 sampled tables with starting seed 2000000. b. Kruskal Wallis Test c. Grouping Variable: GROUP
Jonckheere-Terpstra检验
这个检验处理的问题和Kruskal-Wallis检 验类似,零假设都是各个总体的位置参数 相同,但这里的备选假设为各个总体的位 置参数按升幂排列(如为降幂排列,可把 总体编号颠倒顺序即为升幂排列)。 注意这里所说的位置参数和前面的 Kruskal-Wallis检验中的位置参数意义一 样。
Kruskal Wallis 检验——SPSS实现
使用house.sav数据。 选项为Analyze-Nonparametric Tests-K Independent Samples。 把变量(这里是price)选入Test Variable List; 再把数据中用1、2、3来分类的变量group输入 Grouping Variable,在Define Groups输入1、2、 3。 在下面Test Type选中Kruskal-Wallis H。 点Exact时打开的对话框中可以选择精确方法 (Exact),Monte Carlo抽样方法(Monte Carlo) 或用于大样本的渐近方法(Asymptotic only)。 最后OK即可
方差分析对应的非参检验
——Kruskal Wallis 检验(对应单因素) ——Friedman检验(对应双因素)
Kruskal Wallis 检验
这个检验的目的是看多个总体的位置参数是 否一样。 方法和Wilcoxon-Mann-Whitney检验的思想 类似。 假定有k个总体。 先把从这个k个总体来的样本混合起来排序, 记各个总体观测值的秩之和为Ri,i=1,…,k。 显然如果这些Ri很不相同,就可以认为它们 位置参数相同的零假设不妥(备选假设为各 个位置参数不全相等)。
Friedman秩和检验——双因素
参数统计中讨论了两因子试验设计数据的 方差分析,那里所用的F检验需要假定总体 的分布为正态分布。 有 一 种 非 参 数 方 差 分 析 方 法 , 称 为 Friedman ( 两 因 子 ) 秩 和 检 验 , 或 Friedman方差分析。
它适用于两个因子的各种水平的组合都有一个观 测值的情况。
i j
Jonckheere-Terpstra检验——house
Jonckheere-Terpstra Test a PRICE Number of Levels in GROUP N Observed J-T Statistic Mean J-T Statistic Std. Deviation of J-T Statistic Std. J-T Statistic Asymp. Sig. (2-tailed) Exact Sig. (2-tailed) Exact Sig. (1-tailed) Point Probability 3 75 1229.500 925.000 102.299 2.977 .003 .003 .001 .000
Ri Rij , i 1,..., k
j 1
Friedman秩和检验
这样做的目的是在每个区组内比较处理。
例如, 同个年龄段中比较药品的疗效比不分年龄来比较 疗效要合理; 在同一个部位比较不同的材料要比混合起来比较要合 理等等。
k 2
这里要引进的Friedman统计量定义为
Kruskal Wallis 检验
Kruskal-Wallis检验统计量为
R 12 H 3( N 1) N ( N 1) i 1 ni
公式中ni为第i个样本量,而N为各个样本量之和(总 样本量)。 如果观测值中有大小一样的数值,这个公式会有稍 微的变化。 这个统计量在位置参数相同的零假设下有渐近的自 由度为k-1的c2分布。 Kruskal-Wallis检验仅仅要求各个总体变量有相似 形状的连续分布。
Friedman秩和检验
假定第一个因子有 k 个水平(称为处理, treatment ),第二个因子有 b 个水平(称 为区组);因此一共有 k×b = kb 个观测值。 这里之所以称一个因子为处理,是因为这 是我们想要看该因子各水平是否对试验结 果有显著的不同。 而另一个因子称为区组,不同的区组也可 能对结果有影响。下面是一个例子。
Friedman秩和检验——SPSS实现
使用fert.sav数据。 选项为Analyze-Nonparametric Tests-K Related Samples。 然后把变量(这里是a、b、c)选入Test Variable List。 在下面Test Type选中Friedman。 在点Exact时打开的对话框中可以选择精确方法 (Exact),Monte Carlo抽样方法(Monte Carlo) 或用于大样本的渐近方法(Asymptotic only)。 最后OK即可
