如何用几何画板画椭圆
数学中常用几何画板绘制椭圆

数学中常⽤⼏何画板绘制椭圆圆锥曲线是⾼中数学的重点和难点,也是历来⾼考的必考内容,所以对于⾼中⽣来说,弄懂圆锥曲线这块难啃的⾻头,是很有必要的。
其中要熟练掌握的圆锥曲线之⼀就是椭圆,它是圆锥与平⾯的截线,其实要想画出椭圆,其⽅法不⽌⼀种,下⾯就⼀起来通过学学椭圆的五种画法。
⽅法⼀、利⽤椭圆第⼀定义构造椭圆椭圆第⼀定义:平⾯内到两个定点的距离之和等于定长2a(a>0)的点的轨迹就是椭圆,按照此定义可画出椭圆,具体步骤如下:1.单击“圆⼯具”,在画板的适当位置任意画⼀个圆,将圆⼼的标签改为F1。
单击“点⼯具”,在圆上任意画⼀点C,同时选中点F1和点C,执⾏“构造”-“线段”命令,构造出线段F1C。
单击“点⼯具”,在线段F1C任意画⼀点F2。
2.在圆上任意画⼀点E,并构造线段EF1和线段EF2。
选中线段EF2,执⾏“构造”-“中点”命令,构造线段EF2的中点F。
3.选中线段EF2和点F,执⾏“构造”-“垂线”命令,构造出线段EF2的垂直平分线j。
同时选中线段EF1和直线j,选择“构造”-“交点”命令,构造线段EF1和直线j的交点G。
4.选中点G和点E(把点E称做是点G的相关点,改变G点的位置,点E的位置也跟着改变),选择“构造”-“轨迹”命令,可画出椭圆。
拖动点B 和点F2可改变椭圆的形状。
⽅法⼆、利⽤椭圆第⼆定义画椭圆椭圆的第⼆定义:设动点M(x, y)与定点F(c, 0)的距离和它到定直线l: x=a2/c的距离的⽐是常数(a>c>0),则点M的轨迹是椭圆。
点F 是椭圆的⼀个焦点,直线l是椭圆中对应于焦点F的准线,常数e=c/a(0<e<1)。
具体的操作步骤如下:步骤⼀打开⼏何画板,使⽤“点⼯具”画任意⼀点F,使⽤“线⼯具”画直线L(点F不在L上)。
过点F作⼀条直线,在直线上取⼀点P;步骤⼆选中点F、P执⾏“度量”--“距离”命令,度量FP的长度;选中点F和度量的FP的长度,执⾏“构造”--“以圆⼼和半径绘圆”构造以点F为圆⼼,FP为半径的圆。
几何画板中的度量功能实验报告:椭圆的画法

几何画板中的度量功能实验报告一、 实验目的1. 学习应用数学知识原理来指导绘制圆锥曲线。
2. 掌握几何画板中的建立坐标系,绘制已知点以及运用几何画板中内置计算器计算比值的方法,掌握度量菜单的用法。
3. 应用几何画板中的操作类按钮的功能动态显示圆锥曲线的变化状况。
二、 实验原理圆锥曲线基本定义,椭圆的参数方程以及椭圆的标准方程。
实验内容:根据椭圆的不同定义,标准方程以及参数方程,绘制不同的椭圆曲线。
三、 实验仪器PC 计算机; 软件工具:几何画板5.04 四、实验课时:6课时 五、实验步骤 (一)知识储备椭圆的第一定义:平面内与两定点F 1、F 2(即焦点)的距离的和等于常数的动点P 的轨迹叫做椭圆. 其数学表达式为:|PF 1|+|PF 2|=2a (2a >|F 1F 2|),焦距:|F 1F 2|=2c ≤2a.椭圆的第二定义:平面内到定点F(c ,0)的距离和到定直线l :ca x 2=(F 不在l 上)的距离之比为常数,即离心率ace =(0<e<1)的点的轨迹是椭圆. (二)椭圆的画法:1、根据椭圆的第一定义画椭圆:2种画法。
2、缩放法画椭圆3、双圆法画椭圆(三)各种画法的实验步骤1、根据椭圆的第一定义画椭圆:有两种画法 画法一:(1)新建页:【文件】-【文档选项】-【增加页】-【空白页面】,命名为:根据椭圆的第一定义画椭圆——画法一。
(2)构造控制台:选择【线段工具】,在空白处画线段AB ,选中线段AB ,【构造】-【构造线段上的点】(点C ),选中点C ,【度量】-【点的值】(xx ____上在AB C ),【数据】-【计算】-输入 :上在____1AB C ,选中比值,鼠标右击-【标记比值】。
(3)画圆:选择【点工具】,在空白处,作点D 、点E ,双击点D ,选中点E ,【变换】-【缩放】-【按标记比进行缩放】-【确定】,得到点E ’(通过拖动点C ,可以控制点E ’的位置,从而改变下面的椭圆的离心率。
几何画板生成椭圆曲线八种方法

按住shift键,同时选中外圆圆周上的点E和外圆圆周,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“单向”、“绕圆c2”、“快速地”,按下“动画”按钮确定。
这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆。完成,存盘退出。
几何画板生成椭圆曲线八法
国家教育部推荐的教育软件《几何画板》提供曲线的动态变化,便于观察与验证。如很好的开发它的功能,制作出富于表现力的动态效果的课件,培养学生对抽象曲线的理解和想象能力有极大的帮助。下面就用绘制椭圆曲线的八种方法的同行们商榷。
一、定义法(到两定点的距离和等于定长)
选取“线段”工具,在绘图板中作一线段AB(线段AB的长度为椭圆的长轴长2a)。用“点”工具在线段上任取一点C,按住shift键先后选中A,C点,选择“变换”→“标记向量 "A→C"”。
在圆周上任去一点F,同时选中点F和点A,按Ctrl+L键作出线段FA。再同时选中点F和线段FA,选择“作图”→“垂线”作出该圆的切线。
选中该切线和垂线j,按Ctrl+I键作出交点G,同样的方法作出该切线和垂线k的交点H。连接点G和点E(同时选中两点,按Ctrl+L键),连接点H和点D。作出线段GE和线段HD的交点I(同时选中两条线段,按Ctrl+I键)。选中线段FA,按Ctrl+H键隐藏。
三、同心圆法。
选择“文件”→“新绘图”,选择“图表”→“建立坐标轴”,用“圆”工具作两圆心为原点的同心圆(外圆半径长就是最终椭圆的长半轴长a,内圆半径长就是最终椭圆的短半轴长b),选中点B和圆周上的点C和D,按Ctrl+H键隐藏。
用几何画板绘制椭圆的方法

用几何画板绘制椭圆的方法作椭圆的方法很多,在此仅举4种方法。
例1:利用椭圆的定义作椭圆。
[简要步骤]:(1)作点A、B,以及线段CD(定长);(2)以点A为圆心,CD为半径作圆,并在圆A上任意取一点E;(3)连接AE、BE,并作BE的垂直平分线FG,交BE于点F,交AE于点G;(4)同时选中点G和点E,作轨迹,如图1。
图1例2:利用椭圆的参数方程作椭圆。
本例的作图原理就是先计算x = a cos t,y = b sin t(-π≤t ≤π),然后根据算得的x、y的值作出点(x,y),最后作出轨迹。
[简要步骤]:(1)显示坐标轴,在x、y轴上分别取点C、D,测量并计算出点C的横坐标和点D的纵坐标,然后将标签分别改为a和b;(2)以任意点E为圆心,点F为圆上一点作圆,在圆上任取一点G,测量角FEG的值,并将标签改为t;(3)将角度设置为弧度制,计算a cos t和b sin t的值,并依次选中,画出点H (a cos t,b sin t);(4)同时选中点H和点G,作轨迹,如图2。
图2例3:利用椭圆的参数方程的几何意义作椭圆。
[简要步骤]:(1)作水平线段AB,在线段AB上取一点C,以点A为圆心,分别以点B、C为圆上一点作两个同心圆,在大圆上任取一点D,连接AD,交小圆于点E;(2)过点D作线段AB的垂线,并过点E作垂线的垂线,两线交于点F;(3)同时选中点D和点F,作轨迹,如图3。
图3例4:利用压缩圆的方法作椭圆。
我们知道,将圆压缩就成了椭圆,因此,我们可以以椭圆的短轴与长轴之比作为压缩比,将圆压缩成椭圆。
[简要步骤]:(1)作线段AB,以线段AB的中点C为圆心,以点B为圆上一点作圆,在圆上任取一点D;(2)过点D作线段AB的垂线,交线段AB于点E;(3)作线段FG、GH,依次选中线段FG、GH,并标识为比例;(4)以点E为缩放中心,将点D以标识的比例压缩,得点D';(5)同时选中点D和点D',作轨迹,如图4。
几何画板生成椭圆曲线八种方法

选择“文件”→“新绘图”,选择“图表”→“建立坐标轴”,用“圆”工具作两圆心为原点的同心圆(外圆半径长就是最终椭圆的长半轴长a,内圆半径长就是最终椭圆的短半轴长b),选中点B和圆周上的点C和D,按Ctrl+H键隐藏。
选择“显示”→“线型”→“虚线”,在外圆圆周上任取一点E,按住shift键,同时选中点A和点E,按Ctrl+L作出线段AE,同时选中线段AE和内圆圆周,按Ctrl+I键作出交点F。
2.按住shift键,先后选中点F,选择“显示”→“追踪点”,同样选中点G和点C,选择“显示”→“追踪点”。
按住shift键,先后选中点C和线段AB,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“双向”、“沿着线段j”、“慢慢地”,按“动画”按钮完成设置。这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆。完成,存盘退出。
同时选中点A和点D,按Ctrl+L键作线段AD。再同时选中垂线k和线段AD定值。
选中点F,按Ctrl+T键追踪点F。选中点D和圆周,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“单向”、“绕圆c1”、“正常地”,按“动画”按钮完成设置。这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆(如图4)。另外您也可以同时选中点F和点D,选择“作图”→“轨迹”也可以作出该椭圆。完成,存盘退出
二、准线法(到定点的距离与到定直线的距离之比为常数e)
打开一个新的绘图板,选择“图表”→“建立坐标轴”。
用“线段”工具作线段CD,在线段CD上任取一点E。同时选中点C和点E,选择“度量”→“距离”,量出CE的长。同样量出CD的长。
按住shift键,选中量出的CE和CD的距离,按鼠标右键弹出对话框,选择“度量”→“计算”。在打开的计算器中选择“数值”→“距离(C到E)”。选择“/”→“距离(C到D)”→“确定”。在绘图板上就会出现CE和CD的比值。用“文本工具”双击该值,弹出“度量值格式”对话框,选择“T文本格式”。 将“距离(C到E)/距离(C到D)”改成“e”,确定,完成改变。选中点B,按Ctrl+H键隐藏,在X轴上取点F(F为椭圆的一个焦点)。作线段GH,在其上取点I。用上面的方法量出GI的距离,并将其距离名称改为c。选中c和e的值,打开计算器,将c除以e的值求出,并将其名改为a。
用几何画板画椭圆的六种方法

用几何画板画椭圆的六种方法椭圆是平面几何中常见的图形,具有许多特点和性质。
在绘制椭圆时,有多种方法可以使用。
下面将介绍六种常用的绘制椭圆的方法。
1. 绳和两个钉:这是最简单的方法之一。
取一根绳,将两个钉固定在纸上,钉的距离确定椭圆的长轴,绳长为椭圆的周长。
将绳套在两个钉上,再以笔紧绷绳子,沿纸面移动绳子的笔尖,即可得到一个完美的椭圆。
2. 立兰德椭圆仪:这是一种专门用于绘制椭圆的工具。
它由两个互相垂直的固定圆和一个移动圆组成。
通过调整移动圆的位置,使其切割固定圆的位置在不同角度,便可绘制出各种椭圆。
3. 画平行线法:在纸上画一条长直线,作为椭圆的长轴。
然后,在长轴上选择几个等分点,并与长轴垂直的方向上画平行线。
接下来,再在每个平行线上选择等分点,并连结相邻点,最终得到椭圆。
4. 两点距离法:选择椭圆上的两个任意点,并利用细线连接它们。
然后,取一根较长的尺,在椭圆外围固定两个点,使其到线的距离相同。
移动尺的另一段,让尺上的铅笔碰触到线,并沿着椭圆移动,最终形成一个椭圆。
5. 推拉法:选取一块矩形硬纸板或卡纸,将其弯曲成圆筒形。
两端的直径确定椭圆的长短轴。
然后,在圆筒上连接两个焦点,并用铅笔固定在纸上固定一个点,同时将纸沿着直径滑动,同时保持焦点的位置变化,最终形成一个椭圆。
6. 辅助圆法:在纸上确定椭圆的长轴和短轴的长度。
以长轴为直径,在一张纸上画一个大圆;再以短轴为直径,在同一张纸上画一个小圆。
以每个圆的切点为圆心,连结两个切点,最终形成一个完美的椭圆。
这几种方法都能够帮助我们绘制出精确的椭圆。
根据实际需求和使用条件的不同,我们可以选择适合自己的方法来画椭圆。
希望这些方法对您有所帮助!。
人教版A版高中数学选修1-1第二章 圆锥曲线与方程2.1 椭圆 信息技术应用《几何画板》探究点的轨迹---椭圆教

x2 a2
+
y2 b2
=1
(a>b>0)
y2 a2
+
x2 b2
=1(a>b>0)
3.椭圆的几何性质:
e c (0 e 1) a
课件名
用《几何画板》探究点的轨迹:椭圆
概念重温
1.如图所示,一圆形纸片的圆心为O,F是圆内 一定点,M是圆周上一动点,把纸片折叠使M 与F重合,然后抹平纸片,折痕为CD,设CD与 OM交于点P,则点P的轨迹是
课课件件名 名
用《几何画板》探用究《几点何画的板》轨探迹究点:的轨椭迹:圆椭圆
焦半径公式:
焦点在x轴:|MF1| = a + ex , 左加右减
|MF2| = a - ex
焦点在y轴:|MF1| = a + ey , 下加上减
|MF2| = a - ey
课课件件名 名
用《几何画板》探用究《几点何画的板》轨探迹究点:的轨椭迹:圆椭圆
椭圆的第二定义
1、定义:平面内到一个定点F和一条定直线 l
(F不在 l上) 的距离的比为常数e(0<e<1)的点
M的轨迹,叫椭圆。定点F叫焦点,定直线 l 叫准 线。
2、定义式:
_|_M___F__1_|_ d1
=e
_|_M___F__2_|_ d2
=e
左对左,右对右
课件名
用《几何画板》探究点的轨迹:椭圆
椭圆的方程与准线方程
x2 a2
+
y2 b2
=1
左对左,右对右
右准线 方程:
x=
a2 c
左准线 方程:
x=-ac2
左准线 左准线 右准线
几何画板椭圆第一定义的模拟实验步骤

几何画板椭圆第一定义的模拟实验步骤
以下是模拟实验椭圆第一定义的步骤:
1. 准备实验材料:一张几何画板、一支铅笔和一根细线。
2. 在几何画板上找到一个合适的中心点,并用铅笔在该点做一个小标记。
3. 使用针将细线的一端固定在几何画板上的中心点上。
4. 用铅笔将细线的另一端固定在画板上适当的位置,确保线条拉直,并且线长稍长于几何画板的两个半径之和。
5. 将铅笔以一定的角度保持固定,然后将细线沿着画板来回移动,绕着中心点旋转线条。
6. 在细线被拉挺的同时,保持细线与铅笔尖端的距离始终不变。
7. 观察细线运动时留下的痕迹,这些痕迹将形成一个闭合的曲线。
8. 这个曲线即为椭圆。
根据椭圆的定义,椭圆是平面上所有距离到两个固定焦点的距离之和恒定的点的轨迹。
这个模拟实验能够帮助你直观地理解椭圆第一定义,即两个焦点和椭圆上所有点到这两个焦点距离之和的恒定关系。
参与实验的过程可以帮助你更好地理解和记忆椭圆的特征。
用几何画板画椭圆的方法
用几何画板画椭圆的方法
椭圆是圆锥曲线重要的一部份,用几何绘图工具绘制椭圆不仅可以使图形画得更准确,还能很好地显示椭圆的一些性质。
本文就向大家介绍几何画板圆锥曲线中的椭圆怎么画。
1.构造线段与中点。
选择“直线工具”,画出线段AB,选择“构造”—“中点”命令,画出线段AB的中点C。
使用线段工具绘制线段AB并构造中点C
2.构造圆。
依次选中点C、点A,选择“构造”—“以圆心和圆周上的点绘圆”命令,绘制出以点C为圆心经过点A的圆C。
选中点C、点A后构造以点C为圆心经过点A的圆C
3.构造垂线与交点。
选择“点工具”,在圆周上任意作一点D,选中点D和线段AB,选择“构造”—“垂线”命令,绘制出线段AB的垂线,与线段AB的交点为E。
绘制点D后构造线段AB的垂线并与之交于E点
4.隐藏圆和直线。
选中圆C和直线DE,选择“显示”—“隐藏路径对象”命令,隐藏圆C和直线DE。
选中圆C和直线DE后将之隐藏
5.构造线段和中点。
选择“线段工具”,绘制出线段DE。
选择“构造”—“中点”命令,绘制出线段DE的中点F。
用线段工具绘制出线段DE后构造其中点F
6.绘制椭圆。
依次选中点D、点F,选择“构造”—“轨迹”命令,绘制出椭圆。
如下图所示。
使用“构造”—“轨迹”命令绘制出椭圆
7.隐藏点与线段。
选中点D、点E、点F、线段DE,选择“显示”—“隐藏对象”命令,椭圆绘制完成。
隐藏点D、E、F和线段DF
以上向大家详细介绍了用几何画板画椭圆的方法,相信大家对此已经有所掌握。
人教A版高二数学《椭圆及其标准方程》课件

设M(x, y)是椭圆上任意一点,
M
椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正 常数2a (2a>2c) ,则F1、F2的坐 标分别是(c,0)、(c,0) .
F1 0 F x
2
由椭圆的定义得,限制条件:| MF1 | | MF2 | 2a
代入坐标 | MF1 | (x c)2 y2 ,| MF2 | (x c)2 y2
点 焦点的位 x2 , y2 项中哪个分母大,焦点就在哪一条
置的判定
坐标轴上.
15
x2 变式1:椭圆的方程为:3
y2 7
1
,
则
a=____7_,b=____3___,c=___2____,焦点坐
标为:(0_,_2_)和__(__0_,-_2_)_焦距等于_____4_____;曲
线上一点P到焦点F2的距离为3,则点P到另 一个焦点F1的距离等于___2__7___3_,则 △F1PF2的周长为_2__7___4_____ y
25 16
25 16
思考:求合适下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-4,0)和(4,0),且椭
圆经过点(5,0).
y
解:因为椭圆的焦点在 x 轴上,设
x2 a2
y2 b2
1(a
>
b>
0).
由椭圆的定义知
F1 O
F2 P x
2a (5 4)2 (0 0)2 (5 4)2 (0 0)2 10,
所以 a 5.
又因为 c 4,所以 b2 a2 c2 25 16 9.
因此,所求椭圆的标准方程为
x2 y2 1. 25 9
定义法 20
用几何画板研究椭圆的画法
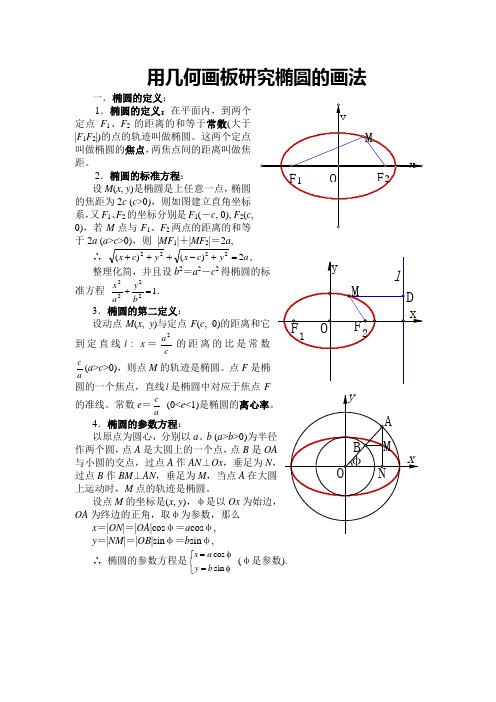
用几何画板研究椭圆的画法一.椭圆的定义:1.椭圆的定义:在平面内,到两个定点F 1、F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,两焦点间的距离叫做焦距。
2.椭圆的标准方程:设M (x , y )是椭圆是上任意一点,椭圆的焦距为2c (c >0),则如图建立直角坐标系,又F 1、F 2的坐标分别是F 1(-c , 0), F 2(c , 0),若M 点与F 1、F 2两点的距离的和等于2a (a >c >0),则 |MF 1|+|MF 2|=2a ,∴a y c x y c x 2)()(2222=+-+++,整理化简,并且设b 2=a 2-c 2得椭圆的标准方程 12222=+by a x .3.椭圆的第二定义:设动点M (x , y )与定点F (c , 0)的距离和它到定直线l : x =ca2的距离的比是常数ac(a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F的准线。
常数e =ac(0<e <1)是椭圆的离心率。
4.椭圆的参数方程:以原点为圆心,分别以a 、b (a >b >0)为半径作两个圆,点A 是大圆上的一个点,点B 是OA 与小圆的交点,过点A 作AN ⊥Ox ,垂足为N ,过点B 作BM ⊥AN ,垂足为M ,当点A 在大圆上运动时,M 点的轨迹是椭圆。
设点M 的坐标是(x , y ),φ是以Ox 为始边,OA 为终边的正角,取φ为参数,那么x =|ON |=|OA |cos φ=a cos φ, y =|NM |=|OB |sin φ=b sin φ,∴ 椭圆的参数方程是⎩⎨⎧φ=φ=sin cos b y a x (φ是参数).二.椭圆的画法: 画法1:1.在x 轴上取两点F 1、F 2,使|OF 1|=|OF 2|,用它们作为两个焦点; 2.在图形外作一条线段CD ,使|CD |=2a ,(|CD |>|F 1F 2|); 3.以O 为中心,在x 轴上取两点A 1、A 2,使|A 1A 2|=|CD |;4.在CD 上分别取C '、D ',使|CC '|=|A 1F 1|=|DD '|;作线段C 'D ',并用“作图”菜单中的“对象上的点”功能在C 'D '上作点M ;5.分别以F 1、F 2为圆心,用|CM |、|MD |为半径作圆,两圆相交于P 1、P 2两点;同样方法分别以F 1、F 2为圆心,用|DM |、|CD |为半径作圆,两圆相交于P 3、P 4两点;并将这四个点定义为“追踪点”;6.依次选中点M 、点P 1 (或点M 、点P 2),用“作图”菜单中的“轨迹”功能,作出椭圆。
“几何画板”绘制椭圆的几种典型作法

选择 < 度量 /距离 ) 度量 出线 段 n和 c的长 度 ; , 按
一
2
,2
Al+一 键 打 开计 算器 , t 计算 “ 一c选 中 一c选 - . ,
C
择 < 换 /标 记 距 离 ) 选 中点 C, 择 < 换 /平 变 . 选 变
一
2
移 )平 移距 离 为 ( 一c , 向为 0度 , 到点 F, , _ “ )方 得
1 根 据 椭 圆第 一定 义 作椭 圆
( )打开 几何 画板 , 择 ( 辑 /参 数 选 项 > 1 选 编 , 单击 “ 文本 ” 项 卡 , 所有 新 建 的 点前 的方框 中 选 在 画对 号 , 后 确 定.用 “ 线 段 ”工 具 , 线 段 然 画 作 A 线段 AB 的 长度 为椭 圆 的长 轴 长 2 ) 用 “ B( a. 画 点”工具 在线 段 A 上任 取一 点 C, B 用选 择工 具选 中 A, C点 , 择 ( 选 变换 /标 记 向量 >A ~> C . “ ”
2 根 据 椭 圆第 二定 义 作 椭 圆( 准线法)
( )打开 一个 新 画板 , “ 直 线”工具 作 两 1 用 画
条 直线 , 直 线 Z 准线 , 一 条 直线 AB 与直 线 使 为 另 垂 直. 中两 条直 线 , 择 ( 图 /交 点 ) 作 出交 选 选 作 ,
点 C; 两 条 直 线 外 , 两 条 线 段 和 , 在 画 使 > c .
“ 几何画板” 绘制椭圆的几种典型作法
陈 永 胜
( 林师范大学数学学院 , 林 吉 吉 四平 1 60 ) 30 0
摘
要: 几何 画 板 是 一 个 优 秀的 专 业 学科 平 台 软 件 , 表 了 当代 专 业 工 具 平 台 类 教 学 软 件 的 发 展 方 向 . 代 它 以数 学 为根 本 , 动 态几 何 ” 以“ 为特 色来 动 态 表 现 设 计 者 的 思 想 , 为探 索 几何 奥 秘 提 供 一 个 新 的 工 具。 绍 使 用 “ 介 几何 画 板 ” 画椭 圆 的 几种 典 型 作 法 , 圆 第 一 定 义 、 圆 第 二 定 义 、 角 坐 标 方 程 、 椭 椭 直 参
完整word版椭圆的画法word文档良心出品

几何画板简明教程椭圆的画法和性质第九章椭圆的定义:一.y的距离的FF、1.在平面内,到两个定点21这的点的轨迹叫做椭圆。
F|)和等于常数(大于|F2M两焦点间的距离叫做焦点,两个定点叫做椭圆的焦距x:2.椭圆的标准方程FOF 椭圆的焦距是椭圆是上任意一点,x, y)设M(21F、,则如图建立直角坐标系,又F为2c (c>0)21、点与F(的坐标分别是F-c, 0), F(c, 0),若M112+MF|F两点的距离的和等于2a (a>c>0),则|12,a|MF|=222222ay2x?c)(x?c)??y??(1-图9 , ∴222得椭圆的标准方程-b整理化简,并且设c=ay l22yx1??. 22M ba D 3.椭圆的第二定义:x的距离和它到定直c, 0)M设动点(x, y)与定点F(FOF2ca21l的M>0)x=的距离的比是常数(a>c,线则点: cal是椭圆是椭圆的一个焦点,直线轨迹是椭圆。
点Fc是椭圆e<1)中对应于焦点F的准线。
常数e=(0<a2 图9-的离心率。
4.椭圆的参数方程:y为半径作两个>0)a>b以原点为圆心,分别以a、b (与小圆的交点,B是OA点圆,A是大圆上的一个点,点A,垂AN,过点A作AN⊥Ox,垂足为NB作BM⊥过点点的轨迹是椭圆。
足为M,当点A在大圆上运动时,M MB x为OAφ),是以Ox为始边,M设点的坐标是(x, y?|为参数,那么终边的正角,取φON |x=|ON|=OA|cosφ=acosφ,,φφ=bsin||y=NM|=OB|sin?x?acos?).φ是参数∴椭圆的参数方程是(??siny?b?3 -图9 43第九章椭圆的画法和性质二.椭圆的画法:画法1:y24-图9 ,用它们作为两个焦点;OF||OF|=|1.在x轴上取两点F、F,使2211;F|)(|CD|>|FCD.在图形外作一条线段,使|CD|=2a,221 |;|=|CDAx轴上取两点A、A,使|A3.以O为中心,在2211,并用“作图”菜单中的D';作线段C'||AF|=DD'|'4.在CD上分别取C、D',使|CC'|=11 M;D'上作点“对象上的点”功能在C'两点;同样方法P为半径作圆,两圆相交于P、||CM|、|MD5.分别以F、F为圆心,用2121两点;并将这四个点定P为半径作圆,两圆相交于P、|、|CD|DM分别以F、F为圆心,用|4123义为“追踪点”;,用“作图”菜单中的“轨迹”功能,作出椭圆。
(完整word版)几何画板实例教程
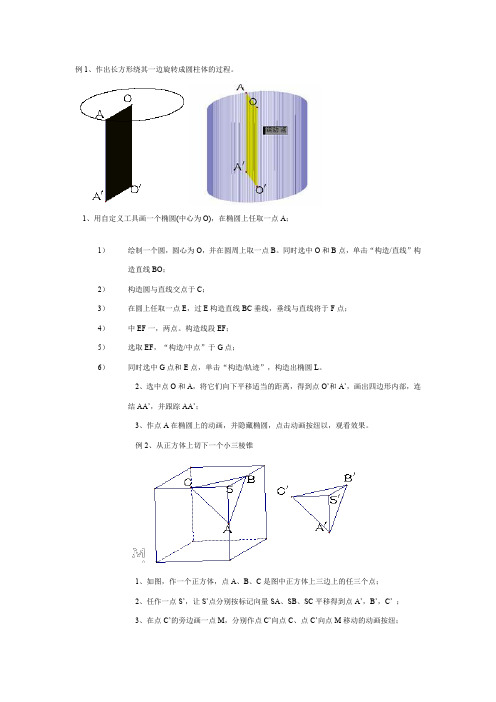
例1、作出长方形绕其一边旋转成圆柱体的过程。
1、用自定义工具画一个椭圆(中心为O),在椭圆上任取一点A;1)绘制一个圆,圆心为O,并在圆周上取一点B。
同时选中O和B点,单击“构造/直线”构造直线BO;2)构造圆与直线交点于C;3)在圆上任取一点E,过E构造直线BC垂线,垂线与直线将于F点;4)中EF一,两点。
构造线段EF;5)选取EF,“构造/中点”于G点;6)同时选中G点和E点,单击“构造/轨迹”,构造出椭圆L。
2、选中点O和A,将它们向下平移适当的距离,得到点O’和A’,画出四边形内部,连结AA’,并跟踪AA’;3、作点A在椭圆上的动画,并隐藏椭圆,点击动画按纽以,观看效果。
例2、从正方体上切下一个小三棱锥1、如图,作一个正方体,点A、B、C是图中正方体上三边上的任三个点;2、任作一点S’,让S’点分别按标记向量SA、SB、SC平移得到点A’,B’,C’ ;3、在点C’的旁边画一点M,分别作点C’向点C、点C’向点M移动的动画按纽;4、用不同颜色标出立体图形的侧面,隐藏多余的图形。
例3、作正六边形在平面内的投影1、如图,点O为旋转中心,点A旋转60度生成点B,点B旋转60度生成点C,……;作正六边形A BCDEF的内部,任选一点M,连结DM、BM,作直线AB;2、在正六边形内部(边沿)选一点N,过N分别作NN’垂直直线AB于点N’,NP平行于DM,过N’作N’P平行于BM,BM交NP于点P;3、选中点N和点P,点击轨迹命令,隐藏多余的图形,拖动点M可改变投影的形状。
例4、作一个旋转的正方体1、作线段a、b,选中a、b标记线段比;2、作圆O,作一条经过点O的直线l,在圆O上取一点A,让它以O为中心旋转90度得A’;3、作AC垂直直线l于点C,标记点C,,让点A按标记比缩放得点B,同理将点A’缩放得到点D,作点A在圆O上和动画,隐藏多余的图形;4、让点B和D绕点O旋转180度得点E和F,作四边形BDEF,让四边形BDEF向上平移适当距离,连结对应顶点。
几何画板中椭圆的几种构造方法

几何画板中椭圆的几种构造方法几何画板中椭圆的几种构造方法高二8班第二组在数学学习过程中我们发现有很多题目都能得到椭圆的方程。
我们组把它们整理发现利用几何画板也可以有很多方法来构造椭圆的图象,于是把几种画法整理如下:椭圆的构造方法一:借助于椭圆的第一定义椭圆的第一定义:平面内到两个定点F 1,F 2的距离之和为定值2a (2a >|F1F 2|)的点的轨迹。
(1)以O 为圆心,2a 为半径作圆,在圆上任取一点P ,在圆内任取一点A ;(2)连接PO 、PA ,作PA 的中垂线与PO 交于点M ,连接MA ;(3)将点M 定义为“追踪点”,选中点P ,让点P 在圆上任意转动可得到点M 的轨迹为以O ,A为焦点长轴长为2a 的椭圆。
如图:图中的MP=MA,所以OM+MA=OM+MP=OP=圆的半径,符合椭圆的第一定义。
椭圆的构造方法二:借助于椭圆的第二定义椭圆的第二定义:设动点M (x , y ) 与定点F (c , 0) 的距离和它到定直线l : x =ca a 2c 的距离的比是常数(a >c >0),则点M 的轨迹是椭圆。
点F 是椭圆的一个焦点,直线l 是椭圆中对应于焦点F 的准线。
常数e =ca (0(1)取点F 和直线L ,(点F 不在L 上)。
过点F 作一条直线,在直线上取一点P ;(2)以F 为圆心以FP 为半径作圆,度量FP的长度,取参数e=0.8(可改为其他小于1的正数) ,计算FP/e;(3)过P 点作直线L 的垂线,交L 于M 点,以M 为圆心,以FP/e为半径做圆,交垂线于N点,过N 作L 的平行线,交圆F 于A ,B 两点;(4)追踪A ,B 两点,让P 在直线PF 上任意移动可得椭圆方程。
椭圆的构造方法三:借助椭圆的参数方程1.以坐标原点O 为圆心,分别以a 、b(a>b>0)为半径画两个圆;2.在大圆上取一点A ,连接OA 与小圆交于点B ;3.过点A 作AN 垂直于Ox 轴,垂足为N ;作BM 垂直于AN ,垂足为M ;4.分别选中点M 和点A ,用“作图”菜单中的“轨迹”功能,画出椭圆。
用几何画板画椭圆的六种方法刘秀梅

用几何画板画椭圆的六种方法刘秀梅[ 录入者:编辑05 | 时间:2009-01-17 | 来源:本站| 浏览:[ 109次]椭圆在平面解析几何的教学中是一个重要的内容,利用几何画板软件可以很准确地画出椭圆图形,为教师的教和学生的学都带来了方便。
下面介绍六种画椭圆的方法。
1.利用椭圆定义椭圆定义:到两定点的距离之和为定长的点的轨迹。
利用此定义来画,步骤如下:(3)构造线段PF的中垂线MN,与线段PF交于M,与线段PF交于N;(4)构造点P在圆上的动画,追踪点M,M的轨迹就是椭圆(如图1)。
2.利用菱形画椭圆步骤如下:(1)画一个菱形ABCD,对称轴为AC、BD;(2)过D构造AB上的垂线,垂足为P,DP交AC于O,标记AC、BD为镜面,做出点P关于AC的对称点P′,关于BD的对称点P″;(3)顺次选取OPP′构造圆上的弧,再以BD为镜面,构造出对称弧;(4)顺次选取DP″P构造圆上的弧,再以AC为镜面,构造出对称弧,四段弧围成椭圆(如图2)。
3.利用定长线段的滑动一条线段AB(|AB|=2a)的两端A和B分别在x轴和y轴上滑动,线段AB的中点的轨迹就是椭圆。
步骤如下:(1)建立坐标系xoy,在x轴上任取一点M,构造线段OM,使|OM|=|AB|=2a;(2)在线段OM上任取一点A,以A为圆心,以OM为半径构造圆,交y轴于点B;(3)构造线段AB,在AB上任取一点P(非中点),利用点反射或旋转构造点P 关于x轴、y轴、原点的对称点P″、P′、P?苁,追踪点P、P′、P″、P?苁;(4)构造点A在线段OM上的动画,点P、P′、P″、P?苁的轨迹就是椭圆(如图3)。
值得一提的是椭圆规就是利用这个原理制成的,只不过点P取在了线段AB的延长线上。
4.利用参考圆画椭圆步骤如下:(1)以原点O为圆心,分别以a、b(a>b)为半径做两个圆;(2)任取大圆上的一点A,构造线段OA交小圆于点B,过点A作AN⊥OX(x轴),垂足为N;(3)过点B作BM⊥AN,垂足为M,构造点M关于y轴的对称点M′,追踪点M和M′;(4)构造点A在大圆上的动画,点M、M′的轨迹就是椭圆(如图4)。
运用几何画板绘制椭圆的有效方法

在圆锥曲线中,曲线上的点到定点的距离与到定直线的距离的商是常数e,且0<e<1时为椭圆。
椭圆教学是中学数学教学中的重点和难点,椭圆的知识和图像都极为抽象,学生很难理解。
不仅如此,有些教师在绘制椭圆图形时也会感到困难,并且准确性不够。
而运用几何画板软件画出的椭圆既准确又美观,还能增加教学的趣味性,引发学生的学习兴趣,可以让学生轻松、直观地观察并理解椭圆的定义及其性质,从而收到很好的教学效果。
几何画板以点、线、圆作为基础图形,对这些基础图形进行拼接、平移、变换、度量、构造、轨迹追踪以及对基本图形的性质进行运用。
学生可以在此过程中探究图形的内在关系并发现数学的本质,探究数学的奥妙和趣味性,激发学习数学的兴趣。
笔者结合自身教学经验,在总结、归纳、提炼和创新的基础上整理出七种常用的运用几何画板绘制椭圆的方法,分享如下:一、定义法定义法的原理是圆锥曲线的统一定义,即焦点距离与到准线距离的商是定值的点的轨迹。
椭圆的定义,即平面内一个动点到两个定点的距离之和等于常数,这个动点的轨迹叫椭圆,这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距。
绘制的具体步骤为:打开软件,新建文件,在绘画板内画线段AB 的同时在AB 上绘制出C 点,然后在AB 外选取D 、E 两点,满足DE >AB ;选中A 、C 两点进行标记向量,然后通过标记向量将D 平移,得到D ;选中D 和D 点,绘制出一个以D 为圆心,以D 和D 间距离为半径的圆并且隐藏;同理,标记B 、C 两个点为标记向量,并且作出E 的平移点到E 点,构造出圆,隐藏E 点;运用点工具做出两个圆周交点为F 、G 两点。
接下来分两种方法研究。
分别选中F 、C 和G 、C 两组点进行构造轨迹绘制出椭圆曲线,如图1所示。
图2定义法动态绘制椭圆点击F 点,点击显示、追踪交点,同理操作G 点;点击C 点,选择操作类按钮、动画、确定,完成设置;点击绘画板上的动画键,绘画板就绘制出一个椭圆,如图2所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何用几何画板画椭圆一、定义法(到两定点的距离和等于定长)选取“线段”工具,在绘图板中作一线段AB(线段AB的长度为椭圆的长轴长2a)。
用“点”工具在线段上任取一点C,按住shift键先后选中A,C点,选择“变换”→“标记向量"A→C"”。
再用“点”工具再用点工具任取一点D,选中点D,选择“变换”→“平移”,选中“按标记的向量”,然后确定,会得到点D'。
按住shift键,先后选中点D和D',选择“作图”→“以圆心和圆周上的点画圆”,选中点D',按Ctrl+H键将其隐藏。
按住shift键,先后选中B,C点,选择“变换”→“标记向量"B→C"”。
用点工具另作一点E,使其与D点的距离小于线段AB的长(线段DE的长为2c),选中点E,选择“变换”→“平移”,选中“按标记的向量”,然后确定,会得到点E'。
按住shift键,先后选中点E和E',选择“作图”→“以圆心和圆周上的点画圆”,选中点E',按Ctrl+H键将其隐藏。
按住shift键,选中两个圆的圆周,选择“作图”→“交点”(或按Ctrl+I键),作出交点F和G。
以下可以分两个方向进行:1.按住shift键,先后选中点F和点C,选择“作图”→“轨迹”,作出椭圆的上半部分;同理先后选中点G和点C,作出椭圆的下半部分(如图1)。
2.按住shift键,先后选中点F,选择“显示”→“追踪点”,同样选中点G和点C,选择“显示”→“追踪点”。
按住shift键,先后选中点C和线段AB,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“双向”、“沿着线段j”、“慢慢地”,按“动画”按钮完成设置。
这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆。
完成,存盘退出。
二、准线法(到定点的距离与到定直线的距离之比为常数e)打开一个新的绘图板,选择“图表”→“建立坐标轴”。
用“线段”工具作线段CD,在线段CD上任取一点E。
同时选中点C和点E,选择“度量”→“距离”,量出CE的长。
同样量出CD的长。
按住shift键,选中量出的CE和CD的距离,按鼠标右键弹出对话框,选择“度量”→“计算”。
在打开的计算器中选择“数值”→“距离(C到E)”。
选择“/”→“距离(C到D)”→“确定”。
在绘图板上就会出现CE和CD的比值。
用“文本工具”双击该值,弹出“度量值格式”对话框,选择“T文本格式”。
将“距离(C到E)/距离(C到D)”改成“e”,确定,完成改变。
选中点B,按Ctrl+H键隐藏,在X轴上取点F(F为椭圆的一个焦点)。
作线段GH,在其上取点I。
用上面的方法量出GI的距离,并将其距离名称改为c。
选中c和e的值,打开计算器,将c除以e的值求出,并将其名改为a。
选中a的计算值,选择“图表”→“绘制度量值”,弹出“绘制度量值”对话框。
选择“H 在横(x)轴”,确定,作出垂直于x轴的一条直线。
选中c的度量值,选择“变换”→“标记距离”,选中F点,选择“变换”→“平移”,弹出“平移”对话框,选择“按标记的距离”,确定,作出点F平移后的点F'。
先后选中点F和点F',选择“作图”→“以圆心和圆周上的点画圆”。
选中该圆周和上面作出的垂直于x轴的直线,按Ctrl+I绘出交点J和K。
选中点J和点K,选择“显示”→“追踪点”。
选中点I和线段GH,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“双向”、“沿着线段n”、“慢慢地”,按“动画”按钮完成设置。
这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆(如图2)选中CE、CD、e、c和a的值,按Ctrl+H隐藏。
完成,存盘退出。
三、同心圆法。
选择“文件”→“新绘图”,选择“图表”→“建立坐标轴”,用“圆”工具作两圆心为原点的同心圆(外圆半径长就是最终椭圆的长半轴长a,内圆半径长就是最终椭圆的短半轴长b),选中点B和圆周上的点C和D,按Ctrl+H键隐藏。
选择“显示”→“线型”→“虚线”,在外圆圆周上任取一点E,按住shift键,同时选中点A和点E,按Ctrl+L作出线段AE,同时选中线段AE和内圆圆周,按Ctrl+I 键作出交点F。
按住shift键,同时选中点E和纵坐标轴,选择“作图”→“平行线”,作出一直线,再同时选中点F和横坐标轴,选择“作图”→“平行线”,作出另一直线。
同时选中这两条直线,按Ctrl+I键作出交点G。
以下可以分两个方向进行:1.选择“显示”→“线型”→“细线”,同时选中交点G和外圆圆周上的点E,选择“作图”→“轨迹”就作出了椭圆(如图3)。
完成,存盘退出。
选择“显示”→“线型”→“细线”,选中点G,选择“显示”→“追踪点”。
按住shift键,同时选中外圆圆周上的点E和外圆圆周,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“单向”、“绕圆c2”、“快速地”,按下“动画”按钮确定。
这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆。
完成,存盘退出。
四、单圆法(1)打开一个新的绘图板,选取“圆”工具作一圆(圆的半径长即2a),选中圆周上的点B,按Ctrl+H隐藏。
在圆的内部任选一点C(A,C即椭圆的交点)。
在圆周上任取一点D,同时选中点C和点D,按Ctrl+L键作线段CD。
选中线段CD,按Ctrl+M作出CD的中点E,再同时选中点E和线段CD,选择“作图”→“垂线”,作出垂线k。
同时选中点A和点D,按Ctrl+L键作线段AD。
再同时选中垂线k和线段AD,按Ctrl+I键作出交点F,想一想,点F到点A和点C的距离是不是定值。
选中点F,按Ctrl+T键追踪点F。
选中点D和圆周,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,选择“单向”、“绕圆c1”、“正常地”,按“动画”按钮完成设置。
这时,绘图板上会出现一个“动画”按钮,双击“动画”按钮,就会自动画出椭圆(如图4)。
另外您也可以同时选中点F和点D,选择“作图”→“轨迹”也可以作出该椭圆。
完成,存盘退出五、单圆法(2)打开一个新的绘图板,选择“图表”→“建立坐标轴”,选中点B,按Ctrl+H键隐藏。
用“圆”工具作一圆,圆心为原点A,圆周上的控制点为C,选中点C,按Ctrl+H 键隐藏。
选中圆周和纵坐标轴,按Ctrl+I键作出交点D、E,在圆周上任取一点F。
选择工具箱里的“直线”工具(按下“线段”工具按钮,向右拖动鼠标,就会看到“直线”工具按钮),同时选中点E和点F,按Ctrl+L键作出过点E、F的直线。
选中点F和纵坐标轴,选择“作图”→“平行线”,作出平行于y轴的直线。
选中该直线和横坐标轴,按Ctrl+I键作出交点G。
同时选中点D和点G,按Ctrl+L键作出过点D、G的直线。
同时选中直线EF 和直线DG,按Ctrl+I键作出交点H。
选中点H,选择“显示”→“追踪点”。
同时选中点F和它所在的圆周,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,设定为“单向”、“绕圆c1”、“正常地”,按“动画”按钮确定,这时绘图板上会出现“动画”按钮此时双击“动画”按钮就会自动画出椭圆(如图5)。
完成,存盘退出。
六、三角形法。
打开一个新的绘图板,选择“图表”→“建立坐标轴”,选中点B,按Ctrl+H隐藏。
选取“线段”工具,作一任意长度的线段CD。
在纵坐标轴上任取两点E、F,使得该两点到坐标原点A的距离都大于线段CD的长。
选中点E、F,按Ctrl+L键作出线段EF。
在纵坐标轴上取一点G,使得线段AG的长小于CD。
选中点G和线段CD,选择“作图”→“以圆心和半径画圆”。
选中该圆周和横坐标轴,按Ctrl+I键作出交点H和I。
选中H点,按Ctrl+H键隐藏。
选中点I和线段CD,选择“作图”→“以圆心和半径画圆”。
选中两个圆周,按Ctrl+I 键作出交点K和J。
选中点J,按Ctrl+H键隐藏。
同时选中点G、I和K,按Ctrl+L键作出三角形。
双击坐标原点A,将其标记为中心(也可按Ctrl+F键,还可选择“变换”→“标记中心"A"”来完成该操作)。
选中点K,选择“变换”→“旋转”,弹出旋转对话框。
对话框中应该显示“关于中心原点A”,否则就是中心设得不正确。
将框中的度数改为180,确定,就会的到点K'。
同时选中点K和K',选择“显示”→“追踪点”。
再同时选中点G和线段EF(选EF时需要注意:在线段EF上单击是选中纵坐标轴,而非线段EF,再单击才是选中线段EF,然后需要单击纵坐标轴上线段EF以外的地方来取消对纵坐标轴的选中,上述操作都需要按住shift键)。
选择“编辑”→“操作类按钮”→“动画”,弹出匹配路径对话框,设置为“双向”、“沿着线段k”、“慢慢地”,按“动画”按钮完成设置。
此时双击“动画”按钮就会自动画出椭圆(如图6)。
完成,存盘退出。
另外,有两点需要注意:1.只要是相交的两条直线就可以作出椭圆,不一定要选择坐标系的x轴和y轴。
2.三角形GIK只要是固定形状不变就可以了,不一定要选择正三角形,选正三角形只是为了作图的方便七、包络线法。
打开一个新的绘图板,用“圆”工具作一圆,圆心为A。
在圆内部任取一点C,在圆周上任取一点D,连接AC和CD。
选中线段CD,按Ctrl+M键作出线段CD 的中点E,选中点E和线段CD。
选择“作图”→“垂线”作出一垂线。
选中该垂线,选择“显示”→“追踪直线”。
同时选中点D和它所在的圆周,选择“编辑”→“操作类按钮”→“动画”,弹出“匹配路径”对话框,设定为“单向”、“绕圆c1”、“慢慢地”,按“动画”按钮确定,这时绘图板上会出现“动画”按钮。
此时双击“动画”按钮就会自动画出椭圆(如图7)。
完成,存盘退出。
八、切线法。
打开一个新的绘图板,选择“图表”→“建立坐标轴”,选中点B,按Ctrl+H键隐藏。
用“圆”工具作一圆,圆心为原点A,圆周上的控制点为C,选中点C,按Ctrl+H 键隐藏。
选中圆周和横坐标轴,按Ctrl+I键作出交点D、E。
选中点D和横坐标轴,选择“作图”→“垂线”,作出垂线j,同样的方法作出过E点垂直于横坐标轴的直线k。
在圆周上任去一点F,同时选中点F和点A,按Ctrl+L键作出线段FA。
再同时选中点F和线段FA,选择“作图”→“垂线”作出该圆的切线。
选中该切线和垂线j,按Ctrl+I键作出交点G,同样的方法作出该切线和垂线k 的交点H。
连接点G和点E(同时选中两点,按Ctrl+L键),连接点H和点D。
作出线段GE和线段HD的交点I(同时选中两条线段,按Ctrl+I键)。
选中线段FA,按Ctrl+H键隐藏。
选中点I,选择“显示”→“颜色”,将颜色改为红色。
