中考试题相似三角形的应用.docx
2025届中考数学复习专项(相似三角形-手拉手旋转型综合应用)练习(附答案)

2025届中考数学复习专项(相似三角形-手拉手旋转型综合应用)练习1.如图(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出ΔOB1C1;(2)点B的对应点B1的坐标是,点C的对应点C1的坐标是.2.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.(1)求证:△ABC∽△ADE;(2)判断△ABD与△ACE是否相似?并证明.3.如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC,AC的中点,连接DE.(1)求:的值;(2)将△CDE绕点C逆时针方向旋转一定的角度,的大小有无变化?请仅就图2的情形给出证明.4.如图,在△ABC与△DEC中,已知∠ACB=∠DCE=90°,AC=6,BC=3,CD=5,CE=2.5,连接AD,BE.(1)求证:△ACD∽△BCE;(2)若∠BCE=45°,求△ACD的面积.5.问题背景:如图(1),已知△ABC∽△ADE,求证:△ABD∽△ACE;尝试应用:如图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE =30°,AC与DE相交于点F.点D在BC边上,,求的值.6.如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,求证:(1)△ABC∽△ADE(2)若AC:BC=3:4,求BD:CE为多少7.【问题背景】如图1,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,由已知可以得到:①△ ≌△ ;②△ ∽△ .【尝试应用】如图2,在△ABC和△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE =30°,求证:△ACE∽△ABD.【问题解决】如图3,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE =30°,AC与DE相交于点F,点D在BC上,,求的值.8.如图,点B在线段CD上,在CD的同一侧作两个等腰直角△ABC和△BDE,且∠ACB =∠BED=90°,AD与CE,BE分别交于点P,M,连接PB.(1)若AD=k•CE,则k的值是;(2)求证:△BMP∽△DME;(3)若BC=,P A=3,求PM的长.9.如图1,在Rt△ABC中,AC=BC=5,等腰直角△BDE的顶点D,E分别在边BC,AB 上,且BD=,将△BDE绕点B按顺时针方向旋转,记旋转角为α(0°≤α<360°).(1)问题发现当α=0°时,的值为,直线AE,CD相交形成的较小角的度数为;(2)拓展探究试判断:在旋转过程中,(1)中的两个结论有无变化?请仅就图2的情况给出证明:(3)问题解决当△BDE旋转至A,D,E三点在同一条直线上时,请直接写出△ACD的面积.。
九年级数学相似三角形典型例题

九年级数学相似三角形典型例题一、利用相似三角形的判定定理证明相似例1:已知:在△ABC和△DEF中,∠A = ∠D = 60°,AB = 4,AC = 8,DE = 2,DF = 4。
求证:△ABC∽△DEF。
解析:1. 我们看相似三角形的判定定理。
对于两个三角形,如果它们的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
2. 在本题中:计算公式,公式。
并且已知∠A = ∠D = 60°。
因为公式且∠A = ∠D,所以根据相似三角形判定定理中的“两边对应成比例且夹角相等的两个三角形相似”,可以得出△ABC∽△DEF。
二、相似三角形性质的应用(求边长)例2:已知△ABC∽△A'B'C',相似比为公式,若AB = 6,则A'B'的长为多少?解析:1. 因为相似三角形对应边成比例。
设A'B' = 公式。
已知相似比公式。
2. 又已知公式,AB = 6,所以公式。
通过交叉相乘可得:公式。
即公式,解得公式,所以A'B'的长为9。
三、利用相似三角形解决实际问题(测量高度)例3:在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,求这棵大树的高度。
解析:1. 因为在同一时刻,太阳光下不同物体的高度和影长成正比。
设大树的高度为公式米。
可以得到两个相似三角形,一个是由小强及其影子构成,另一个是由大树及其影子构成。
2. 根据相似三角形的性质,对应边成比例。
则公式。
交叉相乘可得:公式。
计算得公式,解得公式米。
所以这棵大树的高度是9.6米。
浙教新版九年级上册《4.5 相似三角形的性质及其应用》2024年同步练习卷(3)+答案解析

浙教新版九年级上册《4.5相似三角形的性质及其应用》2024年同步练习卷(3)一、选择题:本题共4小题,每小题3分,共12分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.如图所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G均在小正方形的顶点上,则的重心是()A.点GB.点DC.点ED.点F2.如图,在中,E,G分别是AB,AC上的点,,的平分线AD交EG于点F,若,则()A.B.C.D.3.如图,的两条中线AD和BE相交于点G,过点E作交AD于点F,则FG:AG是()A.1:4B.1:3C.1:2D.2:34.如图,正方形ABCD中,E为CD的中点,,交BC于点F,则与的大小关系为()A.B.C.D.无法确定二、填空题:本题共6小题,每小题3分,共18分。
5.如图,在中,点D,E分别是BC,AC的中点,AD与BE相交于点若,则EF的长是______.6.如图,AD是的高,AE是的外接圆的直径,且,,,则的直径______.7.点G是的重心,,如果,那么AB的长是______.8.如图,E,F分别为AC,BC的中点,D是EC上一点,且若,,则BE的长为______.9.如图,在等腰中,,,点E在边CB上,,点D在边AB上,,垂足为F,则AD的长为______.10.如图,点D在的边BC上,已知点E、点F分别为和的重心,如果,那么两个三角形重心之间的距离EF的长等于______.三、解答题:本题共3小题,共24分。
解答应写出文字说明,证明过程或演算步骤。
11.本小题8分已知,如图,在中,CD是斜边上的中线,交BC于点F,交AC的延长线于点∽吗?为什么?你能推出结论吗?请试一试.12.本小题8分已知:如图,在中,点D、E分别在边BC、AB上,,AD与CE相交于点F,求证:;求证:13.本小题8分如图,在中,,,动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒,连接若与相似,求t的值;连接AN,CM,若,求t的值.答案和解析1.【答案】B【解析】解:取BC的中点N,取AC的中点M,连接AN,BM,如图所示,则AN与BM的交点为D,故点D是的重心,故选:取BC的中点N,取AC的中点M,连接AN,BM,然后根据图形可知AN与BM的交点为D,即可得到点D 为的重心.本题考查三角形的重心,解答本题的关键是明确三角形的重心是三角形中线的交点.2.【答案】C【解析】解:,,,,∽,故选:根据两组对应角相等可判断∽,可得,则可得出结论.本题考查了相似三角形的判定与性质,灵活运用定理是关键.3.【答案】A【解析】【分析】本题考查的是三角形的重心的概念和性质、平行线分线段成比例定理的应用,三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍,根据重心的性质得到,,根据平行线分线段成比例定理计算即可.【解答】解:的两条中线AD和BE相交于点G,点G是的重心,,,,,::4,故选:4.【答案】C【解析】解:,,,,∽,且相似比为2,,,又,∽,易证∽,求得CF的长,可得根据勾股定理即可求得AE、EF的长,即可判定∽,即可解题.本题考查了相似三角形的判定,相似三角形对应边比值相等的性质,相似三角形对应角相等的性质,本题中求证∽是解题的关键.5.【答案】3【解析】解:点D,E分别是BC,AC的中点,,且,,,,故答案为:由题意可知,DE是的中线,则,且,可得,代入BF的长,可求出EF的长,进而求出BE的长.本题主要考查三角形中位线,平行线分线段成比例等知识,熟练掌握相关知识是解题的关键.6.【答案】【解析】【分析】本题考查了圆周角定理,相似三角形的性质和判定的应用,解此题的关键是求出∽首先根据两个对应角相等可以证明三角形相似,再根据相似三角形的性质得出关于AE的比例式,计算即可.【解答】解:由圆周角定理可知,,,,∽::AC,,,,::5,,故答案为:7.【答案】6【解析】解:如图,AD为AB边上的中线,点G是的重心,,,,故答案为先根据三角形重心的性质得到,则,然后根据直角三角形斜边上的中线性质得到AB的长.本题考查了三角形的重心:重心到顶点的距离与重心到对边中点的距离之比为2:也考查了直角三角形斜边上的中线性质.8.【答案】【解析】解:,,,∽,,,,E,F分别为AC,BC的中点,,,解得:故答案为:由可得:,结合公共角,可证得∽,从而利用相似三角形的对应中线之比等于相似比即可求BE的长.本题主要考查相似三角形的判定与性质,解答的关键是明确相似三角形的对应中线的之等于相似比.9.【答案】【解析】解:过D作于H,在等腰中,,,,,,,,,,∽,,,,,,,故答案为:过D作于H,根据等腰三角形的性质得到,,求得,得到,根据相似三角形的性质即可得到结论.本题考查了相似三角形的判定和性质,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.10.【答案】【解析】解:如图,连接AE并延长交BD于G,连接AF并延长交CD于H,点E、F分别是和的重心,,,,,,,,,,∽,,,故答案为:连接AE并延长交BD于G,连接AF并延长交CD于H,根据三角形的重心的概念、相似三角形的性质解答.本题考查了三角形重心的概念和性质,三角形的重心是三角形中线的交点,三角形的重心到顶点的距离等于到对边中点的距离的2倍.11.【答案】证明:,,,,,∽;为的中线,,,又,,又是公共角,∽,,即【解析】根据题意,得,,则,易证∽;由中,CD是斜边上的中线,得,则,又,所以,又是公共角,所以∽,即可得出;本题主要考查了直角三角形和相似三角形的判定与性质,掌握直角三角形斜边上的中线等于斜边的一半,是解答本题的关键.12.【答案】证明:,,,,,,∽,,;∽,,即,,,∽,,,,【解析】根据等腰三角形的性质得到,,推出∽,根据相似三角形的性质得到,于是得到;根据相似三角形的性质得到,即,推出∽,根据相似三角形的性质得到,于是得到,等量代换即可得到结论.本题考查了相似三角形的判定和性质,等腰三角形的性质,三角形的外角的性质,证得∽是解题的关键.13.【答案】解:,,,,由题意得,,当∽时,,即,解得:;当∽时,,即,解得:,综上所述,与相似时,t的值为或;如图,过点M作于点D,,,∽,,,,,,,,,,,,,,,∽,,即,解得:【解析】根据勾股定理求出AB,分∽、∽两种情况,根据相似三角形的性质列出比例式,计算即可;过点M作于点D,分别证明∽,∽,根据相似三角形的性质列出比例式,计算即可.本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.。
相似三角形的性质及应用练习题1

相似三角形的性质及应用练习卷一、填空题1.已知两个相似三角形的相似比为3, 则它们的周长比为;2.若△ABC∽△A′B′C′, 且, △ABC的周长为12cm, 则△A′B′C′的周长为;3、如图1, 在△ABC中, 中线BE、CD相交于点G, 则= ;S△GED: S△GBC= ;4.如图2, 在△ABC中, ∠B=∠AED, AB=5, AD=3, CE=6, 则AE= ;5.如图3, △ABC中, M是AB的中点, N在BC上, BC=2AB, ∠BMN=∠C, 则△∽△ ,相似比为 , = ;6、如图4, 在梯形ABCD中, AD∥BC, S△ADE: S△BCE=4: 9, 则S△ABD: S△ABC= ;7、如图5, 在△ABC中, BC=12cm, 点D、F是AB的三等分点, 点E、G是AC的三等分点, 则DE+FG+BC= ;8、两个相似三角形的周长分别为5cm和16cm, 则它们的对应角的平分线的比为;9、两个三角形的面积之比为2: 3, 则它们对应角平分线的比为 , 对应边的高的比为;对应边的中线的比周长的比10、已知有两个三角形相似, 一个边长分别为2、3、4, 另一个三角形最长边长为12, 则x、y的值为;二、选择题11.下列多边形一定相似的为()A.两个矩形B.两个菱形C.两个正方形D.两个平行四边形12、在△ABC中, BC=15cm, CA=45cm, AB=63cm, 另一个和它相似的三角形的最短边是5cm, 则最长边是()A.18cmB.21cmC.24cmD.19.5cm13、如图, 在△ABC中, 高BD.CE交于点O, 下列结论错误的是()A.CO·CE=CD·CA B、OE·OC=OD·OBC.AD·AC=AE·AB D、CO·DO=BO·EO14.已知, 在△ABC 中, ∠ACB=900, CD ⊥AB 于D, 若BC=5, CD=3, 则AD 的长为( )A.2.25B.2.5C.2.75D.315.如图, 正方形ABCD 的边BC 在等腰直角三角形PQR 的底边QR 上,其余两个顶点A.D 在PQ 、PR 上, 则PA :PQ 等于( )A.1:B.1: 2C.1: 3D.2: 316.如图, D 、E 分别是△ABC 的边AB 、AC 上的点, = =3,且∠AED=∠B, 则△AED 与△ABC 的面积比是( )A 、1: 2B 、1: 3C 、1: 4D 、4: 9三、解答题17、如图, 已知在△ABC 中, CD=CE, ∠A=∠ECB, 试说明CD2=AD ·BE 。
专题4.2 相似三角形的应用(基础)(解析版)

专题4.2 相似三角形的应用目录相似三角形的应用(影子问题) (1)相似三角形的应用(路灯和影长) (3)相似三角形的应用(平面镜测高) (5)相似三角形综合应用 (8)相似三角形与几何综合运用 (12)相似三角形的应用(影子问题)【例1】在相同时刻的物高与影长成比例,如果高为1.5m的测杆的影长为3m,那么影长为30m的旗杆的高是( )A.15m B.16m C.18m D.20m【解答】解:设影长为30m的旗杆的高是xm,Q在相同时刻物高与影长成比例,高为1.5m的测杆的影长为3m,\1.5330x=,解得15()x m=.故选:A.【变式训练1】《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈10=尺,1尺10=寸),则竹竿的长为( )A.五丈B.四丈五尺C.一丈D.五尺【解答】解:设竹竿的长度为x尺,Q竹竿的影长=一丈五尺15=尺,标杆长=一尺五寸 1.5=尺,影长五寸0.5=尺,\1.5150.5x=,解得45x=(尺).故选:B .【变式训练2】小明身高1.5米,在操场的影长为2米,同时测得教学大楼在操场的影长为60米,则教学大楼的高度应为( )A .45米B .40米C .90米D .80米【解答】解:Q 在相同时刻,物高与影长组成的直角三角形相似,1.5:2\=教学大楼的高度:60,解得教学大楼的高度为45米.故选:A .【变式训练3】小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB 的影长OC 为16米,OA 的影长OD 为20米,小明的影长FG 为2.4米,其中O 、C 、D 、F 、G 五点在同一直线上,A 、B 、O 三点在同一直线上,且AO OD ^,EF FG ^.已知小明的身高EF 为1.8米,求旗杆的高AB .【解答】解://AD EG Q ,ADO EGF \Ð=Ð,90AOD EFG Ð=Ð=°Q ,AOD EFG \D D ∽,\AO OD EF FG =,即201.8 2.4AO =,15AO \=,同理得BOC AOD D D ∽,\BO OC AO OD =,即161520BO =,12BO \=,15123AB AO BO \=-=-=(米),答:旗杆的高AB 是3米.相似三角形的应用(路灯和影长)【例2】如图,小明同学用自制直角三角形纸板DEF 测量树的高度AB ,他调整自己的位置,设法使斜边DF 保持水平,并且边DE 与点B 在同一直线上.已知纸板的两条边50DF cm =,40DE cm =,测得边DF 离地面的高度 1.5AC m =,12CD m =,则树高AB = m .【解答】解:在Rt DEF D 中,222DE EF DF +=,即:2224050EF +=,30EF \=,由题意得:90BCD DEF Ð=Ð=°,CDB EDF Ð=Ð,DCB DEF \D D ∽,CB DC EF DE=,300.3EF cm m ==Q ,400.4DE cm m ==,12CD m =,\120.30.4BC =,解得:9BC =米,1.5AC m =Q ,1.5910.5()AB AC BC m \=+=+=.故答案是:10.5【变式训练1】如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m 时,标准视力表中最大的“E ”字高度为72.7mm ,当测试距离为3m 时,最大的“E ”字高度为( )A.4.36mm B.29.08mm C.43.62mm D.121.17mm 【解答】解:由题意得://CB DF,\DF AD BC AB=,3AD m=Q,5AB m=,72.7BC mm=,\372.75DF=,43.62() DF mm\=,故选:C.【变式训练2】利用标杆CD测量建筑物的高度的示意图如图所示,若标杆CD的高为1.5米,测得2DE=米,18BD=米,则建筑物的高AB为米.【解答】解://AB CDQ,EBA ECD\D D∽,\CD EDAB EB=,即1.52218AB=+,15AB\=(米).故答案为:15【变式训练3】如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为.【解答】解://DE BCQ,ADE ACB\D D∽,即DE AE BC AB=,则40.84 3.5h=+,1.5h\=,经检验, 1.5h=是原方程的解,故答案为:1.5米.相似三角形的应用(平面镜测高)【例3】如图是小玲设计用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB BD^,CD BD^.且测得 1.4AB=米, 2.1BP=米,12PD=米.那么该古城墙CD的高度是米.【解答】解:APB CPDÐ=ÐQ,ABP CDPÐ=Ð,ABP CDP\D D∽\AB BPCD PD=即1.42.112CD=解得:8CD=米.【变式训练1】如图,为了测量操场上一棵大树的高度,小英拿来一面镜子,平放在离树根部5m的地面上,然后她沿着树根和镜子所在的直线后退,当她后退1m时,正好在镜中看见树的顶端.小英估计自己的眼睛到地面的距离为1.6m,则大树的高度是m.【解答】解:ABC DBEÐ=Ð=°,ACB DEBÐ=ÐQ,90∽,ABC DBE\D D\=,::BC BE AC DE即1:5 1.6:DE=,\=,DE m8()故答案为:【变式训练2】如图,在测量旗杆高度的数学活动中,某同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部.若眼睛距离地面 1.5AB m=,BC m=,同时量得2 =,则旗杆高度DE=m.12CD m^,Q,DE BD^【解答】解:AB BD\Ð=Ð=°,90ABC EDCQ,ACB DCEÐ=Ð∽,ABC EDC\D D\AB BC DE CD=,\1.5212 DE=,9() DE m\=,故答案为:9【变式训练3】春暖花开,草长莺飞,学校开展了校外实践活动某数学社团成员小明、小王和小丽发现在活动根据地远处的小山坡上有一棵小树,如图所示,记小树的位置为点E,他们想利用皮尺、平面镜等测量工具测量小树到山脚下的距离(即DE的长度):小明站在点B处,让小丽移动平面镜至点C处,此时小明在平面镜内可以看到点E.小王、小丽用皮尺测得BC为3米,CD为18米,同时测得120CDEÐ=°.已知小明的眼睛到地面的距离1.5AB=米,请根据以上数据,求DE的长度.(结果保留根号)【解答】解:过E作EF BC^于F,120CDEÐ=°Q,60EDF\Ð=°,设EF为x米,DF=米,DE x=米,90B EFCÐ=Ð=°Q,ACB ECDÐ=ÐQ,ABC EFC\D D∽,\AB BC EF FC=,\1.5x=,解得:x=,=),答:DE米.相似三角形综合应用【例4】青龙寺是西安最著名的樱花观赏地,品种达到了13种之多,每年3、4月陆续开放的樱花让这里成为了花的海洋.一天,小明和小刚去青龙寺游玩,想利用所学知识测量一棵樱花树的高度(樱花树四周被围起来了,底部不易到达).小明在F处竖立了一根标杆EF,小刚走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上.此时测得小刚的眼睛到地面的距离 1.6DC=米;然后,小刚在C处蹲下,小明平移标杆到H处时,小刚恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小刚的眼睛到地面的距离==米,2CF=米, 1.6FH=米,点C、F、H、A在一条EF GH0.8MC=米.已知 2.4直线上,点M在CD上,CD AC^.根据以上测量过^,AB AC^,EF AC^,GH AC程及测量数据,请你求出这棵樱花树AB的高度.^于点P,交EF于点N,过点M作MQ AB^于点Q,交GH 【解答】解:过点D作DP AB于点K,==,2由题意可得:DP MQ ACAP DC==米,==米,MK CH=, 1.6DN CFAQ HK MC===米.0.8Ð=Ð=°,END BPDÐ=ÐEDN BDPQ,90DEN DBP \D D∽,\BP DP EN DN=,\1.62.4 1.62 AB AC-=-.GMK BMQ Ð=ÐQ,90GKM BQMÐ==°,GMK BMQ\D D∽\BQ QM GK MK=.\0.82.40.82 1.6 AB AC-=-+.8.8AB\=(米).答:这棵樱花树AB的高度是8.8米.【变式训练1】某校社会实践小组为了测量古塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,古塔的塔尖点B正好在同一直线上,测得 1.2EC=米,将标杆向后平移到点G处,这时地面上的点F,标杆的顶端点H,古塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与古塔底处的点A在同一直线上),这时测得 1.8FG=米,20CG=米,请你根据以上数据,计算古塔的高度AB.【解答】解:根据题意得,EDC EBAD D∽,FHG FBAD D∽,\DC ECBA EA=,GH FGAB AF= DC HG=Q,\FG EC AF EA=,\1.8 1.21.820 1.2CA AC=+++,40CA\=(米),\2 1.21.240 AB=+,68.7AB\»米,答:古塔的高度AB约为68.7米.【变式训练2】学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑AB的高度(如图1).如图2,在地面BC上取E,G两点,分别竖立两根高为2m的标杆EF和GH,两标杆间隔EG为23m,并且古建筑AB,标杆EF和GH在同一竖直平面内,从标杆EF后退2m到D处,从D处观察A点,A,F,D三点成一线;从标杆GH后退4m到C处,从C处观察A点,A,H,C三点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度.【解答】解:设BE y=m,由题意可知,ABD FEDD D∽,ABC HGCD D∽,\EF EDAB BD=,GC HGBC AB=,2EF HG==Q,\ED GC BD BC=,\242423y y=+++,解得:23()y m=,则ED EFBD AB=,即22232AB=+,解得:25()AB m=,答:该古建筑的高度为25米.【变式训练3】阳光明媚的一天实践课上,亮亮准备用所学知识测量教学楼前一座假山AB的高度,如图,亮亮在地面上的点F处,眼睛贴地观察,看到假山顶端A、教学楼顶端C在一条直线上.此时他起身在F处站直,发现自己的影子末端和教学楼的影子末端恰好重合于点G处,测得2FG=米,亮亮的身高EF为1.6米.假山的底部B处因有花园围栏,无法到达,但经询问和进行部分测量后得知,9BF=米,点D、B、F、G在一条直线上,CD DG^,AB DG^,EF DG^,已知教学楼CD的高度为16米,请你求出假山的高度AB.【解答】解:CD DG^Q,EF DG^,//EF CD\,GEF GCD\D D∽,\EF GFCD GD=,即1.621692DB=++,解得9BD=.CD DG^Q,AB DG^,//AB CD\,FAB FCD\D D∽,\AB FBCD FD=,即91699AB=+,解得8AB =,\假山的高度AB 为8米.相似三角形与几何综合运用【例5】如图,ABC D 是一块锐角三角形余料,边120BC mm =,高80AD mm =,要把它加工成矩形零件PQMN ,使一边在BC 上,其余两个顶点分别在边AB 、AC 上.(1)求证:APQ ABC D D ∽;(2)若这个矩形的边:2:1PN PQ =,则这个矩形的长、宽各是多少?【解答】解:(1)Q 四边形PNQM 为矩形,//MN PQ \,即//PQ BC ,APQ ABC \D D ∽;(2)设边宽为x mm ,则长为2x mm ,Q 四边形PNMQ 为矩形,//PQ BC \,AD BC ^Q ,PQ AD \^,80212080x x -=//PQ BC Q ,APQ ABC \D D ∽,\PQ AH BC AD=,由题意知PQ x =mm ,80AD mm =,120BC mm =,2PN x =mm ,\80212080x x -=,解得30x =,260x \=.即长为60mm ,宽为30mm .答:矩形的长60mm ,宽为30mm .【变式训练1】如图,一块直角三角形木板,直角边AB 的长为1.5米,三角形的面积为1.5平方米,工人师傅要用它截取一个面积最大的正方形桌面,请甲、乙两位同学设计加工方案,甲同学的设计方案如图(1),乙同学的设计方案如图(2),你认为哪位同学设计的正方形面积大?请说明理由.【解答】解:甲同学设计的正方形面积大,理由如下:1.5AB m =Q ,三角形的面积为1.5平方米,2BC m \=,设正方形边长为x m ,图(1)中,//DE AB Q ,CDE CBA \D D ∽,\DE CD AB BC =,\21.52x x -=,解得67x =;图(2)中,由勾股定理得, 2.5()AC m ===,过点B 作BH AC ^于H ,交DE 于P ,由面积得1122AC BH AB BC ´´=´´,2 1.56()2.55BH m ´\==,//DE AC Q ,BDE BAC \D D ∽,\DE BP AC BH=,\6562.55x x -=,解得3037x =,Q 630737>,\甲同学设计的正方形面积大.【变式训练2】一块材料的形状是等腰ABC D ,底边120BC cm =,高120AD cm =.(1)若把这块材料加工成正方形零件,使正方形的一边在BC 上,其余两个顶点分别在AB ,AC 上(如图1),则这个正方形的边长为多少?(2)若把这块材料加工成正方体零件(如图2,阴影部分为正方体展开图),则正方体的表面积为多少?【解答】解:(1)设正方形边长EH 为x cm ,AD Q 是ABC D 的高,90ADB \Ð=°,Q 四边形EFGH 是正方形,//EH BC \,90AKE ADB \Ð=Ð=°,//EH BC Q ,AEH ABC \D D ∽,\EH AK BC AD =,\120120120x x -=,60x \=,答:这个正方形的边长为60cm ;(2)设正方形边长MN 为a cm ,AD Q 为ABC D 的高,90ADB \Ð=°,//MN BC Q ,90APM ADB \Ð=Ð=°,//MN BC Q ,AMN ABC \D D ∽,\MN AP BC AD =,\1204120120a a -=,24a \=,2266243456a \=´=,答:正方体的表面积为23456cm .【变式训练3】如图,ABC D 是等腰三角形铁板余料,其中20AB AC cm ==,24BC cm =,若ABC D 上截出一矩形零件DEFG ,使EF 在边BC 上,点D 、G 分别在AB 、AC 上.(1)设EF xcm =,2DEFG S ycm =矩形,试写出y 与x 的函数关系式;(2)问截得的矩形DEFG 的长、宽为何值时,该矩形的面积等于三角形铁板余料面积的一半?【解答】解:(1)ABC D Q 是等腰三角形,AH BC ^,12BH CH BC \==(三线合一),则16()AH cm =,设EF xcm =,2S ycm =矩形,Q 四边形DGFE 是矩形,//DG BC \,ADG ABC \D D ∽,故AP DG AH BC =,即1624AP x =,故23AP x =.222(16)1633y DG DE x x x x \=×=-=-+;(2)根据题意得,2211162416322x x -+=´´´,解得:12x =,21683x \-=,答:矩形DEFG 的长、宽分别为12和8时,该矩形的面积等于三角形铁板余料面积的一半.一.选择题(共8小题)1.一个直角三角形木架的两条直角边的边长分别是30cm ,40cm .现要做一个与其相似的三角形木架,如果以60cm 长的木条为其中一边,那么另两边中长度最大的一边最多可达到( )A .60cmB .75cmC .100cmD .120cm【解答】解:Q 一个直角三角形木架的两条直角边的边长分别是30cm ,40cm ,\50()cm =,Q 现要做一个与其相似的三角形木架,以60cm 长的木条为其中一边,\当另两边中长度最大的一边最长,则两三角形的相似比为:30:601:2=,故设要做的三角形最长边长为:502100()cm ´=.故选:C .2.如图,在测量旗杆高度的数学活动中,小达同学在脚下放了一面镜子,然后向后退,直到他刚好在镜子中看到旗杆的顶部.若眼睛距离地面 1.5AB =米,同时量得2BC =米,10CD =米,则旗杆高度DE 为( )A .7.5米B .403米C .7米D .9.5米【解答】解:AB BD ^Q ,DE BD ^,90ABC EDC \Ð=Ð=°,ACB DCE Ð=ÐQ ,ABC EDC \D D ∽,\AB BC DE CD=,1.5210DE =,7.5DE \=,故选:A .3.如图,有一块三角形余料ABC ,120BC mm =,高线90AD mm =,要把它加工成一个矩形零件,使矩形的一边在BC 上,点P 、M 分别在AB ,AC 上,若满足:2:1PM PQ =,则PQ 的长为( )A .36mmB .40mmC .50mmD .120mm【解答】解:如图,设AD 交PN 于点K .:2:1PM PQ =Q ,\可以假设2MP k =mm ,PQ k =mm .Q 四边形PQNM 是矩形,//PM BC \,APM ABC \D D ∽,AD BC ^Q ,//BC PM ,AD PN \^,\PM AK BC AD =,\29012090k k -=,解得36k =,36PQ mm \=.故选:A .4.如图,王华把一面很小的镜子水平放置在离树底(点)8B 米的点E 处,然后沿着直线BE 后退到点D ,这时恰好在镜子里看到树梢(点)A ,已知4DE =米,王华目高 1.6CD =米,则树的高度AB为( )A.4.8米B.3.2米C.8米D.20米【解答】解:根据题意得CED AEBÐ=ÐQ,CDE ABEÐ=Ð,CED AEB\D D∽,::CD AB DE BE\=,即1.6:4:8AB=,3.2AB\=,答:树的高度AB为3.2m.故选:B.5.如图,某“综合与实践”小组为测量河两岸A,P两点间的距离,在点A所在岸边的平地上取点B,C,D,使A,B,C在同一条直线上,且AC AP^;使CD AC^且P,B,D三点在同一条直线上.若测得10AB m=,2BC m=,6CD m=,则A,P两点间的距离为( )A.60m B.40m C.30m D.20m【解答】解:AP AC^Q,CD AC^,90A C\Ð=Ð=°,ABP CBDÐ=ÐQ,APB DCB\D D∽,\AB AP BC DC=,10AB m=Q,2BC m=,6CD m=,10630()2AB DC AP m BC ×´\===.故选:C .6.据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O ,物体AB 在幕布上形成倒立的实像CD .若物体AB 的高为6cm ,小孔O 到物体和实像的水平距离BE ,CE 分别为8cm ,6cm ,则实像CD 的高度为( )A .4cmB .4.5cmC .5cmD .6cm【解答】解://AB CD Q ,OAB OCD \D D ∽,\CD CE AB BE =,\668CD =,4.5CD \=答:实像CD 的高度为4.5cm ,故选:B .7.如图,小明同学用自制的直角三角形纸板DEF 测量树的高度AB ,他调整自己的位置,设法使斜边DF 保持水平,并且边DE 与点B 在同一直线上.已知纸板的两条直角边30DE cm =,15EF cm =,测得边DF 离地面的高度 1.6AC m =,10CD m =,则树高AB 长为( )A .21.6mB .6.6mC .20.6mD .7.6m【解答】解:D D Ð=ÐQ ,DEF BCD Ð=Ð,DEF DBC\D D∽,\DE CDEF BC=,即30100015BC=,解得:500BC=,5BC m\=,1.6AC m=Q,1.65 6.6()AB AC BC m\=+=+=,即树高6.6m.故选:B.8.大约在两千四五百年前,如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是9cm,则蜡烛火焰的高度是( )A.6cm B.8cm C.10cm D.12cm【解答】解:设蜡烛火焰的高度是x cm,由相似三角形对应高的比等于相似比得到:10159x=.解得6x=.即蜡烛火焰的高度是6cm.故选:A.二.填空题(共4小题)9.古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测金字塔的高度.如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA 是268米,则金字塔的高度BO是 134 米.【解答】解:据相同时刻的物高与影长成比例,设金字塔的高度BO 为x 米,则可列比例为,42268x=,解得:134x =,经检验,134x =是原方程的解,134BO \=.故答案为:134.10.如图,小卓利用标杆EF 测量旗杆AB 的高度,测得小卓的身高 1.8CD =米,标杆 2.4EF =米,1DF =米,11BF =米,则旗杆AB 的高度是 9 米.【解答】解:CG 的延长线交AB 于H ,如图,易得 1.8GF BH CD m ===,1CG DF m ==,11GH BF m ==,2.4 1.80.6EG EF GF m m m \=-=-=,//EG AH Q ,CGE CHA \D D ∽,\EG CG AH CH =,即0.61111AH =+,7.2AH \=,7.2 1.89()AB AH BH m \=+=+=,即旗杆AB 的高度是9m .故答案为:9.11.有一块三角形的草坪,其中一边的长为10m.在这块草坪的图纸上,这条边的长为5cm.已知图纸上的三角形的周长为15cm,则这块草坪的周长为 30 m.【解答】解:设这块草坪的周长为x m,根据题意可得:10515x=,解得:30x=,故答案为:30.12.如图是步枪在瞄准时的示意图,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD 为50cm,若从眼睛到准星的距离OE为0.5m,则眼睛到目标的距离OF为 125 m.【解答】解:设眼睛到目标的距离为x m,0.8OE m=,0.20.002AB cm m==,500.5CD cm m==,//AB CDQ,OBE ODF\D D∽,\AB OE CD OF=,即0.0020.5 0.5x=,解得125x=.答:眼睛到目标的距离OF为125m,故答案为:125.三.解答题(共3小题)13.位于沱河南岸的永城沱南生态广场,有座雕塑《汉韵南风袅袅歌》,雕塑由主体和书着《永城赋》的基座两部分构成(如图),其立意是“这里是汉兴腹地,这里是豫东江南¼¼”九1×班数学社团的同学们想利用学过的测量旗杆高度的方法测量这座雕塑(含基座,下同)的高度(从雕塑周围地平面算起),已知负责测量的小永身高为h米(眼睛以上的高度忽略不计),测量时小永的影长为a米,雕塑的影长为b米;利用小镜测量时,小永离镜子的距离为c米,镜子离雕塑的最高点所在直线的距离为d米.请你帮助小永选择其中一个方案,画出图形并计算出雕塑的高度(结果用含字母的式子表示).【解答】解:Q小永身高为h米(眼睛以上的高度忽略不计),测量时小永的影长为a米,雕塑的影长为b米,\雕塑的高度hba=米,答:雕塑的高度为hba米.14.如图,利用标杆BE测量建筑物CD的高度.已知标杆BE高1.2m,测得 1.6AB m=,28AC m=,点A,E,D在同一直线上,点B在AC上.求该建筑物CD的高度.【解答】解:EB AC^Q,DC AC^,90EBA DCA\Ð=Ð=°,A AÐ=ÐQ,EBA DCA\D D∽,\BE AB CD AC=,1.2BE=Q, 1.6AB=,28AC=,\1.2 1.628 CD=,21 CD\=,\该建筑物CD的高度是21m.15.为了加快城市发展,保障市民出行方便,某市在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥AF的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A ,再在河岸的这一边选出点B 和点C ,分别在AB 、AC 的延长线上取点D 、E ,使得//DE BC .经测量,120BC =米,210DE =米,且点E 到河岸BC 的距离为60米.已知AF BC ^于点F ,请你根据提供的数据,帮助他们计算桥AF 的长度.【解答】解:如图所示,过E 作EG BC ^于G ,//DE BC Q ,ABC ADE \D D ∽,\47AC BC AE DE ==,\43AC EC =,AF BC ^Q ,EG BC ^,//AF EG \,ACF ECG \D D ∽,\AF AC EG EC =,即4603AF =,解得80AF =,\桥AF 的长度为80米.。
相似三角形的应用-2022年中考数学一轮复习考点(浙江专用)(解析版)

考点15 相似三角形的应用【命题趋势】相似三角形的应用在中考中主要考察热点有:8字图、A字图等简单相似模型。
出题类型可以是选择填空这类小题,也可以是18~19这类解答题,难度通常不大,问题背景多以现实中的实物如树高、楼高、物体尺寸等为背景,提炼出数学模型,进而利用(或构造)简单相似模型求解长度等问题。
【中考考查重点】一、相似三角形在实际生活中的应用二、位似图形三、相似三角形与函数综合考向一:相似三角形在实际生活中的应用相似三角形在实际生活中的应用:(一)建模思想:建立相似三角形的模型(二)常见题目类型:1.利用投影、平行线、标杆等构造相似三角形求解2.测量底部可以到达的物体的高度3.测量底部不可以到达的物体的高度4.测量河的宽度【同步练习】1.如图,小明周末晚上陪父母在马路上散步,他由灯下A处前进4米到达B处时,测得影子BC长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子DE长为()A.1米B.2米C.3米D.4米【分析】依据△CBF∽△CAP,即可得到AP=8,再依据△EDG∽△EAP,即可得到DE 长.【解答】解:由FB∥AP可得,△CBF∽△CAP,∴=,即=,解得AP=8,由GD∥AP可得,△EDG∽△EAP,∴=,即=,解得ED=2,故选:B.2.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为()A.2米B.3米C.米D.米【分析】由题意知:△ABE∽△CDE,得出对应边成比例即可得出CD.【解答】解:由题意知:AB∥CD,则∠BAE=∠C,∠B=∠CDE,∴△ABE∽△CDE,∴=,∴=,∴CD=3米,故选:B.3.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.5m,木竿PQ的影子有一部分落在了墙上,它的影子QN=1.8m,MN=0.8m,木竿PQ的长度为.【分析】根据同一时刻物高与影长成正比列式求解即可.【解答】解:设木竿PQ长为xm,依题意得=,解得x=1.6,答:木竿PQ长度为1.6m,故答案为:1.6m.4.如图,有一块三角形余料,它的边BC=100m,高线AH=80m,要把它加工成矩形零件,使矩形的一边EF在BC上,其余两个顶点D、G分别在边AB、AC上,设矩形DEFG的一边长DE=xm,矩形DEFG的面积为S.(1)矩形DEFG的另一边长DG是多少?(用关于x的代数式表示)(2)求S关于x的函数表达式和自变量x的取值范围.(3)当x为多少时,矩形DEFG的面积S有最大值?最大值是多少?【分析】(1)利用矩形的性质,DG∥EF,利用同位角相等,证△ADG∽△ABC,利用相似三角形的性质求解即可;(2)由(1)可知,DG=(80﹣x),然后即可求出用x表示的矩形面积的关系式.(3)利用配方法求出最大值即可.【解答】解:(1)∵四边形DEFG是矩形,∴DG∥EF,∴∠ADG=∠ABC,∠AGD=∠ACB,∴△ADG∽△ABC,∴=,∴=,∴DG=(80﹣x)(m);(2)矩形面积S=x•(80﹣x)=﹣x2+100x(0<x<80);(3)∵S=﹣(x2﹣80x)=﹣(x﹣40)2+2000,∵﹣<0,∴x=40时,S的值最大,最大值为2000.答:当x=40时,S的值最大,最大值为2000m2.考向二:位似图形位似图形满足的条件:①所有经过对应点的直线都相交于同一点(该点叫做位似中心);②这个交点到两个对应点的距离之比都相等(这个比值叫做位似比)【同步练习】1.如图,BC∥ED,下列说法不正确的是()A.AE:AD是相似比B.点A是两个三角形的位似中心C.B与D、C与E是对应位似点D.两个三角形是位似图形【分析】根据位似变换的概念和性质判断即可.【解答】解:A、当BC∥ED时,△AED∽△ACB,AE:AC是相似比,本选项说法不正确,符合题意;B、点A是两个三角形的位似中心,本选项说法正确,不符合题意;C、B与D、C与E是对应位似点,本选项说法正确,不符合题意;D、两个三角形是位似图形,本选项说法正确,不符合题意;故选:A.2.如图,已知△ABC和△ADE是以点A为位似中心的位似图形,且△ABC和△ADE的周长比为2:1,则△ABC和△ADE的位似比是()A.1:4B.4:1C.1:2D.2:1【分析】利用位似的性质求解.【解答】解:∵△ABC和△ADE是以点A为位似中心的位似图形,∴△ABC∽△ADE,位似比等于相似比,∵△ABC和△ADE的周长比为2:1,∴△ABC和△ADE的相似比为2:1,∴△ABC和△ADE的位似比是2:1.故选:D.3.如图,在网格图中,以O为位似中心,把△ABC缩小到原来的,则点A的对应点为()A.D点B.E点C.D点或G点D.D点或F点【分析】作射线AO,根据位似变换的概念判断即可.【解答】解:作射线AO,由图可知,点D和点G都在射线AO上,且=,=,则点A的对应点为D点或G点,故选:C.4.如图,在7×4方格纸中,点A,B,C都在格点上,用无刻度直尺作图.(1)在图1中的线段AC上找一个点E,使AE=AC;(2)在图2中作一个格点△CDE,使△CDE与△ABC相似.【分析】(1)构造相似比为的相似三角形即可解决问题;(2)利用勾股定理的逆定理判断出∠ACB=90°,从而解决问题.【解答】解:(1)如图,构造相似比为的相似三角形,则点E即为所求;(2)如图,∵BC2=5,AC2=20,AB2=25,∴BC2+AC2=AB2,∴∠ACB=90°,AC=2BC,∴△CDE即为所求.5.如图,在平面直角坐标系中,△ABC的顶点为A(2,1),B (1,3),C(4,1),若△A1B1C1与△ABC是以坐标原点O为位似中心的位似图形,点A、B、C的对应点分别为A1、B1、C1,且A1的坐标为(4,2).(1)请在所给平面直角坐标系第一象限内画出△A1B1C1;(2)分别写出点B1、C1的坐标.【分析】(1)(2)利用点A和点A1的坐标特征确定位似比为2,然后把点B、C的横纵坐标都乘以2得到点B1、C1的坐标,然后描点即可.【解答】解:(1)如图,△A1B1C1;(2)点B1的坐标为(2,6),点C1的坐标为(8,2).考向三:相似三角形与函数综合【方法提炼】【同步练习】1.(2021•无棣县二模)如图(1)所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②;③当0<t≤5时,;④当秒时,△ABE∽△QBP;其中正确的结论是()A.①②③B.②③C.①③④D.②④【分析】据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E 时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED 的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.【解答】解:根据图(2)可得,当点P到达点E时,点Q到达点C,∵点P、Q的运动的速度都是1cm/秒,∴BC=BE=5,∴AD=BE=5,故①小题正确;又∵从M到N的变化是2,∴ED=2,∴AE=AD﹣ED=5﹣2=3,相似三角形与函数的综合重点是利用相似三角形的性质,设置参数,构建对应函数模型,再利用函数的性质求解后续问题在Rt△ABE中,AB===4,∴cos∠ABE==,故②小题错误;过点P作PF⊥BC于点F,∵AD∥BC,∴∠AEB=∠PBF,∴sin∠PBF=sin∠AEB==,∴PF=PB sin∠PBF=t,∴当0<t≤5时,y=BQ•PF=t•t=t2,故③小题正确;当t=秒时,点P在CD上,此时,PD=﹣BE﹣ED=﹣5﹣2=,PQ=CD﹣PD=4﹣=,∵=,==,∴=,又∵∠A=∠Q=90°,∴△ABE∽△QBP,故④小题正确.综上所述,正确的有①③④.故选:C.2.(2020•达州)如图,在梯形ABCD中,AB∥CD,∠B=90°,AB=6cm,CD=2cm.P 为线段BC上的一动点,且和B、C不重合,连接P A,过点P作PE⊥P A交射线CD于点E.聪聪根据学习函数的经验,对这个问题进行了研究:(1)通过推理,他发现△ABP∽△PCE,请你帮他完成证明.(2)利用几何画板,他改变BC的长度,运动点P,得到不同位置时,CE、BP的长度的对应值:当BC=6cm时,得表1:BP/cm…12345…CE/cm…0.83 1.33 1.50 1.330.83…当BC=8cm时,得表2:BP/cm…1234567…CE/cm… 1.17 2.00 2.50 2.67 2.50 2.00 1.17…这说明,点P在线段BC上运动时,要保证点E总在线段CD上,BC的长度应有一定的限制.①填空:根据函数的定义,我们可以确定,在BP和CE的长度这两个变量中,的长度为自变量,的长度为因变量;②设BC=mcm,当点P在线段BC上运动时,点E总在线段CD上,求m的取值范围.【分析】(1)根据两角对应相等两三角形相似证明即可.(2)①根据函数的定义判断即可.②设BP=xcm,CE=ycm.利用相似三角形的性质构建二次函数,利用二次函数的性质求出y的最大值即可解决问题.【解答】(1)证明:∵AB∥CD,∴∠B+∠C=180°,∵∠B=90°,∴∠B=∠C=90°,∵AP⊥PE,∴∠APE=90°,∴∠APB+∠EPC=90°,∵∠EPC+∠PEC=90°,∴∠APB=∠PEC,∴△ABP∽△PCE.(2)解:①根据函数的定义,我们可以确定,在BP和CE的长度这两个变量中,BP的长度为自变量,EC的长度为因变量,故答案为:BP,EC.②设BP=xcm,CE=ycm.∵△ABP∽△PCE,∴=,∴=,∴y=﹣x2+mx=﹣(x﹣m)2+,∵﹣<0,∴x=m时,y有最大值,∵点E在线段CD上,CD=2cm,∴≤2,∴m≤4,∴0<m≤4.1.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中最大的“”字高度为72.7mm,当测试距离为3m时,最大的“”字高度为()A.121.17mm B.43.62mm C.29.08mm D.4.36mm【分析】直接利用平行线分线段成比例定理列比例式,代入可得结论.【解答】解:由题意得:CB∥DF,,∵AD=3m,AB=5m,BC=72.7mm,,∴DF=43.62(mm),故选:B.2.如图,点A,B都在格点上,若BC=,则AC的长为()A.B.C.2D.3【分析】根据相似三角形的判定和性质可以得到AB的长,然后由图可知AC=AB﹣BC,然后代入数据计算即可.【解答】解:作CD⊥BD于点D,作AE⊥BD于点E,如右图所示,则CD∥AE,∴△BDC∽△BEA,∴,∴=,解得BA=2,∴AC=BA﹣BC=2﹣=,故选:B.3.国旗法规定:所有国旗均为相似矩形,在下列四面国旗中,其中只有一面不符合标准,这面国旗是()A.B.C.D.【分析】根据已知条件分别求出矩形的长与宽的比,即可得到结论.【解答】解:A、=,B、=,C、=,D、=,∵==≠,∴B选项不符合标准,故选:B.4.如图,△ABC与△A′B′C′位似,位似中心为点O,,△ABC的面积为9,则△A′B′C′面积为()A.B.6C.4D.【分析】根据位似图形的概念得到△ABC∽△A′B′C′,根据相似三角形的面积之比等于相似比的平方解答.【解答】解:根据题意知,△ABC∽△A′B′C′,∵,∴△ABC的面积:△A′B′C′面积=9:4.又∵△ABC的面积为9,∴△A′B′C′面积为4.故选:C.5.如图,△ABC和△A′B′C′是以点O为位似中心的位似图形,若OA:AA′=2:5,则△ABC与△A′B′C′的周长比为()A.2:3B.4:3C.2:9D.4:9【分析】根据题意求出OA:OA′=2:3,根据相似三角形的性质求出AC:A′C′,根据相似三角形的性质计算即可.【解答】解:∵OA:AA′=2:5,∴OA:OA′=2:3,∵△ABC和△A′B′C′是以点O为位似中心的位似图形,∴AC∥A′C′,△ABC∽△A′B′C′,∴△AOC∽△A′OC′,∴AC:A′C′=OA:OA′=2:3,∴△ABC与△A′B′C′的周长比为2:3,故选:A.6.小明的身高为1.6m,某一时刻他在阳光下的影子长为2m,与他邻近的一棵树的影长为10m,则这棵树的高为m.【分析】在同一时刻物高和影长成正比,即在同一时刻的两个问题物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.【解答】解:设这棵树的高度为xm,根据相同时刻的物高与影长成比例,则可列比例为:,解得:x=8.故答案为:8.7.据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD(点A、B的对应点分别是C、D).若物体AB的高为6cm,小孔O到物体和实像的水平距离BE、CE分别为8cm、6cm,则实像CD的高度为cm.【分析】根据相似三角形的判定和性质定理即可得到答案.【解答】解:∵AB∥CD,∴△OAB∽△OCD,∴,∴,∴CD=4.5,答:实像CD的高度为4.5cm,故答案为:4.5.8.小丽想利用所学知识测量旗杆AB的高度,如图,小丽在自家窗边看见旗杆和住宅楼之间有一棵大树DE,小丽通过调整自己的位置,发现半蹲于窗边,眼睛位于C处时,恰好看到旗杆顶端A、大树顶端D在一条直线上,小丽用测距仪测得眼睛到大树和旗杆的水平距离CH、CG分别为7米、28米,眼睛到地面的距离CF为3.5米,已知大树DE的高度为7米,CG∥BF交AB于点G,AB⊥BF于点B,DE⊥BF于点E,交CG于点H,CF⊥BF于点F.求旗杆AB的高度.【分析】根据相似三角形的判定与性质得出比例式求解即可.【解答】解:由题意知BG=HE=CF=3.5米,∴DH=DE﹣CF=7﹣3.5=3.5(米),∵AB⊥BF,DE⊥BF,∴AG∥DH,∴△CDH∽△CAG,∴=,即,∴AG=14米,∴AB=AG+GB=14+3.5=17.5(米),∴旗杆AB的高度为17.5米.9.如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成矩形零件PQMN,使一边在BC上,其余两个顶点分别在边AB、AC上.(1)求证:△APQ∽△ABC;(2)若这个矩形的边PN:PQ=1:2,则这个矩形的长、宽各是多少?【分析】(1)根据矩形的对边平行得到BC∥PQ,利用“平行于三角形的一边的直线截其他两边或其他两边的延长线,得到的三角形与原三角形相似”判定即可.(2)设宽为xmm,则长为2xmm,同(1)列出比例关系求解即可.【解答】解:(1)∵四边形PNQM为矩形,∴MN∥PQ,即PQ∥BC,∴△APQ∽△ABC;(2)设边宽为xmm,则长为2xmm,∵四边形PNMQ为矩形,∴PQ∥BC,∵AD⊥BC,∴PQ⊥AD,∵PN:PQ=1:2,∴PQ为长,PN为宽,∵PQ∥BC,∴△APQ∽△ABC,∴=,由题意知PQ=2xmm,AD=80mm,BC=120mm,PN=xmm,∴=,解得x=,2x=.即长为mm,宽为mm.答:矩形的长mm,宽为mm.10.(2022•禅城区校级模拟)如图①,四边形ABCD是矩形,AB=1,BC=2,点E是线段BC上一动点(不与B、C两点重合),点F是线段BA延长线的一动点,连接DE,EF,DF,EF交AD于点G,设BE,AF=y,已知y与x之间的函数关系式如图②所示,(1)图②中y与x的函数关系式为;(2)求证:△CDE∽△ADF;(3)当△DEG是等腰三角形时,求x的值.【分析】(1)利用待定系数法可得y与x的函数表达式.(2)利用两边成比例夹角相等证明△CDE∽△ADF即可.(3)分三种情况:①若DE=DG,则∠DGE=∠DEG,②若DE=EG,如图①,作EH ∥CD,交AD于H,③若DG=EG,则∠GDE=∠GED,分别列方程计算可得结论.【解答】(1)解:设y=kx+b,由图象得:当x=1时,y=2,当x=0时,y=4,代入得:,,∴y=﹣2x+4(0<x<2).故答案为:y=﹣2x+4(0<x<2).(2)证明:∵BE=x,BC=2∴CE=2﹣x,∴==,=,∴=,∵四边形ABCD是矩形,∴∠C=∠DAF=90°,∴△CDE∽△ADF,∴∠ADF=∠CDE.(3)解:假设存在x的值,使得△DEG是等腰三角形,①若DE=DG,则∠DGE=∠DEG,∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,∴∠DGE=∠GEB,∴∠DEG=∠BEG,在△DEF和△BEF中,,∴△DEF≌△BEF(AAS),∴DE=BE=x,CE=2﹣x,在Rt△CDE中,由勾股定理得:1+(2﹣x)2=x2,x=.②若DE=EG,如图①,作EH∥CD,交AD于H,∵AD∥BC,EH∥CD,∴四边形CDHE是平行四边形,∴∠C=90°,∴四边形CDHE是矩形,∴EH=CD=1,DH=CE=2﹣x,EH⊥DG,∴HG=DH=2﹣x,∴AG=2x﹣2,∵EH∥CD,DC∥AB,∴EH∥AF,∴△EHG∽△F AG,∴=,∴=,∴x1=,x2=(舍),经检验x=是分式方程的解,∴x=.③若DG=EG,则∠GDE=∠GED,∵AD∥BC,∴∠GDE=∠DEC,∴∠GED=∠DEC,∵∠C=∠EDF=90°,∴△CDE∽△DFE,∴=,∵△CDE∽△ADF,∴==,∴=,∴2﹣x=,∴x=.综上,x=或或.1.(2021·浙江绍兴)如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则树的高度AB长是()A.2m B.3m C.m D.m【分析】利用相似三角形的性质求解即可.【解答】解:∵AB∥OP,∴△CAB∽△CPO,∴,∴,∴AB=2(m),故选:A.2.(2021·浙江嘉兴)如图,在直角坐标系中,△ABC与△ODE是位似图形,则它们位似中心的坐标是.【分析】根据图示,对应点所在的直线都经过同一点,该点就是位似中心.【解答】解:如图,点G(4,2)即为所求的位似中心.故答案是:(4,2).3.(2021·浙江温州)如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点A′,B′.若AB=6,则A′B′的长为()A.8B.9C.10D.15【分析】根据位似图形的概念列出比例式,代入计算即可.【解答】解:∵图形甲与图形乙是位似图形,位似比为2:3,AB=6,∴=,即=,解得,A′B′=9,故选:B.4.(2021·浙江金华)如图1是一种利用镜面反射,放大微小变化的装置.木条BC上的点P处安装一平面镜,BC与刻度尺边MN的交点为D,从A点发出的光束经平面镜P反射后,在MN上形成一个光点E.已知AB⊥BC,MN⊥BC,AB=6.5,BP=4,PD=8.(1)ED的长为.(2)将木条BC绕点B按顺时针方向旋转一定角度得到BC′(如图2),点P的对应点为P′,BC′与MN的交点为D′,从A点发出的光束经平面镜P′反射后,在MN上的光点为E′.若DD′=5,则EE′的长为.【分析】(1)由题意可得,△ABP∽△EDP,则=,进而可得出DE的长;(2)过点E′作∠E′FG=∠E′D′F,过点E′作E′G⊥BC′于点G,易得△ABP′∽△E′FP′,由此可得=,在Rt△BDD′中,由勾股定理可求出BD′的长,可求出∠BD′D的正切值,设P′F的长,分别表示E′F和E′D′及FG和GD′的长,再根据BD′=13,可建立等式,可得结论.【解答】解:(1)如图,由题意可得,∠APB=∠EPD,∠B=∠EDP=90°,∴△ABP∽△EDP,∴=,∵AB=6.5,BP=4,PD=8,∴=,∴DE=13;故答案为:13.(2)如图2,过点E′作∠E′FD′=∠E′D′F,过点E′作E′G⊥BC′于点G,∴E′F=E′D′,FG=GD′,∵AB∥MN,∴∠ABD′+∠E′D′B=180°,∴∠ABD′+∠E′FG=180°,∵∠E′FB+∠E′FG=180°,∴∠ABP′=∠E′FP′,又∠AP′B=∠E′P′F,∴△ABP′∽△E′FP′,∴=即,=,设P′F=4m,则E′F=6.5m,∴E′D′=6.5m,在Rt△BDD′中,∠BDD′=90°,DD′=5,BD=BP+PD=12,由勾股定理可得,BD′=13,∴cos∠BD′D=,在Rt△E′GD′中,cos∠BD′D==,∴GD′=2.5m,∴FG=GD′=2.5m,∵BP′+P′F+FG+GD′=13,∴4+4m+2.5m+2.5m=13,解得m=1,∴E′D′=6.5,∴EE′=DE+DD′﹣D′E′=13+5﹣6.5=11.5.故答案为:11.5.5.(2021·浙江湖州)已知在平面直角坐标系xOy中,点A是反比例函数y=(x>0)图象上的一个动点,连结AO,AO的延长线交反比例函数y=(k>0,x<0)的图象于点B,过点A作AE⊥y轴于点E.(1)如图1,过点B作BF⊥x轴,于点F,连接EF.①若k=1,求证:四边形AEFO是平行四边形;②连结BE,若k=4,求△BOE的面积.(2)如图2,过点E作EP∥AB,交反比例函数y=(k>0,x<0)的图象于点P,连结OP.试探究:对于确定的实数k,动点A在运动过程中,△POE的面积是否会发生变化?请说明理由.【分析】(1)①设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,﹣),得出AE=OF,AE∥OF,由平行四边形的判定可得出结论;②过点B作BD⊥y轴于点D,如图1,证明△AEO∽△BDO,由相似三角形的性质得出,则可得出答案;(2)过点P作PH⊥x轴于点H,PE与x轴交于点G,设点A的坐标为(a,),点P 的坐标为(b,),则AE=a,OE=,PH=﹣,证明△AEO∽△GHP,由相似三角形的性质得出,解方程得出,由三角形面积公式可得出答案.【解答】(1)①证明:设点A的坐标为(a,),则当点k=1时,点B的坐标为(﹣a,﹣),∴AE=OF=a,∵AE⊥y轴,∴AE∥OF,∴四边形AEFO是平行四边形;②解:过点B作BD⊥y轴于点D,如图1,∵AE⊥y轴,∴AE∥BD,∴△AEO∽△BDO,∴,∴当k=4时,,即,∴S△BOE=2S△AOE=1;(2)不改变.理由如下:过点P作PH⊥x轴于点H,PE与x轴交于点G,设点A的坐标为(a,),点P的坐标为(b,),则AE=a,OE=,PH=﹣,∵四边形AEGO是平行四边形,∴∠EAO=∠EGO,AE=OG,∵∠EGO=∠PGH,∴∠EAO=∠PGH,又∵∠PHG=∠AEO,∴△AEO∽△GHP,∴,∵GH=OH﹣OG=﹣b﹣a,∴,∴﹣k=0,解得,∵a,b异号,k>0,∴,∴S△POE=×OE×(﹣b)=×(﹣b)=﹣,∴对于确定的实数k,动点A在运动过程中,△POE的面积不会发生变化.1.(2021•温州模拟)如图,在正六边形桌面中心正上方有一盏吊灯,在灯光下,桌面在水平地面的投影是一个面积为m2的正六边形,已知桌子的高度为0.75m,桌面边长为1m,则吊灯距地面的高度为()A.2.25m B.2.3m C.2.35m D.2.4m【分析】首先根据正六边形的面积可得正六边形的边长,进而可通过构造相似三角形,由相似三角形性质求出.【解答】解:设正六边形的边长是xm,则x•x••6=,解得x=1.5,如图,依题意知DF=FE=0.5米,FG=0.75米,CG=0.75米,∵DE∥BC,∴△F AE∽△GAC,∴,即=,解得:AF=1.5,∴AG=1.5+0.75=2.25(m),答:吊灯距地面的高度为2.25m.故选:A.2.(2021•临海市一模)如图,为测量楼高AB,在适当位置竖立一根高2m的标杆MN,并在同一时刻分别测得其落在地面上的影长AC=20m,MP=2.5m,则楼高AB为()A.15m B.16m C.18m D.20m【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,即可求解.【解答】解:∵,即,∴楼高=16米.故选:B.3.(2022•温州模拟)如图,在4×7的方格中,点A,B,C,D在格点上,线段CD是由线段AB位似放大得到,则它们的位似中心是()A.点P1B.点P2C.点P3D.点P4【分析】延长CA、DB交于点P 1,根据位似中心的概念得到答案.【解答】解:延长CA、DB交于点P1,则点P1为位似中心,故选:A.4.(2021•嘉兴二模)如图,在直角坐标系中,△ABC的顶点B的坐标为(﹣1,1),现以坐标原点O为位似中心,作与△ABC的位似比为的位似图形△A'B'C',则B'的坐标为()A.B.C.或D.或【分析】根据以原点为位似中心的对应点的坐标关系,把B点的横纵坐标都乘以或﹣得到B'的坐标.【解答】解:∵位似中心为坐标原点,作与△ABC的位似比为的位似图形△A'B'C',而B的坐标为(﹣1,1),∴B'的坐标为(﹣,)或(,﹣).故选:C.5.(2021•嘉善县一模)如图,在平面直角坐标系中,点A的坐标为(1,0),点D的坐标为(3,0),若△ABC与△DEF是位似图形,则的值是()A.B.C.D.【分析】根据位似图形的概念得到AC∥DF,【解答】解:∵点A的坐标为(1,0),点D的坐标为(3,0),∴OA=1,OD=3,即=,∵△ABC与△DEF是位似图形,∴AC∥DF,∴△OAC∽△ODF,∴==,故选:B.6.(2021•瑞安市一模)数学兴趣小组计划测量公路上路灯的高度AB,准备了标杆CD,EF及皮尺,按如图竖直放置标杆CD与EF.已知CD=EF=2米,DF=2米,在路灯的照射下,标杆CD的顶端C在EF上留下的影子为G,标杆EF在地面上的影子是FH,测得FG=0.5米,FH=4米,则路灯的高度AB=米.【分析】延长CG交FH于M,根据相似三角形的判定和性质解答即可.【解答】解:如图,延长CG交FH于M,∵∠GMF=∠CMD,∠GFM=∠CDM=90°,∴△GFM∽△CDM,∴,设FM为a米,则a=(a+2)×,解得:a=,设BD=x米,AB=y米,同理可得,△CMD∽△AMB,∴,,可得,,整理得:,解得:,经检验是分式方程组的解,∴AB=5米.故答案为:5.7.(2022•鹿城区校级一模)如图,在8×8的网格中,△ABC是格点三角形,请分别在图1和图2中按要求作图.(1)在图1中以O为位似中心,作格点三角形△A1B1C1,使其与△ABC位似比为1:2.(2)在图2中作格点线段BM⊥AC.【分析】(1)连接OA,OB,OC,取OA,OB,OC的中点A1,B1,C1,连接A1B1,B1C1,C1A1即可;(2)利用数形结合的思想作出线段BM即可.【解答】解:(1)如图,△A1B1C1即为所求;(2)如图,线段BM即为所求.8.(2021•永嘉县校级模拟)已知一块等腰三角铁板废料如图所示,其中AB=AC=50cm,BC=60cm,现要用这块废料裁一块正方形DEFG铁板,使它的一边DE落在△ABC的一腰上,顶点F、G分别落在另一腰AB和BC上,求;(1)等腰三角形ABC的面积S△ABC;(2)正方形DEFG的边长.【分析】(1)过A作AH⊥BC于H,根据等腰三角形的性质得到BH=BC=30(cm),根据勾股定理得到AH===40(cm),由三角形的面积公式即可得到结论;(2)过B作BM⊥AC交FG于N,根据三角形的面积公式得到BM=48(cm),根据正方形的性质得到FG∥DE,根据相似三角形的性质即可得到结论.【解答】解:(1)过A作AH⊥BC于H,∵AB=AC=50cm,BC=60cm,∴BH=BC=30(cm),∴AH===40(cm),∴S△ABC=BC•AH=60×40=1200(cm2);(2)过B作BM⊥AC交FG于N,则S△ABC=AC•BM=1200,∵AC=50cm,∴BM=48(cm),∵四边形DEFG是正方形,∴FG∥DE,∴BN⊥FG,△BFG∽△BAC,∴=,∴,∴FG=,∴正方形DEFG的边长为.9.(2021•海曙区模拟)如图是某公园的一台滑梯,滑梯着地点B与梯架之间的距离BC=4m.(1)现在某一时刻测得身高1.8m的小明爸爸在阳光下的影长为0.9m,滑梯最高处A在阳光下的影长为1m,求滑梯的高AC;(2)若规定滑梯的倾斜角(∠ABC)不超过30°属于安全范围,请通过计算说明这架滑梯的倾斜角是否符合安全要求?【分析】(1)直接利用同一时刻太阳光下影长与物体高度成比例进而得出答案;(2)直接利用锐角三角函数关系得出∠ABC的取值范围.【解答】解:(1)由题意可得:=,解得:AC=2(m),答:滑梯的高AC为2m;(2)∵tan∠ABC===<tan30°=,∴∠ABC<30°,∴这架滑梯的倾斜角符合安全要求.10.(2021•婺城区校级模拟)已知在菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D 不重合),且∠PCQ=30°.(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;(3)联结PQ,直线PQ与直线BC交于点E,如果△QCE与△BCP相似,求线段BP的长.【分析】(1)如图1中,作PH⊥BC于H.解直角三角形求出BH,PH,在Rt△PCH中,理由勾股定理即可解决问题.(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.证明△POQ∽△BOC,推出∠OPQ=∠OBC=30°=∠PCQ,推出PQ=CQ=y,推出PC=y,在Rt△PHB 中,BH=x,PH=x,根据PC2=PH2+CH2,可得结论.(3)分两种情形:①如图2中,若直线QP交直线BC于B点左侧于E.②如图3中,若直线QP交直线BC于C点右侧于E.分别求解即可.【解答】解:(1)如图1中,作PH⊥BC于H.∵四边形ABCD是菱形,∴AB=BC=4,AD∥BC,∴∠A+∠ABC=180°,∵∠A=120°,∴∠PBH=60°,∵PB=3,∠PHB=90°,∴BH=PB•cos60°=,PH=PB•sin60°=,∴CH=BC﹣BH=4﹣=,∴PC===.(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.∵四边形ABCD是菱形,∴∠ABD=∠CBD=30°,∵∠PCQ=30°,∴∠PBO=∠QCO,∵∠POB=∠QOC,∴△POB∽△QOC,∴=,∴=,∵∠POQ=∠BOC,∴△POQ∽△BOC,∴∠OPQ=∠OBC=30°=∠PCQ,∴PQ=CQ=y,∴PC=y,在Rt△PHB中,BH=x,PH=x,∵PC2=PH2+CH2,∴3y2=(x)2+(4﹣x)2,∴y=(0≤x<8).(3)①如图2中,若直线QP交直线BC于B点左侧于E.此时∠CQE=120°,∵∠PBC=60°,∴△PBC中,不存在角与∠CQE相等,此时△QCE与△BCP不可能相似.②如图3中,若直线QP交直线BC于C点右侧于E.则∠CQE=∠B=QBC+∠QCP=60°=∠CBP,∵∠PCB>∠E,∴只可能∠BCP=∠QCE=75°,作CF⊥AB于F,则BF=2,CF=2,∠PCF=45°,∴PF=CF=2,此时PB=2+2,③如图4中,当点P在AB的延长线上时,∵△QCE与△BCP相似,∴∠CQE=∠CBP=120°,∴∠QCE=∠PCB=15°,作CF⊥AB于F.∵∠FCB=30°,∴∠FCP=45°,∴BF=BC=2,CF=PF=2,∴PB=2﹣2.综上所述,满足条件的PB的值为2+2或2﹣2.。
相似三角形的应用练习题(带答案

是矩形,
∵四边形
是正方形,
∴
,
∵
,
,
∴
,
∴ ∴四边形
, 为正方形.
( 2 )仿照勤奋小组同学的作法作图,如图 与图 所示,矩形
即为所作.
图
图
( 3 )如图 ,作
的高 ,交 于 ,
∵
的面积
,
∴
,
∵
,
设
,则
,
,
,
∵
,
∴
,
∴
,
∴
,
解得
,
∴
,
∴
,
∴矩形
的面积
,
同理,在矩形
中,若
,可求出
,
∴
,
,
∴矩形
的面积
.
.
,
,
.若点 是 边上的一点,将
, 交 于,
,则
,
D
10
【答案】
;
【解析】 作
于,
∵
,
,
∴
,
∴
,
∴
,
由折叠及
得:
,
∴易得
,
∴
,
又∵
,
∴
,
∴
,
∴
.
【标注】【知识点】翻折问题与勾股定理;相似A字型
3. 如图,矩形
的顶点 在 轴的正半轴上,点 、点 分别是边 、 上的两个点.将
沿 折叠,使点 落在 边上的三等分点 上(点 靠近点 ),过点 作
,使 , 位于边 上, , 分别位于边 , 上.(在备用图中完成,不写作法,保
留作图痕迹)
( 3 )解决问题: 在( )的条件下,已知
相似三角形的性质及应用(解析版)

4.5相似三角形的性质及应用一、相似三角形的性质1.相似三角形的对应角相等,对应边的比相等. 2. 相似三角形中的重要线段的比等于相似比.相似三角形对应高,对应中线,对应角平分线的比都等于相似比. 要点:要特别注意“对应”两个字,在应用时,要注意找准对应线段. 3. 相似三角形周长的比等于相似比∽,则由比例性质可得:4. 相似三角形面积的比等于相似比的平方∽,则分别作出与的高和,则21122=1122ABCA B C BC AD k B C k A D S k S B C A D B C A D '''''''⋅⋅⋅⋅=='''''''''⋅⋅△△要点:相似三角形的性质是通过比例线段的性质推证出来的. 二、三角形的重心三角形三条中线的交点叫做三角形的重心,三角形的重心分每一条中线成1:2的两条线段.OEFDABC即12OD OE OF OA OB OC === . 要点:H OEFDAB C过点E 作EH ∥BC 交AD 于H ,根据三角形的中位线平行于第三边并且等于第三边的一半可得CD=2EH ,从而得到BD=2EH ,再根据△BDO 和△EHO 相似,利用相似三角形对应边成比例列出比例式计算即可得证1=2OE HE OB BD ,同理其他比例也可以得到. 三、相似三角形的应用1.测量高度测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.要点:测量旗杆的高度的几种方法:平面镜测量法 影子测量法 手臂测量法 标杆测量法2.测量距离测量不能直接到达的两点间的距离,常构造如下两种相似三角形求解。
1.如甲图所示,通常可先测量图中的线段DC 、BD 、CE 的距离(长度),根据相似三角形的性质,求出AB 的长.2.如乙图所示,可先测AC 、DC 及DE 的长,再根据相似三角形的性质计算AB 的长.要点:1.比例尺:表示图上距离比实地距离缩小的程度,比例尺= 图上距离/ 实际距离;2.太阳离我们非常遥远,因此可以把太阳光近似看成平行光线.在同一时刻,两物体影子之比等于其对应高的比;3.视点:观察事物的着眼点(一般指观察者眼睛的位置); 4. 仰(俯)角:观察者向上(下)看时,视线与水平方向的夹角. 一、单选题1.两三角形的相似比是2:3,则其对应角的角平分线之比是( ) A .2:3 B .2:3 C .4:9 D .8:27 【解答】B【提示】根据相似三角形对应角平分线的比等于相似比解答即可. 【详解】解:∵两三角形的相似比是2:3, ∴相似三角形对应角平分线的比是2:3,故选:B .【点睛】本题考查了相似三角形的性质,主要利用了相似三角形对应角平分线的比,对应高的比,对应中线的比都等于相似比的性质.2.已知ABC DEF ∽△△,ABC 与DEF 的面积之比为1:2,若BC 边上的中线长为1,则EF 边上的中线长是( ) A .2 B .2 C .3D .4【解答】A【提示】由ABC DEF ∽△△,ABC 与DEF 的面积之比为1:2可知:相似比为1:2,则对应中线的比为1:2,即可求出答案.【详解】∵ABC DEF ∽△△,ABC 与DEF 的面积之比为1:2 ∴相似比为1:2 ∴其对应中线的比为1:2 ∵BC 边上的中线长为1 ∴EF 边上的中线长是2 故选:A【点睛】本题主要考查了相似三角形的相似比的相关知识点,熟练掌握相似三角形面积比、相似比、对应边的高线、中线的比的关系是解题的关键,属于基础知识题.3.如图点D 、E 分别在△ABC 的两边BA 、CA 的延长线上,下列条件能判定ED ∥BC 的是( ).A .AD DEAB BC =; B .AD AE AC AB =;C .AD AB DE BC ⋅=⋅; D .AD AC AB AE ⋅=⋅. 【解答】D【提示】根据选项选出能推出ADE ABC ∆∆∽,推出D B ∠=∠或E C ∠=∠的即可判断. 【详解】解:A 、∵AD DEAB BC =,EAD BAC ∠=∠,不符合两边对应成比例及夹角相等的相似三角形判定定理. 无法判断ADE ∆与ABC ∆相似,即不能推出//DE BC ,故本选项错误;B 、AD AE AC AB =EAD BAC ∠=∠, ADE ACB ∴∆∆∽,E B ∴∠=∠,D C ∠=∠,即不能推出//DE BC ,故本选项错误;C 、由AD AB DE BC ⋅=⋅可知AB DEBC AD =,不能推出DAE BAC ∆∆∽,即不能推出D B ∠=∠,即不能推出两直线平行,故本选项错误;D 、∵AD AC AB AE ⋅=⋅,AD AEAB AC ∴=,EAD BAC ∠=∠, DAE BAC ∴∆∆∽,D B ∴∠=∠,//DE BC ∴,故本选项正确;故选:D .【点睛】本题考查了相似三角形的性质和判定和平行线的判定的应用,主要考查学生的推理和辨析能力,注意:有两组对应边的比相等,且这两边的夹角相等的两三角形相似. 4.已知ABC 与DEF 相似,且A D ∠=∠,那么下列结论中,一定成立的是( ) A .B E ∠=∠ B .AB ACDE DF =C .相似比为AB DED .相似比为BCEF【解答】D【提示】根据相似三角形的性质对不同的对应角和对应边进行分类讨论.【详解】解:∵B 可以与E 对应,也可以与F 对应,∴∠B=∠E 或∠B=∠F ,A 不一定成立; 同上,AB 可以与DE 对应,也可以与DF 对应,∴AB AC DE DF =或AB ACDF DE =,B 不一定成立;同上,AB 可以与DE 对应,也可以与DF 对应,∴相似比可能是AB DE ,也可能是ABDF ,C 不一定成立;∵∠A=∠D ,即∠A 与∠D 是对应角,∴它们的对边一定是对应比,即BC 与EF 是对应比,∴相似比为BCEF ,∴D 一定成立, 故选D .【点睛】本题考查相似三角形的性质,注意相似三角形的性质是针对对应角和对应边而言的. 5.如图,小明站在 C 处看甲、乙两楼楼顶上的点 A 和点 E .C ,E ,A 三点在同一直线上,B ,C 相距 20 米,D ,C 相距 40 米,乙楼的高 BE 为 15 米,小明的身高忽略不计,则甲楼的高 AD 为 ( )A .40 米B .20 米C .15 米D .30 米【解答】D【提示】证明ADC EBC ∽△△,利用相似三角形的性质解答即可. 【详解】解:由题意可知:90ADC ∠=︒,90EBC ∠=︒,C ∠是公共角,∴ADC EBC ∽△△, ∴AD DCEB BC =, ∵20m BC =,40m DC =,15m BE =, ∴40=15=30m 20DC AD EB BC =⨯⨯.故选:D【点睛】本题考查相似三角形的判定及性质,解题的关键是熟练掌握相似三角形的判定及性质. 6.如图,在Rt △ABC 中,90ACB ∠=,CD AB ⊥垂足为D ,那么下列结论错误的是( )A .22AC BD BC AD ⋅=⋅B .22BC BD CD AB ⋅=⋅C .AD BC AC CD ⋅=⋅ D .CD BC AC BD ⋅=⋅ 【解答】B【提示】根据直角三角形的性质与相似三角形的判定可知△ADC ∽△CDB ∽△ACB ,利用相似三角形的对应线段成比例即可求解. 【详解】∵∠ACB=90°,CD ⊥AB , ∴△ADC ∽△CDB ∽△ACB ∴AC2=AD·AB ,BC2=BD·AB ,故22AC BD BC AD ⋅=⋅,A 正确,B 错误;∵△ADC ∽△CDB∴AD AC CDCD BC BD == ∴AD BC AC CD ⋅=⋅,CD BC AC BD ⋅=⋅,C,D 选项正确; 故选B.【点睛】此题主要考查相似三角形的判定与性质,解题的关键是熟知直角三角形的性质及相似三角形的判定.7.如图,E ,F 是平行四边形ABCD 对角线AC 上两点,AE=CF=14AC .连接DE ,DF 并延长,分别交AB ,BC 于点G ,H ,连接GH ,则ADG BGHS S △△的值为( )A .12B .23C .34D .1【解答】C【提示】首先证明AG :AB=CH :BC=1:3,推出GH ∥AC ,推出△BGH ∽△BAC ,可得223924ADC BAC BGHBGHS S BA SSBG ()()====,13ADG ADCSS=,由此即可解决问题.【详解】∵四边形ABCD 是平行四边形 ∴AD=BC ,DC=AB , ∵AC=CA , ∴△ADC ≌△CBA , ∴S △ADC=S △ABC ,∵AE=CF=14AC ,AG ∥CD ,CH ∥AD ,∴AG :DC=AE :CE=1:3,CH :AD=CF :AF=1:3, ∴AG :AB=CH :BC=1:3, ∴GH ∥AC , ∴△BGH ∽△BAC , ∴223924ADC BAC BGHBGHS S BA S SBG ()()====,∵13ADG ADCS S=,∴913434ADG BGHS S=⨯=.故选C .【点睛】本题考查平行四边形的性质、相似三角形的判定和性质、全等三角形的判定和性质、等高模型等知识,解题的关键是灵活运用所学知识解决问题,属于中考选择题中的压轴题.8.如图,在正方形ABCD 中,ABP 是等边三角形,AP 、BP 的延长线分别交边CD 于点E 、F ,联结AC 、CP 、AC 与BF 相交于点H ,下列结论中错误的是( )A .AE=2DEB .CFP APHC .CFP APCD .2CP PH PB =⋅【解答】C【提示】A.利用直角三角形30度角的性质即可解决问题. B.根据两角相等两个三角形相似即可判断.C.通过计算证明∠DPB≠∠DPF ,即可判断.D.利用相似三角形的性质即可证明. 【详解】解:∵四边形ABCD 是正方形, ∴∠D=∠DAB=90°, ∵△ABP 是等边三角形, ∴∠PAB=∠PBA=∠APB=60°, ∴∠DAE=30°, ∴AE=2DE ,故A 正确; ∵AB ∥CD ,∴∠CFP=∠ABP=∠APH=60°,∵∠PHA=∠PBA+∠BAH=60°+45°=105°, 又∵BC=BP ,∠PBC=30°, ∴∠BPC=∠BCP=75°, ∴∠CPF=105°,∴∠PHA=∠CPF ,又易得∠APB=∠CFP=60°, ∴△CFP ∽△APH ,故B 正确; ∵∠CPB=60°+75°=135°≠∠DPF , ∴△PFC 与△PCA 不相似,故C 错误; ∵∠PCH=∠PCB-∠BCH=75°-45°=30°, ∴∠PCH=∠PBC , ∵∠CPH=∠BPC , ∴△PCH ∽△PBC ,∴PC PHPB PC =,∴PC2=PH•PB ,故D 正确, 故选:C .【点睛】本题考查相似三角形的判定和性质,等边三角形的性质,正方形的性质,直角三角形30度角的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.9.如图所示,D 、E 分别是ABC ∆的边AB 、BC 上的点,且//DE AC ,AE 、CD 相交于点O .若45::2DOE COA S S ∆∆=,则BDES ∆与CDE S ∆的比是( )A .1:2B .1: 3C .2:3D .2:5 【解答】C【提示】利用相似三角形的性质解决问题即可. 【详解】解:∵//DE AC , ∴DEO CAO ∆∆∽, ∵45::2DOE COA S S ∆∆=,∴2425DE AC ⎛⎫=⎪⎝⎭,∴25DE AC =, ∵//DE AC , ∴25BE DE BC AC ==, ∴23BE EC =,∴BDES ∆与CDE S ∆的比2:3=,故选:C .【点睛】本题主要考查的是相似三角形的性质和判定,熟练掌握相似三角形的性质和判定定理是解题的关键.10.如图,正方形ABCD 和正方形CGFE 的顶点,,C D E 在同一条直线上,顶点, ,B C G 在同一条直线上.O 是EG 的中点,EGC ∠的平分线GH 过点D ,交BE 于点H ,连接FH 交EG 于点M ,连接OH 交EC 于点N .则BCCG 的值为( )A .31-B .3C .21-D .2【解答】C【详解】∵四边形ABCD 和四边形CGFE 是正方形,,,BC DC CE CG BCE DCG ∴==∠=∠.在BCE和DCG △中,,,(),,BC DC BCE DCG BCE DCG SAS BEC BGH CE CG =⎧⎪∠=∠∴∴∠=∠⎨⎪=⎩≌.90BGH CDG ∠+∠=︒,,90CDG HDE BEC HDE ∠=∠∴∠+∠=︒.GH BE ∴⊥.GH 平分,EGC BGH EGH ∠∴∠=∠.()BGH EGH ASA ∴≌.BH EH ∴=.又O 是EG 的中点,//HO BG ∴.D C DHN G ∴∽△△.DN HN DC CG ∴=.设HN a =,正方形ECGF 的边长是2b ,则2BC a =,22,,22b a aCD a NC b a b -==∴=,即2220a ab b +-=,解得(12)a b =-+或(12)a b =--(舍去),则221,212a BCb CG =-∴=-.二、填空题11.若两个相似三角形的面积比是9:25,则对应边上的中线的比为 _________. 【解答】3:5【提示】根据相似三角形的性质:相似三角形对应边上的中线之比等于相似比即可得出答案. 【详解】∵两个相似三角形的面积比是9:25 ∴两个相似三角形的相似比是3:5 ∴对应边上的中线的比为3:5 故答案为:3:5.【点睛】本题主要考查相似三角形的性质,掌握相似三角形的性质是解题的关键. 12.如图,△ABC ∽△CBD ,AB=9,BD=25,则BC=______.【解答】15【提示】根据相似三角形的性质列出比例式,代入计算即可求解. 【详解】解:∵△ABC ∽△CBD ,∴AB CBCB BD =,即2BC AB BD =⨯, AB=9,BD=25,2292522515BC AB BD ∴=⨯=⨯==,15BC =∴, 故答案为:15【点睛】本题考查了相似三角形的性质,根据相似三角形的性质列出比例式是解题的关键. 13.一个三角形三边长度之比为2:5:6,另一个与它相似的三角形最长边为24,则三角形的最短边为_________. 【解答】8【提示】首先设与它相似的三角形的最短边的长为x ,然后根据相似三角形的对应边成比例,即可得方程,解此方程即可求得答案.【详解】解:设与它相似的三角形的最短边的长为x ,则 2624x =,∴8x =;∴三角形的最短边为8. 故答案为:8.【点睛】此题考查了相似三角形的性质.此题比较简单,注意掌握相似三角形的对应边成比例定理的应用.14.如图,在矩形ABCD 中,E 是BC 的中点,连接AE ,过点E 作EF AE ⊥交DC 于点F .若4AB =,6BC =,则DF 的长为______.【解答】74【提示】结合矩形的性质证明BAECEF ∆∆可求得CF 的长,再利用DF CD DF =-可求解.【详解】解:四边形ABCD 为矩形,90B C ∴∠=∠=︒,4CD AB ==,90BAE AEB ∴∠+∠=︒,EF AE⊥,90AEF∴∠=︒,90AEB CEF∴∠+∠=︒,BAE CEF∴∠=∠,BAE CEF∴∆∆,::AB CE BE CF∴=,E是BC的中点,6BC=,3BE CE∴==,4AB=,4:33:CF∴=,解得94CF=,97444DF CD DF∴=-=-=.故选:7 4.【点睛】本题主要考查矩形的性质,相似三角形的判定与性质,证明BAE CEF∆∆是解题的关键.15.用杠杆撬石头的示意图如图所示,P是支点,当用力压杠杆的A端时,杠杆绕P点转动,另一端B向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的B端必须向上翘起8cm,已知杠杆的动力臂AP与阻力臂BP之比为4:1,要使这块石头滚动,至少要将杠杆的A端向下压_____cm.【解答】32【提示】首先根据题意画出图形,然后根据△APM∽△BPN有AP AMBP BN=,然后再利用动力臂AP与阻力臂BP之比为4:1和8BN≥即可求出AM的最小值.【详解】解:如图:AM、BN都与水平线垂直,即AM∥BN;∴△APM∽△BPN;∴APBP=AMBN,∵杠杆的动力臂AP与阻力臂BP之比为4:1,∴AMBN=41,即AM=4BN;∴当BN≥8cm时,AM≥32cm;故要使这块石头滚动,至少要将杠杆的端点A 向下压32cm . 故答案为:32.【点睛】本题主要考查相似三角形的判定及性质的应用,掌握相似三角形的判定及性质是解题的关键. 16.如图,已知,20,60AB BC ACBAD DAE AD DE AE ︒︒==∠=∠=,则DAC ∠的度数为_________.【解答】40°【提示】由AB BC ACAD DE AE ==可判定△ABC ∽△ADE ,得到∠BAC=∠DAE ,再根据20BAD ︒∠=,60DAE ︒∠=,可得出∠DAC 的度数.【详解】解:∵AB BC ACAD DE AE ==, ∴~ABC ADE , ∴60BAC DAE ︒∠=∠=, 又∵20BAD ︒∠=, ∴40DAC ︒∠=. 故答案为:40°.【点睛】本题考查了相似三角形的判定和性质,解题的关键是能根据AB BC ACAD DE AE ==判定出△ABC ∽△ADE.17.如图,已知在ABC 中,90C ∠=︒,10AB =,1cot 2B =,正方形DEFG 的顶点G 、F 分别在边AC 、BC 上,点D 、E 在斜边AB 上,那么正方形DEFG 的边长为_____.【解答】207【提示】作CM ⊥AB 于M ,交GF 于N ,由勾股定理可得出AB ,由面积法求出CM ,证明△CGF ∽△CAB ,再根据对应边成比例,即可得出答案. 【详解】作CM ⊥AB 于M ,交GF 于N ,如图所示: ∵Rt △ABC 中,∠C =90°,AB =10,1cot B 2=,∴设BC =k ,则AC =2k ,AB2=AC2+BC2,即:102=(2k )2+k2,解得:k =25, ∴BC =25,AC =45, ∴CM =AC BC AB ⋅=452510⨯=4,∵正方形DEFG 内接于△ABC , ∴GF =EF =MN ,GF ∥AB , ∴△CGF ∽△CAB ,∴CN GF =CM AB ,即4EF EF410-=, 解得:EF =207;故答案为:207.【点睛】本题考查的是相似三角形的判定和性质、正方形的性质、勾股定理等知识;正确作出辅助线、灵活运用相似三角形的判定定理和性质定理是解题的关键.18.如图,在ABC 中,90ACB ∠=︒,AC BC =,点E 是边AC 上一点,以BE 为斜边往BC 侧作等腰Rt BEF △,连接,CF AF ,若6AB =,四边形ABFC 的面积为12,则AE =_________,AF =_________.【解答】 234【提示】如图,过点E 作EH AB ⊥于H ,过点F 作FQ AC ⊥,交AC 的延长线于Q ,由面积和差关系可求3BCF S ∆=,通过证明ABE CBF ∆∆∽,可得2()ABE BCF S AB S BC∆∆=,可求2EH =,由勾股定理可求AE ,BE ,EF 的长,通过证明BEH EFQ ∆∆∽,可得2BE EH BH EF QF EQ ===,可求22EQ =,2QF =,由勾股定理可求解.【详解】解:如图,过点E 作EH AB ⊥于H ,过点F 作FQ AC ⊥,交AC 的延长线于Q ,90ACB ∠=︒,AC BC =,2AB BC ∴,=6AB ,32AC BC ∴==四边形ABFC 的面积为12,12ABC BCF S S ∆∆∴+=, 3BCF S ∆∴=,等腰Rt BEF ∆,2BE BF ∴,45EBF∠=︒,=45ABC ∠︒,ABE CBF ∴∠=∠,2AB BE BC FB == ABE CBF ∴∆∆∽,∴2()ABE BCF S AB S BC ∆∆=, 326ABE S ∆∴=⨯=,∴162AB EH ⨯=,2EH ∴=,45CAB ∠=︒,EH AB ⊥,45CAB AEH ∴∠=∠=︒,2AH EH ∴==,222AE EH ==,4BH ∴=,2CE =,2221825BE CE BC ∴=+=+=,10EF ∴=,180AEH BEH FEB QEF ∠+∠+∠+∠=︒, 90BEH FEQ ∴∠+∠=︒,且90BEH EBH ∠+∠=︒EBH QEF ∴∠=∠,且90Q BHE ∠=∠=︒,BEH EFQ ∴∆∆∽, ∴2BE EH BHEF QF EQ ===, 22EQ ∴=,2QF =, 42AQ ∴=,2232234AF AQ QF ∴=+=+=,故答案为:22,34.【点睛】本题考查了相似三角形的判定和性质,等腰直角三角形的性质,勾股定理等知识,利用相似三角形的性质求出EH 的长是本题的关键.三、解答题19.如图,在ABP 中,C ,D 分别是,AP BP 上的点.若4,5,6,3CD CP DP AC BD =====.(1)求证:ABP DCP ∽△△; (2)求AB 的长. 【解答】(1)见解析(2)AB=8【提示】(1)△ABP与△DCP有公共角,分别计算PDPC与APBP的值,得到PD PCPA PB=,根据相似三角形的判定定理得出结论;(2)运用相似三角形的性质计算即可.(1)证明:∵CD=CP=4,DP=5,AC=6,BD=3,∴AP=AC+CP=6+4=10,BP=BD+DP=3+5=8,∴54PDPC=,10584APBP==,∴PD APPC BP=,即PD PCPA PB=,∵∠DPC=∠APB,∴△ABP∽△DCP;(2)解:∵△ABP∽△DCP,∴AB PBCD PC=,即844AB=,∴AB=8.【点睛】本题考查了相似三角形的判定与性质,属于基础题.解决问题的关键是掌握:有两边对应成比例且夹角相等的两个三角形相似.20.如图,在矩形ABCD中,AB:BC=1:2,点E在AD上,BE与对角线AC交于点F.(1)求证:△AEF∽△CBF;(2)若BE⊥AC,求AE:ED.【解答】(1)见解析(2)1:3【提示】(1)根据矩形的性质得到AD∥BC,然后根据相似三角形的判断方法可判断△AEF∽△CBF;(2)设AB=x,则BC=2x,利用矩形的性质得到AD=BC=2x,∠BAD=∠ABC=90°,接着证明△ABE∽△BCA,利用相似比得到AE=12x,则DE=32x,从而可计算出AE:DE.(1)解:证明:∵四边形ABCD为矩形,∴AD∥BC,∴△AEF∽△CBF;(2)设AB=x,则BC=2x,∵四边形ABCD为矩形,∴AD=BC=2x,∠BAD=∠ABC=90°,∵BE⊥AC,∴∠AFB=90°,∵∠ABF+∠BAF=90°,∠BAC+∠ACB=90°,∴∠ABF=∠ACB,∵∠BAE=∠ABC,∠ABE=∠BCA,∴△ABE∽△BCA,∴AE ABAB BC=,即2AE xx x=,∴AE=12x,∴DE=AD-AE=32x,∴AE:DE=13:22x x=1:3.【点睛】本题考查了三角形相似的判定与性质,应注意利用图形中已有的公共角、公共边等条件,同时利用相似三角形的性质进行几何计算.也考查了矩形的性质.21.如图,为了测量平静的河面的宽度EP,在离河岸D点3.2米远的B点,立一根长为1.6米的标杆AB,在河对岸的岸边有一根长为4.5米的电线杆MF,电线杆的顶端M在河里的倒影为点N,即PM PN=,两岸均高出水平面0.75米,即0.75DE FP==米,经测量此时A、D、N三点在同一直线上,并且点M、F、P、N N共线,点B、D、F共线,若AB、DE、MF均垂直与河面EP,求河宽EP是多少米?【解答】河宽为12米【提示】连接DF ,根据题意可得出四边形DEPF 为矩形,由ADB NDF ∽△△可求得DF ,便可解决问题.【详解】解:如图,连接DF ,∵点B 、D 、F 共线,DE 、MF 均垂直与河面EP ,且0.75DE FP ==, 4.5MF =, ∴四边形DEPF 为矩形, ∴DF EP =,∴ 4.50.75 5.25PN FM FP =+=+=, ∴ 5.250.756FN PN FP =+=+=, ∵AB 、DE 、MF 均垂直与河面EP , ∴90ABD NFD ∠=∠=︒, ∵ADB NDF ∠=∠, ∴ADB NDF ∽△△; ∴AB NFBD DF =, ∵ 1.6AB =, 3.2BD =, ∴1.663.2DF =,∴12DF =, ∴12EP =(米). 答:河宽EP 是12米.【点睛】本题主要考查了相似三角形的性质与判定,矩形的判定和性质等知识.关键是构造和证明三角形相似.22.如图,已知AD ,BC 相交于点E ,且△AEB ∽△DEC ,CD =2AB ,延长DC 到点G ,使CG =12CD ,连接AG .(1)求证:四边形ABCG 是平行四边形;(2)若∠GAD =90°,AE =2,CG =3,求AG 的长. 【解答】(1)证明见解析; (2)35AG =【提示】(1)根据相似三角形的性质可得AB ∥CD ,再由CD =2AB ,CG =12CD ,可得AB =CG ,即可证明;(2)由平行四边形的性质可得AG ∥BC ,可得∠AEB =90°,再由CG =3可得AB =3,利用勾股定理可得BE ,再由相似三角形的性质可得CE ,从而得出BC ,即可求解. (1)证明:∵△AEB ∽△DEC , ∴∠B =∠BCD , ∴AB ∥CD , 即AB ∥CG ,∵CD =2AB ,CG =12CD ,∴AB =CG ,∴四边形ABCG 是平行四边形; (2)解:∵四边形ABCG 是平行四边形,AE =2,CG =3, ∴AG ∥BC ,AG =BC ,AB =CG =3, ∵∠GAD =90°, ∴∠AEB =90°,在Rt △ABE 中,由勾股定理可得:BE 22AB AE -即BE =22325-=,∵△AEB ∽△DEC , ∴12BE AB CE CD ==, ∴CE =25,∴BC =BE+CE =35, ∴AG =BC =35.【点睛】本题考查相似三角形的性质,勾股定理,平行四边形的判定与性质,解题的关键是熟练掌握相似三角形的性质,勾股定理的运用,平行四边形的判定与性质.23.如图,在△ABC 中,AD 是角平分线,点E 是边AC 上一点,且满足ADE B ∠=∠.(1)证明:ADB AED ∆∆;(2)若3AE =,5AD =,求AB 的长. 【解答】(1)见解析(2)253【提示】(1)证出∠BAD=∠EAD .根据相似三角形的判定可得出结论; (2)由相似三角形的性质可得出AD ABAE AD =,则可得出答案. (1)∵AD 是∠BAC 的角平分线, ∴∠BAD=∠EAD . ∵∠ADE=∠B , ∴△ADB ∽△AED . (2)∵△ADB ∽△AED , ∴AD ABAE AD =,∵AE=3,AD=5, ∴535AB =, ∴253AB =. 【点睛】本题考查了相似三角形的判定与性质以及三角形内角和定理,熟练掌握相似三角形的判定定理和性质定理是解题的关键.24.已知:平行四边形ABCD ,E 是BA 延长线上一点,CE 与AD 、BD 交于G 、F .求证:2CF GF EF =⋅.【解答】见解析【提示】根据平行四边形的性质得到AD BC ∥,AB CD ∥,得到△DFG ∽△BFC ,△DFC ∽△BFE ,根据相似三角形的性质列出比例式,计算即可. 【详解】证明:∵四边形ABCD 是平行四边形, ∴AD BC ∥,AB CD ∥,∴△DFG ∽△BFC ,△DFC ∽△BFE ∴GF DF CF BF =,CF DFEF BF =, ∴GF CFCF EF =, 即2CF GF EF =⋅.【点睛】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.25.如图,已知cm,cm,23,36,117AD a AC b BC AC B D ===∠∠=︒=︒,ABC DAC △∽△.(1)求AB 的长;(2)求DC 的长; (3)求BAD ∠的度数.【解答】(1)32cm a ;(2)2cm3b ;(3)153︒【提示】(1)由ABC DAC △∽△,可得:,AB BCAD AC =再代入数据可得答案;(2)由ABC DAC △∽△,可得:,AC BCDC AC =再代入数据可得答案;(3)由ABC DAC △∽△,可得:117,36,BAC D B DAC ∠=∠=︒∠=∠=︒再利用角的和差可得答案; 【详解】解:(1)23,,BC AC AD a ==3,2BC AC ∴= ABC DAC △∽△,,AB BCAD AC ∴= 3,2AB a ∴= 3.2AB a ∴=(2) ABC DAC △∽△,,AC BCDC AC ∴= 而3,,2BC AC b AC == 3,2b DC ∴=2.3DC b ∴=(3) ABC DAC △∽△,36,117,B D ∠=︒∠=︒117,36,BAC D B DAC ∴∠=∠=︒∠=∠=︒11736153.BAD BAC DAC ∴∠=∠+∠=︒+︒=︒【点睛】本题考查的是相似三角形的性质,掌握相似三角形的对应角相等,对应边成比例是解题的关键.26.如图,在四边形ABCD 中,AC ,BD 交于点F .点E 在BD 上,且BAE CAD ∠=∠,AB ACAE AD =.(1)求证:ABC AED ∽△△. (2)若20BAE ∠=︒,求∠CBD 的度数. 【解答】(1)证明见解析 (2)20︒【提示】(1)根据两边对应成比例,且夹角相等,两个三角形相似,即可证明.(2)根据(1)中ABC AED ∽△△,得出ADB ACB ∠=∠,再根据对顶角相等,AFD BFC ∠=∠,证得AFD BFC ∽△△,得出CBD CAD BAE ∠=∠=∠,即可求解. (1)∵BAE CAD ∠=∠∴BAE EAF CAD EAF ∠+∠=∠+∠, ∴BAC DAE ∠=∠, AB ACAE AD =,∵在ABC 和AED △中, AB ACAE AD BAC DAE ⎧=⎪⎨⎪∠=∠⎩,∴ABC AED ∽△△. (2)∵ABC AED ∽△△, ∴ADB ACB ∠=∠,又∵AFD BFC ∠=∠,对顶角相等,∴AFD BFC ∽△△, ∴CBD CAD ∠=∠,∵BAE CAD ∠=∠,20BAE ∠=︒,∴20CAD ∠=︒, 故答案为:20︒.【点睛】本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键. 27.如图,四边形ABCD 为正方形,且E 是边BC 延长线上一点,过点B 作BF ⊥DE 于F 点,交AC 于H 点,交CD 于G 点.(1)求证:△BGC ∽△DGF ; (2)求证:GD AB DF BG ⋅=⋅; (3)若点G 是DC 中点,求GFCE 的值.【解答】(1)见解析 (2)见解析 (3)5GF CE=【提示】(1)由正方形性质和题干已知垂直条件得直角相等,后由对顶角相等,进而得到△BGC ∽△DCF .(2)由第一问的结论可得到相似比,既有DG BC DF BG ⋅=⋅,然后因为正方形四边相等,进行等量代换即可求出证明出结论.(3)通过ASA 判定出△BGC ≌△DEC ,进而根据第一问结论可得△BGC ∽△DGF ,然后通过相似比设未知数,赋值CG x =,即可求出GFCE 的值.(1)证明:∵四边形ABCD 是正方形 ∴90BCD ADC ∠=∠=︒ ∵BF DE ⊥ ∴90GFD ∠=︒ ∴BCD GFD ∠=∠,又∵BGC DGF ∠=∠, ∴△BGC ∽△DCF . (2)证明:由(1)知△BGC ∽△DGF , ∴BG BCDG DF =, ∴DG BC DF BG ⋅=⋅ ∵四边形ABCD 是正方形, ∴AB BC =∴DG AB DF BG ⋅=⋅. (3)解:由(1)知△BCC ∽△DGF , ∴FDG CBG ∠=∠,在△BGC 与△DEC 中,,{,=,CBG CDE BCG DCE BC CD ∠=∠∠=∠ ∴△BGC ≌△DEC (ASA ) ∴CG EC = ∵G 是CD 中点 ∴CG DG = ∴::GF CE CF DC = ∵△BGC ∽△DGF ∴::GF DG CG BG =在Rt △BGC 中,设CG x =,则2BC x =,BC =∴CG BG =∴GF CE=【点睛】本题主要考查了正方形的性质,全等三角形判定和性质,相似三角形判定和性质等知识点,熟练运用相似三角形判定和性质是解题的关键.28.如图1,在ABC 中,90ACB ∠=︒,AC BC =,点D 是AB 边上一点(含端点A 、B ),过点B 作BE 垂直于射线CD ,垂足为E ,点F 在射线CD 上,且EF BE =,连接AF 、BF .(1)求证:ABF CBE ∽;(2)如图2,连接AE ,点P 、M 、N 分别为线段AC 、AE 、EF 的中点,连接PM 、MN 、PN .求PMN ∠的度数及MNPM 的值;(3)在(2)的条件下,若2BC =PMN 面积的最大值.【解答】(1)证明见解析;(2)135PMN ∠=;=2MN PM 3)14 【提示】(1)根据两边对应成比例,夹角相等判定即可.(2)PMN ∠的值可以根据中位线性质,进行角转换,通过三角形内角和定理求解即可,MNPM 的比值转换为AFCE 的比值即可求得.(3)过点P 作PQ 垂直于NM 的延长线于点Q ,12PMN S MN PQ =△,将相关线段关系转化为CE ,可得关系218PMN S CE =△,观察图象,当2CE BC == 【详解】(1)证明:∵90ACB ∠=︒,AC BC = ∴2AB BC =,45ABC BAC ∠=∠= ∵BE 垂直于射线CD , ∴90,BEF ∠= 又∵EF BE =∴2FB EB =,45FBE EFB ∠=∠= ∵+ABC ABE ABE FBE ∠∠=∠+∠ 即:ABF CBE ∠=∠又∵2AB BFCB BE == ∴ABF CBE ∽(2)解:∵点P 、M 、N 分别为线段AC 、AE 、EF 的中点∴//PM CN ,//MN AF ,11,22PM CE MN AF== ∴MPN CNP ∠=∠,CNM EFA ∠=∠∴+MPN MNP CNP MNP CNM EFA ∠∠=∠+∠=∠=∠ 又∵ABF CBE ∽ ∴90AFB CEB ∠=∠= 又∵45EFB ∠=∴904545EFA AFB BFE ∠=∠-∠=-= ∴+45MPN MNP ∠∠=又∵++180MPN MNP PMN ∠∠∠= ∴18045135PMN ∠=-=又∵12=12AFMN AFPM CECE = 又∵ABF CBE ∽ ∴=2AF AB CE CB = ∴=2MNPM(3)如下图:过点P 作PQ 垂直于NM 的延长线于点Q , 135,PMN ∠=︒ 45,PMQ MPQ ∴∠=︒=∠,PQ ∴= 111221222228216PMNS MN PQ AF PM AF CE AF CE ==⨯⨯==△又∵BC =∴AF =∴221168PMN S CE ==△∴当CE 取得最大值时,PMN 取得最大值, ,BE CE ⊥E ∴在以BC 的中点为圆心,BC 为直径的圆上运动,∴当CE CB ==CE 最大,∴11=2=84S ⨯, 【点睛】本题考查的是三角形相似和判定、以及三角形面积最大值的求法,根据题意找见相关的等量是解题关键.。
九年级数学相似三角形的应用练习题解答题.doc
【本文由书林工作坊整理发布,如有疑问可关注私信。
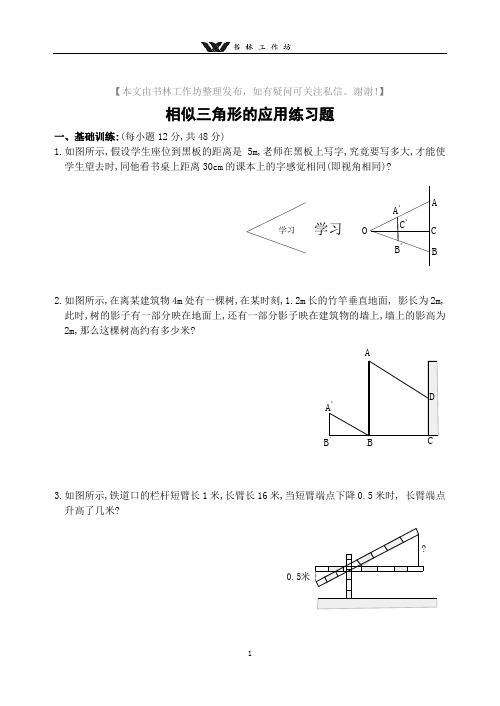
谢谢!】相似三角形的应用练习题一、基础训练:(每小题12分,共48分)1.如图所示,假设学生座位到黑板的距离是5m,老师在黑板上写字,究竟要写多大,才能使学生望去时,同他看书桌上距离30cm 的课本上的字感觉相同(即视角相同)?学习学习A 'C 'B 'OC BA2.如图所示,在离某建筑物4m 处有一棵树,在某时刻,1.2m 长的竹竿垂直地面, 影长为2m,此时,树的影子有一部分映在地面上,还有一部分影子映在建筑物的墙上,墙上的影高为2m,那么这棵树高约有多少米?3.如图所示,铁道口的栏杆短臂长1米,长臂长16米,当短臂端点下降0.5米时, 长臂端点升高了几米?0.5米4.如图所示,零件的外径为a,要求它的厚度x,需要求出内孔的直径AB, 但不能直接量出AB,现用一个交叉钳(两臂长AC和BD相等)去量,如果OA:OC=OB:OD=n,且量得CD=b,求厚x.度二、提高训练:(每小题16分,共32分)1.如图所示,小华在晚上由路灯A走向路灯B,当他走到点P时, 发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时, 发现他身前影子的顶部刚好接触到路灯B的底部,已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.(1)求两个路灯之间的距离;(2)当小华走到路灯B时,他在路灯A下的影长是多少?2.如图所示,学校的围墙外有一旗杆AB,甲在操场上C 处直立3m 高的竹竿CD, 乙从C 处退到E 处恰好看到竹竿顶端D 与旗杆顶端B 重合,量得CE=3m, 乙的眼睛到地面的距离FE=1.5m,丙在C 1处也直立3m 高的竹竿C 1D 1,乙从E 处退后6m 到E 1处, 恰好看到两根竹竿和旗杆重合,且竹竿顶端D 1与旗杆顶端B 也重合,量得C 1E 1=4m,求旗杆AB 的高.C 1E 1F 1ABD 1DCFE三、中考题与竞赛题:(共20分)如图所示,梯形ABCD 中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB 上确定点P 的位置,使得以P,A,D 为顶点的三角形与以P,B,C 为顶点的三角形相似.PABDC答案: 一、1.解:如图所示,有△OAB∽△OA′B ′,量得课本正文中的字的大小为0.4cm×0.35cm,∴字高A′B′=0.4cm,因此'''AB OCA B OC=, 又∵OC=500cm,OC′=30cm,∴AB=5000.4730⨯≈(cm), 同理字的宽度为5000.3530⨯≈6(cm),∴老师黑板上的字的大小应为7cm×6cm(高×宽). 2.4.4m. 3.8米. 4.2n ab-. 二、1.(1)18m. (2)3.6m. 2.10.5m.三、解:(1)若点A,P,D 分别与点B,C,P 对应,即△APD∽△BCP,∴AD APBP BC =, ∴273AP AP =-, ∴AP 2-7AP+6=0, ∴AP=1或AP=6,检测:当AP=1时,由BC=3,AD=2,BP=6, ∴AP ADBC BP=, 又∵∠A=∠B= 90°,∴△APD∽△BCP. 当AP=6时,由BC=3,AD=2,BP=1, 又∵∠A=∠B=90°, ∴△APD∽△BCP.(2)若点A,P,D 分别与点B,P,C 对应,即△APD∽△BPC.∴AP AD BP BC =,∴273AP AP =-, ∴AP=145.检验:当AP=145时,由BP=215,AD=2,BC=3,∴AP ADBP BC=, 又∵∠A=∠B=90°,∴△APD∽△BPC.14 5、6 处.因此,点P的位置有三处,即在线段AB距离点A1、。
相似三角形应用题

4.在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
经开学习中心学科教师辅导讲义
学员姓名:年级:初三课时数:3课时
学科教师:辅导科目:数学授课时间段:
课题
中考第20题相似三角形实际应用题
教学目的
1、复习巩固相似三角形知识点
2、使学生熟练利用相似三角形解实际应用题
教学内容
解直角三角形小题和大题中都有可能出现,小题会出现选题中,大题出现在20题!
知识点1:三角形相似的判定方法
1、(2010•宁德)我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直.已知装饰画的高度AD为0.66米,
求:(1)装饰画与墙壁的夹角∠CAD=_________度(精确到1°);
1、定义法:三个对应角相等,三条对应边成比例的两个三角形相似.
2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角
形与原三角形相似.
3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两
(完整word版)九年级数学相似三角形的性质及应用(教师版)知识点+典型例题+详细答案(良心出品必属

相似三角形的性质及应用【学习目标】1、探索相似三角形的性质,能运用性质进行有关计算;2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题)【要点梳理】要点一、相似三角形的性质1 •相似三角形的对应角相等,对应边的比相等2. 相似三角形中的重要线段的比等于相似比相似三角形对应高,对应中线,对应角平分线的比都等于相似比3. 相似三角形周长的比等于相似比JP CA则匚m厂•AB+BC^CA kA'B^^^+k^A1由比例性质可得:4. 相似三角形面积的比等于相似比的平方曲BC CA.詡,「,则分别作出「二'与沁丁的高1 1BC AD k BC k ADS亠和」l ,则石注二屮27 =k2S AABZ丄BC AD2要点诠释:相似三角形的性质是通过比例线段的性质推证出来的•要点二、相似三角形的应用1. 测量高度测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.要点诠释:测量旗杆的高度的几种方法:平面镜测量法影子测量法手臂测量法标杆测量法2. 测量距离测量不能直接到达的两点间的距离,常构造如下两种相似三角形求解。
1如甲图所示,通常可先测量图中的线段DC BD CE的距离(长度),根据相似三角形的性质,求出AB的长.2 .如乙图所示,可先测AC DC及DE的长,再根据相似三角形的性质计算AB 的长.要点诠释:1 •比例尺:表示图上距离比实地距离缩小的程度,比例尺=图上距离/实际距离;2•太阳离我们非常遥远,因此可以把太阳光近似看成平行光线•在同一时刻,两物体影子之比等于其对应高的比;3 •视点:观察事物的着眼点(一般指观察者眼睛的位置);4•仰(俯)角:观察者向上(下)看时,视线与水平方向的夹角.【典型例题】类型一、相似三角形的性质△ ABB A DEF若厶ABC的边长分别为5cm 6cm 7cm,而4。
陕西中考相似三角形应用真题汇总

2.如图,一人拿着一支刻有厘米分划的小尺,他站在距 电线杆约30米的地方,把手臂向前伸直,小尺竖直,看 到尺上约12个分划恰好遮住电线杆,已知臂长约60厘米 .求电线杆的高.
3.如图,一条东西走向的笔直公路,点A、B表示公 路北侧间隔150米的两棵树所在的位置,点C表示电 视塔所在的位置.小王在公路PQ南侧直线行走,当 他到达点P的位置时,观察树A恰好挡住电视塔,即 点P、A、C在一条直线上,当他继续走180米到达点Q 的位置时,以同样方法观察电视塔,观察树B也恰好 挡住电视塔.假设公路两侧AB∥PQ,且公路的宽为 60米,求电视塔C到公路南侧PQ的距离.
(13年)一天晚上,李明和张龙利用灯光下的影子长 来测量一路灯D的高度.如图,当李明走到点A处时, 张龙测得李明直立身高AM与其影子长AE正好相等; 接着李明沿AC方向继续向前走,走到点B处时,李 明直立时身高BN的影子恰好是线段AB,并测得 AB=1.25m.已知李明直立时的身高为1.75m,求路 灯的高度CD的长.(精确到0.1m)
如图,已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所 使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息, 求出“望月阁”的高AB的长度.
已知:AB⊥BM,ED⊥BM, GF⊥BM ED=1.5 米,CD=2米, DF=16米,FH=2.5米, FG=1.65米
求:AB=?米
21.(15年陕西)晚饭后,小聪和小军在社区
梳理信息:
已知:∠ACH=45° DG=5m, FG=2m, EF=1.6m, CD=0.5m,
求:AB=?m H
解:如图,过点C作CH⊥AB于点H,设AB=X, 则CH=BD,BH=CD=0.5, 则AH=X-0.5 在Rt△ACH中,∠ACH=45°, ∴CH=AH=X-0.5, 则BD=CH=X-0.5 ∵EF⊥FB,AB⊥FB,∴∠EFG=∠ABG=90°. 由题意知∠EGF=∠AGB, ∴△EFG∽△ABC
中考中相似三角形的实际应用

中考中相似三角形的实际应用河南何冬玲以现实生活为背景的问题,已成为近年中考题的一个亮点,它有利于动手操作能力、识图能力及运用数学知识解决实际问题能力的培养.本文就以年中考题为例进行说明.例(芜湖市课改实验区)小胖和小瘦去公园玩标准的跷跷板游戏,两同学越玩越开心,小胖对小瘦说:“真可惜!我只能将你最高翘到米高,如果我俩各边的跷跷板再伸长相同的一段长度,那么我就能翘到米,甚至更高!”()你认为小胖的话对吗?请你作图分析说明;()你能否找出将小瘦翘到米高的方法?试说明.解:()小胖的话不对.小胖说“真可惜!我现在只能将你最高翘到米高”,情形如图所示,是标准跷跷板支架的高度,是跷跷板一端能翘到的最高高度米,是地面.∵,,,∴.∴.又∵此跷跷板是标准跷跷板,,∴,而米,得米.若将两端同时都再伸长相同的长度,假设为米.如图所示,米,米.∵,∴,即.∴,同理可得.∴,由米,得米.综上所述,跷跷板两边同时都再伸长相同的一段长度,跷跷板能翘到的最高高度始终为支架高度的两倍,所以不可能翘得更高.()方案一:如图所示,保持长度不变.将延长一半至,即只将小瘦一边伸长一半.使,则.由,得,∴米.方案二:如图所示,将支架升高米.,,又因为米.∴,∴米.点评:本例利用相似三角形性质解决了生活中常见的跷跷板游戏问题,达到了学以致用的目的,很有实际意义.个人整理,仅供交流学习--------------------------------------------------------------------------------------------------------------------。
相似三角形的应用(重点题专项讲练)(人教版)(原卷版)

相似三角形的应用【典例1】如图,身高1.5米的李强站在A处,路灯底部O到A的距离为20米,此时李强的影长AD=5米,李强沿AO所在直线行走12米到达B处.(1)请在图中画出表示路灯高的线段和李强在B处时影长的线段;(2)请求出路灯的高度和李强在B处的影长.【思路点拨】(1)利用中心投影的性质画出图形即可;(2)设HO=x米,由证得△AED∽△OHD得ADDO =AEHO求出HO的值,再证明△FBC∽△HOC得到BCCO=BFHO,从而求解.【解题过程】解:(1)如图HO,BC即为所求(2)由题意知:BF=AE=1.5米,OA=20米,AB=12米,∴BO=OA−AB=20−12=8米设HO=x米∴∠HOA=∠EAD=90°又∴∠D=∠D∴△AED∽△OHD∴AD DO =AEHO即1.5x =525解得,x=7.5∴∠FBC=∠HOD=90°又∴∠FCB=∠FCO∴△FBC∽△HOC∴BC CO =BFHO即BC8+BC =1.57.5解得BC=2答:路灯高度为7.5米,BC长2米1.(2022·浙江绍兴·模拟预测)如图,身高1.2m的小淇晚上在路灯(AH)下散步,DE为他到达D处时的影子.继续向前走8m到达点N,影子为FN.若测得EF=10m,则路灯AH的高度为()A.6m B.7m C.8m D.9m2.(2022·河北·石家庄二十三中九年级阶段练习)如图,花丛中有一路灯杆AB.在灯光下,小明在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时小明的影长GH=5米.如果小明的身高为1.7米,则路灯杆AB的高度(精确到1米)为()A.5米B.6米C.7米D.8米3.(2022·河北·大名县束馆镇束馆中学三模)一种燕尾夹如图1所示,图2是在闭合状态时的示意图,图3是在打开状态时的示意图(数据如图,单位:mm),则从闭合到打开B,D之间的距离减少了()A.25 mm B.20mm C.15 mm D.8mm4.(2022·全国·九年级专题练习)有一等腰三角形纸片ABC,AB=AC,裁剪方式及相关数据如图所示,则得到的甲、乙、丙、丁四张纸片中,面积最大的是()A.甲B.乙C.丙D.丁5.(2022·江苏无锡·九年级期中)一块直角三角形木板,它的一条直角边AC长为1cm,面积为1cm2,甲、乙两人分别按图∴、∴把它加工成一个正方形桌面,则∴、∴中正方形的面积较大的是()A.∴B.∴C.一样大D.无法判断6.(2022·全国·九年级单元测试)如图,大楼ABCD(可以看作不透明的长方体)的四周都是空旷的水平地面.地面上有甲、乙两人,他们现在分别位于点M和点N处,M、N均在AD的中垂线上,且M、N到大楼的距离分别为60米和20√3米,又已知AB长40米,AD长120米,由于大楼遮挡着,所以乙不能看到甲.若乙沿着大楼的外面地带行走,直到看到甲(甲保持不动),则他行走的最短距离长为________米.7.(2022·全国·九年级专题练习)图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽AB=1.2厘米,托架斜面长BD=6厘米,它有C到F共4个档位调节角度,相邻两个档位间的距离为0.8厘米,档位C到B的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长AG是15厘米,O 是支点且OB=OE=2.5厘米(支架的厚度忽略不计).当支架调到E档时,点G离水平面的距离GH为__________cm.8.(2022·浙江金华·一模)将一本高为17cm(即EF=17cm)的词典放入高(AB)为16cm的收纳盒中(如图1).恰好能盖上盒盖时,测得底部F离收纳盒最左端B处8cm,若此时将词典无滑动向右倒,书角H的对应点H′恰为CD中点.(1)收纳盒的长BC=_______;(2)现将若干本同样的词典放入此有盖的收纳盒中,如图2放置,则最多有________本书可与边BC有公共点.9.(2022·浙江杭州·九年级专题练习)如图,某种吊车由固定机架和三根连杆组成.已知连杆AB=12米,CD=10米,CE=9米,其支点A,D的距离为5米,支点B,C的距离为3米,点A,D到地面l的垂直高度分别为4米和8米.当EC和CD共线时(如图1),点E到地面l的距离为__________米;改变连杆之间的夹角使CE与l平行(如图2),此时点E到地面l的高度为___________米.10.(2022·浙江·翠苑中学九年级期中)如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子的示意图;(2)如果小亮的身高AB=1.5m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.11.(2022·河南·泌阳县光亚学校九年级阶段练习)延时课上,老师布置任务如下:让王林(AB)站在B点处去观测10m外的位于D点处的一棵大树(CD),所用工具为一个平面镜P和必要的长度测量工具(B、P、D在一直线上).已知王林身高1.6m,大树高6.4m,请问如何放置平面镜P才能观测到大树的顶端?12.(2022·辽宁·沈阳市第二十三中学九年级期中)如图,在水平桌面上的两个“E”,当点P1,P2,O在一条直线上时,在点O处用∴号“E”(大“E”)测得的视力与用∴号“E”(小“E”)测得的视力效果相同.(1)△P1D1O与△P2D2O相似吗?请说明理由.(2)图中b1,b2,l1,l2满足的数量关系为___________.(3)若b1=3.2cm,b2=2cm,∴号“E”的测量距离l1=8m,要使得测得的视力相同,则∴号“E”的测量距离l2为___________m.13.(2022·陕西·西安市西航一中九年级期中)如图,小明欲测量一座古塔的高度,他拿出一根杆CD竖直插在地面上,然后自己退后,使眼睛通过杆的顶端C刚好看到塔顶A,若小明的眼睛E离地面1.5米,杆顶端C离地面2.4米,小明到杆的距离DF=2米,杆到塔底的距离DB=32米,E、C、H在同一直线上且EH⊥AB 于H,交CD于点G,求这座古塔的高度.14.(2022·陕西·西安工业大学附中九年级期中)为了加快城市发展,保障市民出行方便,某市在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥AF 的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB、AC的延长线上取点D、E,使得DE∥BC.经测量,BC=120米,DE=210米,且点E 到河岸BC的距离为60米.已知AF∴BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度.15.(2022·广东·佛山市南海区南海实验中学九年级期中)九年级二班的兴趣小组想去测量学校升旗杆的高度,如图所示,小逸同学眼睛A与标杆顶点F、升旗杆顶端E在同一直线上,已知小逸眼睛距地面AB的长为1.7m,标杆FC的长为3.2m,测得BC的长为2m,CD的长为4m,求升旗杆的高ED.16.(2022·山西省运城市运康中学校九年级阶段练习)小明想用镜子测量一棵松树AB的高度,但因树旁有一条河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图所示,第一次他把镜子放在C点,人在F点时正好在镜子中看到树尖A的像;第二次把镜子放在D点,人在H点正好看到树尖A的像.已知小明的眼睛到地面的距离EF=GH=1.7m,量得CD=12m,CF=1.8m,DH=3.8m.已知点B、C、F、D、H在一条直线上,AB⊥BH,EF⊥BH,GH⊥BH,请你求出松树AB的高.17.(2022·全国·九年级单元测试)某天晚上,小明看到人民广场的人行横道两侧都有路灯,想起老师数学课上学习身高与影长的相关知识,于是自己也想实际探究一下.为了探究自己在两路灯下的影长和在两路灯之间的位置关系,小明在网上从有关部门查得左侧路灯(AB)的高度为4.8米,右侧路灯(CD)的高度为6.4米,两路灯之间的距离(BD)为12米,已知小明的身高(EF)为1.6米,然后小明在两路灯之间的线段上行走(如图所示),测量相关数据.(1)若小明站在人行横道的中央(点F是BD的中点)时,小明测得自己在两路灯下的影长FP=米,FQ=米;(2)小明在移动过程中,发现在某一点时,两路灯产生的影长相等(FP=FQ),请问时小明站在什么位置,为什么?18.(2022·全国·九年级专题练习)阅读以下文字并解答问题:在“测量物体的高度”活动中,某数学兴趣小组的3名同学选择了测量学校里的三棵树的高度,在同一时刻的阳光下,他们分别做了以下工作:小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如1图).小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如2图),墙壁上的影长为1.2米,落在地面上的影长为2.4米.小明:测得丙树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如3图).身高是1.6米的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2米.(1)在横线上直接填写甲树的高度为______米,乙树的高度为________米﹔(2)请求出丙树的高度.1112。
中考试题探究 相似三角形的实际应用

第20课时 相似三角形的实际应用(5年4考,7分)1典例“串”考点2陕西5年真题、副题“明”考法典例“串”考点模型一 利用“标杆”测高图形题设已知BC、DE、BD,求AB构建等量利用△ABC∽△ADE可求得AD,AB=AD-BD 关系式1. 如图,某数学兴趣小组的同学利用标杆测量旗杆AB的高度.将一根5米高的标杆CD竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛离地面的距离EF为1.6米,求旗杆AB的高度.第1题图解:如解图,过点E 作EH ⊥AB 于点H ,交CD 于点G .由题意可得四边形EFDG 、GDHB 都是矩形,AB ∥CD ∥EF .∴△ECG ∽△EAH,由题意可得EG =FD =3,GH =BD =30,CG =CD -GD =CD -EF =5-1.6=3.4,∴AH =34米,∴AB =AH +HB =34+1.6=35.6米.答:旗杆AB 的高为35.6米.第1题解图模型二 中心投影图形题设已知:CG 、CD 、CE 、EF 、HE ,求AB 的高已知:AD 、DG 、CH 、EF 、BE ,求DE 的长构建等量关系式由投影可知△DCG ∽△DBA 和△FEH ∽△FBA ,联立两个比例式,可求出BC 和AB由投影可知△AGD ∽△ACH 和△BFE ∽△BCH ,列比例式可求得AH 、BH ,DE =AH +BH -AD -BE2. 某天晚上,小颖、小华和小林想测量小区门口路灯的高度.如图,相邻的两盏路灯AC、BD高度相等,小颖站在E点处,此时她身后的影子的顶部刚好接触到路灯AC的底部;小华站在F点处,此时他身后影子的顶部刚好接触到路灯BD的底部.这时,小林测得EF=10.2米.已知AB=20米,小颖身高ME=1.6米,小华身高NF=1.75米,AC、BD、ME、NF均与地面垂直.请你根据以上数据计算路灯的高度.(结果精确到0.1米)第2题图解:设AE=x,则BF=20-10.2-x=9.8-x,∵ME∥BD,∴△AME∽△ADB,∵NF∥AC,∴△BNF∽△BCA,∴BD≈6.8,答:路灯的高度约为6.8米.模型三 平行投影图形题设已知:AB 、BE 、CD ,求DF 的高已知:AB 、AC 、DE 、EF ,求DG 的高构建等量关系式直接得出△ABE ∽△CDF ,列比例式求解过点F 作FH ⊥DG ,垂足为H ,由题知△ABC ∽△HFG ,求出GH , DG =EF +GH3. 如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.请你根据以上测量数据,求电线杆AB的高度.第3题图解:如解图,过点C 作CG ⊥AB 于点G ,则四边形CDBG 为矩形,∴GC =BD =3米,GB =CD =2米.∵∠NMF =∠AGC =90°,NF ∥AC ,∴∠NFM =∠ACG ,∴△NMF ∽△AGC,∴AB =AG +GB =6+2=8米,答:电线杆AB 的高为8米.第3题解图模型四 镜面反射、投影图形题设已知∠α、AB 、AO 、OC ,求CD 的高已知AB 在水中的倒影为BD ,及EF 、EC 、CB ,求AB构建等量关系式直接得出△ABO ∽△CDO ,列比例式求解直接得出△FEC ∽△DBC ,列比例式求解4. 小雁塔位于唐长安城安仁坊荐福寺内,又称“荐福寺塔”,是西安的标志性建筑之一.在一次社会实践中,小梅和小鹏想通过测量小雁塔的高度,来检验自己掌握知识和运用知识的能力.如图,由于无法直接到塔的底部,小梅在D处利用测角仪测得塔顶A的仰角为25°,同时小鹏在C、B之间的地面上放置一平面镜(平面镜厚度不计),当小鹏移动平面镜至E处时,小梅恰好通过平面镜看到了塔顶A.经测量,DC=1.5米,CE=3米.已知DC⊥CB,AB⊥CB,且C、E、B在同一条直线上,不考虑其它因素,请你根据题中提供的相关信息,计算小雁塔的高A B.(结果精确到0.1米,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47).第4题图解:如解图,过点D作DF⊥AB于点F,则四边形BCDF是矩形,∴BC=DF,BF=CD=1.5米,∵∠DEC=∠AEB,∠DCE=∠ABE=90°,∴△DCE∽△ABE,设AB=x,则BE=2x,∴AF=x-1.5,DF=BC=3+2x,在Rt△AFD中,tan25°=解得x≈48.5,即AB≈48.5米,答:小雁塔的高AB约为48.5米.第4题解图模型五 固定视角图形题设已知AB、BC、BE,求BD构建等量关系式由一对直角和一锐角相等构造相似三角形,即△ABD∽△CBE,再列比例关系式求解5. 如图,小明想通过自己所学的知识测量一段笔直的高架桥MN上DQ段的运行距离,设计了如下的测量方案:已知在高架桥的一侧有一排居民楼AB(楼顶AB与高架桥MN 在同一水平面上,且AB与点D正好在同一直线上),测得AB=35米,小明先站在A处,测得视线与高架桥MN的垂直距离AH=15米,小明又站在B处,使得视线与BQ在一条直线上,此时测得BQ=45米,且∠QBA=90°,求此高架桥上DQ段的运行距离.第5题图解:根据题意得∠AHD =∠QBA =90°,∠ADH =∠QDB ,∴△ADH ∽△QDB,∵AH =15米,BQ =45米,AB =35米,在Rt △AHD 中,根据勾股定理得AD 2=AH 2+DH 2,∴(3DH -35)2=152+DH 2,解得AD =3DH -35.解得DH =20或DH =6.25(舍去),答:此高架桥上DQ 段的运行距离为75米.解得DQ =75(米).陕西5年真题、副题“明”考法命题点相似三角形的实际应用(5年4考)1. (2018陕西20题7分)周末,小华和小亮想用所学的数学知识测量家门前小河的宽,测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C、A共线.已知:CB⊥AD,ED⊥AD,测得BC=1 m,DE=1.5 m,BD=8.5 m,测量示意图如图所示.请根据相关测量信息,求河宽AB.第1题图解:∵CB⊥AD,ED⊥AD,∴CB∥ED.又∵∠CAB=∠EAD,∴△ABC∽△ADE,(3分)∵BC=1 m,DE=1.5 m,BD=8.5 m,AD=AB+BD,∴AB=17 m,答:河宽AB为17 m. (7分)2. (2015陕西20题7分)晚饭后,小聪和小军在社区广场散步.小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A 点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)第2题图解:由题意得∠CAD=∠MND=90°,∠CDA=∠MDN,∴△CAD∽△MND,∴MN=9.6.(3分)又∵∠EBF=∠MNF=90°,∠EFB=∠MFN,∴△EBF∽△MNF,(5分)解得BE≈1.75.(6分)答:小军的身高BE约为1.75米.(7分)3. (2015陕西副题20题7分)周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处.这样观测到的两个点A、B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、MN、M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.测得GE=5米,EN=12.3米,NN′=6.2米.请你根据以上信息,求出遮阳篷的宽AB是多少米?(结果精确到0.01米)第3题图解:如解图,延长MM′交DE于点P,∵AG、DE、MN、M′N′均垂直于EF,MN=M′N′,∴四边形M′MNN′和四边形PMNE均为矩形,∴MM′=NN′=6.2,PM=EN=12.3.(2分)∵AB∥CD∥PM,∴△ACD∽△DPM,△ABD∽△MM′D ,解得AB≈2.52.答:遮阳篷的宽AB约为2.52米.(7分)第3题解图4. (2016陕西20题7分)某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量.于是他们首先用平面镜进行测量,方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C.镜子不动,小亮看着镜面上的标记,他来回走动,走到点D 时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合.这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米;然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.如图,已知:AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计.请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.第4题图解:由题意得∠ABC=∠EDC=∠GFH=90°,∠ACB=∠ECD,∠AFB=∠GHF. ∴△ABC∽△EDC,△ABF∽△GFH,(3分)解得AB=99米.答:“望月阁”的高AB为99米.(7分)5. (2019陕西20题7分)小明想利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午,他和学习小组的同学们带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示.于是,他们先在古树周围的空地上选择了一点D,并在点D处安装了测倾器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5 m,并在点G处的地面上水平放置了一个小平面镜,小明沿BG方向移动,当移动到点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2 m,小明眼睛与地面的距离EF=1.6 m,测倾器的高CD=0.5 m.已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高AB.(小平面镜的大小忽略不计)第5题图解:如解图,过点C 作CH ⊥AB 于点H ,则CH =BD ,BH =CD =0.5.(1分)在Rt △ACH 中,∠ACH =45°,∴AH =CH =BD .∴AB =AH +BH =BD +0.5.(2分)∵EF ⊥FB ,AB ⊥FB ,∴∠EFG =∠ABG =90°.由题意,易知∠EGF =∠AGB ,∴△EFG ∽△ABG .(4分)解得BD =17.5 m .(6分)∴AB =17.5+0.5=18(m).答:这棵古树的高AB 为18 m .(7分)第5题解图6. (2019陕西副题20题7分)新学期,小华和小明被选为升旗手,为了更好地完成升旗任务,他俩想利用测倾器和阳光下的影子来测量学校旗杆的高度P A.如图所示,旗杆直立于旗台上的点P处,他们的测量方法是:首先,在阳光下,小华站在旗杆影子的顶端F处,此时,量得小华的影长FG=2 m,小华身高EF=1.6 m;然后,在旗杆影子上的点D处,安装测倾器CD,测得旗杆顶端A的仰角为49°,量得CD=0.6 m,DF=6 m,旗台高BP=1.2 m.已知在测量过程中,点B、D、F、G在同一水平直线上,点A、P、B在同一条直线上,AB、CD、EF均垂直于BG.求旗杆的高度PA.(参考数据:sin49°≈0.8,cos49°≈0.7,tan49°≈1.2)第6题图解:如解图,过点C 作CH ⊥AB 于点H ,则CH =BD ,BH =CD =0.6.在Rt △AHC 中,tan49°=∴AH =1.2BD .∴AB =AH +HB =1.2BD +0.6.(3分)连接AF 、EG .由题意,可得△EFG ∽△ABF.解得BD =10.5,∴AB =13.2.(6分) ∴PA =AB -PB =13.2-1.2=12(m).答:旗杆的高度PA 约为12 m .(7分)第6题解图点击链接至练习册。
九年级数学下册272相似三角形相似三角形的应用例析素材(新版)新人教版.docx

相似三角形的应用例析相似三角形是平面儿何中的重要的内容之一,其应用十分广泛.举例说明如下.1、测量底部不能到达的建筑物的高例1如图,花从中有一路灯杆AB.在灯光下,小明在D点处的影长DE二3米,沿BD方向行走到达G点,DG二5米,这时小明的影长GII = 5米.如果小明的身高为1. 7米,求路灯杆AB的高度(精确到0. 1米).2、测量池塘宽例2如图,有一池塘要测量两端AB的距离,可先在平地上取一个可以直接到达A和B 的点C,连接AC并延长至D,使AC并延长至D,使CD = -CA,连接BC并延长至E,使5CE = -CB,连接ED,如果量出DE = 25m ,那池塘宽多少?53、利用影长测量建筑物的高度例3高4m的旗杆在水平地面上的影子长6m,此时测得附近一个建筑物的影子2 24m,求该建筑物的高度.4、测量电线杆的高例4如图,一人拿着一支刻有厘米刻度的小尺,站在距电线杆约30m 的地方,把手臂 向前伸直,小尺竖直,看到尺上约12个刻度恰好遮住电线杆,己知手臂长约60cm,求电线 杆的高.5、测量台阶例5汪老师要装修自己带阁楼的新居(右图为新居剖而图),在建造客厅到阁楼的楼 梯AC 时,为避免上楼时墙角F 碰头,设计墙角F 到楼梯的竖直距离FG 为1. 75饥 他量得 客厅高AB=2. 8/77,楼梯洞口宽&=2乩 阁楼阳台宽EF = 3/〃.请你帮助汪老师解决下列问 题:(1)要使墙角F 到楼梯的竖直距离FG 为1.75/77, 少米?阶宽耍大于20c 加问汪老师应该将楼梯建儿个台阶?为什么?楼梯底端C 到墙角D 的距离CD 是多(2)在(1)的条件下,为保证上楼时的舒适感, 楼梯的每个台阶小于20c/〃,每个台卜:参考答案【分析】 根据题意得:AB 丄BH, CD 丄BH, FG 丄BH,在 RtAABE 和 RtACDE4b TAB 丄BH, CD 丄BH,ACD//AB,可证得:AABE^ACDE,同理:竺—匹—AB HG+GD+BD即佥=諾而’解之得:BD=7-販将BD=7・5代入①得:AB 二5. 95m^6m.答:路灯杆AB 的髙度约为6m ・【点评】 本题通过多次平行线,利用相似三角形解决.把实际问题转化为相似问题, 建立数学模型,做到学以致用.例2:【分析】这个问题的实质是△ECDs^BCA,利用两个三角形相似求池塘宽v CD = -CA, CE = -CB 解: 5 5CD CE 1■ ------ — __* CA ~ CB _ 5又 VZECD=ZBCAA AECD^ABCADE CD 1• _____ __ _____ _ __ * AB - AC - 5・•・ AB = 5DE = 5 x 25 = 125(m)【点评】 通过测量池塘宽,能够综合运用三角形相似的判定条件和性质解决问题,发 展数学应用意识,加深对相似三角形的理解和认识.例3:又CD=FG=1・7nu 由①、②可得:DE _ HG DE+BD 一 HG + GD + BD【分析】画出上述示意图,即可发现:即该建筑物的高度是16m.例4:【分析】 本题所叙述的内容可以画出如图那样的儿何图形,即DF 二60cm 二0. 6m, DF = AF J 4F = GFGF 二 12cm 二0. 12m, CE 二30m,求 BC ・由于△ ADF<^ AAEC, £C = AC ,又△ AGFs/\ABC,二 AC~ BC t DF _ GF:.~EC~~BC ,从而可以求出BC 的长.解:TAE 丄EC, DF 〃EC,.\ZADF=ZAEC, ZDAF=ZEAC,AADF^AAEC.DF _ AFA = AC.又 GF 丄EC, BC 丄EC,・・・GF 〃BC, ZAFG 二ZACB, ZAGF 二ZABC,•••△AGF S AABC,AF _ GF:,~AC =~BC ,DF _ GF:.~EC =~BC .又T DF 二60cm 二0. 6m, GF 二12cm 二0. 12cm, EC=30m,BC=6m.即电线杆的高为6m.【点评】“测量电线杆的高”问题本身就是利用数学问题去处理实际问题,还有许多 实际问题都可以用数学问题来解决,运用相似三角形相似的相关知识解决在生活屮的一些实 际问题;必须要正确地理解知识的内涵,比如手臂向前伸直与地面平行,刻度平行于电线杆, 由此构造“相似三角形对应成比例的线段” •在应用过程中,要时时围绕三角形相似这一宗 旨• 例5:【分析】 (1)根据题意有AF//BC, ・・・ZACB 二ZGAF,又ZABC 二ZAFG 二90° ,・•・△ ABCs AGFA.B rC 所以仝_=竽A B B C于是得,BC= AB A f BXBC=16 (m).・BC..---- 二——得BC=3. 2 (m), CD二2+3-3. 2=1. 8 (m). FG(2)设楼梯应建n个台阶,则0. 2n>2.8, 0. 2n<3. 2,解得14<n<16, ・••楼梯应建15个台阶.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学科:数学
专题:相似三角形的应用
主讲教师:黄炜北京四中数学教师
重难点易错点解析
在构造相似模型时,务必找准对应边.
题一
题面:如图所示,AB是斜靠在墙壁上的长梯,梯脚B距离墙角1.6m,梯上点D距离墙1.4m,BD长0.55m,则梯子长为( )
A.3.85m B.4.00m C.4.40m D.4.50m
金题精讲
题一
题面:在已知半圆内,求作内接正方形.
位似变换
满分冲刺
题一
题面:如图,小明准备测量学校旗杆AB的高度,当他发现斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成30°角,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度.
相似三角形的应用
题二
题面:如图,正方形ABCD和正方形OEFG中,点A和点F的坐标分别为(3,2),(-1,-1),则两个正方形的位似中心的坐标是_________.
位似中心、平面直角坐标系
题三
题面:在已知三角形内,求作内接正方形.
相似三角形的应用
讲义参考答案重难点易错点解析
题一
答案:C.
金题精讲
题一
答案:正方形EFGH即为所求.
满分冲刺
题一
答案:20324
3
m.
题二
答案:位似中心的坐标是(1,0)或(-5,-2).
题三
答案:方法1:利用位似形的性质作图法(图16)
图16
作法:(1)在AB上任取一点G',作G'D'⊥BC;
(2)以G'D'为边,在△ABC内作一正方形D'E'F'G';
(3)连结BF',延长交AC于F;
(4)作FG∥CB,交AB于G,从F,G各作BC的垂线FE,GD,那么DEFG就是所求作的内接正方形.
方法2:利用代数解析法作图(图17)
图17
(1)作AH(h)⊥BC(a);
(2)求h+a,a,h的比例第四项x;
(3)在AH上取KH=x;
(4)过K作GF∥BC,交两边于G,F,从G,F各作BC的垂线GD,FE,那么DEFG就是所求的内接正
方形.
初中数学试卷
鼎尚图文**整理制作。
