因子分析实验报告
因子分析实验报告

因子分析实验报告一、实验目的因子分析是一种多元统计分析方法,旨在将多个相关变量归结为少数几个综合因子,以简化数据结构和揭示潜在的变量关系。
本次实验的主要目的是通过因子分析方法,对给定的数据集进行分析,提取主要因子,并解释其含义和实际应用价值。
二、实验数据来源及描述本次实验所使用的数据来源于一项关于消费者购买行为的调查。
该数据集包含了 500 个样本,每个样本包含了 10 个变量,分别是:价格敏感度、品牌忠诚度、产品质量感知、售后服务满意度、促销活动参与度、购买频率、购买金额、购买渠道偏好、口碑传播意愿和推荐他人购买意愿。
这些变量反映了消费者在购买过程中的不同方面的态度和行为,通过对这些变量的分析,可以更好地了解消费者的购买模式和偏好,为企业的市场营销策略提供决策依据。
三、实验方法及步骤1、数据预处理首先,对数据进行了缺失值处理。
对于存在少量缺失值的变量,采用了均值插补的方法进行填充。
然后,对数据进行了标准化处理,以消除量纲的影响,使得不同变量之间具有可比性。
2、因子提取运用主成分分析法(PCA)进行因子提取。
通过计算相关矩阵的特征值和特征向量,确定因子的个数。
根据特征值大于 1 的原则,初步确定提取 3 个因子。
3、因子旋转为了使因子更具有可解释性,采用了方差最大正交旋转(Varimax rotation)方法对因子进行旋转。
4、因子解释对旋转后的因子载荷矩阵进行分析,解释每个因子所代表的含义。
四、实验结果及分析1、因子载荷矩阵经过旋转后的因子载荷矩阵如下:|变量|因子 1|因子 2|因子 3|||||||价格敏感度|075|-012|021||品牌忠诚度|018|072|-015||产品质量感知|025|068|028||售后服务满意度|022|065|031||促销活动参与度|032|-025|078||购买频率|015|028|072||购买金额|012|025|068||购买渠道偏好|028|-035|052||口碑传播意愿|018|032|058||推荐他人购买意愿|021|035|055|2、因子解释因子 1 主要反映了消费者对产品本身相关因素的关注,包括价格敏感度、产品质量感知、售后服务满意度等,可命名为“产品相关因子”。
因子分析报告

实验名称:因子分分析一、实验目的和要求通过上机操作,完成spss软件的因子分析二、实验内容和步骤7.7R型聚类如图所示选择将6个变量选入变量框中分别点击descriptive rotation 选项,进行以下操作As Factor Analysis: Descri-Statistics -------------------Urii variate descrptiv&s口帕1 solutiorirCor relation Matri»-[可Coefficients 日[v>\9gnifiuwri亡已levels Reproduced0 Dderrtii nent □ Anti -image巨kMO and Bflrtleti'^tesd of sphericrlyContinue |Cancel Help点击extract ion点击optionsMissing ValuesJ Exclude cases listwisBExclude ceses ^air\*iseRepiac亡Mh meanCoefTi cierit Displav FormatSuppress absolute values less thane结果如下所示Correlation Matrix aa. Determinant = .037上表为相关矩阵,给出了6个变量之间的相关系数。
主对角线系数都为1,从表中我们可知,变量与变量之间有的会高度相关,有的相关性比较低,语文与历史,语文与英语,英语与历史都是高度相关的,其他的相关度较低上表为KMO和Bartlett检验表,KMO检验是对变量是否适合做因子分析的检验, 根据Kaiser常用度量标准,由于KMO=0.755 ,表明此时一般适合做因子分析。
Extraction Method: PrincipalComponent Analysis.上表为公因子方差,给出了该次分析中从每个原始变量中提取的信息,从表中可以看出除了化学外,主成分几乎都包含了其余各个变量至少80%的信息。
因子分析实验报告

因子分析实验报告因子分析实验报告引言:因子分析是一种常用的统计分析方法,用于探索变量之间的内在关系。
通过因子分析,我们可以找到隐藏在观测变量背后的潜在因素,从而更好地理解数据的结构和解释变量之间的关系。
本实验旨在通过因子分析方法,对某一特定数据集进行分析,以探索其内在因素和变量之间的关系。
实验设计:本实验选取了一个涉及消费者购买行为的数据集,包含了多个观测变量,如消费金额、购买频率、品牌忠诚度等。
我们希望通过因子分析,找出这些变量背后的潜在因素,以便更好地理解消费者购买行为的本质。
实验步骤:1. 数据准备:首先,我们收集了一份关于消费者购买行为的数据集,包含了1000个样本和10个观测变量。
这些变量包括消费金额、购买频率、品牌忠诚度等。
我们将这些变量进行了标准化处理,以消除量纲差异。
2. 因子提取:接下来,我们使用主成分分析方法进行因子提取。
主成分分析是一种常用的因子提取方法,通过线性变换将原始变量转化为一组互相无关的主成分。
我们计算了每个主成分的特征值和特征向量,并选取了特征值大于1的主成分作为因子。
3. 因子旋转:在因子提取后,我们进行了因子旋转,以使得因子更易于解释。
常用的因子旋转方法有方差最大旋转和极大似然旋转等。
在本实验中,我们选择了方差最大旋转方法,以最大化因子的方差。
4. 因子解释:最后,我们对提取出的因子进行解释。
通过观察每个因子所对应的变量载荷,我们可以确定每个因子的含义和影响因素。
同时,我们还计算了每个因子的方差贡献率,以评估其在解释总体方差中的贡献程度。
实验结果:经过因子分析,我们成功地提取出了3个主要因子,并对其进行了旋转和解释。
这些因子分别代表了消费者的购买能力、购买偏好和品牌忠诚度。
具体而言,第一个因子与消费金额和购买频率相关,代表了消费者的购买能力;第二个因子与购买偏好和购买意愿相关,代表了消费者的购买偏好;第三个因子与品牌忠诚度相关,代表了消费者对品牌的忠诚程度。
因子分析实验报告

因子分析实验报告1. 引言因子分析是一种常用的数据分析方法,用于探索和解释观测变量背后的潜在因子结构。
它可以帮助我们发现变量之间的关联性,进而理解数据的本质和结构。
本实验报告旨在通过一个因子分析的具体案例,介绍因子分析的步骤和相关概念。
2. 实验设计2.1 数据收集首先,我们需要收集一组观测变量的数据。
在本实验中,我们选择了一个市场调查问卷作为数据源。
该问卷包含了多个问题,涉及不同的主题,如消费习惯、生活方式等。
我们将这些问题作为观测变量,以便进行因子分析。
2.2 变量选择在进行因子分析之前,我们需要对观测变量进行筛选和选择。
一般来说,我们会选择那些具有较高相关性的变量用于因子分析。
在本实验中,我们将根据变量之间的相关系数矩阵进行选择。
2.3 数据预处理在进行因子分析之前,我们还需要对数据进行一些预处理操作。
这可能包括缺失值处理、异常值处理、数据标准化等。
我们需要确保数据的可靠性和一致性,以获得准确的因子分析结果。
3. 因子分析步骤3.1 因子提取因子提取是因子分析的关键步骤。
它用于从观测变量中提取潜在因子。
常用的因子提取方法包括主成分分析法、最大方差法等。
在本实验中,我们将采用主成分分析法进行因子提取。
3.2 因子旋转因子旋转是为了使提取的因子更易解释和解读。
它通过改变因子载荷矩阵的结构,使得每个因子只与少数几个观测变量相关联。
常用的因子旋转方法包括方差最大旋转法、正交旋转法等。
在本实验中,我们将采用方差最大旋转法进行因子旋转。
3.3 因子解释因子解释是根据旋转后的因子载荷矩阵,对提取的因子进行解释和命名的过程。
我们需要分析每个因子与观测变量之间的关系,以确定每个因子所代表的概念或主题。
在本实验中,我们将尝试解释每个因子,并为其命名。
4. 实验结果经过因子分析的步骤,我们得到了旋转后的因子载荷矩阵。
根据这个矩阵,我们可以解释每个因子所代表的概念,并为其命名。
以下是我们得到的部分结果:•因子1:消费习惯因子,包括购买力、消费水平等变量。
SPSS因子分析实验报告
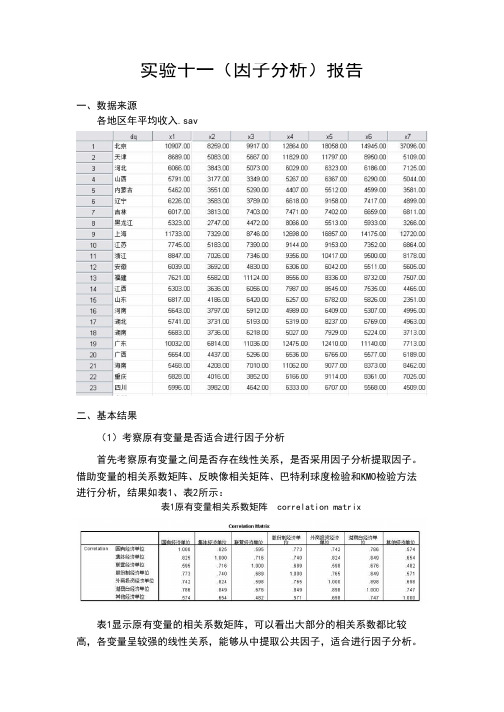
实验十一(因子分析)报告一、数据来源各地区年平均收入.sav二、基本结果(1)考察原有变量是否适合进行因子分析首先考察原有变量之间是否存在线性关系,是否采用因子分析提取因子。
借助变量的相关系数矩阵、反映像相关矩阵、巴特利球度检验和KMO检验方法进行分析,结果如表1、表2所示:表1原有变量相关系数矩阵 correlation matrix表1显示原有变量的相关系数矩阵,可以看出大部分的相关系数都比较高,各变量呈较强的线性关系,能够从中提取公共因子,适合进行因子分析。
表2 KMO and Bartlett's Test由表2可知,巴特利特球度检验统计量观测值为,p值接近0,显著性差异,可以认为相关系数矩阵与单位阵有显著差异,同时KMO值为,根据Kaiser给出的KMO度量标准可知原有变量适合进行因子分析。
(2)提取因子进行尝试性分析:根据原有变量的相关系数矩阵,采用主成分分析法提取因子并选取大于1的特征值。
具体结果见表3:可知,initial一列是因子分析初始解下的共同度,表明如果对原有7个变量采用主成分分析法提取所有特征值,那么原有变量的所有方差都可以被解释,变量的共同度均为1。
事实上,因子个数小于原有变量的个数才是因子分析的目的,所以不可以提取全部特征值。
第二列表明港澳台经济单位、集体经济单位以及外商投资经济单位等变量的绝大部分信息(大于83%)可被因子解释。
但联营经济、其他经济丢失较为表3因子分析中的变量共同度(一)严重。
因此,本次因子提取的总体效果不理想。
重新制定提取特征值的标准,指定提取2个因子,分析表4:可以看出,此时所有变量的共同度均较高,各个变量的信息丢失较少。
因此,本次因子提取的总体效果比较理想。
表4因子分析的变量共同度(二)表5中,第一列是因子编号,以后三列组成一组,每组中数据项为特征值、方差贡献率、累计方差贡献率。
第一组数据项(2-4列)描述因子分析初始解的情况。
在初始解中由于提取了7个因子,因此原有变量的总方差均被解释,累计方差贡献率为100%。
因子分析实验报告范本

因子分析实验报告范本(8)对实验结果进行分析研究5、预习抽查、提问及成绩(请按优,良,中,及格,不及格五级评定)6、未抽查学生的预习成绩(请按优,良,中,及格,不及格五级评定,由教师评阅实验报告时确定)第二部分:实验过程记录(可加页)1、实验原始记录(包括实验数据记录,实验现象记录,实验过程发现的问题等)第一步:导入数据交作® 编勘视图茁fttg(D)炜飘D 分折他)图羽〔① 起H■幵数据俸回3檢素…■关闭Q Ct甘斗Q 探存Ctrl-S另存M£0...1舲股票代冯蛋票启称星玉每股收主营业务临入万元主营壮务和净利掏万元总资庐万元总氏储万元am万元净资庐万元1600519蛊州茅台9.3500217181918531611D69333536615&831023:625034133 2520*ST 風圈 4.3100 765S9 91S3 4360£9 5321S J3330 34 48773 2304 洋河战储370001230535 735376 396274 29^0921D08495 3719206974 E00694大酋股盼 3.5100244355349&401 1029551M0G9409297431E177205 551 格力电器 3.27® 9341Q06 35387J6982755 1595O3B3 11073129 1140772596 600392 广杀朋珠 2.42008612 5149 02756 2&35B1 1041310 25314B76031B8亚邦股粘 2.380019276S9613051512365843105490 10 260053 8300386 飞天诚信 2.3200 73471 31617 18937 1452S8 13802 13 131J869 33B 建茉动力 2.2200 5614B38 1196345 J44543 12291644 8253531 4B4038113 10300Q95三六五网•-■'ill3275730342117353B773BO536080720 111600340 痒夏車舊 2 130******** 5SI71492821171O454E07 0757223 75 1697464 12333 美的菓团 2.120010908416 2724175895296 115822077164805 7D 4417492 13601336新华■保晞 2.030010992500770400&3250061043000663669001246B2100 14 E0Q742 一汽宣錐 1.0300 321935 44368 39B42E25EQ323354120392142 15538 云甫白药 1.0700 1331752397977 194470 1471992397999 37 1074393 1660D436片甘腐 1.06001067735215223877338619&37^025274S21 17 600104 上芫棄团1,0500 46954731 528B0772CMO93238147695 2127279010 16674997 106D3168 张普罢思 1.B400 5B567 41D699995 8347S 1031789 7315819601533匠城汽生 1.BJ0042665B9105313355S625543O55J2317249213113305 2060081G 妄怯信托1,6100135026 109457 S209Q22956270060:45 1594&4图1数据第二步:将数据标准化fe9.36004.3100口十"gn丄H L H教IM也…,貝谒股J締出(①…■本©•••r Trnrsn点击分析f 描述统计f 描述。
《多元统计实验》因子分析实验报告一

《多元统计实验》因子分析实验报告newscore2 #显示以第二因子得分排序结果newscore3<-newscore[order(newscore[,4],decreasing=T),] #按第三因子得分排序newscore3 #显示以第三因子得分排序结果newscore4<-newscore[order(newscore[,5],decreasing=T),] #按因子综合得分排序newscore4 #显示以因子综合得分排序结果三、实验结果分析下图为数据标准化后相关系数矩阵图,可以看出x3、x8、x4之间的存在较大的相关性,这些消费指标之间存在较强的线性相关关系,适合用因子分析模型进行分析,下面用极大似然估计法进行因子分析。
将公共因子设置为3个,从下运行结果可以看出,累计方差贡献率达到了83.36%,说明选择3个是合适的,从初始载荷阵可以看出消费指标无法准确的解释因子的含义,故我们在进行基于极大似然法的正交旋转。
由下图旋转得到的因子载荷估计,居住(x3)、生活用品及服务(x4)、交通通信(x5)、教育文化娱乐(x6)、医疗保健(x7)和其他用品及服务(x8)在因子f1上的载荷分别为0.772、0.679、0.663、0.858、0.733、0.692,这六个消费指标反映了日常消费,因此f1命名为日常消费因子;x1在f2上反映了食品烟酒的消费,因此f2命名为食品烟酒因子;x2在f3上反映了衣着的消费,因此命名为衣着因子。
也由此可得到因子分析模型:x*1≈0.208f1+0.975f2+ε1x*2≈0.220f1+0.972f3+ε2x*3≈0.772f1+0.510f2+ε3x*4≈0.679 f1+0.361 f2+0.405f3+ε4x*5≈0.663 f1+0.440 f2+0.271 f3+ε5x*6≈0.858 f1+0.262 f2+ε6x*7≈0.733 f1+0.350 f3+ε7x*8≈0.692 f1+0.522 f2+0.391+ε8从下图的各因子得分结果,可以看出,在第一因子上得分多的为上海、北京、天津;第二因子上得分多的为北京、上海、云南;第三因子得分多的为海南、广东、上海;但是这样得到的结果,较难找,因此我们对得分分别按第一因子和第二因子以及第三因子进行排序可直观看出。
因子分析实验报告范本

因子分析实验报告范本一、实验目的本次因子分析实验旨在探究多个变量之间的潜在结构关系,通过降维的方法提取出主要的公共因子,以更简洁、有效地解释数据中的信息。
二、实验数据来源及描述实验数据来源于_____调查,共收集了_____个样本,涉及_____个变量。
这些变量包括但不限于:1、变量 1:_____,用于衡量_____。
2、变量 2:_____,反映了_____。
3、变量 3:_____,其代表的含义是_____。
三、实验方法1、数据预处理对缺失值进行处理,采用_____方法进行填充。
对数据进行标准化处理,以消除量纲的影响。
2、因子提取方法选用主成分分析法提取公共因子。
根据特征根大于 1 的原则确定因子个数。
3、因子旋转方法采用方差最大化正交旋转,以使因子更具有可解释性。
四、实验步骤1、导入数据使用统计软件(如 SPSS)将数据文件导入。
2、数据预处理按照上述预处理方法进行操作。
3、因子分析在软件中选择因子分析模块,设置相应的参数进行分析。
4、结果解读观察公因子方差表,了解每个变量被公共因子解释的程度。
查看总方差解释表,确定提取的公共因子个数及解释的总方差比例。
分析旋转后的成分矩阵,解读公共因子的含义。
五、实验结果1、公因子方差变量 1 的公因子方差为_____,表明公共因子能够解释其_____%的方差。
变量 2 的公因子方差为_____,意味着公共因子对其的解释程度为_____%。
2、总方差解释提取了_____个公共因子,其特征根分别为_____、_____、_____。
这_____个公共因子累计解释了总方差的_____%。
3、旋转后的成分矩阵公共因子 1 在变量 1、变量 2 上有较高的载荷,分别为_____、_____,可以将其解释为_____因素。
公共因子 2 在变量 3、变量 4 上的载荷较大,分别为_____、_____,代表了_____方面。
六、结果讨论1、因子的可解释性提取的公共因子在实际意义上具有一定的合理性和可解释性,能够较好地概括原始变量所包含的信息。
实验报告-因子分析(多元统计)精选全文

精选全文完整版可编辑修改实验报告主成分分析(综合性实验)(Principal component analysis)实验原理:主成分分析利用指标之间的相关性,将多个指标转化为少数几个综合指标,从而达到降维和数据结构简化的目的。
这些综合指标反映了原始指标的绝大部分信息,通常表示为原始指标的某种线性组合,且综合指标间不相关。
利用矩阵代数的知识可求解主成分。
实验题目一:将彩色胶卷在显影液下处理后在不同情形下曝光,然后通过红、绿、蓝三种滤色片并在高、中、低三种密度下进行测量,每个胶卷有高红、高绿、高蓝、中红、…、低蓝等九个指标(分别记为X1-X9九个变量)。
试验了108个胶卷,由数据已算得如下协差阵:(S2a1)177 179 95 96 53 32 -7 -4 -3419 245 131 181 127 -2 1 4302 60 109 142 4 4 11158 102 42 4 3 2137 96 4 5 6128 2 2 834 31 3339 3948实验要求:(1)试从协差阵出发进行主成分分析;(2)计算方差累积贡献率;(3)作Scree图,并结合(2)的结果确定主成分的个数;(4)试对结果进行解释。
实验题目二:下表中给出了不同国家及地区的男子径赛记录:(t8a6)Country 100m(s) 200m(s)400m(s)800m(min)1500m(min)5000m(min)10,000m(min)Marathon(mins)Argentina 10.39 20.81 46.84 1.81 3.7 14.04 29.36 137.72 Australia 10.31 20.06 44.84 1.74 3.57 13.28 27.66 128.3 Austria 10.44 20.81 46.82 1.79 3.6 13.26 27.72 135.9 Belgium 10.34 20.68 45.04 1.73 3.6 13.22 27.45 129.95 Bermuda 10.28 20.58 45.91 1.8 3.75 14.68 30.55 146.62 Brazil 10.22 20.43 45.21 1.73 3.66 13.62 28.62 133.13 Burma 10.64 21.52 48.3 1.8 3.85 14.45 30.28 139.95 Canada 10.17 20.22 45.68 1.76 3.63 13.55 28.09 130.15 Chile 10.34 20.8 46.2 1.79 3.71 13.61 29.3 134.03 China 10.51 21.04 47.3 1.81 3.73 13.9 29.13 133.53 Columbia 10.43 21.05 46.1 1.82 3.74 13.49 27.88 131.35 Cook Islands 12.18 23.2 52.94 2.02 4.24 16.7 35.38 164.7 Costa Rica 10.94 21.9 48.66 1.87 3.84 14.03 28.81 136.58 Czechoslovakia 10.35 20.65 45.64 1.76 3.58 13.42 28.19 134.32 Denmark 10.56 20.52 45.89 1.78 3.61 13.5 28.11 130.78 Dominican Republic 10.14 20.65 46.8 1.82 3.82 14.91 31.45 154.12 Finland 10.43 20.69 45.49 1.74 3.61 13.27 27.52 130.87 France 10.11 20.38 45.28 1.73 3.57 13.34 27.97 132.3 German (D.R.) 10.12 20.33 44.87 1.73 3.56 13.17 27.42 129.92 German (F.R.) 10.16 20.37 44.5 1.73 3.53 13.21 27.61 132.23 Great Brit.& N. Ireland 10.11 20.21 44.93 1.7 3.51 13.01 27.51 129.13 Greece 10.22 20.71 46.56 1.78 3.64 14.59 28.45 134.6 Guatemala 10.98 21.82 48.4 1.89 3.8 14.16 30.11 139.33 Hungary 10.26 20.62 46.02 1.77 3.62 13.49 28.44 132.58 India 10.6 21.42 45.73 1.76 3.73 13.77 28.81 131.98Indonesia 10.59 21.49 47.8 1.84 3.92 14.73 30.79 148.83 Ireland 10.61 20.96 46.3 1.79 3.56 13.32 27.81 132.35 Israel 10.71 21 47.8 1.77 3.72 13.66 28.93 137.55 Italy 10.01 19.72 45.26 1.73 3.6 13.23 27.52 131.08 Japan 10.34 20.81 45.86 1.79 3.64 13.41 27.72 128.63 Kenya 10.46 20.66 44.92 1.73 3.55 13.1 27.38 129.75 Korea 10.34 20.89 46.9 1.79 3.77 13.96 29.23 136.25 D.P.R Korea 10.91 21.94 47.3 1.85 3.77 14.13 29.67 130.87 Luxembourg 10.35 20.77 47.4 1.82 3.67 13.64 29.08 141.27 Malaysia 10.4 20.92 46.3 1.82 3.8 14.64 31.01 154.1 Mauritius 11.19 22.45 47.7 1.88 3.83 15.06 31.77 152.23 Mexico 10.42 21.3 46.1 1.8 3.65 13.46 27.95 129.2 Netherlands 10.52 20.95 45.1 1.74 3.62 13.36 27.61 129.02 New Zealand 10.51 20.88 46.1 1.74 3.54 13.21 27.7 128.98 Norway 10.55 21.16 46.71 1.76 3.62 13.34 27.69 131.48 Papua New Guinea 10.96 21.78 47.9 1.9 4.01 14.72 31.36 148.22 Philippines 10.78 21.64 46.24 1.81 3.83 14.74 30.64 145.27 Poland 10.16 20.24 45.36 1.76 3.6 13.29 27.89 131.58 Portugal 10.53 21.17 46.7 1.79 3.62 13.13 27.38 128.65 Rumania 10.41 20.98 45.87 1.76 3.64 13.25 27.67 132.5 Singapore 10.38 21.28 47.4 1.88 3.89 15.11 31.32 157.77 Spain 10.42 20.77 45.98 1.76 3.55 13.31 27.73 131.57 Sweden 10.25 20.61 45.63 1.77 3.61 13.29 27.94 130.63 Switzerland 10.37 20.46 45.78 1.78 3.55 13.22 27.91 131.2 Taipei 10.59 21.29 46.8 1.79 3.77 14.07 30.07 139.27 Thailand 10.39 21.09 47.91 1.83 3.84 15.23 32.56 149.9 Turkey 10.71 21.43 47.6 1.79 3.67 13.56 28.58 131.5 USA 9.93 19.75 43.86 1.73 3.53 13.2 27.43 128.22 USSR 10.07 20 44.6 1.75 3.59 13.2 27.53 130.55Western Samoa 10.82 21.86 49 2.02 4.24 16.28 34.71 161.83 (数据来源:1984年洛杉机奥运会IAAF/AFT径赛与田赛统计手册)实验要求:(1)试求主成分,并对结果进行解释;(2)试用方差累积贡献率和Scree图确定主成分的个数;(3)计算各国第一主成分的得分并排名。
因子分析实验报告

电子科技大学政治与公共管理学院本科教学实验报告(实验)课程名称:数据分析技术系列实验电子科技大学教务处制表电子科技大学实验报告学生:晨飞学号:27指导教师:高天鹏一、实验室名称:电子政务可视化实验室二、实验项目名称:因子分析三、实验原理使用SPSS软件的因子分析对数据样本进行分析相关分析的原理:步骤一:将原始数据标准化。
因子分析的第一步是主成分分析,将总量较多的因素通过线性组合的方式组合成几个因素,且这些因素之间相互独立。
步骤二:建立变量的相关系数矩阵RAnalyse->Dimention Ruduction-> Fctor ->Extraction->勾选Correlation matrix可以输出相关系数矩阵,相关系数矩阵计算了变量之间两两的pearson相关系数。
步骤三:适用性检验使用Bartlett球形检验或者KMO球形检验来检验样本是否适合进行因子分析。
评价标准:KMO检验用于检验变量间的偏相关系数是否过小,一般情况下,当KMO大于0.9时效果最佳,小于0.5时不适宜做因子分析。
Bartlett球形检验用于检验相关系数矩阵是否是单位阵,如果结论是不拒绝该假设,则表示各个变量都是各自独立的。
步骤四:根据因子贡献率选取因子,特征值和特征向量构建因子载荷矩阵A。
处于简化和抽取核心的思想,一般会按照某种标准选取前几个对观测结果影响较大的因素构建因子载荷矩阵,一般的标准是选取特征根大于1的因子。
并要求累积贡献率达到90%以上。
步骤五:对A进行因子旋转因子旋转的目的是使因子载荷矩阵的结构发生变化,使每个变量仅在一个因子上有较大载荷。
是将因子矩阵在一个空间里投影,使单个向量的投影在仅在一个变量的方向有较大的值,这样做可以简化分析。
步骤六:计算因子得分:计算因子得分是计算在不同样本水平下观测指标的水平的方式。
计算因子得分需要用到因子得分计算函数,这个计算的结果是无量纲的,仅表示各因子在这个水平下观测指标的值,这也是因子分析的目标,将不可观测的目标观测量用一个函数与可以观测的变量联系起来。
多元统计实验报告--因子分析

多元统计实验报告设计题目:因子分析一、分析数据1995年我国社会发展状况的数据二、基本原理因子分析的基本思想是把每个研究变量分解为几个影响因素变量,将每个原始变量分解成两部分因素,一部分是由所有变量共同具有的少数几个公共因子组成的,另一部分是每个变量独自具有的因素,即特殊因子。
三、实验步骤及其结果分析1、选择Analyze→Data Reduction→Factor,打开Factor Analysis主对话框;2、选择变量X1至X6,点击向右的箭头按钮,将六个变量移到Variable栏中;3、点击Descriptives…按钮,打开Descriptives子对话框。
在此对话框的Statistics下选择Initial solution;Correlation Matrix下选择coefficients,单击Continue按钮,返回Factor Analysis主对话框;4、单击Extraction…按钮,打开Extraction子对话框。
在此对话框的Method 下选择Principal components;Analyze下选择Correlation Matrix;Extract下选择Number of Factor,并在其右端的矩形框键入6;Display下选择Unrotated factor 和Scree plot,单击Continue按钮,返回Factor Analysis主对话框;点击OK按钮,显示结果清单。
(1)相关矩阵从表Correlation Matrix(相关矩阵)可知,各变量间存在较强的相关关系,因此有必要进行因子分析。
表中主对角线上的元素为1,表明变量自身于自身的相关系数为1。
(2)解释总方差从表Total Variance Explained(解释总方差)可知,前三个因子一起解释总方差的93.466%(累计贡献率),这说明前三个因子提供了原始数据的足够信息。
5、根据以上分析提取因子情况,单击Extraction…按钮,打开Extraction子对话框。
主成分分析和因子分析实验报告

主成分分析和因子分析实验报告目录主成分分析和因子分析实验报告 (1)引言 (1)研究背景 (1)研究目的 (2)研究意义 (3)主成分分析 (4)主成分分析的概念 (4)主成分分析的原理 (5)主成分分析的步骤 (6)因子分析 (7)因子分析的概念 (7)因子分析的原理 (8)因子分析的步骤 (8)实验设计 (9)数据收集 (9)数据预处理 (11)主成分分析实验 (11)因子分析实验 (13)实验结果与分析 (14)主成分分析结果 (14)因子分析结果 (15)结果对比与讨论 (16)结论与展望 (17)实验结论 (17)实验不足与改进方向 (17)后续研究建议 (18)参考文献 (19)引言研究背景主成分分析(Principal Component Analysis,简称PCA)和因子分析(Factor Analysis,简称FA)是多元统计分析中常用的降维技术,广泛应用于数据挖掘、模式识别、图像处理、金融风险评估等领域。
这两种方法可以帮助我们从大量的变量中提取出最为重要的信息,简化数据集,减少冗余信息,同时保留原始数据的主要特征。
随着信息技术的迅速发展,数据的规模和复杂性不断增加,传统的统计分析方法已经无法满足对大规模数据的处理需求。
在这种背景下,主成分分析和因子分析成为了研究者们的关注焦点。
它们能够对高维数据进行降维处理,提取出最为重要的特征,从而更好地理解和解释数据。
主成分分析是一种无监督学习方法,通过线性变换将原始数据映射到一个新的坐标系中,使得新坐标系下的变量之间不相关。
这样做的好处是可以减少数据的维度,同时保留了原始数据的主要信息。
主成分分析的基本思想是找到能够最大程度解释数据方差的投影方向,即找到一组新的变量,使得它们之间的协方差为零。
这些新的变量被称为主成分,它们按照解释方差的大小排序,前几个主成分能够解释原始数据中大部分的方差。
因子分析是一种潜变量模型,它假设观测数据是由一组潜在因子和测量误差共同决定的。
SPSS因子分析实验报告

SPSS因子分析实验报告一、实验目的本次实验旨在运用 SPSS 软件进行因子分析,以探索和简化数据结构,发现潜在的因子,并对变量之间的关系进行深入理解。
通过因子分析,我们希望能够提取主要的公共因子,解释数据中的大部分变异,为进一步的数据分析和决策提供有价值的信息。
二、实验数据来源本次实验所使用的数据来源于具体数据来源。
该数据集包含了具体变量描述等多个变量,共样本数量个观测值。
这些数据反映了数据所涉及的研究对象或领域的相关情况。
三、实验步骤1、数据预处理首先,对原始数据进行了初步的检查和清理。
检查了数据中是否存在缺失值,并对缺失值进行了适当的处理(如删除含缺失值的观测、用均值或中位数插补等)。
同时,对数据进行了标准化处理,以消除量纲的影响,使不同变量在相同的尺度上进行比较。
2、适用性检验在进行因子分析之前,需要对数据进行适用性检验,以确定数据是否适合进行因子分析。
常用的检验方法包括巴特利特球形检验(Bartlett's Test of Sphericity)和 KMO 检验(KaiserMeyerOlkin Measure of Sampling Adequacy)。
巴特利特球形检验的原假设是相关系数矩阵为单位矩阵,即变量之间相互独立。
如果检验结果显著(p 值小于 005),则拒绝原假设,表明变量之间存在相关性,适合进行因子分析。
KMO 检验用于评估变量之间的偏相关性。
KMO 值越接近 1,表明数据越适合进行因子分析;一般认为,KMO 值大于 06 时适合进行因子分析。
3、提取因子根据适用性检验的结果,确定可以进行因子分析后,使用主成分法(Principal Component Analysis)或主轴因子法(Principal Axis Factoring)等方法提取因子。
在提取因子时,需要确定提取因子的个数。
常用的确定因子个数的方法有特征值准则(Eigenvalue Criterion)和碎石图(Scree Plot)。
因子分析实验报告

因子分析实验报告引言概述:因子分析是一种多变量统计分析方法,用于确定一组观测变量中的潜在因子结构。
通过因子分析,我们可以分析一个大量的观测变量,将其归纳为较少数量的相互关联的因子,从而简化复杂的数据结构。
本实验旨在通过实际应用因子分析方法,对潜在因子结构进行探索和解释。
正文内容:1.因子分析的基本原理1.1数据预处理1.1.1数据清洗1.1.2数据标准化1.2因子提取方法1.2.1主成分分析法1.2.2最大似然法1.2.3主轴法1.3因子旋转方法1.3.1方差最大旋转法(Varimax)1.3.2极简旋转法(Simplimax)1.3.3最大似然旋转法(Promax)1.4因子解释和命名1.4.1因子载荷1.4.2解释方差1.4.3因子命名2.实验设计和数据收集2.1实验目的和假设2.2实验设计2.3数据收集方法2.4样本选择和数量3.数据分析和结果解释3.1因子提取3.1.1因素的选择3.1.2因子提取方法的比较3.1.3因子间关系3.2因子旋转3.2.1旋转前的因子载荷3.2.2旋转后的因子载荷3.2.3旋转后的因子解释3.3因子的可解释变异3.3.1总方差解释比例3.3.2单个因子的方差解释比例3.3.3组合因子的方差解释比例4.结果分析和讨论4.1因子结构和因子载荷4.2因子的解释和命名4.3因子的解释力度和相关性4.4结果的稳定性和可靠性4.5结果与假设的一致性5.实验总结和建议5.1实验结果总结5.2实验中的问题和限制5.3进一步研究方向和建议5.4实验应用和意义文末总结:通过本次因子分析实验,我们成功地应用了因子分析方法对观测变量进行了潜在因子结构的探索和解释。
通过数据分析和结果解释,我们得到了一组有意义和可解释的因子结构,并对其进行了详细的分析和讨论。
我们还总结了本次实验的结果、问题和限制,并提出了进一步研究方向和建议。
本实验对研究者在实际应用因子分析方法时提供了宝贵的经验和指导。
因子分析实验报告

因子分析实验报告因子分析实验报告引言:因子分析是一种常用的统计方法,用于研究变量之间的关系和潜在结构。
通过因子分析,可以将一组观测变量转化为较少的潜在因子,从而减少数据的复杂性,提取出变量背后的共同因素。
本实验旨在探究因子分析在数据分析中的应用,并通过实例分析来展示其效果。
实验设计:本实验选取了一个由20个观测变量组成的数据集,包括心理测试中的各项指标。
首先,我们对数据进行了描述性统计分析,包括计算均值、方差等指标,以了解数据的基本情况。
接下来,我们使用因子分析方法对数据进行了降维处理,提取出主要的潜在因子。
最后,我们对提取出的因子进行了解释,并分析了各个因子与观测变量之间的关系。
实验结果:在描述性统计分析中,我们发现数据集中的观测变量具有一定的相关性,但并不完全一致。
这表明存在一些共同的潜在因子,可以通过因子分析来提取。
在进行因子分析时,我们采用了主成分分析法,通过计算特征值和特征向量,确定了最重要的潜在因子。
根据特征值-特征向量的结果,我们提取了3个主要因子,这些因子解释了总方差的70%以上。
接下来,我们对提取出的因子进行了命名和解释。
第一个因子被命名为“情绪状态”,它包括了焦虑、抑郁和情绪波动等观测变量。
第二个因子被命名为“自信与社交能力”,它包括了自尊、社交能力和自信等观测变量。
第三个因子被命名为“认知能力”,它包括了记忆力、注意力和思维敏捷等观测变量。
进一步分析发现,这些因子与观测变量之间存在一定的相关性。
例如,情绪状态因子与焦虑、抑郁等观测变量呈正相关,而与自尊、社交能力等观测变量呈负相关。
这些结果表明,通过因子分析可以揭示出变量之间的内在关系,为后续的数据分析和研究提供了重要线索。
讨论与结论:本实验通过因子分析方法,成功地将一个包含20个观测变量的数据集转化为3个潜在因子。
这些因子能够解释数据集中70%以上的总方差,具有较好的降维效果。
通过对提取出的因子进行解释和分析,我们发现了变量之间的内在关系,并为进一步的研究提供了重要线索。
实验报告5 因子分析

S P S S操作实验题目:因子分析实验类型:基本操作实验目的:掌握因子分析的基本原理及方法实验内容:数据是34名运动员十项全能的比赛成绩。
试采用因子分析的方法来提取公共因子,分析衡量运动员运动成绩的指标。
1、对数据进行KMO和Bartlett检验。
2、使用主成分分析方法,并且在公因子特征值大于1的基础上选择公因子的数目,确定公因子的个数。
3、利用最大方差法求出旋转后的因子载荷矩阵,确定对应公因子经济含义。
4、根据因子载荷矩阵写出标准化的跳远、铅球与公因子之间的函数表达式。
5、求出数据中第一个学生和最后一个学生的的公因子得分。
实验步骤:1、点击“变量视图”,将十项全能成绩改为“X1、X2……X10”,选择“分析”—“降维”—“因子分析”,然后进入到了“因子分析”的界面,将“X1、X2……X10”项选为“变量”;2、选择“描述”项,然后勾选“单变量描述性”“原始分析结果”“系数”“显著性水平”“行列式”“KMO和Bartlett的球形度检验”,点击“继续”;3、点击“抽取”项,选择“主成分”方法,基于特征值大于“1”,点击“继续”;4、点击“旋转”项,选择“最大方差法”,勾选“旋转解”和“载荷图”,点击“继续”;5、点击“因子得分”项,勾选“保存为变量”(旋转)和“显示因子系数得分矩阵”,方法为“回归”,点击“继续”;6、“选项”项为默认项,点击“确定”,得到所需结果。
实验结果:1.对数据进行KMO和Bartlett检验。
KMO 和 Bartlett 的检验取样足够度的 Kaiser-Meyer-Olkin 度量。
.788Bartlett 的球形度检验近似卡方211.586 df 45 Sig. .000通过KMO检验和Bartlett检验的结果发现,KMO的值为0.788,比较接近1,表示适合做因子分析。
Bartlett 的球形度卡方检验的P值为0.000,拒绝原假设,即总体变量是相关的。
可以进行因子分析。
主成分分析因子分析实验报告

主成分分析因子分析实验报告引言:方法:数据集:本次实验使用的数据集是关于一组学生的各项成绩数据,包括语文、数学、英语等科目的成绩。
数据集共有100个样本,每个样本包含5个特征。
主成分分析(PCA):主成分分析的主要思想是通过线性变换将原始数据映射到一个新的坐标系中,使得数据在新的坐标系下的方差最大化。
这样可以使得数据在新的坐标系下尽可能地被压缩到一维或者二维空间中,从而实现降维的目的。
在本次实验中,我们将对数据集进行主成分分析,寻找数据中的主要结构。
因子分析(Factor Analysis):因子分析的主要思想是假设观测数据是由一组潜在因子和测量误差组成的。
因子分析试图通过最大似然估计的方法找出最可能的潜在因子,并将观测数据映射到潜在因子的空间中。
在本次实验中,我们将使用因子分析探索数据集中的潜在因子结构。
结果:主成分分析(PCA):通过主成分分析,我们发现数据集的前两个主成分可以解释约80%的数据方差。
这表明数据在二维空间下已经能够充分表示原始数据的特征。
同时,我们还可以观察到各个特征在主成分空间中的投影,从而了解不同特征之间的相关性。
因子分析(Factor Analysis):通过因子分析,我们找到了数据集中的两个主要因子,分别是“数理化”因子和“语言能力”因子。
这两个因子可以代表数据中的大部分信息,与原始特征之间存在着较高的相关性。
因子分析帮助我们发现了数据中的潜在结构,并解释了数据之间的关系。
讨论:主成分分析和因子分析是两种常用的数据降维技术,能够通过线性变换和潜在因子的挖掘来发现数据的主要结构和潜在信息。
在本次实验中,我们使用这两种方法对一个学生成绩数据集进行了分析,发现了数据中的主要结构和隐藏因子。
通过主成分分析,我们找到了能够解释数据80%方差的主成分,并可视化了数据在主成分空间中的表现。
通过因子分析,我们发现了数据中的两个主要因子,并解释了数据中的潜在结构。
结论:主成分分析和因子分析是一种强大的数据分析工具,能够帮助我们更好地理解数据并发现数据中的潜在结构。
因子血清鉴定实验报告

实验名称:因子血清鉴定实验目的:通过对血清中特定因子的检测,评估其存在与否,为临床诊断提供依据。
实验时间:2023年X月X日实验地点:XX医院检验科实验人员:XX一、实验原理因子血清鉴定是一种检测血清中特定因子存在与否的方法。
该实验基于抗原-抗体反应原理,通过特异性抗体与待测因子结合,形成抗原-抗体复合物,从而实现对特定因子的定性或定量分析。
二、实验材料1. 样本:患者血清(A、B、C、D、E)2. 试剂:- 抗体:针对特定因子的抗体(IgM型、IgA型、IgG型、IgE型)- 底物:酶联底物- 显色剂:TMB(3,3'-5,5'-四甲基联苯胺)- 阴性对照:已知不含特定因子的血清- 阳性对照:已知含有特定因子的血清3. 仪器:- 酶标仪- 移液器- 微量板三、实验方法1. 将抗体分别加入微量板孔中,每孔加入100μl抗体,37℃孵育1小时。
2. 洗板:用洗涤液洗板3次,每次2分钟。
3. 加入待测血清,每孔加入100μl,37℃孵育1小时。
4. 洗板:同上。
5. 加入底物,每孔加入100μl,37℃孵育30分钟。
6. 洗板:同上。
7. 加入显色剂,每孔加入100μl,37℃孵育10分钟。
8. 洗板:同上。
9. 在酶标仪上测定各孔的吸光度(OD值)。
四、实验结果1. 阴性对照:各孔OD值均低于阈值。
2. 阳性对照:各孔OD值均高于阈值。
3. 待测血清:- A血清:OD值低于阈值,未检测到特定因子。
- B血清:OD值低于阈值,未检测到特定因子。
- C血清:OD值高于阈值,检测到特定因子。
- D血清:OD值低于阈值,未检测到特定因子。
- E血清:OD值低于阈值,未检测到特定因子。
五、实验结论根据实验结果,患者C血清中检测到特定因子,其余患者血清未检测到特定因子。
结合临床诊断,可初步判断患者C可能患有与该特定因子相关的疾病。
六、实验讨论1. 本实验采用抗原-抗体反应原理,具有较高的灵敏度和特异性。
主成分分析因子分析实验报告

主成分分析因子分析实验报告实验目的:实验步骤:1.收集数据:我们选择了一个包含10个观测变量的数据集,其中包括身高、体重、年龄、血压等变量。
数据集总共有100个样本。
2.数据预处理:在进行主成分分析和因子分析之前,我们首先进行数据预处理,包括缺失值填充、异常值处理和数据标准化等。
通过这些步骤,我们可以确保数据的准确性和可靠性。
3. 主成分分析(PCA):在进行PCA之前,我们需要确定主成分的数量。
我们使用Kaiser准则和累计方差解释比来确定主成分的个数。
接下来,我们使用PCA方法进行主成分分析,并计算每个主成分的贡献率和累计贡献率。
此外,我们还绘制了特征值图,以便更好地理解主成分的贡献。
4. 因子分析(FA):在进行因子分析之前,我们需要确定因子的数量和旋转方法。
我们使用Bartlett球形检验和Kaiser-Meyer-Olkin (KMO)测度来确定因子的数量。
然后,我们使用最大方差旋转方法进行因子分析,以获得更清晰和可解释的因子结构。
我们计算每个因子的贡献率和累计贡献率,并通过因子载荷矩阵来解释因子和变量之间的关系。
5.结果分析:根据主成分和因子的贡献率和解释性,我们可以确定最重要的主成分和因子。
通过对主成分和因子的解释,我们可以深入了解变量之间的关联性和结构。
此外,我们还可以利用主成分和因子进行变量降维,以便更好地理解和解释数据。
实验结果:在主成分分析中,我们确定了3个主成分,其中第一个主成分的贡献率为35%,第二个主成分的贡献率为22%,第三个主成分的贡献率为16%。
累计贡献率达到73%,说明这3个主成分可以很好地解释观测变量之间的关系。
从特征值图中可以看出,前3个主成分的特征值明显大于其他主成分。
在因子分析中,我们确定了2个因子,并使用最大方差旋转方法进行了因子分析。
第一个因子解释了25%的方差,第二个因子解释了18%的方差。
因子载荷矩阵显示了变量和因子之间的关系,可以用来解释因子的含义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子科技大学政治与公共管理学院本科教学实验报告
(实验)课程名称:数据分析技术系列实验
电子科技大学教务处制表
电子科技大学
实验报告
学生姓名:刘晨飞学号:2013120101027
指导教师:高天鹏
一、实验室名称:电子政务可视化实验室
二、实验项目名称:因子分析
三、实验原理
使用SPSS软件的因子分析对数据样本进行分析
相关分析的原理:
步骤一:将原始数据标准化。
因子分析的第一步是主成分分析,将总量较多的因素通过线性组合的方式组合成几个因素,且这些因素之间相互独立。
步骤二:建立变量的相关系数矩阵R
Analyse->Dimention Ruduction-> Fctor ->Extraction->勾选Correlation matrix可以输出相关系数矩阵,相关系数矩阵计算了变量之间两两的pearson相关系数。
步骤三:适用性检验
使用Bartlett球形检验或者KMO球形检验来检验样本是否适合进行因子分析。
评价标准:
KMO检验用于检验变量间的偏相关系数是否过小,一般情况下,当KMO大于0.9时效果最佳,小于0.5时不适宜做因子分析。
Bartlett球形检验用于检验相关系数矩阵是否是单位阵,如果结论是不拒绝该假设,则表示各个变量都是各自独立的。
步骤四:根据因子贡献率选取因子,特征值和特征向量构建因子载荷矩阵A。
处于简化和抽取核心的思想,一般会按照某种标准选取前几个对观测结果影响较大的因素构建因子载荷矩阵,一般的标准是选取特征根大于1的因子。
并要求累积贡献率达到90%以上。
步骤五:对A进行因子旋转
因子旋转的目的是使因子载荷矩阵的结构发生变化,使每个变量仅在一个因子上有较大载荷。
是将因子矩阵在一个空间里投影,使单个向量的投影在仅在一个变量的方向有较大的值,这样做可以简化分析。
步骤六:计算因子得分:
计算因子得分是计算在不同样本水平下观测指标的水平的方式。
计算因子得分需要用到因子得分计算函数,这个计算的结果是无量纲的,仅表示各因子在这个水平下观测指标的值,这也是因子分析的目标,将不可观测的目标观测量用一个函数与可以观测的变量联系起来。
四、实验目的
理解因子分析的含义,以及数学原理,掌握使用spss进行因子分析的方法,并能对spss因子分析产生的输出结果进行分析。
五、实验内容及步骤
本次实验包含两个例子:
实验步骤:
(0) 问题描述
实验一题目要求:对我国主要城市的市政基础设施情况进行因子分析。
实验二题目要求:主要城市日照数sav为例,其中的变量包括城市的名称“city”、各个月份的日照数
(1)实验二步骤:执行analyze->dimention reduction->factor->rotation如下勾选
(2) 执行Analyse->Dimention Ruduction,打开分析窗口
打开参数设置窗口
加入变量
(3)点击Descripitives,选择initial solution(输出原始分析结果)、coefficients(输出相关系数矩阵)、勾选进行KMO和bartlett球形检验,完成之后点击continue回到参数设置窗口
输出选项
(4)点击Extraction输出碎石图,完成之后点击continue回到参数设置窗口
勾选输出碎石图
(5)勾选输出因子得分,完成之后点击continue回到参数设置窗口
输出因子得分
(6)选择缺失的值用均值代替,完成之后点击continue回到参数设置窗口
均值代替缺失数据
(7)点击OK,输出分析结果
六、实验器材(设备、元器件):
计算机、打印机、硒鼓、碳粉、纸张
七、实验数据及结果分析
(1) 实验一主要结果及分析:
KMO and Bartlett's Test
Kaiser-Meyer-Olkin Measure of Sampling Adequacy. .856
Bartlett's Test of Sphericity Approx. Chi-Square 281.248
df 15
Sig. .000
KMO and Bartlett's球形检验的结果
从表里的结果可以看出,KMO的检验值为0.856,一般KMO值大于0.9认为适合做因子分析,这个值为0.856接近0.9,适合做因子分析。
相关系数矩阵
从这个表格中可以看出这六个变量之间有很高的相关度,需要标准化。
变量共同度表
这个表,表示提取公共因子之后各个变量的共同度,就是原始信息的保留度,例如第一个变量有95.4%的信息被保留下来了。
主成分表
按照之前的设置,保留了一个特征值大于1的因子,这个因子的贡献率为88%
特征值和变量的散点图
可以看出,除了第一个因子之外其他的因子特征值都很小。
Component Matrix a
Component
1
年末实有道路长度(公里).977
年末实有道路面积(万平方米).959
城市桥梁(座).862
城市排水管道长度(公里).961
城市污水日处理能力(万立方
.939
米)
城市路灯(盏).927
因子负荷矩阵
这个可以用来表示因子的线性组合。
Component Score Coefficient Matrix
Component
1
年末实有道路长度(公里).185
年末实有道路面积(万平方米).182
城市桥梁(座).163
城市排水管道长度(公里).182
城市污水日处理能力(万立方米).178
城市路灯(盏).176
因子得分系数矩阵
用主成分分析方法得出的因子得分系数矩阵,可以计算因子得分函数。
这个只选择出一个因子,这个实际上没有意义
(2) 实验二结果及分析:
Communalities
Initial Extraction
一月日照时数 1.000 .915
二月日照时数 1.000 .918
三月日照时数 1.000 .896
四月日照时数 1.000 .933
五月日照时数 1.000 .882
六月日照时数 1.000 .778
七月日照时数 1.000 .617
八月日照时数 1.000 .874
九月日照时数 1.000 .754
十月日照时数 1.000 .863
十一月日照时数 1.000 .847
十二月日照时数 1.000 .854
变量共同度表.
主成分表
选取了前三个特征解大于1的值
Component Matrix a
Component
1 2 3
一月日照时数.852 -.435 -.015
二月日照时数.854 -.419 -.115
三月日照时数.869 -.275 -.257
四月日照时数.805 -.079 -.528
五月日照时数.888 -.033 -.303
六月日照时数.764 .439 -.038
七月日照时数.364 .644 -.265
八月日照时数.465 .809 .066
九月日照时数.794 .295 .192
十月日照时数.800 .251 .400
十一月日照时数.825 -.275 .300
十二月日照时数.562 -.164 .715
因子载荷矩阵
显示提取出来的三个因子的线性组合
Rotated Component Matrix a
Component
1 2 3
一月日照时数.837 -.014 .463
二月日照时数.882 .013 .375
三月日照时数.901 .163 .241
四月日照时数.903 .340 -.049
五月日照时数.834 .392 .179
六月日照时数.405 .730 .285
七月日照时数.128 .763 -.134
八月日照时数-.031 .917 .178
九月日照时数.376 .588 .516
十月日照时数.297 .528 .704
十一月日照时数.592 .081 .700
十二月日照时数.140 .018 .913
旋转之后的因子载荷矩阵
使各因子的载荷不再集中,可以看出,第一个因子主要由前5个变量决定,中间的因子主要由中间三个因子决定,后面的一个因子主要由后四个因子决定
Component Transformation Matrix
Component 1 2 3
1 .754 .437 .491
2 -.432 .892 -.131
3 -.495 -.113 .861
因子转换矩阵
八、实验结论
因子分析可以有效降低维度,抽取对观测指标影响最大的几个变量的线性组合,简化研究的过程。
九、总结及心得体会
有了数据分析软件可以节省大量的数据分析的时间,但是根据数据分析的结果对样本数据进行评估还是需要人员操作,看不懂分析的结果,不懂得分析结果的意思就无法进行接下来的工作,所以我们不仅要熟练掌握数据分析的方法,还要了解其中的原理,这样才能充分发挥软件给我们带来的好处,有意识地利用软件帮助我们进行计算,而不只是模仿教程上面的操作步骤,得出自己也看不懂的分析结果。
十、对本实验过程及方法、手段的改进建议
可以选取不能进行因子分析的例子,体会因子分析使用的限制。
