第29课时 《一元一次方程解法》3导学案
《一元一次方程》教案及导学案

一元一次方程教案一、教学目标:知识与技能1、再次培养学生会设出未知数,根据问题寻找相等关系、再根据相等关系列出方程的能力;2、理解一元一次方程、方程的解等概念;3、掌握检验某个值是不是方程的解的方法;过程与方法在解决实际问题的过程中探讨数量关系、列方程的方法,训练学生运用新知识解决实际问题的能力. 情感态度与价值观:鼓励学生进行观察思考,发展合作交流的意识和能力.二、教学重点:建立一元一次方程的概念,以及寻找相等关系、列出方程.三、教学难点:根据具体问题中的等量关系,列出一元一次方程。
四、教学过程设计一元一次方程导学案一、学习目标:1、会设出未知数,根据问题寻找相等关系、再根据相等关系列出方程;2、理解一元一次方程、方程的解等概念;3、掌握检验某个值是不是方程的解的方法;二、学习重点:建立一元一次方程的概念,以及寻找相等关系、列出方程. 三、学习难点:根据具体问题中的等量关系,列出一元一次方程。
(一)自主学习1、自学课本第79页内容完成下列问题 观察下面方程的特点(1)4x =24; (2)1700+150x=2450 (3)0.52x-(1-0.52x)=80 (1)从未知数的个数来看: (2)从未知数的次数来看: (3)从方程两边是否为整式来看:小结:像上面方程,它们都含有 个未知数(元),未知数的次数都是 ,这样的 方程叫做一元一次方程。
2、自学课本第80页,知道什么是方程的解,及检验一个值是否为方程的解. 检验2和-3是否为方程2x+4=x+1 的解。
解:当x=2时, 左边= = , 右边= = ,∵左边 右边(填=或≠) ∴x=2 方程的解(填是或不是) 当x=-3 时,左边= = , 右边= = , ∵左边 右边(填=或≠) ∴x=-3 方程的解(填是或不是) (二)组际合作展风采1、判断下列方程是不是一元一次方程: (1)23-x=一7: (2)2a-b=3(3 )y+3=6y-9; (4)0.32 m-(3+0.02 m) =0.7. (5)x 2=1 (6)61x(7)1082->-x ;(8)132≠+-x2、若方程3x a-4=5(a 已知,x 未知)是一元一次方程,则a 等于( ) A.任意有理数 B.0 C.1 D.0或1 3、x=2是下列方程( )的解.A.2x=6B.(x-3)(x+2)=0C.x 2=3 D.3x-6=04、 小颖种了一株树苗,开始时树苗高为40厘米,栽种后树苗每周长高约15厘米,大约几周后树苗长高到1米.(只列式,不求解)5、A 、B 两地相距 200千米,一辆小车从A 地开往B 地,3小时后离B 地还有20千米,求小卡车的平均速度(三)训练指导提能力1、x=3是下列哪个方程的解?( ) A. 3x-1-9=0 B. x=10-4x C. x(x-2)=3 D. 2x-7=122、已知x -5与2x -4的值互为相反数,列出关于x 的方程.3、x 、y 是两个有理数,“x 与y 的和的13等于4”用式子表示为( ). A .143x y ++= B .143x y += C .1()43x y += D .以上都不对 4、检验2和3-是否为方程2125-=--x x 的解。
(完整word版)一元一次方程导学案(DOC)

一元一次方程导学案【学习目标】1、知道什么是方程,会判断一个数学式子是算式还是方程;2、能根据简单的实际问题列一元一次方程,并了解其步骤;3、会判断方程的解。
【学习重点】一元一次方程的含义。
【学习难点】根据简单的实际问题列一元一次方程。
课前自主学习(查阅教材和相关资料,完成下列内容)考点一.方程的概念1、含有的等式叫方程。
考点二.一元一次方程的概念1.只含有个未知数,未知数的次数都是次的方程,叫做一元一次方程。
考点三.列方程遇到实际问题时,要先设字母表示 ,然后根据问题中的 ,最后写出含有未知数的 ,就能列出方程.归纳:列方程解实际问题的步骤:第一步: ,第二步: ,第三步: .考点四.解方程及方程的解的含义解方程就是求出使方程中等号左右两边的的值,这个值就是方程的 .【重要思想】1.类比思想:算式与方程的对比2.转化思想:把实际问题转化为数学问题,特别是方程问题.学练提升问题1:判断下列数学式子X+1, 0.5x-x, 2x-3=7, 3x+2=2x-5 , 2x2+3x-8=0,x+2y=7.是方程有 ,是一元一次方程有【规律总结】【同步测控】1.自己编造两个方程: , .2.自己编造两个一元一次方程: , .问题2.根据问题列方程:1.用一根长24cm的铁丝未成一个正方形,正方形的变长是多少?2.一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间他到规定的检修时间2450小时?【同步测控】根据下列问题,设未知数,列出方程1.环形跑道一周长400m,沿跑道跑多少周,可以跑3000m?2.甲种铅笔每只0.3元,乙种铅笔铅笔每只0.6元,用9元钱买了两种铅笔共20支,两种铅笔各买了多少支?【规律总结】【同步测控】1.一个梯形的下底比上底多2cm,高是5cm,面积是40cm2,求上底.2.x的2倍于10的和等于18;3.比b的一半小7的数等于a与b的和;4.把1400元奖学金按照两种奖项将给22名学生,其中一等奖每人200元,二等奖每人50元,获得一等奖的学生多少人?问题三、判断方程的根1.判断下列各数X=1,x=2,x=-1,x=0.5.那个是方程2x+3=5x-3的解?2.当x= 时,方程3x-5=1 两边相等?等式性质导学案【学习目标】1、了解等式的两条基本性质,并会用数学式子表示;2、能利用等式的基本性质解简单的方程; 【学习重点】理解等式的两条基本性质。
3.3 解一元一次方程的解法(3)导学案

七年级数学上册第三章《一元一次方程》导学案课题 3.3 解一元一次方程的算法(3) 姓名:编号;第5号执教者班级:七年级组长评价设计者申寿军教学时间课时 1学习方法学生先自学课本,并独立完成自主学习部分,然后小组讨论交流、展示;教师指导、辅导。
教学目标1.在具体情景中建立方程模型.2.能准确应用去括号法则解一元一次方程。
教学重、难点重点:利用去括号的法则解含括号的一元一次方程。
难点:解含多重括号的一元一次方程教学过程一激情引趣,导入新课1 下面去括号是否正确?(1)2-(3x-5)=2-3x-5,(2) 5x- 3(2x-4)=5x-6x-122下图中马路的旁边栽了几颗树?间隔几段?段数和棵数有什么规律?下面我们就来看一道与植树有关的问题二合作交流,探究新知1 问题1现有树苗若干棵,计划栽在一段公路的一侧,要求路的两端各栽1棵,并且每2棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔5.5米栽一棵,则树苗正好用完.你能算出原有树苗的棵数和这段路的长度吗?(做完后交流做法)2 尝试练习:(1 )解方程:115223x x x ⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭(2) 下面方程的解法对不对?如果不对,请改正。
解方程:2(23)25x x +=+解:去括号,得 4325x x +=+移项,得 4235x x +=-化简,得 915x =- 方程两边除以95,得:x= -95(3) 解下了方程,并口算检验:①(4y+8)+(3y-7)=0 ,② 2(2x-1)-2(4x+3)=7③()3434x x -=三 应用迁移,巩固提高1 解含有多重括号的方程例1 解方程:13222[]232393y ⎛⎫--= ⎪⎝⎭2 实践应用例2 如果代数式8x-9与6-2x 的值互为相反数,则x 的值是多少?例3 如果用C 表示摄氏温度(℃),f 表示华氏温度(℉),那么c 和f 之间的关系是“c=59(f-32)” 已知C=15,求f.四 冲刺奥赛例4 已知关于x 的方程3[x-2 (x-3a )]=4x,和3151128x a x +--=有相同的解,求这个解。
一元一次方程的解法导学案

课题:3.3一元一次方程的解法(1)教学目标:探索解一元一次方程的步骤,会用移项法解一元一次方程。
重点难点:掌握解一元一次方程的步骤,并会解简单的一元一次方程。
教学过程1.小组交流讨论如何解上面的方程2.观察上面的方程:应该怎样变形,才能使它向x=a(常数)的形式转化呢? 根据 ,得到方程,得到方程根据 ,解得x=3.将原方程和变形之后的方程相比,你有什么发现?4.思考:(1)观察上面方程的变形,哪些项改变了在原方程中的位置?怎样变的?这些项有什么变化?(2)什么是移项?移项的根据是什么?攀登科学高峰,就像登山运动员攀登珠穆朗玛峰一样,要克服无数艰难险阻,懦夫和懒汉是不可能享受到胜利的喜悦和幸福的。
--陈景润一、 发现结论 二、生成结论请欣赏一首诗:太阳下山晚霞红,牧童把鸭赶回笼,黄鸭在外闹哄哄,三五成群进笼中,黄鸭数量加三十,一打一笼十五笼,爷爷考问鸭几何,牧童摇头不知数。
你能列出方程来解决这个问题吗?(3)上面解方程“移项”的目的是什么?(4)“移项”应注意什么问题?1. 解方程(1)60402=-x (2)60402-=+x(3)3020+-=+x x2. 请你编一个一元一次方程并解这个一元一次方程.3. 在 中填上适当的数,使得方程的解为2=x=-12xA 类三、变式炼知四、分层反馈1.解方程(1)95-=+x (2) x x -=-17102B 类2. 按照如图所示的操作步骤,若输出的值为47,求输入的数。
输入x×7 -9 输出3.如果式子32-x 与式子9+x 互为相反数,求x 的值。
C 类4.已知231+=x y ,x y -=42,当x 取何值时,21y y =?5. 如果3=x 是方程15-=-m x 的解,求m 的值。
组评:。
第29课时 《一元一次方程解法》3导学案(新)

第 1 页第29课时 《一元一次方程解法》3导学案知识目标:1、利用等式性质解含分母的方程; 2、利用比例性质解含分母方程。
知识点一:利用等式性质解含分母的方程等式性质:在等式两边同时乘以一个数,结果仍是等式。
因为方程:就是含有未知数的等式,所以,对于方程也有: 在方程两边同时乘以一个数,结果仍是方程。
1、在方程:123x =的两边乘以6,即:16623x ⨯=⨯,得到 了一个不含分母的方程:32x =2、 在方程:1123x +=的两边乘以6,即:(1)16623x +⨯=⨯,得到了一个不含分母的方程:3(1)2x +=。
我们发现:式子(1)2x +中多了一对括号。
3、在方程:11123x x ++=-的两边乘以6,即:(1)16166623x x +⨯+⨯=⨯-⨯,得到了一个不含分母的方程:3(1)626x x ++=-。
我们发现:方程左边中不含分母的“1”,也乘了6,方程右边中的“x -”也乘了6。
这说明:等式两边每一项都要乘同一个数,体现了等式性质。
通过上面3题,可以知道:任何一个含分母的方程都可以转化为不含分母的方程。
并且可以知道去分母时要注意的事项是:1、分子中是多项式时,要加括号。
(如第2、3题) 2、方程中不含分母的项,也要乘以同一个数。
(如第3题)3、乘的数是最小公倍数。
学习方法指导第 2 页例:(根据等式性质去分母解方程)11123x xx +--=- 解:去分母:(1)(1)6166623x x x +-⨯-⨯=⨯-⨯ 3(1)662(1x x x +-=-- 去括号:336622x x x +-=-+合并同类项:3382x x -=-移项: 3832x x -=- 合并同类项:51x -=系数化成1:15x =-练习:26135x x x +-+=- 51312423x x x-+-=- 14223x x +-+= 1231337x x -+=-仔细观察去分母的过程: 想一想:为什么每一项都乘以6?为什么分子中出现了括号?3x 532x 35-=- 2546+=--x x x138547=+--x x 332121x x -=-+作业:1、方程:124x =去分母后,得到的方程是 2、方程:2323x x+-=去分母后,得到的方程是 3、方程:21223x x-+=+去分母后,得到的方程是 4、方程:12123x xx -+-=+去分母后,得到的方程是解方程14223x x +-+=1231337x x -+=-3y 181y 961y 5--+=+ 51312423x x x-+-=- 26135x x x +-+=-()1132152x x --=。
人教版数学七年级上册导学案:3.3《解一元一次方程》(3课时)

课型:学习新知课主备人:审定人:执教者:执教时间:班级:组别:学生姓名:【课程目标】会解一元一次方程。
【学习目标】会解带有括号的一元一次方程及相关的实际问题。
【学法指导】从生活中抽象出数学问题学习新知,并用新知识解决实际问题。
【学习过程】一、知识链接1、化简⑴-2a+(2a-1) ⑵m+n-(m-n) ⑶a+2(a-3) ⑷3x-3(x-5)2、解方程:5x+2=7x-8二、自主学习阅读教材P93-95页,勾画出重难点。
问题:某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度。
这个工厂去年上半年每月平均用电多少度?(用方程求解)解:设上半年每月平均用电x度,则下半年每月平均用电度;上半年共用电度,下半年共用电度。
列方程为。
x 的形式转化呢?这个方程与上一节课所解方程有何不同点?怎样使这个方程向a试一试吧,老师相信你一定行!注:1.方程中若有括号时,去括号是常用的化简步骤,根据,先,然后再、、系数化为1。
a.当括号前是“-”号,去括号时,各项都要。
括号前有数字,则要乘遍括号内所有项,不能,并注意符号。
小组评价组长签名三、交流展示解下列方程:(1)2x-(x+10)=5x+2(x-1) (2)3x-7(x-1)=3-2(x+3)讨论:解一元一次方程的步骤是什么?四、当堂检测解下列方程:(1)3(x-2)=x-(8-8x) (2)3x-2(x+3)=4(x-1)+7(3)4x + 3(2x–3)=12 -(x +4) (4) 3x-2[ 3(x - 1) -2(x+2)]=3(18-x)五、学后反思学习等级小组评价教师评价课型:学习新知课主备人:审定人:执教者:班级:组别:学生姓名:【课程目标】会解一元一次方程,会用一元一次方程解决实际问题。
【学习目标】1. 灵活求解解一元一次方程;2.会用一元一次方程解决实际问题。
【学习过程】一、自主学习1、解方程3221211245 x x x+-+-=-2、解一元一次方程的一般步骤及每步注意事项是①__________ 注意:;②__________ 注意:;③注意:;④__________注意:;⑤__________注意:;3、利用分数的基本性质,把下列式子的分母化成整数.(1)0.120.4________0.3x -= ; (2) 0.20.3__________0.05a -= .学习等级______________小组评价___________二、合作交流用你最喜欢的方法解下列方程(尽量用你最简便的方法做):(1)0.10.2130.020.5x x -+-= ; (2)111[(3)3]0222y --= .【当堂检测】1、对于方程()x x 31]322134[41=--变形,第一步较好的方法是( ) A 、去分母 B 、去括号 C 、移项 D 、合并同类项2、解方程(1)0.520.3(0.52)0.030.2x x x ++-= ; (2)21215[(1)]75452x x x --=-- .3、甲、乙两车同时从A ,B 两地相向而行,两车的相遇点距A 、B 两地中点处8km,已知甲车速度是乙车速度的1.2倍,求A 、B 两地的路程。
一元一次方程的解法导学案

一元一次方程(预习展示课) 2014-11-92.会验证一个数是否是方程的解.一. 忆一忆:1.指出下列各式哪些是方程,为什么?○1235+= ,○2235x +=,○323x + ○41602x -=,○569y +=,○6236y -= ○72m 310n +=,○8315xy += ,○9m 3-7=9 方程有(填序号) 二、学一学:2.观察○4和○5每个方程中未知数的个数是 个,未知数的次数是 次. 程;(要理解记住)其中“元”指方程中的未知数,“次”指未知数的次数. ①观察1中的方程,一元一次方程有 (填序号)②请再举几例一元一次方程. 3.可以发现:当x=6时,方程4x=24的等号左边= 4x =4×6=24,右边=24,即左边=右边,也三、议一议:1.x=3和x=4中哪一个是方程3x+2=11的解?为什么?2.x=1000和x=2000中哪一个是方程0.52x -(1-0.52)x=80的解? 3.如果x=3是关于x 的方程2x -a=0(即x 是未知数,其它都是已知数)的解,那么数a= . 四、练一练1.判断下列各式哪些是方程?哪些不是?(1)34+=6 ( ) (2)21x =( ) (3) 3()7x y +=( ) (4)210x +≥( )2.判断下列各方程那些是一元一次方程?哪些不是?(1)4x =( )(2)6x y +=( )(3)220x x +-=( )(4)241x x-=( ) 3.试估计下列方程后面括号中的数是否为方程的解?并说明理由.(1)3x -8=2x -4 (x=4); (2)()x x x 3+20=4-25=40 解:将x=4代入原方程:左边=348⨯-= . 右边=244⨯-= .∵左边 右边(填“=”或“≠”) ∴x =4 原方程的解.(填“是”或“不是”)检测试题 姓名 分数1.判断下列各方程那些是一元一次方程?哪些不是?(1)3+2y y =( )(2)7m n +=-( )(3)2y 20y +-=( )(4)24x x-=( )2.判断下列方程后面括号中的数是否为方程的解?并说明理由. x -5+5=-20(x =5)等式的性质(预习展示课) 2014-11-10学习目标:1.记住等式的性质并会用字母表示.2.会根据等式的性质将等式变形. 一、记一记 :用等号连接表示相等关系的式子叫做等式. 二、学一学:1.已知等式235+=,则236++ 56+,23m +- 5m -,23()a b +++=5+ . 由1总结出等式的性质1:2.(1)由55a b -=-得到555____a b -+=-+,所以___a =,根据等式性质1(2)由x a y a +=+得到____x a a y a +-=+-,所以___x =,根据 3.已知等式236⨯=,则235⨯⨯ 65⨯, 23m ⨯⨯ 6m ⨯(23)6⨯÷ 66÷,(23)n ⨯÷ 6(0)n n ÷≠ 由3总结出等式的性质2: 4.(1)若3x=6,得到x=2,其根据是 .即等式两边同时乘13(或除以3) (2)若1122x y -=-得到x=y 其根据是 .即 . 三、试一试.1.用适当的数或式子填空,使所得的结果仍是等式,并说明根据的使等式的哪一条性质. (1)如果6x y -=,那么____6x y y -+=+,所以____x =,根据 ; (2)如果324x -=,那么13____24()3x -⨯=⨯-,所以____x =,根据 ; (3)如果152a =,那么125____2a ⨯=⨯,所以____a =,根据 ; 2.精心选一选.下列用等式性质对等式的变形正确的是( )(A )若37,x y +=-则711x y +=- (B)若1136x -=,则2x =-等式的性质检测A 姓名运用等式的性质填空. (1)95x +=,等式两边同时 ,得: x+9 =5 ,(这一步的根据是 ). 所以___x =. (2)122x -=, 等式两边同时 ,得:1___2___2x -=,(这一步的根据是 ). 所以___x =等式的性质检测B 姓名运用等式的性质填空. (1)123x -=,等式两边同时 ,得: x -12 =3 ,(这一步的根据是 ). 所以___x =. (2)153x -=, 等式两边同时 ,得:1___5___3x -=,(这一步的根据是 ). 所以___x =解方程(1)(系数化1)(预习展示课)2014-11-11学习目标:1.会利用等式性质解形如ax=b (a ≠0)的一元一次方程;2.会检验方程的解是否正确;3.记住解方程和检验的书写格式.一.忆一忆:1.如果x -7=12,那么x -7+ =12+7,所以____x =,根据 ;2.如果26x -=,那么12____6()2x -⨯=⨯-,所以____x =,根据 ;3.如果153a =,那么135____3a ⨯=⨯,所以____a =,根据 ; 4. 如果x 1--5=43,那么x 1--5+5=43+ ,所以1____3x -=,根据 。
第三章 一元一次方程导学案[人教版初一七年级]
![第三章 一元一次方程导学案[人教版初一七年级]](https://img.taocdn.com/s3/m/e578a704360cba1aa811dade.png)
3.1.1从算式到方程[学习目标]能根据题意用字母表示未知数,然后分析出等量关系,再根据等量关系列出方程。
[学习重点]能根据题意用字母表示未知数,然后分析出等量关系,再根据等量关系列出方程。
[学习难点]体会找等量关系,会用方程表示简单实际问题。
[学习过程]问题1:根据条件列出式子1、数的关系:①比a大10的数:;②b的一半与7的差:;③x的2倍减去10:;④某数x的30%与这个数的2倍的积:;⑤a的3倍与a的2的商:;2、基本图形关系:①正方形的边长为a,则面积为,周长为;②长方形的长为a,宽为b,则面积为,周长为;③圆的半径为r,则周长为,面积为;④三角形的三边长分别为a、b、c,则周长为,若长为a的边上的高为h,则面积为;⑤正方体的棱长为a,则体积为,表面积为;⑥长方体的长、宽、高分别为a、b、c,则长方体的体积为,表面积为;⑦圆柱的底面圆半径为r,高为h,则侧面积为,体积为;⑧梯形的上、下底长分别为a、b,高为h,则面积为。
3、其他关系:①某商品原价为a元,降价20%后售价为元;②某商品原价为a元,升价20%后售价为元;③某商品原价为a元,打七五折后售价为元;④某商品每件x元, 买a件共要花元;⑤汽车每小时行驶v千米,行驶t小时后的路为千米;⑥某建筑队一天完成一件工程的121,x天完成这件工程的;练习一根据条件列出式子①比a小7的数:;②x的三分之一与9的和:;③x的3倍减去x的倒数:;④某数x的一半与b的积:;⑤x与y的平方差:;问题2:根据条件列出等式:①比a大5的数等于8:;②b的一半与7的差为6:;③x的2倍比10大3:;④比a的3倍小2的数等于a与b的和:;⑤某数x的30%比它的2倍少34:;问题3:根据下面实际问题中的数量关系,设未知数列出方程:①用一根长为24cm的铁丝围成一个正方形,正方形的边长为多少?解:设正方形的边长为x cm,列方程得:。
②某校女生人数占全体学生数的52%,比男生多80人,这个学校有多少学生?解:设这个学校学生数为x,则女生数为,男生数为,依题意得方程:。
解一元一次方程(三)导学案

3. 3解一元一次方程(三)----去分母[学习目标] 会运用等式性质2正确去分母解一元一次方程。
[重点难点] 重点:去分母解方程。
难点:去分母时,不含分母的项会漏乘公分母,及没有对分子加括号。
[学习过程][复习]1、解方程:(1)95)3(+=--x x ;(2))212(22--=-x x2、求下列各数的最小公倍数:(1)2,3,4(2)3,6,8。
(3)3,4,18。
**在上面的复习题1中,可以保留分母,也可以去掉分母,得到整数系数,这样做比较简便。
所以若方程中含有分母,则应先去掉分母,这样过程比较简便。
[例1] 解方程:43312-=-x x 解:两边都乘以 ,去分母,得去括号,得 ,移项,得 ,合并同类项,得 ,系数化为1,得。
[同步练习一] 解方程:655314+=-x x[例2] 解方程:31241213--+=-+x x x x解:两边都乘以 ,去分母,得去括号,得移项, 得合并同类项,得系数化为1, 得[同步练习二] 解方程:632141+-=+-x x[练习三] 解方程:(1)5131+=-x x ;(2)51131+=--x x ;(3)512131+-=+-x x ;[小结]1、含有分母的方程的解法。
2、解一元一次方程的一般步骤为:①分母,②去括号,③移项,④合并同类项,⑤ 系数化为1 .2、 去分母时要注意什么?(两点)[课后作业] A 组 解方程:(1)4232+=-x x ;(2)21141+=--x x ;(3)223131x x --=--;(4)32213415x x x --+=-;(5)162312=+-+x x ;(6)5124121223+--=-+x x x ;(7)5222123--=--x x x(8)32221+-=--x x x 。
B 组 1、k 取何值时,代数式31+k 的值比213+k 的值小1?2、一件工作由一个人做要50小时完成,现在计划由一部分人先做5小时,再增加8人和他们一起做10小时,完成了这项工作,问:先安排多少人工作?。
3.3 一元一次方程的解法导学案

一元一次方程的解法【知识回顾】1.下列等式的变形是否正确?正确的打“ √ ”,错误的打“ⅹ ”(1)由2=x+3得x=3+2 ( )(2)由32x=-8得x=-12 ( )(3)由 5y+2=7y+8得7y-5y=8-2 ( )2.回答下列问题:(1)由等式a=b ,能不能得到等式a+2=b+2?为什么?(2)由等式22b a,能不能得到等式a=b ?为什么?【学习目标】1.了解等式的基本性质在解方程中的作用.2.会解一元一次方程,并经历和体会解方程中的“转化”的过程和思想.3.了解一元一次方程解法的一般步骤,并能正确灵活应用.【学习重点与难点】重点:会利用等式的性质解方程难点:正确灵活解方程学习过程:一、导入新课:上节课我们学习了“等式的性质”,这一节课我们来学习如何利用等式的性质来解一元一次方程.二、新知学习:(一)移项1.自学要求:请认真看课本本节的内容,并明确两个问题:①什么是方程的移项?②方程的移项与等式的基本性质有什么关系?2.自学检测:(1)把方程中的某一项_________后,从方程的一边________另一边,这种变形叫做移项.(2)对比下列的变形,并体会其不同之处对方程3x-4=1求解运用等式的基本性质:3x –4+4=1+4 ( )3x = 5 ( ) x =35 ( )运用移项:3x=1+4 ( )3x=5 ( ) x=35( )3.练习把下列的方程中的含有未知数的项移到方程的一边,常数项移到另一边:(1)2=x+3(2)5y+2=3y+8(3)4x –3=0你得到了什么结论:___________________________________________.(二)一元一次方程的解法1.自学要求:请认真阅读课本每道解答过程,注意每一种方程的解题步骤和方法.2.对应训练(1)解方程的最根本目的是____________,也就是把未知数的___________化为1.(2)请说出下列方程的第一步的解题步骤和依据① x –3=12 ② -3y=-15③ 11x+3=5(2x+1) ④ 13223-=--x x(3)纵观所有的例题可以看出,本节主要体现了___________的数学思想和方法.(4)解一元一次方程的基本步骤为_______、_______、_______、______、________.小结:____________________________________________________.【精练反馈】基础部分1. 解方程中,移项的依据是( )A.加法交换律B.乘法分配律 C.等式的性质 D.以上都不是2.解下列方程①-2x=4,x=________. ②-3x=0,x=________.③3x-4=-1,x=________.3.已知关于x 的方程ax+4=0的解是x=-2,则a=________.4.以x=1为解的一元一次方程是__________.(只需填写满足条件的一个方程即可)5.下面的移项对不对?如果不对,应如何改正?(1)从x +5=7,得到x =7+5(2)从5x =2x -4,得到5x -2x =4(3)从8+x =-2x -1到x +2x =-1-8通过第5题告诉我们,“移项”要注意什么?能力提高部分6.解方程:(1)3x=12+2x ; (2)-6x-7=-7x+1(3)3(2x+5)=2(4x+3)–3 (4)x 4352x =+ (5))2(2)1(5121+-=-x x (6)3-(4x-3)=7(7)(x-2)-(2-x)=4(8)8-9x=9-8x (9)181x 561x 2=+-- (10)62x 12x 23x +-=-- 7.已知y 1=4x+8,y 2=3x –7(1) 当x 取何值时,y 1=y 2?(2) 当x 取何值时,y 1与y 2 互为相反数?知识拓展部分8.小李在解方程513a x -= (x 为未知数)时,误将x -看作x +,得方程的解为2x =-,则原方程的解为( )A.3x =-B.0x =C.2x =D.1x =9.对于有理数,,,a b c d ,规定一种运算a bad bc c d =- ,如101(2)02222=⨯--⨯=-- ,那么当2425(3)5x -=- 时,则x 等于( ) A.34- B.274 C.234- D.134- 10.小强的练习册上有一道方程题,其中一个数被墨汁涂染了,变成了332131∆--=⎪⎭⎫ ⎝⎛+--x x x ,他翻了书后的答案,知道这个方程的解为5。
数学:3.3《解一元一次方程2(3)》 精品导学案(人教版七年级上)

数学:3.3《解一元一次方程(二)(3)》学案(人教版七年级上)----去分母【学习目标】:会运用等式性质2正确去分母解一元一次方程。
【学习重点】 :去分母解方程。
【学习难点】:去分母时,不含分母的项会漏乘公分母,及没有对分子加括号。
【导学指导】一、知识链接1、解方程: (1) 4-3(2-x)=5x (2)2x =3x-12、求下列各数的最小公倍数:(1)2,3,4;(2)3,6,8;(3)3,4,18;在上面的1、(2)中,可以保留分母,也可以去掉分母,得到整数系数,这样做比较简便。
所以若方程中含有分母,则应先去掉分母,这样过程比较简便。
二、自主探究1.解方程:43312-=-x x 解:两边都乘以 ,去分母,得 依据去括号,得 依据 移项,得 依据合并同类项,得 依据系数化为1,得 依据练习:解方程:655314+=-x x例4 解方程:3123213--=-+x x x 解:两边都乘以 ,去分母,得去括号,得移项, 得合并同类项,得系数化为1, 得【课堂练习】1.小明是个“小马虎”下面是他做的题目,我们看看对不对?如果不对,请帮他改正。
(1)方程1024x x --=去分母,得214x x -+=; (2)方程1136x x -+=去分母,得122x x +-=; (3)方程11263x x --=去分母,得312x x --= ; (4)方程1123x x -=+去分母,得3261x x -=+。
2. 课本第101页练习(1)32213415x x x --+=-; (2)5124121223+--=-+x x x ;【要点归纳】:1、解一元一次方程的一般步骤为:①去分母,②去括号,③移项,④合并同类项,⑤ 系数化为1 。
2、去分母时要注意什么?(两点)【拓展训练】解方程:(1)632141+-=+-x x ; (2)223131x x --=--;【总结反思】:教师个人研修总结在新课改的形式下,如何激发教师的教研热情,提升教师的教研能力和学校整体的教研实效,是摆在每一个学校面前的一项重要的“校本工程”。
七年级数学解一元一次方程导学案无答案新人教版
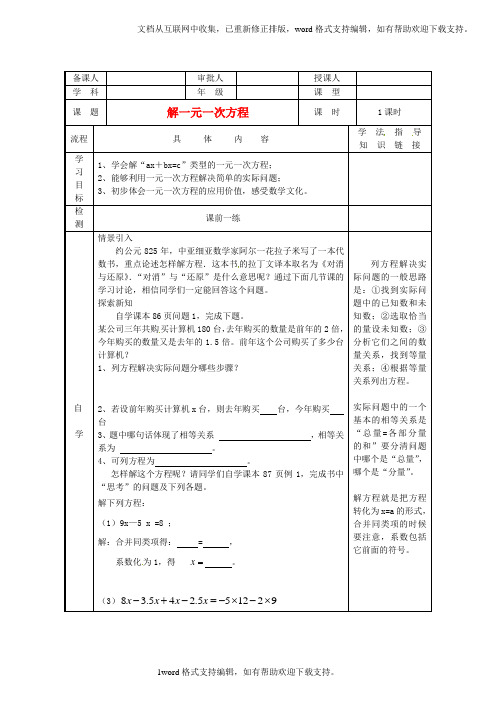
备课人审批人授课人学科年级课型课题解一元一次方程课时1课时流程具体内容学法指导知识链接学习目标1、学会解“ax+bx=c”类型的一元一次方程;2、能够利用一元一次方程解决简单的实际问题;3、初步体会一元一次方程的应用价值,感受数学文化。
检测课前一练自学情景引入约公元825年,中亚细亚数学家阿尔一花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.“对消”与“还原”是什么意思呢?通过下面几节课的学习讨论,相信同学们一定能回答这个问题。
探索新知自学课本86页问题1,完成下题。
某公司三年共购买计算机180台,去年购买的数量是前年的2倍,今年购买的数量又是去年的1.5倍。
前年这个公司购买了多少台计算机?1、列方程解决实际问题分哪些步骤?2、若设前年购买计算机x台,则去年购买台,今年购买台3、题中哪句话体现了相等关系,相等关系为。
4、可列方程为。
怎样解这个方程呢?请同学们自学课本87页例1,完成书中“思考”的问题及下列各题。
解下列方程:(1)9x—5 x =8 ;解:合并同类项得: = ,系数化为1,得=x。
(3)921255.245.38⨯-⨯-=-+-xxxx列方程解决实际问题的一般思路是:①找到实际问题中的已知数和未知数;②选取恰当的量设未知数;③分析它们之间的数量关系,找到等量关系;④根据等量关系列出方程。
实际问题中的一个基本的相等关系是“总量=各部分量的和”要分清问题中哪个是“总量”,哪个是“分量”。
解方程就是把方程转化为x=a的形式,合并同类项的时候要注意,系数包括它前面的符号。
解:合并同类项得: = ,系数化为1,得=x。
归纳:解形如ax+bx=c的方程步骤是:① ,②。
自学教材87页,参照例2完成下题有一列数,按一定的规律排列成1,-2,4,-8,16,-32,…,其中某三个相邻的数的和是192,这三个数各是多少?1、数列的规律是2、若设三个数中的第一个数为x,那么后面与它相邻的数是,。
数学七年级上册第28课时《解一元一次方程》导学案

第28课时 第4章第2节 解一元一次方程[学习目标]1.了解方程的解,解方程的概念;2.掌握运用等式的基本性质解简单的一元一次方程;3.经历体会解方程中的转化思想.[活动方案]活动一 在探求方程的解的过程中,寻求解方程的方法怎样求一元一次方程2x +1=5,2x +(12-x )=20,13 x -4=14 x -1,8+6(n -1)=140,5+x =14 (32+x )中未知数的值呢?1.填表: 当x =_____时,方程2x +1=5两边相等.2.试一试:分别把0、1、2、3、4代入下列方程,哪一个值能使方程两边相等?(1)2x -1=5;(2)3x -2=4x -3.3.什么叫做方程的解,及解方程?活动二 回顾等式的性质,探求如何用等式性质解方程1. 阅读课本99页2. 思考等式有什么性质?3.方程是等式吗?你能否参照等式的性质解下列方程:(1)x +5=2; (2)-2x =4.活动三 学会解方程例 解方程(1)x+3=-2; (2)3x=5-2x[检测反馈] (仔细做看谁学得棒)1.在1、3、-2、0中,方程2x-1=-5的解为.方程x-12=1的解为.2.判断下列变形是否正确①由3x+1=5,得3x=4 ;②由2y+a=b+2y,得a=b;③由12x=1,得x=12;④4由8x=16,得x=2。
3.利用等式性质,解下列方程:62x)1(-=+(2)3x34x-=-【巩固提升】(认真完成 做最好的你)1.用适当的数或整式填空,使所得的结果仍为等式。
(1)如果43+-=x x ,那么+x 3( )4=;(2)如果247=-x ,那么+=27x ( );(2)如果521=y ,那么=y ⨯5( ); (3)如果721=a ,那么=a ÷7( )。
2.如果ma=mb,那么下列变形不一定正确的是( )A.ma+1=mb+1 B.ma-3=mb-3C.-0.5ma= -0.5mb D.a=b3.下列方程变形,不正确的是( )A .234+=x x ,得2=xB .225-=+x ,得522--=xC .由238-=x x ,得238=-x xD .由2364+=-x x ,得6234+=-x x4.下列是解方程83=+x 的几种求解过程,其中正确的是 ( )A .53883=-===+x xB .113883++===+x xC .38+=x ,即11=xD .38-=x ,即5=x5.若已知x =2是关于x 的方程2x +3k =4的解,则k 的值为多少?6.利用等式性质,解下列方程:(1)25=+x (2)93-=-x(3)2153=+x (4)356=--x(5)2332-=x (6)1634=-x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第29课时 《一元一次方程解法》3导学案
知识目标:1、最小公倍数; 2、等式性质;
3、去分母法解方程。
能力目标:转化思想
知识点一: 最小公倍数(小学知识)
1、2与3的最小公倍数是 ;
2、4与6的最小公倍数是 ;
3、2、3、4的最小公倍数是 ;
4、4、6、10的最小公倍数是 ; 知识点二:等式性质 1、等式的性质是: 2、如果1
23x =,那么正确的是( )
A 、23x =
B 、12x
= C 、13x = D 、32x =
3、如果1123x x
+-=,那么正确的是( ) A 、2(1)3(1)x x +=- B 、3(1)2(1)x x +=- C 、112x x +=- D 、113x
x -+=
4、如果11123
x x
+-=+,那么正确的是( ) A 、3(1)2(1)x x +=- B 、31216x x +=⨯-+ C 、
3(1)2(1)6x x +=-+ D 、3(1)2(1)2x x +=-+ 学生探究问题
知识点三:去分母法解方程
1112
3
x x +-=+
解法一:方程可化为:
111112233x x +=-
+
合并同类项,得:
1141223
3x x +=- 移项,得:
1141233
2
x x +=
-
合并同类项,得:
556
6
x =
系数化成1,得: 1x =
解法二: 去分母,得:3(1)2(1)6x x +=-+ 去括号,得:33226x x +=-+ 合并同类项,得:3382x x +=- 移项,得:3283x x +=- 合并同类项,得:55x =
系数化成1,得:1x =
练习: 1、3
x 532
x 35-=
- 2、
2
54
6+=
--x x x
3、138
547
=+--x x 4、332121x
x -=-+ 作业: 1、2与5的最小公倍数是 ; 2、4与3的最小公倍数是 ; 3、5、3、2的最小公倍数是 ; 4、4、2、5的最小公倍数是 ; 5、方程:1
24
x =去分母后,得到的方程是 6、方程:2323
x x
+-=去分母后,得到的方程是 7、方程:21223x x
-+=+去分母后,得到的方程 是 8、方程:12123
x x
x -+-=+去分母后,得到的 方程是
解下列含分母的方程
14
2
23x x +-+
=
12313
3
7
x
x -+=
-
3
y 181y 961y 5--+=+
513124
2
3
x x x -+-=
-
2613
5
x x x +-+
=-
()113215
2
x x -
-=。
