应力应变曲曲线和动态力学性能测试课
材料力学性能-第一章-应力应变曲线和弹性变形

2021年10月24日 第一章 单向静载下材料的力学性能 星期日 纯弹性型
大多数玻璃、陶瓷、 岩石、低温下的金属
弹性-均匀塑性型
许多金属和合金、部 分陶瓷和非晶态高聚物
2021年10月24日 第一章 单向静载下材料的力学性能 星期日
低温和高应变 速率下的fcc金属。 其塑性变形常常是 通过孪生实现的。 当孪生速率超过夹 头运动速率时出现 此种类型曲线。
弹性-不均匀塑性型
2021年10月24日 第一章 单向静载下材料的力学性能 星期日
弹性-不均匀塑 性-均匀塑性型
弹性-不均匀塑 性-均匀塑性型
一些bcc的铁基合金 和若干有色合金。
一些结晶态的高聚 物和未经拉伸的非晶 态高聚物
2021年10月24日 第一章 单向静载下材料的力学性能 星期日 同一种材料在不同拉伸条件下其应 力-应变曲线也会不同。比如,退火低 碳钢在低温下脆性大大增加,其拉伸曲 线就只有弹性变形部分。
表1-2 几种常用材料的比弹性模量
材料
铜 钼 铁 钛 铝 铍 氧化铝 碳化硅
比弹性模量/×108cm 1.3 2.7 2.6 2.7 2.7 16.8 10.5 17.5
2021年10月24日 第一章 单向静载下材料的力学性能 星期日 三、弹性比功 表示金属材料吸收弹性变形功的能力。
用金属材料开始塑性 σ
2021年10月24日 第一章 单向静载下材料的力学性能 星期日
影响因素
弹性变形是原子间距在外力作用
下可逆变化的结果,因而弹性模量E与
原子间作用力和原子间距都有关系。原 子间作用力取决于原子本性和晶格类
型,故E也取决于原子本性与晶格类
型。
2021年10月24日 第一章 单向静载下材料的力学性能 星期日
材料的应力应变曲线

材料的应力应变曲线材料的应力应变曲线是材料力学性能的重要参数之一,它能够反映材料在外力作用下的变形和破坏过程,对于材料的设计和使用具有重要的指导意义。
在工程实践中,对材料的应力应变曲线进行分析和研究,可以帮助工程师更好地选择合适的材料,并预测材料在各种工况下的性能表现。
应力应变曲线通常是通过材料拉伸试验得到的,拉伸试验是一种常用的材料力学性能测试方法,通过在材料上施加拉伸力,使其发生变形,然后记录施加力和变形量的关系,就可以得到材料的应力应变曲线。
应力应变曲线一般包括弹性阶段、屈服阶段、塑性阶段和断裂阶段。
在应力应变曲线中,弹性阶段是指材料在受到外力作用下,发生线性弹性变形的阶段。
在这个阶段内,材料的应变与应力成正比,满足胡克定律。
当外力撤去时,材料可以完全恢复到最初的形状,不会留下永久变形。
弹性阶段的斜率即为材料的弹性模量,它是材料刚度和变形能力的重要指标。
屈服阶段是指材料在受到一定应力作用后,开始出现应变不再与应力成正比的现象。
这个阶段的应力称为屈服强度,对于金属材料来说,屈服强度是材料的重要参数之一,它可以反映材料开始发生塑性变形的能力。
屈服点之后,材料进入塑性阶段。
塑性阶段是指材料在屈服点之后,继续受到应力作用而产生明显的塑性变形的阶段。
在这个阶段内,材料的应力逐渐增加,而应变也随之增加,材料会出现明显的颈缩现象。
塑性阶段的性能表现对于材料的加工性能和使用性能有着重要的影响。
最后是断裂阶段,当材料受到的应力达到其抗拉强度时,就会发生断裂现象。
在这个阶段,材料会突然断裂,失去承载能力。
对于工程设计来说,抗拉强度是一个重要的设计参数,它可以帮助工程师选择合适的材料,并预测材料的破坏形式和破坏位置。
总的来说,材料的应力应变曲线是材料力学性能的重要指标,它可以帮助工程师更好地了解材料的性能特点,指导工程设计和材料选择。
通过对应力应变曲线的分析和研究,可以更好地预测材料在各种工况下的性能表现,为工程实践提供重要的参考依据。
65号钢应力应变曲线试验研究

65号钢应力-应变曲线试验研究摘要:使用CMT5105型电子万能试验机对65号钢进行单轴拉伸试验,得到其应力-应变曲线和拉伸时的机械性能,通过理论推导得到其真应力-真应变曲线。
最后采用Ramberg-Osgood 公式,利用最小二乘法获取65号钢试验数据的拟合曲线,以用于有限元等进一步研究中。
关键词:65号钢单轴拉伸试验应力-应变曲线Ramberg-Osgood公式Experimental Study on Stress-Strain Curves of Steel No.65 Abstract: CMT5105 electronic universal testing machine is used for the uniaxial tensile test of steel no.65. The stress-strain curve and the mechanical properties of tensile are obtained. The true stress-true strain curve is obtained through theoretical derivation. Finally, Ramberg-Osgood equation is used and the least squares method is applied to obtain the experimental data curve fitting of steel no.65, which will be used for further studies such as finite element.Key Words: Steel No.65; Uniaxial Tensile Test; Stress-Strain Curves; Ramberg-Osgood equation. 前言目前国内关于65号钢的疲劳寿命研究相对来说比较少,对其性能的了解还不足以应用到实际工程中。
应力应变曲线解析

金属材料的变形与再结晶
1 金属的应力-应变曲线 2 金属的塑性变形 3 回复与再结晶 4 金属热变形、蠕变与超塑性
1
第1页/共27页
A
典型的结晶高聚合物材料具有此特
征,这与其结构有关。
B
23
第23页/共27页
不同类型材料典型的拉伸应力-应变曲线
退火低碳钢: 在拉伸应力-应变曲线上,出现屈服平台,平台的延伸长度
随钢的含碳量增加而减少。 当含碳量增至0.6%以上,平台消失。
24
第24页/共27页
其它类型材料的应力-应变曲线
拉伸速率对材料应力-应变曲线的影响 26
第26页/共27页
感谢您的欣赏!
27
第27页/共27页
材料由弹性连续过渡到塑性变形,塑性变形时无锯齿形平台, 变形时总伴随着加工硬化。
19
第19页/共27页
3)第Ⅲ种类型:弹性-不均匀塑性变形 在正常弹性后,有一系列锯齿叠加在抛物线型曲线上。 此类材料特性:是由于材料内部不均匀变形所致。
出现的情况: (1)面心立方金属在低温和高应
变率下,其塑变通过孪生进行。 标距的长度随孪生带的成核和生
E
E-材料的弹性模量(杨氏模量)
特点:具有可逆应力-应变曲线 和不出现塑性变形的特征。
典型材料:如玻璃、岩石、多种 陶瓷、高交联度的高聚合物和低 温下的某些金属材料。
此类材料抗脆性(低能量)断裂 的能力是极需注意的问题。
14
第14页/共27页
苏打石灰玻璃:应力-应变曲线只显示弹性变形,没有塑性 变形立即断裂,这是完全脆断的情形。
金属材料力学性能的应力—应变曲线测定与分析

0 引言应力应变曲线是描述金属材料在受力过程中应力与应变之间的关系的曲线。
它是对金属材料力学行为的定量描述,对评估金属材料的力学性能具有重要的意义。
李凯[1]提出了一种基于数字图像相关技术(Digital Image Correlation,以下简称DIC)来获取材料全过程真实应力-应变关系的方法,测试并对比X65和X80管道钢的真实应力-应变曲线.对比分析焊接接头各局部区域的力学性能,研究发现本次实验试件的焊缝区虽然具有较高的屈服强度,但其应变硬化性能及抗拉强度却低于母材区,最终导致断裂发生在焊缝区。
该方法对于获取焊缝区、热影响区的局部真实本构关系,实现焊接接头分区测试具有较强的实际意义。
王璐[2]采用分子动力学模型,研究体积分数为15%,SiC 颗粒尺寸和SiC、TiN 和TiC 颗粒单一增强和混合类型对其增强的铁基复合材料力学性能的影响规律,计算复合材料的应力-应变曲线,探索在原子尺度的强化机理和载荷传递的微观机制。
1 真应力-真应变曲线的测试基本原理应力-真应变曲线实际上指的是,首先,由符合计量要求的拉伸试验机或万能试验机配备纵向引伸计测试获得的工程应力-应变曲线,然后,再利用公式(1)(2)或(3),分别对真应力和真实塑性应变进行计算,最终将其绘制成真应力-真应变曲线。
真实应力计算公式:+∆ 1 1真实应变计算公式:2近似真实应变计算公式:(1)真实应变计算公式: 1真实应变计算公式:e =×2近似真实应变计算公式:e =ln 1+ 3在这个公式中,E 是以表示的材料的弹性模数;ε是以毫米/毫米计算的试验得到的应变值(请注意,不是百分比,若为百分比,则必须首先除以100);S 是以MPa 表示的真应力;F 是力的数值,单位为N;S 是初始横截面面积(mm 2)。
上述公式的基础,运用体不变性原则,求出了在拉伸过程中的截面面积。
所以,这一方法并不适合于非均匀变形的材料。
2真应力-真应变曲线的测试条件及测试方法2.1测试准备2.1.1试样的选择和制备根据GB/T2975-2018《钢及钢产品力学性能试验取样位置及试样制备》,对试样样品进行了采样,并根据GB/T2281-2018《金属材料拉伸试验第1部分:室温试验方法》中R4样品的加工,对样品进行了低应力研磨,并对样品进行了抛光处理,以避免样品中存在的缺陷对测试结果产生较大的影响[3]。
材料力学性能(2)应力应变曲线

拉伸试验得到的应力应变,通常是指工程应力和工程应变,用于计算应力应变的横截面积和长度,是未变形的初始横截面积和初始长度(便于测量)。
与之对应的,还有真应力和真应变,用于计算应力应变的横截面积和长度,是变形后的横截面积和长度。
在应力低于比例极限的情况下,应力σ与应变ε成正比,即σ=Εε;式中E为常数,称为弹性模量或杨氏模量,是正应力与正应变的比值,弹性模量的单位与应力的单位相同。
剪切模量的定义与之类似,是切应力与切应变的比值。
金属的应力应变曲线,通常分为四个阶段:弹性阶段、屈服阶段、应变硬化阶段和颈缩断裂阶段。
注意:不同的材料,应力应变曲线会有差异,并不是每种材料都会表现出上述四个阶段。
屈服强度材料的屈服强度,是指材料开始发生塑性变形时所对应的应力。
由于不同材料应力应变曲线变化各异,通常很难确定在多大的应力下,材料开始屈服。
实际应用中,也会用到以下几种定义屈服点的方式:弹性极限(Elastic Limit)The lowest stress at which permanent deformation can be measured. 能检测到塑性变形的最小应力。
比例极限(Proportional Limit)The point at which the stress-straincurve becomes nonlinear. 应力-应变曲线开始出现非线性的应力。
很多金属材料的弹性极限和比例极限几乎是一样的。
偏移屈服点(Offset Yield Point 或 Proof Stress)有些材料的应力应变曲线,弹性阶段和塑性阶段之间没有明显的分界点。
可以采用某个指定的很小的塑性应变,通常是0.2%,对应的应力作为屈服点。
真应力和真应变前面拉伸试验得到的工程应力(σ)和工程应变(ε),是基于试件未变形的初始横截面积(A0)和初始长度(L0)计算的。
而实际中,随着载荷的变化,横截面积和长度都是在发生变化的。
应力应变曲线 (2)

应力应变曲线引言应力应变曲线是材料力学测试中常用的曲线,它描述了材料在外部施加力的作用下发生的应变程度以及对应的应力大小。
通过分析应力应变曲线,可以了解材料的力学性质和变形行为,对于工程设计和材料选择具有重要的意义。
实验方法通常,获得材料的应力应变曲线需要进行拉伸试验。
拉伸试验一般按照国际标准ASTM E8或ISO 6892进行,主要步骤如下: 1. 准备试样:根据标准要求,制备符合尺寸要求的金属试样。
2. 固定试样:将试样夹紧在拉伸试验机上,确保试样的两端无法移动。
3. 施加载荷:通过拉伸试验机施加逐渐增加的力,使试样受到拉伸力的作用。
4. 记录数据:在拉伸过程中,通过传感器测量和记录试样的变形量和受力情况。
5. 绘制曲线:根据记录的变形量和受力数据,绘制应力应变曲线。
应力应变曲线的特征应力应变曲线通常有以下几个特征: 1. 弹性阶段:在应力较小的范围内,材料会发生弹性变形,即当力作用于材料时,材料会发生形变。
如果施加的力被移除,材料将恢复到其初始状态。
在这个阶段,应力与应变成正比关系,曲线呈直线。
2. 屈服点:当材料承受的应力达到一定值时,材料开始发生塑性变形,即在去除力时,材料不会完全恢复至初始状态。
该点称为屈服点,其应力值通常用来衡量材料的强度。
3. 塑性阶段:在超过屈服点后,材料仍然能够承受更大的应力而不发生断裂。
材料发生塑性变形,应变值随着应力的增加而逐渐增大。
曲线由直线变为曲线段,呈现出先上升后下降的形态。
4. 极限强度:应力应变曲线的极限强度是指材料能够承受的最大应力值,超过该值材料将发生断裂。
5. 断裂阶段:当超过极限强度后,材料就会发生断裂,应力应变曲线出现陡峭下降。
应力应变曲线的应用应力应变曲线在工程应用中具有重要的意义: 1. 材料选择:通过分析应力应变曲线,可以评估材料的强度、韧性和可塑性等力学性能,对于工程中合理选择材料具有指导意义。
2. 结构设计:应力应变曲线可以提供材料的变形行为信息,对于工程结构的设计和可靠性分析具有重要的参考价值。
金属材料应力-应变曲线

个重要指标。
• (3)强化阶段 抗拉强度 b
经过屈服阶段后,曲线从c点又开始逐渐上升,说
明要使应变增加,必须增加应力,材料又恢复了抵抗变 形的能力,这种现象称作强化,ce段称为强化阶段(加 工硬化)。曲线最高点所对应的应力值记作, 称为材
料个重的要抗指拉标强。度(或强度极限),b 它是衡量材料强度的又一
bt
o
σbt—拉伸强度极限(约为140MPa)。它是 衡量脆性材料(铸铁)拉伸的唯一强度指标。
二、压缩时的应力——应变曲线 1、试样及试验条件
常 温 、 静 载
§9-5
2、低碳钢压缩实验
(MPa) 400
低碳钢压缩 应力应变曲线
E(b)
C(s上)
f1(f)
低碳钢拉伸
g
(e) B
D(s下)
应力应变曲线
力学性质:在外力作用下材料在变形和破坏方面所 表现出的力学性能
一、拉伸时的应力——应变曲线
试
件
和
实
验 条 件
常 温 、
静
载
1、 试件
(1)材料类型:
低碳钢: 塑性材料的典型代表; 灰铸铁: 脆性材料的典型代表;
标距
L0
(2)标准试件:
d0
标点
尺寸符合国标的试件;
2.标用标距于准:测试试件的:等截面部分长度;
(4)缩颈断裂阶段
曲线到达e点前,试件的变形是均匀发生的, 曲线到达e点,在试件比较薄弱的某一局部(材 质不均匀或有缺陷处),变形显著增加,有效横 截面急剧减小,出现了缩颈现象,试件很快被 拉断,所以ef段称为缩颈断裂阶段。
4.塑性指标 试件拉断后,弹性变形消失,但塑性变形仍保 留标。常用的塑性指标有两个:
工程材料中重要曲线之一材料应力-应变曲材料的力学性能1力学

工程材料中重要曲线之一材料应力-应变曲一、材料的力学性能1、力学性能:材料在外力作用时所表现的性能(又称机械性能),如强度、塑性、硬度、韧性及疲劳强度等。
2、变形:材料在外力的作用下将发生形状和尺寸变化。
外力去除后能够恢复的变形称为弹性变形,外力去除后不能够恢复的变形称为塑性变形。
3、(应力-应变曲线)应力-应变曲线:是描述应力与应变关系的曲线,它是根据标准试样所承受的载荷与变形量的变化所绘制的关系曲线。
二、弹性与刚度1、弹性极限:在应力-应变曲线中,OA段为弹性变形阶段,此时卸掉载荷,试样恢复到原来尺寸。
A 点多对应的应力为材料承受最大弹性变形的应力称为弹性极限,用σp表示。
2、比例极限:其中OA′部分为一斜直线,应力与应变呈比例关系,A′点所对应的应力为保持这种比例关系的最大应力称为比例极限,用σe表示。
由于大多数材料的A点和A′点几乎重合在一起,一般不做区分。
3、弹性模量E:在弹性形变范围内,应力与应变的比值称为弹性模量,用E来表示。
弹性模量是材料最稳定的性质之一,它的大小主要取决于材料的本性,除随温度升高而逐渐降低外,其他强化材料的手段如热处理、冷热加工、合金化等对弹性模量的影响很小。
4、刚度:材料受力时抵抗弹性变形的能力,可以通过增加横截面积或改变截面形状的方法来提高零件的刚度。
三、强度与塑性1、强度定义:材料在外力作用下抵抗变形和破坏的能力。
根据加载方式的不同,强度指标有许多种,其中以拉伸试验测得的屈服强度和抗拉强度两个指标应用最多。
2、屈服强度(1)屈服现象:应力超过B点后,材料将发生塑性变形。
在BC段,材料发生塑性变形而应力不会增加的现象。
(2)屈服强度:B点所对应的应力称为屈服强度,用σs表示。
屈服强度反映材料抵抗永久变形的能力,是最重要的零件设计指标之一。
3、抗拉强度(1)颈缩现象:CD段为均匀变形阶段。
在这一阶段,应力随应变增加而增加,产生应变强化。
变形超过D点后,试样开始发生局部塑性变形,即出现颈缩。
9-1应力-应变曲线课堂使用

L L0 L
L0
L0
试样标距 L0
弹性极限: σe 屈服极限:σs, σ0.2
加工硬化(应变硬化)
抗拉强度: σb
工程应力-应变基曲础教线学
断裂强度: σk
延伸率:δ=(Lk-L0)/L0
断面收缩率:ψ=(F0-Fk)/F0
4
2、工程应力σ -应变ε曲线
用静拉伸应力σ-应变ε曲线,可得出许多重要性能指标:
弹性模量 E :主要用于零件的刚度设计。
屈服强度σs 和抗拉强度σb :主要用于零件的强度设计。 特别是:抗拉强度σb 和弯曲疲劳强度有一定比例关系,进
一步为零件在交变载荷下使用提供参考。 而材料的塑性,断裂前的应变量:主要是为材料在冷热变形
时的工艺性能作参考。
5 基础教学
2、工程应力σ -应变ε曲线
主要表现:在试验中,外力不增 加(保持恒定)试样仍继续伸长; 或外力增加到一定数值时突然下 降,随后,在外力不增加或上下 波动下,试样继续伸长变形。这 便是“屈服现象”。
22 基础教学
5)第Ⅴ种类型:弹性-不均匀塑性-均匀塑性变形 它有一个上屈服点A,接着载荷下降。 其中:OA-弹性;AB-不均匀塑变;BC-均匀塑变。
出现的情况: (1)面心立方金属在低温和高应
变率下,其塑变通过孪生进行。 标距的长度随孪生带的成核和生
长间歇地突然伸长,当试样中瞬 时应变率超过试验机夹头运动速 率,则载荷就下降。
20 基础教学
(2)含碳的体心立方铁基固溶体及铝的低溶质固溶体。 由于溶质原子或空位与晶格位错相互作用的结果所致。
若应力足够大,位错可从溶质 原子簇中挣脱,载荷就下降。
若溶质原子足够快地扩散开, 就可将位错重新锁住,则须再 增大载荷才使变形继续下去。
熟练绘制应力-应变曲线图
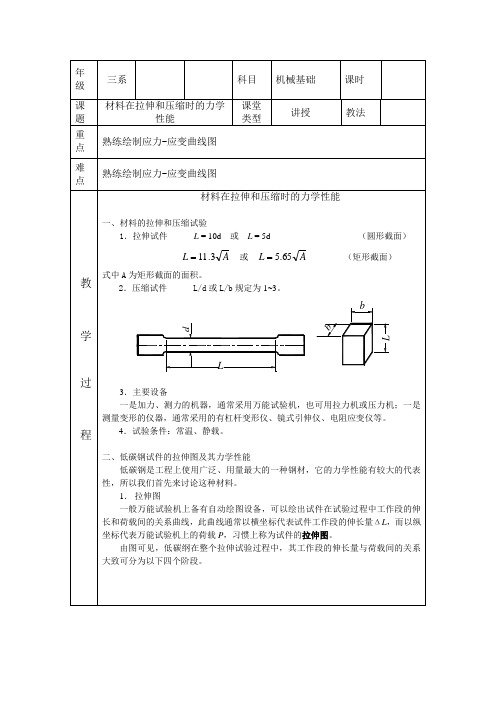
第Ⅳ阶段──局部变形阶段 从曲线最高点到试件断裂的一点是材料的破坏阶 段。试件某一段内的横截面开始收缩,出现所谓“颈缩”现象。在此阶段,由于“颈 缩”部分的横截面面积急剧缩小,因此,荷载反而下降,一直到试件被拉断。
试件的尺寸无关,可以代表材料的力学性能。此曲线称为应力—应变曲线,即
曲线。
教
D
AB C
学
b
s e
P
过
O
程
E F
小 结 熟练绘制应力-应变曲线图
作业 情况
拉伸图一般万能试验机上备有自动绘图设备可以绘出试件在试验过程中工作段的伸长和荷载间的关系曲线此曲线通常以横坐标代表试件工作段的伸长量l而以纵坐标代表万能试验机上的荷载p习惯上称为试件的拉伸图
年 级
三系
科目 机械基础
课时
课 材料在拉伸和压缩时的力学 课堂
题
性能
类型
重 点
熟练绘制应力-应变曲线图
讲授
教法
测量变形的仪器,通常采用的有杠杆变形仪、镜式引伸仪、电阻应变仪等。
程
4.试验条件:常温、静载。
二、低碳钢试件的拉伸图及其力学性能 低碳钢是工程上使用广泛、用量最大的一种钢材,它的力学性能有较大的代表
性,所以我们首先来讨论这种材料。 1. 拉伸图 一般万能试验机上备有自动绘图设备,可以绘出试件在试验过程中工作段的伸
第Ⅱ阶段──屈服阶段或流动阶段 在变形继续增长的过程中,荷载保持在某 一数值附近上下波动。如果略去这一微小的变化,则可认为荷载保持不变,而变形 继续迅速增加,这一现象通常称为屈服或流动。若试件表面经过抛光,此时可见到 与轴线成 450方向的条纹,它们是由于材料沿试件的最大剪应力面发生滑移而出现的, 称为滑移线。
应力应变曲线材料力学ppt课件

8
(2)屈服阶段 屈服点
s
曲线超过b点后,出现了一段锯齿形曲线, 这—阶段应力没有增加,而应变依然在增加,材 料好像失去了抵抗变形的能力,把这种应力不增 加而应变显著增加的现象称作屈服,bc段称为屈
服阶段。屈服阶段曲线最低点所对应的应力 s
第五节 应力——应变曲线
1
力学性质:在外力作用下材料在变形和破坏方面所 表现出的力学性能
一、拉伸时的应力——应变曲线
试 件 和 实 验 条 件
§9-4
常 温 、 静 载
2
1、 试件
(1)材料类型:
低碳钢: 塑性材料的典型代表; 灰铸铁: 脆性材料的典型代表;
标距
L0
(2)标准试件:
d0
标点
尺寸符合国标的试件;
1、弹性阶段ob E
P — 比例极限 e — 弹性极限
E tan
7
(1)弹性阶段 比例极限σp
oa段是直线,应力与应变在此段成正比关系,材
料符合虎克定律,直线oa的斜率 tan E 就是材
料的弹性模量,直线部分最高点所对应的应力值 记作σp,称为材料的比例极限。曲线超过a点,图 上ab段已不再是直线,说明材料已不符合虎克定 律。但在ab段内卸载,变形也随之消失,说明ab 段也发生弹性变形,所以ab段称为弹性阶段。b点 所对应的应力值记作σe ,称为材料的弹性极限。
、 值越大,其塑性越好。一般把 ≥5%的材
料称为塑性材料,如钢材、铜、铝等;把 <5%的
材料称为脆性材料,如铸铁、混凝土、石料等。 11
工程应用:冷作硬化
e
d
不同材料应力应变曲线分解

不同材料应力应变曲线分解
应力-应变曲线是材料力学性能测试中常见的曲线,它反映了材料在外
界施加载荷时的应变行为。
不同材料的应力-应变曲线形状和特性有一
定的差异,可以根据材料的性质和特点将其分解为不同的部分。
1. 弹性阶段:在应力小于材料的屈服强度时,材料表现出线性弹性行为。
这个阶段应力和应变成正比,称为胡克定律。
材料在这个阶段内
具有良好的恢复性。
2. 屈服阶段:当应力逐渐增大,达到或超过材料的屈服强度(或屈服点),材料会发生塑性变形,应变会出现非线性增加。
在这个阶段内,
材料的应力会逐渐减小,但并不恢复原状。
3. 塑性流动阶段:当应力继续增大,材料会出现塑性流动,此时应力
和应变关系呈非线性增长。
材料的应变会持续增加,而应力不再减小。
4. 极限强度阶段:当应力接近材料的极限强度时,材料会出现明显的
变形和破坏,应变急剧增加。
5. 断裂阶段:当应力超过材料的极限强度时,材料会发生断裂,应变
突然增加并导致材料失效。
需要注意的是,不同材料的应力-应变曲线可能会有所不同,例如金属
材料的应力-应变曲线常常显示出明显的屈服点和流动平台。
而非金属
材料如陶瓷和聚合物等,可能会表现出更加复杂的曲线形状。
材料的
温度、应变速率等因素也会对应力-应变曲线产生影响。
电子拉力机测定聚合物的应力-应变曲线

上海衡翼橡胶材料实验报告第页〔共页〕实验名称:电子拉力机测定聚合物的应力-应变曲线一.实验目的1.掌握拉伸强度的测试原理和测试方法,掌握电子拉力机的使用方法及共工作原理;2.了解橡胶在拉伸应力作用下的形变行为,测试橡胶的应力-应变曲线;3.通过应力-应变曲线评价材料的力学性能〔初始模量、拉伸强度、断裂伸长率〕;4.了解测试条件对测试结果的影响;5.熟悉高分子材料拉伸性能测试标准条件。
二.实验原理随着高分子材料的大量使用,人们迫切需要了解它的性能。
而拉伸性能是高分子聚合物材料的一种基本的力学性能指标。
拉伸试验是力学性能中一种常用的测试方法,它是在规定的试验温度、湿度和拉伸速度下,试样上沿纵向施加拉伸载荷至断裂。
在材料试验机上可以测定材料的屈服强度、断裂强度、拉伸强度、断裂伸长率。
影响高聚物实际强度的因素有:1〕化学结构。
链刚性增加的因素都有助于增加强度,极性基团过密或取代基过大,阻碍链段运动,不能实现强迫高弹形变,使材料变脆。
2)相对分子质量。
在临界相对分子质量之前,相对分子质量增加,强度增加,越过后拉伸强度变化不大,冲击强度随相对分子质量增加而增加,没有临界值。
3)支化和交联。
交联可以有效增强分子链间的联系,使强度提高。
分子链支化程度增加,分子间作用力小,拉伸强度降低,而冲击强度增加。
4)应力集中。
应力集中处会成为材料破坏的薄弱环节,断裂首先在此发生,严重降低材料的强度。
5)添加剂。
增塑剂、填料。
增强剂和增韧剂都可能改变材料的强度。
增塑剂使大分子间作用力减少,降低了强度。
又由于链段运动能力增强,材料的冲击强度增加。
惰性填料只降低成本,强度也随之降低,而活性填料有增强作用。
6)结晶和取向。
结晶度增加,对提高拉伸强度、弯曲强度和弹性模量有好处。
结晶尺寸越小,强度越高。
取向使材料的强度提高几倍甚至几十倍,此外,取向后可以阻碍裂缝向纵深方向发展。
7)外力作用速度和温度。
衡翼拉伸试验中提高拉伸速度和降低温度都会使强度降低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在实际拉伸过程中,试样的截面积A的变化更为复杂多
样。有的试样会均匀地逐渐变细,而有些则突然变细成 颈。以后截面积A基本保持不变。只是细颈进一步伸长, 直到被拉伸为止。这就是被称为“冷拉”现象。
3.实验原材料和仪器设备
原材料 聚丙烯(PP),聚苯乙烯(PS) 仪器设备 万能电子拉力机(日本岛津AG-10KNA)、游标卡尺、 直尺。 万能电子拉力机测试主体结构示意图,如图1-1所 示。
0 sin t
0 sin(t )
E 0和 0分别为应力和应变的幅值,将应力表达式展 式中 开:
0 cos sin(t ) 0 sin cost
应力波可分解为两部分,一部分与应力同相位,峰 值为 0 cos ,与储存的弹性能有关,另一部分与应变有 90°的相位差,峰值为 0 sin ,与能量的损耗有关。定 义储能模量( E ),损耗模量( E )和力学损耗( tan ):
图1-1 万能电子拉力机测试主体结构示意图 1-传感器;2-主架;3-横梁控制器;4-夹具;5-横梁;6-记录仪; 7-控制台开关;8-控制面板;9-显示屏
4. 实验步骤
试样制备 调换和安装拉伸试验用夹具 设定试验条件 键入样品参数
5. 问题讨论
(1) 改变试样的拉伸速率会对试验产生什么影响? (2) 在试验过程中,试样的截面积变化会对最终谱图 产生什么影响?你认为在现有的试验条件下能否 真实地获得或通过计算获得瞬时的截面积?
E ( 0 / 0 )sin sin E tan cos E
E ( 0 / 0 )cos
复数模量可表示为: E* E iE E E E 其绝对值为: 在交变应力作用下,样品在每一周期内所损耗的机 械能可通过下式计算: W (t )d (t ) 3 E 02
4.实验步骤
样品 共混样品制备 试条制备 用刀将薄膜裁成宽5~10mm,长30mm试条备用 DMTA测试部分: 接通DMTA电源,预热20分钟。 点击电脑屏幕上的RSI软件,在“Utilities”中选 “Instrument online”进行联机。 在DMTA面板上,上扳“sample chamber motion control”开启炉子,去除T-bar上的所有夹具。 “Utilities”“calibrate instrument”“calcheck” “continue””进行弹簧常数检测,将检测值和 原值进行比较,只要在20%的误差允许范围 内,即可按“accept”进行下一步。
式中 P——拉伸截荷,N; A——试样的瞬时截面积,mm2。 如果与之相应时刻内,试样的标线长度由L被拉伸为 L+dL,则真应变δ为: L dL L L L (1-4) ln ln( 0 ) ln(1 ) (100%)
L0
L
L0
L0
假定试样在大形变时体积不变,即AL=A0L0,则真应 力可表示为: P PL P σ' = = = (1+ ε) = σ(1+ ε) A A 0 L0 A 0 (1-5) 真应变δ和真应力可由标称应变ε和标称应力σ通过式 (1-4)和式(1-5)求得。
升温速率:0.1℃/min~40℃/min(400℃后25℃/min) 降温速率:0.1℃/min~20℃/min 或改变频率:频率范围:1.6×10-3~200Hz。最后 可得到,和对温度(T)、频率(Hz)或时间(t)的图 谱。本机配置计算机,可通过计算机设置测试条件,完 成条件控制、数据处理及打印谱图。
动态力学分析法 研究两相聚合物的相容性
1. 实验目的要求
掌握使用DMTA-IV型动态粘弹谱仪测定聚合物的 复合模量、储能模量、损耗模量和阻尼模量的原 理及方法。 通过数据分析,了解共试样上加一个正弦伸长应力,频率为,振 幅为,则应变也可以以正弦方式改变,应力与应变之 间有一相位差,可分别表示为:
2 2
W 与 E 成正比,因此,样品损耗机械能的能力高低可
以用 E 或 tan 值的大小来衡量。 动态力学分析对分子运动特别灵敏。当一定温度下 高分子链段运动频率与仪器施加频率一致时,由于链段 运动而产生的分子间摩擦作用能最大限度地损耗机械 能,此时 tan 值达到最大值。储能模量也随温度上升而 大幅度下降。 若所研究的样品为两组分体系,如果两组分完全不 相容,样品形成明显的两相结构,此时,-T曲线和-T
σ=P/A0 (MPa) (1-1) 式中:P为拉伸载荷;A0为试样的初始截面。试样的伸长 率即应变ε为 ε=ΔL/L0 (100%) (1-2) 式中:L0为试样标定线间的初始长度;ΔL为拉伸后标定 线长度的变化量。 对于形变很大的聚合物材料,由于拉伸过程中试样 的截面积发生变化。从曲线直接得到的标称拉伸力学性 能已经不符合实际情况。故必须转化成真应力和真应 变,以求得真实拉伸力学性能。 真应力为: (MPa) (1-3) σ' = P/A
曲线有两个转变区,对应于两种不同的相。若两相聚合物 有一定相容性,则随着相容性的改善,-T曲线上逐渐由两 个转变峰过渡为一个宽转变峰。
3. 仪器
DMTA-IV型动态粘弹谱仪主机炉内结构如图所示。 样品通过夹具(拉伸、压缩、剪切、悬臂梁、三点弯曲等 夹具),T-bar与驱动器,应力传感器和位移检测器相连 接。试样在预张力(最大值:15N)的作用下由驱动器施 加一固定频率的正弦伸缩振动。预张力的作用是使试样在 受到伸缩振动时始终产生张应力。应力传感器和位移检测 器分别检测到同样振动频率的正弦应力和应变讯号,经仪 器信号处理器处理,直接给出,和值。测量过程中通过控 制样品炉的升温程序:炉温范围:-150℃~600℃(注意: 设置温度禁止超过材料熔点)
