培优训练3.doc
素养培优专练3

素养培优专练(三)一、功能在实际情境中的应用(一)功能在生产、生活中的应用1.(2020·天津高考)(多选) 复兴号动车在世界上首次实现速度350 km/h自动驾驶功能,成为我国高铁自主创新的又一重大标志性成果。
一列质量为m的动车,初速度为v0,以恒定功率P在平直轨道上运动,经时间t达到该功率下的最大速度v m,设动车行驶过程所受到的阻力F保持不变。
动车在时间t内()A.做匀加速直线运动B.加速度逐渐减小C.牵引力的功率P=F v mD.牵引力做功W=12m v2m-12m v2答案BC解析动车加速的过程功率恒定,根据P=F牵v可知,动车的牵引力减小,根据牛顿第二定律得F牵-F=ma,可知动车的加速度减小,所以动车做加速度减小的加速直线运动,A错误,B正确;当加速度为0时,牵引力等于阻力,列车达到最大速度v m,则牵引力的功率P=F v m,C正确;动车的功率恒定,在时间t内,牵引力做功W=Pt,根据动能定理得Pt-Fs=12m v 2m-12m v2,故W>12m v2m-1 2m v 2,D错误。
(二)功能在体育运动、活动中的应用2. (2021·河北省二轮复习联考一)跳伞运动被视为“勇敢者的运动”,惊险又刺激。
在一次跳伞训练中,一名跳伞运动员打开降落伞后,先减速下降一段时间,此后匀速向下直线运动。
下列说法正确的是()A.在减速下降阶段,下降同样的高度,运动员的动能变化量可能不相等B.在减速下降阶段,下降同样的高度,运动员的重力势能变化量不相等C.在匀速下降阶段,运动员的机械能守恒D.在匀速下降阶段,运动员的重力势能不变答案 A解析因为在减速下降阶段,跳伞运动员未必是匀减速下落,所受合力不一定恒定,则下降同样的高度,运动员的动能变化量不一定相等,A正确;重力势能变化量只与高度变化有关,下降同样的高度,重力势能变化量一定相等,B错误;机械能包括动能和势能,运动员匀速下降时,v不变,则动能不变,高度减小,则重力势能减小,所以运动员的机械能减小,C、D错误。
六年级数学培优3.doc

2.汽车上有男乘客45人,若女乘客人数减少10%,恰好与男乘客人么回来比去时少用______小时.4.在一个停车场,共有24辆车,其中汽车是4个轮子,摩托车是3个轮子,这些车共有86个轮子,那么三轮摩托车有______辆.5.有6个学生都面向南站成一行,每次只能有5个学生向后转,则最少要做______次能使6个学生都面向北.6.如图所示为一。
个棱长6厘米的正方体,从正方体的底面向内挖去一个最大的圆锥体,则剩下的体积是原正方体的百分之______(保留一位小数).7.掷两粒骰子,出现点数和为7、为8的可能性大的是______.8.老妇提篮卖蛋.第一次卖了全部的一半又半个,第二次卖了余下的一半又半个,第三次卖了第二次余下的一半又半个,第四次卖了第三次余下的一半又半个.这时,全部鸡蛋都卖完了.老妇篮中原有鸡蛋______个.10.把33,51,65,77,85,91六个数分为两组,每组三个数,使两组的积相等,则这两组数之差为______.大的分数为 。
6、某班有49名同学,其中男同学的52和女同学的83参加了数学小组,那么这个班中没有参加数学小组的同学有( )名。
7、甲、乙两人背诵英语单词,甲比乙每天多背8个,乙因生病,中途停止10天。
40天后,乙背的单词正好是甲的一半,甲背单词( )个。
8、买电影票,5元、8元、12元一张的一共150张,用去1140元,其中5元和8元的张数相等,5元的电影票有( )。
9、甲、乙、丙三种货物,如果购买甲3件、乙7件、丙1件共花3.15元;如果购买甲4件、乙10件、丙1件共花4.20元,那么购买甲、乙、丙各1件需 ( )元。
二、解答题:1、学校要建一段围墙,由甲、乙、丙三个班完成,已知甲班单独干需要20小时完成,乙班单独干需要24小时完成,丙班单独干需要28小时完成,如果先由甲班工作1小时,然后由乙班接替甲班干1小时,再由丙班接替乙班干1小时,再由甲班接替接替丙班干1小时,……三个班如此交替着干,那么完成此任务共用了多少时间?(6分)2.图中,每个小正方形的面积均为1个面积单位,共9个面积单位,则图中阴影部分面积为多少个面积单位?3.小红到商店买一盒花球,一盒白球,两盒球的数量相等,花球原价是2元钱3个,白球原价是2元钱5个.新年优惠,两种球的售价都是4元钱8个,结果小红少花了5元钱,那么,她一共买了多少个球?4、快车从甲地开往乙地,慢车从乙地开往甲地,两车同时出发相向而行,8小时在途中相遇。
小学一年级数学培优训练题及答案三

小学一年级数学培优训练题及答案三1.3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?【答案】想:可先求出3箱梨比3箱苹果多的重量,再加上3箱苹果的重量,就是3箱梨的重量。
解:45+5×3=45+15=60(千克) 答:3箱梨重60千克。
2. 已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?【答案】想:由已知条件可知,一张桌子比一把椅子多的288元,正好是一把椅子价钱的(10-1)倍,由此可求得一把椅子的价钱。
再根据椅子的价钱,就可求得一张桌子的价钱。
解:一把椅子的价钱:288÷(10-1)=32(元)一张桌子的价钱:32×10=320(元)答:一张桌子320元,一把椅子32元。
3.有趣的水杯下面是两块一样的红色颜料,各放一块到杯子里,哪杯水更红一些?为什么?【答案】【教学思路】先让学生观察,两个杯子盛着的水不一样多.如果往两个杯子里各放一块红色颜料,那么水少的杯子里的水更红一些,水多的杯子里面的水颜色就淡一些.因为这里渗透了浓度问题,学生光凭想象和生活的经验来解答是比较有限,而且不透彻.所以我们可以通过直观的实验来说明道理,红色颜料可以用红墨水来代替.4.有趣的水杯把鹅蛋、鸡蛋、鸽蛋分别放入3个碗里,猜猜它们分别放在哪个碗里?【答案】2号碗放的是鹅蛋,3号碗放的是鸡蛋,1号碗放的是鸽子蛋.5.把瓶子里的铁块拿出来后三个杯子里的水一样多.哪个瓶子里面拿出来的铁块最大?【答案】拿走铁块后每个杯子的水都一样多,那么原来杯子里面水多的说明放入的铁块大,杯子里面水少的放入的铁块小.从图中知道:3号瓶水位高,拿出来的铁块一定最大.6.将大小不同的两块石头放入盛水相同的两个瓶中,哪个瓶中放入的是大石头?【答案】瓶里盛水相同时,放入的石头大则水位就升得高,放入的石头小,则水位就升得少.l号瓶水位高,说明l号瓶里放入的是大石头.7.三杯糖水一样甜,哪杯水里放进去的糖最少?答案:8.在50以内(包括50),十位上的数字比个位上的数字大的两位数一共有多少个?【教学思路】这道题如果先把50以内的数写出来然后再来数一数,就太麻烦了.我们可以通过列表的方法来进行分别列举,这样更容易找到答案:9.】数字趣味题小小鸡,真神气,圆脑袋,圆身体,尖脚尖嘴大眼睛,翘翘尾巴展展翅,青草地里找虫吃。
苏科版七上第三章《代数式》解答题培优训练(三)(有答案).doc

苏科版七上第三章《代数式》解答题培优训练(三)班级:姓名:得分:一、解答题1.已知,A在数轴上表示的数是单项式-5秒的系数,B表示的数是多项式x2y + 15的常数项.~40~0 5 W~15~20*(1)数轴上点A表示的数是,点B表示的数是;(2)若一动点F从点A出发,以3个单位长度/秒速度由A向B运动;动点。
从原点。
出发,以1个单位长度/秒速度向B运动,点P、Q同时出发,点Q运动到B 点时两点同时停止.设点。
运动时间为I秒.%1若尸从人到B运动,则F点表示的数为,。
点表示的数为.(用含£ 的式子表示) %1当f为何值时,点F与点。
之间的距离为2个单位长度。
2,已知整式M = x 2 + Sax-x- 1,整式M与整式N之差是3x 2 + 4ctx-x(l)求出整式N;⑵若a是常数,且2M + N的值与x无关,求。
的值.3.“冏” Song)是中文地区网络社群间一种流行的表情符号,像一个人脸郁闷的神情,被赋予“郁闷、悲伤、无奈”之意.如图所示,一张边长为10的正方形的纸片, 剪去两个一样的小直角三角形和一个长方形得到一个“冏”字图案(阴影部分).设剪去的小长方形长和宽分别为x, y,剪去的两个小直角三角形的两直角边长也分别为 x, y.(1)用含有X,y的代数式表示图中“冏"的面积;(2)若|x — 4| + (y — 3尸=0时,求此时"冏"的面积.4.阅读材料,解答下列问题:例:当a = 5,则\a\ = |5| = 5,故此时“的绝对值是它本身;当a = 0时,|a| = 0, 故此时a 的绝对值是0;当a <。
时,如a = -5,则|a| = |5| = -(5) = 5,故此时a 的绝对值是它的相反数.综上所述,一个数的绝对值要分三种情况,即(> 0)|a| = {0(a = 0)这种分析方法涌透了数学中的分类讨论思想.请仿照例中的分类(-a(a < 0)讨论,解决下面的问题:(1)|-4+5|=—;|-|-3| =—;(2)如果|% + 1| = 2,求X的值;(3)若数轴上表示数a的点位于-3与5之间,求|ct + 3| + |a - 5|的值;(4)当£1=时,|a — l| + |a + 5| + |a — 4|的值最小,最小值是—5.嘉淇准备完成题目:化简:(口/ + 8* + 6) —(8X + 5/ + 2),发现系数“口”印刷不清楚.(1)他把“口”猜成3,请你化简:(3濯+ 8x + 6)- (8x + 5%2 + 2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“口”是几?6.已知A = 3a2b-2ab2 + abc,小明错将“24 — B”看成“2A + B”,算得结果为4a2b — 3ab2 + 4abc.(1)计算B的表达式;(2)求2A-B的结果;(3)小强说(2)中的结果的大小与c的取值无关,对吗?7.观察算式.12=-X1X2X36l2 + 22=ix2x3x5612+22+32=-X3X4X76我们称这样的式子为连等式.(1)请写出一个式子:I2 + 22 + 32 + 42 =;(2)请用n表示式子的规律:* + 22 + 32 + 42 + ... + n2 =(3)根据你所得的规律求:II2 + 122 + 132 + 142 + - + 182 + 192的值.8.【问题】若a + b = 10,则沥的最大值是多少?【探究】探究一:当a - b = 0时,求沥值.显然此时,a = b = 5,贝ijab = 5 x 5 = 25探究二:完成下表:探究三:设a = 5 + x,贝阳 =, ab =, 11:匕时当x=时,,活最大;【结论】若a + b = 10,则ab的最大值是【拓展】(1)若“、力为两个正数,且满足a + b = m,则沥的最大值是;⑵a、b、c为三个正数,且满足a + b + c = m,则沥c的最大值是。
Unit 3培优练习- 2024-2025学年人教版英语七年级上册

24秋七年级英语培Unit 3培优练习单元词汇专练一、根据句意提示,填写出单词的适当形式。
1. Our classroom has a big ______/skriːn/ on the wall.2. We often play basketball in the sports _____/fiːld/.3. Shelly goes to Mr Chen's ______(办公室) to ask questions.4. Students enjoy doing exercises in the g____.5. Teachers' Day is a s______ day.6. There are three dining _____(hall) in our school.7. This film is so ________(amaze).8. Alice knows the ___________(important) of reading.So she reads every day.9. This is a modern _________(build) in our school.10. Each student has a desk ________(draw) in the classroom.二、根据汉语意思完成英语句子。
每空一词。
1. 教室后面还有另外一块黑板。
There is another blackboard ___ ____ ______ ___ the classroom.2. 新教室与旧教室大不相同。
The new classroom is so _________ _____ the old one.3. 学生们通常在学校上课。
Students usually have lessons ___ ______.4. 学校图书馆在美术楼的对面。
The school library is ______ ______ the art building.5. 我们学校前面有两棵高高的树。
小学六年级培优训练3

知识点一:火车过桥问题。
【列车过桥问题公式】(桥长+列车长)÷速度=过桥时间;(桥长+列车长)÷过桥时间=速度;速度×过桥时间=桥、车长度之和。
例:一列火车长150米,每秒钟行19米。
全车通过长800米的大桥,需要多少时间?练习:(1)一列火车长200米,它以每秒10米的速度穿过200米长的隧道,从车头进入隧道到车尾离开隧道共需要多少秒?(2)一座桥长3000米,一列火车以每分钟800米的速度过桥,从火车头上桥到火车尾离开桥共用了4.5分钟,这列火车的车身长多少米?(3)少先队员357人排成三路纵队去参观画展.队伍行进的速度是20米/分,前面两人都相距1米.现在队伍要通过一座长702米的桥,整个队伍从上桥到离桥共需要几分钟?知识点二:行程问题行程问题的公式:速度×时间=路程路程÷时间=速度路程÷速度=时间相遇问题公式:速度和×相遇时间=相遇路程相遇路程÷速度和=相遇时间相遇路程÷相遇时间=速度和追击问题公式:追及路程÷速度差=追及时间速度差×追及时间=追及路程追及路程÷追及时间=速度差1、甲乙两人从相距54千米的两地,同时相向而行,甲每小时行4千米,乙每小时行5千米,几小时后两人相遇?2、甲乙两车相距70千米,两车同时而行,甲车每小时行55千米,乙车每小时行45千米,经过几小时甲车追上乙车?例题2:甲乙两辆汽车同时从东西两地相向开出,甲车每小时行66千米,乙车每小时行58千米,两车在离中点36千米处相遇,求东西两地相距多少千米?练习:(1)快、慢两车同时从两城相向出发,4小时后在离中点18千米处相遇,已知快车每小时行70千米,慢车每小时行多少千米?(2)一辆客车和一辆货车同时由甲乙两地相向开出,在离中点15千米的地方相遇,已知客车与货车的速度比是4:3,求甲乙两地相距多少千米?(3)甲车从A地到B地,乙车从B地到A地,当甲车行了全程的80%,乙行了3全程的时,甲、乙两车又相距40千米,则A、B两地之间的路程是多少千米?5。
初中数学分式方程的增根、无解问题填空题培优训练3(附答案详解)

初中数学分式方程的增根、无解问题填空题培优训练3(附答案详解)1.关于x 的方程1322m x x x -+=--有增根,则m =______. 2.关于x 的方程22x m x +-=1的解是正数,则m 的取值范围是________ . 3.若关于x 的分式方程12111a x x x x --=---有增根,则a =__________. 4.若关于x 的分式方程111x xm +--=2有增根,则m =_____. 5.已知关于x 的方程2x a x 2-+=1的解是负值,则a 的取值范围是______. 6.若数a 关于x 的不等式组()()11223321x x x a x ⎧-≤-⎪⎨⎪-≥-⎩恰有两个整数解,且使关于y 的分式方程132211y a y y--=---的解为正数,则所有满足条件的整数a 的值之和是_______. 7.我们知道方程2312x x x ++=-的解是45x =.现给出另一个方程(1)2311(1)2y y y +++=++-,它的解是__________. 8.若数a 使关于x 的不等式组2122274x x x a-⎧≤-+⎪⎨⎪+>-⎩,有且仅有四个整数解,且使关于y 的分式方程2222a y y+=--有非负数解,则所有满足条件的整数a 的值之和是________________.9.用换元法解方程22111x x x x --=-时,如果设2x y x 1=-,那么所得到的关于y 的整式方程为_____________10.关于x 的分式方程3111m x x+=--的解为正数,则m 的取值范围是___________. 11.使得关于x 的不等式组6101131282x a x x -≥-⎧⎪⎨-+<-+⎪⎩有且只有4个整数解,且关于x 的分式方程14ax x --+274x -=-8的解为正数的所有整数a 的值之和为________. 12.若关于 x 的方程18mx x += 的解是x=14,则 m= ________________.13.关于x 的分式方程2111x k x x x ++=++的解为非正数,则k 的取值范围是____. 14.方程333x m x x -=--有增根则m 的值是 ____. 15.若关于x 的方程2126339m x x x x ++=+--有增根,则m 的值是__________________. 16.若关于x 的分式方程x 2322m m x x ++=--的解为正实数,则实数m 的取值范围是____.17.关于x 的分式方程5x x -+2=m x 5-有增根,那么m =_____. 18.已知关于x 的方程22x m x ++=3的解是非负数,则m 的取值范围是_____. 19.若分式方程22x m x x=--有增根,则m 的值为__________. 20.若整数a 使关于x 的分式方程21222a x x +=--的解为正数,使关于y 的不等式组2350y a y +>⎧⎨+<⎩ 无解,则所有满足条件的整数a 的值之和是_____. 21.若关于x 的分式方程1x m x --﹣3x =1无解,则m 的值为_____. 22.若分式方程544x a x x =+--有增根,则a 的值为____. 23.若关于x 的方程122x m x x +=--有增根,则m 的值是________. 24.若关于x 的一元一次不等式组1322x x a x⎧-≤⎪⎨⎪-<-⎩所有整数解的和为-9,且关于y 的分式方程22142a y a y y +-=--有整数解,则符合条件的所有整数a 为__________. 25.若关于x 的方程201x b x -=-的解是非负数,则b 的取值范围是__________. 26.若解方程333x m x x =--出现增根,则m 的值是______. 27.若关于 x 的方程1222x m x x-=+--产生增根,那么 m 的值是_____. 28.已知关于x 的方程22x m x --=3的解是正数,则m 的取值范围为_________. 29.已知分式方程2322356x x m x x x x ---=---+的解为正数,则m 的取值范围为_____.30.若关于x 的分式方程211k x x x =---的解为正数,则满足条件的非负整数k 的值为____.31.若关于x 的方程25211--=---a x x的解为非负数,且关于x 的不等式组122260x a x ⎧≥-⎪⎨⎪->⎩有且仅有5个整数解,则符合条件的所有整数a 的和是__________. 32.有 6 张卡片,上面分别标有 0,1,2,3,4,5 这 6 个数字,将它们背面洗匀后,任意抽出一张,记卡片上的数字为 a ,若数 a 使关于 x 的分式方程2211a x x+=--的解为正数,且使关于 y 的不等式组2132y y y a +⎧->⎪⎨⎪≤⎩的解集为y < −2,则抽到符合条件的 a 的概率为_________;33.若关于x 的方程111m x x x ----=0有增根,则m 的值是______. 34.关于x 的方程2334ax a x +=-的解为x =1,则a =______. 35.若关于x 的分式方程211k x +=-的解是正数,则k 的取值范围是__________. 36.关于x 的方程12ax x +-=−1的解是正数,则a 的取值范围是________. 37.若关于x 的分式方程21326x m x x -=--有增根,则m 的值是______。
2024年部编版七年级上册语文周末复习培优训练试卷及答案 (3)

周末提优3第三单元学习任务群:学习生活总分:50 分建议用时:45 分钟得分:基础型学习任务群[荣德原创]为更好地巩固近期所学内容,某班学生分为“现代文小组”和“文言文小组”,对第三单元展开学习。
请你阅读两个小组的成果,完成相关问题。
1. 下面是“现代文小组”制作的口袋书,请你阅读其中几页,完成相关任务。
(9 分)(1)任务一:第1 页中有四个词语存在书写错误,请你在下面写出正确的字形。
(4 分)①___________ ②___________ ③___________ ④___________(2)任务二:第2 页中有两个字的读音标注错误,请你改正。
(2 分)①___________应读作___________ ②___________应读作___________(3)任务三:第3 页中个别词语的归类出现错误,___________应该是名词,___________应该是动词,___________既不是动词也不是名词。
(3 分)2. “文言文小组”研读了《〈论语〉十二章》,邀请你参与,一起完成学习任务。
(11 分)(1)任务一:明义• 理解内容下面句中加点词的解释,有误的一项是(2 分) ( )A. 学而时.习之(按时)B. 传.不习乎(传授,这里指老师传授的知识)C. 三军可夺.帅也(夺取)D. 切.问而近思(恳切)(2)任务二:广识•了解文化下面文学及文化常识,说法错误的一项是(2 分) ( )A. 儒家是先秦诸子百家之一,脱胎自周朝礼乐传统, 代表人物有孔子、老子、孟子、庄子。
B. “箪”,古代盛饭用的圆形竹器, 也有用芦苇等制成的。
C. 文言文中的“水”指的是冷水,“汤”指的是热水。
D. “匹夫”泛指平民百姓,除此之外,平民百姓还可以用“布衣”来代称。
(3)任务三:记言• 书写运用请根据语境进行默写。
(7 分)文学社的同学们想要为外国友人表演一场话剧。
请你依据《〈论语〉十二章》的内容将下面的剧本补充完整。
七年级数学暑期培优专题训练(综合3)

七年级数学暑期培优专题训练(综合3)班级 姓名1.下列等式从左到右的变形中,是因式分解的是A .x 2-9+6x =(x +3)(x -3)+6xB .(x +5)(x -2)=x 2+3x -10C .x 2-8x +16=(x -4)2D .6ab =2a ·3b2.将一副三角板按如图方式叠放,则∠a 等于A .30°B .45°C .60°D .75°3.为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m ,东西方向缩短3m ,则改造后的长方形草坪面积与原来正方形草坪面积相比A .减少9m 2B .增加9m 2C .保持不变D .增加6m 24.如图,射线OC 的端点O 在直线AB 上,∠1的度数x °是∠2的度数y °的2倍多10°,则可列正确的方程组为A .18010x y x y +=⎧⎨=+⎩B .180210x y x y +=⎧⎨=+⎩C .180102x y x y +=⎧⎨=-⎩D .90210x y y x +=⎧⎨=-⎩5.如图,△DAC 和△EBC 均是等边三角形,AE 、BD 分别与CD 、CE 交于点M 、N ,有如下结论:①△ACE ≌△DCB ;②△ACM ≌△DCN ;③CM =CN;④OC 平分∠AOB .其中,正确结论的个数是A .4个B .3个C .2个D .1个二、填空题:本大题共12小题,每小题3分,共36分.把答案直接填在答题纸相对应的位置上.6.()2301220132-⎛⎫+-- ⎪⎝⎭= . 7.最薄的金箔的厚度为0.000000091m ,用科学记数法表示为 m .8.如图,己知∠1=∠2,AC =AD ,还需要什么条件,就能使△ABC ≌△AED ,把所需要的条件写在横线上, (只需写出一个满足条件即可).9.已知243x y k x k +=⎧⎨=+⎩,如果x 与y 互为相反数,则k = . 10.已知:a +b =32,ab =1,化简(a -2)(b -2)的结果是 .11.若4x 2+m x +9是一个完全平方式,则实数m 的值是 .12.如图,在△ABC 中,DE 是AC 的垂直平分线,AE =3cm .△ABD 的周长为13cm ,则△ABC 的周长是 .13.已知:234x t y t =+⎧⎨=-⎩,则x 与y 的关系式是 . 14.如图,五边形ABCDE 中,∠A =140°,∠B =120°,∠E =90°,CP 和DP 分别是∠BCD 、∠EDC的外角平分线,且相交于点P ,则∠CPD = .15.如图,方格纸中△ABC 的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,图中与△ABC 全等的格点三角形共有__________个(不含△ABC).三、解答题:16.计算下列各式:(1)5(a 4)3+(-2a 3)2·(-a 2)3-a 15÷a 3;(2)先化简,再求值:(2a +b )(2a -b )+3(2a -b )2+(-3a )(4a -3b ),其中a =-1,b =-2.17.把下列各式分解因式:(1 )6a 2b -9ab 2+3ab ; (2)a 3-6a 2-7a ; (3)(x 2+x )2-(x +1)2.18.解下列方程组:(1)15,55(1);x y x y -=+⎧⎨+=-⎩ (2)54,2310,38.x y z x y z x y z --=⎧⎪+-=⎨⎪++=⎩19. 已知:如图,在△ABC 中,BE 、CF 分别是AC 、AB 两条边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连AD 、AG .试判断AG 与AD 的关系,并说明理由。
九年级培优训练题组3

12. 如图, P 在边长为 1 的等边△ ABC 的边 AB 上, 点 过点 P 作 PE ⊥ AC 于 E ,
Q 为 BC 延长线上一点,且 PA = CQ ,连 PQ 交 AC 育网站:
2
精锐教育·教务管理部
中国领先的高端教育连锁集团 13.如图, n + 1 个上底、两腰长皆为 1,下底长为 2 的等腰梯形的下底均在同一直线上.联结 AP 、 AP2 、 1
精锐教育网站:
3
精锐教育·教务管理部
中国领先的高端教育连锁集团 15.计算: 4 sin 60 −
(
1 3 − 2 − − 12 + . 2
0
)
−1
16.如图,台风中心位于点 P ,并沿东北方向想、 PQ 移动.已知台风移动的速度为 30 千米/时,受影响区域 的半径为 200 千米, B 市位于点 P 的北偏东 75°方向上,距离点 P 320 千米处. (1)本次台风是否会影响 B 市?如果有影响,请给出证明;如果没有影响,说明理由; (2)求这次台风影响 B 市的时间.
2
(1)求抛物线的解析式; (2)如果点 P 由点 A 出发沿 AB 边以 2cm / s 的速度向点 B 运动,同时点 Q 由点 B 出发沿 BC 边以 1cm / s 的 速度向点 C 运动.当其中一点到达终点时,另一点也随之停止运动.设 S = PQ ①试求出 S 与运动时间 t 之间的函数关系式,并写出 t 的取值范围; ②当 S =
Sn =
.
14.如图,已知在正方形 ABCD 外取一点 E ,连接 AE , BE , DE .过点 A 作 AE 的垂线交 ED 于点 P .若
AE = AP = 1, PB = 5 .下列结论:
六年级数学培优训练3

第3课时工程问题一、引入工程问题是应用题中的一个类型,是研究工作效率、工作时间和工作总量之间相互关系的一类问题。
这三个量之间的关系如下:工作效率×工作时间=工作总量;工作总量÷工作时间=工作效率;工作总量÷工作效率=工作时间。
二、新授例1 一项工程,甲乙两队合作需12天完成,乙丙两队合作需15天完成,甲丙两队合作需20天完成。
如果三队合作,需要几天完成?分析:假设这项工程为1个单位,则甲乙合作的效率为1/12,乙丙合作的效率为1/15,甲丙合作的效率为1/20。
因此,甲乙丙三队的工作效率的2倍为(1/12+1/15+1/20),即甲乙丙三队合作的工效为(1/12+1/15+1/20)÷2=1/10,从而三队合作完成这项工作的时间为1÷1/10=10天。
解答:1÷[(1/12+1/15+1/20)÷2]=10(天)答:甲乙丙三队合作需要10天完成。
例2 现有一项工程,甲单独做63天,再由乙做28天可以完成。
如果甲乙合作需48天完成。
现在甲先做42天,然后由乙来做,问乙还要多少天完成?分析:设工程总量为1,已知甲乙合作的工作效率为1/48;又甲干63天乙干28天也可以完成,因此甲做63-48=15天,相当于乙做48-28=20天,所以甲的工作效率是乙的工作效率的4/3,从而乙的工效为:1/48÷(1+4/3)=1/112,甲的工效为1/112×4/3=1/84。
解答:63-48=15 48-28=20 20÷15=4/31/48÷(1+4/3)=1/112 1/112×4/3=1/84(1-1/84×42)÷1/112=56(天)答:乙再做56天可以完成这项工程。
例3 师徒两人合作生产一批零件,6天可以完成任务。
师傅先做了5天后,因事外出,有徒弟接着做3天,共完成任务的7/10。
人教版(五四制)2019-2020七年级数学上册期中综合复习培优训练题3(含答案)

人教版(五四制)2019-2020七年级数学上册期中综合复习培优训练题3(含答案)1.甲、乙两班共有88人,若从甲班调3人到乙班,那么两班人数正好相等,设甲班原有人数是x人,可列出方程()A.88﹣x=x﹣3 B.(88﹣x)+3=x﹣3C.88+x=x﹣3 D.(88﹣x)+3=x2.张萌的手中有长方形ABCD(AD∥BC)和长方形EFGH(EH∥FG)两张纸片,她将这两张纸片按如图所示的方式放置,测得FG,EH分别交AD于M,N两点,并测得∠MFC=30°,则∠ANH的度数为()A.120°B.130°C.140°D.150°3.如图,直线AB,CD被直线EF所截,下列判断中不正确的是( )A.∠3=∠6B.∠2=∠6C.∠1和∠4是内错角D.∠3和∠5是同位角4.如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠EPF=70°,则∠BEP的度数为()A.50°B.55°C.60°D.65°5.下列式子中是一元一次方程的是()A.﹣2=5 B.2x﹣3 C.x=y D.3x=06.如果方程2x+1=3和的解相同,则a的值为()A.7 B.5 C.3 D.07.随着通讯市场竞争日异激烈,某通讯公司的手机市话收费标准每分钟降低了元后,再次下调了,现在的收费标准是每分钟元,则原收费标准每分钟为多少元()A.B.C.D.8.如图,AB∥CD,FE⊥DB,垂足为E,∠1=60°,则∠2的度数是()A.60°B.50°C.40°D.30°9.方程的解是()A.B.C.1 D.-110.一家服装商场,以1 000元/件的价格进了一批高档服装,出售时标价为1 500元/件,后来由于换季,需要清仓处理,因此商场准备打折出售,但仍希望保持利润率不低于5%,那么该商场至多可以打________折.A.9 B.8 C.7 D.611.若x与﹣3的差为1,则x的值是_____.12.如图,直线AB,CD相交于点O,OE⊥AB于点O,若∠EOC=60°,则∠BOD度数是_____.13.当________时,与的值相等.14.方程的解为:_____________.15.甲、乙两人练习赛跑,若甲让乙先跑10米,则甲跑5秒种就能追上乙.若甲让乙先跑2秒钟,则甲跑4秒种就能追上乙,则甲每秒跑____米,乙每秒跑____米.16.在同一平面内有四条直线a、b、c、d,已知:a∥d,b∥c,b∥d,则a和c的位置关系是_____.17.一群小孩分一堆苹果,1人3个多7个,1人4个少3个,则有_____ 个小孩,_____个苹果.18.18.已知三角形ABC ,若将三角形ABC 平移后,得到三角形A′B′C′,且点A(1,0)的对应点A′的坐标是(-1,0),则三角形ABC 是向左平移_______个单位得到三角形A′B′C′.19.如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角的度数分别是_____________.20.如图所示,AB ∥CD,试解决下列问题:(1)在图(1)中,∠1+∠2等于多少度?请说明理由;(2)在图(2)中∠1+∠2+∠3等于多少度?请说明理由;(3)在图(n)中,试探究∠1+∠2+∠3+∠4+…+∠n 等于多少度.21.如图所示,在△ABC 中,AB=AC ,∠A=60°,BD ⊥AC 于点D ,DG ∥AB ,DG 交BC 于点G ,点E 在BC 的延长线上,且CE=CD .(1)求∠ABD 和∠BDE 的度数;(2)写出图中的等腰三角形(写出3个即可).22.某超市在“元旦”促销期间规定:超市内所有商品按标价的80%出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:(符号a x b ≤<表示x 是大于或等于a ,而小于b 的数)根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额=商品的折扣+相应的奖券金额,例如:购买标价为440元的商品,则消费金额为: 44080%352⨯=元,获得的优惠额为: ()440180%40128⨯-+=元. (1)购买一件标价为840元的商品,求获得的优惠额.(2)对于标价在600元与900元之间(含600元和900元)的商品,顾客购买标价为多少元的商品时可以得到925的优惠率.(设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价)23.一位商人来到一个新城市,想租一套房子,A家房主的条件是:先交2 000元,然后每月交租金380元,B家房主的条件是:每月交租金580元.(1)这位商人想在这座城市住半年,那么租哪家的房子合算?(2)这位商人住多长时间时,租两家房子的租金一样?24.已知,∠AOB=90°,点C在射线OA上,CD∥OE.(1)如图1,若∠OCD=120°,求∠BOE的度数;(2)把“∠AOB=90°”改为“∠AOB=120°”,射线OE沿射线OB平移,得O′E,其他条件不变,(如图2所示),探究∠OCD、∠BO′E的数量关系;(3)在(2)的条件下,作PO′⊥OB垂足为O′,与∠OCD的平分线CP交于点P,若∠BO′E=α,请用含α的式子表示∠CPO′(请直接写出答案).25.为鼓励居民节约用电,某省试行阶梯电价收费制,具体执行方案如下:例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?26.如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为A(a,0),B(0,b),C(2,4),且方程3x2a+b+11﹣2y3a﹣2b+9=0 是关于x,y 的二元一次方程.(1)求A、B 两点坐标;(2)如图1,设D 为坐标轴上一点,且满足S△ABD=S△ABC,求D 点坐标.(3)平移△ABC 得到△EFG(A 与E 对应,B 与F 对应,C 与G 对应),且点E 的横、纵坐标满足关系式:5x E﹣y E=4,点F 的横、纵坐标满足关系式x F﹣y F=4,求G 的坐标.27.解下列方程(1)x﹣4=2﹣5x (2)(3)(4)参考答案1.B【解析】【分析】设甲班原有人数是x人,根据甲、乙两班共有88人,若从甲班调3人到乙班,那么两班人数正好相等可列出方程.【详解】设甲班原有人数是x人,则(88﹣x)+3=x﹣3.故答案选B.【点睛】本题考查了一元一次方程,解题的关键是根据实际问题抽象出一元一次方程.2.D【解析】如图,∵AD∥BC,EH∥FG,∴∠1=∠2,∠2=∠3,∴∠3=∠1=∠MFC=30°,∴∠ANH=180°-∠3=180°-30°=150°.故答案选D.3.B【解析】解:A.根据对顶角相等可得∠3=∠6,故此选项不合题意;B.∠2和∠6是同位角,不一定相等,故此选项符合题意;C.∠1和∠4是内错角,故此选项不合题意;D.∠3和∠5是同位角,故此选项不合题意;故选B.4.A【解析】分析:本题只要根据角平分线的性质得出∠EFD的度数,然后根据平行线的性质得出∠BEF的度数,从而得出答案.详解:∵∠PEF=90°,∠EPF=70°,∴∠EFP=20°,∵FP平分∠EFD,∴∠EFD=40°,∵AB∥CD,∴∠BEF=180°-40°=140°,又∵∠PEF=90°,∴∠BEP=50°,故选A.点睛:本题主要考查的就是平行线的性质以及角平分线的性质,属于基础题型.熟记平行线的性质是解决本题的关键.5.D【解析】【分析】只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做一元一次方程.由一元一次方程的定义可得:判断一个方程是否为一元一次方程,首先判断它是不是方程,主要看:①是不是等式;②有没有未知数,有未知数的等式是方程.其次看是不是整式方程,即未知数不能出现在分母中.最后看未知数的个数和次数,未知数的个数只能有1个,且次数是1次的.满足上述三个条件的式子才可断定为一元一次方程.本题就是根据上述判断方法进行判断得出结论的.【详解】解:A、该方程属于分式方程,故本选项错误;B、2x﹣3不是方程,故本选项错误;C、该方程中含有2个未知数,属于二元一次方程,故本选项错误;D、该方程符合一元一次方程的定义,故本选项正确.故选:D.【点睛】本题考查一元一次方程的判定,解题关键是方程两边都是整式.6.A【解析】【分析】先求出的解,然后把求得的方程的解代入即可求出的值.【详解】∵,∴.把代入,得,解之得,.故选A.【点睛】本题主要考查方程的解的概念和一元一次方程的解法,熟练掌握一元一次方程的解法是解答本题的关键.7.D【解析】【分析】此题要根据题意列出代数式.可先求下调了25%前的价格,再求原价.也可列方程求解.【详解】解:①算术求解:b÷(1-25%)+a=b+a.②列方程求解:设原收费标准每分钟为x元,则(x-a)(1-25%)=b,解得x=b+a.故选:D.【点睛】解答本题的实质是实现从基本数量关系的语言表述到用字母表示一种转化,设出未知数,借助方程,列出等式,从而求出答案.8.D【解析】【分析】由EF⊥BD,∠1=60°,结合三角形内角和为180°即可求出∠D的度数,再由“两直线平行,同位角相等”即可得出结论.【详解】解:在△DEF中,∠1=60°,∠DEF=90°,∴∠D=180°-∠DEF-∠1=30°.∵AB∥CD,∴∠2=∠D=30°.故选:D.【点睛】本题考查平行线的性质以及三角形内角和为180°,解题关键是根据平行线的性质,找出相等、互余或互补的角.9.B【解析】【分析】方程去分母,移项合并,将x系数化为1,即可求出解.【详解】解:去分母得:-1+3x=6x,移项合并得:3x=-1,解得:x=.故选B.【点睛】此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,即可求出解.10.C【解析】试题解析:设该种商品最多可打折,根据题意,得解得所以最多可打7折.11.-2【解析】分析:根据解方程的步骤:移项,移项要变号,合并同类项,进行计算即可.详解:根据题意得:x+3=1,移项得:x=1-3,合并同类项得:x=-2.故答案为:-2.点睛:本题主要考查了解一元一次方程,解题过程中关键是要注意符号问题.12.30°【解析】【分析】根据垂直的定义可得∠AOE=90°,再结合角的和差关系可求出∠AOC的度数;然后根据∠AOC和∠BOD组成了一个平角,即可求出∠BOD的度数.【详解】∵OE⊥AB,∴∠AOE=90°.∵∠EOC=60°,∴∠AOC=90°-60°=30°,∴∠BOD=∠AOC=30°.故答案为:30°【点睛】本题考查了垂直的定义,对顶角的性质及角的运算,得到图形中各个角之间的关系是关键. 13.【解析】【分析】根据题意列出方程,求出方程的解即可得到x的值.【详解】根据题意得:5(x﹣2)=2[7x﹣(4x﹣3)]去括号得:5x﹣10=14x﹣8x+6移项合并得:x=﹣16.故答案为:﹣16.【点睛】本题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.14.=【解析】【分析】利用等式性质2,等号两边同乘即可求解.【详解】,等号两边同乘,得x=.故答案为:【点睛】此题考查了等式的性质,熟练掌握等式的性质是解此题的关键.15. 6 4【解析】设甲每秒跑x米,则乙每秒跑x−105=(x−2)米,根据题意得:4x=6(x−2),去括号得:4x=6x−12,解得:x=6,则甲每秒跑6米,乙每秒跑4米。
文科数学培优强化训练3

2012届上砂中学文科数学培优强化训练3一、选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若复数11z i =-,23z i =+,则复数12z z z =⋅在复平面内对应的点位于A.第一象限B. 第二象限C. 第三象限D. 第四象限 2.已知集合2{|10},{|560}M x x N x x x =-<=-+>,则M N = A. {|1}x x < B.{|12}x x << C.{|3}x x > D. ∅ 3. 命题“(,),,,2330x y x R y R x y ∃∈∈++<”的否定是( )A. 000000(,),,,2330x y x R y R x y ∃∈∈++<B. 000000(,),,,2330x y x R y R x y ∃∈∈++≥C. (,),,,2330x y x R y R x y ∀∈∈++≥D. (,),,,2330x y x R y R x y ∀∈∈++>4.某中学为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用图1的条形图表示。
根据条形图可得这50名学生这一天平均每人的课外阅读时间为A.0.67(小时) B.0.97(小时) C.1.07(小时) D.1.57(小时) 5.已知函数()lg(1)lg(1)f x x x =-++,()lg(1)lg(1)g x x x =--+,则 A .()f x 与()g x 均为偶函数 B .()f x 为奇函数,()g x 为偶函数 C .()f x 与()g x 均为奇函数 D .()f x 为偶函数.()g x 为奇函数 6.已知向量(4,3)=a , (2,1)=-b ,如果向量λ+a b 与b 垂直,则|2|λ-a b 的值为 A .1 BC.5 D.7.已知四棱锥V ABCD -,底面ABCD 是边长为3的正方形,VA ⊥平面ABCD ,且4VA =,则此四棱锥的侧面中,所有直角三角形的面积的和是A. 12B.24C.27D.368.已知实数x y ,满足2201x y x y x +≤⎧⎪-≤⎨⎪≤≤⎩,,,则23z x y =-的最大值是A.6-B.1-C.4D.69.已知函数()y f x =,将()f x 的图象上的每一点的纵坐标保持不变,横坐标扩大到原来的2倍,然后把所得的图象沿着x 轴向左平移2π个单位,这样得到的是1sin 2y x =的图象,那么函数()y f x =的解析式是 A.1()sin 222x f x π⎛⎫=- ⎪⎝⎭B. 1()sin 222f x x π⎛⎫=+ ⎪⎝⎭C. 1()sin 222x f x π⎛⎫=+ ⎪⎝⎭D. 1()sin 222f x x π⎛⎫=- ⎪⎝⎭10.观察下图2,可推断出“x ”应该填的数字是A .171B .183C .205D .268二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题)11.高三某班学生每周用于数学学习的时间(单位:小时)与数学成绩y (单位:分)之间有如下数据:根据统计资料,该班学生每周用于数学学习的时间的中位数是 ; 根据上表可得回归方程的斜率为3.53,截距为13.5,若某同学每周用于数学学习的时间为18 小时,则可预测该生数学成绩 是 分(结果保留整数).12.已知椭圆的方程是125222=+y ax (5a >),它的两个焦点分别为12,F F ,且12||8F F =,弦AB (椭圆上任意两点的线段)过点1F ,则2ABF ∆的周长为 13.如果实数,x y 满足等式22(2)3x y -+=,那么xy的最大值是( )14.(坐标系与参数方程选做题)在极坐标系中,直线(sin cos )2ρθθ-=被圆4sin ρθ=截得的弦长为 15.(几何证明选讲选做题)如图3,PAB 、PCD 为⊙O 的两条割线,若PA=5,AB=7,CD=11,2AC =,则BD 等于三、解答题:本大题共6小题,满分80分. 解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知数列{}n a 是一个等差数列,且21a =,55a =-.(I )求{}n a 的通项n a 和前n 项和n S ;(II )设52n n a c -=,2n cn b =,证明数列{}n b 是等比数列. 17. (本题满分13分)在ABC ∆中,角,,A B C 的对边分别为,,,a b c 6B π=,4cos ,5A b ==(Ⅰ)求a 的值;(Ⅱ)求sin(2)A B -的值;18.(本小题满分13分)2012年春节前,有超过20万名广西、四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年,为防止摩托车驾驶人因长途疲劳驾驶,手脚僵硬影响驾驶操作而引发交事故,肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾乘人员休息站,让过往返乡过年的摩托车驾驶人有一个停车休息的场所。
培优辅导3 观察、归纳与猜想(含答案)-

3.创造的基石──观察、归纳与猜想知识纵横当代著名科学家波普尔说过:我们的科学知识,是通过未经证明的和不可证明的预言,通过猜测,通过对问题的尝试性解决,通过猜想而进步的。
从某种意义上说,一部数学史就是猜想与验证猜想的历史。
20世纪数学发展中巨大成果是,1995年英国数学家维尔斯证明了困扰数学界长达350•多年的“费尔马大猜想”,而著名的哥德巴赫猜想,已经历经了两个半世纪的探索,尚未被人证实猜想的正确性。
当一个问题涉及相当多的乃至无穷多的情形时,我们可以从问题的简单情形或特殊情况入手,通过对简单情形或特殊情况的试验,从中发现一般规律或作出某种猜想,从而找到解决问题的途径或方法,这种研究问题的方法叫归纳猜想法,是创造发明的基石。
例题求题【例1】(1)用●表示实圆,用○表示空心圆,现有若干实圆与空心圆按一定规律排列如下:●○●●○●●●○●○●●○●●●○●○●●○●●●○……问:前2001个圆中,有_______个空心圆. (2001年江苏省泰州市中考题)(2)古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,则第24个三角形数与第22个三角形数的差为__________.(2003年舟山市中考题) 思路点拨 (1)仔细观察,从第一个圆开始,若干个圆中的实圆数循环出现,而空心圆的个数不变;(2)每个三角形数可用若干个数表示.解:(1)667 提示:每9个圆一组中实圆个数循环出现,而空心圆每组3个;(2)(1+2+3+…+24)-(1+2+3+…+22)=47.【例2】观察下列图形,并阅读图形下面的相关文字:两条直线相交, 三条直线相交, 四条直线相交,最多有1个交点最多有3个交点最多有6个交点像这样,10条直线相交,最多交点的个数是( )A.40个B.45个C.50个D.55个(2001年湖北省荆门市中考题) 思路点拨随着直线数的增加,最多交点也随着增加,从给定的图形中,•探讨每增加一条直线,最多交点的增加数与原有直线数的关系,是解本例的关键.解:选B.提示:每增加一条直线,最多交点的增加数与原有直线数相同,问题就转化为求1+2+3+…+9的和.【例3】化简999n ⋅⋅⋅个×999n ⋅⋅⋅个+1999n ⋅⋅⋅个(第18届江苏省竞赛题)思路点拨 先考察n=1,2,3时的简单情形,然后作出猜想,这样,化简的目标更加明确.解:原式=102n【例4】古人用天干和地支记次序,其中天干有10个:甲乙丙丁戊己庚辛壬癸;地支有12个:子丑寅卯辰巳午未申酉戌亥,将天干的10个汉字和地支的12个汉字分别循环排列如如下两行:甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸……子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥……从左向右数,第1列是甲子,第3列是丙寅…,问当第二次甲和子在同一列时,该列的序号是多少? (第12届“希望杯”邀请赛试题) 思路点拨 把“甲”、“子”在第一行、第二行出现的位置分别用相应的代数式表示,将实际问题转化为数学问题求解。
培优试题3
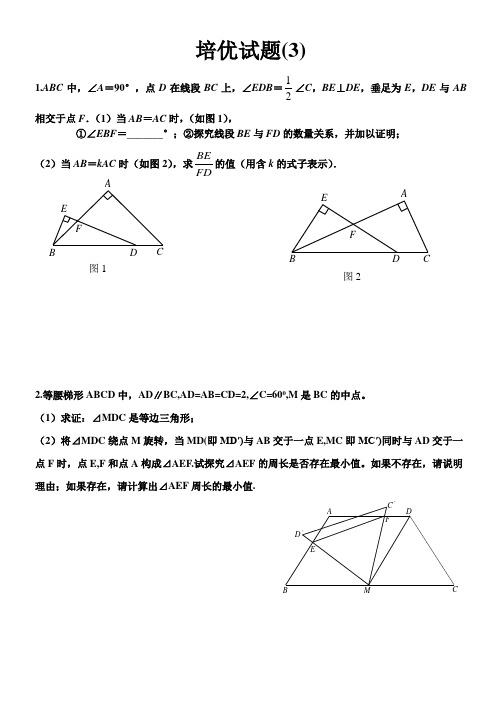
培优试题(3)1.ABC 中,∠A =90°,点D 在线段BC 上,∠EDB =12∠C ,BE ⊥DE ,垂足为E ,DE 与AB 相交于点F .(1)当AB =AC 时,(如图1),①∠EBF =_______°;②探究线段BE 与FD 的数量关系,并加以证明; (2)当AB =kAC 时(如图2),求BEFD的值(用含k 的式子表示).2.等腰梯形ABCD 中,AD ∥BC,AD=AB=CD=2,∠C=600,M 是BC 的中点。
(1)求证:⊿MDC 是等边三角形;(2)将⊿MDC 绕点M 旋转,当MD(即MD′)与AB 交于一点E,MC 即MC′)同时与AD 交于一点F 时,点E,F 和点A 构成⊿AEF.试探究⊿AEF 的周长是否存在最小值。
如果不存在,请说明理由;如果存在,请计算出⊿AEF 周长的最小值.D 'C 'M FEDCB A图1图2AB CD EFF E DCBA3在□ABCD 中,∠BAD 的平分线交直线BC 于点E ,交直线DC 于点F .(1)在图1中证明CE CF =;(2)若90ABC ∠=︒,G 是EF 的中点(如图2),直接写出∠BDG 的度数; (3)若120ABC ∠=︒,FG ∥CE ,FG CE =,分别连结DB 、DG (如图3),求∠BDG 的度数.GDDD4.如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,(1)的值为;(2)求证:AE=EP;(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.5.已知△ABC为等边三角形,点D为直线BC上一动点(不与点B,C重合),以AD为边作菱形ADEF(A,D,E,F按顺时针排列),使∠DAF=60°,连接CF.(1)如图1,当点D在边BC上时,直接写出AC,CF,CD之间的关系。
初一数学第二学期培优3

AB C P R图(乙)A BC图(甲)AC DR图(乙)A CD 图(甲)2A.0B.1C.2D.3内折出 PCR ,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C= °. 5.探究(1)如图①∠1+∠2与∠B +∠C 有什么关系?为什么?(2)把图①△ABC 沿DE 折叠,得到图②,填空:∠1+∠2_______∠B +∠C(填“>”“<”“=”),当∠A =40°时,∠B +∠C +∠1+∠2=______(3)如图③,是由图①的△ABC 沿DE 折叠得到的,如果∠A =30°,则x +y =360°-(∠B +∠C +∠1+∠2)=360°- = , 猜想∠BDA +∠CEA 与∠A 的关系为图③5.如图,射线OX ⊥OY ,A 、B 为OX 、OY 上两动点,∠OAB 的平分线与∠ABO 的外角平分线所在直线交于点C 。
试问:∠C 的度数是否随点A 、B 的运动而发生变化?若变化,请说明理由;若不变化,求出∠C 的值.Y XCB OA6.如图①,在△ABC 中,AD ⊥BC 于D ,AE 平分∠BBAC . (1)若∠B=30°,∠C=70°,则∠DAE= ; (2)若∠C-∠B=30°,则∠DAE= ; (3)你能探求出∠DAE 与∠B 、∠C 之间的关系吗?;(4)如图②将点A 在AE 上移动到点F,FD ⊥BC 于点D,其他条件不变,那么(3)中的结论还成立吗?说明理由.(5)如图③,当∠C <∠B 时我们发现上述结论不成立,但为了使结论的统一与完美,我们不妨规定:角度也有正负,规定顺时针为正,逆时针为负.例如:∠DAE=-18°,则∠EAD=18°,作出上述规定后,上述结论还成立吗? ;若∠DAE=-7°,则∠B-∠C= °.图①FCDE BA 图②图③。
九年级数学培优3(有答案)

九年级数学培优33、轮船顺流航行时m 千米/小时,逆流航行时(m-6)千米/小时,则水流速度( B )A 、2千米/小时 B 、3千米/小时 C 、6千米/小时 D 、不能确定6、函数y=(m 2-1)x 2-(3m-1)x+2的图象与x 轴的交点情况是 ( C ) A 、当m ≠3时,有一个交点 B 、1±≠m 时,有两个交 C 、当1±=m 时,有一个交点 D 、不论m 为何值,均无交点7、如果两圆的半径分别为R 和r (R>r ),圆心距为d ,且(d-r)2=R 2,则两圆的位置关系是( B ) A 、内切B 、外切C 、内切或外切D 、不能确定11、若|x|=x ,则-x 一定是( D )A 、正数B 、非负数C 、负数D 、非正数 若|x|=x,则X 是零或正数, -X 则为零或负数,即为非正数。
所以,要选D 。
12、两个有理数的和除以这两个有理数的积,其商为0,则这两个有理数为( C ) A 、互为相反数 B 、互为倒数 C 、互为相反数且不为0 D 、有一个为024、反比例函数xy 2=,当x ≤3时,y 的取值范围是( C ) A 、y ≤32 B 、y ≥32 C 、y ≥32或y<0 D 、0<y ≤3228、若关于x 的方程21=+-ax x 有解,则a 的取值范围是( B ) A 、a ≠1 B 、a ≠-1 C 、a ≠2 D 、a ≠±129.下列图形中既是中心对称图形,又是轴对称图形的是( A ) A 、线段 B 、正三角形 C 、平行四边形 D 、等腰梯形 29、已知dcb a =,下列各式中不成立的是( C ) A 、dc b ad c b a ++=-- B 、d b c a d c 33++= C 、bd ac b a 23++= D 、ad=bc39.△ABC 的三边a 、b 、c 满足a ≤b ≤c ,△ABC 的周长为18,则( D ) A 、a ≤6 B 、b<6 C 、c>6 D 、a 、b 、c 中有一个等于638、△ABC 的三边a 、b 、c 满足a ≤b ≤c ,△ABC 的周长为18,则(C ) A 、a ≤6 B 、b<6 C 、c>6 D 、a 、b 、c 中有一个等于642、如图,把直角三角形纸片沿过顶点B 的直线BE (BE 交CA 于E )折叠,直角顶点C 落在斜边AB 上,如果折叠后得到等腰三角形EBA ,那么下列结论中(1)∠A=300(2)点C 与AB 的中点重合 (3)点E 到AB 的距离等于CE 的长,正确的个数是( D ) A 、0 B 、1 C 、2 D 、343、不等式6322+>+x x 的解是( C ) A 、x>2 B 、x>-2 C 、x<2 D 、x<-244、在一次函数y=2x-1的图象上,到两坐标轴距离相等的点有( B ) A 、1个 B 、2个 C 、3个 D 、无数个 49、把aa 1--(a 不限定为正数)化简,结果为( B )A 、aB 、a- C 、-aD 、-a-53、设a 、b 是方程x 2-12x+9=0的两个根,则b a +等于( C )A 、18B 、6C 、23D 、±23 54、下列命题中,正确的个数是( B )①等边三角形都相似 ②直角三角形都相似 ③等腰三角形都相似④锐角三角形都相似⑤等腰三角形都全等 ⑥有一个角相等的等腰三角形相似⑦有一个钝角相等的两个等腰三角形相似 ⑧全等三角形相似A 、2个B 、3个C 、4个D 、5个14、(2009黄石)已知二次函数y=ax 2+bx+c (a ≠0)的图象如图3所示, 下列结论:①abc >0 ②2a+b <0 ③4a -2b+c <0 ④a+c >0, 其中正确结论的个数为( C )39.已知二次函数c bx ax y ++=2的图象如图所示,下列结论:①0>abc ;② c a b +<;③ 024>++c b a ;④ b c 32<;⑤ )(b am m b a +>+,(1≠m 的实数)其中正确的结论有( )。
七年级上册数学培优专题训练3 定义新运算附解析学生版

七年级上册数学培优专题训练3 定义新运算附解析学生版一、单选题(共10题;共20分)1.(2分)如果规定符号“*”的意义为:a*b =a×ba+b,则2∗(−3)的值是( ) A .6 B .-6C .65D .-652.(2分)现定义一种新运算“*”,规定a ∗b =b 2−a ,如3∗1=12−3=−2,则(−2)∗(−3)等于( ) A .11B .-11C .7D .-73.(2分)规定新运算“⊕”: 对于任意实数a 、b 都有 a ⊕b =ab −a +b −1 ,例如: 2⊕5=2×5−2+5−1 , 则方 程 2⊕x =1 的解是( ) A .23B .1C .43D .534.(2分) 对于有理数 a , b ,定义 a ⊙b =2a −b ,则 [(x −y)⊙(x +y)]⊙3x 化简后得( ) A .−x +y B .−x −6y C .−x +6y D .−x +4y5.(2分)任意四个有理数a 、b 、c 、d ,定义了一种新运算:|a cb d |=ad −bc ,若|23x 1x|=6,则x 的值为( ) A .2B .3C .6D .−66.(2分)若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则 2017!2016! 的值为( )A .2017B .2016C .2017!D .2016!7.(2分)已知 C 32= 3×21×3=3, C 35= 5×4×31×2×3=10, C 64= 6×5×4×31×2×3×4=15,……观察以上计算过程,寻找规律.计算 C 85=( ) A .72B .56C .42D .408.(2分)已知:[x]表示不大于x 的最大整数.例:[3.6]=3,[﹣0.9]=﹣1,现定义:{x}=x ﹣[x],例:{1.6}=1.6﹣[1.6]=0.6,计算{4.9}﹣{﹣1.8}的结果为( ) A .6.7B .3.1C .1.1D .0.79.(2分)我们常用的十进制数,如2639=2×103+6×102+3×101+9,我国古代《易经》一书记载,远古时期,人们通过在绳子上打结来记录数量,如图,一位母亲在从右到左依次排列的绳子上打结,并采用七进制(如2513=2×73+5×72+1×71+3),用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )A .1435天B .565天C .365天D .13天10.(2分)已知有理数 a ≠1 ,我们把 11−a 称为 a 的差倒数,如:2的差倒数是 11−2=−1 ,-1的差倒数是 11−(−1)=12 .如果 a 1=−3 , a 2 是 a 1 的差倒数, a 3 是 a 2 的差倒数, a4 是a 3 的差倒数…依此类推,那么 a 1−a 2+a 3−a 4⋯+a 2017−a 2018+a 2019−a 2020 的值是( ) A .-3B .−114C .114D .1312二、填空题(共10题;共10分)11.(1分)规定一种新运算:a⊕b =a 2﹣2b ,若2⊕ [ 3 ⊕(﹣x )]=6,则x 的值为 12.(1分)如果定义新运算: a※b =a+b a−b(a ≠b) ,那么(1⊕2)⊕3的值为 .13.(1分)定义一种新运算“⊕”:对于任意有理数x 和y ,x⊕y= xy +a(x +y)+1 (a 为常数).例如:2⊕3=2×3+(2+3)a+1=5a+7.若2⊕(-1)的值为3,则a 的值为 .14.(1分)定义新运算:对于任意实数a ,b ,都有a⊕b =a (a ﹣b )+1,等式右边是通常的加法、减法及乘法运算,比如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5.则(﹣2)⊕3= .15.(1分)如图定义一种新运算“⊕”,如:2⊕1= 2+2×12=2;x⊕y =x+2yx,则(4⊕2)⊕(﹣1)= .16.(1分)已知a ,b 均为有理数,现我们定义一种新的运算,规定:a#b =a 2+ab ﹣5,例如:1#2=12+1×2﹣5=﹣2,则(﹣3)#6的值是 .17.(1分)已知a ,b 为有理数,如果规定一种新的运算“⊕”,规定:a⊕b =2b ﹣3a ,例如:1⊕2=2×2﹣3×1=4﹣3=1,计算:(3⊕2)⊕5= .18.(1分)符号“ Σ ”表示和,如 ∑4i=1a i =a 1+a 2+a 3+a 4 ,则 ∑3a i 5i=1−∑(2a i −3)5i=1−∑a i 5i=1= .19.(1分)符号“f ”表示一种运算,它对一些数的运算结果如下:①f(1)=0,f(2)=1,f(3)=2,f(4)=3,…;②f(12)=2,f(13)=3,f(14)=4,f(15)=5,….利用以上规律计算:f(12008)−f(2008)= .20.(1分)在计算1+3+32⋅⋅⋅+3100的值时,可设S =1+3+32+⋅⋅⋅+3100,①则3S =3+32+33+⋅⋅⋅+3101②.∴②-①,得2S =3101−1,所以S =3101−12,试利用上述方法求1+8+82+⋅⋅⋅+82004的值: .三、解答题(共9题;共96分)21.(5分)若“三角表示运算a ﹣b+c ,“方框” 表示运算x ﹣y+z+w.求:×表示的运算,并计算结果.22.(10分)已知x ,y 为有理数,现规定一种新运算“⊗”,满足x ⊗y =xy −2021.(1)(5分)求(2⊗5)⊗(−4)的值;(2)(5分)记P =a ⊗(b −c),Q =a ⊗b −a ⊗c ,请猜想P 与Q 的数量关系,并说明理由.23.(10分)设a ,b ,c ,d 为实数,则我们把形如|a bc d|的式子叫做二阶行列式,它的运算法则用公式表示为|abcd|=ad −bc ,请利用此法则解决以下问题: (1)(5分)求|12−12|的值; (2)(5分)若|231−x5|=22,求x 的值.24.(15分)用“⊕”定义一种新运算:对于任意有理数a 和b ,规定a⊕b =ab 2+2ab +a ,如:1⊕3=1×32+2×1×3+1=16.(1)(5分)求(-2)⊕3的值;(2)(5分)若( a+12 ⊕3)⊕ (−12) =8,求a 的值;(3)(5分)若2⊕x =m , (14x) ⊕3=n (其中x 为有理数),写出m ,n 的大小.25.(20分)用“⊕”定义一种新运算:对于任何有理数x 和y ,规定x⊕y ={2x +12y(x ≤y)y −12x(x >y).(1)(5分)求2⊕(﹣3)的值;(2)(5分)若(﹣a 2)⊕2=m ,求m 的最大整数;(3)(5分)若关于n 的方程满足:1⊕n =﹣32n ﹣2,求n 的值;(4)(5分)若−13A =13t 3−83t 2−2t −2,12B =−12t 3+2t 2+3t+1,且A⊕B =﹣2,求5+12t ﹣2t 3的值.26.(12分)对于有理数a ,b ,定义了一种新运算“⊕”为:a※b ={2a −b(a ≥b)a −23b(a <b),如:5⊕3=2×5﹣3=7,1※3=1−23×3=−1.(1)(1分)计算:①2⊕(﹣1)= ;②(-4)⊕(﹣3)= ; (2)(5分)若3⊕m =﹣1+3x 是关于x 的一元一次方程,且方程的解为x =2,求m 的值; (3)(5分)若A <B ,A =﹣x 3+4x 2﹣x+1,B =﹣x 3+6x 2﹣x+2,且A⊕B =﹣3,求2x 3+2x 的值.27.(7分)阅读下列材料,并解决下面的问题:我们知道,加减运算是互逆运算,乘除运算也是互逆运算,其实乘方运算也有逆运算,如我们规定式子23=8可以变形为log 28=3,log 525=2也可以变形为52=25.在式子23=8中,3叫做以2为底8的对数,记为log 28.一般地,若a n =b(a >0且a ≠1,b >0),则n 叫做以a 为底b 的对数,记为log a b(即log a b =n),且具有性质:①log a b n =nlog a b ;②log a a n =n ;③log a M +log a N =log a (M ⋅N),其中a >0且a ≠1,M >0,N >0. 根据上面的规定,请解决下面问题:(1)(1分)计算:log 31 ;log 1025+log 104(请直接写出结果); (2)(5分)已知x =log 32,请你用含x 的代数式来表示y ,其中y =log 372(请写出必要的过程).28.(10分)对于数轴上的两点P ,Q 给出如下定义:P ,Q 两点到原点O 的距离之差的绝对值称为P ,Q 两点的友好距离,记为(POQ ).例如:P ,Q 两点表示的数,如图1所示:则(POQ )=|PO ﹣QO |=|2﹣1|=1.(1)(5分)A ,B 两点表示的数,如图所示:①A ,B 两点的友好距离为 ▲ ;②若C 为数轴上一点(不与点O 重合),且(AOB )=2(AOC ),求点C 表示的数;(2)(5分)M ,N 为数轴上的两点(点M 在点N 左边),且MN =4,若(MON )=2,直接写出点N表示的数.29.(7分)定义:若A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离2倍,我们就称点C是[A,B]的美好点.例如;如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是[A,B]的美好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是[A,B]的美好点,但点D是[B,A]的美好点.如图2,M,N为数轴上两点,点M所表示的数为−7,点N所表示的数为2.(1)(1分)点E,F,G表示的数分别是−3,6.5,11,其中是[M,N]美好点的是;写出[M,N]美好点H所表示的数是.(2)(5分)现有一只电子蚂蚁P从点N开始出发,以2个单位每秒的速度向左运动.当t 为何值时,点P恰好为[N,M]的美好点?答案解析部分1.【答案】A【解析】【解答】解:由题意得:2∗(−3)=2×(−3)2+(−3)=−6−1=6,故答案为:A . 【分析】根据 a*b =a×ba+b, 计算求解即可。
数学培优3

数学培优(3)1、从甲地到乙地,某人步行比乘公交车多用3.6小时,已知步行速度为每小时8千米,公交车的速度为每小时40千米,设甲、乙两地相距x千米,则列方程为。
2、与铁路平行的一条公路上有一行人与骑自行车的人同时向南行进。
行人的速度是每小时3.6km,骑自行车的人的速度是每小时10.8km。
如果一列火车从他们背后开来,它通过行人的时间是22秒,通过骑自行车的人的时间是26秒。
⑴行人的速度为每秒多少米?⑵这列火车的车长是多少米?3、一次远足活动中,一部分人步行,另一部分乘一辆汽车,两部分人同地出发。
汽车速度是60千米/时,步行的速度是5千米/时,步行者比汽车提前1小时出发,这辆汽车到达目的地后,再回头接步行的这部分人。
出发地到目的地的距离是60千米。
问:步行者在出发后经过多少时间与回头接他们的汽车相遇(汽车掉头的时间忽略不计)4、一列火车匀速行驶,经过一条长300m的隧道需要20s的时间。
隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10s,根据以上数据,你能否求出火车的长度?火车的长度是多少?若不能,请说明理由。
5、甲、乙两地相距x千米,一列火车原来从甲地到乙地要用15小时,开通高速铁路后,车速平均每小时比原来加快了60千米,因此从甲地到乙地只需要10小时即可到达,列方程得。
6、甲、乙两人在400米长的环形跑道上跑步,甲分钟跑240米,乙每分钟跑200米,二人同时同地同向出发,几分钟后二人相遇?若背向跑,几分钟后相遇?7、工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.该工艺品每件的进价、标价分别是多少元?8、某车间有16名工人,每人每天可加工甲种零件5个或乙种零件4个.在这16名工人中,一部分人加工甲种零件,其余的加工乙种零件.•已知每加工一个甲种零件可获利16元,每加工一个乙种零件可获利24元.若此车间一共获利1440元,•求这一天有几个工人加工甲种零件.9、某蔬菜公司的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,•经粗加工后销售,每吨利润可达4500元,经精加工后销售,每吨利润涨至7500元,当地一家公司收购这种蔬菜140吨,该公司的加工生产能力是:如果对蔬菜进行精加工,每天可加工16吨,如果进行精加工,每天可加工6吨,•但两种加工方式不能同时进行,受季度等条件限制,公司必须在15天将这批蔬菜全部销售或加工完毕,为此公司研制了三种可行方案:方案一:将蔬菜全部进行粗加工.方案二:尽可能多地对蔬菜进行粗加工,没来得及进行加工的蔬菜,•在市场上直接销售.方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.你认为哪种方案获利最多?为什么?10、某家电商场计划用9万元从生产厂家购进50台电视机.已知该厂家生产3•种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案.(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,•销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,你选择哪种方案?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
培优训练3:化学(离子)方程式的书写
1.(2018·天津理综,7节选)下图中反应①是制备SiH4的一种方法,其副产物MgCl2·6NH3是优质的镁资源。
回答下列问题:
(1)在一定条件下,由SiH4和CH4反应生成H2和一种固体耐磨材料(写化学式)。
(2)为实现燃煤脱硫,向煤中加入浆状Mg(OH)2,使燃烧产生的SO2转化为稳定的Mg化合物,写出该反应的化学方程式:。
解析(1)由SiH4和CH4反应生成H2和一种固体耐磨材料,显然该耐磨材料为原子晶体SiC。
(2)煤燃烧产生的SO2与Mg(OH)2反应生成MgSO3,MgSO3具有还原性,易被空气中的氧气氧化为MgSO4,反应的化学方程式为2Mg(OH)2+2SO2+O2===2MgSO4+2H2O。
答案(1)SiC
(2)2Mg(OH)2+2SO2+O2===2MgSO4+2H2O
2.过二硫酸(结构如图)是一种白色晶体,其酸及盐均为强氧化剂。
(1)(NH4)2S2O8在水溶液中的电离方程式为。
(2)在Ag+及加热的条件下,S2O2-8可将溶液中的Mn2+氧化为MnO-4,该反应的离子方程式为
,观察到的现象是。
(3)由氯磺酸(ClSO3H)与过氧化氢作用可得固态的过二硫酸,该反应的化学方程式
为 。
解析 (2)由过二硫酸结构可知,分子中S 元素处于最高价+6价,其中的-1价
O 具有强氧化性,则离子方程式:5S 2O 2-8+2Mn 2++8H 2O=====Ag +
△2MnO -4+10SO 2-4+16H +,由于生成MnO -4,溶液会变为紫色。
答案 (1)(NH 4)2S 2O 8===2NH +4+S 2O 2-8
(2)2Mn 2++5S 2O 2-8+8H 2O=====Ag +△2MnO -4+10SO 2-4+16H + 溶液颜色变为紫色
(3)2ClSO 3H +H 2O 2===H 2S 2O 8↓+2HCl
3.无水氯化铝在生产、生活中应用广泛。
(1)氯化铝在水中的电离方程式为 。
(2)工业上用a g 铝土矿粉(主要成分为Al 2O 3,含有Fe 2O 3、SiO 2等杂质)制取无水
氯化铝的一种工艺流程如图所示:
已知:
物质
SiCl 4 AlCl 3 FeCl 3 FeCl 2 沸点/℃ 57.6 180(升华) 300(升华) 1 023
①步骤Ⅰ中焙烧时除了生成三种固体单质外,还可以使固体水分挥发、气孔数目
增多,其作用是 (要求写出两种),
步骤Ⅰ中生成非金属单质的反应的化学方程式
为 。
②步骤Ⅲ的尾气经冷却至室温后,用足量的NaOH 冷溶液吸收,写出吸收过程中
发生反应的离子方程式。
解析 (1)AlCl 3在水溶液中能完全电离,属于强电解质,电离方程式为AlCl 3===Al 3
++3Cl -。
(2)①步骤Ⅰ中焙烧时,固体水分挥发,可以防止后续步骤生成的AlCl 3
水解;气孔数目增多,可以增大步骤Ⅱ中反应物的接触面积,加快反应速率。
由
题意知,铝土矿粉中含有SiO 2杂质,SiO 2与焦炭在高温下反应生成单质Si ,故步
骤Ⅰ中生成非金属单质的反应的化学方程式为SiO 2+2C=====△Si +2CO ↑。
②步
骤Ⅲ的尾气经冷却至室温后,主要有Cl 2、O 2和CO 2,用足量的NaOH 冷溶液吸
收时,发生反应的离子方程式为Cl 2+2OH -===Cl -+ClO -+H 2O 和CO 2+2OH -
===CO 2-3+H 2O 。
答案 (1)AlCl 3===Al 3++3Cl -
(2)①防止后续步骤生成的AlCl 3水解;增大步骤Ⅱ中反应物的接触面积,加快反
应速率 SiO 2+2C=====△Si +2CO ↑
②Cl 2+2OH -===Cl -+ClO -+H 2O 、CO 2+2OH -===CO 2-3+H 2O
4.高铁酸钾(K 2FeO 4)是一种易溶于水,高效的多功能水处理剂。
工业上通常先制
得高铁酸钠,然后在一定温度下,向高铁酸钠溶液中加入KOH 至饱和,从而使
高铁酸钾析出。
(1)高铁酸钾中铁元素的化合价为 ,推测其具有的化学性质是 。
(2)高铁酸钾与水反应生成O 2、Fe(OH)3(胶体)和KOH 。
①该反应的离子方程式为 。
②高铁酸钾作为水处理剂起到的作用是 。
(3)①在无水条件下制备高铁酸钠的主要反应为2FeSO 4+a Na 2O 2===2Na 2FeO 4+
b X +2Na 2SO 4+
c O 2↑,该反应中物质X 的化学式为 ,b 与c 的关系
是 。
②一定温度下,向高铁酸钠溶液中加入KOH 至饱和可析出高铁酸钾,原因是 。
(4)在碱性条件下,由氯化铁、氯气可制备出高铁酸钾,写出该反应的离子方程式: 。
解析 (1)根据化合物中各元素化合价的代数和为零,可得铁元素的化合价为+6;
高铁酸钾中铁元素处于最高价态,则高铁酸钾具有强氧化性。
(2)①高铁酸钾与水
反应生成O 2,同时它本身被还原生成Fe(OH)3,反应的离子方程式为4FeO 2-4+
10H 2O===4Fe(OH)3(胶体)+8OH -+3O 2↑。
②高铁酸钾具有强氧化性,作为水处
理剂能起到杀菌消毒的作用,同时其还原产物为Fe(OH)3胶体,又能起到净水的作用。
(3)①根据元素守恒可知,X应是Na2O,根据钠元素守恒,有2a=8+2b,根据氧元素守恒有2a=8+b+2c,两式联立,可得b=2c。
②一定温度下,向高铁酸钠溶液中加入KOH至饱和可析出高铁酸钾,原因是该条件下高铁酸钾的溶解度小于高铁酸钠的溶解度。
(4)用氯气在碱性条件下氧化氯化铁可制备高铁酸钾,根据得失电子守恒、原子守恒及电荷守恒,反应的离子方程式为2Fe3++3Cl2+16OH-===2FeO2-4+6Cl-+8H2O。
答案(1)+6强氧化性(2)①4FeO2-4+10H2O===4Fe(OH)3(胶体)+8OH-+3O2↑②杀菌消毒、净水
(3)①Na2O b=2c②相同条件下高铁酸钾的溶解度小于高铁酸钠的溶解度
(4)2Fe3++3Cl2+16OH-===2FeO2-4+6Cl-+8H2O
5.铜是与人类关系密切的有色金属。
已知:常温下,在溶液中Cu2+稳定,Cu+易在酸性条件下发生反应:2Cu+===Cu2++Cu。
大多数+1价铜的化合物是难溶物,如Cu2O、CuI、CuCl、CuH等。
一定条件下,在CuSO4中加入NH5反应生成氢化亚铜(CuH)。
(1)已知NH5是离子化合物且所有原子都达到稀有气体的稳定结构,请写出NH5的电子式:。
(2)写出CuH在过量稀盐酸中有气体生成的反应的离子方程式:。
(3)将CuH溶解在适量的稀硝酸中,完成以下化学方程式:
CuH+HNO3=== Cu(NO3)2+H2↑++。
解析(1)NH5的所有原子都达到稀有气体的稳定结构,即氮原子的最外层达到8电子稳定结构,所有氢原子达到2电子稳定结构,说明NH5是由NH+4和H-组成
的离子化合物,电子式为。
(2)CuH溶解在稀盐酸中,CuH中的H失电子,盐酸中的H+得电子,产生的气体为氢气,酸性溶液中2Cu +===Cu2++Cu,故离子方程式为2CuH+2H+===Cu2++Cu+2H2↑。
(3)Cu+在酸
性条件下发生反应2Cu+===Cu2++Cu,稀硝酸具有强氧化性,能把铜氧化为硝酸铜,CuH具有还原性,因此二者反应生成氢气、一氧化氮气体、铜离子、H2O,其化学方程式为6CuH+16HNO3===6Cu(NO3)2+3H2↑+4NO↑+8H2O。
答案(1)
(2)2CuH+2H+===Cu2++Cu+2H2↑
(3)616634NO↑8H2O。
