第二章传输线理论
第2章传输线理论

j z
1 2Z0
(U1
I1Z0 )e
j z
(2―2―14)
同样可以写成三角函数表达式
U (z)
U1 cos z
jZ0
sin z
I
(
z)
j
U1 Z0
sin
z
I1
cos
z
(2―2―15)
第2章 传输线理论
三、入射波和反射波的叠加 由式(2―2―5)和式(2―2―6)两式可以看出,传输线 上任意位置的复数电压和电流均有两部分组成,即有
U (z)
A1e j z
A2e j z
Ui(z) Ur(z)
I
(z)ຫໍສະໝຸດ 1 Z0A1e j z
1 Z0
A2e j z
Ii(z)
Ir(z)
(2―2―16)
第2章 传输线理论
根据复数值与瞬时值的关系,并假设A1、A2为实数, 则沿线电压的瞬时值为
u(z,t) Re[U (Z )e ji ] A1 cos(t z) A2 cos(t z)
式中v0为光速。由此可见,双线和同轴线上行波电
压和行波电流的相速度等于传输线周围介质中的光速,
它和频率无关,只决定周围介质特性参量ε,这种波称为
无色散波。
第2章 传输线理论
(三) 相波长λp
相波长λp是指同一个时刻传输线上电磁波的相位相 差2π的距离,即有
p
2
vp f
vpT
0 r
(2―3―5)
第2章 传输线理论
这种路的分析方法,又称为长线理论。事实上,“场” 的理论和“路”的理论既是紧密相关的,又是相互补充 的。有些传输线宜用“场”的理论去处理,而有些传输 线在满足一定条件下可以归结为“路”的问题来处理, 这样就可借用熟知的电路理论和现成方法,使问题的处 理大为简化。
第二章-传输线理论

第二章 传输线理论
根据传输线上的分布参数是否均匀分布,可将其分为 均匀传输线和不均匀传输线。我们可以把均匀传输线分割
成许多小的微元段dz (dz<<λ),这样每个微元段可看作集 中参数电路,用一个Γ型网络来等效。于是整个传输线可
等效成无穷多个Γ型网络的级联
第二章 传输线理论
2 - 2 无耗传输线方程及其解 一、传输线方程
即:
( ) I (z) = Ii2e jβ z + Ir2e- jβ z = Ii2 e jβ z + e- jβ z = 2Ii2 cos β z
( ) u(z,t) =
2Ui2
sin
β
z cos ω t
+
φ 2
+π
2
i(z,t) =
2
Ii2
cos β
z cos(ω t
+
φ) 2
第二章 传输线理论
=
-
Ur (z) Ir (z)
=
R0 + jωL1 G0 + jωC1
对于无耗传输线( R0 = 0, G0 = 0 ),则
Z0 =
L1 C1
对于微波传输线 ,也符合。
平行双线 同轴线 特性阻抗
在无耗或低耗情况下,传输线的特性阻抗为一实数, 它仅决定于分布参数L1和C1,与频率无关。
第二章 传输线理论
l = (2n +1) λ (n = 0,1,2,)
4
1.传输线上距负载为半波长整数倍的各点的输入阻抗等于负载阻抗;
2.距负载为四分之一波长奇数倍的各点的输入阻抗等于特性阻抗的
平方与负载阻抗的比值;
3.当Z0为实数,ZL为复数负载时,四分之一波长的传输线具有变换阻 抗性质的作用。
第二章 传输线理论总结

当Z0为实数时,电压入射波与电流入射波的相位 相同;电压反射波与电流反射波相位相反。
三、 传输线的特性参数
1、特性阻抗Z0
将传输线上导行波的电压与电流之比定义为传输线的 特性阻抗, 用Z0来表示, 其倒数称为特性导纳, 用Y0来表
示。
由定义得 Z 0
R1 jL1 G1 jC1
可见特性阻抗Z0通常是个复数, 且与工作频率有关。 它由传输 线自身分布参数决定而与负载及信源无关, 故称为特性阻抗。
或者
二、传输线方程
2. 时谐均匀传输线方程
a. 时谐传输线方程
对于时谐电压和电流, 可用复振幅表示为 v(z, t)=Re[V(z)e jωt] i(z, t)=Re[I(z)e jωt] 将上式代入(2.1-1)式, 即得时谐传输线方程:
dV ( z ) ( R1 jL1 ) I ( z ) Z1 I ( z ) dz (2.1-3) dI ( z ) (G1 jC1 )V ( z ) Y1V ( z ) dz Z1 R1 jL1 传输线单位长度的串联阻抗 式中 传输线单位长度的并联导纳 Y1 G1 jC1
(2.1-11)
二、传输线方程
2. 时谐均匀传输线方程
c. 电压、电流的定解
V (d ) VL chd I L Z 0 shd VL I (d ) shd I L chd Z0
写成矩阵形式:
(2.1-12)
chd V (d ) I (d ) shd Z0
无耗线 j L1C1
低耗线
0, L1C1
(2.1-22)
R1 G1Z 0 c d 2Z 0 2
(2.1-23)
微波技术基础 第2章 传输线理论

内容提要
一、传输线基本概念
1、传输线的种类
2、分布参数及分布参数电路
二、传输线方程的解
1、传输线方程的解
2、入射波和反射波
三、传输线的特性参量
传播常数、特性阻抗、相速和相波长、输入阻抗、反
射系数、驻波比(行波系数)和传输功率
2020/1/23
1
西安电子科技大学
四、均匀无耗传输线工作状态的分析
,
a b
ad
D
a
W
, d
L1(H / m)
ln b 2 a
D D2 d2
ln
d
d
W
C1(F / m)
2 / ln b
a
/ ln D D2 d 2
d
W
d
R1( / m)
Rs
2
1 a
1 b
2Rs
d
2Rs W
G1(S / m)
数电路,用一个 型网络来等效。于是整个传输线可等效成 无穷多个 型网络的级联.
2020/1/23
6
西安电子科技大学
二、传输线方程
i(z,t)
L1 z
(z, t) R1 z
G1z
i(z z,t)
C1z (z z,t)
z
1) 一般传输线方程或电报方程
z,t z z,t z,t z
2
2
I (d ) VL ILZ0 e d VL ILZ0 e d I (d ) I (d )
2Z0
2Z0
V (d) ch d
I
(d
第2.1章 传输线理论

——→与低频状态完全不同。
第二章 传输线理论
传输线理论 长线理论
传输线是以TEM导模方式传 输电磁波能量。 其截面尺寸远小于线的长度, 而其轴向尺寸远比工作波长大 时,此时线上电压只沿传输线 方向变化。
一维分布参数电路理论
第二章 传输线理论
1)长线理论
传输线的电长度:传输线的几何长度 l 与其上 工作波长l的比值(l/l)。
当f =2GHz时
wLl = 2.3碬 3 / m > > Rl 10 wCl = 1.89S / m > > Gl
可忽略R和G的影响。——低耗线
第二章 传输线理论
P17表2.1-1给出了双导线、同轴线和平行板传输线的 分布参数与材料及尺寸的关系。
同轴线 a:内导体半径 b:外导体半径 m,e:填充介质 L(H/m)
①终端条件解:
边界条件: V (l ) = VL , I (l ) = I L
第二章 传输线理论
将上式代入解中: V = A e- g l + A e g l L 1 2
IL = 1 ( A1eZ0
gl
V ( z ) = A1e- g z + A2 eg z I ( z) = 1 ( A1e- g z - A2eg z ) Z0
第二章 传输线理论
2)时谐均匀传输线方程
a)时谐传输线方程 电压和电流随时间作正弦变化或时谐变化,则
电压电流的瞬时值可用复数来表示:
v ( z , t ) = V0 cos(wt + y v ( z )) = Re 轾 e jwt e jy v ( z ) = Re 轾( z )e j wt V0 V 犏 犏 臌 臌 i ( z , t ) = I 0 cos(wt + y I ( z )) = Re 轾e jwt e jy I ( z ) = Re 轾 z )e j wt I0 I( 犏 犏 臌 臌
第二章传输线理论2-Smith圆图

C
O
开路点(D点),其坐标为(1,0)
r , x , | |1, , 0
2019/9/19
D
8
(2) 圆图上有三条特殊线
圆图上实轴CD为X=0的轨迹,
右半轴为电压波腹点的轨迹,
线上的值为驻波比ρ读数
左半轴为电压波节点的轨迹,
线上的R值为行波系数K的读数
D
最 外 面 的 单 位 圆 为 R=0 的 纯
2019/9/19
18
例4
测量获得
Z SC in
j106,ZiOnC
j23.6
终端接负载后输入阻抗 Zin 25 j70 求负载阻抗?
解:Z0
Z Z SC OC in in
50
z SC in
j2.12
向电源
d
2
arctg
(
z SC in
)
0.18
Y d g jb
Z d r jx
2019/9/19
12
r
g 1
g
2
i2
1Leabharlann 1g
2
i b=1
b=0.5 容纳
电导圆方程
i g=1 g=2
2019/9/19
0
b=
shorted.c
0
b=0 open.
感纳 b=-0.5
电纳圆b=方-1程
1
2. 以系统不变量|Γ|作为Smith圆图的基底.在无耗传输线中,
|Γ|是系统的不变量。所以由|Γ|从0到1的同心圆作为Smith圆 图的基底,使我们可能在一有限空间表示全部工作参数Γ 、 和ρ。 Z (d )
第二章 传输线理论

b
b
d
a
b h( z ) ln (2.27a) a
I ( z ) H ( , z)d 2g ( z)(2.27b)
0
2
从式(2.27)消去式(2.26)中的h(z)和g(z),并代入同轴线的L、 C和G,则得到同轴线电报方程:
V ( z ) jLI ( z ) (2.28a) z I ( z ) (G jC )V ( z ) (2.28b) z
注意: 在传输线上提到的波长,往往是指的是传输线的波
导波长,它与自由空间的波长不一定相同,因此对应的相
速也不相同。
2.1.2 无耗传输线
无耗传输线,有
0
即
j j LC (2.12a)
由此可知传输线的特征阻抗有
L v Z0 Lv (2.13) C C
上式说明,只要求出传输线的单位长度电感、电容和相 速三者中的两个,就可以求出传输线的特征阻抗。
2.2.3 无耗同轴线的传播常数、特征阻抗和 功率流
由无耗传输线的条件
R0 G0
则电场和磁场的波动方程:
2 E z 2 H
2
E 0
2
z 2
2 H 0
传播常数、波阻抗和特征阻抗和功率流
LC ZW
V0 1 Z0 I 0 2
由: 可知:
V ( 0) ZL I ( 0)
负载阻抗的特性直接关系到传输线上反射波和入射波的
变化,从而影响到传输线参考面上总电压和总电流。 当端接负载等于传输线特征阻抗时,传输线上无反射。
微波技术基础
(2007版) 教材 《微波工程》第三版 (DAVID M.POZAR)
第二章 传输线理论

Microwave Technique
2、低频大损耗情况(工频传输线) j R jLG jC
L R,C G
RG ,
0,
Z0
R G
传输线上不呈现波动过程,只带来一定衰减,衰减α为常数。
3、高频小损耗情况:
L R, C G
2 1
图2.1 传输线的一个长度增量(a)电压电流(b)等效电路
在1处使用KVL:
v( z ,t ) Rzi(
z
,
t
)
Lz
i
z
,
t
v(
z
z
,
t
)
0
t
在2处使用KCL:
i( z ,t ) Gzv( z z,t ) Cz vz z,t i( z z,t ) 0
(2.10)
相速
vP
f
(2.11)
Microwave Technique
电报方程解的讨论
1、一般情况:(有耗)
V ( z) V (0)ez V_ (0)ez
I ( z) V (0) ez V (0) ez
Z0
Z0
YZ j R jLG jC
引言
Microwave Technique
基本概念
长线(long line):传输线几何长度与工作波长λ可比拟,需用分布参数 电路描述。 短线(short line):传输线几何长度与工作波长λ相比可忽略不计,可 用集总参数分析。 二者分界:l/λ > 0.05 分布参数(distributed parameter):R、L、C和G 。
电磁场课件第二章传输线的基本理论

1正弦时变条件下传输线方程
令信源角频率已知 ,线上的电压、电流皆为正弦时变规律(或称为谐变),这样具有普遍性意义。
2 方程的通解
典型波动方程的解 传播常数和波阻抗
3 已知信源端电压和电流时的解
求待定系数
边界条件
解的具体形式
用到的数学公式
4 已知负载端电压和电流时的解
边界条件 求待定系数
信号各频率成分的幅值传输过程中无变化(衰减常数)。
均匀无损耗传输线无频率失真,即为无色散系统。
一般情况,衰减常数及相移常数与频率关系复杂,是色散系统。
均匀无损耗传输特性
行波,没有反射波
驻波,反射波和入射波振幅相同
混合波
相向两列行波叠加结果
3 传输线上任一位置处的输入阻抗
传输线上任一位置处的输入阻抗定义为该点电压和电流的比值。
传输线是用以传输电磁波信息和能量的各种形式的传输系统的总称。
微波传输线是用以传输微波信息和能量的各种形式的传输系统的总称,它的作用是引导电磁波沿一定方向传输, 因此又称为导波系统, 其所导引的电磁波被称为导行波。
一、传输线的概念
1
一般将截面尺寸、形状、媒质分布、材料及边界条件均不变的导波系统称为规则导波系统, 又称为均匀传输线。
考察点位置,实际上和传输线长度有关,
在线电磁波的频率,
外接负载阻抗的阻抗,
传输线的波阻抗(特征阻抗)。
输入阻抗决定因素
输入阻抗和传输线相对长度关系
四分之一波长线:阻抗变换性 二分之一波长线:阻抗不变性 是无损耗传输线的一个重要特性
例2–1 均匀无损耗传输线的波阻抗75Ω,终端接50Ω纯阻负载,求距负载端0.25λ、0.5λ位置处的输入阻抗。若信源频率分别为50MHz、100MHz,求计算输入阻抗点的具体位置。
第二章 传输线理论

二、特性阻抗
无耗传输线
R0 0, G0 0
L0 Z0 C0
微波传输线
R0 L0 , G0 C0
L0 Z0 C0
在无耗或低耗情况下,传输线的特性阻抗为一实 数,它仅决定于分布参数L0和C0,与频率无关。
z
式中
R0 j L0 Z0 G0 jC0
R0 j L0 G0 jC0 j
二、传输线方程的解
1.已知传输线终端电压U2和电流I2,沿线电压电流表达式
U z A1e z A2e z 1 I z A1e输线种类
TEM波传输线
TE波和TM波传输线
表面波传输线
一、传输线种类
传输线的基本要求: 能量损耗小 传输效率高 功率容量大 工作频带宽 尺寸小且均匀 常用的微波传输线: 平行双线、波导、同轴线、带状线、微带线
1长线
定义:传输线的几何尺度与线上传输电磁 波波长比值大于或接近于1。
2-2 传输线方程及其解
一、传输线方程
传输线方程是研究传输线上电压、电流变化 规律及其相互关系的方程。
dz 段传输线的等效电路
一、传输线方程
u u t , z i i t , z
u z , t dz du z, t z 微分角度 di z , t i z , t dz z
分布电感效应: 高频电流会在导体周围产生高频磁场,磁 场也是沿线分布的,这就是分布电感效应
第二章 传输线理论(第二部分)

z = jx | Γ |=1
纯感性(pure inductive) ) 等电抗圆
匹配
朝 电 源
x>0 感性平面 开路
短路
朝 负 载
x < 0 容性平面
等电阻圆
实轴--纯阻性 实轴--纯阻性 --
z =r
SWR = r r > 1 SWR = 1 r <1 r
Microwave Technique
纯容性(pure capacitive) )
Smith 圆图
1939年由 年由Bell实验室的 实验室的P.H. Smith发明 年由 实验室的 发明 在形象化传输线现象和解决阻抗匹配问题时十分有用 Smith圆图是现在最流行的 圆图是现在最流行的CAD软件和测试设备的重要部分 圆图是现在最流行的 软件和测试设备的重要部分 本质上是Γ在极坐标中的图形(单位圆) 本质上是 在极坐标中的图形(单位圆) 在极坐标中的图形 任意阻抗值均能在Γ平面中找到相应的点 任意阻抗值均能在 平面中找到相应的点(4D) 平面中找到相应的点
反射系数Γ图 反射系数 图
反射系数图最重要的概念是相角走向。 最重要的概念是相角走向 反射系数图最重要的概念是相角走向。
Γ (l ) = ΓL e −2 jβl = ΓL e jθ
式中l是 处与参考面之间的距离,是向电源的。因此,向电源是反射系 式中 是z=0处与参考面之间的距离,是向电源的。因此,向电源是反射系 数的负角方向;反之,向负载是反射系数的正角方向 负角方向 是反射系数的正角方向。 数的负角方向;反之,向负载是反射系数的正角方向。 圆图上旋转一周为λ / (而不是λ )。 圆图上旋转一周为λg/2(而不是λg)。
Microwave Technique
第二章传输线理论1

双线
a
D
a
平板传输线
w d
L C
µ b ln 2π a
µ D arcch π 2a
πε ′
arcch( D / 2a)
Rs / π a
µd
W
2π ε ′ ln b / a
Rs 1 1 ( + ) 2π a b
ε ′W
d
2 Rs / W
ωε ′′W
d
R G
(1)
应用泰劳公式
∂u(z,t) u(z +dz,t) =u(z,t) + dz +L ∂z ∂i(z,t) i(z +dz,t) =i(z,t) + dz +L ∂z
∂u(z +dz,t) ∂u(z,t) ∂ u(z,t) = + dz +L 且 : 有 ∂z ∂z ∂z∂t
微波传输线, 其电路参数(R、 、 、 及 微波传输线 其电路参数 、L、C、G)及 电路物理量(u、i),都是沿线分布的 是 z,t 的 电路物理量 、 ,都是沿线分布的(是 , 函数),称之为分布参数电路, 函数 ,称之为分布参数电路,必须用传输线理 论来研究。 论来研究。
三、均匀传输线及其等效电路
例:设双导线的分布电感 L0=0.999nH/mm, 设双导线 分布电感 分布电容 C0=0.0111pF/mm ; 时引入的串联电抗 工作在 f= 50Hz时引入的串联电抗、并联导纳: 时引入的串联电抗、并联导纳:
XLf=50Hz=ωL=2πf L0=314×10-3µΩ /mm ω π × Bcf=50Hz=ωC=2πf C0 =3.49×10-12 S /mm ω π ×
用图2-4所示线上电压 或电流 用图 所示线上电压(或电流 随空间位置分布状况 所示线上电压 或电流)随空间位置分布状况 来说明长、短线的区别: 来说明长、短线的区别
微波技术第二章 传输线理论06

j2 z
L
e
j
L
2 z
L
e
j
EXIT
反射系数与阻抗的关系
输入阻抗与反射系数间的关系
Z in z U z I z U i z 1 z I i z 1 z Z0 1 z 1 z
z
j t
z
cos t z A 2 e
j t
cos t z = u i z , t u r z , t
i z , t Re I z e A1 Z0 e
z
A2 Z0 e
z
入射电压
cos t z
U z I z
.
.
A1 e 1 Z0
z
A2 e
z
z
A e
1
A2 e
z
式中,
Z0
R 0 j L 0 G 0 j C 0
R0
j L 0 G 0 j C 0 j
1 1
1
EXIT
第二章 传输线理论
传输线上反射波的大小,可用反射系数的模、驻波比 和行波系数三个参量来描述。 反射系数模的变化范围为 驻波比的变化范围为
,,
0 1
1
行波系数的变化范围为
0 K 1
传输线的工作状态一般分为三种: (1)行波状态 (2)行驻波状态 (3)驻波状态
j z j z
A2 A1
e
j2 z
微波技术 第二章 传输线基本理论
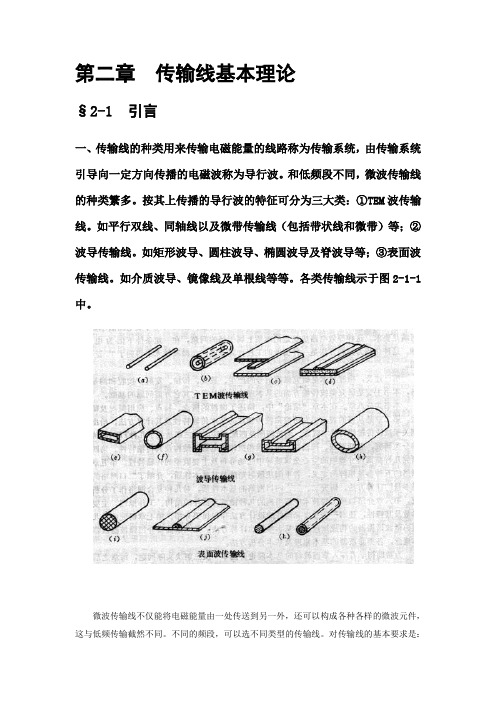
第二章传输线基本理论§2-1 引言一、传输线的种类用来传输电磁能量的线路称为传输系统,由传输系统引导向一定方向传播的电磁波称为导行波。
和低频段不同,微波传输线的种类繁多。
按其上传播的导行波的特征可分为三大类:①TEM波传输线。
如平行双线、同轴线以及微带传输线(包括带状线和微带)等;②波导传输线。
如矩形波导、圆柱波导、椭圆波导及脊波导等;③表面波传输线。
如介质波导、镜像线及单根线等等。
各类传输线示于图2-1-1中。
微波传输线不仅能将电磁能量由一处传送到另一外,还可以构成各种各样的微波元件,这与低频传输截然不同。
不同的频段,可以选不同类型的传输线。
对传输线的基本要求是:损耗小、效率高;功率容量大;工作频带宽;尺寸小且均匀。
二、分布参数的概念“长度”有绝对长度与相对长度两种概念。
对于传输线的“长”或“短”,并不是以其绝对长度而是以其与波长比值的相对大小而论的。
我们把比值称为传输线的相对长度。
在微波领域里,波长以厘米或毫米计。
虽然传输线的长度有时只不过是几十厘米甚至几个毫米,比如传输频率为3GHz的同轴电缆虽只有半米长,但它已是工作波长的5倍,故须把它称为“长线”;相反,输送市电的电力传输线(频率为50Hz)即使长度为几千米,但与市电的波长(6000千米)相比小得多,因此只能称为“短线”而不能称为“长线”。
微波传输线都属于“长线”的范畴,故本章又可称作长线的基本理论。
前者对应于低频率传输线。
它在低频电路中只起连接线的作用,因频率低,其本身分布参数所引起的效应过错全可以忽略不计,所以在低频电路中只考虑时间因子而忽略空间效应,因而把电路当作集中参数电路来处于是允许的。
后者对应于微波传输线。
因为频率很高时分布参数效应不能再忽视了,传输线不能仅当作连接线,它将形成分布参数电路,参与整个电路的工作。
因而传输线在电路中所引起的效应必须用传输线理论来研究。
亦即,在微波传输线上处处存在分布电阻、分布电感,线间处处存在分布电容和漏电电导。
第二章传输线理论

(3)传输线上电压和电流的通解: 对(2.1-3)再次取导数有
d 2V ( z ) dI ( z ) ( R1 jL1 ) Z1 (Y1V ( z )) Z1Y1V ( z ) 2 dz dz d 2 I ( z) dV ( z ) (G1 jC1 ) Y1Z1 I ( z( ) 2.1 6 ) 2 dz dz
(iii)信号源和负载条件解:如图所示已知始信号源的电 动式为EG,内阻为ZG,负载的阻抗为ZL
V ( z ) A1e Z A2 eZ V (0) V0 A1 A2 EG I 0 Z G (1) V (l ) VL A1e l A2 el ( 2) I ( z) 1 ( A1e Z A2 eZ ) Z0 1 ( A1 A2 ) I 0 Z 0 ( A1 A2 )(3) Z0 1 V ( A1e l A2 el ) L ( 4) Z0 ZL
另d l z , 表示从负载端接处向源 方向d处,则该处的电压和电 流可以表示为: VL Z 0 I L d VL Z 0 I L d V (d ) e e 2 2 V Z 0 I L d VL Z 0 I L d I (d ) L e e (2.1 11) 2Z 0 2Z 0
I (0) I 0
联立求解有: V Z0 I0 V Z0 I0 A1 0 , A2 0 2 2 对于传输线上任意一点 z处的电压和电流可以表 示为: V Z 0 I 0 z V0 Z 0 I 0 z V ( z ) A1e z A2 ez 0 e e 2 2 V Z 0 I 0 z V0 Z 0 I 0 z 1 I ( z) ( A1e z A2 ez ) 0 e e(2.1 14) Z0 2 2
传输线基本理论

平行双导线、同轴线的等效电路参数计算公式列于表 2-1。
表 2-1 平行双导线、同轴线的等效电路参数 R'、G'、L'和 C'
参数
同轴线
平行双导线
单位
R'
Rs
2π
1 a
+
1 b
Rs
πa
Ω/m
L'
µ 2π
ln(b
/
a)
µ π
ln (d
/
2a)
+
(d / 2a)2 − 1
H/m
2πσ
G'
ln(b / a)
有耗传输线方程的解
13
对于有损耗的情况,如果传播常数 k 与特征阻抗 Zc(或导纳 Yc)的定义为
jk = (R'+ jωL')(G'+ jωC')
1
Zc
= Yc
=
R'+ jωL' G'+ jωC'
那么传输线方程
dV (z) = −(R'+ jωL')I (z)
dz
dI (z) = −(G'+ jωC')V (z)
将上式代入传输线方程
∂V (z,
∂z
t
)
=
−
R'
I
(z,
t
)
+
L'
∂I
(z,
∂t
t
)
∂I
(z,
∂z
t
)
=
−G'V
(z,
t
)
电信传输原理及应用第二章 传输线理论 1

注:Z从终端起 从终端起
U ( z ) = U 2 chγ z + I 2 Z C shγ z
将A1, A2代入整理后可得 :
I ( z ) = U 2 shγ z + I 2 chγ z ZC
18
第2章 传输线理论
传输线方程的解 3
2. 已知传输线始端电压 1和电流 1,沿线电压电流表达式 已知传输线始端电压U 和电流I 这时将坐标原点z=0选在始端较为适宜。 这时将坐标原点 选在始端较为适宜。将始 选在始端较为适宜 端条件U 代入式, 端条件 (0)=U1, I (0)=I1代入式,同样可得沿线 的电压电流表达式为
其中横电磁波只存在于多导体系统中, 其中横电磁波只存在于多导体系统中,而横磁 波和横电波一般存在于单导体系统中, 波和横电波一般存在于单导体系统中,它们是 色散波。 色散波。
3
第2章 传输线理论
传输线的分类
TEM或准 或准TEM传输线: 传输线: 或准 传输线
4
第2章 传输线理论
13
第2章 传输线理论
均匀传输线的分布参数
14
第2章 传输线理论
均匀传输线方程及其稳态解
把均匀传输线分割成许多小的微元段dz (dz<<λ), 这样每个微元段可看作集中参数电路,用一个Γ 型网络来等效。于是整个传输线可等效成无穷多 个Γ 型网络的级联
15
第2章 传输线理论
11
第2章 传输线理论
分布参数电路
•某一双线传输线分布电感为 某一双线传输线分布电感为L=1nH/mm,分布电容 某一双线传输线分布电感为 , 为C=0.01pF/mm。 。 •在低频率f •在低频率f =50Hz 时, 传输线上每毫米引入的串联 在低频率 电抗和并联电纳分别为:X 电抗和并联电纳分别为 L=3.14×10e-7 /mm, × , Bc=3.14×10e-12 S/mm。可见,低频时分布参数很 × 。可见, 可忽略。 小,可忽略。 •当高频率为 =5×109Hz 时,XL=31.4 /mm, 当高频率为f × 当高频率为 , Bc=3.14×10e-4 S/mm。显然,此时分布参数不可忽 × 。显然, 略,必须加以考虑。 必须加以考虑。
传输线理论

几何长度l与工作波长λ相比可以忽略不计传输线, 用集总参数进行描述。应用电路理论分析。
分界线可认为是: l / 0.05
2.1.2 分布参数及传输线等效电路模型
Low frequencies(short line) wavelengths >> wire length current (I) travels down wires easily for efficient power transmission measured voltage and current not dependent on position along wire
集 总 参 数 电 路
分 布 参 数 电 路
2.1.2 分布参数及传输线等效电路模型 例
100Km长的高压线,工作频率50Hz,电长度 l / 0.017
---- 短线
1cm长的传输线,工作频率为3GHz,电长度 l / 0.1
---- 长线
2.1.2 分布参数及传输线等效电路模型 分布参数(distributed parameter)
➢可以从场的角度以某种TEM传输线导出 ➢可以从路的角度,由分布参数得到
采用电路理论分析 对时諧情况求通解
得到一般传输线方程 最后根据传输线端接条 件求出传输线方程定解
2.2.1 传输线方程
a.一般传输线方程
按照泰勒级数展开,并忽略高次项
应用基尔霍夫定律
v(z z,t) v(z,t) v(z,t) z z
第二章 传输线理论
本章学习提要:
❖又称一维分布参数电路理论,是微波电路设计 和计算的理论基础。
❖从路的观点研究传输线在微波运用下的传输特 性,讨论用史密斯圆图进行阻抗计算和阻抗匹 配的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
standing wave solution
V ( z ) = V o+ e − j β z + V o− e j β z I (z) = I e
+ o − jβ z
+I e
− o
jβ z
V o+ − jβ z V o− j β z e e = − Zo Zo
2-6
路
• Reflection coefficient (applications in measurement, radar, and remote sensing)
2-8
路
(derivation) 1 T 1 T v(z, t )i(z,t )dt = ∫ Re[V (z)e jwt ]Re[ I ( z)e jwt ]dt T ∫0 T 0 1 T1 1 = ∫ [V (z)e jwt + V * ( z)e− jwt ] [ I ( z)e jwt + I * ( z)e− jwt ]dt T 0 2 2 1 T = ∫ [V (z) I ( z)e j 2 wt + V * ( z) I * ( z)e− j 2 wt + V ( z) I * ( z) + V * ( z) I ( z)]dt 4T 0 T 1 1 = [V ( z) I * ( z) + V * ( z) I ( z)]∫ dt = 2Re[V ( z) I * ( z)]T 0 4T 4T 1 = Re[V ( z) I * ( z)] 2 1 1 1 = Re{[Vo+ e− jβz + Vo−e jβz ] [Vo+ e− jβz − Vo−e jβz ]*} = Re{[Vo+ e− jβz + Vo−e jβz ][Vo+*e jβz − Vo−*e− jβz ]} Zo 2 2Z o Pin (z) =
V − ( − l ) V o− e − jβ l Γ (−l ) ≡ + = + jβ l = Γ L e − j 2 β l = e − jβ l Γ L e − jβ l V (−l ) Vo e V o− ∵ Γ (0) = + ≡ Γ L Vo
• Input impedance (applications in circuit design) Z + jZ o tan β l V (−l ) = Zo L Z in ( − l ) ≡ I (−l ) Z o + jZ L tan β l
+ − o
wave
G + jwC
I o+
I o−
( derivation ) γ dV ( z ) = −γVo+ e − γz + γVo− e γz = − ( R + jwL ) I ( z ) → I ( z ) = (Vo+ e − γz + Vo− e γz ) dz R + jwL Vo+ − γz Vo− γz R + jwL =I ( z ) + I ( z ) = e + e ⇒ Zo = = Zo Zo γ 2-3
2-5
路
2.3 The terminated lossless transmission line
Zo
Source match
I(-l) Zo, Γs=0 + V(-l) Γ(-l) Z in ( − l ), Pin ( − l ) -l ΓL ZL
0 z Pinc (0) Pin (0), or Ptrans (0)
ΓL
e jβ l (1 + Γ L e j
ΓL
e − j 2β l )
e − j 2βl Γ L − 2 β l = π → V m in = V o+ (1 − Γ L )
Γ L − 2 β l = 0 → V m ax = V o+ (1 + Γ L ),
• Time-average input power flow
→ Z in (0) = Z in
( Z L + Z o ) e jβ l + ( Z L − Z o ) e − jβ l Z L ( e jβ l + e − jβ l ) + Z o ( e jβ l − e − jβ l ) e jβ l + Γ L e − jβ l = Z o jβ l = Zo = Zo e − Γ L e − jβ l ( Z L + Z o ) e jβ l − ( Z L − Z o ) e − jβ l Z L ( e jβ l − e − jβ l ) + Z o ( e jβ l + e − jβ l ) Z L cos β l + jZ o sin β l Z + jZ o tan β l = Zo L jZ L sin β l + Z o cos β l Z o + jZ L tan β l
e
0m
− αz
P + ( z ) = P + (0) e −2 αz
1m
z
2-4
路
2. phase constant phase velocity
β=
2π w = vp λ w β
wavelength group velocity
vp =
2π β d β −1 vg = ( ) dw λ=
3. characteristic impedance (wave impedance)
( derivation ) Z in
l=0
V o+ e jβ l + V o− e − jβ l V o+ e jβ l (1 + Γ L e − 2 jβ l ) 1 + Γ L e − 2 jβ l V (−l ) = = Z o + jβ l = Z o + jβ l = Zo I (−l ) V o e − V o− e − jβ l V o e (1 − Γ L e − 2 jβ l ) 1 − Γ L e − 2 jβ l Z − Zo 1+ ΓL V (0) ≡ ZL = Zo ⇒ ΓL = L I (0) 1− ΓL ZL + Zo
+ −
R + jwL G + jwC
路
time-domain solution v ( z,t ) = Vo+ e − αz cos( wt − βz + ∠ Vo+ ) + Vo− e αz cos( wt + βz + ∠ Vo− ) i ( z,t ) = I o+ e − αz cos( wt − βz + ∠ I o+ ) + I o− e αz cos( wt + βz + ∠ I o− )
Chapter 2 Transmission Line Theory
2.1 The lumped-element circuit model for a transmission line transmission line or telegrapher equation, traveling wave solution 2.3 The terminated lossless transmission line Zin, Γ, VSWR time-average power flow 2.4 The Smith chart Zin-plot conformal mapped on Γ-plot 2.5 The quarter-wave transformer frequency response, TDR 2.6 Generator and load mismatches impedance match, conjugate match 2.7 Lossy transmission lines low loss line, distortionless line perturbation method
= Zo
2-7
路
• Voltage standing wave ratio VSWR ≡ Vmax = 1 + ΓL
Vmin 1 − ΓL
V o+
( d eriva tio n ) V ( − l ) = V o+ e j β l + V o− e − j β l = V o+ e j β l (1 + Γ L e − j 2 β l ) = V o+ e j V ( − l ) = V o+ 1 + Γ L e j
incident
• Traveling wave solution
V ( z ) = V + ( z ) + V − ( z ) = Vo+ e − γz + Vo− e γz
I+(z) I(z)
I¯(z)
reflected wave
+ + + V V V+(z) V(z) V¯(z) I ( z ) = I + ( z ) + I − ( z ) = I o+ e − γz + I o− e γz = o e − γz − o e γz Zo Zo - + − V R + jwL Vo z ⇒ Z ≡ = = − o : characteristic impedance
Discussion: 1. attenuation constant
V + (1m) = V + (0m) e −α α = ln V + (0m) V (1m)
