平面的基本性质PPT课件

合集下载

【ppt课件】9[1].1.1《平面的基本性质》课件(1)(旧人教第二册下B)-精品文档

2．观察（1）、（2）、（3）三个图形，模型说明它们的位置关系有什么不同，并用字母表示各个平面．
(1)
(2)
(3)
3．请将以下四图中，看得见的部分用实线描出．
(1)
(2)
(3)
(4)
4．如图所示，用符号表示以下各概念： ①点A、B在直线a上； ②直线a在平面内 ③点O不在平面内；点C在平面内；直线b不在平面内；
b、绝对平
c、无限延伸性
4、点、线、面的位置关系（集合语言表示法）Q NhomakorabeaP
点A 在平面a内，
A

点Ｐ在直线l上，
Pl
Ql
点B 在平面a外， B
点Q不在直线l上，
直线 L 在平面 a 之外
(I) (II) L
L
A

l∥α
L A
直线L在平面a 内,

L
表示为：
L
直线a与b 相交于点A,
．

3、平面的空间感觉：（1）一个平面把空间分成_____________部分；
（2）二个平面把空间分成_____________部分；
（3）三个平面把空间分成_____________部分。
（4）正方体把空间分成______________部分
作业：绿书P5－7素质检测
练习： 1、书本P5 1－ 7
E
上
王新敞
奎屯新疆
A H D G B F C P
王新敞
奎屯
新疆
练习： 1．判断下列命题的真假，真的打“√”，假的打“×” （1）可画一个平面，使它的长为4cm，宽为2cm．（2）一条直线把它所在的平面分成两部分，一个平面把空间分成两部分．（3）一个平面的面积为20 cm2．（4）经过面内任意两点的直线，若直线上各点都在这个面内，那么这个面是平面．

新教材高中数学第八章立体几何初步8.4.1平面课件新人教A版必修第二册ppt

③
×
如三棱锥的四个顶点相连的四边形不能确定
一个平面
④
√
平面是空间中点的集合,是无限集
答案:④
4.设平面α与平面β交于直线l,A∈α,B∈α,且直线AB∩l=C,则
直线AB∩β=
.
解析:∵α∩β=l,AB∩l=C,∴C∈β,C∈AB,∴AB∩β=C.
答案:C
∴由基本事实3可知,点P在平面ABC与平面α的交线上,同理可
证Q,R也在平面ABC与平面α的交线上.
∴P,Q,R三点共线.
本例换为:如图所示,在正方体ABCD-A1B1C1D1中,设线段A1C
与平面ABC1D1交于点Q,如何说明B,Q,D1三点共线?
证明:如图所示,连接A1B,CD1.
显然B∈平面A1BCD1,D1∈平面A1BCD1.
④两条平行线确定一个平面
A.①②
B.②③
C.②④
D.③④
(2)两个平面若有三个公共点,则这两个平面(
A.相交
B.重合
C.相交或重合
D.以上都不对
)
解析:(1)不在同一条直线上的三点确定一个平面.圆上三个点
不会在同一条直线上,故可确定一个平面,∴①不正确,②正确.
当四点在一条直线上时不能确定一个平面,③不正确.根据平
且 P∈l
3.做一做:如图所示,在空间四边形各边AD,AB,BC,CD上分别
取E,F,G,H四点,如果EF,GH交于一点P,求证:点P在直线BD
上.
证明:∵EF∩GH=P,
∴P∈EF,且P∈GH.
又EF⊂平面ABD,GH⊂平面CBD,
∴P∈平面ABD,且P∈平面CBD,
即P∈平面ABD∩平面CBD,平面ABD∩平面CBD=BD,

平面的基本性质(2)(PPT)4-3

脂(松脂)混和加热。猪油和松树脂都是含碳的有机化合物，
推论
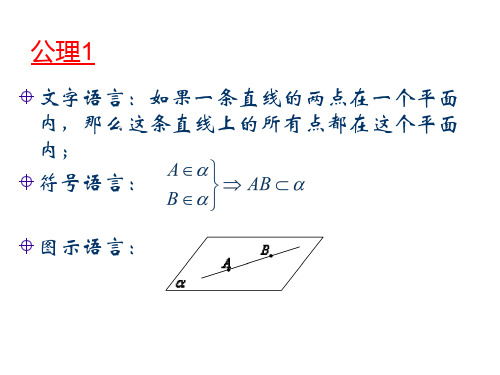
经过一条直线和直线外的一点有且只有一个平面；经过两条相交直线有且只有一个平面；经过两条平言：如果一条直线的两点在一个平面内，那么这条直线上的所有点都在这个平面内；符号语言：
图示语言：
直线和平面的位置关系
高三数学总复习攻略
色素沉着、角化过度或疣状增生，也可见白细胞减少或贫血。已公认长期接触砷化物可致皮肤癌和肺癌。急性经口中毒应及早洗胃，活性炭g，及氧化镁～ 4g或蛋清水(4只鸡蛋清加水杯拌匀)有助于除去胃内残余的砷化合物。二巯基丙磺酸钠、二巯基丁二酸钠有较好的解毒效果。慢性中毒者应停止砷接触，并积极驱砷治疗。车间空气中砷化物(三氧化；安馨3021 安馨3021 ；二砷和五氧化二砷最高容许浓度为.mg/m;地面水最高含砷量不得超过.4mg/L;大气日平均最高容许浓度为.mg/m。 [4] 发现简史编辑含砷矿石含砷矿石古代罗马人称砷的硫化物矿叫auripigmentum。"auri"表示"金黄色"，"Pigmentum"是指"颜料"；二者组合起来就是"金黄色的颜料"。这首先见于世纪罗马博物学家普林尼的著作中。今天英文中雌黄的名称orpiment 正由这一词演变而来的。 [] 世纪希腊医生第奥斯科里底斯叙述焙烧砷的硫化物以制取三氧化二砷，用于医药中。 [] 三氧化二砷在中国古代文献中称为砒石或砒霜。这个"砒"字由"貔"而来。貔传说是一种吃人的凶猛野兽。这说明中国古代人们早已认识到它的毒性，常常出现在中国古典小说和戏剧中。 [] 小剂量砒霜作为药用在中国医药书籍中最早出现在公元 7年宋朝人编辑的《开宝本草》中。 [] 世纪中叶中国北魏末期农学家贾思勰(xie)编著的农学专著《齐民要术》中讲到：将雄黄、雌黄研成粉末，与胶水泥和，浸纸可防虫蠹(dU)(蛀虫)。明末宋应星编著的《天工开物》中讲到三氧化二砷在农业生产中的应用："陕、洛之间，忧虫蚀者，或以砒霜拌种子……" [] 将黄色砷的硫化物在空气中焙烧后就转变成白色的三氧化二砷。这种明显的物质间的转变引起中外炼金术士和炼丹家的兴趣。西方炼金术士们把雌黄称为帝王黄，用蛇作为砷的符号。 [] 中国炼丹家称硫磺、雄黄和雌黄为三黄，视为重要的药品。公元4世纪前半叶中国炼丹家、古药学家葛洪(～年)在《抱朴子内篇》卷十一《仙药》中记述着："又雄黄……饵服之法，或以蒸煮之；或以酒饵；或先以硝石化为水，乃凝之；或以玄胴肠裹蒸于赤土下；或以松脂和之；或以三物炼之，引之如布，白如冰。……。这是葛洪讲述服用雄黄的方法：或者蒸煮它，或者用酒浸泡，或者用硝酸钾(硝石)溶液溶解它。用硝酸钾溶解它会生成砷酸钾KAsO4，受热会分解生成三氧化二砷AsO，砒霜。或者与猪油(玄胴肠或猪大肠)共热；或者与松树

高B数学必修二课件平面的基本性质与推论

空间向量的线性运算
空间向量的加法运算
空间向量的减法运算
空间向量加法运算遵循平行四边形法则或三角形法则。两个空间向量相加，其和向量也是一个空间向量，其大小等于两个向量的大小之和，方向遵循平行四边形法则或三角形法则。
空间向量减法运算遵循三角形法则。两个空间向量相减，其差向量也是一个空间向量，其大小等于两个向量的大小之差，方向遵循三角形法则。
直线在平面内的判定
判定定理
如果一条直线上的两个点在平面内，则这条直线在平面内。
推论
如果一条直线与一个平面有一个公共点，且这条直线在平面内，则这条直线完全在平面内。
直线与平面平行的判定与性质
判定定理
如果一条直线与一个平面没有公共点，则这条直线与这个平面平行。
性质定理
如果一条直线与一个平面平行，那么过这条直线的任一平面与这个平面的交线与这条直线平行。
空间向量在平面几何中的拓展应用
01
向量在解析几何中的应用
通过向量的坐标表示和运算，可以建立平面解析几何的基本概念和性质
，如直线的方程、圆的方程等。
02
向量在物理中的应用
向量在物理中有着广泛的应用，如力、速度、加速度等都是向量，通过
向量的运算可以解决物理中的实际问题。
03
向量在计算机图形学中的应用
计算机图形学是研究计算机生成和操作图形的科学，向量在计算机图形
学中有着重要的应用，如向量的线性变换可以实现图形的缩放、旋转和
平移等操作。
06
总结与展望
平面的基本性质与推论的总结
平面的基本性质
平面是无限延展的，没有边界；平面内任意两点可以确定一条直线，且该直线在平面内；不在同一直线上的三点确定一个平面。

平面的基本性质及三大公理ppt课件

直线与平面的关系：l ,l
如果要把一根木条固定在墙面上,至少需要几个钉子?
文公理1:如果一条直线上的
字两个点在平面内,那么这条
语言
直线上所有的点都在这个图形语言
平面内.
符
α AB
号
Al, B l, A, B
直AB
语言
关键词: 两作点用, ：用所有来证明或
证明： AB , AC
B,C BC
你骑车放学回家了,到家时如何才能把自行车停稳?
B
A
C
公理２经过不在同一直线上的三点有且只有一个平面.
B
α 。A
C
表示为:
A、B、C不共线 A、B、C确定一个平面 .
推论1:过直线和直线外一点,有且只有一个平面.
推论2:过两条相交直线,有且只有一个平面 .
例题
一、平面的概念
平面和点、直线一样,它是构成空间图形的基本要素之一，是一个只描述而不定义的原始概念.
(1)数学中所说的平面在空间是无限伸展的（直线是无限延伸的）
(2)平时接触到的平面实例都只是平面的一部分
1.平面的基本概念:
几何里的平面的特征:
1.平 2.无限延展 3.不计厚薄
（不是凹凸不平）（没有边界）
（没有质量）
二、平面的画法
直线是无限延伸的,通常我们画出直线的一部分来表示直线,同样地,我们也可以画出平面的一部分来表示平面.
通常用平行四边形来画平面 1、一个平面在不同的摆放状态下的画法
当平面水平放置的时，候通常把平行四边形的锐角画成4 5
2、两个平面在不同的位置关系下的画法

平面的基本性质ppt8 人教课标版

苏教版高中数学教材必修2 第1章立体几何初步
1.2 点、线、面之间的位置关系
平面的基本性质
公理1常用于判定点在面内： P∈l，l⊂P∈．公理2常用于：
①找两平面的交线；
②判定点在线上： P∈，P∈，且∩＝l P∈l．
苏教版高中数学教材必修2 第1章立体几何初步
1.2 点、线、面之间的位置关系
苏教版高中数学教材必修2 第1章立体几何初步
1.2 点、线、面之间的位置关系
推论1证明二：在直线l上任取两点A，B． ∵P∈l ∴A，B，P确定一个平面．
又A∈l，B∈l，A∈，B∈，
∴l⊂．故直线l和点A确定一个平面．
苏教版高中数学教材必修2
第1章立体几何初步
1.2 点、线、面之间的位置关系
苏教版高中数学教材必修2
第1章立体几何初步
1.2 点、线、面之间的位置关系
练习：
1．两个平面重合的条件是（ D ）
A．有三个公共点
B．有无数多个公共点 C．有一条公共直线 D．有三个公共点，且三点不共线
苏教版高中数学教材必修2
第1章立体几何初步
1.2 点、线、面之间的位置关系
2．下列命题中正确的个数为（ C ） a．三点确定一个平面；b．过三点至少有一个平面；c．四条线段顺次首尾连接，所得图形必为平面图形；d．两两平行的三条直线必在同一平面内；e．两两相交的三条直线必在同一平面内；f．在空间，两组对边分别平行的四边形是平行四边形；g．在空间，两组对边分别相等的四边形是平行四边形； h．梯形为平面图形． A． 1 个 B．2个 C． 3 个 D． 4 个
苏教版高中数学教材必修2 第1章立体几何初步
1.2 点、线、面之间的位置关系

《平面的基本性质》课件

平面解析几何在实际问题中的应用案例
物理学中的应用
在物理学中，许多概念和公式可以通过平面解析几何来描述和解释，例如力学、电磁学和光学中的许多概念。
工程学中的应用
在工程学中，平面解析几何被广泛应用于机械设计、建筑设计、航空航天等领域。
计算机图形学中的应用
在计算机图形学中，平面解析几何是生成和处理二维图形的基础，例如在游戏开发、动画制作和计算机视觉等领域的应用。
THANKS FOR WATCHING
感谢您的观看
平面与几何体的关系
总结词
平面是几何体的重要组成部分，它可以作为几何体的边界或表面。
详细描述
在几何学中，许多常见的几何体都是由平面构成的。例如，长方体的每个面都是一个平面，球体的表面也是一个平面。此外，平面还可以用来定义其他几何体的形状和大小，例如通过平面的交线来定义三维空间的形状。
CHAPTER 02
平面上的直线的方程
两点式方程
通过平面上两点的坐标，可以求出直线的方程。
点斜式方程
已知直线上的一个点和直线的斜率，可以求出直线的方程。
平面上的点与直线的位置关系
点在直线上
如果一个点的坐标满足直线的方程，则该点在直线上。
点在直线外
如果一个点的坐标不满足直线的方程，则该点在直线外。
CHAPTER 04
与线性代数的联系
线性代数提供了研究平面几何对象（如向量、矩阵和线性变换）的工具。
平面解析几何的发展历程与未来展望
发展历程
从早期的欧几里得几何到文艺复兴时期的笛卡尔几何，再到现代的解析几何，平面解析几何经历了漫长的发展历程。
未来展望
随着数学和其他学科的发展，平面解析几何将继续发展，与其他数学分支的交叉将更加深入，新的研究方法和视角也将不断涌现。

中职教育数学《平面及基本性质》课件

例、求证三角形ABC的三条边在同一个平面内。
方法：利用推论２
Ｂ
Ｃ
题目变型：两两相交且不过同一点的三条直线共面。
如图，在长方体ＡＢＣＤ－Ａ１Ｂ１Ｃ１Ｄ１中，
Ｐ为棱ＢＢ１的中点，画出由Ａ１，Ｃ１，Ｐ三点所确定
的平面与长方体表面的交线．
分析：因为点Ｐ既在平面
证明：设直线a、b满足a平行于b ，由平行线的定义，直线a、b在同一平面内，这就是说，过直线a、b有平面α。
设点A为直线a上任一点，则点A在直线b外，点A 和直线b在过直线a、b的平面α内，由公理3的推论1，过点A和直线b的平面只有一个。过直线a、b的平面只有一个。
反馈练习
1、选择题:
D （１)两个平面的公共点的个数可能有......( )
图形语言：通常用平行四边形来表示平面．
D
C
A
B
平面α、平面AC 、平面ABCD
表示：1、通常用希腊字母 , , 等来表示，如：
平面，2、用表示平行四边形的两个相对顶点的字母来表示，如：平面AC．3、用平面的顶点字母表示，如平面ABCD
(1) 当平面是水平放置的时候，通常把平行四边形的锐角画成45°，横边画成邻边长的2倍。
A
B
(2)点与平面的位置关系：
点A在平面α内：记为：A∈α
点B不在平面α上：记为：B∈ α α
B A
文字叙述
图形表示
符号表示
直线l在平面α内
l α
直线l在平
l
l
面α外
α
α
直线l1 l2交于点Ｐ
平面α 、 ß相交于直线 l
P l1
l2
l
l l1 l2 P

《平面的基本性质》公开课课件

平面的基本性质
复习回顾
公理 1 如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内．
Al, B l, A, B l
公理2 如果两个平面有一个公共点，那么它们还有其他公共点，且所有这些公共点的集合是一条过这个公共点的直线。
公理3 经过不在同一条直线上的三点，有且只有一个平面
五、【小结】
1.公理3的三个推论：推论1 经过一条直线和这条直线外的一点，有且只有一个平面推论2 经过两条相交直线，有且只有一个平面推论3 经过两条平行直线，有且只有一个平面 2.公理3及其三个推论的作用是确定平面 3.证明若干个点、线共面的方法． (Байду номын сангаас证其中某些点、线确定一个平面,再证剩余点、线落在此平面内)
AB α.(公理1)同理BC α，AC α，所以AB，BC，
CA三直线共面.
证共面问题，可先由公理3（或推论）证某些元素确定一个平面，再证其余元素都在此平面内；或者指出给定的元素中的某些元素在一个平面内，再证两个平面重合．
怎样的直线a我们就说它在平面外？
推论3 经过两条平行直线，有且只有一个平面
推论1 经过一条直线和这条直线外的一点，有且只有一个平面推论2 经过两条相交直线，有且只有一个平面推论3 经过两条平行直线，有且只有一个平面
例题讲解
例1 直线AB、BC、CA两两相交，交点分别为A、B、C，判断这三条直线是否共面，并说明理由。(如图)
所以经过点A和直线a有且只有一个平面
例题讲解
解法二:因为A在直线BC外，所以过点A和直线BC确定
平面α.(推论1)，因为A∈α，B∈BC，所以B∈α.故AB α，同理AC α，所以AB，AC，BC共面.

平面的基本性质(2)课件

4条直线相交于一点时：条直线相交于一点时： (3)每 (3)每2条直线都 (1)4条直线 (1)4条直线确定一平面时全共面时
(2)有3条直线有条直线共面时三条直线相交于一点, 三条直线相交于一点,用其中的两条确定平面,最多可以确定可以确定6 确定平面,最多可以确定6个。
2个平面分空间有两种情况：个平面分空间有两种情况：个平面分空间有两种情况 (1)两平面没有 (1)两平面没有 (2)两平面有公 (2)两平面有公公共点时共点时
练习5 练习
有公共点， ① ×若直线 a 与平面 α 有公共点，则称 aα ②两个平面可能只有一个公共点． ×两个平面可能只有一个公共点． ③四条边都相等的四边形是菱形． ×四条边都相等的四边形是菱形．
（２）已知空间四点中，无三点共线，则可确定已知空间四点中，无三点共线， A．一个平面． B．四个平面．
α 内,但不在平面 β 内但不在平面
新疆王新敞
奎屯
α
α
α
2.正方体的各顶点如图所示， 2.正方体的各顶点如图所示，正方体的三正方体的各顶点如图所示个面所在平面 A1C1 , A1 B, B1C 分别记作 α、β、γ 试用适当的符号填空。试用适当的符号填空。
(1)A _______, B1 _______ α α 1
复习提问
点A在直在直线a上上点A在直在直线a外外点A在平在平面α内内点A在平在平面a外外
●
A
●
a
A∈a ∈ a A
A
a
●
α
A A
●
A∈α
Aα
元素（点）与集合（直线与平面）与平面）之间的关系

平面基本性质第二课时PPT课件

因为点A、B、C分别在直线a、b上，所以它们在过a、 b的平面内。由由公理3，过A、B、C三点的平面只有一个，过直线a、b的平面只有一个。
平面的基本性质推论3:经过两条平行直线，有且只有一个平面.
b
a
a // b 有且只有一个平面，使a ,b
推论3 经过两条平行直线，有且只有一个平面
（3）空间四点中，三点共线是这四个点共面的( ) A．充分但不必要条件 B．必要但不充分条件 C．充分必要条件 D．既非充分条件，也非必要条件
直 l在线内平l，面，记 l不直作在内线平 l，；
直 l 和线 m 相直 A ，交线 l m 记于 A （ A 是作点 A 的简
直 l于线平相面交 A ，于 l记点 A 作
平与面平相面交l，与记直作线 l。
公理1:如果一条直线上的两个点在平面内,那么这条直线上所有的点都在这个平面内.
AB
符号语言作用
怎样的直线a我们就说它在平面外？
平面的基本性质
公理2:如果两个平面有一个公共点，那么它们还有其他的公共点，且所有的这些点的集合是一条过这个点的直线
符号语言作用
l
P
平面的基本性质公理3:经过不在同一条直线上的三个点，有且只有一个平面.
推论1 经过一条直线和这条直线外的一点，有且只有一个平面
求证：过点A和直线a可以确定一个平面
唯一性: 如果经过点A和直线a的平面还有一个平面β，那么
A∈β， a β，因为B∈a，C∈a，所以B∈β，C∈β.(公理1)故不
共线的三点A，B，C既在平面α内又在平面β内.所以平面α和平面 β重合.(公理3)
（A）0 （B）1 （C）2 （D）０或无数

人教版高中数学平面(共22张PPT)教育课件

①直线 AC1在平面 CC1B1B内；错误
C D
B A
C1 D1
B1 A1
在正方体 AB 中A C 1 ，B 1 C 判1 D D 1 断下列命题是否正确，并说明理由：
③由点A，O，C可以确定一个平面；错误
C
D
O
B A
C1 D1
B1 A1
5、在正方体 ABA C 1B 1 C 1 D D 1中，判断下列命题是否正确，并说明理由：
人
的
一
生
说
白
了
，
也
就
是
三
万
余
天
，
贫
穷
与
富
贵
，
都
是
一
种
生
活
境
遇
。
懂
得
爱
自
己
的
人
，
对
生
活
从
来
就
没
有
过
高
的
奢
望
，
只
是
对
生
存
的
现
状
欣
然
接
受
。
漠
漠
红
尘
，
芸
芸
众
生
皆
是
客
，
时
光
深
处
，
流
年
似
水
，
转
瞬
间
，
光
阴
就
会
老
去
，
留
在
心
头
的
，
只
是
弥
留
在
时

平面的基本性质.ppt

于是可得到 M∈面 ABD∩面 BCD＝BD. 即点 M 在直线 BD 上。
有关共面、共线、共点问题的证明方法 1．证明共面问题证明共面问题，一般有两种证法：一是由某些元素确定一个平面，再证明其余元素在这个平面内；二是分别由不同元素确定若干个平面，再证明这些平面重合． 2．证明三点共线问题证明空间三点共线问题，先考虑两个平面的交线，再证有关的点都是这两个平面的公共点．或先由某两点作一直线，再证明其他点也在这条直线上． 3．证明三线共点问题证明空间三线共点问题，先证两条直线交于一点，再证明第三条直线经过这点，把问题转化为证明点在直线上的问题．而这条直线往往归结为平面与平面的交线．
A, B, C三点不共线
B A
C
有且只有一个平面，使A , B , C
基本性质3：如果不重合的两个平面有一个公共点，那么它们有且只有一条过这个点的公共直线。符号语言：
P P
l且P l
四、跟踪训练巩固新知
问题4：（教材 P38—3）一扇门，可以想象成平面的一部分，通常用两个合页把它固定在门框的一边上，当门不锁上的时候，可以自由转动，如果门锁上，则门就固定在墙面上，这个事实说明平面具有哪条基本性质?
五、小结归纳布置作业
课堂小结：
1、平面的基本性质、推论及应用：
2、有关共面、共线、共点问题的证明方法
作业： 1、教材P38----A组、 B组 2、学案
基本性质1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内. B A A 符号语言：直线 AB B 基本性质2：经过不在同一条直线上的三点，有且只有一个平面。符号语言：
4、（教材P37——思考与讨论变式）