标数法C版

合集下载

标数法

一、加法原理概念引入生活中常有这样的情况，就是在做一件事时，有几类不同的方法，而每一类方法中，又有几种可能的做法．那么，考虑完成这件事所有可能的做法，就要用加法原理来解决．例如:王老师从北京到天津，他可以乘火车也可以乘长途汽车，现在知道每天有五次火车从北京到天津，有4趟长途汽车从北京到天津．那么他在一天中去天津能有多少种不同的走法？分析这个问题发现，王老师去天津要么乘火车，要么乘长途汽车，有这两大类走法，如果乘火车，有5种走法，如果乘长途汽车，有4种走法．上面的每一种走法都可以从北京到天津，故共有5+4=9种不同的走法．在上面的问题中，完成一件事有两大类不同的方法．在具体做的时候，只要采用一类中的一种方法就可以完成．并且两大类方法是互无影响的，那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数．二、加法原理的定义一般地，如果完成一件事有k 类方法，第一类方法中有1m 种不同做法，第二类方法中有2m 种不同做法，…，第k 类方法中有k m 种不同做法，则完成这件事共有12 k N m m m =+++……种不同方法，这就是加法原理．加法原理运用的范围：完成一件事的方法分成几类，每一类中的任何一种方法都能完成任务，这样的问题可以使用加法原理解决．我们可以简记为：“加法分类，类类独立”．分类时，首先要根据问题的特点确定一个适合于它的分类标准，然后在这个标准下进行分类；其次，分类时要注意满足两条基本原则：① 完成这件事的任何一种方法必须属于某一类； ② 分别属于不同两类的两种方法是不同的方法．知识要点第8讲标数法只有满足这两条基本原则，才可以保证分类计数原理计算正确．运用加法原理解题时，关键是确定分类的标准，然后再针对各类逐一计数．通俗地说，就是“整体等于局部之和”．三、加法原理解题三部曲1、完成一件事分N 类；2、每类找种数（每类的一种情况必须是能完成该件事）；3、类类相加树形图法、标数法及简单的递推一、树形图法“树形图法”实际上是枚举的一种，但是它借助于图形，可以使枚举过程不仅形象直观，而且有条理又不重复遗漏，使人一目了然．【例 1】（难度等级 ※※※）A 、B 、C 三个小朋友互相传球，先从A 开始发球(作为第一次传球)，这样经过了5次传球后，球恰巧又回到A 手中，那么不同的传球方式共多少种？(2005年《小数报》数学邀请赛)【解析】如图，A 第一次传给B ，到第五次传回A 有5种不同方式．同理，A 第一次传给C ，也有5种不同方式．所以，根据加法原理，不同的传球方式共有5510+=种．C B CC B AAB A B CCBA【巩固】（难度等级 ※※※）一只青蛙在A ，B ，C 三点之间跳动，若青蛙从A 点跳起，跳4次仍回到A 点，则这只青蛙一共有多少种不同的跳法？【解析】 6种，如图，第1步跳到B ，4步回到A 有3种方法；同样第1步到C 的也有3种方法．根据加法原理，共有336+=种方法．AA A BCAB C BA【例 2】（难度等级 ※※※）甲、乙二人打乒乓球，谁先连胜两局谁赢，若没有人连胜头两局，则谁先胜三局谁赢，打到决出输赢为止．问：一共有多少种可能的情况？【解析】如下图，我们先考虑甲胜第一局的情况：图中打√的为胜者，一共有7种可能的情况．同理，乙胜第一局也有 7种可能的情况．一共有 7＋7=14（种）可能的情况．二、标数法适用于最短路线问题，需要一步一步标出所有相关点的线路数量，最终得到到达终点的方法总数．标数法是加法原理与递推思想的结合．【例 3】（难度等级 ※※）如图所示，沿线段从A 到B 有多少条最短路线？GFE D C BA111064332111AB【解析】图中B 在A 的右上方，因此从A 出发，只能向上或者向右才能使路线最短，那么反过来想，如果到达了某一个点，也只有两种可能：要么是从这个点左边的点来的，要么是从这个点下边的点来的．那么，如果最后到达了B ，只有两种可能：或者经过C 来到B 点，或者经D 来到B 点，因此，到达B 的走法数目就应该是到达C 点的走法数和到达D 点的走法数之和，而对于到达C 的走法，又等于到达E 和到达F 的走法之和，到达D 的走法也等于到达F和到达G的走法之和，这样我们就归纳出：到达任何一点的走法都等于到它左侧点走法数与到它下侧点走法数之和，根据加法原理，我们可以从A点开始，向右向上逐步求出到达各点的走法数．如图所示，使用标号方法得到从A到B共有10种不同的走法．【巩固】（难度等级※※）如图，从A点到B点的最近路线有多少条？BA10204111111B6243310A【解析】使用标号法得出到B点的最近路线有20条．【例 4】（难度等级※※）如图，某城市的街道由5条东西向马路和7条南北向马路组成，现在要从西南角的A处沿最短的路线走到东北角B出，由于修路，十字路口C不能通过，那么共有＿＿＿＿种不同走法．AA【解析】本题是最短路线问题．要找出共有多少种不同走法，关键是保证不重也不漏，一般采用标数法．如上图所示，共有120种．另解：本题也可采用排除法．由于不能经过C，可以先计算出从A到B的最短路线有多少条，再去掉其中那些经过C的路线数，即得到所求的结果．对于从A到B的每一条最短路线，需要向右6次，向上4次，共有10次向右或向上；而对于每一条最短路线，如果确定了其中的某6次是向右的，那么剩下的4次只能是向上的，从而该路线也就确定了．这就说明从A到B的最短路线的条数等于从10次向右或向上里面选择6次向右的种数，为610C．一般地，对于m n⨯的方格网，相对的两个顶点之间的最短路线有mm nC+种．本题中，从A到B的最短路线共有610C种；从A到C的最短路线共有26C种，从C到B的最短路线共有24C种，根据乘法原理，从A到B且必须经过C的最短路线有2264C C⨯种，所以，从A到B且不经过C的最短路线有622106421090120C C C-⨯=-=种．【例 5】（难度等级※※※）如图所示，从A点到B点，如果要求经过C点或D点的最近路线有多少条？【解析】1、方格图里两点的最短路径，从位置低的点向位置高的点出发的话，每到一点（如C、D点）只能向前或者向上．2、题问的是经过C点，或者D点；那么A到B点就可以分成两条路径了A--C---B；A---D---B，那么也就可以分成两类．但是需要考虑一个问题——A到B点的最短路径会同时经过C和D点吗？最短路径只能往上往前，经过观察发现C、D不会同时出现在最短路径上了．3、A---C---B，那么C就是必经之点了，就需要用到乘法原理了．A---C，最短路径用标数法标出，同样C---B点用标数法标注，然后相乘A---D---B，同样道理．最后结果是735+420=1155条．【例 6】如图1为一幅街道图，从A出发经过十字路口B，但不经过C走到D的不同的最短路线有条.【解析】到各点的走法数如图2所示.ACBD1118126666633211DB CA图1图2所以最短路径有18条.【例 7】小王在一年中去少年宫学习56次，如图所示，小王家在P点，他去少年宫都是走最近的路，且每次去时所走的路线正好互不相同，那么少年宫在________点处．EC【解析】本题属最短路线问题．运用标数法分别计算出从小王家P点到A、B、C、D、E点的不同路线有多少条，其中，路线条数与小王学习次数56相等的点即为少年宫．因为，从小王家P点到A点共有不同线路84条；到B点共有不同线路56条；到C点共有不同线路71条；到D点共有不同线路15条；到E点共有不同线路36条．所以，少年宫在B点处．【例 8】（难度等级※※※）在下图的街道示意图中，有几处街区有积水不能通行，那么从A 到B的最短路线有多少种？AB1111111111455511136162151422 1111 1311B A【解析】因为B在A的右下方，由标号法可知，从A到B的最短路径上，到达任何一点的走法数都等于到它左侧点的走法数与到它上侧点的走法数之和．有积水的街道不可能有路线经过，可以认为积水点的走法数是0．接下来，可以从左上角开始，按照加法原理，依次向下向右填上到各点的走法数．如右上图，从A到B的最短路线有22条．【例 9】（难度等级※※※）在下图的街道示意图中，C处因施工不能通行，从A到B的最短路线有多少条？CBA6033311122221111CBA【解析】因为B 在A 的右上方，由标号法可知，从A 到B 的最短路径上，到达任何一点的走法数都等于到它左侧点的走法数与到它下侧点的走法数之和．而C 是一个特殊的点，因为不能通行，所以不可能有路线经过C ，可以认为到达C 点的走法数是0．接下来，可以从左下角开始，按照加法原理，依次向上向右填上到各点的走法数．如图，从A 到B 的最短路线有6条．【巩固】（难度等级 ※※※）在下图的街道示意图中，C 处因施工不能通行，从A 到B 的最短路线有多少种？CB A【解析】因为B 在A 在右下方，由标号法可知，从A 到B 的最短路径上，到达任何一点的走法数都等于到它左侧点的走法数与到它上侧点的走法数之和.而C 是一个特殊的点，因为不能通行，所以不可能有路线经过C ，可以认为到达C 点的走法数是0.接下来，可以从左上角开始，按照加法原理，依次向下向右填上到各点的走法数.如图，从A 到B 的最短路线有6条．【例 10】（难度等级 ※※※）如下表，请读出“我们学习好玩的数学”这9个字，要求你选择的9个字里能连续(即相邻的字在表中也是左右相邻或上下相邻)，这里共有多少种完15111310146151132【解析】方法一：标数法．第一个字只能选位于左上角的“我”，以后每一个字都只能选择前面那个字的下方或右方的字，所以本题也可以使用标号法来解：(如右上图，在格子里标数)共70种不同的读法．方法二：组合法．仔细观察我们可以发现，按“我们学习好玩的数学”走的路线就是向右走四步，向下走四步的路线，而向下和向右一个排列顺序则代表了一种路线．所以总共有4870C 种不同的读法．【例 11】（难度等级 ※※※）如图，沿着“北京欢迎你”的顺序走（要求只能沿着水平或竖直方向走），一共有多少种不同的走法？北北京北北京欢京北欢迎欢你113112*********【解析】沿着“北京欢迎你”的顺序沿水平或竖直方向走，北以后的每一个字都只能选择上面的或左右两边的字，按加法原理，用标号法可得右上图．所以一共有11种走法．【巩固】（难度等级 ※※※）如下表，请读出“我们学习好玩的数学”这9个字，要求你选择的9个字里能连续(即相邻的字在表中也是左右相邻或上下相邻)，这里共有多少351511113451014610151512013570321【解析】第一个字只能选位于左上角的“我”，以后每一个字都只能选择前面那个字的下方或右方的字，所以本题也可以使用标号法来解：(在格子里标数)共70种不同的读法．【例 12】（难度等级※※※）在下图中，用水平或者垂直的线段连接相邻的字母，当沿着这些线段行走是，正好拼出“APPLE”的路线共有多少条？A|A—P—A| | |A—P—P—P—A| | | | |A—P—P—L—P—P—A| | | | | | |A—P—P—L—E—L—P—P—A1|1—3 —1| | |1—2—7 —2—1| | | | |1—2—4—15—4—2—1| | | | | | | 1—2—4—8—31—8—4—2—1【解析】要想拼出英语“APPLE”的单词，必须按照“A→P→P→L→E”的次序拼写．在图中的每一种拼写方式都对应着一条最短路径．如下图所示，运用标号法原理标号得出共有31种不同的路径．【巩固】如图1，用水平线或竖直线连结相邻汉字，沿着这些线读下去，正好可以读成“祖国明天更美好”，那么可读成“祖国明天更美好”的路线有条.【解析】如图2所示，利用加法原理，将读到各个字的路线数写在每个字下方，共有不同的路线721127-=(条).祖祖国祖祖国明国祖祖国明天明国祖祖国明天更天明国祖祖国明天更美更天明国祖祖国明天更美好美更天明国祖图1祖1祖1国3祖1祖1国2明7国2祖1祖1国2明4天15明4国2祖1祖1国2明4天8更31天8明4国2祖1祖1国2明4天8更16美63更16天8明4国2祖1祖1国2明4天8更16美32好127美32更16天8明4国2祖1图2【巩固】(第三届“希望杯”2试试题)右图中的“我爱希望杯”有______种不同的读法.杯杯杯杯杯望望望望希希希爱爱我161511353211111111杯杯杯杯杯望望望望希希希爱爱我【解析】“我爱希望杯”的读法也就是从“我”走到“杯”的方法.如上右图所示，共16种方法.【例 13】如图1所示，科学家“爱因斯坦”的英文名拼写为“Einstein”，按图中箭头所示方向有种不同的方法拼出英文单词“Einstein”.i111111i图1图2【解析】由E n s t e i n→i→→→→→→的拼法如图2所示.根据加法原理可得共有303060+=(种)不同拼法.【例 14】（难度等级※※※）图中有10个编好号码的房间，你可以从小号码房间走到相邻的大号码房间，但不能从大号码走到小号码，从1号房间走到10号房间共有多少种不同的走法？【解析】我们可以把这个图展开，用箭头标出来就更直观了，然后采用我们学的标数法．【例 15】（难度等级 ※※※）国际象棋中“马”的走法如图1所示，位于○位置的“马”只能走到标有×的方格中，类似于中国象棋中的“马走日”．如果“马”在88⨯的国际象棋棋盘中位于第一行第二列（图2中标有△的位置），要走到第八行第五列（图2中标有＠的位置），最短路线有________条．【2008年北京“数学解题能力展示”读者评选活动】第@图图1题@图2【解析】最后一步的可能如图1，倒数第二步的可能如图2，倒数第三步的可能如图3．最后36312++=（种）．图3图2@11112122图1@111122163321111@【例 16】（难度等级 ※※※）从北京出发有到达东京、莫斯科、巴黎和悉尼的航线，其他城市间的航线如图所示(虚线表示在地球背面的航线)，则从北京出发沿航线到达其他所有城市各一次的所有不同路线有多少？【解析】第一站到东京的路线有10条：⎧⎪⎪⎪⎧→→⎪→⎨⎪→→⎩⎪⎪⎧⎧→→⎪⎪⎨→⎪⎪⎩→→→⎨⎨→⎧⎪⎪→⎨⎪⎪→⎩⎩⎪⎪⎧⎧→⎪→⎪⎨⎪→⎪⎩→⎪⎨→⎧⎪⎪→⎨⎪⎪→⎩⎩⎩莫斯科巴黎悉尼纽约悉尼巴黎莫斯科巴黎悉尼纽约悉尼巴黎北京东京莫斯科纽约悉尼巴黎悉尼纽约巴黎莫斯科纽约莫斯科巴黎悉尼纽约莫斯科巴黎莫斯科纽约同理，第一站到悉尼、巴黎、莫斯科的路线各有10条，不同的路线共有10440⨯=条．【例 17】一个实心立方体的每个面分成了四部分．如图所示，从顶点P 出发，可找出沿图中相连的线段一步步到达顶点Q 的各种路径．若要求每步沿路径的运动都更加靠近Q ，则从P 到Q 的各种路径的数目为几？QP1818666333322111111QP【解析】因为正方体每个面的对面也有同样的路径，最靠近Q 的有三个点，从P 点到这三个点都是18种路径．故有18354⨯=三、简单递推：斐波那契数列的应用对于某些难以发现其一般情形的计数问题，可以找出其相邻数之间的递归关系，有了这一递归关系就可以利用前面的数求出后面的数，这种方法称为递推法．【例 18】（难度等级※※※）一楼梯共10级，规定每步只能跨上一级或两级，要登上第10级，共有多少种不同走法？【解析】登1级2级3级4级 ......10级1种方法2种3种5种 ......？我们观察每级的种数，发现这么一个规律：从第三个数开始，每个数是前面两个数的和；依此规律我们就可以知道了第10级的种数是89.其实这也是加法的运用：假如我们把这个人开始登楼梯的位置看做A0，那么登了1级的位置是在A1，2级在A2... A10级就在A10．到A3的前一步有两个位置；分别是A2和A1．在这里要强调一点，那么A2到A3既然是一步到了，那么A2、A3之间就是一种选择了；同理A1到A3也是一种选择了．同时我们假设到n级的选择数就是An ．那么从A0到A3就可以分成两类了：第一类：A0 ---- A1 ------ A3，那么就可以分成两步．有A1×1种，也就是A1种；(A1 ------ A3是一种选择)第二类：A0 ---- A2 ------ A3，同样道理有A2．类类相加原理：A3 = A1＋A2，依次类推An = An-1 + An-2．【例 19】（难度等级※※※）1×2的小长方形(横的竖的都行)覆盖2×10的方格网，共有多少种不同的盖法．【解析】如果用12⨯的长方形盖2n ⨯的长方形，设种数为n a ,则11a =，22a =,对于3n ≥，左边可能竖放1个12⨯的，也可能横放2个12⨯的，前者有-1n a 种，后者有-2n a 种，所以-1-2n n n a a a =+,所以根据递推，覆盖210⨯的长方形一共有89种．【例 20】（难度等级 ※※※）如下图，一只蜜蜂从A 处出发，回到家里B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？BAAB 1357946821235813213455891【解析】蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬近相邻大号码的蜂房．明确了行走路径的方向，就可以运用标数法进行计算．如右图所示，小蜜蜂从A 出发到B 处共有89种不同的回家方法．【巩固】小蜜蜂通过蜂巢房间，规定只能由小号房间进入大号房间问小蜜蜂由A 房间到达B 房间有多少种方法？【解析】斐波那契数列第八项．21种．【例 21】每对小兔子在出生后一个月就长成大兔子，而每对大兔子每个月能生出一对小兔子来．如果一个人在一月份买了一对小兔子，那么十二月份的时候他共有多少对兔子？【解析】第一个月，有1对小兔子；第二个月，长成大兔子，所以还是1对；第三个月，大兔子生下一对小兔子，所以共有2对；第四个月，刚生下的小兔子长成大兔子，而原来的大兔子又生下一对小兔子，共有3对；第五个月，两对大兔子生下2对小兔子，共有5对； ……这个特点的说明每月的大兔子数为上月的兔子数，每月的小兔子数为上月的大兔子数，即上上月的兔子数，所以每月的兔子数为上月的兔子数与上上月的兔子数相加．依次类推可以列出下表：经过月数：---1---2---3---4---5---6---7---8---9---10---11---12 兔子对数：---1---1---2---3---5---8--13--21--34--55--89--144 所以十二月份的时候总共有144对兔子．【例 22】树木生长的过程中，新生的枝条往往需要一段“休息”时间供自身生长，而后才能萌发新枝．一棵树苗在一年后长出一条新枝，第二年新枝“休息”，老枝依旧萌发新枝；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则依次“休息”．这在生物学上称为“鲁德维格定律”．那么十年后这棵树上有多少条树枝？【解析】一株树木各个年份的枝桠数，构成斐波那契数列：1，2，3，5，8，13，21，34，55，89，……所以十年后树上有89条树枝．【例 23】对一个自然数作如下操作：如果是偶数则除以2，如果是奇数则加1，如此进行直到得数为1操作停止．问经过9次操作变为1的数有多少个？【解析】可以先尝试一下，倒推得出下面的图：2410131112514302831643215167683421其中经1次操作变为1的1个，即2，经2次操作变为1的1个，即4，经3次操作变为1的2个，是一奇一偶，以后发现，每个偶数可以变成两个数，分别是一奇一偶，每个奇数变为一个偶数，于是，经1、2、…次操作变为1的数的个数依次为：1，1，2，3，5，8，…这一串数中有个特点：自第三个开始，每一个等于前两个的和，即即经过9次操作变为1的数有34个.为什么上面的规律是正确的呢？道理也很简单. 设经过n 次操作变为1的数的个数为n a ,则1a =1，2a =1，3a =2，… 从上面的图看出，1n a +比n a 大.一方面，每个经过n 次操作变为1的数，乘以2，就得出一个偶数，经过1n +次操作变为1；反过来，每个经过1n +次操作变为1的偶数，除以2，就得出一个经过n 次操作变为1的数. 所以经过n 次操作变为1的数与经过1n +次操作变为1的偶数恰好一样多.前者的个数是n a ,因此后者也是n a 个.另一方面，每个经过n 次操作变为1的偶数，减去1，就得出一个奇数，它经过1n +次操作变为1，反过来.每个经过1n +次操作变为1的奇数，加上1，就得出一个偶数，它经过n 次操作变为1. 所以经过n 次操作变为1的偶数经过1n +次操作变为1的奇数恰好一样多.而由上面所说，前者的个数就是1n a -,因此后者也是1n a -.经过n +1次操作变为1的数，分为偶数、奇数两类，所以11n n n a a a +-=+，即上面所说的规律的确成立.。

标数法

次 ,故合乎条件的正方形的个数为1244 = 31.
参考文献 : [1 ] 董迎新. 中考加分题对教学的启示 [J ] . 中小学数学
(教师版) ,2004 (122) . [2 ] 周士藩. 对一道中考加分题的思考 [J ] . 中小学数学
(教师版) ,2004 (3) . [3 ] 季小冬. 对一道中考加分题的再思考[J ] . 中小学数学
图 9 图 10
于是 , f (3 ,4) = 4(3 + 7 + 5 + 11) + 2(8 + 15)
= 150. 当 n ≥5 时 , A 、B 、C 、E、F、G 六类格点各有 4 个 , D 、H 两类格点各有 2 ( n + 1 - 6) = 2 n - 10 个 ,各类格点的标数如图 11 、12 所示.
2007 年第 9 期
= 60 n - 92. 16 , n = 1 ; 50 , n = 2 ;
综上 , f (3 , n) = 96 , n = 3 ; 150 , n = 4 ; 60 n - 92 , n ≥5.
如何求出 f ( m , n) 的计算公式 ? 这是一个相当复杂的问题 ,用标数法似乎难于获解 , 因此 ,改进方法无疑是十分必要的.
训练题
(7)
》的选择题
3
的条件应为“
……使
AE EB
=
FC DF
=
2
007.
……”,填空题 1 的解答“ ……p
=
2 xy x+ y
=
40 2
011470 .
……”应为“ ……p =
2 xy x+ y
=
50 2

【典型例题】五年级数学下册第一单元观察物体(三)(含答案)

2021-2022学年五年级数学下册典型例题系列之第一单元观察物体（三）（原卷版）编者的话：《2021-2022学年五年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的，该系列主要包含典型例题和专项练习两大部分。

典型例题部分是按照单元顺序进行编辑，主要分为计算和应用两大部分，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和期末真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

本专题是第一单元观察物体（三）典型例题部分。

本部分内容主要是观察立体图形的几种类型题，考试多以填空、选择、判断等基础题型为主，题目比较简单，建议选取着重点进行讲解，一共划分为五个考点，欢迎使用。

【考点一】根据立体图形观察物体。

【方法点拨】根据立体图形观察物体时：1.从不同位置观察立体图形的形状，一般是从前面、上面、左面三个方向观察，所看到的形状一般是不同的。

2.在画观察到的图形时，遵循三个原则：长对正、高平齐、宽相等。

【典型例题】画出从不同方向观察到的图形。

【对应练习1】如图的物体分别从正面、左面、上面看到的图形是什么？请你在方格纸上画出来。

【对应练习2】分别画出从正面、上面、左面看到的形状。

【对应练习3】请把对应的序号填在横线上．（1）从上面看是的有（）。

（2）从前面看是的有（）。

（3）从左面或右面看是的有（）。

【考点二】根据平面图形还原立体图形。

【方法点拨】根据平面图还原立体图形：1.从上面看到的图形中，小正方形内部的数表示的是在这个位置上所用的小正方体的个数。

2.从正面看到的图形中，视线从前往后，每列中最大的数即为这一列最高层的层数。

3.从左面看到的图形，视线从左往右，每行中最大的数即为这一行最高层的层数。

【典型例题】一个立体图形，从正面看到图形是，从上面看到的图形是，从右面看到的图形是，这个立体图形可能是（）。

A． B．C． D．【对应练习1】一个几何体，从正面看是，从左面看是，这个几何体可能是（）。

奥数标数法练习计数之标数法经典例题讲解

奥数标数法练习计数之标数法经典例题讲解解答：第1步：在起点A处标1。

再观察点B，要想到达点B，只有一个入口A，所以在B点也标1。

第2步：再观察点C，要想到达点C,它有两个入口A和B，所以在点C处标1＋1＝2。

同理重复点F，点D，点E，点G，点H，点I【第三篇】分析:既然要走最短路线,自然是不能回头走,所以从A地到B地的过程中只能向右或向下走.我们首先来确认一件事,如下图从A地到P点有m种走法,到Q点有n种走法,那么从A地到B 地有多少种走法呢?就是用加法原理,一共有m+n种走法.这个问题明白了之后,我们就可以来解决这道例题了:首先由于只能向右或向下走,那么最上面一行和最左边一列的每一个点都只能有一种走法,(因为不可以走回头路).我们就在这些交点的旁边标记上一个数字,代表走到这个位置有多少种方法.【第四篇】有一个5位数,每个数字都是1,2,3,4,5中的一个,并且相临两位数之差是1.那么这样的5位数到底有多少个呢?(数字可以重复) 这是一道数论的题目,但是我们也可以使用标数法来解答,并且非常直观.到第一站可以有5种选择,每种选择有一种走法,那么下一站,走1号门就只有一种走法(就是第一站走的2号门),走2号门就有2种走法(第一站走1号或3号门)走3号门也是2种走法(第一站走2号门或4号门)走4号门2种走法(第一站走3号门或者5号门)走5号门只有一种走法(第一站走的是4号门)我们发现在这一站经过某个门有多少种走法,正好等于他左上和右上的两个数字和.于是我们可以将数字标全.这道题的答案就是42种,虽然很多同学会用枚举法也能做出42种,但是一旦这道题给的不是5位数,而是7位数,9位数的话,枚举法就显得无力了.这种时候标数法是个不错的选择.可以用到标数法的问题有很多，大家掌握这种方法之后可以解决很多平时看起来很麻烦的题目。

计数第06讲_标数法(学生版)A4

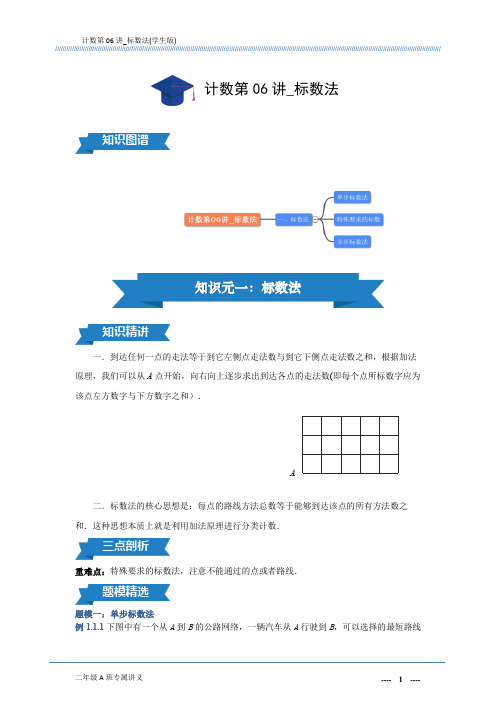
一．到达任何一点的走法等于到它左侧点走法数与到它下侧点走法数之和，根据加法原理，我们可以从A 点开始，向右向上逐步求出到达各点的走法数(即每个点所标数字应为该点左方数字与下方数字之和）．二．标数法的核心思想是：每点的路线方法总数等于能够到达该点的所有方法数之和．这种思想本质上就是利用加法原理进行分类计数．重难点：特殊要求的标数法，注意不能通过的点或者路线．题模一：单步标数法例1.1.1下图中有一个从A 到B 的公路网络，一辆汽车从A 行驶到B，可以选择的最短路线计数第06讲_标数法A一共有________条？BA例1.1.2下图是一个街道的示意图，实线表示道路，从B到A，只能向右或向上或右斜上方沿着道路前进，则一共有_________种不同的走法．AB例1.1.3在图所示中，从“北”字开始，每次向下移动到一个相邻的字可以读出“北京奥运会”．那么一共有多少种不同的读法？北京京奥奥奥运运运运会会会会会题模二：特殊要求的标数例1.2.1在如图所示的街道示意图中，C处因施工不能通行，那么从A到B处的最短路线有________条．例 1.2.2有一只蚂蚁沿着下图中的方格线从A爬到B，每次只能向右爬一格或向上爬一格．图中画着黑点的地方必须通过，那么这只蚂蚁可以选择____________条不同的路线．例1.2.3如图，从A 出发经过十字路口D ，但不经过线段BC （不过点B 、C ），不同的最短路径有多少条？题模三：多步标数法例1.3.1如图所示，国际象棋中的棋子“皇后”从左下角走到右上角，每步只能向右、向上或者向右上移动任意多格，一共有多少种不同的走法？A ．168B ．178C ．188D ．198随练1.1如图，从A 点沿线段走到B 点，每次只能向上或向右走一步，共有多少种不同走法？DABCBA随练1.2在下图中，从A点沿线段走到B点，每次只能向上或向右走一步，共有多少种不同走法？BA随练1.3如图，从A出发经过十字路口D，但不经过线段BC（不过点B、C），不同的最短路径有多少条？DBCA随练1.4如图，从A出发经过十字路口D，但不经过线段BC（不过点B、C），不同的最短路径有多少条？DB CA随练1.5如图所示，亚瑟王要沿路线从A地前往B地拿去圣剑Excalibur，但路中有许多恶魔使得部分道路无法通行，那么亚瑟王现在要取得圣剑的最短路线共有_________条．（圆圈表示恶魔占据的地方）随练 1.6如图所示，国际象棋中的棋子“皇后”从左下角走到右上角，每步只能向右、向上或者向右上移动任意多格，一共有多少种不同的走法？作业1如图，有一个48 的棋盘，现将一枚棋子放在棋盘左下角格子A处，要求每一步只能向棋盘右上或右下走一步（如从C 走一步可走到D 或E ），那么将棋子从A 走到棋盘右上角B 处共有_______种不同的走法．作业2在下图中，从A 点沿线段走到B 点，每次只能向上或向右走一步，共有多少种不同走法？作业3一只兔子沿着方格的边从A 到B ,规定上只能往上或往右走，但是必须经过一座独木桥MN ,这只兔子有______________种不同的走法．ABABNM作业4一只甲虫沿着下图中的方格线从A 爬到B ，每次只能向右爬一格或向上爬一格．请问：（1）图中C 、D 两点必须都通过，那么这只甲虫可以选择多少条不同的路线？（2）图中C 、D 两点只通过其中的一个点，那么这只甲虫可以选择多少条不同的路线？图中C 、D 两点都不通过，那么这只甲虫可以选择多少条不同的路线？作业5如图，从A 处到B 的最短路线中，必通过十字路口C 和D 的，共有多少条？作业6一种蜂房编号如图所示，左上角有一只小蜜蜂，还不会飞，只会向相邻的蜂房爬行，且方向只能是向右、右上、右下方爬，它爬行到8号蜂房，共有____种路线．ABCDB AC D1 35 7 8642。

标数法求表面积

标数法求表面积
摘要：
一、引言
二、标数法的概念与原理
三、标数法在求表面积中的应用
四、标数法的优势与局限性
五、总结与展望
正文：
一、引言
在数学中，求解表面积问题是一项常见任务。

在各种求解方法中，标数法具有较高的准确性和通用性。

本文将详细介绍标数法的原理，以及在求表面积中的应用。

二、标数法的概念与原理
标数法，又称“标记法”，是一种求解数学问题的方法。

它通过引入一种新的数——标数，将问题转化为标数之间的关系，从而简化问题的求解过程。

标数法适用于各种几何图形，如求面积、体积等。

三、标数法在求表面积中的应用
标数法在求表面积问题中具有广泛的应用。

以矩形为例，假设矩形的长为a，宽为b，则矩形的表面积S=2ab+2bc+2ac。

通过引入标数，我们可以将矩形的面积表示为S=2ab+2bc+2ac=2(a+b+c)·(a+b+c)-
2(a+b+c)+2(a+b+c)-2ac，进一步化简得到S=4(a+b+c)-4ac。

这样，我们
就将矩形表面积的求解问题转化为标数之间的关系问题。

四、标数法的优势与局限性
标数法的优势在于，它能够将复杂的问题转化为简单的问题，从而降低问题的求解难度。

同时，标数法具有较高的通用性，适用于各种几何图形。

然而，标数法也存在局限性，对于某些特殊问题，可能需要结合其他方法进行求解。

五、总结与展望
总之，标数法是一种求解数学问题的有效方法，尤其在求解表面积问题时具有显著优势。

通过对标数法的原理和应用进行深入了解，可以帮助我们更好地应对各种数学问题。

标数法C版

8
1.
标数法
预习
如图，从 A 地出发去 B 地，请问共有几种不同的最短路线？
B
A
【答案】56 【分析】标数如下，共有 56 种最短路线.
19 7 3 1 2 1 3 1 7 4 1 19 12 5 1 56 37 18 6 1
2.
如图，从 A 地出发去 B 地，请问共有几种不同的最短路线？
Bபைடு நூலகம்
A
【答案】26 【分析】标数如下，共有 26 种最短路线.
32
三年级春季第 8 讲标数法（C 版）
6.
用 10 个形如“
”的棋子覆盖 2 10 的棋盘（“
；有多少种不同的摆法？ ”）
【答案】89 【分析】最右侧要么是一“竖”，要么是两“横”；一“竖”即 9+1 的结构，两“横”即 8+2 的结构，可见 10 列的摆法，等于 9 列的摆法和 8 列的摆法之和；1 列的摆法有 1 种，2 列的摆法有 2 种；则 1， 2，3，4，...，10 列的摆法分别有：1，2，3，5，8，13，21，34，55，89，其中 10 列的摆法有 89 种. 7. 一场足球比赛的结束后，甲乙两队的进球数为 3 : 4，且整场比赛中甲队的进球数量从未领先乙队，请问，两队在比赛中的进球顺序有多少种情况？【答案】14 【分析】在 3´ 4 的方格表中，设两队从左下角为 0:0，乙队进一球则向右走一格，甲队进一球则向上走一格，最终 3:4 则走到了右上角，其中图示斜线上方的交点表示甲队领先，则不允许走到，标数可得，两队的进球顺序有 14 种.
D
4.
一只蜜蜂从 A 处出发，回到家里 B 处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？

行测数量关系技巧：标数法进阶篇

行测数量关系技巧：标数法进阶篇通过标数法基础篇的学习相信大家已经基本掌握了标数法这一解题方法，并在涉及到最短路线的方法数这类题型中运用自如。

随着行测考试的日渐成熟，数学运算中的各种方法或多或少有一些延伸或变形，标数法也是如此，本文主要讲解标数法的进阶题型。

首先，回顾一道标准的标数法题目。

例1.小张从华兴园到软件公司上班要经过多条街道(软件公司在华兴园的东北方)。

假如他只能向东或者向北行走，则他上班不同走法共有：A.12种B.15种C.20种D.10种通过标数法基础篇的学习，我们已经了解了标数法是指将到达每个点的方法数标注在点的旁边的一种解题方法，通常运用在求最短路线方法数的题目中。

标数法的核心步骤是观察一个点能从哪些点走过来就把这些点的数加起来作为该点的方法数。

这道例题中规定了只能向东或者向北走，按照要求走就不会存在绕路的情况，那么这样从华兴园到软件公司的走法就是最短路线。

我们可以利用标数法的核心对原图进行标数：在路线方向和路线经过的点明确的情况下，我们能够利用标数法很快得出结果，上述例题从华兴园到到软件公司的方法数为10种，故答案为D。

其次，我们来学习标数法延伸后的第一类题目。

此类题目中不直接给出路线方向或路线经过的点，需要考生自行理解转化为标数模型求解。

例2.如图所示，有两排蜂房，一只蜜蜂从左下角的1号蜂房开始去8号蜂房，假设只朝右上或右下逐个爬行。

则不同的走法有：A.16种B.18种C.21种D.24种例题二中并没有给出明确的路线方向也没有路线中经过的点，需要我们根据题目的表述进行理解。

我们可以把每一个蜂房理解为路线中经过的点，路线方向是左下角的蜂房可以朝右侧相邻的两个蜂房移动(注意“只朝右上或右下逐个爬行”中的右上或右下应理解为整体观察的情况，即只向右侧的蜂房爬行)。

然后我们再采取标数法进行解题，如下图所示。

故从1号蜂房到8号蜂房共有21种方法，此题选C。

再次，我们来学习标数法延伸后的第二类题目。

小学奥数教师版-7-1-3 加法原理之树形图及标数法

分析这个问题发现，王老师去天津要么乘火车，要么乘长途汽车，有这两大类走法，如果乘火车，有 5 种走法，如果乘长途汽车，有 4 种走法．上面的每一种走法都可以从北京到天津，故共有 5+4=9 种不同的走法．
在上面的问题中，完成一件事有两大类不同的方法．在具体做的时候，只要采用一类中的一种方法就可以完成．并且两大类方法是互无影响的，那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数．
一般地，对于
m
n
的方格网，相对的两个顶点之间的最短路线有
Cm mn
种．
本题中，从 A 到 B 的最短路线共有 C160 种；从 A 到 C 的最短路线共有 C62 种，从 C 到 B 的最短路线共
有 C42 种，根据乘法原理，从 A 到 B 且必须经过 C 的最短路线有 C62 C42 种，所以，从 A 到 B 且不经
的走法数目就应该是到达 C 点的走法数和到达 D 点的走法数之和，而对于到达 C 的走法，又等于到
达 E 和到达 F 的走法之和，到达 D 的走法也等于到达 F 和到达 G 的走法之和，这样我们就归纳出：
到达任何一点的走法都等于到它左侧点走法数与到它下侧点走法数之和，根据加法原理，我们可以
从 A 点开始，向右向上逐步求出到达各点的走法数．如图所示，使用标号方法得到从 A 到 B 共有 10
1
3
6
10
B
1
2
3
4
1
1
1
A
【题型】解答
【解析】图中 B 在 A 的右上方，因此从 A 出发，只能向上或者向右才能使路线最短，那么反过来想，如果到
达了某一个点，也只有两种可能：要么是从这个点左边的点来的，要么是从这个点下边的点来的．那

标数法求表面积

标数法求表面积摘要：1.表面积的定义与意义2.标数法的概念与原理3.标数法求表面积的步骤与应用4.实例分析与计算5.标数法求表面积的优缺点6.与其他求表面积方法的比较正文：在我们日常生活中，经常会遇到各种形状的物体，如何快速准确地求出它们的表面积是一项重要任务。

今天，我们就来学习一种求表面积的方法——标数法。

一、表面积的定义与意义表面积是指一个物体外部所有面的总面积。

在数学、物理等领域，表面积是一个重要的几何概念。

求表面积的方法有很多，其中标数法就是一种简单实用的方法。

二、标数法的概念与原理标数法，又称度量法，是通过计算物体各面的面积与侧棱长的乘积之和来求得表面积的方法。

它的基本原理是：将物体的每个面看作一个平面，用侧棱长（或高）乘以该面的面积，得到每个面的度量值，最后将各面的度量值相加，即可得到物体的表面积。

三、标数法求表面积的步骤与应用1.确定物体的形状，计算各面的面积。

2.测量物体的侧棱长（或高）。

3.将各面的面积与侧棱长（或高）相乘，得到每个面的度量值。

4.将各面的度量值相加，得到物体的表面积。

标数法适用于各种形状的物体，如长方体、立方体、圆柱、圆锥等。

在实际应用中，我们可以根据物体的具体形状和尺寸，灵活运用标数法求解表面积。

四、实例分析与计算以一个长方体为例，长为a，宽为b，高为c。

根据标数法，我们可以计算其表面积：1.计算各面的面积：- 前后两个面的面积：ab- 左右两个面的面积：ac- 上下两个面的面积：bc2.计算侧棱长：- 长方体的侧棱长为c。

3.计算各面的度量值：- 前后两个面的度量值：ab × c- 左右两个面的度量值：ac × c- 上下两个面的度量值：bc × c4.计算表面积：- 表面积= 前后两个面度量值之和+ 左右两个面度量值之和+ 上下两个面度量值之和= (ab × c + ac × c + bc × c) × 2五、标数法求表面积的优缺点优点：1.方法简单，易于掌握。

标数法知识点总结

标数法模块一、知识点一、标数法利用加法原理解决最短路线有几条的方法二、过程1. 确定目标方向2. 起点开始横竖标“1”3. 做加法PS:每个点的数，表示从起点到这个点最短路线的条数三、类型1. 基本型(“田”字型)2. 非“田”字型3. 必过：套框；必不过：标0或去线4. 拼读文字、字母型5. 蜂房型模块二、例题精讲【基本型】如图所示，从A点沿线段走最短路线到B点，共有多少种不同的最短路线?B[解答] B在A的右上方，每次只能向右或向上，标数可得共有10种不同的最短路线A【非田型】小君家到学校的道路如图所示.从小君家到学校有种不同的走法. (只能沿图中向右向下的方向走)小君家学校[解析]标数法如图，共10条不同走法. 只要每次都想一下，它上一步在哪里，它可以从哪个点过过来!【必过、必不过型】艾迪和薇儿准备去看望养老院的李奶奶，如下图(1) 他们从学校经过市中心到养老院的最短路线共有几条呢?[解析]先要到达市中心，可以先把市中心当成终点，然后再从市中心出发到达养老院，标数可得有60种方法。

养老院(2) 他们从学校不经过市中心到养老院的最短路线共有几条呢?[解析]不经过市中心，说明到达市中心的方法为0,可以直接标0;可以把周围4条线去掉，标数可得有66种方法。

(也可以用到达终点的所有方法，减去经过市中心的方法)养老院(3)傍晚时，市中心附近下了一场大雨，附近的路均无法通行，请问到养老院的最短路线共有几条呢学校[解析]里面每个点标0,得到有35条。

养老院【拼读型】如图所示，科学家“爱因斯坦”的英文名拼写为“Einstein”, 按图中箭头所示方向有种不同的方法拼出英文单词“Einstein”[解析]由E→i→n→s→t→e→i→n拼读顺序，进行标数可得：30+30=60种【蜂房型】一只蜜蜂从A处出发, 回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行, 共有多少种回家的方法?[解析]向右指的正右、右上、右下都可以，所以标数得，有89种.。

标数法口诀

标数法口诀以下是五个符合要求的口诀：《标数法口诀一》一二三四依次来，标数其实很简单。

一条路走到底，就像直线不拐弯。

二路分开左右看，选择清楚不犯难。

三路好比岔路口，仔细思考再向前。

四路如同多方向，冷静判断别慌乱。

从小数字开始算，一步一步记心间。

遇到复杂也别怕，耐心标数全搞定它。

《标数法口诀二》标数法呀真奇妙，小朋友们要记牢。

一是起点认真找，方向明确不能跑。

二是过程慢慢瞧，步骤清晰不混淆。

三看分支怎么绕，条理清楚才最好。

四要终点确认好，大功告成哈哈笑。

就像走路一步步，稳稳当当不会错。

大家快来一起学，轻松掌握没话说。

《标数法口诀三》标数如同走楼梯，一步一步向上移。

一是基础要打实，稳稳站立不偏移。

二把台阶看仔细，顺序不能出问题。

三走起来有规律，不慌不忙有秩序。

四到终点心欢喜，收获成果笑嘻嘻。

好像游戏玩通关，快乐感觉在心田。

学会标数用处大，解题不再困难啦。

《标数法口诀四》标数法，要学会，听我来讲小口诀。

一开头，别乱走，目标明确才不忧。

二中间，思路展，多种可能都看见。

三过程，耐心点，仔细分析不能倦。

四结尾，答案显，大功告成笑开颜。

如同搭积木一般，稳稳当当建家园。

快来一起用标数，知识海洋任你游。

《标数法口诀五》标数就像建房子，一砖一瓦有次序。

一是先把地基打，基础牢固才不怕。

二是开始砌墙壁，横竖整齐又美丽。

三将屋顶慢慢盖，遮风挡雨有依赖。

四等房子全建成，满心欢喜好高兴。

好比画画一步步，精彩作品就出炉。

小朋友们快练习，标数轻松就学会。

(word完整版)最短路线问题——标数法的应用

(word 完整版)最短路线问题——标数法的应用
计数的基本方法-—标数法
例1:沿着下图所显示的线段,从A 点到B 点，有多少条最短路线?
I
C
例2：沿着下图所显示的线段，从A 点到B 点，有多少条最短路线？（1)
（2）
例3：沿下图所示的线段，从A
完整版)最短路线问题——标数法的应用
例4：如图,求A 到B 沿网格线的最短路线数：
（1）必须经过点C ；（2）必须经过线段EF ；（3）不经过点C ；（4）不经过线段EF;
例5：按下图箭头所指的方向行走，从A 到达Z 有多少种不同行走路线？
本章小结：
1.什么是标数法？
答：在每个点上标记出从起点出发到此点的路线数的一种计数方法。

2.如何使用标数法解决长方形网络图中的最短路线问题？答:
1. 确定标数的方向；
2. 将与起点共直线的点上标上数字1；
3. 画出每个小方格对角线；
(word完整版)最短路线问题——标数法的应用4.把每个小方格内对角线顶点上的两个数字相加，和标记在剩下的那个点上；
2。

如何使用标数法解决路线数问题？
答：
1.从某一点出发到另一点只有一条路线的时候，则后点上标记的数字应该和前一点相同;
2.如果到达某一点必须经过与这个点相邻的两个或几个点时，则该点上标记的数字是能够到达这一点的相
邻的两个或几个点上标记的数字之和。

四年级数学：标数法

四年级数学：标数法标数法：是一种技巧性很强的方法，掌握好了方法，可以快速解决相关题型。

标数法的技巧：1、把起点标为1；2、之后每个点上的数=所有来这个点的“正确”方向上各自最近点上数之和。

如果只有一个正确方向过来这个点，那么就把唯一的一个方向上最近的点上数挪过来。

3、如果目标在起点的右上方，那么必须往右，往上或者往右上方向走。

如右图：（1）某个点，从左边来，从下边来，所有数为A+B，（2）某个点，只能从左边来，把A数挪过来。

（3）某个点，只能往上走，把B数挪过来。

一、基础例题1、如图小明要从家去学校，图中的线段是街道。

小明只能沿着街道从家去学校，那么请问小明最短最合理的路线有多少种？2、从学校到图书馆，所走路线最短最合理的走法一共有多少种？3、图中的线路表示的是小刚从家到学校所能经过的所有街道，问小刚上学一共有多少条不同的最短路线？4、如图，要从点A到点B去，问最短的线路有多少种？5、现在要从点A到点B去，但是C点正在施工，不能经过。

问最短的路线有多少种？6、小明要从学校去少年宫，但是不能经过A点，问最短路线有多少种？7、如图是一街道的平面图，从A点到B点有多少种最近的走法？8、小明从A点步行到Z点,只能往右或者往下走，路线如图所示，那么小明从A 点到Z点的最短路线有多少条？二、拓展例题1、按照图中箭头所指的方向行走，那么从A点到I点一共有多少条不同的路线？2、按照图中箭头所指的方向行走，那么从A点到G点一共有多少条不同的路线？3、一只小蜜蜂呀，从点A出发，A回到家B，每次只能从一个蜂房爬向右侧相邻的蜂房而不准逆行，一共有多少种回家的方法？（右侧：正右，右上，右下三种都算右侧方向。

）4、如图所示，科学家爱因斯坦的英文名拼写为“Einstein”按照图中箭头所指方向有多少种不同的方法拼出英文单词“Einstein”？5、图中有10方格编好号码的方向，你可以从小号码房间走到相邻的大号码房间，但是不能从大号码房间走到小号码房间，从1号房间走到10号房间共有多少种不同的走法？6、图中是关于A、B、C的公路网，汽车从A点到B点再到C点可以选择不绕远路的不同路线各有几种？7、在右边的街道示意图中，C处因为施工不可以通过，问从A点到B点的最短路线有多少条？8、如图所示从A点到B点沿着网格线不经过线段CD和EF的最短路线的条数有多少条？作业：1、从点A到点B的最短路线有几条？只可以向右或者向下走。

卡特兰数标数法

卡塔兰数（Catalan number）是一个在组合数学中常见的数列，它出现在各种计数
问题中。

卡塔兰数以比利时数学家欧仁·查尔斯·卡塔兰（1814-1894）的名字命名。

在标准法中，卡塔兰数通常用 Cn 表示，其中 n 是非负整数。

卡塔兰数的计算可用
标数法（标准法）进行。

标数法是一种用于计算卡塔兰数的递推方法。

下面是卡塔兰数的标数法的详细解释：
1.定义：卡塔兰数满足以下递推关系：
C0 = 1, Cn = Σ(Ci * Cn-1-i) (i 从 0 到 n-1)
2.计算方法：标数法是一种递归方法，用于计算卡塔兰数。

它基于卡塔兰数
的递推关系，可以从 C0 开始逐步计算出后续的卡塔兰数。

C0 = 1
C1 = C0*C0 = 1
C2 = C0*C1 + C1*C0 = 2
C3 = C0*C2 + C1*C1 + C2*C0 = 5
C4 = C0*C3 + C1*C2 + C2*C1 + C3*C0 = 14
...
3.应用：卡塔兰数在组合数学中有广泛的应用，包括组合计数问题、图论、
几何学、树的计数等方面。

4.性质：卡塔兰数具有许多重要的组合性质和递推关系，它们在不同的组合
计数问题中扮演着重要角色。

卡塔兰数标数法提供了一种计算卡塔兰数的简便方法。

它的递归结构使得可以使用简单的递归算法来计算任意阶数的卡塔兰数。

在组合数学和计算机科学领域，卡塔兰数具有重要的应用和意义。

小学计数知识学习习题：标数法(含答案)

小学计数知识学习：标数法习题一小学计数知识学习：标数法习题二1. 如图所示，小明家在A地，小学在B地，电影院在C地。

1.小明从家里去学校，走最短的线路，有多少种走法?2.小明从家里去电影院，走最短线路，有多少种走法?小学计数知识学习：标数法习题三如图，从一楼到二楼有12梯，小明一步只能上1梯或2梯，问小明从1楼上到2楼有多少种走法？小学计数知识学习：标数法习题四一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？解答：蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房。

明确了行走路径的方向，就可运用标数法进行计算。

如图所示，小蜜蜂从A出发到B处共有89种不同的回家方法。

小学计数知识学习：标数法习题五例1．按图中箭头所指的方向行走，从A到I共有多少条不同的路线？解答：第1步：在起点A处标1。

再观察点B，要想到达点B，只有一个入口A，所以在B点也标1。

第2步：再观察点C，要想到达点C,它有两个入口A和B，所以在点C处标1＋1＝2。

同理重复点F，点D，点E，点G，点H，点I小学计数知识学习：标数法习题六分析:既然要走最短路线,自然是不能回头走,所以从A地到B地的过程中只能向右或向下走. 我们首先来确认一件事,如下图从A地到P点有m种走法,到Q点有n种走法,那么从A地到B地有多少种走法呢?就是用加法原理,一共有m+n种走法.这个问题明白了之后,我们就可以来解决这道例题了:首先由于只能向右或向下走,那么最上面一行和最左边一列的每一个点都只能有一种走法,(因为不可以走回头路).我们就在这些交点的旁边标记上一个数字,代表走到这个位置有多少种方法.小学计数知识学习：标数法习题七有一个5位数,每个数字都是1,2,3,4,5中的一个,并且相临两位数之差是1.那么这样的5位数到底有多少个呢?(数字可以重复)这是一道数论的题目,但是我们也可以使用标数法来解答,并且非常直观.到第一站可以有5种选择,每种选择有一种走法, 那么下一站,走1号门就只有一种走法(就是第一站走的2号门),走2号门就有2种走法(第一站走1号或3号门)走3号门也是2种走法(第一站走2号门或4号门)走4号门2种走法(第一站走3号门或者5号门)走5号门只有一种走法(第一站走的是4号门)我们发现在这一站经过某个门有多少种走法,正好等于他左上和右上的两个数字和.于是我们可以将数字标全.这道题的答案就是42种,虽然很多同学会用枚举法也能做出42种,但是一旦这道题给的不是5位数,而是7位数,9位数的话,枚举法就显得无力了.这种时候标数法是个不错的选择.可以用到标数法的问题有很多，大家掌握这种方法之后可以解决很多平时看起来很麻烦的题目。

计数之标数法经典例题讲解【三篇】

计数之标数法经典例题讲解【三篇】
导读：本文计数之标数法经典例题讲解【三篇】，仅供参考，如果觉得很不错，欢迎点评和分享。

【第一篇】一只蜜蜂从A处出发，回到家里B处，每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行，共有多少种回家的方法？
解答：蜜蜂“每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行”这意味着它只能从小号码的蜂房爬进相邻的大号码的蜂房。

明确了行走路径的方向，就可运用标数法进行计算。

如图所示，小蜜蜂从A出发到B处共有89种不同的回家方法。

【第二篇】例1．按图中箭头所指的方向行走，从A到I共有多少条不同的路线？
解答：第1步：在起点A处标1。

再观察点B，要想到达点B，只有一个入口A，所以在B点也标1。

第2步：再观察点C，要想到达点C,它有两个入口A和B，所以在点C处标1＋1＝2。

标数法求表面积

标数法求表面积
（原创实用版）
目录
1.引言
2.标数法的定义和原理
3.标数法在求表面积中的应用
4.标数法的优点和局限性
5.结论
正文
【引言】
标数法是一种求解几何问题的有效方法，广泛应用于计算几何中。

本文将介绍标数法在求表面积中的应用，帮助读者更好地理解和掌握这一方法。

【标数法的定义和原理】
标数法是一种通过给定图形的某些特征（如边、角等）赋予标号，然后利用这些标号进行计算的方法。

它的原理是将复杂的几何问题转化为简单的代数问题，从而简化求解过程。

【标数法在求表面积中的应用】
在求表面积时，我们可以先给定图形的各个面赋予标号，然后利用标数法计算各个面的面积。

具体步骤如下：
1.确定图形的各个面，并为每个面赋予一个标号；
2.计算每个面的边数，并将其与相应的标号相乘；
3.根据面的性质（如三角形、四边形等），计算每个面的面积；
4.将所有面的面积相加，得到图形的总表面积。

【标数法的优点和局限性】
标数法的优点在于它可以将复杂的几何问题转化为简单的代数问题，从而降低问题的难度。

此外，标数法具有较强的通用性，适用于多种几何图形。

然而，标数法也有其局限性，对于某些特殊情况，使用标数法可能不够简便。

【结论】
总之，标数法是一种求解表面积的有效方法，具有较强的通用性和简便性。

标数法C版

标数法

标数法

【典型例题】五年级数学下册第一单元观察物体(三)(含答案)

奥数标数法练习 计数之标数法经典例题讲解

计数第06讲_标数法(学生版)A4

标数法求表面积

标数法C版

行测数量关系技巧：标数法进阶篇

小学奥数教师版-7-1-3 加法原理之树形图及标数法

标数法求表面积

标数法知识点总结

标数法口诀

(word完整版)最短路线问题——标数法的应用

四年级数学：标数法

卡特兰数 标数法

小学计数知识学习习题：标数法(含答案)

计数之标数法经典例题讲解【三篇】

标数法求表面积

奥数标数法练习计数之标数法经典例题讲解

卡特兰数标数法