应力状态分析和强度理论(例题)
应力状态分析与强度理论-习题与答案

(A)受力构件横截面上各点的应力情况
(B)受力构件各点横截面上的应力情况
(C)构件未受力之前,各质点之间的相互作用力状况
(D)受力构件内某一点在不同横截面上的应力情况
2、一实心均质钢球,当其外表面迅速均匀加热,则球心O点处的应力状态是()
(A)单向拉伸应力状态(B)平面应力状态
(A)铸铁为塑性材料
(B)铸铁在三向压应力状态下产生塑性变形
(C)铸铁在单向压应力作用下产生弹性变形
(D)材料剥脱
7、混凝土立方试块在作单向压缩试验时,若在其上、下表面上涂有润滑剂,则试块破坏时将沿纵向裂开,其主要原因是()
(A)最大压应力(B)最大剪应力
(C)最大伸长线应变(D)存在横向拉应力
8、一中空钢球,内径d=20cm,内压p=15Mpa,材料的许用应力 =160Mpa,则钢球壁厚t只少是()
(A)t=47㎜(B)t=2.34㎜
(C)t=4.68㎜(D)t=9.38㎜
9、将沸水注入厚玻璃杯中,有时玻璃杯会发生破裂,这是因为()
(A)热膨胀时,玻璃杯环向线应变达到极限应变,从内、外壁同时发生破裂
(B)玻璃材料抗拉能力弱,玻璃杯从外壁开始破裂
(C)玻璃材料抗拉能力弱,玻璃杯从内壁开始破裂
(D)水作用下,玻璃杯从杯底开始破裂
因圆柱与钢筒之间的空隙 ,而 > ,故圆柱受钢筒弹性约束。设柱与筒之间的作用力为p,则铝柱中各点处主应力为
钢筒中各点处主应力为
设铝柱和钢筒的径向应变分别为 ,变形协变条件为
即
于是
得
p=2.74Mpa
故钢筒周向应力为
即
得
所以则其相当应力为
由于 <0.5
材料力学第七章应力状态和强度理论

x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y
x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2
x
y
2
4 2 xy
x
yx xy x
y
R c
x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2
40
x y
2 0.431MPa
sin( 80 ) xy cos(80 )
C
C
C
例题3:已知梁上的M、Q,试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q = 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa
材料力学应力状态和强度理论

x 122.5MPa x 64.6MPa
σy 0
τ y 64.6
(122.5 , 64.6)
D1
B2
o
C
B1
(0 , - 64.6)
由 x , x 定出 D1 点 由 y , y 定出 D2 点 以 D1D2 为直径作应力圆。
D2
A1,A2 两点的横坐标分别代表 a 点的两个主应力
1 oA1 150MPa
1 x 136.5MPa
σ x 136.5MPa σy 0
τx0 τy0
2 3 0
D2 (0,0)
D1(136.5,0)
x 136.5MPa
b
σ1
σ x 136.5MPa τ x 0
σy 0
τy0
1 所在的主平面就是 x 平面 , 即梁的横截面 C 。
解析法求 a 点的主平面和主应力
解: x 100MPa, y 20MPa, x 40MPa, 300
20
300
100 40
x 100MPa, y 20MPa, x 40MPa, 300
x
2
y
x
2
y
cos
2
x
sin
2
x
2
y
sin
2
x
cos
2
300
100
(20) 2
100
(20) 2
cos( 600)
m
F
A
F
m
A
F
F
A
A 点 横截面 m—m 上的应力为: F
A
n
m
F
A
F
m
n
F
A
2
材料力学习题参考答案2011年7月-第22章应力状态和强度理论

22-6 图示受力板件,试证明A 点处各截面的正应力、剪应力均为零证明:若在尖点A 处沿自由边界取三角形单元体如图所示,设单元体 、面上的应力分量为、和、,自由边界上的应力分量为,则有由于、,因此,必有、、。
这时,代表A 点应力状态的应力圆缩为 坐标的原点,所以A 点为零应力状态。
22-7 图示槽形刚体,在槽内放置一边长为10mm 、的立方钢块,钢块顶面受到合力为P=8kN 的均布压力作用,试求钢块的三个主应力和最大剪应力。
已知材料的弹性模量GPa E 200=,泊松比3.0=μ。
解: 选取坐标轴x 、y 、z 如图。
x σ=0, σz =-10101083⨯⨯=-80MPa ,εy =1E 〔σy -μ(σz +σx )〕=1E〔σy -μσz 〕=0 由此得 σy =μσz =0.3×(-80)=-24 MPa 。
Pxzyo将x σ、y σ、z σ按代数值大小排列,得三个主应力为 σ1=0 、σ2 =-24 MPa 、σ3=-80 MPa 。
最大剪应力 τm a x =σσ132-=280=40 MPa 。
22-12 试比较图示正方形棱柱体在下列两种情况下的相当应力3xd σ:(a )棱柱体自由受压:(b )棱柱体在刚性方模内受压。
弹性常数E 、μ均为已知.解:对于图(a )中的情况,应力状态如图(c )对于图(b )中的情况,应力状态如图(d )所以,,22-20 N O.28a普通热轧工字钢简支梁如图所示。
今由贴在中性层上某点K处、与轴线夹45º角方向上的应变片测得ε45º=-260×10-6。
已知钢材的E=210GPa,μ=0.28。
求作用在梁上的载荷F P。
应力状态分析 、强度理论、组合变形

Page57
BUCT
解:1 T=3×0.25 = 0.75KN.M
2 MxY =7×0.22 = 1.54KN.M
3 MxY中=7×0.22×0.5 =0.77KN.M
4 MxZ=3.5×0.4= 1.4KN.M
5
M总
M
2 z
M
2 y
=1.6
6
r3
1 W
M 2 T 2 [ ]
Page28
BUCT
化工设备机械 基础
然后叠加
= + = Pcos / A + Pl sin y / Iz
1 = N / A + M / Wz
2 = N / A - M / Wz
Page29
BUCT
例题5-5
化工设备机械 基础
Page30
BUCT
化工设备机械 基础
Page31
BUCT
uf 达到某一数值时,材料失效。
强度条件:
1 2
[(1
2
)2
(
2
3
)2
(
3
1)2
]
[]
Page21
BUCT
化工设备机械 基础
r1 1
r2 1-μ(σ2 - σ3 )
r3 1 3 2 4 2
r4
1 2
2 3 2
r3
( M )2 4( T )2 1
W
Wp
W
M 2 T 2 [ ]
Page2
BUCT
§1 应力状态的概念
化工设备机械 基础
一、问题的提出
杆件在基本变形时横截面上应力的分布规律
1. 轴向拉压:
应力状态分析及强度理论习题讲解

答案:
D
四、计算
1. 构件内危险点应力状态如图所示,试作强度校核: 1)材料为铸铁,已知许用拉应力 t 30MPa,压应力 90MPa;3)材料仍为铸铁,应力分量中 为压应力。
15MPa
c 90MPa,泊松比 =0.25;2)材料为铝合金,
15MPa
45 , 45
90 90
45 45
45
x
O
45 , 45
(b)
45
45
x
(c)
(d)
4.用电阻应变仪测得空心钢轴表面一点与母线成45 方向 上的正应变 45 200 103。已知该轴转速为120r / min , 外径D 120mm,内径d 80mm,钢材E 210GPa, =0.28, 求轴传递的功率。
45
a b
1
45
1
3
O
45 3
x
(b)
4 WP D 1 12 10 1 8 /12 16 16 272.3 106 m 3 n E 所以 N WP 45 9550 1 120 210 109 272.3 106 200 103 112kW 9550 1 0.28 3 4 3 6
n
dA
y
30
120
1
t
30
20
1 2
x
2
40 30
(b)
4 5,26 B C
68
240
3)作应力圆(图(c)) (1)取比例尺,1cm-20MPa,在 - 坐标平 面内作点1(+20,0)、2(-40,0);
《材料力学》第7章应力状态和强度理论习题解.
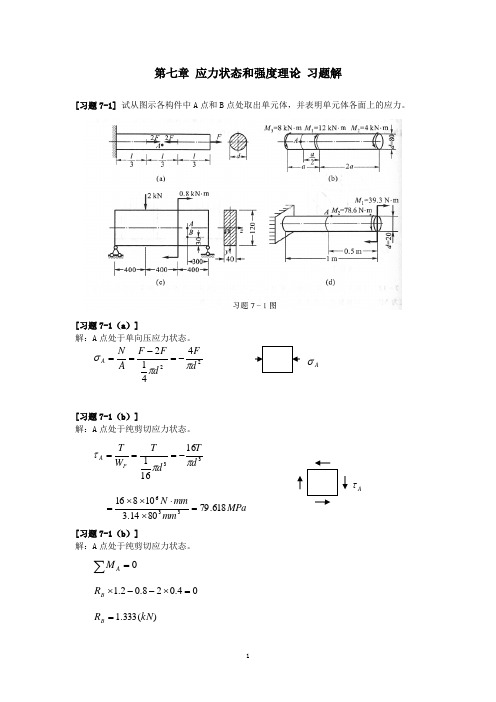
第七章 应力状态和强度理论 习题解[习题7-1] 试从图示各构件中A 点和B 点处取出单元体,并表明单元体各面上的应力。
[习题7-1(a )]解:A 点处于单向压应力状态。
224412d F d F F A N A ππσ-=-==[习题7-1(b )]解:A 点处于纯剪切应力状态。
3316161d T d T W T P A ππτ-===MPa mm mm N 618.798014.310816336=⨯⋅⨯⨯=[习题7-1(b )]解:A 点处于纯剪切应力状态。
0=∑AM04.028.02.1=⨯--⨯B R )(333.1kN R B =)(333.1kN R Q B A -=-=MPa mmN A Q A 417.01204013335.15.12-=⨯⨯-=⨯=τB 点处于平面应力状态MPamm mm mm N I y M zB B 083.21204012130103.0333.1436=⨯⨯⨯⋅⨯⨯==σMPa mm mm mmN b I QS z zB 312.0401204012145)3040(1333433*-=⨯⨯⨯⨯⨯⨯-==τ[习题7-1(d )]解:A 点处于平面应力状态MPa mm mm N W M zA A 064.502014.3321103.39333=⨯⨯⋅⨯==σMPa mm mm N W T PA 064.502014.3161106.78333=⨯⨯⋅⨯==τ [习题7-2] 有一拉伸试样,横截面为mm mm 540⨯的矩形。
在与轴线成045=α角的面上切应力MPa 150=τ时,试样上将出现滑移线。
试求试样所受的轴向拉力F 。
解:AFx =σ;0=y σ;0=x τ 004590cos 90sin 20x yx τσστ+-=A F 2045=τ 出现滑移线,即进入屈服阶段,此时,1502045≤=AFτ kN N mm mm N A F 6060000540/30030022==⨯⨯==[习题7-3] 一拉杆由两段沿n m -面胶合而成。
材料力学习题应力状态和强度理论

应力状态分析与强度理论基 本 概 念 题一、选择题1. 三种应力状态分别如图(a )、(b )、(c )所示,则三者间的关系为( )。
A .完全等价B .完全不等价C .图(b )、图(c )等价D .图(a )、图(c )等价题1图2. 已知应力情况如图所示,则图示斜截面上的应力为( )。
(应力单位为 MPa)。
A .70-=ασ,30-=ατB .0=ασ,30=ατC .70-=ασ,30=ατD .0=ασ,30-=ατ3. 在纯剪切应力状态中,其余任意两相互垂直截面上的 正应力,必定是( )。
A .均为正值B .一为正值一为负值C .均为负值 题2图D .均为零值4. 单元体的应力状态如图所示,由x 轴至1σ方向的夹角为( )。
A .︒5.13 B .︒-5.76 C .︒5.76 D .︒-5.13题4图 题5图5. 单元体的应力状态如图所示,则主应力1σ、2σ分别为( )。
(应力单位MPa). -33-A .901=σ,102-=σB .1001=σ,102-=σC .901=σ,02=σD .1001=σ,02=σ 6. 如图6所示单元体最大剪应力max τ为( )。
A .100 MPaB .50 MPaC .25 MPaD .0题6图 题7图7. 单元体如图所示,关于其主应力有下列四种答案,正确的是( )。
A .1σ>2σ,03=σ B .3σ<2σ<0,03=σ01=σ C .1σ>0,2σ= 0,3σ<0,1σ<3σ D .1σ>0,2σ= 0,3σ<0,1σ>3σ8. 已知应力圆如图7-22所示,图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力,则与应力圆所对应的单元体为( )。
A .图(a )B .图(b )C .图(c )D .图(d )题8图9. 在图示四种应力状态中,其应力圆具有相同的圆心和相同的半径是( )。
-34-题9图A .图(a )、图(d )B .图(b )、图(c )C .图(a )、图(b )、图(c ) 、图(d )D .图(a )、图(d )、图(b )、图(c )10. 如图所示,较大体积的钢块上开有一贯穿的槽,槽内嵌入一铝质立方体,铝块受到均布压力P 作用,假设钢块不变形,铝块处于( )。
7工程力学(下)—应力分析与强度理论2

ν
(
)
由于忽略铜块与钢块上凹坑之间的摩擦, 由于忽略铜块与钢块上凹坑之间的摩擦,所以 σx,σy,σz都是主应力,且 , 都是主应力,
σ 1 = σ 2 = −15.5 MPa σ 3 = −30 MPa
∴σ 1 = 44.3MPa
σ 3 = −20.3MPa
1 0.3 ε z = [0 − υ (σ x + σ y )] = − ( − 20.3 + 44.3) × 10 6 E 210 × 10 9 = − 34.3 × 10 − 6
边长a 例7-8 边长 =0.1 m的铜质立方体置于刚性很 的铜质立方体置于刚性很 大的钢块中的凹坑内(图 , 大的钢块中的凹坑内 图a),钢块与凹坑之间无 间隙。 间隙。试求当铜块受均匀分布于顶面的竖向外 加荷载F 加荷载 =300 kN时,铜块内的主应力、最大 时 铜块内的主应力、 切应力。已知铜的弹性模量E 切应力。已知铜的弹性模量 =100 GPa,泊松 , 比n=0.34。铜块与钢块上凹坑之间的摩擦忽略 = 。 不计。 不计。
思考题: 已知单元体上的应力, 思考题: 已知单元体上的应力,求 σ x τ x .
解:σ α = 120MPa、τ α = 80MPa、
(MPa)
α = 30°、σ y = 0
σα = σx
2 2 3 3 = σx − τ x = 120MPa 4 2 +
τx
σx120Fra bibliotek80σx
30°
cos 60° − τ x sin 60°
[材料力学]材料力学试题库精选题解精选题8_应力状态_强度理论.docx
![[材料力学]材料力学试题库精选题解精选题8_应力状态_强度理论.docx](https://img.taocdn.com/s3/m/9169fcbc5f0e7cd185253626.png)
应力状态强度理论1.图示单元体,试求 (1) 指定斜截而丄的应力;(2) 主应力大小及主平而位置,并将主平而标在单元体上。
F<T r — CT V解:(1) (y (/ = — ----- + ---------- cos 2a 一 g sin 2& = 76.6 MPar r/ = ----- sin + r v cos2a =-32.7 MPaCc£X-50 ± 加 +(—129.9)2 = _50 ±1506=100 MPa, (r 2 = 0 , 6=-200 MPa解:b 、=150 MPa,「=—120 MPayx由 r = ----------- sin 2Q +「cos 2a = —~~— = -804522得 6 =-10 MPa3.—点处两个互成45°平面上的应力如图所示,其屮<7未知,求该点主应力。
max bmin81.98 MPa-121.98a = 81.98 MPa, <r 2 = 0 , cr 3 = -121.98 MPa^0=larctan(^^) = l arctan2 CT X -cr v 2402.某点应力状态如图示。
试求该点的主应力。
解:取合适坐标轴令6=25 MPa, r x =-129.9 MPa120"-- ----- sin 2a + T cos 2a = 0 得 = -125 MPa 2 -100MPa-200150 MPacr cr + cr所以max= __ ±2214.22MPa一74.226=214.22 MPa, cr2 = 0, <r3 = -74.22 MPa4.图示封闭薄壁圆筒,内径d=100 mm,壁厚f = 2 mm,承受内床“ =4 MPa, 外力偶矩M“=0・192 kN-mo求靠圆筒内壁任一点处的主应力。
解・・r常九严停32a=^- = 5Q MPax 4t<r v二四= 100 MPa、2tmax bmin 100.7MPa 49.356=100.7 MPa, 6=49.35 MPa, (r3 = -4 MPa5.受力体某点平面JL的应力如图示,求其主应力大小。
5-应力状态分析-强度理论-组合变形(共37张)

dt
d
sx
s y
cos2 2t xy sin 2
0
设极值切应力所在平面外法线与x轴正向夹角为α1,则由
上式得
tan
21
s
x s 2t xy
y
第17页,共37页。
(5-7)
17
5 应力状态(zhuàngtài)分析 强度理论(续)
式(5-7)亦有两个解 和1
1
, 说明两个极值
2
切应力所在平面互相垂直。由上式解出sin2α1和cos2α1,
强度条件:
s1 (s 2 s 3 ) s
(5-15)
适用条件:这一理论可较好地解释石料、混凝土等脆性材料压
缩时的破坏现象。
31
第31页,共37页。
5 应力状态分析 强度(qiángdù)理论(续)
2、塑性屈服理论
(1)最大切应力理论(第三强度理论)
观点:最大切应力是引起材料破坏的主要因素。即无论
2
比较式(5-5)和式(5-7),可见
(5-9)
tan 21
1
tan 2 0
cot 2 0
tan
2
0
2
——说明极值切应力所在平面与主平面成45º角。
21
2 0
2
1
0
4
19
第19页,共37页。
5 应力状态分析 强度理论(续)
[例5-2]分析拉伸试验时低碳钢试件出现(chūxiàn)滑移线的原因。
第10页,共37页。
5 应力状态分析(fēnxī) 强度理论(续)
利用三角函数公式
cos2 1 cos2
2
sin2 1 cos2
2
工程力学第13章应力状态分析和强度理论

max
m in
x
y
2
(
x
2
y
)2
2 xy
——主应力的大小
3)、 切应力 的极值及所在截面
由
x
y
2
sin 2
xy cos 2 ,
令 d
0
d 1
tan
21
x 2 xy
y
(1 ; 1 1 900 )
——最大切应力 所在的位置
z
x
y y
x
z x
2
I 3 1
(1)求平行于σ1的方向面的应力σα 、 τα ,其上之应力与σ1 无关.
1
3
II 2
(2)求平行于σ2的方向面的应力σα、 τα ,其上之应力与σ2 无关.
2
III 1 3
2
(3)求平行于σ3的方向面的应力σα 、 τα ,其上之应力与σ3 无关.
例2、槽形刚体内放置一边长为a = 10 cm 正方形钢块,试求钢 块的三个主应力。F = 8 kN,E = 200 GPa, μ = 0.3。
Fy
解:1) 研究对象ຫໍສະໝຸດ 正方形钢块y F 80 MPa, A
x
?,
z 0.
x 0, y ?, z ? .
y
x b
a
c x x
y
b x
x
a y
c
y t
n 单元体各面面积
x bc : dA
ab: dAcos ac : dAsin
设:斜截面面积为dA,由分离体平衡得:
第十二章 应力状态和强度理论习题
试题答案:
解:(1)
(2)
(3)
, ,
8、求图示木梁截面 上点 与轴线成 角方向的线应变 。已知 , , ,材料的弹性模量 ,泊松比 。
试题答案:
解:在点B,正应力为零,只有切应力,为纯剪切应力状态。
,
9、设地层由石灰岩组成,其密度 ,泊松比 。计算离地面 深处的地压应力。
(2)
(3)
12、受内压的薄壁圆筒,已知内压为 ,平均直径为 ,壁厚为 ,弹性常数为 、 。试确定圆筒薄壁上任一点的主应力、主应变及第三、第四强度理论的相当应力。
解: , ,
13、构件中危险点的应力状态如图所示。试选择合适的准则对以下两种情形作强度校核:1.构件为钢制
= 45MPa, = 135MPa, = 0, = 0,
1、层合板构件中微元受力如图所示,各层板之间用胶粘接,接缝方向如图中所示。若已知胶层剪应力不得超过1MPa。试分析是否满足这一要求。
解:
MPa
MPa,不满足。
2从构件中取出的微元受力如图所示,其中AC为无外力作用的自由表面。试求:x和xy。
解:应用应力解析公式,有
MPa
据此,解得
MPa
Mpa
3、已知一点的应力状态如图。试求其主应力及其方向角,并确定最大切应力值。
许用应力 = 160MPa。
2.构件材料为铸铁
= 20MPa, =25MPa, = 30MPa, = 0, = 30MPa。
解:
1. 强度满足。
2. 强度满足。
14、炮筒横截面如图示。在危险点处 , ,第二个主应力 ,且垂直于图面。材料的 ,试用第三强度和第四强度理论进行强度校核。
知识资料材料力学知识资料应力状态分析和强度理论(三)组合变形压杆稳定(新版)

需要课件请或强度理论(一)强度理论的概念1.材料破坏的两种类型材料破坏型式不仅与材料本身的材质有关,而且与材料所处的应力状态、加载速度温度环境等因素有关。
材料在常温、静载荷下的破坏型式主要有以下两种:脆性断裂材料在无显然的变形下骤然断裂。
塑性屈服(流动) 材料浮上显著的塑性变形而丧失其正常的工作能力。
2.强度理论在复杂应力状态下关于材料破坏缘故的假设,称为强度理论。
研究强度理论的目的,在于利用容易应力状态下的实验结果,来建立材料在复杂应力状态下的强度条件。
(二)四个常用的强度理论四个常用强度理论的强度条件可以统一地写成式中σr称为相当应力,其表达式为最大拉应力理论σr1=σ1(第一强度理论)最大拉应变理论σr2=σ1-ν(σ1+σ2)(第二强度理论)最大剪应力理论σr3=σ1-σ3(第三强度理论)形状改变比能理论(第四强度理论)[σ]为材料的许用应力。
第1 页/共18 页对于工程上常见的一种二向应力状态如图5—9—3所示,其特点是平面内某一方向的正应力为零。
设σy=0,则该点的主应力为代入(5—9-15)式得:第三强度理论(最大剪应力理论)的相当应力为第四强度理论(形状改变比能理论)的相当应力为最大拉应力理论、最大拉应变理论是关于脆性断裂的强度理论;最大剪应力理论、形状改变比能理论是关于塑性屈服的强度理论。
强度理论的选用在三向拉应力作用下,材料均产生脆性断裂,故宜用第一强度理论;而在三向压缩应力状态下,材料均产生屈服破坏,故应采用第三或第四强度理论。
当材料处于二向应力状态作用下时:脆性材料易发生断裂破坏,宜用第一或第二强度理论;塑性材料易发生塑性屈服破坏,宜用第三或第四强度理论。
[例5-9-1] 已知构件上某点的应力单元体如图5-9-4(a),(b)所示(图中应力单位为MPa)。
试求指定斜截面上的应力。
[解] 图示单元体处于平面应力状态。
(1)在图示坐标中代人公式(5-9-1)、(5-9-2)得σα、τσ方向如图中所示。
第8章例题-强度理论-纯剪切

例 试按强度理论建立纯剪切应力状态的强度条件,并寻求 许用切应力和许用拉应力之间的关系。 y 解 圆轴扭转时,三个主应力为
1 , 2 0, 3
纯剪切的强度条件为 [ ] 塑性材料:
3
1
n
45
x
第三强度理论 r3 1 3 2 [ ] [ ] 0.5[ ] 第四强度理论
工 程 力 学 第 8 章 应 力 状 态 理 论 与 强 度 理 论
版权所有 张强 钟艳玲
例 试按强度理论建立纯剪切应力状态的强度条件,并寻求 许用切应力和许用拉应力之间的关系。 y 解 圆轴扭转时,三个主应力为
1 , 2 0, 3
纯剪切的强度条件为 [ ] 脆性材料: 第一强度理论 r1 1 [ ] 第二强度理论
例 试按强度理论建立纯剪切应力状态的强度条件,并寻求 许用切应力和许用拉应力之间的关系。 y
[ ] (0.8 1)[ ](脆性材料) [ ] (0.5 0.6)[ ](塑性材料)
3
1
n
45
x3Βιβλιοθήκη 31n
45
x
[ ] [ ]
r2 1 ( 2 3 ) (1 ) [ ]
比如铸铁, 0.25
0.8[ ]
1
[ ] (0.8 1)[ ](脆性材料)
工 程 力 学 第 8 章 应 力 状 态 理 论 与 强 度 理 论
r4
1 2
[(1 2 )2 ( 2 3 )2 ( 3 1 )2 ]
3 [ ]
0.577[ ]
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
50 x 100 x 100 cos 600 0
300
2
2
100MPa x
(3)求主应力:因为τxy = 0,所以有
1 100 MPa 2 0 3 100 MPa
(4)求最大剪应力:
100 100 100MPa
max
例题
例7-4 薄壁锅炉的平均直径D=1060 mm,壁厚t=25 mm,蒸气压力p=2.5 MPa,材料许用应力
[σ]=40 MP;按最大剪应力理论校核锅炉的强度。
σ’ p
σ’
p
σ’’
σ’’
强度不够,重新设计 pD
r3
1
3
2t
t
pD
2
0.033m
(5)用最大形状改变比能理论计算
210 109
3.11104
τα
σα
300
τxy
p.5
例题
例题
例7-4 薄壁锅炉的平均直径D=1060 mm,壁厚t=25 mm,蒸气压力p=2.5 MPa,材料许用应力
[σ]=40 MP;按最大剪应力理论校核锅炉的强度。
σ’ p
σ’
p
σ’’
σ’’
解:(1)由横截面分离体的平衡条件
' Dt p 1 D2 4
例题
(d) (1)应力分量 (2)用解析法求斜截面上的应力
(3)应力圆
p.9
例题
例题
例7-6. 已知应力状态如图所示,图中的应力单位为MPa。试求:
(1)主应力大小,主平面位置;(2)在单元体上给出主平面位置及主应力方向;(3)最大剪应力。
解: (1)应力分量
应力圆
(2)求主平面位置和主应力大小
p.10
2 60 80 40
1
20 450 0 22.50 0 90 112 .50
40MPa 60MPa 80MPa
(2)求主应力:
m a x m in
x
y
2
x
y
2
2
2 xy
80 40
例题
例题
3
4
5
2
应力状态分析和 6
1
强度理论
7
11
8 10
9
p.1
例题
例题
例7-1 已知图示单元体上的应力为σx=80MPa,σy=-40MPa,τxy’=-60MPa;求主应力、主平面、剪应 力极值和极值平面,并在单元体上表示出来。
解:(1)求主平面:
tg 2 0
2 xy x y
(3)求剪应力的极值和位置
40MPa 60MPa
m m
ax in
x
y
2
2
xy2
80MPa
80
40 2
602
2
84.9MPa 84.9MPa
α1 = α0+45 0 = 67.5 0 , 对应τmax
2
104.8MPa 64.9MPa
按代数值大小排列:
;
80
40
2来自6022
1 104 .8MPa 2 0 3 64.9MPa
由于σx >σy,则α0=22.50对应σ1
p.2
例题
例题
例7-1 已知图示单元体上的应力为σx=80MPa,σy=-40MPa,τxy’=-60MPa;求主应力、主平面、剪应 力极值和极值平面,并在单元体上表示出来。
' pD 26.5MPa 4t
(2)由纵截面分离体的平衡条件
2'' lt pDl
(3)确定主应力
'' pD 53MPa 2t
1 '' , 2 ' , 3 0
(4)用最大剪应力强度理论计算
r3 1 3 53MPa
p.6
例题
0.0285m
p.7
例题
例7-5 .在图示各单元体中,试用解析法和应力圆求斜面ab上的应力。应力单位为MPa。
例题
解:(a) (1)应力分量
(2)用解析法求斜截面上的应力
(3)应力圆
(-70、0)
τ (35,36.5)
600
σ (70、0)
p.8
例题
例7-5 .在图示各单元体中,试用解析法和应力圆求斜面ab上的应力。应力单位为MPa。
求:(1)A点在指定斜截面上的应力。(2)A点主应力的大小及方向,并用单元体表示。
解:(1)A点的应力状态 属二向应力状态,应力分量是
p.12
例题
例题
例7-7. 薄壁圆筒的扭转-拉伸示意图如图所示。若P=20kN,T=600NN·m,且d=50mm,=2mm。试
2
p.4
例题
例题
例7-3 图示钢轴上作用一个力偶M=2500 kNm,已知D=60 mm,E=210 GPa, µ=0.28;圆轴表面上 任一点与母线成α =300方向上的正应变。
解:(1)取A点的单元体,应力状态为:
xy
T Wt
M
1 D3
58.95MPa
x y 0 16
(4)在单元体上标出它们的位置;
σ1
τmax
α0
σ3
p.3
例题
例7-2 已知图示正三角形单元体上的应力,求主应力和最大剪应力。 50MPa
解:(1)取出正三角形一半(直角三角形),分析如图;
50MPa 300
86.6MPa
σx
86.6MPa
例题
50MPa 86.6MPa 100MPa
100MPa
(2)求σx的值;
例题
例题
例7-6. 已知应力状态如图所示,图中的应力单位为MPa。试求:
(1)主应力大小,主平面位置;(2)在单元体上给出主平面位置及主应力方向;(3)最大剪应力。
(2)求主平面位置和主应力大小
(3)最大剪应力
p.11
例题
例题
例7-7. 薄壁圆筒的扭转-拉伸示意图如图所示。若P=20kN,T=600NN·m,且d=50mm,=2mm。试
M A
300
(2)求斜截面上的正应力
300 xy sin 600 51.05MPa
σα+90o
300900 xy sin 2400 51.05MPa
(3)计算斜截面上的应变
1
300
E 300
1200
1 51.5 0.28 51.5106
1 2 2 2
r4
21
2
2
3
3
1
45.9MPa
强度不够,重新设计
r4
1 2 2 2
2
1
2
2
3
3
1
3 pD
4t
t
3 pD
4
