第5章习题解答2
《电力系统分析》第5章 习题解答

第五章思考题及习题答案5-1什么是电力系统的有功功率备用容量?为什么要设置备用容量?答:系统的电源容量超出发电厂发出的有功功率的总和的部分,称为系统的备用容量。
系统设置有功功率备用容量为了满足频率调整的需要,以保证在发电、供电设备发生故障或检修时,以及系统负荷增加时,系统仍有足够的发电容量向用户供电,保证电力系统在额定频率下达到有功平衡。
5-2 电力系统频率偏移过大的影响有哪些?答:频率偏移过大时,主要有以下影响:(1)电动机的转速和输出功率随之变化,会严重地影响产品的质量。
(2)会影响各种电子设备工作的精确性。
(3)对电力系统的正常运行影响很大。
对汽轮发电机叶片都有不良影响;电厂用的许多机械如水泵、风机等在频率降低时都要减小出力,因而影响发电设备的正常运行,使整个发电厂的有功出力减小,从而导致系统频率的进一步下降;频率降低时,异步电动机和变压器的励磁电流增大,为了不超越温升限额,不得不降低发电机的发出功率;频率降低时,系统中的无功功率负荷将增大,无功功率损耗增加,这些都会给电力系统无功平衡和电压调整增加困难。
总之,由于所有设备都是按系统额定频率设计的,系统频率质量的下降将影响各行各业。
而频率过低时,甚至会使整个系统瓦解,造成大面积停电。
5-3 什么是电力系统负荷的有功功率—静态频率特性?何为有功功率负荷的频率调节效应?K的大小与哪些因素有关?L答:系统处于运行稳定时,系统中有功负荷随频率的变化特性称为负荷的有功功率—静态频率特性。
当系统有功平衡破坏而引起频率变化时,系统负荷也参与对频率的调节(当频率变化时,系统中的有功功率负荷也将发生变化),这种特性有助于系统中的有功功率在新的频率下重新达到平衡,这种现象称为负荷的频率调节效应。
K的数值取决于全电力系统各类负荷的比重。
L5-4什么是电力系统发电机组的有功功率—静态频率特性?何为发电机组的单位调节功率?K的大小与哪些因素有关?G答:发电机输出的有功功率与频率之间的关系称为发电机组的有功功率一频率静态特性。
第5章感应电机习题与解答

C ;D 。
答A
6.★三相异步电动机气隙增大,其他条件不变,则空载电流( )。
A 增大 ; B 减小 ;
C 不变 ; D 不能确定。
答A
7.三相感应电动机等效电路中的附加电阻 上所消耗的电功率应等于():
A输出功率 ;B输入功率 ;
C电磁功率 ;D总机械功率 。
答D
8.与普通三相感应电动机相比,深槽、双笼型三相感应电动机正常工作时,性能差一些,主要是()。
答A
12.★设计在 电源上运行的三相感应电动机现改为在电压相同频率为 的电网上,其电动机的()。
A 减小, 减小, 增大;B 减小, 增大, 减小;
C 减小, 减小, 减小;D 增大, 增大, 增大。
答C
13.一台绕线式感应电动机,在恒定负载下,以转差率 运行,当转子边串入电阻 ,测得转差率将为()( 已折算到定子边)。
。
答1,
4.★感应电动机起动时,转差率 ,此时转子电流 的值, ,主磁通比,正常运行时要 ,因此起动转矩 。
答 1,很大,很小,小一些,不大
5.★一台三相八极感应电动机的电网频率 ,空载运行时转速为735转/分,此时转差率为,转子电势的频率为。当转差率为0.04时,转子的转速为,转子的电势频率为。
答0.02, , ,
6.三相感应电动机空载时运行时,电机内损耗包括,,,和,电动机空载输入功率 与这些损耗相平衡。
答定子铜耗,定子铁耗,机械损耗,附加损耗
7.三相感应电机转速为 ,定子旋转磁场的转速为 ,当 时为运行状态;当 时为运行状态;当 与 反向时为运行状态。
答电动机,发电机,电磁制动
8.增加绕线式异步电动机起动转矩方法有 ,。
A4极, ; B6极, ;
第5章思考题和习题解答

第五章 电气设备的选择5-1 电气设备选择的一般原则是什么?答:电气设备的选择应遵循以下3项原则:(1) 按工作环境及正常工作条件选择电气设备a 根据电气装置所处的位置,使用环境和工作条件,选择电气设备型号;b 按工作电压选择电气设备的额定电压;c 按最大负荷电流选择电气设备和额定电流。
(2) 按短路条件校验电气设备的动稳定和热稳定 (3) 开关电器断流能力校验5-2 高压断路器如何选择? 答:(1)根据使用环境和安装条件来选择设备的型号。
(2)在正常条件下,按电气设备的额定电压应不低于其所在线路的额定电压选择额定电压,电气设备的额定电流应不小于实际通过它的最大负荷电流选择额定电流。
(3)动稳定校验(3)max shi i ≥ 式中,(3)sh i 为冲击电流有效值,max i 为电气设备的额定峰值电流。
(4)热稳定校验2(3)2th th ima I t I t ∞≥式中,th I 为电气设备在th t 内允许通过的短时耐热电流有效值;th t 为电气设备的短时耐热时间。
(5)开关电器流能力校验对具有分断能力的高压开关设备需校验其分断能力。
设备的额定短路分断电流不小于安装地点最大三相短路电流,即(3).max cs K I I ≥5-3跌落式熔断器如何校验其断流能力?答:跌落式熔断器需校验分断能力上下限值,应使被保护线路的三相短路的冲击电流小于其上限值,而两相短路电流大于其下限值。
5-4电压互感器为什么不校验动稳定,而电流互感器却要校验?答:电压互感器的一、二次侧均有熔断器保护,所以不需要校验短路动稳定和热稳定。
而电流互感器没有。
5-5 电流互感器按哪些条件选择?变比又如何选择?二次绕组的负荷怎样计算? 答:(1)电流互感器按型号、额定电压、变比、准确度选择。
( 2)电流互感器一次侧额定电流有20,30,40,50,75,100,150,200,400,600,800,1000,1200,1500,2000(A )等多种规格,二次侧额定电流均为5A ,一般情况下,计量用的电流互感器变比的选择应使其一次额定电流不小于线路中的计算电流。
第5章 北邮信号与系统课后习题解答

1 s2
e s 1
(4)
2
(t)
3e 2 t u (t )
2
s
3
2
(5)L
[
1 2a
3
(sin
at
at
cos at)]
1 2a3
(s2
a
a2
a
d ds
( s2
s
a2
))
1 2a2
( s2
1 a2
s2 a2 (s2 a2)2
)
1 (s2 a2)2
1)]
e(s2) s2
其波形题 5-3 解图所示。
f1 (t ) 1
f2 (t) 1
t
1
t
f3 (t) e2
t
f4 (t)
e-2
1
t
5-4 解:
题 5-3 解图
(a)L [ f1(t)] L [E[u(t t1) u(t t1 )] E[u(t t2) u(t t2 )]]
1[ (s2
s 1)2
]
1 2
t
sin
t
由拉氏变换的积分性质
L
1[
(
s
2
2
1)2
]
t
sin d
sin t
t cos t
,t
0
0
或:
s
1 2
1
sin
t
,
(s2
2 1)2
sin t *sin t
sin t t cos t
第5章振动和波动习题解答

第5章 振动和波动5-1 一个弹簧振子 m=:0.5kg , k=50N ;'m ,振幅 A = 0.04m ,求 (1) 振动的角频率、最大速度和最大加速度;(2) 振子对平衡位置的位移为 x = 0.02m 时的瞬时速度、加速度和回复力; (3) 以速度具有正的最大值的时刻为计时起点,写出振动方程。
频率、周期和初相。
A=0.04(m) 二 0.7(rad/s) 二-0.3(rad)⑷10.11(Hz) T 8.98(s)2 n、5-3证明:如图所示的振动系统的振动频率为1 R +k 2式中k 1,k 2分别为两个弹簧的劲度系数,m 为物体的质量V max 二 A =10 0.04 = 0.4(m/s) a max 二 2A =102 0.04 =4(m/s 2) ⑵设 x =Acos(,t :;;■『),贝Ud x vA sin(,t 「)dtd 2xa一 dt 2--2Acos(「t 亠 ^ ) - - 2x当 x=0.02m 时,COS (;:, t :忙)=1/ 2, sin( t 「)= _、一3/2,所以 v ==0.2、.3 ==0.346(m/s) 2a = -2(m/s )F 二 ma = -1(N)n(3)作旋转矢量图,可知:2x =0. 0 4 c o st(1 0)25-2弹簧振子的运动方程为 x =0.04cos(0.7t -0.3)(SI),写出此简谐振动的振幅、角频率、严...U ・」|1岛解:以平衡位置为坐标原点,水平向右为 x 轴正方向。
设物体处在平衡位置时,弹簧 1的伸长量为Xg ,弹簧2的伸长量为x 20,则应有_ k ] X ]0 ■木2乂20 = 0当物体运动到平衡位置的位移为 X 处时,弹簧1的伸长量就为x 10 X ,弹簧2的伸长量就为X 20 -X ,所以物体所受的合外力为F - -k i (X io X )k 2(X 20 -x)- -(匕 k 2)x2d x (k i k 2)dt 2 m上式表明此振动系统的振动为简谐振动,且振动的圆频率为5-4如图所示,U 形管直径为d ,管内水银质量为 m ,密度为p 现使水银面作无阻尼 自由振动,求振动周期。
机械制造技术基础(第2版)第五章课后习题答案

《机械制造技术基础》部分习题参考解答第五章工艺规程设计5-1 什么是工艺过程?什么是工艺规程?答:工艺过程——零件进行加工的过程叫工艺过程;工艺规程——记录合理工艺过程有关内容的文件叫工艺规程,工艺规程是依据科学理论、总结技术人员的实践经验制定出来的。
5-2 试简述工艺规程的设计原则、设计内容及设计步骤。
5-3 拟定工艺路线需完成哪些工作?5-4试简述粗、精基准的选择原则,为什么同一尺长方向上粗基准通常只允许用一次?答:粗、精基准的选择原则详见教材P212-214。
粗基准通常只允许用一次的原因是:粗基准一般是毛面,第一次作为基准加工的表面,第二次再作基准势必会产生不必要的误差。
5-5加工习题5-5图所示零件,其粗、精基准应如何选择(标有 符号的为加工面,其余为非加工面)?习题5-5图a)、b)、c)所示零件要求内外圆同轴,端面与孔轴线垂直,非加工面与加工面间尽可能保持壁厚均匀;习题5-5图d)所示零件毛坯孔已铸出,要求孔加工余量尽可能均匀。
习题5-5图解:按题目要求,粗、精基准选择如下图所示。
5-6为什么机械加工过程一般都要划分为若干阶段进行?答:机械加工过程一般要划分为粗加工阶段、半精加工阶段、精加工阶段和光整加工阶段。
其目的是保证零件加工质量,有利于及早发现毛坯缺陷并得到及时处理,有利于合理使用机床设备。
5-7 试简述按工序集中原则、工序分散原则组织工艺过程的工艺特征,各用于什么场合?5-8什么是加工余量、工序余量和总余量?答:加工余量——毛坯上留作加工用的材料层;工序余量——上道工序和本工序尺寸的差值;总余量——某一表面毛坯与零件设计尺寸之间的差值。
5-9 试分析影响工序余量的因素,为什么在计算本工序加工余量时必须考虑本工序装夹误差和上工序制造公差的影响?5-10习题5-10图所示尺寸链中(图中A0、B0、C0、D0是封闭环),哪些组成环是增环?那些组成环是减环?习题5-10图解:如图a),A0是封闭环,A1, A2, A4, A5, A7, A8是增环,其余均为减环。
第5章 刚体的定轴转动 习题解答

对飞轮,由转动定律,有 式中负号表示摩擦力的力矩方向与角速度 方向相反。
联立解得
以 F 100 N 等代入上式,得
Fr R 2 (l1 l2 ) F J mRl1
5-1
第 5 章 刚体的定轴转动
2 0.40 (0.50 0.75) 40 100 rad s 2 60 0.25 0.50 3 t
由以上诸式求得角加速度
(2)
Rm1 rm2 g I m1 R 2 m2 r 2 0.2 2 0.1 2
1 1 10 0.202 4 0.102 2 0.202 2 0.102 2 2
9.8 6.13 rad s 2
T2 m2 r m2 g 2 0.10 6.13 2 9.8 20.8N T1 m1 g m1 R 2 9.8 2 0.2. 6.13 17.1N v 2a1h 2 Rh 2 6.13 0.2 2 2.21 m s 1
M M f J 1
t1
。移去力矩 M 后,根据转动定律,有
M f J 2
2
联立解得此转轮的转动惯量
0 t2
J
M 20 17.36 kg m 2 1 1 1 100 2 1 60 10 100 t1 t2
v0
6(2 3 3m M l J l 1M (1 2 ) (1 ) 2 ml 2 3m 12 m
(2) 由①式求得相碰时小球受到的冲量为:
I Fdt mv mv mv0
负号说明所受冲量的方向与初速度方向相反。
电工技术第五章 三相电路习题解答

139第五章 三相电路[练习与思考]5-1-1 对称三相电源的三相绕组作星形联接时,设线电压uAB=380sin(ωt+30o)V ,试写出相电压uB 的三角函数式及相量式。
解:V t u B )120sin(220︒-=ωV U B ︒-∠=∙1202110 5-1-2 三角形联接的对称三相电源,空载运行时三相电源会不会在三相绕组所构成的闭合回路中产生电流?如果一相电源电压极性接反,则闭合回路中是否有电流通过?解:空载运行时,电源回路中无电流通过。
如果一相电源电压极性接反,则闭合回路中有电流通过。
5-2-1 为什么电灯开关一定要接在相线(火线)上?解:因为电灯是单相负载,当开关断开时,电灯灯头不带电,以便于安全维修和更换。
如果开关接在零线上,当其断开时,电灯灯头依然带电(接在火线上),作业时会造成触电事故。
5-2-2 三相四线制电路中,中线阻抗为零。
若星形负载不对称,则负载相电压是否对称?如果中线断开,负载电压是否对称?解:三相四线制电路中,若星形负载不对称,负载相电压仍然对称;如果中线断开,负载电压将不对称。
5-2-3 三相四线制电路中,电源线的中性线上规定不得加装保险丝,这是为什么? 解:如果电源线的中性线上加装保险丝,一旦由于某种原因造成保险丝熔断,接成Y 型的各组单相负载上的各相相电压将不会对称,有的相电压可能会超过单相负载的额定电压,造成损坏;有的相电压可能会低于额定电压,使得负载不能正常工作。
因此源线的中性线上规定不得加装保险丝。
5-3-1 三相负载对称是指下述三种情况下的哪一种:⑴|Z AB |=|Z BC |=|Z CA |;⑵φAB =φBC =φCA ;⑶Z AB =Z BC =Z CA 。
、解:三相负载对称是指(3),阻抗模相等,阻抗角相等。
5-3-2 已知对称三角形联接的三相电路中A 相负载线电流A 010∠=∙A I ,试写出其余各相线电流与相电流。
解:A I B ︒-∠=∙12010 A I C ︒+∠=∙12010140A I AB ︒∠=∙308.5 A I BC ︒-∠=∙908.5 A I CA ︒∠=∙1508.55-4-1 同一三相负载,采用三角形联接和星形联接接于线电压相同的三相电源上,试求这两种情况下负载的线电流、相电流及有功功率的比值。
电路与模拟电子技术(第二版第五章习题解答

第五章 电路的暂态分析5.1 题5.1图所示各电路在换路前都处于稳态,求换路后电流i 的初始值和稳态值。
解:(a )A i i L L 326)0()0(===-+,换路后瞬间 A i i L 5.1)0(21)0(==++ 稳态时,电感电压为0, A i 326==(b )V u u C C 6)0()0(==-+, 换路后瞬间 02)0(6)0(=-=++C u i 稳态时,电容电流为0, A i 5.1226=+=(c )A i i L L 6)0()0(11==-+,0)0()0(22==-+L L i i 换路后瞬间 A i i i L L 606)0()0()0(21=-=-=+++ 稳态时电感相当于短路,故 0=i(d )2(0)(0)6322C C u u V +-==⨯=+ 换路后瞬间 6(0)63(0)0.75224C u i A ++--===+(a)(b)(d)(c)C2ΩL 2+6V -题5.1图i稳态时电容相当于开路,故 A i 12226=++=5.2 题5.2图所示电路中,S 闭合前电路处于稳态,求u L 、i C 和i R 的初始值。
解:换路后瞬间 A i L 6=,V u C 1863=⨯= 06=-=L R i i031863=-=-=C L C u i i0==+R C L Ri u u ,V u u C L 18-=-=5.3 求题5.3图所示电路换路后u L 和i C 的初始值。
设换路前电路已处于稳态。
解:换路后,0)0()0(==-+L L i i ,4mA 电流全部流过R 2,即(0)4C i mA +=对右边一个网孔有:C C L u i R u R +⋅=+⋅210由于(0)(0)0C C u u +-==,故2(0)(0)3412L C u R i V ++==⨯=5.4 题5.4图所示电路中,换路前电路已处于稳态,求换路后的i 、i L 和 u L 。
大学物理基础教程答案第05章习题分析与解答

5-1 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常数,R 为摩尔气体常数,则该理想气体的分子数为( )。
(A )PV m (B )PV kT (C )PV RT (D ) PVmT解:由N p nkT kT V ==得,pVN kT=,故选B 5-2 两个体积相同的容器,分别储有氢气和氧气(视为刚性气体),以1E 和2E 分别表示氢气和氧气的内能,若它们的压强相同,则( )。
(A )12E E = (B )12E E > (C )12E E < (D ) 无法确定 解:pV RT ν=,式中ν为摩尔数,由于两种气体的压强和体积相同,则T ν相同。
又刚性双原子气体的内能52RT ν,所以氢气和氧气的内能相等,故选A 5-3 两瓶不同种类的气体,分子平均平动动能相同,但气体分子数密度不同,则下列说法正确的是( )。
(A )温度和压强都相同 (B )温度相同,压强不同 (C )温度和压强都不同(D )温度相同,内能也一定相等解:所有气体分子的平均平动动能均为32kT ,平均平动动能相同则温度相同,又由p nkT =可知,温度相同,分子数密度不同,则压强不同,故选B5-4 两个容器中分别装有氦气和水蒸气,它们的温度相同,则下列各量中相同的量是( )。
(A )分子平均动能 (B )分子平均速率 (C )分子平均平动动能 (D )最概然速率解:分子的平均速率和最概然速率均与温度的平方根成正比,与气体摩尔质量的平方根成反比,两种气体温度相同,摩尔质量不同的气体,所以B 和D 不正确。
分子的平均动能2i kT ε=,两种气体温度相同,自由度不同,平均动能则不同,故A 也不正确。
而所有分子的平均平动动能均为k 32kT ε=,只要温度相同,平均平动动能就相同,如选C 5-5 理想气体的压强公式 ,从气体动理论的观点看,气体对器壁所作用的压强是大量气体分子对器壁不断碰撞的结果。
第5章 反馈放大电路 习题解答

第五章习题参考答案5-1 试判断图5-22所示集成运放电路的反馈类型。
a) b)图5-22题5-1的图答 (a )F R 、1R :引入串联电压负反馈。
(b )F R 、1R :引入了正反馈。
5-2 电路如图5-23所示,解答下列为题: 1)1F R 引入了何种反馈,其作用如何? 2)2F R 引入了何种反馈,其作用如何?图5-23 题5-2图解 1)1F R 、3E R 引入的是直流电流并联负反馈。
其作用是稳定静态电流2E I 。
其稳定过程如下:↓↓→↓→↑→↑→↑→↑→2211122E B C C B E E I I U I I U I2)2F R 引入的是交、直流电压串联负反馈。
其作用是交流电压串联负反馈可改善放大器的性能,如提高电压放大倍数的稳定性、减小非线性失真、抑制干扰和噪声、展宽放大电路的通频带等。
由于是电压负反馈还可使反馈环路内的输出电阻降低)1(AF +倍。
由于是串联反馈可使反馈环路内的输入电阻增加)1(AF +倍。
2F R 引入的直流电压串联负反馈的作用是稳定静态电压2C U ,其稳定过程如下:↓↑→↑→↓→↓→↑→↑→2211112C C C C B E C U I U I I u U5-3 在图5-24所示的两级放大电路中,(1)那些是直流负反馈;(2)哪些是交流负反馈,并说明其类型;(3)如果F R 不接在T 2的集电极,而是接在C 2与L R 之间,两者有何不同?(4)如果F R 的另一端不是接在T 1的发射极,而是接在它的基极,有何不同,是否会变为正反馈?5-24 题5-3图解 1)1E R 、2E R 直流串联电流负反馈,F R 、1E R 直流电压串联负反馈。
2)F R 、1E R 交流电压串联负反馈。
3)如果F R 不接在T 2的集电极,而是接在C 2与L R 之间,则F R 、1E R 只有交流电压串联负反馈,没有直流反馈。
4)如果F R 的另一端不是接在T 1的发射极,而是接在它的基极,则变为正反馈。
电磁场原理习题与解答(第5章)

第五章习题答案5-2 如题图所示,一半径为a 的金属圆盘,在垂直方向的均匀磁场B 中以等角速度ω旋转,其轴线与磁场平行。
在轴与圆盘边缘上分别接有一对电刷。
这一装置称为法拉第发电机。
试证明两电刷之间的电压为22ωBa 。
证明:,选圆柱坐标, ρφe vB e B e v B v E z ind=⨯=⨯=其中 φρωe v=22ωρρωρερρa B d B e d e v B l d E aal ind====⎰⎰⎰∙∙∴证毕 5-3解:5-4 一同轴圆柱形电容器,其内、外半径分别为cm r 11=、cm r 42=,长度cm l 5.0=,极板间介质的介电常数为04ε,极板间接交流电源,电压为V t 10026000u πsin =。
求s t 0.1=时极板间任意点的位移电流密度。
解法一:因电源频率较低,为缓变电磁场,可用求静电场方法求解。
忽略边沿效应,电容器中的场为均匀场,选用圆柱坐标,设单位长度上内导体的电荷为τ,外导体电荷为τ-,因题图5-2zvρ此有ρρπετe 2E 0=21r r <<ρ1200222121r r d dl E u r r r r lnπετρρπετ===⎰⎰∙1202r r u ln=∴πετ所以ρρer r u E 12 ln =, ρρεer r u D 12ln=2A/mρρππρερεe t 10010026000r r e tu r r tD J 1212dcos ln ln ⨯=∂∂=∂∂=当s t 1=时2512A/m10816100100260004108584ρρρππρe e J d--⨯=⨯⨯⨯⨯=.cos ln .解法二:用边值问题求解,即⎪⎩⎪⎨⎧=====∇401u 02ρϕρϕϕ 由圆柱坐标系有0)(1=∂∂∂∂ρϕρρρ(1)解式(1)得 21ln c c +=ρϕ由边界条件得: 4u c 1ln -= u c 2=u 4u +-=∴ρϕln ln所以 ρρπϕe 4t10026000Eln sin =-∇=ρρπεεe 4t 100260004E D 0ln sin ==ρπρπεe 1004t 100260004t D J 0D⨯=∂∂=ln cos当s t 1=时)(.25D mAe 10816J ρρ-⨯=5-5由圆形极板构成的平板电容器)(d a >>见题图所示,其中损耗介质的电导率为γ、介电系数为ε、磁导率为μ,外接直流电源并忽略连接线的电阻。
四川大学物理习题册第五章解答2
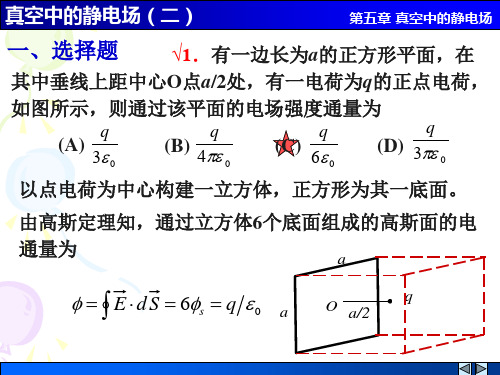
x2
r02
真空中的静电场(二)
第五章 真空中的静电场
s E1 2 0
取x轴正方向为正
E2
s 2 0
1
x
x2
r02
x 0,
E
E1
E2
s 2 0
s 2 0
1
x x2
r02
2 0
sx
x2 r02
x 0,
面上均匀带电,电荷面密度为s.试求通过小孔中心O并
与平面垂直的直线上各点的场强和电势.(提示:选O 点的电势为零).
解: 用割补法,该带电体=无限大平面(+s) +圆屏(-s)
由高斯定理可得,无限大平面场强
s E1 2 0 x 由场强叠加原理可得,圆屏场强
E2
s 2 0
1
x
为常数,则场强分布为 Ex=
,Ey=
.
U Ex x 2Ax
Ey
U y
2By
真空中的静Hale Waihona Puke 场(二)第五章 真空中的静电场
三、计算题 1. 如图,带电细线弯成半径为R的半圆形,
电荷线密度为=0sinq,式中0为一常数,q为半径R与
x轴所成的夹角.试求环心O处的电场强度.
解: 在细线取一线段元,由点电荷的场强公式有
d
E
dq
4 0R2
er
0
sinq Rdq 4 0R2
cosq i sinq j
y E
dE
0
sinq cosq i sin2 q j dq
第五章习题解答

习 题 五1. 设V 是数域F 上向量空间,假如V 至少含有一个非零向量α,问V 中的向量是有限多还是无限多?有没有n (n ≥ 2)个向量构成的向量空间? 解 无限多;不存在n (n ≥ 2)个向量构成的向量空间(因为如果F 上一个向量空间V 含有至少两个向量, 那么V 至少含有一个非零向量α , 因此V 中含有α , 2α , 3α , 4α , …,这无穷多个向量互不相等,因此V 中必然含有无穷多个向量).2. 设V 是数域F 上的向量空间,V 中的元素称为向量,这里的向量和平面解析几何中的向量α,空间解析几何中的向量β有什么区别?解 这里的向量比平面中的向量意义广泛得多,它可以是多项式,矩阵等,不单纯指平面中的向量.3. 检验以下集合对所指定的运算是否构成数域F 上的向量空间.(1)集合:全体n 阶实对称矩阵;F :实数域;运算:矩阵的加法和数量乘法;(2)集合:实数域F 上全体二维行向量;运算: (a 1, b 1)+ (a 2, b 2)=(a 1+a 2, 0) k • (a 1, b 1)=(ka 1, 0)(3)集合:实数域上全体二维行向量;运算: (a 1, b 1)+ (a 2, b 2)=(a 1+a 2, b 1+b 2)k •( a 1, b 1)=(0, 0)解 (1) 是; (2) 不是(因为零向量不唯一);(3) 不是(不满足向量空间定义中的(8)).4. 在向量空间中,证明,(1) a (-α)=-a α=(-a ) α ,(2) (a -b )α=a α-b α ,a ,b 是数,α是向量.证明 (1) a a a a =+-=+-))(()(αααα 0= 0ααa a -=-∴)(又 ==+-=+-a a a a a 0))(()(ααα 0ααa a -=-∴)(综上, .)()(αααa a a -=-=-(2) ααααααb a b a b a b a -=-+=-+=-)())(()(.5. 如果当k 1=k 2=…=k r =0时,k 1α1+k 2α2+…+k r αr =0, 那么α1, α2, …, αr 线性无关. 这种说法对吗?为什么?解 这种说法不对. 例如设α1=(2,0, -1), α2=(-1,2,3), α3=(0,4,5), 则0α1+0α2+0α3=0. 但α1, α2, α3线性相关, 因为α1+2α2-α3=0.6. 如果α1, α2, …, αr 线性无关,而αr +1不能由α1, α2, …, αr 线性表示,那么α1, α2,…, αr , αr +1线性无关. 这个命题成立吗?为什么? 解 成立. 反设α1, α2,…, αr , αr +1线性相关,由条件α1, α2, …, αr 线性无关知αr +1一定能由α1, α2, …, αr 线性表示,矛盾.7. 如果α1, α2, …, αr 线性无关,那么其中每一个向量都不是其余向量的线性组合. 这种说法对吗?为什么?解 对. 反设 αi = k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k r αr ,则 k 1α1+k 2α2+…k i -1αi-1+(-1) αi +k i+1αi +1 +…+k r αr =0. 由于-1≠0, 故α1, α2, …, αr 线性相关.8. 如果向量α1, α2, …, αr 线性相关,那么其中每一个向量都可由其余向量线性表示. 这种说法对吗?为什么?解 不对. 设α1=(1,0) , α2=(2,0) , α3=(0,1) , 则α1, α2, α3线性相关, 但α3不能由α1, α2线性表示.9. 设α1= (1, 0, 0), α2= (1, 2, 0), α3=(1, 2, 3)是F 3中的向量,写出α1, α2, α3的一切线性组合. 并证明F 3中的每个向量都可由{α1, α2, α3}线性表示.解 k 1α1+k 2α2+k 3α3 k 1, k 2 , k 3∈F .设k 1α1+k 2α2+k 3α3=0,则有⎪⎩⎪⎨⎧==+=++030220332321k k k k k k , 解得 k 1= k 2 =k 3=0.故α1, α2, α3线性无关.对任意(a,b,c)∈F 3, (a,b,c)=3213)32())322((αααc c b c ba +-+--,所以F 3中的每个向量都可由{α1, α2, α3}线性表示.10. 下列向量组是否线性相关(1) α1= (1, 0, 0), α2= (1, 1, 0), α3=(1, 1, 1);(2) α1=(3, 1, 4), α2=(2, 5, -1), α3=(4, -3, 7).解 (1) 线性无关; (2) 线性无关.11. 证明,设向量α1, α2, α3线性相关,向量α2, α3, α4线性无关,问:(1) α1能否由α2, α3线性表示?说明理由;(2) α4能否由α1, α2, α3线性表示?说明理由.解 (1)因为α2, α3线性无关而α1, α2, α3线性相关,所以α1能由α2, α3线性表示;(2)反设α4能由α1, α2, α3线性表示,但α1能由α2, α3线性表示,故α4能由α2, α3线性表示,这与α2, α3, α4线性无关矛盾,所以α4不能由α1, α2, α3线性表示.12. 设α1= (0, 1, 2), α2= (3, -1, 0), α3=(2, 1, 0),β1= (1, 0, 0), β2= (1, 2, 0), β3=(1, 2, 3)是F 3中的向量. 证明,向量组{α1, α2, α3}与{β1, β2, β3}等价.证明 (β1, β2, β3)=(321,,εεε)A(α1, α2, α3)= (321,,εεε)B其中A=⎪⎪⎪⎭⎫ ⎝⎛300220111, B=⎪⎪⎪⎭⎫ ⎝⎛-002111230.易验证A , B 均可逆, 这样 (β1, β2, β3) = (α1, α2, α3 )(B -1A )(α1, α2, α3) = (β1, β2, β3)(A -1B ) ,故向量组{α1, α2, α3}与{β1, β2, β3}等价.13. 设数域F 上的向量空间V 的向量组{α1, α2, …, αs }线性相关,并且在这个向量组中任意去掉一个向量后就线性无关. 证明,如果∑=s i i ik 1α=0 (k i ∈F ),那么或者k 1=k 2=…=k s =0, 或k 1,k 2,…,k s 全不为零.证明 由条件∑=s i i ik 1α=0 (k i ∈F )知k i αi = - (k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs ) (*)(1) 当k i =0时,(*)式左边等于零,故k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs =0. 由于这s -1个向量线性无关,所以k 1=k 2=…=k s =0.(2) 当k i ≠0时, αi = -ik 1(k 1α1+k 2α2+…k i -1αi-1+k i+1αi +1 +…+k s αs ),下证对于任意i j s j ≠∈},,2,1{ 时k j ≠0. 反设k j =0, 则αi 可由s -2个向量线性表示.这与任意s -1个向量线性无关矛盾,所以此时k 1,k 2,…,k s 全不为零.14. 设α1=(1, 1), α2=(2, 2), α3=(0, 1) , α4=(1, 0)都是F 2中的向量. 写出{α1, α2, α3, α4}的所有极大无关组.解 α1, α3 ; α1, α4 ; α2 ,α3 ; α2 ,α4 ; α3 ,α4 .15. 设A 1=⎪⎪⎭⎫ ⎝⎛-2001,A 2=⎪⎪⎭⎫ ⎝⎛-0021, A 3=⎪⎪⎭⎫ ⎝⎛0120,A 4=⎪⎪⎭⎫ ⎝⎛-2142∈M 2×2(F ). 求向量空间M 2×2(F )中向量组{A 1, A 2,A 3, A 4}的秩及其极大无关组. 解 秩{A 1, A 2,A 3, A 4}=3, {A 1, A 2,A 3}是向量组{A 1, A 2, A 3, A 4}的一个极大无关组.16.设由F 4中向量组{α1=(3,1,2,5),α2=(1,1,1,2),α3=(2,0,1,3),α4 =(1,-1,0,1),α5 =(4,2,3,7)}. 求此向量组的一个极大无关组.解 (α1,α2,α3,α4,α5)= (4321,,,εεεε)A , 其中A=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-71325301122101141213, 则秩A =2. 又(α1,α2 )= (4321,,,εεεε)B , 其中B =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛25121113. 秩B =2, 故{α1,α2}线性无关, 它是向量组{α1,α2,α3,α4,α5}的一个极大无关组.17. 证明,如果向量空间V 的每一个向量都可以唯一表成V 中向量α1, α2, …, αn 的线性组合,那么dim V =n .证明 由条件零向量可唯一的表示成α1, α2, …, αn 的线性组合, 这说明α1, α2, …, αn 线性无关, 故可作为V 的基, 从而dim V =n .18. 设β1, β2,…,βn 是F 上n (>0)维向量空间V 的向量,并且V 中每个向量都可以由β1, β2,…,βn 线性表示. 证明, {β1, β2,…,βn }是V 的基.证明 由条件标准正交基{ e 1, e 2, …,e n }可由β1, β2,…,βn 线性表示, 反过来β1, β2,…,βn 又可由{ e 1, e 2, …,e n }线性表示,所以{ e 1, e 2, …,e n }和{β1, β2,…,βn }等价. 由{ e 1, e 2, …,e n }线性无关知{β1, β2,…,βn }线性无关,又因V 中每个向量都可以由β1, β2,…,βn 线性表示, 由基的定义知{β1, β2,…,βn }是V 的基.19. 复数集C 看作实数域R 上的向量空间(运算: 复数的加法,实数与复数的乘法)时,求C 的一个基和维数.解 基为{1, i }; dim C =2.20. 设V 是实数域R 上全体n 阶对角形矩阵构成的向量空间(运算是矩阵的加法和数与矩阵的乘法). 求V 的一个基和维数.解 基为E ii (i =1,2, …,n ); dim V =n .21. 求§5.1中例9给出的向量空间的维数和一个基.解 任意一个不等于1的正实数都可作为V 的基; dim V =1.22. 在R 3中,求向量α=(1, 2, 3)在基ε1=(1, 0, 0),ε2=(1, 1, 0),ε3=(1, 1, 1)下的坐标.解 (-1,-1,3)T .23. 求R 3中由基{α1, α2, αs }到基{β1, β2, β3 }的过渡矩阵,其中α1=(1, 0, -1), α2=(-1, 1, 0), α3=(1, 2, 3),β1=(0, 1, 1), β2=(1, 0, 1), β3=(1, 1, 1).解 所求过渡矩阵为⎪⎪⎪⎭⎫ ⎝⎛-32204230061. 24. 设{α1, α2,…, αn }是向量空间V 的一个基,求由这个基到基{α3, α4, …, αn ,α1, α2}的过渡矩阵.解 所求过渡矩阵为⎪⎪⎭⎫ ⎝⎛-0022n I I . 25. 已知F 3中向量α关于标准基ε1=(1, 0, 0),ε2=(0, 1, 0) ,ε3=(0, 0, 1)的坐标是(1, 2, 3),求α关于基β1=(1, 0, 1), β2=(0, 1, 1), β3=(1, 1, 3)的坐标.解 (1,2,0)T .26. 判断R n 的下列子集哪些是子空间(其中R 是实数域,Z 是整数集).(1) {(a 1, 0, …, 0, a n )| a 1, a n ∈R };(2) {(a 1, a 2, …, a n )|∑==ni i a 10,a 1, a 2, …, a n ∈R };(3) {(a 1, a 2, …, a n )|a i ∈Z , i =1, 2, …, n };解 (1) 是; (2) 是; (3) 不是(数乘不封闭).27. 设V 是一个向量空间,且V ≠{0}. 证明,V 不能表成它的两个真子空间的并集.证明 设W 1与W 2是V 的两个真子空间(1) 若21W W ⊆,则W 1⋃W 2= W 2≠V ;(2) 若21W W ⊇,则W 1⋃W 2= W 1≠V ;(3) 若21W W ⊄且12W W ⊄, 取1W ∈α但2W ∉α,2W ∈β但1W ∉β, 那么1W ∉+βα,否则将有1)(W ∈=-+βαβα,这与1W ∉β矛盾, 同理2W ∉+βα, 所以V 中有向量21W W ∉+βα,即V ≠21W W .28. 设V 是n 维向量空间,证明V 可以表示成n 个一维子空间的直和.证明 设{α1, α2,…, αn }是向量空间V 的一个基, (α1), (α2) ,…, (αn )分别是由α1, α2,…, αn 生成的向量空间, 要证(α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn )(1) 因为{α1, α2,…, αn }是V 的一个基, 所以V 中任一向量α都可由α1, α2,…, αn 线性表示, 此即(α1+α2+…+αn )= (α1)+ (α2)+…+ (αn ).(2) 对任意i ≠j ∈{1,2,…, n },下证 (αi )∩ (αj )={0}. 反设存在0 ≠∈x (αi )∩ (αj ),由∈x (αi )知存在k F ∈使得x =k αi ; 由 x ∈ (αj )知存在F l ∈使得x =l αj , 从而αi =kl αj , 即α1与α2线性相关, 矛盾, 所以 (αi )∩ (αj )={0}. 综上, (α1+α2+…+αn )= (α1)⊕ (α2)⊕…⊕ (αn ).29. 在R 3中给定两个向量组α1=(2, -1, 1, -1), α2=(1, 0, -1, 1),β1=(-1, 2, -1, 0), β2=(2, 1, -1, 1).求 (α1, α2)+ (β1, β2) 的维数和一个基.解 取R 4的标准正交基{4321,,,εεεε},于是(α1, α2, β1, β2)= (4321,,,εεεε)A ,其中 A =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------1011111112012112 , 秩A = 4. 故α1, α2, β1, β2线性无关, 又因为 (α1, α2)∩ (β1, β2)={0},所以dim (α1, α2) + dim (β1, β2)= 4,{ α1, α2, β1, β2}是它的基.30. 设W 1, W 2都是向量空间V 的子空间,证明下列条件是等价的:(1) W 1⊆W 2;(2) W 1∩W 2=W 1;(3) W 1+W 2=W 2.证明 (i) (1)⇒(2) 因为W 1⊆W 2 , 所以W 1∩W 2=W 1. (ii) (2)⇒(3) W 1+W 2 ={α1+α2 | α1∈W 1, α2∈W 2} 由(2)知对任意α∈W 1, 都有α∈W 2 , 所以W 1+W 2 ={α1+α2 | α1, α2∈W 2}=W 2 .(iii) (3)⇒(1) W 1+W 2 ={α1,+α2 | α1∈W 1, α2∈W 2}=W 2 , 说明对任意α∈W 1, 都有α∈W 2 , 此即W 1⊆W 2 .31. 设V 是实数域R 上n 阶对称矩阵所成的α2向量空间;W 是数域R 上n 阶上三角矩阵所成的向量空间,给出V 到W 的一个同构映射.解 对∈∀A V (A =(a ij )且a ij = a ji )和B ∈W (B =(a ij ),当i>j 时, a ij =0) 定义f : V → WA B 易验证f 是V 到W 的一个同构映射.32. 设V 与W 都是数域F 上的向量空间,f 是V 到W 的一个同构映射,证明{α1, α2, …, αn }是V 的基当且仅当{f (α1), f (α2), …, f (αn )}是W 的基.证明 设{α1, α2, …, αn }是V 的基.(1) 由α1, α2, …, αn 线性无关知f (α1), f (α2), …, f (αn ) 线性无关.(2) 任取∈ηW , 由f 是同构映射知存在∈ξV 使得f (ξ)=η.但ξ=∑=n i i ia 1α, a i ∈F , f (ξ)=f (∑=n i i i a 1α)=)(1∑=n i i i f a α=η. 由η的任意性知{f (α1), f (α2), …, f (αn )}是W 的基.反过来, {f (α1), f (α2), …, f (αn )}是W 的基(1) 由f (α1), f (α2), …, f (αn )线性无关知α1, α2, …, αn 线性无关.(2) 任取∈ξV , 由f 是同构映射知存在∈ηW 使得f (ξ)=η.但η=∑=n i i i f k 1)(α= f (∑=n i i i k 1α), k i ∈F , 从而ξ=∑=ni i i k 1α, k i ∈F .由ξ的任意性知{ α1, α2, …, αn }是V 的基.补 充 题1. 设W 1, W 2是数域F 上向量空间V 的两个子空间. α,β是V 的两个向量,其中α∈W 2,但α∉ W 1,β∉W2. 证明:(1)对于任意k ∈F ,αβk +∉W 2;(2)至多有一个k ∈F ,使得αβk +∈W 1.证明 (1)反设存在k 1∈F 使得αβ1k +∈W 2 , 又α∈W 2 , 因此β=β+ k 1α-k 1α∈W 2 , 这与β∉W 2矛盾. 所以对于∀k ∈F ,αβk +∉W 2 .(2)若有k 1, k 2∈F , k 1≠k 2使得αβ1k +, αβ2k +∈W 1, 那么。
电磁场与电磁波(第三版)课后答案第5章

第五章习题解答5.1真空中直线长电流I 的磁场中有一等边三角形回路,如题 5.1图所示,求三角形回路内的磁通。
解根据安培环路定理,得到长直导线的电流I 产生的磁场2IrB e穿过三角形回路面积的磁通为d SB S32322[d ]d d 2db db zd dI I z z xxxx由题 5.1图可知,()tan63x d zx d ,故得到32d 3db dIx dxx3[ln(1)]223Ib d b d5.2通过电流密度为J 的均匀电流的长圆柱导体中有一平行的圆柱形空腔,如题 5.2图所示。
计算各部分的磁感应强度B ,并证明腔内的磁场是均匀的。
解将空腔中视为同时存在J 和J 的两种电流密度,这样可将原来的电流分布分解为两个均匀的电流分布:一个电流密度为J 、均匀分布在半径为b 的圆柱内,另一个电流密度为J 、均匀分布在半径为a 的圆柱内。
由安培环路定律,分别求出两个均匀分布电流的磁场,然后进行叠加即可得到圆柱内外的磁场。
由安培环路定律d CI B l,可得到电流密度为J 、均匀分布在半径为b 的圆柱内的电流产生的磁场为2222b b bbbbr bbr br J r B J r 电流密度为J 、均匀分布在半径为a 的圆柱内的电流产生的磁场为2222a a aaaar aar ar J r B J r 这里a r 和br 分别是点a o 和b o 到场点P 的位置矢量。
将aB 和bB 叠加,可得到空间各区域的磁场为圆柱外:22222babab a r rBJr r ()br b 圆柱内的空腔外:2022ba aar BJr r (,)b ar b r a 空腔内:22b aBJr r J d()ar a 式中d 是点和b o 到点a o 的位置矢量。
由此可见,空腔内的磁场是均匀的。
5.3下面的矢量函数中哪些可能是磁场?如果是,求其源变量J 。
dbIzx题 5.1 图Sbr ar Jboao ab题5.2图d(1) 0,r ar H e B H(圆柱坐标)(2) 0(),x y ay ax H e e BH(3) 0,x y axay H e e BH(4) 0,ar He BH (球坐标系)解根据恒定磁场的基本性质,满足0B 的矢量函数才可能是磁场的场矢量,否则,不是磁场的场矢量。
第五章 热力学第二定律与熵 习题解答解析

证明:假设绝热线与等温线相交于两点A和B,从而围城一个闭合 区域,分两种情况讨论。
⑴ 绝热线在等温线的下面。假设此循环是顺时针的,则此过程
P
对外做功,而在整个循环中只从单一热源吸热
A
并全部用来对外做功,而不产生其它影响,这
CB D
违反了热二律的开尔文表述,因此,这种情况 下,等温线不能和绝热线相交于两点
多大距离位置? ⑶ 物体系的总熵增加多少?
分析:开始时活塞是固定的,放松以后活塞振动起来,说明开始时
活塞两边压强不等,物质的量也不等。考虑到气缸内的氦气
和氖气作为一个整体它不可能对外做功,而开始时整个物体
系(气缸以及内部的气体和外面的水)的温度均匀地处于 25℃,它不可能和外界交换热量。所以一开始气缸以及内部 气体的内能就不变,温度不变,以后温度应该仍然不变,谁 的温度也不变。
PHe VHe P'HelS
PNe VNe P'Ne(0.8 l )S P'He (0.8 l)S
l 0.6m;
Ne
1 3
mol
⑶ 整个气体的熵变等于氦气和氖气熵变之和。
S
SHe
SNe
0.6
0.3
S S
HedV V
0.2 S
0.5 S
NedV V
Rln2
1 3
R
ln
2 5
3.22JK 1
因而是不可逆的。应该设想水所经历的是另一个其始、末态
都和他的初、末态相同的可逆过程。例如,水在等压条件下 依次和一系列的温度从T1逐步上升到T2的热源相接触,相邻 两热源之间的温差满足△T/T<<1的条件。只有水达到新的平 衡态后,才脱开原来的热源,再和下一个温度的热源相接触, 使达到下一热源的温度…如此使得水的温度也逐步从从T1上 升到T2。这样就可以认为水在任何时刻的温度几乎都是处处 相等的,它始终满足热学平衡条件,因而是可逆的。由于这两 个可逆和不可逆过程的始末两态相同,因而熵变相同。
矩阵理论第五章课后习题解答

第五章课后习题解答1. 设000c c=cc c c A .讨论c 取何值时A 为收敛矩阵. 解:由于()()22c cλ=cc c c c c λλλλλ-----=+---3E A ,所以A 的特征值为12c λ=,23c λλ==-,于是=A ()2r c ,而矩阵A 收敛的充要条件是<A ()1r 即1122c -<<. 2. 若()lim k k →∞=AA ,证明()lim k k →∞=A A ,其中(),k m n ⨯∈A A C , 为m n ⨯C 中的任何一种矩阵范数,并问该命题的逆命题是否成立,为什么?证:由于()()lim lim 0k k k k →∞→∞=⇔-=AA A A ,再利用矩阵范数的三角不等式推知()()k k -≤-AA A A ,所以有()lim 0k k →∞-=A A ,即()lim k k →∞=AA .该命题的逆命题不成立,例如取⎛⎫- ⎪= ⎪ ⎪⎝⎭A ()1(1)10k k k ,⎛⎫= ⎪⎝⎭A 1010,并取矩阵范数为Frobenius范数,则有→∞→∞===A A ()lim limk k k ,但→∞A ()lim k k 不存在,所以→∞≠AA ()lim k k .3. 设()()()(),,lim lim k m n k n l k k k k ⨯⨯→∞→∞∈∈==AC B C A A,B B,证明()()lim k k k →∞=A B AB .证:→∞→∞=⇔-=A BAB A B AB ()()()()lim lim 0k k k k k k ,利用矩阵范数的性质有-=-+-A BAB A B AB AB AB ()()()()()()k k k k k k≤-+-AA B A B B ()()()()()k k k≤-+-B A A A B B ()()()()k k k由已知条件→∞→∞==AA B B ()()lim ,lim k k k k 及第2题结论知→∞-=A A ()lim 0,k k→∞-=B B ()lim 0k k ,→∞=B B ()lim k k .由此可见上面不等式的右边趋于0, 所以→∞-=A B AB ()()lim 0k k k .4. 设()()()1lim ()k n n k k k ⨯-→∞∈=AC ,A A,A 和1-A 都存在,证明()11lim()k k --→∞=A A .证:记adj A 为矩阵A 的伴随矩阵,ij A 为A 中元素ij a 的代数余子式,则()()1()adj ()det k k k -=A A A, 其中adj ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭A A A A A A A A A A ()()()11211()()()()12222()()()12.k k k n k k k k n k k k nn nn易知(k)ij A 是A ()k 中元素的1n -次多项式,由多项式函数的连续性知(k)ij ij =A →∞A lim k ,故adj adj →∞=AA ()lim k k .同理d e t A ()k 是A ()k 中元素的n 次多项式,所以det det →∞=≠AA ()lim 0k k ,于是adj adj det det --→∞→∞===A A A A AA ()()11()lim ()lim k k k k k . 5. 设矩阵级数∞=∑A ()k k收敛(绝对收敛),证明()k k ∞=∑PAQ 也收敛(绝对收敛),且 ()()00k k k k ∞∞==⎛⎫= ⎪⎝⎭∑∑PA Q P A Q , 其中()k m n s m n l ⨯⨯⨯∈∈∈AC ,P C ,Q C .证:记 ()()()0()N NN k k k k ====∑∑SPA Q P A Q ,于是()()()()0lim (lim )()N k N k k N N k k k ∞∞→∞→∞======∑∑∑PAQ SP A Q P A Q可见若∞=∑A ()k k收敛,则()k k ∞=∑PAQ 也收敛.如果()k k ∞=∑A绝对收敛,则()0k k ∞=∑A 收敛.又由于≤≤PA Q PA Q A ()()()k k k c ,其中c 是与k 无关的正常数,由比较判别法知()k k ∞=∑PA Q 收敛,故()0k k ∞=∑PA Q 也绝对收敛.6. 讨论下列幂级数的敛散性:⑴ 2117113kk k ∞=⎛⎫ ⎪--⎝⎭∑; ⑵ 018216kkk k ∞=-⎛⎫⎪-⎝⎭∑. 解: (1) 设1713⎡⎤=⎢⎥--⎣⎦A可求得A 的特征值为221-==λλ,所以=A ()2r . 幂级数∑∞=121k k x k的收敛半径为1)1(lim lim 221=+==∞→+∞→k k a a r k k k k . 由=>A ()2r r 知矩阵幂级数211k k k∞=∑A 发散.(2) 设1821-⎡⎤=⎢⎥-⎣⎦B ,可求得B 的特征值为31-=λ,52=λ,所以()=B 5r .又因幂级数∑∞=06k kk x k 的收敛半径 6166lim lim 11=+==+∞→+∞→k k a a r k k k k k k ,<B ()r r ,所以矩阵幂级数06kkk k ∞=∑B 绝对收敛. 7. 计算00.10.70.30.6kk ∞=⎛⎫⎪⎝⎭∑.解:设0.10.70.30.6⎡⎤=⎢⎥⎣⎦A ,由于0.91∞=<A ,故矩阵幂级数0kk ∞=∑A 收敛,且其和为1472()393-⎡⎤-=⎢⎥⎣⎦E A . 8. 设,n n⨯∈=A B C,AB BA ,证明sin()sin cos cos sin cos()cos cos sin sin +=++=-A B A B A B,A B A B A B .证:由=AB BA ,有e e e +=A B A B,()()11sin()()()22i i i i i i e e e e e e i i +-+--+=-=-A B A B A B A B A B 1[(cos sin )(cos sin )(cos sin )(cos sin )]2i i i i i=++---A A B B A A B Bsin cos cos sin =+A B A B同理可证:cos()cos cos sin sin +=-A B A B A B .9. 设210001010⎛⎫ ⎪= ⎪ ⎪⎝⎭A ,求te A ,sin t A .解:()()()31120λλλλ-=+--=E A求得A 的特征值为11-=λ,12=λ,23=λ,于是存在可逆矩阵111310310-⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦P ,101110336642--⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P 使得1112--⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦P AP . 再根据矩阵函数值公式得 ()21,,t t t t e diag e e e --=A P P⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--++---=------t t tt t t t t t t t tt t t e e e e e e e e e e e e e e e 33330333303234661222 ()()1sin sin ,sin ,sin 2t diag t t t -=-A P P=sin 24sin 22sin 2sin 24sin 1006sin 606sin 0tt t t t t t --⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦10. 设126103114--⎛⎫⎪=- ⎪ ⎪--⎝⎭A ,求,cos .t e t A A解:由 ()λλλλλ+--=-=-=-E A 331261310114得A 的特征值1λ=,解齐次线性方程组3()0-=A E x ,即2261130113x --⎛⎫⎪--= ⎪ ⎪--⎝⎭得1λ=的两个无关特征向量12(1,1,0),(2,1,1)T T αα=-=.又对2α,因非齐次方程组322()βα-=A E 相容,故可求得解2(1,0,0)T β=-.由122,,ααβ构造可逆矩阵121110010--⎛⎫ ⎪= ⎪ ⎪⎝⎭P ,1011001113--⎛⎫ ⎪= ⎪ ⎪--⎝⎭P ,使 1100011001-⎛⎫⎪= ⎪ ⎪⎝⎭P AP 为A 的Jordan 标准形.于是1001210001112260110000113000100011313t tt t t t t t t t e e t t t e P e te P e te e t t t e e t t t -⎛⎫⎛⎫-----⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪===-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪----+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭A1cos 002sin cos 2sin 6sin cos 0cos sin sin cos sin 3sin 00cos sin sin cos 3sin t t t tt t t t t t t t t t t t t t t t t t t t t t t -+-⎛⎫⎛⎫ ⎪ ⎪=-=+- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭A P P .11. 设1000110001100011⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭A ,求ln A . 解:方法一:事实上,可证明()[()]TTf f =A A 成立. 本题中TA 为一约当标准形矩阵,由()ln()f =A A 知(1)0,(1)1,(1)1,(1)2f f f f ''''''===-=.所以(1)(1)110(1)(1)012!3!2310(1)11(1)(1)01ln()[ln()]102!2201(1)(1)11100(1)32TTT T f f f f f f f f f f '''''⎛⎫⎛⎫⎛⎫'-⎪ ⎪ ⎪⎪ ⎪ ⎪''⎪⎪ ⎪'-====-⎪⎪ ⎪⎪⎪ ⎪' ⎪⎪ ⎪- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭A A方法二:对A 求得P ,使得11111111-⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦P AP J ,再得到1000010001ln ln 1002111032-⎡⎤⎢⎥⎢⎥⎢⎥=⋅⋅=-⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦A P J P .12. 设()t A 和1()t -A 均为n 阶可微矩阵,证明111()()()()d t d t t t dt dt ---⎛⎫=- ⎪⎝⎭A A A A .证:对1()()t t -=A A E 两端关于t 求导数可得11()()()()0d t d t t t dt dt--⋅+⋅=A A A A . 两边左乘1()t -A 并移项即得111()()()()d t d t t t dt dt ---⎛⎫=- ⎪⎝⎭A A A A .13. 设()(),T m n f tr ⨯=∈X X X X R ,求dfd X. 解: 这是数量函数对矩阵变量的导数.设()ijm nx ⨯=X ,则()()2211m nT st Fs t f x tr =====∑∑X XX X . 又因为()21,2,,;1,2,,ij ijfx i m j n x ∂===∂ ,所以 ()22ij m n ijm ndf f x d x ⨯⨯⎛⎫∂=== ⎪ ⎪∂⎝⎭X X . 14. 设,,()m nn F ⨯∈∈=A Rx R x Ax ,求()(),dF dF d d Tx x x x . 解:设 ()ijm na ⨯=A ,12(,,,)Tn x x x =x , 由于111(),,Tn nk k mk k k k F a x a x ==⎛⎫== ⎪⎝⎭∑∑x Ax所以()1,,,T i mi i F a a x ∂=∂ ()11111,,,,,,,,.TTm n mn n dF F F a a a a d x x ⎛⎫∂∂== ⎪∂∂⎝⎭x 而 11111,,n T nm mn a a dF F Fd x x aa ⎡⎤⎛⎫∂∂⎢⎥=== ⎪⎢⎥∂∂⎝⎭⎢⎥⎣⎦Ax .15. 设(),det 0,det n n f ⨯∈≠=X R X X X .证明1(det )()T dfd -=X X X. 证:设()ijn nx ⨯=X ,记ij x 的代数余子式为ij X ,X 的伴随矩阵为adj X .将det X 按第i 行展开,得11()i i ij ij in in f =det x x x =++++X X X X X ,所以(),1,2,,ij ijfi j n x ∂==∂X ,从而有()()()()()11det (det )T T Tij n n df adj d --⨯====X X X X X X X.。
第5章和第6章重点思考题和习题解答
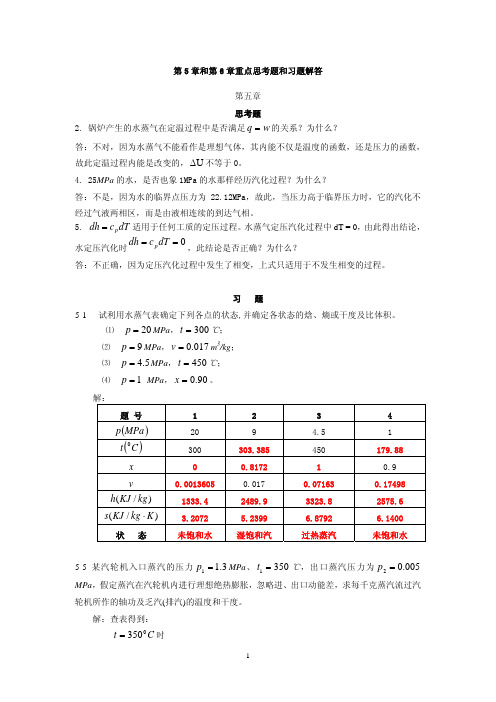
输出净功:
wnet = w2 − w1 = 392.82 − 240.46 = 152.36kJ / kg
循环吸热量:
q1 = h3 − h2 = cP (T3 − T2 ) = 1004.5 × (873 − 534.38) = 340.14kJ / kg
热效率: 或 热效率:
η = wnet = 152.36 = 44.8% q1 340.14
kJ/(kg.K);h2’=137.72 kJ/kg,h2’’=2560.6 kJ/kg
x = s2 − s2 ' = 6.6446 − 0.4761 = 0.779 s2 ''−s2 ' 8.393 − 0.4761
h2 = xh2 ''+(1 − x)h2 ' = 0.779 × 2560.6 + (1 − 0.779) ×137.72 = 2025.1 kJ/(kg.K)
5. dh = c pdT 适来自于任何工质的定压过程。水蒸气定压汽化过程中 dT = 0,由此得出结论, 水定压汽化时 dh = c pdT = 0 ,此结论是否正确?为什么?
答:不正确,因为定压汽化过程中发生了相变,上式只适用于不发生相变的过程。
习题
5-1 试利用水蒸气表确定下列各点的状态,并确定各状态的焓、熵或干度及比体积。
⑴ p = 20 MPa, t = 300 ℃; ⑵ p = 9 MPa, v = 0.017 m3/kg;
⑶ p = 4.5 MPa, t = 450 ℃;
⑷ p = 1 MPa, x = 0.90 。
解:
题号
1
2
3
p(MPa )
20
9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.8 在有16根地址总线的微机系统中,根据下面两种情 况设计存储器片选的译码电路及其存储芯片的连接电路。 (1)采用1Kx4位存储芯片,形成32KB存储器。 (2)采用2Kx8位存储芯片,形成32KB存储器。
答:(1)64片
5.8 在有16根地址总线的微机系统中,根据下面两种情 况设计存储器片选的译码电路及其存储芯片的连接电路。 (1)采用1Kx4位存储芯片,形成32KB存储器。 (2)采用2Kx8位存储芯片,形成32KB存储器。
5.18 试为某8位微机系统设计一个具有16KB ROM和 48KB RAM的存储器。 (1)选用EPROM芯片2716组成只读存储器ROM,从 0000H地址开始。 (2)选用SRAM芯片6264组成随机存取存储器RAM。 (3)分析每个存储芯片的地址范围。 答:(1)2716芯片:2^11x8=2KB,所以需要8片2716。 (2)6264芯片:2^13x8=8KB,所以需要6片6264 (3)每个存储芯片的地址范围如下: 0000H-07FFH,0800H-0FFFH,1000H-17FFH,1800H-1FFFH, 2000H-27FFH,2800H-2FFFH,3000H,37FFH,3800H-3FFFH, (11根地址线(2KB),对应111_1111_1111B) 4000H-5FFFH,6000H-7FFFH,8000H-9FFFH,0A00H-0BFFFH, 0COOOH-0DFFFH,0E000H-OFFFFH (13根地址线(8KB),对应1_1111_1111_1111B)
5.20 在8088系统中,地址线20根,数据线8根,设计 192Kx8位的存储系统,其中数据区为128Kx8,选用芯片 62128( 128Kx8 ),置于CPU寻址空间的最底端,程序 区为64Kx8位,选用27256(32Kx8),置于寻址空间的最高 端,写出地址分配关系,画出所设计的原理电路图。
答:(1)32片 (采用A0-A13寻址,所以空间为16KB, (16Kx8)/(2Kx2)=32 (2)RAM1:0FA800H-OFAFFFH (1111_1010_1xxx_xxxx_xxxx) RAM2:0FB000H-0FB7FFH 注意:地址是20位 (1111_1011_0xxx_xxxx_xxxx)
M/IO
A18 A19
这里A15-A19来自 地址锁存器的输出
5.24 已知某16位微机系统的CPU与RAM连接的部分示意 图如(P199页)习题图5.47所示,若RAM采用每片容量 为2Kx2位的芯片,试填空回答下列问题: (1)根据题意,本系统需要该芯片多少片? (2)如图5.47所示,设由74LS138的Y5和Y6端分别引出 引线连至RAM1和RAM2两组芯片的端,则RAM1和 RAM2的地址范围分别是多少?
答: (1)数据区的地址空间:00000H-1FFFFH (2^17=128K),程序区的地址空间:0FFFFF0F0000H (2^16=64K) (2)图如下。
RD WR ALE STB地址:00000H-1FFFFH
A17 A18 ≥1 A19 A0-A16 D0-D7 A0-A14
5.13 如果存储器的速度慢与CPU不相配合,应采用什 么措施?
答:在总线周期内插入若干个等待周期。
5.15 用1Kx2的RAM芯片,组成8KB的存储容量,需要 多少RAM芯片?多少根地址线?多少芯片组? 答:8KB/(1KX2)= (8KX8)/(1KX2)=32(片),需要13根地 址线,(2^13=8K),其中4片为一组,所以需要8个芯片组。
628128 128KB CE WE OE
A8-A19 AD0-AD7 8088
DT/R DEN
收发器 8286 T OE 74LS138 G1 G2A G2B A15 A16 A17 A B C Y6 Y7
U1 27256 D0-D7 32KB CE OE
A0-A14 U2 27256 D0-D7 32KB CE OE U1地址:0F0000H-0F7FFFH U2地址:0F8000H-0FFFFFH
5.5 设有一个具有13位地址和8位字长的存储器,试问: (1)存储器能存储多少字节信息? (2)如果存储器由1Kx4位RAM芯片组成,共计需要多 少片? (3)需要用哪几位高地址做片选译码来产生芯片选择信 号? 答:(1)8KB(8K字节信息)。 (2)16片 (3)A10,A11,A12
5.6 下列RAM各需要多少地址线进行寻址?需要多少条 数据I/O线? 答(1) 512Kx4位------19条地址线,4条数据I/O线 (2)1kx4位------10条地址线,4条数据I/O线
答:(2)16片
5.12 存储器与CPU之间的连接,有哪几种连接线?应 考虑哪几方面的问题?
答:(1)地址线,数据线和控制线。(AB,DB和CB) (2)应考虑的问题
1.CPU外部总线的负载能力 2.各种信号线的配合与连接 3.CPU的时序与存储器的存储速度之间的匹配 4.存储器的地址分配及片选信号的产生
