概率论典型例题第2章

合集下载

概率论第二章习题答案

概率论第二章习题答案习题1：离散型随机变量及其分布律设随机变量X表示掷一枚公正的六面骰子得到的点数。

求X的分布律。

解答：随机变量X的可能取值为1, 2, 3, 4, 5, 6。

由于骰子是公正的，每个面出现的概率都是1/6。

因此，X的分布律为：\[ P(X=k) = \frac{1}{6}, \quad k = 1, 2, 3, 4, 5, 6 \]习题2：连续型随机变量及其概率密度函数设随机变量Y表示从标准正态分布中抽取的数值。

求Y的概率密度函数。

解答：标准正态分布的概率密度函数为高斯函数，其形式为：\[ f(y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}}, \quad -\infty < y < \infty \]习题3：随机变量的期望值已知随机变量X的分布律为：\[ P(X=k) = p_k, \quad k = 1, 2, ..., n \]求X的期望值E(X)。

解答：随机变量X的期望值定义为：\[ E(X) = \sum_{k=1}^{n} k \cdot p_k \]习题4：随机变量的方差继续使用习题3中的随机变量X，求X的方差Var(X)。

解答：随机变量X的方差定义为期望值的平方与每个值乘以其概率之和的差：\[ Var(X) = E(X^2) - (E(X))^2 \]其中，\( E(X^2) = \sum_{k=1}^{n} k^2 \cdot p_k \)习题5：二项分布设随机变量X表示n次独立伯努利试验中成功的次数，每次试验成功的概率为p。

求X的分布律和期望值。

解答：X服从参数为n和p的二项分布。

其分布律为：\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k = 0, 1, ..., n \]X的期望值为：\[ E(X) = np \]结束语：以上是概率论第二章的一些典型习题及其解答。

概率论第二章习题及答案

三、一些常用的离散型随机变量
1) Bernoulli分布如果随机变量 X 的分布律为
PX 0 1 p q ， PX 1 p
或
P{ X k } p q
X P
k 1 k
(k 0 , 1)
1 p
0 1-p
则称随机变量 X 服从参数为 p 的 Bernoulli分布．记作 X ~ B1 ， p . 其中0 p 1 为参数
第二章随机变量及其分布
一、随机变量的定义
设E是一个随机试验，S是其样本空间．若对每一个
S , 都有唯一确定的一个实数X 与之对应 , 则称
X 为一个随机变量.

S
X
R
第二章习题课
二、离散型随机变量的分布律
设离散型随机变量 X 的所有可能取值为 x1 ， x2 ，， xk ，并设
如果连续型随机变量X 的密度函数为（I）
1 2 2 x f x e 2 其中， 0 为参数，则称随机变量X 服从参数为， 2 的
正态分布．记作
f (x)
x 2
X ~ N ，

2

0
第二章随机变量及其分布
4）几何分布
若随机变量 X 的分布律为
PX k q k 1 p
k 1， 2，
其中 p 0，q 0，p q 1
则称随机变量 X 服从参数为 p的几何分布．
返回主目录
第二章随机变量及其分布
5）超几何分布
如果随机变量 X 的分布律为

x

f ( t )dt,

概率论第二章习题解答(全)

概率论第二章习题1考虑为期一年的一张保险单，若投保人在投保一年内意外死亡，则公司赔付20万元，若投保人因其它原因死亡，则公司赔付5万元，若投保人在投保期末自下而上，则公司无需传给任何费用。

若投保人在一年内因意外死亡的概率为0.0002，因其它原因死亡的概率为0.0010，求公司赔付金额的分崣上。

解设赔付金额为X ，则X 是一个随机变量，取值为20万，5万，0，其相应的概率为0.0002；0.0010；0.9988，于是得分布律为X20（万）5万0xp 0.00020.00100.99882.（1）一袋中装有5只球，编号为1,2，3,4，5。

在袋中同时取3只，以X 表示取出的3只球中的最大号码，写出随机变量X 的分布律（2）将一颗骰子抛掷两次，以X 表示两次中得到的小的点数，试求X 的分布律。

解（1）在袋中同时取3个球，最大的号码是3,4，5。

每次取3个球，其总取法：35541021C ⋅==⋅，若最大号码是3，则有取法只有取到球的编号为1,2，3这一种取法。

因而其概率为22335511{3}10C P X C C ====若最大号码为4，则号码为有1,2，4；1，3,4；2，3，4共3种取法，其概率为23335533{4}10C P X C C ====若最大号码为5，则1，2,5；1,3，5；1，4,5；2,3，5；2,4，5；3,4，5共6种取法其概率为25335566{5}10C P X C C ====一般地3521)(C C x X p x -==，其中21-x C 为最大号码是x 的取法种类数，则随机变量X 的分布律为X 345xp 101103610（2）将一颗骰子抛掷两次，以X 表示两次中得到的小的点数，则样本点为S ＝｛（1,1），（1,2），（1,3），…，（6,6）｝，共有36个基本事件，X 的取值为1,2，3,4，5,6，最小点数为1，的共有11种，即（1,1，），（1,2），（2,1）…，（1,6），（6,1），11{1}36P X ==；最小点数为2的共有9种，即（2,2），（2,3），（3,2），…，（3,6），（6,3），9{2}36P X ==；最小点数为3的共有7种，7{3}36P X ==；最小点数为4的共有5种，5{4}36P X ==；最小点数为5的共有3种，3{5}36P X ==；最小点数为6的共有1种，1{6}36P X ==于是其分布律为X 123456kp 11369367365363361363设在15只同类型的产品中有2只次品，在其中取3次，每次任取1只，作不放回抽样，以X 表示取出的次品的次数，（1）求X 的分布律；（2）画出分布律的图形。

概率论与数理统计2.第二章练习题(答案)

第二章练习题（答案）一、单项选择题1．已知连续型随机变量X 的分布函数为⎪⎩⎪⎨⎧≥<≤+<=ππx x b kx x x F ,10,0,0)( 则常数k 和b 分别为（ A ）（A ）0,1==b k π （B ）π1,0b k = （C ）0,21==b k π （D ）π21,0==b k ． 2.下列函数哪个是某随机变量的分布函数（ A ）A. f （x ）={xa e −x 22a,x ≥01, x <0(a ＞0); B. f （x ）={12cosx, 0< x <π0, 其他C. f （x ）={cosx, −π2< x <π20, 其他D. f （x ）={sinx, −π2< x <π20, 其他3.若函数()f x 是某随机变量X 的概率密度函数，则一定成立的是（ C ） A. ()f x 的定义域是[0,1] B. ()f x 的值域为[0,1] C. ()f x 非负 D. ()f x 在(,)-∞+∞内连续4. 设)1,1(~N X ，密度函数为)(x f ，则有（ C ） A.{}{}00>=≤X P X P B. )()(x f x f -= C. {}{}11>=≤X P X P D. )(1)(x F x F --=5. 设随机变量()16,~μN X ，()25,~μN Y ，记()41-<=μX P p ，()52+>=μY P p ，则正确的是（ A ）.（A ）对任意μ，均有21p p = （B ）对任意μ，均有21p p < （C ）对任意μ，均有21p p > （D ）只对μ的个别值有21p p = 6. 设随机变量2~(10,)X N ，则随着的增加{10}P X （ C ）A.递增B.递减C.不变D.不能确定7.设F 1(x )与F 2(x )分别为随机变量X 1、X 2的分布函数,为使F (x )=aF 1(x )-bF 2(x )是某一随机变量的分布函数,在下列给定的多组数值中应取 ( A )A . a =53, b =52-; B . a =32, b =32;C . 21-=a ， 23=b ; D . 21=a , 23-=b .8.设X 1与X 2是任意两个相互独立的连续型随机变量，它们的概率密度函数分别为f 1(x )和f 2(x )，分布函数分别为F 1(x )和F 2(x )，则 ( D ) (A) f 1(x )+f 2(x ) 必为某个随机变量的概率密度；（B ）f 1(x )•f 2(x ) 必为某个随机变量的概率密度；（C ）F 1(x )+F 2(x ) 必为某个随机变量的分布函数； (D) F 1(x ) •F 2(x ) 必为某个随机变量的分布函数。

概率论第二章

第二章随机变量及其分布习题全解习题2–11.一批产品中含有正品和次品，从中每次任取一件，有放回地连取3次，以X 表示取到的次品数．(1)写出X 的可能取值及对应事件的样本点；(2)设该批产品的次品率为p ，求X 的取值概率．解有放回地连取3次，每次都可能取到次品，且取到次品的概率均为p .(1)X 的可能取值为0,1,2,3；对应事件的样本点为{0}{(,,)}X ==正正正{1}{(,,),(,,),(,,)}X ==次正正正次正正正次{2}{(,,),(,,),(,,)}X ==次次正次正次正次次{3}{(,,)}X ==次次次(2)每次取到次品的概率为p ，连取3次相当于3重伯努利试验，故33{}(1),0,1,2,3k k k P X k C p p k -==-=2.从自然数1,2,3,4中无放回地连取两个数，以X 表示两数之差的绝对值．(1)写出X 的可能取值及对应事件的样本点；(2)求X 的取值概率．解从1,2,3,4中无放回地连取两个数，样本空间{(,)|,1,2,3,4}Ωi j i j i j ==≠；含有2412P =个样本点，各样本点等可能出现．(1)两数之差的绝对值X 可能取值1,2,3；对应事件的样本点为{1}{(1,2),(2,1),(2,3),(3,2),(3,4),(4,3)}X =={2}{(1,3),(3,1),(2,4),(4,2)}X =={3}{(1,4),(4,1)}X ==(2)根据X 取值所对应事件的样本点数，求得6{1}12P X ==，4{2}12P X ==，2{3}12P X ==可统一表示为4{},1,2,36kP X k k -===3.将一颗骰子连掷两次，以X 表示掷出的最大点数，求X 的可能取值及相应的取值概率．解一颗骰子连掷两次，其样本空间{(,)|,1,2,,6}Ωi j i j == 含有2636=个样本点，各样本点等可能出现．掷出的最大点数X 可能取值1,2,,6 ，对应事件{}{(,1),,(,),(1,),,(1,)}X k k k k k k k ==- 含有21k -个样本点，故X 的取值概率为21{},1,2,,636k P X k k -=== 4.某车站每60分钟发一班车，乘客在任意时刻随机到达车站．以X 表示乘客的候车时间，求(1)X 的可能取值范围；(2)乘客候车超过20分钟的概率．解考虑任一时间段内的前后两班车，发车间隔为60分钟．(1)如果乘客到达车站正好赶上前一班车发车，则候车时间0X =；否则要等后一班车，候车时间(0,60)X ∈，故X 的可能取值范围为区间[0,60)．(2)记前一班车发车时刻为0，乘客在发车间隔时间区间[0,60)内随机到达车站，候车超过20分钟意味着乘客在时间区间(0,40)内到达．根据几何概率有(0,40)402{20}603[0,60)P X >===区间的长度区间的长度5.向一个半径为1米的圆形靶子射击，设射击都能中靶，并且命中靶上任一同心圆的概率与该圆的面积成正比．以X 表示弹着点与圆心的距离，求(1)X 的可能取值范围；(2)命中靶上半径为x 的同心圆的概率．解考虑由弹着点确定的以X 为半径的同心圆．(1)因为射击都能中靶，故X 的可能取值范围为区间[0,1]．(2)对任一[0,1]x ∈，事件{0}X x ≤≤表示命中靶上半径为x 的同心圆，其概率为2{0},0P X x x λπλ≤≤=>由{01}X Ω≤≤=，有{01}1P X λπ≤≤==可得1λπ=，故命中靶上半径为x 的同心圆的概率为2{0},01P X x x x ≤≤=≤≤习题2–21.下列各表是否为离散型随机变量的分布律？(1)1010.10.50.6X P--(2)1230.10.30.5X P(3)2312311112222kX k P解根据分布律的基本性质判别：(1)否，因为{1}0.10P X =-=-<，不满足非负性．(2)否，因为31{}0.10.30.50.91k P X k ===++=≠∑，不满足规范性．(3)是，因为10,1,2,2k k >= ；且1112kk ∞==∑，满足分布律的基本性质．2.求下列随机变量X 的分布律中的常数a ．(1){},1,2,,aP X k k N N=== ；(2){},1,2,3,42k kaP X k k ===；(3){}2,1,2,k P X k a k === ．解根据分布律的规范性计算：(1)由11Nk a a N N N===∑，可得1a =．(2)由()4112341312248168kk ka a a ==+++==∑，可得813a =．(3)由1122lim 11n kn k a a a a ∞→∞=-==-∑，应有211a a =-，可得13a =．3.某射手用5发子弹射击目标，每次射击的命中率为p ．如果命中目标就停止射击，否则一直射击到子弹耗尽，求射击次数X 的分布律．解X 的可能取值为1,2,3,4,5．当5k <时，第k 次射击命中目标，前1k -次射击均未命中，有1{}(1),1,2,3,4k P X k p p k -==-=当5k =时，前4次射击均未命中，第5次射击可能命中也可能不中，有454{5}(1)(1)(1)P X p p p p ==-+-=-综上求得X 的分布律为23412345(1)(1)(1)(1)X Ppp pp p p pp ----4.袋内有1个白球和2个黑球，从中每次任取一球，连取两次，以X 表示取到白球的次数．求下列两种情况下X 的分布律．(1)第一次取球后不放回；(2)第一次取球后放回．解袋内仅有一个白球，无放回取球至多取到一次，有放回取球至多取到两次．(1)无放回取球时，X 的可能取值为0,1．根据超几何分布，有21223{},0,1k kC C P X k k C -===计算得到X 的分布律为011233X P(2)有放回取球时，X 的可能取值为0,1,2．根据二项分布，有()()2211{}1,0,1,233kkk P X k Ck -==-=计算得到X 的分布律为012441999X P5.重复进行伯努利试验，设每次试验成功的概率为p ，以X 表示取得第r 次成功时的试验次数，求X 的分布律．解X 的可能取值为,1,r r + ．事件{}X k =意味着第k 次试验为成功，且前1k -次试验中有1r -次成功，故X 的分布律为11(1)(1)111{}(1)(1),,1,r r k r r r k rk k P X k C p p p C p p k r r ---------==-=-=+ 6.数轴上一质点从原点出发，每次以概率p 向右移动或以概率1p -向左移动一个单位，且各次移动相互独立．以n X 表示第n 次移动后质点的坐标，求n X 的分布律．解事件{}n X k =表示经过n 次移动后质点的坐标为k ．将n 次移动视作n重伯努利试验，设其中有i 次向右移动，j 次向左移动，则有,i j n i j k +=-=，故k 与n 的奇偶性相同，且,22n kn k i j +-==由此求得n X 的分布律为222(1),,2,4,,{}0,n k n k n kn n C p p k n n n nP X k ++-⎧⎪-=--+-+==⎨⎪⎩其他7.某车间共有9台机床，各台机床在工作中开动的概率均为0.2，且工作状态相互独立．如果供给该车间的电力至多允许6台机床同时开动，求出现电力不足状况的概率．解以X 表示同时开动的机床数，则X 服从二项分布(9,0.2)B ，分布律为99{}0.2(10.2),0,1,,9k k k P X k C k -==-= 当6X >时将出现电力不足状况，出现的概率为999977{6}{}0.20.80.0003k k k k k P X P X k C -==>====∑∑8.设某商店每月销售某种商品的数量服从参数为8的泊松分布，求该种商品月初应准备多少库存，才能有99%以上的把握保证当月不脱销．解以X 表示当月销售量，则X 服从泊松分布(8)P ，分布律为88{},0,1,2,!k P X k e k k -===设月初准备库存为n ，要有99%以上的把握保证当月不脱销，应有88{}0.99!k nk P X n e k -=≤=≥∑查泊松分布表可得15n =．9.设某交叉路口在t 分钟内通过的汽车数服从参数与t 成正比的泊松分布，已知在1分钟内没有汽车通过的概率为0.2，求在2分钟内最多有一辆汽车通过的概率．解以t X 表示t 分钟内通过的汽车数，则t X 服从泊松分布()P t λ，分布律为(){},0,1,2,!k tt t P X k e k k λλ-===根据1分钟内没有汽车通过的概率1{0}0.20!P X e λλ-===可得ln 5λ=，故2分钟内最多有一辆汽车通过的概率为112ln5220(2ln 5)1{1}{}(12ln 5)!25k k k P X P X k e k -==≤====+∑∑10.一批种子的发芽率为0.995，从中任取600粒做发芽试验，用泊松分布近似计算600粒种子中没有发芽的比例不超过1%的概率．解每粒种子不发芽的概率为10.9950.005p =-=，以X 表示600粒种子中没有发芽的种子数，则X 服从二项分布(600,0.005)B ，分布律为600600{}0.005(10.005),1,2,,600kk k P X k C k -==-= 用参数6000.0053np λ==⨯=的泊松分布(3)P 近似计算，有33{},1,2,,600!k P X k e k k -=≈= 故600粒种子中没有发芽的比例不超过1%，即6X ≤的概率为6633{6}{}0.9665!k k k P X P X k e k -==≤==≈=∑∑11.设某厂共有100台设备，各台设备的状态相互独立，且发生故障的概率均为0.01．求下列两种情况下，设备发生故障而不能得到及时修理的概率．(1)配备5名维修工，每人负责20台设备；(2)配备3名维修工，共同负责100台设备．解如果同一时刻发生故障的设备数超过相应负责的维修工数，则故障不能得到及时修理．(1)以,1,2,,5i X i = 分别表示5名维修工各自负责的20台设备中同时发生故障的设备数，则i X 相互独立，均服从二项分布(20,0.01)B ．当任一1i X >时，将有设备发生故障而不能及时修理，其概率为{}{}()555111512020{1}1{1}1{1}10.010.990.0815iiii i i kkkk PX P X P X C ===-=>=-≤=-≤=-=∏∑ (2)以X 表示100台设备中同时发生故障的设备数，则X 服从二项分布(100,0.01)B ．当3X >时，将有设备发生故障而不能及时修理，其概率为331001000{3}1{3}1{}10.010.990.0184k kk kk P X P X P X k C =-=>=-≤=-==-=∑∑12.设一天内进入某商场的顾客数服从参数为λ的泊松分布，每位顾客购物的概率为p ，且各位顾客是否购物相互独立．以X 表示一天内在该商场购物的顾客数，求X 的分布律．解以Y 表示一天内进入商场的顾客数，则Y 服从泊松分布()P λ，有n 位顾客进入商场的概率为{},0,1,2,!nP Y n e n n λλ-===在进入商场的n 位顾客中，购物的顾客数X 服从二项分布(,)B n p ，故在Y n =的条件下，X k =的条件概率为{|}(1),0,1,2,,k k n k n P X k Y n C p p k n-===-= 根据全概率公式，求得X 的分布律为(1){}{}{|}(1)![(1)]!()!!(),0,1,2,!nk kn kn n kn kk kn k k k p n kk pP X k P Y n P X k Y n e C p p n e p p e p ek n k k p e k k λλλλλλλλλλ∞∞--==---∞-=-======⋅--==-==∑∑∑即X 服从参数为p λ的泊松分布．习题2–31.下列函数是否为随机变量的分布函数？(1)0,1(),0121,1x F x x x <⎧⎪⎪=≤<⎨⎪≥⎪⎩；(2)0,01(),0121,1x F x x x <⎧⎪⎪=≤≤⎨⎪>⎪⎩；(3)21(),1F x x x=-∞<<+∞+．解根据分布函数的基本性质判别．(1)是，因为()F x 满足非减性，规范性和右连续性．(2)否，因为1(10)1(1)2F F +=≠=，不满足右连续性．(3)否，因为()F x 在(0,)+∞内递减，且()0F +∞=，不满足非减性和规范性．2.设下列函数为随机变量X 的分布函数，求常数,a b ．(1)01(),1111x F x ax b x x ≤-⎧⎪=+-<≤⎨⎪>⎩，，；(2)()arctan ,F x a b x x =+-∞<<+∞；(3)0()sin ,1x a F x x a x b x b ≤⎧⎪=<≤⎨⎪>⎩，，．解根据分布函数的基本性质分析计算．(1)根据()F x 的右连续性，应有(10)0(1)(10)1(1)F a b F F a b F -+=-+==-+==+=由此可得12a b ==．(2)根据()F x 的规范性，应有()02F a bπ-∞=-=，()12F a bπ+∞=+=由此可得11,2a b π==．(3)根据()F x 的右连续性和非减性，应有(0)sin 0()(0)1sin ()F a a F a F b b F b +===+===且()F x 在(,]a b 上单调非减，由此可得2,2,0,1,2,2a kb k k πππ==+=±± ．3.设离散型随机变量X 的分布律为210112X Paa -求常数a ，并求分布函数()F x ．解根据分布律的非负性和规范性，应有210,12a a a ≥++=由此可得312a -=，故X 的分布律为10113123222X P---并由分布律求得X 的分布函数为0,11,102()3,0121,1x x F x x x <-⎧⎪⎪-≤<⎪=⎨⎪≤<⎪⎪≥⎩4.某设备在试运行过程中，有3个独立的部件可能需要调准，其概率分别为0.1,0.2和0.3．以X 表示需要调准的部件数，求X 的分布律和分布函数．解记第i 个部件需要调准的事件为,11,2,3i A =．则123123123123123123123123{0}{}0.90.80.70.504{1}{}0.0560.1260.2160.398{2}{}0.0140.0240.0540.092{3}{}0.10.20.30.006P X P A A A P X P A A A A A A A A A P X P A A A A A A A A A P X P A A A ===⨯⨯====++====++====⨯⨯= 综上求得X 的分布律为01230.5040.3980.0920.006X P根据分布律求得X 的分布函数为0,00.504,01()0.902,120.994,231,3x x F x x x x <⎧⎪≤<⎪⎪=≤<⎨⎪≤<⎪⎪≥⎩5.设离散型随机变量X 的分布函数为0,00.2,01()0.5,120.8,231,3x x F x x x x <⎧⎪≤<⎪⎪=≤<⎨⎪≤<⎪⎪≥⎩求：(1)X 的分布律；(2)概率{03}P X <<；(3)条件概率{03}P X X ><解根据分布函数求出分布律，再计算有关概率．(1)由()F x 的间断点及{}()(0)P X x F x F x ==--，求得X 的分布律为01230.20.30.30.2X P(2)根据X 的分布律求得{03}{1}{2}0.30.30.6P X P X P X <<==+==+=(3)按条件概率的定义及X 的分布律，可得{03}0.6{03}0.75{3}0.8P X P X X P X <<><===<习题2–41.设随机变量X 的密度函数为sin 0()20x x f x π⎧<<⎪=⎨⎪⎩，，其他求概率{}63P X ππ≤≤，并求分布函数()F x ．解根据密度函数()f x ，所求概率为{}336631()sin 632PX f x dx xdx ππππππ-≤≤===⎰⎰注意到密度函数()0f x =的区间上积分为零，求得分布函数为0200,0()()sin ,02sin ,20,01cos ,021,2xxx F x f t dt tdt x tdt x x x x x πππππ-∞⎧<⎪⎪==≤<⎨⎪⎪≥⎩⎧<⎪⎪=-≤<⎨⎪⎪≥⎩⎰⎰⎰2.设随机变量X 的密度函数为,01()0,a x x f x <<⎧=⎨⎩其他求：(1)常数a ；(2)常数c ，使{}{}P X c P X c <=>；(3)分布函数()F x .解(1)根据密度函数的规范性，有12()13f x dx a xdx a +∞-∞===⎰⎰由此可得32a =．(2)由{}{}1{}P X c P X c P X c <=>=-<，有2{}1P X c <=，故32031{}()22ccP X c f x dx xdx c -∞<====⎰⎰由此可得314c =．(3)由密度函数3,012()0,x x f x ⎧<<⎪=⎨⎪⎩其他求得分布函数为01030,03()(),0123,120,0,011,1xx x F x f t dt t dt x t dt x x x x x -∞⎧<⎪⎪⎪==≤<⎨⎪⎪≥⎪⎩<⎧⎪=≤<⎨⎪≥⎩⎰⎰⎰3.设随机变量X 的密度函数为||(),x f x ae x -=-∞<<+∞求常数a ，并求分布函数()F x ．解根据密度函数的规范性，有0||0()21x x x f x dx ae dx ae dx ae dx a +∞+∞+∞---∞-∞-∞==+==⎰⎰⎰⎰由此可得12a =．由密度函数||1()2x f x e -=，求得分布函数为001,02()()1,021,0211,02x t xxt t x x e dt x F x f t dt e dt e dt x e x e x -∞-∞--∞-⎧<⎪==⎨⎪+≥⎩⎧<⎪=⎨⎪-≥⎩⎰⎰⎰⎰4.设随机变量X 的分布函数为2,0()0,0x a be x F x x -⎧+>⎪=⎨≤⎪⎩求常数,a b ；并求密度函数()f x ．解根据分布函数的右连续性和规范性，有(00)(0)0a b F F +=+==，()1F a +∞==由此可得1,1a b ==-．由分布函数21,0()0,0x e x F x x -⎧->⎪=⎨≤⎪⎩求导得到密度函数为22,0()()0,0x xe x f x F x x -⎧>⎪'==⎨≤⎪⎩5.设随机变量X 的密度函数()f x 为偶函数，已知()0.8F a =，求()F a -的值，并求概率{0}P X a ≤≤和{}P X a >．解对任意的x ，由()()f x f x -=可得()()()()1()1()xxxxF x f t dt f u du f u du f u du F x -+∞-∞+∞-∞-==--==-=-⎰⎰⎰⎰特别地，当0x =时，有(0)1(0)F F =-，即(0)0.5F =．根据以上结果，分别求得()1()10.80.2{0}()(0)0.80.50.3{||}()[1()]0.2(10.8)0.4F a F a P X a F a F P X a F a F a -=-=-=≤≤=-=-=>=-+-=+-=6.设随机变量X 服从区间(0,5)上的均匀分布，对X 进行3次独立观测，求至多有一次观测值小于2的概率．解根据均匀分布的定义，X 的密度函数为1,055()0x f x ⎧<<⎪=⎨⎪⎩，其他在每次观测中，观测值小于2的概率为221{2}()0.45P X f x dx dx -∞<===⎰⎰以Y 表示3次观测中观测值小于2的次数，则(3,0.4)Y B ，故所求概率为11330{1}{}(0.4)(0.6)0.648k k k k k P Y P Y k C -==≤====∑∑7.设随机变量X 服从区间(2,6)-上的均匀分布，求一元二次方程20t X t X ++=有实根的概率．解根据均匀分布的定义，X 的密度函数为1,268()0x f x ⎧-<<⎪=⎨⎪⎩，其他方程20t X t X ++=有实根的充分必要条件为24X X ≥，即0X ≤或4X ≥，故所求概率为622411{4}{0}{4}0.588P X X P X P X dx dx -≥=≤+≥=+=⎰⎰8.设某元件的使用寿命X (单位:小时)服从参数0.002λ=的指数分布，求：(1)该元件在使用500小时内损坏的概率；(2)该元件在使用1000小时后未损坏的概率；(3)该元件在使用500小时未损坏的情况下，可以再使用500小时的概率．解根据指数分布的定义，X 的密度函数为0.0020.002,0()0,0xe xf x x -⎧>⎪=⎨≤⎪⎩由此分别求得(1)该元件在使用500小时内损坏的概率为5000.0021{500}0.0021x P X e dx e --<==-⎰(2)该元件在使用1000小时后未损坏的概率为0.00221000{1000}0.002x P X e dx e +∞-->==⎰(3)根据指数分布的无记忆性，该元件在使用500小时未损坏的情况下，可以再使用500小时的概率为0.0021500{1000|500}{500}0.002x P X X P X e dx e +∞-->>=>==⎰9.设顾客在银行排队等候的时间X (单位:分)服从参数0.1λ=的指数分布．某顾客每周去一次银行办理业务，如果等候时间超过20分钟就离开，求该顾客一个月内至少有一次未办成业务的概率．解根据指数分布的定义，X 的密度函数为0.10.1,0()0,0xe xf x x -⎧>⎪=⎨≤⎪⎩故等候时间超过20分钟的概率为0.1220{20}0.1x P X e dx e +∞-->==⎰该顾客一个月内去银行4次，以Y 表示未办成业务的次数，则2(4,)Y B e - ，至少有一次未办成业务的概率为24{1}1{0}1(1)P Y P Y e -≥=-==--10.设随机变量X 服从正态分布2(,)N μσ，已知{}0.9P X c μ-≤=，求{}P X c μ->．解由2(,)X N μσ 可知，其密度函数曲线关于x μ=对称，有{}{}P X c P X c μμ-<-=->根据已知条件{}0.9P X c μ-≤=，可以求得(){}{}{}2{}21{}2(10.9)0.2P X c P X c P X c P X c P X c μμμμμ->=->+-<-=->=--≤=⨯-=11.设随机变量X 的密度函数为24481(),8x x X f x e x π++-=-∞<<+∞求：(1)X 服从何种分布；(2)概率{2}P X <-，{2}P X >，{44}P X -≤≤；(3)满足{}0.95P X c ≤>的常数c 的允许值．解X 的密度函数可表为222(2)4482211()822x x x X f x e eππ+++--⋅==⋅(1)对照正态分布2(,)N μσ的密度函数22()21()2x f x eμσπσ--=可知2(2,2)X N - ．(2)将X 标准化，查标准正态分表求得{}{}{}2{2}0(0)0.522{2}1{2}121(2)0.022822{44}13(3)(1)(3)(1)10.842X P X PX P X P X P X P X P ΦΦΦΦΦΦ+<-=<==+>=-≤=-<=-=+-≤≤=-<<=--=+-=(3)根据题意，要满足{}()222{}0.95222X c c P X c P=Φ+++≤=≤>反查标准正态分表可得2 1.652c +≥，故 1.3c ≥．12.设某车床加工的产品的直径服从正态分布2(100,0.2)N ，如果产品直径在1000.3±之间为合格，求该车床加工的产品的合格率．解以X 表示该车床加工的产品的直径，则2(100,0.2)X N ．根据产品标准，当99.7100.3X ≤≤时为合格，故产品的合格率为{}99.7100100100.3100{99.7100.3}0.20.20.2(1.5)( 1.5)2(1.5)10.8664X P X PΦΦΦ---≤≤=≤≤=--=-=13.设某车间每名工人每月完成的产品数服从正态分布2(3000,50)N ，按规定全车间有3%的工人可获超产奖，求获奖者每月至少要完成的产品数．解以X 表示每名工人每月完成的产品数，则2(3000,50)X N ．记获奖者每月至少要完成的产品数为c ，根据获超产奖的比例，有{}()30003000{}1{}15050300010.0350X c P X c P X c Pc Φ--≥=-<=-<-=-=由此可得()30000.9750c Φ-=，反查标准正态分布表得30001.8850c -=故获奖者每月至少要完成的产品数3094c =．14.设某课程的考试成绩服从正态分布2(75,)N σ，并且95分以上所占比例为2.5%．以达到60分为及格，求该课程的考试及格率．解以X 表示该课程考试成绩，则2(75,)X N σ ．根据95分以上比例，有{}()75957520{95}1{95}110.025X P X P X PΦσσσ-->=-≤=-≤=-=由此可得()200.975Φσ=，反查标准正态分布表得201.96σ=即201.96σ=，故该课程的考试及格率为{}()()()756075{60}1{60}115151 1.470.929X P X P X PσσΦΦΦσσ--≥=-<=-<=--===习题2–51.设随机变量X 的分布律为210120.10.150.20.250.3X P--求Y X =和(1)Z X X =-的分布律．解根据X 的分布律，有2101221012(1)620020.10.150.20.250.3X X X X P---将相同的取值合并，分别求得Y X =和(1)Z X X =-的分布律为0120.20.40.4Y P，0260.450.450.1Z P2.设随机变量X 的分布律为1{},1,2,2kP X k k ===求()sin2Y X π=的分布律．解相应于X 的取值，有()1,41sin 0,2,1,2,3,21,43X n Y X X n n X n π-=-⎧⎪====⎨⎪=-⎩根据X 的分布律，分别计算Y 的取值概率，有4111211431112{1}{41}21511{0}{2}2318{1}{43}215n n n n n n n n n P Y P X n P Y P X n P Y P X n ∞∞-==∞∞==∞∞-===-==-==========-==∑∑∑∑∑∑综上求得()sin2Y X π=的分布律为101258151515Y P-3.设随机变量X 的密度函数为21(),(1)f x x x π=-∞<<+∞+定义X 的函数110,1111X Y X X -≤-⎧⎪=-<<⎨⎪≥⎩，，求Y 的分布律．解根据X 的密度函数，分别计算Y 的取值概率，有121212111{1}{1}(1)411{0}{11}(1)211{1}{1}(1)4P Y P X dx x P Y P X dx x P Y P X dx x πππ--∞-+∞=-=≤-==+==-<<==+==≥==+⎰⎰⎰综上求得Y 的分布律为101211444Y P-4.设随机变量X 的密度函数为||,11()0,X x x f x -<<⎧=⎨⎩其他求2Y X =服从的分布．解由X 的取值区间(1,1)-可知2Y X =的取值区间为[0,1)．当0y <时，有(){}0Y F y P Y y =≤=；当1y ≥时，有(){}1Y F y P Y y =≤=；当01y ≤<时，在X 的取值区间(1,1)-上，有2(){}{}{}||yY yF y P Y y P X y P y X y x dx y-=≤=≤=-≤≤==⎰综上求得2Y X =的分布函数为0,0(),011,1Y y F y y y y <⎧⎪=≤<⎨⎪≥⎩由此可知2(0,1)Y X U = ．5.设随机变量X 服从区间(1,1)-上的均匀分布，求||X Y e -=的密度函数．解根据均匀分布的定义，X 的密度函数为1,112()0,X x f x ⎧-<<⎪=⎨⎪⎩其他由X 的取值区间(1,1)-可知||X Y e -=的取值区间为1(,1]e -．当1y e -≤或1y >时，有()0Y f y =．当11e y -<≤时，在X 的取值区间(1,1)-上，有||ln 11ln (){}{}{||ln }{1ln }{ln 1}11221ln 1()()X Y y y Y Y F y P Y y P e y P X y P X y P y X dx dxy f y F y y---=≤=≤=≥-=-<≤+-≤<=+=+'==⎰⎰综上求得||X Y e =的密度函数为11,1()0,Y e y yf y -⎧<<⎪=⎨⎪⎩其他其中()Y F y 在1y =处不可导，取(1)0Y f =．6.设随机变量X 服从区间(),22ππ-上的均匀分布，求sin Y X =的密度函数．解根据均匀分布的定义，X 的密度函数为1,22()0,X x f x πππ⎧-<<⎪=⎨⎪⎩其他由X 的取值区间(),22ππ-可知sin Y X =的取值区间为(1,1)-．在X 的取值区间(),22ππ-上，函数sin y x =严格单调且可导，其反函数为arcsin x y =，按公式求得sin Y X =的密度函数为2(arcsin )|(arcsin )|,11()0,11110X Y f y y y f y y y π'-<<⎧=⎨⎩⎧-<<⎪-=⎨⎪⎩其他其他7.设随机变量X 服从参数为λ的指数分布，求(0)Y a X b a =+>的分布函数和密度函数．解根据指数分布的定义，X 的密度函数为,0()0,xX e x f x x λλ->⎧=⎨≤⎩由X 的取值区间(0,+)∞及0a >，可知Y a X b =+的取值区间为(,)b +∞．当y b ≤时，有(){}0,()()0Y Y Y F y P Y y f y F y '=≤===；当y b >时，在X 的取值区间(0,+)∞上，有{}0()()(){}{}01()()Y y bx a y b ay b aY Y F y P Y y P a X b y y bP X e dxa ef y F y eaλλλλλ------=≤=+≤-=<≤==-'==⎰综上求得Y a X b =+的分布函数和密度函数为()()1,()0,,()0,y b a Y y b a Y e y bF y y b e y b af y y b λλλ----⎧⎪->=⎨⎪≤⎩⎧>⎪=⎨⎪≤⎩8.设随机变量X 服从标准正态分布(0,1)N ，求X Y e =的密度函数．解根据标准正态分布的定义，X 的密度函数为221(),2x x e x ϕπ-=-∞<<+∞由X 的取值区间(,)-∞+∞可知X Y e =的取值区间为(0,)+∞．在X 的取值区间(,)-∞+∞上，函数x y e =严格单调且可导，其反函数为ln x y =，按公式求得X Y e =的密度函数为2(ln )2(ln )|(ln )|,0()001,020,0X Y y f y y y f y y e y y y π-'>⎧=⎨≤⎩⎧>⎪=⎨⎪≤⎩，9.设随机变量X 服从区间(,)a b 上的均匀分布，证明(0)Y c X d c =+≠仍服从均匀分布．证仅证明0c >的情形．根据均匀分布的定义，X 的密度函数为1,()0X a x b b af x ⎧<<⎪-=⎨⎪⎩其他由X 的取值区间(,)a b 及0c >，可知Y c X d =+的取值区间为(,)ac d bc d ++．在X 的取值区间(,)a b 上，函数y c x d =+严格单调且可导，其反函数为y dx c-=，按公式求得Y c X d =+的密度函数为()(),()01,()0,XY y d y d f ac d y bc d c c f y ac d y bc d b a c '--⎧+<<+⎪=⎨⎪⎩⎧+<<+⎪-=⎨⎪⎩，其他其他由此即知(,)Y c X d U ac d bc d =+++ ．同理可证，对于0c <的情形，有(,)Y c X d U bc d ac d =+++ ．10.设随机变量X 服从参数1λ=的指数分布，证明X Y e -=和1X Z e -=-均服从区间(0,1)上的均匀分布．证根据指数分布的定义，X 的密度函数为,0()0,0xX e x f x x ->⎧=⎨≤⎩由X 的取值区间(0,)+∞可知，X Y e -=和1X Z e -=-的取值区间均为(0,1)．在X 的取值区间(0,)+∞上，函数x y e -=和1x z e -=-均严格单调且可导，其反函数分别为ln x y =-和ln(1)x z =--，按公式分别求得X Y e -=和1X Z e -=-的密度函数为(ln )|(ln )|,01()01,010,[ln(1)]|[ln(1)]|,01()01,010,X Y X Z f y y y f y y f z z z f z z '--<<⎧⎪=⎨⎪⎩<<⎧⎪=⎨⎪⎩'----<<⎧⎪=⎨⎪⎩<<⎧⎪=⎨⎪⎩，其他其他，其他其他由此即知(0,1)X Y e U -= ，1(0,1)X Z e U -=- ．总习题二1.从五个数1,2,3,4,5中任取三个数，以X 表示取到的最大数，求X 的分布律．解从1,2,3,4,5中任取三个数，共有3510C =种不同取法．可能取到的最大数3,4,5X =，相应的概率为2135{},3,4,5k C P X k k C -===计算得到X 的分布律为345136101010X P2.电台每小时报时一次，某人睡觉醒来不知时间而等待电台报时，求等待时间不超过15分钟的概率．解以分钟为单位．如果醒来时恰好电台报时，则等待时间0X =；否则等待时间(0,60)X ∈，故X 的可能取值范围为区间[0,60)．等待时间不超过15分钟意味着在时间区间[45,60)内醒来．根据几何概率有[45,60)151{15}604[0,60)P X ≤===区间的长度区间的长度3.重复进行伯努利试验，设每次试验成功的概率为p ，将试验进行到成功和失败都出现为止．以X 表示试验次数，求X 的分布律．解设事件k A 为“第k 次试验首次成功”，k B 为“第k 次试验首次失败”，2,3,k = ．则事件{}k k X k A B == ，且k k A B =∅，故X 的分布律为11{}()()()(1)(1),2,3,k k k k k k P X k P A B P A P B p p p p k --===+=-+-=4.设随机变量X 的分布律为21010.512X Paa --求常数a ，并求X 的分布函数．解根据分布律的非负性和规范性，有21200.5(12)1a a a -≥⎧⎪⎨+-+=⎪⎩由此可得112a =-．根据X 的分布律1010.51.5221X P---求得X 的分布函数为0,10.5,10()20.5,011,1x x F x x x ⎧<-⎪-≤<⎪=⎨-≤<⎪⎪≥⎩5.设自动生产线经过调整后出现次品的概率为0.01p =，生产过程中出现次品时立即调整生产线，以X 表示两次调整之间所生产的合格品数，求：(1)X 的分布律；(2)两次调整之间能以0.9的概率保证至少生产多少个合格品．解X 的可能取值为0,1,2, ．事件{}X k =表示连续生产k 个合格品后，第1k +个产品出现次品而需调整生产线．(1)X 的分布律为{}(0.99)0.01,0,1,2,k P X k k ==⨯=(2)两次调整之间至少生产k 个合格品的概率为{}{}(0.99)0.01(0.99),0,1,2,i k i ki kP X k P X i k ∞∞==≥===⨯==∑∑要以0.9的概率保证至少生产k 个合格品，应有(0.99)0.9k =，由此解得ln 0.910.48ln 0.99k ==故两次调整之间以0.9的概率保证至少生产10个合格品．6.对目标进行500次射击，设每次射击命中的概率为0.01，且每次射击命中与否相互独立，用泊松分布近似计算至少命中2次的概率．解以X 表示命中次数，则(500,0.01)X B ，至少命中2次的概率为15005000{2}1{1}1(0.01)(10.01)kk kk P X P X C -=≥=-≤=--∑根据500n =，0.01p =，由参数5np ==λ的泊松分布近似求得155{2}110.040.96!k k P X e k -=≥≈-=-=∑7.设在任一长为t 年的时间间隔内的地震发生次数()N t 服从参数为λt 的泊松分布，以T 表示距下次地震发生的间隔年数．求：(1)三年内发生地震的概率；(2)三年内不发生地震而下一个三年内发生地震的概率；(3)在三年内不发生地震的情况下，下一个三年内发生地震的概率．解根据题意，t 年内地震发生次数()N t 的分布律为(){()},0,1,2,!k tt P N t k e k k -===λλ记间隔年数T 的分布函数为()F t ，则当0t <时，有(){}0F t P T t =≤=；当0t ≥时，注意到{}T t >等价于{()0}N t =，有(){}1{}1{()0}1tF t P T t P T t P N t e -=≤=->=-==-λ综上可得T 的分布函数为1,0()0,0te t F t t λ-⎧-≥⎪=⎨<⎪⎩(1)三年内发生地震的概率为3{3}(3)1P T F e -≤==-λ(2)三年内不发生地震而下一个三年内发生地震的概率为36{36}{6}{3}(6)(3)P T P T P T F F e e --<≤=≤-≤=-=-λλ(3)在三年内不发生地震的情况下，下一个三年内发生地震的概率为3633{6,3}{36}{6|3}1{3}1{3}P T T P T e e P T T e P T P T e----≤><≤-≤>====->-≤λλλλ8.某型号元件的使用寿命X 服从参数为λ的指数分布，用若干该型号元件组成一个系统，设各元件损坏与否相互独立．以Y 表示系统的寿命，求下列两个系统寿命Y 的密度函数．(1)由n 个该型号元件组成的串联系统；(2)由n 个该型号元件组成的并联系统．解以i X 表示第i 个元件的使用寿命．由题意知i X 独立同分布，记其分布函数为()F x ，密度函数为()f x ，则1,0,0(),()0,00,0xxe x e x F xf x x x ---≥>⎧⎧==⎨⎨<≤⎩⎩λλλ(1)对于串联系统，其寿命Y 的分布函数为()11(){}1{}1{}11{}1[1()]Y nni i i i nF y P Y y P Y y P X y P X y F y ===≤=->=->=--≤=--∏∏求导得到密度函数为1,0()()[1()]()00nλyn Y Y nλe y f y F y n F y f y y -->⎧'==-=⎨≤⎩，(2)对于并联系统，其寿命Y 的分布函数为1(){}{}[()]nnY i i F y P Y y P X y F y ==≤=≤=∏求导得到密度函数为11(1),0()()[()]()00λy n λyn Y Y nλe e y f y F y n F y f y y ----->⎧'===⎨≤⎩，9.设电源电压X 服从正态分布2(220,25)N ，某电子元件当电压低于200V 时损坏的概率为0.1；当电压在200240V V 时损坏的概率为0.001；当电压高于240V 时损坏的概率为0.2，求：(1)该电子元件损坏的概率；(2)该电子元件损坏时，电源电压在200240V V 的概率．解设事件A 为“该电子元件损坏”，记电压状态123{220},{220240},{240}B X B X B X =<=≤≤=>由2(220,25)X N ，有{}()220220220{}252525X x x P X x PΦ---≤=≤=查标准正态分布表可得()()()123(){200}0.810.80.212(){200240}120.2120.576(){240}1{240}10.80.212P B P X P B P X P B P X P X ΦΦΦ=<=-=-==≤≤=-⨯==>=-≤=-=(1)根据全概率公式，该电子元件损坏的概率为31(){}(|)0.10.2120.0010.5760.20.2120.064i i i P A P B P A B ===⨯+⨯+⨯=∑(2)根据贝叶斯公式，该电子元件损坏时，电压在200240V V 的概率为2222(,){}(|)0.0010.576(|)0.009()()0.064P A B P B P A B P B A P A P A ⨯====10.设某门课程的考试成绩服从正态分布2(70,10)N ，如果规定优秀的比例为5%，求获得优秀的最低分数．解设获得优秀的最低分数为c ．由考试成绩2(70,10)X N ，以及优秀比例为5%，应有{}()707070{}1{}110.05101010X c c P X c P X c P---≥=-<=-<=-=Φ由此可得()700.9510c -=Φ，反查标准正态分布表得70 1.6510c -=故获得优秀的最低分数86.5c =．11.设非负随机变量X 的密度函数为()X f x ，求Y X =的密度函数．解由X 的取值区间[0,)+∞可知Y X =的取值区间为[0,)+∞．当0y =时，可取()0Y f y =．当0y >时，在X 的取值区间(0,)+∞上，函数y x =严格单调且可导，其反函数为2x y =，按公式求得Y X =的密度函数为222()(),0()002(),00,0X Y X f y y y f y y y f y y y '>⎧=⎨≤⎩>⎧=⎨≤⎩，12.设随机变量X 的密度函数为1||,11()0,X x x f x --<<⎧=⎨⎩其他求2Y X =的密度函数．解由X 的取值区间(1,1)-可知2Y X =的取值区间为[0,1)．当0y <或1y ≥时，有()0Y f y =．当01y ≤<时，在X 的取值区间(1,1)-上，有20(){}{}{}(1||)2(1)21()()1,01Y yyy Y Y F y P Y y P X y P y X y x dx x dx y yf y F y y y-=≤=≤=-≤≤=-=-=-'==-<<⎰⎰综上求得2Y X =的密度函数为11,01()0,Y y yf y ⎧-<<⎪=⎨⎪⎩其他其中()Y F y 在0y =处不可导，取(0)0Y f =．。

《概率论与数理统计》习题及答案第二章

《概率论与数理统计》习题及答案第二章1．假设一批产品中一、二、三等品各占60%，30%，10%，从中任取一件，发现它不是三等品，求它是一等品的概率.解设i A =‘任取一件是i 等品’ 1,2,3i =，所求概率为13133()(|)()P A A P A A P A =，因为 312A A A =+所以 312()()()0.60.30.9P A P A P A =+=+=131()()0.6P A A P A ==故1362(|)93P A A ==. 2．设10件产品中有4件不合格品，从中任取两件，已知所取两件中有一件是不合格品，求另一件也是不合格品的概率.解设A =‘所取两件中有一件是不合格品’i B =‘所取两件中恰有i 件不合格’ 1, 2.i = 则12A B B =+11246412221010()()()C C C P A P B P B C C =+=+，所求概率为2242112464()1(|)()5P B C P B A P A C C C ===+. 3．袋中有5只白球6只黑球，从袋中一次取出3个球，发现都是同一颜色，求这颜色是黑色的概率.解设A =‘发现是同一颜色’，B =‘全是白色’，C =‘全是黑色’，则 A B C =+，所求概率为336113333611511/()()2(|)()()//3C C P AC P C P C A P A P B C C C C C ====++ 4．从52张朴克牌中任意抽取5张，求在至少有3张黑桃的条件下，5张都是黑桃的概率.解设A =‘至少有3张黑桃’，i B =‘5张中恰有i 张黑桃’，3,4,5i =，则345A B B B =++，所求概率为555345()()(|)()()P AB P B P B A P A P B B B ==++51332415133********1686C C C C C C ==++. 5．设()0.5,()0.6,(|)0.8P A P B P B A ===求()P A B 与()P B A -.解 ()()()() 1.1()(|) 1.10P AB P A P B P A B P A P B A =+-=-=-= ()()()0.60.40.2P B A P B P AB -=-=-=.6．甲袋中有3个白球2个黑球，乙袋中有4个白球4个黑球，今从甲袋中任取2球放入乙袋，再从乙袋中任取一球，求该球是白球的概率。

概率论与数理统计第2章例题

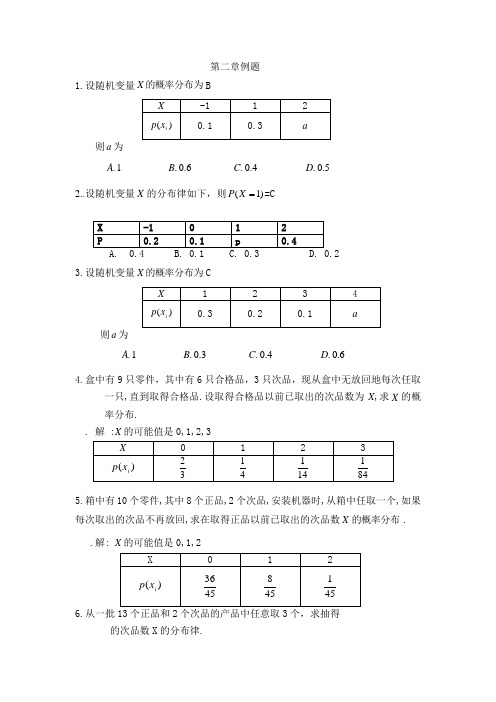
第二章例题1.设随机变量的概率分布为X B则a为1.A6.0.B4.0.C5.0.D2..设随机变量X的分布律如下，则(1)P X =CX C3.设随机变量的概率分布为则a为1.A3.0.B4.0.C6.0.D4.盒中有9只零件，其中有6只合格品，3只次品，现从盒中无放回地每次任取一只,直到取得合格品.设取得合格品以前已取出的次品数为X,求X的概率分布.. 解 :X的可能值是0,1,2,35.箱中有10个零件,其中8个正品,2个次品,安装机器时,从箱中任取一个,如果X. 每次取出的次品不再放回,求在取得正品以前已取出的次品数的概率分布.解: X的可能值是0,1,26.从一批13个正品和2个次品的产品中任意取3个，求抽得的次品数X的分布律.解31331522(0),35C P X C ===1221331512(1),35C C P X C ===212133151(2),35C C P X C === 分布律：取1个球，每次取出的黑球不再放回去，直至取到白球为止，求取球次数X 的分布律. 解 1P =25 2P =620 3P =1260 4P =6608.有10件产品,其中有2件是次品.现从中不放回地任取2件,求取得的产品中的次品数X 的分布律. 解,4528)0(21028===C C X P 451)2(,4516)1(210222101812======C C X P C C C X P 9. 一袋中有5个乒乓球，编号为1,2,3,4,5,在其中同时取三个，以X 表示取出的三个球中的最大号码，试求X 的分布律. 解6.0)5(,3.0)4(,1.01)3(3524352335=========CCX P C C X P C X P10．设随机变量X 的分布列为),2,1,0(,!)( ===k k ak X P kλ确定常数a 解：1!0=∑+∞=k kk a λ1!=∑+∞=k kk a λ, 1=λae , λ-=e a1.设连续型随机变量X 的概率密度和分布函数分别为()f x 和()F x ，则下列选项中正确的是 CA ．()01f x ≤≤B ．()()P X x F x ==C ．()()P X x F x =≤D ．()()P X x f x ==2.设连续型随机变量X 的密度函数为()f x ，分布函数为()F x ，则下列选项正确的是CA ．()()P X x f x ==B ．()()P X x F x ==C ．()()P X x F x <=D ． 0()1f x ≤≤3.=<<⎩⎨⎧≤≤=)121(,,010,2)(X P x x x f X 则其它的概率密度为设随机变量 B 1.A 43.B 31.C 21.D4. 随机变量X 的分布密度为⎩⎨⎧<<=其他020)(x kx x ϕ则k=__________ 1/25.设随机变量X 的概率密度为()Ax ,x ;f x ,⎧≤≤=⎨⎩2010其它，常数A 为BA. －2B. 3C. 1D. 46.设随机变量X 的概率密度为()Ax,x ;f x ,≤≤⎧=⎨⎩020其它，常数A 为 BA. 2B. 0.5C. －2D. 47.设连续随机变量X 的分布函数为()22,0;0,0.x A Be x F x x -⎧⎪+>=⎨⎪ ≤⎩ (1)求系数A 和B ；(2)()12P X <<.解 (1)()lim 11x F x A →+∞=⇒=()()0lim 01x F x F B →=⇒=-(2)()()()()12212210.4712P X F F e e --<<=-=-= 8.设连续随机变量X 的密度函数为()1;0, 1.x f x x <= ≥⎩(1)求系数A ；(2)1122P X ⎛⎫-<< ⎪⎝⎭.解 (1)()11f x dx A π+∞-∞=⇒=⎰(2)()1212111223P X f x dx -⎛⎫-<<== ⎪⎝⎭⎰ …9.⎪⎩⎪⎨⎧<≥=1000,01000,1000)():(2x x x x f X 概率密度为小时单位某种型号电子管的寿命,只任取互独立设各电子管损坏与否相现有一大批此种管子5),(,求其中至少有2 只寿命大于1500小时的概率.解:321000)1500(15002==>⎰+∞dx x X P令Y 为任取5只,寿命大于1500小时的管子数,)32,5(~B Y9547.0243232)1()0(1)2(===-=-=≥Y P Y P Y P 10.设随机变量X 在[0，2]上服从均匀分布，则概率密度()f x =()1022x f x ⎧≤≤⎪=⎨⎪⎩其它正态分布1.随机变量()2~,X N μσ，则X 落在区间(),μσμσ-+内的概率是_____________ (用()1Φ表示) ()211Φ- 2.~(2,4)X N ，则()0P X <=CA ．()1ΦB ．()121-ΦC ．()11-ΦD ．()11+Φ3.设)36,2(~N X 则P （X ≤8）=AA. )1(ΦB. )2(ΦC. 1-)1(ΦD. 1-)2(Φ4.设),(~2σμN X ,随σ的增大, 则}{σμ<-X P CA. 增减不定B. 单调减小C. 保持不变 D . 单调增大 5.).91(),2,3(~2<<-X P N X 求若)9987.0)3(,9772.0)2(,8413.0)1((=Φ=Φ=Φ已知)2()3()91(:-Φ-Φ=<<-X P 解9759.01)2()3(=-Φ+Φ=6.=≤)7(),9,1(X P N X 求服从正态分布设随机变量_________ 0.9772,.)9987.0)3(,9772.0)2(,8413.0)1((=Φ=Φ=Φ已知7. 设)01.0,3(~N X , 求}1.0|3{|>-X P (结果表示为)1(Φ的形式).解 }1.0|3{|1}1.0|3{|<--=>-X P X P)1(22)]1()1([1Φ-=-Φ-Φ-=8. 已知)9,108(~N X ，求}111105{<<X P , }3|108{|>-X P (结果表示为)(x Φ的形式).解 1)1(2)1()1()3108105()3108111(}111105{-Φ=-Φ-Φ=-Φ--Φ=<<X P)1(22)1)1(2(1}3|108{|1}3|108{|Φ-=-Φ-=≤--=>-X P X P9. 设随机变量X 与Y 均服从正态分布，22~(,4),~(,5)X N Y N μμ ，}{}{124,5p P X p P Y μμ=≤-=≥+，试说明：对于任何实数μ，都有12p p =. 解 ()(){4}{1}1114X P X P μμ-≤-=≤-=Φ-=-Φ (){5}{1}115Y P Y P μμ-≥+=≥=-Φ, 结论成立10.设总体X 服从正态分布()212,2N ，抽取容量为25的简单随机样本，求样本均值X 大于12.5的概率.（()1.250.8944Φ=）解 ⎪⎪⎭⎫⎝⎛>-=>25.15/212)5.12()252,12(~2X P X P N X ----4分 ()1 1.2510.89440.1056=-Φ=-= ----7分11.在电源电压不超过200伏、位于200～240伏和超过240伏三种情况下，某种电子元件损坏的概率分别为0.1,0.0010.2和，假设电源电压)25,220(~2N X 。

概率论第二章

第二章典型习题一、选择题1、设随机变量X的分布函数F（x）=P{X=1}=（）A、0B、C、-D、-2、设离散型随机变量X的概率分布为P{X=i}=c，i=1,2，…，其中c＞0是常数，则（）A、p=B、p=C、p=c+1D、0<p<1的任意数3、设随机变量X服从指数分布, 则随机变量Y=min{X,2}的分布函数( )A、是连续函数B、至少有两个间断点C、是阶梯函数D、恰好有一个间断点4、设f（x）是连续性随机变量X的概率密度，则f（x）一定是A、可积函数B、单调函数C、连续函数D、可积函数，k=0,1,2，…，则常数a=（）5.设随机变量X的概率分布为P{X=k}=a！A、B、C、D、6.设随机变量X服从正态分布N（μ,σ），则随σ的增大，概率P{|X-μ| <σ}应该（A）单调增大（B）单调减小（C）保持不变（D）增减不定7设随机变量X服从正态分布N（μ，），Y~N（μ，）；记=P{X≤μ-4}，=P{X≥μ+5}，则（）（A）（B）（C）（D）因μ未知，无法比较和的大小8.设随机变量X的密度函数为（x），Y=-2X+3，则Y的密度函数为（A）-（）（B）（）（C）-（）（D）（）9.设（x）与（x）分别是随机变量与的分布函数，为使F（x）=a（x）-b（x）是某一随机变量的分布函数，在下列给定的各组数值中应取（）（A）a=，b=（B）a=，b=（C）a=—，b=（D）a=，b=二、填空题1、设离散型随机变量X的概率密度是P{X=i}=，i=0,1，则p=2、设离散型随机变量X的分布函数F（x）=＜则随机变量|X|的分布函数3、设X是在区间（0,1）内取值的连续性随机变量，而Y=1-X，已知P{X≤0.29}=0.75，则满足P{Y≤k}=0.25的常数k=4、设f（x）=k（∞＜＜∞）是一概率密度，则k=若k满足概率等式P{X5、设随机变量X的概率密度为F(x)=其他≥k}=，则k的取值范围是（）6、设随机变量X的服从正态分布N（μ，1），已知P{X≤3}=0.975，则P{X≤-0.92}=7、设随机变量X的服从正态分布N（μ，），且二次方程+4y+X=0无实根的概率为0.5，则μ=8、设随机变量X的分布函数F（X），常数a＞0，则＋∞－∞（）=a三、解答题1、袋中装有大小相同的10只球，编号为0,1,2，…，9，从中任取一只，观察其编号，按“大于5，“等于5”，“小于5”三种情况定义随机变量X，并写出X的分布律和分布函数。

概率论2章习题

P{X=2}=P(A1A2A3)+P(A1A2A3)+P(A1A2A3)=P(A1)P(A2|A1)P(A3|A1A2)
+P(A1)P(A2|A1)P(A3|A1A2) +P(A1)P(A2|A1)P(A3|A1A2)
2 1 13 2 13 1 13 2 1 1 15 14 13 15 14 13 15 14 13 35
P{X<0}=P{X>a}=0
Xx 0
(1)若x<0, {Xx}是不可能事件, F(x)=P{X≤x} =0 .
ax
(2)若0≤x≤a , 事件A表示“质点落在[0,a]中小区间[0,x] 则 P(A)=P{0≤X内≤x”}与, 该小区间的长度x成比例,
令 P{0≤X≤x}=kx , (0≤x≤a),
qk-rpr =(1-p)k-rpr.
故Y的分布律为
P{Y
k}
k r
11
pr (1
p)kr ,
k r,r 1,
7. 设事件A在一次试验中发生的概率为0.3,当A发生不少于3次时, 指示灯发出信号.(1)进行了5次重复独立试验,求指示灯发出信号的概率;(2)进行了7次重复独立试验,求指示灯发出信号的概率.
T(以日计)服从指数分布,其概率密度为
fT
(t)
1 241
e
x
241,
t0
求分布函数FT(t),并求概率P{50<T<100}.
0,
其它
解
t0, FT (t)
t
fT (t)dt 0
t>0, FT (t)
t
fT (t)dt
t 1 et 0 241
241dt

《概率论与数理统计》第02章习题解答.docx

=0.2(0.2 + 0.2-0.2 x 0.2) = 0.072
P{ X = 1} = P[人(瓦U瓦)U孔A ] = 0.8(0.2 + 0.2-0.04) + 0.2 x (0.8)2
= 0.416
P{X=2} =P( £%為)=(0.8)3=0.512
3、据信有20%的美国人没有任何健康保险，现任意抽查12个美国人，以X表示15人无任何健康保险的人数(设各人是否有健康保险是相互独立的)，问X服从什么分布，写出X的分布律，并求下列情况下无任何健康保险的概率
解:(1)P{X>1}=f(x)dx=j"-(4-x2)dr = (-X- — X3)
"9927
（2）―叫刃’叩沟心］刃
22
27
10-R
£二0丄2,…，10
27■■
592
(3)P{y=2}=C^(—)2x(—)8=0.2998
s99s9?
p{r>2}= 1- p{r=0} - p{y=1}= 1-(—)° x(―)10- ^0(—)J(—)9= 0.5778
J；(0.2 + 1.2y)dy
—oo
y v _1
-1 < y < 0
0<y<\
0
0.2y + 0.2
0.6/+0.2j + 0.2
1
y <-1
0<y<l
沖1
P{0<Y<0.5} = F(0.5)-F(0) = 0.2+0.2x0.5 + 0.6x(0.5)2-0.2 = 0.25
P{y > 0.1} = 1-F(0」)=1一0.2-0.2x0」一0.6x0= 0.774

概率统计(概率论)第二章练习题答案及解析

第二章习题与答案同学们根据自己作答的实际情况，并结合总正误率和单个题目正误统计以及答案解析来总结和分析习题！！！标红表示正确答案标蓝表示解析1、为掌握商品销售情况，对占该地区商品销售额60%的10家大型商场进行调查，这种调查方式属于( )。

A普查B抽样调查【解析：抽取一部分单位进行调查；习惯上将概率抽样（根据随机原则来抽取样本）称为抽样调查】C重点调查【解析：在调查对象中选择一部分重点单位进行调查的一种非全面调查】D统计报表2、人口普查规定标准时间是为了（）。

A确定调查对象和调查单位B避免资料的重复和遗漏。

C使不同时间的资料具有可比性D便于登记资料【解析：规定时间只是为了统计该时间段内的人口数据，没有不同时间数据对比的需要】3、对一批灯泡的使用寿命进行调查，应该采用( )。

A普查 B重点调查 C典型调查D抽样调查4、分布数列反映( )。

A总体单位标志值在各组的分布状况B总体单位在各组的分布状况【解析：课本30页1.分布数列的概念一段最后一句】C总体单位标志值的差异情况D总体单位的差异情况5、与直方图比较，茎叶图( )。

A没有保留原始数据的信息B保留了原始数据的信息【解析：直方图展示了总体数据的主要分布特征，但它掩盖了各组内数据的具体差异。

为了弥补这一局限，对于未分组的原始数据则可以用茎叶图来观察其分布。

课本P38】C更适合描述分类数据D不能很好反映数据的分布特征6、在累计次数分布中，某组的向上累计次数表明( )。

A大于该组上限的次数是多少B大于该组下限的次数是多少C小于该组上限的次数是多少【解析：向上累计是由变量值小的组向变量值大的组累计各组的次数或频率，各组的累计次数表明小于该组上限的次数或百分数共有多少。

课本P33】D小于该组下限的次数是多少7、对某连续变量编制组距数列，第一组上限为500，第二组组中值是750，则第一组组中值为 ( )。

A. 200B. 250C. 500D. 300【解析：组中值=下限+组距/2=上限+组距/2】8、下列图形中最适合描述一组定量数据分布的是( )。

概率论与数理统计第二章习题及答案

概率论与数理统计习题第二章随机变量及其分布习题2-1 一袋中装有5只球，编号为1，2，3，4，5.在袋中同时取3只，以X 表示取出的3只球中的最大号码，写出X 随机变量的分布律.解：X 可以取值3，4，5，分布律为1061)4,3,2,1,5()5(1031)3,2,1,4()4(1011)2,1,3()3(352435233522=⨯====⨯====⨯===C C P X P C C P XP C C P X P 中任取两球再在号一球为中任取两球再在号一球为号两球为号一球为也可列为下表X ： 3， 4，5 P ：106,103,101习题2-2 进行重复独立试验，设每次试验成功的概率为p ，失败的概率为p -1)10(<<p .（1）将试验进行到出现一次成功为止，以X 表示所需的试验次数，求X 的分布律.（此时称X 服从以p 为参数的几何分布.）（2）将试验进行到出现r 次成功为止，以Y 表示所需的试验次数，求Y 的分布律.（此时称Y 服从以p r ,为参数的巴斯卡分布.）（3）一篮球运动员的投篮命中率为%45.以X 表示他首次投中时累计已投篮的次数，写出X 的分布律，并计算X 取偶数的概率.解：（1）P (X=k )=qk －1p k=1,2,……（2）Y=r+n={最后一次实验前r+n －1次有n 次失败，且最后一次成功},,2,1,0,)(111 ===+=-+--+n p q C p p q C n r Y P r n n n r r n n n r 其中 q=1－p ，或记r+n=k ，则 P {Y=k }= ,1,,)1(11+=----r r k p p C rk r r k（3）P (X=k ) = (0.55)k －10.45k=1,2…P (X 取偶数)=311145.0)55.0()2(1121===∑∑∞=-∞=k k k k X P习题2-3 一房间有同样大小的窗子，其中只有一扇是打开的。

概率论与数理统计习题及答案第二章.doc

习题 2-21. 设 A 为任一随机事件 , 且 P ( A )= p (0< p <1). 定义随机变量1, 发生 ,XA0, 不发生 .A写出随机变量 X 的分布律 .解 { =1}= ,{ =0}=1- p .P X p P X或者X 0 1P1- pp2. 已知随机变量X 只能取 -1,0,1,2 四个值 , 且取这四个值的相应概率依次为1 , 3 , 5 , 7. 试确定常数 c ,并计算条件概率 P{ X1 | X0} .2c 4c 8c 16c解由离散型随机变量的分布律的性质知，1 3 571,2c4c8c 16c37所以 c .161P{ X1}8所求概率为{ <1|X0 }=2c.P XP{ X 0}1 5 7252c 8c 16c3. 设随机变量 X 服从参数为 2, p 的二项分布 , 随机变量 Y 服从参数为 3, p 的二项分布 ,若P{X ≥1}5, 求P{Y ≥1}.9解注意 p{x=k}=C n k p k q n k , 由题设 5P{ X ≥1}1 P{ X0} 1 q 2 ,9故 q1 p2 从而.3P{Y ≥1} 1 P{ Y 0}1 (2 )3 19 .3 274. 在三次独立的重复试验中 , 每次试验成功的概率相同 , 已知至少成功一次的概率19为, 求每次试验成功的概率 .27解设每次试验成功的概率为p , 由题意知至少成功一次的概率是19，那么一次都27没有成功的概率是8 . 即 (1 p)38 ,故p = 1 .272735. 若 X 服从参数为的泊松分布 ,且P{X1} P{ X 3}, 求参数 .解由泊松分布的分布律可知 6 .6. 一袋中装有 5 只球 , 编号为 1,2,3,4,5.在袋中同时取 3 只球, 以 X 表示取出的 3 只球中的最大号码 , 写出随机变量 X 的分布律 .解从 1，2，3，4，5 中随机取 3 个，以 X 表示 3 个数中的最大值， X 的可能取值是 3，4，5，在 5 个数中取 3 个共有C 5310 种取法 .{ =3} 表示取出的 3 个数以 3 为最大值， P{=3}=C 22= 1;C 53 10{ =4} 表示取出的 3 个数以 4 为最大值， P{=4}=C 323 ;C 53 10 { =5} 表示取出的 3 个数以 5 为最大值， P{=5}=C 423 .5 C 53X 的分布律是X 3 45P13310105习题 2-31. 设 X 的分布律为X -11P求分布函数( ), 并计算概率 { <0},{ <2},{-2 ≤ <1}.F xPXPXPX0, x 1, 解 (1)0.15, 1≤ x 0,F ( x )=0≤ x 1,0.35, 1,x ≥1.(2) P { X <0}= P { X =-1}=; (3) P { X <2}= P { X =-1}+ P { X =0}+P { X =1}=1; (4) P {-2 ≤ x <1}= P { X =-1}+ P { X =0}=.2. 设随机变量 X 的分布函数为( ) = + arctan x - ∞< <+∞.F xA Bx试求 : (1) 常数 A 与 B ; (2)X 落在 (-1, 1] 内的概率 .解 (1) 由于 (- ∞)=0,(+∞)=1, 可知F FA B()1 12A, B.A B( )122于是F ( x) 1 1arctan x, x .2(2) P{ 1X ≤1} F (1) F ( 1)1 1 1 1arctan( 1))( arctan1) (2 21 1 1 1 () 1 .2424 23. 设随机变量 X 的分布函数为F ( x )=0,x 0, x,0≤x 1,1,x ≥1,求 P { X ≤ -1}, P { < X <}, P {0< X ≤ 2}.解 P {X ≤ 1} F( 1) 0,P {< X <}= F - F {}- P { X =}=, P {0< X ≤2}= F (2)- F (0)=1.5.X 的绝对值不大于1;P{ X1}1 1}1 假设随机变量 ,P{X; 在事件{ 1 X 1} 出现的条件下 ,84X 在 (-1,1) 内任一子区间上取值的条件概率与该区间的长度成正比 . (1) 求 X 的分布函数 F ( x) P{ X ≤ x }; (2)求 X 取负值的概率 p .解 (1) 由条件可知 ,当 x1时,F ( x) 0 ;当 x 1 时 , F ( 1) 1;当 x 1时 , 8F (1)= P { X ≤ 1}= P ( S )=1.所以P{ 1 X1} F (1) F ( 1)P{X 1}1 1 514.88易见 , 在 X 的值属于 (1,1) 的条件下 , 事件 { 1 X x} 的条件概率为P{ 1 X ≤ x | 1X 1} k[ x( 1)],取 x =1 得到 1= k (1+1),所以 k = 1.2x 1 . 因此P{ 1 X ≤x | 1 X 1}于是 , 对于1 x 1 ,有2P{ 1X ≤ x} P{ 1X ≤ x, 1 X 1}P{ 1 X 1} P{ 1 X ≤ x | 1 X 1}5 x 1 5x 5 . 对于 x ≥1,8 2 16有 F ( x) 1. 从而0, x 1, F ( x)5x 7 , 1x 1,161, ≥x1.(2) X 取负值的概率p P{ X0} F(0) P{ X0} F (0) [F(0)F (0 )] F (0 )7 . 习题 2-4161. 选择题设 f ( x)2x, x [0, c],则 f ( x) 是某一随机变量的概率(1)0,x如果 c =(),[0, c].密度函数 .(A)1(B)1.(C) 1.(D)3.2.3c2f ( x)dx 11 ,于是 c 1解由概率密度函数的性质可得2xdx, 故本题应选 (C ).(2) 设 X ~ N (0,1), 又常数 c 满足 P{ X ≥ c} P{ X c} , 则 c 等于 ( ).(A) 1.(B) 0.(C)1 (D) -1..2解因为P{ X ≥ c} P{ X c} ,所以 1 P{ X c} P{ X c} , 即2P{ Xc} 1, 从而 P{X c} 0.5 , 即 ( c) 0.5 , 得 c =0. 因此本题应选 (B).(3) 下列函数中可以作为某一随机变量的概率密度的是( ).cos x, x [0, ],1x2,(A)f (x)(B)f (x),0,其它 .20,其它 .1( x) 2x≥22e,≥ 0,e , x0, (C)f (x) (D)f ( x)20, x0.0,x 0.解由概率密度函数的性质f ( x)dx 1 可知本题应选 (D).(4) 设随机变量X ~ N(,42) , Y~N(,52), P 1P{X ≤4 },P 2 PY ≥ 5 }, 则( ).(A) 对任意的实数 , P 1P 2 . (B) 对任意的实数 , P 1 P 2 .(C) 只对实数的个别值 ,有P 1 P 2 . (D) 对任意的实数 , P P .12解由正态分布函数的性质可知对任意的实数, 有P 1( 1) 1 (1) P 2 .因此本题应选 (A).Xf xf (x)f ( x)F x(5) 设随机变量的概率密度为 , 且 , 又( )为分布函数 , 则对任意实数 a , 有 ( ).a(A)F ( a) 1∫0 f (x)dx .(B)F ( a)(C) F ( a)F ( a) . (D) Fa解由分布函数的几何意义及概率密度的性质知答案为1 a2 ∫0f ( x)dx.2F ( a) 1 .(B).(6) 设随机变量X 服从正态分布N (1, 12 ) , Y 服从正态分布 N ( 2, 22) ,且P{ X11} P{ Y21},则下式中成立的是 (). (A) σ1 < σ2 .(B)σ 1 > σ 2 .(C)μ1 <μ2 .(D)μ1 >μ2 .解答案是 (A). XN(0 1)u 满足(7) 设随机变量服从正态分布对给定的正数, 数(0,1),P{ X u }, 若P{X x}, 则 x 等于 ().(A)u .(B)u.(C)u 1-.(D)u 1.2122解答案是 (C).2. 设连续型随机变量 X 服从参数为的指数分布 ,要使P{ kX 2k}1成立 ,4应当怎样选择数 k ?解因为随机变量 X 服从参数为的指数分布 , 其分布函数为F ( x)1 e x , x 0,0,x ≤ 0.由题意可知1 P{ k X 2k} F(2k) F ( k) (1 e2 k )(1 e k ) e k e 2 k .4于是kln 2.3. 设随机变量 X 有概率密度f ( x) 4 x 3 , 0 x 1, 0,其它 ,要使 P{ X ≥ a}P{ Xa} ( 其中 a >0) 成立 , 应当怎样选择数 a ?解由条件变形 , 得到 1P{ Xa} P{ Xa},可知P{ X a} 0.5 ,于是a3dx 0.5,因此 a14x.424. 设连续型随机变量 X 的分布函数为0,x 0,F ( x)x 2 , 0≤x ≤1,1,x 1,求: (1)X 的概率密度 ; (2) P{0.3 X 0.7} .解 (1)根据分布函数与概率密度的关系F ( x)f ( x) ,可得f (x)2x, 0 x 1,0, 其它 .(2)P{0.3 X0.7}F (0.7) F (0.3) 0.720.320.4 .5. 设随机变量 X 的概率密度为2x,0≤ x ≤1,f ( x ) ＝其它 ,0,求P {X ≤ 1}与P {1＜ X ≤2}.241}11 1解P{X ≤ 22xdx x 22 ;24P{ 1 X ≤2}1 2 xdx x 2 1 15 .1444 166. 设连续型随机变量 X 具有概率密度函数x,0 x ≤1,f ( x) Ax,1x ≤2,0,其它 .求 : (1) 常数 A ； (2) X 的分布函数 F ( x ).解 (1) 由概率密度的性质可得11 2( A x)dx1 x2xdx12于是A 2；(2) 由公式 F ( x) xf ( x)dx可得当 x ≤0 时 , F ( x) 0 ; 当 0x ≤1时 ,F( x)x1 x2 ;xdx2当 1x ≤2时 ,F ( x)1x(2xdx1当 x >2 时,F ( x) 1.0,1 x2 , 所以F ( x)2 x 22x1,2112[ Ax x 2]A 1,21x 2 x)dx 2x1;2x ≤ 0,0 x ≤ 1,1 x ≤ 2,1,x2.7. 设随机变量 X 的概率密度为1f ( x) 4( x 1), 0 x 2,0, 其它 ,对 X 独立观察 3 次, 求至少有 2 次的结果大于 1 的概率 . 解根据概率密度与分布函数的关系式P{ a X ≤ b} F (b) F ( a)b f ( x)dx ,a可得P{ X 1} 21 ( x 1)dx 54.1 8 所以 , 3 次观察中至少有2 次的结果大于 1 的概率为C 2(5)2(3) C 3 ( 5)3 175 .8 8 2568 4x 2 8. 设 X ~U(0,5) , 求关于 x 的方程 4 Xx 2 0 有实根的概率 .解随机变量 X 的概率密度为1, ≤ x 5,f ( x)50, 其它 ,若方程有实根 , 则16 X 232≥0, 于是 X 2 ≥ 2. 故方程有实根的概率为P { X 2 ≥2}= 1P{ X 2 2}1 P{2 X2}1 21dx0 512 .59. 设随机变量 X ~ N(3,22) .(1)计算 P{2 X ≤5} , P{ 4 X ≤10}, P{| X | 2}, P{X 3}；(2)确定 c 使得P{ X c} P{ X ≤ c}; (3) 设 d 满足 P{ X d}≥0.9 , 问 d 至多为多少？解 (1) 由 P { a <x ≤ b }= P { a3 X 3 ≤ b 3 } Φ( b 3 ) Φ( a 3)公式,得到2 2 2 22XΦ(1) Φ( 0.5) 0.5328P,{2< ≤5}=P {-4< X ≤10}= Φ(3.5) Φ( 3.5) 0.9996,P{|X|2}=P{X2} +P{X2}=1 2 32 3Φ() +Φ(2 ) =,2P{ X 3} =1 P{ X ≤3} 1Φ( 3 3 ) 1 Φ(0) = .2(2) 若P{Xc}P{ X ≤ c} , 得 1P{ X ≤ c}P{ x ≤ c} ,所以P{ X ≤ c} 0.5由 Φ(0) =0 推得c3 0, 于是 c =3.2 Φ(d3(3)P{ X d}≥ 0.9 即1)≥ 0.9 , 也就是2Φ( d 3 )≥ 0.9 Φ(1.282) ,2因分布函数是一个不减函数, 故(d 3)≥ 1.282,2解得d ≤ 3 2 ( 1.282) 0.436 .10. 设随机变量 X ~ N (2, 2) , 若 P{0 X4} 0.3 , 求 P{X 0} .解因为X ~ N2,所以 ZX~ N(0,1). 由条件 P{0 X4} 0.3可知0.3 P{0 X4}0 2X 24 22(2P{}( )) ,于是 222 ( )10.3从而 ( )0.65 .,P{X 0}P{X202}(22 所以) 1( ) 0.35.习题 2-5 1. 选择题(1) 设 X 的分布函数为 F ( x ), 则 Y 3 X 1 的分布函数 G y 为( ).(A) F (1 1 (B)F (3 y 1) .y) .3311(C)3F ( y) 1.(D)F ( y).3 3解由随机变量函数的分布可得 , 本题应选 (A).(2) 设X~N 01 ,令YX 2, 则Y ~().(A)N( 2, 1). (B)N(0,1) . (C) N( 2,1) . (D)N (2,1) .解由正态分布函数的性质可知本题应选 (C).2. 设 X ~ N(1,2), Z 2X 3 , 求 Z 所服从的分布及概率密度 . 解若随机变量 X ~ N(,2) , 则 X 的线性函数 YaX b 也服从正态分布 , 即Y aX b ~ N( a b,( a ) 2). 这里 1,2 , 所以 Z ~ N(5,8) .概率密度为1 ( x 5) 2f (z)16,x.e43. 已知随机变量 X 的分布律为X -1137P(1) 求＝2－ X 的分布律； (2) 求＝3＋ 2分布律 .YYX解 (1)2－X-5-1123P(2)3＋X 23 41252P4. 已知随机变量 X 的概率密度为1， 1 x 4，f X ( x)＝2 x ln 20，其它，且 Y ＝2－ X , 试求 Y 的概率密度 .解先求Y的分布函数F Y ( y):F Y ( y) = P{ Y ≤ y}P{2X ≤ y}P{X ≥2 y}2 y1 P{ X 2y} =1-f X ( x)dx.于是可得 Y 的概率密度为1, 1 2 y4,f Y ( y)f X (2y)(2 y)=2(2 y) ln 20,其它 .1, 2 y1,f Y ( y)即2(2 y) ln 20,其它 .5. 设随机变量 X 服从区间 (-2,2) 上的均匀分布, 求随机变量 YX 2 的概率密度 .解由题意可知随机变量 X 的概率密度为f X ( x)1 ,2 x2,40, 其它 .因为对于 0<y <4,F Y ( y) P{ Y ≤ y} P{ X 2 ≤ y} P{y ≤ X ≤ y }F X ( y ) F X ( y ) .于是随机变量YX 2 的概率密度函数为f Y ( y)1 f X ( y )11 , 0 y 4.f X ( y )y4 2 y2 yf ( y)1 , 0 y 4,即4 y0,其它 .总习题二1. 一批产品中有 20%的次品 , 现进行有放回抽样 , 共抽取 5 件样品 . 分别计算这 5 件样品中恰好有 3 件次品及至多有 3 件次品的概率 .解以 X 表示抽取的 5 件样品中含有的次品数 . 依题意知 X ~ B(5,0.2) .(1) 恰好有 3 件次品的概率是 P X C 5 0.2 3 0.8 .{ =3}= 3 23(2) 至多有 3 件次品的概率是C 5k 0.2k 0.85 k .k 02. 一办公楼装有 5 个同类型的供水设备 . 调查表明 , 在任一时刻 t 每个设备被使用的概率为 . 问在同一时刻(1) 恰有两个设备被使用的概率是多少？ (2) 至少有 1 个设备被使用的概率是多少？ (3) 至多有 3 个设备被使用的概率是多少？(4) 至少有 3 个设备被使用的概率是多少？解以 X 表示同一时刻被使用的设备的个数，则X ~B (5,,{ = }=k k5 kP X kC 50.1 0.9, k =0,1, ,5.(1) 所求的概率是 P XC 50.1 0.90.0729 ;{ =2}=223(2)所求的概率是 P X(1 0.1)5 0.40951 ;{ ≥ 1}=1(3)所求的概率是{ ≤ 3}=1-P{ =4}- { =5}=;P XXP X(4) 所求的概率是 P { X ≥ 3}= P { X =3}+ P { X =4}+ P { X =5}=.3. 设随机变量 X 的概率密度为xkf ( x)e , x ≥0,0， x0,1且已知k θ, 求常数.,2k x解由概率密度的性质可知dx1得到 k =1.e1x1由已知条件1, 得.1 e dx2ln 24. 某产品的某一质量指标 X ~ N(160, 2 ) , 若要求 P{120 ≤X ≤ 200} ≥, 问允许最大是多少 ?解由P{120 ≤ ≤ 200} P{ 120 160 X160 200 160X≤ ≤ }= ( 404040) (1( ))2 ( ) 1≥,( 40 ) ≥ , 40最大值为 .得到查表得 ≥ , 由此可得允许5.设随机变量 X 的概率密度为( x ) = e -| x | , - ∞< <+∞.φX A x试求 : (1) 常数 ; (2) {0< <1}; (3)的分布函数 .AP X解 (1)由于(x)dxAe |x|dx 1, 即2 Ae x dx 1故 2A = 1, 得1到A = .2所以φ( x ) =1 e -|x |.2(2) P {0< X <1} = 11 xdx1 ( e x 11 e 10.316.e2 ) 220 (3)因为 F ( x)x1 e |x| 得到2 dx,11当 x <0 时 , F ( x)x x x ,2 e dx 2e当 x ≥0 时,F ( x)1 0x1 xe x1 x,2e dx2dx 1 e21e x ,x0,所以 X 的分布函数为F ( x)21 ex,1 x ≥ 0.2。

概率论第二章+习题

第二章随机变量与概率分布一、单项选择题1．设随机变量的密度函数p(x)= ⎩⎪⎨⎪⎧ 2x x[0、A] 0 其他, 则常数 A=( )A 、1/4B 、1/2C 、1D 、22．设随机变量的分布列为P{=k}=C2k ，k=1,2,…，则常数C= ( )A 、1/4B 、1/2C 、1D 、23．设 ~ N (, 2 )，且概率密度 p(x) =16e -(x-2)2/6 ，则正确的为 ( ) A 、= 3 , =2 B 、=2, =3 C 、=2, = 3 D 、= 2 , = 34．设随机变量的密度函数 p(x) = ⎩⎪⎨⎪⎧Asinx ， x[0，]0，其它，则A=( )A 、1B 、1/2C 、1/4D 、2 5．设离散型随机变量X 的分布列为错误!其分布函数为F(x),则 F(3/2) = ( ) A 、 B 、0.3 C 、 D 、6．设随机变量的分布列为⎣⎢⎡⎦⎥⎤1 2 4P 1/4 1/2 , 则常数 = ( )A 、1/8B 、1/4C 、1/3D 、1/2 7．在相同条件下，相互独立地进行5次射击，每次射击时命中目标的概率为，则击中目标的次数的概率分布为 ( )A 、二项分布 B(5,B 、普阿松分布P(2)C 、均匀分布 U, 3)D 、正态分布 N(3, 52) 8．某射手对目标独立地进行射击，直到击中目标为止，设每次击中的概率为2/3，则击中目标前的射击次数X 的概率分布为 ( )A 、P{X=k}= C n k (23 ) k (13 ) n – k , k=0,1,2,…,nB 、P{X=k}= kk! e –1 , >0, k=0,1,2,…,n C 、P{X=k}= (23 ) (13 )k k=0,1,2,…D 、P{X=k}= (23 ) (13 )k-1 k=0,1,2,…9．设随机变量的密度函数为p(x)，且p(-x)=p(x)，F(x)是的分布函数，则对任意的实数a,有( )A 、F(-a)=1- ⎠⎛0a p(x)dx B 、F(-a)=12 - ⎠⎛0a p(x)dx C 、F(-a)=F(a) D 、F(-a)=2F(a)-110．设随机变量的密度函数为p(x)= ⎩⎪⎨⎪⎧x 0<x ≤12-x 1<x ≤20 其它，则P{<}等于 ( )A 、B 、C 、⎠⎛0(2-x)dxD 、⎠⎛1(2-x)dx二、填空题11．设随机变量的分布函数为 F(x)= ⎩⎪⎨⎪⎧0 x<0sinx 0x</21 x/2, 则 F(/4)= 。

(完整版)概率论第二章随机变量及其分布答案

概率论与数理统计练习题系专业班姓名学号第二章随机变量及其分布（一）一．选择题：1．设X 是离散型随机变量，以下可以作为X 的概率分布是 [ B ]（A ）1234111124816Xx x x x p （B ） 123411112488X x x x x p （C ）1234111123412Xx x x x p（D ） 1234111123412X x x x x p -2．设随机变量ξ的分布列为 01230.10.30.40.2X p )(x F 为其分布函数，则)2(F =[ C ]（A ）0.2 （B ）0.4 （C ）0.8 （D ）1 二、填空题：1．设随机变量X 的概率分布为0120.20.5X p a ，则a = 0.32．某产品15件，其中有次品2件。

现从中任取3件，则抽得次品数X 的概率分布为 P{X=0}=22/35;P{X=1}=12/35; P{X=2}=1/353．设射手每次击中目标的概率为0.7,连续射击10次，则击中目标次数X 的概率分布为 P{X=k}=k kkC -⨯10103.07.0,10,,0Λ=k 或X~B(10,0.7)三、计算题：1．同时掷两颗骰子，设随机变量X 为“两颗骰子点数之和”求：（1）X 的概率分布；（2）(3)P X ≤；（3）(12)P X >(1) P{X=2}= P{X=12}=1/36; P{X=3}= P{X=11}=1/18;P{X=4}= P{X=10}=1/12; P{X=5}= P{X=9}=1/9;P{X=6}= P{X=8}=5/36;P{X=7}=1/6(2) P{X=2}=1/36; P{X=3}=1/18 (3) P{X>12}=02．产品有一、二、三等品及废品四种，其中一、二、三等品及废品率分别为60%，10%，20%及10%，任取一个产品检查其质量，试用随机变量X 描述检查结果。

概率论第二章习题参考解答

概率论第二章习题参考解答1. 用随机变量来描述掷一枚硬币的试验结果. 写出它的概率函数和分布函数. 解: 假设ξ=1对应于"正面朝上",ξ=0对应于反面朝上. 则 P (ξ=0)=P (ξ=1)=0.5 . 其分布函数为⎪⎩⎪⎨⎧≥<≤<=11105.000)(x x x x F 2. 如果ξ服从0-1分布, 又知ξ取1的概率为它取0的概率的两倍, 写出ξ的分布律和分布函数.解: 根据题意有 P (ξ=1)=2P (ξ=0) (1) 并由概率分布的性质知 P (ξ=0)+P (ξ=1)=1 (2) 将(1)代入(2)得3P (ξ=0)=1, 即P (ξ=0)=1/3 再由(1)式得 P (ξ=1)=2/3因此分布律由下表所示ξ0 1 P 1/32/3而分布函数为⎪⎩⎪⎨⎧>=<≤<=11103/100)(x x x x F 3. 如果ξ的概率函数为P {ξ=a }=1, 则称ξ服从退化分布. 写出它的分布函数F (x ), 画出F (x )的图形. 解: ⎩⎨⎧≥<=ax a x x F 10)(, 它的图形为ax1 0F (x )4. 一批产品分一,二,三级, 其中一级品是二级品的两倍, 三级品是二级品的一半, 从这批产品中随机地抽取一个检验质量, 用随机变量描述检验的可能结果, 写出它的概率函数. 解设ξ取值1,2,3代表取到的产品为一,二,三级, 则根据题意有 P (ξ=1)=2P (ξ=2) (1)P (ξ=3)=P (ξ=2)/2 (2) 由概率论性质可知P (ξ=1)+P (ξ=2)+P (ξ=3)=1 (3)(1),(2)代入(3)得:2P (ξ=2)+P (ξ=2)+P (ξ=2)/2=1解得P (ξ=2)=2/7, 再代回到(1)和(2)得 P (ξ=1)=4/7, P (ξ=3)=1/7 则概率函数为)3,2,1(271)(3=⨯==-i i P i ξ或列表如下: ξ 123P 4/7 2/7 1/75. 一批产品20个, 其中有5个次品, 从这批产品中随意抽取4个, 求这4个中的次品数ξ的分布律.解: 基本事件总数为420C n =,有利于事件{ξ=i }(i =0,1,2,3,4)的基本事件数为ii i C C n -=4155, 则001.01731911718192051234)4(031.0171952121545171819201234)3(2167.01718191415231212141545171819201234)2(4696.01718191314151231314155171819201234)1(2817.01719137123412131415171819201234)0(445420115354202152542031515420415=⋅⋅=⋅⋅⋅⋅⋅⋅⋅====⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅====⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅====⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅====⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅===C C P C C C P C C C P C C C P C C P ξξξξξ ξ1234P 0.2817 0.4696 0.2167 0.031 0.0016. 一批产品包括10件正品, 3件次品, 有放回地抽取, 每次一件, 直到取得正品为止, 假定每件产品被取到的机会相同, 求抽取次数ξ的概率函数.解: 每次抽到正品的概率相同, 均为p =10/13=0.7692, 则每次抽到次品的概率q =1-p =0.2308则ξ服从相应的几何分布, 即有),3,2,1(1331310)(1=⎪⎭⎫⎝⎛⋅===-i pq i P i i ξ7. 上题中如果每次取出一件产品后, 总以一件正品放回去, 直到取得正品为止, 求抽取次数ξ的分布律.解: 这样抽取次数就是有限的, 因为总共只有3件次品, 即使前面三次都抽到次品,第四次抽时次品已经全部代换为正品, 因此必然抽到正品, 这样ξ的取值为1,2,3,4. 不难算出,0027.0131132133)4(0328.01312132133)3(1953.01311133)2(7692.01310)1(=⋅⋅===⋅⋅===⋅=====ξξξξP P P Pξ 1234P 0.7692 0.1953 0.0328 0.00278. 自动生产线在调整之后出现废品的概率为p , 当在生产过程中出现废品时立即重新进行调整, 求在两次调整之间生产的合格品数ξ的概率函数.解: 事件ξ=i 说明生产了i 次正品后第i +1次出现废品, 这是i +1个独立事件的交(1次发生i 次不发生, 因此有P (ξ=i )=p (1-p )i , (i =0,1,2,…)9. 已知随机变量ξ只能取-1,0,1,2四个值, 相应概率依次为cc c c 167,85,43,21, 确定常数c 并计算P {ξ<1|ξ≠0}.解: 根据概率函数的性质有1}2{}1{}0{}1{==+=+=+-=ξξξξP P P P即1167854321=+++cc c c 得2.3125163716710128167854321==+++=+++=c 设事件A 为ξ<1, B 为ξ≠0, (注: 如果熟练也可以不这样设)则32.0258167852121}2{}1{}1{}1{)0{}01{)()(}0|1{==++==+=+-=-==≠≠⋂<==≠<ξξξξξξξξξP P P P P P B P AB P P 10. 写出第4题及第9题中各随机变量的分布函数. 解: 第4题:⎪⎪⎩⎪⎪⎨⎧≥<≤<≤<=31327/6217/410)(x x x x x F第9题:当x <-1时: F (x )=P (ξ≤x )=0 当-1≤x <0时: F (x )=P (ξ≤x )=P (ξ=-1)=2162.03125.22121=⨯=c 当0≤x <1时: F (x )=P (ξ≤x )=P (ξ=-1)+P (ξ=0)=5405.03125.243214321=⎪⎭⎫ ⎝⎛+=+c c 当1≤x <2时: F (x )=P (ξ≤x )=P (ξ=-1)+P (ξ=0)+P (ξ=1)=8108.03125.2854321854321=⎪⎭⎫ ⎝⎛++=++c c c 当x ≥2时: F (x )=P (ξ≤x )=1 综上所述, 最后得:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<≤--<=21218108.0105405.0012162.01)(x x x x x x F 11. 已知ξ~⎪⎩⎪⎨⎧<<=其它1021)(x xx ϕ, 求ξ的分布函数F (x ), 画出F (x )的图形.解: 当x <0时: F (x )=0;当0≤x <1时:xx xt x t dt t dt t dt dt t x F xxx=-==+-⋅==+==+--∞-∞-⎰⎰⎰⎰00012112121210)()(12102100ϕ 当x ≥1时: F (x )=1 综上所述, 最后得⎪⎩⎪⎨⎧≥<≤<=111000)(x x xx x F 图形为10 xF (x )112. 已知ξ~⎩⎨⎧<<=其它0102)(x x x ϕ, 求P {ξ≤0.5}; P (ξ=0.5);F (x ).解: 25.005.020)(}5.0{225.0025.005,0|=-==+==≤⎰⎰⎰∞-∞-x xdx dx dx x P ϕξ, 因ξ为连续型随机变量, 因此取任何点的概率均为零, 所以P {ξ=0.5}=0,求F (x ): 当x <0时, F (x )=0 当0≤x <1时, 220|20)()(x t tdt dt dt t x F xxx==+==⎰⎰⎰∞-∞-ϕ 当x ≥1时, F (x )=1 综上所述, 最后得:⎪⎩⎪⎨⎧≥<≤<=111000)(2x x x x x F 13. 某型号电子管, 其寿命(以小时计)为一随机变量, 概率密度⎪⎩⎪⎨⎧≥=其它0100100)(2x x x ϕ, 某一个电子设备内配有3个这样的电子管, 求电子管使用150小时都不需要更换的概率.解: 先求一个电子管使用150小时以上的概率P (ξ≥150)为:3215010012100100)()150(|150121502150==+-===≥∞++-+∞+∞⎰⎰x dx xdx x P ϕξ 则3个这样的电子管构成贝努里独立试验概型, 试验三次发生三次的概率为2963.027832)3(33==⎪⎭⎫⎝⎛=p14. 设连续型随机变量ξ的分布函数为:⎪⎩⎪⎨⎧≥<≤<=111000)(2x x Ax x x F 求系数A ; P (0.3<ξ<0.7); 概率密度φ(x ).解: 因ξ是连续型随机变量, 因此F (x )也必是连续曲线, 则其在第二段(0,1)区间的曲线必能和第三段(1,+∞)的曲线接上, 则必有 A ×12=1, 即A =1. 则分布函数为⎪⎩⎪⎨⎧≥<≤<=111000)(2x x x x x F P (0.3<ξ<0.7)=F (0.7)-F (0.3)=0.72-0.32=0.49-0.09=0.4概率密度φ(x )为⎩⎨⎧<≤='=其它0102)()(x x x F x ϕ15. 服从柯西分布的随机变量ξ的分布函数是F (x )=A +B arctg x , 求常数A ,B ;P {|ξ|<1}以及概率密度φ(x ). 解: 由F (-∞)=0, 得A +Barctg (-∞)=02=-πB A(1)再由F (+∞)=1,得12)arctg(=+=+∞+πB A B A(2)综和(1),(2)两式解得π1,21==B A 即x x F arctg 121)(π+=5.0214411111)1()1()11()1|(|==⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--==--=--=<<-=<πππππξξarctg arctg F F P P2111)()(x x F x +⋅='=πϕ16. 服从拉普拉斯分布的随机变量ξ的概率密度||)(x Ae x -=ϕ, 求系数A 及分布函数F (x ).解: 这实际上是一个分段函数, φ(x )可重新写为⎩⎨⎧<≥=-0)(x Aex Ae x xxϕ 根据性质1)(=⎰+∞∞-dx x ϕ, 又因φ(x )为偶函数, 因此有1222)(|==-==∞+-+∞-+∞∞-⎰⎰A Aedx Aedx x x xϕ, 则有A =1/2因此⎪⎩⎪⎨⎧<≥==--02102121)(||x e x e ex x x x ϕ.求分布函数F (x ). 当x <0时, 有xxtxt x e e dt e dt t x F 212121)()(====∞-∞-∞-⎰⎰ϕ当x ≥0时, 有x x xtxt t x e e e dt e dt e dt t x F ----∞-∞--=+-=-=+==⎰⎰⎰21121212121212121)()(00ϕ 综上所述, 最后得⎪⎩⎪⎨⎧≥-<=-0211021)(x e x ex F x x17. 已知⎩⎨⎧<<+-=其它01031212)(~2x x x x ϕξ, 计算P {ξ≤0.2|0.1<ξ≤0.5}解: 设事件A ={ξ≤0.2}, B ={0.1<ξ≤0.5}, 则要计算的是条件概率P (A |B ), 而)()()|(B P AB P B A P =, 而事件AB ={ξ≤0.2}∩{0.1<ξ≤0.5}={0.1<ξ≤0.2} 因此有148.03.006.0004.06.024.0032.0)1.0301.06001.04()2.0304.06008.04()364(d )31212()(}2.01.0{)(2.01.0232.01.022.01.0=-+-+-=⨯+⨯-⨯-⨯+⨯-⨯==+-=+-==≤<=⎰⎰x x x xx x dx x P AB P ϕξ256.03.006.0004.05.15.15.0)1.0301.06001.04()5.0325.06125.04()364(d )31212()(}5.01.0{)(5.01.0235.01.025.01.0=-+-+-=⨯+⨯-⨯-⨯+⨯-⨯==+-=+-===≤<=⎰⎰x x x xx x dx x P B P ϕξ最后得5781.0256.0148.0)()()|(}5.01.0|2.0{====≤<≤B P AB P B A P P ξξ18. 已知xxce x +-=2)(~ϕξ, 确定常数c .解: 首先证明普阿松广义积分π=⎰+∞∞--x e xd 2, 因为函数2x e -并不存在原函数, 因此需要一技巧. 令⎰+∞∞--=x eI x d 2, 则⎰⎰⎰+∞∞-+∞∞-+-+∞∞--=⎥⎦⎤⎢⎣⎡=y x e x e I y x x d d d )(22222作极坐标代换, 令θθsin ,cos r y r x ==, 则积分区间为全平面, 即θ从0积到2π, r 从0积到+∞, 且θd d d d r r y x =, 因此有πππθπ====∞+-+∞-+∞-⎰⎰⎰020202222)d(212rr r e r e rdr ed I , 所以I =π.现确定常数c , 由性质1)(=⎰+∞∞-dx x ϕ,1d d 41)21(414141212222====⎰⎰⎰+∞∞---+∞∞-+-⋅⋅+-+∞∞-+-πcedx ecex cex cex x x xx得421πe c =19. 已知⎩⎨⎧>>=-其它)0()(~λλϕξλa x e c x x, 求常数c 及P {a -1<ξ≤a +1}.解: 由性质1)(=⎰+∞∞-dx x ϕ得1d d 0)(|==-=+=-∞+-+∞-∞-+∞∞-⎰⎰⎰aax ax ace ce x e c x dx x λλλλϕ 解得 aec λ=, 因此有⎩⎨⎧>>=--其它)0()()(λλϕλa x e x a x则λλλλλλϕξ---+---+--=-==+==+≤<-⎰⎰⎰⎰e e due x ex x x a a P u u a aa x a a a a 1d d 0d )()11(|111)(111η ξ 01234560 0.202 0.174 0.113 0.062 0.049 0.023 0.004 1 0 0.099 0.064 0.040 0.031 0.020 0.006 2 0 0 0.031 0.025 0.018 0.013 0.008 30.001 0.002 0.004 0.011求边缘概率分布, 与是否独立?解: 按下表计算ξ与η的边缘分布: η ξ 0123456p i (1)0 0.202 0.174 0.113 0.062 0.049 0.023 0.004 0.627 1 0 0.099 0.064 0.040 0.031 0.020 0.006 0.260 2 0 0 0.031 0.025 0.018 0.013 0.008 0.095 3 00.001 0.0020.004 0.011 0.018 p j (2)0.202 0.273 0.208 0.128 0.100 0.060 0.029ξ0 1 2 3 P0.6270.260 0.095 0.018 以及的边缘分布如下表所示:η0 1 2 3 4 5 6 P0.2020.2730.2080.1280.10.060.029当i =1及j =0时,因202.026.0}0{}1{0}0,1{)2(0)1(110⨯====≠====ηξηξP P p p P p因此ξ与η相互间不独立.21. 假设电子显示牌上有3个灯泡在第一排, 5个灯泡在第二排. 令ξ,η分别表示在某一规: η ξ 0 1 2 3 4 5 0 0.01 0.01 0.03 0.05 0.07 0.09 1 0.01 0.02 0.04 0.05 0.06 0.08 2 0.01 0.03 0.05 0.05 0.05 0.06 30.010.010.040.060.060.05试计算在规定时间内下列事件的概率: (1) 第一排烧坏的灯泡数不超过一个; (2) 第一排与第二排烧坏的灯泡数相等;(3) 第一排烧坏的灯泡数不超过第二排烧坏的灯泡数.解: 假设事件A 为第一排烧坏的灯泡数不超过一个, B 为第一排与第二排烧坏的灯泡数相等, C 为第一排烧坏的灯光数不超过第二排烧坏的灯泡数. 则事件A 发生的概率为上表中头两排概率之和52.008.006.005.004.002.001.009.007.005.003.001.001.0)(104=++++++++++++==∑∑==i j ij p A P事件B 发生的概率为上表中从0行0列开始的斜对角线之和14.006.005.002.001.0)(3=+++==∑=i ii p B P事件C 发生的概率为上表中斜对角线上右的各个数相加(包括斜对角线上的数), 但为减少运算量, 也可以考虑其逆事件C 的概率, 然后用1减去它. 而C 的概率为上表中斜对角线的左下角的所有概率之和(不包括斜对角线):89.011.01)04.001.003.001.001.001.0(1)(1)(=-=+++++-=-=C P C P22. 袋中装有标上号码1,2,2的3个球, 从中任取一个并且不再放回, 然后再从袋中任取一球, 以ξ, η分别记为第一,二次取到球上的号码数, 求(ξ,η)的分布律(袋中各球被取机会相同).解: 因为有两个2一个1, 因此第一次取到2号的概率为P (ξ=2)=2/3, 第一次取到1号的概率为P (ξ=1)=1/3. 第一次取到2号后还剩下一个2号一个1号, 则在此条件下第二次取到1号的概率P (η=1|ξ=2)=P (η=2|ξ=2)=1/2. 而第一次取到1号后还剩下两个2号, 因此这时P (η=1|ξ=1)=0, P (η=2|ξ=1)=1. 综上所述并用乘法法则可得312132)2|2()2()2,2(312132)2|1()2()1,2(31131)1|2()1()2,1(0031)1|1()1()1,1(22211211=⨯=========⨯=========⨯=========⨯========ξηξηξξηξηξξηξηξξηξηξP P P p P P P p P P P p P P P pη ξ 1 2 1 0 1/3 21/31/3)0,2()31,1()1,1()0,0(--且相应的概率依次为1/6, 1/3, 1/12, 5/12. 列出(ξ,η)的概率分布表, 写出关于η的边缘分布. 解: 从上面数组可知ξ只取-1,0,2这三个值, 而η只取0,31,1这三个值, 因此总共可构成九个. 概率分布表及η的边缘分布计算如下 η ξ 0 1/3 1 -1 0 1/12 1/3 0 1/62 5/12 0 0p j(2) 7/12 1/12 1/3η0 1/3 1P7/12 1/12 1/324. 袋中装有标上号码1,2,2,3的4个球, 从中任取一个并且不再放回, 然后再从袋中任取一球, 以ξ, η分别记为第一,二次取到球上的号码数, 求(ξ,η)的分布律(袋中各球被取机会相同).解: 第一次取到号码1,2,3的概率为P{ξ=1}=P(ξ=3)=1/4P{ξ=2}=1/2在第一次取到号码i条件下,第二次取到号码j的概率各为P{η=1|ξ=1}=P{η=3|ξ=3}=0P{η=2|ξ=1}=P{η=2|ξ=3}=2/3P{η=3|ξ=1}=P{η=1|ξ=3}=1/3P{η=1|ξ=2}=P{η=3|ξ=2}=1/3P{η=2|ξ=2}=1/3则p11=P{ξ=1,η=1}=P{ξ=1}P{η=1|ξ=1}=0p12=P{ξ=1,η=2}=P{ξ=1}P{η=2|ξ=1}=1/6p13=P{ξ=1,η=3}=P{ξ=1}P{η=3|ξ=1}=1/12p21=P{ξ=2,η=1}=P{ξ=2}P{η=1|ξ=2}=1/6p22=P{ξ=2,η=2}=P{ξ=2}P{η=2|ξ=2}=1/6p23=P{ξ=2,η=3}=P{ξ=2}P{η=3|ξ=2}=1/6p31=P{ξ=3,η=1}=P{ξ=3}P{η=1|ξ=3}=1/12p32=P{ξ=3,η=2}=P{ξ=3}P{η=2|ξ=3}=1/6p33=P{ξ=3,η=3}=P{ξ=3}P{η=3|ξ=3}=0即联合概率分布表如下表所示ηξ 1 2 31 0 1/6 1/122 1/6 1/6 1/63 1/12 1/6 025. 表示随机地在1-4的4个整数中取出的一个整数，η表示在1-ξ中随机地取出的一个整数值，求(ξ,η)的联合概率分布.解: 因ξ取四个数中的任何一个概率相等, 因此有P{ξ=i}=1/4, (i=1,2,3,4)而在ξ=i的条件下, (i=1,2,3,4), η取1到i的概率也相同,为1/i, 即P{η=j|ξ=i}=1/i, (i=1,2,3,4;j=1-i)因此有p ij=P{ξ=i,η=j}=P{ξ=i}P{η=j|ξ=i}=1/(4i), (i=1,2,3,4; j=1-i),联合概率分布如下表所示:η ξ 1 2 3 4 1 1/4 0 0 0 2 1/8 1/8 0 0 3 1/12 1/12 1/12 0 41/161/161/161/1626. 已知(ξ,η)~⎪⎩⎪⎨⎧≤≤+=其它04,0)sin(),(πϕy x y x c y x ,试确定常数c 并求η的边缘概率密度.解: 根据性质1),(=⎰⎰+∞∞-+∞∞-dydx y x ϕ, 有1)12(]220122[)]4sin([sin )]4cos([cos )]cos([)sin(40440404040=-=+--=+-=+-=+-=+⎰⎰⎰⎰c c x x c x x dx c y x dx c dydx y x c ππππππππ解得12)12)(12(12121+=+-+=-=c ,因此,⎪⎩⎪⎨⎧≤≤++=其它04,0)sin()12(),(πϕy x y x y x求η的边缘概率密度: 当40π≤≤y 时:)8sin(22)12()]4cos()[cos 12()cos()12()sin()12(),()(4042ππϕϕκπ+-+==+-+==++-=++==⎰⎰∞+∞-y y y y x dx y x dx y x y上式后一等式利用了三角函数公式2sin 2sin2cos cos A B A B B A -+=-, 而计算三角函数8sin π的值, 又是在已知224cos=π的前提下,利用半角公式2cos 12sin θθ-=得222222124cos18sin-=-=-=ππ当y 取区间]4,0[π之外的值时, 0)(1=y ϕ.因此最后得:⎪⎩⎪⎨⎧≤≤+-+=其它040)8sin(22)12()(2ππϕy y y27. 已知ξ服从参数p =0.6的0-1分布, 在ξ=0及ξ=1条件下, 关于η的条件分布分别如下二表所示:η 1 2 3 P {η|ξ=0}1/4 1/2 1/4 η 1 2 3 P {η|ξ=1}1/21/61/3求二元随机变量(,)的联合概率分布, 以及在≠1时关于的条件分布. 解: 根据题意已知P {ξ=0}=1-p =1-0.6=0.4, P {ξ=1}=p =0.6 则根据乘法法则有:p 01=P {ξ=0,η=1}=P {ξ=0}P {η=1|ξ=0}=0.4×(1/4)=0.1 p 02=P {ξ=0,η=2}=P {ξ=0}P {η=2|ξ=0}=0.4×(1/2)=0.2 p 03=P {ξ=0,η=3}=P {ξ=0}P {η=3|ξ=0}=0.4×(1/4)=0.1 p 11=P {ξ=1,η=1}=P {ξ=1}P {η=1|ξ=1}=0.6×(1/2)=0.3 p 12=P {ξ=1,η=2}=P {ξ=1}P {η=2|ξ=1}=0.6×(1/6)=0.1 p 13=P {ξ=1,η=3}=P {ξ=1}P {η=3|ξ=1}=0.6×(1/3)=0.2 η ξ 1 2 3 0 0.1 0.2 0.1 10.30.10.2由表中可以算出P {η≠1}=1-P {η=1}=1-(p 01+p 11)=1-0.4=0.6 P {ξ=0,η≠1}=p 02+p 03=0.2+0.1=0.3 P {ξ=1,η≠1}=p 12+p 13=0.1+0.2=0.3 因此有5.06.03.0}1{}1,1{}1|1{5.06.03.0}1{}1,0{}1|0{==≠≠==≠===≠≠==≠=ηηξηξηηξηξP P P P P P则在η≠1时关于ξ的条件分布律如下表所示:ξ0 1 P {ξ|η≠0} 0.5 0.528. 第22题中的两个随机变量ξ与η是否独立？当ξ=1时η的条件分布是什么？ : η ξ 1 2 1 0 1/3 21/31/3, 因为 P {ξ=1}=1/3, P {η=1}=1/3 而P {ξ=1,η=1}=0≠P {ξ=1}P {η=1} 在ξ=1条件下, 因13/13/1}1{}2,1{}1|2{03/10}1{}1,1{}1|1{================ξηξξηξηξξηP P P P P P因此在此条件下η服从单点分布或退化分布, 只取值为2, 取值为2的条件概率为1.ξ-2 -1 0 1/2 P 1/4 1/3 1/12 1/3η-1/2 1 3 P1/21/41/4=p i (1)p j (2), 算得联合分布律如下表所示 η ξ -1/2 1 3 -2 1/8 1/16 1/16 -1 1/6 1/12 1/12 0 1/24 1/48 1/48 1/21/61/121/12根据此联合分布律可算出43129611211)2/1,2/1()1,1(1)0(1)0(121484481161)1,0()3,2()1(==--==-==-=-=-==+-=≠+==+===+=-===+ηξηξηξηξηξηξηξP P P P P P P30. 测量一矩形土地的长与宽, 测量结果得到如下表所示的分布律(长与宽相互独立), 求周长度ξ 29 30 31 P 0.30.50.2解: 因ζ=2ξ+2η, 可知ζ的取值为96,98,100,102,104, 又因ξ与η独立, 因此有 P {ζ=96}==P {ξ=29}P {η=19}=0.3×0.3=0.09P {ζ=98}=P {ξ=29}P {η=20}+P {ξ=30}P {η=19}=0.3×0.4+0.5×0.3=0.27 P {ζ=100}=P {ξ=29}P {η=21}+P {ξ=30}P {η=20}+P {ξ=31}}P {η=19}==0.3×0.3+0.5×0.4+0.2×0.3=0.35P {ζ=102}=P {ξ=30}P {η=21}+P {ξ=31}P {η=20}=0.3×0.5+0.2×0.4=0.23 P {ζ=104}=P {ξ=31}P {η=21}=0.2×0.3=0.06 因此ζ的分布律如下表所示: 周长ζ 96 98 100 102 104 P0.090.270.350.230.06η的分布.R 10 11 12 13 P0.10.40.30.2, ξ的取值为62.83, 69.12,ξ62.83 69.12 75.4 81.68 P 0.1 0.4 0.3 0.2 η314.16 380.13 452.39 530.93 P0.10.40.30.232. 一个商店每星期四进货, 以备星期五,六,日3天销售, 根据多周统计, 这3天销售件数 ξ110 11 12 P 0.2 0.7 0.1 ξ213 14 15 P 0.30.60.1宽度η 19 20 21 P0.30.40.3ξ317 18 19 P 0.1 0.8 0.1问三天销售总量∑==31i iξη这个随机变量可以取哪些值?如果进货45件, 不够卖的概率是多少? 如果进货40件, 够卖的概率是多少?解: 因η的取值为ξ1,ξ2,ξ3三个随机变量可能取值之和, 因此可能的取值为从10+13+17=40到12+15+19=46之间的每一个整数值, 即40,41,42,43,44,45,46. 因此, 如进货15件, 不够卖的概率在η取值为46时出现, 即 P {η=46}=P {ξ1=12}P {ξ2=15}P {ξ3=19}=0.1×0.1×0.1=0.001 如进货40件, 够卖的概率发生在η取值为40时出现, 即P {η=40}=P {ξ1=10}P {ξ2=13}P {ξ3=17}=0.2×0.3×0.1=0.006 33. 求出第22题中ξ+η的分布律.ξ与η的联合分布律如下表: η ξ 1 2 1 0 1/3 21/31/3则P {+=2}=P {=1,=1}=0P {ξ+η=3}=P {ξ=1,η=2}+P {ξ=2,η=1}=2/3 P {ξ+η=4}=P {ξ=2,η=2}=1/3 ξ+η3 4 P 2/3 1/334. 求出第23题中ξ-η的分布律解: 因(ξ , η)只取下列数组中的值：)0,2()31,1()1,1()0,0(--且相应的概率依次为1/6, 1/3, 1/12, 5/12.因此ξ-η也只取0-0=0, -1-1=-2, -1-1/3=-4/3, 2-0=2这四个值, 相应的概率也还是依次为1/6, ξ-η-2 -4/3 0 2 P 1/3 1/12 1/6 5/1235. 已知P {ξ=k }=a /k , P {η=-k }=b /k (k =1,2,3), ξ与独立, 确定a ,b 的值; 求出(ξ,η)的联合概率分布以及ξ+η的概率分布. 解: 由概率分布的性质有131211}{31=⎪⎭⎫⎝⎛++==∑=a k P k ξ, 解得 5455.0116312111==++=a,191411}{31=⎪⎭⎫⎝⎛++=-=∑=b k P k η 解得 7347.04936914111==++=b 因此有P {ξ=1}=0.5455, P {ξ=2}=0.5455/2=0.2727, P {ξ=3}=0.1818 P {η=-1}=0.7347, P {η=-2}=0.1837, P {η=-3}=0.0816 因ξ与η独立, 则有p 11=P {ξ=1,η=-1}=P {ξ=1}P {η=-1}=0.5455×0.7347=0.4008 p 12=P {ξ=1,η=-2}=P {ξ=1}P {η=-2}=0.5455×0.1837=0.1002 p 13=P {ξ=1,η=-3}=P {ξ=1}P {η=-3}=0.5455×0.0816=0.0445 p 21=P {ξ=2,η=-1}=P {ξ=2}P {η=-1}=0.2727×0.7347=0.2004 p 22=P {ξ=2,η=-2}=P {ξ=2}P {η=-2}=0.2727×0.1837=0.0501 p 23=P {ξ=2,η=-3}=P {ξ=2}P {η=-3}=0.2727×0.0816=0.0223 p 31=P {ξ=3,η=-1}=P {ξ=3}P {η=-1}=0.1818×0.7347=0.1336 p 32=P {ξ=3,η=-2}=P {ξ=3}P {η=-2}=0.1818×0.1837=0.0333 p 33=P {ξ=3,η=-3}=P {ξ=3}P {η=-3}=0.1818×0.0816=0.0148 η ξ -1-2-31 0.4008 0.1002 0.0445 2 0.2004 0.0501 0.0223 30.1336 0.0333 0.0148计算+的概率分布: P {ξ+η=-2}=p 13=0.0445P {ξ+η=-1}=p 12+p 23=0.1002+0.0223=0.1225P {ξ+η=0}=p 11+p 22+p 33=0.4008+0.0501+0.0148=0.4657 P {ξ+η=1}=p 21+p 32=0.2004+0.0333=0.2337 P {ξ+η=2}=p 31=0.1336即ξ+η的概率分布率如下表所示ξ+η-2 -1 0 1 2 P 0.0445 0.1225 0.4657 0.2337 0.133636. 已知服从区间[0,1]上的均匀分布, 求的函数=3+1的概率分布. 解: 根据题意知ξ的概率密度φξ(x )为⎩⎨⎧≤≤=其它0101)(x x ξϕ 则η的分布函数为)31(}31{}13{}{)(-=-≤=≤+=≤=x F x P x P x P x F ξηξξη 对其求导得η的概率密度与ξ的概率密度间的关系为⎪⎩⎪⎨⎧≤≤=⎪⎩⎪⎨⎧≤-≤=-=-'='=其它其它041310131031)31(31)31(31)()(x x x x F x F x ϕϕξηη即η服从在区间[1,4]上的均匀分布.37. 已知ξ～⎪⎩⎪⎨⎧>+=其它0)1(2)(2x x x πϕ, ξηln =, 求η的概率密度.解: 求η的分布函数F η(x )为)(}{}{ln }{)(x x e F e P x P x P x F ξηξξη=≤=≤=≤=因e x 总大于0, 而当x 大于0时F ξ(x )为x t t t dt t x F x xxarctg 2arctg 2d )1(2)()(|002πππϕξ==+==⎰⎰∞- 因此有x x e e F x F arctg 2)()(πξη==则η的概率密度为其分布函数的求导:xx ee x F x 212)()(+⋅='=πϕηη。

(完整版)概率论第二章答案

习题2-21. 设A 为任一随机事件, 且P (A )=p (0<p <1). 定义随机变量1,,0,A X A =⎧⎨⎩发生不发生.写出随机变量X 的分布律.解 P {X =1}=p , P {X =0}=1-p . 或者2. 已知随机变量X 只能取-1,0,1,2四个值, 且取这四个值的相应概率依次为cc c c 167,85,43,21. 试确定常数c , 并计算条件概率}0|1{≠<X X P . 解由离散型随机变量的分布律的性质知，13571,24816c c c c+++= 所以3716c=. 所求概率为 P {X <1| X0≠}=258167852121}0{}1{=++=≠-=cc c c X P X P . 3. 设随机变量X 服从参数为2, p 的二项分布, 随机变量Y 服从参数为3, p 的二项分布, 若{P X ≥51}9=, 求{P Y ≥1}.解注意p{x=k}=kk n k n C p q -,由题设5{9P X =≥21}1{0}1,P X q =-==-故213qp =-=. 从而{P Y ≥32191}1{0}1().327P Y =-==-=4. 在三次独立的重复试验中, 每次试验成功的概率相同, 已知至少成功一次的概率为1927, 求每次试验成功的概率.解设每次试验成功的概率为p , 由题意知至少成功一次的概率是2719，那么一次都没有成功的概率是278. 即278)1(3=-p , 故 p =31. 5. 若X 服从参数为λ的泊松分布, 且{1}{3}P X P X ===, 求参数λ.解由泊松分布的分布律可知6=λ.6. 一袋中装有5只球, 编号为1,2,3,4,5. 在袋中同时取3只球, 以X 表示取出的3只球中的最大号码, 写出随机变量X 的分布律.解从1，2，3，4，5中随机取3个，以X 表示3个数中的最大值，X 的可能取值是3，4，5，在5个数中取3个共有1035=C 种取法.{X =3}表示取出的3个数以3为最大值，P{X =3}=2235C C =101;{X =4}表示取出的3个数以4为最大值，P{X =4}=1033523=C C ;{X =5}表示取出的3个数以5为最大值，P{X =5}=533524=C C .X 的分布律是1. 设X求分布函数解 (1) F (x )=0,1,0.15,10,0.35,01,1,1.x x x x <-⎧⎪-<⎪⎨<⎪⎪⎩≤≤≥(2) P {X <0}=P {X =-1}=0.15;(3) P {X <2}= P {X =-1}+P {X =0}+P {X =1}=1; (4) P {-2≤x <1}=P {X =-1}+P {X =0}=0.35. 2. 设随机变量X 的分布函数为F (x ) = A +B arctan x -∞<x <+∞.试求: (1) 常数A 与B ; (2) X 落在(-1, 1]内的概率.解 (1) 由于F (-∞) = 0, F (+∞) = 1, 可知()0112,.2()12A B A B A B πππ⎧+-=⎪⎪⇒==⎨⎪+=⎪⎩ 于是 11()arctan ,.2F x x x π=+-∞<<+∞(2) {11}(1)(1)P X F F -<=--≤1111(arctan1)(arctan(1))22ππ=+-+-11111().24242ππππ=+⋅---=3. 设随机变量X 的分布函数为F (x )=0, 0,01,21,1,,x xx x <<⎧⎪⎪⎨⎪⎪⎩ ≤ ≥求P {X ≤-1}, P {0.3 <X <0.7}, P {0<X ≤2}.解 P {X 1}(1)0F -=-=≤,P {0.3<X <0.7}=F (0.7)-F {0.3}-P {X =0.7}=0.2,P {0<X ≤2}=F (2)-F (0)=1.5. 假设随机变量X 的绝对值不大于1;11{1},{1}84P X P X =-===; 在事件{11}X -<<出现的条件下, X 在(-1,1)内任一子区间上取值的条件概率与该区间的长度成正比. (1) 求X 的分布函数(){F x P X =≤x }; (2) 求X 取负值的概率p .解 (1) 由条件可知, 当1x <-时, ()0F x =; 当1x =-时,1(1)8F -=;当1x =时, F (1)=P {X ≤1}=P (S )=1. 所以115{11}(1)(1){1}1.848P X F F P X -<<=---==--=易见, 在X 的值属于(1,1)-的条件下, 事件{1}X x -<<的条件概率为{1P X -<≤|11}[(1)]x X k x -<<=--,取x =1得到 1=k (1+1), 所以k =12. 因此{1P X -<≤|11}12x X x -<<=+. 于是, 对于11x -<<, 有 {1P X -<≤}{1x P X =-<≤,11}x X -<<{11}{1|11}≤P X P X x X =-<<-<-<< 5155.8216x x ++=⨯=对于x ≥1, 有() 1.F x = 从而0,1,57(),11,161,1.x x F x x x <-+=-<<⎧⎪⎪⎨⎪⎪⎩≥ (2) X 取负值的概率7{0}(0){0}(0)[(0)(0)](0).16p P X F P X F F F F =<=-==---=-=习题2-41. 选择题 (1) 设2, [0,],()0, [0,].x x c f x x c ∈=∉⎧⎨⎩ 如果c =( ), 则()f x 是某一随机变量的概率密度函数. (A)13. (B) 12. (C) 1. (D) 32.解由概率密度函数的性质()d 1f x x +∞-∞=⎰可得02d 1cx x =⎰, 于是1=c , 故本题应选(C ).(2) 设~(0,1),XN 又常数c 满足{}{}P X c P X c =<≥, 则c 等于( ).(A) 1. (B) 0. (C) 12. (D) -1.解因为{}{}P X c P X c =<≥, 所以1{}{}P X c P X c -<=<,即2{}1P X c <=, 从而{}0.5P X c <=,即()0.5c Φ=, 得c =0. 因此本题应选(B).(3) 下列函数中可以作为某一随机变量的概率密度的是( ).(A)cos ,[0,],()0,x x f x π∈=⎧⎨⎩其它. (B) 1,2,()20,x f x <=⎧⎪⎨⎪⎩其它.(C)22()2,0,()0,0.≥x x f x x μσ--=<⎧⎩ (D) e ,0,()0,0.≥x x f x x -=<⎧⎨⎩ 解由概率密度函数的性质()1f x dx +∞-∞=⎰可知本题应选(D).(4) 设随机变量2~(,4)XN μ, 2~(,5)Y N μ, 1{X P P =≤4μ-}, {2P P Y =≥5μ+}, 则( ).(A) 对任意的实数12,P P μ=. (B) 对任意的实数12,P P μ<. (C) 只对实数μ的个别值, 有12P P =. (D) 对任意的实数12,P P μ>. 解由正态分布函数的性质可知对任意的实数μ, 有12(1)1(1)P P ΦΦ=-=-=. 因此本题应选(A).(5) 设随机变量X 的概率密度为()f x , 且()()f x f x =-, 又F (x )为分布函数, 则对任意实数a , 有( ).(A)()1d ()∫aF a x f x -=-. (B) 01()d 2()∫aF a x f x -=-.(C) ()()F a F a -=. (D) ()2()1F a F a -=-.解由分布函数的几何意义及概率密度的性质知答案为(B). (6) 设随机变量X服从正态分布211(,)N μσ,Y服从正态分布222(,)N μσ,且12{1}{1},P X P Y μμ-<>-< 则下式中成立的是( ).(A) σ1 < σ2. (B) σ1 > σ2. (C) μ1 <μ2. (D) μ1 >μ2.解答案是(A).(7) 设随机变量X 服从正态分布N (0,1), 对给定的正数)10(<<αα, 数αu 满足{}P X u αα>=, 若{}P X x α<=, 则x 等于( ).(A)2u α . (B) 21α-u. (C)1-2u α. (D) α-1u .解答案是(C).2. 设连续型随机变量X 服从参数为λ的指数分布, 要使1{2}4P k X k <<=成立, 应当怎样选择数k ?解因为随机变量X 服从参数为λ的指数分布, 其分布函数为1e ,0,()0,0.≤x x F x x λ-->=⎧⎨⎩由题意可知221{2}(2)()(1e )(1e )e e 4k k k k P k X k F k F k λλλλ----=<<=-=---=-.于是ln 2k λ=.3. 设随机变量X 有概率密度34,01,()0,x x f x <<=⎧⎨⎩其它, 要使{}{}≥P X a P X a =<(其中a >0)成立, 应当怎样选择数a ?解由条件变形,得到1{}{}P X a P X a -<=<,可知{}0.5P X a <=, 于是304d 0.5a x x =⎰,因此a =.4. 设连续型随机变量X 的分布函数为20,0,()01,1,1,,≤≤x F x x x x <=>⎧⎪⎨⎪⎩求: (1) X 的概率密度; (2){0.30.7}P X <<.解 (1) 根据分布函数与概率密度的关系()()F x f x '=,可得2,01,()0,其它.x x f x <<⎧=⎨⎩ (2)22{0.30.7}(0.7)(0.3)0.70.30.4P X F F <<=-=-=.5. 设随机变量X 的概率密度为f (x )＝2,01,0,x x ⎧⎨⎩≤≤ 其它, 求P {X ≤12}与P {14X ＜≤2}.解{P X ≤12201112d 224}x x x ===⎰;1{4P X <≤12141152}2d 1164x x x ===⎰. 6. 设连续型随机变量X 具有概率密度函数,01,(),12,0,x x f x A x x <=-<⎧⎪⎨⎪⎩≤≤其它.求: (1) 常数A ；(2) X 的分布函数F (x ).解 (1) 由概率密度的性质可得12221121111d ()d []122x x A x x xAx x A =+-=+-=-⎰⎰,于是2A =；(2) 由公式()()d x F x f x x -∞=⎰可得当x ≤0时,()0F x =;当0x <≤1时, 201()d 2xF x x x x ==⎰;当1x <≤2时, 2101()d (2)d 212x x F x x x x x x =+-=--⎰⎰;当x >2时,()1F x =.所以220,0,1()221, 2.1,021,12x F x x x x x x x =->⎧⎪⎪<⎪⎨⎪-<⎪⎪⎩≤≤,≤,7. 设随机变量X 的概率密度为1(1),02,()40,x x f x ⎧⎪⎨⎪⎩+<<=其它,对X 独立观察3次, 求至少有2次的结果大于1的概率.解根据概率密度与分布函数的关系式{P a X <≤}()()()d bab F b F a f x x =-=⎰,可得2115{1}(1)d 48P X x x >=+=⎰.所以, 3次观察中至少有2次的结果大于1的概率为223333535175()()()888256C C +=. 8. 设~(0,5)X U , 求关于x 的方程24420x Xx ++=有实根的概率.解随机变量X 的概率密度为105,()50,,x f x <=⎧⎪⎨⎪⎩≤其它,若方程有实根, 则21632X -≥0, 于是2X ≥2. 故方程有实根的概率为 P {2X ≥2}=21{2}P X -<1{P X =-<<1d 5x =-15=-.9. 设随机变量)2,3(~2N X.(1) 计算{25}P X <≤, {410}P X -<≤, {||2}P X >, }3{>X P ； (2) 确定c 使得{}{};P X c P X c >=≤ (3) 设d 满足{}0.9P X d >≥, 问d 至多为多少？解 (1) 由P {a <x ≤b }=P {33333}()()22222a Xb b a ΦΦ-----<=-≤公式, 得到P {2<X ≤5}=(1)(0.5)0.5328ΦΦ--=, P {-4<X ≤10}=(3.5)( 3.5)0.9996ΦΦ--=,{||2}P X >={2}P X >+{2}P X <-=123()2Φ--+23()2Φ--=0.6977,}3{>X P =133{3}1()1(0)2P X ΦΦ-=-=-≤=0.5 .(2) 若{}{}≤P X c P X c >=,得1{}{}P X c P x c -=≤≤,所以{}0.5P X c =≤由(0)Φ=0推得30,2c -=于是c =3. (3){}0.9≥P X d > 即13()0.92d Φ--≥, 也就是3()0.9(1.282)2d ΦΦ--=≥,因分布函数是一个不减函数, 故(3)1.282,2d --≥ 解得 32( 1.282)0.436d +⨯-=≤.10. 设随机变量2~(2,)X N σ, 若{04}0.3P X <<=, 求{0}P X <.解因为()~2,X N σ2,所以~(0,1)X Z N μσ-=. 由条件{04}0.3P X <<=可知02242220.3{04}{}()()X P X P ΦΦσσσσσ---=<<=<<=--,于是22()10.3Φσ-=, 从而2()0.65Φσ=. 所以{{}2020}P P X X σσ==--<<22()1()0.35ΦΦσσ-=-=. 习题2-51. 选择题(1) 设X 的分布函数为F (x ), 则31Y X =+的分布函数()G y 为( ).(A) 11()33F y -. (B) (31)F y +.(C)3()1F y +. (D)1133()F y -. 解由随机变量函数的分布可得, 本题应选(A).(2) 设()~01,XN ,令2Y X =--, 则~Y ( ).(A)(2,1)N --. (B)(0,1)N . (C)(2,1)N -. (D)(2,1)N .解由正态分布函数的性质可知本题应选(C).2. 设~(1,2),23X N Z X =+, 求Z 所服从的分布及概率密度. 解若随机变量2~(,)X N μσ, 则X 的线性函数Y aX b =+也服从正态分布, 即2~(,()).Y aX b N a b a μσ=++ 这里1,μσ==, 所以Z ~(5,8)N .概率密度为()f z=2(5)16,x x ---∞<<+∞.3. 已知随机变量X 的分布律为(1) 求解 (1)(2)4. ()X f x ＝1142ln 20x x <<⎧⎪⎨⎪⎩，　，　，　其它，且Y ＝2－X , 试求Y 的概率密度.解先求Y 的分布函数)(y F Y :)(y F Y ={P Y ≤}{2y P X =-≤}{y P X=≥2}y -1{2}P Xy =-<-=1-2()d yX f x x --∞⎰.于是可得Y 的概率密度为()(2)(2)Y X f y f y y '=---=12(2)ln 20,.,124,其它y y -⎧<-<⎪⎨⎪⎩即 121,2(2)ln 20, ,()其它.Y y y f y -<<-⎧⎪=⎨⎪⎩5. 设随机变量X 服从区间(-2,2)上的均匀分布, 求随机变量2YX =的概率密度.解由题意可知随机变量X 的概率密度为()0,.1,22,4其它X f x x =⎧-<<⎪⎨⎪⎩因为对于0<y <4,(){Y F y P Y =≤2}{y P X =≤}{y P =X}(X X F F =-.于是随机变量2YX =的概率密度函数为()Y fy (X X f f =+0 4.y =<<即()04,0,.其它f y y =<<⎩总习题二1. 一批产品中有20%的次品, 现进行有放回抽样, 共抽取5件样品. 分别计算这5件样品中恰好有3件次品及至多有3件次品的概率.解以X 表示抽取的5件样品中含有的次品数. 依题意知~(5,0.2)X B .(1) 恰好有3件次品的概率是P {X =3}=23358.02.0C .(2) 至多有3件次品的概率是k k k k C-=∑5358.02.0.2. 一办公楼装有5个同类型的供水设备. 调查表明, 在任一时刻t 每个设备被使用的概率为0.1. 问在同一时刻(1) 恰有两个设备被使用的概率是多少？ (2) 至少有1个设备被使用的概率是多少？ (3) 至多有3个设备被使用的概率是多少？ (4) 至少有3个设备被使用的概率是多少？解以X 表示同一时刻被使用的设备的个数，则X ~B (5,0.1),P {X =k }=k kkC -559.01.0,k =0,1, (5)(1) 所求的概率是P {X =2}=0729.09.01.03225=C ; (2)所求的概率是P {X ≥1}=140951.0)1.01(5=--;(3) 所求的概率是 P {X ≤3}=1-P{X =4}-P {X =5}=0.99954;(4) 所求的概率是P {X ≥3}=P {X =3}+P {X =4}+P {X =5}=0.00856. 3. 设随机变量X 的概率密度为e ,0,()00,≥，x k x f x x θθ-=<⎧⎪⎨⎪⎩且已知1{1}2P X>=, 求常数k , θ.解由概率密度的性质可知e d 1xkx θθ-+∞=⎰得到k =1.由已知条件111e d 2xx θθ-+∞=⎰, 得1ln 2θ=.4. 某产品的某一质量指标2~(160,)X N σ, 若要求{120P ≤X ≤200}≥0.8, 问允许σ最大是多少?解由{120P ≤X ≤}200120160160200160{}X P σσσ---=≤≤=404040()(1())2()1ΦΦΦσσσ--=-≥0.8,得到40()Φσ≥0.9, 查表得40σ≥1.29, 由此可得允许σ最大值为31.20.5. 设随机变量X 的概率密度为φ(x ) = A e -|x |, -∞<x <+∞.试求: (1) 常数A ; (2) P {0<X <1}; (3) X 的分布函数.解 (1) 由于||()d e d 1,x x x A x ϕ+∞+∞--∞-∞==⎰⎰即02e d 1x A x +∞-=⎰故2A = 1, 得到A =12.所以 φ(x ) =12e -|x |.(2) P {0<X <1} =111111e e d (e )0.316.0222xxx ----=-=≈⎰(3) 因为||1()e d ,2xx F x x --∞=⎰ 得到当x <0时, 11()e d e ,22x x xF x x -∞==⎰当x ≥0时, 00111()e d e d 1e ,222x x x xF x x x ---∞=+=-⎰⎰所以X 的分布函数为 1,0,2()11,0.2xx x F x x -⎧<⎪⎪=⎨⎪-⎪⎩e e ≥。

概率论第二章练习题

第二章一、基本题目1. 做一系列独立的试验，每次试验成功的概率为p ，求：(1) n 次试验中成功次数X 的分布律；(2)在n 次成功之前已经失败次数Y 的分布律；(3)不断试验至首次成功时试验次数Z 的分布律。

2. 一批产品共有25件，其中5件次品，从中随机地一个一个取出检查，共取4次，设X 为其中的次品数，若（1）每次取出的产品仍放回；（2）每次取出的产品不再放回。

写出两种情况下X 的分布律。

3. 某公司有400台计算机, 在一天中任一台报修的概率是. 请给出一天中报修台数X 的分布律(需陈述建立过程和依据), 并计算报修不超过3台计算机的概率.4.设每天到达炼油厂的油船数服从λ=2的泊松分布. 现港口有三台设备, 一天内一台设备只能为一条油船服务, 若一天中有多于三艘油船到达,多余的油船必需调往其他港口. 求:(1) 某天必需调离油船的概率.(2) 为在90%的日子里能容许安排所有的油船,现有设备应增设至几台(3) 每天最可能到达的油船数是几艘并给出其概率.解已知到达炼油厂的油船数X ~P (2)5. 从一批子弹中任意抽出10发试射，若至多只有一发子弹落在靶心2厘米以外，则接受该批子弹。

设弹着点与靶心的距离X （厘米）的概率密度为⎪⎩⎪⎨⎧<<=-其他,030,)(2x Axe x f x 试求：(1)系数A ；（2）该批子弹被接受的概率.6. 在长为L 的线段上随机选取一点，将其分为两段，求短的一段与长的一段之比小于1/4的概率7.两台新的电子仪器寿命分别为21,X X ,)36,42(~1N X ,)9,45(~2N X , 若需连续使用仪器46小时，问选用哪一台仪器较好8. 设测量误差)10,0(~2N X ，求在100次独立重复测量中至少有3次测量误差的绝对值大于的概率，并用泊松分布求其近似值.9. 设某电子元件寿命X （小时）服从参数为λ的指数分布.若要求该元件寿命在1200小时以上的概率达到(1)求λ的最大取值（λ称为该元件的失效率）；(2) 若一个该种元件已使用300小时，求它能用到900小时以上的概率。

概率论第二章习题(答案)

A．1 e1
. 设随机变量 X 的方差为 2，则根据切比雪夫不等式有（C）
A． P X EX 2 1
4
C. P X EX 2 1
2
B. P X EX 2 3
4
D． P X EX 2 1
2
二．填空与计算题
1. 设随机变量 X 服从参数为 1 的泊松分布,则 P X EX 2 .
C. E( X C)2 E( X )2 D. E( X C)2 E( X )2
16. 设随机变量 X 的分布函数为 F (x) ，则随机变量Y 2 X 1的分布函数为（D）
A．
F
y 2
1
B.
2F(y) 1
C. 1 F ( y) 1
2
2
D．
F
y 2
1 2
17. 设随机变量 X 的密度函数为 f (x) ，则随机变量Y 3 2 X 的密度函数为（B）
度，
f (x) af1(x), bf2 (x),
x 0, (a 0,b 0)
x0
为概率密度，则 a,b 应满足（A）．
A ．2a 3b 4 ； B ．3a 2b 4 ； C ．a b 1； D ．a b 2 .
11.
设随机变量 X
服从正态分布
N
(1
,
2 1
)
，随机变量 Y
服从正态分布
解: 由 EX 2 2 ， P X EX 2 P X 2 e1 . 2
2. 设随机变量 X 概率分布为 P X k C (k 0,1, 2,) ，则
A. a 3 5,b 2 5 ; B. a 2 3, b 2 3 ;
C. a 1 2 , b 3 2 ; D. a 1 2 ,b 3 2 .

《概率论》第二章习题

第二章事件与概率1、字母M ，A ，X ，A ，M 分别写在一张卡片上，充分混合后重新排列，问正好得到顺序MAAM 的概率是多少？解：这五个字母自左往右数，排第i 个字母的事件为A i ，则42)(,52)(121==A A P A P ，21)(,31)(1234123==A A A A P A A A P 1)(12345=A A A A A P 。

利用乘法公式，所求的概率为()()()()12345123412312154321)()(A A A A A P A A A A P A A A P A A P A P A A A A A P =301121314252=⋅⋅⋅⋅= 2、有三个孩子的家庭中，已知有一个是女孩，求至少有一个男孩的概率。

解：有三个孩子的家庭总共有23=8个类型。

设A={三个孩子中有一女}，B={三个孩子中至少有一男}，A 的有利场合数为7，AB 的有利场合为6，依题意所求概率为P （B|A ），则 ()768/78/6)()(===A P AB P A B P . 3、若M 件产品中包含m 件废品，今在其中任取两件，求：（1）已知取出的两件中有一件是废品的条件下，另一件也是废品的条件概率；（2）已知两件中有一件不是废品的条件下，另一件是废品的条件概率；（3）取出的两件中至少有一件是废品的概率。

3、解：（1）M 件产品中有m 件废品，m M -件正品。

设A={两件有一件是废品}，B={两件都是废品}，显然B A ⊃，则 ()1122()/m M m m M P A C C C C -=+ 22/)(M m C C B P =，题中欲求的概率为)(/)()(/)()|(A P B P A P AB P A B P ==121/)(/221122---=+=-m M m C C C C C C M m m M m M m . （2）设A={两件中有一件不是废品}，B={两件中恰有一件废品}，显然A B ⊂，则(),/)(2112M m M m m M C C C C A P --+= 211/)(M m M m C C C B P -=. 题中欲求的概率为)(/)()(/)()|(A P B P A P AB P A B P ==12/)(/2112211-+=+=---m M m C C C C C C C M m M m m M M m M m . （3）P{取出的两件中至少有一件废品}=())1()12(/2211---=+-M M m M m C C C C M m m M m .4、袋中有a 只黑球，b 只白球，甲乙丙三人依次从袋中取出一球（取后不放回），试分别求出三人各自取得白球的概率（3≥b ）。

概率论典型例题第2章

概率论第二章习题答案

概率论第二章习题及答案

概率论第二章习题解答(全)

概率论与数理统计2.第二章练习题(答案)

概率论第二章

《概率论与数理统计》习题及答案 第二章

概率论与数理统计第2章例题

概率论第二章

概率论2章习题

《概率论与数理统计》第02章习题解答.docx

概率统计(概率论)第二章练习题答案及解析

概率论与数理统计第二章习题及答案

概率论与数理统计习题及答案第二章.doc

概率论 第二章+习题

(完整版)概率论第二章随机变量及其分布答案

概率论第二章习题参考解答

(完整版)概率论第二章答案

概率论第二章练习题

概率论第二章习题(答案)

《概率论》第二章习题

《概率论与数理统计》习题及答案第二章

概率论第二章+习题