正交基和标准正交基
合集下载
标准正交基
A1
,
A2
,
An
, An En
（8）
练习：
1.设1 (0,1,1,0,0),2 (1,1,0,1,0),3 (4,5,0,0,1). 求L(1, 2 ,3 )的一个标准正交基.
答案：
标准正交基为：
1
1 2
(0,1,1,0,0), 2
1 10
因为 m n,
所以必有向量 不能被 1,2, ,m 线性表出，
作向量 m1 k11 k22 kmm ( 0)
ki R 待定．
证明续： 从正交向量组的性质知
(i ,m1 ) ( ,i ) ki (i ,i ), i 1, 2, , m.
证明 设有一组数 k1, k2 , , kr使得
k11 k22 krr 0 等号两边的向量分别和1作内积
k11 k22 krr , 1 0, 1 展开得 k1 1,1 k2 2,1 kr r ,1 0
L(1, 2 , , i ) L(1,2, ,i ), i 1, 2, , n
证： 基本方法─逐个构成出满足要求的 1,2 ,
首先，可取
1
1
| 1
|1
.
,n .
证明续：
一般地，假定已求出 1,2 , ,m 是单位正交的 ，且
L(1, 2 , , i ) L(1,2 , ,i ), i 1, 2, , m (4) 当 m n 时，因为有 m1 L(1, 2 , , m ), 由(4)知 m1不能被 1,2 , ,m线性表出．
于是取
ki
( ,i ) , (i ,i )
线性代数第五章 正交性
b = (-1, -1, 2, 2),
中每一个正交.
c = (3, 2, 5, 4),
20
练 习：
设 q1=
1 2
(1,1,1,1)T, q2=
1 2
(1,1,1,
1)T,
用两种方法将它们扩充成 4的一组规范正交基.
作业：
5.1节练习: 1. 2.
5.4节练习: 1. 2.
5.6节练习: 8.
课后练习:
在欧氏空间 4里找出两个单位向量，使它们同时与向量
a = (2, 1, -4, 0),
v2 ||v2||
正 交
基
vn=
xn
xn, v1,
v1 v1
v1
xn, v2,
v2 v2
v2
…
xn, vn1 vn1, vn1
vn1
un
=
vn ||vn||
Span(x1, x2, . . . , xn ) = Span(v1, v2, . . . , vn )
例5
设V = span(x1, x2, x3, x4),求 V的一组规范正交基. 其中x1= (1,−1, 1,−1)T, x2 = (1, 1, 3,−1) T , x3= (2,0, 4,−2)T , x4 = (3, 7, 1, 3)T .
||x|| ||y||
定 理 1 | xTy | ||x|| ||y|| 柯西-施瓦兹不等式 定 理 2 x y xT y = 0 称 x 和 y 正交 .
推广至更一般 向量空间 V
3
内积(P213 5.4 内积空间)
定 义 在向量空间V上定义一种运算，在这种运算下，V 中任意 一对向量 x 和 y，都对应一个实数，记作 x, y，若还满足: 对任意的 x, y, z ∈ V 及 s, t ∈ R，成立 (1) x, x 0 , 取等号当且仅当 x = 0 .
图形学欧氏空间具体概念
2. n 维欧氏空间 中的线性变换 σ 是正交变换 维欧氏空间V中的线性变换 交矩阵． 交矩阵．
(α , β ) ≤ α β
三、欧氏空间中向量的夹角（续） 欧氏空间中向量的夹角（
〈α , β 〉 = arc cos (α , β )
α β
( 0 ≤ 〈α , β 〉 ≤ π )
(α , β ) = 0
定义： 为欧氏空间中两个向量， 定义：设 α、β为欧氏空间中两个向量，若内积
正交或互相垂直， 则称 α 与 β 正交或互相垂直，记作 α ⊥ β . 注： ① 零向量与任意向量正交 零向量与任意向量正交.
3) 非零向量 α 的单位化： α α . 的单位化：
1
三、欧氏空间中向量的夹角
1. 柯西－布涅柯夫斯基不等式 柯西－ 对欧氏空间V中任意两个向量 α、β 对欧氏空间V
线性相关时等号成立. 当且仅当 α、β 线性相关时等号成立. 2. 欧氏空间中两非零向量的夹角 定义: 为欧氏空间， 中任意两非零向量， 夹角定义为 α 定义: 设V为欧氏空间， 、β 为V中任意两非零向量，α、β 的夹角定义为 ，有
π α ⊥ β ⇔ 〈α , β 〉 = 即 cos〈α , β 〉 .= 0 , ② 2
3. 勾股定理 为欧氏空间， 设V为欧氏空间，∀α , β ∈ V , α ⊥ β ⇔ α + β 2 = α 2 + β 为欧氏空间 推广：若欧氏空间V中向量 两两正交， 推广：若欧氏空间 中向量 α 1 ,α 2 ,⋯ ,α m 两两正交， 即 (α i ,α j ) = 0, i ≠ j , i , j = 1, 2,⋯ , m 2 2 2 2 α1 + α 2 + ⋯ + α m = α1 + α 2 + ⋯ + α m . 则
(α , β ) ≤ α β
三、欧氏空间中向量的夹角（续） 欧氏空间中向量的夹角（
〈α , β 〉 = arc cos (α , β )
α β
( 0 ≤ 〈α , β 〉 ≤ π )
(α , β ) = 0
定义： 为欧氏空间中两个向量， 定义：设 α、β为欧氏空间中两个向量，若内积
正交或互相垂直， 则称 α 与 β 正交或互相垂直，记作 α ⊥ β . 注： ① 零向量与任意向量正交 零向量与任意向量正交.
3) 非零向量 α 的单位化： α α . 的单位化：
1
三、欧氏空间中向量的夹角
1. 柯西－布涅柯夫斯基不等式 柯西－ 对欧氏空间V中任意两个向量 α、β 对欧氏空间V
线性相关时等号成立. 当且仅当 α、β 线性相关时等号成立. 2. 欧氏空间中两非零向量的夹角 定义: 为欧氏空间， 中任意两非零向量， 夹角定义为 α 定义: 设V为欧氏空间， 、β 为V中任意两非零向量，α、β 的夹角定义为 ，有
π α ⊥ β ⇔ 〈α , β 〉 = 即 cos〈α , β 〉 .= 0 , ② 2
3. 勾股定理 为欧氏空间， 设V为欧氏空间，∀α , β ∈ V , α ⊥ β ⇔ α + β 2 = α 2 + β 为欧氏空间 推广：若欧氏空间V中向量 两两正交， 推广：若欧氏空间 中向量 α 1 ,α 2 ,⋯ ,α m 两两正交， 即 (α i ,α j ) = 0, i ≠ j , i , j = 1, 2,⋯ , m 2 2 2 2 α1 + α 2 + ⋯ + α m = α1 + α 2 + ⋯ + α m . 则
标准正交基
ki R 待定．
§2 标准正交基
从正交向量组的性质知
( i , m1 ) ( , i ) ki ( i , i ),
于是取
( , i ) ki , ( i , i )
i 1,2, , m .
i 1,2, , m ,
可得 ( i , m 1 ) 0 ,
( i , j ) 1 i j， 0 i j
i , j 1,2,, n
(1)
③ n 维欧氏空间V中的一组基 1 , , n 为标准正交基 当且仅当其度量矩阵 A ( i , j ) En . ④ n 维欧氏空间V中标准正交基的作用: 设 1 , , n为V的一组标准正交基，则
§2 标准正交基
例2. 在 R[ x ]4 中定义内积为
( f , g ) f ( x ) g( x )dx
1 1
求 R[ x ]4 的一组标准正交基． (由基 1, x , x 2 , x 3 出发作正交化)
2 3 1, x , x , x 解: 取 1 2 3 4
§2 标准正交基
3
3 x i y j z k , x i y j z k R 设 1 1 1 2 2 2 ① 从 ( , i ) x1 , ( , j ) y1 , ( , k ) z1 得 ( , i ) i ( , j ) j ( , k ) k
2 再单位化得标准正交向量组 1 ,2 ,,m .
i
1 | i |
i , i 1,2,, m
§2 标准正交基
例1. 把 1 (1,1,0,0), 2 (1,0,1,0),
2.6.Rn的标准正交基
T
2. 长度的性质
(1) || || 0 , 且
设 , 为 Rn 中的向量， k R . || || = 0 = 0 ; (2) || k || = | k | · || ; || (3) |T | || || · || , 且 |T | = || || · || || ||
例如，设 = (1, 1, 1, 1)T , = (1, -2, 0, -1)T , = (3, 0, -1, -2)T ,
1 2 T (1, 1, 1, 1) 2, 0 1
则
3 0 T (1, 1, 1, 1) 0, 1 2
解 = (d1 , d2 , … , dn)T = d11 + d22 + … + dnn , 由于
即 = (d , d , … , d )T = d ,d2 +… ,dn+，恰为d , , d ) … + 的各个分量. 在标准基下的坐标为 (d1
1 2 n 1 1 2 2 n n
1. 内积的定义
定义 2.18 设 = (a1 , a2 , … , an)T , = (b1 , b2 … , bn)T 为 Rn 中的两个向量，
b1 则 n b2 T (a1 , a2 , , an ) a1b1 a2b2 anbn ai bi i 1 b 称为向量 与 的内积. n 显然， T R .
类似可证 k2 = 0, … , ks = 0.
因为 1 与 i (i = 2, 3, … T s) 正交, 所以 1Ti = 0, , T
2. 长度的性质
(1) || || 0 , 且
设 , 为 Rn 中的向量， k R . || || = 0 = 0 ; (2) || k || = | k | · || ; || (3) |T | || || · || , 且 |T | = || || · || || ||
例如，设 = (1, 1, 1, 1)T , = (1, -2, 0, -1)T , = (3, 0, -1, -2)T ,
1 2 T (1, 1, 1, 1) 2, 0 1
则
3 0 T (1, 1, 1, 1) 0, 1 2
解 = (d1 , d2 , … , dn)T = d11 + d22 + … + dnn , 由于
即 = (d , d , … , d )T = d ,d2 +… ,dn+，恰为d , , d ) … + 的各个分量. 在标准基下的坐标为 (d1
1 2 n 1 1 2 2 n n
1. 内积的定义
定义 2.18 设 = (a1 , a2 , … , an)T , = (b1 , b2 … , bn)T 为 Rn 中的两个向量，
b1 则 n b2 T (a1 , a2 , , an ) a1b1 a2b2 anbn ai bi i 1 b 称为向量 与 的内积. n 显然， T R .
类似可证 k2 = 0, … , ks = 0.
因为 1 与 i (i = 2, 3, … T s) 正交, 所以 1Ti = 0, , T
4-2标准正交基
3
α1，α2，…，αm两两正交，则称α1，α2，…，αm是V的 ， 两两正交， ， 的 ， 又都是单位向量， 一个正交基；如果α1，α2，…，αm又都是单位向量， 一个正交基； 正交基 的一个标准正交基 则称α1，α2，…，αm是V的一个标准正交基. ， 的一个标准正交基.
定义4.7 定义4.7 设α1，α2，…，αm是欧氏空间 的一个基.如果 ， 是欧氏空间V的一个基.
1 1 1 1 1 1 α 3 = ,− ,0, ,0 为R4的一个基 ,α 4 = − , , 的一个基. 2 2 2 2 2 2
T T
说明 1）自然基 1，e2，…，en是Rn标准正交基. 标准正交基. ）自然基e ，
T
T
4
3）向量空间V的任意向量α ，在V中的一个标准正交基 ）向量空间 的任意向量 中的一个标准正交基 α1，α2，…，αm下的坐标为： = k α + k α + L + k α ， 下的坐标为： α
由单位向量组成的正交向量组称为标准正交向量组. 由单位向量组成的正交向量组称为标准正交向量组. 标准正交向量组
2
正交向量组是线性无关的. 定理4.2 正交向量组是线性无关的. 定理 ， 是正交向量组， 证 设α1，α2，…，αm是正交向量组，并有一组数使 k1α1 + k2α2 + … + kmαm= 0. ， ， ， ）对上式的两边做内积， 用αi（i=1，2，…，m）对上式的两边做内积，得 <k1α1 + k2α2 + … + kmαm ,αi >= <0 ,αi> 0 k1<α1, αi> + k2<α2, αi> + … + km<αm, αi>= 0 因α1, α2, …, αm两两正交, 所以<αi, αj>= 0( i ≠ j, )， 两两正交 所以 ， 故 ki<αi，αi>=0，（i=1，2，…，m） ， ， ， ， ） 所以< 因αi ≠ 0，所以 αi，αi>≠0，故ki =0（i=1，2，…，m）. ， （ ， ， ， ） 于是向量组α1，α2，…，αm线性无关 ， 线性无关.
α1，α2，…，αm两两正交，则称α1，α2，…，αm是V的 ， 两两正交， ， 的 ， 又都是单位向量， 一个正交基；如果α1，α2，…，αm又都是单位向量， 一个正交基； 正交基 的一个标准正交基 则称α1，α2，…，αm是V的一个标准正交基. ， 的一个标准正交基.
定义4.7 定义4.7 设α1，α2，…，αm是欧氏空间 的一个基.如果 ， 是欧氏空间V的一个基.
1 1 1 1 1 1 α 3 = ,− ,0, ,0 为R4的一个基 ,α 4 = − , , 的一个基. 2 2 2 2 2 2
T T
说明 1）自然基 1，e2，…，en是Rn标准正交基. 标准正交基. ）自然基e ，
T
T
4
3）向量空间V的任意向量α ，在V中的一个标准正交基 ）向量空间 的任意向量 中的一个标准正交基 α1，α2，…，αm下的坐标为： = k α + k α + L + k α ， 下的坐标为： α
由单位向量组成的正交向量组称为标准正交向量组. 由单位向量组成的正交向量组称为标准正交向量组. 标准正交向量组
2
正交向量组是线性无关的. 定理4.2 正交向量组是线性无关的. 定理 ， 是正交向量组， 证 设α1，α2，…，αm是正交向量组，并有一组数使 k1α1 + k2α2 + … + kmαm= 0. ， ， ， ）对上式的两边做内积， 用αi（i=1，2，…，m）对上式的两边做内积，得 <k1α1 + k2α2 + … + kmαm ,αi >= <0 ,αi> 0 k1<α1, αi> + k2<α2, αi> + … + km<αm, αi>= 0 因α1, α2, …, αm两两正交, 所以<αi, αj>= 0( i ≠ j, )， 两两正交 所以 ， 故 ki<αi，αi>=0，（i=1，2，…，m） ， ， ， ， ） 所以< 因αi ≠ 0，所以 αi，αi>≠0，故ki =0（i=1，2，…，m）. ， （ ， ， ， ） 于是向量组α1，α2，…，αm线性无关 ， 线性无关.
四规范正交基(标准正交基)
四.规范正交基(标准正交基)
1.规范正交基的概念 定义3 设 n 维向量 e1 ,e2 , ,er是向量空间V V R n 的一个基,如果
e1 ,e2 ,,er
是两两正交的单位向量,则称
e1 ,e2 ,,er
显然,若
是向量空间V的一个规范正交基.
e1 ,e2 ,,er
j
是V的一个规范正交基。
T T
x P Px
x x x
T
按‖x‖表示向量长度, ‖x‖=‖y‖说明经正交变换 向量的长度保持不变,这是正交变换的优良特性。
作业:
161页
1 (2)
2
3
1 0 它的基础解系为 1 0 , 2 1 1 1
令 1 1 , 2 2 ,
则 α3 与α1,α2 正交,显然α1与α2 线性无关,
施密特标准正交化.
因此可用
1 b1 1 取b1 = α1 , 则e1 0 , b1 2 1
1 b2 1 则e2 2 b2 2 1
1 2 取b2 2 2 , e1 e1 1 1 2
3 再把 α3单位化，得 e3 3
3
1 1 1 , 3 1
ቤተ መጻሕፍቲ ባይዱ
解：显然P的每个列向量是两两正交的单位向量.所以 P为正交矩阵。
例5 设e1 , e2 ,, en是Rn的一个 规范正交基.A为正交矩阵.
试证.Ae1 , Ae2 , , Aen也是R 的一个规范正交基.
n
证 由于
i
Ae , Ae Ae
j i
T
T
1.规范正交基的概念 定义3 设 n 维向量 e1 ,e2 , ,er是向量空间V V R n 的一个基,如果
e1 ,e2 ,,er
是两两正交的单位向量,则称
e1 ,e2 ,,er
显然,若
是向量空间V的一个规范正交基.
e1 ,e2 ,,er
j
是V的一个规范正交基。
T T
x P Px
x x x
T
按‖x‖表示向量长度, ‖x‖=‖y‖说明经正交变换 向量的长度保持不变,这是正交变换的优良特性。
作业:
161页
1 (2)
2
3
1 0 它的基础解系为 1 0 , 2 1 1 1
令 1 1 , 2 2 ,
则 α3 与α1,α2 正交,显然α1与α2 线性无关,
施密特标准正交化.
因此可用
1 b1 1 取b1 = α1 , 则e1 0 , b1 2 1
1 b2 1 则e2 2 b2 2 1
1 2 取b2 2 2 , e1 e1 1 1 2
3 再把 α3单位化，得 e3 3
3
1 1 1 , 3 1
ቤተ መጻሕፍቲ ባይዱ
解：显然P的每个列向量是两两正交的单位向量.所以 P为正交矩阵。
例5 设e1 , e2 ,, en是Rn的一个 规范正交基.A为正交矩阵.
试证.Ae1 , Ae2 , , Aen也是R 的一个规范正交基.
n
证 由于
i
Ae , Ae Ae
j i
T
T
2.6 标准正交基
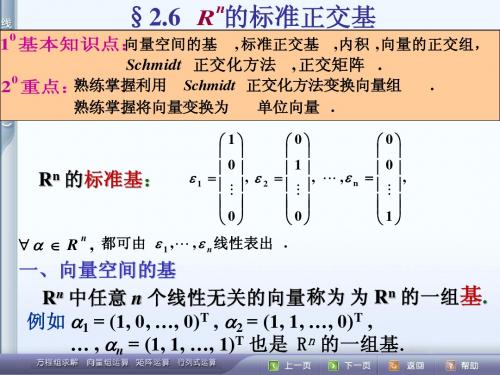
则称a1 , a2 , … , an 为 向量 在基 1 , 2 ,, n 下的坐标， 记作 ( a1 , a2 , … , an ) .
二、向量的内积
1.Def .
给定Rn中向量
a1 a2 an
n i1
b1 b2 , bn
i j 0
T
1 0 0 1 2 0 0
0 0 , n 1
是两两正交的.
( i j ; i , j 1, 2 , ..., s )
则称向量组1, 2,…,s 为正交向量组. 正交向量组1,2,…,s 中无零向量.
§2.6 R 的标准正交基
n
0
向量空间的基 , 标准正交基 , 内积 , 向量的正交组， 1 基本知识点： Schmidt 正交化方法 , 正交矩阵 . 0 熟练掌握利用 Schmidt 正交化方法变换向量组 . 2 重点：
熟练掌握将向量变换为 单位向量 .
1 0 0 0 1 0 , , , n , 1 2 0 0 1
a1 a2 an
n R ,
都可由 1 , , n 线性表出 .
a1 0 0
0 0 0 a2 a 1 1 a 2 2 a n n an 0
QTQ=
sin
co s sin
1 cos 0
0 1
高等代数第九章 2第二节 标准正交基
换句话说 结论 一组基为标准正交基的<＝>是它的度量矩 阵为单位矩阵.
返回
上页
下页
因为度量矩阵是正定矩阵的，根据第五章关 于正定二次型的结果，正定矩阵合同于单位矩阵. 这说明在n维欧氏空间中存在一组基，它的度量矩 阵是单位矩阵. 由此断言
结论 在n维欧氏空间中，标准正交基是存在的. 在标准正交基下，向量的坐标可以通过内积 简单地表示出来，即 (1 , )1 ( 2 , ) 2 ( n , ) n (2)
返回
上页
下页
例3 欧氏空间Rn的基
i (0,,0, 1 ,0,,0） i 1, 2 ,, n
（i）
是Rn的一个标准正交基.
返回
上页
下页
(5)
(5)式相当于一个矩阵的等式
ATA=E ，
或者
返回
(6)
A-1=AT .
上页 下页
我们引入
定义7 n级实数矩阵A称为正交矩阵，如果ATA=E . 因此，以上分析表明，由标准正交基到标准正 交基的过渡矩阵是正交矩阵；反过来，如果第一组 基是标准正交基，同时过渡矩阵是正交矩阵，那么
第二组基一定也是标准正交基.
向量η1,η2,…,ηn .
| 1 | 求出η1,η2,…,ηm ，它们是单位正交的，具有性质
返回 上页 下页
首先，可取 1
1
1 . 一般地，假定已经
L(ε1,ε2,…,εi)=L(η1,η2,…,ηi)，i=1,2, …,m.
下一步求ηm+1. 因为L(ε1,ε2,…,εm)=L(η1,η2,…,ηm)，所以εm+1 不能被线性表出. 按定理1证明的方法，作向量
返回 上页 下页
返回
上页
下页
因为度量矩阵是正定矩阵的，根据第五章关 于正定二次型的结果，正定矩阵合同于单位矩阵. 这说明在n维欧氏空间中存在一组基，它的度量矩 阵是单位矩阵. 由此断言
结论 在n维欧氏空间中，标准正交基是存在的. 在标准正交基下，向量的坐标可以通过内积 简单地表示出来，即 (1 , )1 ( 2 , ) 2 ( n , ) n (2)
返回
上页
下页
例3 欧氏空间Rn的基
i (0,,0, 1 ,0,,0） i 1, 2 ,, n
（i）
是Rn的一个标准正交基.
返回
上页
下页
(5)
(5)式相当于一个矩阵的等式
ATA=E ，
或者
返回
(6)
A-1=AT .
上页 下页
我们引入
定义7 n级实数矩阵A称为正交矩阵，如果ATA=E . 因此，以上分析表明，由标准正交基到标准正 交基的过渡矩阵是正交矩阵；反过来，如果第一组 基是标准正交基，同时过渡矩阵是正交矩阵，那么
第二组基一定也是标准正交基.
向量η1,η2,…,ηn .
| 1 | 求出η1,η2,…,ηm ，它们是单位正交的，具有性质
返回 上页 下页
首先，可取 1
1
1 . 一般地，假定已经
L(ε1,ε2,…,εi)=L(η1,η2,…,ηi)，i=1,2, …,m.
下一步求ηm+1. 因为L(ε1,ε2,…,εm)=L(η1,η2,…,ηm)，所以εm+1 不能被线性表出. 按定理1证明的方法，作向量
返回 上页 下页
正交基与标准正交基
标准正交基到正交基的转换
01
定义
标准正交基是单位正交基，即每个基向量的模长为1。正交基则是线性
空间的一组基，满足两两正交的性质。
02
转换方法
将标准正交基中的每个向量乘以该向量的模长，即可得到正交基。
03
数学表示
设${mathbf{e}_1, mathbf{e}_2, ldots, mathbf{e}_n}$为标准正交基，
在信号处理中的应用
信号表示
正交基可以用于表示信号，例如傅里叶变换将信 号表示为正弦和余弦函数的正交基。
信号分离
利用正交基可以将复合信号分离成简单的分量， 便于分析和处理。
信号压缩
通过选择重要的正交基函数，可以实现信号压缩， 减少存储和传输的开销。
在量子力学中的应用
量子态表示
在量子力学中，正交基用于表示量子态，特别是使用 波函数。
02
标准正交基的概念
定义
定义
标准正交基是线性空间的一组基，其 中每个向量都与其余向量正交，且模 长为1。
解释
标准正交基中的向量是线性独立的，且 它们的模长都为1，这意味着它们没有 长度，只有方向。此外，这些向量之间 相互垂直，即它们正交。
性质
唯一性
对于给定的线性空间，标准正交 基不是唯一的。也就是说，可以 有多种不同的标准正交基来表示 同一个线性空间。
则正交基为${|mathbf{e}_1| mathbf{e}_1, |mathbf{e}_2| mathbf{e}_2,
ldots, |mathbf{e}_n| mathbf{e}_n}$。
判断两个基是否正交，需要计算它们的点积。如果点积为0，则两个基正交。 正交意味着两个基向量在空间中垂直，不共线。
第二节标准正交基
(5)
(5) 式相当于一个矩阵的等式
ATA = E ，
(6)
或者
A-1 = AT .
定义 7 n 级实数矩阵 A 称为正交矩阵，如
果 ATA = E . 因此，以上分析表明，由标准正交基到标准正
交基的过渡矩阵是正交矩阵；反过来，如果第一组 基是标准正交基，同时过渡矩阵是正交矩阵，那么
第二组基一定也是标准正交基. 最后我们指出，根据逆矩阵的性质，由
i j.
(1)
显然，(1) 式完全刻画了标准正交基的性质. 换句
话说，一组基为标准正交基的充分必要条件是：
它的度量矩阵为单位矩阵. 因为度量矩阵是正定的.
根据第五章关于正定二次型的结果，正定矩阵合同 于单位矩阵. 这说明在 n 维欧氏空间中存在一组基, 它的度量矩阵是单位矩阵. 由此可以断言，在 n 维 欧氏空间中，标准正交基是存在的.
理 1 证明中的方法，作向量
m
m1 m1 ( m1,i )i . i 1
显然
m +1 0 , 且 (m +1 , i) = 0 ，i = 1 , 2 , … , m .
令
m1
m1 | m1
|
.
则 1 , 2 , … , m , m +1 就是一单位正交向量组.
同时
L(1 , 2 , … , m +1 ) = L(1 , 2 , … , m +1) .
交向量组的方法称为施密特(Schimidt)正交化过程.
三、举例
例1 设
1
1
4
a1 2 , a2 3 , a3 1 ,
1
1
0
试用施密特正交化过程把这组向量变成单位正交
第四章1欧几里得空间的定义与基本性质2标准正交基与正交变换
这样共可得到 n 个两两正交的单位特征向量 1 ,2 , ,n .
3. 以这些向量为列构成正交矩阵 P (1,2 , ,n ),
有 P 1 AP diag(l1, ,l1, ,ls , ls ).
3 2 4
例： 设
A
2 4
0 2
2 3
求正交矩阵 P ，使得 P 1 AP 为对角阵。
14
性质: (1)若 A为正交矩阵，则 | A |=±1.
(2)实矩阵 A 为正交矩阵的充要条件为 A1 A . (3)实矩阵 A为正交矩阵的充要条件是：
A的行(列)向量组为两两正交的单位向量组。
例: 设 A 为三阶非零实方阵, 且 aij = Aij , 其中Aij 是 aij 的代数余子式, i , j = 1, 2, 3. 证明 : |A| = 1, 且 A 是正交矩阵.
1
得基础解系
p1
2 0
,
0
p2
2 1
.
21
先正交化：
1
b1
p1
2 0
,
0 1 4
b2
p2
[b1 , [b1 ,
p2 ] b1 ]
b1
2 1
4 5
2 0
1 5
2 5
再单位化：
1
1
1 5
2 0
,
4
2
1 35
2 5
22
当 l3 8 时，齐次线性方程组为 A 8E x 0
a
2 n
称 || α || 为向量 α 的长度（模或范数）。
特别地，当 || || 1 时，称 α 为单位向量。
由α
(≠
0)求出单位向量
||
||
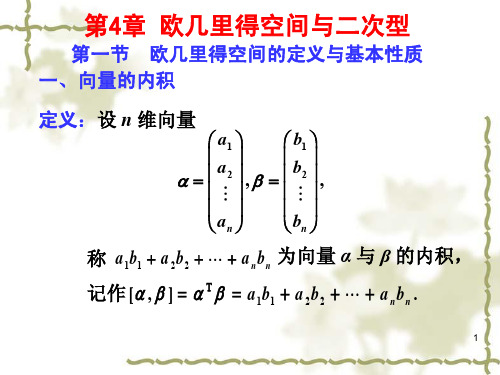
3. 以这些向量为列构成正交矩阵 P (1,2 , ,n ),
有 P 1 AP diag(l1, ,l1, ,ls , ls ).
3 2 4
例： 设
A
2 4
0 2
2 3
求正交矩阵 P ，使得 P 1 AP 为对角阵。
14
性质: (1)若 A为正交矩阵，则 | A |=±1.
(2)实矩阵 A 为正交矩阵的充要条件为 A1 A . (3)实矩阵 A为正交矩阵的充要条件是：
A的行(列)向量组为两两正交的单位向量组。
例: 设 A 为三阶非零实方阵, 且 aij = Aij , 其中Aij 是 aij 的代数余子式, i , j = 1, 2, 3. 证明 : |A| = 1, 且 A 是正交矩阵.
1
得基础解系
p1
2 0
,
0
p2
2 1
.
21
先正交化：
1
b1
p1
2 0
,
0 1 4
b2
p2
[b1 , [b1 ,
p2 ] b1 ]
b1
2 1
4 5
2 0
1 5
2 5
再单位化：
1
1
1 5
2 0
,
4
2
1 35
2 5
22
当 l3 8 时，齐次线性方程组为 A 8E x 0
a
2 n
称 || α || 为向量 α 的长度（模或范数）。
特别地，当 || || 1 时，称 α 为单位向量。
由α
(≠
0)求出单位向量
||
||
镜面反射的标准正交基
镜面反射的标准正交基
在光学中，镜面反射通常涉及到标准正交基的概念。
标准正交基是一组正交（垂直）且长度为1的基向量，用于描述一个空间中的方向。
在光学中，通常使用三个基向量来表示光线的传播方向。
常见的标准正交基通常选择为：
1. 入射光方向基向量(i)：
* 表示光线从光源入射到表面的方向。
2. 反射光方向基向量(r)：
* 表示光线从表面反射出去的方向。
3. 法线方向基向量(n)：
* 表示表面的法线方向，即垂直于表面的方向。
这三个基向量通常构成右手坐标系，其中法线方向(n) 与入射光方向(i) 和反射光方向(r) 共同构成一个右手坐标系。
光的反射通常遵循著名的“反射定律”，即入射角等于反射角。
这可以用以下向量关系表示：
[ r = i - 2(i \cdot n) \cdot n ]
其中：
* (r) 是反射光方向向量，
* (i) 是入射光方向向量，
* (n) 是法线方向向量，
* (\cdot) 表示向量点积。
在这个公式中，(i \cdot n) 表示入射光方向与法线方向的点积。
根据反射定律，反射光方向(r) 是入射光方向(i) 经过镜面反射后的方向。
这种标准正交基和向量关系是在描述镜面反射光学现象时常用
的概念。
矩阵的标准正交基
矩阵的标准正交基是指一组相互正交的单位向量，这些单位向量的排列构成一个正交矩阵。
标准正交基的一个重要性质是，任意一个向量都可以唯一地表示为基向量的线性组合。
设n维欧几里得空间的一个标准正交基为{e_1, e_2, ..., e_n}，其中e_i ≺e_j（i < j），那么这个标准正交基具有以下性质：
1. e_i ⊥ e_j (i ≠ j)
2. e_i ∈ R^n, ||e_i|| = 1 (i = 1, 2, ..., n)
3. 对于任意一个向量v ∈ R^n，有v = Σai * e_i，其中ai为实数。
求解标准正交基的方法有Gram-Schmidt正交化等。
首先选取一个向量作为基向量，然后在该向量上进行正交化，得到一个新的向量，将其作为新的基向量，继续进行正交化，直到得到n个相互正交的单位向量。
标准正交基在矩阵中的应用广泛，例如求解线性方程组、求解特征值和特征向量等问题。
在求解这些问题时，通常需要将矩阵表示为标准正交基的线性组合，以便于进行计算和分析。