人教A版高中数学必修五1.1 正弦定理和余弦定理
人教A版必修5第1章《正弦定理和余弦定理》ppt导学课件

根据勾股定理知△ABC 是直角三角形. 4、 已知 a,b,c 分别为△ABC 三个内角 A,B,C 的对边,acosC+ 3asinC-b-c =0. (1)求 A; (2)若 a=2,△ABC 的面积为 3,求 b, c. 【解析】本题考查正弦定理.(1)利用正 弦定理边化角结合两角和差公式化简求 解; (2)利用三角形面积公式及余弦定理 求解. 【答案】 (1)由 acosC+ 3asinC-b-c= 0 及正弦定理得
.
【解析】本题考查正弦定理 . 在三角形中【解析】本题考查正弦定理.由正弦定理, 需要考虑大边对大角,三个内角的和不能得 sin B= 2, 2 0 超过 180 .利用正弦定理求得∠B,根据大 ∵a>b,∴∠A>∠B. 边对大角,故∠B =30°,勾股定理求得 ∴∠B 只有一解.∴∠B=45°. c. 【答案】45°.
人教(A)数学 · 必修5 对点助学PPT
【知识目标】
1、理解正弦定理和余弦定理公 式的推导过程;
正弦定理和余弦定理
【学习目标】
1、会根据正弦定理和余弦定理 解三角形(知三求一) ; 2、会利用正弦定理和余弦定理 进行边角的相互转化2 3, b=6,
B=60°或 120°.
a
sin A
=
= =2R sin B sin C
b
c
(R 为△ABC 的外接圆半径).
统一为“边”之间的关系式或“角” 【答案】由正弦定理 a = b sin A sin B 之间的关系式. 3 1 1 可得 = ,∴sin B= , sin 60° sin B 2
【对点巩固】
故∠B=30°或 150°.由 a>b,
高中数学人教版必修5课件:1.1.1正弦定理(系列三)

典型例题 例1 已知一三角形中a=2 3 ,b=6,A=30°,判断三角形是
否有解,若有解,解该三角形.
解 a=2 3,b=6,a<b,A=30°<90°.
又因为bsinA=6sin30°=3,a>bsinA,
所以本题有两解,由正弦定理得,
sinB=bsian
A=6sin 2
30°= 3
23,故B=60°或120°.
跟踪训练1 在△ABC中,角A、B、C所对的边分别为a、b、
c,已知A=60°,a= 3,b=1,则c等于
(B )
A.1 B.2 C. 3-1 D. 3
解析 由正弦定理sina A=sinb B,可得sin 630°=sin1 B,
∴sinB=12,故∠B=30°或150°.由a>b,
得∠A>∠B,∴∠B=30°,故∠C=90°,
由勾股定理得c=2.
例2 在△ABC中,若∠A=120°,AB=5,BC=7,求△ABC 的面积.
解 如图,由正弦定理,
得sin
1720°=sin5
, C
∴sinC=5143,且∠C为锐角(∠A=120°).∴cosC=1114. ∴sinB=sin(180°-120°-∠C)=sin(60°-∠C) = 23cosC-12sinC= 23×1114-12×5143=3143.
证明 作AD⊥BC,垂足为D, 则AD=AB·sinB,又AD=AC·sinC,
∴csinB=bsinC.
∴S△ABC=12BC·AD =12acsinB=12absinC. 同理S△ABC=12absinC=12bcsinA.
∴S△ABC=12absinC=12bcsinA=12acsinB.
人教版高中数学必修五正弦定理和余弦定理课件

解的情况
A为钝角或直角
a>b a≤b
一解 无解
a<bsinA
无解
A为锐角
a=bsinA bsinA<a<b
一解 两解
a≥b
一解
思考 : 在ABC中, a x, b 2, A 450,若这个三角形有
两解,则x的取值范围是 _____2_,_2____
正弦定理的推论: =2R (R为△ABC外接圆半径) (边换角)
在已知三边和一个角的情况下:求另一个角 ㈠用余弦定理推论,解唯一,可以免去判断舍取。 ㈡用正弦定理,计算相对简单,但解不唯一,要进行 判断舍取。
练习1:在△ABC中,已知
解:
=31+18 =49
∴b=7
练习2:
在△ABC中, a 7,b 4 3, c 13 ,求△ABC的最小角。
解:
72 (4 13)2 ( 13)2 274 3
二、可以用正弦定理解决的两类三角问题: (1)知两角及一边,求其它的边和角; (2)知三角形任意两边及其中一边的对角,求其它
的边和角(注意判断解的个数)
思考:你能用正弦定理来解释为什么在三角形中越大
的角所对的边就越大吗?
分析:设△ABC的三个角所对边长分别是a、b、c,
且∠A≥∠B≥∠C,
(1)若△ABC是锐角或直角三角形 ∵正弦函数y=sinx在 [0, ]上是增函数 2
2A 2k 2B 或 2A 2k 2B(k Z)
0 A,B ,∴k 0,则A B或A+B=
故△ABC为等腰三角形或直角三角形.
2
针对性练习 1、已知△ABC中,sin2A=sin2B+sin2C,且 b sinB=c sinC,则△ABC的形状是
人教版高一必修五第一章正弦定理和余弦定理

CD a sinB
S ABC
1 1 AB CD ac sin B 2 2
C a
同理:S ABC S ABC
1 ab sinC; 2 1 bc sin A. 2
b
B
c D
A
正弦定理:在一个三角形中各边和它所对角的正弦的比 相等.
A
C 且 B 180 ( A C ) 105
b c 解:∵ sin B sin C
c sin B 10 sin 105 b 19 sin C sin 30
例2:在
ABC中,已知a=20cm,b=28cm,A=40°,解三角形
(角度精确到1 ° ,边长精确到1cm). b sin A 28 sin 40 解:根据正弦定理, sin B 0.899 a 20 因为0<B<180 ,所以B 64或 116 (1)当B≈64°时, C=180°-(A+B)≈180°-(40°+64°)=76°
例题1
2
4
正弦定理
(1)在ABC中,已知b 12, A 30 ,
3.定理的应用举例 例1 在ABC 已知 解三角形. 变式:若将a=2 改为c=2,结果如何? 通过例题你发现了什么一般性结论吗?
A 300 , B 1350 , a 2
,
小结:知道三角形的两个内角和任何一边,利 用正弦定理可以求出三角形中的其它元素。
例 2、 已知a=16, b= 16 3, A=30° . 已知两边和其中一边 解三角形(2)将 A=30° 变为B= 30° 呢? 的对角,求其他边和角 a b 解:由正弦定理 C
新人教A版必修5高中数学正弦定理、余弦定理(一)

正弦定理、余弦定理(一)教学目标:进一步熟悉正、余弦定理内容,能够应用正、余弦定理进行边角关系的相互转化,判断三角形的形状,证明三角形中的三角恒等式;通过正、余弦定理在边角互换时所发挥的桥梁作用来反映事物之间的内在联系;通过三角恒等式的证明来反映事物外在形式可以相互转化而内在实质的不变性.教学重点:利用正、余弦定理进行边角互换.教学难点:1.利用正、余弦定理进行边角互换时的转化方向;2.三角恒等式证明中结论与条件之间的内在联系的寻求.教学过程:Ⅰ.复习回顾前面两节课,我们一起学习了正弦定理、余弦定理的内容,并且接触了利用正、余弦定理解三角形的有关题型.下面,我们先来回顾一下正、余弦定理的内容.正弦定理、余弦定理实质上反映了三角形内的边角关系,运用定理可以进行边与角之间的转换,这一节,我们将通过例题分析来学习正、余弦定理的边角转换功能在证明三角恒等式及判断三角形形状时的应用.Ⅱ.讲授新课[例1]已知△ABC ,BD 为B 的平分线,求证:AB ∶BC =AD ∶DC分析:前面大家所接触的解三角形问题是在一个三角形内研究问题,而 B 的平分线BD 将△ABC 分成了两个三角形:△ABD 与△CBD ,故要证结论成立,可证明它的等价形式:AB ∶AD =BC ∶DC ,从而把问题转化到两个三角形内,而在三角形内边的比等于所对角的正弦值的比,故可利用正弦定理将所证继续转化为AB sin ∠ADB =AD sin ∠ABD ,BC sin ∠BDC =DCsin ∠DBC,再根据相等角正弦值相等,互补角正弦值也相等即可证明结论.证明:在△ABD 内,利用正弦定理得:AB sin ∠ADB =AD sin ∠ABD ,即AB AD =sin ∠ADB sin ∠ABD在△BCD 内,利用正弦定理得:BC sin ∠BDC =DC sin ∠DBC ,即BC DC =sin ∠BDC sin ∠DBC. ∵BD 是B 的平分线.∴∠ABD =∠DBC ,∴sin ABD =sin DBC .∵∠ADB +∠BDC =180°,∴sin ADB =sin (180°-∠BDC )=sin BDC∴AB AD =sin ∠ADB sin ∠ABD =sin ∠BDC sin ∠DBC =BC DC ,∴AB BC =AD DC评述:此题可以启发学生利用正弦定理将边的关系转化为角的关系,并且注意互补角的正弦值相等这一特殊关系式的应用.[例2]在△ABC 中,求证:a 2sin2B +b 2sin2A =2ab sin C分析:此题所证结论包含关于△ABC 的边角关系,证明时可以考虑两种途径:一是把角的关系通过正弦定理转化为边的关系,若是余弦形式则通过余弦定理;二是把边的关系转化为角的关系,一般是通过正弦定理.另外,此题要求学生熟悉相关的三角函数的有关公式,如sin2B =2sin B ·cos B 等,以便在化为角的关系时进行三角函数式的恒等变形.证明一:(化为三角函数)a 2sin2B +b 2sin2A=(2R sin A )2·2sin B ·cos B +(2R sin B )2·2sin A ·cos A=8R 2sin A ·sin B (sin A cos B +cos A sin B )=8R 2sin A sin B sin C=2·2R sin A ·2R sin B ·sin C =2ab sin C所以原式得证.证明二:(化为边的式子)左边=a 2·2sin B cos B +b 2·2sin A ·cos A=a 2·2b k ·a 2+c 2-b 22ac +b 2·2a k ·b 2+c 2-a 22bc=ab kc(a 2+c 2-b 2+b 2+c 2-a 2) =ab kc ·2c 2=2ab ·c k =2ab sin C 评述:由边向角转化,通常利用正弦定理的变形式:a =2R sin A ,b =2R sin B ,c =2R sin C ,在转化为角的关系式后,要注意三角函数公式的运用,在此题用到了正弦二倍角公式sin2A =2sin A ·cos A ,正弦两角和公式sin (A +B )=sin A ·cos B +cos A ·sin B ;由角向边转化,要结合正弦定理变形式以及余弦定理形式二.三角形的有关证明问题,主要围绕三角形的边和角的三角函数展开,从某种意义上来看,这类问题就是有了目标的含边和角的式子的化简问题.[例3]已知A 、B 、C 是△ABC 的三个内角,且满足(sin A +sin B )2-sin 2C =3sin A sin B求证:A +B =120°分析:要证A +B =120°,由于A +B +C =180°,只要证明C =60°,而已知条件为三角函数关系,故应考虑向三角函数的转化,又在0°~180°之间,余弦值所对应角唯一,故可证明cos C =12 ,而由余弦定理cos C =a 2+b 2-c 22ab,所以应考虑把已知的角的关系式转化为边的关系.证明:由(sin A +sin B )2-sin 2C =3sin A ·sin B可得sin 2A +sin 2B -sin 2C =sin A ·sin B又∵sin A =a k ,sin B =b k,sin C =c k, ∴a 2k 2 +b 2k 2 -c 2k 2 =a k ·b k整理得a 2+b 2-c 2=ab∴cos C =a 2+b 2-c 22ab =12又0°<C <180°,∴C =60°∴A +B =180°-C =120° 评述:(1)有关三角形内角的证明,选择余弦值与正弦值相比较,要省去取舍的麻烦.但注意在根据三角函数值求角时,应先确定角的范围;(2)在将已知条件中角的关系转化为边的关系时,运用了正弦定理的变形式:a =2R sin A ,b =2R sin B ,c =2R sin C ,这一转化技巧,要求学生熟练掌握.[例4]在△ABC 中,b cos A =a cos B ,试判断三角形的形状.分析:三角形形状的判断,可以根据角的关系,也可根据边的关系,所以在已知条件的运用上,可以考虑两种途径:将边转化为角,将角转化为边,下面,我们从这两个角度进行分析.解法一:利用余弦定理将角化为边.∵b cos A =a cos B∴b ·b 2+c 2-a 22bc =a ·a 2+c 2-b 22ac∴b 2+c 2-a 2=a 2+c 2-b 2∴a 2=b 2 ∴a =b故此三角形是等腰三角形.解法二:利用正弦定理将边转化为角.∵b cos A =a cos B又b =2R sin B ,a =2R sin A∴2R sin B cos A =2R sin A cos B∴sin A cos B -cos A sin B =0∴sin (A -B )=0∵0<A ,B <π,∴-π<A -B <π∴A -B =0,即A =B故此三角形是等腰三角形.评述:(1)在判定三角形形状时,一般考虑两个方向进行变形,一个方向是边,走代数变形之路,通常是正、余弦定理结合使用;另一个方向是角,走三角变形之路.通常是运用正弦定理.要求学生要注重边角转化的桥梁——正、余弦定理;(2)解法二中用到了三角函数中两角差的正弦公式,但应注意在根据三角函数值求角时,一定要先确定角的范围.另外,也可运用同角三角函数的商数关系,在等式sin B ·cos A =sin A cos B 两端同除以sin A sin B 得cot A =cot B ,再由0<A ,B <π,而得A =B .为巩固本节所学的解题方法,下面我们进行课堂练习.Ⅲ.课堂练习1.在△ABC 中,证明下列各式:(1)(a 2-b 2-c 2)tan A +(a 2-b 2+c 2)tan B =0(2)cos2A a 2 -cos2B b 2 =1a 2 -1b 2 . 证明:(1)左边=(a 2-b 2-c 2)sin A cos A +(a 2-b 2+c 2)sin B cos B=(a 2-b 2-c 2)·a k ·2bc b 2+c 2-a 2 +(a 2-b 2+c 2)·b k ·2ac a 2+c 2-b 2=2abc k [-(b 2+c 2-a 2)b 2+c 2-a 2 +a 2+c 2-b 2a 2+c 2-b 2] =2abc k(-1+1)=0=右边 故原命题得证.(2)左边=1-2sin 2A a 2 -1-2sin 2B b 2 =(1a 2 -1b 2 )-2sin 2A k 2 sin 2A +2sin 2B k 2 sin 2B=1a 2 -1b 2 -2k 2 +2k 2 =1a 2 -1b 2 =右边 故原命题得证.评述:(1)在(1)题证明时应注意两点:一是切化弦的思路,二是结合正、余弦定理将角的关系转化为边的关系;(2)(2)题证明过程中用到了余弦二倍角的公式,而此公式有三种形式cos2A =cos 2A -sin 2A =2cos 2A -1=1-2sin 2A ,由于考虑到等式右端为边的关系,故选用第三种形式,在转化为边的关系时较为简便.2.在△ABC 中,已知sin B ·sin C =cos 2A 2,试判断此三角形的类型. 解:∵sin B ·sin C =cos 2A 2 ,∴sin B ·sin C =1+cos A 2∴2sin B ·sin C =1+cos [180°-(B +C )]将cos (B +C )=cos B cos C -sin B sin C 代入上式得cos B cos C +sin B sin C =1∴cos(B-C)=1又0<B,C<π,∴-π<B-C<π∴B-C=0,∴B=C故此三角形是等腰三角形.评述:(1)此题在证明过程中,要用到余弦二倍角公式cos A=2cos2A2-1的逆用,要求学生注意;(2)由于已知条件就是三角函数关系式,故无需向边的关系转化,而是进行三角函数式的恒等变形.Ⅳ.课时小结通过本节学习,我们熟悉了正、余弦定理在进行边角关系转换时的桥梁作用,并利用正、余弦定理对三角恒等式进行证明以及对三角形形状进行判断.其中,要求大家重点体会正、余弦定理的边角转换功能.Ⅴ.课后作业补充作业:1.在△ABC中,已知sin Asin C=sin(A-B)sin(B-C),求证:2b2=a2+c2.证明:由已知得sin(B+C)sin(B-C)=sin(A+B)·sin(A-B)cos2B-cos2C=cos2A-cos2B2cos2B=cos2A+cos2C2·1-cos2B2=1-cos2A2+1-cos2B2∴2sin2B=sin2A+sin2C由正弦定理可得2b2=a2+c2.2.在△ABC中,A=30°,cos B=2sin B- 3 sin C.(1)求证:△ABC为等腰三角形;(提示B=C=75°)(2)设D为△ABC外接圆的直径BE与AC的交点,且AB=2,求AD∶DC的值. 答案:(1)略(2)1∶ 3。
高中数学第一章解三角形1.1正弦定理和余弦定理1.1.2余弦定理人教A版必修5

∴A=60°,C=180°-(A+B)=75°.
探究 2 已知三边(三边关系)解三角形 例 2 (1)在△ABC 中,若 a=7,b=4 3,c= 13,则 △ABC 的最小角为( )
πππ π A.3 B.6 C.4 D.12 (2)在△ABC 中,角 A,B,C 的对边分别为 a,b,c, 已知 a-b=4,a+c=2b,且最大角为 120°,求此三角形的 最大边长. 答案 (2)见解析
2.做一做
(1)在△ABC 中,角 A,B,C 所对的边分别为 a,b,c, 5π
若 a=1,b= 7,c= 3,则 B=____6____. (2) 已知 △ABC 的 三边 分 别为 2,3,4 , 则此 三 角形是
___钝__角___三角形.
π (3)在△ABC 中,若 a2+b2-c2=ab,则角 C 的大小为 ___3_____.
解析 (1)因为 c<b<a,所以最小角为角 C. 所以 cosC=a2+2ba2b-c2=429×+74×8-4 133= 23, 所以 C=π6,故选 B.
(2)已知 a-b=4,且 a>b,且 a=b+4,又 a+c=2b, 则 b+4+c=2b,所以 b=c+4,则 b>c,从而 a>b>c,所以 a 为最大边,A=120°,b=a-4,c=a-8.
解 利用边的关系判断, 由正弦定理,得sinC=c,
sinB b 由 2cosAsinB=sinC,得 cosA=2ssininCB=2cb, 又 cosA=b2+2cb2c-a2,∴2cb=b2+2cb2c-a2,即 a=b.
又(a+b+c)(a+b-c)=3ab,∴(a+b)2-c2=3ab, ∴b=c, 综上 a=b=c,∴△ABC 为等边三角形.
正弦定理和余弦定理1 高中数学(人教)

课堂合作探究
KETANG HEZUO TANJIU
问题导学
当堂检测
解:在△ABC 中,C=180° -(A+B)=180° -(60° +45° )=75° . sin 75° =sin(45° +30° ) =sin 45° cos 30° +cos 45° sin 30° =2 ×
2 3 2 2 2 1 2 ( 3+1Leabharlann . 4第一章解三角形
1.1 正弦定理和余弦定理
1.1.1
正弦定理
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
目标导航
预习引导
1.会推导正弦定理; 学习目标 2.会用正弦定理解一些简单的三角形度量问题; 3.能用正弦定理判断三角形的形状. 重点难点 重点:应用正弦定理进行边角转化,解决三角形问题; 难点:正弦定理的理解及推导.
������������ ������������ ������ =BD=2R.故 =2R,即 =2R. sin������ sin������ sin������ ������������ ������������
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
������ 2������ ������ 2������ ������ 2������
课前预习导学
KEQIAN YUXI DAOXUE
课堂合作探究
KETANG HEZUO TANJIU
目标导航
预习引导
2.解三角形 (1)一般地,把三角形的三个角 A,B,C 和它们的对边 a,b,c 叫做三角 形的元素. (2)已知三角形的几个元素求其他元素的过程叫做解三角形.
人教版高中数学必修五目录

人教版高中数学必修五目录 1.1正弦定理与余弦定理1.1.1正弦定理1.1.2余弦定理1.2应用举例第二章数列2.1数列2.1.1数列2.2.2数列的递推公式(选学)2.2等差数列2.2.1等差数列2.2.2等差数列的前n项和2.3等比数列2.3.1等比数列2.3.2等比数列的前n项和第三章不等式3.1不等关系与不等式3.2均值不等式3.3一元二次不等式及其解法3.4不等式的实际应用领域3.5二元一次不等式(组)与简单的线性规划问题如何努力学习高中数学一·培养良好的学习兴趣自学数学最出色的方法就是把数学培育成自己的嗜好。
嗜好高中数学就可以有兴趣回去课堂教学高中数学的自学方法,有兴趣才可以构成自学的主动性和积极性。
养好较好的自学习惯,并把它培育成自学兴趣存有这几点建议:(1)课前预习,对所有学识产生疑问,产生好奇心。
(2)听讲中要协调老师授课,满足用户感官的兴奋性,听讲重点化解复习中疑点,把老师课堂的回答·停滞·教具和模型的模拟的都视作观赏音乐,及时提问老师课堂回答,培育思索与老师同步性,提升精神,把老师对你的回答的评价,变成鞭策自学的动力。
(3)思考问题注意归纳,挖掘你的学习的潜力。
(4)听讲中特别注意老师传授时的数学思想,多问什么必须这样的思索,这样的方法怎样就是产生的?把概念回归自然。
所有学科都是从实际问题中产生归纳的,数学概念也回归于现实生活,如角的概念·直角坐标系的产生·极坐标的产生都是从实际生活中抽象出来的。
只有回归现实才能对概念理解切实可靠,有应用概念判断·推理时会准确。
二、弄清楚概念、性质与基本方法弄清概念、性质和基本方法是每个学科学习的第一步也是最重要的一步,如果概念没有弄清就去解题是没有不碰壁的。
正确理解概念再做习题就比较容易了,通过习题的演算反过来还可以进一步理解概念与性质。
要弄清概念、性质和基本方法,就要先复习老师上课所讲的东西,要看一看课本上的相关内容。
高中数学必修五-正弦定理与余弦定理

正弦定理与余弦定理知识集结知识元正弦定理公式知识讲解1.正弦定理【知识点的知识】1.正弦定理和余弦定理定理正弦定理余弦定理内容=2R(R是△ABC外接圆半径)a2=b2+c2﹣2bc cos A,b2=a2+c2﹣2ac cos B,c2=a2+b2﹣2ab cos C变形形式①a=2R sin A,b=2R sin B,c=2R sin C;②sin A=,sin B=,sin C=;③a:b:c=sin A:sin B:sin C;④a sin B=b sin A,b sin C=c sin B,a sin C=c sin A cos A=,cos B=,cos C=解决三角形的问题①已知两角和任一边,求另一角和其他两条边;②已知两边和其中一边的对角,求另一边和其他两角①已知三边,求各角;②已知两边和它们的夹角,求第三边和其他两角在△ABC中,已知a,b和角A时,解的情况A为锐角A为钝角或直角图形关系式a=b sin A b sin A<a<b a≥b a>b一解两解一解一解解的个数由上表可知,当A为锐角时,a<b sin A,无解.当A为钝角或直角时,a≤b,无解.2、三角形常用面积公式1.S=a•h a(h a表示边a上的高);2.S=ab sin C=ac sin B=bc sin A.3.S=r(a+b+c)(r为内切圆半径).【正余弦定理的应用】1、解直角三角形的基本元素.2、判断三角形的形状.3、解决与面积有关的问题.4、利用正余弦定理解斜三角形,在实际应用中有着广泛的应用,如测量、航海、几何等方面都要用到解三角形的知识(1)测距离问题:测量一个可到达的点到一个不可到达的点之间的距离问题,用正弦定理就可解决.解题关键在于明确:①测量从一个可到达的点到一个不可到达的点之间的距离问题,一般可转化为已知三角形两个角和一边解三角形的问题,再运用正弦定理解决;②测量两个不可到达的点之间的距离问题,首先把求不可到达的两点之间的距离转化为应用正弦定理求三角形的边长问题,然后再把未知的边长问题转化为测量可到达的一点与不可到达的一点之间的距离问题.(2)测量高度问题:解题思路:①测量底部不可到达的建筑物的高度问题,由于底部不可到达,因此不能直接用解直角三角形的方法解决,但常用正弦定理计算出建筑物顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.②对于顶部不可到达的建筑物高度的测量问题,我们可选择另一建筑物作为研究的桥梁,然后找到可测建筑物的相关长度和仰、俯角等构成三角形,在此三角形中利用正弦定理或余弦定理求解即可.点拨:在测量高度时,要理解仰角、俯角的概念.仰角和俯角都是在同一铅锤面内,视线与水平线的夹角.当视线在水平线之上时,成为仰角;当视线在水平线之下时,称为俯角.例题精讲正弦定理公式例1.已知△ABC中,角A,B,C所对的边分别是a,b,c.若A=45°,B=30°,a=,则b=()A.B.1 C.2 D.例2.在△ABC中,角A,B,C的对边分别为a,b,c,若,则B=()A.B.C.D.或例3.在△ABC中,已知三个内角为A,B,C满足sin A:sin B:sin C=3:5:7,则C=()A.90°B.120°C.135°D.150°利用正弦定理解三角形知识讲解【正余弦定理的应用】1、解直角三角形的基本元素.2、判断三角形的形状.3、解决与面积有关的问题.4、利用正余弦定理解斜三角形,在实际应用中有着广泛的应用,如测量、航海、几何等方面都要用到解三角形的知识例题精讲利用正弦定理解三角形例1.在△ABC中,a,b,c是内角A,B,C所对的边.若a>b,则下列结论不一定成立的()A.A>B B.sin A>sin BC.cos A<cos B D.sin2A>sin2B例2.在△ABC中,角A,B,C的对边分别是a,b,c,且,则角A的大小为()A.B.C.D.例3.在△ABC中,三内角A,B,C的对边分别为a,b,c,若sin B =b sin A,则a=()A .B .C.1 D.三角形面积公式的简单应用知识讲解1.余弦定理【知识点的知识】1.正弦定理和余弦定理定理正弦定理余弦定理内容=2R(R是△ABC外接圆半径)a2=b2+c2﹣2bc cos A,b2=a2+c2﹣2ac cos B,c2=a2+b2﹣2ab cos C变形形式①a=2R sin A,b=2R sin B,c=2R sin C;②sin A=,sin B=,sin C=;③a:b:c=sin A:sin B:sin C;④a sin B=b sin A,b sin C=c sin B,a sin C=c sin A cos A=,cos B=,cos C=解决三角形的问题①已知两角和任一边,求另一角和其他两条边;②已知两边和其中一边的对角,求另一边和其他两角①已知三边,求各角;②已知两边和它们的夹角,求第三边和其他两角A为锐角A为钝角或直角图形关系式a=b sin A b sin A<a<b a≥b a>b 解的个数一解两解一解一解由上表可知,当A为锐角时,a<b sin A,无解.当A为钝角或直角时,a≤b,无解.例题精讲三角形面积公式的简单应用例1.已知△ABC的内角A,B,C的对边分别为a,b,c,且(a+b)2=c2+ab,B=30°,a=4,则△ABC的面积为()A.4 B.3C.4D.6例2.设△ABC的三个内角A,B,C成等差数列,其外接圆半径为2,且有,则三角形的面积为()A.B.C.或D.或例3.在△ABC中角ABC的对边分别为a、b、c,cos C=,且a cos B+b cos A=2,则△ABC面积的最大值为()A.B.C.D.利用余弦定理解三角形当堂练习填空题练习1.如图,O在△ABC的内部,且++3=,则△ABC的面积与△AOC的面积的比值为_____.练习2.锐角△ABC的内角A,B,C的对边分别为a,b,c,已知c2-8=(a-b)2,a=2c sin A,则△ABC的面积为____.练习3.在△ABC中,内角A,B,C的对边分别为a,b,c,已知,则的最大值是____.解答题练习1.'在△ABC中,角A,B,C所对的边分别为a,b,c,且满足.(1)求角B的大小;(2)若D为AC的中点,且BD=1,求S△ABC的最大值.'练习2.'在△ABC中,角A、B、C的对边分别是a、b、c,若(a+c)sin B-b sin C=b cos A.(1)求角A;(2)若△ABC的面积为4,a=6,求△ABC的周长.'练习3.'△ABC内角A,B,C所对的边分别为a,b,c.若。
人教A版高中数学必修5第一章 解三角形1.1 正弦定理和余弦定理教案

专题22正弦定理和余弦定理1.掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题;1.正、余弦定理在△ABC 中,若角A ,B ,C 所对的边分别是a ,b ,c ,R 为△ABC 外接圆半径,则 定理正弦定理余弦定理内容a sin A =b sin B =csin C=2R a 2=b 2+c 22bc cos__A ;b 2=c 2+a 22ca cos__B ; c 2=a 2+b 2-2ab cos__C常见变形(1)a =2R sin A ,b =2R sin__B ,c =2R sin_C ;(2)sin A =a 2R ,sin B =b 2R ,sin C =c2R ;(3)a ∶b ∶c =sin__A ∶sin__B ∶sin__C ;(4)a sin B =b sin A ,b sin C =c sin B ,a sin C =c sin Acos A =b 2+c 2-a 22bc ;cos B =c 2+a 2-b 22ac ;cos C =a 2+b 2-c 22ab2.S △ABC =12ab sin C =12bc sin A =12ac sin B =4R =12(a +b +c )·r (r 是三角形内切圆的半径),并可由此计算R ,r .高频考点一 利用正弦定理、余弦定理解三角形例1、(1)在△ABC 中,已知a =2,b =6,A =45°,则满足条件的三角形有( ) A .1个 B .2个 C .0个D .无法确定(2)在△ABC 中,已知sin A ∶sin B =2∶1,c 2=b 2+2bc ,则三内角A ,B ,C 的度数依次是________.(3)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =3,sin B =12,C =π6,则b =________.答案 (1)B (2)45°,30°,105° (3)1 解析 (1)∵b sin A =6×22=3,∴b sin A <a <b .解得b =1.【感悟提升】(1)判断三角形解的个数的两种方法①代数法:根据大边对大角的性质、三角形内角和公式、正弦函数的值域等判断. ②几何图形法:根据条件画出图形,通过图形直观判断解的个数.(2)已知三角形的两边和其中一边的对角解三角形.可用正弦定理,也可用余弦定理.用正弦定理时,需判断其解的个数,用余弦定理时,可根据一元二次方程根的情况判断解的个数. 【变式探究】(1)已知在△ABC 中,a =x ,b =2,B =45°,若三角形有两解,则x 的取值范围是( ) A .x >2 B .x <2 C .2<x <2 2D .2<x <2 3(2)在△ABC 中,A =60°,AC =2,BC =3,则AB =________. 答案 (1)C (2)1解析 (1)若三角形有两解,则必有a >b ,∴x >2,又由sin A =a b sin B =x 2×22<1,可得x <22,∴x 的取值范围是2<x <2 2. (2)∵A =60°,AC =2,BC =3, 设AB =x ,由余弦定理,得BC 2=AC 2+AB 2-2AC ·AB cos A ,化简得x 2-2x +1=0, ∴x =1,即AB =1.高频考点二 利用正弦、余弦定理判定三角形的形状例2、(2015·浙江)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c ,已知A =π4,b 2-a2=12c 2. (1)求tan C 的值;(2)若△ABC 的面积为3,求b 的值. 解 (1)由b 2-a 2=12c 2及正弦定理得(2)由tan C =2,C ∈(0,π)得 sin C =255,cos C =55,因为sin B =sin(A +C )=sin ⎝ ⎛⎭⎪⎫π4+C ,所以sin B =31010,由正弦定理得c =223b ,又因为A =π4,12bc sin A =3,所以bc =62,故b =3. 【感悟提升】(1)对于面积公式S =12ab sin C =12ac sin B =12bc sin A ,一般是已知哪一个角就使用哪一个公式.(2)与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化. 【变式探究】四边形ABCD 的内角A 与C 互补,AB =1,BC =3,CD =DA =2. (1)求C 和BD ;(2)求四边形ABCD 的面积.解 (1)由题设A 与C 互补及余弦定理得BD 2=BC 2+CD 2-2BC ·CD cos C =13-12cos C ,① BD 2=AB 2+DA 2-2AB ·DA cos A =5+4cos C .②由①②得cos C =12,BD =7,因为C 为三角形内角,故C =60°. (2)四边形ABCD 的面积S =12AB ·DA sin A +12BC ·CD sin C=⎝ ⎛⎭⎪⎫12×1×2+12×3×2sin60° =2 3.高频考点三 正弦、余弦定理的简单应用例3、设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( )A.锐角三角形B.直角三角形C.钝角三角形D.不确定答案 B【感悟提升】(1)判断三角形形状的方法①化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.②化角:通过三角恒等变形,得出内角的关系,从而判断三角形的形状,此时要注意应用A +B +C =π这个结论. (2)求解几何计算问题要注意①根据已知的边角画出图形并在图中标示; ②选择在某个三角形中运用正弦定理或余弦定理.【变式探究】(1)在△ABC 中,内角A ,B ,C 所对的边长分别是a ,b ,c ,若c -a cos B =(2a -b )cos A ,则△ABC 的形状为( ) A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形(2)如图,在△ABC 中,已知点D 在BC 边上,AD ⊥AC ,sin∠BAC =223,AB =32,AD =3,则BD 的长为______.答案 (1)D (2) 3∴△ABC 为等腰或直角三角形.(2)sin∠BAC =sin(π2+∠BAD )=cos∠BAD ,∴cos∠BAD =223.BD 2=AB 2+AD 2-2AB ·AD cos∠BAD=(32)2+32-2×32×3×223,即BD 2=3,BD = 3.高频考点三 和三角形面积有关的问题【例3】 (2016·全国Ⅰ卷)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos C (a cosB +b cos A )=c .(1)求C ;(2)若c =7,△ABC 的面积为332,求△ABC 的周长. 解 (1)由已知及正弦定理得,2cos C (sin A cos B +sin B ·cos A )=sin C ,2cos C sin(A +B )=sinC ,故2sin C cos C =sin C . 由C ∈(0,π)知sin C ≠0, 可得cos C =12,所以C =π3.(2)由已知,12ab sin C =332,又C =π3,所以ab =6,由已知及余弦定理得,a 2+b 2-2ab cos C =7,故a 2+b 2=13, 从而(a +b )2=25.所以△ABC 的周长为5+7. 【方法规律】三角形面积公式的应用原则(1)对于面积公式S =12ab sin C =12ac sin B =12bc sin A ,一般是已知哪一个角就使用哪一个公式.(2)与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化.【变式探究】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,满足(2a -b )cos C -c cos B =0.(1)求角C 的值;(2)若三边a ,b ,c 满足a +b =13,c =7,求△ABC 的面积.1.【2016高考新课标3理数】在ABC △中,π4B =,BC 边上的高等于13BC ,则cos A =( ) (A )310 (B )10 (C )10- (D )310-【答案】C【解析】设BC 边上的高为AD ,则3BC AD =,所以225AC AD DC AD =+=,2AB AD=.由余弦定理,知22222210cos 210225AB AC BC A AB AC AD AD+-===-⋅⨯⨯,故选C . 2.【2016高考新课标2理数】ABC ∆的内角,,A B C 的对边分别为,,a b c ,若4cos 5A =,5cos 13C =,1a =,则b = . 【答案】21133.【2016高考天津理数】在△ABC 中,若AB ,120C ∠=o ,则AC = ( ) (A )1(B )2(C )3(D )4【答案】A【解析】由余弦定理得213931AC AC AC =++⇒=,选A.4.【2016高考江苏卷】在锐角三角形ABC 中,若sin 2sin sin A B C =,则tan tan tan A B C 的最小值是 ▲ . 【答案】8. 【解析】sin sin()2sin sin tan tan 2tan tan A B+C B C B C B C==⇒+=,又tan tan tan tan tan 1B+CA=B C -,因tan tan tan tan tan tan tan 2tan tan tan tan tan 8,A B C A B C A B C A B C =++=+≥≥即最小值为8.5.(2016·山东卷)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知b =c ,a 2=2b 2(1-sinA ),则A =( )A.3π4 B.π3 C.π4 D.π6解析 在△ABC 中,由b =c ,得cos A =b 2+c 2-a 22bc =2b 2-a 22b 2,又a 2=2b 2(1-sin A ),所以cos A =sin A ,即tan A =1,又知A ∈(0,π),所以A =π4,故选C.答案 C【2015高考天津,理13】在ABC ∆ 中,内角,,A B C 所对的边分别为,,a b c ,已知ABC ∆的面积为 ,12,cos ,4b c A -==- 则a 的值为 . 【答案】【解析】因为0A π<<,所以sin 4A ==,又1sin 242ABC S bc A bc ∆===∴=,解方程组224b c bc -=⎧⎨=⎩得6,4b c ==,由余弦定理得2222212cos 64264644a b c bc A ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭,所以8a =.【2015高考北京,理12】在ABC △中,4a =,5b =,6c =,则sin 2sin AC= .【答案】1【解析】222sin 22sin cos 2sin sin 2A A A a b c a C C c bc +-==⋅2425361616256⨯+-=⋅=⨯⨯【2015高考新课标1,理16】在平面四边形ABCD 中,∠A =∠B =∠C =75°,BC =2,则AB 的取值范围是 . 【答案】(62-,6+2)AB 的取值范围为(62-,6+2).【2015江苏高考,15】(本小题满分14分) 在ABC ∆中,已知ο60,3,2===A AC AB . (1)求BC 的长; (2)求C 2sin 的值 【答案】(17(243【2015高考湖南,理17】设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,,tan a b A =,且B 为钝角. (1)证明:2B A π-=;(2)求sin sin A C +的取值范围. 【答案】(1)详见解析;(2)29,]28. 【解析】(1)由tan a b A =及正弦定理,得sin sin cos sin A a AA bB ==,∴sin cos B A =,即sin sin()2B A π=+,又B 为钝角,因此(,)22A πππ+∈,故2B A π=+,即2B A π-=; (2)由(1)知,()C A B π=-+(2)2022A A πππ-+=->,∴(0,)4A π∈,于是sin sin sin sin(2)2A C A A π+=+-2219sin cos 22sin sin 12(sin )48A A A A A =+=-++=--+,∵04A π<<,∴20sin A <<221992(sin )488A <--+≤,由此可知sin sin A C +的取值范围是29]28.(2014·湖北卷)某实验室一天的温度(单位:℃)随时间t (单位:h)的变化近似满足函数关系:f (t )=10-3cos π12t -sin π12t ,t ∈[0,24).(1)求实验室这一天的最大温差.(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?即sin ⎝⎛⎭⎪⎫π12t +π3<-12.又0≤t <24,因此7π6<π12t +π3<11π6,即10<t <18.故在10时至18时实验室需要降温.(2014·江西卷)已知函数f (x )=sin(x +θ)+a cos(x +2θ),其中a ∈R,θ∈⎝ ⎛⎭⎪⎫-π2,π2.(1)当a =2,θ=π4时,求f (x )在区间[0,π]上的最大值与最小值;(2)若f ⎝ ⎛⎭⎪⎫π2=0,f (π)=1,求a ,θ的值.【解析】(1)f (x )=sin ⎝ ⎛⎭⎪⎫x +π4+2cos ⎝⎛⎭⎪⎫x +π2=22(sin x +cos x )-2sin x =22cos x -22sin x =sin ⎝ ⎛⎭⎪⎫π4-x .因为x ∈[0,π],所以π4-x ∈⎣⎢⎡⎦⎥⎤-3π4,π4,故f (x )在区间[0,π]上的最大值为22,最小值为-1. (2)由⎩⎪⎨⎪⎧f ⎝ ⎛⎭⎪⎫π2=0,f (π)=1,得⎩⎪⎨⎪⎧cos θ(1-2a sin θ)=0,2a sin 2θ-sin θ-a =1. 又θ∈⎝ ⎛⎭⎪⎫-π2,π2,知cos θ≠0, 所以⎩⎪⎨⎪⎧1-2a sin θ=0,(2a sin θ-1)sin θ-a =1,解得⎩⎪⎨⎪⎧a =-1,θ=-π6.(2014·四川卷)已知函数f (x )=sin ⎝ ⎛⎭⎪⎫3x +π4.(1)求f (x )的单调递增区间;(2)若α是第二象限角,f ⎝ ⎛⎭⎪⎫α3=45cos ⎝⎛⎭⎪⎫α+π4cos 2α,求cos α-sin α的值.当sin α+cos α=0时,由α是第二象限角,得α=3π4+2k π,k ∈Z,此时,cos α-sin α=- 2.当sin α+cos α≠0时,(cos α-sin α)2=54.由α是第二象限角,得cos α-sin α<0,此时cos α-sin α=-52. 综上所述,cos α-sin α=-2或-52. (2013·北京卷)在△ABC 中,a =3,b =2 6,∠B=2∠A. (1)求cos A 的值; (2)求c 的值.【解析】(1)因为a =3,b =2 6,∠B=2∠A, 所以在△ABC 中,由正弦定理得3sin A =2 6sin 2A .所以2sin Acos A sin A =2 63.故cos A =63. (2)由(1)知cos A =63,所以sin A =1-cos 2A =33. 又因为∠B=2∠A,所以cos B =2cos 2A -1=13.所以sin B =1-cos 2B =2 23.在△ABC 中,sin C =sin(A +B) =sin AcosB +cos Asin B =5 39. 所以c =a sin Csin A=5.(2013·全国卷)设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,(a +b +c)(a -b +c)=ac. (1)求B ; (2)若sin Asin C =3-14,求C.=32, 故A -C =30°或A -C =-30°,因此C =15°或C =45°. (2013·浙江卷)已知α∈R,sin α+2cos α=102,则tan 2α=( ) A.43 B.34 C .-34 D .-43 【答案】C【解析】由(sin α+2cos α)2=1022'得sin 2α+4sin αcos α+4cos 2α=104=52,4sin αcos α+1+3cos 2α=52,2sin 2α+1+3×1+cos 2α2=52,故2sin 2α=-3cos 2α2,所以tan2α=-34,选择C.(2013·重庆卷)4cos 50°-tan 40°=( ) A. 2 B.2+32C. 3 D .2 2-1 【答案】C1.在△ABC 中,AB =3,AC =1,B =30°,△ABC 的面积为32,则C =( ) A.30° B.45°C.60°D.75°解析 法一 ∵S △ABC =12·AB ·AC ·sin A =32,即12×3×1×sin A =32,∴sin A =1, 由A ∈(0°,180°),∴A =90°,∴C =60°.故选C. 法二 由正弦定理,得sin B AC =sin C AB ,即12=sin C 3,sin C =32,又C ∈(0°,180°),∴C =60°或C =120°. 当C =120°时,A =30°,S △ABC =34≠32(舍去).而当C =60°时,A =90°, S △ABC =32,符合条件,故C =60°.故选C. 答案 C2.在△ABC 中,角A ,B ,C 对应的边分别为a ,b ,c ,若A =2π3,a =2,b =233,则B 等于( )A.π3B.5π6C.π6或5π6D.π6解析∵A=2π3,a=2,b=233,∴由正弦定理asin A=bsin B可得,sin B=basin A=2332×32=12.∵A=2π3,∴B=π6.答案 D3.在△ABC中,cos2B2=a+c2c(a,b,c分别为角A,B,C的对边),则△ABC的形状为( ) A.等边三角形 B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形答案 B4.△ABC的内角A,B,C的对边分别为a,b,c,则“a>b”是“cos 2A<cos 2B”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件解析因为在△ABC中,a>b⇔sin A>sin B⇔sin2A>sin2B⇔2sin2A>2sin2B⇔1-2sin2A<1-2sin2B⇔cos 2A<cos 2B.所以“a>b”是“cos 2A<cos 2B”的充分必要条件.答案 C5.已知△ABC的内角A,B,C的对边分别为a,b,c,且c-bc-a=sin Asin C+sin B,则B等于( ) A.π6B.π4C.π3D.3π4答案 C解析 根据正弦定理a sin A =b sin B =csin C =2R ,得c -b c -a =sin A sin C +sin B =ac +b, 即a 2+c 2-b 2=ac ,得cos B =a 2+c 2-b 22ac =12,故B =π3,故选C.6.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若(a 2+c 2-b 2)tan B =3ac ,则角B 的值为________. 答案π3或2π3解析 由余弦定理,得a 2+c 2-b 22ac=cos B ,结合已知等式得cos B ·tan B =32, ∴sin B =32,∴B =π3或2π3. 7.在△ABC 中,若b =5,B =π4,tan A =2,则a =______.答案 2108.已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a =2,且(2+b )(sin A -sin B )=(c -b )sin C ,则△ABC 面积的最大值为________. 答案3解析 由正弦定理,可得(2+b )(a -b )=(c -b )·c . ∵a =2,∴a 2-b 2=c 2-bc ,即b 2+c 2-a 2=bc .由余弦定理,得cos A =b 2+c 2-a 22bc =12.∴sin A =32. 由b 2+c 2-bc =4,得b 2+c 2=4+bc . ∵b 2+c 2≥2bc ,即4+bc ≥2bc ,∴bc ≤4. ∴S △ABC =12bc ·sin A ≤3,即(S △ABC )max = 3.9.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a ≠b ,c =3,cos 2A -cos 2B =3sin A cos A -3sin B cos B . (1)求角C 的大小;(2)若sin A =45,求△ABC 的面积.由a <c ,得A <C ,从而cos A =35,故sin B =sin(A +C )=sin A cos C +cos A sin C=4+3310, 所以,△ABC 的面积为S =12ac sin B =83+1825.10.如图,在△ABC 中,B =π3,AB =8,点D 在BC 边上,且CD =2,cos∠ADC =17.(1)求sin∠BAD ; (2)求BD 、AC 的长.在△ABD 中,由正弦定理得 BD =AB ·sin∠BADsin∠ADB =8×3314437=3.在△ABC 中,由余弦定理得AC 2=AB 2+BC 2-2AB ·BC ·cos B=82+(2+3)2-2×8×5×12=49.所以AC =7.11.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且a 2-(b -c )2=(2-3)bc ,sin A sin B =cos 2C2,BC 边上的中线AM 的长为7.(1)求角A 和角B 的大小; (2)求△ABC 的面积.解 (1)由a 2-(b -c )2=(2-3)bc , 得a 2-b 2-c 2=-3bc ,∴cos A =b 2+c 2-a 22bc =32,(2)由(1)知,a =b ,由余弦定理得AM 2=b 2+(a2)2-2b ·a2·cos C =b 2+b 24+b 22=(7)2,解得b=2,故S △ABC =12ab sin C =12×2×2×32= 3.12.设f (x )=sin x cos x -cos 2⎝ ⎛⎭⎪⎫x +π4.(1)求f (x )的单调区间;精品文档. (2)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若f ⎝ ⎛⎭⎪⎫A 2=0,a =1,求△ABC 面积的最大值.解 (1)由题意知f (x )=sin 2x 2-1+cos ⎝ ⎛⎭⎪⎫2x +π22=sin 2x 2-1-sin 2x 2=sin 2x -12. 由-π2+2k π≤2x ≤π2+2k π,k ∈Z, 可得-π4+k π≤x ≤π4+k π,k ∈Z ; 由π2+2k π≤2x ≤3π2+2k π,k ∈Z, 可得π4+k π≤x ≤3π4+k π,k ∈Z . 所以f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤-π4+k π,π4+k π(k ∈Z ); 单调递减区间是⎣⎢⎡⎦⎥⎤π4+k π,3π4+k π(k ∈Z ). (2)由f ⎝ ⎛⎭⎪⎫A 2=sin A -12=0,得sin A =12, 由题意知A 为锐角,所以cos A =32. 由余弦定理a 2=b 2+c 2-2bc cos A ,可得1+3bc =b 2+c 2≥2bc ,即bc ≤2+3,且当b =c 时等号成立. 因此12bc sin A ≤2+34.所以△ABC 面积的最大值为2+34.。
(人教版)数学必修五:1《正弦定理和余弦定理(1)》ppt课件 公开课精品课件

2
3+1 4.
根据正弦定理,得 a=cssiinnCA=2ssiinn7650°°
= 22×3+23 1= 6( 3-1), 4
b=cssiinnCB=2ssiinn7455°°= 22×3+221=2( 3-1). 4
[方法总结] (1)已知任意两角和一边,解三角形的步骤: ①由三角形内角和定理求出第三个角; ②由正弦定理公式的变形,求另外的两边. (2)注意事项: 已知内角不是特殊角时,往往先求出其正弦值,再根据以 上步骤求解.
1.正弦定理 在一个三角形中,各边和它所对角的正弦的比相等,即
正弦定理的向量法证明: 证明:(向量法) 当△ABC 是锐角三角形时,如图(1)所示, 过点 A 作单位 向量 i 垂直于 AB,因为A→C=A→B+B→C,所以 i·A→C=i·A→B+i·B→C, 所以 b·cos(90°-A)=c·cos90°+a·cos(90°-B),即 bsinA=asinB, 得sianA=sibnB.同理可得sianA=sincC,所以sianA=sibnB=sincC.
1.任意三角形的内角和为________;三条边满足:两边之 和________第三边,两边之差________第三边,并且大边对 ________,小边对________.
2.直角三角形的三边长a,b,c(斜边)满足________定 理,即________.
[答案] 1.180° 大于 小于 大角 小角 2.勾股 a2 +b2=c2
运用正弦定理求有关三角形的面积问题
已知在△ABC 中,c=2 2,a>b,C=π4,tanA·tanB =6,试求三角形的面积.
[分析] 本题可先求 tanA,tanB 的值,由此求出 sinA 及 sinB, 再利用正弦定理求出 a,b 及三角形的面积.
正弦定理-高二数学人教版(必修5)

第一章 解三角形1.1 正弦定理和余弦定理1.1.1 正弦定理1.正弦定理在ABC △中,若角A ,B ,C 对应的三边分别是a ,b ,c ,则各边和它所对角的正弦的比相等,即____________.正弦定理对任意三角形都成立.2.解三角形一般地,把三角形的三个角A ,B ,C 和它们的对边a ,b ,c 叫做三角形的____________.已知三角形的几个元素求其他元素的过程叫做____________.K 知识参考答案:1.sin sin sin a b c ==A B C2.元素 解三角形K —重点 正弦定理的变形和推广、正弦定理在解三角形中的应用 K —难点 三角形解的个数的探究、三角形形状的判断K —易错 解三角形时要明确角的取值范围,同时注意对角的讨论正弦定理的常见变形及推广(1)sin sin sin ,,,sin sin ,sin sin ,sin sin sin sin sin A a C c B ba Bb A a Cc A b C c B B b A a C c ======. (2)sin sin sin sin sin sin sin sin sin sin sin sin a b c a b a c b c a b cA B C A B A C B C A B C+++++======+++++. (3)::sin :sin :sin a b c A B C =. (4)正弦定理的推广:2sin sin sin a b cR A B C===,其中R 为ABC △外接圆的半径. (1)已知△ABC 中,sin :sin :sin =1:2:3A B C ,则a:b:c =_____________;(2)已知△ABC 中,∠A =60︒,3a ,则++sin +sin +sin a b cA B C=_____________.【答案】(1)1:2:3;(2)2.【解析】(1)根据正弦定理的变形,可得=sin :sin :sin =1:2:3a:b:c A B C . (2)方法1:设=sin sin a b A B ==(>0)sin ck k C,则有sin sin sin a k Ab k Bc k C ===,,, 从而sin sin sin sin sin sin sin sin sin a b c k A k B k C k A B C A B C ++++++++==,又32sin sin60a k A ===︒,所以sin sin sin a b c A B C ++++=2. 方法2:根据正弦定理的变形,可得2sin sin sin sin a b c aA B C A++++==.【名师点睛】熟记正弦定理的变形,可使解题过程更加简捷,从而达到事半功倍的效果.在ABC △中,求证:22sin 2sin 22sin a B b A ab C +=.【答案】证明见解析.【解析】设ABC △外接圆的半径为R ,则2sin ,2sin ,a R A b R B == 于是222222sin 2sin 2(2sin )sin 2(2sin )sin 28sin sin (sin cos cos sin )8sin sin sin 22sin 2sin sin 2sin ,a Bb A R A B R B A R A B A B A B R A B CR A R B C ab C +=+=+==⋅⋅⋅=所以22sin 2sin 22sin a B b A ab C +=. 【解题技巧】===2sin sin sin a b c R A B C的两种变形的应用: (1)(边化角)2sin ,2sin ,2sin a R A b R B c R C ===; (2)(角化边)sin ,sin ,sin 222a b cA B C R R R===. 正弦定理在解三角形中的应用、三角形解的个数的探究1.正弦定理可以用来解决下列两类解三角形的问题:(1)已知两角和任意一边,求其他的边和角; (2)已知两边和其中一边的对角,求其他的边和角. 2.三角形解的个数的探究(以已知a b ,和A 解三角形为例) (1)从代数角度来看①若sin sin 1b AB=a >,则满足条件的三角形的个数为0,即无解; ②若sin sin 1b AB=a=,则满足条件的三角形的个数为1;③若sin sin 1b AB=a<,则满足条件的三角形的个数为1或2. 注:对于(3),由sin 0sin 1b AB=a<<可知B 可能为锐角,也可能为钝角,此时应由“大边对大角”、“三角形内角和等于180°”等进行讨论. (2)从几何角度来看①当A 为锐角时:一解一解 两解 无解②当A 为钝角或直角时:一解 一解 无解 无解(1)已知在ABC △中,10,45,30c A C ==︒=︒,则a =_______,b =_______,B =_______;(2)已知在ABC △中,3,60,1b B c ==︒=,则a =_______,A =_______,C =_______; (3)已知在ABC △中,6,45,2c A a ==︒=,求b 和,B C .【答案】(1)102,5652+,105︒;(2)2,90︒,30︒;(3)见解析. 【解析】(1)10,45,30180()105c A C B A C ==︒=︒∴=︒-+=︒,,由sin sin a c A C =,得sin 10sin 45102sin sin 30c A a C ⨯︒===︒, 由sin sin b c B C =,得sin 10sin10562205652sin sin 304c B b C ⨯︒+===⨯=+︒.(2)∵sin 1sin 601,sin sin sin 23b c c B C B C b ⨯︒=∴===, ,60,b c B C B >=︒∴<,C 为锐角,30,90C A ∴=︒=︒,∴222=+=c b a .(3)sin 6sin 453,sin sin sin 22a c c A C A C a ⨯︒=∴===, sin ,60c A a c C <<∴=︒或120︒,∴当60C =︒时,sin 6sin 7575,31sin sin 60c B B b C︒=︒===+︒,当120C =︒时,sin 6sin1515,31sin sin 60c B B b C ︒=︒===-︒. 31,75,60b B C ∴=+=︒=︒或31,15,120b B C =-=︒=︒.【解题技巧】(1)已知三角形的两角与一边解三角形时,由三角形内角和定理可以计算出三角形的另一角,由正弦定理可计算出三角形的另两边.(2)已知两边和其中一边的对角解三角形时,先用正弦定理求出另一边所对的角的正弦值,若这个角不是直角,则利用三角形中“大边对大角”看能否判断所求这个角是锐角,①当已知的角为大边所对的角时,则能判断另一边所对的角为锐角;②当已知的角为小边所对的角时,则不能判断,此时就有两解,再分别求解即可;③然后由三角形内角和定理求出第三个角;④最后根据正弦定理求出第三条边.三角形形状的判断判断三角形形状的常用方法——边化角,已知条件中同时包含边角关系,判断三角形形状时,将边化为角,从三角变换的角度来研究角的关系和特征,进而判断三角形的形状.一般来说,这种方法能够判断的三角形都是特殊的三角形,如直角三角形、等腰三角形、等边三角形、等腰直角三角形.在ABC △中,已知sin sin sin a b Ba B A+=-,且cos()cos 1cos 2A B C C -+=-,则ABC △是 A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形【答案】B【解析】设ABC △的外接圆半径为R ,由正弦定理的推广,得sin 2a A R =,sin 2bB R=,代入sin sin sin a b B a B A +=-,可得a b ba b a+=-,即22b a ab -=. 因为cos()cos 1cos 2A B C C -+=-,所以2cos()cos()2sin A B A B C -++=, 即2sin sin sin A B C =. 由正弦定理的推广可得2()222a b cR R R⋅=,所以2ab c =, 由22b a ab -=及2ab c =可得222b a c =+,所以ABC △是直角三角形. 故选B .【名师点睛】注意到a ,b ,c 在条件式中是齐次线性关系,因此可以考虑利用正弦定理将边化为角.通过角的特征或者关系来判断三角形的形状.忽略角的取值范围而出错在ABC △中,若3C B =,求cb的取值范围. 【错解】由正弦定理,可得22sin sin 3sin 2cos cos 2sin =2cos cos 24cos 1sin sin sin c C B B B B B B B B b B B B +===+=-, 220cos 1,14cos 13B B ≤<∴-≤-<,由0,0b c >>,可得03cb<<. 故cb的取值范围为(0,3). 【错因分析】错解中没有考虑角B 的取值范围,误认为角B 的取值范围为(0,180)︒︒. 【正解】由正弦定理可得22sin sin 3sin 2cos cos 2sin =2cos cos 24cos 1sin sin sin c C B B B B B B B B b B B B +===+=-, 2180,3,045,cos 12A B C C B B B ++=︒=∴︒<<︒<<, 214cos 13B ∴≤-<,即13cb<<, 故cb的取值范围为(1,3). 【名师点睛】解三角形时要注意三角形的内角为正角且必须满足三角形内角和定理,这是解题中的隐含条件,应特别注意.忽略对角的讨论而出错已知在ABC △中,4,22,30,a b B ===︒ 求角,A C 和边c .【错解】由正弦定理sin sin a b A B =可得422sin sin 30A =︒, 2sin ,452A A ∴==︒,1803045105C ∴=︒-︒-︒=︒,62,sin105sin sin 4c b C B +=︒=,sin 232sin b C c B ∴==+. 【错因分析】错解中由正弦定理求出角A 的正弦值后误认为角A 是锐角,从而导致错误. 【正解】由正弦定理,sin sin a b A B =得422sin sin 30A =︒, 2sin ,2A ∴=,45a b A >∴=︒或135︒.当45A =︒时,1803045105C =︒-︒-︒=︒,62sin ,sin105,232sin sin 4sin c b b Cc C B B+=︒=∴==+;当135A =︒时,1803013515C =︒-︒-︒=︒,62sin ,sin15,232sin sin 4sin c b b Cc C B B-=︒=∴==-. 综上,45,105,232A C c =︒=︒=+或135,15,232A C c =︒=︒=-.【名师点睛】在ABC △中,已知两边和其中一边的对角解三角形时,可先用正弦定理求出另一边的对角,此时解的个数可能不确定,应注意讨论,避免漏解导致错误.1.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,83,6,60a b A ===︒,则sin B = A .2B 6C 2D 32.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若a =45B =︒,2b =,则A =A .30︒或150︒B .30︒C .150︒D .45︒3.在ABC △中,若∠A =60°,∠B =45°,BC =AC =A .B .CD 4.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,已知A :B :C =1:2:3,则a :b :c =A .1:2:3B .C .D .5.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,b =,4B π∠=,tan A =,则a =A .210B .C .10D .26.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若cos cos sin b C c B a A +=,则ABC △的形状为A .锐角三角形B .直角三角形C .钝角三角形D .不能确定7.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,15,18,30a b A ===︒,则此三角形解的个数为 A .0 B .1 C .2D .不能确定8.已知ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,且cos A :cos B =b :a ,则ABC △是 A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形9.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若8a =,60B =︒,75C =︒,则b =______________.10.在ABC △中,角A ,C 的对边分别为a ,c ,其中1=a ,33=c 3A π=,则角=C ______________.11.在ABC △中,若B =30°,AB =23,AC =2,则ABC △的周长为______________. 12.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,己知A −C =90°,a +c =2b ,求C .13.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若a =52b ,A =2B ,则cos B = A 5 B 5C 5 D 5 14.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,已知π,3,23A a b ===,则B = A .π6 B .π4 C .π3D .π215.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,已知π3,6,3a b A ===,则角B 等于 A .π4B .3π4C .π4或3π4D .以上都不正确16.在ABC △中,角A ,B ,C 的对边为a ,b ,c ,若cos (2)cos c a B a b A -=-,则ABC △是A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰或直角三角形17.在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若cos cos cos A B Ca b c==,则ABC △是 A .有一内角是30°的三角形 B .等边三角形C .等腰直角三角形D .有一内角是30°的等腰三角形18.在ABC △中,已知31,6,15b c B =-==︒,则边长a =A .31+或2B .31+C .2D .2319.在ABC △中,已知2AB AC =,30B =︒,则A =______________.20.如图所示,在一个坡度一定的山坡AC 的顶上有一高度为25m 的建筑物CD .为了测量该山坡相对于水平地面的坡角θ,在山坡的A 处测得15DAC ∠=︒,沿山坡前进50m 到达B 处,又测得45DBC ∠=︒.根据以上数据计算可得cos θ=______________.21.如图,在ABC △中,点D 在BC 边上,π72cos 42CAD AC ADB ∠==∠=,,. (1)求sin C 的值;(2)若5BD =,求AD 的长.22.(2017山东理)在ABC △中,角A ,B ,C 的对边分别为a ,b ,c .若ABC △为锐角三角形,且满足sin (12cos )2sin cos cos sin B C A C A C +=+,则下列等式成立的是 A .2a b = B .2b a = C .2A B =D .2B A =23.(2017新课标全国Ⅰ文)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin sin (sin cos )0B A C C +-=,a =2,c 2,则C =A .π12 B .π6 C .π4D .π324.(2017新课标全国Ⅱ文)ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,若2cos cos cos b B a C c A =+,则B =______________.25.(2017新课标全国Ⅲ文)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b ,c =3,则A =______________.26.(2018北京理)在△ABC 中,7a =,8b =,1cos 7B =-. (1)求A ∠;(2)求AC 边上的高.1.【答案】D【解析】∵83,6,60a b A ===,由sin sin a b A B =得sin 3sin .8b A B a ==故选D . 2.【答案】B【解析】在ABC △中,由sin sin a b A B =得21sin sin sin 4522a A Bb ===︒,由于a b <,所以A B <,所以30A =︒,故选B . 3.【答案】B【解析】由正弦定理得23sin 60sin 45AC =︒︒,所以AC =23sin 452 2.sin 60︒=︒故选B .4.【答案】C【解析】因为在ABC △中,A +B +C =π,且A :B :C =1:2:3,所以A =6π,B =3π,C =2π,由正弦定理的变形,得a :b :c =sin A :sin B :sin C 13=1=22::1:3:2.故选C .6.【答案】B【解析】由已知可得2sin cos cos sin sin B C B C A +=,∴2sin()sin B C A +=,∴sin 1A =,∴π2A =,三角形为直角三角形.故选B . 7.【答案】C【解析】由正弦定理可得sin 18sin 303sin 155b A B a ︒===,因为b a >,所以30B A >=︒,所以角B 可能是锐角,也可能是钝角,所以此三角形有两解,故选C .8.【答案】D【解析】由正弦定理可得cos sin cos sin A b BB a A==,即sin A cos A =sin B cos B ,所以sin2A =sin2B ,即2A =2B 或2A +2B =π,即A =B 或A +B =2π,故ABC △是等腰或直角三角形.故选D .9.【答案】46【解析】∵60B =︒,75C =︒,∴45A =︒,∵sin sin a bA B=,∴82322b=,∴46b =. 10.【答案】π6【解析】由正弦定理可得313πsin sin 3C =,即212333sin =⨯=C ,所以π6C =或5π6,又a c <,所以π6C =.12.【答案】o =15C .【解析】由正弦定理可得sin sin 2A C B +=,又由于o o90=180()A C B A C -=-+,,故cos sin 2)C C A C +=+o 22)22C C =+=,即22sin cos 2,22C C C +=o cos(45)cos 2C C -=. 因为o o 090C <<,所以o 2=45C C -,即o =15C . 13.【答案】B【解析】由正弦定理,得sin sin a A b B =,所以a =52b 可化为sin sin A B =52.又A =2B ,所以sin 2sin B B =52,所以cos B =54.故选B . 14.【答案】D【解析】在ABC △中,由正弦定理可得2πsin sin sin 133b B A a ==⨯=,又0πB <<,所以B =π2,故选D . 15.【答案】 A【解析】在ABC △中,∵π3,6,3a b A ===,∴36πsin sin sin sin 3a b A B B =⇒=2sin 2B ⇒=,又63b a =<=,∴π03B A <<=,∴π4B =,故选A .16.【答案】D【解析】由正弦定理和已知条件可得sin sin cos 2sin cos sin cos C A B A A B A -=-, 所以sin()sin cos 2sin cos sin cos ,A B A B A A B A +-=- 即cos (sin sin )0A B A -=,所以cos 0A =或sin sin 0B A -=,即90A =︒或=A B .故ABC △是等腰三角形或直角三角形. 故选D .18.【答案】A【解析】由正弦定理可得,sin 63sin 231c B C b ===-, 在ABC △中,c b >,60C ∴=或120.当60C =时,105A =︒,sin 6sin10531sin c A a C ︒∴===; 当120C =时,45A =︒,此时sin 6sin 452sin c A a C ︒∴===. 综上,可得31a =或2.故选A .19.【答案】105︒或15︒【解析】由正弦定理得sin sin AB AC C B =,得sin 2sin 2sin 302AB B C AC ==︒=, 由AB AC >,得C B >,所以45C =︒或135︒,从而105A =︒或15︒.21.【答案】(1)45;(2)22. 【解析】(1)因为2cos ADB ∠=72sin ADB ∠= 又π4CAD ∠=,所以π4C ADB =∠-, 所以πππ722224sin sin()sin coscos sin 4445C ADB ADB ADB =∠-=∠⋅-∠⋅==. (2)在ACD △中,由sin sin AD ACC ADC =∠,可得sin 22sin AC C AD ADC⋅==∠. 22.【答案】A【解析】由题意知sin()2sin cos 2sin cos cos sin A C B C A C A C ++=+, 所以2sin cos sin cos 2sin sin 2B C A C B A b a =⇒=⇒=,故选A . 23.【答案】B【解析】由sin()sin (sin cos )0A C A C C ++-=可得sin cos cos sin sin sin A C A C A C ++-sin cos 0A C =,即πsin (sin cos )2sin()04C A A C A +=+=,所以3π4A =.由正弦定理sin sin a c A C =可得223πsin sin 4C =,即1sin 2C =,因为c a <,所以C A <,所以π6C =,故选B . 24.【答案】π3【解析】由正弦定理可得12sin cos sin cos sin cos sin()sin cos 2B B A C C A A C B B =+=+=⇒=π3B ⇒=. 25.【答案】75︒【解析】由正弦定理sin sin b c B C=,可得36sin 22sin 32b C Bc ⨯===,结合b c <可得45B =︒,则18075A B C =︒--=︒. 26.【答案】(1)π3A ∠=;(2)AC 边上的高为332. 【解析】(1)在△ABC 中,因为1cos 7B =-,所以π(,)2B ∈π,所以243sin 1cos 7B B =-=. 由正弦定理7sin sin sin a b A B A =⇒=8437,所以3sin 2A =. 因为π(,)2B ∈π,所以π(0,)2A ∈,所以π3A ∠=(2)在△ABC 中,3114333sin sin()sin cos sin cos ()272714C A B A B B A =+=+=⨯-+⨯=. 如图所示,在△ABC 中,sin h C BC =,所以3333sin 7142h BC C =⋅=⨯=, 所以AC 边上的高为332.。
人教版高中必修51.1正弦定理和余弦定理课程设计

人教版高中必修5-1.1 正弦定理和余弦定理课程设计一、引言正弦定理和余弦定理是高中数学中的基础概念,在解决三角形相关问题时经常会用到。
本课程设计将围绕正弦定理和余弦定理展开,旨在通过讲解和丰富的实例,帮助学生深入理解这两个概念,提高学生解决实际问题的能力。
二、教学目标本课程设计主要的教学目标包括:1.理解正弦定理和余弦定理的定义和含义,并能运用正确公式计算相关量;2.能解决使用正弦定理和余弦定理求解三角形中各角度和边长的问题,并能熟练运用所学知识解决类似问题;3.培养学生对数学概念的深刻理解,提高数学分析、解题和推理的能力。
三、教学重点和难点1. 教学重点•正弦定理和余弦定理的定义和含义;•正弦定理和余弦定理的公式和运用;•求解三角形相关问题的思路和方法。
2. 教学难点•正弦定理和余弦定理的理解与运用;•正弦定理和余弦定理的推导过程说明;•如何分析实际问题,确定合适的求解方法。
四、教学内容和方法1. 教学内容1) 正弦定理•正弦定理的概念和含义;•正弦定理的公式和运用;•正弦定理的推导过程说明;•正弦定理的实际应用。
2) 余弦定理•余弦定理的概念和含义;•余弦定理的公式和运用;•余弦定理的推导过程说明;•余弦定理的实际应用。
2. 教学方法本课程设计将采用以下教学方法:•讲授法:通过对正弦定理和余弦定理的原理、公式和运用的讲解,向学生阐述相关概念并理解其原理;•实例分析法:通过较为典型的实例分析、讨论问题,帮助学生理解正弦定理和余弦定理的实际应用;•独立思考法:通过举例让学生通过自己的思考和分析实际问题,确定求解方法解决问题,培养学生分析问题、解决问题的能力。
五、教学评价教学评价主要从以下方面进行:•学生课堂发言和问题讨论表现;•学生课后作业完成情况;•学生课后课程练习题完成情况以及参与竞赛、奥数活动表现;•学生在考试中的表现。
六、教学资源为了更好地实行授课过程中,需要准备以下资源:•课程讲义;•课件尠存储设备:如电脑、U盘等;•相关参考资料:如教材、习题集等。
人教版必修五1.1.1正弦、余弦定理课件

B. acos A bcos B
C. asin B bsin A
D. acos B bcos A
(2)若A,B,C是⊿ABC的三个内角,则
sinA+sinB__>__sinC.
(3)在ABC中,C 2B,则sin 3B 等于(B) sin B
A.b/a
B.a/b
C.a/c
D.c/a
正弦定理、余弦定理
正弦定理、余弦定理
例题讲授
例1,在ABC中,已知A 32.0, B 81.8, a 42.9cm,解三角形 解:根据三角形内角和定理, C 180 ( A B) 180 (32.0 81.8 ) 66.2 根据正弦定理,b asin B 42.9sin 81.8 80.1(cm)
c a sin C 20sin 24 13(cm). sin A sin 40
正弦定理、余弦定理
例题讲授
例3 在 ABC 中,B 45,C 60,a 2( 3 1) ,求
ABC的面积S.
解: A 180 (B C ) 75
A
∴由正弦定理得 b a sin B 2(
3
1)(
练习:
(1)在 ABC 中,一定成立的等式是( C )
A. asin A bsinB
B. acos A bcos B
C. asin B bsin A
D. acos B bcos A
(2)在 ABC中,若
a cos
A
b cos B
c cos C
,则 ABC 是(
D)
2
2
2
A.等腰三角形
B.等腰直角三角形
sin A sin 32.0 根据正弦定理,c asin C 42.9sin 66.2 74.1(cm)
高中数学必修五第一章《正弦定理和余弦定理》1.1.1正弦定理

§1.1 正弦定理和余弦定理1.1.1 正弦定理学习目标 1.掌握正弦定理的内容及其证明方法.2.能运用正弦定理与三角形内角和定理解决简单的解三角形问题.知识点一 正弦定理思考1 如图,在Rt △ABC 中,a sin A ,b sin B ,csin C分别等于什么?答案a sin A =b sin B =c sin C=c . 思考2 在一般的△ABC 中,a sin A =b sin B =csin C 还成立吗?答案 在一般的△ABC 中,a sin A =b sin B =csin C 仍然成立.梳理 在任意△ABC 中,都有a sin A =b sin B =c sin C,这就是正弦定理. 特别提醒:正弦定理的特点(1)适用范围:正弦定理对任意的三角形都成立.(2)结构形式:分子为三角形的边长,分母为相应边所对角的正弦的连等式.(3)刻画规律:正弦定理刻画了三角形中边与角的一种数量关系,可以实现三角形中边角关系的互化.知识点二 解三角形一般地,把三角形的三个角A ,B ,C 和它们的对边a ,b ,c 叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.1.对任意△ABC ,都有a sin A =b sin B =csin C.(√)2.任意给出三角形的三个元素,都能求出其余元素.(×) 3.在△ABC 中,已知a ,b ,A ,则三角形有唯一解.(×)类型一 正弦定理的证明例1 在钝角△ABC 中,证明正弦定理. 考点 正弦定理及其变形应用 题点 正弦定理的理解证明 如图,过C 作CD ⊥AB ,垂足为D ,D 是BA 延长线上一点,根据正弦函数的定义知,CD b =sin ∠CAD =sin(180°-A )=sin A ,CD a =sin B . ∴CD =b sin A =a sin B . ∴a sin A =bsin B. 同理,b sin B =csin C .故a sin A =b sin B =c sin C. 反思与感悟 (1)用正弦函数定义沟通边与角内在联系,充分挖掘这些联系可以使你理解更深刻,记忆更牢固.(2)要证a sin A =bsin B ,只需证a sin B =b sin A ,而a sin B ,b sin A 都对应CD .初看是神来之笔,仔细体会还是有迹可循的,通过体会思维的轨迹,可以提高我们的分析解题能力.跟踪训练1 如图,锐角△ABC 的外接圆O 半径为R ,角A ,B ,C 对应的边分别为a ,b ,c ,证明:asin A=2R .考点 正弦定理及其变形应用 题点 正弦定理的理解证明 连接BO 并延长,交外接圆于点A ′,连接A ′C , 则圆周角A ′=A .∵A ′B 为直径,长度为2R , ∴∠A ′CB =90°, ∴sin A ′=BC A ′B =a 2R ,∴sin A =a 2R ,即asin A =2R .类型二 已知两角及一边解三角形例2 在△ABC 中,已知A =30°,B =60°,a =10,解三角形. 考点 用正弦定理解三角形 题点 已知两角及一边解三角形 解 根据正弦定理,得b =a sin B sin A =10sin 60°sin 30°=10 3. 又C =180°-(30°+60°)=90°. ∴c =a sin C sin A =10sin 90°sin 30°=20.反思与感悟 (1)正弦定理实际上是三个等式:a sin A =b sin B ,b sin B =c sin C ,a sin A =csin C ,每个等式涉及四个元素,所以只要知道其中的三个就可以求另外一个.(2)因为三角形内角和为180°,所以已知两角一定可以求出第三个角. 跟踪训练2 在△ABC 中,已知a =18,B =60°,C =75°,求b 的值. 考点 用正弦定理解三角形 题点 已知两角及一边解三角形 解 根据三角形内角和定理,得A =180°-(B +C )=180°-(60°+75°)=45°. 根据正弦定理,得b =a sin B sin A =18sin 60°sin 45°=9 6.类型三 已知两边及其中一边的对角解三角形例3 在△ABC 中,已知c =6,A =45°,a =2,解三角形. 考点 用正弦定理解三角形题点 已知两边及其中一边对角解三角形解 ∵a sin A =c sin C ,∴sin C =c sin A a =6sin 45°2=32,∵C ∈(0°,180°),∴C =60°或C =120°. 当C =60°时,B =75°,b =c sin B sin C =6sin 75°sin 60°=3+1; 当C =120°时,B =15°,b =c sin B sin C =6sin 15°sin 120°=3-1. ∴b =3+1,B =75°,C =60°或b =3-1,B =15°,C =120°. 引申探究若把本例中的条件“A =45°”改为“C =45°”,则角A 有几个值? 解 ∵a sin A =c sin C ,∴sin A =a sin C c =2·226=33.∵c =6>2=a ,∴C >A .∴A 为小于45°的锐角,且正弦值为33,这样的角A 只有一个. 反思与感悟 已知三角形两边和其中一边的对角解三角形的方法:首先用正弦定理求出另一边所对的角的正弦值,若这个角不是直角,当已知的角为大边所对的角时,则能判断另一边所对的角为锐角,当已知的角为小边所对的角时,则不能判断,此时就有两组解,再分别求解即可;然后由三角形内角和定理求出第三个角;最后根据正弦定理求出第三条边. 跟踪训练3 在△ABC 中,若a =2,b =2,A =30°,则C =________. 考点 用正弦定理解三角形题点 已知两边及其中一边对角解三角形 答案 105°或15°解析 由正弦定理a sin A =b sin B ,得sin B =b sin A a =2sin 30°2=22.∵B ∈(0°,180°),∴B =45°或135°,∴C =180°-45°-30°=105°或C =180°-135°-30°=15°.1. 在△ABC 中,一定成立的等式是( ) A .a sin A =b sin B B .a cos A =b cos B C .a sin B =b sin AD .a cos B =b cos A考点 正弦定理及其变形应用 题点 正弦定理的变形应用 答案 C解析 由正弦定理a sin A =bsin B ,得a sin B =b sin A ,故选C.2.在△ABC 中,sin A =sin C ,则△ABC 是( ) A .直角三角形 B .等腰三角形 C .锐角三角形D .钝角三角形 考点 用正弦定理解三角形题点 利用正弦定理进行边角互化解三角形 答案 B解析 由sin A =sin C 及正弦定理,知a =c , ∴△ABC 为等腰三角形.3.在△ABC 中,已知a =8,B =60°,C =75°,则b 等于( ) A .4 2 B .4 3 C .4 6D .4考点 用正弦定理解三角形 题点 已知两角及一边解三角形 答案 C解析 易知A =45°,由a sin A =b sin B 得b =a sin B sin A=8×3222=4 6. 4.在△ABC 中,a =3,b =2,B =π4,则A =________.考点 用正弦定理解三角形题点 已知两边及其中一边对角解三角形 答案 π3或2π3解析 由正弦定理,得sin A =a sin Bb=3×222=32, 又A ∈(0,π),a >b ,∴A >B ,∴A =π3或2π3.5.在△ABC 中,已知a =5,sin C =2sin A ,则c =________. 考点 正弦定理及其变形应用 题点 正弦定理的变形应用 答案 2 5解析 由正弦定理,得c =a sin Csin A=2a =2 5.1. 正弦定理的表示形式:a sin A =b sin B =csin C =2R ,或a =k sin A ,b =k sin B ,c =k sin C (k >0). 2. 正弦定理的应用范围(1)已知两角和任一边,求其他两边和其余一角. (2)已知两边和其中一边的对角,求另一边和其余两角.3. 已知三角形两边和其中一边的对角解三角形的方法 (1)首先由正弦定理求出另一边对角的正弦值.(2)如果已知的角为大边所对的角,由三角形中大边对大角、大角对大边的法则能判断另一边所对的角为锐角,由正弦值可求唯一锐角.(3)如果已知的角为小边所对的角,则不能判断另一边所对的角为锐角,这时由正弦值可求得两个角,要分类讨论.一、选择题1.在△ABC 中,a =5,b =3,则sin A ∶sin B 的值是( ) A.53 B.35 C.37 D.57 考点 用正弦定理解三角形题点 利用正弦定理进行边角互化解三角形 答案 A解析 根据正弦定理,得sin A sin B =a b =53.2.在△ABC 中,a =b sin A ,则△ABC 一定是( ) A .锐角三角形 B .直角三角形 C .钝角三角形D .等腰三角形考点 正弦定理及其变形应用 题点 正弦定理的变形应用 答案 B解析 由题意有a sin A =b =bsin B,则sin B =1,又B ∈(0,π),故角B 为直角,故△ABC 是直角三角形. 3.在△ABC 中,若sin A a =cos Cc ,则C 的值为( )A .30°B .45°C .60°D .90° 考点 正弦定理及其变形应用 题点 正弦定理的变形应用 答案 B解析 由正弦定理知sin A a =sin Cc ,∴sin C c =cos Cc,∴cos C =sin C ,∴tan C =1, 又∵C ∈(0°,180°),∴C =45°,故选B.4.在△ABC 中,若A =105°,B =45°,b =22,则c 等于( ) A .1 B .2 C. 2 D. 3 考点 用正弦定理解三角形 题点 已知两角及一边解三角形 答案 B解析 ∵A =105°,B =45°,∴C =30°. 由正弦定理,得c =b sin C sin B =22sin 30°sin 45°=2.5.在△ABC 中,a =15,b =10,A =60°,则cos B 等于( ) A .-223 B.223 C .-63 D.63考点 用正弦定理解三角形题点 已知两边及其中一边对角解三角形 答案 D解析 由正弦定理,得15sin 60°=10sin B ,∴sin B =10sin 60°15=10×3215=33. ∵a >b ,∴A >B ,又∵A =60°,∴B 为锐角. ∴cos B =1-sin 2B =1-⎝⎛⎭⎫332=63. 6.在△ABC 中,已知A =π3,a =3,b =1,则c 的值为( )A .1B .2 C.3-1 D. 3 考点 用正弦定理解三角形题点 已知两边及其中一边对角解三角形 答案 B解析 由正弦定理a sin A =bsin B,可得3sinπ3=1sin B ,∴sin B =12,由a >b ,得A >B ,∴B ∈⎝⎛⎭⎫0,π3,∴B =π6. 故C =π2,由勾股定理得c =2.7.在△ABC 中,B =π4,BC 边上的高等于13BC ,则sin A 等于( )A.310B.1010C.55D.31010 考点 用正弦定理解三角形 题点 正弦定理解三角形综合 答案 D解析 如图,设BC 边上的高为AD ,不妨令AD =1.由B =π4,知BD =1.又AD =13BC =BD ,∴DC =2,AC =12+22= 5.由正弦定理知,sin ∠BAC =sin B ·BC AC =225·3=31010.8.在△ABC 中,若A =60°,B =45°,BC =32,则AC 等于( ) A .4 3 B .2 3 C. 3 D.32考点 用正弦定理解三角形 题点 已知两角及一边解三角形 答案 B解析 由正弦定理得,BC sin A =AC sin B ,即32sin 60°=AC sin 45°,所以AC =3232×22=23,故选B.二、填空题9.在△ABC 中,若C =2B ,则cb的取值范围为________.考点 用正弦定理解三角形题点 利用正弦定理、三角变换解三角形 答案 (1,2)解析 因为A +B +C =π,C =2B ,所以A =π-3B >0,所以0<B <π3,所以12<cos B <1.因为c b =sin C sin B =sin 2Bsin B =2cos B ,所以1<2cos B <2,故1<cb<2.10.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若cos A =45,cos C =513,a =1,则b =_____.考点 用正弦定理解三角形 题点 已知两角及一边解三角形 答案2113解析 在△ABC 中,由cos A =45,cos C =513,可得sin A =35,sin C =1213,sin B =sin(A +C )=sin A cos C +cos A ·sin C =6365,又a =1,由正弦定理得b =a sin B sin A =2113.11.锐角三角形的内角分别是A ,B ,C ,并且A >B .则下列三个不等式中成立的是______. ①sin A >sin B ; ②cos A <cos B ;③sin A +sin B >cos A +cos B . 考点 用正弦定理解三角形题点 利用正弦定理、三角变换解三角形 答案 ①②③解析 A >B ⇔a >b ⇔sin A >sin B ,故①成立. 函数y =cos x 在区间[0,π]上是减函数, ∵A >B ,∴cos A <cos B ,故②成立. 在锐角三角形中,∵A +B >π2,∴0<π2-B <A <π2,函数y =sin x 在区间⎣⎡⎦⎤0,π2上是增函数, 则有sin A >sin ⎝⎛⎭⎫π2-B ,即sin A >cos B , 同理sin B >cos A ,故③成立.三、解答题12.已知在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,c =10,A =45°,C =30°,求a ,b 和B .考点 用正弦定理解三角形题点 已知两角及一边解三角形解 ∵a sin A =c sin C, ∴a =c sin A sin C =10sin 45°sin 30°=10 2. B =180°-(A +C )=180°-(45°+30°)=105°.又∵b sin B =c sin C, ∴b =c sin B sin C =10sin 105°sin 30°=20sin 75° =20×6+24=5(6+2). 13.在△ABC 中,A =60°,a =43,b =42,求B .考点 用正弦定理解三角形题点 已知两边及其中一边对角解三角形解 由正弦定理a sin A =b sin B ,得sin B =22, ∵a >b ,∴A >B .∴B 只有一解,∴B =45°.四、探究与拓展14.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,a =x ,b =2,B =45°.若△ABC 有两解,则x 的取值范围是( )A .(2,+∞)B .(0,2)C .(2,22)D .(2,2)考点 用正弦定理解三角形题点 已知两边及其中一边对角解三角形答案 C解析 因为△ABC 有两解,所以a sin B <b <a ,即x sin 45°<2<x ,所以2<x <22,故选C.15.已知下列各三角形中的两边及其中一边的对角,判断三角形是否有解,有解的作出解答.(1)a =10,b =20,A =80°;(2)a =23,b =6,A =30°.考点 用正弦定理解三角形题点 已知两边及其中一边对角解三角形解 (1)a =10,b =20,a <b ,A =80°<90°,讨论如下:∵b sin A =20sin 80°>20sin 60°=103,∴a <b sin A ,∴本题无解.(2)a =23,b =6,a <b ,A =30°<90°,∵b sin A =6sin 30°=3,a >b sin A ,∴b sin A <a <b ,∴本题有两解.由正弦定理得sin B =b sin A a =6sin 30°23=32, 又∵B ∈(0°,180°),∴B =60°或B =120°.当B =60°时,C =90°,c =a sin C sin A =23sin 90°sin 30°=43; 当B =120°时,C =30°,c =a sin C sin A =23sin 30°sin 30°=2 3. ∴当B =60°时,C =90°,c =43;当B =120°时,C =30°,c =2 3.。
新人教A版必修5高中数学1.1正弦定理和余弦定理学案
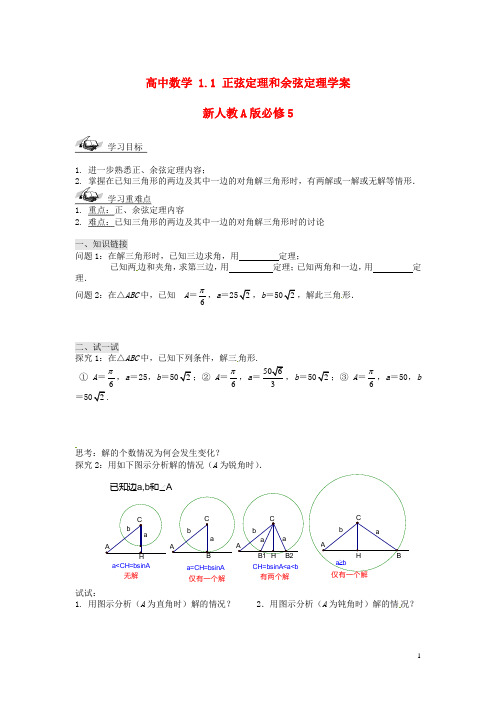
高中数学 1.1 正弦定理和余弦定理学案新人教A 版必修5学习目标1. 进一步熟悉正、余弦定理内容;2. 掌握在已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形. 学习重难点1. 重点:正、余弦定理内容2. 难点:已知三角形的两边及其中一边的对角解三角形时的讨论一、知识链接问题1:在解三角形时,已知三边求角,用 定理;已知两边和夹角,求第三边,用 定理;已知两角和一边,用 定理.问题2:在△ABC 中,已知 A =6π,a =252,b =502,解此三角形.二、试一试探究1:在△ABC 中,已知下列条件,解三角形.① A =6π,a =25,b =502;② A =6π,a =5063,b =502;③ A =6π,a =50,b=502.思考:解的个数情况为何会发生变化?探究2:用如下图示分析解的情况(A 为锐角时).babab a baa 已知边a,b 和∠A仅有一个解有两个解仅有一个解无解a ≥b CH=bsinA<a<b a=CH=bsinA a<CH=bsinAAC B ACB1ABACB2CHHH试试:1. 用图示分析(A 为直角时)解的情况? 2.用图示分析(A 为钝角时)解的情况?※ 模仿练习例1. 在∆ABC 中,已知80a =,100b =,45A ∠=︒,试判断此三角形的解的情况.变式:在∆ABC 中,若1a =,12c =,40C ∠=︒,则符合题意的b 的值有_____个.例2. 在∆ABC 中,60A =︒,1b =,2c =,求sin sin sin a b cA B C++++的值.变式:在∆ABC 中,若55a =,16b =,且1sin 22032ab C =,求角C .三、总结提升 ※ 学习小结1. 已知三角形两边及其夹角(用余弦定理解决);2. 已知三角形三边问题(用余弦定理解决);3. 已知三角形两角和一边问题(用正弦定理解决);4. 已知三角形两边和其中一边的对角问题(既可用正弦定理,也可用余弦定理,可能有一解、两解和无解三种情况).※ 知识拓展在∆ABC 中,已知,,a b A ,讨论三角形解的情况 :①当A 为钝角或直角时,必须a b >才能有且只有一解;否则无解; ②当A 为锐角时,如果a ≥b ,那么只有一解; 如果a b <,那么可以分下面三种情况来讨论: (1)若sin a b A >,则有两解;(2)若sin a b A =,则只有一解;(3)若sin a b A <,则无解.当堂检测1. 已知a 、b 为△ABC 的边,A 、B 分别是a 、b 的对角,且sin 2sin 3A B =,则a bb +的值=( ). A. 13 B. 23 C. 43 D. 532. 已知在△ABC 中,sin A ∶sin B ∶sin C =3∶5∶7,那么这个三角形的最大角是( ). A .135° B .90° C .120° D .150°3. 如果将直角三角形三边增加同样的长度,则新三角形形状为( ). A .锐角三角形 B .直角三角形 C .钝角三角形 D .由增加长度决定4. 在△ABC 中,sin A :sin B :sin C =4:5:6,则cos B = .5. 已知△ABC 中,cos cos b C c B =,试判断△ABC 的形状 .课后作业1. 在∆ABC中,a xcm=,2b cm=,45B∠=︒,如果利用正弦定理解三角形有两解,求x 的取值范围.2. 在∆ABC中,其三边分别为a、b、c,且满足2221sin24a b cab C+-=,求角C.课后反思。
新人教A版高中数学(必修5)1.1《正弦定理和余弦定理》

数学5 第一章解三角形章节总体设计(一)课标要求本章的中心内容是如何解三角形,正弦定理和余弦定理是解三角形的工具,最后落实在解三角形的应用上。
通过本章学习,学生应当达到以下学习目标:(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。
(2)能够熟练运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的生活实际问题。
(二)编写意图与特色1.数学思想方法的重要性数学思想方法的教学是中学数学教学中的重要组成部分,有利于学生加深数学知识的理解和掌握。
本章重视与内容密切相关的数学思想方法的教学,并且在提出问题、思考解决问题的策略等方面对学生进行具体示范、引导。
本章的两个主要数学结论是正弦定理和余弦定理,它们都是关于三角形的边角关系的结论。
在初中,学生已经学习了相关边角关系的定性的知识,就是“在任意三角形中有大边对大角,小边对小角”,“如果已知两个三角形的两条对应边及其所夹的角相等,那么这两个三角形全”等。
教科书在引入正弦定理内容时,让学生从已有的几何知识出发,提出探究性问题:“在任意三角形中有大边对大角,小边对小角的边角关系.我们是否能得到这个边、角的关系准确量化的表示呢?”,在引入余弦定理内容时,提出探究性问题“如果已知三角形的两条边及其所夹的角,根据三角形全等的判定方法,这个三角形是大小、形状完全确定的三角形.我们仍然从量化的角度来研究这个问题,也就是研究如何从已知的两边和它们的夹角计算出三角形的另一边和两个角的问题。
”设置这些问题,都是为了加强数学思想方法的教学。
2.注意加强前后知识的联系加强与前后各章教学内容的联系,注意复习和应用已学内容,并为后续章节教学内容做好准备,能使整套教科书成为一个有机整体,提高教学效益,并有利于学生对于数学知识的学习和巩固。
本章内容处理三角形中的边角关系,与初中学习的三角形的边与角的基本关系,已知三角形的边和角相等判定三角形全等的知识有着密切联系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学学习材料金戈铁骑整理制作1.1 正弦定理和余弦定理一、填空题1.在△ABC 中,sin 2A ≤sin 2B +sin 2C -sin B sin C ,则A 的取值范围是________. 解析 由题意和正弦定理,得a 2≤b 2+c 2-bc ,b 2+c 2-a 2≥bc ,cos A =b 2+c 2-a 22bc ≥12,所以0<A ≤π3.答案 ⎝⎛⎦⎥⎤0,π32.若△ABC 的内角A ,B ,C 所对的边为a ,b ,c 满足(a +b )2-c 2=4,且C =60°,则ab 的值为________.解析 由(a +b )2-c 2=4及余弦定理,得c 2=a 2+b 2-2ab cos 60°=(a +b )2-3ab ,所以ab =43.答案433.在△ABC 中,若b =1,c =3,C =2π3,则a =________.解析 由正弦定理,有3sin2π3=1sin B , 即sin B =12.又C 为钝角,所以B 必为锐角,所以B =π6,所以A =π6.故a=b =1.答案 14.在△ABC 中,已知5210a c A =,=,=30,则B 等于________.解析 根据正弦定理sin sin a c A C =,得sin 1102sin 2252c A C a ⨯===. ∴C=45或C=135.当C=45时,B=105; 当C=135时,B=15. 答案 105或155.如图,在△ABC 中,D 是边AC 上的点,且AB =AD,2AB =3BD ,BC =2BD ,则sin C =________.解析 设AB =a ,∴BD =23a , BC =2BD =43a , cos A =AB 2+AD 2-BD 22AB ·AD =2a 2-43a22a 2=13∴sin A =1-cos 2A =223由正弦定理知sin C =AB BC ·sin A =34×223=66. 答案 666.在△ABC 中,若S △ABC =14(a 2+b 2-c 2),那么角C =________.解析 根据三角形面积公式得,S =12ab sin C =14(a 2+b 2-c 2),∴sin C =a 2+b 2-c 22ab .又由余弦定理:cos C =a 2+b 2-c 22ab,∴sin C =cos C ,∴C =π4.答案 π47.在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c ,且b 2+c 2=bc +a 2,则角A 的大小为________.解析 由余弦定理,得cos A =b 2+c 2-a 22bc =12,所以A =π3.答案π38.已知△ABC 中,AB =2,C =π3,则△ABC 的周长为________(用含角A 的三角函数表示).解析 由正弦定理,得△ABC 的周长为a +b +c =2sin A sin π3+2sin Bsinπ3+2=43sin A +43sin ⎝⎛⎭⎪⎫2π3-A +2=23sin A +2cos A +2=4sin ⎝ ⎛⎭⎪⎫A +π6+2. 答案 4sin ⎝⎛⎭⎪⎫A +π6+29.已知△ABC 的一个内角为120°,并且三边长构成公差为4的等差数列,则 △ABC 的面积为________.解析 不妨设A =120°,c <b ,则a =b +4,c =b -4,于是由cos 120°=b 2+b -2-b +22b b -=-12,解得b =10,S =12bc sin 120°=15 3.答案 15 310. 在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若a 2-b 2=3bc ,sin C =23sin B ,则A 角大小为________. 解析 由a 2-b 2=3bc ,c =23b ,得a 2=7b 2,所以cos A =b 2+c 2-a 22bc =b 2+12b 2-7b 243b 2=32,所以A =π6. 答案π611.在锐角△ABC 中,BC=1,B=2A,则cos AC A的值等于 ,AC 的取值范围为 .解析 设2A B θθ=⇒=.由正弦定理得sin2sin AC BC θθ=, ∴122cos cos AC AC θθ=⇒=.由锐角△ABC 得0290θ<<0⇒45θ<<, 又0<180390θ-<30⇒60θ<<,故3045θ<<22⇒<cos 32θ<, AC=2cos θ,∴(23)AC ∈,.答案 2 (23),12.△ABC 中,a ,b ,c 分别为A ,B ,C 的对边,如果a ,b ,c 成等差数列,B =30°,△ABC 的面积为32,那么b =________.解析 由a ,b ,c 成等差数列,得2b =a +c . 平方得a 2+c 2=4b 2-2ac . 又△ABC 的面积为32,且B =30°,故由S △ABC =12ac sin B =12ac sin 30°=14ac =32,得ac =6,所以a 2+c 2=4b 2-12.由余弦定理cos B =a 2+c 2-b 22ac =4b 2-12-b 22×6=b 2-44=32.解得b 2=4+2 3.又因为b 为边长,故b =1+ 3. 答案 1+ 313.在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若b a +a b =6cos C ,则tan Ctan A +tan Ctan B的值是________. 解析 利用正、余弦定理将角化为边来运算,因为b a +ab =6cos C ,由余弦定理得a 2+b 2ab =6·a 2+b 2-c 22ab ,即a 2+b 2=32c 2.而tan C tan A +tan C tan B =sin C cos C ⎝ ⎛⎭⎪⎫cos A sin A +cos B sin B =sin C cos C ·sin Csin A sin B=c 2ab ·a 2+b 2-c 22ab =2c 2a 2+b 2-c 2=2c 232c 2-c2=4.答案 4 二、解答题14.在△ABC 中,已知角A ,B ,C 的对边分别为a ,b ,c ,且(a +b +c )(b +c -a )=3bc . (1)求A ;(2)若B -C =90°,c =4,求b .(结果用根式表示)解析 (1)由条件,得(b +c )2-a 2=3bc ,即b 2+c 2-a 2=bc ,∴cos A =b 2+c 2-a 22bc =12.∵0°<A <180°,∴A =60°. (2)由⎩⎨⎧B +C =120°,B -C =90°得B =105°,C =15°.由正弦定理得b sin105°=4sin15°,即b =4sin105°sin15°,∴b =4tan75°,∵tan75°=tan(45°+30°)=1+tan30°1-tan30°=2+3,∴b =8+4 3.15.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知B =C,2b =3a . (1)求cos A 的值; (2)cos ⎝⎛⎭⎪⎫2A +π4的值.解析 (1)由B =C,2b =3a ,可得c =b =32a , 所以cos A =b 2+c 2-a 22bc=34a 2+34a 2-a 22×32a ×32a=13. (2)因为cos A =13,A ∈(0,π),所以sin A =1-cos 2A =223,cos 2A =2cos 2A -1=-79,sin2A =2sin A cos A =429. 所以cos ⎝ ⎛⎭⎪⎫2A +π4=cos 2A cos π4-sin 2A sin π4=⎝ ⎛⎭⎪⎫-79×22-429×22=-8+7218.16.设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知a =1,b =2, cos C =14.(1)求△ABC 的周长; (2)求cos(A -C )的值.解析 (1)因为c 2=a 2+b 2-2ab cos C =1+4-4×14=4.所以c =2.所以△ABC 的周长为a +b +c =1+2+2=5. (2)因为cos C =14,所以sin C =1-cos 2C =1-⎝ ⎛⎭⎪⎫142=154.所以sin A =a sin C c =1542=158.因为a <c ,所以A <C ,故A 为锐角, 所以cos A =1-sin 2A =1-⎝ ⎛⎭⎪⎫1582=78. 所以cos(A -C )=cos A cos C +sin A sin C =78×14+158×154=1116.17.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A -2cos C cos B =2c -ab.(1)求sin Csin A的值; (2)若cos B =14,△ABC 的周长为5,求b 的长.解析 (1)由正弦定理得a =2R sin A ,b =2R sin B ,c =2R sin C (R 为△ABC 外接圆半径),所以cos A -2cos C cos B =2c -a b =2sin C -sin Asin B,即sin B cos A -2sin B cos C =2sin C cos B -sin A cos B , 即有sin(A +B )=2sin(B +C ),即sin C =2sin A ,所以sin Csin A=2. (2)由(1)知sin C sin A =2,所以有ca=2,即c =2a ,又因为△ABC 的周长为5, 所以b =5-3a ,由余弦定理及cos B =14得b 2=c 2+a 2-2ac cos B ,即(5-3a )2=(2a )2+a 2-4a 2×14,解得a =1, 所以b =2.18.在△ABC 中,角A ,B ,C 所对边的长分别是a ,b ,c ,且cos 〈AB →,AC →〉=14.(1)求sin 2B +C 2+cos 2A 的值;(2)若a =4,b +c =6,且b <c, 求a ,c 的值. 解析 (1)sin 2B +C 2+cos 2A=12[1-cos(B +C )]+(2cos 2A -1) =12(1+cos A )+(2cos 2A -1) =12⎝ ⎛⎭⎪⎫1+14+⎝ ⎛⎭⎪⎫18-1=-14.(2)由余弦定理,得a 2=b 2+c 2-2bc cos A ,即a 2=(b +c )2-2bc -2bc cos A , 即16=36-52bc ,∴bc =8.由⎩⎨⎧b +c =6,bc =8,b <c ,可求得⎩⎨⎧b =2,c =4.。
