初二数学等边三角形[人教版]

合集下载

人教版数学八年级上册.等边三角形的性质与判定经典课件

∴ ∠C = 600
∴∠ A=600
∴AB=AC=BC
人教版数学八年级上册.等边三角形的性质与判定经典课件
人教版数学八年级上册.等边三角形的性质与判定经典课件
等边三角形的判定方法:
• 1.三边相等的三角形是等边三角形. •2.三个内角都等于60 °的三角形是等边三角形. •3.有一个内角等于60 °的等腰三角形是等边三角形.
人教版数学八年级上册.等边三角形的性质与判定经典课件
判定有一个角是60°的等腰三角形是等边三角形. 二如果一个等腰三角形中有一个角是60°，
那么这个三角形是等边三角形。第一种情况：当顶角是600时。第二种情况：当底角是600时。
人教版数学八年级上册.等边三角形的性质与判定经典课件
人教版数学八年级上册.等边三角形的性质与判定经典课件
探索星空：探究性质三
3、等边三角形是轴对称图形吗?有几条对称轴?
A
B
C
等边三角形是轴对称图形，它有三条对称轴。
人教版数学八年级上册.等边三角形的性质与判定经典课件
人教版数学八年级上册.等边三角形的性质与判定经典课件
等边三角形的性质
1 .三条边相等
A
1
F
D
B
2
E3 C
人教版数学八年级上册.等边三角形的性质与判定经典课件
人教版数学八年级上册.等边三角形的性质与判定经典课件
我们这节课学习了哪些知识? 谈谈你的体会.
人教版数学八年级上册.等边三角形的性质与判定经典课件
人教版数学八年级上册.等边三角形的性质与判定经典课件人教版数学八年级上册.等边三角形的性质与判定经典课件

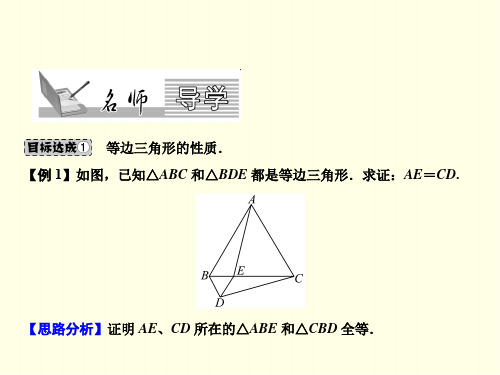
初二上数学课件(人教版)-等边三角形

形，点D、E分别在BC、AC边上，AE=CD，AD与BE
交于点F.
（1）求证：△ABE≌△CAD；
（2）求∠AFB的度数.
证明（1）∵△ABC为等边三角形，
： ∴∠BAC＝∠ABC＝∠C＝60°，AB＝AC＝BC，
AB＝CA 在△ABE和△CAD中， ∠BAE＝∠ACD
∴△ABE≌△CAD.
AE＝CD，
分别是EB、CD的中点，易证：CD＝BE，△AMN是等边三角
形.当△ADE绕A点旋转到图②的位置，△AMN是否还是等
边三角形？若是，请给出证明；若不是，请说明理由.
解：△AMN是等边三角形. AB＝AC
证明：在△ABE和△ACD中 ∠B1 AE=∠CAD=60° BD2＝BE，
∴△ABE≌△ACD（SAS），
3.顶角为60°的等腰三角形是等边三角形吗？为什么？
4.有一个底角为60°的等腰三角形是等边三角形吗？
探究二：含30°角的直角三角形的性质
5.让同学们拿出一块含有30°角的直角三角板，并测量较短直角边与斜边之间有什么样的数量关系.
等边三角形 15°
120°
A
3
例1：如图①，若△ABC和△ADE为等边三角形，M、N
（2）∵△ABE≌△CAD（已证）, ∴∠ABE＝∠CAD，
又∵∠CAD＋∠BAD＝60°, ∴∠ABE＋∠BAD＝60°，
又∵∠BFD＝∠BAF＋∠ABF，∴∠BFD＝60°，
∴∠AFB=180°-60°=120°
本课时学习了等边三角形的判定与性质.在直角三角形中，30°角所对的直角边等于斜边的一半.
推荐课后完成 “课后练案”内容.
∴△AMN为等边三角形.
例2：如图，在△ABC中,AB＝AC,D、E是 △ABC内的两点,AD平分 ∠BAC,∠EBC=∠E=60°.若BE8＝6cm,DE＝2cm, 解则析BC：＝如_图__，cm延. 长AD交BC于M，

初二上数学课件(人教版)-等边三角形的性质与判定

(1)证明：∵AB＝AC，又 D 是 BC 中点，∴AD⊥BC，又 AB 平分∠DAE， ∴∠DAB＝∠EAB，又∠E＝∠ADB＝90°，AB＝AB，∴△ADB≌△AEB， ∴AD＝AE； (2)解：△ABC 是等边三角形，由△ADB≌△AEB，得∠EBA＝∠ABC，又 AB＝AC，∴∠ABC＝∠C，由 BE∥AC，得∠EBA＋∠ABC＋∠C＝180°， ∴∠C＝60°，∴△ABC 是等边三角形．
证明：易证△BCD≌△ACE(SAS)，得∠EAC＝∠B，又∠B＝∠ACB，∴∠ EAC＝∠ACB，∴AE∥BC.
13．如图，点 P 是等边三角形 ABC 内一点，连接 PA、PB、PC，以 BP 为边构造△BPD，连接 CD，使得 AP＝CD，∠1＝∠2.求证：△BPD 是等边三角形．
证明：∵△ABC 是等边三角形，∴AB＝CB.在△ABP 和△CBD 中，
角形；④有两个内角都是 60°的等腰三角形是等边三角形．以上结论正确的
有( D )
A．1 个
B．2 个
C．3 个
D．4 个
9．在△ABC 中，AD⊥BC，垂足为 D，并且 BD＝CD，则△ABC 的形状是等腰三角形，要使△ABC 是等边三角形，一般还要补充条件：一个内角为60° ．
10．如图，在等边三角形 ABC 中，BO、CO 分别平分∠ABC、∠ACB，OE ∥AB，OF∥AC.若 BE＝3cm，则△OEF 的周长为 9cm ．
【规范解答】∵AB＝AC，∴∠ABC＝∠C.∵DA＝DC，∴∠DAC＝∠C， ∵∠ADB＝∠C＋∠DAC，∴∠ADB＝2∠ABD.∵DA⊥AB，∴∠ADB＋∠ ABD＝90°.∴∠ADB＝60°.∵AE＝AD，∴△ABD≌△ABE.∴BD＝EB.∴△ BDE 是等边三角形．

初二数学等边三角形[人教版]

二次结构泵https:// 二次结构柱输送泵与传统灌注施工工艺的对比：1、一台构造柱施工设备的施工工作量为200根/天(每根柱子按0.18立方)，相当于48人灌注工人的工作量。经比较构造柱施工设备可缩短灌注工程90%的施工工作周期，并且每日可节省几千元工资。2、构造柱施工设备一人操作就可开工，但传统的灌注施工工作强度大，因此要时刻面临缺工施工，困难等问题.二次结构柱输送泵是吸收国内外先进技术基础上研制成的一种新型多功能施工机械，该产品具有广泛用途，可用于建筑砂送，二次结构柱输送泵岩土工程注浆大面积喷涂高、操作方便，安全可靠，易于维修保养，结构紧凑，移动灵活，本产品采用凸轮式转动，二次结构柱输送泵活塞结构自动控压设制，流量大，使用寿命长，能够输送配比1:2.5的砂浆，该产到国际同行先进水平二次结构柱输送泵，该泵机质量轻，装有行走轮，方便移动，设计独特，可直接放于楼面现场浇注，并且不受泵送高度的限制。有效的解决构造柱浇注过程中出现的顶部接近底梁段难以高质量浇注的问题，二次结构柱保证构造柱的平整度和观感质量。适用于超高层的细石混凝土输送，建筑楼层群体构造柱浇柱二次结构柱输送泵送效率高，泵送系统是人工施工的数倍，这样有效的提高了生产效率，节省了劳动成本。二次结构柱输送泵的研制，解决了某工况下的混凝土难以泵送的问题，从而提高了施工的进度，降低了劳动的强度，减少了施工过程中对人工成本的投入二次结构柱输送泵，不仅实现了轻巧与高相结合的概念，还能让你的工作变得更加的安全省力，具体优点如下：公司体积一般的设备而言显得更小，重量更轻，可以用于隧道、罐桩等领域，在施工的过程中，你可以任意穿梭于热饿和面积较小的场所，操作起来也更加的方便省力。公司液压室内二次结构柱输送泵双泵的冲击小，可靠性更高，使用途中安全可于新上任的师傅来说心里更加的有自信，操作起来也会变得更加的熟练。公司技术上采用了筛选过滤的技术，防止其他东西进入车身内，造成损伤，增加了元件的使用寿命。二次构造柱浇筑泵和混凝土地泵，得到了越来越多人的认可。在使用这些设备时安装管道成了一项最重要的工作，安装不当及容易造成故障。下面就为您详细讲解了设备管道的布置方法。构造柱泵和混凝土地泵布管，应根据工程和施工场点，最大骨料粒径、输送泵型号、输送距离及输送难易程度等进行选择与配置。构造柱泵和混凝土地泵布管时，应尽量缩短管线长度，少用弯管和软管；在同一条管线中，应采用相同管径的混凝土输送管；同时采用新、旧配管时，应将新在泵送压力较大处，管线应固定牢靠，管接头应严密，不得漏浆；应使用无龟裂，无凹凸损伤和无弯折的配管。构造柱泵和混凝土地泵布管方式：二次构造柱专用泵的操作步骤：1.向下泵送混凝土时，应先把输送管上气阀打开，待输送管下土有了一定压力时，方可关闭气阀。2.混凝土泵送即将结束前，应正确计算尚需用的混凝土数量，并应及时告知混凝土搅拌处。3.泵送过程中，废弃的和泵送终止时多余的混凝土，应按预先确定的处理方法和场所，及时进行妥善处理。4.泵时，二次构造柱输送泵，应将混凝土泵和输送管清洗干净。5.排除堵塞，重新泵送或清洗混凝土泵时，布料设备的出口应朝安全方向，以防堵塞物或废浆高速飞出伤人。6.当多台混凝土泵同时泵送或与其他输送方法组合输送混凝土时，应预各自的输送能力、浇筑区域和浇筑顺序。并应分工明确、互相配合、统一指挥。7.混凝土输送泵在泵送过程中，若需接长3m以上(含3m)的输送管时，仍应预先用水和水泥浆或水泥砂浆，进行湿润和润滑管道内壁。8.混凝土泵送过程中，不下的输送管内的混凝土撒落在未浇筑的地方构造柱输送泵Байду номын сангаас介：又称混凝土输送泵，是利用压力将混凝土沿管道连续输送的机械。小型混凝土泵车主要由泵体和输送管组成，泵体装在汽车底盘上，再装备可伸缩或屈折的布料杆，就组成泵 1，释放的日益扩大的稳定性。2，确保电源输入是正常。3，去切换确认或推翻转移。4，之前用水湿喂缸,或之前添加一个薄、流动的材料。5，饲料开始工作。6，列窗体，如清朝和次生构造柱泵送料机，打开后您完成其余，然后移动之前壶嘴插入极板取出。7，停止应休息一会后，干净的水，以防止二次构造柱泵下一步不能正常工作。二次构造柱泵机械厂家分析机械工业废水处理技术现状从工程设计、施工、设备研发、制造、安装、运营等方面可从事系列服务。近年来在我国北方也逐渐兴起了一些颇具实力的环保企业。今后我国机械工业含油废水处理技术创新发展前规划磁吸附分离法主要借助磁性物质作为载体，利用油珠的磁化效应，将磁性颗粒与含油废水相结合，使油吸附在磁性颗粒上，再通过分离装置，将磁性物质及其吸附的油留在磁场中，从而达到油水分离的目的。新型二次构造柱泵、二次浇注专用设备优点如下：二次构造柱泵上料机泵机的使用功率非常小，只有7.5kw，在无电源的情况下只需配一台小型的发电机即可工作。二次构造柱泵上料机是国内体小的混凝土输送泵，是许多狭窄施工环境的理想选择。二次构造柱泵上量轻，移动方便。二次构造柱泵上料机配置高，全液压操作，性能稳定，结构紧凑，故障率低，寿命长。二次构造柱泵上料机泵机价格实惠，有微型砂浆泵，微型细石混凝土泵，微型混凝土泵三种配置供客户选择。采用活塞结构自动空压工作压力大，泵送距离远，泵送高度高二次构造柱泵原理：1.全液控换向液压系统，回路优化设计，发热损耗低，二次构造柱液压浇筑泵系统更稳定。2.S管阀采用高锰钢铸造成型，易磨损面堆焊抗磨材料；眼镜板和切割环采用高硬耐磨合压耐磨。3.活塞采用进口原材料，油缸密封及关键电气部件采用进口元件。4.二次构造柱液压浇筑泵布局合理，维护空间大。设计严谨，兼顾经济性与可靠性，性价比高。二次构造柱专用泵特点：该泵机质量轻，装有行走轮，方便移动，设特，移动方便，运行平稳，操作简单，使用寿命长。泵送系统是人工施工的10倍，节约时间和劳动成本，提高劳动生产效率。可直接放于楼面现场浇注，并且不受泵送高度的限制。产业升级是中国经济转型的基本驱动力。虽然经济转型还包括体制改革等方面的内容，但产业升级不仅具有独立于其他因素（如市场机制）的内容，而且是衡量转型是否成功的唯一标志（即生产力标准）。二次构造柱泵有效的解决构造柱程中出现的顶部接近底梁段难以高质量浇注的问题，保证构造柱的平整度和观感质能够有效的解决构造柱浇注过程中出现的顶部接近底梁段难以高质量浇注的问题。二次构造柱泵优点：1、二次结构细石砂浆专用浇筑泵可实现远距离高层建混凝土、砂浆等输送。2、分配阀采用先进的S管阀，密封性好、结构简单可靠。眼睛板和浮动切割环采用硬质合金，耐磨性好、寿命长、更换方便，切割环采用可自动补偿间隙结构。3、控制方式用电-液控制，具有完善的电-液过载保护及示系统；具有反泵操作功能，容易排除堵塞故障；泵送速度可以调节，能满足各种工况需求。4、集中润滑系统由程序自动控制启停及运转时间，有效延长转动件的使用寿命。5、接触器和按钮开关等电器组件，防护等级可达到IP65，采用制，工作可靠，控制线路简单，电器箱配备开关，便于操作。6、主要密封件采用优质密封件，杜绝了液压系统的内外泄漏。二次构造柱浇筑泵的适用范围：广泛用于一些特殊的施工环境如：铁路公路隧道，引水洞，涵洞，矿洞，桥洞等洞施工，还包括水利工程，水电工程，边坡支护，地下施工作业，基础的灌装工程，大型群楼建筑的构造柱浇注等等。

初二数学等边三角形[人教版]

TPM导入时的常见问题TPM咨询服务中心TPM管理培训公司概述：TPM管理是一种根本性改进活动，它需要组织内部的所有的人力资源的参与。随着高精尖设备越来越多的代替人工从事生产任务，引入TPM管理机制，可建立适合司情的新型设备管理模式，全面提升设备指标，促进设备向零故障迈进，那么导入TPM常见的问题有哪些呢？TPM常见问题1、以为只要培训了，员工就会做了。正确的做法：需要与实践相结合，培训了，未必完全懂了，听懂了，未必就会做了。精益TPM是实践的哲学，需要在做中学，学中做。 2、以为精益TPM的每个阶段不需要太长时间，每一两月可以完成一个阶段，一年就可以完成TPM的7个阶段。正确的理解：TPM重在调理企业的体质，就如同人吃中药调理体质，需要足够的时间才能见效，中药调理没有速效药，否则就成毒药了。一般每个阶段需要6-8个月时间。 3、以为做TPM管理，只做好就行了，没有必要浪费时间去记录和总结。正确的理解：这次做好了，不代表下一次也能做好，A员工做了，不代表B员工也能做好，只有把好的做法和经验总结出来并编制成标准化的文件，才能有传承性，所以员工需要养成记录和总结的习惯，没有记录就没有管理，没有总结就没有提升。 4、认为员工的年龄太大，文化程度低，TPM就没有办法推行。正确的理解：年龄与文化程度，确实是推行后台升级的影响因素之一，但，这不是主要因素，TPM强调的是全员参与，营造良好的改善氛围，形成比学赶帮超的文化，只要员工有了强烈的改善意愿，员工有改善的能力，无论年龄大小、文化高低，同样可以取得好的推行效果。 5、以为小改善不是改善，因为小改善不能带来直接的经济效益。正确的做法：改善，无关乎大小，小改善也是改善。只要是员工主动提出来的改善，哪怕再小，也需要肯定和鼓励，没有树木，无以成森林，所以，要鼓励微创新，微改善，也许可以带来大效果。盲目导入精益TPM导致失败：有些企业认为TPM很简单，相关的书籍也很多，网上更是有海量的资料可以参考，不需要请顾问公司，自已完全有能力做好。所以，就选择自主推行，往往结果都不会太满意，最后都是不了了之。还有些企业，崇尚外部的一些大师级的培训老师，认为听了几场培训，自已就领悟了，然后就开始带领员工热火朝天的干起来了，甚至认为自已干的不错：原来TPM不就是这么回事吗。但对比一些经过专业顾问公司辅导过的同行企业，发现自已跟别人的水平相差甚远。 TPM管理常见问题与对策：1、高层管理者有急躁的情绪：建议：作为高层管理者，首先要有正确的认知，TPM管理类似中药治病与调理体制。要深知改变群体的思维模式及价值观不可能一蹴而就，需要一定的时间来磨合与积淀；项目前期宜采用以点带面的方式，忌全面铺开。 2、中层管理者不重视：建议：首先明确责任，中层管理者是项目推进部门第一责任人；其次奖惩结合，不能只有奖励没有惩罚，惩罚以面子为主，辅以经济惩罚；第三加强培训宣传，让中层管理者认识到真正的好处；第四建立会议体系，将项目作为一项工作，定期总结汇报。 3、员工参与度不高：建议：建立激励机制，对员工侧重精神和物质的奖励；开展多样化的活性化活动，让员工在‘游戏’的感觉中潜移默化；优先解决改善员工工作条件的改善项目，先让员工受益； TPM设备管理改善的五大要点TPM管理体系作为先进企业管理的主要内容，TPM管理在企业的实施关系着企业的可持续发展，TPM管理不但改善企业的生产设备，还提高企业的设备创新能力和员工的综合素质。很多企业意识到企业的竞争就是企业的管理模式的竞争。企业推行TPM管理如何落地？TPM咨询服务中心TPM设备管理培训公司根据多年辅导经验总结企业设备管理改善的五大落地要点如下：TPM个别改善要点一、设备的点检、保养和修理这是设备管理方面的中心环节，也是工作量最大的部分。企业要合理制订设备的点检、维护保养和修理等方面的计划，并采用先进的检修技术进行定期检修与保养。 2、核心设备的评价这是指企业须根据技术先进、经济合理的原则和生产的需要，正确地选择核心设备。同时要组织专家团队定期评价，确保设备在最佳的方式生产。 3、设备的改良企业需根据生产经营的规模、产品的品种与质量，以及发展新产品、改造老产品的需要，有计划、有重点地对现有设备进行改良与升级，进而提高生产效率及降低成本。 4、设备使用设备使用管理是指针对设备的特点，正确合理地使用设备、安排生产任务。这样，企业可以减轻设备的亏损、延长使用寿命，防止设备和人身事故的发生，减少和避免设备闲置等。 5、设备的日常管理（1）主要包括设备的分类、登记、编号、封存、报废、事故处理和技术资料管理等。（2）设备的封存和迁移。企业对闲置不用或停用三个月以上的设备，应由车间提出计划，经生产部门和设备管理部门审核，报企业领导批准后进行封存。封存的设备应采取防尘、防潮、防锈等措施，并要定期维护和检查。当企业生产工艺改变需要迁移设备时，必须由生产工艺部门提出方案，经设备管理部门审查，企业领导批准后，办理迁移手续后方可迁移。（3）设备的调拨和报废。对本企业已不适用，长期闲置不用或利用率极低的设备应予调出。企业调出的设备，需报有关部门批准，并做好账务处理后方可调出。调出的形式有出租和有偿转让两种。由于超过使用年限而结构陈旧、精度低劣、生产效率低、能源消耗高，或由于事故造成损坏而在经济上、技术上都不值得修复改装的设备，都可报废。企业要报废的设备，通常由使用部门提出申请，设备管理部门组织有关部门进行技术鉴定，并报请上级主管部门批准后方可报废。（4）设备的事故处理。由于非正常损坏而导致设备效能降低或不能使用即为设备事故。企业应采取积极有效措施，预防各种事故的发生。当设备发生事故后，应积极组织抢修，分析原因并进行严肃处理，从中吸取经验教训并采取有效措施，防止类似事故的发生。凡是人为原因所引起的设备事故，应视情节轻重给予处分。对重大设备事故及处理情况要及时向上级主管部门报告。（5）设备技术资料的管理。建立设备档案、积累设备技术资料及加强设备资料的管理是做好设备管理的重要环节。设备档案一般包括设备出厂检验单、设备进厂验收单、设备安装工程记录单、设备修理卡片、定期检查记录、设备的全套图纸、说明及检修工艺文件等。设备档案是保证设备正确使用、对设备进行检查和维护修理的重要依据。智泰咨询认为通过对设备技术资料的分析，可以掌握设备的技术状况和零部件磨损的程度，从而制订出切合实际的检查修理计划，预防设备事故的发生。（6）设备管理的评价指标设备运动过程既然存在物质和价值两种运动形态，就要求从技术和经济两个方面加强对设备的管理，以求得设备的技术状态最佳和设备的维修费用最经济。

八年级初二数学上册 13.3.2 等边三角形(第2课时) 【教学课件PPT】

Rt△ABC 中,∠C =90°,∠B =2∠A,∠B 和∠A 各是多少度?边AB 与BC 之间有什么关系?
证明:∵∠B+∠A =180°– ∠C=90°, ∠B=2∠A,
∴∠B=60°,∠A=30°. ∴ AB=2BC.
探究新知
素养考点 2 利用直角三角形性质解决实际问题
例4 如图是屋架设计图一部分,点D 是斜梁AB 中点,立柱 BC,DE 垂直于横梁AC,AB =7.4 cm,∠A =30°,立柱BC,DE 有多长?
∴EF=2EH=2,∠FEO=∠FOE.
∴OF=EF=2．
課堂检测
基础巩固题
1.如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分
与地面成30°角,这棵树在折断前高度为( ) B
A．6米 B．9米
C．12米 D．15米
2.某市在旧城绿化改造中,计划在一块如图所示△ABC空地上种植
草皮优化环境,已知∠A＝150°,这种草皮每平方米售价a元,则购买
B
图中BC,DE 分别是哪个直角三角形直角边?它们所对锐角分别是多少度?
D
A
E
C
探究新知
解:∵DE⊥AC,BC ⊥AC, ∠A=30 °,
∴BC=
1 2
AB,
DE= 1 AD.
2
B
∴BC=
1 2
AB=
1 2
×7.4=3.7(m).
D
又AD=
1 2
AB,
A
E
C
∴DE=
1 2
AD=
1 ×3.7=1.85
2
∴BC
=
1 2
AB．
B
C
D
探究新知方法点拨

人教版八年级数学上册等边三角形

反过来怎么样——逆向思维
命题:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.是真命题吗? 如果是,请你证明它.
已知:如图,在△ABC中,∠ACB=900,BC= 1 AB.
求证:∠A=300.
2
A
B
C
反过来怎么样——逆向思维
证明:如图, 延长BC至D,使CD=BC,连接AD.
概念性质
等有二腰条边三角相等形
等有三边条边三角轴一条 1、等边对等角 2、三线合一 3、对称轴三条
判定
1、定义 2等角对等边
1定义 2两个角是600 3等腰三角形有一个 600
我能行 3
将两个含有板有30°的三角尺如图摆放在一起,你能借助这个图形,找到Rt△ABC的直
A 300
C
这是一个通过线段之间的关系来判定一个角的具体度数(300)的根据之一.
比一比：看谁算的快
1.如图：在Rt△ABC中 ∠A=300,AB+BC=12cm 则AB=__８___cm Ｂ
３００
Ｃ
Ａ
2.如图:△ABC是等边三角形，
A
AD⊥BC,DE⊥AB,若AB=8cm,
BD=４＿ｃ＿ｍ＿， BE=_２__ｃ_ ｍ E
∴∠A=300(直角三角形两锐角互余).
回顾反思 4
几何的三种语言
定理:在直角三角形中, 如果一条直角边等于斜边的一半,那么它所对的锐角等于300.
在△ABC中
∵∠ACB=900,BC=AB/2(已知),
∴∠A=300(在直角三角形中,如果一条直
B
′ 角边等于斜边的一半,那么它所对的锐角
等于300).

部编版八年级数学上册《等边三角形》PPT课件

第三单元轴对称
3.4 等边三角形
人教版数学（八年级上）
知识回顾
什么是等边三角形？它与一般三角形有什么区别？
一般三角形
等腰三角形
有二条边相等一般三角形
等腰三角形｛
底≠腰底＝腰
定义：三条边都相等的三角形叫做等边三角形。等边三角形也叫做正三角形是特殊的等腰三角形
等边三角形
等边三角形
名称
等腰三角形
证明
∵ △ABC 是等边三角形， ∴ ∠A =∠ABC =∠ACB =60°． ∵ DE∥BC， ∴ ∠ABC =∠ADE，
∠ACB =∠AED. ∴ ∠A =∠ADE =∠AED. ∴ △ADE 是等边三角形.
A
B
C
D
E
变式2 若点D、E 在边AB、AC 的反向延长线上，且DE∥BC，结论依然成立吗？
A
E F
B
D
C
如图, △ABC为等边三角形, ∠ 1= ∠ 2= ∠ 3 (1)求∠EDF的度数. (2)△DEF为等边三角形吗?为什么?
B
A
1F
3
D
E
2
C
已知 △ A B C 是等边三角形 , D, E , F 分别是各边上的一点 , 且 AD=BE=CF.
试说明△ DEF是等边三角形.
证明：∵AB＝AC ∴∠B＝∠C 同理 ∠A＝∠B ∴∠A＝∠B＝∠C 又∵∠A＋∠B＋∠C＝180° ∴∠A＝∠B＝∠C＝60°
几何语言：在△ABC中 ∵AB＝AC＝BC ∴∠A＝∠B＝∠C＝60°
A
B
C
3. 等边三角形有三条对称轴
A
B
C
三条对称轴

初二数学等边三角形[人教版]

像薛敏这样的小丫头片子，除了了有几分姿色，无父无母无权无势，沦落到靠帮餐馆帮工维持生计，他许大财主年纪虽然已经可以做她的父亲，但他哪里看得上眼，将他娶回去做第八房夫人。以游人熊挖心的凶名，别的山寨想要收留他，并不是一件容易的事，但水白云对此毫无芥蒂，更把宋贵、黄勇、陈猛男、何易等四人周到的安排在宾馆里，礼节备至。 “有道理，我听你的！” 但他左边的袖子，却被豹子的利爪撕得粉碎。 “听说过修道的人自爆金丹，给别人雷霆一击吗？”
无枪和无矛扑了上去，抱住无剑的尸身，号啕大哭。呼吸，屋子里有呼吸。 “是啊，我对你很满意！” “我们走，我来殿后！” 最使人恐怖的是，何易的横练功夫，竟然已经到了匪夷所思的地步。何易刚才舍命攻击自己这一招，将后背全部卖给了无枪。
华语作文
“别，别，你别哭，我不会强迫你的，你……你走吧！” 游人熊刚才杀的这个人，已经是这次狩猎的最后一名被杀者，其余的，都已经死在他身后如狼似虎的兄弟们的手里。游人熊的红脸殷红如血，拍着何易的肩膀，高声的道：“想不到，我雪山派竟然出了你这样的人才，从今天开始，我就授你实权心目，从此以后，你是我雪山派第五位心目，统领最精锐的前锋营，做我游人熊的亲兵队队长。” “那就用冰雪……净化你的灵魂，洗涤你的心胸吧！” 至少在正式的场合交手，他从未失手过。
但他的脸色充满迷惘，喃喃道：“那个冰雪的世界，是真，还是假？” 但何易当此地步，义愤填膺，哪里顾得了这么多，叱责道：“游大哥，你是人，他们也是人，为什么一定要杀他们，杀了之后，尸体还要这样被作践？” “是啊，你不就是仗着刀法厉害，武功稀松住手！” “好，孩子，从此以后，我们也许永不分离，你静下心来，待我讲其中的缘由原原本本的告诉你！” “我……我现在就练？” “小子，你这是透支体能，你知道吗，再这样下去，你活不过二十岁？”老龙又开始训斥了。

人教版八年级数学上册(教案).2等边三角形

（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解等边三角形的基本概念。等边三角形是三边长度相等的三角形，它具有独特的性质和应用。在几何学中，等边三角形是非常重要的基本图形。
2.案例分析：接下来，我们来看一个具体的案例。通过分析等边三角形在建筑、艺术等领域的应用，了解它如何帮助我们解决问题。
3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了等边三角形的基本概念、判定方法、性质和面积计算。同时，我们也通过实践活动和小组讨论加深了对等边三角形的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
-掌握等边三角形面积公式的推导过程：学生需要理解并记住面积公式的推导过程，这涉及到数学抽象和逻辑推理的能力。
-在实际问题中识别和应用等边三角形的知识：学生需要具备一定的观察能力和问题分析能力，才能将等边三角形的知识应用到实际问题中。
举例解释：
-通过对比不同类型的三角形，让学生明确等边三角形的判定条件，并能够识别。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“等边三角形在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.重点难点解析：在讲授过程中，我会特别强调等边三角形的判定方法和面积计算这两个重点。对于难点部分，我会通过举例和比较来帮助大家理解。

人教版八年级数学上册12.3.2等边三角形(1)课件 (共16张PPT)

投无路了，你只要足够坚定，运气会眷顾你；永远不要轻易放弃，或许再坚持下这个坎儿就过去了，一旦熬过阴霾，你会发现发现自己会变的无比强大。人生在世没有什么过不去的坎儿，如果遇到挫折和困难，我们必须激
励自己努力前行。不少朋友会写一些励志的话语贴在办公桌上，那么励志的句子致自己简短有哪些？今天小编就为大家整理了经典有气质内涵的句子，看看正能量的句子经典语句，让自己的每一天都充满生机，向着美好的未来前行！一、励志的句子致自己简短1、前方无绝路，希望在转角。2、穷则思变，既要变，又要实干。3、欲望如海水，越喝越渴。4、不去追逐，永远不会拥有。不往前走，永远原地停留。5、勇气不是感觉不到恐惧而是感觉到恐惧也继续做下去。、只有一条路不能选择，那就是放弃。7、只要还有明天，今天就永远是起跑线。8、现实很近又很冷，梦想很远却很温暖。9、松驰的琴弦，永远奏不出时代的强音。10、东西，让你羡慕，却不能拥有;有些错过，让你留恋，却终生遗憾。11、人生应该树立目标，否则你的精力会白白浪费。12、前方无绝路，希望在转角。13、最后的措手不及是因为当初游刃有余的自14、瞄准天上的星星，或许你永远也射不到，但却比你瞄准树梢射得高远。15、一个人有生就有死，但只要你活着，就要以最好的方式活下7、过去是经历，现在是尝试，未来是期待。经历过，尝试着，就有期待。18、别放弃你的梦想，迟早有一天它会在你手里发光。19、一个人拥有什么样的性格，就拥有什么样的世界。20、当你停下来休息的时候，不要忘记别人还在奔跑。二、经典有气质内涵的句子1、不要问自己收获了多少果实，而是要问自己今天播种了多少种子。2、别为小小的委屈难过，人生在世，注定要受许多委屈。智者懂得隐忍，原谅周围的那些人，让我们在宽容中壮大。3、如果你热爱一件事，那么你整天都能埋头于这件事而不觉得无聊，这样你才能在这个领域内出类拔萃。如果你全力以赴地去做你真心热爱的事情，那没有人会是你的对手。4、把圈子变小，把语言变干净，把成绩往上提，把故事往心里收一收，现在想要的以后都会有。5、随着年龄的增长，人总会变得越来越宽容，所以很多事情到最后并不是真的解决了，而是算了吧。6、人和人真是说不清的劫数，你为了一个人辗转反侧夜不能寐，那个人又为了别人，神魂颠倒食不知味。7、突然发现有些感情，有些事，不是几句煽情的文字就能决定的，终究抵不过内心的波涛汹涌以及现实的无奈。8、过去的人，有他们出现的意义，但不要太念念不忘。过去的人有过去的好，但最好的，都是你身边的那个。9、不是谁辜负了誓言，而是被时间扯淡了思念。0、总有一天，你会在我的世界里下落不明，我会在你的世界里杳无音信1、在前进的路上，别急着一口气狂奔到底。静得下心，才能守住目标，沉得住气，才能持续发力。以笃志力行的心态，做久久为功的努力，踏踏实实的你，终将变得很了不起。2、不再向往单纯，而是让心底的单纯唤醒梦魇迷住的躁动与孤寂，于是慢慢的，开始懂得了感恩，懂得了珍惜，懂得了生命中那些真正重要的东西，有一种单纯的幸福幸福。3、我们总是喜欢拿顺其自然，来敷衍人生道路上的荆棘坎坷，却很少承认，真正的顺其自然，其实是竭尽所能之后的不强求，而非两手一摊的不作为。4、因为平时你们没有利益冲突，自然相安无事。但有些人就是一旦触及利益，就绝不会忍耐你。所以啊，看一个人爱不爱你，重点是看有矛盾时，他会不会忍你。忍你的是好心，吼你的要当心。5、心，是静的才好，能静下来的，才是心情。不然，烦躁中怎么能让自己染上心思。心思，是美的那种，女子的心思就是在安静的时间里，想一些事，看一本书，想一个人，那种心情只能在静的环境里生存。6、如果自己都在偷懒，命运又怎么会认可你。别再虚度光阴，叫醒那个沉睡的自己。记住，只要开始，就永远不晚。7、人最大的对手，往往不是别人，而是自己的懒惰。别指望撞大运，运气不可能永远在你身上，任何时候都要靠本事吃饭。你必须拼尽全力，才有资格说自己的运气不好。

人教版初二数学上册：等边三角形(提高)知识讲解

等边三角形（提高）【学习目标】1. 掌握等边三角形的性质和判定.2. 掌握含30°角的直角三角形的一个主要性质．3. 熟练运用等边三角形的判定定理与性质定理进行推理和计算．【要点梳理】【高清课堂：389303 等边三角形，知识要点】要点一、等边三角形等边三角形定义：三边都相等的三角形叫等边三角形.要点诠释：由定义可知，等边三角形是一种特殊的等腰三角形．也就是说等腰三角形包括等边三角形．要点二、等边三角形的性质等边三角形的性质：等边三角形三个内角都相等，并且每一个内角都等于60°. 要点三、等边三角形的判定等边三角形的判定：（1）三条边都相等的三角形是等边三角形；（2）三个角都相等的三角形是等边三角形；（3）有一个角是60°的等腰三角形是等边三角形．要点四、含30°的直角三角形含30°的直角三角形的性质定理：在直角三角形中，如果有一个锐角是30°，那么它所对的直角边等于斜边的一半. 要点诠释：这个定理的前提条件是“在直角三角形中”，是证明直角三角形中一边等于另一边（斜边）的一半的重要方法之一，通常用于证明边的倍数关系. 【典型例题】类型一、等边三角形1、（2015秋·黄冈期中）如图，已知点B 、C 、D 在同一条直线上，ABC ∆和DCE ∆都是等边三角形，BE 交AC 于F ，AD 交CE 于H. （1）求证：△BCE ≌△ACD ；（2）求证：FH ∥BD.【答案与解析】（1）证明： ABC ∆和DCE ∆都是等边三角形 ∴BC ＝AC ，CE ＝CD ，∠BCA ＝∠ECD ＝60°∴∠BCA+∠ACE=∠ECD+∠ACE ，即∠BCE=∠ACD在△BCE 和△ACD 中BCE ACD CE B A D C C C ∠=∠==⎧⎪⎨⎪⎩∴△BCE ≌△ACD （SAS ）（2）由（1）知△BCE ≌△ACD 则∠CBF=∠CAH ，BC=AC又∵ABC ∆和DCE ∆都是等边三角形，且点B 、C 、D 在同一条直线上， ∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF ，在△BCF 和△ACH 中CBE CAH BC ACBCF ACH ∠=∠=∠=∠⎧⎪⎨⎪⎩∴△BCF ≌△ACH （ASA ） ∴CF=CH ，又∵∠FCH ＝60°∴△CHF 是等边三角形 ∴∠FHC ＝∠HCD=60°， ∴FH ∥BD【总结升华】本题考查等边三角形的判定与性质及全等三角形的判定与性质，熟知全等三角形的判定定理是解答此题的关键。

人教版八年级上13.3.2 等边三角形(1)(含答案)

13.3.2等边三角形（1）一．选择题（共8小题）1．如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中∠α+∠β的度数是（）A． 180°B． 220°C． 240°D． 300°2．下列说法正确的是（）A．等腰三角形的两条高相等C．有一个角是60°的锐角三角形是等边三角形B．等腰三角形一定是锐角三角形D．三角形三条角平分线的交点到三边的距离相等3．在△ABC中，①若AB=BC=CA，则△ABC为等边三角形；②若∠A=∠B=∠C，则△ABC 为等边三角形；③有两个角都是60°的三角形是等边三角形；④一个角为60°的等腰三角形是等边三角形．上述结论中正确的有（）A． 1个B． 2个C． 3个D． 4个4．如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于（）A． 25° B． 30°C．45°D． 60°5．如图，已知D、E、F分别是等边△ABC的边AB、BC、AC上的点，且DE⊥BC、EF⊥AC、FD⊥AB，则下列结论不成立的是（）A．△DEF是等边三角形B．△ADF≌△BED≌△CFEC．DE=AB D．S△ABC=3S△DEF6．如图，在△ABC中，D、E在BC上，且BD=DE=AD=AE=EC，则∠BAC的度数是（）A． 30°B． 45°C． 120°D． 15°7．如图，在△ABC中，AB=AC，∠A=120°，BC=6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为（）A． 4cm B． 3cm C． 2cm D． 1cm第1 题第4题第5题第7题8．已知∠AOB=30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1，O，P2三点所构成的三角形是（）A．直角三角形B．钝角三角形C．等腰三角形D．等边三角形二．填空题（共10小题）9．已知等腰△ABC中，AB=AC，∠B=60°，则∠A=_________度．10．△ABC中，∠A=∠B=60°，且AB=10cm，则BC=_________cm．11．在△ABC中，∠A=∠B=∠C，则△ABC是_________三角形．12．如图，将两个完全相同的含有30°角的三角板拼接在一起，则拼接后的△ABD的形状是_________．13．如图，M、N是△ABC的边BC上的两点，且BM=MN=NC=AM=AN．则∠BAN=_________．第13题第14题第15题14．如图，用圆规以直角顶点O为圆心，以适当半径画一条弧交两直角边于A、B两点，若再以A为圆心，以OA为半径画弧，与弧AB交于点C，则∠AOC等于_________．15．如图，将边长为6cm的等边三角形△ABC沿BC方向向右平移后得△DEF，DE、AC 相交于点G，若线段CF=4cm，则△GEC的周长是_________cm．16．如图，在等边△ABC中，D、E分别是AB、AC上的点，且AD=CE，则∠BCD+∠CBE= _________度．第16 题第17题第18题17．三个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=_______°．18．如图，△ABD与△AEC都是等边三角形，AB≠AC．下列结论中，正确的是_________．①BE=CD；②∠BOD=60°；③∠BDO=∠CEO．三．解答题（共5小题）19．如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．（1）求证：△ABE≌△CAD；（2）求∠BFD的度数．20．如图，D是等边△ABC的边AB上的一动点，以CD为一边向上作等边△EDC，连接AE，找出图中的一组全等三角形，并说明理由．21．已知，如图，延长△ABC的各边，使得BF=AC，AE=CD=AB，顺次连接D，E，F，得到△DEF为等边三角形．求证：（1）△AEF≌△CDE；（2）△ABC为等边三角形．22．已知：如图，在△ABC中，AB=BC，∠ABC=120°，BE⊥AC于点D，且DE=DB，试判断△CEB的形状，并说明理由．23．已知：如图1，点C为线段AB上一点，△ACM，△CBN都是等边三角形，AN交MC 于点E，BM交CN于点F．（1）求证：AN=BM；（2）求证：△CEF为等边三角形；（3）将△ACM绕点C按逆时针方向旋转90°，其他条件不变，在图2中补出符合要求的图形，并判断第（1）、（2）两小题的结论是否仍然成立（不要求证明）．13.3.2等边三角形三、CDDBDCCD四、9、60；10、10；11、等边；12、等边三角形；13、90度；14、60度；15、6；16、60；17、130；18、①②三、19、（1）证明：∵△ABC为等边三角形，∴∠BAC=∠C=60°，AB=CA，即∠BAE=∠C=60°，在△ABE和△CAD中，，∴△ABE≌△CAD（SAS）．（2）解：∵∠BFD=∠ABE+∠BAD，又∵△ABE≌△CAD，∴∠ABE=∠CAD．∴∠BFD=∠CAD+∠BAD=∠BAC=60°．20、解答：解：△BDC≌△AEC．理由如下：∵△ABC、△EDC均为等边三角形，∴BC=AC，DC=EC，∠BCA=∠ECD=60°．从而∠BCD=∠ACE．在△BDC和△AEC中，，∴△BDC≌△AEC（SAS）．21、解答：证明：（1）∵BF=AC，AB=AE（已知）∴FA=EC（等量加等量和相等）．（1分）∵△DEF是等边三角形（已知），∴EF=DE（等边三角形的性质）．（2分）又∵AE=CD（已知），∴△AEF≌△CDE（SSS）．（4分）（2）由△AEF≌△CDE，得∠FEA=∠EDC（对应角相等），∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF（等量代换），△DEF是等边三角形（已知），∴∠DEF=60°（等边三角形的性质），∴∠BCA=60°（等量代换），由△AEF≌△CDE，得∠EFA=∠DEC，∵∠DEC+∠FEC=60°，∴∠EFA+∠FEC=60°，又∠BAC是△AEF的外角，∴∠BAC=∠EFA+∠FEC=60°，∴△ABC中，AB=BC（等角对等边）．（6分）∴△ABC是等边三角形（等边三角形的判定）．（7分）22、解答：解：△CEB是等边三角形．（1分）证明：∵AB=BC，∠ABC=120°，BE⊥AC，∴∠CBE=∠ABE=60°．（3分）又DE=DB，BE⊥AC，∴CB=CE．（5分）∴△CEB是等边三角形．（7分）23、（1）证明：∵△ACM，△CBN是等边三角形，∴AC=MC，BC=NC，∠ACM=60°，∠NCB=60°，∴∠ACM+∠MCN=∠NCB+∠MCN，即：∠ACN=∠MCB，在△ACN和△MCB中，AC=MC，∠ACN=∠MCB，NC=BC，∴△ACN≌△MCB（SAS）．∴AN=BM．（2）证明：∵△AC N≌△MCB，∴∠CAN=∠CMB．又∵∠MCF=180°﹣∠ACM﹣∠NCB=180°﹣60°﹣60°=60°，∴∠MCF=∠ACE．在△CAE和△CMF中∠CAE=∠CMF，CA=CM，∠ACE=∠MCF，∴△CAE≌△CMF（ASA）．∴CE=CF．∴△CEF为等腰三角形．又∵∠ECF=60°，∴△CEF为等边三角形．（3）解：如右图，∵△CMA和△NCB都为等边三角形，∴MC=CA，CN=CB，∠MCA=∠BCN=60°，∴∠MCA+∠ACB=∠BCN+∠ACB，即∠MCB=∠ACN，∴△CMB≌△CAN，∴AN=MB，结论1成立，结论2不成立．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

人气最好的捕鱼游戏
[问答题,简答题]常见的稀土元素的价态有哪些？ [单选,A1型题]“想象”这种心理活动属于（）。A.情感过程B.意志过程C.意识过程D.个性特征E.认识过程 [单选]数字出版产品制作的一般流程不包括（）。A.内容整合B.产品规范化C.建立数据库D.产品测试 [单选]矿井中硫化氢最高允许浓度为（）。A、0.0005%B、0.0024%C、0.00066% [名词解释]Web服务器 [单选,A1型题]下列各项，不属于温燥证临床表现的是（）。A.发热有汗B.咽喉疼痛C.口渴饮水D.舌红脉浮数E.无汗头痛 [单选]“管理的艺术在于驾驭信息”的含义是（）。A、管理者要善于掌握信息，提高信息的时效性B、管理者要善于转换信息，实现信息的价值C、管理者要善于对信息分类，掌握战略级信息，完成企业战略目标D、管理者要善于将企业内部的物质流转换成信息流 [单选]6[综合知识试题1]某图的邻接矩阵如下所示，则该图为（）。A.B.C.D.ABCD [判断题]海绵动物由于具有特殊的水沟系结构，故对漂浮生活能很好的适应。?（）A.正确B.错误 [单选,A2型题,A1/A2型题]下列哪项不是湿淫证的特点（）A.易阻遏气机B.多损伤阳气C.只能从寒化D.病程黏滞缠绵E.病性重浊趋下 [单选,A1型题]下列哪种症状、体征和检查可确诊为后尿道完全断裂（）A.会阴部血肿B.下腹及骨盆部皮下瘀斑C.骨盆挤压痛D.插导尿管不能进入膀胱E.尿道造影，见造影剂外溢于后尿道周围未进入膀胱 [单选]能够用于激光光动力疗法的药物是（）A.吲哚青绿B.荧光素钠C.丙酮D.血卟啉衍生物E.甲醇 [单选]某些疾病夜间病情加重的原因多为()A．病室空气污浊通气不良B．机体内CO潴留C．卧位不适D．迷走神经兴奋性增高E．病室嘈杂，影响睡眠 [单选]被誉为“东方的希波克拉底誓言”，指出医务人员不仅要有精湛的医疗技术，还要拥有良好医德的著作是（）。A.《本草纲目》B.《大医精诚》C.《神农本草经》D.《黄帝内经》E.《千金方》 [单选,A2型题,A1/A2型题]点彩红细胞胞质中的颗粒为（）A.残存变性的DNAB.残存变性的RNAC.残存变性的脂蛋白D.核糖体E.金属颗粒沉淀 [单选,A2型题,A1/A2型题]下列哪一项不是结核性脑膜炎的并发症（）.A.脑出血B.脑积水C.继发性癫痫D.脑性瘫痪E.脑神经障碍 [单选,A4型题,A3/A4型题]男，10月，呕吐3天，腹泻4天，因无尿8小时入院，诊断重度等渗脱水伴酸中毒、营养不良。给以补液后12小时纠正脱水、酸中毒，16小时突然出现惊厥。治疗应采取的措施是()A．脱水B．补钙C．补钾D．补钠E．补镁 [单选]准时制生产的目标是（）。A.节约装配时间、减少装配中可能出现的问题B.通过产品的合理设计使产品易生产C.彻底消除无效劳动造成的损失D.有效地利用各种生产资源 [单选,A2型题,A1/A2型题]DSA要使一直径2mm的血管及其内径1mm的狭窄与一直径4mm的血管及其内径2mm的狭窄成像一样清晰，可以（）A.将碘浓度加倍B.将曝光量加倍C.将视野加倍D.将矩阵加倍E.将像素大小加倍 [单选]上皮组织具有保护、吸收、（）和感觉等功能。A.呼吸B.消化C.分泌D.排泄 [单选]从事国际航行船舶上的中国船员，凭本人的登陆、住宿。（）A.出境、入境证件B.护照C.海员证D.以上都是 [单选]关于急性肾衰竭下列哪项是不正确的（）A.肾功能短期内迅速减退B.肾小球滤过率下降C.既往均无慢性肾脏病史D.有水、电解质、酸碱平衡紊乱E.常伴有少尿 [单选]依据糖尿病诊断标准，确诊糖尿病选用（）A.全血血糖B.血浆血糖C.糖化血红蛋白D.尿糖定性E.24小时尿糖定量 [单选]属于PSC初始检查的内容是（）。A.船舶证书B.船体构造C.无线电设备D.操作性检查 [单选]85％深度烧伤伤员的创面焦痂处理方法，选择（）A.保痂下，有计划的分期切痂植皮B.中草药保痂蚕食脱痂植皮C.一次切痂植皮D.自然脱痂植皮E.保痂 [判断题]弱电综合布线，在一室外的一些走线位置我们可以共沟不共管。A.正确B.错误 [问答题,简答题]现实市场的形成需要具备哪些条件？ [判断题]买卖合同是出卖人转移标的物的所有权于买受人，买受人支付价款的合同。（）A.正确B.错误 [填空题]A，B两组分等摩尔扩散的代表单元操作是（），A在B中单向扩散的代表单元操作是（）。 [单选]下列哪种疾病容易导致压力负荷过重引起的心衰（）A.主动脉瓣关闭不全B.二尖瓣关闭不全C.动脉导管未闭D.肺动脉瓣狭窄E.甲状腺功能亢进症 [单选]以下哪项不是体外受精胚胎移植的适应证？（）A.不明原因性不孕B.宫颈因素不孕C.子宫内膜异位症D.双侧输卵管阻塞E.子宫内膜结核 [单选]下列各项中，不属于事业单位净资产项目的是()。A.事业结余B.固定基金C.专用基金D.应缴预算款 [单选]一条高速公路的通信系统由（）子系统构成。A.光纤数字传输系统、数字程控交换系统、会议电视系统、通信电源系统、光电缆工程及通信管道工程B.光纤数字传输系统、数字程控交换系统、有线广播系统、通信电源系统、光电缆工程及通信管道工程C.光纤数字传输系统、数字程控交换系 [判断题]推动长三角水稻农业发展的动力是人口压力.A.正确B.错误 [单选,A1型题]肾损伤后哪项护理措施不正确（）A.严密观察生命体征B.观察疼痛性质及程度C.绝对卧床休息D.向患者介绍肾损伤知识E.尽早离床活动 [单选]用户登录了网络系统，越权使用网络信息资源，这属于（）。A.身份窃取B.非授权访问C.数据窃取D.破坏网络的完整性 [判断题]在概括河流图形时，首先要研究河流的弯曲状和曲折系数。A.正确B.错误 [单选]下列不同环境中，相同的起火物最容易起火的为（）。A、富氧区B、缺氧区C、正常的室内环境D、真空区 [填空题]常用的服装面料有（）、（）、（）、（）、（）、（）。 [单选,A2型题,A1/A2型题]可以诱发鱼、禽、大鼠和猴子等多种动物肝癌的真菌毒素是（）。A.烟曲霉毒素B.橘青霉毒素C.黄曲霉毒素D.展青霉毒素E.赭曲霉毒素

初二数学等边三角形[人教版]

人教版数学八年级上册.等边三角形的性质与判定经典课件

初二上数学课件(人教版)-等边三角形

初二上数学课件(人教版)-等边三角形的性质与判定

初二数学等边三角形[人教版]

初二数学等边三角形[人教版]

八年级初二数学上册 13.3.2 等边三角形(第2课时) 【教学课件PPT】

人教版八年级数学上册等边三角形

部编版八年级数学上册《等边三角形》PPT课件

最新人教版初二上册数学【等边三角形(第一课时)】教学课件

初二数学等边三角形[人教版]

人教版八年级数学上册(教案).2等边三角形

人教版八年级数学上册12.3.2等边三角形(1)课件 (共16张PPT)

人教版初二数学上册：等边三角形(提高)知识讲解

最新人教版初中数学八年级上册 13.3.2《等边三角形》含有30度角的直角三角形课件

人教版八年级上13.3.2 等边三角形(1)(含答案)

初二数学等边三角形[人教版]

人教版数学八年级 上册.等边三角形的性质与判定经典课件

初二上数学课件(人教版)-等边三角形

初二上数学课件(人教版)-等边三角形的性质与判定

初二数学等边三角形[人教版]

初二数学等边三角形[人教版]

八年级初二数学上册 13.3.2 等边三角形(第2课时) 【教学课件PPT】

人教版八年级数学上册等边三角形

部编版八年级数学上册《等边三角形》PPT课件

最新人教版初二上册数学【等边三角形(第一课时)】教学课件

初二数学等边三角形[人教版]

人教版八年级数学上册(教案).2等边三角形

人教版八年级数学上册12.3.2等边三角形(1)课件 (共16张PPT)

人教版初二数学上册：等边三角形(提高)知识讲解

最新人教版初中数学八年级上册 13.3.2《等边三角形》含有30度角的直角三角形课件

人教版八年级上13.3.2 等边三角形(1)(含答案)

人教版数学八年级上册.等边三角形的性质与判定经典课件