矢量场标量场散度梯度旋度的理解
矢量场,标量场,散度,梯度,旋度的理解教学内容

矢量场,标量场,散度,梯度,旋度的理解1.梯度 gradient设体系中某处的物理参数(如温度、速度、浓度等)为w,在与其垂直距离的dy 处该参数为w+dw,则称为该物理参数的梯度,也即该物理参数的变化率。
如果参数为速度、浓度或温度,则分别称为速度梯度、浓度梯度或温度梯度。
在向量微积分中,标量场的梯度是一个向量场。
标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
更严格的说,从欧氏空间Rn到R的函数的梯度是在Rn某一点最佳的线性近似。
在这个意义上,梯度是雅戈比矩阵的一个特殊情况。
在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。
梯度一词有时用于斜度,也就是一个曲面沿着给定方向的倾斜程度。
可以通过取向量梯度和所研究的方向的点积来得到斜度。
梯度的数值有时也被成为梯度。
在二元函数的情形,设函数z=f(x,y)在平面区域D内具有一阶连续偏导数,则对于每一点P(x,y)∈D,都可以定出一个向量(δf/x)*i+(δf/y)*j这向量称为函数z=f(x,y)在点P(x,y)的梯度,记作gradf(x,y)类似的对三元函数也可以定义一个:(δf/x)*i+(δf/y)*j+(δf/z)*k 记为grad[f(x,y,z)]2.散度气象学中指:散度指流体运动时单位体积的改变率。
简单地说,流体在运动中集中的区域为辐合,运动中发散的区域为辐散。
用以表示的量称为散度,值为负时为辐合,此时有利于天气系统的的发展和增强,为正时表示辐散,有利于天气系统的消散。
表示辐合、辐散的物理量为散度。
微积分学→多元微积分→多元函数积分中:设某量场由 A(x,y,z) = P(x,y,z)i + Q(x.y,z)j + R(x,y,z)k 给出,其中 P、Q、R 具有一阶连续偏导数,∑是场内一有向曲面,n 是∑在点 (x,y,z) 处的单位法向量,则∫∫A·ndS 叫做向量场 A 通过曲面∑向着指定侧的通量,而δP/δx + δQ/δy + δR/δz 叫做向量场 A 的散度,记作 div A,即 div A = δP/δx + δQ/δy + δR/δz。
梯度散度和旋度——定义及公式

梯度散度和旋度——定义及公式梯度、散度和旋度是矢量场的重要属性,它们帮助我们理解和描述矢量场的变化特征。
梯度表示了矢量场的变化率和方向,散度表示了矢量场的流出或流入程度,旋度表示了矢量场的循环或旋转程度。
在物理学、工程学和应用数学等领域,梯度、散度和旋度被广泛应用于描述流体力学、电磁场和温度分布等问题。
首先,让我们来看看梯度的定义和公式。
梯度表示了矢量场在一个点上的最大变化率和该变化的方向。
对于一个标量场(只有大小没有方向的场),梯度是一个矢量场。
设f(x,y,z)是一个三维空间中的标量场,梯度∇f(x,y,z)可以表示为:∇f(x,y,z)=(∂f/∂x,∂f/∂y,∂f/∂z)其中,∂f/∂x、∂f/∂y和∂f/∂z分别表示f对x、y和z的偏导数。
梯度的大小表示了函数在该点上变化最快的方向。
接下来,我们来看看散度的定义和公式。
散度表示了矢量场的流出或流入程度。
对于一个三维矢量场F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z)),它的散度∇·F可以表示为:∇·F=∂P/∂x+∂Q/∂y+∂R/∂z其中,∂P/∂x、∂Q/∂y和∂R/∂z分别表示F的各个分量对x、y和z的偏导数。
散度的值正表示流出,负表示流入。
最后,我们来看看旋度的定义和公式。
旋度表示了矢量场的循环或旋转程度。
对于一个三维矢量场F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z)),它的旋度∇×F可以表示为:∇×F=(∂R/∂y-∂Q/∂z,∂P/∂z-∂R/∂x,∂Q/∂x-∂P/∂y)其中,∂R/∂y-∂Q/∂z、∂P/∂z-∂R/∂x、∂Q/∂x-∂P/∂y分别表示F的各个分量对x、y和z的偏导数之差。
旋度的大小表示了场的循环或旋转的强度。
梯度、散度和旋度提供了一种描述矢量场的数学工具,帮助我们分析矢量场的性质和行为。
通过计算这些属性,我们可以得到关于矢量场的重要信息,如流体的速度分布、电磁场的演化和温度场的变化。
旋度梯度散度方向导数

旋度梯度散度方向导数旋度、梯度、散度和方向导数是微分几何中的一些基本概念,它们在物理学、工程学和应用数学中都有广泛的应用。
本文将对旋度、梯度、散度和方向导数进行详细的介绍和解释。
1. 旋度旋度是矢量场的一个重要属性,用于描述矢量场的旋转性质。
在三维空间中,一个矢量场的旋度可以表示为向量的叉乘形式,即旋度矢量。
旋度矢量的大小表示旋转的强度,方向则表示旋转的方向。
旋度的计算公式为:∇ × F = (∂Fz/∂y - ∂Fy/∂z) i + (∂Fx/∂z - ∂Fz/∂x) j + (∂Fy/∂x - ∂Fx/∂y) k其中,F = Fx i + Fy j + Fz k 是一个矢量场,∂/∂x、∂/∂y、∂/∂z 分别表示对 x、y、z 的偏导数。
2. 梯度梯度是标量场的一个重要属性,用于描述标量场的变化率。
在三维空间中,一个标量场的梯度可以表示为矢量的形式,即梯度矢量。
梯度矢量的大小表示变化率的大小,方向则表示变化率的方向。
梯度的计算公式为:∇f = (∂f/∂x) i + (∂f/∂y) j + (∂f/∂z) k其中,f 是一个标量场,∂f/∂x、∂f/∂y、∂f/∂z 分别表示对 x、y、z 的偏导数。
3. 散度散度是矢量场的一个重要属性,用于描述矢量场的收敛或发散性质。
在三维空间中,一个矢量场的散度可以表示为矢量的点乘形式,即散度标量。
散度标量的大小表示收敛或发散的强度,正值表示收敛,负值表示发散。
散度的计算公式为:∇ · F = (∂Fx/∂x) + (∂Fy/∂y) + (∂Fz/∂z)其中,F = Fx i + Fy j + Fz k 是一个矢量场,∂Fx/∂x、∂Fy/∂y、∂Fz/∂z 分别表示对 x、y、z 的偏导数。
4. 方向导数方向导数是标量场在给定方向上的变化率。
在三维空间中,标量场的方向导数可以表示为梯度矢量和给定方向单位矢量的点乘形式。
方向导数的大小表示变化率的大小,方向则表示变化率的方向。
第3讲 矢量分析(2)

P 穿出该六面体的净通量为
Fx Fy Fz S F dS x xyz y xyz z xyz
根据定义,则得到直角坐标系中的散度 表达式为
F lim
S
F dS V
V 0
Fx Fy Fz x y z
u • 0 —— u(M)沿l 方向无变化。 l
方向导数的概念
问题:在什么方向上变化率最大、其最大的变化率为多少?
3. 标量场的梯度
标量场的场函数为 ( x, y, z, t ) a.方向导数:
d 空间变化率,称为方向导数。 dl
P1
dn
P
P2
dl
d 为最大的方向导数。 dn
0
0 d
b.梯度 定义:标量场中某点梯度的大小为该点最大的方向导数, 其方向为该点所在等值面的法线方向。 d ˆ an 数学表达式: grad dn
计算
d d d n d cos d a a ˆn ˆl dn dl d n dl d n d grad d l
l1 l2 l3 l4
Fy1y Fz 2 z Fy 3 y Fz 4 z
Fy1 Fy M
Fy z
M
z 2
z
3
4 z M
C 2
Fz y Fz 2 Fz M y M 2 Fy z Fy 3 Fy M z M 2 F y Fz 4 Fz M z y M 2
Si
散度定理是闭合曲面积分
与体积分之间的一个变换关系。
散度体积分=闭合面通量
三. 矢量场的环流和旋度
1. 矢量场的环流与旋涡源
旋度梯度散度

旋度梯度散度旋度、梯度和散度是向量分析中的三个重要概念,它们在物理学、工程学和应用数学中具有广泛的应用。
本文将就旋度、梯度和散度这三个概念展开讨论,介绍它们的定义、性质以及在实际问题中的应用。
一、旋度的定义和性质旋度是一个向量场的一个重要特征,它描述了向量场的旋转性质。
在三维空间中,给定一个向量场F(x, y, z),其旋度定义为:rot F = (∂Fz/∂y - ∂Fy/∂z, ∂Fx/∂z - ∂Fz/∂x, ∂Fy/∂x - ∂Fx/∂y)其中,Fx、Fy、Fz分别表示向量场F在x、y、z方向上的分量。
旋度的几何意义是:旋度的大小表示向量场的旋转速率,而旋度的方向表示旋转轴的方向。
换言之,旋度可以告诉我们向量场在某一点上是否存在旋转,并且可以确定旋转轴的方向。
旋度具有一些重要的性质。
首先,旋度是一个向量,它的方向垂直于曲面元素的法向量,并且符合右手法则。
其次,旋度与向量场的平面性质相关,当旋度为零时,向量场是无旋的,即向量场在任意闭合路径上的线积分为零;当旋度不为零时,向量场是有旋的,即向量场在某些路径上的线积分不为零。
二、梯度的定义和性质梯度是一个标量场的一个重要特征,它描述了标量场的变化率和变化方向。
在三维空间中,给定一个标量场φ(x, y, z),其梯度定义为:grad φ = (∂φ/∂x, ∂φ/∂y, ∂φ/∂z)梯度的几何意义是:梯度的大小表示标量场变化最快的方向,而梯度的方向与变化率最大的方向一致。
梯度具有一些重要的性质。
首先,梯度是一个向量,它的方向指向标量场变化最快的方向,并且变化率最大;其次,梯度的大小表示标量场变化的速率,大小越大表示变化越快;最后,梯度是无旋的向量场,即梯度场的旋度为零。
三、散度的定义和性质散度是一个向量场的一个重要特征,它描述了向量场的发散性质。
在三维空间中,给定一个向量场F(x, y, z),其散度定义为:div F = ∂Fx/∂x + ∂Fy/∂y + ∂Fz/∂z散度的几何意义是:散度的大小表示向量场在某一点上的发散程度,正值表示向外发散,负值表示向内汇聚。
散度,旋度,梯度

《散度,旋度,梯度》1、散度:可用于表征空间各点矢量场发散的强弱程度,物理上,散度的意义是场的有源性。
当div F>0 ,表示该点有散发通量的正源(发散源);当div F<0 表示该点有吸收通量的负源(洞或汇);当div F=0,表示该点无源。
2、旋度是向量分析中的一个向量算子,可以表示三维向量场对某一点附近的微元造成的旋转程度。
这个向量提供了向量场在这一点的旋转性质。
旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴,它和向量旋转的方向满足右手定则。
旋度向量的大小则是绕着这个旋转轴旋转的环量与旋转路径围成的面元的面积之比。
3、梯度:是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值。
对散度的理解梯度: 运算的对像是纯量,运算出来的结果会是向量在一个纯量场中,梯度的计算结果会是"在每个位置都算出一个向量,而这个向量的方向会是在任何一点上从其周围(极接近的周围,学过微积分该知道甚么叫极限吧?)纯量值最小处指向周围纯量值最大处.而这个向量的大小会是上面所说的那个最小与最大的差距程度"举例子来讲会比较简单,如果现在的纯量场用一座山来表示,纯量值越大的地方越高,反之则越低.经过梯度这个运操作数的运算以后,会在这座山的每一个点上都算出一个向量,这个向量会指向每个点最陡的那个方向,而向量的大小则代表了这个最陡的方向到底有多陡.散度: 运算的对像是向量,运算出来的结果会是纯量散度的作用对像是向量场,如果现在我们考虑任何一个点(或者说这个点的周围极小的一块区域),在这个点上,向量场的发散程度,如果是正的,代表这些向量场是往外散出的.如果是负的,代表这些向量场是往内集中的.一样,举例子:因为散度的作用对像是向量场,所以就不能用上面所讲的山来想象,这次要想象一个大广场里挤了很多人,如果每个人都在到处走动,是不是可以把每个人的行动都看成是一个向量,假如现在某人放了一个屁,周围的人(可能包含他自己)都想要赶快闪远一点,就会发现,在这块区域的人都往这小块区域以外的方向移动.对啦…这就是散度(你也可以想说是闪远一点的闪度…冷…),大家如果散得越快,散得人越多,这个散度算出来就就越大.旋度: 运算的对像是向量,运算出来的结果会是向量旋度的作用对象也是向量场,这次直接用上面的例子来讲:如果现在散开的众人都是直直的往那个屁的反方向散开,这时候你看到这些人的动线是不是就是一个标准的幅射状?不过事实上,每个人在闻到屁的时候是不会确切的知道屁到底是来自哪个方向的.而可能会走错方向,试过之后才发现不对劲,越找越臭.这时候你看到众人的走向不见得就是一个幅射状(大家都径向移动),而可能有一些切向移动的成份在(以屁发点为中心来看)旋度对应的就是这些切向移动的情况,相对来讲,散度对应的其实就是径向移动的情况.而一个屁,虽然可能会像上述的造成一些切向的移动,但理论上来讲,并不会使散开的众人较趋向于顺时钟转,或逆时钟转.在这种情况,顺时钟转的情况可以看作与逆时钟转的情况抵消,因此,在这情况下,旋度仍然是零.也就是说,一个屁能造成散度,而不会造成旋度…而甚么时候是有旋度的呢?如果这时候音乐一放,大家开始围着中间的营火手拉手跳起土风舞(当然是要绕着营火转的那种啦)这时候就会有旋度没有散度啦.(刚刚一直放屁的那位跑出去找厕所的除外)以上这三个,有一点一定要记得的.不论是梯度,散度,旋度,都是一种local的量(纯量,向量),所考虑的都是任何一点(其周围极接近,极小的小范围)的情况.以上举的例子因为要容易了解,所以都是针对二度空间向量为例,而且都是很大的东西,但广场是一个点,营火晚会也是一个点,纳须弥于芥子,这就请自行想象吧。
散度、旋度、梯度释义

散度、旋度、梯度释义散度、旋度、梯度是矢量分析中的重要概念,通常用于描述矢量场的特性。
1. 散度(Divergence)散度是指矢量场在某一点上的流出量与流入量之差,也就是说,它描述了矢量场的源和汇在该点的情况。
如果某一点的散度为正,表示该点是矢量场的源,矢量场从该点向外扩散;如果散度为负,表示该点是矢量场的汇,矢量场汇聚于该点;如果散度为零,则表示该点是矢量场的旋转中心。
数学上,散度用向量微积分的形式来表示,它是矢量场的散度算子作用于该点处的矢量的结果。
散度算子用符号“∇·”表示,因此,该点的散度可以用以下公式来计算:div F = ∇·F其中,F表示矢量场,div F表示该点的散度。
2. 旋度(Curl)旋度是指矢量场在某一点上的旋转程度,也就是说,它描述了矢量场在该点处的旋转方向和强度。
如果某一点的旋度为正,表示该点周围的矢量场是顺时针旋转的;如果旋度为负,表示该点周围的矢量场是逆时针旋转的;如果旋度为零,则表示该点周围的矢量场没有旋转。
数学上,旋度用向量微积分的形式来表示,它是矢量场的旋度算子作用于该点处的矢量的结果。
旋度算子用符号“∇×”表示,因此,该点的旋度可以用以下公式来计算:curl F = ∇×F其中,F表示矢量场,curl F表示该点的旋度。
3. 梯度(Gradient)梯度是指矢量场在某一点上的变化率,也就是说,它描述了矢量场在该点处的变化方向和强度。
如果某一点的梯度为正,表示该点处的矢量场在该方向上增强;如果梯度为负,表示该点处的矢量场在该方向上减弱;如果梯度为零,则表示该点处的矢量场没有变化。
数学上,梯度用向量微积分的形式来表示,它是矢量场的梯度算子作用于该点处的标量函数的结果。
梯度算子用符号“∇”表示,因此,该点的梯度可以用以下公式来计算:grad f = ∇f其中,f表示标量函数,grad f表示该点的梯度。
梯度、散度和旋度——定义及公式

梯度、散度和旋度——定义及公式1 哈密顿算子(Hamiltion Operator )哈密顿算子本身没有含义,只有作用于后面的量才有实际意义;它是一个微分算子,符号为∇。
三维坐标系下,有=i j k x y z∂∂∂∇++∂∂∂ 或者 (,,)x y z ∂∂∂∇=∂∂∂ 其中,,i j k 分别为xyz 方向上的单位矢量。
2 梯度(Gradient ) 2.1 梯度的定义梯度是哈密顿算子直接作用于函数f 的结果(f 可以是标量和向量)。
(,,)f f f f f f grad f f i j k x y z x y z ∂∂∂∂∂∂=∇=++=∂∂∂∂∂∂ 标量场的梯度是向量,标量场中某一点的梯度指向标量场增长最快的地方,梯度的长度是最大变化率。
2.2 梯度的性质∇c=0∇(RS)= ∇R+∇S21()(),0R S R R S S S S∇=∇-∇≠ [()]()f S f S S '∇=∇其中,C 为常数,R 、S 为两个标量场,f 为一连续可微函数。
3 散度(Divergence )散度是哈密顿算子与矢量函数f 点积的结果,是一个标量。
设矢量函数=(,,)x y z x y z f f i f j f k f f f =++则散度表示为: (,,)(,,)y x z x y z f f f div f f f f f x y z x y z∂∂∂∂∂∂=∇==++∂∂∂∂∂∂ 散度是描述空气从周围汇合到某一处或从某一处散开来程度的量。
它可用于表征空间各点矢量场发散的强弱程度,物理上,散度的意义是场的有源性。
当0div f >,该点有散发通量的正源(发散源);当0div f <,该点有吸收通量的负源(洞或汇); 当=0div f ,该点无源。
4 旋度(Curl, Rotation )旋度是哈密顿算子与矢量函数f 叉积的结果,是一个矢量,设矢量函数=(,,)x y z x y z f f i f j f k f f f =++则旋度:=rot ()()()y y x x z z x y zij k f f f f f f curl f f f i j k xy z y zz x x y f f f ∂∂∂∂∂∂∂∂∂=∇⨯==-+-+-∂∂∂∂∂∂∂∂∂ 旋度是矢量分析中的一个矢量算子,可以表示三维矢量场对某一点附近的微元造成的旋转程度。
矢量分析:旋度、散度、梯度

矢量三重积: Vector triple production
A (B C) B( AC) C( A B)
公式右边为“BAC-CAB”, 故称为“Back -Cab”法则, 以便记忆。
例:
给定两矢量 A 2xˆ 3yˆ 4zˆ 和 B 6xˆ 4yˆ 1zˆ ,求 A B 在 C xˆ yˆ zˆ 上的分量。
s
q
4 r2
s
ds
q
4 r2
4 r 2
q
这证明在此球面上所穿过的电通量 e 的源正是点电荷q。
例:
球面S上任意点的位置矢量为 r xˆx yˆy zˆz rˆr,
试利用散度定理计算 r ds
解:
S
r x y z 3 x y z
r ds rdv 3 dv 3 4 r3 4 r3
Curl
[ A nˆ lim
l A dl ]max
S 0
S
2、旋度的物理意义
1) 矢量A的旋度是一个矢量, 其大小是矢量A在给定点处的最大 环量面密度, 其方向就是当面元的取向使环量面密度最大时,
该面元矢量的方向 nˆ 。
2) 它描述A在该点处的旋涡源强度。
3) 若某区域中各点curl A=0, 称A为无旋场或保守场。
无源场f可以表示为另一个矢量场的旋度即202161075可将矢量场f表示为一个无源场fs和无旋场f因而可定义一个标量位函数u和矢量位函数a使得202161076常用的矢量恒等式202161077202161078矢量分析小结基本内容矢量场的表示方法和代数运算和乘积运算亥姆霍兹方程202161079基本要求了解矢量场散度的定义掌握其计算方法和物理意义
关于梯度、旋度和散度的直观理解

关于梯度、旋度和散度的直观理解散度为零,说明是无源场;散度不为零时,则说明是有源场(有正源或负源)若你的场是一个流速场,则该场的散度是该流体在某一点单位时间流出单位体积的净流量. 如果在某点,某场的散度不为零,表示该场在该点有源,例如若电场在某点散度不为零,表示该点有电荷,若流速场不为零,表是在该点有流体源源不绝地产生或消失(若散度为负).一个场在某处,沿着一无穷小的平面边界做环积分,平面法向量即由旋度向量给定,旋度向量的长度则是单位面积的环积分值.基本上旋度要衡量的是一向量场在某点是否有转弯. 梯度: 运算的对像是纯量,运算出来的结果会是向量在一个纯量场中,梯度的计算结果会是"在每个位置都算出一个向量,而这个向量的方向会是在任何一点上从其周围(极接近的周围,学过微积分该知道甚么叫极限吧?)纯量值最小处指向周围纯量值最大处.而这个向量的大小会是上面所说的那个最小与最大的差距程度"举例子来讲会比较简单,如果现在的纯量场用一座山来表示,纯量值越大的地方越高,反之则越低.经过梯度这个运操作数的运算以后,会在这座山的每一个点上都算出一个向量,这个向量会指向每个点最陡的那个方向,而向量的大小则代表了这个最陡的方向到底有多陡.散度: 运算的对像是向量,运算出来的结果会是纯量散度的作用对像是向量场,如果现在我们考虑任何一个点(或者说这个点的周围极小的一块区域),在这个点上,向量场的发散程度,如果是正的,代表这些向量场是往外散出的.如果是负的,代表这些向量场是往内集中的.一样,举例子:因为散度的作用对像是向量场,所以就不能用上面所讲的山来想象,这次要想象一个大广场里挤了很多人,如果每个人都在到处走动,是不是可以把每个人的行动都看成是一个向量,假如现在某人放了一个屁,周围的人(可能包含他自己)都想要赶快闪远一点,就会发现,在这块区域的人都往这小块区域以外的方向移动.对啦..这就是散度(你也可以想说是闪远一点的闪度....冷....),大家如果散得越快,散得人越多,这个散度算出来就就越大.旋度: 运算的对像是向量,运算出来的结果会是向量旋度的作用对象也是向量场,这次直接用上面的例子来讲:如果现在散开的众人都是直直的往那个屁的反方向散开,这时候你看到这些人的动线是不是就是一个标准的幅射状??不过事实上,每个人在闻到屁的时候是不会确切的知道屁到底是来自哪个方向的.而可能会走错方向,试过之后才发现不对劲,越找越臭.这时候你看到众人的走向不见得就是一个幅射状(大家都径向移动),而可能有一些切向移动的成份在(以屁发点为中心来看)旋度对应的就是这些切向移动的情况,相对来讲,散度对应的其实就是径向移动的情况.而一个屁,虽然可能会像上述的造成一些切向的移动,但理论上来讲,并不会使散开的众人较趋向于顺时钟转,或逆时钟转.在这种情况,顺时钟转的情况可以看作与逆时钟转的情况抵消,因此,在这情况下,旋度仍然是零.也就是说,一个屁能造成散度,而不会造成旋度....而甚么时候是有旋度的呢??如果这时候音乐一放,大家开始围着中间的营火手拉手跳起土风舞(当然是要绕着营火转的那种啦)这时候就会有旋度没有散度啦.(刚刚一直放屁的那位跑出去找厕所的除外) 以上这三个,有一点一定要记得的.不论是梯度,散度,旋度,都是一种local的量(纯量,向量),所考虑的都是任何一点(其周围极接近,极小的小范围)的情况.以上举的例子因为要容易了解,所以都是针对二度空间向量为例,而且都是很大的东西,但广场是一个点,营火晚会也是一个点,纳须弥于芥子,这就请自行想象吧.分享:。
散度旋度梯度

散度散度是向量分析中的一个向量算子,将向量空间上的一个向量场(矢量场)对应到一个标量场上。
散度描述的是向量场里一个点是汇聚点还是发源点,形象地说,就是这包含这一点的一个微小体元中的向量是“向外”居多还是“向内”居多。
举例来说,考虑空间中的静电场,其空间里的电场强度是一个矢量场。
正电荷附近,电场线“向外”发射,所以正电荷处的散度为正值,电荷越大,散度越大。
负电荷附近,电场线“向内”,所以负电荷处的散度为负值,电荷越大,散度越小。
定义定义向量场的散度,首先要引入通量的概念。
给定一个三维空间中的向量场以及一个简单有向曲面,则向量场通过曲面的通量就是曲面每一点上的场向量在曲面法向方向上的分量的积分:其中是积分的面积元,n是Σ在点(x,y,z)处的单位法向量。
如果曲面是封闭的,例如球面,那么通常约定法向量是从里朝外的,所以这时候的通量是描述曲面上的场向量朝外的程度。
通量描述了一定区域(也就是)中向量场的方向趋势,散度则是这个性质的一种局部描述[1]:7-8,也就是说,从散度在一点的值,我们可以看出向量场在这点附近到底倾向发散或收敛。
要算某一点的散度,先求包含这一点的某一个封闭曲面的通量除以封闭曲面围起来的微小体元的体积(这体积用表示)得到的比值,向量场在点的散度即是这比值在体元趋向于点时的极限。
用数学公式表示即:[2]:4如果用Nabla算子表示的话,向量场的散度记作:[2]:5从定义中可以看出,散度是向量场的一种强度性质,就如同密度、浓度、温度一样,它对应的广延性质是一个封闭区域表面的通量,所以说散度是通量的体密度[1]:7-8。
物理上,散度的意义是场的有源性。
某一点或某个区域的散度大于零,表示向量场在这一点或这一区域有新的通量产生,小于零则表示向量场在这一点或区域有通量湮灭。
这样的点或区域分别称为向量场的正源(发散源)和负源(洞)[1]:8。
举例来说,假设将太空中各个点的热辐射强度向量看做一个向量场,那么某个热辐射源(比如太阳)周边的热辐射强度向量都指向外,说明太阳是不断产生新的热辐射的源头,其散度大于零。
矢量运算(梯度、散度、旋度)与拉普拉斯算符公式整理
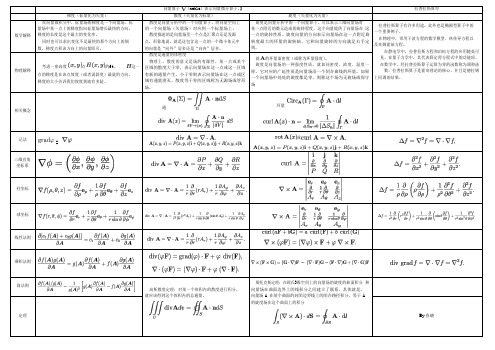
向量算子 (nabla )表示向量微分算子。
】拉普拉斯算符梯度(标量化为矢量)散度(矢量化为标量)旋度(矢量化为矢量)数学解释在向量微积分中,标量场的梯度是一个向量场。
标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
同时也可以求出变化不是最快的那个方向上的倒数,梯度点积该方向上的向量即可。
散度是向量分析中的一个向量算子,将向量空间上的一个向量场(矢量场)对应到一个标量场上。
散度描述的是向量场里一个点是汇聚点还是发源 点,形象地说,就是这包含这一点的一个微小体元中 的向量是“向外”居多还是“向内”居多。
旋度是向量分析中的一个向量算子,可以表示三维向量场对 某一点附近的微元造成的旋转程度。
这个向量提供了向量场在 这一点的旋转性质。
旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴,它和向量旋转的方向满足右手定则。
拉普拉斯算子有许多用途,此外也是椭圆型算子中的 一个重要例子。
在物理中,常用于波方程的数学模型、热传导方程以 及亥姆霍兹方程。
在静电学中,拉普拉斯方程和泊松方程的应用随处可见。
在量子力学中,其代表薛定谔方程式中的动能项。
在数学中,经拉普拉斯算子运算为零的函数称为调和函 数;拉普拉斯算子是霍奇理论的核心,并且是德拉姆 上同调的结果。
物理解释考虑一座高度 点 的ft 。
这一 点的梯度是在该点坡度(或者说斜度)最陡的方向。
梯度的大小告诉我们坡度到底有多陡。
散度是通量的体密度物理上,散度的意义是场的有源性。
某一点或某个区域的散度大于零,表示向量场在这一点或这一区域有新的通量产生,小于零则表示向量场在这一点或区域有通量湮灭。
散度等于零的区域称为无源场或管形场。
就 的环量面密度(或称为环量强度)。
旋度是向量场的一种强度性质,就如同密度、浓度、温度一 样,它对应的广延性质是向量场沿一个闭合曲线的环量。
如果一个向量场中处处的旋度都是零,则称这个场为无旋场或保守场相关概念通环量记法=或三维直角坐标系柱坐标球坐标线性法则乘积法则商法则高斯散度定理:对某一个体积内的散度进行积分, 就应该得到这个体积内的总通量。
向量场与标量场的梯度散度与旋度

向量场与标量场的梯度散度与旋度向量场与标量场的梯度、散度与旋度一、引言在物理学和数学中,向量场和标量场是两个基本的概念。
向量场是指在每个点上都有一个向量的场,而标量场是指在每个点上都有一个标量的场。
本文将介绍向量场与标量场的概念以及它们的梯度、散度和旋度。
二、向量场的概念向量场是指在空间中的每个点上都有一个向量的场。
向量场可以用箭头表示,箭头的方向表示向量的方向,箭头的长度表示向量的大小。
向量场可以描述物理量的分布情况,如速度场、电场等。
三、标量场的概念标量场是指在空间中的每个点上都有一个标量的场。
标量场可以用等高线表示,等高线的密集程度表示标量的大小。
标量场可以描述温度场、压力场等物理量的分布情况。
四、向量场的梯度向量场的梯度表示其在空间中的变化率。
在数学中,向量场的梯度可以用偏导数表示。
对于一个二维向量场F(x, y),其梯度∇F(x, y)可以表示为:∇F(x, y) = (∂F/∂x, ∂F/∂y)其中,∂F/∂x表示F关于x的偏导数,∂F/∂y表示F关于y的偏导数。
梯度的方向表示向量场变化的方向,梯度的大小表示变化的快慢。
五、标量场的梯度标量场的梯度表示其在空间中的变化率。
在数学中,标量场的梯度可以用梯度算子表示。
对于一个标量场φ(x, y),其梯度∇φ(x, y)可以表示为:∇φ(x, y) = (∂φ/∂x, ∂φ/∂y)其中,∂φ/∂x表示φ关于x的偏导数,∂φ/∂y表示φ关于y的偏导数。
梯度的方向表示标量场变化的方向,梯度的大小表示变化的快慢。
六、向量场的散度向量场的散度表示其在空间中的发散情况。
在数学中,向量场的散度可以用散度算子表示。
对于一个二维向量场F(x, y),其散度∇·F(x, y)可以表示为:∇·F(x, y) = (∂F/∂x + ∂F/∂y)其中,∂F/∂x表示F关于x的偏导数,∂F/∂y表示F关于y的偏导数。
散度表示向量场的流入流出情况,散度为正表示有流出的趋势,散度为负表示有流入的趋势。
梯度散度旋度的表达式和物理意义

梯度散度旋度的表达式和物理意义梯度、散度和旋度是矢量分析中的重要概念,用于描述矢量场的性质和变化规律。
它们在物理学、工程学等领域中具有广泛的应用。
本文将分别介绍梯度、散度和旋度的表达式及其物理意义。
一、梯度的表达式和物理意义梯度是矢量场中变化最快的方向和变化率的量化表示。
对于一个标量场,其梯度表示了该场在每个点上的变化率和变化方向。
梯度的表达式可以用微分算符∇(读作nabla)来表示,梯度算符作用于标量场可以得到一个矢量场,其表达式如下:∇φ = (∂φ/∂x)i + (∂φ/∂y)j + (∂φ/∂z)k其中,φ表示标量场,(∂φ/∂x)、(∂φ/∂y)、(∂φ/∂z)分别表示φ对x、y、z的偏导数,i、j、k分别表示坐标轴x、y、z方向的单位矢量。
梯度的物理意义是表示标量场在空间中的变化率和变化方向。
梯度的大小表示了标量场在某一点上的变化率,而梯度的方向表示了变化最快的方向。
例如,在温度场中,梯度的大小表示了温度的变化速率,而梯度的方向表示了温度变化最快的方向。
二、散度的表达式和物理意义散度是矢量场中的源和汇的量化表示,用来描述矢量场的流入和流出情况。
对于一个矢量场,其散度表示了该场在每个点上的流出或流入速率。
散度的表达式可以用梯度算符∇和点乘运算来表示,散度算符作用于矢量场可以得到一个标量场,其表达式如下:div A = ∇·A = (∂A_x/∂x) + (∂A_y/∂y) + (∂A_z/∂z)其中,A表示矢量场,A_x、A_y、A_z分别表示A在x、y、z方向上的分量。
散度的物理意义是表示矢量场在某一点上的流出或流入速率。
散度的正值表示矢量场在该点上的流出,负值表示矢量场在该点上的流入,而散度为零表示该点上不存在源和汇。
例如,在电场中,散度的正值表示电场从该点流出,负值表示电场流入该点。
三、旋度的表达式和物理意义旋度是矢量场中的旋转性质的量化表示,用来描述矢量场的旋转情况。
关于梯度、旋度和散度的直观理解

关于梯度、旋度和散度的直观理解梯度、旋度和散度是向量场中常用的概念,它们在物理学、数学、计算机图形学等多个领域中有广泛的应用。
本文将从直观的角度出发,简单介绍这三个概念。
梯度:在向量场中,梯度描述的是向量场在某一点处变化最快的方向和大小。
在数学上,梯度是一种向量算子,表示一个标量函数的变化速率最快的方向。
例如,在地形高度图中,我们可以用梯度描述地面的坡度,地形越陡峭,梯度值越大。
梯度的方向指向函数取最大值的方向,大小表示变化率的大小。
因此,梯度经常用来计算曲面的切向和法向。
在梯度场中,梯度表示每个位置的变化的方向和大小,也可以用来计算位势场中的力场。
旋度:在向量场中,旋度描述向量场的局部旋转性质,即向量场在一个点处的“自旋”程度。
在数学上,旋度是一种向量算子,对于一种三维向量场,旋度可以描述在某一点处该向量场的局部旋转程度和方向。
旋度的大小与该点附近的环形的“自旋率”成正比,方向垂直于该环面,总是环面法线的方向。
在物理学中,旋度经常用于描述涡旋和旋转性质,例如涡旋流场、电场和磁场等。
散度:在向量场中,散度描述的是向量场在一个点上的大小,即向量场在某一点处的“源”或“汇”程度。
在数学上,散度是一种向量算子,用来描述一个三维向量场在某一点上的流入流出程度,它表示物质或能量在该点上出现的“净量”(散度为正表示物质或能量从该点流出,散度为负表示物质或能量从该点流入)。
在物理学中,散度经常用来描述电偶极子、电荷密度、质量流量等现象。
梯度、旋度和散度在数学上是三个不同的概念,但它们在物理学中具有紧密的联系。
例如,旋度和散度可以用于磁场、电场、流体动力学等领域的描述。
在现实中,物质和能量在空间中流动和转移,这些现象都可以用梯度、旋度和散度来描述。
因此,对于物理学、数学和计算机图形学等领域的研究人员来说,掌握这三个概念的基本含义和运算方法非常重要。
6矢量分析:旋度、散度、梯度

ˆx y ˆy z ˆr, ˆz r rx
x y z r 3 x y z
4 3 3 S r ds V rdv 3V dv 3 3 r 4 r
§1 .3 环量与旋度, 斯托克斯定理
Curl, circulation, The Stokes’s theorem
这个极限的意义就是环量的面密度, 或称环量强度。
由于面元是有方向的, 它与封闭曲线l的绕行方向成右手螺旋关系,
因此在给定点处, 上述极限值对于不同的面元是不同的。 为此, 引入旋度(curl或rotation):
ˆ lim Curl A n
2、旋度的物理意义
[ A dl ]max
散度可用算符 哈密顿 表示为
divA A
哈密顿
ˆ ˆ z ˆ x y x y z
拉普拉斯2
2 2 2 2 2 2 x y z
divA 0
divA 0
divA 0
正源
负源
无源
散度的基本运算公式
C 0
C为常矢量
和或差: Vector addition or subtraction
则
ˆBx y ˆBy z ˆBz Bx
ˆ( Ax Bx ) y ˆ ( Ay By ) z ˆ( Az Bz ) A B x
图 1 -2 矢量的相加和相减
1 .1 .2 标量积和矢量积
矢量的相乘有两种定义: 标量积(点乘)和矢量积(叉乘)。 定义:标量积A· B是一标量, 其大小等于两个矢量模值相 乘, 再乘以它们夹角αAB(取小角, 即αAB≤π)的余弦:
ˆ分量第一项是y→z, x
矢量场,标量场,散度,梯度,旋度的理解

1.梯度gradient设体系中某处的物理参数(如温度、速度、浓度等)为w,在与其垂直距离的dy处该参数为w+dw,则称为该物理参数的梯度,也即该物理参数的变化率。
如果参数为速度、浓度或温度,则分别称为速度梯度、浓度梯度或温度梯度。
在向量微积分中,标量场的梯度是一个向量场。
标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
更严格的说,从欧氏空间Rn到R的函数的梯度是在Rn某一点最佳的线性近似。
在这个意义上,梯度是雅戈比矩阵的一个特殊情况。
在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。
梯度一词有时用于斜度,也就是一个曲面沿着给定方向的倾斜程度。
可以通过取向量梯度和所研究的方向的点积来得到斜度。
梯度的数值有时也被成为梯度。
在二元函数的情形,设函数z=f(x,y)在平面区域D内具有一阶连续偏导数,则对于每一点P(x,y)∈D,都可以定出一个向量(δf/x)*i+(δf/y)*j这向量称为函数z=f(x,y)在点P(x,y)的梯度,记作gradf(x,y)类似的对三元函数也可以定义一个:(δf/x)*i+(δf/y)*j+(δf/z)*k 记为grad[f(x,y,z)]2.散度气象学中指:散度指流体运动时单位体积的改变率。
简单地说,流体在运动中集中的区域为辐合,运动中发散的区域为辐散。
用以表示的量称为散度,值为负时为辐合,此时有利于天气系统的的发展和增强,为正时表示辐散,有利于天气系统的消散。
表示辐合、辐散的物理量为散度。
微积分学→多元微积分→多元函数积分中:设某量场由A(x,y,z) = P(x,y,z)i + Q(x.y,z)j + R(x,y,z)k 给出,其中P、Q、R 具有一阶连续偏导数,∑是场内一有向曲面,n 是∑在点(x,y,z) 处的单位法向量,则∫∫A·ndS 叫做向量场A 通过曲面∑向着指定侧的通量,而δP/δx + δQ/δy + δR/δz 叫做向量场A 的散度,记作div A,即div A = δP/δx + δQ/δy + δR/δz。
电磁场基础--二、梯度、散度和旋度数学定义

电磁场基础--⼆、梯度、散度和旋度数学定义⼆、梯度、散度和旋度数学定义2.1哈密顿算⼦哈密顿引进的⼀个⽮性微分算⼦称为哈密顿算⼦或▽算⼦:优点:在运算中既有微分⼜有⽮量的双重运算性质,其优点在于可以把对⽮量函数的微分运算转变为⽮量代数的运算,从⽽可以简化运算过程,并且推导简明扼要,易于掌握。
⾝并⽆意义,就是⼀个算⼦,同时⼜被看作是⼀个⽮量,在运算时,具有⽮量和微分的双重⾝份。
运算规则为:其梯度、散度及旋度⽤▽算⼦表⽰为(u 为标量;A为⽮量):2.2 拉普拉斯算⼦拉普拉斯算⼦是n维中的⼀个⼆阶微分算⼦,定义为(▽f)的(▽·f)。
因此如果f是⼆阶可微的实函数,则f的拉普拉斯算⼦定义为:f的拉普拉斯算⼦也是笛卡尔xi中的所有⾮混合⼆阶:数学表⽰式⼆维空间:其中x与y代表 x-y 平⾯上的笛卡尔:的表⽰为:三维空间:笛卡尔下的表⽰为:的表⽰为:2.3 梯度数学定义标量u的哈密顿算⼦运算。
梯度本质:作⽤对象:标量场运算对象:标量运算结果:向量(⽮量)梯度针对⼀个标量场(势场),衡量⼀个标量场的变化⽅向。
梯度为0说明该势场是个等势场。
其结果为向量。
2.4 散度数学定义散度表⽰是的场分量沿各⾃⽅向上的变化规律。
哈密顿算⼦与⽮量A(->)的点积为⽮量A的散度。
散度本质:作⽤对象:向量场运算对象:向量运算结果:标量散度针对⼀个向量场,衡量⼀个向量场的单位体积内的场强。
散度为0说明这个场没有源头。
其结果为标量。
2.5 旋度数学定义旋度表⽰是的各个分量沿着与它们相垂直的⽅向上的变化规律。
哈密顿算⼦与⽮量A的叉乘,即为⽮量旋度。
旋度本质:作⽤对象:向量场运算对象:向量运算结果:向量旋度针对⼀个向量场,衡量⼀个向量场的⾃旋。
旋度为0说明这个场是个保守场(⽆旋场),保守场⼀定是某个标量场的梯度场。
其结果为⽮量。
2.6 ⽮量场的旋度与散度的意义:数量()场的梯度与⽮量场的和可表⽰为:与拉普拉斯算⼦的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矢量场标量场散度梯度
旋度的理解
公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]
1.梯度 gradient
设体系中某处的物理参数(如温度、速度、浓度等)为w,在与其垂直距离的dy处该参数为w+dw,则称为该物理参数的梯度,也即该物理参数的变化率。
如果参数为速度、浓度或温度,则分别称为速度梯度、浓度梯度或温度梯度。
在向量微积分中,标量场的梯度是一个向量场。
标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
更严格的说,从欧氏空间Rn到R的函数的梯度是在Rn某一点最佳的线性近似。
在这个意义上,梯度是雅戈比矩阵的一个特殊情况。
在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性函数,也就是线的斜率。
梯度一词有时用于斜度,也就是一个曲面沿着给定方向的倾斜程度。
可以通过取向量梯度和所研究的方向的点积来得到斜度。
梯度的数值有时也被成为梯度。
在二元函数的情形,设函数z=f(x,y)在平面区域D内具有一阶连续偏导数,则对于每一点P(x,y)∈D,都可以定出一个向量
(δf/x)*i+(δf/y)*j
这向量称为函数z=f(x,y)在点P(x,y)的梯度,记作gradf(x,y)
类似的对三元函数也可以定义一个:(δf/x)*i+(δf/y)*j+(δf/z)*k 记为grad[f(x,y,z)]
2.散度
气象学中指:
散度指流体运动时单位体积的改变率。
简单地说,流体在运动中集中的区域为辐合,运动中发散的区域为辐散。
用以表示的量称为散度,值为负时为辐合,此时有利于天气系统的的发展和增强,为正时表示辐散,有利于天气系统的消散。
表示辐合、辐散的物理量为散度。
微积分学→多元微积分→多元函数积分中:
设某量场由 A(x,y,z) = P(x,y,z)i + Q,z)j + R(x,y,z)k 给出,其中 P、Q、R 具有一阶连续偏导数,∑是场内一有向曲面,n 是∑在点 (x,y,z) 处的单位法向量,则∫∫A·ndS 叫做向量场 A 通过曲面∑向着指定侧的通量,而δP/δx + δQ/δy + δR/δz 叫做向量场A 的散度,记作 div A,即 div A = δP/δx + δQ/δy + δR/δz。
上述式子中的δ为偏微分(partial derivative)符号。
3旋度
表示曲线、流体等旋转程度的量
4.矢量和标量场
假设有一个三维空间,显然空间的每一个点都能用坐标(x, y, z)唯一地标识出来。
假如给空间的每一个点都赋予一个数字,那么整个空间就充满了数字。
此时,这个充满数字的三维空间在数学上就叫做“场”。
上述的场叫做标量场,因为单纯的一个数字叫做“标量(scalar)”。
如果我们给空间的每一个点都赋予一个矢量(vector),即一个既有大小,又有方向的东西,那么整个空间就变成充满了矢量,这个空间就叫做矢量场。
矢量场中的每一点都对应于一个矢量,而矢量能够根据规则进行各种运算,例如加、减和乘等(数学上没有矢量的除法)。
显然,我们可以对整个矢量场中的每一个矢量同时进行某种运算,例如同时将它们乘以一个数,或加上一个数等。
但是我们可以对整个矢量场进行一些更复杂的运算,其中散度就是其中一种。
三维空间中的一个矢量可以沿x、y和z方向分解,现假设空间的某一点被赋予的矢量能够沿着这3个方向分解为大小为P、Q和R的三个分量,表示为(P,Q,R)。
注意,由于空间中每个点被赋予的矢量一般来说是不同的,所以P、Q和R的大小在空间的不同的点一般有不同的值,也就是说P、Q和R中每一个都是x、y和z的函数。
对三维矢量场来说,我们可以对其中一个点的矢量,假设为(P,Q,R)进行以下操作:
1、求出dP/dx+dQ/dy+dR/dz的值,其中dP/dx表示求P对x的一阶偏导数,其余雷同;
2、将这个值赋予这个点
对整个矢量场的每个点均进行以上运算,就等于给整个三维空间的每个点都赋予了一个值,于是我们就得出了一个新的标量场,这个标量场就叫做原来的矢量场的散度(divergence),这种运算就叫做“对矢量场取散度”。
除了散度运算以外,我们还可以对矢量场进行其它的运算,例如旋度运算(curl)。
跟散度运算不同,旋度运算的结果不是标量场,而是另一个矢量场。
而涡度就是一个速度场的旋度,显然涡度是一个矢量场的一个类型。
