比的意义和基本性质 练习题
比的意义和比的基本性质练习课

复习旧知,整体回顾
(1)、什么叫做比?比的各部分名称是什么?
举例:( ):( )=( )÷( )
(2)、什么是比的基本性质?
举例:( ):( )=( ):( ) (0除外)
(3)、什么叫做比值?一般求比值方法是什么?
举一个求比值的例子: (4)、怎样化简比?举一个化简比的例子:
4 9
,大米和面粉的比是( )。 ).
6、一条水渠,已修好了 ,还剩下60米,已修的和剩下的长度之比是(
7 4
5 8
• 小结:
这节课我们学了什么?
追问:既然比的后项不能是0,而足球赛中常出现的
“2:0”的意义是什么?它是一个比吗?
(2)小强身高1米,他爸爸身高173厘米,小强和他爸爸
身高的比是1:173
(3)比的前项和后项都乘一个相同的数,比值不变。
(4) 既可以看作一个分数,也ห้องสมุดไป่ตู้以看作4:5
2、填空 (1)一辆汽车2小时行驶100千米,这辆汽
(5)两个正方形边长的比是2:1,它们周 长的比是 ( ) ,面积的比是()。
目标检测。 1、写同样多的作业,李莉用12分钟,王祥用15分钟, 李莉与王祥的最简单的速度比是( ). 2、把3克盐放入12克水中,盐与盐水重量的最简整 数比是( ).
3、练习 十一第3题
4、练习 十一第5题
1、配制一种盐水,在120克水中放了5克盐。 ⑴写出盐和水的克数的比,并化简。 盐和水的克数的比是5∶120。 5∶120=1∶24 ⑵写出盐和盐水的克数的比,并化简。 盐和盐水的克数的比是5∶125。 5∶125=1∶25 ⑶写出水和盐水的克数的比,并化简。 水和盐水的克数的比是120∶125。 120∶125=24∶25
六年级上数学比的意义和比的基本性质练习题-2019年精选教学文档

六年级上数学比的意义和比的基本性质练习题学习是劳动,是充满思想的劳动。
查字典数学网为大家整理了比的意义和比的基本性质练习题,让我们一起学习,一起进步吧!
填空:
1,一车水果重1.8吨,按2:3:5的比例分配给甲,乙,丙三个水果店,乙水果店分得这批水果的().
2,甲数比乙数多,甲数与乙数的比是().
3,甲,乙,丙三个数的平均数是15,甲,乙,丙三个数的比是2:3:4,甲数是().
4、东风小学六年级人数是五年级人数的,五年级与六年级人数的比是().
5,把3克盐放入12克水中,盐与盐水重量的最简整数比是().
6,把(5平方米):(50平方分米)化成最简整数比是( ),它们的比值是( ).
7,甲数除以乙数的商是1.5,甲数与乙数的最简整数比是( ). 8,写同样多的作业,李莉用12分钟,王祥用15分钟,李莉与王祥的最简单的速度比是( ).
9,把1与它的倒数的比化成最简整数比是( ),比值是( ). 10,4分:时的比值是( ),最简整数比是( ).
11,把:0.75化成最简单的整数比是( ),比值是( ).
12,1:0.75化成最简单的整数比是( ),比值是( ).
13,:0.125化成最简单的整数比是( ),读作( ),比值是( ),读作( ).
欢迎大家去阅读由小编为大家提供的比的意义和比的基本性质练习题大家好好去品味了吗?希望能够帮助到大家,加油哦!。
比与比例的知识点与练习题

比与比例的知识点与练习题比例的意义和性质比的意义和性质1.比的意义:两个数相除叫做比。
冒号“:”是比号,读作“比”。
比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
比的前项相当于被除数,后项相当于除数,比值相当于商。
比值通常用分数表示,也可以用小数表示,有时也可能是整数。
比的后项不能是零。
比的前项相当于分子,后项相当于分母,比值相当于分数值。
2.比的性质:比的前项和后项同时乘上或者除以相同的数(除外),比值不变,这叫做比的基本性质。
比的化简可以根据比的基本性质进行,结果必须是一个最简比。
比例的意义和性质1.比例的意义:表示两个比相等的式子叫做比例。
组成比例的四个数,叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
2.比例的基本性质:在比例里,两个外项的积等于两个内项的积。
3.解比例:根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个数比例中的另外一个未知项。
求比例中的未知项,叫做解比例。
练比例的意义和性质练题1.填空。
1) 两个比相等的式子叫做比例。
2) 组成比例的四个数叫做比例的项。
两端的两项叫做外项,中间的两项叫做内项。
3) 在比例里,两个外项的积等于两个内项的积。
4) 求比例中的未知项,叫做解比例。
5) 比值相等的两个比就相等。
2.按要求写比例。
1) 例如:1:2可以表示为2:4.2) 3:5=6:10.3) 1:2和2:1:10.4) 3:2:5:12.5) 17:3/5=68:12,所以比例为17:3/5=68:12.6) 2/3:6/2=4:9.3.按要求转化。
1) 6:8=3:4,8:6=4:3,24:6=4:1,2:3=8:12.2) 7:8=14:16,7:16=14:32,8:7=16:14,16:7=32:14.3) 7a=6b,a:b=6:7.4) 3/5a=4/9b,a:b=4:5/27.5.如果甲数的4/5与乙数的7/9相等,则甲数与乙数的比是多少?解:设甲数为4x,乙数为5y,则有:4x/(5y) = 7/9解得:x/y = 35/36因此甲数与乙数的比为4x/5y = 140/180 = 7/96.男生人数的5/8与女生人数的5/9相等,那么女生人数与男生人数的比是多少?解:设男生人数为5x,女生人数为8y,则有:5x/(8y) = 5/9解得:x/y = 8/9因此女生人数与男生人数的比为8y/5x = 72/25选择题:1.比例5:3=15:9的内项3增加6,要使比例成立,外项9应该增加多少?解:内项3增加6,变为9,比例变为5:3=15:9+6,即5:3=21:15因此,外项9应该增加6,变为15.答案:⑴62.把2千克盐加入15千克水中,盐与盐水重量的比是多少?解:盐水总重量为17千克,盐的重量为2千克,因此盐与盐水重量的比为2:17.答案:⑶2:173.下面的比中能与3:8组成比例的是多少?解:3:8的比值为0.375,只有1.5:4的比值也为0.375,因此1.5:4能与3:8组成比例。
小学六年级数学上册练习题第四单元-比

小学六年级数学上册练习题第四单元-比第一课时 比的意义班级: 姓名:巩固达标 一、填空。
(1)在4:7=中,( )是比的前项,( )是比的后项,比值是( )。
(2)43=( )÷( ) =( ):( )(3)人体血液中,红细胞的平均寿命是120天,血小板的平均寿命是10天。
红细胞与血小板的寿命的比是( )。
(4)--辆“复兴号”高铁3小时行驶了1050km,这列高铁行驶的路程和时间的比是( ) :( ),比值是( ),比值表示( )。
(5)一条公路已修了全长的125,已修的和未修的比是( ),未修的和全长的比是( )。
(6)比与分数、除法的联系。
( )(7) 甲数是乙数的4倍,甲、乙两数的比是( ),乙数与两数和的比是( )。
(8)在100克水中加入10克盐,盐和盐水的比是( )。
二、判断。
(对的画“√”,错的画“X”)(1)在今年一场足球比赛中,法国1:0战胜比利时,所以比的后项为0。
( )(2) 小明的身高125cm,弟弟的身高是1m,小明和弟弟身高的比是125:1。
( )三、求下面各比的比值。
0.36 : 0.45 1.5t:400kg 32:9420分: 0.25时能力拓展应用题。
1、小明体重40千克,相当于小军的910,小华的体重是小军的65。
小华体重多少千克?2、修一条工路,第一天修了全长的,第二天修的比第一天的少50米,两周共修了160米,这条路一共有多长?3、学校有彩色粉笔48盒,比白粉笔的少3盒,学校有白粉笔多少盒?4、一满杯糖水正好是200 g,其中含糖20g 。
从杯中倒出20g 糖水后,再往杯里加满水,这时杯子里的糖与水的质量比是多少?第二课时 比的基本性质班级: 姓名:巩固达标 1、填空(1).填表后再说一说比与分数、除法有怎样的关系。
(2)如果把3: 7的前项加上12,要使比值不变,后项应加上( )。
(3)12:16=( ):4=18÷( )=( ):0.8=32(4)甲数的43等于乙数的32,那么甲、乙两数的最简整数比是( ):( )。
比的意义及比的基本性质

2、比与除法、分数又有什 么不同?
比和除法、分数的联系和区别
联
比
系(相
当
于)
区 别
一种 关系
一种 运算 一种 数
比的前项 :比号 比的后项 比值 ÷除号
—分数线
除法 被除数
分数 分 子
除数
商
分母 分数值
比的后项可以是0吗?
• 做一做: • 1、小敏和小亮在文具店买同样的本子。小 敏买了6本,花了1.8元。 小亮买了8本,花 了2.4元。 小敏和小亮买的练习本之比是 • ( ):( ),比值是( ) ,花钱 数之比是( ) :( ),比值是( )。
• ( ): ( )
• 0.75:2 =(0.75×100): (2×100) • =75:200=( ): ( )
• 例如:15
﹕
3 10 = 15÷10= 2
• 前项 比号 后项 比值 • 根据分数与除法的关系,两个数的比也可以写成 分数形式。例如:15:10也可以写成 15 • 仍读作“15 比10”。 10
比值通常用分数表示,能 除尽时也可以用小数表示, 能整除时就用整数表示。
想一想:
1、比的前项、后项和比值 分别相当于除法算式和分 数中的什么?
• 6 :8= (6×2) • 6 :8 = (6÷2)
: (8×2) =12 : 16 : (8÷2) = 3 : 4
• 6÷8 = (6÷2) : (8÷2) =3 ÷4 • 你能根据比和分数的关系研究比的规律吗?
比的前项和后项同时乘或除以相同的数 (0除外)比值不变。
• 这叫做比的基本性质 • 根据比的基本性质,可以把比化成最简单 的整数比。
六年级数学下册《比例的意义和性质》练习题(附答案解析)

六年级数学下册《比例的意义和性质》练习题(附答案解析)学校:___________姓名:___________班级:____________一、选择题1.能与11:34组成比例的是()。
A.4∶3B.3∶4C.1:43D.1:342.下面每组中的四个数,不能组成比例的是()。
A.2,0.25,3,0.375B.18,8,5.4,24C.5452,,,3767D.30,25,6,1253.下面能与3∶8组成比例的是()。
A.8∶3B.15∶40C.0.2∶0.6 4.下列哪个选项中的四个数不能组成比例。
()A.3,5,9,15B.1,2,3,4C.12,13,16,19D.2,4,7,145.如果a、b都是不为0的数,且56a=78b,则a和b的大小关系是()。
A.a<b B.a=b C.a>b6.能与13∶14组成比例的是()。
A.4∶13B.13∶4C.4∶3D.3∶47.下面各比中,能与0.14∶0.1组成比例的是()。
A.0.8∶0.25B.28∶20C.13∶35D.14∶18.在比例里,两个外项的积等于两个内项的积。
这叫做()。
A.比例的基本性质B.比例C.比例的外项9.根据下图中的信息判断,下列等式不成立的是()。
A.a∶c=d∶b B.a b=c dC.b d=c a10.如果a×3=b×4,那么a∶b=()。
A.4∶3B.3∶4C.1∶12二、填空题11.12的因数共有______个,选择其中的4个因数,把它们组成一个比例是______。
12.在30的因数中选择4个奇数组成一个比例:( )。
根据比例的基本性质把它改写成乘法等式:( )。
13.比值是2的一个比例是( )。
14.如果2a=3b(a、b≠0),那么a∶b=( )∶( );如果a∶b=5∶2 ,那么a∶5=( )∶( )。
15.比值是35的两个比可以为( ),( ),这两个比组成比例是( ).16.一个比例,等号左边的比和等号右边的比一定是( )的。
六年级数学:《比的意义和基本性质》试题

其实,任何一门学科都离不开死记硬背,关键是记忆有技巧,“死记”之后会“活用”。不记住那些基础知识,怎么会向高层次进军?尤其是语文学科涉猎的范围很广,要真正提高学生的写作水平,单靠分析文章的写作技巧是远远不够的,必须从基础知识抓起,每天挤一点时间让学生“死记”名篇佳句、名言警句,以及丰富的词语、新颖的材料等。这样,就会在有限的时间、空间里给学生的脑海里注入无限的内容。日积月累,积少成多,从而收到水滴石穿,绳锯木断的功效。2、计划生产1800个零件,第一天生产了计划的,第二天生产了计划的。还剩下计划的几分之几没生产?还剩下多少个没生产?
六年级数学:《比的意义和基本性质》试题
二、求比值:
12:8 0.4:0.12
“教师”一称最接近的“老师”概念,最早也要追溯至宋元时期。金代元好问《示侄孙伯安》诗云:“伯安入小学,颖悟非凡貌,属句有夙性,说字惊老师。”于是看,宋元时期小学教师被称为“老师”有案可稽。清代称主考官也为“老师”,而一般学堂里的先生则称为“教师”或“教习”。可见,“教师”一说是比较晚的事了。如今体会,“教师”的含义比之“老师”一说,具有资历和学识程度上较低一些的差别。辛亥革命后,教师与其他官员一样依法令任命,故又称“教师”为“教员”。三、解决问题:
单靠“死”记还不行,还得“活”用,姑且称之为“先死后活”吧。让学生把一周看到或听到的新鲜事记下来,摒弃那些假话套话空话,写出自己的真情实感,篇幅可长可短,并要求运用积累的成语、名言警句等,定期检查点评,选择优秀篇目在班里朗读或展出。这样,即巩固了所学的材料,又锻炼了学生的写作能力,同时还培养了学生的观察能力、思维能力等等,达到“一石多鸟”的效果。以上就是六年级数学:《比的意义和基本性质》试题全文,希望能给大家带来帮助!
比的基本性质练习题

填空:
1. 9:5中( 9 )是前项,( 5 )是后项,比值是( )。
2. 如果A:B=C,那么A是比的( 前项 ( 后项 ),C是比的( 比值
),B是比的 )。
3. 从A地道B地一共180千米,客车要行2小时,货车要行3小 时。
(1)客车所行路程与所用时间的比是( 180:2 ),比值是( 90 (2)客车所用时间与货车所用时间的比是( 2:3 ),比值是( )。 )。
( (
4 3 4 4 7 3
) )
2.六(2)班男生28人,女生21人。
女生人数与男生人数的比是( 3 )∶( 4 ) 男生人数与女生人数的比是( 4 )∶( 3 ) 男生人数( 4 )份,女生人数( 3 )份 4 男生人数是女生的 3 3 女生人数是男生的 4 4 男生人数占全班人数的 7 女生人数占全班人数的 3
(4)第二次制作零件个数和所用时间的比是( 520: 6.5 ), 比值是( 8 0 )。 3 5. 如果A:B= ,那么2A:2B= 5 6. 一根绳子全长2.4米,用去0.6米,用去的绳子和全长的比是 ( 0.6: 2.4 ),比值是( )。
化简比并求比值
21:35 0.8:0.32 0.3吨:150千克 0.65:1.3
பைடு நூலகம்
(3)货车与客车的速度比是( 90:60),比值是(
)。
4. 某工厂制作一种零件,第一次8小时加工了640个,第二次 6.5小时加工了520个。 (1)第一次制作零件个数与第二次制作零件个数的比是 ( 640:520 ),比值是( )。 (2)第一次所用时间与第二次所用时间的比是( 8 : 6.5 ), 比值是( )。 (3)第一次制作零件个数与所用时间的比是(640: 8 比值是( 8 0 )。 ),
六年级比的意义和基本性质练习题
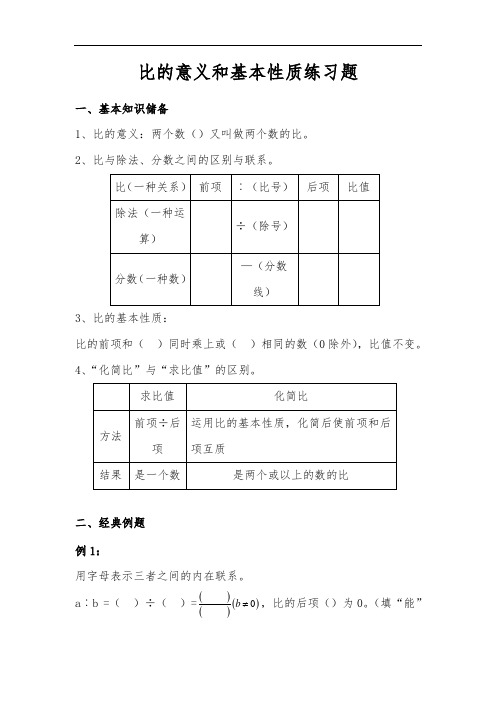
比的意义和基本性质练习题一、基本知识储备1、比的意义:两个数()又叫做两个数的比。
2、比与除法、分数之间的区别与联系。
3、比的基本性质:比的前项和( )同时乘上或( )相同的数(0除外),比值不变。
4、“化简比”与“求比值”的区别。
二、经典例题 例1:用字母表示三者之间的内在联系。
a ︰b =( )÷( )=()()()0b ≠,比的后项()为0。
(填“能”或“不能”)举一反三1:一袋洗衣粉重320克,一块香皂重80克。
洗衣粉与香皂的重量比是(),比值是();香皂与洗衣粉的重量比是(),比值是()。
例2:盐与水的比是1︰10,则盐︰盐水=(︰),水︰盐=(︰),盐水︰水=(︰)。
举一反三2:两个正方形边长比是1︰3,这两个正方形的周长比是(︰)面积比是(︰)。
例3:男生与女生的人数比是3︰4,男生比女生少() ()。
举一反三3:1、某班有男生20人,女生30人,男生与全班人数的比是(),女生比男生多() ()。
2、甲数除以乙数的商是43,甲数与乙数的比是()。
例4:易错题分析1、在4︰9中,如果比的前项加上8,要使比值不变,后项应加上()。
易错题分析2、A ︰B=2︰3,B ︰C=4︰5,那么A ︰B ︰C=(︰︰)。
易错题分析3、一项工程,甲单独完成需要6小时完成,乙单独完成需要5小时完成,甲、乙工作效率之比是(︰)。
举一反三4:1、在3︰8中,如果比的前项加上15,要使比值不变,后项应加上()。
2、A ︰B=3︰4,B ︰C=5︰6,那么A ︰B ︰C =(︰︰)。
3、一辆汽车从甲地开往乙地,3小时到达,返回时4小时到达,前往速度与返回速度的比是(︰)。
三、迁移拓展 例1、如果532CB A ==(其中A 、B 、C 都不等于0),那么A ︰B ︰C=(︰︰)。
举一反三7:如果2A=3B=4C (其中A 、B 、C 都不等于0),那么A ︰B ︰C=(︰︰)。
例2、有两个重叠的正方形,大正方形的边长是5厘米,小正方形的边长是4厘米,重叠部分的面积是9平方厘米,求阴影部分面积。
比的意义及比的基本性质

第十讲 比的意义及比的基本性质【典型例题1】求下列各式的比值:(1)4.5:217; (2)312:611 (3)36分:0.4时.解析:(1)4.5:217= 4.5÷7.5=0.6;或 4.5:217=29÷215=29×152=53.(2)312:611=37÷67=37×76=2.(3)0.4时=0.4×60=24分; 36分:0.4时=36分÷24分=211点评:此题考查的是比与比值的概念;掌握正确、熟练地求比值的方法. 【知识点】1.比a 、b 是两个数或两个同类的量,为了把b 和a 相比较,将a 与b 相除,叫做a与b 的比.记作a:b ,或写成ba,其中b ≠0;a 叫做比的前项,b 叫做比的后项.2.比值 比的前项除以比的后项所得的商叫做比值。
求比值时注意: (1)得到的结果是一个数(分数或小数,有时是整数). (2)求两个同类量的比值时,如果单位不同,必须把这两个量化成相同的单位. (注意:比是解决同类量之比). 【基本习题限时训练】1. 求54:45的比值,结果正确的是:( ) A 、2516 B 、1625 C 、16﹕25 D 、 25﹕16【解】A2. 求2周: 5天的比,结果正确的是:( )A 、14:5B 、542 C 、5:14 D 、 2.8【解】C3. 某中学预备(2)的学生人数为40人,其中男生17人,则该班男生人数与女生人数的比值是:( )A 、4017B 、1723C 、17﹕23D 、 2317【解】D 【拓展题1】一项工程,甲队用15天完成,乙队用18天完成,求甲队与乙队的工作效率的比值.【解析】(1÷15) ﹕(1÷18)= 151:181=151÷181=151×18=115【点评】把这项工程看成整体“1”,工作效率=工作总量÷工作时间,所以甲队和乙队的工作效率分别是151和181【拓展题2】如图,在ΔABC 中BC=10厘米,BD 是BC 的52,求ΔABD 和ΔABC 的面积之比.【解析】BD=10×52=4厘米;BC=10厘米;BD 上高的长=BC 上高的长;ΔABD 的面积:ΔABC 的面积=(21×BD ×BD 上高):(21×BC ×BC 上高)=(21×4):(21×10)=2:5.【点评】 三角形的面积公式是21×底边长×底边长上的高,而ΔABD 和ΔABC的边长可以取B D 、BC 它们底边上的高是同一条高,由已知条件只要求出B D 长就可以求出这两个三角形的面积比.【典型例题2】已知41:x=213,求x.解析:因为41:x=213;所以41÷x=213;由 x=41÷213;可得x=41×72;所以x=141.点评:要求正确理解分数、除法、比的关系和区别,从而求出所求的未知数。
(完整版)比与比例的知识点与练习题

比率的意义和性质一.知识点1、比的意义和性质( 1)比的意义:两个数相除又叫做两个数的比。
“:”是比号,读作“比” 。
比号前面的数叫做比的前项,比号后边的数叫做比的后项。
比的前项除今后项所得的商,叫做比值。
同除法比较,比的前项相当于被除数,后项相当于除数,比值相当于商。
比值平常用分数表示,也能够用小数表示,有时也可能是整数。
比的后项不能够是零。
依照分数与除法的关系,可知比的前项相当于分子,后项相当于分母,比值相当于分数值。
( 2)比的性质比的前项和后项同时乘上也许除以相同的数(0 除外),比值不变,这叫做比的基本性质。
(3)求比值和化简比求比值的方法:用比的前项除今后项,它的结果是一个数值能够是整数,也能够是小数或分数。
依照比的基本性质能够把比化成最简单的整数比。
它的结果必定是一个最简比,2、比率的意义和性质(1)比率的意义表示两个比相等的式子叫做比率。
组成比率的四个数,叫做比率的项。
两端的两项叫做外项,中间的两项叫做内项。
(2)比率的基本性质在比率里,两个外项的积等于两个两个内向的积。
(3)解比率依照比率的基本性质,若是已知比率中的任何三项,就可以求出这个数比率中的别的一个未知项。
求比率中的未知项,叫做解比率。
二、练习比率的意义的基本性质练习题一、填空。
1.()叫做比率。
2.()叫做比率的项。
()叫做比率的外项,()叫做比率的内项。
3.()这叫做比率的基本性质。
4.()叫做解比率。
5.两个比的()相等,这两个比就相等。
二、按要求写比率。
1.写出一个你喜欢的比率。
2.写出一个比值是3/5 的比率。
3.一个比率的两个外项互为倒数,一个内项是1/10 ,写出吻合条件的一个比率。
4 .一个比率的两个内项的积是4/5 ,一个外项是 3/8 ,写出吻合条件的一个比率。
5.一个比率,组成比率的比的比值是1/4 ,两个外项分别是17 和 3/5 ,写出这个比率。
6.有两个比,比值都是2/3 ,第一个比的后项与第二个比的前项都是6,把这两个比组成比率。
(完整版)比的意义和基本性质练习题

比的意义一、细心填写:1.两个数相除又叫做这两个数的()。
比前项除以后项所得的商叫()。
2、甲数是12, 乙数是18.(1)甲与乙的比是()∶( )。
(2)乙与甲的比是( )∶()。
(3)甲与甲乙两数和的比是()∶( )。
(4)乙与甲乙两数和的比是()∶()。
(5)甲乙两数差与甲乙两数和的比是()∶()。
3.小明3分钟走了240米, 小杰5分钟走了350米。
(1)小明与小杰行走时间的比是(), 比值是( )。
(2)小明与小杰行走路程的比是( ), 比值是()。
(3)小明路程与时间的比是(), 比值是(), 比值表示( )。
(4)小杰路程与时间的比是( ),比值是(), 比值表示().(5)小明行走速度与小杰行走速度的比是( ).4.某校六年级一班男生人数是女生人数的。
男生人数与女生人数的比是()。
女生人数与全班人数的比是( )。
全班人数与女生人数的比是().5.苹果比梨多, 苹果与梨的比是( ), 梨与苹果和梨和的比是( ).5.甲数是乙数的3倍,乙数和甲数的比是()。
6、一段路,甲走完全程用7小时, 乙走完全程用6小时, 甲、乙的时间比是(),甲与乙的速度比是()。
7、两个正方形的边长的比是1∶3, 它们的周长比是()。
8、2∶13=( )÷()=()()95=( )∶()=()÷()9、将5克糖放入20克水中, 糖与糖水的比是( ).三、求比值。
12: 8 0。
4:0。
12 :5: 41 4.5:0.9 0.75:4130分钟∶41时 0.75吨∶250千克 400厘米∶0.8米比的基本性质一、细心填写1.( ),叫做比的基本性质.2.16:20=32: ( ) =( )÷10 = = ( ): 0.2( ): 16= = =( )÷24=3: ( )=( )÷20=0.250.8÷1.2=4÷( )=8: ( )==( ): 27=28÷( )=( ): ( )=0.625=15÷( )= =20: ( )3.火车4小时行驶了600千米,路程和时间的最简整数比是( ), 比值是( )。
2022-2023学年人教版数学六年级下册比例的意义和性质练习题(含答案)

2022-2023学年人教版数学六年级下册比例的意义和性质练习题学校:___________姓名:___________班级:___________一、选择题1.下列能与12∶13组成比例的是( )。
A .2∶3B .13∶14C .3∶2D .34∶132.下面各组的两个比,可以组成比例的是( )。
A .13 ∶ 16和12∶14B .12∶9和9∶6C .8.4∶2.1和1.2∶8.43.能与11:43组成比例的是( )。
A .13:4B .4∶3C .3∶4D .1:434.如果a 、b 都是不为0的数,且56a =78b ,则a 和b 的大小关系是( )。
A .a <bB .a =bC .a >b5.下列各数中,( )不能与2、8、10组成比例。
A .58B .85C .52D .406.若乙数的56与甲数的34相等(甲、乙两数均不为0)则乙数∶甲数=( )。
A .10∶9B .9∶10C .56∶347.下面的( )可以和23:35组成比例。
A .35:23B .10:9C .9:108.若y∶3=2∶x (x ,y 都不为0),下列式子中成立的是( )。
A .3x =2yB .x =6yC .xy =6D .2x =3y9.用2,3,6,9组成的比例中,正确的是( )。
A .2396:=:B .2:36:9C .3269:=:10.如果a×3=b×4,那么a∶b =( )。
A .4∶3B .3∶4C .1∶12二、填空题11.一个比例的两个外项都是6,且两个比值都是4,则这个比例可以写成( )。
12.写出比值是35的两个比:( )、( )。
再把它们组成比例:( )。
13.在比例2.4:7.215:45中,内项是( )和( ),外项是( )和( )。
14.一个比例中,两个比的比值都是0.8,两个内项都是2,这个比例是( )。
15.比值是35的两个比可以为( ),( ),这两个比组成比例是( ).16.一个比例,等号左边的比和等号右边的比一定是( )的。
比的基本性质

比的意义和基本性质一、细心填写:1、鸡有80只,鸭有100只,鸡和鸭只数的比是( ),比值是( )。
2、长方形长3分米,宽12厘米,长与宽的比是( ),比值是( )。
3、小李5小时加工60个零件,加工个数与时间的比是( ),比值是( )。
4、一本书读了55页,45页没有读,已读与总数的比是( ),比值是( )。
5、甲数相当于乙数的92,甲数与乙数的比是( ),乙数与甲数的比是( )。
6、三好学生占全班人数的81,三好学生与全班人数的比是( )。
7、白兔只数的31与黑兔相等。
白兔与黑兔的比是( ),白兔与黑兔的比是( )8、若A ÷B =5(A 、B 都不等于0)则A :B =( ):( ) 若A =B (A 、B 都不等于0) 则A :B =( ):( ) 二、求比值:32:94 0.3:0.023321:113 0.21:6.348:36 0.5: 527:3.5 3: 1161:0.1259072二、应用题1、节日期间,某商场的商品一律按原价的78 销售。
某品牌毯子现价是每条280元,这种毯子原来的单价是多少元?2、有一面三角形小旗,面积是320 平方米,它的底是65 米,高是多少米?3、有一种油桶,最多能装汽油92 平方米,它的底是65 米,高是多少米?4、某校书法兴趣小组有40人,是科技小组人数的23 ,科技小组的人数是舞蹈组的34 。
舞蹈组有多少人?5、工地上有三堆石子,第一堆中80吨,第二堆的质量是第一堆的75 ,第三堆的质量是第二堆的1516 。
先估计哪一堆石子最重,再算一算这堆石子的重量?6、家电商城运进了110台电视机,第一个月卖出这些电视机的511 ,第二个月卖出的台数是第一个月的45 。
这两个月各卖出多少台电视机?7、(1)一瓶酱油25 千克,6天用完,平均每天用多少千克? (2)一桶酱油6千克,装容量25 千克的瓶里,可以装多少瓶?。
《比的意义和基本性质》练习题

比的意义和基本性质(一)一、细心填写:1、鸡有80只,鸭有100只,鸡和鸭只数的比是( ),比值是( )。
2、长方形长3分米,宽12厘米,长与宽的比是( ),比值是( )。
3、小李5小时加工60个零件,加工个数与时间的比是( ),比值是( )。
4、一本书读了55页,45页没有读,已读与总数的比是( ),比值是( )。
5、甲数相当于乙数的92,甲数与乙数的比是( ),乙数与甲数的比是( )。
6、三好学生占全班人数的81,三好学生与全班人数的比是( )。
7、白兔只数的31与黑兔相等。
白兔与黑兔的比是( ),白兔与黑兔的比是( ) 8、若A ÷B =5(A 、B 都不等于0)则A :B =( ):( )若A =B (A 、B 都不等于0) 则A :B =( ):( )9、 填写比、除法和分数的关系。
比 比的前项除法 除数分数 --- 分数线 分数值10、( )又叫做两个数的比。
( )叫做比值。
11、43=( ):( ) =( )÷( )12、在100克水中加入10克盐,盐和盐水的比是( )。
13、男工人数是女工人数的52,男、女工人数的比是( )。
14、甲数是乙数的4倍,甲、乙两数的比是( ),乙数与两数和的比是( )。
15、甲数比乙数多41,甲数与乙数的比是( ),比值是( )。
16、( ),叫做比的基本性质。
17、16:20=32:( ) =( )÷10 =()4=()80=1.6( ) =( ):0.218、火车4小时行驶了600千米,路程和时间的最简整数比是( ),比值是( )。
19、甲数是乙数的3倍乙数与甲数的比是( ),比值是( )。
20、601班男生与女生人数的比是2:3,女生占全班的( ),男生占全班的( )。
21、甲数是乙数的32,乙数与甲数的比是( ),甲数与乙数的比是( )。
二、求比值:12:8 0.4:0.12 5: 41 4.5:0.9 31:65 32:910 0.75:41 4: 41 35:45 360:450 0.3:0.15 18: 32 6:0.36 203:54 0.6:52 32:6 三、化简比:35:45 360:450 0.3:0.15 18: 32 6:0.36 203:54 0.6:52 32:683:21 0.75: 43 24: 31 6.4:0.16 2.25:9 815:32 54:83 31:41四、判断是否:1、54可以读作“6比7”。
六年级数学比的意义和基本性质练习题

六年级数学比的意义和基本性质练习题
39、比的意义和基本性质(一)
一、细心填写:
1、鸡有80 只,鸭有100 只,鸡和鸭只数的比是(),比值是()。
2、长方形长3 分米,宽12 厘米,长与宽的比是(),比值是()。
3、小李5 小时加工60 个零件,加工个数与时间的比是(),比值是()。
4、一本书读了55 页,45 页没有读,已读与总数的比是(),比值是()。
5、甲数相当于乙数的,甲数与乙数的比是(),乙数与甲数的比是()。
6、三好学生占全班人数的,三好学生与全班人数的比是()。
7、白兔只数的与黑兔相等。
白兔与黑兔的比是(),白兔与黑兔的比是()
8、若A÷B=5(A、B 都不等于0)则A:B=( ):( )
若A=B(A、B 都不等于0)则A:B=( ):( )
二、求比值:
:0.3:0.02
: 0.21:6.3
48:36 0.5:
7:3.5 3:1:0.125 三、解决问题:。
人教版册数学比的意义和基本性质》练习题

人教版册数学《比的意义和基本性质》练习题 The document was prepared on January 2, 202139、比的意义和基本性质(一)一、细心填写:1、鸡有80只,鸭有100只,鸡和鸭只数的比是( ),比值是( )。
2、长方形长3分米,宽12厘米,长与宽的比是( ),比值是( )。
3、小李5小时加工60个零件,加工个数与时间的比是( ),比值是( )。
4、一本书读了55页,45页没有读,已读与总数的比是( ),比值是( )。
5、甲数相当于乙数的92,甲数与乙数的比是( ),乙数与甲数的比是( )。
6、三好学生占全班人数的81,三好学生与全班人数的比是( )。
7、白兔只数的31与黑兔相等。
白兔与黑兔的比是( ),白兔与黑兔的比是( )8、若A ÷B =5(A 、B 都不等于0)则A :B =( ):( )若A =B (A 、B 都不等于0) 则A :B =( ):( )二、求比值:32:94 : 3321:113 : 48:36 : 52 7: 3: 116 1: 9072 三、解决问题:1、一辆汽车从甲地到乙地,每小时行80千米,用了43小时,返回时只用了85小时。
返回时每小时行多少千米2、商店售出2筐橙子,每筐24千克。
售出的橙子占水果总数的116,售出的香蕉占水果总数的41。
售出香蕉多少千克40、比的意义和基本性质(二)一、细心填写:12)叫做比值。
3、43=( ):( ) =( )÷( ) 4、在100克水中加入10克盐,盐和盐水的比是( )。
5、男工人数是女工人数的52,男、女工人数的比是( )。
6、甲数是乙数的4倍,甲、乙两数的比是( ),乙数与两数和的比是( )。
7、甲数比乙数多41,甲数与乙数的比是( ),比值是( )。
二、求比值:12:8 :5: 41 : 31:65 32:910 :41 4: 41 三、解决问题:1、小明体重40千克,相当于小军的910,小华的体重是小军的65。
六下数学 比例 知识点总结+题型训练 完整版带答案

二、填空题。
1、在比例4.2/5.6=6/8中,( 4.2 )和( 8 )是外项,( 5.6 )和( 6 )是内项。 2、在比例里,如果两个外项互为倒数,其中一个内项是0.4 ,则另外一个内项是( 2.5 ) 3、a:7=5:b中,( a )和( b )是外项,( 7 )和( 5 )是内项,a×b=( 35 )。 4、如果4a=7b,那么a:b=( 7 ):( 4 );b:a=( 4 ): (7)
5、填空:12:9的比值是( 4/3 ),1/3:1/4的比值 是( 4/3 ),把这两个比写成比例是(12:9=1/3:1/4 )。 6、填空:12的因数有(1,2,3,4,6,12),用其中的4个 因数组成比例是(1):(2)=(6):(12) 7、用两个比值都是0.8的组成比例,比例式是( 4:5=0.8:1)。 8、如果a×7=b÷2,那么a:b=(1):(14)。
一、比例的基本意义和性质
知识点总结: 1、比的意义:( 两个数相除又叫两个数的比 )
比例的意义:( 表示两个比相等的式子 )
如2.4:1.6=60:40是一个比例,2:3=4:6是一个比例
2、比和比例之间的联系与区别: 表示两个比相等的式子叫做“比例”。如2:3=4:6 关系:“比”是研究两个量之间的关系,所以它有(两项); “比例”是研究相关联的两种量中两组相对应数的关系,所以 比例是由(四项)组成。 比例是由比组成的,如果两个比相等, 那么这两个比就可以组成比例。成比例的两个比的比值一定相 等。 区别: “比”是表示两个数相除的关系 比由两项组成(前项、 后项) 任意两个数都能组成比 。“比例”是表示两个比相等 的关系 比例由四项组成(两个内 项、两个外项) 任意四个数 不一定都能组成比例
16、已知a b c d均大于0,请根据4/a=10/b=18/c=20/d把
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
比的意义和基本性质练习题
一、填空题
1、填写比、除法和分数的关系。
2、( )又叫做两个数的比。
( )叫做比值。
3、4
3
=( ):( ) =( )÷( )
5、男工人数是女工人数的
5
,男、女工人数的比是( )。
6、甲数是乙数的4倍,甲、乙两数的比是( ),乙数与两数和的比是( )。
7、甲数比乙数多4
1
,甲数与乙数的比是( ),比值是
( )。
8、( ),叫做比的基本性质。
9、16:20=32:( ) =( )÷10 =
()
4
=
()80
=1.6( ) =
( ):0.2
10、火车4小时行驶了600千米,路程和时间的最简整数比是
( ),比值是( )。
11、甲数是乙数的3倍乙数与甲数的比是( ),比值是( )。
12、601班男生与女生人数的比是2:3,女生占全班的( ),男生占全班的( )。
13、甲数是乙数的3
2
,乙数与甲数的比是( ),甲数与乙数的
比是( )。
二、求比值:
12:8 0.4:0.12 5: 4
1
4.5:0.9
31:65 32:910 0.75:41 4:41
35:45 360:450 0.3:0.15 18: 3
2
6:0.36 203:54 0.6:52 3
2
:6
三、化简比:
35:45 360:450 0.3:0.15 18: 3
2
6:0.36 203:54 0.6:52 3
2
:6
83:21 0.75: 43 24: 31
6.4:0.16
2.25:9 815:3
2
54:83 31:41
四、判断是否正确: 1、54
可以读作“5比4”………………………………………( ) 2、比的前项和后项同时乘一个相同的数,比值不变………( ) 3、比的基本性质与商不变的性质是一致的………………( ) 4、10克盐溶解在100克水中,这时盐和盐水的比是1:10( )
5、比的前项乘5,后项除以5
1。
比值不变 ………………( )
6、男生比女生多5
2
,男生与女生人数的比是7:5 ………( )
7、59
既可以看作分数,也可以看成一个比 ……………( )
8、“宽是长的几分之几”与“宽与长的比”,意义相同,结果表达形不同。
( )。
