系统辨识第五章作业

合集下载

系统辨识习题解答（最新）

系统辨识习题解答1-14、若一个过程的输入、输出关系可以用MA 模型描述，请将该过程的输入输出模型写成最小二乘格式。

提示：①提示：① MA MA 模型z k D z u k ()()()=-1②定义tt q )](,),1(),([)(,],,,[10n k u k u k u k d d d n --== h 解：因为MA 模型z k D z u k ()()()=-1，其中n n z d z d d z D ---+++= 1101)(，从而)()1()()(10n k u d k u d k u d k z n -++-+= 所以当定义t t q )](,),1(),([)(,],,,[10n k u k u k u k d d d n --== h ，则有最小二乘格式：)()()()()(0k e k h k e k h d k z ni i i +=+=å=q t，其中e(k)e(k)是误差项。

是误差项。

2-3、设)}({k e 是一个平稳的有色噪声序列，为了考虑这种噪声对辨识的影响，需要用一种模型来描述它。

请解释如何用白噪声和表示定理把)(k e 表示成AR 模型、MA 模型和ARMA 模型。

解：根据表示定理，在一定条件下，有色噪声e(k)可以看成是由白噪声v(k)驱动的线性环节的输出，该线性环节称为成形滤波器，其脉冲传递函数可写成)()()(111---=z C z D z H 即)()()()(11k v z D k e z C --=其中cc n n zc z c z C ---+++= 1111)(dd nn zd z d z D ---+++= 1111)(根据其结构，噪声模型可区分为以下三类：根据其结构，噪声模型可区分为以下三类：自回归模型（自回归模型（AR AR 模型）： )()()(1k v k e z C =- 平均滑动模型（平均滑动模型（MA MA 模型）： )()()(1k v z D k e -= 自回归平均滑去模型（自回归平均滑去模型（ARMA ARMA 模型）： )()()()(11k v z D k e z C --=3－4、根据离散Wiener-Hopf 方程，证明å-=D -D +=10221P N j P P P Mz j g N t a k g N t a N k R )(ˆ)(ˆ)()(解：由于M 序列是循环周期为t N P D ，12-=PP N ，t D 为M 序列移位脉冲周期，自相关函数近似于d 函数，a 为M 序列的幅度。

系统辨识作业

1.1讨论系统方程为：（信噪比）至少30%)()1()()1()(k e k u k b k ay k y +-=-+)(k e 为零均值白噪声， =)(k a =)(k b要求对系统参数辨识进行讨论（1）定常系统 a=0.8,b=0.5参数递推估计（2）时变系统取不同值是的不同结果并讨论。

（1）取初值P (0)=I 、∧θ（0）=0选择方差为1的白噪声作为输入信号u （k ），L=300，采用RLS 算法进行参数估计，代码及仿真结果图如下：clear all ;close all ;a=[1 0.8]';b=[0.5]';d=1; %对象参数na=length(a)-1;nb=length(b)-1; %na 、nb 为A 、B 阶次L=300; %仿真长度uk=zeros(d+nb,1); %输入初值：uk(i)表示u(k-i) yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列 xi=sqrt(0.1)*randn(L,1); %白噪声序列theta=[a(2:na+1);b]; %对象参数真值thetae_1=zeros(na+nb+1,1); %thetae 初值 P=10^6*eye(na+nb+1); for k=1:Lphi = [-yk;uk(d:d+nb)]; %´此处phi 为列向量 y(k)=phi'*theta + xi(k); %采集输出数据%递推最小二乘法K=P*phi/(1+phi'*P*phi);thetae( : ,k)=thetae_1 + K*(y(k)-phi'*thetae_1); P=(eye(na+nb+1)-K*phi')*P;%更新数据thetae_1 = thetae( : ,k);for i=d+nb:-1:2 uk(i)=uk(i-1); enduk(1)=u(k); for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endplot([1:L],thetae); %line([1,L],[theta,theta]); xlabel('k');ylabel('参数估计a、b');legend('a_1','b_0');axis([0 L -2 2]);图1-1 递推最小二乘法的参数估计结果（2））取初值P(0)=I、∧θ（0）=0选择方差为1的白噪声作为输入信号u（k），取分别为0.91,0.95,0.98,1.00时，L=600，采用FFRLS算法进行参数估计，代码及仿真图如下所示：clear all;close all;a=[1 0.8]';b=[0.5]';d=1; %对象参数na=length(a)-1;nb=length(b)-1; %na、nb为A、B阶次L=600; %仿真长度uk=zeros(d+nb,1); %输入初值：uk(i)表示u(k-i)yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); %白噪声序列thetae_1=zeros(na+nb+1,1); %thetae初值P=10^6*eye(na+nb+1);lambda=0.98; %遗忘因子范围[0.9 1]for k=1:Lif k==301a=[1 0.6]';b=[0.3]'; %对象参数突变endtheta( : ,k)=[a(2 : na+1);b]; %对象参数真值phi = [-yk;uk(d:d+nb)]; %´此处phi为列向量y(k)=phi'*theta( : ,k) + xi(k); %采集输出数据%遗忘因子递推最小二乘法·¨K=P*phi/(lambda+phi'*P*phi);thetae( : ,k)=thetae_1 + K*(y(k)-phi'*thetae_1);P=(eye(na+nb+1)-K*phi')*P/lambda;%更新数据thetae_1 = thetae( : ,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endsubplot(1,2,1)plot([1:L],thetae(1:na,:));hold on;plot([1:L],theta(1:na,:),'k:'); xlabel('k');ylabel('参数估计a');legend('a_1');axis([0 L -2 2]);subplot(1,2,2)plot([1:L],thetae(na+1:na+nb+1,:));holdon;plot([1:L],theta(na+1:na+nb+1,:),'k:');xlabel('k');ylabel('参数估计b');legend('b_0');axis([0 L -0.5 2]);图1-2-1 遗忘因子递推最小二乘法的参数估计结果（λ=0.91）图1-2-2 遗忘因子递推最小二乘法的参数估计结果（λ=0.95）图1-2-3遗忘因子递推最小二乘法的参数估计结果（ =0.98）图1-2-4 遗忘因子递推最小二乘法的参数估计结果（λ=1）由以上可以看出，技术对于参数突变的系统，采用FFRLS算法也能够有效地进行参数估计。

系统辨识大作业

系统辨识大作业系统辨识大作业1.考虑如下系统y() 1.5(1)0.7(2)(3)0.5(4)()k y k y k u k u k k ξ--+-=-+-+式中，()k ξ为白噪声。

取初值6(0)10P I =，ˆ(0)0θ=。

分别选择M 序列和方差为1的正态分布白噪声作为输入信号()u k ，采用递推最小二乘算法进行参数估计，迭代L=400步停止计算。

要求i) 给出基本迭代公式；ii) 画出程序流程框图；iii) 画出输入输出数据曲线、参数估计曲线、误差曲线；(提示：产生长度为L 方差为1的正态分布白噪声的MATLAB 命令为 randn （L,1）。

)答：选择如下形式的辨识模型)()4()3()2()1()(2121k k u b k u b k z a k z a k z ξ+-+-=-+-+设输入信号的取值是1．从1=k 到16=k 的M 序列，采用4位移位寄存器产生，幅度为0.03；2. 方差为1、长度为L 的正态分布白噪声，用randn(L,1)命令产生；i) 基本的迭代公式为1ˆˆˆ()(1)()[()()(1)]1()(1)()()(1)()()()[()()](1)T T T k k k z k k k k k k k k k k k I k k k θθθ-⎧=-+--⎪⎪⎡⎤=--+⎨⎢⎥Λ⎣⎦⎪⎪=--⎩K h K P h h P h P K h Pii) 程序流程框图iii)源代码与输入输出曲线、参数估计曲线、误差曲线%最小二乘递推算法辨识程序(输入信号采用M序列)clear %清理工作间变量L1=15; % M序列的周期L2=400; %迭代L2步后停止y1=1;y2=1;y3=1;y4=0; %四个移位寄存器的输出初始值%用4位移位寄存器生成M序列for i=1:L1; %开始循环，长度为L1x1=xor(y3,y4); %第一个移位寄存器的输入是第三个与第四个移位寄存器的输出的“或”x2=y1; %第二个移位寄存器的输入是第一个移位寄存器的输出x3=y2; %第三个移位寄存器的输入是第二个移位寄存器的输出x4=y3; %第四个移位寄存器的输入是第三个移位寄存器的输出y(i)=y4; %取出第四个移位寄存器的幅值为"0"和"1"的输出信号，即M序列if y(i)>0.5,u(i)=-0.03; %如果M序列的值为"1", 辨识的输入信号取“-0.03”else u(i)=0.03; %如果M序列的值为"0", 辨识的输入信号取“0.03”end %小循环结束y1=x1;y2=x2;y3=x3;y4=x4; %为下一次的输入信号做准备end %大循环结束，产生输入信号ufigure(1); %第1个图形stem(u),grid on %显示出输入信号径线图并给图形加上网格z(2)=0;z(1)=0; %设z的前两个初始值为零for k=3:15; %循环变量从3到15z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %输出采样信号endfigure(2); %第2个图形stem(z),grid on %显示出输出信号径线图并给图形加上网格%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0，即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,14)]; %被辨识参数矩阵的初始值及大小e=zeros(4,15); %相对误差的初始值及大小num=0; %迭代次数初始化for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x); %开始求K(k)k1=p0*h1*x1; %求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出p(k)的值p0=p1; %给下次用num=num+1; %迭代次数加1if num==L2break; %如果参数收敛情况满足要求，终止计算end %小循环结束end %大循环结束c,e %显示被辨识参数及其误差(收敛)情况%分离参数a1=c(1,:); a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:); ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(3); %第3个图形i=1:15; %横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1，a2，b1，b2的各次辨识结果title('Parameter Identification with Recursive Least Squares Method') %图形标题figure(4); %第4个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1，a2，b1，b2的各次辨识结果的收敛情况title('Identification Precision') %图形标题输入输出曲线：参数估计曲线和误差曲线：%最小二乘递推算法辨识程序(输入信号采用正态白噪声)clear %清理工作间变量L2=400; %迭代L2步后停止%产生白噪声输入信号u=randn(L2,1); %产生长度为L2、方差为1的正态白噪声作为输入figure(1); %绘制输入信号图形stem(u),grid on %显示出输入信号径线图并给图形加上网格z(2)=0;z(1)=0; %设z的前两个初始值为零for k=3:15; %循环变量从3到15z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2); %输出采样信号endfigure(2); %绘制输出信号图形stem(z),grid on %显示出输出信号径线图并给图形加上网格%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0，即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,14)]; %被辨识参数矩阵的初始值及大小e=zeros(4,15); %相对误差的初始值及大小num=0; %迭代次数初始化for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x); %开始求K(k)k1=p0*h1*x1; %求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出p(k)的值p0=p1; %给下次用num=num+1; %迭代次数加1if num==L2break; %如果参数收敛情况满足要求，终止计算end %小循环结束end %大循环结束c,e %显示被辨识参数及其误差(收敛)情况%分离参数a1=c(1,:); a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:); ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(3); %第3个图形i=1:15; %横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1，a2，b1，b2的各次辨识结果title('Parameter Identification with Recursive Least Squares Method') %图形标题figure(4); %第4个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1，a2，b1，b2的各次辨识结果的收敛情况title('Identification Precision') %图形标题输入输出曲线：参数估计曲线：2.考虑如下确定性系统() 1.5(1)0.7(2)(3)0.5(4)y k y k y k u k u k --+-=-+-采用梯度校正算法进行参数估计，通过相对误差准则停止计算。

第五章练习题

第五章练习题一、选择题1、下列开环传递函数所表示的系统，属于最小相位系统的是（）。

(A) ()()12151++-s s s (B) Ts Ts +-11 （T>0）(C) ()()13121+++s s s (D) ()()232-++s s s s【答案】C 【知识点】第五章【解析】该题考查考生什么是最小相位系统。

最小相位系统：若系统传递函数G(s)的所有零点和极点均在s 平面的左半平面，则该系统称为最小相位系统。

所以，答案为C 。

2.对数幅频特性的渐近线如图所示，它对应的传递函数G(s)为( )A. 1+TsB.1 1+TsC. 1TsD. (1+Ts)2【答案】A【知识点】第五章【解析】该题考查考生典型环节的伯德图。

图中为一阶微分环节对数幅频特性的渐近线。

所以，答案为A。

3.图示对应的环节为( )A. TsB.1 1+TsC. 1+TsD. 1 Ts【答案】C【知识点】第五章【解析】该题考查考生典型环节的乃奎斯特图。

图中为一阶微分环节的乃奎斯特图。

所以，答案为C。

4.若系统的Bode图在ω=5处出现转折(如图所示)，这说明系统中有( )环节。

A. 5s+1B. (5s+1)2C. 0.2s+1D. 10212(.)s【答案】D【知识点】第五章【解析】该题考查考生由伯德图估计最小相位系统。

由图可以看出转折点为5，并且是由-20dB/dec →-60dB/dec ，所以，必然是在5这个转折点处，出现了两个惯性环节。

因此，答案为D 。

5.已知系统的传递函数G(s)=se Ts K τ-+1，其幅频特性｜G(j ω)｜应为( )A. K T e 1+-ωτB. K T e 1+-ωτωC. K T e 2221+-ωτωD. K T 122+ω【答案】D【知识点】第五章【解析】该题考查考生频率特性。

题目中的传递函数包括延迟环节，容易迷惑考生。

但延迟环节对系统的幅频特性无影响。

所以，答案为D 。

系统辨识第五章讲义

6
1
选取Ts的经验公式：
a）按过渡时间T95选择(Ts ＝(1/150~1/50) T95)； b）按系统主要时间常数Ta选择
Ts ＝(0.05~0.1) Ta ； c ) 按系统最小时间常数Tmin选择
Ts ＝(0.2~0.4) Tmin ； d）按香农采样定理选择Ts
（一般按该法选择的Ts偏大）,实践中Ts再缩小 10倍也许合适。
－ 0.643
ai
1.018
bi
J
592.65
t
2
－1.015 0.337
3
－1.118 0.624
－ 0.178
4
－1.157 0.756
－0.412 0.187
1.068 －0.520
1.115 －0.660
0.263
1.085 －0.733
0.409 －0.146
469.64 12.57
389.50 9.67
优点——完全客观的准则，不要求建模者主观判断☺
缺点——需要事先已知噪声的概率分布
21
五．残差检验定阶
分析：LS、GLS、RELS等方法获得无偏估计条件
要求残差为白噪声；
如果假定的模型阶数n小于系统真实阶数，则计算得出的残差不是白色的；
反之，残差接近白噪声，则说明模型阶数不
低于系统阶数的数值。检验方法：1）计算残差 εˆ(k) = y(k) − xT (k)θˆ
5
二．采样间隔的选择
采样间隔Ts的选取，对模型参数辨识有很大影响。 Ts太大，描述系统动态性质的精确性降低了。 Ts太小，（1）相邻几次采样数据相差太小，容易在解参数估计值时出现病态方程，产生计算上的困难；
（2）参数估计的较小误差都会对模型的输入输出特性造成显著影响；

系统辨识大作业.

一、问题描述考虑仿真对象：()0.9(1)0.15(2)0.02(3)0.7(1)0.15(2)()z k z k z k z k u k u k e k +-+-+-=---+ e() 1.0e(1)0.41e(2)(),~(0,1)k k k v k v N λ+-+-=式中，u(k)和z(k)是输入输出数据，v(k)是零均值、方差为1的不相关的随机噪声；u(k)采用与e(k)不相关的随机序列。

1. 设计实验，产生输入输出数据；2. 使用基本最小二乘法估计参数；3. 考虑其他适用于有色噪声的辨识方法估计参数；4. 模型验证。

二、问题分析对于单输入单输出系统（Single Input Single Output, SISO ），如图 1所示，将待辨识的系统看作“灰箱”，它只考虑系统的输入输出特性，而不强调系统的内部机理。

图 1中，输入u(k)和输出z(k)是可以测量的，1()G z -是系统模型，用来描述系统的输入输出特性，y(k)是系统的实际输出。

1()N z -是噪声模型，v(k)是均值为零的不相关随机噪声，e(k)是有色噪声。

图 1 SISO 系统的“灰箱”结构对于SISO 随机系统，被辨识模型()G z 为：12121212()()()1n n nn b z b z b z y z G z u z a z a z a z ------+++==++++ 其相应的差分方程为11()()()n ni i i i y k a y k i b u k i ===--+-∑∑若考虑被辨识系统或观测信息中含有噪声，被辨识模型可改写为11()()()()n ni i i i z k a y k i b u k i v k ===--+-+∑∑式中，z(k)为系统输出量的第k 次观测值；y(k)为系统输出量的第k 次真值，y(k-1)为系统输出量的第k-1次真值，以此类推；u(k)为系统的第k 个输入值，u(k-1)为系统的第k-1个输入值；v(k)为均值为0的不相关随机噪声。

(完整word版)2003版系统辨识最小二乘法大作业

西北工业大学系统辩识大作业题目：最小二乘法系统辨识一、问题重述：用递推最小二乘法、加权最小二乘法、遗忘因子法、增广最小二乘法、广义最小二乘法、辅助变量法辨识如下模型的参数离散化有z^4 - 3.935 z^3 + 5.806 z^2 - 3.807 z + 0.9362---------------------------------------------- =z^4 - 3.808 z^3 + 5.434 z^2 - 3.445 z + 0.8187噪声的成形滤波器离散化有4.004e-010 z^3 + 4.232e-009 z^2 + 4.066e-009 z + 3.551e-010-----------------------------------------------------------------------------=z^4 - 3.808 z^3 + 5.434 z^2 - 3.445 z + 0.8187采样时间0.01s要求：1.用Matlab 写出程序代码；2.画出实际模型和辨识得到模型的误差曲线；3.画出递推算法迭代时各辨识参数的变化曲线；最小二乘法:在系统辨识领域中 ,最小二乘法是一种得到广泛应用的估计方法 ,可用于动态 ,静态 , 线性 ,非线性系统。

在使用最小二乘法进行参数估计时 ,为了实现实时控制 ,必须优化成参数递推算法 ,即最小二乘递推算法。

这种辨识方法主要用于在线辨识。

MATLAB 是一套高性能数字计算和可视化软件 ,它集成概念设计 ,算法开发 ,建模仿真 ,实时实现于一体 ,构成了一个使用方便、界面友好的用户环境 ,其强大的扩展功能为各领域的应用提供了基础。

对于一个简单的系统 ,可以通过分析其过程的运动规律 ,应用一些已知的定理和原理,建立数学模型 ,即所谓的“白箱建模 ”。

但对于比较复杂的生产过程 ,该建模方法有很大的局限性。

由于过程的输入输出信号一般总是可以测量的 ,而且过程的动态特性必然表现在这些输入输出数据中 ,那么就可以利用输入输出数据所提供的信息来建立过程的数学模型。

(完整)系统辨识大作业汇总,推荐文档

参数递推估计是指被辨识的系统，每取得一次新的测量数据后，就在前一次估计结果的基础上，利用新引入的测量数据对前一次估计的结果进行修正，从而递推地得出新的参数估计值。这样，随着新测量数据的引入，一次接一次地进行参数估计，直到估计值达到满意的精确程度为止。最小二乘递推算法的基本思想可以概括为：
当前的估计值ˆ(k) =上次估计值ˆ(k 1) +修正项即新的估计值ˆ(k) 是在旧的估计值ˆ(k 1) 的基础上，利用新的观测数据对旧的估计值进行修正而成的。
可以看出，取 (k) 1的时候，加权最小二乘估计就退化成了最小二乘参数估计的递推算法（Recursive Least Squares, RLS）。加权参数 1 可以在
(0,1]范围内选择，如果选 1 1，所有的采样数据都是等同加权的，如果
(k)
1 1,则表示对新近获得的数据给予充分大的加权因子，而削弱历史观测 (k)
可以根据生成的白噪声序列和输入序列，以及必要的 0 初始值，带入表达式即可得到采样输出数据。
2. 差分模型阶检验在实际场景中，辨识模型的阶数和纯时延往往是未知的，在很多情况下仅
仅依靠猜测。在模型的阶数和纯时延不确定时，设系统模型为
n
n
y(t) ai y(t i) bj y(t i) (t)
数据的影响。实际计算时，需要首先确定初始参数ˆ(0) 和 P(0) 。
P(0) 2I 为充分大实数
一般说来选取
(0)
为充分小的向量
对于这样的系统，使用最小二乘法参数估计的递推算法进行辨识可以得到无偏估计，但是如果噪声模型必须用 C(z1)v(k) 表示时，此时就无法得到无偏估计了，因为该方法没有把噪声模型考虑进去。
K (k) P(k 1)h(k)[hT (k) p(k 1)h(k) 1 ]1

系统辨识第五章

第五章统计学方法预备知识在实际过程中和信号测量中不可避免地会受到各种干扰或噪声的影响，当这些随机性干扰或噪声在试验结果中成为不可忽略的因素时，需要采用统计学的方法对过程进行辨识，而本章主要讲述统计学中需要用到的概率知识、最小二乘法和慢时变参数的递推估计。

5.1概率统计基本知识在实验结果中存在一个变量，该变量不能预先知道取哪个值，这样的变量称为随机变量，而随机变量分为离散性和连续型两种。

对于这样一种变量，要完全描述一个随机现象的特性，就需要知道在实验中各种可能结果出现的机会是多少，即随机变量的概率分布。

对于离散型的随机变量，其概率分布为：i i p x X P ===}{，11=∑=Ni i p式中，X 是一个随机变量，X=i x 代表某一件事；{}.P 表示事件的概率；i p 为i x 对应的概率。

对于一个连续型随机变量x ，其概率分布是一个函数，为：}{)(x X P x F <=概率分布也是随机变量分布律之一，如设()x F 连续可微，概率密度可定义为：dx x dF x p )()(=若用()(){}dx x X x P x dF dx x p +<<=表示概率元素，则变量X 落入区间()b a ,的概率为：{}()⎰=<<badx x p b X a P而X 落入区间()x ,∞-的概率为：()()⎰∞-=xdx x p x F而且X 落入区间()+∞∞-,的概率为：()⎰+∞∞-=1dx x p在实际问题中，使用一个变量往往不够，需要使用多个随机变量才能描述一个实际问题。

本章中讨论的是二维随机变量。

二维随机变量概率分布：称两个事件X<x ，Y<y 同时实现的概率为随机变量（X,Y ）的概率分布，即：},{),(y Y x X P y x F <<=二维随机变量的概率密度为：yx y x F y x p ∂∂∂=),(),(2 条件概率密度：即在某个条件下某件事情发生的概率，如()()()B A P B P B A P |=⋂从而可得到()()()B P B A P B A P ⋂=|均值：也称为数学期望，它表示大量重复某一实验，其结果的平均。

系统辨识基础课程作业

《系统辨识基础》课程作业■ 课程编号：40250203 ■ 课程序号：0■ 课程名称：系统辨识基础Fundamentals of System Identification■ 任课教师：萧德云■ 学时：总学时48，3学时/周 ■ 学分：3学分■ 教材：方崇智萧德云，《过程辨识》，清华大学出版社，1988■ 说明：本课程作业可分两次交给辅导教师杜宇健批改，第一次（1、2、3、4章）讲完第4章后交，第二次（5、13、6章）讲完第6章后交，期末考试之前作业必须交齐。

作业与实验共占总成绩的20％。

■ 课程作业第1章1、举例说明数学模型的定义及其用途。

2、建模有哪两种基本方法，它们有什么本质的区别？3、辨识建模的基本出发点是什么？4、叙述辨识所用模型的含义，并用数学表达式给出辨识模型的满意度描述。

5、叙述利用辨识方法建立系统数学模型所应该遵循的基本原则。

6、论述“过程辨识”P11图1.7和1.8各自对问题的描述含义和区别。

7、最小二乘格式输入向量h ()k 的元素应满足什么要求？8、“过程辨识”P520 1.3。

9、试解释辨识定义的实用意义（突出辨识的三要素概念）。

10、“过程辨识”P520 1.4。

11、“过程辨识”P520 1.5。

12、“过程辨识”P520 1.6。

13、“过程辨识”P520 1.7。

14、若一个过程的输入、输出关系可以用MA 模型描述，请将该过程的输入输出模型写成最小二乘格式。

提示：① MA 模型z k D z u k ()()()=-1② 定义ττθ)](,),1(),([)(,],,,[10n k u k u k u k d d d n --== h15、将下列模型写成最小二乘格式A z z kB z u k D z v k ()()()()()()---=+111 16、“过程辨识”P520 1.9。

提示：①最小二乘格式z H w L L L =+θ②数据矩阵H L u u u N u L u L u L N =-----⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥()()()()()()01112 ③概率密度 )]()(21exp[)2()|(222θθσπσθτH z H z z ---=-wL w p④Fisher 矩阵⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=θ∂θ∂θ∂θ∂τ)|(log )|(log E z z M p p⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=H H w H w H ττττσσσ2221E 11E w w w17、举例说明有关模型方程误差的概念。

系统辨识作业汇总

系统建模方法大作业1.考虑如下系统y() 1.5(1)0.7(2)(3)0.5(4)()k y k y k u k u k k ξ--+-=-+-+式中，()k ξ为白噪声。

取初值6(0)10P I =，ˆ(0)0θ=。

分别选择M 序列和方差为1的正态分布白噪声作为输入信号()u k ，采用递推最小二乘算法进行参数估计，迭代L=400步停止计算。

要求i) 给出基本迭代公式；ii) 画出程序流程框图；iii) 画出输入输出数据曲线、参数估计曲线、误差曲线；提示：产生长度为L 方差为1的正态分布白噪声，相应的MATLAB 命令为 randn （L,1）。

1=+10**[*0*1]k p h h p h-（1）z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-3)+0.5*u(k-4)h1=[-z(k-1),-z(k-2),u(k-3),u(k-4)]c1=c0+k1*[z(k)-h1'*c0]（2）（3）1.当输入为M序列时L=15; % M序列的周期y1=1;y2=1;y3=1;y4=0; %四个移位寄存器的输出初始值for i=1:L; %开始循环，长度为Lx1=xor(y3,y4); %第一个移位寄存器的输入是第三个与第四个移位寄存器的输出的x2=y1; %第二个移位寄存器的输入是第一个移位寄存器的输出x3=y2; %第三个移位寄存器的输入是第二个移位寄存器的输出x4=y3; %第四个移位寄存器的输入是第三个移位寄存器的输出y(i)=y4; %取出第四个移位寄存器的幅值为"0"和"1"的输出信号，即M 序列if y(i)>0.5,u(i)=-0.03; %如果M序列的值为"1", 辨识的输入信号取“-0.03” else u(i)=0.03; %如果M序列的值为"0", 辨识的输入信号取“0.03” end %小循环结束y1=x1;y2=x2;y3=x3;y4=x4; %为下一次的输入信号做准备end %大循环结束，产生输入信号ufigure(1); %第一个图形title('输入M序列') %图形标题stem(u),grid on %显示出输入信号径线图并给图形加上网格z(4)=0;z(3)=0;z(2)=0;z(1)=0; %设z的前四个初始值为零for k=5:15; %循环变量从3到15z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-3)+0.5*u(k-4); %输出采样信号end%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0，即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,14)]; %被辨识参数矩阵的初始值及大小e=zeros(4,15);for(n=1:400); %迭代次数for k=5:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-3),u(k-4)]';x=h1'*p0*h1+1;x1=inv(x); %开始求K(k)k1=p0*h1*x1; %求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出 p(k)的值p0=p1; %给下次用%如果参数收敛情况满足要求，终止计算end%小循环结束end %大循环结束c,e %显示被辨识参数及其误差(收敛)情况%分离参数a1=c(1,:);a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:);ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(2); %第二个图形i=1:15; %横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1，a2，b1，b2的各次辨识结果title('递推最小二乘参数辨识') %图形标题figure(3); %第三个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1，a2，b1，b2的各次辨识结果的收敛情况title('辨识精度') %图形标题辨识曲线图：2当输入为随机正态分布时u=randn(L,1); %产生随机正态分布白噪声figure(1); %第一个图形title('输入正态分布白噪声') %图形标题stem(u),grid on %显示出输入信号径线图并给图形加上网格z(4)=0;z(3)=0;z(2)=0;z(1)=0; %设z的前四个初始值为零for k=5:15; %循环变量从3到15z(k)=1.5*z(k-1)-0.7*z(k-2)+u(k-3)+0.5*u(k-4); %输出采样信号end%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0，即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,14)]; %被辨识参数矩阵的初始值及大小e=zeros(4,15);for(n=1:400); %迭代次数for k=5:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-3),u(k-4)]';x=h1'*p0*h1+1;x1=inv(x); %开始求K(k)k1=p0*h1*x1; %求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出 p(k)的值p0=p1; %给下次用%如果参数收敛情况满足要求，终止计算end%小循环结束end %大循环结束c,e %显示被辨识参数及其误差(收敛)情况%分离参数a1=c(1,:);a2=c(2,:);b1=c(3,:);b2=c(4,:);ea1=e(1,:);ea2=e(2,:);eb1=e(3,:);eb2=e(4,:);figure(2); %第二个图形i=1:15; %横坐标从1到15plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1，a2，b1，b2的各次辨识结果title('递推最小二乘参数辨识') %图形标题figure(3); %第三个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1，a2，b1，b2的各次辨识结果的收敛情况title('辨识精度') %图形标题辨识曲线：2.考虑如下确定性系统() 1.5(1)0.7(2)(3)0.5(4)y k y k y k u k u k --+-=-+-采用梯度校正算法进行参数估计，通过相对误差准则停止计算。

系统辨识答案

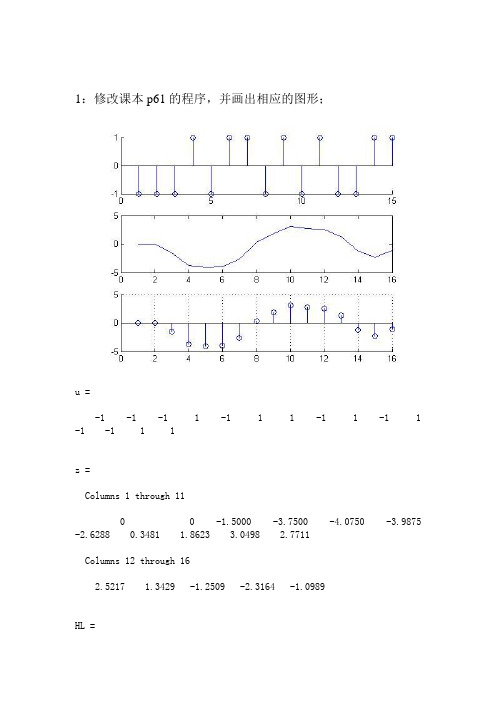
1：修改课本p61的程序，并画出相应的图形；u =-1 -1 -1 1 -1 1 1 -1 1 -1 1 -1 -1 1 1z =Columns 1 through 110 0 -1.5000 -3.7500 -4.0750 -3.9875 -2.6288 0.3481 1.8623 3.0498 2.7711Columns 12 through 162.5217 1.3429 -1.2509 -2.3164 -1.0989HL =0 0 -1.0000 -1.00001.5000 0 -1.0000 -1.00003.7500 1.5000 1.0000 -1.00004.0750 3.7500 -1.0000 1.0000 3.9875 4.0750 1.0000 -1.0000 2.6288 3.9875 1.0000 1.0000 -0.3481 2.6288 -1.0000 1.0000 -1.8623 -0.3481 1.0000 -1.0000 -3.0498 -1.8623 -1.0000 1.0000 -2.7711 -3.0498 1.0000 -1.0000 -2.5217 -2.7711 -1.0000 1.0000 -1.3429 -2.5217 -1.0000 -1.00001.2509 -1.3429 1.0000 -1.00002.3164 1.2509 1.0000 1.0000 ZL =-1.5000-3.7500-4.0750-3.9875-2.62880.34811.86233.04982.77112.52171.3429-1.2509-2.3164-1.0989c =-1.50000.70001.00000.5000a1 =-1.5000a2 =0.7000b1 =1b2 =0.50002：修改课本p63的程序，并画出相应的图形（V的取值范围为54-200）；V = [54.3000, 61.8000, 72.4000, 88.7000, 118.6000, 194.0000]τP = [61.2000, 49.5000, 37.6000, 28.4000, 19.2000, 10.1000]τZL = [4.1141, 3.9020, 3.6270, 3.3464, 2.9549, 2.3125]τHL =-3.9945 1.0000-4.1239 1.0000-4.2822 1.0000-4.4853 1.0000-4.7758 1.0000-5.2679 1.0000c4 =1.40429.6786alpha = 1.4042beita = 1.5972e+0043：表1中是在不同温度下测量同一热敏电阻的阻值，根据测70时的电阻量值确定该电阻的数学模型，并求出当温度在C︒值。

系统辨识与建模智慧树知到课后章节答案2023年下湘潭大学

系统辨识与建模智慧树知到课后章节答案2023年下湘潭大学湘潭大学第一章测试1. A system is a unity composed of various parts that are interconnectedconstrained and interacted with each other and have certain overallfunctions and comprehensive behaviors.（）A:对 B:错答案:对2.Which one is not belong to modern control theory system?（）.A:System identification B:Modern control theory C:State estimationD:Automatic control答案:Automatic control3.建立数学模型的方法可大体分为：（）.A:观测法 B:理论分析法 C:测试法 D:实验法答案:理论分析法;测试法4.下列哪些属于非参数模型?（）A:权序列模型 B:输入输出模型 C:状态空间模型 D:脉冲响应模型答案:权序列模型;脉冲响应模型5.针对水箱进行机理建模时，我们应该凭借哪种关系建立公式？（）.A:水箱流入量和流出量之差为流入水流量的增量 B:水箱流入量和流出量之差为液位的增量 C:水箱流入量和流出量之差为液体存储量的变化率 D:水箱流入量和流出量之差为流出水流量的增量答案:水箱流入量和流出量之差为液体存储量的变化率第二章测试1.下面哪些内容不属于系统辨识的基本内容？（）A:观测数据 B:模型结构辨识 C:模型验证 D:模型参数辨识答案:观测数据2.白噪声过程没有“记忆性”，也就是说t时刻的数值与t时刻以前的值无关，也不影响t时刻以后的将来值。

（）A:对 B:错答案:对3.关于白噪声的均匀分布计算问题，将产生的（0，1）均匀分布的随机数通通减去0.5，然后乘以存储器f中预置的系数，这里取f=2，从而得到新的分布（）。

系统辨识期末作业

系统辨识期末作业一、系统辨识“系统辨识”是研究如何利用系统试验或运行的、含有噪声的输入输出数据来建立被研究对象数学模型的一种理论和方法。

系统辨识是建模的一种方法，不同的学科领域，对应着不同的数学模型。

从某种意义上来说，不同学科的发展过程就是建立他的数学模型的过程。

辨识问题可以归结为用一个模型来表示客观系统(或将要构造的系统)本质特征的一种演算，并用这个模型把对客观系统的理解表示成有用的形式。

当然也可以有另外的描述，辨识有三个要素：数据，模型类和准则。

辨识就是按照一个准则在一组模型类中选择一个与数据拟合得最好的模型。

总而言之，辨识的实质就是从一组模型类中选择一个模型，按照某种准则，使之能最好地拟合所关心的实际过程的静态或动态特性。

通过系统辨识建立对象数学模型的依据是：研究表明，从外部对一个系统的认识，是通过其输入输出数据来实现的，既然数学模型是表述一个系统动态特性的一种描述方式，而系统的动态特性的表现必然蕴含在它变化的输入输出数据中。

所以，通过记录系统在正常运行时系统的输入输出数据，或者通过测量系统在人为输入作用下的输出响应，然后对这些数据进行适当的系统处理、数学计算和归纳整理，提取数据中蕴含的系统信息，从而建立被控对象的数学描述，这就是系统辨识。

即系统辨识就是一种利用数学的方法从输入输出数据序列中提取对象数学模型的方法。

下面从三个方面来对系统辨识进行介绍：1、统辨识的方法（1）、经典的系统辨识办法在经典控制理论中，所分析研究的是单输入单输出系统，经常用到的系统模型是频率响应、权函数和传递函数。

所以早期系统辨识工作的主要内容也就是寻求描述单变量系统的频率特性、权函数和系统的传递函数。

早期的系统辨识所用的方法大多是在一定的连续时间性的输入信号下（非周期的或周期的），观测被识对象对这种输入作用的响应，例如频率响应或阶跃响应。

根据需要，再由这些响应特性求出系统的参数模型。

这些方法有阶跃响应法、频率特性法和相关分析法。

系统辨识作业及答案

系统辨识作业及答案一．问答题1. 介绍系统辨识的步骤。

答：（1）先验知识和建模目的的依据；（2）实验设计；（3）结构辨识；（4）参数估计；（5）模型适用性检验。

2. 考虑单输入单输出随机系统，状态空间模型[])()(11)()(11)(0201)1(k v k x k y k u k x k x +=+=+ 转换成ARMA 模型。

答：ARMA 模型的特点是u(k)=0,[])()(11)()(0201)1(k v k x k y k x k x +=??=+3. 设有一个五级移位寄存器，反馈取自第2级和第3级输出的模2加法和。

试说明：（1）其输出序列是什么？（2）是否是M 序列？（3）它与反馈取自第4级与第3级输出模2加法和所得的序列有何不同？（4）其逆M 序列是什么？答：（1）设设输入序列1 1 1 1 1111018110107101006010015100114001113011112111111）（）（）（）（）（）（）（）（()()()()()()()01110161110115110101410100)13(0100112100111 10011110011109()()()()()()()001112401110)23(111012********* 010020010011910011180011117()()()()()()()()10011320011131011103000111291101028101002701001261001125 其输出序列为：1 1 1 1 1 0 0 1 0 1⑵不是M 序列⑶第4级与第3级模2相加结果100108001007010006100015000114001113011112111111）（）（）（）（）（）（）（）（()()()()()()()11110161110115110101410101)13(0101112101101 10110010110019()()()()()()()110012410010)23(001002201000211 000120000111900111180111117()()()()()()()()01111321111031111013011010291010128010112710110260110025 不同点：第2级和第3级模二相加产生的序列，是从第4时刻开始，每隔7个时刻重复一次；第4级与第3级模2相加产生的,序列，是从第2时刻开始每隔15个时刻重复一次。

合工大系统辨识作业及答案

系统辨识作业一、简答题1 系统辨识的实验设计应包含那些内容？答：系统辨识实验设计应包含选择实验信号、采样时间、辨识时间、输入输出数据长度等。

2 判断下列是否为一个正确周期的M 序列，并说明原因。

111100010011011 111100********* 答：不是M 序列，因为M 序列的周期为15，由M 序列的性质知序列中“1”的状态应为8个而第一个中有9个所以不是M 序列3证明加权最小二乘估计的无偏性。

证明：加权最小二乘估计的解为：()1ˆTT WLSW WY θ-=ΦΦΦ 其中Φ为输入矩阵 W 为加权矩阵 Y 为输出矩阵。

()()11ˆ()T T WLS T TE W W e E W We θθθ--⎡⎤⎡⎤=ΦΦΦΦ+⎣⎦⎢⎥⎣⎦⎡⎤=+ΦΦΦ⎢⎥⎣⎦由于Φ与e 统计独立，则()10T T E W We -⎡⎤ΦΦΦ=⎢⎥⎣⎦即ˆWLS E θθ⎡⎤=⎣⎦所以ˆWLSθ是无偏估计量，命题得证。

4比较最小二乘法、广义最小二乘法和辅助变量法的优缺点。

答：基本最小二乘对低噪声有效，参数估计值可很快收敛到真值，所需计算量相对较少，但对实际噪声估计有偏。

广义最小二乘法：计算量大，可能不收敛，可能是有偏估计。

但如果对噪声模型用随机逼近法，而对过程模型采取最小二乘法则获得较好形式的广义最小二乘法。

辅助变量法可以一次性完成计算，但是计算量也大，对初值选择很敏感。

5答：对于n 阶系统与n+1阶系统参数估计之间有如下的关系：对于n+1阶系统 ()()()11()()A z y k B z u k e k --=+设其待估参数为()011111...(1)(2)T T Tn n n n n b a b a b a b θθθ++⎡⎤⎡⎤+==⎣⎦⎣⎦ 则(1)()[()]T n A Y n θθθ=-Φ-Φ由题目知n=2时系统参数为准确值，则n=3时按照上式去计算，估算出的系数必远远偏离系统模型参数值。

北航《系统辨识》课程作业

7
姓名：xx
学号：SYxx
2013/11/30
xlabel('迭代次数') ylabel('误差') hold off figure(2); plot(-1.5-error1,'b'); hold on plot(0.7-error2,'c') hold on plot(1-error3,'g') hold on plot(0.5-error4,'y') hold on plot(-1-error5,'m') hold on plot(0.2-error6,'r') legend('a1','a2','b1','b2','d1','d2',-1) title('参数估计值变化') xlabel('迭代次数') ylabel('参数') hold off 2. 题目 2 程序 clc close all total=1500; sigma=1.0; %M 序列输入 A1=1;A2=1;A3=1;A4=0; for i=1:1:total x1=xor(A3,A4); x2=A1; x3=A2; x4=A3; OUT(i)=A4; if OUT(i)<0.5 u(i)=1; else u(i)=-1; end A1=x1;A2=x2;A3=x3;A4=x4; end figure(1) stem(u,'r') grid on
6
%噪声
姓名：xx
学号：SYxx
2013/11/30
v_da2(k)=y(k-2)-d1*v_da2(k-1)-d2*v_da2(k-2); v_db1(k)=-u(k-1)-d1*v_db1(k-1)-d2*v_db1(k-2); v_db2(k)=-u(k-2)-d1*v_db2(k-1)-d2*v_db2(k-2); v_dd1(k)=-v(k-1)-d1*v_dd1(k-1)-d2*v_dd1(k-2); v_dd2(k)=-v(k-2)-d1*v_dd2(k-1)-d2*v_dd2(k-2); d_theta=[v_da1(k),v_da2(k),v_db1(k),v_db2(k),v_dd1(k),v_dd2(k)]'; J_d=J_d+v(k)*d_theta; JJ_d=JJ_d+d_theta'*d_theta; end bef=theta; theta=theta-inv(JJ_d)*J_d; v(1)=v(N+1);v(2)=v(N+2); v_da1(1)=v_da1(N+1);v_da2(1)=v_da2(N+1);v_db1(1)=v_db1(N+1);v_db2 (1)=v_db2(N+1);v_dd1(1)=v_dd1(N+1);v_dd2(1)=v_dd2(N+1); v_da1(2)=v_da1(N+2);v_da2(2)=v_da2(N+2);v_db1(2)=v_db1(N+2);v_db2 (2)=v_db2(N+2);v_dd1(2)=v_dd1(N+2);v_dd2(2)=v_dd2(N+2); %求取误差 error1(j)=-1.5-theta(1); error2(j)=0.7-theta(2); error3(j)=1-theta(3); error4(j)=0.5-theta(4); error5(j)=-1-theta(5); error6(j)=0.2-theta(6); v_error(j)=v(N+2); j=j+1; end theta%输出估计参数 %作图 figure(1); plot(error1) hold on plot(error2) hold on plot(error3) hold on plot(error4) hold on plot(error5,'r') hold on plot(error6,'r') title('参数估计误差')

系统辨识第5章线性动态模型参数辨识最小二乘法

度函数
，则称uS(uk()为) “持续激励”信号。
● 定义4 一个具有谱密度 Fn (为z 1的) 平f1z稳1 信f2号z 2u(k)称fn为z nn 阶
“持续激励”Fn信(e号j )，2 S若u (对) 一0 切形如 Fn (e j ) 0
的滤波器，关系式
，意味着
。
● 定理2 设输入信号u(kR)u是(0)平稳R随u (1机) 信号，Ru (如n 果1)相关函数矩阵

式中
zL H L nL
nzHLLL[[zn(h(hh11TT)T),((,(zL12n())()22)),,,,znz(((LzLzL)(()]10]))1)
z(1 na ) z(2 na )
z(L na )
u(0) u(1)
u(L 1)
u(1 nb )
u(2
nb
)
u(L nb )
5.2 最小二乘法的基本概念
● 两种算法形式
① 批处理算法：利用一批观测数据，一次计算或经反复迭代，
以获得模型参数的估计值。
②
递推算法：在上次模型参数估计值
ˆ
(k
1)的基础上，根据当
前获得的数据提出修正，进而获得本次模型参数估计值ˆ (k )，
广泛采用的递推算法形式为
(k ) (k 1) K (k )h(k d )~z (k )
z(k ) h (k ) n(k )
式中z(k)为模型输出变量，h(k)为输入数据向量，为模型参
数向量，n(k)为零均值随机噪声。为了求此模型的参数估计值，可以利用上述最小二乘原理。根据观测到的已知数据序列
和{z(k)} ，{h极(k小)} 化下列准则函数
L
J ( ) [z(k ) h (k ) ]2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

摘要系统辨识是描述各种各样系统运动规律的一种方法论，是研究系统的一种有效工具。

利用这个工具可以对我们要研究的系统进行定量描述。

随着现代控制理论的迅速发展，系统辨识得到迅速而蓬勃发展，并已经成功运用与多种工程应用领域。

但针对有色噪声干扰系统，传统的辨识方法不能得到良好的参数估计，而工程上大多系统都为有色噪声干扰系统。

有色噪声干扰系统的一类系统为广义输出误差模型，本文对白噪声和有色噪声两种噪声干扰下运用最小二乘法，递推最小二乘法分别比较噪声的不同，以及进一步得出最小二乘法的适用性。

进一步研究广义最小二乘法对有色噪声系统辨识的改进。

关键词：系统辨识；白噪声；有色噪声；最小二乘；递推最小二乘；广义最小二乘ABSTRACTthe law of motion of the system identification is to describe the various system and an effective tool for the system. It also can be used to study quantitative description of the system. With the rapid development of modern control theory,the development of system identification has been rapid and vigorous , and has been successfully applied to a variety of engineering applications. However, the traditional identification methods can't get good parameter estimation in engineering systems for colored noise . Colored noise jamming system is for generalized output error model.under two kinds of noise of white noise and color noise ,by using the least square method and the recursive least square method ,respectively to compare the different noise, and to furtherconcluded that the applicability of the least-square method. To further studied the improvement of generalized least squares identification of colored noise system.KEY WORDS: system identification,white noise, colored noise.,least squares;,recursive least squares,the generalized least squares目录摘要 (1)第一章系统辨识 (2)1.1辨识的定义 (2)1.2辨识的内容和步骤 (3)1.3辨识目的 (3)1.4先验知识 (3)1.5数据预处理 (4)1.6模型结构辨识 (4)1.7模型参数辨识 (4)1.8模型检验 (4)第二章题目详解 (5)2.1.1最小二乘法 (5)2.1.2递推法 (8)2.2.1最小二乘法 (12)2.2.2递推法 (13)2.3广义最小二乘法 (15)附录 (16)第一章系统辨识1.1辨识的定义Zadeh对辨识的定义（1962年）辨识就是在输入和输出数据的基础上，从一组给定的模型类中，确定一个与所测系统等价的模型。

Liung 对辨识的的定义（1978年）系统辩识有三个要素——数据、模型类和（等价）准则。

系统辩识是按照一个准则，在模型类中选择一个与数据拟合得最好的模型。

Liung 认为，实际系统的复杂性很难找到一个适用的模型与之等价。

因此，系统辩识的任务只是要求从输入输出数据出发，找到一个与实际系统相逼近的模型。

该定义体现了逼近的观点。

系统辨识是在输入和输出观测的基础上，从指定的一类模型中确定一个与系统等价的模型。

1.2辨识的内容和步骤简单地说，辨识就是一种从观测到的含有噪声的输入输出数据中提取数学模型的方法。

根据现场的情况，辨识可以离线进行，也可以在线进行；辨识的内容主要包括四个方面：实验设计，模型结构辨识，模型参数辨识，模型检验。

1.3辨识目的明确模型应用的最终目的很重要，因为它将决定模型的类型，精度要求和采用哪种辨识方法等问题。

1.4先验知识对于给定的过程进行辨识之前，要通过一些手段对过程有一些了解粗略的掌握一些过程和数据，这些先验知识对实验设计将其指导作用。

1.5数据预处理输入输出数据通常含有直流或交流成分，任何方法都无法消除对系统精度的影响。

此外，高频成分也是不利的。

因此需对输入数据进行零均值化和剔除高频成分预处理。

1.6模型结构辨识模型结构辨识包括模型验前结构和模型结构参数两部分。

1.7模型参数辨识当模型结构确定之后，就需要进行模型参数辨识。

方法很多，最基本，应用最广的是最小二乘法。

但是最小二乘法也有一些重大缺陷，比如过程辨识受到有色噪声污染时，他几乎比能适应。

1.8模型检验模型检验是辨识过程不可或缺的步骤之一。

但是，它没有一般方法可循。

它和模型结构问题密切相关。

如果模型结构不合适，模型检验是不能通过的。

第二章题目详解2.1.1最小二乘法一个单输入－单输出线性定常系统的差分方程)()1()()()2()1()(1021n k u b L k u b k u b n k x a L k x a k x a k x n n -++-+=-++-+-+式中)(k u 为输入信号，)(k x 为理论上的输出值。

)(k x 通过观测得到，在观测过程中往往附加有随机干扰。

观测值用)(k y 表示：)()()(k v k x k y += ξ（k ）=v （k ）+Σ)(i k v a i - 则∑∑+-+--=)()()()(k i k u b i k y a k y i i ξ；如果 u （k ）也有测量误差，则在ξ（k ）中应包含这一测量误差。

ζφθ+=Y 则()YTTθθφφ1ˆ-=原题设为二阶系统，且θ的真值已知，输入)(k u 已知，求)(k y ，并且由输入输出序列得出参数估值，其程序已在matlab中实现。

实验结果如下图：2.1.2递推法图1.2 最小二乘递推算法辨识的Malab6.0程序流程图Matlab仿真结果：c =Columns 1 through 121.6420 0 1.6420 0 0 0 0 0 0 0 0 00.7150 0 0.7150 0 0 0 0 0 0 0 0 00.3900 0 0.3689 0 0 0 0 0 0 0 0 00.3500 0 0.2298 0 0 0 0 0 0 0 0 0Columns 13 through 240 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0Columns 25 through 300 0 0 0 0 00 0 0 0 0 00 0 0 0 0 00 0 0 0 0 0e =Columns 1 through 120 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 -0.0540 0 0 0 0 0 0 0 0 00 0 -0.3433 0 0 0 0 0 0 0 0 0Columns 13 through 240 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0Columns 25 through 300 0 0 0 0 00 0 0 0 0 00 0 0 0 0 00 0 0 0 0 0结果分析：仿真结果表明，大约递推到第五步时，参数辨识的结果基本达到稳定状态。

此时，参数的相对变化量E ≤0.000000005。

从整个辨识过程来看，精度的要求直接影响辨识的速度。

虽然最终的精度可以达到很小，但开始阶段的相对误差会很大。

2.2.1最小二乘法题设将白噪声改为有色噪声，)2()1()()(21-+-+=k a k a k k εεεξ；有色噪声可以看做是白噪声经过成型滤波器后得到的。

Matlab 仿真结果：结果分析：由于所用的输出观测值有有色噪声成分，所以辨识结果有误差，且用最小二乘法计算得到的参数估计误差较大。

2.2.2递推法结果：结果分析：第一问和第二问的区别只是噪声不同，但是从仿真结果图像来看，都是从第五步开始达到稳定状态的，但有色噪声参数辨识显然误差更大更明显。

2.3广义最小二乘法广义最小二乘法辨识的计算步骤如下：（1）应用已得到的输入和输出数据 u(k) 和y(k) (2)计算残差e(k),并用其代替)(k ξ （3）计算和)(k u -和)(k y -(4)应用得到的)(k u -和)(k y -，)()()()()()2(1)1(1k k b k a u z y z ε+=--，再用最小二乘法重新估计θ ，得θ的第2次估值 θ)2( 。

然后按步骤⑵计算残差 e(k) 。

重新估计f ，得到估值 f)2( 。

再按步骤⑶计算y)2(和u)2(，按步骤⑷求θ 的第3次估计θ)3( 。

重复上循环步骤，直到θ 的估值θ收敛为止。

附录程序%1.1 二阶系统的最小二乘一次完成算法辨识程序，在光盘中的文件名：FLch3LSeg1.m u=[1.147,0.201,-0.787,-1.589,-1.052,0.866,1.152,1.573,0.626,0.433,-0.958,0.81,-0.044,0.947,-1.4 74,-0.719,-0.086,-1.099,1.45,1.151,0.485,1.633,0.043,1.326,1.706,-0.340,0.89,1.444,1.177]; %系统辨识的输入信号为一个周期的M序列y=zeros(1,30); %定义输出观测值的长度w=0.1*randn(1,30)for k=3:30y(k)=-1.642*y(k-1)-0.715*y(k-2)+0.39*u(k-1)+0.35*u(k-2)+w(k); %用理想输出值作为观测值endsubplot(3,1,1) %画三行一列图形窗口中的第一个图形stem(u) %画输入信号u的径线图形subplot(3,1,2) %画三行一列图形窗口中的第二个图形i=1:1:30; %横坐标范围是1到16，步长为1plot(i,y) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中的第三个图形stem(y),grid on %画出输出观测值z的径线图形，并显示坐标网格u,y %显示输入信号和输出观测信号%L=30%数据长度HL=[-y(2) -y(1) u(2) u(1);-y(3) -y(2) u(3) u(2);-y(4) -y(3) u(4) u(3);-y(5) -y(4) u(5) u(4);-y(6) -y(5) u(6) u(5);-y(7) -y(6) u(7) u(6);-y(8) -y(7) u(8) u(7);-y(9) -y(8) u(9) u(8);-y(10) -y(9) u(10) u(9);-y(11) -y(10) u(11) u(10);-y(12) -y(11) u(12) u(11);-y(13) -y(12) u(13) u(12);-y(14) -y(13) u(14) u(13);-y(15) -y(14) u(15) u(14);-y(16) -y(15) u(16) u(15);-y(17) -y(16) u(17) u(16);-y(18) -y(17) u(18) u(17);-y(19) -y(18) u(19) u(18);-y(20) -y(19) u(20) u(19);-y(21) -y(20) u(21) u(20);-y(22) -y(21) u(22) u(21);-y(23) -y(22) u(23) u(22);-y(24) -y(23) u(24) u(23);-y(25) -y(24) u(25) u(24);-y(26) -y(25) u(26) u(25);-y(27) -y(26) u(27) u(26);-y(28) -y(27) u(28) u(27);-y(29) -y(28) u(29) u(28)] %给样本矩阵HL赋值Y=[y(3);y(4);y(5);y(6);y(7);y(8);y(9);y(10);y(11);y(12);y(13);y(14);y(15);y(16);y(17);y(18);y(19) ;y(20);y(21);y(22);y(23);y(24);y(25);y(26);y(27);y(28);y(29);y(30)] % 给样本矩阵z L赋值%Calculating Parametersc1=HL'*HL; c2=inv(c1); c3=HL'*Y; c=c2*c3 %计算并显示a1=c(1), a2=c(2), b1=c(3),b2=c(4) %从中分离出并显示a1 、a2、b1、b2%1.2 RLS递推最小二乘辨识c0=[1.642 0.715 0.39 0.35]'; %被辨识参数的初始值p0=10^6*eye(4,4); %直接给出初始状态P0，即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,29)]; %被辨识参数矩阵的初始值及大小e=zeros(4,30); %相对误差的初始值及大小u=[1.147,0.201,-0.787,-1.589,-1.052,0.866,1.152,1.573,0.626,0.433,-0.958,0.81,-0.044,0.947,-1.4 74,-0.719,-0.086,-1.099,1.45,1.151,0.485,1.633,0.043,1.326,1.706,-0.340,0.89,1.444,1.177]; %系统辨识的输入信号为一个周期的M序列y=zeros(1,30); %定义输出观测值的长度w=0.5*randn(1,30);for k=3:30y(k)=-1.642*y(k-1)-0.715*y(k-2)+0.39*u(k-1)+0.35*u(k-2)+w(k); %用理想输出值作为观测值endfor k=3:30; %开始求Kh1=[-y(k-1),-y(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K的值d1=y(k)-h1'*c0;c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*(h1'*p0*h1+1); %求出p(k)的值p0=p1; %给下次用if e2<=Ebreak; %如果参数收敛情况满足要求，终止计算end %小循环结束end %大循环结束c,e %显示被辨识参数及其误差(收敛)情况%分离参数a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:); ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:);figure(2); %第二个图形i=1:30; %横坐标从1到30plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1，a2，b1，b2的各次辨识结果title('Parameter Identification with Recursive Least Squares Method') %图形标题figure(3); %第三个图形i=1:30; %横坐标从1到30plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1，a2，b1，b2的各次辨识结果的收敛情况title('Identification Precision') %图形标题%2.1 二阶系统的最小二乘一次完成算法辨识程序，在光盘中的文件名：FLch3LSeg1.m u=[1.147,0.201,-0.787,-1.589,-1.052,0.866,1.152,1.573,0.626,0.433,-0.958,0.81,-0.044,0.947,-1.4 74,-0.719,-0.086,-1.099,1.45,1.151,0.485,1.633,0.043,1.326,1.706,-0.340,0.89,1.444,1.177]; %系统辨识的输入信号为一个周期的M序列y=zeros(1,30); %定义输出观测值的长度w=0.1*randn(1,30);for k=3:30W(k)=w(k)+1.642*w(k-1)+0.715*w(k-2)y(k)=-1.642*y(k-1)-0.715*y(k-2)+0.39*u(k-1)+0.35*u(k-2)+W(k); %用理想输出值作为观测值endsubplot(3,1,1) %画三行一列图形窗口中的第一个图形stem(u) %画输入信号u的径线图形subplot(3,1,2) %画三行一列图形窗口中的第二个图形i=1:1:30; %横坐标范围是1到16，步长为1plot(i,y) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线subplot(3,1,3) %画三行一列图形窗口中的第三个图形stem(y),grid on %画出输出观测值z的径线图形，并显示坐标网格u,y %显示输入信号和输出观测信号%L=30%数据长度HL=[-y(2) -y(1) u(2) u(1);-y(3) -y(2) u(3) u(2);-y(4) -y(3) u(4) u(3);-y(5) -y(4) u(5) u(4);-y(6) -y(5) u(6) u(5);-y(7) -y(6) u(7) u(6);-y(8) -y(7) u(8) u(7);-y(9) -y(8) u(9) u(8);-y(10) -y(9) u(10) u(9);-y(11) -y(10) u(11) u(10);-y(12) -y(11) u(12) u(11);-y(13) -y(12) u(13) u(12);-y(14) -y(13) u(14) u(13);-y(15) -y(14) u(15) u(14);-y(16) -y(15) u(16) u(15);-y(17) -y(16) u(17) u(16);-y(18) -y(17) u(18) u(17);-y(19) -y(18) u(19) u(18);-y(20) -y(19) u(20) u(19);-y(21) -y(20) u(21) u(20);-y(22) -y(21) u(22) u(21);-y(23) -y(22) u(23) u(22);-y(24) -y(23) u(24) u(23);-y(25) -y(24) u(25) u(24);-y(26) -y(25) u(26) u(25);-y(27) -y(26) u(27) u(26);-y(28) -y(27) u(28) u(27);-y(29) -y(28) u(29) u(28)] %给样本矩阵HL赋值Y=[y(3);y(4);y(5);y(6);y(7);y(8);y(9);y(10);y(11);y(12);y(13);y(14);y(15);y(16);y(17);y(18);y(19) ;y(20);y(21);y(22);y(23);y(24);y(25);y(26);y(27);y(28);y(29);y(30)] % 给样本矩阵z L赋值%Calculating Parametersc1=HL'*HL; c2=inv(c1); c3=HL'*Y; c=c2*c3 %计算并显示a1=c(1), a2=c(2), b1=c(3),b2=c(4) %从中分离出并显示a1 、a2、b1、b2%2.2 RLS递推最小二乘辨识c0=[1.642 0.715 0.39 0.35]'; %被辨识参数的初始值p0=10^6*eye(4,4); %直接给出初始状态P0，即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,29)]; %被辨识参数矩阵的初始值及大小e=zeros(4,30); %相对误差的初始值及大小u=[1.147,0.201,-0.787,-1.589,-1.052,0.866,1.152,1.573,0.626,0.433,-0.958,0.81,-0.044,0.947,-1.4 74,-0.719,-0.086,-1.099,1.45,1.151,0.485,1.633,0.043,1.326,1.706,-0.340,0.89,1.444,1.177]; %系统辨识的输入信号为一个周期的M序列y=zeros(1,30); %定义输出观测值的长度w=0.5*randn(1,30);for k=3:30W(k)=w(k)+1.642*w(k-1)+0.715*w(k-2)y(k)=-1.642*y(k-1)-0.715*y(k-2)+0.39*u(k-1)+0.35*u(k-2)+W(k); %用理想输出值作为观测值endfor k=3:30; %开始求Kh1=[-y(k-1),-y(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1;x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K的值d1=y(k)-h1'*c0;c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*(h1'*p0*h1+1); %求出p(k)的值p0=p1; %给下次用if e2<=Ebreak; %如果参数收敛情况满足要求，终止计算end %小循环结束end %大循环结束c,e %显示被辨识参数及其误差(收敛)情况%分离参数a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:); ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:);figure(2); %第二个图形i=1:30; %横坐标从1到30plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1，a2，b1，b2的各次辨识结果title('Parameter Identification with Recursive Least Squares Method') %图形标题figure(3); %第三个图形i=1:30; %横坐标从1到30plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1，a2，b1，b2的各次辨识结果的收敛情况title('Identification Precision') %图形标题%3 广义最小二乘递推法u=[1.147,0.201,-0.787,-1.589,-1.052,0.866,1.152,1.573,0.626,0.433,-0.958,0.81,-0.044,0.947,-1.4 74,-0.719,-0.086,-1.099,1.45,1.151,0.485,1.633,0.043,1.326,1.706,-0.340,0.89,1.444,1.177]; %系统辨识的输入信号为一个周期的M序列y=zeros(1,30); %定义输出观测值的长度w=0.1*randn(1,30);for k=3:30y(k)=-1.642*y(k-1)-0.715*y(k-2)+0.39*u(k-1)+0.35*u(k-2)+w(k); %用理想输出值作为观测值endcf0=[0.001 0.001 0.001 0.001]';pf0=10^6*eye(4);E=0.000000005;ef=zeros(4,30);nc=2; % 设定噪声模型的最高阶次ce0=zeros(nc,1);pe0=eye(nc);v1=0;for k=nc+1:30zf(k)=[1 ce0']*y(k:-1:k-nc)';uf(k)=[1 ce0']*u(k:-1:k-nc)'; % 计算zf(k)、uf(k)hf=[-zf(k-1),-zf(k-2),uf(k-1),uf(k-2)]'; % 构造hf(k)jf=hf'*pf0*hf+1; jf=inv(jf);kf=pf0*hf*jf; % 准备并求出kf的值df=zf(k)-hf'*cf0;cf1=cf0+kf*df; % 求出theta的估计值ef1=(cf1-cf0)./cf0; % 求出两次估计值之间的相对误差并保存pf1=(eye(4)-kf*hf')*pf0; % 求出pf的值% 以下为噪声模型参数估计h=[-y(k-1),-y(k-2),u(k-1),u(k-2)]';v1(k)=y(k)-h'*cf1;he=-v1(k-1:-1:k-nc)'; % 构造噪声模型参数估计时的he(k)ze=he'*pe0*he+1; ze=inv(ze);ke=pe0*he*ze; % 准备并求出ke的值de=v1(k)-he'*ce0; ce1=ce0+ke*de; % 求出theta的估计值pe1=(eye(nc)-ke*he')*pe0; % 求出pe的值ee1=(ce1-ce0)./(ce0+eps);% 保存各种参数供下次循环和作图用cf0=cf1;cf(:,k)=cf1;pf0=pf1;ef0=ef1;ef(:,k)=ef1;ce0=ce1;pe0=pe1;ee0=ee1;% 如果满足以下条件，则跳出循环if (abs(ef1)<E)&&(ef1~=0)=0if abs(ee1)<Ej1=k;break;endendend% 分离估计参数a1=cf(1,:);a2=cf(2,:);b1=cf(3,:);b2=cf(4,:);ea1=ef(1,:);ea2=ef(2,:);eb1=ef(3,:);eb2=ef(4,:);end% 绘图figurej=1:k;plot(j,a1,'r',j,a2,'b',j,b1,'m',j,b2,'k');title('NSR=0.1时有色噪声影响下广义最小二乘递推法系统参数辨识结果'); xlabel('噪声模型的最高阶次');ylabel('系统参数辨识结果');axis tightlegend('a1=-1.5','a2=0.7','b1=2','b2=0.5')grid on;figureplot(j,ea1,'r',j,ea2,'b',j,eb1,'m',j,eb2,'k');title('NSR=0.1时有色噪声影响下广义最小二乘递推法系统参数辨识误差'); xlabel('递推次数');ylabel('系统参数辨识误差');axis([1,1024,-0.02,0.02]);grid on;legend('a1','a2','b1','b2')- 21 -。