理论力学第八章点的合成运动和例题讲解
合集下载
理论力学 第八章
x o ' = x o ' (t ) 牵连运动方程 y o ' = y o ' ( t ) = ( t )
动系与定系之间的坐标变换关系
x = xO′ + x′ cos y′sin y = yO′ + x′ sin + y′ cos
沿半径为r的圆 例8-1 点M相对于动系 Ox′y′ 沿半径为 的圆 相对于动系 周以速度v作匀速圆周运动 圆心为O 作匀速圆周运动(圆心为 周以速度 作匀速圆周运动 圆心为 1 ） ，动系x′y′ O Oxy 以匀角速度ω绕点 作定轴转动， 相对于定系 以匀角速度 绕点O作定轴转动， 绕点 作定轴转动 如图所示。 重合， 重合。 如图所示。初始时x′y′ 与 与 重合 O Oxy 重合，点M与O重合。 的绝对运动方程。 求：点M的绝对运动方程。 的绝对运动方程
. 已知: 已知 ω, OA, = r, OO1 = l, OA水平 求: ω1 = ?
解:
1．动点：滑块A ． 动系：摇杆AB 2. 运动分析 绝对运动:绕O点的圆周运动
相对运动:沿O1B的直线运动 牵连运动:绕O1轴定轴转动
√ √ √
3.
ve = va sin = ωr
r
2 2
l +r ve r2ω ∴ω1 = = 2 2 O A l +r 1
4. 绝对运动方程 vt vt x = x′ cos y′ sin = r1 cos r cosωt r sin r sin ωt y = x′ sin + y′ cos = r1 cos vt sin ωt + r sin vt co-3 用车刀切削工件的直径端面，车刀刀尖 M沿水平轴 作往复运动，如图所示。设oxy为定坐 沿水平轴x作往复运动 沿水平轴 作往复运动，如图所示。 为定坐 标系，刀尖的运动方程为 x = bsin (ωt ) 。工件以 标系， 逆时针转向转动。 等角速度 ω逆时针转向转动。 求：车刀在工件圆端面上切出的痕迹。 车刀在工件圆端面上切出的痕迹。
点的合成运动(相对牵连绝对运动)(课堂)-2022年学习资料
理论力学-第八章京的合刻-1
第八章点的合成运动->☑§8-1-点的合成运动的概念-§8-2点的速度合成定理->☒-§8-3牵连运动为平 时点的加速度合成定理->§8-4牵连运动为转动时点的加速度合成定理-☑习题课
运动学-前两章中我们研究点和刚体的运动，一般都是以地面为参考-体的。然而在实际问题中，还常常要在相对于地面 动着的参-考系上观察和研究物体的运动。例如，从行驶的汽车上观看飞-机的运动等，坐在行驶的火车内看下雨的雨点 向后斜落的等-为什么在不同的坐标系或参考体上观察物体的运动会有不-同的结果呢？我们说事物都是相互联系着的。 面我们就将研-究参考体与观察物体运动之间的联系。为了便于研究，下面先-来介绍有关的概念。-§8-1点的合成 动的概念-一.坐标系：-1静坐标系：把固结于地面上的坐标系称为静坐标系，简称静系。-2动坐标系：把固结于相 于地面运动物体上的坐标系，-称为动坐标系，简称动系。例如在行驶的汽车。-3
运动学-四.动点的选择原则：-般选择主动件与从动件的连接点，它是对两个坐标系都有-运动的点。-五.动系的选 原则：-动点对动系有相对运动，且相对运动的轨迹是已知的，-或者能直接看出的。-下面举例说明以上各概念：-动 ：AB杆上A点-动系：固结于凸轮O上-静系：固结在地面上-5
运动学-绝对运动：-直线-相对运动：-曲线（圆弧）-A-牵连运动：直线平动-n-雌-y
运动学-B-[例2]曲柄摆杆机构-已知：OA=r,0,OO,=l图示瞬时OA⊥O0-a-求：摆杆O,B角速 o-解：取OA杆上A点为动点，摆杆OB为动系，-基座为静系。-绝对速度v。=ro方向⊥OA-相对速度y,= 方向1O1B-牵连速度v。=?方向⊥OB-由速度合成定理y=,+y。作出速度平行四边形如图示。-Onie20-9u.-040me-0Ar-1.r2w=2w-∩-16
第八章点的合成运动->☑§8-1-点的合成运动的概念-§8-2点的速度合成定理->☒-§8-3牵连运动为平 时点的加速度合成定理->§8-4牵连运动为转动时点的加速度合成定理-☑习题课
运动学-前两章中我们研究点和刚体的运动，一般都是以地面为参考-体的。然而在实际问题中，还常常要在相对于地面 动着的参-考系上观察和研究物体的运动。例如，从行驶的汽车上观看飞-机的运动等，坐在行驶的火车内看下雨的雨点 向后斜落的等-为什么在不同的坐标系或参考体上观察物体的运动会有不-同的结果呢？我们说事物都是相互联系着的。 面我们就将研-究参考体与观察物体运动之间的联系。为了便于研究，下面先-来介绍有关的概念。-§8-1点的合成 动的概念-一.坐标系：-1静坐标系：把固结于地面上的坐标系称为静坐标系，简称静系。-2动坐标系：把固结于相 于地面运动物体上的坐标系，-称为动坐标系，简称动系。例如在行驶的汽车。-3
运动学-四.动点的选择原则：-般选择主动件与从动件的连接点，它是对两个坐标系都有-运动的点。-五.动系的选 原则：-动点对动系有相对运动，且相对运动的轨迹是已知的，-或者能直接看出的。-下面举例说明以上各概念：-动 ：AB杆上A点-动系：固结于凸轮O上-静系：固结在地面上-5
运动学-绝对运动：-直线-相对运动：-曲线（圆弧）-A-牵连运动：直线平动-n-雌-y
运动学-B-[例2]曲柄摆杆机构-已知：OA=r,0,OO,=l图示瞬时OA⊥O0-a-求：摆杆O,B角速 o-解：取OA杆上A点为动点，摆杆OB为动系，-基座为静系。-绝对速度v。=ro方向⊥OA-相对速度y,= 方向1O1B-牵连速度v。=?方向⊥OB-由速度合成定理y=,+y。作出速度平行四边形如图示。-Onie20-9u.-040me-0Ar-1.r2w=2w-∩-16
高中物理课件第八章 点的合成运动
ve1 vA a1
r ae1
r aA
ar An
ar At
aren1
aret1
a2nr ar
r aC1
2r e
r vr
0
va ?
r va
r ve1
r vr1
r a
t A
A
O1
ar et1
r M vr
r
ar
n A
vA
ar en1
1
1
vrev1ra
解得：
ae l(0 cos 02 sin ) B
由于杆ABC作平移，
aD ae l(0 cos 02 sin )
r ae
D
C
22
第八章 点的合成运动［习题课］ 题型二：
2、曲柄滑块机构， 牵连运动为定轴转动
23
第八章 点的合成运动［习题课］
习题4 （例题3）刨床的急回机构如图所示。曲柄
9
第八章 点的合成运动［习题课］
牵连运动为平移/定轴转动 求解基本参量的练习
10
第八章 点的合成运动［习题课］
砂 习粒题M1 相图对示于筛箱砂体机的，速曲度柄为Ovr1rA，=O图2B示=位a，置且AO1BA=BO1O902。，
杆O1A的角速度为1 ，角加速度为1 ，AM a / 2 ,
第八章 点的合成运动
习题课
1
知识的回顾
1、点作曲线运动
ar
r an
r at
v2
nr
dv r
dt
2、定轴转动刚体上的点
理论力学第八章点的合成运动
3
实例三
描述一个长杆在平面内同时作直线运动和回转运动的合成运动，讨论合成运动对 杆心运动特性的影响。
合成运动中的矢量操作
在合成运动中，我们经常需要进行矢量的加法、减法和乘法等操作。这些操作可以帮助我们推导、计算和分析 合成运动的各种特性。
合成运动的应用及展望
应用
合成运动的概念和原理广泛应用于物理学、工程学和运动学等领域，为我们理解和解决复杂 的运动问题提供了有力的工具。
点的合成运动的基本概念
点的合成运动是指多个点以各自不同的速度和方向同时运动，并在同一时间 到达相对位置的运动方式。它是合成运动的基本形式之一。
合成运动的示意图和公式推导
示意图
通过示意图展示合成运动的过程和结果，帮助加深 理解。
公式推导
推导合成运动的公式，使我们能够定量描述和计算 合成运动的各个特性。
质点运动的合成运动
质点的合成运动是指质点在运动过程中，同时具有平移运动和旋转运动的一 种复杂运动形式。在合成运动中，质点的运动轨迹会呈现出特定的形态和规 律。
质点合成运动实例分析
1
实例一
分析一个小球在倾斜平面上同时进行滚动和滑动的合成运动，探讨其运动规律和 性质。
2
实例二
研究一个弹射体在水平飞行过程中受到重力和空气阻力合成运动的影响，揭示合 成运动对物体运动轨迹的影响。
理论力学第八章点的合成 运动
欢迎大家来到本次关于理论力学第八章点的合成运动的精彩演讲。在本次演 讲中，我们将深入探讨合成运动的定义、基本概念、示意图与公式推导，以 及质点运动的合成运动等内容。
合成运动的定义
合成运动是指由多个简单的运动相结合而成的复杂运动。它将两个或多个运 动矢量合成为一个合成矢量，从而形成全新的运动方式。
理论力学之点的合成运动
1
60o
O1
x
点M .
x
va= ve + vr va = 0.2 m/s
0.5cm
解得: ve= 0.17m/s=2× 0.866 ; vr= 0.1m/s ; 2= 0.2r26ad/s
例题. 具有园弧形滑道的曲柄滑道机构,用来使滑 道 BC获得间歇的往复运动.已知曲柄以匀角速 度 =10 rad/s 绕O轴转动, OA=10cm ,园弧道的 半径 r = 7.5cm. 当曲柄转到图示位置sin = 0.6 时, 求滑道BC的速度.
5
例题.曲柄导杆机构 的运动由滑块 A带动,
B
已知OA= r且转动的 角速度为.试分析滑 块 A的运动.
O
C A
D
动点：滑块A；动系：固连在BCD杆
*、机构运动特点：一运动物体上有一固定点始终与另一 运动物体接触，且在其上运动。
则：动点：固定接触点；动系：另一运动物体。
6
例题. 平底凸轮机构 如图示. 凸轮 O 的半径 为R,偏心距OA=e,以匀 角速度绕O转动,并带 B 动平底从动杆 BCD运 动. 试确定动点并分析 其运动.
Va=Ve/cos= … =2; Vr=Ve tan= … =1
22
例题. 斜面CD与水平成 角,并以 v = 10cm/s 沿水平方向运动.求杆AB的速度vA.
C
v
B
A D
23
解:取杆AB的A端为动点. 动系固连在斜面上。
C
动点A的绝对运 v 动---铅垂直线运 动。
B
vr
va
ve
va B
1 O1
ve
vr
A(A´)
绝对运动—以O1为中心 r为半径
理论力学点的合成运动
例 8-4 曲柄OA以匀角速度 w绕O轴转动，其上
套有小环 M，而小环 M又在固定的大圆环上运动，大 圆环的半径为 R。
试求当曲柄与水平线成的角 j ωt 时，小环 M
的绝对速度和相对曲柄 OA 的相对速度。
A
M w
R
O
j
C
解：（1）选择动点及 动系： 小环M为动点，动系固连在 OA上。
（2）分析三种运动：绝 对运动为圆周运动，相对运 动为沿OA的直线运动，牵连 运动为定轴转动。
y
OA杆转动的角速度为
O
wOA
ve OC
ve 2r
3u 6r
y
wOA B
j va vr
A
r ve C
x
u x
8.3 牵连运动是平动时点的加速度合成定理
在图8-9中，设 Oxyz为定系，Oxyz为动系且作平
动，M为动点。动点M在动系中的坐标为 x、y 、z， 动系单位矢量为 i、 j、k。动系平动，i、j、k 的
Oxyz 作某种运动，在瞬时t，动系连同相对轨迹AB在
定系中的I位置，动点则在曲线 AB
上的 M 点。经过时间间 隔 t ，动系运动到定系 中的II位置，动点运动到
点 M。 如果在动系上观
察点M 的运动，则它沿 曲线 AB 运动到点 M2。
z B
M2
vr
z
M O
A
O I
x
va
M B
ve M1
z
O x A
例 8-1 汽车以速度 v1 沿直线的道路行驶，雨滴 以速度 v2 铅直下落，试求雨滴相对于汽车的速度。
v1
解： 因为雨滴相对运动的汽车有运动，所以本题 为点的合成运动问题，可应用点的速度合成定理求解。
3理论力学 第八章点的合成运动解析
? ? tg ?1 v?
v平
[例8-2] 曲柄摆杆机构
φ
已知：OA= r , ? , OO1=l 图示瞬时OA? O
求：摆杆O1B角速度? 1
解：取套筒A点为动点，摆杆O1B为动系.基座为静系。
绝对速度va = r ?
相对速度vr = ?
方向? OA 方向//O1B
牵连速度ve = ?
方向? O1B
由速度合成定理 va ? vr ? ve 作出速度平行四边形 如图示。
r
ve ? va sin? ? r? ?
r2? l2
又?ve ? O1 A?? 1,
? ? 1 ? Ov1eA?
1? r 2 ?l2
r 2?
r2?
l2
?
r
r 2?
2 ? l2
（
）
[例8-3]圆盘凸轮机构
已知：OC＝e , R ? 3e , ? （匀角速度）
vr
va
A veva
B
aa
ar
va
A
Baen
ae?
练习三
解:
A
?
?
o
B
A
? ?
o
ve ? OB??
va
B
vr
动系:OA杆； 动点:滑块B
A
? ?
arn
o
aen ? OB?? 2
ar?
B
aa
a?e ? OB??
[例8-1] 桥式吊车。 已知：小 车水平运行，速度为v平， 物块A相对小车垂直上升 的速度为v? 。求物块A的运 行速度。
一、实例 : M点运动
地面: 摆线， 车箱: 圆。
二、复合运动的一般模型
工程力学—点的合成运动习题及解答
第八章 点的合成运动习题及解答P189 8-5. 已知 OA=l ，曲杆BCD 的速度为v ，BC=a; 求：A 点的速度与x 的关系。
解：取曲杆上的点B 为动点，OA 杆为动系，则r e a v v v +=v v a =,得22a e a x a .v sin .v v +==φ,a x a.v OB v 22e0+==ω=A v .v l .0=ωl ,a x a .22+P190 8-7. 已知 两种机构中2m .0a O O 21==, 杆 A O 1的角速度1ω=3rad/s,030=θ;求：杆A O 2A O 1的角速度2ω.解: 图 (a) , 取杆A O 1上的A 点为动点，杆A O 2为动系，图 (b) , 取杆A O 2上的A 点为动点，杆A O 1为动系，由: r e av v v += 分别作速度矢量图。
由图 (a) 解出23a.cos30.v v 10a e ω==，,s /rad 5.12A O v 12e 2===ωω由图 (b) 解出32.a .cos30v v 10e a ω==， ,s /5rad .12A O v 12e 2===ωω.s /rad 232A O v 12a 2===ωωP190 8-9. 已知 ==V v AB 常数，当t=0时，0=ϕ；求：045=ϕ时，点C 的速度的大小。
解: 取杆AB 上的A 点为动点，杆OC 为动系，由: r e av v v += 作速度矢量图。
ϕϕcos .v cos .v v a e ==，lcos .a OA OC .v v e c ϕ==解出 l a.cos vv 2c ϕ=，当045=ϕ时， 2l av v c =P190 8-10. 已知，轮C 半径为R ，偏心距OC=e, 角速度 ω=常数；求：00=ϕ时，平底杆AB 的速度。
解: 取轮心C 为动点，平底杆AB 为动系，由: r e av v v += 作速度矢量图。
8理论力学
线运动.
D
动系的牵连运动—沿x轴的直线平动. vD
va= ve + vr va = r ve = vD= v
v 解得: va sin
v r sin
16
例题8-7.平底凸轮机构如图
示. 凸轮 O 的半径为R,偏心 距OA = e,以匀角速度 绕 B O 转动,并带动平底从动杆 BCD运动. 试求该瞬时杆 BCD的速度.
动系O—x´y´
e x´
y´
A的绝对运动—以B为中心 l 为 半径的园运动.
x A的相对运动—沿凸轮O边缘的曲线运动.
牵连运动—动系随凸轮O且角速度为的定轴转动.
牵连点—凸轮O上被AB杆的A端盖住的A´点且随凸轮
O作角速度为的定轴转动.
va= ve + vr va = l AB
解得:
AB
e l
22
ve = rsin
将它表示成转角的函数.
B
D
C e O A
26
解:取偏心园凸轮的 B
D
中心C为动点.
建立静系O—x y和 动系A—x´y´
y
ve va
C e vr
O
A
y´
x
x´
C的绝对运动—以O为中心为e半径的园运动.
C的相对运动—平行于 y´ 轴的直线运动.
牵连运动—动系沿水平直线作往复平动.
va= ve + vr
长 r,以匀角速1转动.试分析滑
O2
块A的运动.
5
O
例题8-3.曲柄导杆机构
的运动由滑块 A带动,已
B
C
知OA= r且转动的角速
A
度为.试分析滑块 A的
理论力学8
摇杆绕固定轴O1来回摆动。设曲柄长OA=r，两轴间距离OO1 l
求曲柄在水平位置瞬时，摇杆O1B绕O1轴的角速度1及滑块A相
对摇杆O1B的相对速度。
运动学/点的合成运动
解：
选取动点： OA 上的A点 动系： O1B 定系： 基座
运 绝对运动：圆周运动 动 分 相对运动：直线运动 析 牵连运动：定轴转动 ：
运动学/点的合成运动
另一方面，在实际问题中，不仅要在固联在地面上
的参考系上还要在相对于地面运动着的参考系上观察和
研究物体的运动。下面先看几个例子。
沿直线轨道纯滚动 的圆轮，研究轮缘上A 点的运动，对于地面上 的观察者，是旋轮线轨 迹，对站在轮心上的观 察者是圆。
A点的运动可看成随轮心的平移与绕轮心转动的合成。
运动学/点的合成运动
MM MM1 M1M 将上式两边同时除以t并取 t0得
lim MM lim MM1 t 0 t t 0 t
lim
M1M
t 0 t
va ve vr
即：在任一瞬时动点的绝对速度等于牵连速度与相对速
度的矢量和，这就是点的速度合成定理。
点的速度合成定理是瞬时矢量式，共包括大小‚方向 六个元素，已知任意四个元素，就能求出其它两个。
运动学/点的合成运动
例如，直管OB以匀角速度绕定轴O转动，小球M
以速度u在直管OB中作相对的匀速直线运动，如图示。 将动坐标系固结在OB管上，以小球M为动点。随着动 点M的运动，牵连点在动坐标系中的位置在相应改变。 设小球在t1、t2瞬时分别到达M1、M2位置，则动点的 牵连速度分别为
ve1 OM1
运动学/点的合成运动
第八章
点的合成运动
在前两章中研究点和刚体的运动时，认为地球（ 参考体）固定不动,将坐标系（参考系）固连于地面。 因此，点和刚体的运动是相对固定参考系而言的。
求曲柄在水平位置瞬时，摇杆O1B绕O1轴的角速度1及滑块A相
对摇杆O1B的相对速度。
运动学/点的合成运动
解：
选取动点： OA 上的A点 动系： O1B 定系： 基座
运 绝对运动：圆周运动 动 分 相对运动：直线运动 析 牵连运动：定轴转动 ：
运动学/点的合成运动
另一方面，在实际问题中，不仅要在固联在地面上
的参考系上还要在相对于地面运动着的参考系上观察和
研究物体的运动。下面先看几个例子。
沿直线轨道纯滚动 的圆轮，研究轮缘上A 点的运动，对于地面上 的观察者，是旋轮线轨 迹，对站在轮心上的观 察者是圆。
A点的运动可看成随轮心的平移与绕轮心转动的合成。
运动学/点的合成运动
MM MM1 M1M 将上式两边同时除以t并取 t0得
lim MM lim MM1 t 0 t t 0 t
lim
M1M
t 0 t
va ve vr
即：在任一瞬时动点的绝对速度等于牵连速度与相对速
度的矢量和，这就是点的速度合成定理。
点的速度合成定理是瞬时矢量式，共包括大小‚方向 六个元素，已知任意四个元素，就能求出其它两个。
运动学/点的合成运动
例如，直管OB以匀角速度绕定轴O转动，小球M
以速度u在直管OB中作相对的匀速直线运动，如图示。 将动坐标系固结在OB管上，以小球M为动点。随着动 点M的运动，牵连点在动坐标系中的位置在相应改变。 设小球在t1、t2瞬时分别到达M1、M2位置，则动点的 牵连速度分别为
ve1 OM1
运动学/点的合成运动
第八章
点的合成运动
在前两章中研究点和刚体的运动时，认为地球（ 参考体）固定不动,将坐标系（参考系）固连于地面。 因此，点和刚体的运动是相对固定参考系而言的。
理论力学第八章 点的合成运动(Y)
aC
五、牵连运动为定轴转动时的加速度合成定理
aa ae ar ac
点的加速度合成定理：动点在某瞬时的绝对加速度等于该瞬 时的牵连加速度、相对加速度与科氏加速度的矢量和。 科氏加速度
ac 2e vr 大小: ac 2e vr sin
平行时， 00 或 180 0
车轮轮缘上一点M的运动分析
O1
如果站在地面上观察时，车轮边缘上任一点的轨迹都是悬轮线 如果站在汽车上观察时，车轮边缘上任一点的轨迹都是圆
飞机螺旋浆上点P 的运动分析
如果在飞机上观察螺旋桨上P点的运动轨迹是一个圆。 如果在地面上观察，则P点的轨迹就是螺旋线。
2、两种坐标系与三种运动
（1）两种坐标系
60
vA O1 A
ve vC v A
vCD va ve cos O1 A cos 10cm / s
vC
1、加速度分析
牵连运动——AB杆作平动。
aa ae ar
a A aC ae O1 A
2
2
2
aCD aa ee sin O1 A sin 34.6cm / s
一、绝对运动、相对运动与牵连运动 二、速度合成定理 三、矢量表示角速度，角加速度 四、牵连运动是平动时的加速度合成定理 五、牵连运动是定轴转动时的加速度合成 定理
一、绝对运动、相对运动与牵连运动 1、运动的相对性
从不同的参考系观察同一点的运动，其结果是不相同的 物体对于不同的参考系，运动各不相同。
ve
va
va l
——垂直于OA
牵连运动（牵连点的运动）——T 形杆上A点作水平直线运动
ve 大小未知，方向沿水平。
点的合成运动
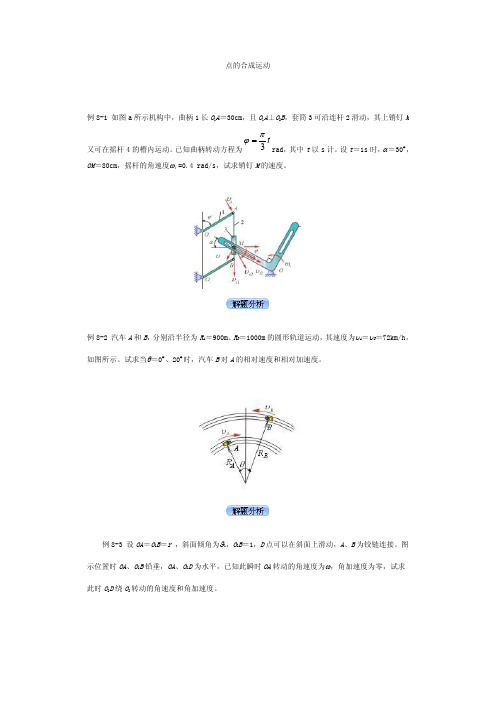
点的合成运动例8-1 如图a所示机构中，曲柄1长O1A＝30cm，且O1A⊥O2B，套筒3可沿连杆2滑动，其上销钉M又可在摇杆4的槽内运动。
已知曲柄转动方程为t3πϕ=rad，其中t以s计。
设t＝1s时，α＝30︒，OM＝80cm，摇杆的角速度ω4=0.4 rad/s，试求销钉M的速度。
例8-2 汽车A和B，分别沿半径为R A＝900m、R B＝1000m的圆形轨道运动，其速度为υA＝υB＝72km/h，如图所示。
试求当θ＝0︒、20︒时，汽车B对A的相对速度和相对加速度。
例8-3 设OA＝O1B＝r ，斜面倾角为ϑ1，O2B＝1，D点可以在斜面上滑动，A、B为铰链连接。
图示位置时OA、O1B铅垂，OA、O2D为水平，已知此瞬时OA转动的角速度为ω，角加速度为零，试求此时O2D绕O2转动的角速度和角加速度。
例8-4 （如图a）所示机构由OA杆与圆柱组成，OA杆长为l，绕定轴O作匀速转动，其角速度为ω。
圆柱在水平面上作纯滚动，求图示位置ϕ= 30︒时，圆柱的角速度与角加速度。
圆柱半径R=20cm，ω= 2rad/s。
例8-5 图示平面机构中，杆AB以匀速u沿水平方向运动，并通过滑块B推动杆OC转动。
试求ϕ=60︒时，杆OC的角加速度和滑块B相对杆OC的加速度。
例8-6 图（a）所示平面机构，直角弯杆ABC绕轴A转动，使套在其上的小环M沿半径为R的固定大圆环运动。
已知cmRAB240==，当弯杆的AB段转至左侧水平位置时，其角速度ω=2rad/s，角加速度α= 2rad/s2，转向如图所示。
试求该瞬时小环M的绝对速度和绝对加速度的大小。
理论力学8—点的合成运动
veபைடு நூலகம்
ω ϕ
O1
ϕ
vr
A
ve = va sin ϕ = rω sin ϕ ve = O1 A × ω1 = r 2ω (l 2 + r 2 )
r 2ω O1 A = (l 2 + r 2 ) → ω1 = 2 2 l +r
例3 水平直杆AB在半径为r的固定圆环上以匀速u竖直下落，如图。 试求套在该直杆和圆环交点处的小环M的速度。 解：以小环M为动点，定系取在地面上，动系取在AB杆上， 动点的速度合成矢量图如图。 由图可得：
vB = v A = ve1 = 10(m / s ),
vr1 = 2v cos 30o = 17.32(m / s )
(2) 求A相对于B的速度，以A为动点，动系固连于B艇。
v e 2 = OA × ω = 50 × v
v a 2 = 10m / s
ρ
= 5m / s
北
vr 2 = ve 2 2 + vr 2 2 = 11.2m / s
O
r vA
R A
r vB
B
解：（1）以车A为动点，静系取在地面上，动系取在车B 上。动点的速度合成矢量图如图。由图可得：
2 2 2 vr1 = v A + ve2 = v A + vB = 75km / h
v A 45 sin α1 = = = 0.6 vr1 75
O
α1 = 36.9o
R
r r r vA vr1 y′ ve x′ α1r A vB B
例1 如图所示，偏心距为e、半径为R的凸轮，以匀角速度ω 绕O 轴转动，杆AB能在滑槽中上下平动，杆的端点A始终与凸轮接触， 且OAB成一直线。求在图示位置时，杆AB的速度。 解：因为杆AB作平动。选取杆 AB的端点A作为研究的动点，动 参考系随凸轮一起绕O轴转动。 点A的绝对运动是直线运动， 相对运动是以凸轮中心C为圆心 的圆周运动，牵连运动则是凸轮 绕O轴的转动。 B
理论力学点的合成运动NN
第八章 点的合成运动
第8章 点的合成运动
8.1 点的合成运动的概念 8.2 点的速度合成定理 8.3 点的加速度合成定理
8.1 点的合成运动的概念
在实际问题中，往往不仅要知道物体相对地球的运动，而 且有时要知道被观察物体相对于地面运动着的参考系的运动情 况。 例如在运动着的飞机、车船上观察其他飞机、车船的运动。
ve2 l2r2 ae2 l2r22
ve2
M2
ae2
r
ve1
M
1
ae1
o
o
重点要弄清楚牵连点的概念
8.1 点的合成运动的概念
点的合成运动
由于牵连运动的存在，使物体的绝对运动和相对运动发生了差别。
如果没有牵连运动，则动点的相对运动就是它的绝对运动； 如果没有相对运动，则动点随同动参考系所作的运动就是它的绝 对运动； 动点的绝对运动既取决于动点的相对运动，也决定于动参考系的 运动即牵连运动，动点的绝对运动可以看成是牵连运动和相对运 动的合成结果。所以绝对运动也称为复合运动或合成运动。
的动点，把动参考系固定在摇杆O1B上。 O
ve
B
vr
点A的绝对运动是以点O为圆心的
圆周运动，相对运动是沿O1B方向的直
A
线 运 动 ， 而 牵 连 运 动 则 是 摇 杆 绕 O1 轴
的摆动。
ve vasinrsin
ve O1A1
r2
(l2 r2)
O1
O 1A (l2r2) 1l2 r 2r2
8.2 点的速度合成定理
va vrve
几点说明
牵连运动是指刚体(动系)的运动；而牵连速度是指刚体
上一点(与动系相重合的点)的速度。 应用速度合成定理时,可利用速度平行四边形中的几何关 系解出未知数。
第8章 点的合成运动
8.1 点的合成运动的概念 8.2 点的速度合成定理 8.3 点的加速度合成定理
8.1 点的合成运动的概念
在实际问题中，往往不仅要知道物体相对地球的运动，而 且有时要知道被观察物体相对于地面运动着的参考系的运动情 况。 例如在运动着的飞机、车船上观察其他飞机、车船的运动。
ve2 l2r2 ae2 l2r22
ve2
M2
ae2
r
ve1
M
1
ae1
o
o
重点要弄清楚牵连点的概念
8.1 点的合成运动的概念
点的合成运动
由于牵连运动的存在，使物体的绝对运动和相对运动发生了差别。
如果没有牵连运动，则动点的相对运动就是它的绝对运动； 如果没有相对运动，则动点随同动参考系所作的运动就是它的绝 对运动； 动点的绝对运动既取决于动点的相对运动，也决定于动参考系的 运动即牵连运动，动点的绝对运动可以看成是牵连运动和相对运 动的合成结果。所以绝对运动也称为复合运动或合成运动。
的动点，把动参考系固定在摇杆O1B上。 O
ve
B
vr
点A的绝对运动是以点O为圆心的
圆周运动，相对运动是沿O1B方向的直
A
线 运 动 ， 而 牵 连 运 动 则 是 摇 杆 绕 O1 轴
的摆动。
ve vasinrsin
ve O1A1
r2
(l2 r2)
O1
O 1A (l2r2) 1l2 r 2r2
8.2 点的速度合成定理
va vrve
几点说明
牵连运动是指刚体(动系)的运动；而牵连速度是指刚体
上一点(与动系相重合的点)的速度。 应用速度合成定理时,可利用速度平行四边形中的几何关 系解出未知数。
【精】理论力学经典例题
m2vB
(m1
vr 2ve 20 cm/s
vr C
O
M
w
ve va A
B
小环M的加速度分析如图所示 ：
aa ae ar aC
O
aC 2wvr 2 0.5 20 w
B
20 cm/s2
aen M ar C
ac
a aA
y
aen w 2 OM
a 向y方向投影,有: a
0.52
cos
20
aen
5 cm/s2
2w
4ew
3
1
8ew 2
3
B h
aC aa
art
A
aen q
arn
C
O
w
aa cosq aen cosq arn aC
aa
2 (2ew2
3
3 16ew2 8ew2 ) 2 ew2
2 33
3
9
例13 图示曲杆OBC绕O轴转动，使套在其上的小环M沿固定直 杆OA滑动。已知OB＝10 cm，OB与BC垂直，曲杆的角速度为 0.5rad/s，求当φ=60°时小环M的速度和加速度。
va ve vr
va
vr
A
ve
ve w OA
q
va ve tanq w OA
32 3
3ew
3
C O w
vr
ve
cosq
2ew
3
4
3ew
3
2
加速度分析如图
aa ae ar aC
aen OA w 2 2ew 2
arn
vr 2 R
16ew 2
33
aC
2wvr
理论力学8—点的合成运动2分解
(2) 应用速度合成定理时,可利用速度平行四边形中的 几何关系解出未知数。也可以采用投影法：即等式左 右两边同时对某一轴进行投影，投影的结果相等。
8.2 点的速度合成定理
通常选动点和动系主要有以下几种情况： 1. 有一个很明显的动点，在题中很容易发现；
2. 有一个不变的接触点，可选该点为动点；
ae 2 ve1
o
M1
ae1
o
ve1 (l r ) ae1 (l r ) 2
2 2
ve 2 l r
ae 2 l 2 r 2 2
重点要弄清楚牵 连点的概念
8.2 点的速度合成定理
rM rO r
r = xi yj zk
8.1 相对运动· 牵连运动· 绝对运动
习惯上把固定在地球上的坐标系称为 定参考系 ， 以oxy坐标系表示；固定在其它相对于地球运动的参考 体上的坐标系称为动参考系，以o'x'y'坐标系表示。 用点的合成运动理论分析点的运动时，必须选定两 个参考系，区分三种运动：
(1) 动点相对于定参考系的运动，称为绝对运动；
第 8 章
点的合成运动
8.1 相对运动· 牵连运动· 绝对运动
8.2 点的速度合成定理
8.3 点的加速度合成定理
在不同的参考系中，对于同一动点，其运动方 程、速度和加速度是不相同的，这就是运动的 相对性。许多力学问题中，常常需要研究同一 点在不同参考系中的速度、加速度的相互关系。
8.1 相对运动· 牵连运动· 绝对运动
z'
k' j'
y'
i'
x'
O' y
理论力学第八章点的合成运动.
y O1M sin
vt 代入 y r sin vt r
12
已知：r, 相对速度v， ＝ωt， 求：点M的绝对运动方程。
3 牵连运动方程
t 0
0
xo' xo 0, yo' yo 0, t
导数上加“～”表示相对导数。
drM ve rO x i y j z k dt
M’为动系上的点，其在 动系上的坐标为常数。
drM va rO x i y j z k x i y j z k 得证。 dt 15
当 0 或 180 时(e // v r ), ac 0
2、牵连运动为平动情况：
e 0 ac 0
a
a
ae ar
24
2、例题分析：
[例1] 矩形板ABCD以匀角速度 绕固定 轴z转动，点M1和点M2分别沿板的对角线 BD和边线CD运动，在图示位置时相对于 A 板的速度分别为 v 1 和 v 2 。 计算：点M1 、 M2的科氏加速度大小, 并 图示方向。
[注1]此时为动点与动参 考体不重合的情况，须 将动系扩大到参考体之 外。 [注2]特殊问题：特点是相接触两个物体的接触点位置都随 时间而变化.此时, 这两个物体的接触点不宜选为动 点，应选择满足选择原则的非接触点为动点。
17
8-2 点的速度合成定理 恰当地选择动点、动系是求解合成运动问题的关键。
例8-1 点M相对于动系 Oxy 沿半径为r的圆周以 速度v作匀速圆周运动(圆心为O1 ） ，动系 Oxy 相对 Oxy 以匀角速度ω绕点O作定轴转动，如图 于定系 所示。初始时 Oxy 与 Oxy 重合，点M与O重合。 求：点M的绝对运动方程。 解: 1 动点：M点
理论力学n第八章 点的合成运动
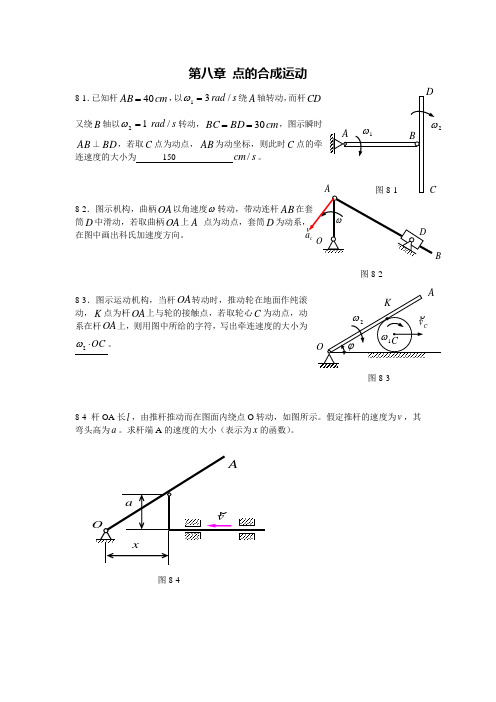
第八章 点的合成运动8-1．已知杆cm AB 40=，以s ra d /31 =ω绕A 轴转动，而杆又绕B 轴以s rad /12 =ω转动，cm BD BC 30==AB ⊥BD ，若取C 点为动点，AB 为动坐标，则此时C 连速度的大小为 150 s cm /。
8-2．图示机构，曲柄OA 以角速度ω转动，带动连杆AB 筒D 中滑动，若取曲柄OA 上A 点为动点，套筒D 在图中画出科氏加速度方向。
8-3．图示运动机构，当杆OA 转动时，推动轮在地面作纯滚动，K 点为杆OA 上与轮的接触点，若取轮心C 为动点，动系在杆OA 上，则用图中所给的字符，写出牵连速度的大小为 2O C ω⋅。
8-4 杆OA 长l ，由推杆推动而在图面内绕点O 转动，如图所示。
假定推杆的速度为v ，其弯头高为a 。
求杆端A 的速度的大小（表示为x 的函数）。
2图8-3图8-4图8-2解：1.取推杆上与OA 杆上的接触点B 为动点，动系在OA 上。
2. 分析三种运动：绝对运动：直线运动 相对运动：直线运动 牵连运动：转动3. 由r e a v v v+=画速度平行四边形 方向√ √ √ 大小√ ？ ？ 22sin ax av v v a e +==α，22ax alv l OBv v e A +=⋅=8-5 在图示机构中，已知O 1O 2=a =200mm ，s rad /31=ω。
求图示位置时杆O 2A 的角速度。
（a ）1.取O 1A 上A 为动点，动系在O 2A 上；2.分析三种运动：绝对运动：圆周运动 1ωa v a = 相对运动：直线运动 牵连运动：转动3. 由r e a v v v+=画速度平行四边形 方向√ √ √ 大小√ ？ ？30cos 30cos 1ωa v v a e ==s r a d a v e5.1230cos 212===ωω8-6 在图示机构中，已知O 1O 2=a =200mm ，s rad /31=ω。
理论力学第8章 点的合成运动
第8章 点的合成运动8-1 如图 8-1 所示，光点 M 沿 y 轴作谐振动，其运动方程为 x = 0， y = a cos(kt +β)如将点 M 投影到感光记录纸上，此纸以等速v e 向左运动。
求点 M 在记录纸上的轨迹。
解 动系O 'x ' y '固结在纸上，点 M 的相对运动 方程x '= v e t ， y '= a cos(kt + β) 消去t 得点 M 在记录纸上的轨迹方程ky '= a cos(x '+β)v e8-2 如图 8-2 所示，点 M 在平面Ox ' y '中运动，图 8-1 运动方程为x '= 40(1− cos t ) ， y '= 40sin t式中t 以 s 计，x '和 y '以 mm 计。
平面Ox ' y '又绕垂直于该平面的轴O 转动，转动方程为 ϕ= t rad ，式中角ϕ为动系的 x '轴与定系的 x 轴间的交角。
求点 M 的相对轨迹和绝对轨迹。
解 由点 M 的相对运动方程可改写为⎛ x ' ⎞⎜⎜⎝40 −1⎟⎟⎠ = −cos ty ' = sin t40上2式两边平方后相加，得点 M 的相对轨迹方程(x '−40)2 + y '2 =1600 图 8-2 由题得点 M 的坐标变换关系式x = x 'cos ϕ− y 'sin ϕ y= x 'sin ϕ+y 'cos ϕ将ϕ= t 和相对运动方程代入，消去t 得点M 的绝对轨迹方程(x + 40)2 + y 2 =16008-3 水流在水轮机工作轮入口处的绝对速度v a =15 m/s ，并与直径成β=60° 角，如图 8-3a 所示，工作轮的半径R = 2 m ，转速n = 30 r/min 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
MM ' 为绝对位移 M1M ' 为相对位移
MM' ＝ MM1 ＋ M1M'
MM' ＝ MM1 ＋ M1M' 将上式两边同除以△t， 取△t →0时的极限，得
lim M M lim M M 1 lim M 1 M t 0 t t 0 t t 0 t
va vevr
即在任一瞬时动点的绝对速度等于其牵连速度与相对速度 的矢量和，这就是点的速度合成定理。 说明：① 点的速度合成定理适用于牵连运动（动系的运动）为
O1B的角速度1。
解：取OA杆上A点为动点，摆杆O1B 为动系，基座为静系。
绝对速度va = r ，方向 OA
相对速度vr = ? 方向//O1B 牵连速度ve = ? 方向O1B
由速度合成定理 va vevr作出速度平行四边形 如图所示。
ve vasin r
r r2 l2
r 2 r2 l2
则
1. 绝对运动：动点相对于静系的运动。 2. 相对运动：动点相对于动系的运动。 点的运动 3. 牵连运动：动系相对于静系的运动。 刚体的运动 在任意瞬时，动坐标系中与动点相重合的点叫牵连点。
绝对运动中动点的速度与加速度称绝对速度 v a 与绝对加速度 a a 相对运动中动点的速度和加速度称相对速度 v r 与相对加速度 a r
§8-2 点的速度合成定理
点的速度合成定理将建立动点的绝对速度、相对速度和牵连 速度之间的关系。
设有一动点M按一定规律沿着固连于动系O’x’y’z’ 的曲线AB 运动, 而曲线AB同时又随同动系O’x’y’z’ 相对静系Oxyz运动。
当t t+△t 时 AB A' B' ， M M' 也可看成M M１ M´
牵连运动：平动； 牵连速度 ve=v平 方向
绝对运动：曲线； 绝对速度 va 的大小、方向待求。
由速度合成定理：vavevr
作出速度平行四边形如图示，则物块A的速度大小和方向为
vAva ve2vr2 v平2 v2
tg 1 v
v平
[例2] 曲柄摆杆机构。已知：OA= r 、 、
OO1=l，图示瞬时，OAOO1 。求：摆杆
牵连运动中牵连点的速度和加速度称牵连速度v e 与牵连加速度a e
四. 动点的选择原则： 选择对动系、静系都为运动的点，例如主动件与从动件
的连接点。 五. 动系的选择原则：
动点对动系有相对运动，且相对运动的轨迹是已知的， 或者是能直接看出的。
下面举例说明以上概念：
动点：AB杆上A点
动系：固结于凸轮Ｏ'上
相对速度 vr = ? 未知，方向CA
牵连速度 ve = OA =2e, 方向
由速度合成定理 va vevr
OA
（翻页请看动画）
作出速度平行四边形 如图所示。
va vetan300 2 e
3 3
vAB
2 3e
3
()
由上述例题知求解合成运动的速度问题的一般步骤为： ①选取动点、动系和静系。 ②对三种运动及其速度进行分析。
同一物体的运动对于不同的参考体来说是不同的。 例如，下雨时，地面上的观察者看雨滴是铅垂向下的， 但对正在行进的车上的观察者来说，雨滴则是倾斜向后的。 又如，沿直线轨道滚动的车轮，站在地面上的人看轮缘上 点M的运动轨迹是一旋轮线，而在行驶着的车中的人看M点， 其轨迹则是一个圆。
二. 动点：所要研究的运动着的点。 三. 三种运动及三种速度与三种加速度
1
ve O1 A
1 r2 l2
r2 r 2
r2 l2 r 2 l 2
（
）
[例3] 圆盘凸轮机构
已知：OC＝e , R 3e , （匀角速度） 图示瞬时, OCCA 且 O、A、B三点共线。
求：从动杆AB的速度。
解：动点取直杆上A点，动系固结于圆盘，
静系固结于基座。
绝对速度 va = ? 待求，方向//AB
[例4] 已知： 凸轮半径 r , 图示时速度 v ， 300 ；杆OA靠在
凸轮上。 求：杆OA的角速度。
分析：相接触的两个物体的接触点位置在各自物体上都随 时间而变化，因此若选两物体的接触点为动点，则相对运动 的分析会较困难。根据上述动点、动系和静系的选择原则， 在此情况下，可选择满足上述两条原则的非接触点为动点。
任何运动的情况。
② 点的速度合成定理是瞬时矢量式，共包括大小、方向 六个元素，已知任意四个元素，就能求出其它两个。
应用举例
[例1] 桥式吊车。已知： 小车水平运行，速度为v平， 物块A相对小车垂直上升的 速度为v。求物块A的运行 速度。
解：选取 动点：物块A 动系：小车 静系：地面
相对运动：直线； 相对速度 vr =v 方向
静系：固结在地面上
绝对运动：直线运动 相对运动：圆弧运动 牵连运动：直度 ：v r
牵连速度 ：v e
绝对加速度：a a
相对加速度：a r 牵连加速度：a e
动点：圆盘上 A点 动系：O'A 摆杆 静系：机架 绝对运动：圆周运动 相对运动：直线运动 牵连运动：定轴转动
动点：摆杆上 A1点 动系：圆盘 静系：机架
绝对运动：圆弧运动 相对运动：曲线运动 牵连运动：定轴转动
若动点A在偏心轮上时 动点：A(在AB杆上) A（在偏心轮上）
动系：偏心轮
AB杆
静系：地面
地面
绝对运动：直线运动 圆周运动（红虚线）
相对运动：圆周运动 曲线运动（未知）
牵连运动：定轴转动 平动
注意：要指明动点在哪个 物体上，且动点不能选在 动系上。
③根据速度合成定理 va vevr作出速度平行四边形。
④根据速度平行四边形，求出未知量。 恰当地选择动点、动系和静系是求解合成运动问题的关键。 动点、动系和静系的选择原则：
①动点、动系和静系须分别属于三个不同的物体，否则绝对、 相对运动中就缺少一种运动，不能成为合成运动。 ②动点相对动系的运动（即相对运动）轨迹易于直观判断 （除已知绝对运动和牵连运动求解相对运动的问题外）。
前两章中我们研究点和刚体的运动，都是以地面为参考体。 然而在实际问题中，还常常要在相对于地面运动着的参考系上 观察和研究物体的运动。如从行驶的汽车上观看飞机的运动， 坐在行驶的火车内看下雨的雨点等。
本章研究同一物体相对于不同参考系的运动及其相互关系。
§8-1 相对运动·牵连运动·绝对运动
一. 坐标系： 静坐标系：固结于地面上的坐标系。简称静系（Oxyz）。 动坐标系：固结于相对于地面运动物体上的坐标系。 简称动系（O’x’y’z’） 。
MM' ＝ MM1 ＋ M1M'
MM' ＝ MM1 ＋ M1M' 将上式两边同除以△t， 取△t →0时的极限，得
lim M M lim M M 1 lim M 1 M t 0 t t 0 t t 0 t
va vevr
即在任一瞬时动点的绝对速度等于其牵连速度与相对速度 的矢量和，这就是点的速度合成定理。 说明：① 点的速度合成定理适用于牵连运动（动系的运动）为
O1B的角速度1。
解：取OA杆上A点为动点，摆杆O1B 为动系，基座为静系。
绝对速度va = r ，方向 OA
相对速度vr = ? 方向//O1B 牵连速度ve = ? 方向O1B
由速度合成定理 va vevr作出速度平行四边形 如图所示。
ve vasin r
r r2 l2
r 2 r2 l2
则
1. 绝对运动：动点相对于静系的运动。 2. 相对运动：动点相对于动系的运动。 点的运动 3. 牵连运动：动系相对于静系的运动。 刚体的运动 在任意瞬时，动坐标系中与动点相重合的点叫牵连点。
绝对运动中动点的速度与加速度称绝对速度 v a 与绝对加速度 a a 相对运动中动点的速度和加速度称相对速度 v r 与相对加速度 a r
§8-2 点的速度合成定理
点的速度合成定理将建立动点的绝对速度、相对速度和牵连 速度之间的关系。
设有一动点M按一定规律沿着固连于动系O’x’y’z’ 的曲线AB 运动, 而曲线AB同时又随同动系O’x’y’z’ 相对静系Oxyz运动。
当t t+△t 时 AB A' B' ， M M' 也可看成M M１ M´
牵连运动：平动； 牵连速度 ve=v平 方向
绝对运动：曲线； 绝对速度 va 的大小、方向待求。
由速度合成定理：vavevr
作出速度平行四边形如图示，则物块A的速度大小和方向为
vAva ve2vr2 v平2 v2
tg 1 v
v平
[例2] 曲柄摆杆机构。已知：OA= r 、 、
OO1=l，图示瞬时，OAOO1 。求：摆杆
牵连运动中牵连点的速度和加速度称牵连速度v e 与牵连加速度a e
四. 动点的选择原则： 选择对动系、静系都为运动的点，例如主动件与从动件
的连接点。 五. 动系的选择原则：
动点对动系有相对运动，且相对运动的轨迹是已知的， 或者是能直接看出的。
下面举例说明以上概念：
动点：AB杆上A点
动系：固结于凸轮Ｏ'上
相对速度 vr = ? 未知，方向CA
牵连速度 ve = OA =2e, 方向
由速度合成定理 va vevr
OA
（翻页请看动画）
作出速度平行四边形 如图所示。
va vetan300 2 e
3 3
vAB
2 3e
3
()
由上述例题知求解合成运动的速度问题的一般步骤为： ①选取动点、动系和静系。 ②对三种运动及其速度进行分析。
同一物体的运动对于不同的参考体来说是不同的。 例如，下雨时，地面上的观察者看雨滴是铅垂向下的， 但对正在行进的车上的观察者来说，雨滴则是倾斜向后的。 又如，沿直线轨道滚动的车轮，站在地面上的人看轮缘上 点M的运动轨迹是一旋轮线，而在行驶着的车中的人看M点， 其轨迹则是一个圆。
二. 动点：所要研究的运动着的点。 三. 三种运动及三种速度与三种加速度
1
ve O1 A
1 r2 l2
r2 r 2
r2 l2 r 2 l 2
（
）
[例3] 圆盘凸轮机构
已知：OC＝e , R 3e , （匀角速度） 图示瞬时, OCCA 且 O、A、B三点共线。
求：从动杆AB的速度。
解：动点取直杆上A点，动系固结于圆盘，
静系固结于基座。
绝对速度 va = ? 待求，方向//AB
[例4] 已知： 凸轮半径 r , 图示时速度 v ， 300 ；杆OA靠在
凸轮上。 求：杆OA的角速度。
分析：相接触的两个物体的接触点位置在各自物体上都随 时间而变化，因此若选两物体的接触点为动点，则相对运动 的分析会较困难。根据上述动点、动系和静系的选择原则， 在此情况下，可选择满足上述两条原则的非接触点为动点。
任何运动的情况。
② 点的速度合成定理是瞬时矢量式，共包括大小、方向 六个元素，已知任意四个元素，就能求出其它两个。
应用举例
[例1] 桥式吊车。已知： 小车水平运行，速度为v平， 物块A相对小车垂直上升的 速度为v。求物块A的运行 速度。
解：选取 动点：物块A 动系：小车 静系：地面
相对运动：直线； 相对速度 vr =v 方向
静系：固结在地面上
绝对运动：直线运动 相对运动：圆弧运动 牵连运动：直度 ：v r
牵连速度 ：v e
绝对加速度：a a
相对加速度：a r 牵连加速度：a e
动点：圆盘上 A点 动系：O'A 摆杆 静系：机架 绝对运动：圆周运动 相对运动：直线运动 牵连运动：定轴转动
动点：摆杆上 A1点 动系：圆盘 静系：机架
绝对运动：圆弧运动 相对运动：曲线运动 牵连运动：定轴转动
若动点A在偏心轮上时 动点：A(在AB杆上) A（在偏心轮上）
动系：偏心轮
AB杆
静系：地面
地面
绝对运动：直线运动 圆周运动（红虚线）
相对运动：圆周运动 曲线运动（未知）
牵连运动：定轴转动 平动
注意：要指明动点在哪个 物体上，且动点不能选在 动系上。
③根据速度合成定理 va vevr作出速度平行四边形。
④根据速度平行四边形，求出未知量。 恰当地选择动点、动系和静系是求解合成运动问题的关键。 动点、动系和静系的选择原则：
①动点、动系和静系须分别属于三个不同的物体，否则绝对、 相对运动中就缺少一种运动，不能成为合成运动。 ②动点相对动系的运动（即相对运动）轨迹易于直观判断 （除已知绝对运动和牵连运动求解相对运动的问题外）。
前两章中我们研究点和刚体的运动，都是以地面为参考体。 然而在实际问题中，还常常要在相对于地面运动着的参考系上 观察和研究物体的运动。如从行驶的汽车上观看飞机的运动， 坐在行驶的火车内看下雨的雨点等。
本章研究同一物体相对于不同参考系的运动及其相互关系。
§8-1 相对运动·牵连运动·绝对运动
一. 坐标系： 静坐标系：固结于地面上的坐标系。简称静系（Oxyz）。 动坐标系：固结于相对于地面运动物体上的坐标系。 简称动系（O’x’y’z’） 。