10 相关和回归分析
第十章 直线回归与相关分析

115 125 128 143 132 121 129 112 120 130 125.5
135 137 128 127 155 132 148 117 134 132 134.5
图10-2 NaCl含量对单位叶面积干物重影响的散点图
Y . X X
含义是:对于变量X的每一个值,都有一个Y 的分布,这个分布的平均数就是该线性函数。
ˆ a bX Y
回归截距 与x值相对应的依变量y的点估计值
此方程称为Y对X的直线回归方程(linear regression equation),画出的直线称为回归线 ( regression line)。
ˆ Y a bx
ˆi ) 2 L ( yi y
i 1 n
Y
最小
编号 1 2 3 4 5 血球体积x /mm3 45 52 56 48 42 红血球数y /106 6.53 6.30 9.52 7.50 6.99 6 7 8 9 10 编号 血球体积x /mm3 35 58 40 39 50 红血球数y /106 5.90 9.49 6.20 6.55 8.72
n n
整理后得:
an b xi yi i1 i1 n n n a xi b xi2 xi yi i1 i1 i1
解正规方程得:
x y ( x )( y ) / n b x ( x ) / n ( x x)( y y) = S S ( x x)
第二节:一元线性回归 1 散点图的绘制
2 一元正态线性回归模型 3 直线回归方程的参数估计和回归方 程的建立 4 直线回归的假设检验
5 直线回归的方差分析
6 直线回归的意义( 自学)
统计学中的相关分析与回归分析的关系

统计学中的相关分析与回归分析的关系统计学是一门研究如何收集、整理、描述和解释数据的学科。
在统计学中,相关分析和回归分析是两个重要的方法,用于了解和探究变量之间的关系。
尽管相关分析和回归分析在某些方面有相似之处,但它们在目的、数据类型和结果解释方面存在一些差异。
相关分析是一种用于衡量和描述两个或多个变量之间关联关系的方法。
相关分析可以帮助我们确定变量之间的线性相关程度,即一个变量的变化伴随着另一个变量的变化。
通过计算相关系数,我们可以了解这种关系的强度和方向。
常用的相关系数包括皮尔逊相关系数和斯皮尔曼等级相关系数。
与此不同,回归分析旨在建立一个数学模型,以描述和预测因变量与自变量之间的关系。
回归分析可以通过拟合曲线或平面来表示变量之间的关系,并用方程式来描述这种关系。
回归分析使用的模型可以是线性回归、多项式回归、对数回归等。
通过回归分析,我们可以根据自变量的值来估计因变量的值,并评估自变量对因变量的影响程度。
虽然相关分析和回归分析在某些情况下可互相转化,但它们具有不同的目标和应用范围。
相关分析主要用于探索变量之间的关系,确定它们之间的关联强度和方向,但不提供因果关系。
而回归分析则旨在建立一个模型,通过这个模型可以对未知的因变量进行预测,并且可以评估自变量对因变量的影响。
此外,相关分析和回归分析适用于不同类型的数据。
相关分析通常用于分析连续变量之间的关系,而回归分析可以应用于连续变量、二分类变量和多分类变量之间的关系。
在实际应用中,相关分析和回归分析常常结合使用。
首先,我们可以通过相关分析来初步检验变量之间是否存在关系。
如果相关分析结果显示两个变量之间存在显著相关性,我们可以进一步使用回归分析来建立一个模型,以更好地理解和预测这种关系。
在总结中,统计学中的相关分析和回归分析是两个相互关联的方法。
相关分析用于探究变量之间的关系和相关性,而回归分析则用于建立一个数学模型,描述和预测因变量与自变量之间的关系。
相关分析和回归分析

即r (x x)( y y) 或r (x x)( y y)
n x y
(x x)2 ( y y)2
•协方差的意义
①显示x与y是正相关还是负相关 协方差为负,是负相关, 协方差为正,是正相关。 ②协方差显示x与y相关程度的大小 当相关点在四个象限呈散乱的分布,相关程度很低 当相关点分布在x与y的平均值线上时,表示不相关 当相关点靠近一直线,表示相关关系密切 当相关点全部落在一直线,表示完全相关
2、相关图被形象地称为相关散点图 3、因素标志分了组,结果标志表现为组平均数,
所绘制的相关图就是一条折线,这种折线又叫 相关曲线。
三、相关系数的计算:
1、符号系数:把两个同平均值的离差数列做对称 比较。
①如果一个数列的离差与另一个数列的离差有很 多同号,就可以认为这两标志之间存在正相关。
②如果大多数为异号,就可以认为他们之间存在 负相关。
.............b
xx x
y x
2
y
xy
1 n
x
y
x2
1 n
x2
当出现权数时:
方程为:a f b xf yf ................a xf b x2 f xyf
解得:a y bx
•相关系数的r的推导公式:
r
n xy x y
n x2 x2 n y2 y2
r
xy nxy
(
x2
2
nx )
y2
2
ny
r
xy x y
回归分析与相关性分析的基本原理与应用

回归分析与相关性分析的基本原理与应用数据分析是现代社会中非常重要的一个领域,在各个行业和领域中都有广泛的应用。
而回归分析和相关性分析是数据分析中经常使用的两种方法,本文将探讨回归分析和相关性分析的基本原理和应用。
一、回归分析的基本原理与应用回归分析是用来研究变量之间关系的一种统计方法,主要用于预测一个变量(因变量)与其他变量(自变量)之间的关系。
具体来说,回归分析可以帮助我们确定自变量对因变量的影响程度以及预测因变量的取值。
回归分析的基本原理是基于线性回归模型,即通过建立一个线性方程来描述因变量和自变量之间的关系。
简单线性回归模型的表达式为:Y = α + βX + ε,其中Y表示因变量,X表示自变量,α和β为回归系数,ε为误差项。
在应用回归分析时,我们需要确定自变量与因变量之间的关系强度以及回归系数的显著性。
这可以通过计算相关系数、拟合优度等统计指标来实现。
此外,回归分析还可以通过预测因变量的取值来进行决策和规划,例如销量预测、市场需求预测等。
二、相关性分析的基本原理与应用相关性分析是用来研究变量之间线性相关关系的一种统计方法,主要用于衡量变量之间的相关性程度。
相关性分析可以帮助我们理解变量之间的相互关系,以及在研究和预测中的应用。
相关系数是用来衡量两个变量之间相关性的指标,最常用的是皮尔逊相关系数。
皮尔逊相关系数的取值范围在-1到1之间,其中-1表示完全负相关,1表示完全正相关,0表示无相关性。
通过计算相关系数可以判断两个变量之间是否存在线性关系,以及线性关系的强弱程度。
在应用相关性分析时,我们可以利用相关系数来进行综合评价和比较。
例如,在市场研究中,我们可以通过相关性分析来确定产品特性与客户购买意愿之间的关系,以指导产品开发和市场推广策略。
三、回归分析与相关性分析的比较回归分析和相关性分析都是研究变量之间关系的统计方法,但它们在方法和应用上存在一些区别。
首先,回归分析主要关注自变量对因变量的影响程度和预测,而相关性分析主要关注变量之间的相关程度。
相关分析与回归分析

这是一种不检验F和Tolerance,一次将全部自变量无条件地
纳入回归方程。
二强行剔除Remove一次性剔除
指定某些变量不能进入方程。这种方法通常同别的方法联合
使用,而不能首先或单独使用,因为第一次使用或单独使用
将意味着没有哪个变量进入方程。
三逐步进入Stepwise
▪ 回归分析是研究客观事物变量间的关系,它是建立在对客
观事物进行大量试验和观察的基础上,通过建立数模型寻
找不确定现象中所存在的统计规律的方法。回归分析所研
究的主要问题就是研究因变量y和自变量x之间数量变化规
律,如何利用变量X,Y的观察值样本,对回归函数进行
统计推断,包括对它进行估计及检验与它有关的假设等。
差
▪ “Plots”
该对话框用于设置要绘制的图形的参数。
“X”和“Y”框用于选择X轴和Y轴相应的变量。
左上框中各项的意义分别为:
• “DEPENDNT”因变量。
• “ZPRED”标准化预测值。
• “ZRESID”标准化残差。
• “DRESID”删除残差。
• “ADJPRED”调节预测值。
• “SRESID”声氏化残差。
利用的是非参数检验的方法。
定序变量又称为有序ordinal变量顺序变
量,它取值的大小能够表示观测对象的某种顺
序关系等级方位或大小等,也是基于“质”因
素的变量。例如,“最高历”变量的取值是:
一—小及以下二—初中三—高中中专技校四—
大专科五—大本科六—研究声以上。由小到大
的取值能够代表历由低到高。
Spearman等级相关系数为
– 四. Multinomial Logistic 多元逻辑分析。
相关与回归分析

对相关系数的说明
(1)相关系数受样本容量n的影响,样本容量要求以 n≥30为宜。
(2)相关系数不是等距量表值,更不是等比量表值。不 能说r=0.5是r=0.25的两倍。 (3)存在相关关系不一定存在因果关系。 (4)计算相关系数要求成对数据,任意两个个体之间的 观测值不能求相关。
(5)没有线性相关,不一定没有关系,可能是非线性的。
第十二章 相关与回归分析
一、相关分析概述
客观事物之间的关系大致可归纳为两大类,即 函数关系:两事物之间的一种一一对应的关系,如商品的 销售额和销售量之间的关系。 共变关系:两事物之间本身没有直接的关系,但它们都受 第三种现象的影响而发生变化。例如春天出生的婴儿与春 天栽种的小树,就其高度而言,表面上看来都在增长,好 像有关,其实,这二者都是受时间因素影响在发生变化, 在它们之间并没有直接的关系。 相关关系:两事物之间的一种非一一对应的关系,例如家 庭收入和支出、子女身高和父母身高之间的关系等。它们 之间存在联系,但又不能直接做出因果关系的解释。相关 关系又分为线性相关和非线性相关。 相关分析是分析事物之间相关关系的数量分析方法。
职工的工作种类与工作价值
工作价值 Y 经济取向型 成就取向型 人际关系取向型 合计:FX
工作种类 X
工人 100 30 20 150 技术人员 70 60 10 140 管理人员 50 20 40 110
回归分析与相关分析

相关分析与回归分析
第11页
根据回归函数的意义,当X取xi时,Y的期望值 应为f(xi),由于随机误差,观察值yi与f(xi)之间有
一定的差距,即:
yi f (xi ) i
i是第i次试验的误差。 对于Y ( y1, y2 , , yn) , X (x1, x2 , , xn )和 (1, 2 , , n ) 有
27 May 2020
相关分析与回归分析
第22页
三、回归方程的检验
1.随机误差 2 的估计
由一元线性回归方程的模型:
yi a bxi i i ~ N (0 , 2 )
Y ~ N (a bx , 2 )
以D剩为基础作为 2的估计是合理的,其估计为
n
n
D剩
2 i
( yi (aˆ bˆxi ))2
27 May 2020
相关分析与回归分析
第8页
第二节 回归分析
一、确定回归函数的思想
要全面地考察两个变量 X、Y 之间的关系,我们就要研究Y 的
条件分布 F (y | X=x ) 随 X 取值 x 的变化情况. 很自然我们会 想到用 F ( y | X=x ) 的数学期望(平均值)来代替它,这样就可 以通过研究 x 与 Y 的条件期望值之间的关系来代表 X 与 Y 之 间的关系. 即:
显著. n个y值的总差异记为D总
n
D总= ( yi y) 2 l yy
程进行预测和控制.
27 May 2020
相关分析与回归分析
第6页
“回归” 一词的历史渊源
“回归”一词最早由Francis Galton引入。英国著
名人类学家Franics Galton(1822-1911)于1885年在
统计学第10讲 相关与回归分析(白)含检验

相关关系的图示
非线性相关
完全正线性相关
完全负线性相关
负线性相关
不相关
正线性相关
四、相关关系的判断
定性分析
是依据研究者的理论知识和实践经 验,对客观现象之间是否存在相关 关系,以及何种关系作出判断。
rXY
●
样本相关系数
样本相关系数通常用
rXY
rXY 表示
__ __ i i __ 2 __ 2 i
( x x )( y y ) (x x) ( y y)
i __ __
式中, 和 y 分别是x和y的样本平均数。 x
特点:样本相关系数是根据从总体中抽取的随机样本 的观测值计算出来的,是对总体相关系数的估 计,它是个随机变量。
916 625
x2 1225 1444 1600 1764 2401 2704 2916 3481 3844 4096 4225 4624 4761 5041 5184 5776 55086
y2 576 625 576 784 1024 961 1369 1600 1681 1600 2209 2500 2401 2601 2304 3364 2617 5
六、回归模型的类型
一个自变量 回归模型
两个及两个以上自变量
一元回归
线性 回归 非线性 回归 线性 回归
多元回归
非线性 回归
10.2 简单线性相关与回归分析
一、简单线性相关系数及检验 二、总体回归函数与样本回归函数 三、回归系数的估计 四、简单线性回归模型的检验 五、简单线性回归模型预测
【毕业论文】相关分析和回归分析
相关分析和回归分析客观事物之间的关系分为函数关系和统计关系,函数关系也就是我们通常所说的一一对应的关系,而统计关系是指两事物之间的一种非一一对应的关系,即当一个变量x取一定值时,另一变量y无法依确定的函数取唯一确定的值。
事物之间的统计关系是普遍存在,且有的关系强,有的关系弱。
相关分析和回归分析都是以不同方式测度事物之间统计关系的有效工具。
实际应用中。
这两种分析方法经常互相结合渗透。
一、相关分析相关分析通过图形和数值两种方式,能够有效的揭示事物之间统计关系的强弱程度。
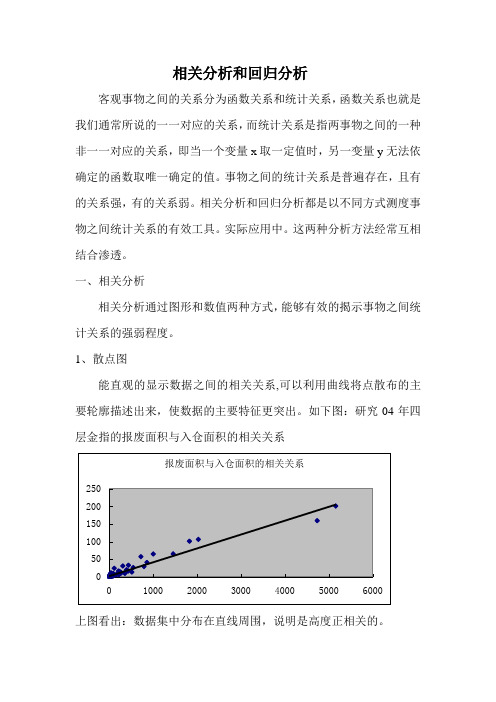
1、散点图能直观的显示数据之间的相关关系,可以利用曲线将点散布的主要轮廓描述出来,使数据的主要特征更突出。
如下图:研究04年四层金指的报废面积与入仓面积的相关关系上图看出:数据集中分布在直线周围,说明是高度正相关的。
2、相关系数散点图能直观的展现变量之间的统计关系,但并不精确。
相关系数以数值的方式精确的反映了两个变量间线形相关的强弱程度。
➢ R=yyxx xy L L L ,其中xx L =∑=--ni ix x12)(,∑=----=ni i i xy y y x x L 1))((,∑=--=ni i yy y y L 12)(.➢ 相关系数R 的取值在-1~+1之间。
➢ R>0表示两变量之间存在正的线性相关关系;R<0表示两变量之间存在负的线性相关关系。
➢ R=1表示两变量存在完全正相关;R=-1表示两变量存在完全负相关;R=0表示两变量不存在线性相关关系。
➢ |R|>0.8表示两变量之间具有较强的线性关系;|R|<0.3表示两变量之间的线性相关关系较弱。
上例中,R=0.974,说明报废面积与入仓面积之间是强正相关的。
二、一元线性回归在实际应用中,我们常常需要考虑某一现象与影响它的最主要因素的关系,回归分析不仅可以揭示变量x 对变量y 的影响大小,还可以由回归方程进行预测和控制。
一元线性回归是最简单的回归模型。
相关分析和回归分析的区别

相关分析和回归分析的区别:1, 在相关分析中,解释变量X与被解释变量Y之间处于平等的位置。
而回归分析中,解释变量与被解释变量必须是严格确定的。
2 相关分析中,被解释变量Y与解释变量X全是随机变量。
而回归,被解释变量Y是随机的,解释变量X可能是随机的,可能是非随机的确定变量。
3 相关的研究主要主要是为刻画两变量间线性相关的密切程度。
而回归不仅可以揭示解释变量X和被解释变量Y的具体影响形式,而且还可以由回归方程进行预测和控制。
如果两变量间互为因果关系,解释变量与被解释变量互换位置,相关分析结果一样,回归分析结果不同。
样本回归函数与总体回归函数的区别: 1 总体是未知的,是客观唯一存在的。
样本是根据样本数据拟合的,每抽取一个样本,变可以拟合一条样本回归线。
2 总体中的β0和β1是未知参数,表现为常数。
而样本中的是随机变量,其具体数值随样本观测值的不同而变化。
3 随机误差ui是实际Yi值与总体函数均值E(Yi)的离差,即Yi与总体回归线的纵向距离,是不可直接观测的。
而样本的残差ei是yi与样本回归线的纵向距离,当拟合了样本回归后,可以计算出ei的具体数值。
一元的五个基本假定:1 随机扰动项ui的均值为零,即E(ui)=02 随机扰动项ui的方差为常数Var(ui)=E[ui-E(ui)]^2=E(ui^2)=σ^23 任意两个随机扰动项ui和uj互不(i不等于j)互不相关,其其协方差为0Cov(ui,uj)=04 随机扰动项ui与解释变量Xi线性无关Cov(ui,Xi)=05 随机扰动项服从正态分布,即ui~N(0,σ^2)样本分段比较法适用于检验样本容量较大的线性回归模型可能存在的递增或递减型的异方差性,思路是首先量样本按某个解释变量从大到小或小到大顺序排列,并将样本均匀分成两段,有时为增强显著性,可去掉中间占样本单位1/4或1/3的部分单位;然后就各段分别用普通最小二乘法拟合回归直线,并计算各自的残差平方和,大的用RSS1,小的用RSS2表示,如果数值之比明显大于1,则存在异方差异方差性的后果:1 参数估计值虽然是无偏的,但却不是有效的。
统计学—10相关与回归分析

(2)设y依x的回归直线方程为yc=a+bx,则
y依x的回归直线方程为yc=24800+0.2x (3)当家庭年收入为150 000,即x =150000时,则家庭消费支出额为
yc=24800+0.2×150000=54800(元) (4)当家庭收入每增加1元,支出平均增加0.2元。
四、估计标准误差
第十讲 相关与回归分析 2
第十讲 相关与回归分析
Correlation Analysis Regression Analysis
一、相关分析的概念 二、简单线性相关分析 三、回归分析 四、估计标准误差
3
一、相关分析的概念
(一)函数关系 (二)相关关系
严格的依存关系
存在S=一πr定2 的依存关系,具光 照体关系值不固定
(1)计算收入与消费支出的相关系数; (2)确定消费支出对于收入的回归方程; (3)估计家庭年收入为150 000时的消费支出额; (4)家庭收入每增加1元,支出平均增加多少元? 解析:(1)设家庭收入为x,家庭消费支出为y,家庭收入与家庭 消费支出之间的相关系数为r, y依x的回归直线方程为yc=a+bx ,由已 知条件可知:
5
二、简单线性相关分析
(一)相关图和相关表
(二)相关系数
1.相关系数的概念
相关系数是在直线相关条件下,说明两现象之间相关关系密切 程度的统计分析指标。
2.相关系数的特点
•计算相关系数的两个变量都是随机变量 •相关系数的取值范围在-1和1之间,其正负号反映正相关或负相关 •两变量为对等关系,可不区分自变量和因变量,其相关系数只有一个值。
correlation analysis Regression analysis
相关分析和回归分析

回归分析和相关分析的联系和区别回归分析(Regression):Dependant variable is defined and can be forecasted by independent variable.相关分析(Correlation):The relationship btw two variables. --- A dose not define or determine B.回归更有用自变量解释因变量的意思,有一点点因果关系在里面,并且可以是线性或者非线形关系;相关更倾向于解释两两之间的关系,但是一般都是指线形关系,特别是相关指数,有时候图像显示特别强二次方图像,但是相关指数仍然会很低,而这仅仅是因为两者间不是线形关系,并不意味着两者之间没有关系,因此在做相关指数的时候要特别注意怎么解释数值,特别建议做出图像观察先。
不过,无论回归还是相关,在做因果关系的时候都应该特别注意,并不是每一个显著的回归因子或者较高的相关指数都意味着因果关系,有可能这些因素都是受第三,第四因素制约,都是另外因素的因或果。
对于此二者的区别,我想通过下面这个比方很容易理解:对于两个人关系,相关关系只能知道他们是恋人关系,至于他们谁是主导者,谁说话算数,谁是跟随者,一个打个喷嚏,另一个会有什么反应,相关就不能胜任,而回归分析则能很好的解决这个问题回歸未必有因果關係。
回歸的主要有二:一是解釋,一是預測。
在於利用已知的自變項預測未知的依變數。
相關係數,主要在了解兩個變數的共變情形。
如果有因果關係,通常會進行路徑分析(path analysis)或是線性結構關係模式。
我觉得应该这样看,我们做回归分析是在一定的理论和直觉下,通过自变量和因变量的数量关系探索是否有因果关系。
楼上这位仁兄说“回归未必有因果关系……如果有因果关系,通常进行路径分析或线性结构关系模式”有点值得商榷吧,事实上,回归分析可以看成是线性结构关系模式的一个特例啊。
相关 分析与回归分析

第二节 相关关系的判断
2.相关表 相关表就是把被研究现象的观察值对应排列所形成的统计表
格。如某地区工业劳动者人数和增加值的历史资料对应排列 如表8-1所示。 相关表中的两行数据叫相关数列,它有别于变量数列。相关 表中的数值是变量的观测值,是实际资料,是样本数据,它 是判别相关关系的基础。在相关表中,如果观测值的分布呈 现一定的规律性,则表明现象间存在相关关系。如随着一个 变量数值的增加或减少,另一个变量的值也大致以某一固定 的速率和数量增加或减少,这就可以初步判别现象间存在相 关关系。如果两个变量的观测值不表现出任何规律性,则可 以判定现象间不存在相关关系。
上一页 下一页 返回
第一节 相关分析的一般问题
2.判定相关关系的表现形态和密切程度 相关关系是一种数量上不严格的相互依存关系。只有当变量间
确实存在高度密切的相关关系时,才可能进行相关分析,对社 会经济现象进行预测、推算和决策。因此,判定现象间存在相 关关系后,需要进一步确定相关关系的表现形态和密切程度。 统计上,一般是通过编制相关表、绘制相关图和计算相关系数 来做出判断的。根据相关图表可对相关关系的表现形态和密切 程度做出一般性的判断,依据相关系数则能做出数量上的具体 分析。在我们判断中学生的学习成绩和身高之间有无相关性时, 如果我们发现有部分相关联的点,我们还要进行相关程度的判 断,看两种现象之间的相关程度的高低,以此来判定其是否具 有研究相关性的必要。
除上例外,在其他方面也都可以编制类似的双变量分组相关 表。如工业企业按产量和成本水平同时分组;对同行业的商 业企业,按企业规模和流通费水平同时分组等。这种双变量 分组相关表,可作为探寻最佳方案、提高经济效益的一种工 具。但是,根据双变量分组表的资料来计算相关分析指标比 较复杂,所以,在相关分析中较少使用。
回归分析与相关性检验方法

回归分析与相关性检验方法引言回归分析和相关性检验方法是统计学中常用的两种分析方法。
它们主要用于研究变量之间的关联程度和预测某一变量对其他变量的影响。
在实际应用中,回归分析和相关性检验方法具有广泛的应用领域,例如经济学、医学、社会科学等。
本文将对回归分析和相关性检验方法进行详细介绍,并给出相应的案例应用。
一、回归分析回归分析是一种统计学方法,用于研究因变量和一个或多个自变量之间关系的强度和方向。
回归分析有两种基本类型:简单线性回归和多元线性回归。
1. 简单线性回归简单线性回归是指当因变量和自变量之间存在一种线性关系时使用的回归分析方法。
简单线性回归的模型可以表示为:$y = \\beta_0 + \\beta_1x + \\epsilon$,其中y表示因变量,x表示自变量,$\\beta_0$和$\\beta_1$是回归系数,表示截距和斜率,$\\epsilon$表示误差项。
简单线性回归的关键是通过最小二乘法估计回归系数,然后进行显著性检验和模型拟合度的评估。
通过显著性检验可以确定回归系数是否显著不为零,进而得出自变量对因变量的影响是否显著。
2. 多元线性回归多元线性回归是指当因变量和多个自变量之间存在一种线性关系时使用的回归分析方法。
多元线性回归的模型可以表示为:$y = \\beta_0 + \\beta_1x_1 +\\beta_2x_2 + ... + \\beta_nx_n + \\epsilon$,其中y表示因变量,x1,x2,...,x n表示自变量,$\\beta_0, \\beta_1, \\beta_2, ..., \\beta_n$表示回归系数,$\\epsilon$表示误差项。
多元线性回归的关键也是通过最小二乘法估计回归系数,并进行显著性检验和模型拟合度的评估。
多元线性回归可以通过检验回归系数的显著性,判断各个自变量是否对因变量产生显著影响。
二、相关性检验方法相关性检验方法是用于检测变量之间关系的非参数统计学方法。
相关分析和回归分析的联系和区别

相关分析和回归分析的联系和区别相关分析和回归分析的联系和区别⼀、总结⼀句话总结:> 1、在回归分析中,y被称为因变量,处在被解释的特殊地位,⽽在相关分析中,x与y处于平等的地位,即研究x与y的密切程度和研究y与x的密切程度是⼀致的;> 2、相关分析中,x与y都是随机变量,⽽在回归分析中,y是随机变量,x可以是随机变量,也可以是⾮随机的,通常在回归模型中,总是假定x是⾮随机的;> 3、相关分析的研究主要是两个变量之间的密切程度,⽽回归分析不仅可以揭⽰x对y的影响⼤⼩,还可以由回归⽅程进⾏数量上的预测和控制.⼆、相关分析和回归分析的联系和区别⼀、回归分析和相关分析主要区别是:1、在回归分析中,y被称为因变量,处在被解释的特殊地位,⽽在相关分析中,x与y处于平等的地位,即研究x与y的密切程度和研究y与x的密切程度是⼀致的;2、相关分析中,x与y都是随机变量,⽽在回归分析中,y是随机变量,x可以是随机变量,也可以是⾮随机的,通常在回归模型中,总是假定x是⾮随机的;3、相关分析的研究主要是两个变量之间的密切程度,⽽回归分析不仅可以揭⽰x对y的影响⼤⼩,还可以由回归⽅程进⾏数量上的预测和控制.⼆、回归分析与相关分析的联系:1、回归分析和相关分析都是研究变量间关系的统计学课题。
2、在专业上研究上:有⼀定联系的两个变量之间是否存在直线关系以及如何求得直线回归⽅程等问题,需进⾏直线相关分析和回归分析。
3、从研究的⽬的来说:若仅仅为了了解两变量之间呈直线关系的密切程度和⽅向,宜选⽤线性相关分析;若仅仅为了建⽴由⾃变量推算因变量的直线回归⽅程,宜选⽤直线回归分析.扩展资料:1、相关分析是研究两个或两个以上处于同等地位的随机变量间的相关关系的统计分析⽅法。
例如,⼈的⾝⾼和体重之间;空⽓中的相对湿度与降⾬量之间的相关关系都是相关分析研究的问题。
2、回归分析是确定两种或两种以上变量间相互依赖的定量关系的⼀种统计分析⽅法。
第10章相关分析及回归分析

第八章相关与回归分析一、本章重点1.相关系数的概念及相关系数的种类。
事物之间的依存关系,能够分为函数关系和相关关系。
相关关系又有单向因果关系和互为因果关系;单相关和复相关;线性相关和非线性相关;不相关、不完全相关和完全相关;正相关和负相关等类型。
2.相关分析,着重掌握如何画相关表、相关图,如何测定相关系数、测定系数和进行相关系数的推断。
相关表和相关图是变量间相关关系的生动表示,对于未分组资料和分组资料计算相关系数的方式是不同的,一元线性回归中相关系数和测定系数有着紧密的关系,取得样本相关系数后还要对整体相关系数进行科学推断。
3.回归分析,着重掌握一元回归的大体原理方式,一元回归是线性回归的基础,多元线性回归和非线性回归都是以此为基础的。
用最小平方式估量回归参数,回归参数的性质和显著性査验,随机项方差的估量,回归方程的显菁性査验, 利用回归方程进行预测是回归分析的主要内容。
4.应用相关与回归分析应注意的问题。
相关与回归分析都有它们的应用范围,必需明白在什么情形下能用,什么情形下不能用。
相关分析和回归分析必需以定性分析为前提,不然可能会闹岀笑话,在进行预测时选取的样本要尽可能分散,以减少预测误差,在进行预测时只有在现有条件不变的情形下才能进行,若是条件发生了转变,原来的方程也就失去了效用。
二、难点释疑本章难点在于计算公式多,不容易记忆,所以更要注重计算的练习。
为了辜握大体计算的内容,最少应认真理解书上的例题,做完本指导书上的全数计算题。
初学者可能会感到本章公式多且复杂,难于记忆,其实只要抓住Lxx、Lxy. Lyy 这三个记号,记住它们的展开式,几个主要的公式就不难记忆了。
若是能自己把这些公式推证一下,弄清其关系,那就更易记住了。
三、练习题(一)填空题1事物之间的依存关系,按照其彼此依存和制约的程度不同,能够分为()和()两种。
2.相关关系按相关关系的情形可分为()和();按自变量的多少分()和();按相关的表现形式分()和();按相关关系的紧密程度分()、()和();按相关关系的方向分()。
第10章 直线回归与相关分析

回归方程的基本条件(性质): 回归方程的基本条件(性质): 性质1 性质1 性质2 性质2 性质3 性质3
ˆ 最小; Q = ∑( y − y)2 = 最小;
ˆ ∑( y − y) = 0
; 。
回 归 直 线 通 过 点 (x, y)
2
ˆ Q = ∑( yi − yi ) = ∑[ yi − (a + bxi )]
二、直线回归的显著性检验
回归关系的假设测验: 回归关系的假设测验: 对于样本的回归方程,必须测定其来自无 对于样本的回归方程,必须测定其来自无 直线回归关系总体的概率大小。只有当这种概 直线回归关系总体的概率大小。 率小于0.05或0.01时,我们才能冒较小的危 或 率小于 时 险确认其所代表的总体存在着直线回归关系。 险确认其所代表的总体存在着直线回归关系。 这就是回归关系的假设测验 。 回归关系的假设测验有两种方法: 测验或F 回归关系的假设测验有两种方法:t测验或F测验
由于x变数的实测区间为[31.7,44.2], 由于x变数的实测区间为[31.7,44.2], [31.7 在应用=48.5-1.1x于预测时,需限定x 在应用=48.5-1.1x于预测时,需限定x的区间 =48.5 于预测时 为[31.7,44.2];如要在x<31.7或>44.2的 [31.7,44.2];如要在x 31.7或 44.2的 区间外延,则必须有新的依据。 区间外延,则必须有新的依据。
整理后可得: 整理后可得:
na + ( ∑ xi )b = ∑ yi ( ∑ xi ) a + ( ∑ x i ) b = ∑ x i y i
2
上式叫做a与b的正规方程组 正规方程组。 正规方程组
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Page 12
➢ 以下资料选自Galton的一项研究,目的是探讨成年 时身高是否与两岁时的身高(单位:英寸)有关。
两岁时的 身高(英寸)
39
30
32
34
35
36
36
30
成年 身高(英寸)
71
63
63
67
68
68
70
64
Medical statistics
医学统计学
直线相关和回归分析
Department of Biostatistics, School of Public Health Nanjing Medical University
直线相关分析
Linear Correlation Analysis
Department of Biostatistics, School of Public Health Nanjing Medical University
➢若两个变量同时增加或减少,变化趋势是同 向的,则两变量之间的关系为正相关 (positive correlation);若一个变量增加时,另 一个变量减少,变化趋势是反向的,则称为 负相关(negative correlation)。
Page 7
直线相关的概念
➢直线相关(linear correlation),又称简单相 关,用以描述两个呈正态分布的变量之间的 线性共变关系,常简称为相关。
Page 8
➢用以说明具有直线关系的两个变量间相关关 系的密切程度和相关方向的指标,称为相关 系数(correlation coefficient),又称为积差 相关系数(coefficient of product-moment correlation),Pearson相关系数 。
➢总体相关系数用希腊字母r表示,而样本相
➢从相关系数r不等于0的总体中抽样,样本相
关系数的分布是偏态的。
Page 19
相关系数的抽样分布(r = - 0.8)
300 200 100
0 -1.0 -0.8 -0.6 -0.4 -0.2 0.0
Page 20
相关系数的抽样分布(r = 0)
300 200 100
0 -1.0 -0.8 -0.6 -0.4 -0.2 0.0 0.2 0.4 0.6 0.8 1.0
Page 13
绘制散点图
71
Y 成年后身高(单位:英寸)
69
67
65
63 30
32
34
36
38
X 2岁时的身高(单位:英寸)
40
Page 14
lXX
X2
2
X
272 2
9318
70.00
n
8
lYY
Y2
2
Y
5342
35712
67.50
n
8
lXY
XY
X Y
n
18221
3
4
Page 26
相关系数的可信区间估计
➢将 r 变换为 z ;
➢根据 z 服从正态分布,估计 Z 的可信区
间;
z ua sz z ua
1 n3
➢再将 z变换回 r 。
Page 27
相关系数的可信区间估计
Fisher’s 变换
r
z
正态近似
Fisher’s 反变换
r的95%CI
Z的95%CI
相关分析:主要内容
➢问题的提出 ➢相关关系与确定性关系 ➢相关和直线相关的概念 ➢直线相关的图示 ➢直线相关系数的计算 ➢直线相关系数的假设检验和区间估计
Page 3
问题的提出
➢以往方法的局限
仅限于考察一个观察指标
Page 4
问题的提出
➢ 人的体重往往随着身高的增加而增加。二者之间 是否存在某种关联?如果存在,可否用身高来推 测体重的多少?
Page 21
相关系数的抽样分布(r =0.8)
300 200 100
0 0 0.2 0.4 0.6 0.8 1.0
Page 22
R.A. Fisher(1921) 的 z 变换
z 1 ln 1 r 2 1r
r
e2z e2z
1 1
z近似服从均数为
1 2
ln(1
r
)
/(1
r
),
标准差为 1/ n 3 的正态分布。
关系数用r表示,取值范围均为[-1,1]。
Page 9
直线相关的图示
正相关
负相关
零相关
零相关
0<r<1 完全正相关
-1<r<0 完全负相关
r=0 零相关
r=0 零相关
r=1
r=-1
r=0
r=0
Page 10
直线相关的图示与相关系数的关系 -01r<r<=r=r-<01<110
Page 11
直线相关系数的计算
➢C =2R ➢S=vt
➢非确定性关系是指两变量在宏观上存在关系, 但并未精确到可以用函数关系来表达。
➢青少年身高随年龄增长而增高; ➢体表面积与体重有关
Page 6
2.相关的概念
➢当两个数值变量之间出现如下情况:当一个 变量增大,另一个也随之增大(或减少),我 们称这种现象为共变,也就是有相关关系。
Page 23
相关系数的z 值的抽样分布(r = - 0.8)
200
150
100
50
0
0
0.5
1.0 1.5
2.0
Page 24
相关系数的z 值的抽样分布(r = 0)
200
150
100
50
0
-2
-1
0
1
2
Page 25
相关系数的z 值的抽样分布(r = 0.8)
200
150
100
50
0
0
1
2
➢H1:ρ≠0,两变量间有直线相关的关系;
➢a =0.05
t 0.9456 7.1196 1 0.94562
82
➢ν=8-2=6
➢以自由度为6查附表2的t界值表,得P<0.01, 按α=0.05的水准拒绝H0,接受H1,认为2岁 时的身高和成年身高之间存在正相关。
Page 18
总体相关系数的区间估计
➢ 儿童所能发出的最长音调往往和年龄有关。同样, 是否可以建立年龄和音调长度的数量关系?
➢ 人的肺活量往往随着胸围的增加而增加。 ➢ 举重运动员所能举起的最大重量是否与他的体重
有关?
Page 5
相关关系与确定性关系
➢所谓确定性关系是指两变量间的关系是函数 关系。已知一个变量的值,另一个变量的值 可以通过这种函数关系精确计算出来。
272 534 8
65.00
Page 15
r lXY
65.00
0.9456
lXX lYY 70.00 67.50
Page 16
相关系数的假设检验
➢H0:r=0,两变量间无直线相关的关系; ➢H1:r≠0。
r0 t
sr
r ,v n2
1 r2 n2
Page 17
➢H0:ρ=0,两变量间无直线相关的关系;
