13-8 热力学第二定律的统计意义【热力学】
第八节热力学第二定律的统计意义和熵的概念

Ω2 = (nV2 /V1 ) N = (V2 ) N
Ω1
n
V1
∴ ∆S = K ln Ω2 = NK ln V2 = υR ln V2
V1
注意:
Ω1
V1
V1
1)熵是状态函数,初末态定,熵定,与过程无关.
2)讨论是针对孤立系统.
若要: ∆S → 0 则 V2 >V1 故方向小→大
4. 开放系统:
熵的改变来自: 熵的产生: dSi 系统内部的不可逆过程引起熵的增加. 熵 流: dSe与外界交换中流入系统的熵(可能有负熵).
S : 熵, (单位 J/K) ; K: 波耳兹曼常数 ; Ω: 微观态数.
2. 熵增: 孤立系统中的一切实际过程都是熵的增加过程.
原理:
d S >0
从状态 1Æ 状态2 熵增为
∆S2 = S2 − S1 = K ln Ω2 − K ln Ω1 = K 若孤立系统进行的是可逆过程,则熵相等.
ln
Ω2 Ω1
dS = dSi + dSe
(三) 熵的宏观表示
熵与过程无关,设计一可逆等温过程, 是气体有状态(T,V1)Æ(T,V2).
可逆等温过程: QT
与(1)式比较: ∆S =
= υRT ln
υRlnV2
V2 V1
V1
∴∆S =QT /T
对无限小过程:(可逆等温)dS = dQ / T
d Q是无限小可逆过程,从外界吸收的热量. T 是系统的温度.
第八节 热力学第二定律的统计意义
和熵的概念
(一) 热二定律的统计意义 (微观态 宏观态)
. VA=VB 任一分子在热运动中出现于A或B的机会相等, 出现 的概率都是1/2. N个分子在A和B中共有2N种分配方式, 而每种分配方式出现的概率都是1/2N .
热力学第二定律

二. 熵(entropy)S
dQ T 0 R
1 R2 R1
2
存在一个与过程 无关的状态量
( 2)
p
d Q (1) d Q T T 0 (1) ( 2)
R1 R2
0
( 2)
V
d Q ( 2) d Q ( 2) d Q 令 S2 S1 S T T T (1) (1) (1) R1 R2 R —任意可逆过程 熵增(量)
10
二 . 不可逆过程是相互沟通的 热二律的 开氏表述
功全部转换成热而不产生其 它影响的过程是不可逆的
(否则热全部转换为功而不产生其它影响成立, 这就违背了热二律的开氏说法。) 热二律的 克氏说法 有限温差热传导不可逆
开氏、克氏 表述的等价
功、热转换 的不可逆性
热传导的 不可逆性
11
实际上,一切不可逆过程都是相互沟通的。 例如: 功变热而不产生其他影 响之不可逆(开氏表述) 可导出 证明: T
25
SCu
Q吸 mc(T1 T2 ) 水恒温吸热:S水 0 T2 T2 T1 T1 S总 S水 SCu mc( 1 ln ) 0(自己证) T2 T2
dT T2 mc mc ln 0 T T1 T1
T2
[例2] 已知: 1mol理气经绝热自由膨胀体积加倍
气体
气体自由膨 胀之不可逆
T
Q T
绝热壁
A=Q 等 价
Q
气体
A=Q
设气体能 气体 T 自动收缩 导致
循环,无变化
不成立 不成立 任何一种不可逆过程的表述,都可作为热力学第 二定律的表述! 12
§4.4 卡诺定理(Carnot theorem)
第六章热力学第二定律

第六章热力学第二定律Second law of thermodynamics ⏹6.1热力学第二定律⏹6.2热现象过程的不可逆性⏹6.3热力学第二定律的统计意义⏹6.4卡诺定理(Carnot theorem)⏹6.5热力学温标(thermodynamic temperature scale)⏹6.6应用卡诺定理的例子⏹*6.7熵(entropy)⏹*6.8熵增加原理(principle of entropy increase)⏹*6.9 熵与热力学几率(thermodynamics probability)6.1 Second law of thermodynamics热力学第一定律给出了各种形式的能量在相互转化过程中必须遵循的规律,但并未限定过程进行的方向。
观察与实验表明,自然界中一切与热现象有关的宏观过程都是不可逆的,或者说是有方向性的。
例如,热量可以从高温物体自动地传给低温物体,但是却不能从低温传到高温。
对这类问题的解释需要一个独立于热力学第一定律的新的自然规律,即热力学第二定律。
●The first law指出:一切热力学过程都应满足能量守恒。
但满足能量守恒的过程是否一定都能进行?●The second law将告诉我们,过程的进行有方向性,满足能量守恒的过程不一定都能进行。
●The second law是在研究如何提高热机效率的推动下逐步被发现的。
提高的热机效率问题成为十九世纪生产中的重要课题。
Two statements of the second law 热功转换传热1851年开尔文-普朗克表述热功转换的角度1850年克劳修斯表述热量传递的角度Kelvin-Planck statement (1851):不可能从单一热源取热,并使之完全转变为有用功而不产生其它影响。
“单一热源”是指温度均匀并且恒定不变的热源若热源不是单一热源,则工作物质就可以由热源中温度较高的一部分吸热而往热源中温度较低的另一部分放热,这样实际上就相当于两个热源。
热学-统计物理6 第6章 热力学第二定律

热功转换
3. 热传导
两个温度不同的物体放在一起,热量将自动地由高温物体 传向低温物体,最后使它们处于热平衡,具有相同的温度。 温度是粒子无规热运动剧烈程度即平均平动动能大小的宏观 标志。初态温度较高的物体,粒子的平均平动动能较大,粒 子无规热运动比较剧烈,而温度较低的物体,粒子的平均平 动动能较小,粒子无规热运动不太剧烈。若用粒子平均平动 动能的大小来区分它们是不可能了,也就是说末态与初态比 较,两个物体的系统的无序度增大了,这种自发的热传导过 程是向着无规热运动更加无序的方向进行的。
热机Q2
A , A
E
Q1
Q1
T1
A Q2
Q1 可
逆 热 机
T2 E’
用反证法,假设
得到
A A Q1 Q1
Q1 Q1
Q1 Q2 Q1 Q2
Q2 Q2
两部热机一起工作,成为一部复合机,结果外界不对复合
机作功,而复合机却将热量 Q1 Q2 Q1 Q2 从低温热源送到高温热源,违反热力学第二定律。
自然界中的自发热传导具有方向性。
通过某一过程,一个系统从某一状态变为另一状态, 若存在另一过程,能使系统与外界同时复原,则原来的过 程就是一个可逆过程。否则,若系统与外界无论怎样都不 能同时复原,则称原过程为不可逆过程。单摆在不受空气 阻力和摩擦情况下的运动就是一个可逆过程。
注意:不可逆过程不是不能逆向进行,而是说当过程逆向 进行时,逆过程在外界留下的痕迹不能将原来正过程的痕 迹完全消除。
现在考虑4个分别染了不同颜色的分子。开始时,4个分 子都在A部,抽出隔板后分子将向B部扩散并在整个容器内无 规则运动。隔板被抽出后,4分子在容器中可能的分布情形如 下图所示:
热力学第二定律的统计解释
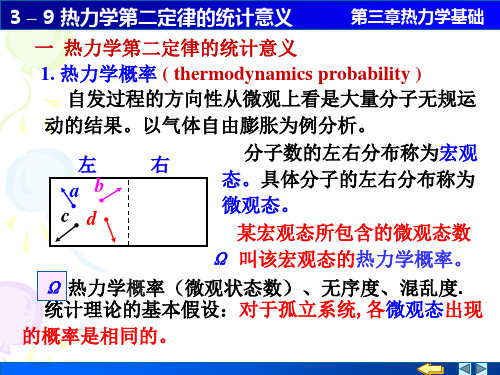
3 – 9 热力学第二定律的统计意义
第三章热力学基础
N1
2
4
N
Ω
(左)
2
22
24
2N
0
N个分子,Ωi
2 N。
若N=100, 则:
Ωi 2100 1030
而左右各半的平衡态及其附近宏观态的热力学概率则
占总微观状态数的绝大比例。 Ω(N左)
一般热力学系统 N的数量级约
N 很大
为1023,上述比例实际上是百分
概率小的状态
概率大的状态
讨论 N 个粒子在空间的分布问题
可分辨的粒子集中在 左空间的概率
N 1, 2
N 2, 4
3 – 9 热力学第二定律的统计意义
第三章热力学基础
b Aa
B
cd
ab
bc
c
a dcd
a bd
a bd
c
1 1264
A
bBa
cd
bd c
a
ab
c d
分子的分布
容器 A
的部
分B
设 S f(),求 f 的函数形式。
由 S 的可加性来分析:
1 S1, 1
1+2
S,
2 S2, 2 1、2彼此独立
∴ 应有: f( ) ln
3 – 9 热力学第二定律的统计意义
第三章热力学基础
S k ln
─ 玻耳兹曼熵公式
1877年玻耳兹曼提出了S ln 。
1900年普朗克引进了比例系数 k 。
ab cd
0
0a
b
c
d
bc ac ab a a d d d bc b
abbc cd d
热力学第二定律统计意义

S = k logW
劳厄: 劳厄:“熵与概率之间的联系是物理学 的最深刻的思想之一。 的最深刻的思想之一。” 熵是一个古老而又年轻的概念。说它古老, 熵是一个古老而又年轻的概念。说它古老, 因为早在100多年前(1854年 100多年前 因为早在100多年前(1854年)就已有人提到了 说它年轻,是因为它有极强的生命力, 它;说它年轻,是因为它有极强的生命力,正 日益广泛地渗透到许许多多的科技领域及日常 生活之中。 生活之中。 熵概念的泛化
说明 熵增原理只能应用于孤立系统,对于开放系统, 熵增原理只能应用于孤立系统,对于开放系统, 熵是可以减少的。 熵是可以减少的。
玻尔兹曼 (Ludwig Boltzmann,1844Boltzmann,18441906) 1906)奥地利理论 物理学家, 物理学家,经典统 计物理学的奠基人 之一。 之一。在它的墓碑 上寓意隽永地铭刻 着
气体分子位置的分布规律
3个分子的分配方式 左半边 右半边 abc 0 ab c bc a ac b a bc
•a •b •c
气体的自由膨胀
b
c
0
ac
ab
abc
(微观态数 3, 宏观态数4, 每一种微观态概率(1 / 23) ) 微观态数2 宏观态数 每一种微观态概率 微观态数 微观态概率 微观态: 微观态: 在微观上能够加以区别的每一种分配方式 宏观态: 宏观态: 宏观上能够加以区分的每一种分布方式 对于孤立系统, 对于孤立系统,各个微观态出现的概率是相同的
增熵乃自然趋势 孔尚任《桃花扇》 孔尚任《桃花扇》 “眼见他起高楼”,起楼是从无序到有序的减 眼见他起高楼” 眼见他起高楼 熵过程,乃逆自然而动; 熵过程,乃逆自然而动; “眼见他楼塌了”,楼塌是从有序到无序的增 眼见他楼塌了” 眼见他楼塌了 熵过程,乃自然趋势。 熵过程,乃自然趋势。 “破坏容易建设难”,热力学第二定律在起作用。 破坏容易建设难” 热力学第二定律在起作用。 破坏容易建设难
热力学第二定律的本质和熵的统计意义

微观状态数的总和
例如:有4个不同颜色的小球a,b,c,d分
装在两个盒子中,总的分装方式应该有16种。 因为这是一个组合问题,有如下几种分配
方式,其热力学概率是不等的。
分配方式
分配微观状态数
(4, 0) C44 1 (3,1) C43 4 (2, 2) C42 6 (1,3) C41 4 (0, 4) C40 1
热力学第二定律的本质和熵的统计意义
热力学第二定律的本质
热与功转换的不可逆性 热是分子混乱运动的一种表现,而功是分子 有序运动的结果。 功转变成热是从规则运动转化为不规则运动, 混乱度增加,是自发的过程; 而要将无序运动的热转化为有序运动的功就 不可能自动发生。
热力学第二定律的本质 气体混合过程的不可逆性 将N2和O2放在一盒内隔板的两边,抽去隔板, N2和O2自动混合,直至平衡。 这是混乱度增加的过程,也是熵增加的过程, 是自发的过程,其逆过程决不会自动发生。
热力学第二定律的本质
热传导过程的不可逆性
处于高温时的系统,分布在高能级上的分子 数较中;
而处于低温时的系统,分子较多地集中在低 能级上。
当热从高温物体传入低温物体时,两物体各 能级上分布的分子数都将改变,总的分子分布的 花样数增加,是一个自发过程,而逆过程不可能 自动发生。
热力学第二定律的本质
从以上几个不可逆过程的例子可以看出:
一切不可逆过程都是向混乱度增加的方向进行, 而熵函数可以作为系统混乱度的一种量度,
这就是热力学第二定律所阐明的不可逆过程 的本质。
熵和热力学概率的关系——Boltzmann公式
热力学概率就是实现某种宏观状态的微观状
态数,通常用 表示。
数学概率是热力学概率与总的微观状态数之比。
第六章-热力学第二定律PPT课件

力学中称为方向性问题。
.
2
3,第二类永动机是不可能实现的
4,热力学第二定律与第一定律 相互独立互相补充
二,热力学第二定律的克劳修斯表述
克劳修斯(Rudolf Clausius,1822-1888),德国物理学家,对热力
学理论有杰出的贡献,曾提出热力学第二定律的克劳修斯表述和熵
的概念,并得出孤立系统的熵增加原理。他还是气体动理论和热力
.
4
3,更简单的克劳修斯表述:热量不可能自发地从低温热源传向高温热源。
通过以上内容,我们来判断以下说法正确与否:
① 功可变成热,热不能变成功。(若 对,举一例说明)
② 功可完全变成热,热不能完全变成功。(若不对,举一反例)
③ 功不能完全变成热,热能完全变成功。
④ 功可完全变成热,但要在外界作用下,热能完全变成功。
2,两种表述将的都是热和功的问题,功不仅限于机械功的广义 功,每一种功热转换过程也可以作为热力学第二定律的表述。
热力学第二定律不是若干典型热学事例的堆积仓库,物理定律也 不能停留在具体的表面描述,真正的热力学定律应当是对物理本 质的描述,不同的表述应当有共同的物理本质,热力学第二定律 应该有更好的叙述。
第六章,热力学第二定律
问题的引入:
1,焦耳理论与卡诺热机理论的矛盾:同属能量转换, 有用功变热可以全部实现,为什么反过来就不能全部 实现,能量转换与守恒定律可没有这样的限制。
2,热机效率始终小于1并不全是技术原因
3,大量与热有关的自然过程仅靠热力学第一定律是不 足以解释的:1)热传递是不可逆的;2)电影散场后, 观众自发离开影院走向各方,却不能自发地重新聚集在 原来的电影院; 3)空气自由膨胀不能自发收缩等。
小结:上述三个不可逆过程,在推理过程中,很容易找到使系统 复原的方法,但这种情况并不多见,并且花费很多精力时间去寻 找系统复原的方法,很不经济。所以,我们必须借助其他方法。
热力学第二定律

§10.8热力学第二定律一、热力学第二定律任务自然界中发生的过程总是有方向的。
热力学第二定律正是反映了自然界中热力学过程的方向性问题,是自然界经验的总结。
二、热力学第二定律的两种表述 1、开尔文表述(开氏表述):不可能制成一种循环动作的热机,只从单一热源吸取热量,使它完全变为有用功而不引起其它变化。
说明:1)前提:即工作物质必须循环动作和其它物体不发生任何变化。
2)开尔文说法是从功热转化的角度出发的,它揭示了功热转换是不可逆的,即3)开尔文表述可等价说成“第二类永动机是不可能制造出来的。
” 2、克劳修斯表述(克氏表述):热量不可能自动地从低温物体传到高温物体。
注意:1)条件:“自动地”2)表明热传递的不可逆性 3、两种表述的等效性1)开尔文说法不成立,则克劳修斯说法也不成立;若开氏说法不成立,则热机可从高温热源吸收热量Q 1,全部用来对外作功A= Q 1;这个功A 可用来驱动一台致冷机,从低温热源吸收热量Q 2,同时向高温热源放出热量Q 2+ A= Q 2+ Q 1。
两者总的效果是低温热源的热量传到了高温热源,而没产生其它影响,显然违反了克劳修斯说法。
2)克劳修斯说法不成立,则开尔文说法也不成立;若克劳修斯说法不成立,即热量可自动地从低温热源传到高温热源。
考虑一台工作于高温热源与低温热源的热机。
从高温热源吸收热量Q 1,向低温热源放出热量Q 2,则Q 2能自动地传到高温热源;两者总的效果是热机把从高温热源吸收的热量全部用来对外作功,这显然违反开氏说法。
由此,可以看出热力学第二定律的表述是多种多样的,而且不同的表述是可以相互沟通的。
三、热力学第二定律的本质 1、可逆过程与不可逆过程一个热力学系统经历一个过程P ,从状态A 变到状态B ,若能使系统进行逆向变化,从状态B 又回到状态A ,且外界也同时恢复原状,我们称过程P 为可逆过程;反之,如果用任何方法都不能使系统和外界完全复原,则称为不可逆过程。
热学练习题

热学练习题16(总18页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、填空题1、系统在条件下,宏观性质的状态叫热力学平衡态。
2、系统在外界影响的条件下,不随时间改变的状态叫热力学平衡态。
3、处于热力学平衡状态的热力学系统,不随时间改变,因此系统的宏观物理量具有确定的。
4、为了表示处于的不同系统具有一个共同的宏观性质,引入了温度概念。
温度与状态参量的关系方程称为。
5、热力学第零定律告诉我们:如果两个热力学系统中的与第三个热力学系统处于,则它们彼此也必定处于。
热力学第零定律的数学表示叫。
6、温度是表示互为热平衡的系统具有共同的物理量;一切互为热平衡的系统都具有相同的。
温度是状态参量的,当系统的状态确定时,系统的温度。
7、建立一种经验温标需要选择;规定;规定,统称为建立温标的三要素。
8、用固定点相同的不同经验温标测量同一物体的温度,所测量的温度值一般,这是由于它们所选用的测温物质,或所选用的测温属性。
(相同或不同)9、定容气体温度计的测温公式为,定压气体温度计的测温公式为,它们与热力学温标所选的固定点(相同或不同)。
10、两只经验温度计用同种标度方法定标,用来测量同一物体的温度,其数值(一定;不一定)相同。
11、定容理想气体温标的测温公式为,定压理想气体温标的测温公式为,用不同的理想气体温标测量同一对象的温度结果(相同或不同)。
理想气体温标能够测温范围为至。
12、摄氏温标与热力学温标的换算关系为 ,摄氏温标的零度相当于热力学温标的 度。
13、量热的基本方法是 法,必须测出的物理量有 和 ,必须使用的仪器有 , 和 。
14、1摩尔气体的范德瓦耳斯方程为 ,其中 表示1摩尔气体所占有的空间, 表示1摩尔气体分子中心可以自由活动的空间。
15、1摩尔气体的范德瓦耳斯方程为 ,其中m V 表示1摩尔气体 的空间,)(b V m -表示1摩尔气体分子 的空间。
16、范德瓦尔斯程()RT b V V a p m m =-⎪⎪⎭⎫ ⎝⎛+2方程中,a 是考虑气体分子间 而引进的修正系数,b 是考虑到气体分子间 对气体分子的 空间进行的修正量。
河北科技大学大学物理答案第9章

第9章思考题9-1 理想气体物态方程是根据哪些实验定律导出的,其适用条件是什么?9-2内能和热量的概念有何不同?下面两种说法是否正确?(1) 物体的温度愈高,则热量愈多;(2) 物体的温度愈高,则内能愈大?9-3 在p-V图上用一条曲线表示的过程是否一定是准静态过程?理想气体经过自由膨胀由状态(p1,V1,T1)改变到状态(p2,V2,T1),这一过程能否用一条等温线表示。
9-4有可能对物体传热而不使物体的温度升高吗?有可能不作任何热交换,而系统的温度发生变化吗?9-5在一个房间里,有一台电冰箱在运转着,如果打开冰箱的门,它能不能冷却这个房间?空调为什么会使房间变凉?9-6根据热力学第二定律判别下列两种说法是否正确?(1) 功可以全部转化为热,但热不能全部转化为功;(2) 热量能够从高温物体传到低温物体,但不能从低温物体传到高温物体。
9-7 一条等温线和一条绝热线是否能有两个交点?为什么?9-8 为什么热力学第二定律可以有许多不同的表述?9-9 瓶子里装一些水,然后密闭起来。
忽然表面的一些水温度升高而蒸发成汽,余下的水温变低,这件事可能吗?它违反热力学第一定律吗?它违反热力学第二定律吗?9-10有一个可逆的卡诺机,以它做热机使用时,若工作的两热源温差愈大,则对做功越有利;当作制冷机使用时,如果工作的两热源温差愈大时,对于制冷机是否也愈有利?(从效率上谈谈)9-11可逆过程是否一定是准静态过程?准静态过程是否一定是可逆过程?有人说―凡是有热接触的物体,它们之间进行热交换的过程都是不可逆过程。
‖这种说法对吗?9-12如果功变热的不可逆性消失了,则理想气体自由膨胀的不可逆性也随之消失,是这样吗?9-13热力学第二定律的统计意义是什么?如何从微观角度理解自然界自发过程的单方向性?9-14西风吹过南北纵贯的山脉:空气由山脉西边的谷底越过,流动到山顶到达东边,在向下流动。
空气在上升时膨胀,下降时压缩。
若认为这样的上升、下降过程是准静态的,试问这样的过程是可逆的吗?9-15 一杯热水置于空气中,他总要冷却到与周围环境相同的温度。
热力学第二定律

不可能把热从低温 物体传到高温物体, 而不引起其它变化
热力学第二定律
1、阐明热力学第二定律的开尔文表述 和克劳修斯表述。论证两种表述的一致 性。 2、介绍可逆过程、不可逆过程的概念。 3、通过气体自由膨胀的微观过程,分 析揭示实际宏观过程的不可逆的原因, 从而阐明热力学第二定律的统计意义。
热力 学第 二定 律的 文字 表述
热力学第一定律
能量守恒与转换定律
能量之间数量的关系
所有满足能量守恒与转换定律 的过程是否都能自发进行
热力学第一定律有两方面的问题没有涉及到:
自发过程的方向性
自发过程:不需要任何外界作用而自动进 行的过程。
热量由高温物体传向低温物体
摩擦生热 水自动地由高处向低处流动 电流自动地由高电势流向低电势
与平衡态的微小偏离,就是涨落(始终存在)。
(二).热力学概率: 某一宏观状态对应的微观状态数叫该 宏观状态的热力学概率..
全部分子自动收缩到左边的 宏观状态出现的热力学概率: 当分子数 N=4 时, 热力学概率=(1/16)=1/24. 当分子数 N=NA(1摩尔)时, 热力学概率
1 1 23 0 NA 610 2 2
热力学第二定律
Back
续上
A B A B
1
4
1/16
4/16
6
6/16
4
4/16 1/16
共 16 种微观态
5 种宏观态
1
6 5 4 3
左4 左3 左2 左1 左0 4个粒子分布
右0 右1 右2 右3 右4
2 1 0
按统计理论的基本假设:对于孤立系统, 各微观状态出现的概率是相同的. 总微观状态数16:
热力学第二定律的统计意义

热力学第二定律的统计意义热力学第二定律是热力学中的一条基本定律,它表明在自然界中存在着一种趋势,即热量自热源向周围环境传递,而不会自动从低温体传向高温体,因此熵(或热力学不可逆性)总是增加的。
然而,这个定律的本质并不明确,这导致了许多学者对它的解释存在争议。
随着物理学的发展,人们发现这个定律与热力学的统计基础有着密切的关系。
首先,我们需要理解热力学中一个基本概念——熵。
熵是一种用来度量系统无序程度的物理量,表示了体系各个微观状态的分布不均匀程度。
通常来说,系统内互相独立的微观变化越多,其熵就越大。
例如,对于一个有序的水晶,在所有原子处于完美排列状态时,其熵最小。
而当温度升高时,原子会破坏这个有序状态,等效于增加了水晶的“混乱程度”,其熵也就增加了。
热力学第二定律实际上是在告诉我们一个事实:任何一个完全隔离的系统,熵不可能永远减少。
也就是说,熵的增加是一个不可逆的过程,这也是热量从高温体传向低温体时熵增加的原因。
概括而言,该定律表明了一个趋势,即系统中的能量将倾向于从高能量的状态向低能量的状态流动,从而使得系统的熵增加。
从统计学的角度来看,热力学第二定律是由这样一个事实推导而来的:在一个大的体系中,微观粒子的随机运动会经常导致某些相对独立事件的不完全或无法恢复性,这些事件包括:1. 分子/原子的碰撞: 分子或原子相互碰撞时,有一部分能量被转移给周围环境中的分子,这会导致大的系统中的能量总体降低;2. 动能的分布: 分子的运动速度分布不服从热力学平衡状态的Maxwell-Boltzmann分布时,也将导致无序增加;3. 热交换: 热量从高温体向低温体传递时,热力学不可逆性也将随之增加。
以上这些现象都会导致系统设在某个起始状态后一段时间后回不到原始状态的情况,这也就是在热力学第二定律中所描述的不可逆性增加。
这个过程是由大量微观粒子的无序运动造成的,也被称为热力学平衡状态的降解。
总体来说,热力学第二定律的统计意义是,它实际上是对许多微观随机过程导致的热力学不可逆性增加的描述。
热力学第二定律的统计意义

热力学第二定律的统计意义
热力学第二定律是热力学中的一个基本定律,它描述了热能的转化过程中存在的不可逆性。
热力学第二定律的统计意义是将宏观不可逆过程与微观粒子运动的随机性联系起来,从而解释热力学第二定律的基本原理。
在热力学中,熵是一个重要的概念,它描述了系统中的混乱程度。
热力学第二定律可以被表述为熵在任何一个孤立系统中总是增加的原则。
这个原则可以通过微观粒子的随机热运动来解释。
在一个系统中,随着时间的推移,分子的位置和速度会随机变化,使得系统的状态逐渐变得更为混乱。
因此,熵增加代表着系统的混乱程度增加,也就是更接近于平均状态。
此外,热力学第二定律还可以通过热力学概率来解释。
热力学概率是指一个系统处于某个状态的概率。
根据热力学第二定律,处于高熵(即更为混乱)状态的概率更大,因为这样的状态更接近于平均状态。
这也反映了分子热运动的随机性,即处于高熵状态的概率更大,因为更多的状态都是高熵状态。
总之,热力学第二定律的统计意义是将宏观的不可逆过程与微观粒子的随机性联系起来,从而解释热力学第二定律的基本原理。
这个原理可以通过系统中的熵增加、分子热运动的随机性以及热力学概率等方面来进行解释。
热力学第二定律的微观解释

分布
详细分布
(宏观态) (微观态)
AB
1
4
6
4
3
1
微观态共有24=16种可能的方式,而且4个分子全 部退回到A部的可能性即几率为1/24=1/16。
一般来说,若有N个分子,则共2N种可能方式,而 N个分子全部退回到A部的几率1/2N.对于真实理想气 体系统N1023/mol,这些分子全部退回到A部的几率
下面从统计观点探讨过程的不可逆性微观意义,并
•由此深入认识第二定律的本质。 不可逆过程的统计性质(以气体自由膨胀为例)
一个被隔板分为A、B相等两部分的容器,装有4
个涂以不同颜色分子。
2
开始时,4个分子都在A部,抽出隔板后分子将向B部
扩散并在整个容器内无规则运动。隔板被抽出后,4
分子在容器中可能的分布情形如下图所示:
•第二定律的统计表述(依然看前例)
左边一列的各种分布仅指出A、B两边各有几个分子,
代表的是系统可能的宏观态。中间各列是详细的分布,
具体指明了这个或那个分子各处于A或B哪一边,代表
的是系统的任意一个微观态。 分布 4个分子在容器中的分布对应5种 (宏观态)
详细分布 (微观态)
宏观态。一种宏观态对应若干种微观态。
顿写一封内容尖刻的信回敬那家伙。 “可以狠狠地骂他一顿。”林肯说。 斯坦顿立刻写了一封措辞强烈的信,然后拿给总统看。 “对了,对了。”林肯高声叫好,“要的就是这个!好好训他一顿,真写绝了,斯坦顿。” 但是当斯坦顿把信叠好装进信封里时,林肯却 叫住他,问道:“你要干什么?” “寄出去呀。”斯坦顿有些摸不着头脑了。 “不要胡闹。”林肯大声说,“这封信不能发,快把它扔到炉子里去。凡是生气时写的信,我都是这么处理的。这封信写得好,写的时候你己经解了气,现在感觉好
热力学第二定律的统计意义

与热力学第二定律的统计表述相比较
熵与热力学 几率有关
玻尔兹曼建 立了此关系
越大,微观态 数就越多,系统 就越混乱越无序。
玻尔兹曼公式:S = k ln
(k为玻尔兹曼常数)
熵的微观意义:系统
热力学第二定律的统计意义
从统计观点探讨过程的不可逆性和熵的微观意义, 由此深入认识第二定律的本质。
不可逆过程的统计性质
(以气体自由膨胀为例) 一个被隔板分为A、B相等两部分的容器,装有 4个涂以不同颜色分子。 开始时,4个分子都在A部,抽出隔板后分子将 向B部扩散并在整个容器内无规则运动。 隔板被抽出后,4分子在容器中可能的分布情形 如下图所示:
平衡态相应于一定宏观 条件下 最大的状态。
热力学第二定律的统计表述: 孤立系统内部所发生的过程总是从包含微观态 数少的宏观态向包含微观态数多的宏观态过渡, 从热力学几率小的状态向热力学几率大的状态 过渡。
熵的微观意义和玻尔兹曼公式
宏观热力学指出:孤立系统内部所发生的过 程总是朝着熵增加的方向进行。
在上例中,均匀分布这种宏观态,相应的微 观态最多,热力学几率最大,实际观测到的 可能性或几率最大。对于1023个分子组成的 宏观系统来说,均匀分布这种宏观态的热力 学几率与各种可能的宏观态的热力学几率的 总和相比,此比值几乎或实际上为100%。 因此,实际观测到的总是均匀分布这种宏观 态。即系统最后所达到的平衡态。
对单个分子或少量分子来说,它们扩散到B部 的过程原则上是可逆的。但对大量分子组成的 宏观系统来说,它们向B部自由膨胀的宏观过 程实际上是不可逆的。这就是宏观过程的不可 逆性在微观上的统计解释。
第二定律的统计表述
(依然看前例) 左边一列的各种分布仅指出A、B两边各有几 个分子,代表的是系统可能的宏观态。 中间各列是详细的分布,具体指明了这个或那 个分子各处于A或B哪一边,代表的是系统的 任意一个微观态。 4个分子在容器中的分布对应5种宏观态。 一种宏观态对应若干种微观态。 不同的宏观态对应的微观态数不同。 均匀分布对应的微观态数最多。 全部退回A边仅对应一种微观态。
热力学第二定律

宏观上解释: 宏观上解释: 功转换为热,是机械能(或电能)转化为内能的过程。 功转换为热,是机械能(或电能)转化为内能的过程。 微观上解释: 微观上解释: 功热转换过程是大量分子有序运动向无序运动转化的过程。 功热转换过程是大量分子有序运动向无序运动转化的过程。
注 意 1 热力学第二定律是大量实验和经验的总结. 热力学第二定律是大量实验和经验的总结.
二。热力学第二定律的宏观表述
1。自然过程的方向性 。 说明孤立系自然过程进行方向的规律是热二定律
m
功热转换过程具有方向性。 功热转换过程具有方向性。 热不能自动转化为功; 热不能自动转化为功; 或通过摩擦而使功变热的过程是不可逆的irreversible 或通过摩擦而使功变热的过程是不可逆的
热传导 (Heat conduction) ) 热量不能自动地由低温物体传向高温物体。 热量不能自动地由低温物体传向高温物体。 热量由高温物体传向低温物体的过程是不可逆的; 热量由高温物体传向低温物体的过程是不可逆的;
气体的 气体体积2 气体体积2 气体体积1 气体体积1 自由扩散 不能自由压缩
自发转化 自发转化 摩擦做功 不能自发 一切与热现象有关的实际宏观过程都是不可逆的! 一切与热现象有关的实际宏观过程都是不可逆的! 物体内能
功热转换
⑴.可逆过程与不可逆过程 在系统状态变化过程中, 在系统状态变化过程中,如果逆过程能重复 正过程的每一状态,而不引起其他变化, 正过程的每一状态,而不引起其他变化,这样的 过程叫做可逆过程 可逆过程。 过程叫做可逆过程。 在不引起其他变化的条件下,不能使逆过程 在不引起其他变化的条件下, 重复正过程的每一状态, 重复正过程的每一状态,或者虽能重复但必然会 不可逆过程。 引起其他变化,这样的过程叫做不可逆过程 引起其他变化,这样的过程叫做不可逆过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一切自发过程的普遍规律
概率小的状态
概率大的状态
讨论 N 个粒子在空间的分布问题
可分辨的粒子集中在左空间的概率 N = 1, W = 1 2
N = 2, W =1 4
可分辨粒子总数 N = 4 n1 1
第 i 种分布的可能状态数 ni
n2 4 各种分布的状态总数 ni 16
n3 6
i
粒子集中在左空间的概率
n3 4
W
1 16
1 24
n5 1 粒子均匀分布的概率
W' 6 3 16 8
N1
2
4
N
1
1
1
1
(W左) 2
22
24
2N
0
三 熵与热力学概率 玻耳兹曼关系式
熵
S k lnW
W 热力学概率(微观状态数)、 无序度、混乱度.
(1)熵的概念建立,使热力学第二定律 得到统一的定量的表述 .
(2)熵是孤立系统的无序度的量度.(平 衡态熵最大.)(W 愈大,S 愈高,系统无序 度愈高.)
玻耳兹曼的墓碑
为了纪念玻耳兹 曼给予熵以统计解释 的卓越贡献 ,他的 墓碑上寓意隽永地刻
着 S k lnW
这表示人们对玻耳兹 曼的深深怀念和尊敬.
耗散结构 (1)宇宙真的正在走向死亡吗?
实际宇宙万物,宇宙发展充满了无序 到有序的发展变化 .(2) Fra bibliotek命过程的自组织现象
生物体的生长和物种进化是从无序到 有序的发展.
一 熵与无序
热力学第二定律的实质:自然界一
切与热现象有关的实际宏观过程都是不可
逆的 .
热功转换 功
完全 热
不完全
有序
无序
热传导 高温物体 自发传热 低温物体 非自发传热
非均匀、非平衡
均匀、平衡
扩散过程
自发
V 外力压缩 V V
二 无序度和微观状态数
不可逆过程的本质
系统从热力学概率小的状态向热力学 概率大的状态进行的过程 .
