第七章-非线性动力学与混沌
非线性动力学中的混沌与分岔现象

非线性动力学中的混沌与分岔现象混沌现象的介绍混沌现象是非线性动力学中一个重要的研究课题,它描述了一种似乎随机的、无规律可循的运动状态。
在混沌现象的研究中,人们发现了一些特征,如灵敏依赖于初始条件、无周期运动和封闭轨道等。
混沌现象的研究对于理解自然界中的复杂系统行为具有重要的意义。
混沌现象最早是由美国数学家Edward Lorenz于20世纪60年代发现的。
他在研究气象学中的大气运动方程时,意外地发现了不确定性的现象。
这个发现被称为“蝴蝶效应”,即当一个蝴蝶在巴西振动翅膀时,可能引发一系列的气流变化,最终导致美国得克萨斯州的一个龙卷风的形成。
这个例子说明了混沌现象中初始条件的微小变化可能引起系统运动的巨大变化。
混沌现象的数学表示混沌现象可以用一些非线性动力学方程描述。
这些方程通常包含了一些非线性项,使得系统的演化不再是简单的线性叠加。
一个经典的混沌系统方程是Lorenz方程:\\frac{{dx}}{{dt}} = \\sigma(y - x),\\frac{{dy}}{{dt}} = x(\\rho - z) - y,\\frac{{dz}}{{dt}} = xy - \\beta z其中,x、y和z是系统的状态变量,t是时间。
σ、ρ和β是一些常数,它们决定了系统的性质。
这个方程描述了一个三维空间中的运动,这种运动就是混沌现象。
分岔现象的介绍分岔现象是混沌现象的一个重要特征,它描述了系统参数发生微小变化时,系统行为的剧烈变化。
简单来说,分岔现象就是系统从一个稳定的演化状态变成多个稳定状态的过程。
分岔现象的经典例子是Logistic映射。
Logistic映射是一种常用的非线性映射,它用于描述生物种群的增长。
Logistic映射的公式为:x_{n+1} = r \\cdot x_n \\cdot (1 - x_n)其中,x_n是第n个时刻的种群密度,x_{n+1}是下一个时刻的种群密度,r是系统的参数,它决定了种群的增长速度。
第七章 非线性动力学与混沌 讲义

2. 线性化方程组的解及其稳定性
12
111 21 1
122 222
试探解:1 Aet ,2 Bet
11
21
12
22
A B
0
ij
( fi x j
)0
11 12 0 21 22
2 T 0
T 11 22
系数矩阵的迹
11 22 12 21 系数行列式的值
特征根
❖ 刘式达,刘式适,《非线性动力学和复杂 现象》,气象出版社,1989
§7.1 引言
一. “非线性动力学”的表观含义
数学上:
f (x) ax b
f
(x)
ax2
bx
c
线性 非线性
定义:力或微分方程含有坐标或速度的非线性项的系 统,称为非线性动力学系统,反之称为线性动力学系统。
例:
mx kx 2x2
1. 定态解 xi 0 i 1,2, , n
x2
平衡点,奇点
x1
2. 发散解
xi 之一或几个随时间无限地偏离初值 x2
爆炸,散射
x1
3. 振荡解
既不趋于无穷大,也不终止于某一点,而是在一定区域内不断变化。
❖ 周期振荡
❖ 准周期振荡
x2 闭合曲线
x1
x2 非闭合曲线
x1
❖ 混沌
相轨迹没有确定的形状周 期、貌似随机的运动。
1,2 T
T 2 4 2
特征矩阵
A1 B1
A2 B2
1 c1 A1e1t c2 A2e2t
2
c1B1e1t
c2 B2e2t
渐进稳定
临界情况 不稳定
1,2 T
T 2 4 2
非线性振动系统的动力学行为

非线性振动系统的动力学行为引言振动是物体在固有频率下的周期性运动。
在自然界和工程领域中,非线性振动系统的研究具有重要意义。
非线性振动系统的动力学行为常常具有复杂性和多样性,如混沌、周期倍增等现象。
本文将探讨非线性振动系统的动力学行为,包括混沌、周期倍增和双稳态等方面。
一、混沌现象混沌是非线性振动系统中一种复杂的动力学行为。
与线性振动系统的周期性运动不同,混沌运动是无规律、无周期的。
混沌现象的出现是由于非线性振动系统中各种非线性项的相互作用导致的。
例如,双摆系统中的混沌现象是由于摆角的非线性耦合引起的。
混沌现象的研究对于理解非线性振动系统的行为具有重要意义。
二、周期倍增现象周期倍增是非线性振动系统中的另一种重要动力学行为。
周期倍增是指系统在某一参数变化的过程中,周期解的周期逐渐增加。
周期倍增现象常常出现在非线性振动系统的临界点附近。
例如,当驱动力的频率接近系统的固有频率时,非线性振动系统可能出现周期倍增现象。
周期倍增现象的研究对于预测和控制非线性振动系统的行为具有重要意义。
三、双稳态现象双稳态是非线性振动系统中的一种特殊现象。
双稳态现象是指系统在某一参数范围内存在两个稳定解。
这意味着系统可以在两个不同的状态之间切换。
双稳态现象的出现是由于非线性项的非线性饱和效应引起的。
例如,光纤中的非线性光学效应可以导致双稳态现象的出现。
双稳态现象的研究对于设计和优化非线性振动系统具有重要意义。
结论非线性振动系统的动力学行为具有复杂性和多样性。
混沌、周期倍增和双稳态是非线性振动系统中常见的动力学现象。
混沌现象是非线性振动系统中无规律、无周期的运动,周期倍增现象是系统周期解周期逐渐增加的现象,双稳态现象是系统存在两个稳定解的现象。
研究非线性振动系统的动力学行为对于理解和应用于实际问题具有重要意义。
总之,非线性振动系统的动力学行为是一个复杂而有趣的研究领域。
通过深入研究非线性振动系统的混沌、周期倍增和双稳态等现象,我们可以更好地理解和控制非线性振动系统的行为,为实际应用提供理论基础和指导。
非线性动力系统混沌运动的分析方法

非线性动力系统混沌运动的分析方法摘要混沌是近20多年来由于计算机的发展而新兴起来的学科。
它一出现,就很快在许多领域得到广泛应用,开阔和加深了人们对许多自然现象的认识。
混沌被誉为是继相对论和量子力学问世以来,二十世纪物理学中的第三次革命。
由于混沌是非线性动力学方程解的一种类型,混沌理论自然与非线性动力学理论紧密相关。
本论文在概述非线性系统和混沌运动特性的基础上,总结了混沌运动的研究方法:时程曲线、相平面图、Poincare映射、功率谱图、Lyapunov 指数和分岔。
以Van der Pol方程为数学模型,编制了计算机程序,利用时程曲线、相平面图、功率谱图和分岔的方法,研究了混沌现象在动力系统中的存在,分析了混沌现象演化的过程。
关键词:非线性系统, 混沌, 相平面, Poincare映射Analysis Methods Of Chaotic Motion InNonlinear Dynamic SystemSpecialty: Information and computing scienceStudent: Yang YadiAdvisor: Zhao FengqunABSTRACTChaos is a new and developing subject with the development of computer in recent more than twenty years. Once appears, it has been generally used in lots of fields. It widens and deepens people’s knowledge to many natural phenomena. Chaos is considered to be the third revolution in physics of the 20th century after the Theory of Relativity and quantum mechanics came out. Because chaos is a type of the solution of nonlinear dynamic equation, chaos theory has a close relation with nonlinear dynamic theory naturally.Nonlinear system and the chaotic motive Characteristics are briefly introduced; the research methods of chaotic motion are summed up in this paper: response curve, phase position map, Poincare mapping, power spectrum map, Lyapunov exponents and the bifurcation. Given an example of the Van der Pol equation, the computer programs are presented in this paper. The existence of the chaotic phenomenon in the dynamic system is proved by using the methods of response curve, phase position map, power spectrum map and the bifurcation, and the evolutionary process of the chaotic phenomenon is also analyzed.KEY WORDS: nonlinear system, chaos, phase position, Poincare mapping目录中文摘要 (i)英文摘要 (ii)1. 绪论 (1)1.1非线性系统与混沌 (1)1.2非线性系统与混沌研究的目的和意义 (2)1.3非线性系统与混沌研究的发展情况 (4)2.混沌及其特征 (6)2.1混沌的定义 (6)2.2混沌运动的特征 (6)2.3奇怪吸引子 (7)3.混沌的研究方法 (9)3.1时程曲线 (9)3.2相平面 (9)3.3庞加莱(Poincare)截面 (11)3.4功率谱 (12)3.5 Lyapunov指数 (17)3.6分岔 (20)4.混沌典型实例分析 (28)5. 结论 (31)致谢.................................................................................. 错误!未定义书签。
第七章 混沌—混乱中的秩序

伯努瓦· 曼德勃罗
混沌与分形
曼德布洛在1960~70年代研究复杂性时,发展出 碎形几何学。他称之为「分形」乃源自拉丁字 “fractus”,意在彰显这些形状的破碎与不规则。 碎形会展现自相似性。这也就是说,无论如何放大 它们,都长得很相似;一个结构的一小部份,看起 来就像整体一样。 自相似性有两种形式:精确的与统计的。假树 显示的图案,在不同放大尺度下都精确重复(下图 左栏)。真树的图案则不会精确重复,只有统计上 的重复(下图右栏)。几乎所有自然界的图案都遵 守统计上的自相似性,帕洛克的绘画亦然。
混沌的应用
1、混沌与艺术
2、混沌与经济学 3、混沌与学习
1、混沌与艺术
一位画家波洛克(杰克逊· 波洛克 Jackson Pollock ) 的创作
纪录片《他妈的,谁是波洛 克》
1948第五号
32
3.2
你觉得波洛克具 备绘画技巧吗?
《周易· 系辞》云:“形而上者谓之道,形而下者谓之 器。”自先秦以来,把造物活动归属于形而下范畴,在文 化观念上“重道轻器”思想历代并不鲜见,但当下的艺术 教育中“重器轻道”现象却相当普遍。
从科学的角度来看,“蝴蝶效应”反映了混沌运 动的一个重要特征:系统的长期行为对初始条件的 敏感依赖性。
一则西方寓言:
丢失一个钉子,坏了一只蹄铁;
坏了一只蹄铁,折了一匹战马; 折了一匹战马,伤了一位骑士; 伤了一位骑士,输了一场战斗; 输了一场战斗,亡了一个帝国。
马蹄铁上一个钉子是否会丢失,本是初始条件的十分微小 的变化,但其“长期”效应却是一个帝国存与亡的根本差别。 这就是军事和政治领域中的所谓“蝴蝶效应”。
A. 孙宙有序地存在之前的那种状态,无形的物质与无穷的空间都处于无 序之中。 B. 极端的混乱与无序。 C. 深远或无底洞。
非线性动力学混沌理论方法及其意义

非线性动力学混沌理论方法及其意义吴 彤(清华大学 科学技术与社会研究所,北京 100084) 摘 要:本文考察了非线性混沌的各类描述定义,研究了混沌的细致分类,讨论和研究了混沌特性以及判别混沌、寻找混沌征兆的方法,区别了混沌与噪声;对混沌理论的认识论和方法论意义进行了四方面的研究:混沌研究对复杂性研究的非线性方法论的意义,混沌和决定论与可预测性的关系,混沌边缘研究意义,建设和避免混沌的关系。
关键词:非线性;混沌;方法;可预测性中图分类号:F22410 文献标识码:A 文章编号:1000-0062(2000)03—0072-08 如果仔细考察人类在自己的生命演化过程中的关注,似乎有两个问题最重要,第一,如何预测未来,第二,是否能够预测未来,因果关系等问题均在此列。
第一个问题是实用性的,而第二个问题则是理论性的,它关系到一种原则和生活的意义。
20世纪中叶以后,当气象学家洛伦兹提出“蝴蝶效应”时,人们了解到,就是完全确定性的动力学方程,也仍然会出现随机性演化。
那么,如何预测未来呢?预测还可能吗?人们现在更害怕混沌理论打破他们对未来可预测性的幻想。
但是这种幻想实在是一种幻象。
其实,从休谟起,科学哲学对归纳问题本质的揭示已经对单一的决定论因果观念给出了不可能的回答。
有哪一个人知道自己的生命和生命之途将如何走向呢?哪一个生命的道路不是在生命演化过程中逐渐完成的呢?其实,宿命论与线性决定论的联系比与随机论的联系更强。
另一方面,也出现了相反的误读和误解。
人们以为,混沌理论如果正确,那么世界将完全不可预测。
似乎混沌理论助长了悲观主义。
其实,混沌理论的出现,一方面揭示了自然界和社会客观存在混沌,谁都无法避免;另一方面,混沌理论对混沌动力学系统的研究,恰恰帮助人们了解混沌现象,对“混沌”不混沌,才能处事(处世)不惊、不乱。
混沌理论在一定意上更支持了决定论,因为它把原来属于随机性的、偶然性的领域,也纳入到决定论的管辖范围内。
混沌理论在非线性动力学中的应用研究

混沌理论在非线性动力学中的应用研究在自然界和社会中,不少现象都呈现出难以预测的混沌态。
混沌现象一度被认为是无规则的,无法用科学方法解释和描述,但混沌理论的发展改变了这一观念,使得我们能够更好地理解并预测混沌现象。
如今,混沌理论已经在非线性动力学领域得到广泛应用。
什么是混沌理论?混沌现象是指一种非线性系统在微小因素下引起的复杂、随机的状态转换。
所谓混沌理论,就是指对混沌现象进行研究,找到其规律和特性的理论。
混沌理论的核心是混沌分形思想,即将混沌的非线性系统抽象成一些规则的几何图像,从而表述它们的结构和特性。
混沌理论的发展历程混沌理论的发展源于70年代。
当代生物学家洛伦茨在研究大气环流问题时得到了一组难以理解的计算结果。
洛伦茨发现,当他用一组非常简单的方程模拟空气流动时,该方程随着时间的变化轨迹从不同的起点展开后,结果却相差无几的奇怪现象。
这种结果使洛伦茨推断出,非线性系统的行为比我们一直认为的要复杂得多。
20世纪90年代初,混沌理论得到了进一步的发展。
通过大量的实验和模拟,研究者们发现:几乎任何的非线性系统都拥有某种形式的混沌现象。
此后,混沌理论在非线性动力学领域得到了大量应用。
混沌理论在非线性动力学中的应用研究非线性动力学是指由非线性系统引起的全部动力学研究。
非线性系统与线性系统的最大区别,在于前者的响应不仅取决于输入信号幅值,还取决于输入信号波形,即非线性系统的输出与输入信号之间存在非线性关系。
混沌理论在非线性动力学中具有重要的应用价值。
现在让我们从以下几个方面来说明。
1.混沌生物学混沌生物学是研究生态系统、种群动态、库仑生命现象等问题的一种新兴的生物学分支。
混沌生物学在描述生物种群量和生态系统变化时,采用了非线性动力学模型。
这些模型通过运用混沌理论,成功地描述了生态系统的特性和演化规律。
在生物多样性存亡问题上,混沌生物学研究可以辅助我们阐明生态系统演化的密度依赖和混沌稳定性。
2.混沌流体力学混沌流体力学是一种研究非线性动力学中的流体系统行为的学科。
第七章 非线性动力学与混沌 讲义

二. 决定性系统与不可预测性
1. 力学决定论及其伟大成就
x m F (x, x, t ) x x 0 , x x 0
t t0
x(t ), x(t )
存在且唯一, 可预测性
1757年,哈雷慧星(Hally comet)按预测回归。 1846年,海王星在预言的位置被发现。 今天,日月蚀的准确预测,宇宙探测器的成功发射与回收。
ij (
f i )0 x j
11 12 0 21 22
T 11 22 系数矩阵的迹 11 22 12 21 系数行列式的值
A1 B 1 A2 B2
T 0
2
特征根
1, 2
T T 2 4 2
xi f i ( x1 , x2 ,, xn )
i 1,2,, n
优点:
四. 相空间(相图)的概念
相空间,也就是状态空间,是由广义坐标和广义动量(速度) 张成的空间,也称相宇。相空间中运动状态的变化轨迹称为相图。
弹簧振子 通解
x 0 x
2 0
x A cos( 0t ) x1 x A0 sin(0t ) x2
设想一位智者在某一瞬间得知激励大自然所有力及组成它的物体 的相互位置,如果这位智者又能对众多的数据进行分析,把宇宙间最 庞大的物体和最轻微的原子的运动凝聚在一个公式中,没有什么事物 是不确定的,将来就像过去一样清晰地展现在眼前。
——拉普拉斯(Laplace,法国数学家,1749-1827)
2. 力学决定论不断受到挑战
x1 x, x2 x
x3 cos t , x4 x3
非线性振动力学中的混沌分析

非线性振动力学中的混沌分析近年来,混沌理论被广泛应用于非线性动力学领域,并在科学研究以及实际应用中发挥了重要作用。
在非线性振动力学中,混沌分析是一种非常有效的方法,旨在研究非线性动力学系统中的混沌现象。
1. 混沌现象简介混沌现象是指那些表现出一定规律性却又极其复杂、几乎无法预测的动态系统。
不像线性系统那样稳定、可预测和规律可循,混沌现象总是会呈现出一定的随机性。
具体而言,混沌现象常会出现于非线性振动力学系统中,这类系统的特征是运动既有局部稳定性,也存在不稳定性。
因此,很难用传统的数学方法来对这些非线性系统进行分析,在这种情况下,混沌分析成为了一种解决方案。
2. 混沌分析的基本原理混沌分析的基本原理是对非线性动力学系统的演变行为进行分析,从而揭示其混沌现象的本质规律。
具体而言,混沌分析常用的方法包括洛伦茨方程、延迟反馈系统、相空间重构等,其中相空间重构也是混沌分析的核心。
该方法将系统的多维状态空间重构成一个简化的流形空间,并进一步将这个流形空间划分成若干个相空间。
这样做的目的在于,将复杂的系统状态转化为易于分析的几何结构,从而分析系统的演变特征以及混沌行为。
3. 混沌分析的实际应用混沌分析的实际应用范围非常广泛,包括通信、控制、金融、生态、化学以及物理等领域。
在通信领域,混沌分析可以用于实现安全的数据传输。
由于混沌系统的不可预测性,使得数据传输更加安全可靠。
在控制领域,混沌分析可以用于实现高效的控制系统。
通过对一些复杂的控制系统进行混沌分析,可以有效地提高控制效率,进而优化生产效益。
在金融领域,混沌分析可以用于预测股市变化。
通过混沌分析,可以揭示出股市变化的本质规律,帮助投资者更好地做出投资决策。
在生态领域,混沌分析可以用于研究气候、生态系统的变化机理。
通过混沌分析,可以揭示出这些生态系统背后的混沌规律,从而采取更加合理的保护措施。
在化学领域,混沌分析可以用于研究化学反应动力学。
通过混沌分析,可以揭示出化学反应背后的混沌规律,有助于优化化学反应过程。
[经济学]非线性动力学浑沌说课讲解
![[经济学]非线性动力学浑沌说课讲解](https://img.taocdn.com/s3/m/fc77ec380812a21614791711cc7931b765ce7b48.png)
朱照宣,1987年,牛顿《原理》三百年祭
• “《原理》发表以来的三百年,牛顿力学经历了两 个阶段。前280年是一阶段。那时认为由运动微 分方程所确定的动态总是确定性的。……后20年 则是另一个阶段。以卡姆定理(KAM)为代表的浑 沌理论提示了决定论和随机论之间、牛顿力学和 统计力学之间没有不可逾越的界线。 ……不仅大 量粒子的系统要用统计力学,两个自由度的保守 系统运动也得用统计力学,连掷骰子本身也既是 决定论的又是概率论的。它从根本上为牛顿力学 摘除了‘机械论’的帽子。”(朱照宣 1987, 第12页)
费格尔
(Herbert Feigl,1902-1988)说
“A causes B” or “A is the cause of B” means that wherever and whenever A occurs it is followed (or attended) by B. Since a precise repetition of A may not be feasible (or discoverable), a less stringent formulation would use something like a mathematical limit process: The more the actual condition A' approximates the conceived (ideal) condition A, the more actual effect B' will approximate the (ideal) effect B.
• There are systems whose trajectories do not monotonically approximate any ideal state. They are sensitive dependence to initial conditions.
混沌与复杂动力系统中的数学方法与应用

混沌与复杂动力系统中的数学方法与应用在现代科学和工程领域中,混沌与复杂动力系统的研究日益受到关注。
混沌指的是一种看似随机、无序而又具有确定性的行为模式,而复杂动力系统则是由多个相互作用的部分组成的系统,其整体行为难以通过简单的规律描述。
为了理解和控制这些系统,数学方法被广泛应用。
本文将介绍混沌与复杂动力系统中常用的数学方法,并探讨它们在实际应用中的作用。
一、非线性动力学与混沌理论在混沌与复杂动力系统的研究中,非线性动力学是一个基础的理论框架。
非线性动力学研究的是非线性系统,即系统的响应不满足线性关系。
非线性动力学理论提供了描述和分析非线性系统行为的数学方法,对于混沌现象的研究起到了重要的作用。
混沌现象最早由美国数学家洛伦兹在20世纪60年代提出,他发现即使是简单的非线性系统,也可能出现极其敏感的依赖于初始条件的行为。
这种行为被称为“蝴蝶效应”,即微小的初始差异可能导致系统演化出完全不同的轨迹。
混沌理论通过数学方法描述了这种复杂而又确定的行为,如迭代映射和微分方程。
二、分形几何与自相似性分形几何是混沌与复杂动力系统中常用的数学工具之一。
分形几何研究的是具有自相似性质的几何图形,即整体和部分之间存在相似的结构。
分形几何的概念由法国数学家曼德博特在20世纪70年代提出,他发现了一类具有无限细节的几何图形,这些图形在任意缩放下都保持自身的形状。
分形几何在混沌与复杂动力系统的研究中有着广泛的应用。
例如,分形维度可以用来描述混沌系统的奇异吸引子的几何结构。
此外,分形几何还可以用来分析复杂系统的空间分布和形态,为理解复杂系统提供了新的视角。
三、网络理论与复杂网络复杂网络是由大量节点和连接构成的网络结构,它在混沌与复杂动力系统的研究中扮演着重要的角色。
网络理论提供了描述和分析复杂网络的数学方法,可以揭示网络的拓扑结构、信息传播和动力学行为。
复杂网络的研究源于20世纪60年代的社会学领域,随着计算机科学和物理学的发展,复杂网络理论逐渐成为一个跨学科的研究领域。
数学家研究发现混沌系统的周期行为与非线性动力学

数学家研究发现混沌系统的周期行为与非线性动力学混沌系统是一类非线性动力系统,它的行为通常被认为是无序和不可预测的。
然而,对混沌系统的研究却是非常有趣的领域,因为它包含着许多有趣且意想不到的现象。
在非线性动力学领域中,最重要的问题之一就是周期行为。
周期行为是指系统在某些时刻会以特定的频率重复其状态。
例如,一个钟摆会在固定的时间间隔内以相同的频率移动。
周期行为可以是简单的,例如单摆的简单周期,也可以很复杂,例如混沌系统。
最初,人们认为混沌系统没有周期行为,因为它们的输出看起来是完全随机的。
但是,一些数学家研究发现,许多混沌系统会表现出周期行为。
这些周期行为可以是多样的,例如简单的定期振荡或者更复杂的“奇异吸引子”。
奇异吸引子是一种非周期性吸引子,其形状复杂多变并且具有非常奇怪的性质。
例如,奇异吸引子的维数可以是小数,而不是整数,这就是所谓的“分数维”。
奇异吸引子的形态经常会被描述为“分叉树状结构”,因为它们在各个阶段中的形态经常类似于树枝的分支。
对于奇异吸引子的研究有一些应用,其中最著名的是在磁共振成像领域中的应用。
磁共振成像是一种用于成像人体内部的非侵入性方法,它可以帮助医生诊断各种疾病,如肿瘤甚至是精神病。
奇异吸引子的一些性质使得它成为磁共振成像的有用方法。
“分叉树状结构”表示各部分的形态分叉,在磁共振成像中,这个分叉结构在图像中体现出来,可以帮助医生更容易地看出病灶的位置以及病变的范围。
另外,周期行为的研究也具有很高的理论重要性。
研究周期行为帮助我们理解非线性动力学中的一些基本原理,例如“稳定性理论”。
稳定性理论是一种用来描述非线性动力系统的稳定性的理论,它告诉我们即使在极端条件下,系统也可能具有稳定的周期行为。
这一原理在电气系统、气候模拟和生物模型等领域中都有重要应用。
总之,数学家们对混沌系统的研究取得了一些非常有趣的结果,它们不仅揭示了混沌系统中的周期行为和奇异吸引子的存在,而且还帮助我们更好地理解非线性动力学的基本原理。
非线性动力学与混沌理论

非线性动力学和混沌理论非线性动力学随着科学技术的发展,非线性问题出现在许多学科之中,传统的线性化方法已不能满足解决非线性问题的要求,非线性动力学也就由此产生。
非线性动力学联系到许多学科,如力学、数学、物理学、化学,甚至某些社会科学等。
非线性动力学的三个主要方面:分叉、混沌和孤立子。
事实上,这不是三个孤立的方面。
混沌是一种分叉过程,孤立子有时也可以和同宿轨或异宿轨相联系,同宿轨和异宿轨是分叉研究中的两种主要对象。
经过多年的发展,非线性动力学已发展出了许多分支。
如分叉、混沌、孤立子和符号动力学等。
然而,不同的分支之间又不是完全孤立的。
非线性动力学问题的解析解是很难求出的。
因此,直接分析非线性动力学问题解的行为(尤其是长时期行为)成为研究非线性动力学问题的一种必然手段。
混沌理论是谁提出的?混沌理论,是系统从有序突然变为无序状态的一种演化理论,是对确定性系统中出现的内在“随机过程”形成的途径、机制的研讨。
美国数学家约克与他的研究生李天岩在1975年的论文“周期3则乱七八糟(Chaos)”中首先引入了“混沌”这个名称。
美国气象学家洛伦茨在2O世纪 6O年代初研究天气预报中大气流动问题时,揭示出混沌现象具有不可预言性和对初始条件的极端敏感依赖性这两个基本特点,同时他还发现表面上看起来杂乱无章的混沌,仍然有某种条理性。
1971年法国科学家罗尔和托根斯从数学观点提出纳维-斯托克司方程出现湍流解的机制,揭示了准周期进入湍流的道路,首次揭示了相空间中存在奇异吸引子,这是现代科学最有力的发现之一。
1976年美国生物学家梅在对季节性繁殖的昆虫的年虫口的模拟研究中首次揭示了通过倍周期分岔达到混沌这一途径。
1978年,美国物理学家费根鲍姆重新对梅的虫口模型进行计算机数值实验时,发现了称之为费根鲍姆常数的两个常数。
这就引起了数学物理界的广泛关注。
与此同时,曼德尔布罗特用分形几何来描述一大类复杂无规则的几何对象,使奇异吸引子具有分数维,推进了混沌理论的研究。
非线性动力学中的混沌现象_王兰芳

非线性动力学中的混沌现象王兰芳 (陕西工学院基础课部 汉中 723003)【摘 要】 本文论述了非线性动力学系统中的长期行为的不可预测性—即混沌现象和非线性系统的特征以及理解混沌的三个要点。
【关键词】 非线性动力学;混沌;初始条件【分类号】 O4本文收到时间:1996-01-19 作者:女 46岁 高级实验师1 前 言在大型计算机没有出现之前,由于解决非线性微分方程的技术条件还不成熟,人们多限于简单地、线性地、有规律地描述动力学问题。
牛顿力学系统一直被认为是确定性的,即认为一系统确定后,就能预测其任意一个时刻的运动状态,只要列出系统的运动方程,在条件给定后,其解是唯一的。
但在近二三十年里,人们发现非线性动力学系统中的长期行为的不可预测性—即混沌现象。
混沌的出现和混沌理论的研究,使物理界的人们更深刻地理解牛顿力学体系的内在含意。
2 非线性系统的特征某一个弹性非线性系统在运动过程中,其运动方程可表示为:X ″+ω20X =-αX ′-εX 3+F cos Ψt (1)这就是著名的Duffing 方程。
左边的第一项X ″为系统的运动加速度,第二项ω20X 为与位移X成正比的恢复力(f =-ω20X );右边的第一项αX ′为阻尼项,第二项εX 3体现了系统的非线性,第三项F cos Ψt 为强迫振动项。
解非线性方程(1)的过程是很复杂的,一般得不到精确的解。
下面我们采用多变量多R 度的近似解法来解(1)式,为了简化取掉阻尼项αX ′和强迫项F cos Ψt 后,(1)式变为:X ″+ω20X =-εX 3(2)取ω0=1,ε是微小量。
多变量多R 度法解方程的方法是:引入m +1个依赖于不同R 度的时间变量。
T m =εm t (m =0,1,2,…,m )(3)第i 个时间变量T i 依次比前一个变量T i -1随时间t 变化的速度减慢一个数量级。
那么非线1997年3月 第13卷第1期陕西工学院学报JOU RNA L OF SHAAN XI INST I T U T E OF T ECHNO LOG Y M arch .1997Vol .13 No .1性方程的解将取以下形式:X (t ;ε)=X (T 0,T 1,…,T m ;ε)=∑m -1m =0εmX m (T 0,T 1,…,T m )+O (ε,T m )O (ε,T m )为近似解∑m -1m =0εmX m (T 0,T 1,…,T m )的余项,m 取多少,则取决于需要近似到那一级。
混沌效应非线性混沌电路(精)

混沌效应一、实验名称 非线性电路振荡周期的分岔与混沌二、实验原理⒈分岔与混沌 ⑴ 逻辑斯蒂映射考虑一条单位长度的线段,线段上的一点用0和1之间的数x 表示。
逻辑斯蒂映射是)1(x kx x -→其中k 是0和4之间的常数。
迭代这映射,我们得离散动力学系统 )1(1n n n x kx x -=+ ,0=n ,1,2…我们发现:①当k 小于3时,无论初值是多少经过多次迭代,总能趋于一个稳定的不动点; ②当k 大于3时,随着k 的增大出现分岔,迭代结果在两个不同数值之间交替出现,称之为周期2循环;k 继续增大会出现4,8,16,32…周期倍化级联;③很快k 在58.3左右就结束了周期倍增,迭代结果出现混沌,从而无周期可言。
④在混沌状态下迭代结果对初值高度敏感,细微的初值差异会导致结果巨大区别,常把这种现象称之为“蝴蝶效应”。
⑤迭代结果不会超出0~1的范围称为奇怪吸引子。
以上这些特点可用图示法直观形象地给出。
逻辑斯蒂映射函数是一条抛物线,所以先画一条)1(x kx y -=的抛物线,再画一条x y =的辅助线,迭代过程如箭头线所示(图1)。
图 1—A 不动点 图1—B 分岔周期2 图1—C 混沌 图1—D 蝴蝶效应图1⑵逻辑斯蒂映射的分岔图 以k 为横坐标,迭代200次以后的x 值为纵坐标,可得到著名的逻辑斯蒂映射分岔图。
X 0X A X B图2逻辑斯蒂映射的分岔图。
k 从2.8增大到4。
⒉ 非线性负阻电路振荡周期的分岔与混沌 ⑴非线性电路与非线性动力学实验电路如图3所示。
它由有源非线性负阻器件R ;LC 振荡器和移相器三部分构成。
图中只有一个非线性元件R ,它是一个有源非线性负阻器件;电感器L 和电容器C2组成一个损耗可以忽略的振荡回路;可变电阻Rv1+Rv2和电容器C1串联将振荡器产生的正弦信号移相输出。
较理想的非线性元件R 是一个三段分段线性元件。
图4所示的是该电阻的伏安特性曲线,从特性曲线显示加在此非线性元件上的电压与通过它的电流极性是相反的。
非线性振动与混沌简介PPT课件
dt2 dt
三种情况: a. f= = = 0;b. f = =0;c. =0,相
应得出简谐振动、阻尼和受迫振动方程。
★简谐振动的相轨线:闭合圈---周期环---。
★阻尼振动的相轨线:从外向内收缩的螺旋线,最终 停止于中点---不动点吸引子--- 。
★受迫振动:经过暂 态之后趋于一稳定的 闭合圈---周期吸引子 或极限环。
单摆方程
ml
d2x dt 2
l
dx dt
mg
sin
x
F
cos t
按泰勒级数 sin x x 1 x3 6
取前两项近似,
适当代换,得到非线性振动方程(杜芬方程)
d 2x dx x x3 f cost
dt2 dt
讨论 运动的演变
1. 线性近似下的单摆运动
21
第21页/共40页
1. 线性近似下的单摆运动 令 =0,退化为线性方程
§3.2 混 沌
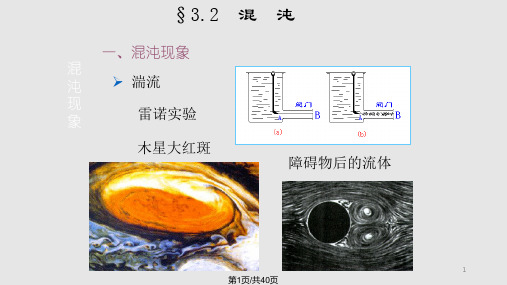
一、混沌现象
混 沌 ➢ 湍流
现 象
雷诺实验
木星大红斑
障碍物后的流体
1
第1页/共40页
湍流
2
第2页/共40页
喷 气 混机 沌尾 现流
燃 烧 的 蜡 烛
象
➢洛仑兹水轮
3
第3页/共40页
➢滴水龙头
混 沌 现 象
➢计算机迭代
x
x2 1的迭代
0.5
5
10 15 20 25 30
o
0.5
对周期点之间的距离之比,以及第相邻两次周期分
岔中的各对周期点之间的距离之比又趋于另一个常
数 ,称为标度因子或普适常数:
= 2.5029078750958928
混沌与非线性动力学在天体物理中的应用

混沌与非线性动力学在天体物理中的应用天体物理学是一门涉及宇宙、太阳系、星云、恒星、行星等各种天体的学科,是研究天文现象及其规律、性质和演化的科学。
在天体物理学的研究中,混沌与非线性动力学的应用日益重要。
混沌现象被认为是一种不存在可预测行为的动力学现象,它的表现为某个系统状态的轨迹在相空间中不断变化,并且永远无法重现某一特定的状态。
对于天体物理学中的系统,比如行星的运动轨迹,混沌现象的存在意味着行星的轨迹变得不可预测,这使得预测天体运动变得更加复杂。
非线性动力学则是研究非线性系统的动力学行为。
在天体物理学中,行星/卫星运动的运动方程是一组非线性微分方程,系统的非线性特征显而易见。
因此,非线性动力学在分析这些天体运动中起着至关重要的作用。
在天体物理学中,混沌和非线性动力学的应用十分广泛。
比如,对太阳系中的天体运动轨迹进行深入研究,可以帮助我们更好地了解各个天体的形成演化过程,了解它们的性质和特点;同时,还可以为制定太空任务和探测器运行计划提供帮助。
具体来看,混沌现象的存在使得天体物理学中行星的轨迹变得不可预测,这一结果使得人们需要寻找新的方式来研究和控制太阳系中的天体。
非线性动力学给出了这种方式。
通过研究非线性系统中的动力学行为,人们可以更好地预测行星等天体的轨迹,了解其演化过程,制定太空任务和探测器运行计划。
此外,在天体物理学中,混沌和非线性动力学还可以用来解决太阳系中天体间的相互作用问题。
当天体间的引力相互作用时,系统的动力学行为是非线性的。
通过研究这种非线性动力学行为,我们可以更好地理解行星之间的引力相互作用,并得到更加准确的轨道预测。
在研究天体物理时,混沌与非线性动力学的应用也会提高计算的效率。
对于复杂的天体系统,使用不断迭代并计算系统状态的方式进行研究,会导致计算量的大幅度增加,而使用混沌现象的分析方法和非线性动力学的理论,可以更有效地处理海量的计算。
总之,混沌与非线性动力学在天体物理学中的应用不仅加深了我们对天体运动的认识,而且对太空任务和探测器的运行计划提供了有力保障。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f i ij ( ) 0 x j
11 12 0 21 22
T 11 22 系数矩阵的迹 11 22 12 21 系数行列式的值
特征矩阵
T 0
2
特征根
T T 2 4 1, 2 2
A1 B 1
t
原点 i 0 是渐进稳定的
参考态
xi 0 也是渐进稳定的。
(2) 两特征根中至少有一个实部为正 原点 i 0 是不稳定的 lim i
t
参考态
xi 0 也是不稳定的。
(3) 两特征根中至少有一个实部为零,另一个实部为负
原点 i 0 是Lyapunov稳定的 参考态 xi 0 处于临界情况。
x
x2
t
时空轨迹 相图
x1
小结
非线性动力学系统
决定性系统与不可预测性(初值敏感性)
一阶自治常微分方程组
相空间
§7.2 运动稳定性分析
一. 非线性方程解的各种形式
i fi ( x1 , x2 ,, xn ) x
1. 定态解
i 1,2,, n i 1,2,, n
x2 x1
代入方程
2 02
当阻尼为正阻尼且很小时 0 0
i , 02 2
x1 x Ae t cos(t ) Ae t [ cos(t ) sin(t )] x2 x 2 2 Ae t sin(t 0 )
x1 x, x2 x
3 x3 cost , x4 x
1 x2 x k 3 F x x x x x3 2 1 1 2 m m m m x 3 x4 2 x x3 4
一阶常微分方程组
数值计算 系统的状态 相空间
例1.
2t x
x0 (0) 1
x0 (0) c 1
1 解: x(t ) 2t t 2 c 2 x(0) x0 (0) c 1
x 0 (t ) 2t
1 2 t 1 2
x(t ) x0 (t ) c 1
x0 (t ) 是Lyapunov稳定的
非线性动力学与混沌
NONLINEAR DYNAMICS AND CHAOS
参考书
林振山,《非线性力学与大气科学》,南京大学
出版社,1993
刘秉正,
《非线性动力学与混沌基础》,东北师 范大学出版社,1994
刘式达,刘式适,《非线性动力学和复杂现象》,
气象出版社,1989
§7.1 引言
一. “非线性动力学”的表观含义
1 x2 x 2 x x1 2 0
2 x12 x2 1 2 2 A ( A0 )
x
x2
t
时空轨迹 相图
x1
阻尼弹簧振子
通解
2x x 0 x
2 0
x Aet
2 0
2 2 0
1 x2 x 2 x 0 x1 2 x2 2
T T 2 4 1, 2 2 3. 奇点的分类 (取非线性方程的奇点为参考态)
(1) 0
T 2 4 0 两根都是实的,且符号相同,此时奇点称为结点。
T 0 不稳定的结点
T 0 稳定的结点
(2) 0 , T 2 4 0, T 0
两根都是复的,此时奇点称为焦点。
lim x(t ) x0 (t ) lim c 2 e t 0
t t
渐进稳定的
三. 线性稳定性分析
1. 线性稳定性定理
i fi ( x1 , x2 ,, xn ) x
i 1,2,, n
设 xi 0 (t ) 为方程的一个解(参考解), 为研究该解的稳定性, 令 xi (t ) xi 0 (t ) i (t ) 为此解附件另一解,称扰动解 。
例2.
解:
tx x
x(t ) t 1 ce
t
x0 (0) 1
x0 (0) 1
c2
x0 (t ) t 1 2et
x(0) x0 (0) 1 c 1 2 c 2
x(t ) x0 (t ) t 1 ce t 1 2e t c 2 e t
1883年,英国流体力学家雷诺(Reynolds)的湍流实验。 (香烟) 1903年,法国数学家昂利•庞伽莱(Henri Poincare)从动力系统 和拓扑学的全局思想出发,指出动力学系统可能存在混沌特征。 1963,美国气象学家洛仑兹(Lorenz)在研究天气预报中大气流 动问题时发现了天气“对初始条件的极端敏感性”,将使长时间 的预测无法进行。后被形象地称为“蝴蝶效应” :一只蝴蝶在巴 西扇一下翅膀,就可能在美国得克萨斯州引起龙卷风。
f ( x, x ) x
2阶,1维
x1 x x 1 x2 x
1 x2 x 2 f ( x1 , x2 ) x
1阶,2维
n+1维自治
(2)非自治的 n维非自治
i 1 xi t , x
Duffing方程
x kx x3 F cost m x
f ( x) x
(1)
x ( x1, x2 ,, xn ) f ( f1, f 2 ,, f n )
设t=t0时方程的解为 x0 (t0 ) ,t时为 x 0 (t ),另一受扰动而偏离它的 解t0时为 x(t0 ) , t时为 x(t )。如果对于任意小的数 0 ,总有一小数 0 存在,使得当 x(t ) x (t ) 时,必有 x(t ) x (t ) , t t 则称解x (t ) 是Lyapunov意义下稳定的,简称Lyapunov稳定的或稳定 0 的。
1. 力学决定论及其伟大成就
F ( x, x , t) x m x 0 x x 0 , x
t t0
(t ) x(t ), x
存在且唯一, 可预测性
1757年,哈雷慧星(Hally comet)按预测回归。 1846年,海王星在预言的位置被发现。
今天,日月蚀的准确预测,宇宙探测器的成功发射与回收。
0 x2 2 0 0 sin x1 2 x2
求定态解
1 0 x 2 0 x
(0,0) 两奇点 ( ,0)
(2k ,0) (2k ,0)
1. 在奇点(0,0)处线性化方程组为
f1 f1 2 2 1 x1 0 x2 0 f 2 f 2 2 1 - 2 2 2 1 2 0 x x 1 0 2 0 1
洛仑兹方程
10x 10 y x 28x y xz y z xy 8 z / 3
初值敏感性
不可预测性,混沌
初值敏感演示
杜芬(Duffing)方程: (带阻尼弹性系统的强迫振动)
x kx x F cost m x
0 0 0 ( x2 y2 ) ( xn yn )
2 2
2 12
两矢量间的距离
(2)
如果解 x 0 (t ) 是稳定的,且 lim x(t ) x 0 (t ) 0 则称此解
t
是渐进稳定的。
(3)
不满足上述条件的解是不稳定的。
设想一位智者在某一瞬间得知激励大自然所有力及组成它的物体 的相互位置,如果这位智者又能对众多的数据进行分析,把宇宙间最 庞大的物体和最轻微的原子的运动凝聚在一个公式中,没有什么事物 是不确定的,将来就像过去一样清晰地展现在眼前。
——拉普拉斯(Laplace,法国数学家,1749-1827)
2. 力学决定论不断受到挑战
3
x10 1,
10 0 x 20 0 x20 1.000001 , x
三. 常微分方程的一般形式
1. 自治方程与非自治方程
F(x, x ) m x F(x, x , t) m x
不显含时间,自治的 显含时间,非自治的
2. 常微分方程一般形式
(1)自治的
T 0
不稳定的焦点
T 0 稳定的焦点
(3) 0, T 0 两根都是纯虚数,解是等幅振荡,此时奇点称为中心。
中心
鞍点
(4)
0
两根都是实数,一正一负,此时奇点称为鞍点。
稳 定 焦 点 不 中稳 心焦 点 鞍点
T 2 4 0
稳定结点
不稳结点
T
T T 2 4 1, 2 2
2. 线性化方程组的解及其稳定性
1 11 1 12 2 2 211 22 2
试探解:1 Aet , 2 Bet
12 A 11 B 0 22 21
i 0 x
平衡点,奇点 2. 发散解
xi 之一或几个随时间无限地偏离初值
爆炸,散射
x2 x1
3. 振荡解
既不趋于无穷大,也不终止于某一点,而是在一定区域内不断变化。
周期振荡
x2
准周期振荡
x2
闭合曲线
x1
非闭合曲线
x1
混沌 相轨迹没有确定的形状周 期、貌似随机的运动。
二. 解的稳定性
Lyapunov稳定性定义:
例: 分析阻尼单摆定态的稳定性
