厦门市初中毕业及高中阶段各类学校招生考试
厦门中考语文试题及答案--完整版

2015年厦门初中毕业及高中阶段各类学校招生考试第一部分积累与运用一、语言积累1.请根据提示填写相应的古诗文。
(1)潮平两岸阔,。
(王湾《次北固山下》)(2)万里赴戎机,。
(《木兰诗》)(3)晓雾将歇,;夕阳欲颓,。
(陶弘景《答谢中书书》)(4)湖上影子,、湖心亭一点,与余舟一芥、。
(张岱《湖心亭看雪》)(5),。
寂寞梧桐深院锁清秋。
(李煜《相见欢》)(6)浊酒一杯家万里,。
(范仲淹《渔家傲·秋思》)(7)古代的仁人志士在“生”与“义”不能得兼时,总会以孟子《鱼我所欲也》中的“,”作为自己选择的标准。
(8)龚自珍在《已亥杂诗》中以落花自比,表达自己不忘报国之志的诗句是:“,。
”二、语言运用2.根据情境,将下列对话补充完整。
中山公园公交站牌前,一位中年妇女正焦急地张望着,你上前热心询问:“(1)”她说:“我急着要到轮渡和旅行团会合,可等了很久也没车。
公交车啥时候能到这儿呢?”你马上拿出手机,查了“无线城市掌上公交”之后,告诉她:“(2)”(提示:请参照右图作答,汽车图标表示公交已到达的站点。
)3.根据提示,完成(1)-(3)小题。
端午时节,粽香阵阵,龙舟竞渡,祭祖祈福。
在闽南,划龙舟、水上捉鸭、走“贡王”等民俗活动异彩纷呈,A家谕..。
厦门的龙舟赛每年都在集美火热开赛。
..yù户晓又是一年竞渡时,这里金鼓齐鸣,B人声顶沸....huì。
健儿们驾着七彩龙舟,劈波斩浪,C锐.nuì不可当..,热闹非凡。
...。
岸上喝彩,水上声嘶,D气冲..chōng斗牛(1)请讲文中的词语“龙舟竞渡”,用正楷字工整地抄写在“田”字格内。
(2)文段中ABCD四处加点的词语,注音与书写都正确...的一项是()(3)端午“赛龙舟·赛诗歌”活动中,有一首描写龙舟赛的诗,顺序被打乱了。
请你将它还原。
竞渡诗【唐】卢肇①鼙鼓动时雷隐隐,兽头凌处雪微微。
②石溪久住思端午,馆驿楼前看发机。
厦门市2005年初中毕业和高中阶段各类学校招生考试9

厦门市2005年初中毕业和高中阶段各类学校招生考试数 学 试 题(满分:150分; 考试时间:120分钟) 考生须知:1. 解答的内容一律写在答题卡上,否则以0分计算. 交卷时只交答题卡,本卷由考场处理,考生不得擅自带走.2. 作图或画辅助线要用0.5毫米的黑色签字笔画好.一、选择题(本大题共7小题,每小题3分,共21分)每小题都有四个选项,其中有且只有一个选项是正确的. 1. 下列计算正确的是A. -1+1=0B. -1-1=0C. 3÷13=1 D. 32=62. 下列事件中是必然事件的是A. 打开电视机,正在播广告.B. 从一个只装有白球的缸里摸出一个球,摸出的球是白球.C. 从一定高度落下的图钉,落地后钉尖朝上.D. 今年10月1日 ,厦门市的天气一定是晴天. 3. 如图1,在直角△ABC 中,∠C =90°,若AB =5,AC =4, 则sin ∠B =A. 35B. 45C. 34D. 434. 下列关于作图的语句中正确的是A. 画直线AB =10厘米.B. 画射线OB =10厘米.C. 已知A 、B 、C 三点,过这三点画一条直线.D. 过直线AB 外一点画一条直线和直线AB 平行. 5. “比a 的32大1的数”用代数式表示是A. 32a +1B. 23a +1C. 52aD. 32a -16. 已知:如图2,在△ABC 中,∠ADE =∠C ,则下列等式成立的是 A. AD AB =AE AC B. AE BC =ADBDC.DE BC =AE AB D. DE BC =AD AB7. 已知:a +b =m ,ab =-4, 化简(a -2)(b -2)的结果是A. 6B. 2 m -8C. 2 mD. -2 m二、填空题(本大题共10小题,每小题4分,共40分) 8. -3的相反数是 . 9. 分解因式:5x +5y = .10. 如图3,已知:DE ∥BC ,∠ABC =50°,则∠ADE = 度. E 图 3D CB A 图 1CBAE 图 2DC A11. 25÷23= . 12. 某班有49位学生,其中有23位女生. 在一次活动中,班上每一位学生的名字都各自写在一张小纸条上,放入一盒中搅匀. 如果老师闭上眼睛从盒中随机抽出一张纸条,那么抽到写有女生名字纸条的概率是 . 13. 如图4,⊙O 的直径AB 垂直于弦CD ,垂足为E ,若∠COD =120°,OE =3厘米,则OD = 厘米.14. 如果甲邀请乙玩一个同时抛掷两枚硬币的游戏,游戏的规则如下:同时抛出两个正面,乙得1分;抛出其他结果, 甲得1分. 谁先累积到10分,谁就获胜.你认为(填“甲”或“乙”)获胜的可能性更大.15. 一根蜡烛在凸透镜下成一实像,物距u ,像距v 和凸透镜的焦距f满足关系式:1u +1v =1f. 若f =6厘米,v =8厘米,则物距u = 厘米.16. 已知函数y =-3x -1-2 2 ,则x 的取值范围是 . 若x 是整数,则此函数的最小值是 .17. 已知平面直角坐标系上的三个点O (0,0)、A (-1,1)、B (-1,0),将△ABO 绕点O 按顺时针方向旋转135°,则点A 、B 的对应点A 1、B 1的坐标分别是A 1( , ) ,B 1( , ) .三、解答题(本大题共9小题,共89分)18. (本题满分7分) 计算: 22+(4-7)÷32+(3)019. (本题满分7分) 一个物体的正视图、俯视图如图5所示,请你画出该物体的左视图并说出该物体形状的名称.20.(1) 求全体参赛选手年龄的众数、中位数;(2) 小明说,他所在年龄组的参赛人数占全体参赛人数的28%.你认为小明是哪个年龄组的选手?请说明理由.图 5俯视图正视图图 421. (本题满分10分) 如图6,已知:在直角△ABC 中,∠C =90°, BD 平分∠ABC 且交AC 于D.(1)若∠BAC =30°,求证: AD =BD ; (2)若AP 平分∠BAC 且交BD 于P ,求∠BPA 的度数.22. (本题满分10分) 某软件公司开发出一种图书管理软件,前期投入的开发、广告宣传费用共50000元,且每售出一套软件,软件公司还需支付安装调试费用200元. (1)试写出总费用y (元)与销售套数x (套)之间的函数关系式;(2)如果每套定价700元,软件公司至少要售出多少套软件才能确保不亏本?23. (本题满分10分) 已知:如图7,P 是正方形ABCD 内一点,在正方形ABCD 外有一点E ,满足∠ABE =∠CBP ,BE =BP ,图 6P DCB A 图 7P ED C B A(1) 求证:△CPB≌△AEB;(2) 求证:PB⊥BE;(3) 若PA∶PB=1∶2,∠APB=135°,求cos∠PAE的值.24. (本题满分12分) 已知抛物线y=x2-2x+m与x轴交于点A(x1,0)、B(x2,0)(x2>x1),(1) 若点P(-1,2)在抛物线y=x2-2x+m上,求m的值;(2)若抛物线y=ax2+bx+m与抛物线y=x2-2x+m关于y轴对称,点Q1(-2,q1)、Q2(-3,q2)都在抛物线y=ax2+bx+m上,则q1、q2的大小关系是(请将结论写在横线上,不要写解答过程);(友情提示:结论要填在答题卡相应的位置上)(3)设抛物线y=x2-2x+m的顶点为M,若△AMB是直角三角形,求m的值.25. (本题满分12分) 已知:⊙O1与⊙O2相交于点A、B,过点B作CD⊥AB,分别交⊙O1和⊙O2于点C、D.(1)如图8,求证:AC是⊙O1的直径;(2)若AC=AD,①如图9,连结BO2、O1 O2,求证:四边形O1C BO2是平行四边形;②若点O1在⊙O2外,延长O2O1交⊙O1于点M,在劣弧︵MB上任取一点E(点E与点B不重合). EB的延长线交优弧︵BDA于点F,如图10所示. 连结AE、AF. 则AE AB(请在横线上填上“≥、≤、<、>”这四个不等号中的一个)并加以证明.(友情提示:结论要填在答题卡相应的位置上)图 8图9图 1026. (本题满分13分) 已知:O 是坐标原点,P (m ,n )(m >0)是函数y = kx(k >0)上的点,过点P 作直线PA ⊥OP 于P ,直线PA 与x 轴的正半轴交于点A (a ,0)(a >m ). 设△OPA 的面积为s ,且s =1+n 44.(1)当n =1时,求点A 的坐标; (2)若OP =AP ,求k 的值;(3 ) 设n 是小于20的整数,且k ≠n 42,求OP 2的最小值.厦门市2005年初中毕业和高中阶段各类学校招生考试数学评分标准及参考答案一、选择题(本大题共7小题,每小题3分,共21分)二、填空题(本大题共10小题,每小题4分,共40分) 8. 3;9. 5(x +y );10. 50度;11. 4;12.2349; 13. 6厘米 14. 甲 ; 15. 24 厘米; 16. x ≤-13 ,-2 ; 17. A 1 (2,0), B 1(22,22)注:8~15题每空4分;16、17题每空2分.第11题写成22不扣分.三、解答题(本大题共9小题,共89分) 18. (本题满分7分) 解:22+(4-7)÷32+(3)0=4-3×23+1…… 4分=4-2+1 …… 5分 =3 …… 7分 注:每步运算1分. 19. (本题满分7分)解: 左视图: …… 3分该物体形状是: 圆柱 . …… 7分 20. (本题满分8分)(1) 解: 众数是:14岁; 中位数是:15岁. …… 4分 (2) 解1:∵ 全体参赛选手的人数为:5+19+12+14=50名 …… 5分又∵ 50×28% …… 6分=14(名) …… 7分∴ 小明是16岁年龄组的选手. …… 8分 解2:∵全体参赛选手的人数为:5+19+12+14=50名 …… 5分 又∵16岁年龄组的选手有14名,而14÷50 …… 6分 =28% …… 7分 ∴ 小明是16岁年龄组的选手. …… 8分 注:第(1)小题的众数、中位数各2分.(1) 证明:∵∠BAC =30°∠C =90° ∴ ∠ABC =60° …… 1分 又∵ BD 平分∠ABC ∴∠ABD =30° …… 2分 ∴ ∠BAC =∠ABD …… 3分 ∴ BD =AD …… 4分 (2) 解1: ∵∠C =90°∴∠BAC +∠ABC =90° …… 5分 ∴ 12(∠BAC +∠ABC)=45° …… 6分 ∵ BD 平分∠ABC ,AP 平分∠BAC∠BAP =12∠BAC ∠ABP =12∠ABC …… 8分即∠BAP +∠ABP =45° …… 9分∴∠APB =180°-45°=135° …… 10分 解2:∵∠C =90° ∴∠BAC +∠ABC =90° …… 5分 ∴ 12(∠BAC +∠ABC)=45° …… 6分 ∵ BD 平分∠ABC ,AP 平分∠BAC∠DBC =12∠ABC ∠PAC =12∠BAC …… 8分∴ ∠DBC +∠PAD =45° …… 9分∴ ∠APB =∠PDA +∠PAD =∠DBC +∠C +∠PAD=∠DBC +∠PAD +∠C =45°+90°=135° …… 10分22. (本题满分10分)(1) 解:y =50000+200x …… 4分 (2) 解1:设软件公司至少要售出x 套软件才能确保不亏本,则有:700 x ≥50000+200x …… 7分 解得:x ≥100 …… 9分 答:软件公司至少要售出100套软件才能确保不亏本. …… 10分 解2:每套成本是50000x +200 …… 5分若每套成本和销售价相等则:700=50000x +200 …… 7分解得:1=100x∴ x =100 …… 9分答:软件公司至少要售100套软件才能确保不亏本. …… 10分 解3:每套成本是50000x +200 …… 5分由题意得:700≥50000x+200 …… 7分解得:1≥100x ∴ x ≥100 …… 9分答:软件公司至少要售100套软件才能确保不亏本. …… 10分 注:第(1)小题的解析式可以不写x 的取值范围.图 6P D CBA(1) 证明:∵ 四边形ABCD 是正方形∴ BC =AB …… 1分 ∵ ∠CBP =∠ABE BP =BE …… 2分 ∴ △CBP ≌△ABE …… 3分 (2) 证明:∵∠CBP =∠ABE∴∠PBE =∠ABE +∠ABP …… 4分=∠CBP +∠ABP =90° …… 5分∴ PB ⊥BE …… 6分(1)、(2)两小题可以一起证明.证明:∵∠CBP =∠ABE∴∠PBE =∠ABE +∠ABP …… 1分=∠CBP +∠ABP =90° …… 2分∴ PB ⊥BE …… 3分 以B 为旋转中心,把△CBP 按顺时针方向旋转90°, …… 4分 ∵ BC =AB ∠CBA =∠PBE =90° BE =BP …… 5分 ∴△CBP 与△ABE 重合∴ △CBP ≌△ABE …… 6分 (3) 解:连结PE∵ BE =BP ∠PBE =90° ∴∠BPE =45° …… 7分 设 AP 为k , 则 BP =BE =2k∴ PE 2=8k 2 …… 8分∴ PE =22k ∵∠BPA =135° ∠BPE =45° ∴∠APE =90° …… 9分 ∴AE =3 k在直角△APE 中: cos ∠PAE =AP AE =13 …… 10分24. (本题满分12分)(1) 解:∵点P (-1,2)在抛物线y =x 2-2x +m 上 …… 1分 ∴ 2=(-1)2 -2×(-1)+m …… 2分 ∴ m =-1 …… 3分 (2) 解: q 1<q 2 …… 7分 (3) 解1:∵ y =x 2-2x +m=(x -1)2 +m -1∴ M (1,m -1) …… 8分 ∵ 抛物线 y =x 2-2x +m 开口向上,且与x 轴交于点A (x 1,0)、B (x 2,0)(x 1<x 2)图 7EP D C B A∴ m -1<0∵ △AMB 是直角三角形,又AM =MB ∴∠AMB =90° △AMB 是等腰直角三角形 …… 9分 过M 作MN ⊥x 轴,垂足为N. 则N (1,0) 又 NM =NA∴ 1-x 1=1-m∴ x 1=m …… 10分 ∴ A (m ,0)∴ m 2-2 m +m =0 ∴m =0 或m =1(不合题意,舍去) …… 12分 解2:又 NM =NA =NB ∴ x 2-x 1=2-2m∴⎩⎨⎧x 2+x 1=2x 2-x 1=2-2m 解得:⎩⎨⎧x 1=m x 2=2-m…… 10分 ∴ A (m ,0)∴ m 2-2 m +m =0∴ m =0 或m =1(不合题意,舍去) …… 12分 25. (本题满分12分)(1) 证明:∵ CD ⊥AB …… 1分∴∠ABC =90° …… 2分 ∴ AC 是⊙O 1的直径 …… 3分(2) ① 证明1:∵ CD ⊥AB ∴∠ABD =90° ∴ AD 是⊙O 2的直径 …… 4分 ∵ AC =AD∵ CD ⊥AB ∴CB =BD …… 5分 ∵ O 1、O 2分别是AC 、AD 的中点∴ O 1O 2∥CD 且 O 1O 2=12CD =CB …… 6分∴ 四边形O 1C BO 2是平行四边形 …… 7分 证明2:∵ CD ⊥AB ∴∠ABD =90°∴ AD 是⊙O 2的直径 …… 4分 ∵ AC =AD∵ CD ⊥AB ∴CB =BD …… 5分 ∵ B 、O 2分别是CD 、AD 的中点∴ BO 2∥AC 且 BO 2=12AC =O 1C …… 6分∴ 四边形O 1C BO 2是平行四边形 …… 7分 证明3:∵ CD ⊥AB ∴∠ABD =90°∴ AD 是⊙O 2的直径 …… 4分 ∵ O 1、O 2分别是AC 、AD 的中点∴ O 1O 2∥CD …… 5分 ∵ CD ⊥AB ∴ CB =BD ∴ B 是CD 的中点图 9图 8∴O 2B ∥O 1C …… 6分 ∴四边形O 1C BO 2是平行四边形 …… 7分 证明4:∵ CD ⊥AB ∴∠ABD =90°∴ AD 是⊙O 2的直径 …… 4分 ∵ AC =AD ∴ O 1C =O 2B∴ ∠C =∠D ------------------------------------------------ 5分 ∵ O 2B =O 2D∴∠O 2B D =∠D ……∴∠C =∠O 2B D ∴O 2B ∥O 1C …… 6分 ∴四边形O 1C BO 2是平行四边形 …… 7分 ② AE > AB …… 8分证明1:当点E 在劣弧︵MC 上(不与点C 重合)时, ∵ AC =AD ∴ ∠ACD =∠ADC∴ ∠AEB =∠ACD =∠ADC =∠AFB∴ AE =AF …… 9分 记AF 交BD 为G ∵ AB ⊥CD∴ AF >AG >AB …… 10分 当点E 与点C 重合时,AE =AC >AB当点E 在劣弧︵CB 上 (不与点B 重合) 时,设AE 交CD 与H , AE >AH >AB …… 11分 综上,AE >AB.…… 12分证明2:当点E 在劣弧︵MC 上(不与点C 重合)时, 连结EC 、DF ,∵ AD 是⊙O 2的直径,即∠AFD =90° ∠EAC =∠EBC =∠DBF =∠DAF∵ AC =AD 直角△AFD ≌直角△AEC∴ AE =AF …… 9分证明3:当点E 在劣弧︵MC 上(不与点C 重合)时,连结EC 、DF ,∵ AD 是⊙O 2的直径,即∠AFD =90° ∵ ∠DBF =∠DAF ∴∠ADF +∠DBF =90° 又∵ ∠DBF =∠EBC ∠ABE +∠EBC =90° ∴ ∠ADF =∠ABE∵ ∠ABE =∠ACE ∴∠ADF =∠ACE ∵ AC =AD ∴ 直角△AFD ≌直角△AEC∴ AE =AF …… 9分 26. (本题满分13分)解:过点P 作PQ ⊥x 轴于Q ,则PQ =n ,OQ =m (1) 当n =1时, s =54…… 1分图 10∴ a =2s n =52…… 3分(2) 解1: ∵ OP =AP PA ⊥OP∴△OPA 是等腰直角三角形 …… 4分 ∴ m =n =a2 …… 5分∴ 1+n 44=12·an即n 4-4n 2+4=0 …… 6分 ∴ k 2-4k +4=0∴ k =2 …… 7分 解2:∵ OP =AP PA ⊥OP∴△OPA 是等腰直角三角形 …… 4分 ∴ m =n …… 5分 设△OPQ 的面积为s 1 则:s 1=s2∴ 12·mn =12(1+n 44) 即:n 4-4n 2+4=0 …… 6分 ∴ k 2-4k +4=0∴ k =2 …… 7分 (3) 解1:∵ PA ⊥OP , PQ ⊥OA∴ △OPQ ∽△OAP 设:△OPQ 的面积为s 1,则s 1s =PO 2AO 2…… 8分 即:12k 1+n 44 =n 2+k 2n2 4 (1+n 44)2n2化简得:2n 4+2k 2-k n 4-4k =0 …… 9分(k -2)(2k -n 4)=0 ∴k =2或k =n 42(舍去) …… 10分∴当n 是小于20的整数时,k =2. ∵ OP 2=n 2+m 2=n 2+k 2n2又m >0,k =2,∴ n 是大于0且小于20的整数 当n =1时,OP 2=5 当n =2时,OP 2=5当n =3时,OP 2=32+432=9+49=859 …… 11分当n 是大于3且小于20的整数时,即当n =4、5、6、…、19时,OP 2得值分别是: 42+442、52+452、62+462、…、192+4192∵192+4192>182+4182>…>32+432>5 …… 12分 ∴ OP 2的最小值是5. …… 13分解2: ∵ OP 2=n 2+m 2=n 2+k 2n2=n 2+22n2=(n -2n )2 +4 …… 11分当n =2n时,即当n =2时,OP 2最小;又∵n 是整数,而当n =1时,OP 2=5;n =2时,OP 2=5 …… 12分 ∴ OP 2的最小值是5. …… 13分 解3:∵ PA ⊥OP , PQ ⊥OA ∴ △OPQ ∽△P AQPQ QA =OQPQ…… 8分 n a -m =mn化简得:2n 4+2k 2-k n 4-4k =0 …… 9分(k -2)(2k -n 4)=0 ∴k =2或k =n 42(舍去) …… 10分解4:∵ PA ⊥OP , PQ ⊥OA ∴ △OPQ ∽△P AQs 1s -s 1=OQ 2PQ2 …… 8分 化简得:2n 4+2k 2-k n 4-4k =0 …… 9分(k -2)(2k -n 4)=0 ∴k =2或k =n 42(舍去) …… 10分解5:∵ PA ⊥OP , PQ ⊥OA ∴ △OPQ ∽△OAP ∴OP OA =OQOP…… 8分 ∴ OP 2=OQ·OA化简得:2n 4+2k 2-k n 4-4k =0 …… 9分(k -2)(2k -n 4)=0∴k =2或k =n 42(舍去) …… 10分。
福建省厦门市2022年初中毕业及高中阶段各类学校招生考试化学试卷

福建省厦门市2022年初中毕业及高中阶段各类学校招生考试化学试卷(试卷满分:100分;考试时间:90分钟)考生注意:1.本学科有两张试卷,一是答题卡,另一是本试题(共7页25题)。
请将全部答案填在答题卡的相应答题栏内,否则不能得分。
2.可能用到的相对原子质量:H—1 C—12 O—16 K-39一、选择题(本题15小题,共30分,每小题仅有一个..正确选项,请在答题卡选择题栏内用2B铅笔将正确选项涂黑)题记:化学此在我们身边,化学与我们息息相关1.小明的食谱中有猪肉、米饭、食盐、矿泉水。
从均衡营养的角度,小明还需增加摄入A.蛋白质 B.糖类 C.无机盐 D.维生素2.右图是人体不可缺少的钙元素的原子结构示意图,则钙原子的A.质子数为20 B.电子层数为3C.最外层电子数为10 D.核外电子数为403.下列说法,你认为正确的是A.人类利用的能量都是通过化学反应获得的B.现代化学技术可在只有水的条件下生产汽油C.CO2会使全球变暖,所以大气中CO2越少越好D.在使用乙醇等新型燃料时,也要注意可能造成的环境污染4.下列事故处理方法,不正确的是A.电器着火,立即用水扑灭B.炒菜时油锅着火,立即盖上锅盖C.厨房煤气管道漏气,立即关闭阀门并开窗通风D.图书馆内图书着火,立即用液态二氧化碳灭火器扑灭5.常用抗生素“先锋Ⅵ”为粉末状固体,每瓶含“先锋Ⅵ”0.5g,注射时应配成质量分数不高于20%的溶液,则使用时每瓶至少需加入蒸馏水A.1mL B. 2 mL C. 3mL D. 4 mL题记:化学是二十一世纪最有用,最有创造力的中心学科6.在厦参加国际磷化学会议的科学家认为无磷洗涤剂洗涤效果差,污染更严重,建议在建立磷回收机制后,重新使用加有磷化合物的含磷洗涤剂。
对此的下列说法不正确的是A.含磷洗涤剂含有磷元素 B.只要解决污染问题,可能重新使用含磷洗涤剂C.含磷洗涤剂含有磷单质 D.研究高效无污染的洗涤剂仍是化学家的任务7.下列科技成果不属于化学成就的是A.厦大研制的二十四面体铂纳米晶粒催化剂比传统铂催化剂的催化效率高4倍B.美国科学家罗杰发现“真核转录的分子基础”,获得诺贝尔奖C.厦门纳润公司川高分子材料生产的“隐形手套”,可保护人手不被浓硫酸腐蚀D.美国科学家约翰等发现“宇宙微波背景辐射的黑体形式”,获得诺贝尔奖8.随着科技的发展,人们有可能通过操纵单个原子来制造分子。
(整理)厦门中考数学试卷

2011年厦门市初中毕业及高中阶段各类学校招生考试数 学(试卷满分: 150分 考试时间120分钟 )一、选择题(本大题有7小题,每小题3分,共21分。
每小题都有四个选项,其中有且只有一个选项是正确的) 1.化简|2|-等于( )A .2B . 2-C .2±D .122.下列事件中,必然事件是( )A .掷一枚普通的正方体骰子,骰子停止后朝上的点数是1B . 掷一枚普通的正方体骰子,骰子停止后朝上的点数是偶数C . 掷一枚普通的硬币,掷得的结果不是正面就是反面D . 从99个红球和一个白球的布袋中随机取出一个球,这个球是红球 3.下列物体中,俯视图为矩形的是( )A .B .C .D . 4.下列计算结果正确的是( )A .2a a a ⋅=B .22(3)6a a = C .22(1)1a a +=+ D .2a a a +=5.如图1,在正方形网格中,将△ABC 绕点A 旋转后得到△ADE ,则下列旋转方式中,符合题意的是 A .顺时针旋转90° B .逆时针旋转90° C .顺时针旋转45° D .逆时针旋转45°6.已知⊙O 1,和⊙O 2的半径分别为5和2,O 1 O 2=3,则⊙O 1,和⊙O 2的位置关系是 A .外离 B .外切 C .相交 D .内切7. 如图2,铁道口的栏杆短臂OA 长1m ,长臂OB 长8m ,当短臂外端A 下降0.5m 时,长臂外端B 升高 A .2m B .4m C .4.5 D .8m图1 图2二、填空题(本大题有10小题,每小题4分,共40分) 8.13的相反数是 。
9.若∠A =30°,则∠A 的补角是 。
10.将1 200 000用科学记数法表示为 。
11.某年6月上旬,厦门市日最高气温气温如下表所示:那么这些日最高气温的众数为 ℃12.一个n 边行的内角和是720°,则边数n = 。
2023年厦门市中考英语真题及答案

厦门2023年初中毕业及高中阶段各类学校招生考试英语试题(满分:150分;考试时间:120分钟)第一部分(选择题)(二)基础知识与运用(每题1分,共30分)V.选择填空:从A、B、C中,选出一种最佳答案完毕句子。
21. —Well, a bowl of noodles with beef and tomato. OK, then what _______ would you like, sir?—A small bowl, please.A. priceB. timeC. size22. Thank you so much. I really like ________ scarf you gave me yesterday. It looks very nice.A. aB. theC. /23. —Who helped you repair the MP4?—________. I repaired it all by myself.A. SomebodyB. AnybodyC. Nobody24. —Mum, I got the best grade in the English test today.—Well done, son. I’m very ________ of you.A. proudB. tiredC. afraid25. —Do you know Jimmy?—Sure. He is one of my best friends. I know him very ________.A. littleB. wellC. alone26. The world is becoming smaller and smaller because the Internet gets us ________.A. closerB. biggerC. farther27. —How do you like the songs sung by Jay Chou?—They are wonderful, ________ I can’t hear the words clearly sometimes.A. thoughB. becauseC. so28. Many kinds of animals are ________. We must do something to save them.A. on holidayB. in dangerC. on show29. —Why don’t you take the computer, Nick? I know you’re a computer fan.—It’s too expensive. I can’t ________ it.A. sellB. borrowC. afford30. He has no ideas of his own, so he always ________ his friends about everything.A. plays withB. argues withC. agrees with31. —Do you like the song You and Me?—Of course. It ________ great.A. soundsB. looksC. smells32. You needn’t write letters to your cousin. You ________ chat with her by instead.A. mustB. have toC. can33. —Jane, hurry up! It’s time to leave.—OK. ________.A. I comeB. I’ve comeC. I’m coming34. —Excuse me, sir. This is a non-smoking room.—Oh, sorry. I ________ the sign.A. don’t seeB. didn’t seeC. won’t see35. —________were you away from school last term?—More than two weeks.A. How oftenB. How longC. How soon36. The Chinese mainland pandas, Tuan Tuan and Y uan Yuan, ________ to Taiwan on Dec. 23, 2023.A. sentB. were sendingC. were sent37. —What do you do?—________.A. I’m a reporterB. I like doing sportsC. I have to go now38. —Could you tell me ________? I must find her.—Sorry. I don’t know. But she was here just now.A. where Kitty wasB. where Kitty isC. where is Kitty39. —I will take my driving test tomorrow.—________!A. CheersB. Good luckC. Congratulations40. —I was terribly ill yesterday, so I missed the match.—________.A. I’m sorry to hear thatB. I don’t like the matchC. The match was greatVI. 完形填空:从A、B、C中,选择一种最佳答案,使短文意思完整。
厦门市教育局关于印发厦门市2024年高中阶段学校招生工作方案的通知

厦门市教育局关于印发厦门市2024年高中阶段学校招生工作方案的通知文章属性•【制定机关】厦门市教育局•【公布日期】2024.03.01•【字号】厦教发〔2024〕12号•【施行日期】2024.03.01•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】教育综合规定正文厦门市教育局关于印发厦门市2024年高中阶段学校招生工作方案的通知各区教育局,市直属中小学、中等职业学校,市招考中心,市教科院等有关单位:《厦门市2024年高中阶段学校招生工作方案》已经研究通过,现予印发,请遵照执行。
厦门市教育局2024年3月1日厦门市2024年高中阶段学校招生工作方案为贯彻落实中共中央国务院关于深化新时代教育评价和推进普通高中育人方式改革精神,根据教育部、福建省教育厅和我市有关考试招生制度改革意见等,制定本方案。
一、组织领导成立厦门市2024年中招领导小组,统一领导全市高中阶段学校招生工作。
厦门市教育招生考试中心(以下简称“市招考中心”)负责组织报名、考务、评卷和录取等工作,厦门市教育科学研究院(以下简称“市教科院”)负责市级统考科目命题工作。
各区相应成立中招领导小组,负责本区中招工作。
各校成立招生工作小组,开展本校中招工作。
二、报名(一)报名时间全市统一报名时间为2024年3月6日至3月11日;因特殊原因错过报名的,可于3月22日至3月23日补报名。
(二)报名片区全市划分为三个招生报名片区,即思明湖里片区、集美海沧片区、同安翔安片区。
考生应在相应招生片区的报名点报名:1.学籍所在校。
2.各区指定的社会报名点。
(三)报名对象1.本市学籍的应届初中毕业生,原则上在学籍所在校报名。
2.本市户籍在外地就学的应届初中毕业生,在户籍所在区社会报名点报名。
3.具有同等学力的本市户籍社会青年(含往届生),在户籍所在区社会报名点报名。
(四)报名注意事项1.补报名考生统一到户籍所在区社会报名点报名。
2.高中阶段学校在校生不得报名。
厦门市中考招生考试

厦门市中考招生考试[文档模板范本]厦门市中考招生考试一、考试时间和地点1.考试时间:2022年6月12日(星期六)2.报到时间:上午8:00-8:303.考试时间:上午9:00-11:304.考试地点:厦门市内各中学(详见准考证)二、考试内容1.语文:阅读理解、完形填空、翻译、作文(时间:120分钟)2.数学:选择题、填空题、解答题(时间:120分钟)3.英语:阅读理解、完形填空、短文填空、翻译、作文(时间:120分钟)4.物理:选择题、填空题、解答题(时间:80分钟)5.化学:选择题、填空题、解答题(时间:80分钟)6.历史:选择题、填空题、解答题(时间:80分钟)7.思品:选择题、简答题、论述题(时间:80分钟)三、考生注意事项1.考生应提前一天查看准考证,并确认考试地点。
2.考试前半小时报到,考试开始前请提前领取试卷和答题卡。
3.考生应当按规定时间完成答题,并在规定的时间内交回试卷和答题卡。
4.考试期间禁止做弊,一经发现,将取销考试资格。
5.考生在考试期间如有身体不适、特殊情况等,应及时向监考人员说明情况。
四、考试评分标准1.试题总分265分,满分600分。
2.各科目满分如下:语文150分,数学100分,英语150分,物理80分,化学80分,历史80分,思品75分。
3.各科目评分标准根据教育部门规定执行,具体详情请咨询当地考试中心。
总结:本文档所涉及简要注释如下:1.厦门市中考招生考试:指厦门市所举办的针对中学毕业生的入学考试。
2.试卷和答题卡:考试时提供给考生的题目和答题用纸。
其中,试卷是考生在答题卡上填写答案的依据。
本文档所涉及的法律名词及注释:暂无。
厦门市2019年中考数学试题含答案(word版)

2019年厦门市初中毕业及高中阶段各类学校招生考试数 学(试卷满分:150分 考试时间:120分钟)准考证号 姓名 座位号注意事项:1.全卷三大题,27小题,试卷共4页,另有答题卡. 2.答案一律写在答题卡上,否则不能得分.3.可直接用2B 铅笔画图.一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确) 1. 反比例函数y =1x的图象是A . 线段B .直线C .抛物线D .双曲线2. 一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,投掷这样的骰子一次,向上一面点数是偶数的结果有A .1种B . 2种C . 3种D .6种3. 已知一个单项式的系数是2,次数是3,则这个单项式可以是 A . -2xy 2 B . 3x 2 C . 2xy 3 D . 2x 34. 如图1,△ABC 是锐角三角形,过点C 作CD ⊥AB ,垂足为D ,则点C 到直线AB 的距离是 A . 线段CA 的长 B .线段CD 的长 C . 线段AD 的长 D .线段AB 的长 5. 2—3可以表示为A .22÷25B .25÷22C .22×25D .(-2)×(-2)×(-2)6.如图2,在△ABC 中,∠C =90°,点D ,E 分别在边AC ,AB 上, 若∠B =∠ADE ,则下列结论正确的是A .∠A 和∠B 互为补角 B . ∠B 和∠ADE 互为补角C .∠A 和∠ADE 互为余角D .∠AED 和∠DEB 互为余角图27. 某商店举办促销活动,促销的方法是将原价x 元的衣服以(45x -10) 元出售,则下列说法中,能正确表达该商店促销方法的是A . 原价减去10元后再打8折B . 原价打8折后再减去10元C . 原价减去10元后再打2折D . 原价打2折后再减去10元8. 已知sin6°=a ,sin36°=b ,则sin 2 6°=A . a 2B . 2aC . b 2D . b9.如图3,某个函数的图象由线段AB 和BC 组成,其中点 A (0,43),B (1,12),C (2,53),则此函数的最小值是A .0B .12C .1D .53图310.如图4,在△ABC 中,AB =AC ,D 是边BC 的中点,一个圆过点A ,交边AB 于点E ,且与BC 相切于点D ,则该圆的圆心是 A .线段AE 的中垂线与线段AC 的中垂线的交点 B .线段AB 的中垂线与线段AC 的中垂线的交点 C .线段AE 的中垂线与线段BC 的中垂线的交点 D .线段AB 的中垂线与线段BC 的中垂线的交点图4二、填空题(本大题有6小题,每小题4分,共24分)11.不透明的袋子里装有1个红球、1个白球,这些球除颜色外无其他差别.从袋子中随机摸出一个球,则摸出红球的概率是 . 12.方程x 2+x =0的解是 .13.已知A ,B ,C 三地位置如图5所示,∠C =90°,A ,C 两地的距离是B ,C 两地的距离是3 km ,则A ,B 两地的距离是 km ;若A 地在C 地的正东方向,则B地在C 地的 方向.14.如图6,在矩形ABCD 中,对角线AC ,BD 相交于点O ,E 是边AD 的中点, 图5若AC =10,DC =25,则BO = ,∠EBD 的大小约为 度 分.(参考数据:tan26°34′≈12)15.已知(39+813)×(40+913)=a +b ,若a 是整数,1<b <2,则a = . 图616.已知一组数据1,2,3,…,n (从左往右数,第1个数是1,第2个数是2,第3个数是3,依此类推,第n 个数是n ).设这组数据的各数之和是s ,中位数是k ,则s = (用只含有k 的代数式表示). 三、解答题(本大题有11小题,共86分)17.(本题满分7分)计算:1-2+2×(-3)2 . 18.(本题满分7分)在平面直角坐标系中,已知点A (-3,1),B (-2,0)C (0,1),请在图7中画出△ABC ,并画出与△ABC关于原点O 对称的图形. 图7 19.(本题满分7分)计算:xx +1+x +2x +1.20.(本题满分7分)如图8,在△ABC 中,点D ,E 分别在边AB ,AC 上,若DE ∥BC , AD =3 ,AB =5,求DEBC的值.21.(本题满分7分)解不等式组⎩⎨⎧2x >2,x +2≤6+3x .22.(本题满分7分)某公司欲招聘一名工作人员,对甲、乙两位应聘者进行面试和笔试,他们的成绩(百分制)如下表所示.若公司分别赋予面试成绩和笔试成绩6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?23.(本题满分7分)如图9,在△ABC 中,AB =AC ,点E ,F 分别是边AB ,AC 的中点,点D 在边BC 上. 若DE =DF ,AD =2,BC =6,求四边形AEDF 的周长.图924.(本题满分7分)已知实数a ,b 满足a -b =1,a 2-ab +2>0,当1≤x ≤2时,函数y =ax (a ≠0)的最大值与最小值之差是1,求a 的值.25.(本题满分7分)如图10,在平面直角坐标系中,点A (2,n ),B (m ,n )(m >2),D (p ,q )(q <n ),点B ,D 在直线y =12x +1上.四边形ABCD 的对角线AC ,BD 相交于点E ,且AB ∥CD ,CD =4,BE =DE ,△AEB 的面积是2.求证:四边形ABCD 是矩形.图1026.(本题满分11分)已知点A (-2,n )在抛物线y =x 2+bx +c 上. (1)若b =1,c =3,求n 的值; (2)若此抛物线经过点B (4,n ),且二次函数y =x 2+bx +c 的最小值是-4,请画出点P (x -1,x 2+bx +c )的纵坐标随横坐标变化的图象,并说明理由.27.(本题满分12分)已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB,延长DA,CB相交于点E.(1)如图11,EB=AD,求证:△ABE是等腰直角三角形;(2)如图12,连接OE,过点E作直线EF,使得∠OEF=30°.当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.图112019年厦门市初中毕业及高中阶段各类学校招生考试数学参考答案说明:解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照评分量表的要求相应评分.一、选择题(本大题共10小题,每小题4分,共40分)二、填空题(本大题共6小题,每题4分,共24分)11. 12 12. 0,-1 13. 5;正北14. 5,18,26 15. 1611 16. 2k 2-k三、解答题(本大题共9小题,共86分) 17.(本题满分7分)解: 1-2+2×(-3)2=-1+2×9=17. ……………………………7分 18.(本题满分7解:……………………………7分19.(本题满分7分) 解:xx +1+x +2x +1=2x +2x +1……………………………5分 =2 ……………………………7分 20.(本题满分7分)解:∵ DE ∥BC ,∴ △ADE ∽△ABC . ……………………………4 ∴ DE BC =ADAB . ……………………………6分 ∵ AD AB =35,∴ DE BC =35. ……………………………7分21.(本题满分7分)解:解不等式2x >2,得x >1. ……………………………3分解不等式x +2≤6+3x ,得x ≥-2. ……………………………6分不等式组⎩⎨⎧2x >2,x +2≤6+3x的解集是x >1. ……………………………7分22.(本题满分7分)解:由题意得,甲应聘者的加权平均数是6×87+4×906+4=88.2. ……………………………3分乙应聘者的加权平均数是6×91+4×826+4=87.4. ……………………………6分∵88.2>87.4,∴甲应聘者被录取. ……………………………7分 23.(本题满分7分)解:∵AB =AC ,E ,F 分别是边AB ,AC 的中点,∴AE =AF =12AB . ……………………………1分又∵DE =DF ,AD =AD ,∴△AED ≌△AFD . ……………………………2分 ∴∠EAD =∠F AD .∴AD ⊥BC , ……………………………3分 且D 是BC 的中点.在R t △ABD 中,∵E 是斜边AB 的中点,∴DE =AE . ……………………………6分 同理,DF =AF .∴四边形AEDF 的周长是2AB . ∵BC =6,∴BD =3.又AD =2,∴AB =13.∴四边形AEDF 的周长是213. ……………………………7分 24.(本题满分7分)解1:由a -b =1,a 2-ab +2>0得,a >-2. ……………………………2分∵a ≠0,(1)当-2<a <0时, ……………………………3分 在1≤x ≤2范围内y 随x 的增大而增大, ∴ a2-a =1. ∴ a =-2 ……………………………4分 不合题意,舍去.(2)当a >0时, ……………………………5分 在1≤x ≤2范围内y 随x 的增大而减小,∴ a -a2=1.∴ a =2. ……………………………6分 综上所述a =2. ……………………………7分解2:(1)当a <0时, ……………………………1分 在1≤x ≤2范围内y 随x 的增大而增大, ∴ a2-a =1. ∴ a =-2. ……………………………2分 ∴ b =-3.而a 2-ab +2=0,不合题意,∴a ≠-2. ……………………………3分 (2)当a >0时, ……………………………4分 在1≤x ≤2范围内y 随x 的增大而减小, ∴ a -a2=1.∴ a =2. ……………………………5分 ∴ b =1. 而a 2-ab +2=4>0,符合题意,∴ a =2. ……………………………6分 综上所述, a =2. ……………………………7分25.(本题满分7分)解1:∵ AB ∥CD ,∴∠EAB =∠ECD ,∠EBA =∠EDC . ∵ BE =DE ,∴ △AEB ≌△CED . ……………………………1分 ∴ AB =CD =4.∵AB ∥CD ,∴四边形ABCD 是平行四边形. ……………………………2分 A (2,n ),B (m ,n )(m >2), ∴ AB ∥x 轴,且CD ∥x 轴.∵ m >2,∴m =6. ……………………………3分 ∴n =12×6+1=4.∴ B (6,4). ∵△AEB 的面积是2,∴△AEB 的高是1. ……………………………4分 ∴平行四边形ABCD 的高是2. ∵ q <n , ∴q =2.∴p =2, ……………………………5分 即D (2,2). ∵点A (2,n ),∴DA ∥y 轴. ……………………………6分∴AD ⊥CD ,即∠ADC =90°.∴四边形ABCD 是矩形. ……………………………7分解2:∵AB ∥CD ,∴∠EAB =∠ECD ,∠EBA =∠EDC . ∵ BE =DE ,∴ △AEB ≌△CED . ……………………………1分∴ AB =CD =4. ∵AB ∥CD ,∴四边形ABCD 是平行四边形. ……………………………2分 ∵A (2,n ),B (m ,n )(m >2), ∴ AB ∥x 轴,且CD ∥x 轴.∵ m >2,∴m =6. ……………………………3分 ∴n =12×6+1=4.∴ B (6,4).过点E 作EF ⊥AB ,垂足为F , ∵△AEB 的面积是2,∴EF =1. ……………………………4分 ∵ q <n ,∴点E 的纵坐标是3. ∴点E 的横坐标是4.∴点F 的横坐标是4. ……………………………5分 ∴点F 是线段AB 的中点.∴直线EF 是线段AB 的中垂线.∴EA =EB . ……………………………6分 ∵四边形ABCD 是平行四边形, ∴AE =EC ,BE =ED .∴AC =BD .∴四边形ABCD 是矩形. ……………………………7分 26.(本题满分11分)(1)解:∵ b =1,c =3,∴ y =x 2+x +3. ……………………………2分 ∵点A (-2,n )在抛物线y =x 2+x +3上,∴n =4-2+3 ……………………………3分 =5. ……………………………4分 (2)解:∵点A (-2,n ),B (4,n )在抛物线y =x 2+bx +c 上,∴⎩⎨⎧4-2b +c =n ,16+4b +c =n .∴b =-2.∴顶点的横坐标是-b2=1.即顶点为(1,-4). ∴-4=1-2+c .∴c =-3. ……………………………7分∴P (x -1,x 2-2x -3).∵将点(x ,x 2-2x -3)向左平移一个单位得点P (x -1,x 2-2x -3), ∴将点(x ,x 2-2x -3)的纵坐标随横坐标变化的函数的图象向左平移 一个单位后可得点P (x -1,x 2-2x -3)的纵坐标随横坐标变化的函 数的图象. ……………………………8分 设p =x -1,q =x 2-2x -3,则q =p 2-4.画出抛物线q =p 2-4的图象. ……………………………11分 27.(本题满分12分)(1)证明:∵四边形ABCD 内接于⊙O ,∠ADC =90°,∴∠ABC =90°.∴∠ABE =90°. ……………………………1分 ∵AC 平分∠DCB ,∴∠ACB =∠ACD . ……………………………2分 ∴AB =AD . ……………………………3分 ∵EB =AD ,∴EB =AB . ……………………………4分∴△ABE 是等腰直角三角形. ……………………………5分(2)直线EF 与⊙O 相离.证明:过O 作OG ⊥EF ,垂足为G . 在Rt △OEG 中, ∵∠OEG =30°,∴OE =2OG . ……………………………6分∵∠ADC =90°,∴AC 是直径. 设∠ACE =α,AC =2r . 由(1)得∠DCE =2α,又∠ADC =90°, ∴∠AEC =90°-2α. ∵α≥30°,∴(90°-2α)-α≤0. ……………………………8分 ∴∠AEC ≤∠ACE .∴AC ≤AE . ……………………………9分 在△AEO 中,∠EAO =90°+α, ∴∠EAO >∠AOE .∴EO >AE . ……………………………10分 ∴EO -AE >0.由AC ≤AE 得AE -AC ≥0. ∴EO -AC =EO +AE -AE -AC=(EO -AE )+(AE -AC )>0. ∴EO >AC . 即2OG ≥2r .∴OG >r . ……………………………11分 ∴直线EF 与⊙O 相离. ……………………………12分。
厦门市中考语文试卷及解析

厦门市中考语文试卷及解析2021年厦门市课改实验区初中毕业高中时期各类学校招生考试语文试题第一部分听力(满分:20分)[一]完成1-10题(20分)1.听读徐志摩《再别康桥》中的两句诗,判定最后一个词读音正确的一项:(2分)A.yúncǎiB.yíncǎiC.yúnchǎi2.下面一句话要强调“王大爷快乐极了”,朗读停顿正确的是哪一项?(2分)A.B.C.3.听下面一段话,判定福建省唯独的火炬手跑的是第几棒?(2分)A.第88棒B.第99棒C.第1棒4.听下面一段话,判定这段话要紧说明了什么?(2分)A.观看蚂蚁有助于了解气候变化情形。
B.蚂蚁喜爱在干燥地点挖穴筑巢。
C.有关蚂蚁的谚语通俗生动易念易记。
5.听下面一段话,判定对文段内容概括正确的是哪一项?(2分)A.描画今日“三湾”的优美景观。
B.交代“三湾”治理差不多开始。
C.展现“三湾”治理的美好前景。
听下面一段话,回答第6题和第7题:6.判定与这段话的主旨关系最紧密的是哪一项?(2分)A.师生关系B.儿童天性C.学校治理7.判定这段话中“蹲下来”一词的含义是什么?(2分)A.指两腿尽量弯曲,像坐的模样。
B.指老师要从小孩的角度去明白得学生。
C.指老师说话、做事、穿着要尽量儿童化。
8.听下面一段话,把高尔基的名言正确的记录下来。
(2分)9.听下面一段话,顾客话中的言外之意是什么?(2分)10.在下面这种情形下,你如何样用文明得体的话回答同桌胡小勇?(2分)第二部分语言积存与运用(满分:16+3分)[二]完成11-15题(16+3分)11.古人云:“腹有诗书气自华”。
请依照下列提示填空:(8+3分)(1)生,亦我所欲也,义,亦我所欲也;二者不可得兼,。
(《鱼我所欲也》)(1分)(2)子在川上,曰:“,。
”(《<论语>十则》)(2分)(3)“乡愁”是古今许多诗词共同的主题之一。
厦门市2008年初中毕业和高中阶段各类学校招生考试
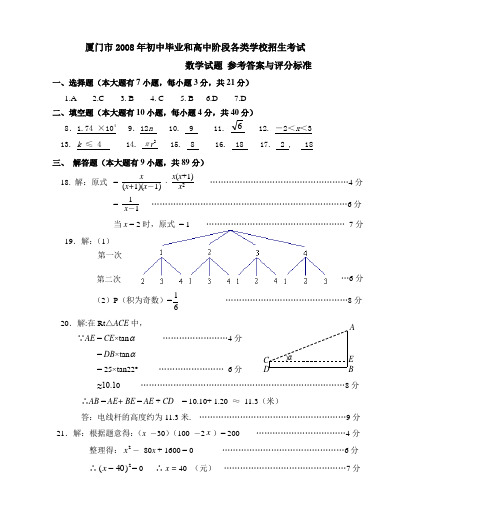
厦门市2008年初中毕业和高中阶段各类学校招生考试数学试题 参考答案与评分标准一、选择题(本大题有7小题,每小题3分,共21分) 1.A 2.C 3. B 4. C 5. B 6.D 7.D 二、填空题(本大题有10小题,每小题4分,共40分)8.1.74 ×1049.12n 10. 9 11. 12. -2<x <313. k ≤ 4 14. πr 215. 8 16. 18 17. 2 , 18 三、 解答题(本大题有9小题,共89分) 18. 解:原式 =x (x+1)(x -1) · x (x +1)x 2 ……………………………………………4分= 1 x -1 ………………………………………………………………6分 当x = 2时,原式 = 1 …………………………………………… 7分19.解:(1)(2)P (积为奇数)=61………………………………………8分 20.解:在Rt △ACE 中,∵AE = CE ×tan α ……………………4分= DB ×tan α= 25×tan22° …………………… 6分≈10.10 …………………………………………………………………8分 ∴AB = AE+ BE = AE + CD = 10.10+ 1.20 ≈ 11.3(米)答:电线杆的高度约为11.3米. ………………………………………………9分 21.解:根据题意得:(x -30)(100 -2x )= 200 ……………………………4分整理得:2x - 80x + 1600 = 0 ………………………………………6分 ∴2)40(-x = 0 ∴ x = 40 (元) ………………………………………7分6EACBD)α …6分第一次第二次∴p = 100-2x = 20(件) …………………………………………8分 答:每件商品的售价应定为40元,每天要销售这种商品20件. ……………9分 22.解:(1)设反比例函数关系式为 y = kx∵反比例函数图象经过点P (-2,1),∴ k = -2 ……………………………2分 ∴反比例函数关系式y = - 2x ……3分(2)∵点Q (1,m )在y = - 2x 上∴m = -2 ………………………………5分 ∴ Q (1, -2) ………………………………6分 (3)示意图 …………………………… 8分当x <-2或0<x <1时,一次函数的值大于反比例函数的值 …………10分 23.(1)证明: ∵ AB = AC∴ ∠C =∠B ……………………………………………………………1分 又OP = OB,∠OPB =∠B ………………………………………………………… 2分 ∴ ∠C = ∠OPB ………………………………………………………… 3分 ∴ OP ∥AD ………………………………4分 又 ∵PD ⊥AC 于D ∴ ∠ADP = 90° ∴ ∠DPO = 90° ………………………………5分 ∴ PD 是⊙O 的切线 ………………………6分 (2)连结AP ,∵AB 是直径,∴ ∠A PB = 90° ………………………………8分 AB = AC = 2, ∠ CAB = 120°∴ ∠ BAP = 60° ………………………………………………………………9分 ∴ BP = 3 ∴ BC = 2 3. ……………………………………………10分 24.解:(1)依题意得:2)1( +(b -1)(-1) + c = -2b …2分∴ b + c = -2 …………………………………………………………3分 (2)当b = 3 时,c = -5 ……………………………………………4分yx-2-1 1∴ y = 2x + 2x -5 = 6)1(2-+x∴ 抛物线的顶点坐标是(-1,-6) ………………………………………6分 (3)当b >3时,抛物线对称轴x = 21--b < -1 , ∴对称轴在点P 的左侧,因为抛物线是轴对称图形,P (-1,-2b ) 且BP = 2P A , ∴ B (- 3,-2b ) …………………9分∴ 21--b = -2 ∴ b = 5 ………………………………10分 又 b +c = -2, ∴c = -7 ……11分 ∴抛物线所对应的二次函数关系式y = 2x + 4x -7 …12解法2.(3)当b >3时,x = 21--b <- 1 , ∴ 对称轴在点P 的左侧,因为抛物线是轴对称图形,∵ P (-1, -2b ),且BP =2P A ,∴ B (- 3,-2b ) ……………………9分∴ 2)3(--3(b -1)+ c = -2b ……………………………………………10分 又b + c = -2 解得:b = 5 c = -7 ……………………11分 ∴这条抛物线对应的二次函数关系式是y = 2x + 4x -7 ……………12分 解法3.(3)∵ b + c = -2,∴ c = -b -2∴ y = 2x +(b -1)x -b - 2 …………………………………………7分 BP ∥x 轴 ∴ 2x +(b -1)x -b - 2 = -2b ……………………………8分 即:2x +(b -1)x +b - 2 = 0解得:x 1 = -1, x 2 = -(b -2) 即 x B = -(b -2) ………………10分 由BP =2P A ∴ -1 +(b -2)= 2×1∴ b = 5, c = -7 …………………………………………………11分 ∴ 这条抛物线对应的二次函数关系式是y = 2x + 4x -7 ……………12分AO P B25.解:(1)连结EF 交AC 于O , 当顶点A 与C 重合时,折痕EF 垂直平分AC ,∴ OA = OC ∠AOE =∠COF = 90° ……………………1分∵ 在平行四边形ABCD 中,AD ∥BC., ∴ ∠EAO = ∠FCO , ∴ △AOE ≌ △COF∴ OE = OF ……………………………………………………………2分∴ 四边形AFCE 是菱形. …………………………………………………3分 (2)四边形AFCE 是菱形, ∴AF = AE = 10 设AB = x , BF = y ∵∠B = 90°∴ x 2+ y 2 = 100 ……………………………………………………………4分 ∴ 2)(y x +-2xy = 100 ①又∵S △ABF = 24 ∴12 xy = 24 则xy = 48 ② …………………… 5分由 ①、②得:2)(y x + = 196 …………………………6分 ∴ x + y = ± 14, x+y = -14(不合题意舍去)∴△ABF 的周长为x + y+ AF = 14 + 10 = 24 ……………………7分 (3) 过E 作EP ⊥AD 交AC 于P ,则P 就是所求的点. ……………………9分 证明:由作法,∠AEP = 90°,由(1)得:∠AOE = 90° , 又 ∠EAO =∠EAP ,∴ △AOE ∽ △AEP ∴ AE AP = AO AE 则 AE 2 = AO ·AP ……………………………………10分 ∵ 四边形AFCE 是菱形 ,∴ AO = 12AC ∴ AE 2 = 12AC ·AP ……………11分∴ 2AE 2 = AC ·AP …………………………………………………12分 26.解:(1)∵∠OAB = 90° OA = 2 , AB = 2 3. ∴ OB = 4 ……………2分∵BM OM = 12 ∴ 4 -OM OM = 12 , ∴ OM = 83……………3分 (2) 由(1)得: OM = 83,∴BM = 43EAC B DO P∵DB ∥OA 易证DB OA = BM OM = 12………………………………………4分 ∴DB = 1 ,D ( 1, 23) …………………………………………5分 ∴ 过OD 的直线所对应的函数关系式是y = 23x(3) 依题意:当0 <t ≤ 83 时,E 在OD 边上, 分别过E 、P 作EF ⊥OA , PN ⊥OA , 垂足分别为F 和N ∵ tan ∠PON =232= 3, ∴∠PON = 60° OP = t ∴ ON = 12 t , PN = 32 t ,∵ 直线OD 所对应的函数关系式是y=23x∴ 设E (n , 23n ) ………………………………………………………7分 易证得 △APN ∽△AEF ∴PN EF = ANAF∴ 32 t 23n = 2-12 t 2-n ……………………………………………………………8分整理得:t2n = 4-t 2-n∴ 8n -n t = 2 t n (8-t ) = 2t ∴ n =2t8-t……………………………9分 由此,S △AOE = 12OA·EF = 12×2×23×2t8-t∴S =43t 8-t (0 < t ≤ 83) 分 当 83<t <4时,点E 在BD 边上, 此时,S = S 梯形OABD -S △ABE ∵DB ∥OA易证:∴△EPB ∽△APO ∴BE OA = BP OP ∴ BE 2 = 4-t ttS △ABE = 12BE·AB = 12× 2(4 -t )t ×23 = 4 -t t ×23∴S = 12(1+2) ×23- (4 -t ) t ×2 3 = 33- 4 -t t ×2 3 = -83t+5 3综上所述:⎪⎪⎩⎪⎪⎨⎧<<+≤<= 4 t 38 35 t38 -38t 0 t -8t 34S …………………………………12分(1)解法2:∵∠OAB = 90°,OA = 2 , AB = 2 3.易求得:∠OBA =30° ∴ OB = 4 ……………………………2分 (3)解法2: 分别过E 、P 作EF ⊥OA , PN ⊥OA , 垂足分别为F 和N , 由(1)得,∠OBA =30°∵OP = t , ∴ON = 12 t , PN = 32 t ,即:P (12 t , 32t )又A ( 2 , 0 ) ,设经过A 、P 的直线所对应的函数关系式是y = kx + b则 ⎩⎪⎨⎪⎧12 tk + b = 32 t 2k + b = 0 解得:k = - 3t 4-t , b = 23t4-t……………………7分∴经过A 、P 的直线所对应的函数关系式是y=- 3t 4-t x + 23t 4-t依题意:当0 < t ≤ 83 时,E 在OD 边上,∴E (n , 23n )在直线AP 上,∴ - 3t 4-t n + 23t4-t = 23n ……………………………………………………8分整理得:t n t -4 - 2t t -4 = 2n∴ n =2t8 -t ………………………………………………………9分8 -t 3当83<t <4时,点E 在BD 上,此时,点E 坐标是(n, 23),因为E 在直线AP 上 ∴ - 3t 4-t n + 23t4-t= 23整理得:t n t -4 + 2t t -4 = 2 ∴8n -nt = 2t∴ n =4t -8t…………………………………………………………11分 BE = 2- n = 2 - 4t -8t = 2(4 -t )t∴S = 12(1+2) ×23- (4 -t ) t ×23= 33- 4 -t t ×2 3 = -83t+5 3综上所述:⎪⎪⎩⎪⎪⎨⎧<<+≤<= 4 t 38 35 t 38 -38t 0 t -8t 34S ……………………………………12分。
2022年厦门市中考数学试题及答案

2022年厦门市初中毕业及高中阶段各类学校招生考试数学〔试卷总分值:150分考试时间:120分钟〕准考证号姓名座位号本卷须知:1.全卷三大题,26小题,试卷共4页,另有答题卡. 2.答案一律写在答题卡上,否那么不能得分. 3.可直接用2B 铅笔画图.一、选择题〔本大题有7小题,每题3分,共21分.每题都有四个选项,其中有且只有一个选项正确〕 1.-2的相反数是A .2B .-2C .±2D .-122.以下事件中,是必然事件的是A .抛掷1枚硬币,掷得的结果是正面朝上B .抛掷1枚硬币,掷得的结果是反面朝上C .抛掷1枚硬币,掷得的结果不是正面朝上就是反面朝上D .抛掷2枚硬币,掷得的结果是1个正面朝上与1个反面朝上 3.图1是一个立体图形的三视图,那么这个立体图形是A .圆锥B .球C .圆柱D .三棱锥4.某种彩票的中奖时机是1%,以下说法正确的选项是 A .买1张这种彩票一定不会中奖B .买1张这种彩票一定会中奖C .买100张这种彩票一定会中奖D .当购置彩票的数量很大时,中奖的频率稳定在1% 5.假设二次根式x -1有意义,那么x 的取值范围是 A .x >1B .x ≥1 C .x <1D .x ≤16.如图2,在菱形ABCD 中,AC 、BD 是对角线, 假设∠BAC =50°,那么∠ABC 等于 A .40°B .50° C .80°D .100°7.两个变量x 和y ,它们之间的3组对应值如下表所示.那么y 与x 之间的函数关系式可能是图1俯视图左视图正视图A .y =xB .y =2x +1C .y =x 2+x +1D .y =3x二、填空题〔本大题有10小题,每题4分,共40分〕 8.计算:3a -2a =.9.∠A =40°,那么∠A 的余角的度数是. 10.计算:m 3÷m 2=.11.在分别写有整数1到10的10张卡片中,随机抽取1张卡片,那么该卡片上的数字恰好是奇数的概率是. 12.如图3,在等腰梯形ABCD 中,AD ∥BC ,对角线AC与BD 相交于点O ,假设OB =3,那么OC =. 13.“x 与y 的和大于1”用不等式表示为.14.如图4,点D 是等边△ABC 内一点,如果△ABD 绕点A逆时针旋转后能与△ACE 重合,那么旋转了度. 15.五边形的内角和的度数是.16.a +b =2,ab =-1,那么3a +ab +3b =;a 2+b 2=.17.如图5,∠ABC =90°,AB =πr ,BC =πr2,半径为r的⊙O 从点A 出发,沿A →B →C 方向滚动到点C 时停止. 请你根据题意,在图5上画出圆心..O 运动路径的示意图; 圆心O 运动的路程是.三、解答题〔本大题有9小题,共89分〕 18.〔此题总分值18分〕〔1〕计算:4÷(-2)+(-1)2×40; 〔2〕画出函数y =-x +1的图象;〔3〕:如图6,点B 、F 、C 、E 在一条直线上,∠A =∠D ,AC =DF ,且AC ∥DF . 求证:△ABC ≌△DEF .19.〔此题总分值7分〕解方程组:⎩⎨⎧3x +y =4,2x -y =1.20.〔此题总分值7分〕:如图7,在△ABC 中,∠C =90°,点D 、E 分别在边AB 、AC上,DE ∥BC ,DE =3,BC =9.图6ABCDFE图4ABCDE图3ABDCOA DE〔1〕求ADAB的值;〔2〕假设BD =10,求sin ∠A 的值. 21.〔此题总分值7分〕A 组数据如下:0,1,-2,-1,0,-1,3.〔1〕求A 组数据的平均数;〔2〕从A 组数据中选取5个数据,记这5个数据为B 组数据.要求B 组数据满足两个条件:①它的平均数与A 组数据的平均数相等;②它的方差比A 组数据的方差大.你选取的B 组数据是,请说明理由. 【注:A 组数据的方差的计算式是S A 2=17[(x 1-—x )2+(x 2-—x )2+(x 3-—x )2+(x 4-—x )2+(x 5-—x )2+(x 6-—x )2+(x 7-—x )2]】22.〔此题总分值9分〕工厂加工某种零件,经测试,单独加工完成这种零件,甲车床需用x 小时,乙车床需用 (x 2-1)小时,丙车床需用(2x -2)小时.〔1〕单独加工完成这种零件,假设甲车床所用的时间是丙车床的23,求乙车床单独加工完成这种零件所需的时间;〔2〕加工这种零件,乙车床的工作效率与丙车床的工作效率能否相同请说明理由. 23.〔此题总分值9分〕:如图8,⊙O 是△ABC 的外接圆,AB 为⊙O 的直径,弦CD 交AB于E ,∠BCD =∠BAC . 〔1〕求证:AC =AD ;〔2〕过点C 作直线CF ,交AB 的延长线于点F ,假设∠BCF =30°,那么结论“CF 一定是⊙O24.〔此题总分值10分〕如图9果点P 在直线y =x -1上,且点P 到直线AB 的距离小于1,那么称点P 是线段AB 的“邻近点〞.〔1〕判断点C(72,52)是否是线段AB 的“邻近点〞,并说明理由;〔2〕假设点Q (m ,n )是线段AB 的“邻近点〞,求m 的取值范围.25.〔此题总分值10分〕□ABCD ,对角线AC 与BD 分别作PE ⊥AC 、PF ⊥BD ,垂足分别为E 、F 〔1〕如图10,假设PE =3,EO =1,求∠EPF 〔2〕假设点P 是AD 的中点,点F 是DO 的中点,图8BF =BC +32-4,求BC 的长.26.〔此题总分值12分〕点A (1,c )和点B (3,d )是直线y =k 1x +b 与双曲线y =k 2x〔k 2>0〕的交点.〔1〕过点A 作AM ⊥x 轴,垂足为M ,连结BM .假设AM =BM ,求点B 的坐标; 〔2〕设点P 在线段AB 上,过点P 作PE ⊥x 轴,垂足为E ,并交双曲线y =k 2x〔k 2>0〕于点N .当PN NE 取最大值时,假设PN =12,求此时双曲线的解析式.2022年厦门市初中毕业及高中阶段各类学校招生考试数学参考答案及评分标准说明:1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;2.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对此题的评阅.如果考生的解答在某一步出现错误,影响后续局部而未改变此题的内容和难度,视影响的程度决定后继局部的给分,但原那么上不超过后续局部应得分数的一半; 3.解答题评分时,给分或扣分均以1分为根本单位. 一、选择题〔本大题共7小题,每题3分,共21分〕题号 1 2 3 4 5 6 7 选项ACADBCB二、填空题〔本大题共10小题,每题4分,共40分〕 8. a . 9. 50°.10. m .11.12. 12. 3. 13. x +y >1.14. 60.15. 540°. 16. 5; 6. 17.;2πr .三、解答题〔本大题共9小题,共89分〕 18.〔此题总分值18分〕〔1〕解:4÷(-2)+(-1)2×40=-2+1×1 ··································································· 4分 =-2+1 ······································································· 5分 =-1.6分〔2〕解:正确画出坐标系8分正确写出两点坐标10分 画出直线12分〔3〕证明:∵AC ∥DF ,……13分∴∠ACB =∠DFE .……15分ABCFE又∵∠A =∠D ,……16分 AC =DF ,……17分 ∴△ABC ≌△EDF . ……18分19.〔此题总分值7分〕解1:⎩⎨⎧3x +y =4,①2x -y =1. ②①+②,得1分 5x =5,2分 x =1.4分将x =1代入①,得 3+y =4,5分 y =1.6分∴⎩⎨⎧x =1,y =1.7分 解2:由①得 y =4-3x . ③1分 将③代入②,得2x -(4-3x ) =1.2分 得x =1.4分将x =1代入③,得 y =4-3×15分 =1.6分∴⎩⎨⎧x =1,y =1.7分 20.〔此题总分值7分〕〔1〕解:∵DE ∥BC ,∴△ADE ∽△ABC .……1分∴AD AB =DEBC.……2分 ∴AD AB =13.……3分〔2〕解1:∵AD AB =13,BD =10,∴AD AD +10=134分 ∴AD =55分经检验,符合题意. ∴AB =15. 在Rt △ABC 中,6分Esin ∠A =BC AB =35. 7分解2:∵AD AB =13,BD =10,∴AD AD +10=134分 ∴AD =55分经检验,符合题意. ∵DE ∥BC ,∠C =90° ∴∠AED =90°在Rt △AED 中,6分 sin ∠A =ED AD =35. 7分解3:过点D 作DG ⊥BC ,垂足为G .∴DG ∥AC .∴∠A =∠BDG .4分又∵DE ∥BC ,∴四边形ECGD 是平行四边形. ∴DE =CG .5分 ∴BG =6.在Rt △DGB 中,6分∴sin ∠BDG =BD GB =35. 7分∴sin ∠A =35.21.〔此题总分值7分〕〔1〕解:A 组数据的平均数是0+1-2-1+0-1+371分=0.3分〔2〕解1:选取的B 组数据:0,-2,0,-1,3. 4分∵B 组数据的平均数是0.5分∴B 组数据的平均数与A 组数据的平均数相同.∴S B 2=145 ,S A 2=167.6分∴145>167.7分 ∴B 组数据:0,-2,0,-1,3.解2:B 组数据:1,-2,-1,-1,3.4分∵B 组数据的平均数是0.5分∴B 组数据的平均数与A 组数据的平均数相同.∵S A 2=167, S B 2=165. 6分∴165>1677分 ∴B 组数据:1,-2,-1,-1,3.22.〔此题总分值9分〕 〔1〕解:由题意得,x =23(2x -2)1分 ∴x =4.2分∴x 2-1=16-1=15(小时).3分答:乙车床单独加工完成这种零件所需的时间是15小时. 4分〔2〕解1:不相同.5分假设乙车床的工作效率与丙车床的工作效率相同,由题意得,6分1x 2-1=12x -2 . 7分 ∴1x +1=12. ∴x =1. 8分经检验,x =1不是原方程的解. ∴原方程无解.9分 答:乙车床的工作效率与丙车床的工作效率不相同. 解2:不相同.5分假设乙车床的工作效率与丙车床的工作效率相同,由题意得,6分 x 2-1=2x -2.7分 解得,x =1.8分此时乙车床的工作时间为0小时,不合题意.9分 答:乙车床的工作效率与丙车床的工作效率不相同. 23.〔此题总分值9分〕〔1〕证明1:∵∠BCD =∠BAC ,∴︵BC =︵BD . ……1分 ∵AB 为⊙O 的直径, ∴AB ⊥CD ,……2分 CE =DE . ……3分∴AC =AD .……4分证明2:∵∠BCD =∠BAC ,∴︵BC =︵BD .1分∵AB 为⊙O 的直径,∴︵BCA =︵BDA .2分 ∴︵CA =︵DA .3分A∴AC =AD .4分证明3:∵AB 为⊙O 的直径,∴∠BCA =90°.1分∴∠BCD +∠DCA =90°,∠BAC +∠CBA =90° ∵∠BCD =∠BAC ,∴∠DCA =∠CBA 2分∴︵CA =︵DA . 3分∴AC =AD .4分〔2〕解1:不正确. 5分连结OC .当 ∠CAB =20°时,6分∵OC =OA ,有∠OCA =20°.∵∠ACB =90°,∴∠OCB =70°.7分 又∵∠BCF =30°, ∴∠FCO =100°,8分 ∴CO 与FC 不垂直.9分∴此时CF 不是⊙O 的切线.解2:不正确.5分连结OC .当 ∠CAB =20°时,6分∵OC =OA ,有∠OCA =20°.∵∠ACB =90°,∴∠OCB =70°.7分 又∵∠BCF =30°, ∴∠FCO =100°,8分在线段FC 的延长线上取一点G ,如下列图,使得∠COG =20°. 在△OCG 中,∵∠GCO =80°, ∴∠CGO =80°. ∴OG =OC . 即OG 是⊙O 的半径.∴ 点G 在⊙O 上. 即直线CF 与圆有两个交点.9分 ∴此时CF 不是⊙O 的切线.解3:不正确.5分连结OC .当 ∠CBA =70°时,6分 ∴∠OCB =70°.7分 又∵∠BCF =30°, ∴∠FCO =100°,8分 ∴CO 与FC 不垂直.9分 ∴此时CF 不是⊙O 的切线.24.〔此题总分值10分〕 〔1〕解:点C(72,52) 是线段AB 的“邻近点〞.1分∵72-1=52,∴点C(72,52)在直线y =x -1上.2分 ∵点A 的纵坐标与点B 的纵坐标相同, ∴AB ∥x 轴.3分∴C(72,52) 到线段AB 的距离是3-52,∵3-52=12<1,4分∴C(72,52)是线段AB 的“邻近点〞.〔2〕解1:∵点Q (m ,n )是线段AB 的“邻近点〞,∴点Q (m ,n )在直线y =x -1上, ∴n =m -1.5分 ① 当m ≥4时,6分 有n =m -1≥3. 又AB ∥x 轴,∴ 此时点Q (m ,n )到线段AB 的距离是n -3.7分 ∴0≤n -3<1. ∴4≤m <5.8分 ② 当m ≤4时,9分 有n =m -1≤3. 又AB ∥x 轴,∴ 此时点Q (m ,n )到线段AB 的距离是3-n . ∴0≤3-n <1. ∴3<m ≤4.10分综上所述, 3<m <5.解2:∵点Q (m ,n )是线段AB 的“邻近点〞,∴点Q (m ,n )在直线y =x -1上, ∴n =m -1.5分 又AB ∥x 轴,∴Q (m ,n )到直线AB 的距离是n -3或3-n ,6分 ① 当0≤n -3<1时,7分 即 当0≤m -1-3<1时, 得 4≤m <5.8分② 当0≤3-n <1时,9分 有0≤3-(m -1)<1时, 得 3<m ≤4.10分 综上所述,3<m <5.25.〔此题总分值10分〕 〔1〕解1:连结PO ,∵PE =PF ,PO =PO , PE ⊥AC 、PF ⊥BD , ∴Rt △PEO ≌Rt △PFO . ∴∠EPO =∠FPO . ……1分在Rt △PEO 中,……2分tan ∠EPO =EO PE =33,……3分∴∠EPO =30°. ∴∠EPF =60°.4分解2:连结PO ,在Rt △PEO 中,1分PO =3+1=2.∴ sin ∠EPO =EO PO =12.2分∴∠EPO =30°. 3分 在Rt △PFO 中,cos ∠FPO =PF PO =32,∴∠FPO =30°. ∴∠EPF =60°. 4分解3:连结PO ,∵PE =PF ,PE ⊥AC 、PF ⊥BD ,垂足分别为E 、F , ∴OP 是∠EOF 的平分线. ∴∠EOP =∠FOP .1分 在Rt △PEO 中,2分tan ∠EOP =PEEO=33分∴∠EOP =60°,∴∠EOF =120°. 又∵∠PEO =∠PFO =90°, ∴∠EPF =60°. 4分〔2〕解1:∵点P 是AD 的中点,∴AP =DP .又∵PE =PF ,∴Rt △PEA ≌Rt △PFD . ∴∠OAD =∠ODA . ∴OA =OD .5分∴AC =2OA =2OD =BD . ∴□ABCD 是矩形.6分∵点P 是AD 的中点,点F 是DO 的中点, ∴AO ∥PF .7分∵PF ⊥BD ,∴AC ⊥BD . ∴□ABCD 是菱形.8分 ∴□ABCD 是正方形.9分∴BD =2BC .F P CBOEDA∵BF =34BD ,∴BC +32-4=324BC . 解得,BC =4.10分解2:∵点P 是AD 的中点,点F 是DO 的中点,∴AO ∥PF .5分∵PF ⊥BD ,∴AC ⊥BD .∴□ABCD 是菱形.6分∵PE ⊥AC ,∴PE ∥OD . ∴△AEP ∽△AOD .∴EP OD =AP AD =12. ∴DO =2PE .∵PF 是△DAO 的中位线,∴ AO =2PF .∵PF =PE ,∴AO =OD .7分∴AC =2OA =2OD =BD .∴□ABCD 是矩形.8分∴□ABCD 是正方形.9分∴BD =2BC .∵BF =34BD ,∴BC +32-4=324BC . 解得,BC =4.10分解3:∵点P 是AD 的中点,∴AP =DP .又∵PE =PF ,∴Rt △PEA ≌Rt △PFD .∴∠OAD =∠ODA .∴OA =OD .5分∴AC =2OA =2OD =BD .∴□ABCD 是矩形.6分∵点P 是AD 的中点,点O 是BD 的中点,连结PO .∴PO 是△ABD 的中位线,∴AB =2PO .7分∵PF ⊥OD ,点F 是OD 的中点,∴PO =PD .∴AD =2PO .∴AB =AD . 8分∴□ABCD 是正方形.9分∴BD =2BC .∵BF =34BD ,∴BC +32-4=324BC . E F A B CD O P解得,BC =4.10分解4:∵点P 是AD 的中点,∴AP =DP .又∵PE =PF ,∴Rt △PEA ≌Rt △PFD .∴∠OAD =∠ODA .∴OA =OD .5分∴AC =2OA =2OD =BD .∴□ABCD 是矩形.6分∵PF ⊥OD ,点F 是OD 的中点,连结PO .∴PF 是线段OD 的中垂线,又∵点P 是AD 的中点,∴PO =PD =12BD 7分 ∴△AOD 是直角三角形, ∠AOD =90°.8分∴□ABCD 是正方形.9分∴BD =2BC .∵BF =34BD ,∴BC +32-4=324BC . 解得,BC =4.10分26.〔此题总分值12分〕〔1〕解:∵点A (1,c )和点B (3,d )在双曲线y =k 2x〔k 2>0〕上, ∴c =k 2=3d 1分∵k 2>0,∴c >0,d >0.A (1,c )和点B (3,d )都在第一象限.∴AM =3d .2分过点B 作BT ⊥AM ,垂足为T .∴BT =2.3分TM =d .∵AM =BM ,∴BM =3d .在Rt △BTM 中,TM 2+BT 2=BM 2,∴d 2+4=9d 2,∴d =22. 点B (3,22) . 4分 〔2〕解1:∵ 点A (1,c )、B (3,d )是直线y =k 1x +b 与双曲线y =k 2x〔k 2>0〕的交点, ∴c =k 2,,3d =k 2,c =k 1+b ,d =3k 1+b .5分 ∴k 1=-13k 2,b =43k 2. ∵A (1,c )和点B (3,d )都在第一象限,∴ 点P 在第一象限.∴PE NE =k 1x +b k 2x=k 1k 2x 2+b k 2x =-13x 2+43x . ······················································· 6分 ∵ 当x =1,3时,PE NE=1; 又∵当x =2时,PE NE 的最大值是43. ∴1≤PE NE ≤43. ·································································· 7分 ∴PE ≥NE .8分∴PN NE =PE NE -1=-13x 2+43x -1.9分 ∴ 当x =2时,PN NE 的最大值是13.10分 由题意,此时PN =12, ∴NE =32.11分 ∴ 点N (2,32) . ∴k 2=3. ∴y =3x.12分 解2:∵A (1,c )和点B (3,d )都在第一象限,∴ 点P 在第一象限.∵PE NE =k 1x +b k 2x=k 1k 2x 2+b k 2x , 当点P 与点A 、B 重合时,PE NE=1, 即当x =1或3时,PE NE=1. ∴ 有 k 1k 2+b k 2=-1,9k 1k 2+3b k 2=-1. 5分 解得,k 1=-13k 2,b =43k 2.∴PE NE =-13x 2+43x .6分 ∵k 2=-3k 1,k 2>0,∴k 1<0.∵PE -NE =k 1x +b -k 2x =k 1x -4k 1+3k 1x=k 1(x 2-4x +3x )=k 1(x -1)(x -3)x,7分 又∵当1≤x ≤3时,(x -1)(x -3)≤0,∴k 1((x -1)(x -3)x)≥0. ∴PE -NE ≥0.8分∴PN NE =PE NE-1 =-13x 2+43x -1.9分 ∴ 当x =2时,PN NE 的最大值是13.10分 由题意,此时PN =12, ∴NE =32. 11分 ∴ 点N (2,32) . ∴k 2=3. ∴y =3x.12分 解3:∵ 点A (1,c )、B (3,d )是直线y =k 1x +b 与双曲线y =k 2x〔k 2>0〕的交点, ∴c =k 2,,3d =k 2,c =k 1+b ,d =3k 1+b .5分k 2=3d ,k 1=-d ,b =4d .∴直线y =-dx +4d ,双曲线y =3d x. ∵A (1,c )和点B (3,d )都在第一象限,∴ 点P 在第一象限.∴PN =PE -NE =-dx +4d -3d x=-d (x 2-4x +3x )=-d (x -1)(x -3)x,6分 又∵当1≤x ≤3时,(x -1)(x -3)≤0,∴-d (x -1)(x -3)x≥0.∴PN =PE -NE ≥0.7分∴PN NE =-dx +4d -3d x 3d x8分 =-13x 2+43x -1.9分 ∴ 当x =2时,PN NE的最大值是13.10分 由题意,此时PN =12,∴NE =32.11分∴ 点N (2,32) .∴k 2=3.∴y =3x .12分。
厦门市2005年初中毕业和高中阶段各类学校招生语文考试

厦门市2005年初中毕业和高中阶段各类学校招生考试语文试题(试卷满分:150分;考试时间:140分钟)考生注意:1.自信沉着,仔细审题,努力展示初中三年的学习成果;2.全卷分四个部分,计30小题;3.答案一律写在答题卡上,否则以0分计算;4.交卷时只交答题卡,本试卷由考场处理,考生不得擅自带走。
第一部分口语交际(满分:20分)[一]完成1—10题(20分)1.听下面几句话,判断哪一句是“创建文明城市”的宣传用语?(2分)A.B.C.2.听一则“阳光读书日”活动通知,判断下列说法正确的是哪一项?(2分)A.活动的主办部门是校教务处。
B.活动时间是本周五下午四点。
C.活动地点是校团委会办公室。
3.听一则新闻报道,判断对新闻主要内容概括正确的是哪一项?(2分)A.翔安隧道正式动工。
B.翔安隧道工程全长9公里。
C.翔安隧道将在4年内完工。
听一则“导游解说词”,回答第4题和第5题。
4.蝴蝶谷的长度是多少?(2分)A.60多米B.80多米C.约200米5.下列有关蝴蝶谷的说法正确的是哪一项?(2分)A.蝴蝶谷位于厦门市集美区。
B.蝴蝶谷因处处有蝴蝶的身影而闻名。
C.蝴蝶谷是一处人工建造的景观。
听下面关于校园“追星族”的争论,回答第6题和第7题。
6.他们争论的焦点是什么?(2分)A.中学生充当“追星族”,对成长没什么好处。
B.现在有的中学生整天追随着一些所谓的青春偶像。
C.中学生充当“追星族”,对成长是否有好处。
7.对他们争论的问题,你有什么看法?简要说出你的理由。
(2分)8.你想用一两句话向你的同桌转述下面这则“翻跟头”奇闻,你该怎么说呢?(2分)9.在下面这种情况下,你该如何向小宁解释“把头抬起来”的言外之意呢?(2分)10.在下面这种情境中,你该怎样说才能表达出自己想与林辉重建友谊的诚意?(2分)第二部分语言积累与运用(满分:29分)[二]完成11—16题(29分)11.古人云:“腹有诗书气自华”。
请根据下列提示填写相应的古诗文:(13分)(1)八百里分麾下炙,五十弦翻塞外声,。
福建厦门市初中毕业和高中阶段学校招生考试语文试卷

福建厦门市初中毕业和高中阶段学校招生考试语文试卷一、考试概况福建厦门市初中毕业和高中阶段学校招生考试为每年的6月举行,考试分为语文、数学、英语三科,满分均为120分。
其中,语文试卷包含听力、阅读、写作三部分,总分为60分,占招生考试总分的50%。
考试时间为120分钟。
二、考试内容1. 听力听力部分是福建厦门市初中毕业和高中阶段学校招生考试语文试卷的第一部分,包括听力理解和听力填空两个环节,共计20分。
听力理解主要考察考生对于口语表达的理解和理解逻辑结构的能力,一般由老师发放听力材料,考生需要根据听到的内容回答问题。
听力填空则要求考生根据听到的内容完成相应单词或短语的填空操作。
2. 阅读阅读部分是语文试卷的重点,共计30分,占整个语文试卷的50%。
试卷包括单选、复合型选择题和阅读理解,试卷内容涵盖文言文、现代文等多种文体,考察考生的阅读能力、理解能力和推理能力。
考生需要对文章的主旨、中心思想、情感倾向等方面进行深入分析。
3. 写作写作部分是试卷的最后一部分,共计10分。
试卷主要考察考生的文化素养和语言表达能力,试卷要求考生在规定的时间内完成一篇小作文,如古诗填空、写作文等。
考生需要注意时间安排、语言规范、格式要求等多重考察要点。
三、考试注意事项1.准备充分。
考生在考试前应该提前了解试卷的题型和考试内容,合理安排时间,保证足够的心理准备和体力准备。
2.注意听力。
由于语音表达的差异,考生在听力部分应该保持警觉,认真聆听老师的语音,特别是听力理解这一环节,要注意理解口音等语音细节,提高听力的准确率。
3.必须遵守考试规定。
考生在考试现场需要仔细阅读答题卡和考试规定,不得在试卷上乱涂乱写,不得在考试时间内与他人交流等。
4.试卷审题。
考生在做试卷时要认真审题,根据题意进行答题,避免偏离题目内容而导致做题失分。
四、考试总结对于每个参加福建厦门市初中毕业和高中阶段学校招生考试的考生来说,语文试卷无疑是最为重要的一部分。
2019年厦门市中考语文试卷及答案

2019年厦门市初中毕业及高中阶段各类学校招生考试语文(试卷满分:150分考试时间:120分钟)准考证号姓名座位号注意事项:1.全卷四个部分,六大题,18小题,试卷共6页,另有答题卡。
2.答案一律写在答题卡上,否则不能得分。
第一部分口语交际(满分:6分)一、完成第1题(6分)1.根据对话情境,回答问题(6分)某中学长期采用电铃声作为上下课的信号。
有位学生特意给校长发了一封电子邮件,建议改变铃声模式。
同学们对此议论纷纷——甲学生我觉得用不着改变。
铃声不就是一种信号嘛,听得清楚就行了。
乙学生老弟,你的耳朵也太缺乏美感了!(众学生善意地笑)优美的铃声可以美化校园文化环境。
电铃声单调刺耳,是该换换了。
丙学生说得好!我觉得校园钟声挺有魅力的。
学校后山钟亭里就有一口大铜钟闲置着,我们为什么不建议校长聘请专人来敲钟呢?丁学生好是好,可太费事了。
我觉得可以用播放“温馨提示语”来代替电铃声,例如“同学们,请做好课前准备,快上课了。
”甲学生这种方式有点拖泥带水,还不如电铃声干脆利落呢!乙学生我也有个主意!建议校长用优美的歌曲来作铃声。
比如《鼓浪屿之波》就挺好听,(哼唱)“鼓浪屿四周海茫茫……”温馨、高雅,多棒啊!(1)同学们议论的话题是什么?(2分)A.优美音乐B.校园铃声C.后山钟亭(2)乙生说“你的耳朵也太缺乏美感了!”其言外之意是什么?(2分)A.甲生不关注校园铃声是否有美感。
B.甲生的耳朵形状长得不太好看。
C.甲生的听力有些迟钝,不够灵敏。
(3)假设你也参加这次讨论,你想表达什么看法呢?请把你想说的话写下来。
(2分)第二部分积累与运用(满分:39分)二、完成2—5题(39分)2.古诗文积累(13分)(1)关关雎鸠,。
(《关雎》)(1分)(2)予独爱莲之,,中通外直……(周敦颐《爱莲说》)(2分)(3)子曰:“岁寒,。
”(《论语》)形象地阐述了身处浊世更显君子风范的哲理。
(1分)(4)一代雄才曹操的诗“如幽燕老将,气韵沉雄”,例如《观沧海》气势恢宏、包容天地万象,“,若出其中;,若出其里”。
厦门市各年中考题

厦门市2002年初中毕业及高中阶段各类学校招生考试语文试题一、(完成1—10题,20分)1.听下面一句话,判断句中最后一个词读音正确的一项是()(2分)A.jīncǎi B.jīngcǎi C.jīngchǎi2.听下面一句话,话中强调“离乡时间很久”的一句是(2分)A.________ B.________ C.________3.听下面一段话,判断话中从几个方面介绍了西海域急需治理的原因?(2分)A.五个B.四个C.三个4.听下面一段话,判断“音乐艺术之路”止于什么地点?()(2分)A.鼓浪屿鹿礁路B.原日本领事馆C.林巧稚纪念馆毓园5.听下面一则广告,判断它是为以下哪一项做广告?()(2分)A.眼镜B.装修C.照相机6.听下面一段话,判断它的中心句是什么?()(2分)A.苏萨是美国著名管乐作曲家B.这首曲子体现了笛子的光彩特点C.苏萨写了一百多首进行曲7.听下面一段话,判断车内标语中“方便”的含义是什么?()(2分)A.上厕所B.合适C.便利8.听下面一段话,判断鲁迅的真实意思是什么?()(2分)A.评价许广平的论文写得好B.批评许广平的论文抄录哆嗦的话太多,很少有自己的见解C.称赞罗素的话很精彩听下面一则小幽默,简要回答第9题和第10题9.怀特太太话中的意思是什么?(2分)10.孩子们说:“我们就有六兄弟啦”的言外之意是什么?(2分)二、(完成11—13题,14+3分)11.根据课文内容填空:(2分,书写不端正者酌扣1—2分)(1)明月别枝惊鹊,______________。
辛弃疾《西江月》)(1分)(2)三人行,______________。
(《〈论语〉六则》)(1分)(3)______________,壮士十年归。
(北朝民歌《木兰诗》)(4)程远独在异国,面对晚霞中森林的奇异风光,心想:加拿大的景色确实迷人,但远离故土的滋味实在不好受。
感叹之中,马致远《天净沙·秋思》中的名句“______________,______________”不觉脱口而出。
厦门市中考英语真题及答案

厦门市中考英语真题及答案2019年厦门市初中毕业及高中阶段各类学校招生考试英语一.选择填空:从A、B、C中,选出一个最佳答案完成句子。
17. ---You look worried. What's your______?---I have trouble in learning math.A. planB. ideaC. problem18. ---I can't find my dictionary.---Is the one on Jack's desk______?---Yes, thank you.A.hisB. yoursC. ours19. ---What does your sister____?---She is tall and thin.A. look likeB. look forC. look up20. ---I really like your backpack, is it______?---I don't know how much it is. It's my brother's.A. expensiveB. heavyC. useful21. ---Jenny, will you still be here this afternoon?---Yeah, I think I'll stay _____five. Then I'm leaving for dinner.A. atB. sinceC. until22. ---I saw David in the teacher's office this morning. Do you know____ he was there?---He slept in geography class.A.whyB. howC. when23. ---____ do you read English newspaper?---I read China Daily every day.How soon B. How often C. How long24. Most of my classmates have had the expensive of takinga plane, but I ____.1.wasn't B. haven't C. won't25. ---Oh, where's my key?---Is it possible that you ____it in the car?A. caughtB. foundC. left26. ---Does Aunt T ara enjoy____?---Yes, She has three dogs, two rabbits, four birds and some fish in her house.A. visiting the zooB. keeping petsC. working on the farm27. ---Excuse me, may I smoke here?---I'm afraid you____. It's not allowed here.A.canB. can'tC. needn't28. I heard that most of Jeff's best books____ when he was sick and poor.A.had writtenB. were writingC. were written29. ---What's the terrible noise upstairs? I can hardly stand that.---Our neighbors ____a party.A.are havingB. were havingC. will have30.---I'm always feeling stressed out before a big exam.---____.You can go out for a walk or listen to some light music.A. Take it easyB. Make a decisionC. Work it out31. ---Would you like to go to the gym with me this Saturday afternoon?---____, but I promised to go swimming with Eric.A.Never mindB. I don't think soC. I'd love toⅥ.完形填空:从A、B、C中,选择一个最佳答案,使短文意思完整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年厦门市初中毕业及高中阶段各类学校招生考试物理一、选择题(共16小题,每小题2分,共32分)1.如图1所示的四个实例中,属于增大压强的是2.以下措施中,从传播过程中减弱噪声的是A.厦门岛内禁止燃放烟花爆竹B.鼓浪屿禁止商家导游使用扩音器C.地铁施工时给机器加润滑油D.部分BRT路段两侧设有透明板墙3.天宫2号空间实验室计划于2016年第三季度择机发射。
空间实验室内适宜宇航员工作生活的气压约为A.100PaB.1 000PaC.10 000PaD.100 000Pa4.荷叶上水珠晶莹透亮,映出荷叶纹理的“清晰”像。
这个像的特点是A.正立放大B.正立等大C.倒立放大D.倒立缩小5.在图2所示的四种剪刀中,最适用于剪开较硬物体的是6.小芳在科技馆用手触摸静电球时,头发丝一根根竖起,形成“怒发冲冠”的有趣现象,如图3所示,竖起的头发丝所带电荷是A.同种电荷B.异种电荷C.正电荷D.负电荷7.动车从启动到离站的过程中,其惯性A.先不变后变大B.保持不变C.先变大后不变D.逐渐变大8.人类首次探测到的引力波是由13亿光年之外的双黑洞合并形成的。
双黑洞的初始质量分别是太阳质量的29倍和36倍,合并后的黑洞质量是太阳的62倍。
亏损的质量以强大引力波的形式释放到宇宙。
经过漫长的旅行抵达地球。
下列说法正确的是A.牛顿预言了引力波的存在B.双黑洞合并过程质量守恒C.该引力波产生于13亿年前D.引力波只能在介质中传播9.与世界能源结构相比,我国目前的能源结构存在不足,如图4所示。
以下措施有利于优化我国能源结构的是A.继续发挥产煤大国的优势B.减小石油和天然气的比重C.严控核能、水电能的开发D.加大可再生能源的开发利用10.某些鱼的沉浮靠鳔的胀缩实现。
原来静止在水中的鱼A.鳔膨胀时浮力小于重力会下沉B.鳔膨胀时浮力大于重力会上浮C.鳔收缩时浮力等于重力仍悬浮D.鳔收缩时浮力大于重力会漂浮11.如图5所示,嫦娥三号着陆器向下喷气获得反推力,以较小速度向月面匀速降落。
着陆器匀速降落时,重力与反推力A.施力物体相同B.是相互作用力C.是一对平衡力D.其合力向下12.老师上课时常用“小蜜蜂”扩音,声音信号由话筒传入扩音器放大后从扬声器播出。
话筒、扬声器的工作原理相当于A.发电机、电动机B.电动机、发电机C.发电机、发电机D.电动机、电动机13.如图6所示,以下四件家用电器正常工作时电流最接近5A的是14.据厦门市气象部门发布的数据,2016年1月25日,岛内东渡观测站和同安莲花观测站测到的最低温度,分别创下了厦门市岛内、外有气象记录以来的最低值。
你认为对应的温度分别是A.-8.8℃、0.1℃B.0.1℃、-8.8℃C.-0.1℃、8.8℃D.8.8℃、-0.1℃15.如图7所示,公交车后门左右扶杆上各装有一个相当于开关的按钮。
当乘客按下任一按钮时,铃声响起,提醒司机有人要下车。
图8中符合要求的电路是16.公共场所严禁吸烟。
小明设计了一种简易烟雾报警控制器,如图9所示。
电路中R0为定值电阻,R为光敏电阻,其阻值随光照强度的增大而减小,烟雾增大到一定程度使电压表的指针偏转到某区域时触发报警系统。
以下做法能使控制器在烟雾较淡时就触发报警的是A.电压表改成大量程B.增大激光强度C.减小R0阻值D.减小电源电压二、填空题(本大题共6小题,没小题2分,共12分)17.在微观尺度下,科学家拍下了超亮的X射线将液体瞬间打得“灰飞烟灭”的情景,如图10所示。
此过程液体吸收X射线的能量,内能,发生的物态变化是。
18.如图11所示,两个表面光滑的铅块相互挤压后粘在一起,说明分子间有;长时间挤压在一起的铅块和金块会相互渗透,说明分子。
19.智能手环可以记录佩戴者的运动情况。
以佩戴者手腕为参照物手环是的;手环数据可由蓝牙通过发送给手机,使用户在朋友圈获得排名和点赞。
20.《康熙几暇格物篇》中记载:“置钱碗底,远视若无,及盛满水时,则钱随水光而显现矣。
”如图12所示,把铜钱放在碗底B处后加适量水,从A处恰好看到铜钱的像在处,用激光笔从A点向处(用图中字母表示)照射,可照亮铜钱。
加满水,从A处看到像的位置将(选填“变高”、“变低”或“不变”)21.如图13是某电热暖手宝的主要参数。
选用水作为吸热或放热物质,是因为水的较大。
已知水的初温为15℃,c水=4.2×103J(kg·℃),接通电源正常工作6min时暖手宝处于状态(选填“通电加热”或“自动断电”)22.如图14所示,两只电表及导线完好。
闭合开关,两只电表示数均为零。
现用一个完好的电阻替换R2,再闭合开关:①若只有电压表示数不为零,则原来的故障是;②若只有电流表示数不为零,则原来的故障是。
三、简答题(本大题1小题,共4分)23.厦门城市名片筼筜湖(图15)原称筼筜港,本是一处避风坞,素有“筼筜渔火”盛誉海堤围筑后筼筜港由海湾变为内湖,海水交换的天然管道被切断。
筼筜湖的水位大部分时间低于外海水位,目前主要利用西堤进水闸门,出水闸门实施进水纳潮和排放潮水,实现潮水与海水的交换,从而改善湖区水质和生态环境。
(1)请结合物理知识简述利用闸门纳潮或排水的过程。
(纳潮和排水任选其一作答)(2)有人建议可利用纳潮和排水两个时段进行潮汐发电,请指出哪个时段更适合,并说明判断依据。
四、作图题(本大题共2小题,每小题2分,共4分)24.在图16中,投出去的篮球在空中飞行,不考虑空气阻力,请在图中画出篮球的受力示意图。
25.图17为上午8:00太阳光经水平镜面反射的光路图,请大家画出一小时后太阳光照射同一点的入射光线及对应的反射光线。
五、实验探究题(本大题共5小题,共28分)26.(4分)利用如图18装置探究平面镜成像特点。
(1)实验时应选较(填“厚”或“薄”)的玻璃板竖立在水平桌面上。
(2)点燃蜡烛A,透过玻璃板观察到A的像,把与A完全相同的蜡烛B放在像的位置观察到B与像完全重合,说明像与物。
(3)将光屏放到像的位置,无法直接在光屏上观察到像,说明说成的像是像。
(4)用方格纸替代白纸,更方便探究像与物关系。
27.(5分)小芳用如图19甲所示的实验装置探究水的沸腾特点。
(1)请指出图甲中的操作错误:。
(2)图乙是根据实验数据画出水的温度随时间变化的曲线。
由图可知,水沸腾时的特点是。
(3)为了说明水在沸腾过程中是否需要吸热,应,观察水是否沸腾。
(4)小芳再次实验时采取两项措施节省了实验时间,请在图乙中大致画出能体现那两项措施的图线。
28.(6分)探究影响滑动摩擦力大小因素的实验装置如图20所示。
在小桶内装入适量的沙子,滑块恰好在水平木板上做匀速直线运动。
(1)为测量滑块受到的滑动摩擦力的大小,应测量,所需测量仪器是。
(2)把毛巾铺在木板上,发现需要装入更多的沙子,滑块才能做匀速直线运动,说明。
(3)小明想用钩码代替沙桶,请你对此作出评价:。
29.(5分)磁感应强度B 用来描述磁场的强弱,国际单位是特斯拉,符号是“T”,为了探究磁铁外轴线上磁感应强度的大小与哪些因素有关,小鹭设计了如图21所示的电路,图甲电源电压6V ,R 为磁感电阻。
其阻值随磁感应强度变化的关系图线如图22.(1)当图乙S2断开,图甲S1闭合时,电流表的示数为mA 。
闭合S1和S2,图乙中滑动变阻器的滑片P 向右移动,图甲中电流表的时速逐渐减小,说明磁感电阻R 处的磁感应强度B 逐渐。
(2)闭合S1和S2,滑片P 不动,沿电磁铁轴线向左移动磁感电阻R ,测出R 离电磁铁左端的距离x 与对应的电流表示数I ,算出R 处磁感应强度B 的数值如下表。
请计算x=5cm 时,B=T (3)综合以上实验可以得出:电磁铁外轴线上磁感应强度随电磁铁电流增大而;离电磁铁越远,磁感应强度越。
30.(8分)用图23甲所示的电路探究“电流与电阻的关系”,电源电压15V 保持不变,滑动变阻器的规格是“50Ω 2A”,阻值为10Ω、20Ω、30Ω、40Ω、50Ω的电阻各一个,电流表量程0~0.6A 、0~3A ,电压表量程0~3V ,0~15V 。
(1)根据图甲将图乙所示的实物图连接完整,电压表量程选择应满足能测量5组数据。
(2)小明将10Ω的电阻接入电路,闭合开关,多次移动滑动变阻器的滑片,记录对应的几组电表示数。
此过程小明实际探究的问题是。
其中自变量是。
(3)要完成预定实验探究任务,滑动变阻器除了保护电阻外,另有一个重要作用是。
(4)下表为另一同学提交的实验数据,林老师指出有的数据不符合实际,你认为不符合实际的是实验次序的数据,理由是。
六、计算题(本大题共3小题,共20分)31.(5分)如图24所示,R1=25Ω,小灯泡L 的规格为“2.5V 0.3A”,电源电压保持不变。
(1)S1、S2都断开时,小灯泡L 正常发光,求电源电压。
(2)S1、S2都闭合时,电流表示数变为0.6A ,求R2的阻值。
32.(7分)“嘉庚号”科考船(图25)于2016年5月8日下水,厦门大学由此成为中国大陆综合性大学中第一所拥有自己的全球级科考船的高校。
科考船满载时排水量为3.5×103t ,在某段航行中牵引力与速度的关系图像是双曲线,如图26所示。
求:(1)科考船满载航行时受到的浮力;(2)请根据图26所示规律计算,科考船航速为20km/h 时受到的牵引力;(3)在该段航行中,科考船发动机每分钟所做的功。
33.(8分)某段输电线由铝绞线组成,为避免冰雪天时因附着冰块变粗变重,造成断线危险,附着在线上的冰重与铝绞线重之比达到8:3时,就必须进行除冰作业。
已知该铝绞线的直径D0=9mm ,ρ铝=2.7×103kg/m3,ρ冰=0.9×103kg/m3,每公里铝绞线的电阻R=0.56Ω。
铝绞线变粗前后横截面均看做圆,如图27所示。
(1)求需要除冰时冰冻变粗铝绞线的直径D 。
(2)有一种除冰方法叫“短路除冰”,即短时间内输电线不经过用电器直接通电,利用导线本身发热熔水。
若短路熔冰时通过铝绞线的电流是600A ,每千克冰熔化需吸热3.36×105J ,熔冰效率为80%,则每公里铝绞线每秒钟可熔冰多少千克?。
