4第四章习题解答
高等代数-第4章习题及解答

第四章 多项式4.1习题,()(),..(-)-(-)()()-(-)()--(-)(-)Z a c ad bc q Z s t ad bc q a c a c b d ab cd ad bc a c b d ab cd a c q a c b d q ab cd ∈-+∴∃∈+==++=++=+1. 设a,b,c,d 已知(a-c)(ad+bc),求证(a-c)(ab+cd)证明:又由 () 得 ()() 即 ,,-()()b d q Zb d q Z ac ab cd ∈∴+∈-+即有 121212,65(-3)13,65(-2)5,65-,65(-3)13(-2)571865-(6528)65(-65)-2828m m m m r c c m c m c c c m m r ⨯⨯∃⨯+⨯==-+∴=2. 一个整数被5除余3,被13除余2,求它被65除的余数解:设所求数为由题知 即 有 令 ,, 则有 故有 1723582957,581-143,-143202,0231414a b a b a b a b b a b a b a ==-=-==-=-=-=-=+=⋅+=⋅+3. 对于下列的整数,分别求出以除所得的商和余数: (1), (2), (3), (4)解:)由带余除法,可表示为 故商为,余数为;)同理得 故商为,余数为; )由 知商为,余数为; 49595b a =+ )由 知商为,余数为。
.()001a b a b b aq q Z b q b a q q a b≠≤=∈≠∴≠∴=≥∴≤4. 证明:若a b,b 0,则证明:由 可得 又 又1,) 1.b ∈=1 1 1115. 设a,b 是不全为零的整数,且a=da ,b=db ,d,a ,b Z.证明d 是a 与b 的一个最大公因数的充分必要条件是(a1111111111[] 4.1.3,,..01(,)1[](,)1''1''1,''u v Z s t ua vb d uda vdb d d ua vb a b a b u a v b a bu v u a v b d d d⇒∃∈+=+=≠∴+=∴=⇐=+=+=+=证明:根据定理得 即 又故有 即 则有 综上所述,结论得证6.(,)1,(,) 1.,(1),,..()()(1),,1,1a b a b ab a b ab d d Z d u v Z s t u a b vab d ua u va b d u v a Z u va Za b =+=+=∈≠∴∃∈++=∴++=∈∴+∈= 证明:若则 证明:反证 假设() 且 故 ()与 () 矛盾 ,17.1..,()(),,.a b ab a b p ab p a p b p p mn a b k k Z p abp b b k p a p b p k m b m k m k n b n k n k p ∴+===+∈∴+ () 设是一个大于的整数且具有以下性质:对于任意整数,,若,则或 证明是一个素数 证明:令 又当 不整除,有,不整除 又有,不整除或; 不整除或 若为合数,那,m k n k p p k p b p 么由可知必为素数,否则 同理可证当不整除时,也必为素数4.2习题224324321.,,(21)(1)251\2(2)(21)()12521-2,1,31k h m x hx x kx x x mx x x k h x hk x h k x h k hk m k h m h k +--+=++--=--+--++--=⎧⎪--====⎨⎪+=-⎩求使 解:对于左边 即有 解之得432322.()242,()25 4.()(),()(),()().f x x x x xg x x x x f x g x f x g x f x g x =+---=--++- 设 计算432443270765432()()4292()()6()0254()()()23913131868kki k i k i f x g x x x x x f x g x x x g x x x x x f x g x a b x x x x x x x x -==+=+--+-=+-=⋅+--+∴==+--++--∑∑解:由题得 令323122223.()59-73,()(53),()().-15-50[()()]3691()()04.()0().()0()()()f x x x xg x x x f x g x f x g x x f x g x s f x f x f x f x f x f x ︒=-++=++⨯=±∂===≠≠=⋅∴ 设求乘积 的次数及其系数和解:根据 得 令 则有 的系数和 证明:当时,是偶次多项式证明:又有 根据定理2 4.2.12()()()()(),()()2f x f x f x f x f x n n N f x n ︒︒︒︒︒∂⋅=∂+∂∂=∈∴∂=的()知 ()()() 再令 () 结论得证2225.(),(),()..()()(),()()()0.(),(),()1221222132212f x g x h x f x xg x xh x f x g x h x g x g f x f h x hg h f g g h f h g h f g f ︒︒︒︒︒︒=+===∂=∂=∂=>=+<=+==+= 设是实数域上的多项式证明如下 若是 则 证明:令 () () () 当 时,有 当 时,有 当 时,有 或 2222214()(),(),()(),(),()()()()06.(),(),()()0(),()1()0(),()h f x f x g x h x f x g x h x f x g x h x f x g x h x f x g x i h x f x xg x x xh x x +========-= 又由题可知 是偶次多项式,又由于是实数域上的多项式 故 的次数不存在 即 求一组满足上题结论的不全为零的复系数多项式解:令 , 即 , 222()()0()()0(),()1xg x xh x f x f x g x i h x ∴+===== 满足条件即 ,4.3 习题3221.()321,()321,()()()().f x x x xg x x x g x f x q x r x =-+-=-+设求用除所得的商式和余数232322217393213212133751337147399299172(),()3999()()()()x x x x x x x x x x x x x x x q x x r x f x g x q x r x --+-+--+-+--+--=-=-=+解: 故 即[]2432322412*********.,,(1)()?012,1(1)()3.()(()()),()(()()),:()(()()()()),(),()m p q x mx x px q p m m m r q m p m m q m x mx x px q g x f x f x g x f x f x g x u x f x u x f x u x u x F x ++++⎧+=-=⎨=-⎩=-=-+++++-+在适合什么条件时,解:由题知当余式时有 即当 时 有 设证明其中为中任意两个12121212121211()(()()),()(()())()(()()()())()(()()()())()(),()()3()()(i g x f x f x g x f x f x g x f x f x f x f x g x f x f x f x f x g x f x g x f x u x F x i +-∴++-+-+∃∀∈=多项式 证明:即 根据多项式整除性质)可知 1122112221,2)..()()(),()()()2()()(1,2)..()(()()()())4.(1)(),(1)(),(1)().11(1)(),(1)(i o s t g x u x f x g x u x f x u x F x i s t g x u x f x u x f x x f x x f x x f x x x f x x f ∃∀∈=+-+-≠±-+ 再根据性质)得 若则证明:1212)(),()[]()()(1)(1)()()(1)(2)x u x u x F x f x u x x f x u x x ∴∃∈=+⎧⎨=-⎩221()()(1)(-1)-(2)(1)()(-1)()2u x u x x x f x x -⨯⨯+= 得212()()()[]2(-1)()21-1()0o u x u x u x F x x f x x x f x -∃=∈=== 故 即 或时,可得出 同样结论成立1212121221212125.(1)()(()()),()()()()(2)()()(),()()()()1(),()1,()1()(()())()()()g x f x f x g x f x g x f x g x f x f x g x f x g x f x g x x f x x f x x g x f x f x g x f x f x +==+=-+ 若则且对吗? 若则或对吗?解:()不对 如 :令 可见 而 不整除 和 (21212122()-1,()1,()1()()()()()()g x x f x x f x x g x f x f x g x f x f x ==+=-)不对如 :令 可见 而 不整除 和(1)(2)6.(1)(1),.,1()1(1)(1),(1)(1).(1)(1)(0),1(1)1,(1)(1)(1)(d n n d q d q d q d d n d n n qd r d q r r d n d x x d n d n d n n qd x x x x x x x x x n qd r r d x x x x x x x x --+--⇐=-=-=-+++--⇒--=+≤<-==-+---- 证明:的充分必要条件是(这里是正整数)证明 设 ,即 则 即 设,令则且212121)(1)(1)0,0.7.()110220()32.(),()[]..(1)()10()(1)(2)()2d q d r x x x r d r d n f x x x f x x x u x u x F x s t x u x f x x u x -∴--≤<=++++∃∈++=++ ,又 故 ,即 设被除的余式为,被除的余式为, 求被 除的余式解:设 , 23120()(2)()[]..()32(3)(1)(2)-(2)(1)()32--10(1)434-10(1)f x u x F x s t f x x x u r x x f x x x u u x r x =∃∈=+++⨯+⨯+=+++=+ 又 , () 有 ()() () 由(),()可得习题4.4432424322432312(1)43243221(-1)1.1)()242,()322;2)()441,() 1.()24221)()()2222f x x x x x g x x x x x f x x x x x g x x x f x x x x x x x A x g x x x x x x x x x +-+=+---=+---=--++=--⎛⎫⎛⎫+----⎛⎫==−−−→ ⎪ ⎪ ⎪+---+---⎝⎭⎝⎭⎝⎭−计算以下各式多项式的最大公因式:解:由 11333221()1()21()42222222200x x xx x x x x x x x x x -++-⎛⎫⎛⎫⎛⎫⎛⎫----−−→−−−→−−−→−−−→ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭224324312(4)222212(-)2(1)12()221(1)()2()44132)()()112333212x x d x x f x x x x x x x A x g x x x x x x x x x x x x +++-++∴=-⎛⎫⎛⎫--++--⎛⎫==−−−→ ⎪ ⎪ ⎪----⎝⎭⎝⎭⎝⎭-⎛⎫⎛⎫--⎛⎫−−−−→−−−→−−−→ ⎪ ⎪ ⎪-+---+⎝⎭⎝⎭⎝⎭−−−→ 由 2311110()1x x x d x -⎛⎫⎛⎫⎛⎫→→ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭∴=2.(),()(),,0,(()(),()())((),()).((),())()()(),()()()()()),()()())(),()(f x g x F x a b c d F ad bc af x bg x cf x dg x f x g x f x g x d x d x f x d x g x d x af x bg x d x cf x dg x h x h x af ∈∈-≠++==∴++∃∀另而,,,并且证明证明:令 即有 ( ( 又设 ()()),()()())-0()()())-()())---()()())()())--()(),()(),()x bg x h x cf x dg x ad bc d bf x af x bg x cf x dg x ad bc ad bc c ag x af x bg x cf x dg x ad bc ad bch x f x h x g x h x d ++≠∴=++=+++∴ (有 (( (( 从而有 ()()()()())()(()(),()())((),())x af x bg x cf x dg x d x af x bg x cf x dg x f x g x ++=++= 即 (, 即 :3.()0,()((),())(()()(),()).()0(),..()()()()()()-()()1((),())(()())((),())(()()(g x h x f x g x f x h x g x g x g x h x s t f x g x h x r x r x f x g x h x f x g x g x r x f x g x f x h x g x ≠=-≠∃=+===-设为任意多项式,证明: 证明: 故 即 由引理可知 , 即 ),())g x1122121212124.1)(,)2)(,)(,)(,,,),,,().1(,),,,,(,),[],..f g hf gh f g f g f f f g g f g g f g h F x f g d d f d g dh fh dh gh dh hf hg f g d u v F x s t uf vg d ===∃∈+=∴证明:是与的最大公因式;此处都是的多项式证明:)设 即 从而有 即 是与的公因式又由 得 112211211212211211221214.4.42)(,),(,),(,[]),;,,,,(,),(,),,,ufh vgh dhdh fh gh f g m f g n m n F x m f m g m f m g mn f f mn f g mn f g mn g g f g m f g n k k l +===∈==∃ 由定理知 是与的最大公因式 设 即 从而有 又由 知 211112222121211221221121212122112112212122112[],..,(,,,)(,)(,)(,,,)l F x s t k f l g m k f l g nk k f f k f l g l k f g l l g g mn mn f f f g f g g g f g f g f f f g f g g g ∈+=+=+++=== 即有 由此可知 从而有4323243232324323235.(),()()()()()((),()):1)()343,()310232)()421659,()25453431033113333102301310u x v x u x f x v x g x f x g x f x x x x x g x x x x f x x x x x g x x x x x x x x x x x x x x x x +==+---=++-=--++=--+⎛⎫+--------→ ⎪++-⎝⎭+2求使解:)(A(x),I )=222322222232230159935993913310230156553296331393555591393132563555555x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ⎛⎫⎪⎪ ⎪+-⎝⎭⎛⎫----⎛⎫---- ⎪→→ ⎪- ⎪++---- ⎪⎝⎭⎝⎭⎛-+⎛⎫-+------ ⎪ ⎪→→--+ ⎪------+- ⎪⎝⎭⎝33-x -x 22243232323231550**321,()55122342165910332540125401x x x x x x x v x x x x x x x x x x x x x x ⎫ ⎪ ⎪ ⎪ ⎪⎭⎛⎫-+- ⎪→ ⎪ ⎪⎝⎭-∴-=⎛⎫⎛⎫--+---++ ⎪→ ⎪ ⎪--+ ⎪⎝⎭--+⎝⎭2 u(x)= 2)(A(x),I )=22222222121223231333332222412(2)1333312231330**1223(),()33x xx x x x x x x x xx x x x x x x x x x x u x v x ⎛⎫-++⎛⎫--+--- ⎪⎪ ⎪⎪→→ ⎪ ⎪--++--+-+- ⎪ ⎪⎝⎭⎝⎭⎛⎫--+- ⎪→ ⎪ ⎪⎝⎭--+∴==4322432436.()1,()(1),,,()().(),()2,()()()()(,,)()(2)(2)(2)1of x Ax Bxg x x A B f x g x f x g x g x f x g x ax bx c a b c F f x ax b a x c b a x b c x c Ax Bx a A =++=-∂==++∈∴=+-+-++-+=++=设试决定使与 的最大公因式为二次多项式解:由于() 即 为最大公因式故不妨设 即有 -23,2,13,-4202013,-4b a B a bc A B c b a b c c A B ⎧⎪=⎪⎪=====-+=⎨⎪-=⎪=⎪⎩∴== 解得 即7.(),()((),())()()()(),((),())1((),())()()()()*()()()()()()()()()()*(),()[].f x g x f x g x u x f x v x g x u x v x f x g x u x f x v x g x u x f x v x g x f x u x f x v x g x g x m x n x F x s =+==+++∃∈设 不全为零,且证明:证明:()有 , 再由 () .()()[()()()()]()()[()()()()]1-()()()()()()11-()())()()()()221()t f x m x u x f x v x g x g x n x u x f x v x g x m x u x f x m x v x g x n x v x g x n x u x f x f x =+=+== 即() () ( () 将()代入(),消去得1-()()1-()()()()()()()()(),(),()01-()()()()()()()()()()()()1()()()()4.4.5((),())1m x u x n x v x g x m x v x g x n x u x f x g x g x n x v x m x u x m x n x u x v x m x n x u x v x m x n x u x v x u x v x =≠∴-+=∴==()()不全为零 即令 由定理 得8.((),()) 1.((),()) 1.,,((),()) 1.1()()()[]()()()()()()((),())1n m n o n n n f x g x n f x g x m n f x g x g x g x k x F x g x k x g x g x g x k x f x g x ===∃∈=∴==设令是任意正整数,证明:由此进一步证明: 对于任意正整数都有证明: 易见 , 即 s.t. (1)又 ()()1()()1()((),())1()(),()[]()()()()()()nn m m m f x g x f x g x k x f x g x x f x l x F x f x l x f x f x f x l x ∴∃∈+=+==∃∈=∴=o u(x),v(x)F[x] s.t. u(x)v(x) (2)v(x) 将(1)代入(2)得 u(x) 由定理4.4.5 知 2易见 f 即 s.t. ((),())1'''()()'()()11'()()'()()1()((),())1n n mn m n f x g x u x f x v x g x u x f x v x g x l x f x g x =∴∃∈+=+== (3)又u (x),v (x)F[x] s.t. (4) 将(3)代入(4)得 由定理4.4.5知 [][]1111119.((),()) 1.((),()())((),()())(()(),()()) 1.((),()())()()(),()()()()[()()]()()()]f x g x f x f x g x g x f x g x f x g x f x g x f x f x g x d x d x F x u x v x F x u x f x v x f x g x d x u x v x =+=+=+=+=∈∴∃∈++=+设 证明: 证明:令 ()s.t. 即 [1()()()()((),())1()1((),()())1((),()())1(()(),()())1f x v xg x d x f x g x d x f x f x g x g x f x g x f x g x f x g x +===+=+=+=故 即 同理可证得 再根据互素性质可知10.()0,()0,:1(),()()()()(),((),())12(),()(),()()()()(),((),())11((),())()1,()()f x g x h x f x g x h x f x h x f x g x h x f x h x g x h x f x g x h x f x g x f x g x d x f x d x m ≠≠===≠=设证明 )若对于任意多项式由可得到则必有 )若对于任意多项式由可得到则必有 证明:) 假设 则有(),()()()()()()()()()()()()()()x g x d x n x m x f x f x g x h x h x f x g x m x f x m x ︒︒=∂<∂∴ 其中 () ()又 (为任意多项式)即有()()((),())12((),())()1()()()()()()()()(),()()()()()()()1((f x m x f x g x f x g x d x f x d x m x h x m x g x f x g x m x g x g x m x f x g x g x m x f x ==≠==∴ 但 不整除,从而矛盾, 故 )假设 ,且 令 即有 () 又),())()()()()()()()1((),())1g x d x f x m x f x g x g x m x f x g x ︒︒︒︒=∴∂>∂∂>∂∴= () ()故 () () 与()矛盾1212111212112211.(),(),,()().1)((),(),,())(((),,()),((),,())),112(),(),,()(),(),,()()()()()()()n n k k n n n n f x f x f x F x f x f x f x f x f x f x f x k n f x f x f x u x u x u x F x u x f x u x f x u x +∈=≤≤-∈+++设证明: )互素的充分且必要条件是存在多项式 ,使得1211121()11((),(),,())(),((),,()(),((),,()()()(),1,2,,()(),1,2,,;()(),1,2,,()(),n n k k n i s t f x f x f x f x d x f x f x d x f x f x d x d x f x i nd x f x s k d x f x t k k nd x d x +=====∴==++∴证明:)设21212()()()(),1,2()(),1,2,,;()(),1,2,,()(),1,2,,()(),2((),(),,())1i s t i n d x d x c x d x i d x f x s k d x f x t k k nc x f x i nc xd x f x f x f x ===++∴=∴= 设结论得证。
第四章 习题答案

第四章的习题及答案4-1 设有一台锅炉,水流入锅炉是之焓为62.7kJ ·kg -1,蒸汽流出时的焓为2717 kJ ·kg -1,锅炉的效率为70%,每千克煤可发生29260kJ 的热量,锅炉蒸发量为4.5t ·h -1,试计算每小时的煤消耗量。
解:锅炉中的水处于稳态流动过程,可由稳态流动体系能量衡算方程:Q W Z g u H s +=∆+∆+∆221体系与环境间没有功的交换:0=s W ,并忽 动能和位能的变化, 所以: Q H =∆设需要煤mkg ,则有:%7029260)7.622717(105.43⨯=-⨯m解得:kg m 2.583=4-2 一发明者称他设计了一台热机,热机消耗热值为42000kJ ·kg -1的油料0.5kg ·min -1,其产生的输出功率为170kW ,规定这热机的高温与低温分别为670K 与330K ,试判断此设计是否合理?解:可逆热机效率最大,可逆热机效率:507.06703301112max =-=-=T T η 热机吸收的热量:1m in210005.042000-⋅=⨯=kJ Q热机所做功为:1m in 102000m in)/(60)/(170-⋅-=⨯-=kJ s s kJ W该热机效率为:486.02100010200==-=Q W η 该热机效率小于可逆热机效率,所以有一定合理性。
4-3 1 kg 的水在1×105 Pa 的恒压下可逆加热到沸点,并在沸点下完全蒸发。
试问加给水的热量有多少可能转变为功?环境温度为293 K 。
解:查水蒸气表可得始态1对应的焓和熵为:H 1=83.93kJ/kg, S 1=0.2962kJ/kg.K 末态2对应的焓和熵为:H 2=2675.9kJ/kg, S 2=7.3609kJ/kg.K)/(0.259293.839.267512kg kJ H H Q =-=-=)/(0.522)2962.03609.7(15.2930.25920kg kJ S T H W sys id =-⨯-=∆-∆=4-4如果上题中所需热量来自温度为533 K 的炉子,此加热过程的总熵变为多少?由于过程的不可逆性损失了多少功? 解:此时系统的熵变不变)./(0647.7K kg kJ S sys =∆炉子的熵变为)./(86.45330.2592K kg kJ T H T Q S sur -=-=∆-==∆ )./(205.286.40647.7K kg kJ S t =-=∆ )/(0.646205.215.2930kg kJ S T W t l =⨯=∆=4-5 1mol 理想气体,400K 下在气缸内进行恒温不可逆压缩,由0.1013MPa 压缩到1.013MPa 。
第四章 交流绕组理论 _ 习题与解答 _

为
;在电枢绕组中所感应的电势频率为
;如 3 次谐波相电势有效值为 E3,
则线电势有效值为
;同步电机三相电枢绕组中一相单独流过电流时,所产
生的 3 次谐波磁势表达式为
。三相绕组流过对称三相电流
时 3 次谐波磁势幅值为
。
答:
τ 3
,3f,0,
Fφ
3
cos
3
π τ
x cosωt ,0
10. ★某三相两极电机中,有一个表达式为δ=F COS(5ωt+ 7θS)的气隙磁势波,这表明:
;
由数学知:相量和总是小于(或等于)其代数和,即 Et( y<τ ) < Et( y=τ ) 及 Eq(q>1) < Eq(q=1) , 故
其比值 即 K y 及 K q 总是小于 1.
4. ★在交流发电机定子槽的导体中感应电动势的频率、波形、大小与哪些因素有关?这些因
素中哪些是由构造决定的,哪些是由运行条件决定的?
绕组串联匝数有关,由构造决定;与频率、每极下磁通量有关,由运行条件决定。
6. ★★试从物理和数学意义上分析,为什么短距和分布绕组能削弱或消除高次谐波电动势?
答: 因谐波电动势 Eφν = 4.44 fν Nk pν kdν Φν ,欲要消除或削弱某次谐波电动势,只需使某次
谐波的短距系数 k pν 或分布系数 kdν 为零(或很小)即可。
τ。
答:ν −1 ν
5. ★三相对称绕组通过三相对称电流,顺时针相序(a-b-c-a),其中 ia = 10 sin ωt ,当 Ia=10A
时,三相基波合成磁势的幅值应位于
;当 Ia =-5A 时,其幅值位于
。
答:A 相绕组轴线处,B 相绕组轴线处。
第四章-混合物化学位-习题-解答

第四章 流体混合物的热力学性质思考题1) 在化工热力学中引入偏摩尔性质的意义何在?在进行化工计算时,什么情况下不能使用偏摩尔量?2) 简述Gibbs-Duhem 方程的用途,说明进行热力学一致性检验的重要性。
3) 简述求混合性质变化的实际用途。
4) 讨论理想气体的混合物和气态理想溶液的区别和联系。
5) 真实气体混合物的非理想性表现在哪几个方面? 6) 说明在化工热力学中引入逸度计算的理由。
7) 解释活度定义中的标准态,为什么要引入不同的标准态?8) 混合物的逸度和逸度系数与它的组元逸度和逸度系数有什么关系?由这种关系我们可以得出什么结论?9) 讨论偏摩尔性质、混合性质变化和超额性质这三个概念在化工热力学中各起的作用。
10) 试总结和比较各种活度系数方程,并说明其应用情况。
计算题1. 某酒厂用96%(wt )的食用酒精配酒,酒中的乙醇含量为56%(wt )。
现决定用1吨食用酒精进行配制,问需加多少水才能配成所需的产品?所得酒有多少m 3?已知在25℃和解:1吨食用酒精中乙醇质量:1*0.96=0.96吨 可配成酒的质量:0.96/0.56=1.714(吨) 所需水的质量:1.714-1=0.714(吨)酒中水的质量:1-0.96+0.714=0.754(吨) 配成的酒的体积22H O EtOH H O EtOH30.9530.754 1.2430.960.718562 1.193281.911842(m )Vt V m V m =⋅+⋅=⨯+⨯=+=2. 298.15K 下,有若干NaCl(B)溶解于1kg 水(A)中形成的溶液,其总体积为2B2/3B B t n 119.0n 773.1n 625.1638.1001V +++= (3cm )。
求B n =0.5mol 时,水和NaCl 的偏摩尔B A V ,V 。
123(),,316.625 1.7730.1192218.625(cm )B AB B B nV V T P n n n n ⎡⎤∂=⎢⎥∂⎣⎦=+⨯⨯+⨯⨯=3322223()31001.3816.625 1.7730.11916.625 1.77320.11921001.12655.5518.022(cm )t B B A AB B B B B B AV n V V n n n n n n n n -=⎡⎤+++--⨯-⨯⎢⎥⎣⎦===3. 在30℃和10.133kPa 下,苯(1)和环几烷(2)的液体混合物的容积数据可用2611(109.416.8 2.64)10V x x -=--⨯表示。
第四章习题解答

第四章习题解4-3 已知调制信号()cos(2000)cos(4000)m t t t ππ=+,载波为4cos10t π,进行单边带调制,试确定该单边带信号的表示式,并画出频谱图。
[解]首先计算()m t 的希尔伯特变换,ˆ()sin(2000)sin(4000)mt t t ππ=+, 然后分别计算上边带与下边带的单边带调制信号。
上边带信号:44444411ˆ()()cos(10)()sin(10)221{[cos(2000)cos(10)sin(2000)sin(10)]2[cos(4000)cos(10)sin(4000)sin(10)]}1[cos(12000)cos(14000)]2U s t m t t mt t t t t t t t t t t t ππππππππππππ=−=−+−=+ 类似地,下边带信号为:1()[cos(8000)cos(6000)]2D s t t t ππ=+。
频谱图:实线为上边带信号,虚线为下边带信号。
4-6 某调制系统如图P4-6所示,为了在输出端同时得到f 1(t )和f 2(t ),试确定接收端的c 1(t)和c (t)f 1(t f 2(t f 1(t )f 2(t )[解] 1020()()cos 2()sin 2s t f t f t f t f t ππ=⋅+如果 10()cos 2c t f t π=,20()sin 2c t f t π= 则11020111()()cos4()sin 4222g t f t f t f t f t ππ⎡⎤=++⋅⎢⎥⎣⎦21020111()()sin 4()cos 4222g t f t f t f t f t ππ⎡⎤=⋅+−⎢⎥⎣⎦通过低通滤波器则输出正好是)(211t f 和)(212t f 。
(相干解调)4-7 设某信道具有均匀的双边噪声功率谱密度()n P f =0.5×10−3W/Hz ,在该信道中传输抑制载波的双边带信号,并设调制信号()m t 的频带限制在5kHz ,而载波为100kHz ,已调信号的功率为10kW 。
第四章 习题解答

1 第四章 习题解答3/150、试用实验方法鉴别晶体SiO 2、SiO 2 玻璃、硅胶和SiO 2 熔体。
它们的结构有什么不同?解答:利用X-射线粉末衍射检测。
晶体SiO 2——质点在三维空间做有规律的排列,各向异性。
SiO 2 熔体——内部结构为架状,近程有序,远程无序。
SiO 2 玻璃——各向同性。
硅胶——疏松多孔。
7/151、SiO 2 熔体的粘度在1000℃时为1014 Pa·s ,在1400℃时为107 Pa·s 。
SiO 2 玻璃粘滞流动的活化能是多少?上述数据为恒压下取得,若在恒容下获得,你认为活化能会改变吗?为什么?解答:(1)根据公式:)exp(0RTE ∆=ηη 1000℃时,η=1014 Pa·s ,T=1000+273=1273K , )1273314.8exp(10014⨯∆=E η (1) 1400℃时,η=107 Pa·s ,T =1400+273=1673K ,)1673314.8exp(1007⨯∆=E η (2) 联立(1)和(2)式解得:η0 = 5.27×10-16 Pa·s ,△E = 713.5 kJ/mol(2)若在在恒容下获得,活化能不会改变。
因为活化能是液体质点作直线运动所必需的能量。
它与熔体组成和熔体[SiO 4]聚合程度有关。
212/151、一种用于密封照明灯的硼硅酸盐玻璃,它的退火点是544℃,软化点是780℃。
求:(1)这种玻璃粘性流动的活化能;(2)它的工作范围;(3)它的熔融范围。
解答:(1)根据公式:)exp(0RTE ∆=ηη 退火点544℃, η=1012Pa·s ,T=544+273=817K , )817314.8exp(10012⨯∆=E η (1) 软化点为780℃,η=4.5×106 Pa·s ,T=780+273=1053K ,)1053314.8exp(104.506⨯∆=⨯E η (2)联立(1)和(2)式解得:η0 = 1.39×10-12 Pa·s ,△E = 373.13 kJ/mol 。
04化工原理第四章习题答案

4-1、燃烧炉的平壁由下列三种材料构成:耐火砖的热导率为,K m W 05.111−−⋅⋅=λ厚度mm 230=b ;绝热砖的热导率为11K mW 151.0−−⋅⋅=λ;普通砖的热导率为11K m W 93.0−−⋅⋅=λ。
若耐火砖内侧温度为C 10000,耐火砖与绝热砖接触面最高温度为C 9400,绝热砖与普通砖间的最高温度不超过C 1300(假设每两种砖之间接触良好界面上的温度相等)。
试求:(1)绝热砖的厚度。
绝热砖的尺寸为:mm 230mm 113mm 65××;(2)普通砖外测的温度。
普通砖的尺寸为:mm 240mm 1200mm 5××。
(答:⑴m 460.02=b ;⑵C 6.344°=t )解:⑴第一层:1121λb t t AQ −=第二层:2232λb t t AQ −=⇒()()32222111t t b t t b −=−λλ⇒()()130940151.0940100023.005.12−=−b ⇒m446.02=b 因为绝热砖尺寸厚度为mm 230,故绝热砖层厚度2b 取m 460.0,校核:()()3940460.0151.0940100023.005.1t −=−⇒C 3.1053°=t ;⑵()()43332111t t b t t b −=−λλ⇒C 6.344°=t 。
4-2、某工厂用mm 5mm 170×φ的无缝钢管输送水蒸气。
为了减少沿途的热损失,在管外包两层绝热材料:第一层为厚mm 30的矿渣棉,其热导率为11K m 0.065W −−⋅⋅;第二层为厚mm 30的石棉灰,其热导率为11K m 0.21W −−⋅⋅。
管内壁温度为C 3000,保温层外表面温度为C 400。
管道长m 50。
试求该管道的散热量。
(答:kW 2.14=Q )解:已知:11 K m 0.065W −−⋅⋅=λ,11 K m 0.21W −−⋅⋅=λ查表得:11K m W 54−−⋅⋅=钢λ()34323212141ln 1ln 1ln 12d d d d d d t t lQλλλπ++−=其中:0606.016.017.0ln ln 12==d d ,302.017.023.0ln ln 23==d d ,231.023.029.0ln ln 34==d d()1m W 28421.0231.0065.0302.0450606.0403002−⋅=++−=πlQ ,kW 2.14W 1042.1502844=×=×=Q 。
第四章 习题答案
习题4.1选择填空1、选用差分放大电路的原因是 A 。
A 、克服温漂B 、 提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ,将使电路的 B 。
A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。
4、设差放电路的两个输入端对地的电压分别为v i1和v i2,差模输入电压为v id ,共模输入电压为v ic ,则当v i1=50mV ,v i2=50mV 时,v id =_0mV __,v ic =_50mV __;当v i1=50mV ,v i2=-50mV 时,v id =_100mA __,v ic =_0mA__;当v i1=50mV ,v i2=0V 时,v id =_50mV __,v ic =_25mA __。
5、电流源常用于放大电路,作为_A ___(A.有源负载,B.电源,C.信号源),使得放大倍数__A __(A.提高,B.稳定)。
6、电压放大电路主要研究的指标是 a 、 b 、 c ;功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、(a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗)7、功率放大电路中,___甲类____功率放大电路导通角最大;_____乙类___功率放大电路效率较高。
(甲类、乙类、甲乙类) 8、甲类功放效率低是因为 B 。
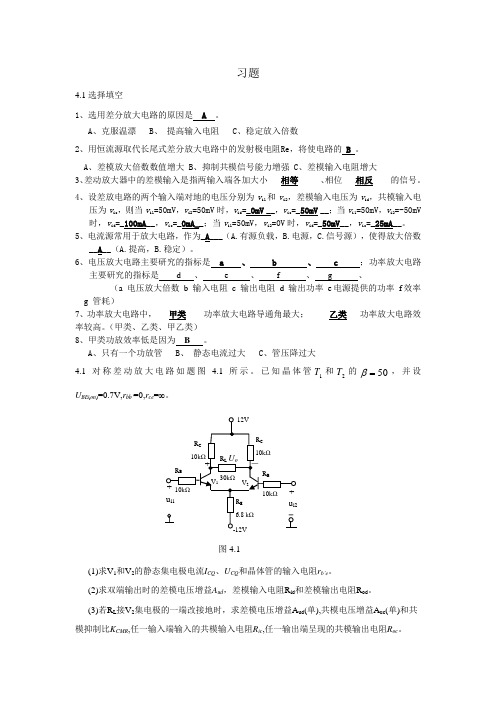
A 、只有一个功放管B 、 静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。
已知晶体管1T 和2T 的50=β,并设U BE (on )=0.7V,r bb ’=0,r ce =∞。
(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。
(2)求双端输出时的差模电压增益A ud ,差模输入电阻R id 和差模输出电阻R od 。
第4章习题及答案

第四章习题及解答4-3 什么是进程?进程与程序的主要区别是什么?答:进程是一个具有一定独立功能的程序关于某个数据集合的一次活动。
进程与程序的主要区别是:(1) 程序是指令的有序集合,是一个静态概念。
进程是程序在处理机的一次执行过程,是一个动态概念。
进程是有生命期的,因创建而产生,因调度而执行,因得到资源而暂停,因撤消而消亡;(2) 进程是一个独立的运行单元,是系统进行资源分配和调度的独立单元,而程序则不是。
(3) 进程与程序之间无一一对应关系。
一个程序可以对应多个进程,一个进程至少包含一个程序。
4-4 图4.2标明程序段执行的先后次序。
其中:I表示输入操作,C表示计算操作,P 表示打印操作,下角标说明是对哪个程序进行上述操作。
请指明:(1)哪些操作必须有先后次序? 其原因是什么?(2)哪些操作可以并发执行? 其原因又是什么?答:(1) ①I n、C n和P n之间有先后顺序要求,这是由于程序本身的逻辑要求。
②使用同一设备的不同的程序段,如C1…C n,I1…I n,P1…P n,之间有先后顺序要求,这是由于设备某一时刻只能为一个程序服务。
(2) 不同程序使用不同设备时,占用不同设备,无逻辑关系,可以并发执行,如I2和C1;I3、C2和P1。
4-9 某系统进程调度状态变迁图如图4.31(1) 什么原因会导致发生变迁2、变迁3、变迁4 ?答:发生变迁2的原因:时间片到发生变迁3的原因:请求I/O或其他系统调用发生变迁4的原因:I/O完成或其他系统调用完成(2) 在什么情况下,一个进程的变迁3 能立即引起另一个进程发生变迁1 ?答:一个进程的变迁3 能立即引起另一个进程发生变迁的条件是,就绪队列非空。
(3) 下列因果变迁是否可能发生?若可能,需要什么条件?a. 2→1;b. 3→2;c. 4→1答:a. 2→1 不需要条件,一定会发生。
b. 3→2 不可能发生。
c. 4→1 可能发生,条件:就绪队列为空,或在可剥夺调度方式下,转变为就绪状态的进程优先级最高。
4第四章金融工程练习题.

4第四章⾦融⼯程练习题.第四章⼀、判断题1、在利率期货交易中,若未来利率上升则期货价格下降。
(√)2、利率期货的标的资产是利率。
(×)3、如果不存在基差风险,则⽅差套期保值⽐率总为1。
(√)4、由于在CBOT交易的债券期货合约的⾯值为10万美元,因此,为了对价值1000万美元的债券资产完全保值,必须持有100份合约。
(×)5、根据逐⽇结算制,期货合约潜在的损失只限于每⽇价格的最⼤波动幅度。
(√)6、如果⽅差套期保值⽐率为1,则这个套期保值⼀定是完美的。
(×)7、随着期货合约越来越临近交割⽇,基差越来越⼤。
(×)8、买⼊和卖出相同品种但交割⽇期不同的两份期货合约⽐单纯买卖⼀份合约需交纳更⾼的保证⾦。
(×)9、以交割⽉份相同但头⼨相反的另⼀份期货合约来对冲原来持仓的合约,称为合约的交割。
(×)10、期货保证⾦实⾏逐⽇结算制。
(√)11、根据短期利率期货的定价公式,远期利率协议价格越⾼,期货价格越低。
(√)⼆、单选题1、利⽤预期利率的上升,⼀个投资者很可能(A)A.出售美国中长期国债期货合约 B 在⼩麦期货中做多头C 买⼊标准普尔指数期货和约D 在美国中长期国债中做多头知识点:利率期货合约解题思路:A。
预期利率上升,则债券价格将下降,因此要出售债券期货合约。
2、在芝加哥交易所按2005年10⽉的期货价格购买⼀份美国中长期国债期货合约,如果期货价格上升2个基点,到期⽇你将盈利(损失)(D)A. 损失2000美元 B 损失20美元 C.盈利20美元 D 盈利2000美元知识点:期权合约收益计算解题思路:D。
期货合约多头,随着合约价格的上涨,盈利增加。
3、在1⽉1⽇,挂牌的美国国债现货价格和期货价格分别为93-6和93-13,你购买了10万美元⾯值的长期国债并卖出⼀份国债期货合约。
⼀个⽉后,挂牌的现货和期货市场价格分别为94和94-09,如果你要结算头⼨,将________A. 损失500美元B. 盈利500美元C. 损失50美元 D 损失5000美元知识点:头⼨结算解题思路:A。
第4章习题解答

第四章 机械振动和机械波4.1什么是简谐振动?分别从运动学和动力学两方面作出解释。
并说明下列运动是不是简谐振动;(1)小球在地面上做完全弹性的上下跳动;(2)小球在半径很大的光滑凹球面底部做小幅度的摆动; (3)曲柄连杆机构使活塞做往复运动。
4.2 若弹簧振子中弹簧本身的质量不可忽略,其振动周期是增加还是减小? 这相当于增加了系统的惯性,振动周期将增加。
4.3 将单摆拉到与竖直方向成ϕ角后,放手任其摆动,则ϕ是否就是其初相位?为什么?单摆的角速度是否是谐振动的圆频率?4.4判断以下说法是否正确?说明理由。
“质点作简谐振动时,从平衡位置运动到最远点需要1/4周期,因此走过该段距离的一半需时1/8周期。
”4.5两个相同的弹簧挂着质量不同的物体,当它们以相同的振幅做简谐运动时,问振动的能量是否相同?4.6什么是波动?振动与波动有什么区别和联系? 4.7试判断下列几种关于波长的说法是否正确. (1)在波传播方向上相邻两个位移相同点的距离; (2)在波传播方向上相邻两个运动速度相同点的距离; (3)在波传播方向上相邻两个振动相位相同点的距离。
4.8当波从一种媒质透入另一种媒质时,下面那些量会改变,哪些量不会改变:波长、频率、波速、振幅。
4.9有人认为频率不同、振动方向不同、相位差不恒定的两列波不能叠加,所以它们不是相干波,这种看法对不对?说明理由。
4.10 波的能量与振幅的平方成正比,两个振幅相同的相干波在空间叠加时,干涉加强的点的合振幅为原来的两倍,能量为原来的四倍,这是否违背能量守恒定律?4.11 一质点作简谐振动)7.0100cos(6ππ+=t x cm 。
某时刻它在23=x cm 处,且向X 轴负向运动,它要重新回到该位置至少需要经历的时间为( ) A 、s 1001 B 、s 2003 C 、s 501 D 、 s 503答案:(B)4.12 一个单摆,如果摆球的质量增加为原来的四倍,摆球经过平衡位置时的速度减为原来的一半,则单摆( )A 、频率不变,振幅不变;B 、频率不变,振幅改变;C 、频率改变,振幅不变;D 、频率改变,振幅改变; B4.13 以频率ν作简谐振动的系统,其动能和势能随时间变化的频率为( ) A 、2/ν B 、ν C 、ν2 D 、ν4 答案:(C)4.14 劲度系数为m N /100的轻弹簧和质量为10g 的小球组成的弹簧振子,第一次将小球拉离平衡位置4cm ,由静止释放任其运动;第二次将小球拉离平衡位置2cm 并给以2cm/s 的初速度任其振动。
[分享]第四章刚体的转动问题与习题解答
![[分享]第四章刚体的转动问题与习题解答](https://img.taocdn.com/s3/m/c9e3663ccec789eb172ded630b1c59eef8c79aab.png)
第四章 刚体的转动 问题与习题解答问题:4-2、4-5、4-94-2如果一个刚体所受合外力为零,其合力矩是否也一定为零?如果刚体所受合外力矩为零,其合外力是否也一定为零?答:一个刚体所受合外力为零,其合力矩不一定为零,如图a 所示。
刚体所受合外力矩为零,其合外力不一定为零,例如图b 所示情形。
4-5为什么质点系动能的改变不仅与外力有关,而且也与内力有关,而刚体绕定轴转动动能的改变只与外力矩有关,而与内力矩无关?答:因为合外力对质点所作的功,等于质点动能的增量;而质点系中内力一般也做功,故内力对质点系的动能的增量有贡献。
而在刚体作定轴转动时,任何一对内力对转轴的力矩皆为一对大小相等、方向相反的力矩,且因定轴转动时刚体转过的角度d θ都一样,故其一对内力矩所作的功()0inij ij ji ij ji W M d M d M M d θθθ=+=+=,其内力功总和也为零,因而根据刚体定轴转动的动能定理可知:内力矩对其转动动能的增量无贡献。
4-9一人坐在角速度为0ω的转台上,手持一个旋转的飞轮,其转轴垂直地面,角速度为ω'。
如果突然使飞轮的转轴倒转,将会发生什么情况?设转台和人的转动惯量为J ,飞轮的转动惯量为J '。
答:(假设人坐在转台中央,且飞轮的转轴与转台的转轴重合)视转台、人和飞轮为同一系统。
(1)如开始时飞轮的转向与转台相同,则系统相对于中心轴的角动量为:10L J J ωω''=+飞轮转轴快速倒转后,飞轮的角速度大小还是ω',但方向与原来相反;如设转台此时的角速度为1ω,则系统的角动量为:21L J J ωω''=-在以上过程中,外力矩为零,系统的角动量守恒,所以有:10J J J J ωωωω''''-=+即 102J Jωωω''=+,转台的转速变大了。
(2)如开始时飞轮的转向与转台相反,则系统相对于中心轴的角动量为:10L J J ωω''=-飞轮转轴快速倒转后,飞轮的角速度大小还是ω',但方向与原来相反;如设转台此时的角速度为1ω,则系统的F 1F 3ab角动量为:21L J J ωω''=+在以上过程中,外力矩为零,系统的角动量守恒,所以有:10J J J J ωωωω''''+=-即 102J Jωωω''=-,转台的转速变慢了。
第四章习题及解答
第四章习题及解答4.1 数字电路设计的基本步骤有哪些?每一步完成的目标任务是什么?见书P48。
4.2 组合逻辑电路的设计为什么可以从卡诺图直接进入?因为逻辑函数可以有多种有表达形式,卡诺图就是其中的一种,因此,直接从卡诺图直接进入设计就是最直接、最有效的一种方式,它简化了设计,更便于化简。
4.3 某车间有A 、B 、C 、D 四台电动机,今要求:(1)A 必须开机;(2)其他三台电动机中至少有两台开机,如不满足上述要求,则指示灯熄灭。
设指示灯亮为“1”,熄灭为“0”,电机开机为“1”,停机为“0”,试用与非门组成指示灯控制电路。
根据题意,用卡诺图表示电机运行的状态,求出输出表达式:F= ABC+ABD+ACD用与非门实现逻辑:4.4 试设计一个供4组使用的智力抢答器电路。
设4组变量分别为:A 、B 、C 、D 。
输出用4个发光二极管,表示抢答结果,灯亮答表达式: F ABCD ABCD ABCD =+++4.5 电话室需对4种电话编码控制,按紧急次序排列优先权由高到底依次为火警电话、急救电话、工作电话、生活电话,其编码为11,10,01,00,试设计该编码电路。
设火警电话、急救电话、工作电话、生活电话为变量A 、B 、C 、D ,编码输出量为X 、Y 。
AB CD01001110000000000001111000 01 11 10 F ABC ABD ACDABC ABD ACD =++=AB C D题4.3图列出编码真值表:4.6 试用3线-8线译码器和门电路实现以下函数:4.7 试用四选一多路选择器实现函数Y ABC AC BC =++。
1. 求出最小项、及最小项反函数非表达式:2. 对比四选一多路选择器表达式:0123Y ABD ABD ABD ABD =+++我们发现用原函数无法用一个四选一选择器实现,但反函数只有三个最小项,因为实际的数据选择器,它们都有两个互补的变量输出,因此从反变量输出端(~W)就可以达到要求了。
第四章习题解答(模电康第五版)

0.5 0
20
iB 10μA
1
2
3
4
5
6 vCE V
回主页 总目录 章目录 上一页 下一页 退出
Rb
VCC VBEQ I BQ
6 0.7 20 10
6
265k
⑶由交流负载线知交流输出范围为0.8~4.5V,故最大 不失真幅度为 4.5 3 1.5V ⑷基极正弦电流的最大幅值为 I Bmax 20μA
ii
ib
I2
Rb2
Re
I EQ
Rs
vi + vs
Rb1 Rb2 rbe
ib
+
Rc
vo RL
- -
Ri
小信号等效电路
直流通路
Ro
回主页 总目录 章目录 上一页 下一页 退出
I EQ I CQ 2.4mA VBQ VBEQ Re I EQ 0.7 2 103 2.4 10 3 5.5V
vi
Rb1 Rb2 Re1 ie
Rc RL vo
vs
- -
回主页 总目录 章目录 上一页 下一页 退出
Av
vo vi
ib Rc // RL ib rbe ie Re1
3.3 5.1
ib RL
'
ib rbe 1 ib Re1
RL
'
rbe 1 Re1
Rb2 Rb1 Rb2 20 Rb1 20
VBQ
VCC
VCC Rb1
VBQ
I1 R c
I BQ I CQ VEQ
5.5
线性代数练习4

T
S ABC
x1 1 x2 2 x3
y1 1 y2 1 . y3 1
证明:因为 AB x2 x1 , y 2 y1 ,0
AC x3 x1 , y3 y1 ,0,从而
x x1 AB AC 0,0 2 x3 x1
y 2 y1 y3 y1
y 5 x 1, 点,直线 y 2 x 3 .
2
2、 将 xOz 坐标面上的抛物线 z 5 x 绕 x 轴旋转一周,求生成的旋转曲面的方程. 解:抛物线 z 5 x 绕 x 轴旋转一周所生成的曲面方程为:
2
( y 2 z 2 ) 5x
3、 将 xOy 坐标面上的双曲线 4 x 9 y 36 分别绕 x 轴及 y 轴旋转一周,求生成的两个旋
6 求下列直线的方程: (1) 经过 A( 1,0,-1),B( 1,1,3)两点.
ቤተ መጻሕፍቲ ባይዱ
(2) 过点 A( 1,-1,2)与直线
x y 2z 1 0 平行. x 2 y 3z 2 0
解: (1)方向向量为 AB 0,1,4 所以直线的方程为
x 1 y z 1 0 1 4
4、 说明下列旋转曲面是怎样形成的: (1) x
2
y2 z2 1; 4 4
5,1,0 ,
也即点 M0( 4,-3,1)在平面 x+2y -z-3=0 上的投影点.
习题 4—5
1、 指出下列方程在平面直角坐标系与空间直角坐标系中各表示什么图形: (1) x y 2 y 0 ;圆,圆柱面
2 2
(2) x 2 y ;抛物线,抛物柱面
2
(3) 4 x 2 y 1;直线,平面 (4)
第四章练习题及参考解答(第四版)计量经济学

第四章练习题及参考解答4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,有人建议你分别进行如下回归:1221i i i Y X u αα=++ 1332i i i Y X u γγ=++(1) 是否存在3322ˆˆˆˆβγβα==且?为什么? (2) 1ˆβ会等于1ˆα或1ˆγ或者两者的某个线性组合吗? (3) 是否有()()22ˆˆVar Var βα=且()()33ˆˆVar Var βγ=?【练习题4.1参考解答】(1) 存在2233ˆˆˆˆαβγβ==且 。
因为 ()()()()()()()22332322222323ˆi iii ii iiii iy x x y x x xx x x x β-=-∑∑∑∑∑∑∑当23X X 与 之间的相关系数为零时,离差形式的230i ixx =∑有 ()()()()223222222223ˆˆi i i i i iiiy x x y x xx x βα===∑∑∑∑∑∑ 同理有: 33ˆˆγβ= (2)会的。
(3) 存在 ()()()()2233ˆˆˆˆvar var var var βαβγ==且 因为 ()()2222223ˆvar 1ix r σβ=-∑当 230r = 时, ()()()22222222223ˆˆvar var 1iix x r σσβα===-∑∑ 同理,有 ()()33ˆˆvar var βγ=4.2 表4.4给出了1995—2016年中国商品进口额Y 、国内生产总值GDP 、居民消费价格指数CPI 的数据。
表4.4 中国商品进口额、国内生产总值、居民消费价格指数资料来源:《中国统计年鉴2017》考虑建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?(3)进行以下回归:121ln ln t t i Y A A GDP v =++ 122ln ln t t i Y B B CPI v =++ 123ln ln t t i GDP C C CPI v =++ 根据这些回归你能对多重共线性的性质有什么认识?(4)假设经检验数据有多重共线性,但模型中32ˆˆββ和在5%水平上显著,并且F 检验也显著,你对此模型的应用有何建议?【练习题4.2参考解答】建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
第4章集成运算放大器习题解答

第4章集成运算放⼤器习题解答第四章习题参考答案4-1 什么叫“虚短”和“虚断”?答虚短:由于理想集成运放的开环电压放⼤倍数⽆穷⼤,使得两输⼊端之间的电压近似相等,即-+≈u u 。
虚断:由于理想集成运放的开环输⼊电阻⽆穷⼤,流⼊理想集成运放的两个输⼊端的电流近似等于零,即0≈=-+i i 。
4-2 理想运放⼯作在线性区和⾮线性区时各有什么特点?分析⽅法有何不同?答理想运放⼯作在线性区,通常输出与输⼊之间引⼊深度负反馈,输⼊电压与输出电压成线性关系,且这种线性关系只取决于外部电路的连接,⽽与运放本⾝的参数没有直接关系。
此时,利⽤运放“虚短”和“虚断”的特点分析电路。
理想运放⼯作在⾮线性去(饱和区),放⼤器通常处于开环状态,两个输⼊端之间只要有很⼩的差值电压,输出电压就接近正、负电压饱和值,此时,运放仍具有“虚断”的特点。
4-3 要使运算放⼤器⼯作在线性区,为什么通常要引⼊负反馈?答由于理想运放开环电压放⼤倍数∞=uo A ,只有引⼊深度负反馈,才能使闭环电压放⼤倍数FA 1u =,保证输出电压与输⼊电压成线性关系,即运放⼯作在线性区。
4-4 已知F007运算放⼤器的开环放⼤倍数dB A uo 100=,差模输⼊电阻Ω=M r id 2,最⼤输出电压V U sat o 12)(±=。
为了保证⼯作在线性区,试求:(1)+u 和-u 的最⼤允许值;(2)输⼊端电流的最⼤允许值。
解(1)由运放的传输特性5o uo 1012===++u u u A 则V 102.1101245--+?===u u(2)输⼊端电流的最⼤允许值为A 106102102.11164id --+?=??==r u I 4-5 图4-29所⽰电路,设集成运放为理想元件。
试计算电路的输出电压o u 和平衡电阻R 的值。
解由图根据“虚地”特点可得0==+-u u图中各电流为601.01--=u i 305.02---=u i 180o f u u i -=- 由“虚断”得f 21i i i =+以上⼏式联⽴,可得V 7.2o =u平衡电阻为Ω==k R 18180//60//30图4-29 题4-5图4-6 图4-30所⽰是⼀个电压放⼤倍数连续可调的电路,试问电压放⼤倍数uf A 的可调范围是多少?图4-30 题4-6图解设滑线变阻器P R 被分为x R 和x P R R -上下两部分。
4-第四章 磁共振成像-课后习题答案

第四章 磁共振影像习题四解答4-1 如何理解加权图像?答: 磁共振成像是多参数成像,图像的灰度反映了各像素上MR 信号的强度,而MR 信号的强度则由成像物体的质子密度ρ、纵向弛豫时间1T 、横向弛豫时间2T 等特性参数决定。
出于分析图像的方便,我们希望一幅MR 图像的灰度主要由一个特定的成像参数决定,这就是所谓的加权图像。
例如图像灰度主要由1T 决定时,就是1T 加权图像;主要由2T 决定时,就是2T 加权图像;主要由质子密度ρ决定时,就是质子密度ρ加权图像。
通过选择不同的序列参数,可以获得同一断层组织无数种不同对比情况的加权图像,以便在最大限度上显示病灶,提高病灶组织和正常组织的对比度。
4-2 简述SE 序列时序和180°脉冲的作用。
答:(1)SE 序列时序为先发射90°射频脉冲经过时间E 12t T =后,再发射180°脉冲,当t =T E 时出现回波峰值,采集信号。
(2)90°脉冲使0M 倒向y '轴,由于0B 的不均匀性造成各个核磁矩旋进的角速度不同,相位很快散开。
经时间T I 后,在x '方向施以180°脉冲使得所有自旋磁矩都绕x '轴旋转180°,但并不改变旋进方向,所以互相远离的核磁矩变为互相汇聚的磁矩,最后汇聚于-y '轴上,使去相位状态的自旋核重新处于同相位状态,抵消了磁场不均匀造成的影响。
4-3 试分析自旋回波T 1加权、T 2 加权的条件及图像对比度形成原理。
答:(1)选择短T E 和短T R ,实现1T 加权。
选择长T E 和长T R 实现T 2加权。
(2)SE 序列T 1对比度的形成: T 1加权像的对比度主要由T R 决定,T 1大的地方I 值小,图像呈现弱信号;T 1小的地方I 值大,图像呈现强信号。
这是因为使用短的T R ,在下一个RF 时,短1T 组织纵向磁化强度矢量必定恢复的比较好,Z M 较大,在90°RF 作用下xy M 就大,信号就强。
第四章习题答案

第四章习题答案习题四答案4.1画出图P4.1由或非门组成的基本RS触发器输出端Q、Q的电压波形,输入端S、R的电压波形如图中所示。
图P4.1解答:已知或非门构成的RS触发器的特征方程如下:?Qn?1?S?RQn ??RS?0根据输入端S、R的波形图,得出输出端Q、Q的电压波形见图A4.1。
4.2 在图P4.2电路中,若CP、S、R电压波形如图中所示,试画出Q、Q端与之对应的电压波形。
假定触发器的初始状态为Q?0。
1图P4.2 解答:见图A4.2图A4.24.3一种特殊的RS触发器如图P4.3所示。
1)试列出状态转换真值表;2)写出次态方程;3)R与S是否需要约束条件?图P4.3解答:1)① CP=0时,SS=1,RR=1,期间Qn?1?Qn,状态保持。
?② CP=1时,?RR?R???SS?S?RR?S?R?S?R2即在CP=1的情况下:若R=0,S=0。
则RR=1,SS=1,有Qn?1?Qn,状态保持。
若R=0,S=1。
则RR=1,SS=0,有Qn?1?1。
若R=1,S=0。
则RR=0,SS=1,有Qn?1?0。
若R=1,S=1。
则RR=0,SS=1,有Qn?1?0。
电路的状态转换真值表如下表所示:2)求次态方程:由上述状态转换真值表,不难得出次态方程:Qn?1?CP?Qn?CP?R?(Qn?S)3)R与S无需约束条件。
4.4 已知主从结构JK触发器J、K和CP的电压波形如图P4.4所示,试画出Q、Q端对应的电压波形。
设触发器的初始状态为Q?0。
图P4.4 解答:见图A4.4图A4.44.5如图P4.5示是主从JK触发器CP和J、K的电压彼形,试画出主触发器QM端和从触发3器Q端的工作波形。
设Q初始态为0。
图P4.5解答:见图A4.5图A4.54.6如图P4.6示电路,设该TTL触发器的初态为0,试画出在CP 作用下的Q端波形图。
图P4.6解答:根据图示可知该触发器的J?1,K?Qn。
由时钟下降沿触发。
线性代数习题答案4

a2 + b2 3 (a2 + b2 3)(a2 − b2 3) a22 − 3b22
a22 − 3b22
3,
a1 ± a2 , b1
± b2;
a1a2
+ 3b1b2 , a1b2
+ a2b1;
a1a2 a22
− 3b1b2 − 3b22
,
(a2b1 − a1b2 a22 − 3b22
)
都是有理数,故 K2 是数域.
x + y = (x1 + y1, x2 + y2 , x3 + y3 )T , 2(x1 + y1) + 3(x2 + y2 ) − (x3 + y3 ) = 0 ⇒ x + y ∈W4 , kx = (kx1, kx2 , kx3)T , 2(kx1) + 3(kx2 ) − (kx3) = 0 ⇒ kx ∈W4 故W4 对 R3 中的加法与数乘运算封闭, 它是 R3 的子空间. (5) W5 = {x ∈ R3 | 2x1 + 3x2 − x3 = 1}; 【解】W5 不是 R3 的子空间. 显然W5 中不含有零向量, 故W5 不是 R3 的子空间. (6) W6 = {x ∈ R3 | x1 − x22 = 0}.
=
a1a2 a22
+ b1b2 + b22
+
(a2b1 a22
− a1b2 ) + b22
i,
a1
± a2 , b1
± b2;
a1a2
− b1b2 , a1b2
+ a2b1;
a1a2 + b1b2 a22 + b22
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1,2-加成生成的中间体正碳离子为P-л共轭和有三个C-H键与其超共轭,而1,4-加成的中间体比其少三个C-H键超共轭。
2.为什么1,4-加成产物比1,2-加成产物稳定?
解:1,2-加成产物有一个C-H键与双键超共扼,而1,4-加成产物有五个C-H键与双键超共扼。与双键超共扼的C-H键越多,产物越稳定。
十四、1,3-丁二烯和氯化氢在醋酸中室温下加成,可以得到78%的CH3CH(Cl)CH=CH2和22%的CH3CH=CHCH2Cl的混合物,此混合物再经过长时间加热或和三氯化铁一起加热,则混合物的组成改变为前者仅占25%,后者占75%,解释原因。
解:低温反应,为动力学控制反应,由中间体的稳定性决定反应主要产物,为1,2-加成为主。
第四章第四章炔烃、二烯烃
第五章
二、用系统命名法或衍生物命名法命名下列化合物。
三、写出下列化合物的构造式。
四、写出1-丁炔与下列试剂作用的反应式。
五、完成下列反应式。
六、以反应式表示以丙炔为原料,并选用必要的无机试剂,合成
下列化合物。
七、完成下列反应式。
八、指出下列化合物可由那些原料通过双烯合成而得。
CH2=CHCH=CHCH=CH2
分子式:C6H8为1,3,5-己三烯。
(完)
作业:94页,2,4,5,6,7,8,9,10,11,14
高温时反应为热力学控制反应,由产物的稳定性决定主要产物,1,4-加成产物比1,2-加成稳定。
十五、一个碳氢化合物,测得其相对分子质量为80,催化加氢时,10mg样品可吸收8.40mL氢气。原样品经臭氧化反应后分解,只得甲醛和乙醛。问这个烃是什么化合物?
解:10mg样品为0.125mmole
8.40mL氢气为0.375mmole。可见化合物分子中有三个双键或一个双键,一个叁键。但是根据臭氧化反应产物,确定化合物分子式为:
十二、试用适当的化学方法将下列混合物中的少量杂志除去。
1,1,除去粗乙烷中少量的乙炔。
解:将混合物通入硝酸银的氨溶液,乙炔生成乙炔银而沉淀除去。
2,2,除去粗乙烯中的少量乙炔。
解:将混合物进行Lindlar催化加氢,则乙炔变为乙烯。
十三、
1.1,3-丁二烯和溴化氢的1,2-加成和14-加成,那种速度快?为什么?
九、以反应式表示以乙炔为原料,并可选用必要无机试剂合成下列化合物。
十、以四个碳原子以下烃为原料合成下列化合物。
十一、用化学方法区别下列各组化合物。
1.乙烷、乙烯、乙炔
解:
乙烷
乙烯
乙炔
Br2/CCl4
不变褪色ຫໍສະໝຸດ 褪色硝酸银氨溶液不变
2.CH3CH2CH2C三CH和CH3C三CCH3
解:分别加入硝酸银氨溶液,有炔银沉淀的位1-丁炔。
