(完整版)正方形的判定方法.
正方形的性质与判定
正方形的性质与判定二、正方形判定方法① 简单地说,要判定一个四边形是正方形,就要判定它既是菱形,又是矩形; 如上表中的判定原理1—4,都是这种方法;② 判定正方形需要四个条件,比较平行四边形、菱形和矩形的判定,判定平行四边形只要两个条件,判定菱形和矩形都要三个条件;③ 也可以先判定一个四边形是平行四边形,再加一个条件判定成菱形(或矩形),最后再加一个条件判定成矩形(或菱形),就成了正方形。
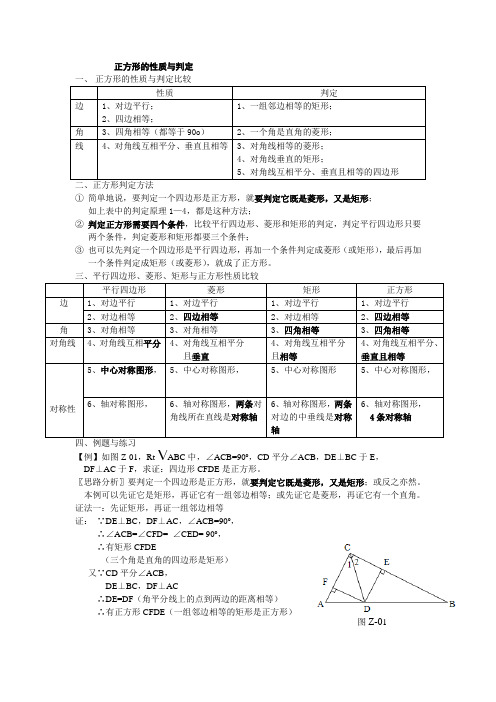
三、平行四边形、菱形、矩形与正方形性质比较四、例题与练习【例】如图Z-01,Rt ABC 中,∠ACB=90o ,CD 平分∠ACB ,DE ⊥BC 于E , DF ⊥AC 于F ,求证:四边形CFDE 是正方形。
〖思路分析〗要判定一个四边形是正方形,就要判定它既是菱形,又是矩形;或反之亦然。
本例可以先证它是矩形,再证它有一组邻边相等;或先证它是菱形,再证它有一个直角。
证法一:先证矩形,再证一组邻边相等 证: ∵DE ⊥BC ,DF ⊥AC ,∠ACB=90o ,∴∠ACB=∠CFD= ∠CED= 90o , ∴有矩形CFDE(三个角是直角的四边形是矩形) 又∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC∴DE=DF (角平分线上的点到两边的距离相等) ∴有正方形CFDE (一组邻边相等的矩形是正方形)图Z-01证法二:先证菱形,再证一个内角为90o 证:∵DE ⊥BC ∴∠DEB=90o ,又∵∠ACB=90o , ∴∠ACB=∠DEB ∴DE ∥CF 同理DF ∥CE ∴有CFDE又∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC∴DE=DF (角平分线上的点到两边的距离相等) ∴有菱形CFDE 又∵∠DEB=90o∴有正方形CFDE (一个角是直角的菱形是正方形) 〖练习〗⒈如图Z-02,矩形ABCD 中,AE 平分∠DAB ,交CD 于E ,EF ⊥AB 于F 求证:四边形AFED 是正方形〖提示〗用“一组邻边相等的矩形是正方形”⒉如图Z-03,在正方形ABCD 中,AE=BF ,AF 、ED 相交于G ①求证:AF=DE ②求证:AF ⊥DE〖提示〗①证ABF ≌DAE (SAS )②证∠2+∠3=90o :由①得∠1=∠3;∠1+∠2=90o⒊① 如图Z-04,正方形ABCD 对角线相交于O ,E 为AC 上一点,过A 作于G ,AG 交BD 于F ,求证:OE=OF 〖提示〗证AOF ≌BOE (AAS )② 如图Z-05,若点E 在AC 的延长线上,AG ⊥BE 交EB 延长线于G ,AG 交DB 延长线于F ,其它条件不变,OE=OF 还成立吗?请证明你的结论图Z-02图Z-03图Z-04图Z-05。
正方形的性质和判定

正方形的性质与判定1.定义:四条边都相等,四个角都是直角的四边形叫做正方形.2.性质:(1)对边平行;(2)四条边都相等;(3)四个角都是直角;(4)对角线互相垂直平分且相等,对角线平分对角;(5) 两条对角线把正方形分成四个全等的等腰直角三角形;(6)中心对称图形,轴对称图形.3.面积:=S 正方形边长×边长=12×对角线×对角线 4.判定:(1)有一个角是直角的菱形是正方形;(2)对角线相等的菱形是正方形;(3)一组邻边相等的矩形是正方形(4)对角线互相垂直的矩形是正方形; (5)对角线互相垂直平分且相等的四边形是正方形;(6)四条边都相等,四个角都是直角的四边形是正方形随堂练习1.菱形、矩形、正方形都具有的性质是( )A .对角线相等B .对角线互相垂直C .对角线互相平分D .对角线平分一组对角2. 已知四边形ABCD 是平行四边形,再从①AB =BC ,②∠ABC =90°,③AC =BD ,④AC ⊥BD 四个条件中,选两个作为补充条件后,使得四边形ABCD 是正方形,现有下列四种选法,其中错误的是( )A .选①②B .选②③C .选①③D .选②④3.如图,在△ABC 中,∠ACB =90°,BC 的垂直平分线EF 交BC 于点D ,交AB 于点E ,且BE =BF ,添加一个条件,仍不能证明四边形BECF 为正方形的是( )A .BC =ACB .CF ⊥BFC .BD =DF D .AC =BF第3题 第4题 第5题 第6题4.如图,在正方形ABCD 的外侧,作等边三角形ADE ,AC 、BE 相交于点F ,则∠BFC 为( )A .45°B .55°C .60°D .75°5.如图,将正方形OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1,),则点B 的坐标为( )A .(1﹣, +1)B .(﹣, +1)C .(﹣1,+1) D .(﹣1,)6.如图,已知正方形ABCD的边长为1,连结AC、BD,CE平分∠ACD交BD于点E,则DE长()A. B. C.1 D.1﹣7.正方形ABCD中E为线段BC上的动点如图①,过A作AF⊥DE,F为垂足,延长AF交DC于G如图②,①求证:AG=DE②连接BF,当E为BC中点时,求证:AB=FB.巩固提升1.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是()A.①② B.②③C.①③ D.②④2.如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为()A. B. C.D.第2题第3题第4题3.如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为()A.2B.3C.23 D 34.一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3 (x)上,已知正方形A 1B 1C 1D 1的边长为1,∠B 1C 1O =60°,B 1C 1∥B 2C 2∥B 3C 3…,则正方形A 2019B 2019C 2019D 2019的边长是( )A.()201821B .()201921C .()201833D .()2019335.如图,正方形CEFG 的边GC 在正方形ABCD 的边CD 上,延长CD 到H ,使DH =CE ,K 在BC 边上,且BK =CE ,求证:四边形AKFH 为正方形.。
正方形判定的5个方法

正方形判定的5个方法正方形是一种非常特殊的四边形,它具有四条相等的边和四个直角。
在计算机图形学中,判定一个图形是否为正方形是一项非常基础的任务。
在本文中,我们将介绍五种判定正方形的方法。
一、基于勾股定理的方法勾股定理指出,在一个直角三角形中,斜边的平方等于两条直角边的平方和。
因此,如果一个四边形是正方形,那么它的对角线长度应该相等。
具体地说,我们可以通过以下步骤来判定一个四边形是否为正方形:1. 计算出四个顶点之间两两之间的距离;2. 找出其中最长和最短的两条距离;3. 如果最长距离等于最短距离,则这个四边形是正方形。
二、基于向量叉积的方法向量叉积是向量运算中的一种重要操作,它可以用来计算两个向量所组成平行四边形面积。
对于任意一个四边形来说,如果它是正方形,则它对角线所组成平行四边形面积应该相等。
因此,我们可以通过以下步骤来判定一个四边形是否为正方形:1. 计算出四个顶点之间两两之间的向量;2. 计算出对角线所组成平行四边形的面积;3. 如果两条对角线所组成平行四边形面积相等,则这个四边形是正方形。
三、基于角度的方法正方形具有四个直角,因此任意两条相邻边所夹的角度应该都是90度。
因此,我们可以通过以下步骤来判定一个四边形是否为正方形:1. 计算出四个顶点之间相邻边所夹的角度;2. 如果所有相邻边所夹的角度都等于90度,则这个四边形是正方形。
四、基于矩阵变换的方法矩阵变换是计算机图形学中非常重要的一种技术,它可以用来进行旋转、缩放和平移等操作。
对于一个正方形来说,我们可以通过将它进行旋转、缩放和平移等操作后,判断变换后的图像是否还是一个正方形。
具体地说,我们可以通过以下步骤来判定一个四边形是否为正方形:1. 将这个四边形通过矩阵变换转化为标准正方形(即所有顶点坐标都在[-1, 1]范围内);2. 判断变换后的图像是否还是一个正方形。
五、基于Hough变换的方法Hough变换是一种常用于图像处理和计算机视觉中的技术,它可以用来检测直线、圆等几何形状。
正方形的判定

矩形
有一组邻边相等
平行四边形
正方形
有一个角是直角
菱形
正方形的判定方法:
• 1、一组邻边相等且有一个角是直角的平行 四边形是正方形
(对角线相等且互相垂直平分的四边形是正方形)
• 2、有一组邻边相等的矩形是正方形 • 3、有一个角是直角的菱形是正方形
判断四边形是正方形有哪些方法?
△CMD≌△ADF
练习.如图(5),在AB上取一点C,以 AC、BC为正方形的一边在同一侧作正 方形AEDC和BCFG连结AF、BD延长 BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF
证明:
如图,已知四边形ABCD和四边形DEFG是正方形,那 么线段AE和DG有什么大小关系?请说明理由。
1、先说明它是矩形,再说明这个矩形 (邻边相等的矩形是正方形) 有一组邻边相等.
2、先说明它是菱形,再说明这个菱形 (有一个角是ቤተ መጻሕፍቲ ባይዱ角的菱形是正方形) 有一个角是直角.
3、先说明它是平行四边形,再说明有 一组邻边相等,并且一个角是直角。
(对角线平分且垂直又相等的四边形是正方形)
巩固练习:判断下列命题是否正确,不是正 方形的补充什么条件能让它成为正方形? • • • • • • 四个角都相等的四边形是正方形; 四条边都相等的四边形是正方形; 对角线相等的菱形是正方形; 对角线互相垂直的矩形是正方形; 对角线垂直且相等的四边形是正方形; 四边相等,有一个角是直角的四边形 是正方形. (×) (×) (√ ) (√ ) (×)
又∵ ∠3+∠2=90°且 ∠1=∠3 ∴ ∠1+∠2=90° ∴ ∠EFG=90° ∴ 四边形EFGH是正方形(有一个角是直角的 菱形是矩形).
正方形的性质及判定(经典讲义)

正方形的性质及判定(经典讲义)正方形的性质及判定(经典讲义)
正方形是几何学中的一种特殊四边形,具有一些独特的性质和
判定方法。
本文档将介绍正方形的性质和判定方法。
正方形的性质
正方形是一种特殊的四边形,具有以下性质:
1. 边长相等:正方形的四条边长度相等。
2. 角度相等:正方形的四个内角均为直角(90度)。
3. 对角线相等:正方形的对角线长度相等且相交于垂直的交点。
4. 对称性:正方形具有4个对称轴,通过中心点垂直的两条对
称轴将正方形分成4个完全相等的部分。
正方形的判定
判定一个四边形是否为正方形可以根据以下方法:
1. 边长判定:如果一个四边形的四条边长度相等,则它是一个正方形。
2. 角度判定:如果一个四边形的四个内角均为直角(90度),则它是一个正方形。
3. 对角线判定:如果一个四边形的对角线长度相等且相交于垂直的交点,则它是一个正方形。
这些方法可以单独或者组合使用来判定一个四边形是否为正方形。
结论
根据正方形的性质和判定方法,我们可以得出以下结论:
- 如果一个四边形满足正方形的性质,即边长相等、角度为直角、对角线相等,那么该四边形是一个正方形。
- 如果一个四边形不满足正方形的任何一个性质,那么该四边形不是一个正方形。
通过理解正方形的性质和判定方法,我们可以准确地识别和判断一个四边形是否为正方形。
正方形的判定

⑸若AB=BC,且AC=BD,则四边形ABCD是
(正方形
)
精品课件
例2、直角三角形ABC中,CD平分∠ACB交AB于D,
DE⊥AC,DF⊥AB。求证:四边形CEDF是正方形。
证明:∵ DE⊥AC,DF⊥AB
∴ ∠DEC=90°, ∠DFC=90° F
而∠ACB=90°
B
D
A
∴ 四边形ABCD为矩形( 有三个角是直角的四边形是矩形 )
证明:
∵四边形ABCD是平行四边形,∠A=900,
∴四边形ABCD是矩形.
A
D
又∵AB=BC,
∴四边形ABCD是正方形.
B
C
精品课件
正方形的判定方法2:
有一个组邻边相等的矩形是正方形
已知:四边形ABCD是矩形,AB=BC.
求证:四边形ABCD是正方形.
D
证明:
∵四边形ABCD是矩形,
B
C
∴∠A=∠B=∠C=∠D=90°,AD=BC,AB=CD.
2
1
∴ ∠EFH=90 °
∴ 四边形EFGH是正方形 (有一个角是直角的菱形是正方形)
精品课件
设计花坛
在一块正方形的花坛上,欲修建两条直的小路 使得两条直的小路将花坛平均分成面积相等的 四部分(不考虑道路的宽度).你有几种方法?
的四边形一定是:(A )
A.正方形
B.菱形
C.矩形
D.平行四边形
精品课件
练习5、已知四边形ABCD是平行四边形,对 角线AC、BD相交于点O。
⑴若AB=BC,则四边形ABCD是( 菱形 ) ⑵若AC=BD,则四边形ABCD是( 矩形 ) ⑶若∠BCD=900,则四边形ABCD是( 矩形 ) ⑷若OA=OB,则四边形ABCD是( 矩形 )
7-平行四边形,矩形,菱形所有判定方法

正方形常用的判定方法有:
1.一组邻边相等的矩形是正方形;
2.一个内角为直角的菱形是正方形;
3.对角线互相垂直的矩形是正方形;
4.对角线相等的菱形是正方形.
正方形不常用的判定方法:
5.对角线互相垂直平分,且相等的四边形是正方形;
6.四边都相等,且有一个内角为直角的四边形是正方形;
7.四边都相等,且对角线相等的四边形是正方形;
8.对角线相等且互相垂直的平行四边形是正方形;
9.一个内角为直角,且一组邻边相等的平行四边形是正方形;
10.对角线平分一个内角的矩形是正方形;
11.两组对边分别平行,且对角线互相垂直且相等的四边形是正方形;
12.两组对角分别相等,且对角线互相垂直且相等的四边形是正方形
矩形的判定方法
1.有一个角是直角的平行四边形是矩形
2.对角线相等的平行四边形是矩形
3.有三个角是直角的四边形是矩形
4.四个内角都相等的四边形为矩形
5.关于任何一组对边中点的连线成轴对称图形的平行四边形是矩形
6.对于平行四边形,若存在一点到两双对顶点的距离的平方和相等,则此平行四边形为矩形
7.对角线互相平分且相等的四边形是矩形
8.对角线互相平分且有一个内角是直角的四边形是矩形
矩形面积
S=ah(注:a为边长,h为该边上的高)
S=ab(注:a为长,b为宽)
菱形4个判定方法
1.四边都相等的四边形是菱形
2.对角线互相垂直的平行四边形是菱形
3.一组邻边相等的平行四边形是菱形
4.对角线互相平分且垂直的四边形是菱形。
正方形的八个判定方法

正方形的八个判定方法一、从边的角度来看1.1 四条边都相等的四边形是正方形。
这就好比一个团队,每个成员都有着相同的实力,大家齐心协力,组成了一个完美的正方形。
就像四条长度一样的木棍,首尾相连,规规矩矩地形成一个正方形。
这是正方形最基本的边的判定方法,如果一个四边形的四条边参差不齐,那肯定不是正方形啦。
1.2 有一组邻边相等并且有一个角是直角的平行四边形是正方形。
想象一下,一个平行四边形本来就规规矩矩的,就像一个规行矩步的人,然后它的一组邻边还相等,就像两只手臂一样长,而且还有一个角是直角,那就像是一个完美的直角拐弯,这样就成了正方形。
这就像一个人本来就品行端正,然后又有了独特的优秀品质,就变得更加完美,就像平行四边形变成正方形一样。
二、从角的角度出发2.1 四个角都是直角的四边形是正方形。
这就像一个房间的四个墙角,都方方正正的,都是直角。
要是一个四边形的角歪七扭八,那肯定不是正方形。
四个直角就像是正方形的灵魂,缺了一个都不行。
这就如同我们做人,要堂堂正正,不能有一点歪斜,正方形的四个直角就是这样的存在,端端正正地摆在那里。
2.2 有三个角是直角的四边形是矩形,而邻边相等的矩形是正方形。
这就好比一个人已经具备了大部分的优秀品质,已经是个不错的矩形了,但是还需要最后一点小提升,那就是邻边相等。
就像一个学生成绩已经很好了,再把某一门学科的成绩也提升到和其他学科一样好,那就更完美了,就像矩形变成正方形一样。
2.3 对角线互相垂直且相等的矩形是正方形。
矩形就像一个已经很规整的框架,但是要成为正方形还需要特殊的条件。
对角线互相垂直且相等就像是给这个框架加上了特殊的加固和装饰,让它成为了正方形。
这就像一件事情本来已经做得不错了,再加上一些独特的元素,就变得更加出色。
三、从对角线的角度考虑3.1 对角线互相垂直平分且相等的四边形是正方形。
这就像是一个神秘的规则,对角线就像四边形的两条神秘线,当它们互相垂直平分且相等的时候,这个四边形就像被施了魔法一样,变成了正方形。
正方形的性质及判定定理

1、对称性 轴对称图形,有 4条对称轴
2、性质
(C)A (1) 它具有平行四边形的一切性质
D(B)
两组对边分别平行且相等,
O
两组对角相等,
对角线互相平分 .
(2) 具有矩形的一切性质
(D)B
四个角都是直角,对角线相等 .
C(A)
(3)具有菱形的一切性质
四条边相等;对角线互相垂直,每条对角线平分一组对角 .
第十三页,编辑于星期二:六点 二十分。
例2 如图所示,正方形 ABCD 中,P为BD上一点,
PM⊥BC于M, PN⊥DC于N. 试说明: AP=MN
证明 : 连接 PC
A
∵PM⊥BC , PN ⊥DC
四边形ABCD 是正方形
D
P
N
∴∠ NCM=90 °
∴四边形 PMCN 是矩形
∴ PC=MN
B
MC
第六页,编辑于星期二:六点 二十分。
想一想:正方形是怎样的 矩形?
正方矩形形
邻边相等的矩形
高效上好每节课 ·快乐上 好 每天学
第七页,编辑于星期二:六点 二十分。
想一想:正方形是怎样的 菱形 ?
正菱方形形
一个角是直角的菱形
高效 上好每节课·快乐上好 每天学
第八页,编辑于星期二:六点 二十分。
平行四边形
B
DE ⊥AC , DF⊥BC
D
A
∴ DE=DF
∴四边形 ABCD是正方形 (有一组邻边相等的矩形是正方形 )
高效 上 好 每 节 课·快乐上好每 天 学
第十六页,编辑于星期二:六点 二十分。
课堂小结
一组邻边相等,并且有 一个角是直角 的平行四边形 叫做正方形.
判定正方形的方法

判定正方形的方法
一、基于几何性质的判定方法:
正方形是一种特殊的四边形,具有以下几何性质:
1.四边相等:正方形的四条边长度完全相等,可以通过测量四边的长度来判断。
2.四角相等:正方形的四个角度完全相等,每个角度为90度。
3.对角线相等:正方形的两条对角线完全相等,在已知四边长的情况下,可以通过勾股定理判断对角线是否相等。
综上所述,如果满足以上几何性质,就可以判定为正方形。
二、基于数学公式的判定方法:
正方形是一种特殊的矩形,具有以下数学公式:
1.周长:正方形的周长公式为4a,其中a为边长。
2.面积:正方形的面积公式为a²,其中a为边长。
在已知周长或面积的情况下,可以通过计算公式得到边长,并判断四边是否相等来判断是否为正方形。
三、基于编程算法的判定方法:
除了几何性质和数学公式的判定方法外,还可以通过编程算法来判定正方形。
1.输入四个点的坐标:首先,需要输入四个点的坐标,分别表示正方形的四个顶点。
2.计算边长:利用欧几里得距离公式计算四条边的长度,然后判断四边是否相等。
3.计算角度:利用向量的概念计算相邻两条边的夹角,然后判断四个角度是否相等且为90度。
4.判断对角线长度:利用勾股定理,计算对角线的长度,然后判断是否相等。
通过上述算法,可以判断输入的四个点是否构成正方形。
综上所述,判断正方形的方法可以从几何性质、数学公式和编程算法等方面进行判定。
根据不同需求和条件,选择适合的方法进行判断。
20.4正方形的判定

想一想:正方形是怎样的矩形?
正方形 矩形
邻边相等 的矩形
矩形 两组 对边
四边形
分别 平行
平行四 边形 菱 形
菱形
平行四边形
正方 形
矩形
一组邻边相等 平行四边形 一内角是直角
正方形
定义:一组邻边相等,且有一个角是直角的平行四边 形叫做正方形
正方形的判定方法:
(可从平行四边形、矩形、菱形为基础)
平行四边形、矩形、菱形、正方形的判定小结
5种识 别方法
一个角是直角且一组邻边相等
----下列说法对吗?
(1)四个角都相等的四边形是正方形
(2)四条边都相等的四边形是正方形
(3)对角线相等的菱形是正方形
(4)对角线互相垂直的矩形是正方形 (5)对角线垂直且相等的四边形是正方形 (6)四边相等,有一角是直角的四边形是正方形
( 正方形 )
3.在四边形ABCD中,O是对角线的交点, 能判定这个四边形是正 方形的是:( A ) A.AO=BO=CO=DO,AC⊥BD B.AD∥BC ∠A=∠C C.AO=CO BO=DO AB=BC D.AC=BD
4.已知:如图,△ABC中.∠ABC=90°,BD是角 平分线,DE⊥AB,DF⊥BC,垂足分别是E、F. 试说明:四边形DEBF是正方形.
ADCE是正方形,说明理由。
A
M
E
N
B
D
C
7、如图,在矩形ABCD中,四个角 的平分线相交于点E、F、G、H, 试说明四边形EFGH是正方形。
E
A
F B G H
D C
回顾平行四边形,矩形,菱形的性质,完成表格前三列
性质 分类 图形
平行四 边形
正方形的性质与判定(2)

(选做题)△ABC中,点O是AC边上的一个动点,过点 O作直线MN∥BC,设交∠ACB的平分线于点E,交 ∠ACB的外角平分线于点F. (1)试证明:OE=OF. (2)当点O运动到线段AC的中点时,四边形AECF是否 是矩形?并证明. (3)在(2)的条件下,当△ABC 满足什么条件时,四边形AECF是 正方形,并证明.
证明:∵四边形ABCD是菱形, ∴四边形ABCD是平行四边形,
AB=AD 又∵∠ABC=90°, ∴四边形ABCD是正方形.(正方形的定义)
几何语言:∵四边形ABCD是菱形,∠ABC=90° ∴四边形ABCD是正方形
(4)对角线相等的菱形是正方形
已知:四边形ABCD是菱形,且AC=BD 求证:四边形ABCD是正方形.
自学指导
阅读P23页做一做及议一议,完成下列问题 1.任意四边形的中点四边形是什么四边形?试探索之. 2.请完成表格: 原四边形 平行四边形 矩形 菱形 正方形
中点四边形 平行四边形 菱形 形状
矩形 正方形
自学检测
请完成下列表格:
原四边形对 角线关系
不相等、不垂直
相等
所得中点四 边形形状
平行四边形
一内角是直角
2、
菱形
(或:对角线相等)
正方 形
菱形法
一组邻边相等
3、 矩形
正方
(或:对角线垂直) 形
矩形法
二、中点四边形的形状由原四边形的对角线决定: 首先是平行四边形;对角线相等则边相等,对角 线垂直则角90°
当堂训练
正方形所有判定方法

判定一个图形是否为正方形,需要满足正方形的定义:四边相等且四个角均为直角。
以下是判定一个四边形是否为正方形的方法:
1.边长相等:正方形的四条边必须相等长。
因此,首先需要测量四条边的长度,如果它们长度相等,则具备成为正方形的一个关键条件。
2.角度判定:正方形的四个内角均为直角(90度)。
可以使用角度测量工具或者画角度的方法来检查四个角是否为直角。
3.对角线相等:正方形对角线相等且相互垂直。
可以通过测量对角线的长度来验证对角线是否相等,并且利用角度测量工具来确定对角线是否垂直。
4.对角线相交于中点:在正方形中,对角线相交于对方的中点,将正方形对角线平分。
可以通过验证对角线是否相交于各自的中点来判断是否为正方形。
5.对称性:正方形具有对称性,即以中心对称,通过验证图形各个部分是否对称可以判定是否为正方形。
综合以上方法,如果一个四边形满足了以上所有条件,即边长相等、四个角均为直角、对角线相等且相互垂直、对角线相交于中点,并且具有对称性,那么这个四边形就可以被判定为正方形。
1.3(2) 正方形的判定

3、判定定理2:有一个角是直角的菱形是正方形。
15:57
4
正方形的判定运用举例
例1.如图,Rt△ABC中, ∠ACB =90°,CD平分∠ACB交AB于点D, DE⊥BC于E,DF⊥AC于F.求证: 四边形CEDF是正方形
证明:∵ DE⊥BC,DF⊥AC,
A E F D
C
F E
B
∴∠DFC=∠DEC=∠ECF=90° 所以四边形CEDF是矩形。
A F D E C
(1)证明:∵DE⊥AC,DF⊥AB, ∴∠BFD=∠CED=90°,又∵BD=CD,BF=CE, ∴Rt△BDF≌Rt△CDE(HL), ∴∠B=∠C. 故 △ABC是等腰三角形;(3分) (2)解:四边形AFDE是正方形. 证明:∵∠A=90°,DE⊥AC,DF⊥AB, ∴四边形AFDE是矩形, 又∵Rt△BDF≌Rt△CDE, ∴DF=DE, 15:57 6 ∴四边形AFDE是正方形.(8分)
3.(2010青岛)已知:如图,在正方形ABCD中, A 点E、F分别在BC和CD上,AE = AF. (1)求证:BE = DF; (2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么 B 特殊四边形?并证明你的结论.
15:57
F
C
D F O E C
8
M
3.如图, CD是线段AB的垂直平分 线;DE⊥AC于点E,DF⊥ BC于点 F.(1)求证:CE=CF; (2)点C运动到什么位置时,四边形 CEDF成为正方形?请说明理由.
15:57
9
4.(1)证明:∵DE⊥AB,DF⊥AC, ∴∠DEB=∠DFC=90°. ∵AB=AC, B ∴∠B=∠C. 又∵DB=DC,△DEB≌△DFC(AAS), ∴DE=DF.
正方形的性质及判定

1.正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形. 2.正方形的性质正方形是特殊的平行四边形、矩形、菱形.它具有前三者的所有性质: ① 边的性质:对边平行,四条边都相等. ② 角的性质:四个角都是直角.③ 对角线性质:两条对角线互相垂直平分且相等,•每条对角线平分一组对角. ④ 对称性:正方形是中心对称图形,也是轴对称图形. 平行四边形、矩形、菱形和正方形的关系:(如图)3.正方形的判定判定①:有一组邻边相等的矩形是正方形. 判定②:有一个角是直角的菱形是正方形.一、正方形的性质【例1】 正方形有 条对称轴.【例2】 已知正方形BDEF 的边长是正方形ABCD 的对角线,则:BDEF ABCD S S =正方形正方形【例3】 如图,已知正方形ABCD 的面积为256,点F 在CD 上,点E 在CB 的延长线上,且20AE AF AF ⊥=,,则BE 的长为FE D CBA【例4】 如图,在正方形ABCD 中,E 为AB 边的中点,G ,F 分别为AD ,BC 边上的点,若1AG =,2BF =,90GEF ∠=︒,则GF 的长为 .正方形的性质及判定正方形菱形矩形平行四边形【例5】 将n 个边长都为1cm 的正方形按如图所示摆放,点12...n A A A ,,,分别是正方形的中心,则n 个正方形重叠形成的重叠部分的面积和为【例6】 如图,正方形ABCD 中,O 是对角线AC BD ,的交点,过点O 作OE OF ⊥,分别交AB CD ,于E F ,,若43AE CF ==,,则EF =OFE DC BA【例7】 如图,正方形ABCD 的边长为2cm ,以B 为圆心,BC 长为半径画弧交对角线BD 于点E ,连接CE ,P 是CE 上任意一点,PM BC ⊥于M ,PN BD ⊥于N ,则PM PN +的值为PNME DC BA【例8】 如图,E 是正方形ABCD 对角线BD 上的一点,求证:AE CE =.EDCBA【例9】 如图,P 为正方形ABCD 对角线上一点,PE BC ⊥于E ,PF CD ⊥于F .求证:AP EF =.F EPDCB A【例10】 如图所示,正方形ABCD 对角线AC 与BD 相交于O ,MN ∥AB ,且分别与AO BO 、交于M N 、.试探讨BM 与CN 之间的关系,写出你所得到的结论的证明过程.M N CDO B A【例11】 如图,已知P 是正方形ABCD 内的一点,且ABP ∆为等边三角形,那么DCP ∠=PDCBA【例12】 已知正方形ABCD ,在AD 、AC 上分别取E 、F 两点,使2ED AD FC AC =∶∶,求证:BEF ∆是等腰直角三角形.GEHDFCBA【例13】 如图,已知E 、F 分别是正方形ABCD 的边BC 、CD 上的点,AE 、AF 分别与对角线BD 相交于M 、N ,若50EAF ∠=︒,则CME CNF ∠+∠= .NMFEDCBA【例14】 如图,四边形ABCD 为正方形,以AB 为边向正方形外作正方形ABE ,CE 与BD 相交于点F ,则AFD ∠=FEDCBA【例15】 如果点E 、F 是正方形ABCD 的对角线BD 上两点,且BE DF =,你能判断四边形AECF 的形状吗?并阐明理由.E CDFBA【例16】 如图,正方形ABCD 中,在AD 的延长线上取点E ,F ,使DE AD =,DF BD =.连结BF 分别交CD ,CE 于H ,G .求证:GHD ∆是等腰三角形.3142FE GHCDBA【例17】 如图,过正方形顶点A 引AE BD ∥,且BE BD =.若BE 与AD 的延长线的交点为F ,求证DF DE =.GFEBDA【例18】 如图所示,在正方形ABCD 中,AK 、AN 是A ∠内的两条射线,BK AK ⊥,BL AN ⊥,DM AK ⊥,DN AN ⊥,求证KL MN =,KL MN ⊥.K NMLDCB A【例19】 如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,连接,BE DG ,求证:BE DG =.GC FEDBA【例20】 (2007年三帆中学期中考试)如图,在正方形ABCD 中,E 为CD 边上的一点,F 为BC 延长线上的一点,CE CF =,30FDC ∠=︒,求BEF ∠的度数.BDCAEF【例21】 已知:如图,在正方形ABCD 中,G 是CD 上一点,延长BC 到E ,使CE CG =,连接BG 并延长交DE 于F .(1)求证:BCG DCE ∆∆≌;(2)将DCE △绕点D 顺时针旋转90︒得到DAE '∆,判断四边形E BGD '是什么特殊四边形?并说明理由.【例22】 若正方形ABCD 的边长为4,E 为BC 边上一点,3BE =,M 为线段AE 上一点,射线BM 交正方形的一边于点F ,且BF AE =,则BM 的长为 .【例23】 如图1,在正方形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 上的点,HA EB FC GD ===,连接EG 、FH ,交点为O . ⑴ 如图2,连接EF FG GH HE ,,,,试判断四边形EFGH 的形状,并证明你的结论;⑵ 将正方形ABCD 沿线段EG 、HF 剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD 的边长为3cm ,1cm HA EB FC GD ====,则图3中阴影部分的面积为_________2cm .图3图1图2H DGC FEBAOH GFEDC BA【例24】 如图,正方形ABCD 对角线相交于点O ,点P 、Q 分别是BC 、CD 上的点,AQ DP ⊥,求证:(1)OP OQ =;(2)OP OQ ⊥.ABCDEF E 'GBO D CA QP【例25】 如图,在正方形ABCD 中,E 、F 分别是AB 、BC 的中点,求证:AM AD =.MFEDCBA【例26】 如图,正方形ABCD 中,E F ,是AB BC ,边上两点,且EF AE FC DG EF =+⊥,于G ,求证: DG DA =G FEC DBA【例27】 如图,点M N ,分别在正方形ABCD 的边BC CD ,上,已知MCN ∆的周长等于正方形ABCD 周长的一半,求MAN ∠的度数NMDCBA【例28】 如图,设EF ∥正方形ABCD 的对角线AC ,在DA 延长线上取一点G ,使AG AD =,EG 与DF交于H ,求证:AH =正方形的边长.HEG CDF B A【例29】 把正方形ABCD 绕着点A ,按顺时针方向旋转得到正方形AEFG ,边FG 与BC 交于点H (如图).试问线段HG 与线段HB 相等吗?请先观察猜想,然后再证明你的猜想.GCHF EDB A【例30】 如图所示,在直角梯形ABCD 中,AD BC ∥,90ADC ∠=︒,l 是AD 的垂直平分线,交AD 于点M ,以腰AB 为边作正方形ABFE ,作EP l ⊥于点P ,求证22EP AD CD +=.lPM FE DC BA【例31】 如图所示,ABCD 是正方形,E 为BF 上的一点,四边形AEFC 恰好是一个菱形,则EAB ∠=______. ABCDEF二、正方形的判定【例32】 四边形ABCD 的四个内角的平分线两两相交又形成一个四边形EFGH ,求证:⑴四边形EFGH 对角互补;⑵若四边形ABCD 为平行四边形,则四边形EFGH 为矩形. ⑶四边形ABCD 为长方形,则四边形EFGH 为正方形.HEFG DCBA【例33】 如图,已知平行四边形ABCD 中,对角线AC 、BD 交于点O ,E 是BD 延长线上的点,且ACE∆是等边三角形.⑴ 求证:四边形ABCD 是菱形;⑵ 若2AED EAD ∠=∠,求证:四边形ABCD 是正方形.OEDCBA【例34】 已知:如图,在ABC ∆中,AB AC =,AD BC ⊥,垂足为点D ,AN 是ABC ∆外角CAM ∠的平分线,CE AN ⊥,垂足为点E . ⑴ 求证:四边形ADCE 为矩形;⑵ 当ABC ∆满足什么条件时,四边形ADCE 是一个正方形?并给出证明.M ENCDBA【例35】 如图,点M 是矩形ABCD 边AD 的中点,2AB AD =,点P 是BC 边上一动点,PE MC ⊥,PF BM ⊥,垂足分别为E 、F ,求点P 运动到什么位置时,四边形PEMF 为正方形.PMF EDC BA【例36】 如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE a AF b ==,,若23EFGH S =,则b a -=H GFEDCBA【例37】 如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为27cm 和211cm ,则CDE∆ 的面积为GFEDCB A【例38】 如图,在正方形ABCD 中,点1P P ,为正方形内的两点,且11PB PD PB AB CBP PBP ==∠=∠,,,则1BPP ∠= P 1PDC BA【例39】 如图,若在平行四边形ABCD 各边上向平行四边形的外侧作正方形,求证:以四个正方形中心为顶点组成一个正方形.PRQ S NMFEDCBA【例40】已知:PA4PB=,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.(1)如图,当∠APB=45°时,求AB及PD的长;(2)当∠APB变化,且其它条件不变时,求PD 的最大值,及相应∠APB的大小.PDCBA。
判定正方形的方法

判定正方形的方法
要判断一个图形是否为正方形,可以使用以下几种方法:
1.边长比较法:
正方形的四条边边长相等,因此可以通过比较每条边的长度来判断该
图形是否为正方形。
首先,可以选择一个任意角的两条边,用勾股定理计
算这两条边的长度之差的绝对值,如果结果为0,则说明这两条边的长度
相等;然后再选择和第一对边相连的另外一条边,用同样的方法进行计算;最后再计算与前两条边相连的第三条边的长度差的绝对值。
如果这三个结
果都为0,则说明这个图形是一个正方形。
2.角度判断法:
正方形的四个内角都是直角(90度),因此可以通过测量图形的内
角来判断是否为正方形。
使用一个角度测量器,依次测量图形的四个内角。
如果所有内角都是直角(90度),则说明这个图形是一个正方形。
3.对角线法:
正方形的四条边互相平分两两相对的内角,并且对角线相等。
因此可
以通过测量图形的对角线是否相等来判断是否为正方形。
首先,通过测量
图形的两条对角线的长度,如果两条对角线的长度相等,则说明这个图形
可能是一个正方形;然后再通过测量图形的四个内角,如果每个内角都是
直角(90度),则可以确认这个图形是一个正方形。
4.尺规作图法:
正方形是尺规作图中的一种基本图形,可以通过尺规作图的方法构造一个正方形。
用尺规作出图形的四条边和四个内角,如果满足正方形的定义,则说明这个图形是一个正方形。
需要注意的是,使用以上方法判断正方形时,应尽量减小测量误差,使用精确的测量工具,并进行多次测量以增加准确性。
此外,在实际应用中,还可以结合多种判断方法进行综合判定,以提高判断的可靠性和准确性。
