1-1_约束和广义坐标解析
chap1-1

换为 变为标量方程
。
(功 ) 即
(能 )
2. 由
得
则
对
中的
作形式上的降阶
注:数学上
分别为二阶和一阶导数,而物理上分
别为加速度和速度。 又 ,则 (函数和反函数)。于是
(I) 式中的右边
因而
注:
因
则
将 (1)、(2)、(3) 代入标量方程 (I) 得到
由于 dq1、dq2、dq3 互相独立,所以
分析力学
教材:理论物理基础教程 (刘连寿主编)
——分析力学部分
讲授:吴少平 办公室:9 –email:wsp@ QQ:997682735 2014 年 2 月
参考书 1.力学
朗道 栗弗席兹
高等教育出版社
(2007年4月第5版)
2.Analytical Mechanics
3.
和
的计算:
(速度
和
的关系)
将
对
求导得到
(
只是
的函数,不是
的函数)
上两式代入 (4),得到
4.粒子的动能:
则
5.代入 (5) 式,得到
6.保守力场: 则
由上两式得
因而
令 L = T – U,则
说明:
① 拉格朗日方程是力学系统的基本运动方程。运动方程 在牛顿力学中为牛顿第二定律,在分析力学中为拉格 朗日方程。牛顿方程:矢量方程;拉格朗日方程:标 量方程。
分析力学是理论物理的第一门课程,具有以下理论
思维的一些特点:
理论物理思维方法
实验观察到的现象 例:光的折射定律
理论家问: 工程师问:
为什么? 理论物理思维方法
唯象规律
做什么? 从现象到本质
广义坐标和约束体系

广义坐标和约束体系在物理学和工程学中,广义坐标和约束体系是描述多体系统运动的重要工具。
广义坐标是一组描述系统状态的独立变量,而约束体系则是一组将系统中各个部分联系在一起的条件。
本文将介绍广义坐标的概念和应用,并探讨约束体系在多体系统动力学中的作用。
一、广义坐标的概念和应用在传统的牛顿力学中,我们常常使用笛卡尔坐标系来描述物体的位置和运动。
然而,在复杂的多体系统中,使用笛卡尔坐标系来描述每个质点的运动往往变得非常复杂。
为了简化问题,引入广义坐标的概念就显得尤为重要。
广义坐标是一组相互独立的变量,它们可以用来描述系统的状态。
与笛卡尔坐标不同的是,广义坐标可以是质点的位置坐标、质点的广义速度、质点的质心位置、刚体的欧拉角等等。
通过引入广义坐标,我们可以用更简洁的方式描述系统的状态,简化求解的过程。
广义坐标的应用十分广泛。
在理论物理中,广义坐标常常用于构建拉格朗日力学和哈密顿力学的数学框架。
在工程学中,广义坐标常常用于描述机械系统中各个零件的运动和变形。
例如,通过引入关节的旋转角度作为广义坐标,可以简化机械臂的运动学分析。
二、约束体系在多体系统动力学中的作用在多体系统中,各个质点之间通常存在一定的约束关系。
这些约束条件可以是几何约束(如刚度约束、长度约束等)或非几何约束(如速度约束、加速度约束等)。
约束体系是将约束条件用方程形式表示的系统。
约束体系在多体系统动力学中发挥着重要作用。
它可以用来限制系统的自由度,从而简化问题的求解。
通过引入拉格朗日乘子的方法,我们可以将约束条件与系统的动力学方程相结合,得到描述系统运动的广义拉格朗日方程。
在这个过程中,广义坐标发挥了重要的作用,它将系统状态映射到一个更简洁的空间中。
约束体系还可以用来分析系统的稳定性和振动特性。
通过线性化约束方程,我们可以得到系统的模态分析,从而了解系统的固有振动频率和模式形态。
这对于设计和优化振动系统非常重要。
三、结论广义坐标和约束体系在多体系统的描述和分析中起到了至关重要的作用。
广 义 坐 标

广义坐标
例如:把小球A用长度为 l 的刚性杆连பைடு நூலகம்起来,用平面 铰链悬挂在O点。小球 A所 满足的约束方程为
x2 y2 l2 0
x
O
l A A0
y
广义坐标
运动约束- 约束方程中含有质点的速度,则被称为运动约束, 或速度约束。通常的约束方程为:
f1
(r1,
r2
,
f
2
(r1,
到了18世纪后期,由于工业的迅速发展,需要研究和解决机器 的各种运动问题。而这些运动恰恰是质点组或者刚体组的约束运动。 由于时代的需要,力学的发展,产生了新的理论和新的方法。
广义坐标
1788年,拉格朗日出版了一本非常有名的著作-叫《分析力学》。 他采用了抽象的数学分析方法,用拉格朗日方程作为力学的基本方程, 发展了牛顿力学。它特别适用于研究约束系统的力学问题。
广义坐标
但是,当我们处理复杂的质点组问题时,实际上存在很大的困难。 因为研究一个自由质点的运动,一般需要求解3个二阶微分方程。n 个自由质点的运动,则需要求解3n个二阶微分方程。当质点组受到k 个约束的时候,方程的数目就变成了3n+k,这就使得问题更为复杂, 求解更加困难。
(2) 分析力学的特点和优势
广义坐标
例如:用刚性杆连接的小球 ,是双面约束。单摆是单面约束。
O
x
O
x
l
A A0 y
x2 y2 l2(双面约束)
l A
A0 y x2 y2 + z2 l2(单面约束)
广义坐标
(4) 完整约束与非完整约束
完整约束 —— 几何约束和可以积分的运动约束,被称为完整约束。
f1(r1, r2 ,
约束的概念与分类

1. 约束的概念与分类 1)约束与约束方程质点系中限制质点运动(位置、速度)的条件称为约束,表为:f x y z xy z t (,,; , , ;)=02)稳定与不稳定约束稳定约束与时间无关:f x y z (,,)=0 不稳定约束与时间相关:f x y z t (,,,)=03)几何与运动约束几何约束亦称位置约束:f x y z t (,,,)=0运动约束又称微分约束:f x y z xy z t (,,; , , ;)=04)可解与不可解约束可解约束:f x y z t (,,,)≤0 不可解约束:f x y z t (,,,)=05)完整系与不完整系完整系:几何、不可解约束系2.广义坐标 对n 个质点组成的质点系,约束为:f x y z t i k i (,,,)(,,...,)==012则独立坐标减少为s=3n-k 个,设独立变量为q q q s 12,,...,称为Lagrange 广义坐标。
独立坐标的个数s=3n-k 为系统的自由度。
不独立变量与广义坐标的关系可表为:x x q q q t y y q q q t z z q q q t i n i i s i i s ii s ===⎧⎨⎪⎩⎪=(,,...,,)(,,...,,)(,,...,,)(,,...,)12121212,此s 个广义坐标确定系统位置。
3.虚位移受约束系在运动过程中各质点的位置既要满足运动微分方程,也要满足约束方程。
同时满足两个方程的运动为真实运动,此时在dt 时间间隔内发生的位移称为实位移,记为d r。
只满足约束方程而与时间无关(δt =0)的位移称为虚位移,记为δr ,它并未实际发生,只是想象中可能发生的位移。
显然,实位移d r 是许多虚位移δr 中的一个。
4.理想约束虚功:作用在质点上的力在任意虚位移δr 上所做的功。
理想约束:约束反力在任意虚位移δr 上所做的虚功之和为零,即,R r i i ⋅=∑δ0。
01-1 分析力学基础

1.1 分析力学基础 1.1.1 直角坐标与广义坐标
燕山大学
Yanshan University
平面直角坐标:用平面上的长度值表示平面上一点位置的坐标。 平面直角坐标系oxy。 三维直角坐标:在二维直角坐标系(oxy)的基础上,再添加一个 垂直于x轴、y轴的坐标轴,称为z轴。x轴、y轴、z轴满足右手定 则,则坐标系oxyz为三维直角坐标。 广义坐标:能决定系统几何位置的彼此独立的量。
Q2 P L sin t cos 0
(3)系统运动微分方程
d L dt q j L Qj q j j 1, 2, , n
燕山大学
Yanshan University
Q1 P sin t 0 Q2 P L sin t cos 0
两个相互啮合的光滑表面所构成的约束
燕山大学
Yanshan University
两曲面相互啮合的约束条件:两曲面不能脱
开,也不能相互嵌入;则有: δrN1=δrN2
N1与N2两者互为作用力与反作用力:
N1= -N2 由于δrT1及δrT2与约束力N1及N2相垂直,因 而约束力在该方向不做功。在虚位移下,约 束力所做的虚功为:
x1 l1 x2 l2
特点:从运动的观点来研究系统的静力平衡问题。 优点:只考虑外力,不必考虑支反力,应用方便。
虚位移
燕山大学
Yanshan University
虚位移:约束允许的微小位移。 (1)虚位移是微小的、即时发生的,即不考虑它们发生的过程。
(2)独立的虚位移数等于系统的自由度数。
对于图示杠杆系统,杠杆两端的虚位移δx1和δx2。由于杠杆是单自 由度系统,因此δx1和δx2只有一个是独立的。
四川大学物理学院理论力学第五章课件 4
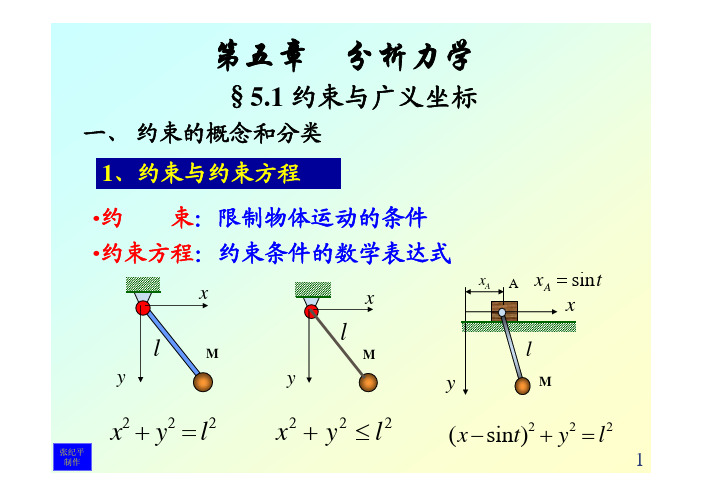
x
x
l
lM
M
y
y
y
xA A xA = sint
x
l
M
x2 + y2 = l2
张纪平 制作
x2 + y2 ≤ l2
(x − sint)2 + y2 = l2
1
2、约束的分类
x 刚性杆
x
l
l
M
M
y
y
x2 + y2 = l2
x2 + y2 ≤ l2
xA A xA = sint
x
y
M
(x −sint)2 + y2 = l2
O
解: 解析法 2个自由度
α
取α、β 为广义坐标
系统所受约束符合虚功原理的适用条件
系统的主动力有 P1, P2 和 F
根据虚功原理,
P1iδ rC + P2 iδ rD + F iδ rB = 0
建立坐标系
P1δ xC + P2δ xD + Fδ yB = 0
张纪平 制作
A
β
F
O
B
α
y
C
l1 β
P1 A l2
F
x
D P2 B
18
P1δ xC + P2δ xD + Fδ yB = 0
yB = l1 cosα + l2 cos β
xC
=
1 2
l1 sin α
O
α
y
C
l1 β
xD
=
l1 sin α
+
1 2
l2
sin
β
1-1&2约束及约束方程、自由度和广义坐标

§1-2 自由度和广义坐标
确定具有完整约束质点系的位置的独立参数的个数称为 质点系的自由度数。 质点系的自由度数。 例如,图1 例如,图1-5两刚性杆连接两小球组成的双摆,确定两小 球位置的直角坐标为 它们必须满足下面两个约束方程
可见有两个独立坐标,即质点系有两个自由度。 确定一个质点系位置的独立参数选取一般不是唯一的 ,如上述双摆,可以选中的任意两个作为独立参数,也 可以选取角作为独立参数。我们把这些能完全确定质点系位置的独 可以选取角作为独立参数。我们把这些能完全确定质点系位置的独 立参数称为质点系的广义坐标。显然,广义坐标数目等于确定质点 立参数称为质点系的广义坐标。显然,广义坐标数目等于确定质点 系位置的独立参数数目。在完整约束的情况下 系位置的独立参数数目。在完整约束的情况下,质点系的广义坐标 在完整约束的情况下, 的数目等于自由度数。 的数目等于自由度数。 如果以 表示一非自由质点系的广义坐标,则各质 点的直角坐标都可以写成这些广义坐标的函数。对于完整、双面和 定常约束,可以写成如下的函数形式
第一章 虚位移定理
§1-1 约束及约束方程
在几何静力学中,我们将限制某物体位移的周围物体 称为该物体的约束。现在从运动学角度来看约束的作用 称为该物体的约束。现在从运动学角度来看约束的作用, 现在从运动学角度来看约束的作用, 一非自由质点系的位置或速度受到某些条件的限制, 一非自由质点系的位置或速度受到某些条件的限制,这种 限制条件称为该质点系的约束。 限制条件称为该质点系的约束。 例如,圆球被限制在水平面上做纯滚动,这是约束 表现为限制圆球中心到水平面的距离保持不变;圆球与水 平面接触点的速度在每瞬时都为零。在一般情况下,约束 对质点系运动的限制可以通过质点系各质点的坐标或速度 的数学方程式来表达,这种表达式称为约束方程 的数学方程式来表达,这种表达式称为约束方程。 约束方程。
第五章 分析力学

mi ɺɺ = Fi + Ri ri
n i=1 i i i
ɺɺ or − mi ri + Fi + Ri = 0
i i i i
r ∑(−m ɺɺ ⋅δr + F ⋅δr + R ⋅δr ) = 0
或 ri = ri (q1, q2 ⋯qs ,t) i =1,2,3,⋯n s < 3n
q1, q2 ⋯qs为广义坐标,可完全描述体系的位形
例如:质点被约束在半径为R的圆周上运动 约束方程:z = 0, x2 + y2 = R2, 引进广义坐标 q =θ x = Rcosθ 则 y = Rsinθ z = 0
4 )令δqα 前的系数 = 0,得 1 Qα = Pl1 sin α = 0, 1 2 2 1 Qβ = P l2 cos β − Fl2 sin β = 0 2 2
P + 2P P 1 2 ∴tgα = , tgβ = 2 2F 2F
§5.3 Lagrange 方程
2. 广义坐标 若体系有k个几何约束,则有 个独立坐标, 若体系有 个几何约束,则有3n-k个独立坐标,引进 个 个几何约束 个独立坐标 引进s个 独立坐标q 独立坐标 1, q2…qs
xi = xi (q1, q2,⋯qs ,t) yi = yi (q1, q2,⋯qs ,t) z = z (q , q ,⋯q ,t) i 1 2 s i
如在 稳定约束 dr为 r中的 中 δ 一个 , 否则 不同 如: ,
dr P’ P
f(x,y,z,t+dt) δr f(x,y,z,t)
理论力学-分析力学

约束、自由度和广义坐标(4/9)
约束的种类 几何约束,微分约束 几何约束(完整约束):限制质点的几何位置 例:Oxy 平面的曲柄连杆的约束
约束方程的一般形式
只存在完整约束的力学系称为完整系
√
约束、自由度和广义坐标(5/9)
微分约束(不完整约束,运动约束):约束方程中含 有时间的一次微分变量(如速度),并且不可解为坐 标之间的关系 例:大环和小盘
不稳定约束情况:摆长随时间变化的单摆
实位移
虚位移
实位移不是虚位移中的一种 虚位移通过约束曲面的切面上
√
虚功原理(3/13)
例:非自由质点组的虚位移
求点 A,B,C 的虚位移
推广:n 个质点组,有 k 个约束
自由度:s = 3n - k 个参量 广义坐标:q1, q2, …, qs 独立变分:dq1, dq2, …, dqs
√
拉格朗日方程(1/8)
达朗贝尔原理
达朗贝尔原理 :体系在任何瞬间的主动力、约束力和逆 效力的和等于零
动力学方程→静力学方程
称为逆效力
逆效力 惯性力
惯性力:在非惯性系,与非惯性系的加速度有关
逆效力:在惯性系,与质点的加速度有关
达朗贝尔-拉格朗日方程
√
拉格朗日方程(2/8)
例:离心调速器由套筒(A, B和C,mA = mB = m)、两拉杆(长l)及两弹簧(系数k) 组成长;已知弹簧无拉伸时,拉杆倾斜
约束力与虚位移垂直:光滑曲面 约束力的虚功之和为零:光滑铰链,绳,杆 虚位移为零:固定点,纯滚动的接触点
非理想约束:分解为理想约束和主动力 粗糙斜面 = 光滑斜面(理想约束) + 摩擦力(主动力)
√
虚功原理(5/13)
工程力学-虚位移原理

− −
rA2 rB3
= =
0 0
rO1 = C1(常向量)
( ) rO31 = C2 常向量
约束个数8=2×4
自由度1=9-8
刚体系自由度 n 的计算公式
三维问题: n = 6Nr − r 二维问题: n = 3Nr − r
Nr :系统中的刚体对象
r –约束的总数;
例6 椭圆摆:判断自由度、选择广义坐标
广义坐标 能够唯一地确定质系位形的独立位形参
数称为系统的广义坐标。
广义坐标数为: n = 3N − r
广义坐标表示为 (q1, q2 ,..., qn )
广义速度
(q&1, q&2 ,..., q&n )
质系中任意质点的矢径 可以用广义坐标表示
ri = ri (q1, q2 ,..., qn , t )
具体函数形式则由约束条件决定。 因此,由广义坐标表示的位置矢量或直角坐标,一 定满足该质点系的约束方程。
对上述两式微分可得
∑ dri
=
k s =1
∂ri ∂qs
dqs
+
∂ri ∂t
dt
或
(i = 1,L, n)
∑ dxi
=
k s =1
∂xi ∂qs
dqs
+
∂xi ∂t
dt
(i = 1,2,L,3n)
r Q
r P
A θ
θ
θ
B
C
−
r Q
解: 解析法 yA = 7a sinθ δ yA = 7a cosθδθ xC = a cosθ δ xC = −a sinθδθ xB = −a cosθ δ xB = a sinθδθ
分析力学-4--达朗贝尔原理及其应用

i 1
i
n
) 0 Fi Ri mi ri (
两边点乘 ri :
) r 0 ( Fi Ri mi ri i
( Fi mi ) ri 0 ri
i
当系统所受约束均为理想约束时, 称
FI mr 达朗伯惯性力是在惯性系中
2、质点系达朗伯原理
对由n个质点所组成的力学体系 对第i个质点: Fi Ri Fij mi ri
( Fi Ri mi ) (i=1,2...n) ri 0 对系统进行累加:
A m1g
l F b
a k l
a l
FI
B
δ yC 2l sin b δ b
F
m2 g y
m1 g
2FI δ xA 2m1 g δ y A (m2 g F ) δ yC 0
C
F 2l (1 cos b )k
FI m1 (e l sin b ) 2
例1:一套滑轮系统悬挂两个重物。设绳和滑轮质量不计, 绳 不可伸长。试求:重力为P1的物体的加速度a1。 自由度1
解:
( P FI1 )δ y1 (P FI2 )δ y2 0 1 2
P FI1 1 a1 g P2 FI 2 a2 g
o
FI 2
x
δ y2 2δ y1 a2 2a1 2 P2 P 1 a1 g 4 P2 P 1
说明:①达朗伯原理仅对建立动力学方程提出了新的线索,
但并未对求解运动微分方程增加任何新的东西;
②对系统所得到的两个公式实际是质点系的质心运动 定理和对固定点角动量定理的另一种表示。
广义坐标

1,2,3,, k
约束
几何约束:约束仅为位置坐标和时间的函数
运动约束:约束既限制质点的位置,
对质点速 度有限制
也限制质点的速度
的约束
约束 约束
可解约束:约束条件为不等式的约束 如软绳约束
不可解约束:约束条件为等式的约束
完整约束:不可解几何约束
如纯滚动条件 x& Rq& 0 x Rq C
(3)、在给定球面中自由运动时,自由度数亦为2,
z
可用直角坐标x,y或球坐标分量q, j
z
oqR
P y
y
xj
x
等来确定其位置。
直角坐标: (x, y) z2 R2 x2 y2
x R sinq cosj存在多值解的数学问题
←
y
R
sinq
sinj
球坐标
z R cosq
我们将用 q 来表示第个广义坐标, 1,2,3,, s
各在r个直i 质角ri 点 坐(q1的 标, q位 系2 ,矢 中是,, q则ss ,个t有)广,义fi坐(r1,标1r2,2,和,,时rN,间;Nt);的 0函s数 3:N位坐1,,矢标2,的表3,广达义式, k
这个特征可在随机发射的机枪子弹通过双缝装甲板墙 的实验中表现出来。
子弹双缝实验
机关枪
a
yy
计
b
yc
数
器
1
缝1
缝2
双 缝 墙
后 障
这是实物粒子颗粒性的反映
12
2
12 1 2
非相干叠加
基于实物粒子的颗粒运动图像,人类建立了
Newton力学,并进一步发展提高为分析力学。
约束、自由度与广义坐标
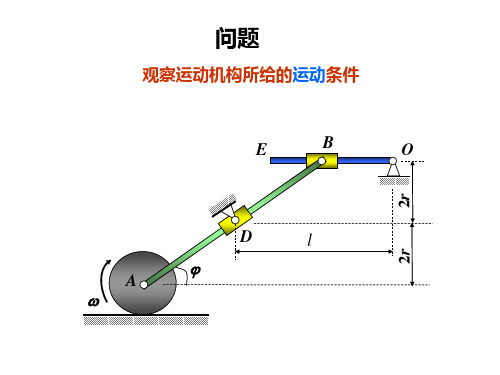
n≥4 s 3n 6 每一根刚杆相当于一个约束,所以约束数为: n≥4
3.自由刚体的广义坐标 刚体的定点运动的描述方法1—欧拉坐标 z3 z2 z1 z0
q
O
绕z0轴转过y角— —进动角 y3
y j
x0
y
j q
y0
ቤተ መጻሕፍቲ ባይዱ
y2
y1
绕x1轴转过q角— —章动角
绕z2轴转过j角— —自转角
x1 x2
x3
xA , y A ,j xB , y B ,q
A B j
xA OAcos b
y A OAsin b
C
q r
D
y
xB OAcosb AB cosj
yB OAsin b ABsin j
xC rq
yC=yD-r
式中: yD OAsin b AB sin j r (1 cosq ) c2
2.自由刚体的自由度 最简单的刚体由4个质点用6根刚杆组成几何不变体 (形如四面体),则自由刚体的自由度为:
k 3 4(质点数) (刚杆数) 6 6
设节点数为n,约束数为s。则写成
k 3n s 6
n=4 此后每增加一个质点就增加3根刚杆。 则一般地:
k 3n s
x y z l0 vt
2 2 2
2
v(匀速)
A
f r ( x1, y1, z1 xn , yn , zn ; t ) 0
(3)完整约束与非完整约束 约束方程中不包含坐标对时间的导数(即质点系中各 质点速度的投影)的约束,称为完整约束。 〈1〉位移约束----全部几何约束 〈2〉运动约束可积分----如纯滚动的圆轮;
周衍柏著理论力学——第五章分析力学 pdf讲义

3
不可解约束:质点始终不能脱离的约束。如质点始终被曲面 约束,即存在约束方程
f ( x, y , z ) = 0 或 f ( x, y , z , t ) = 0 (5.1.3)
约束又可分为几何约束和运动约束。 几何约束又叫做完整约束,它只限制质点在空间的位置,因 而表现为质点坐标的函数,如
f ( x, y , z ) = 0 或 f ( x, y , z , t ) = 0 (5.1.3)
dr P
δr
7
8
9
三、虚功原理 以下讨论只限于不可解约束的情况,设体系在 k 个几何约束 下处于平衡状态。由于体系处于平衡状态,所以体系中每一 个质点都处于平衡状态。 因此任一质点 Pi ,受到主动力的合力 Fi 与约束反力的合力 Ri 满足: (i = 1,2, L , n ) (5.2.3) Fi + Ri = 0 让每一质点在平衡位置发生一虚位移 δr ,则有 Fi ⋅ δr + Ri ⋅ δr = 0 (i = 1,2, L , n ) 上式对各质点求和得:
1
第一节 约束与广义坐标
一、约束的概念和分类 1、力学体系:质点的集合,且质点间存在相互作用,每一 个质点的运动都和其它质点的位置及运动有关,简称体系。 若有 n 个质点,则描述所有质点位置的坐标有 3n 个。 2、约束:限制质点自由运动的条件叫做的约束。 约束一般可表示成质点位置、速度和时间的方程。如:
分析力学

第六章 分析力学引言:到现在为止,我们所讨论的力学问题都是采用牛顿的方法来处理的,因此就称它为牛顿力学。
力学问题除了用牛顿力学的方法处理之外,也可以应用拉格朗日和哈密顿的方法来处理,应用拉格朗日和哈顿方法处理的力学问题通常就称它为分析力学。
分析力学这个名称实际上正是沿用了拉格朗日原著的名称。
拉格朗日《分析力学》这本著作是在1788年写成的。
全书根据一个虚位移原理,用严格的数学分析方法来处理所有的力学问。
全书自始至终没有用到过一张图,拉格朗日本人曾经以此而感到非常满意和十分骄傲。
但是,我们要注意,并不要以为“没有一张图”就能反映出它的最大优点,作为我们做作业的仿效依据,那是不行的。
实际上在现代科学技术中,图是一种必不可少的工具,不要认为科学家所用的方法就占绝对的优势,而一成不变,因为有些内容、结果,往往要受到当时历史条件、科学技术等其他因素所限制。
所以,我们今后在做分析力学部分的题目时,该画的图还是要画的,不要认为大科学家拉格朗日都不画图,那么我也以不作图而引以自豪,这种自豪是…..。
至于,到底什么叫分析力学,没有一本书上,对它有确切的定义。
根据我的理解主要是从研究的手段来区分。
由于,牛顿力学:在求解力学问题时,用的是几何方法和分析方法相结合的手段。
而分析力学:①主要是应用了广义坐标,用广义坐标作为描写机械运动的独立变量。
它的很大优点之一,是在于它从方程组中巧妙地消去了约束,减少了方程组中未知量的个数,从而简化了大量的数学运算,于是也就提高了解题的效率。
这一点在我们今后学了分析力学之后就会体会到。
有些力学题目用牛顿力学的方法去解很难,很费劲,一旦用分析力学的方法去求解,就会显得很容易。
甚至牛顿力学所无法求解的一些复杂的力学问题,然而应用分析力学的方法,常常可以通过比较简单的途径得到解决。
分析力学的优点不仅在于使许多力学问题的求解相当容易,而且在应用和理论方面也起着桥梁作用。
②用处:它们的用处所涉及的方面有:工业上的自动控制、工程技术、理论上的天体力学、量子力学、统计力学以及电动力学等等各个方面。
广义坐标通俗解释

广义坐标通俗解释
广义坐标是用来描述系统位形所需要的独立参数,或者最少参数。
当分析有的问题时(尤其是当有许多约束条件的时候),尽量选择独立的广义坐标。
因为这样可以减少代表约束的变量。
但是,当遇到非完整约束时,或者当计算约束力时,就必须使用关于这约束力的,相应的广义坐标。
广义坐标是不特定的坐标。
假若,我们用一组广义坐标来导引方程,所得到的答案,可以应用于较广泛的问题;并且,当我们最后终于设定这坐标时,答案仍旧是正确的。
拉格朗日力学,哈密顿力学都需要用到广义坐标来表示基要概念与方程。
常用的广义坐标有线量和角量两种。
例如,对约束在空间固定曲线上运动的质点,可用自始点计量的路程s作广义坐标;用细杆约束在竖直平面内摆动的质点,可用杆与铅垂线的夹角θ作广义坐标。
广义坐标对时间的导数称广义速度。
同样,因为问题需要也会有广义加速度、广义动量、广义角动量等。
1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这里: n 质 1点个数
另外有约束方程:
x2 y2 l2 0 z 0
故有: k 约2束个数
故广义坐标个数为: s 3n k 3 2 1
广义坐标可取为: 或 x 或 y 等
注意:在确定广义坐标时,首先要确定广义坐标的个数s,s的确定 不一定非得使用:
s 3n k
还可以判断该质点需要几个独立坐标即可确定其位置,则广义坐标 的个数s即等于几。如下一例题。
x2 y2 l2 0 z 0
今后仅讨论完整、不可解约束力学体系的运动问题.
三、广义坐标
体系 受到(完整)约束数目
一个自由质点
0
n个自由质点
0
n个非自由质点
k
自由度 3 3n 3n-k
独立坐标数目
3
3n 3n-k
=s
因此,我们完全可以用s个独立坐标确切的描述力学体系的位 置,这些独立量不一定是质点的笛卡儿坐标,有时选择某一种 其他坐标会更加方便,于是,人们提出了广义坐标的概念.
第一章 拉格朗日(Lagrange)方程
§1-1 约束和广义坐标
一、牛顿力学的局限性和分析力学的建立:回顾几个概念
主动力: 促使物体运动或有运动趋势的力,如:
(1)物体受力
重力、风力等
约束力: 限制物体运动或有运动趋势的力,如:
示 例 (1)
W
FRA
FRB
示 例 (2)
(2)牛顿运动方程
d 2rv v m dt 2 F合力
分析力学 优势一:
约束越多
自由度越少
独立坐标越少 (引入广义坐标) 广义坐标越少
满足的动力学方程越少
方程越好解
拉格朗日方程
问题越好解决
分析力学 优势二: 加速度、力等矢量 力学特色 牛顿主义 动能、势能等能量 分析力学
电动力学 量子力学 统计物理 相对论
牛顿力学以牛顿定律为基础,借助矢量和几何图形研究力学问题
v F主动力
v R约束力
其显式的得到一般很困难! 用约束方程表示约束情况!
约束方程
约束越多,列出的方程越多!方程越不好解!
牛顿力学 局限二: 力学现象 内在联系 非力学现象(如电磁学等)
牛顿方程 表述方法不同 麦克斯韦方程组
不易找到内在联系
综上,很自然地促使人们探究力学的其他表述形式 —— 分析力学
约束方程: f x, y, z 0或f x, y, z,t 0
常见的完整约束:质点被约束在某一曲线或曲面上运动,则约束方程就是 该曲线或曲面的方程。
x
Example:单摆
x2 y2 l2 0
z置约束
完整约束 完整系
(2)非完整(运动)约束-对体系的位置和速度都进行限制的约束
2、给出在均匀重力场中平面双摆的广义坐标。两个绳长不变。
解:两个质点m1,m2只分别需要1个独立 坐标即可确定其位置,即整个体系只需 2个广义坐标。
对于一个给定的系统, 广义坐标的数目 是一定的, 而广义坐标的选择不是唯一的.
1,2
x1,2
1, x2
x1, x2
v
v
F主动力 R约束力
难点约束力不能事先就给出确切的表达式,而是取决于约束
本身的性质、主动力和物体的运动状态。
牛顿力学 局限一:
m
d 2rv dt 2
v F合力
实际工程技术中迫 切需要解决的问题
必须知道作用在物体上的所有的力——合力
联立 求解
对于非自由质点,即约束运动,运动方程为:
m
d 2rv dt 2
z 0
x vt 2 y2 l2 0
若悬点以匀速v沿x轴运动
为不定常约束
z 0
3、双侧约束和单侧约束
(1)双侧(不可解)约束:体系始终不可脱离的约束(等式)
Example:单摆
x2 y2 l2 0
z 0
(2)单侧(可解)约束:体系可在某个方向脱离的约束(不等式)
Example:单摆中用柔绳代替刚性杆:
约束方程: f x, y, z; x&, y&, z& 0或f x, y, z; x&, y&, z&,t 0
Example:圆盘在竖直平面内沿水平直线的纯滚动
x&c R&
运动约束 速度约束
微分约束
运动约束
经积分可以消去坐标导数 几何约束(完整约束) 不能经积分消去坐标导数 非完整约束
2、定常约束和不定常约束
广义坐标:足以描述(具有s个自由度的)系统位置的任意量
q1, q2,L称, q为s 该体系的广义坐标.常记作
qi i.1, 2,L , s
广义速度 q,i 广义加速度 .qi
说明
1. 广义坐标中的”坐标”的含义已超出几何学的范畴,它的真正含义 就是”独立参量”;
2. 广义坐标可以是线坐标,也可以是角坐标或其他物理量,如面积、 体积、电极化强度、磁化强度等;
牛顿力学
分析力学
代表人物 运动方程
计算方法 描述系统运动状
态的量 研究约束运动时
牛顿 牛顿方程
矢量计算 坐标、动量
给出约束力及约束方程
拉格朗日、哈密顿 拉格朗日方程 哈密顿方程 数学分析
广义坐标、广义动量
无需给出约束力及约束 方程
基本物理量
加速度、力
能量或功
与非力学系统的 联系
不易看出
易于推广
那么, 分析力学到底是什么样子地? 从一个个新的概念入手,慢慢接近了解它!
3. 相应的,广义速度 q既i 可以是线速度,也可以是角速度,或者其
他物理量对时间的变化;
4. 为描述同一系统,广义坐标的选择并不是唯一的,一般地,有许 多组广义坐标都可以完全确定一个给定系统的状态.如何选择最合适 的一组广义坐标——多做练习积累经验。
5. n个质点形成的力学体系的3n个非独立坐标(一般是笛卡儿坐标) 可以用s个独立的广义坐标表示出来:
(1)定常(稳定)约束:约束方程中不显含时间
f x, y, z 0 f x, y, z; x&, y&, z& 0
(2)不定常(不稳定)约束:约束方程中显含时间
f x, y, z,t 0 f x, y, z; x&, y&, z&;t 0
Example:单摆
x2
y2
为l 2定常0 约束
v 特点:注重力 和F 加速度
av运动微分方程
求解质点(质点组)的运动
规律
优点:直观性强。缺点:处理质点组问题,特别是受约束问题特别复杂
分析力学用严格的数学分析方法研究力学问题
特点:注重具有广泛意义的“能量”,扩大坐标概念,引入“广义坐标” 便于研究受约束质点组的力学问题
优点::(1)巧妙的消去“理想约束”,减少了方程组中未知量的个数; (2)观点高,理论完整,涉及范围广,内容丰富 形成许多专门分支 (3)“能量”,“广义坐标” 用于场的研究 量子力学,相对论,统 计物理
二、约束及分类
对于质点组,或称为力学体系:
n个自由质点
独立坐标数目=3n
若受到约束
独立坐标数目<3n
约束:对力学体系中质点的位置和速度所施加的限制条件 约束方程:对限制条件的数学表达式
根据限制条件的性质将约束进行分类:
1、完整约束和非完整约束
与速度无关
(1)完整(几何)约束-仅限制体系在空间的几何位置的约束
xi xi q1, q2,L , qs ,t , yi yi q1, q2,L , qs ,t , i 1, 2L , n s 3n zi zi q1, q2,L , qs ,t ,
或:
rvi rvi q1, q2,L , qs ,t
例题 1、给出单摆的广义坐标。 l
解:广义坐标个数为: s 3n k
