工程力学 理论力学 约束、自由度与广义坐标
《工程力学Ⅰ》课程教学大纲

《工程力学Ⅰ》课程教学大纲课程编号:125111 学分: 4 (4学时/周) 总学时:68大纲执笔人:陈洁大纲审核人:王斌耀一、课程性质与目的工程力学(Ⅰ)(包括静力学、材料力学两部分)是土木工程专业的一门重要的技术基础课,它是各门后续课程的基础,并在许多工程技术领域中有着广泛的应用。
本课程的目的是使学生掌握静力学中一般力系的简化与平衡问题的分析介绍方法;掌握材料力学中构件在拉、压、剪切、扭转和弯曲时的强度与刚度问题的分析计算方法,构件在组合变形时的强度与刚度问题的分析计算方法,以及构件在受压时稳定性问题的分析计算方法等;掌握材料的基本力学性能和基本的材料力学实验方法;初步学会应用基本概念、基本理论和基本分析方法去分析问题和解决问题,为学习一系列后继课程打好必要的基础。
同时结合本课程的特点培养学生分析、解决工程实际问题的能力,提高学生的综合素质。
二、课程基本要求1、掌握力的概念、力的投影和力矩的计算;2、掌握力系简化的方法和一般的简化结果;3、掌握刚体静力学的平衡条件和平衡方程;4、对材料力学的基本概念和基本的分析方法有明确的认识。
5、具有将简单受力杆件简化为力学简图的初步能力,具有力学建模的初步概念与能力。
6、能熟练地做出杆件在基本变形下的内力图、计算其应力和位移、并进行强度和刚度计算。
7、对应力状态理论和强度理论有明确的认识,并能将其应用于组合变形下杆件的强度计算。
8、理解掌握简单超静定问题的求解方法。
9、对能量法的有关基本原理有明确认识,并熟练地掌握一种计算位移的能量方法。
10、对压杆的稳定性概念有明确的认识,能熟练计算轴向受压杆的临界载荷与临界应力,并进行稳定性校核等计算。
11、掌握质点系的质心、刚体的转动惯量、惯性积、惯性主轴和惯性积的平行移轴公式;掌握截面的静矩,形心的位置,惯性矩和惯性积及它们的平行移轴公式,转轴公式。
组合截面的惯性矩、惯性积计算,截面的形心主惯性轴和形心主惯性矩的计算11、对于常用材料在常温下的基本力学性能及其测试方法有初步认识。
第三章 分析力学基础 (理论力学Ⅱ)

yi qk
Fzi
zi ) qk
(k 1,2,,N) (3-7)
则式(3-6)可以写成
N
WF Qkqk 0
k 1
上式中 Qkqk 具有功的量纲
所以称Qk为与广义坐标qk 相对应的广义力
由于广义坐标的独立性 qk可以任一取值
因此若式(3-8)成立 必须有
(3-8)
Q1 Q2 QN 0
yA yB a sin1 1 ,xB a cos1 1
则对应于 1的广义力为
Q1
W1 FAy A FyB FxB
1
1
(e)
将式(e)代入上式 得
保持 1不变 只有 2 时
如图所示
Q1 (FA FB )a sin1 Fa cos1
由式(b)的变分
可得另一组虚位移
yA 0,yB b sin2 2 ,xB b cos2 2
代入对应于 2 的广义力表达式 得
Q2
W2 FAy A FByB FxB
2
2
FBb sin 2 Fbcos2
例 3-2
如图所示 重物A和B分别连接在细绳两端
重物A放置在粗糙的水平面上
重物B绕过定滑轮E铅直悬挂
在设动重滑物轮A重H量的为轴心2P上挂一重物C 重物B重量为P
不计动滑轮H的重量
(3-9)
上式说明
质点系的平衡条件是系统所有的广义力都等于零
这就是用广义坐标表示的质点系的平衡条件
求广义力的方法有两种
一种方法是直接从定义式(3-7)出发进行计算
另一种是利用广义虚位移的任意性 令某一个qk 不等于零 而其他N-1个广义虚位移都等于零 代入
从而
WF Qkqk
Qk
1-1&2约束及约束方程、自由度和广义坐标

§1-2 自由度和广义坐标
确定具有完整约束质点系的位置的独立参数的个数称为 质点系的自由度数。 质点系的自由度数。 例如,图1 例如,图1-5两刚性杆连接两小球组成的双摆,确定两小 球位置的直角坐标为 它们必须满足下面两个约束方程
可见有两个独立坐标,即质点系有两个自由度。 确定一个质点系位置的独立参数选取一般不是唯一的 ,如上述双摆,可以选中的任意两个作为独立参数,也 可以选取角作为独立参数。我们把这些能完全确定质点系位置的独 可以选取角作为独立参数。我们把这些能完全确定质点系位置的独 立参数称为质点系的广义坐标。显然,广义坐标数目等于确定质点 立参数称为质点系的广义坐标。显然,广义坐标数目等于确定质点 系位置的独立参数数目。在完整约束的情况下 系位置的独立参数数目。在完整约束的情况下,质点系的广义坐标 在完整约束的情况下, 的数目等于自由度数。 的数目等于自由度数。 如果以 表示一非自由质点系的广义坐标,则各质 点的直角坐标都可以写成这些广义坐标的函数。对于完整、双面和 定常约束,可以写成如下的函数形式
第一章 虚位移定理
§1-1 约束及约束方程
在几何静力学中,我们将限制某物体位移的周围物体 称为该物体的约束。现在从运动学角度来看约束的作用 称为该物体的约束。现在从运动学角度来看约束的作用, 现在从运动学角度来看约束的作用, 一非自由质点系的位置或速度受到某些条件的限制, 一非自由质点系的位置或速度受到某些条件的限制,这种 限制条件称为该质点系的约束。 限制条件称为该质点系的约束。 例如,圆球被限制在水平面上做纯滚动,这是约束 表现为限制圆球中心到水平面的距离保持不变;圆球与水 平面接触点的速度在每瞬时都为零。在一般情况下,约束 对质点系运动的限制可以通过质点系各质点的坐标或速度 的数学方程式来表达,这种表达式称为约束方程 的数学方程式来表达,这种表达式称为约束方程。 约束方程。
广义坐标自由度自由度

非定常几何约束 若约束方程中明显包含时间t, 这种约束就称为非定常几何约束。
v
x2 y 2 z 2 l0 vt
2
1, y 1, z n , y n , z 1,x n , t ) 0 f j ( x1, y1, z1 xn , yn , zn , x
( j 1, 2, s )
(2)定常约束与非定常约束 定常约束 当约束方程中都不包含时间t时, 这种约束称为定常约束。 定常几何约束 z
O
l
y A
约束方程的一般形式:
x
1, y 1, z n , y n , z 1, x n ) 0 f j ( x1, y1, z1 xn , yn , zn , x
它们被用于描述刚体的位形。
4.受约束刚体的自由度
设刚体数为n,则 k = 6n -S
4、约束刚体的自由度与广义坐标
约束刚体的自由度与广义坐标根据其运动 形式不同有所减小,下表给出刚体在不同的运 动形式时的广义坐标数。
刚体约束情况 刚体上一轴被固定 (定轴转动) 刚体上一点被固定 (定点运动) 刚体被限制作平面平行运 动(平面运动) 刚体被限制作平行移动 (平移) 自由度 1
三、广义坐标、自由度
1、基本概念 自由度:唯一确定质点系空间位置的独立参变量个数
自由度数定义为质点系解除约束时的坐标数减去约束方程数. 空间质点: k 3n s,
平面质点:
k 2n s ,
广义坐标: 用以确定质点系位置的独立参变量
与自由度相对应的独立坐标就是广义坐标.
自由度为k, 取广义坐标: q1 , q2 qk 一般地: n个质点,
自由度和广义坐标.

, t ) 形式复杂; F (r , r
1 t dx (t )dt c1 (t t 0 ) c 2 m t0
• •
c1 , c2
v0 x 0 (物理意义) 分别为 时的速度 和位置坐标 F F F ( x) 2)力 仅为坐标的函数 dx dx dx dx dv F ( x) m x x x v
Fx ( x, y, z; x , y , z , t ) x m F y ( x, y , z ; x , y , z , t ) y m m , y , z Fz ( x, y, z; x , t ) z
(※)
• (※)是二阶微分方程组,给出所有可能的运动,经两次
• 2、非自由质点的运动微分方程 •
质点运动所受的限制 受约束质点为非自由 质点 f ( x, y, z, t ) 0 约束的数学表达式 约束方程 ,如; 质点受到约束后自由度减少一般一个约束减少一个自由 度;约束的数学意义是几何曲线或曲面,物理意义为约 束 反作用力;约束 约束反作用力 非自由质点 自由质 点 约束反作用力为未知量,不完全由约束而定,与质点所 Fx ( x, y, z; x , y , z , t ) R x m x 受 F y ( x, y , z ; x , y , z , t ) R y m y 的其它力和运动状态有关 m , y , z Fz ( x, y, z; x , t ) R z z 两个自由度 四个方程 (1)约束
平面运动
Fx ( x, y; x , y , t) x m , y , t) my Fy ( x, y; x
2 ) F ( r , ; r , t ) m( , r r r 2r ) F ( r , ; r , t ) m ( r ,
运动学-约束自由度广义坐标-分析运动学

非定常的非完整约束
7
广义坐标与自由度
•自由度数(degree of freedom): 自由度数( : 自由度数 确定具有完整约束质点系位置所需独立坐标的个数。 独立坐标的个数 确定具有完整约束质点系位置所需独立坐标的个数。 问题: 问题: M 一个自由质点的自由度是多少? 一个自由质点的自由度是多少? 3 一个自由平面运动刚体的自由度是多少? 一个自由平面运动刚体的自由度是多少?3 一个自由空间运动刚体的自由度是多少?6 一个自由空间运动刚体的自由度是多少? 的自由度数。 例:求图示受约束质点M的自由度数。 求图示受约束质点 的自由度数 自由度: 自由度: k
ψ
(θ , ϕ ) ; (θ ,ψ ) ; (ϕ ,ψ )
对于完整、双面约束的质系,自由度为 , 对于完整、双面约束的质系,自由度为k,则: 完整 的质系 •若选k个广义坐标 q1 , q2 , L, qk ,则各质点的位置矢径: 则各质点的位置矢径: 若选
ri = ri (q1 , q2 , L, qk , t )
z
L
y
x x 2 + y 2 + z 2 = L2
= 3 −1 = 2
• 若有 个质点构成的质点系,存在 个约束方程,则自由度数为: 若有n个质点构成的质点系 存在r个约束方程 则自由度数为: 个质点构成的质点系, 个约束方程, 问题:若是存在r个约束的 个刚体呢? 个约束的n个刚体呢 k = 3 n − r 问题:若是存在 个约束的 个刚体呢?
8
•自由度数(degree of freedom): 自由度数( 自由度数 : 确定具有完整约束质点系位置所需独立坐标的个数。 独立坐标的个数 确定具有完整约束质点系位置所需独立坐标的个数。 问题:若是存在 个约束的 个刚体呢? 个约束的n个刚体呢 问题:若是存在r个约束的 个刚体呢? 问题:静定结构的自由度是多少? 问题:静定结构的自由度是多少?
理论力学-分析力学

约束、自由度和广义坐标(4/9)
约束的种类 几何约束,微分约束 几何约束(完整约束):限制质点的几何位置 例:Oxy 平面的曲柄连杆的约束
约束方程的一般形式
只存在完整约束的力学系称为完整系
√
约束、自由度和广义坐标(5/9)
微分约束(不完整约束,运动约束):约束方程中含 有时间的一次微分变量(如速度),并且不可解为坐 标之间的关系 例:大环和小盘
不稳定约束情况:摆长随时间变化的单摆
实位移
虚位移
实位移不是虚位移中的一种 虚位移通过约束曲面的切面上
√
虚功原理(3/13)
例:非自由质点组的虚位移
求点 A,B,C 的虚位移
推广:n 个质点组,有 k 个约束
自由度:s = 3n - k 个参量 广义坐标:q1, q2, …, qs 独立变分:dq1, dq2, …, dqs
√
拉格朗日方程(1/8)
达朗贝尔原理
达朗贝尔原理 :体系在任何瞬间的主动力、约束力和逆 效力的和等于零
动力学方程→静力学方程
称为逆效力
逆效力 惯性力
惯性力:在非惯性系,与非惯性系的加速度有关
逆效力:在惯性系,与质点的加速度有关
达朗贝尔-拉格朗日方程
√
拉格朗日方程(2/8)
例:离心调速器由套筒(A, B和C,mA = mB = m)、两拉杆(长l)及两弹簧(系数k) 组成长;已知弹簧无拉伸时,拉杆倾斜
约束力与虚位移垂直:光滑曲面 约束力的虚功之和为零:光滑铰链,绳,杆 虚位移为零:固定点,纯滚动的接触点
非理想约束:分解为理想约束和主动力 粗糙斜面 = 光滑斜面(理想约束) + 摩擦力(主动力)
√
虚功原理(5/13)
约束、自由度与广义坐标
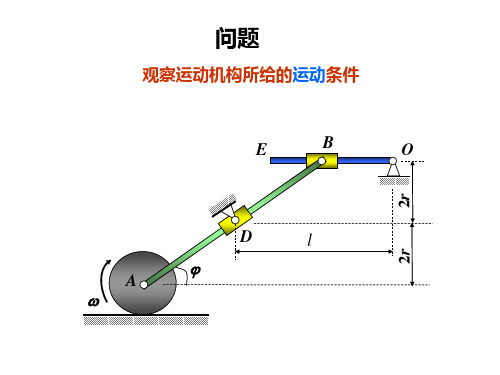
n≥4 s 3n 6 每一根刚杆相当于一个约束,所以约束数为: n≥4
3.自由刚体的广义坐标 刚体的定点运动的描述方法1—欧拉坐标 z3 z2 z1 z0
q
O
绕z0轴转过y角— —进动角 y3
y j
x0
y
j q
y0
ቤተ መጻሕፍቲ ባይዱ
y2
y1
绕x1轴转过q角— —章动角
绕z2轴转过j角— —自转角
x1 x2
x3
xA , y A ,j xB , y B ,q
A B j
xA OAcos b
y A OAsin b
C
q r
D
y
xB OAcosb AB cosj
yB OAsin b ABsin j
xC rq
yC=yD-r
式中: yD OAsin b AB sin j r (1 cosq ) c2
2.自由刚体的自由度 最简单的刚体由4个质点用6根刚杆组成几何不变体 (形如四面体),则自由刚体的自由度为:
k 3 4(质点数) (刚杆数) 6 6
设节点数为n,约束数为s。则写成
k 3n s 6
n=4 此后每增加一个质点就增加3根刚杆。 则一般地:
k 3n s
x y z l0 vt
2 2 2
2
v(匀速)
A
f r ( x1, y1, z1 xn , yn , zn ; t ) 0
(3)完整约束与非完整约束 约束方程中不包含坐标对时间的导数(即质点系中各 质点速度的投影)的约束,称为完整约束。 〈1〉位移约束----全部几何约束 〈2〉运动约束可积分----如纯滚动的圆轮;
理论力学 第2章 虚功原理
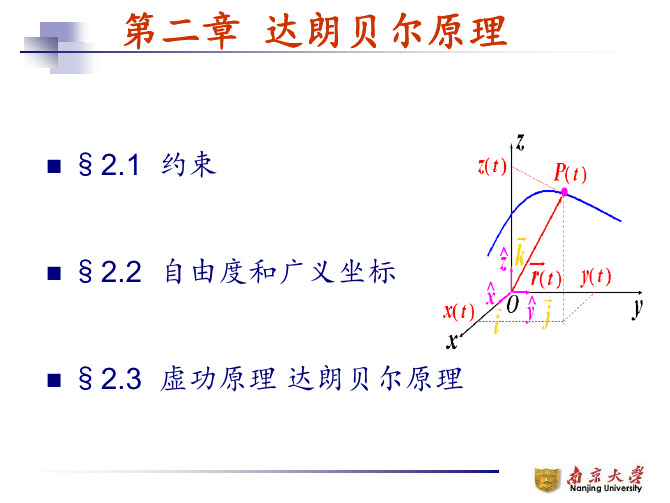
例如:车轮沿直线轨道作纯滚动,xo r 0 是微分方程,
但经过积分可得到 xo r 0 ,该约束仍为完整约束。
2.1 约束
3、定常约束与非定常约束(约束是否与时间有
关?)
x
xA A xA sint
,,
rk
;
r1
,
r2
,,
rk
;
t
)
0
R
o
纯滚动
y
x y
v
y x
xo
xo y
o
R
R
o
x
tan
y x
运动约束 几何约束
2.1 约束
•完整约束(holonomic constraint): 约束方程中不含速度项或含有速度项(可积)的约束
•非完整约束(nonholonomic constraint): 约束方程中含有速度项(不可积)的约束
4、虚位移不只有一个或一组 {rA , rB } {rA,rB}
2.3 虚功原理 达朗贝尔原理
二、虚功
• 虚功(virtual work): W
F
r
作用于质点(系)上的力在虚位移上所作的假想
功。
质点
F Fx
r
i xi
Fy
j
yj
Fzk
zk
W Fxx Fyy Fzz
质点系
• 什么是虚位移 • 什么是虚功 • 什么是虚功原理的适用条件
2.3 虚功原理 达朗贝尔原理
一、实位移和虚位移
( real displacement )
2022年质点系的自由度约束与广义坐标

4. 约束与约束方程 • 某些预先规定的限制条件 • 限制条件的数学形式
5. 几何约束与运动约束 6. 定常约束与非定常约束
f(x,y,z)=0 f(x,y,z,t)=0
7. 双面约束与单面约束
曲柄连杆机构中的滑块
双面定常约束
构成曲柄连杆机构Βιβλιοθήκη z M1(x1,y1,z1)
y
M1(x1,y1)
o M2(x2,y2,z2) y
r=3n-l 不方便。 工程的改进方法
适当选择独立变量描述质点系的位置
广义坐标:独立变量
三、广义坐标应用
1、曲柄连杆机构
y M1(x1,y1)
o
M2(x2,y2) x
x1=Rcos y1=Rsin
z1=0
x2Rco s l2R2si2n
y2=0 z2=0
2、双摆锤
oa
x
M1(x1,y1)
b
• 自由度与约束 • 广义坐标 • 应用
一、质点系的自由度与约束
1. 研究非自由质点系的平衡问题 • 用分析的方法 • 构成平衡问题的理论基础——虚位移原 理
2. 虚位移原理 • 可简洁处理非自由质点系的静力学问题 • 可与达朗伯原理结合,建立普遍形式的 动力学普遍方程
3. 与虚位移原理相关的基本概念 • 自由质点系 • 空间一点的坐标,三个自由度 • n个质点有多少自由度
M2(x2,y2)
y
x1 asi n y1acos
z1 0
x2asinbsi n
y2aco sbco s
z2 0
x o
y M1(x1,y1)
M2(x2,y2) x
M2(x2,y2)
o
x
y M1(x1,y1)
理论力学约束及其分类

理论力学约束及其分类在第一篇静力学中,我们从静力学公理出发,通过力系 的简化,得出刚体的平衡条件,用来研究刚体及刚体系统的 平衡问题。
在这一章里,我们将介绍普遍适用于研究任意质 点系的平衡问题的一个原理,它从位移和功的概念出发,得 出任意质点系的平衡条件。
该原理叫做虚位移原理。
它是研 究平衡问题的最一般的原理,不仅如此,将它与达兰贝尔原 理相结合,就可得到一个解答动力学问题的动力学普遍方程。
一、约束及约束方程 限制质点或质点系运动的各种条件称为约束。
将约束的限制条件以数学方程来表示,则称为约束方程。
例如:平 x 2+y 2=l 2x 2 +y 2=r 2A A -y )2=l 2,y =0AB (x -x )2+(y B AB 二、约束的分类 根据约束的形式和性质,可将约束划分为不同的类型,通常按如下分类:1.几何约束和运动约束限制质点系在空间几何位置的条件称为几何约束。
如前述的平 和 例子中的限制条件 都是几何约束。
几何约束方程的一般形式为f r (x 1, y 1, z 1,×××, x n , y n , z n ) = 0当约束对质点系的运动情况进行限制时,这种约束 条件称为运动约束。
运动约束方程的一般形式为f r (x 1, y 1, z 1,×××, x n , y n , z n , x &1, y &1, z &1,×××, x &n , y &n , z &n ) = 0约束条件不 时间 的约束为 常约束。
当约束条件与时间 , 时间 化时称为 常约束。
前 的例子中约束条件 不 时间 化,它们都是 常约束。
例如: M 一条 过 的系 。
时 l 0, v动 子。
运动约束:v A -r ω=02. 常约束和 常约束x 2+y 2=(l 0-vt )2约束方程中 时间t 几何约束:y A =r例如: 动时。
工程力学 理论力学 约束自由度与广义坐标讲解

自由度 1 3 3 3
广义坐标
j
q ,j,y
x0 , y0 ,q
x0 , y0 , z0
四 实例:机构如图,轮C作纯滚动,试写出约束方程和确定自由度。
1. 刚体数目 3;
xO , yO , b x
2. 定轴转动刚体 OA ;
xA, yA,j
平面运动刚体 AB及轮C ; xB , yB ,q
bO
A
3. 约束方程(在点O 建立直角坐标)
(4)单面约束与双面约束
O
双面约束:在约束方程中用严格的
等号表示的约束。
z
OA为刚性杆: x2 ? y 2 ? z 2 ? l 2
x
约束方程的一般形式:
y
l
A
fr?x1, y1, z1,? ,xn, yn,zn,x?1, y?1, z?1,? , x?n, y?n, z?n,t?? 0
单面约束:在约束方程含有不等号表示的约束 。
xA2
?
y
2 A
?
2
OA
yA
b
O
位形描述: xO , yO , b
x
xO ? 0 约束方程:
yO ? 0
三、广义坐标、自由度 1.基本概念 自由度:唯一确定质点系空间位置的独立坐标个数
自由度定义为质点系解除约束时的坐标数减去约束方程数。 空间质点: k ? 3n ? s, 平面质点: k ? 2n ? s, 广义坐标: 用以确定质点系位置的独立参变量
i=1,2,······ n
2.自由刚体的自由度 最简单的刚体由4个质点用6根刚杆组成几何不变体
(形如四面体),则自由刚体的自由度为 : k ? 3? 4(质点数) ? (6 刚杆数)? 6 设节点数为n,约束数为s。则写成
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.自由刚体的自由度 最简单的刚体由4个质点用6根刚杆组成几何不变体 (形如四面体),则自由刚体的自由度为:
k 3 4(质点数) (刚杆数) 6 6
设节点数为n,约束数为s。则写成
k 3n s 6
n=4 此后每增加一个质点就增加3根刚杆。
k 3n s 则一般地:
x
约束方程:
xO 0
yO 0
三、广义坐标、自由度 1.基本概念
自由度:唯一确定质点系空间位置的独立坐标个数
自由度定义为质点系解除约束时的坐标数减去约束方程数。 空间质点: k 3n s,
平面质点:
k 2n s ,
广义坐标: 用以确定质点系位置的独立参变量 与自由度相对应的独立坐标就是广义坐标。 自由度为k, 取广义坐标: q1 , q2 qk 一般地: n个质点,
对于由n个自由质点组成的自由质点系,则需要3n个 独立坐标,这3n个的坐标集合称为自由质点系的位形。 (3)约束方程 约束可以通过联系坐标、坐标的时间导数以及时间t之 间的关系的数学方程组加以描述,这些数学方程组称之为 约束方程。
3.
约束的分类 几何约束
单摆: O z
l
(1)几何约束与运动约束 y
局部法: 约束方程:
xO 0 yO 0
xO , yO , b xA , y A ,j xD , y D ,q
x
b
A
O
x A OA cos b
y A OA sin b
B j
xB OA cos b AB cosj
q
D
y
yB OA sin b AB sin j
OA cos b AB cosj BD sin q c1
A 如果限制运动的条件仅是 几何性质的,则称为几何约束。
x
x y z l
2 2 2
2
z
M
曲面上的质点:
f ( x, y, z) 0
约束方程的一般形式: x
y
f r ( x1 , y1 , z1 xn , yn , zn ) 0
(r=1,2, ‥ ‥,s)
q r
D B j
xC rq
C
y
yC OA sin b AB sin j r cosq c2
x
整体法: 位形描述
b
A
O
b , j ,q
B j
约束方程:
OA cos b AB cosj BD sin q c1
q
D
y
点D的位置
OA sin b AB sin j BD cosq c2
OA sin b AB sin j BD cosq c2
点D的位置
总计8个约束方程
本例为质点与刚体
y
xA , yA x A , y A ,q
具有同一点
l0
k
x
A
x
广义坐标
q
yA c
q1 x A
q2 q
B
自由度
k 2
问题
本运动机构的自由度
E
B
O 2r
D
w
A
j
2r
l
本运动机构的自由度 O
4.约束方程
n个质点组成的质点系,约束方程的一般形式为:
f r ( x1 , y1 , z1 ,, xn , y n , z n ; x1 , y1 , z1 ,, xn , y n , z n ; t ) 0
(r=1,…,s) 约束方程的个数为:s
静力学问题中涉及的约束都是定常几何约束。
设刚体数为n, 则受约束的空间刚体系的自由度数k = 6n -s
受约束的平面刚体系的自由度数:k=?
5.约束刚体的自由度与广义坐标
约束刚体的自由度与广义坐标根据其运动形式不 同有所减小,下表给出刚体在不同的运动形式时的广 义坐标数。 刚体约束情况 刚体上一轴被固定 (定轴转动) 刚体上仅一点被固定 (定点运动) 刚体仅被限制作平面平行 运动(平面运动) 自由度 1 3 3 广义坐标
r 1,2,, s
(4)单面约束与双面约束 双面约束:在约束方程中用严格的
O
y
等号表示的约束。
OA为刚性杆: x 2 y 2 z 2 l 2
l
z x A
约束方程的一般形式:
f r x1 , y1 , z1 ,, xn , yn , zn , x1 , y1 , z1 ,, xn , yn , zn , t 0
本教材研究:定常、双面、完整约束。
例: 平面刚体位形的描述方法和约束方程
1. 刚体基于两点的描述和约束方程 y A 位形描述:
O
xO , yO xA , yA
xO 0
约束方程:
yO 0
x y OA
2 A 2 A 2
x
2. 刚体基于点线的描述和约束方程 y A
O
b
位形描述: xO , yO , b
受有约束而不能任意运动的质点系则称为非自由质点系。
刚体静力学研究 约束, 是探究约束的 原因-------约束力 运动学研究约束,是 探究约束的结果------运动的限制 y A
x A c1
y A c2
F
O
x
2. 独立坐标、位形空间、约束方程的概念
(1) 坐标
确定一个自由质点在空间的位置需要三个独立参数,这 些参数或代表长度或代表角度,统称坐标。 (2)位形
局部法 总计8个约束方程
4.广义坐标
广义坐标数为 :3n-s=1, 即: 刚体数:n=3
约束方程数:s=8 选广义坐标为:
C B j
b
A
O
q r
D
q j 或
5.自由度计算
qb
或
q q
自由度
k 3*3 s 1
自由度恒等于广义坐标数
整体法: 位形描述 约束方程:
x
b
A
O
b , j ,q
运动约束
如果运动时速度也受到一定条件的限制,则这个条件称为 运动约束。
纯滚动的圆轮:
yC r
y
j
——几何约束
C
x
x jr 0 ——运动约束
x
约束方程的一般形式
f r ( x1 , y1 , z1 xn , yn , zn , x1 , y1 , z1 xn , yn , zn ) 0
约束方程的一般形式为:
f r ( x1 , y1 , z1 ,, xn , yn , zn ) 0
r 1,2,, s
约束方程总是以微分形式表示,不可能积分成有限的 形式的约束称为非完整约束。 运动约束不可积分----碰撞系统,摩擦系统等。
f r ( x1 , y1 , z1 ,, xn , yn , zn ; x1 , y1 , z1 ,, xn , yn , zn ) 0
wO
A l
j
M
D B
vDE
E
五、 总 结
(1)检查刚体(质点)数目 n。 (2)检查各刚体的运动形式。
(3)列写出约束方程。
(4)计算自由度,确定广义坐标。 (a)空间刚体系 k=6n-s,空间质点系 k=3n-s (b)平面刚体系 k=3n-s, 平面质点系 k=2n-s 实用方法:加锁
大胆的假设 小心的求证
x A OA cos b
xA , y A ,j xB , y B ,q
A B j
y A OA sin b
C
q r
D
y
xB OA cos b AB cosj
yB OA sin b AB sin j
xC rq
yC=yD-r
式中: yD OA sin b AB sin j r (1 cosq ) c2
n≥4 每一根刚杆相当于一个约束,所以约束数为:
s 3n 6
n≥4
3.自由刚体的广义坐标 刚体的定点运动的描述方法1—欧拉坐标 z3 z2 z1 z0
q
O
绕z0轴转过y角— —进动角 y3
y j
x0
y
j q
y0
y2
y1
绕x1轴转过q角— —章动角
绕z2轴转过j角— —自转角
x1 x2
x3
刚体的定点运动的描述方法2—卡尔丹坐标
x y z l0 vt
2 2 2
2
v(匀速)
A
f r ( x1 , y1 , z1 xn , yn , zn ; t ) 0
(3)完整约束与非完整约束 约束方程中不包含坐标对时间的导数(即质点系中各 质点速度的投影)的约束,称为完整约束。 〈1〉位移约束----全部几何约束 〈2〉运动约束可积分----如纯滚动的圆轮;
O
y
l
z x A
分析本机构的自由度
E
B
O 2r
D A
j
w
2r
l
分析本机构的自由度
O
wO
A
l
j
M D B
vDE
E
单面约束:在约束方程含有不等号表示的约束。 OA为柔绳: x 2 y 2 z 2 l 2 约束方程的一般形式:
f r x1 , y1 , z1 ,, xn , yn , zn , x1 , y1 , z1 ,, xn , yn , zn , t 0 或 <0
问题
