关于圆锥曲线的切线作法的几种初等思考7页word
第10讲:圆锥曲线的切线

第12讲:圆锥曲线的切线不管是哪一种圆锥曲线的切线,其本质都是圆锥曲线与直线只有一个交点,即联立圆锥曲线方程与直线方程所得到的一元二次方程有且仅有一个根,即0=∆,相信这对于大家来说都不是问题,在这里我们对圆锥曲线的切线做一些总结,以方便大家在最短的时间内解决题目。
(一)椭圆的切线:①12222=+b y a x 在点P(00,y x )处的切线方程为12020=+by y a x x ②过椭圆外一点Q (11,y x )可以做椭圆的两条切线,两切点所在的直线方程为12121=+by y a x x ③直线m kx y +=与椭圆12222=+by a x 相切时,满足2222m b k a =+例:已知P 为椭圆13422=+y x 上一动点,求点P 到直线062=--y x 的最小值与最大值。
(二)双曲线的切线:①1-2222=by a x 在点P(00,y x )处的切线方程为1-2020=b y y a x x②过椭圆外一点Q (11,y x )可以做椭圆的两条切线,两切点所在的直线方程为1-2121=byy a x x ③直线m kx y +=与椭圆12222=+by a x 相切时,满足2222-m b k a =(三)抛物线的切线:①py x 22=上某点P (00,y x )的切线斜率为p x k 0=,点P(px x 2,20),则切线方程为p x x x p x y 2)(2000+-= ,即pxp x x y 2200-=,通过观察我们知道: 与x 轴的交点为)0,2(x ,切线与x 轴的截距为切点处横坐标的一半, 与y 轴的交点为)2-,0(20px ,在y 轴上的截距为切点纵坐标的相反数。
②A (11,y x ),B (22,y x )均在抛物线py x 22=上,请推证A 、B 处两切线及其两切线的交点坐标。
A 点处切线p x p x x y 2211-=B 点处切线pxp x x y 2222-=两条切线的焦点坐标(1212,22x x x x p+) 我们发现:i 、两切线的交点横坐标为两个切点的中点M 的横坐标 ii 、根据前面弦长知识点可知,直线与抛物线的两个交点满足:122x x pb =-(b 为直线与对称轴的截距),那么我们得到:两切线的交点纵坐标(12222x x pbb p p-==-)与直线与对称轴的截距互为相反数 延伸一:过抛物线对称轴上一点(0,b)做直线与抛物线相交于A 、B 两点,过A 、B 分别做抛物线的切线,两切线相交于点Q ,通过几何画板作图我们发现:不论直线绕P(0,b)如何旋转,两切线的交点的纵坐标恒为-b证明:令过P 的直线为y kx b =+,221212(,),(,)22x x A x B x p p联立22x pyy kx b ⎧=⎨=+⎩得122x x pb =-设A 点处切线pxp x x y 2211-=, B 点处切线p x p x x y 2222-=则两条切线的焦点坐标Q (1212,22x x x x p+) ∴12222Q x x pby b p p -===- 证 毕延伸二、过点Q (,)a b (22b pa <)做抛物线的两条切线分别切抛物线于点A 、B , 直线AB 与y 轴的截距为-b斜率22121212222ABx x x x a p p k x x p p-+===- ∴切点弦方程为:ay x b p=-③对于焦点在x 轴上的抛物线,求切线一般联立方程,利用0=∆求解。
关于圆锥曲线的切线作法的再思考

关于圆锥曲线的切线作法的再思考浙江省温州中学 陈相友(邮编 325014)文[1]、文[2]、文[3]已围绕圆锥曲线的切线给出自己不同的几何作法,本文就该问题作些许再思考,期望同仁们指正。
再思考1:文[2] 由一个关于圆的切线判定的平面几何命题,引伸出关于圆锥曲线的一类切线的几何画法命题:命题:如图1,AB 是O 的直径,EB 是O 的切线,直线EA 交O 于D ,点C 是线段BE 的中点,那么DC 是O 的切线。
命题1:如图2,AB 是椭圆的长轴,过B 的直线l AB ⊥,点D 是椭圆上除长轴两端点外任意一点,直线AD 交直线l 于点E ,点C 是线段BE 的中点,那么DC 是椭圆的切线。
命题2:如图3,AB 是双曲线的实轴,过B 的直线l AB ⊥,点D 是双曲线上除实轴两端点外任意一点,直线AD 交直线l 于点E ,点C 是线段BE 的中点, 那么DC 是椭圆的切线。
命题3:如图4,AB 是抛物线的对称轴,B 为顶点,过B 的直线l AB ⊥,点D 是抛物线上除顶点外任意一点,过点D 作直线m ∥AB 交直线l 于点E ,点C 是线段BE 的中点,那么DC 是抛物线的切线。
文[2]已经对引伸推广得到的命题1、命题2、命题3给予论证,而本人以为有必要对三个命题获得的思路的自然之处加以解释。
圆里的结论由几何关系易证,而由圆里的结论推广到椭圆,可以这样理解:椭圆可由长轴圆沿垂直于长轴的方向均匀压缩而得到,压缩后中点仍为中点,切线仍为切线,故知椭圆中作法(命题1)成立。
由椭圆推广到双曲线是命题1到命题2类似自然过渡,然而抛物线中的命题3的出现则有所不同,因为椭圆、双曲线都有两个焦点和两个顶点(椭圆指长轴的两个顶点),而抛物线只有一个焦点和一个顶点,命题3的作法不同于命题1、2,为什么?必须解释。
我的观点是:抛物线作为椭圆向双曲线过渡的曲线可以看作是另一焦点F '(或另一顶点A )位于无穷远处的椭圆或双曲线,这便决定了命题3的DA ∥对称轴,因此E 点的出现如同命题1、2中连接AD 交直线l 所得一样,使三个命题的思路达致真正的统一。
圆锥曲线中的切线问题

圆锥曲线中的切线问题过曲线上一点P(x o ,y o )的切线方程(焦点在x 轴上):圆:200r b)-b)(y -(y a)-a)(x -(x =+;椭圆:12020=+b y y a x x ;双曲线:12020=-b y y a x x ;抛物线:)(00x x p y y +=.证明:以双曲线为例.442222020220220420222022022020242022202222202022222020)(4)1)(b a x (4)2(,012)b a x (x .11.11b a b a a y x b x a x b y b y a x b y y y b y b y ax b y y a x x b y a x b y y a x x ---=---=∆=-+--⎪⎪⎩⎪⎪⎨⎧+=+=⇒⎪⎪⎩⎪⎪⎨⎧=-=-得消去①式平方后除以②式,,,.0012222202202220220,即证,所以,得又=∆=--=-b a b a y a x b b y a x 过曲线外一点P(x o ,y o )作曲线的切线,切点A 、B ,过切点A 、B 的直线方程(焦点在x 轴上):圆:200r b)-b)(y -(y a)-a)(x -(x =+;椭圆:12020=+b y y a x x ;双曲线:12020=-b y y a x x ;抛物线:)(00x x p y y +=.证明:以椭圆为例.设切点),(),,(2211y x B y x A ,以A ,B 为切点的直线方程分别为.1122222121=+=+b y y a x x b y y a x x ,若两切线均是P(x o ,y o )点引出的,即两切线均过点P ,则有.112022********=+=+by y ax x by y ax x ,可知点),(),,(2211y x B y x A 均在直线12020=+b y y a x x 上,所以过切点A ,B 的直线方程为12020=+by y a x x .即证.思考1.(2021全国乙卷)已知抛物线C :x 2=2py(y>0)的焦点为F ,且点F 与圆M :x 2+(y+4)2=1上的点最小值为4.(1)求p ;(2)若点P 在M 上,PA ,PB 是C 的两条切线,A ,B 是切点,求PAB ∆面积的最大值.).520;2(最大值为=p 解:(1)焦点坐标为(0,2p ),于4142p=-+是得到p=2;(2)设P(x 0,y 0),切点为),(),,(2211y x B y x A ,设过点),(11y x A 的方程为x 1x=2(y+y 1),联立x 2=4y ,化为关于x 的一元二次方程X 2-2x 1x+4y 1=0,得0=∆,所以x 1x=2(y+y 1)是抛物线上过A 的切线方程,同理可得x 2x=2(y+y 2)是抛物线上过B 点的切线方程.于是过P(x 0,y 0)作抛物线的切线,则过切点A ,B 的方程为x 0x=2(y+y 0),联立抛物线方程消去y 得X 2-2x 0x+4y 0=0,4|4|d AB P 16441||200200202+-=-+=x y x y x x AB 的距离到,点.520S -5)35(151221S 4-114)4(214|4|1644121d ||21S PAB 00020PAB 2020202030202002002020PAB取最小值为时,当,)(,于是)(而所以∆∆∆=-≤≤----=+==++-=+--+=⋅=y y y y y x y x y x x y x y x x AB 2.已知椭圆)0(12222>>=+b a b y a x 的左右焦点分别为F 1,F 2,且|F 1F 2|=2,点M 在直线x=-2上运动,线段MF 2与椭圆相交于N ,当NF 1⊥x 轴时,直线MF 2的斜率的绝对值为42.(1)求椭圆方程;(2)设P 是椭圆上一点,直线PF 1的斜率与直线MF 2的斜率之积为31-,证明直线MP 始终与椭圆相切.(1222=+y x )解:(1).12.2,0122,,22,22,422222222221=+==--=-====y x a a a c b a a b c c a b k NF MF 所以得所以又得为通径的一半,所以(2)设P(x 0,y 0),M(-2,y 1),设过P 的直线方程为1200=+y y xx ,联立椭圆方程消去x 得,.0,12,884024)2(20202020204020022020=∆=+-+=∆=-+-+所以而,y x x y x x x y y y x y .3131,31.121000021-=-⋅+-=⋅=+y x y k k y y x x MF PF 即由是椭圆的切线方程所以.MP .12M )1,2(M ,10000001与椭圆相切即证明直线满足椭圆的切线切线,点于是点=++-+=y y xx y x y x y。
圆锥曲线的切线
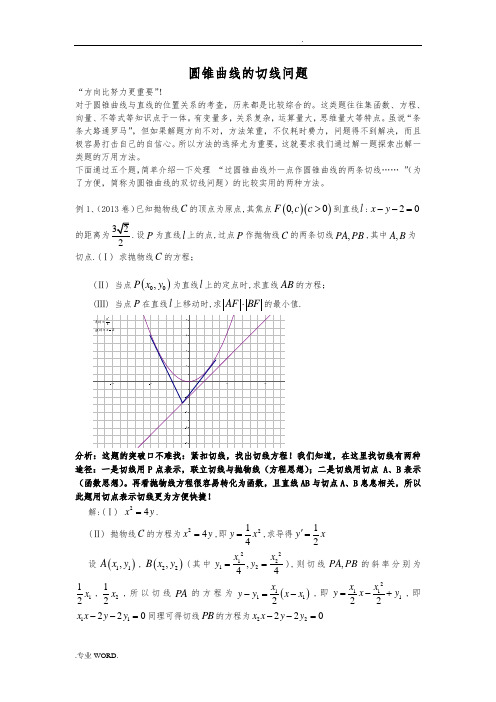
圆锥曲线的切线问题“方向比努力更重要”!对于圆锥曲线与直线的位置关系的考查,历来都是比较综合的。
这类题往往集函数、方程、向量、不等式等知识点于一体。
有变量多,关系复杂,运算量大,思维量大等特点。
虽说“条条大路通罗马”,但如果解题方向不对,方法笨重,不仅耗时费力,问题得不到解决,而且极容易打击自己的自信心。
所以方法的选择尤为重要,这就要求我们通过解一题探索出解一类题的万用方法。
下面通过五个题,简单介绍一下处理 “过圆锥曲线外一点作圆锥曲线的两条切线…… ”(为了方便,简称为圆锥曲线的双切线问题)的比较实用的两种方法。
例1、(2013卷)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线l :20x y --=的距离为2.设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点.(Ⅰ) 求抛物线C 的方程;(Ⅱ) 当点()00,P x y 为直线l 上的定点时,求直线AB 的方程; (Ⅲ) 当点P 在直线l 上移动时,求AF BF ⋅的最小值.分析:这题的突破口不难找:紧扣切线,找出切线方程!我们知道,在这里找切线有两种途径:一是切线用P 点表示,联立切线与抛物线(方程思想);二是切线用切点 A 、B 表示(函数思想)。
再看抛物线方程很容易转化为函数,且直线AB 与切点A 、B 息息相关,所以此题用切点表示切线更为方便快捷! 解:(Ⅰ) 24x y =.(Ⅱ) 抛物线C 的方程为24x y =,即214y x =,求导得12y x '= 设()11,A x y ,()22,B x y (其中221212,44x x y y ==),则切线,PA PB 的斜率分别为112x ,212x ,所以切线PA 的方程为()1112x y y x x -=-,即211122x x y x y =-+,即11220x x y y --=同理可得切线PB 的方程为22220x x y y --=因为切线,PA PB 均过点()00,P x y ,所以1001220x x y y --=,2002220x x y y --= 所以()()1122,,,x y x y 为方程00220x x y y --=的两组解. 所以直线AB 的方程为00220x x y y --=.(Ⅲ) 由抛物线定义可知11AF y =+,21BF y =+, 所以()()()121212111AF BF y y y y y y ⋅=++=+++联立方程0022204x x y y x y--=⎧⎨=⎩,消去x 整理得()22200020y y x y y +-+=由一元二次方程根与系数的关系可得212002y y x y +=-,2120y y y =所以()221212000121AF BF y y y y y x y ⋅=+++=+-+又点()00,P x y 在直线l 上,所以002x y =+,所以22220000001921225222y x y y y y ⎛⎫+-+=++=++ ⎪⎝⎭所以当012y =-时, AF BF ⋅取得最小值,且最小值为92.练习1、椭圆22221x y a b+= (0)ab 的一个焦点为F 为(1,0),已知椭圆的短轴的两个三等分点与一个焦点构成正三角形(1)求椭圆方程(2)已知Q (x0,y0)是椭圆上任一点,求以Q 点为切点的切线方程(3)设P 是直线x=4上一动点,过P 作椭圆的两切线PA 、PB ,求证:直线AB 过定点,并求出该定点坐标。
圆锥曲线的切线切点弦总结归纳(转换坐标系法)

圆锥曲线的切线、切点弦推论总结归纳1、椭圆切线推论:已知椭圆C 方程22221x y a b+=(a>b>0),C 上一点P (00,y x ),过点P 且与C 相切的切线L 方程为:12020=+byy a x x 。
12222=+by a x'2'2()()1x y +=推导:如图所示,当切线'L 斜率存在且不为0时(即切线L 斜率存在且不为0),设'OP 、'L 的斜率分别为1k ,2k ,0010000y ay b k x bx a-==-,由圆的切线性质易知'OP ⊥'L ,即121k k ⋅=-,∴02101bx k k ay -==-,∴由点斜式易得'L 方程为:''0000()y bx xy x b ay a -=--,又'',x yx y a b ==,∴ 0000()y bx x y x b b ay a a-=--,即为椭圆切线L 方程,化简如下:0000y y bx x x b ay a --=-⋅,000022()()y y y x x x b a --=-,2200002222x x y y x y a b a b +=+,又点P(00,y x )是椭圆上一点,∴2200221x y a b +=,即切线L 方程化简后为:0022x x y ya b+=1;易知当切线L 斜率为0时,P (0,b ±),切线L 方程为:y b =±,满足上式;当切线L 斜率不存在时,P (,0a ±)切线L 方程为:x a =±,也满足上式。
综上,推导完毕。
2、直线与椭圆位置关系判定推论:已知椭圆C 方程12222=+by a x (a>b>0),一直线L 方程为:0Ax By C ++=,则L 与C 相交⇔2222A a B b +>2C ;L 与C 相切⇔2222A a B b +=2C ;L 与C 相离⇔2222A a B b +<2C 。
圆锥曲线的切线方程的三种求法

圆锥曲线的切线方程问题侧重于考查圆锥曲线的性质、标准方程以及直线方程的几种形式.此类问题的难度一般不大,对同学们的抽象思维和分析能力的要求较高.下面主要探讨一下求圆锥曲线的切线方程的三种方法.一、向量法在求圆的切线方程时,可巧妙利用圆心和切点的连线垂直于切线的性质来建立关系式.在运用向量法解题时,可先给各条线段赋予方向,求得各条直线的方向向量,然后根据“互相垂直的两个向量的数量积为0”的性质建立圆心、切点、切线之间的关系式,从而求得切线的方向向量以及直线的方程.例1.已知圆O的方程是(x-a)2+(y-b)2=r2,求经过圆上一点M(x0,y0)的圆的切线l的方程.解:设切线l上任意一点N的坐标是(x,y).由(x-a)2+(y-b)2=r2得点O的坐标是(a,b),所以OM=(x0-a,y0-b), MN=(x-x0,y-y0).又因为OM∙MN=0,即[(x-a)-(x0-a)](x0-a)+[(y-b)-(y0-b)](y0-b)=0,所以过圆上的点M(x0,y0)的圆的切线l的方程是:(x0-a)(x-a)+(y0-b)(y-b)=[(x0-a)2+(y0-b)2],所以l的方程:(x0-a)(x-a)+(y0-b)(y-b)=r2.由已知圆的方程与圆上一点的坐标,可得出圆心的坐标,再设出切线上任意一点N的坐标,即可得到与切线垂直的向量,根据向量运算便可求得切线的方程.二、导数法我们知道,导数的几何意义是:该函数曲线在某一点上的切线的斜率,那么在求圆锥曲线的切线方程时,可对曲线的方程进行求导,便可得到曲线在切点处切线的斜率或切点的坐标,根据直线的点斜式方程即可求得切线的方程.例2.设A,B为曲线C:y=x24上两点,A与B的横坐标之和为4.设M为曲线C:y=x24上一点,C在M处的切线与直线AB平行,且AB⊥BM,求直线AB的方程.解:设A(x1,y1),B(x2,y2),则x1≠x2,y1=x124,y2=x224,x1+x2=4,于是直线AB的斜率为k=y1-y2x-x=x1+x24=1.由y=x24,得y,=x2.设M(x3,y3),由题意可知:x32=1,解得x3=2,则M(2,1).设直线AB的方程为y=x+m,故线段AB的中点为N(2,2-m),||MN=||m+1,将y=x+m代入y=x24得x2-4x-4m=0.当Δ=16()m+1>0,即当m>-1时,x1=2+2m+1或x2=2-2m+1,从而可得||AB=2||x1-x2=42(m+1),由||AB=2||MN得42(m+1)=2(m+1),解得m=7,所以直线AB的方程为y=x+7.在求得直线AB的斜率后,便可运用导数法对抛物线的方程求导,得出M点的坐标,再根据韦达定理和弦长公式求得切线的方程.三、几何性质法在解答圆锥曲线问题时,我们经常要用到椭圆、双曲线以及抛物线的几何性质,并结合几何图形,如三角形、梯形、平行四边形的性质来解题.采用几何性质法,关键要根据题意绘制出几何图形,明确各个点、直线、曲线的位置关系,然后运用几何性质来解题.例3.求抛物线C:y2=8x上经过点M(8,8)的切线l的方程.解:由抛物线C:y2=8x可得其焦点F为(2,0),准线方程为:x=-2,过点M(8,8)作准线的垂线,设垂足为N,则N的坐标为(-2,8),又设FN的中点为P,则P的坐标为(0,4),故直线PM的方程为:y=8-48x+4,即x-2y+8=0,所以切线l的方程是:x-2y+8=0.我们根据抛物线的几何性质作出准线,根据图形明确各点、曲线、切线的位置,根据点、直线之间的位置关系以及中点坐标公式建立关系式,求得切线的斜率与方程.相比较而言,几何性质法和导数法比较常用,运用几何性质法和向量法解题过程中的运算量较小.在求圆锥曲线的切线方程时,同学们要结合图形来解题,这样不仅能降低解题的难度,还能提升解题的效率.(作者单位:江苏省阜宁中学)周红芹解题宝典40。
圆锥曲线切线方程的五种求法

2013-12教学实践论———柯西不等式就此“诞生”!而此不等式的应用经常在数学竞赛中出现。
顿时,学生们眼中的喜悦无法言表。
我也深受感染,陶醉其中!从教学实例中我深深体会到:数学教学应充分挖掘学生的潜力,充分调动学生的主观能动性,放手让学生主动探究,教师适时引导,就会有意想不到的收获。
这正如古人云:授之以鱼不如授之以渔。
读懂读通教材及学生,教师在数学教学中才能做到游刃有余。
今后我将不断提高自己的知识素养与教学技能,全身心地投入到新课程的教学中。
(作者单位江苏省南京市栖霞中学烷基苯校区)•编辑刘俊婷切线对于研究圆锥曲线的性质具有十分重要的作用,中学阶段常用的求圆锥曲线的切线方程的方法主要有以下五种:一、向量法在求圆的切线时,可以利用圆心和切点的连线垂直于切线以及向量的内积运算来求。
例1.已知圆O的方程是(x-a)2+(y-b)2=r2,求经过圆上一点M (x0,y0)的圆的切线l的方程.解:设所求切线l上任意一点N的坐标是(x,y)由已知得:点O的坐标是(a,b),且M的坐标是(x0,y0),∴OM=(x-a,y-b,MN=x-x0,y-y0),又∵OM⊥MN∴OM·MN=0即:(x-x0)(x0-a)+(y-y0)(y0-b)=0,即:[(x-a)-(x0-a)](x0-a)+[(y-b)-(y0-b)](y0-b)=0,所以过圆上的点M(x0,y0)的圆的切线l的方程是:(x0-a)(x-a)+(y0-b)(y-b)-[(x0-a)2+(y0-b)2]=0,即:(x0-a)(x-a)+(y0-b)(y-b)=(x0-a)2+(y0-b)2,即l的方程是:(x0-a)(x-a)+(y0-b)(y-b)=r2.二、巧用变换设椭圆方程为x2a2+y2b2=1,我们做变换:x=aμy=bv{,则可把椭圆化为单位圆:μ2+v2=1,从而可将求椭圆的切线方程问题转化为求圆的切线问题:例2.求过椭圆x216+y29=1上一点M(22√,32√2)的切线l方程.解:令μ=x4,v=y3,则椭圆在新坐标系μOv下的方程是:u2+v2=1,点M(22√,32√2)在新坐标系μOv下的坐标是:(2√2,2√2),易知过圆u2+v2=1上的点(2√2,2√2)的切线方程是:2√2μ+2√2v=1,即:μ+v=2√,所以过椭圆上一点M的切线l的方程是:x4+y3=2√,即:3x+4y=122√.值得注意的是:此种方法只对于椭圆问题有效.三、判别式法也可以利用一元二次方程根的判别式来求圆锥曲线的切线方程,这种方法也是中学阶段的常用方法之一.例3.求经过点M(2,1)的双曲线:x2-2y2=2的切线l的方程.解:设l的方程是:y-1=k(x-2)且k≠±2√2,即:y=kx-(2k-1),将它代入方程x2-2y2=2中整理得:(2k2-1)x2-4k(2k-1)x+(8k2-8k+4)=0,由已知得:△=[-4k(2k-1)]2-4(2k2-1)(8k2-8k+4)=0,解得:k=1,故所求切线l的方程为:y=x-(2×1-1),即:x-y-1=0.四、导数法新教材中介绍了微积分的初步知识,我们也可把圆锥曲线的方程看作关于x的隐函数,利用导数求圆锥曲线的切线方程:例4.此处仍以上面的例3为例.解:对方程:x2-2y2=2两边都取关于x的导数,得:2x-4yy′=0,即:y′x=2,y=1=x2y x=2,y=1=1,这就是所求切线的斜率,∴过点M(2,1)的双曲线x2-2y2=2的切线l的方程为:x-y-1=0.五、几何法通过对椭圆、双曲线以及抛物线的几何性质的研究,我们知道:若焦点为F1、F2的椭圆或双曲线上有一点M,则∠F1MF2的平分线一定与圆锥曲线相切;又若焦点为F的抛物线上有一点M,过M作准线的垂线,垂足为N,则FN的中点P与M的连线PM 必与抛物线相切。
圆锥曲线的切线方程求解方法总结

圆锥曲线的切线方程求解方法总结圆锥曲线是代数几何中的重要概念,指由一个平面与一个锥体相交而产生的曲线。
圆锥曲线包括椭圆、抛物线和双曲线,它们在数学和物理学等领域中有广泛的应用。
本文将总结圆锥曲线切线方程的求解方法,并以椭圆、抛物线和双曲线为例进行说明。
一、椭圆的切线方程求解方法椭圆是一个平面上的闭合曲线,其形状类似于椭圆形。
对于椭圆上的一点P,我们要求解的是通过该点的切线方程。
方法1:使用微积分方法求解椭圆的切线方程。
设椭圆的标准方程为x^2/a^2 + y^2/b^2 = 1(其中a和b为椭圆的半长轴和半短轴),点P的坐标为(x0, y0)。
首先对椭圆方程两边求导,得到2x/a^2 + 2y/b^2 * y' = 0。
然后将点P的坐标代入,得到x0/a^2 + y0/b^2 * y' = 0。
最后将此式变形为y' = -x0 * a^2 / (y0 * b^2),即为所求的切线方程。
方法2:使用解析几何方法求解椭圆的切线方程。
设椭圆的焦点为F1和F2,点P在椭圆上的轨迹为OP。
设P点的坐标为(x0, y0),则PF1和PF2的距离之和等于2a,即PF1 + PF2 = 2a。
又根据焦点和点到直线的距离公式,可得切线所在直线与轴的交点Q的坐标为(a^2/x0, b^2/y0),进而得到切线方程的解析式。
二、抛物线的切线方程求解方法抛物线是一个平面上的开口曲线,其形状类似于抛物形。
对于抛物线上的一点P,我们要求解的是通过该点的切线方程。
方法1:使用微积分方法求解抛物线的切线方程。
设抛物线的标准方程为y^2 = 2px(其中p为抛物线的焦点到顶点的距离),点P的坐标为(x0, y0)。
首先对抛物线方程两边求导,得到2yy' = 2p。
然后将点P的坐标代入,得到y0 * y' = p。
最后将此式变形为y' = p / y0,即为所求的切线方程。
方法2:使用解析几何方法求解抛物线的切线方程。
如何计算圆锥曲线的切线

如何計算圓錐曲線的切線
羅驥韡
計算圓錐曲線的切線方程式, 一直是個難題, 尤其是對一般高中生的程度來說, 更何況針 對不同的圓錐曲線 (橢圓、 拋物線、 雙曲線等) 而言, 又有不同的切線公式, 感覺上既不統一又 難以記憶, 所以我在這裡要介紹一種算法, 一種統一的算法, 讓你不管面對何種圓錐曲線, 都可 以直接應用的公式。
探索切線的公式或準則
假設直線通過 A(x1 , y1 )、 B (x2 , y2 ) 兩點, 圓 錐曲線為 ax2 + bxy + cy 2 + dx + ey + f = 0, 那 麼我們利用上述同樣的方法來計算看看, 直線參數 式與圓錐曲線之間, 有沒有任何交點。 首先, 直線參數式為: x = x1 + (x2 − x1 )t y = y1 + (y2 − y1 )t
2 +[ax2 1 + bx1 y1 + cy1 + dx1 + ey1 + f ] = 0
當然, 如果我們要計算這個二次式到底有沒有解, 還要計算它的判別式, 這時你或許會想: 天啊! 它的係數已經如此複雜了, 我們竟然還想去計算它的判別式? 就算我們真的花了九牛二虎之力 把它算出來了, 難道我們還會想去記憶它或應用它嗎? 的確, 我們是遇上了瓶頸, 我們遇到變數 符號太多太長、 複雜難以處理的窘境。 然而, 正是因為面對這樣的窘境, 才讓數學家了解到: 必 須開發新的符號與新的運算規則, 讓我們可以繞過複雜計算的深淵, 繼續邁向推理解題的大道。 以下我們就來介紹這個新的利器。
開發新的運算符號
首先, 我們先來介紹一種 「表格式乘積加總法」: 在左邊的表格中, 2 所在的那一橫列與 3 所在的那一直行, 對到了 數字 5, 這時我們規定: 2 、 3 、 5 要乘起來, 也就是會得到 2 × 3 × 5 = 30
圆锥曲线的切线性质及统一作法

圆锥曲线的切线性质及统一作法在“圆锥曲线的统一定义”一节的教学中,笔者尝试以“统一定义”为理论基础在几何画板上构建三种圆锥曲线的统一作法,以便通过控制离心率的变化来演示三种圆锥曲线的连续变化和相互联系。
然而遇到了不小的困难,在探索新作法过程中,发现了圆锥曲线一个统一的、奇妙的性质。
先看圆锥曲线的统一定义:平面内到一个定点和到一条定直线(定点在直线外)的距离之比等于常数的点的轨迹叫做圆锥曲线。
几何画板生成轨迹的一个重要原则是:寻找一个主动点来提供运动方式,从这个主动点出发,依照确定的步骤作出一个或多个从动点(即构成轨迹的动点),从而生成轨迹。
以“统一定义”为基础的作法中最大的困难在于:从动点需要满足的条件多而分散,不易选取适当的主动点来构建从动点,而且以圆为中介的线段变换使生成的轨迹带有明显的缺陷,即曲线有尖角、断裂等不光滑现象。
于是笔者分别以各自独立的方式生成三种圆锥曲线并置研究,探索出一个共同的性质,从而发现了圆锥曲线的一个新的统一生成方式。
圆锥曲线的统一性质圆锥曲线如图1,记焦点F,顶点A,准线l,过点A作对称轴FA的垂线m,设点P为曲线上任意一点,PFA∠的平分线交l于点Q,交m于点C,延长AC到点E,使AC=CE,则P、E、Q三点共线。
如果圆锥曲线是椭圆(或双曲线),记长轴(或实轴)另一侧顶点为A’,则有A’、P、E、Q四点共线;且直线PC为圆锥曲线的切线由此性质,衍生出圆锥曲线的一个统一作法(如图2),步骤如下1)在平面上取一个点F和一条直线l(点在线外),过点F作直线l的垂线段FD,垂足为D;2)在FD上任取一点记为A,过A作直线m垂直于FD;3)以点F为圆心作任意大小的圆,在圆周上任取一点B,作出直线BF;4)作BFA∠的平分线交l于点Q,交m于点C,延长AC到点E,使AC=CE;图1 图25)作直线QE 交直线BF 于点P ;6)以B 为主动点、P 为从动点生成点P 的轨迹,此轨迹即为圆锥曲线,其中F 为焦点,A 为顶点,l 为准线,AD AF 为离心率。
(完整word版)圆锥曲线知识要点及结论个人总结

《圆锥曲线》知识要点及重要结论一、椭圆1 定义 平面内到两定点21,F F 的距离的和等于常数)2(221F F a a >的点P 的轨迹叫做椭圆。
若212F F a =,点P 的轨迹是线段21F F 。
若2120F F a <<,点P 不存在.2 标准方程 )0(12222>>=+b a b y a x ,两焦点为)0,(),0,(21c F c F -.)0(12222>>=+b a b x a y ,两焦点为),0(),,0(21c F c F -.其中222c b a +=. 3 几何性质椭圆是轴对称图形,有两条对称轴. 椭圆是中心对称图形,对称中心是椭圆的中心. 椭圆的顶点有四个,长轴长为a 2,短轴长为b 2,椭圆的焦点在长轴上。
若椭圆的标准方程为)0(12222>>=+b a b y a x ,则b y b a x a ≤≤-≤≤-,;若椭圆的标准方程为)0(12222>>=+b a b x a y ,则a y a b x b ≤≤-≤≤-,。
二、双曲线1 定义 平面内到两定点21,F F 的距离之差的绝对值等于常数)20(221F F a a <<的点的轨迹叫做双曲线. 若212F F a =,点P 的轨迹是两条射线.若212F F a >,点P 不存在.2 标准方程 )0,0(12222>>=-b a b y a x ,两焦点为)0,(),0,(21c F c F -。
)0,0(12222>>=-b a b y a x ,两焦点为),0(),,0(21c F c F -.其中222b a c +=. 3 几何性质双曲线是轴对称图形,有两条对称轴;双曲线是中心对称图形,对称中心是双曲线的中心。
双曲线的顶点有两个21,A A ,实轴长为a 2,虚轴长为b 2,双曲线的焦点在实轴上.若双曲线的标准方程为)0,0(12222>>=-b a by a x ,则R y a x a x ∈≥-≤,或;若双曲线的标准方程为)0,0(12222>>=-b a bx a y ,则R x a y a y ∈≥-≤,或。
如何计算圆锥曲线的切线

◎ 趙文敏/台灣師範大學數學系正十七邊形的尺規作圖法,是大數學家高斯(Karl Gauss )在他十九歲時所獲得的一項研究成果,它是高斯一生中許許多多數學成果中的第一項。
高斯對他的這一項成果顯然非常喜歡,才會讓正十七邊形的標誌出現在他的墓碑上,永遠陪伴一代大師。
許多人在求學期間都聽說過這些歷史典故,只是可能沒有機會見識到高斯如何以直尺和圓規作出正十七邊形的方法。
在本文中,我們將介紹這個尺規作圖法,更重要的是:當然要證明這個作圖法的正確性。
割圓方程式在歐氏幾何中,哪些邊數的正多邊形可以用尺規作圖,這自然是一個備受關注的問 題。
早在紀元前三世紀時,歐幾里得(Euclid )在他的名著《幾何原本》(Elements ) 中,就已經記載有邊數為3、4、5的正多邊形的尺規作圖法。
至於由3、4、5所衍生的邊數為n 2、32⨯n 、52⨯n 與152⨯n 的正多邊形,其尺規作圖法也早為數學家所熟知。
至於其他邊數的正多邊形,還有哪些確定可以用尺規作圖、或有哪些確定不能用尺規作圖,這兩個問題在歐幾里得之後的兩千年間,數學家們一直無法給出完整的答案。
事實上,正多邊形的尺規作圖這個幾何問題,只利用歐氏幾何學中的理論與方法,是無法解決的。
它必須仰賴數論與代數的理論與方法。
西元1796年,年僅十九歲而就讀於德國哥廷根(Göttingen )大學的高斯,開始喜歡上多項方程式的求解問題,尤其對形如01=-n x 的多項方程式更感興趣。
根據棣美 弗(De Moivre )定理,方程式01=-n x 的n 個根就是nk i n k ππ2sin 2cos+,(N ∈k ,n k ≤≤1)。
在複數平面上,上述n 個複數所代表的點是單位圓的一個內接正n 邊形的n 個頂點,其 中一個頂點是實軸上的單位點1。
因為這個緣故,方程式01=-n x 稱為割圓方程式 (cyclotomic equation )。
除了單位點1外,棣美弗定理只告訴我們其他根的表示法, 卻沒有給出這些根的實際數值。
_圆锥曲线切线的尺规作图简明方法

2 2 其中: a - x1 =
则
y3 + y4 b2 = . 2 m
竖 向 垂 线 EF 中 点 坐 标 为 N'
(
a b , 重合, 命题成立. n m 本命题也可采用初等几何方法证明, 首先证明圆的情
2
2
)
( an ,bm ),与 坐 标 N
这个基本图形包含三对相似三角形 形从图形中分解出来, △AEC∽△OEA∽△OAC, 由于求线段 CE 的长, 根据题目的 条件应选取 △AEC ∽△OEA, 由垂径定理可知 AE = 4 , 选取 比例等 式 CE AE = , 所以得到方程 由 勾 股 定 理 得 OE = 3 , AE OE
个 基 本 图 形, 将 其 分 离 出 来, 显 然 △EMD ∽ △GC' D, 在 EM 是要求的, △EMD 中, 那么△EMD 中哪一条边可以求出 来呢? 由于第二次折叠可以知 MD = 4 , 所以选取比例等式 EM C'G EM C'G = , = , 而 C'D = 6 , 代入得 接下来就是要求出 MD C'D 4 6 BG = GD, C'G 的长度, 由( 1 ) 知 AG = GC' , 设 AG = GC' = x, 2 2 2 BG = GD = 8 - x, 得 6 + x = ( 8 - x) , 可知 AG = GC' = x = 7 7 7 EM 4 , = , 代入比例等式得到方程 解得 EM = . 4 4 6 6 各地的中考试题经常出现这一类包含利用 近几年来, 相似三角形求线段长的题目, 所以教师在相似三角形教学 中应善于把握学生学习中的难点, 有目的地进行这类题型 的训练, 引导学生挖掘出隐含的相似三角形, 利用所学的知 识和方程的思想寻求可行的思路, 让学生准确地把握解题 的关键, 轻松地应对这一类题型, 从而增强学生分析问题、 解决问题的信心. 【参考文献】 [ 1] J] .数 黄炳荣. 利用隐含的相似三角形求线段的长[ 2001 ( 5 ) : 44 - 45. 学教学通讯, [ 2] J] . 高中数理 刘平. 相似三角形中方程思想的应用[
(完整word版)圆锥曲线专题

圆锥曲线的综合问题直线和圆锥曲线问题解法的一般规律“联立方程求交点,根与系数的关系求弦长,根的分布找范围,曲线定义不能忘”.【一】.直线与圆锥曲线的位置关系(1)从几何角度看,可分为三类:无公共点,仅有一个公共点及有两个相异的公共点.(2)从代数角度看,可通过将表示直线的方程代入二次曲线的方程消元后所得一元二次方程解的情况来判断. 1。
设直线l 的方程为Ax +By +C =0,圆锥曲线方程f (x ,y )=0.由Ax+0(,)0{By c f x y +==,消元。
如消去y 后得ax 2+bx +c =0. ①若a =0,当圆锥曲线是双曲线时,直线l 与双曲线的渐近线平行或重合;当圆锥曲线是抛物线时,直线l 与抛物线的对称轴平行或重合. ②若a ≠0,设Δ=b 2-4ac 。
a .Δ > 0时,直线和圆锥曲线相交于不同两点;b .Δ = 0时,直线和圆锥曲线相切于一点;c .Δ < 0时,直线和圆锥曲线没有公共点.2。
“点差法”的常见题型求中点弦方程、求(过定点、平行弦)弦中点轨迹、垂直平分线问题.必须提醒的是“点差法”具有不等价性,即要考虑判别式Δ〉0是否成立.3.直线与圆锥曲线相交时的弦长问题(1)斜率为k 的直线与圆锥曲线交于两点P 1(x 1,y 1),P 2(x 2,y 2),则所得弦长|P 1P 2| = 或|P 1P 2|= .(2)当斜率k 不存在时,可求出交点坐标,直接运算(利用轴上两点间距离公式).1+k 2|x 1-x 2|1+1k 2|y 1-y 2|4.圆锥曲线的中点弦问题遇到中点弦问题常用“根与系数的关系”或“点差法”求解.在椭圆错误!+错误!=1中,以P(x0,y0)为中点的弦所在直线的斜率k=-错误!;在双曲线错误!-错误!=1中,以P(x0,y0)为中点的弦所在直线的斜率k =错误!;在抛物线y2=2px (p〉0)中,以P(x0,y0)为中点的弦所在直线的斜率k=错误!.题型一圆锥曲线中的范围、最值问题【例1】已知抛物线C:y2=4x,过点A(-1,0)的直线交抛物线C于P、Q两点,设错误!=λ错误!.(1)若点P关于x轴的对称点为M,求证:直线MQ经过抛物线C的焦点F;(2)若λ∈错误!,求|PQ|的最大值.[思维启迪](1)可利用向量共线证明直线MQ过F;(2)建立|PQ|和λ的关系,然后求最值.解析:(1)证明设P(x1,y1),Q(x2,y2),M(x1,-y1).∵错误!=λ错误!,∴x1+1=λ(x2+1),y1=λy2,∴y错误!=λ2y错误!,y错误!=4x1,y错误!=4x2,x1=λ2x2,∴λ2x2+1=λ(x2+1),λx2(λ-1)=λ-1,∵λ≠1,∴x2=错误!,x1=λ,又F(1,0),∴错误!=(1-x1,y1)=(1-λ,λy2)=λ错误!=λ错误!,∴直线MQ经过抛物线C的焦点F。
圆锥曲线的切线方程讲义——以一道高考题为例(原创)

因为 P 是 PA, PB 的交点,故 ( x0 , y0 ) 满足:
x0x1 = 2 y1 + 2 y0 ………………① x0x2 = 2y2 + 2y0 ………………②
可知 ( x1, y1 ) , ( x2 , y2 ) 是方程: x0x = 2y + 2y0 的两组解
两边同时除以 a2b2 :
yy0 b2
+
xx0 a2
=
y02 b2
+
x02 a2
因为点 ( x0 , y0 ) 在椭圆上,故
y02 b2
+
x02 a2
=1
所以: xx0 + yy0 = 1. a2 b2
三、应用
(2021 年全国高考乙卷数学(理))已知抛物线 C : x2 = 2 py ( p 0) 的焦点为 F ,且 F 与圆
简单规律: x2 → xx0 , 2 px → px + px → px + px0 (特别注意: ( x0 , y0 ) 为切点)。
二、证明(以椭圆为例)
证明:椭圆
x2 a2
+
y2 b2
= 1( a
b
0) 在 ( x0 ,
y0 ) 的切线方程为
xx0 a2
+
yy0 b2
=1.
证明: 方法、求导法(需要二元求导)
显然 y0 [−5, −3]
P 点在圆上得出
−( y0 + 6)2 + 21 −(−5 + 6)2 + 21 = 20
即: S
圆锥曲线切线切点处理方法

圆锥曲线切线切点处理方法
圆锥曲线切线切点处理方法有两种:
1. 导数法:将圆锥曲线方程化为函数,利用导数法求出函数在点处的切线方程,特别是焦点在轴上常用此法求切线。
2. 根据题中条件设出切线方程,将切线方程代入圆锥切线方程,化为关于(或y)的一元二次方程,利用切线与圆锥曲线相切的充要条件为判别式,即可解出切线方程。
以上是圆锥曲线切线切点处理的两种方法,如需更多信息,可以查阅高等数学专业书籍,或者咨询专业数学学者。
专题14 圆锥曲线切线方程 微点2 圆锥曲线切线方程的常用结论及其应用

(2)过抛物线 上一点 处的切线方程为 ;过抛物线 的外部一点 引两条切线,过两切点的弦所在直线方程为: ;
(3)过抛物线 上一点 处的切线方程为 ;过抛物线 的外部一点 引两条切线,过两切点的弦所在直线方程为: .
同理可得焦点在 轴上的情形.
【结论4】(1)过圆 上一点 切线方程为 ;
(2)当 在椭圆 的外部时,过M引切线有两条,过两切点的弦所在直线方程为 .
【结论5】(1)过双曲线 上一点 处的切线方程为 ;
(2)当 在双曲线 的外部时,过M引切线有两条,过两切点的弦所在直线方程为: .
证明:(1) 的两边对x求导,得 ,得 ,由点斜式得切线方程为 ,即 ,又 所求的切线方程为 .
(1)求椭圆的方程;
(2)直线 与椭圆有唯一的公共点 ,与 轴的正半轴交于点 ,过 与 垂直的直线交 轴于点 .若 ,求直线 的方程.
例6.
6.已知椭圆 与直线 相切于点 ,且点 在第一象限,若直线 与 轴、 轴分别交于点 、 .若过原点O的直线 与 垂直交与点 ,证明: 定值.
【强化训练】
7.若椭圆 的焦点在x轴上,过点 作圆 的切线,切点分别为A、B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是()
下面的结论是从斜率的角度得到已知曲线的切线方程.
【结论8】(1)斜率为k的双曲线 的切线方程为 ;
(2)斜率为k的双曲线 的切线方程为 .
证明:(1)设切线方程为 ,联立 方程得:
,
若 即 , ,
令 化简可得: , ,故切线方程为 .
同理可证情形(2).
【评注】 , ,过双曲线的对称中心不可能作出直线与双曲线相切.
圆锥曲线的切线及切点弦方程.共17页文档

46、法律有权打破平静。——马·格林 47、在一千磅法律里,没有ห้องสมุดไป่ตู้盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人,越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智,自知者明。胜人者有力,自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从高中数学角度出发的圆锥曲线确切线作法的几种思考江苏省淮北中学 连少雷许多资料文献,都介召了圆锥曲线的切线的尺规作法。
那么,作圆锥曲线的切线是否存在规律,有没有统一的初等方法或是尺规作法呢? 先看比较特殊的情况说起,过圆锥曲线上一点的切线方程的一种初等求法:先看一个具体问题:求过椭圆13422=+y x 上一点)23,1(P 的切线方程. 在中学阶段解决此类问题,一般采用∆方法,即设切线方程为)1(23-=-x k y ,代入13422=+y x ,整理得关于x 的一元二次方程:子选手 03124)128()43(2222=--++-++k k x k k x k ,通过判别式∆=0)3124)(43(4)128(2222=--+-+-k k k k k ,解得21-=k ,故所求切线方程为042=-+y x . 这种方法思路直,用到知识少,学生容易掌握,不足之处是运算量偏大,出错率高.那么能否给出一种求解思路简单,而运算量又较小的方法呢?命题:),(00y x P 为圆锥曲线0),(:=y x f C 上一点,则曲线C 上过P 点的切线方程为0)2,2(),(00=---y y x x f y x f (*)证明:因0),(=y x f 为二次曲线方程,知方程(*)代表的是一条直线,记为l .假设直线l 与曲线C 除了点),(00y x P 外还有一个公共点),(111y x P ,则有0),(11=y x f 和0)2,2(),(101011=---y y x x f y x f 同时成立,从而0)2,2(1010=--y y x x f ,这表明),(111y x P 关于点),(00y x P 的对称点)2,2(10102y y x x P --也在曲线C 上,因1,P P 点在直线l 上,故2P 点也在直线l 上,可见直线l 与曲线C 有三个公共点,这与直线与二次曲线最多只有两个公共点矛盾,从而证明了直线l 与曲线C 有且只有一个公共点.(1)当0),(=y x f 表示椭圆时,由于椭圆是封闭曲线,直线l 就是切线,方程(*)即为切线方程.(2)当0),(=y x f 表示双曲线时,只要断定直线l 与双曲线的渐近线不平行,就能证明直线l 就是切线,方程(*)为其切线方程.设双曲线C 方程:)0,0(12222>>=-b a b y a x ,则方程(*):02022020202=-+-x b y a y y a x x b .当00≠y 时,其斜率0202y a x b k =,因渐近线斜率为a b±,若a b y a x b =0202 或aby a x b -=0202,则,000=-ay bx 或,000=+ay bx 从而0202202=-y a x b ,与),(00y x P 在双曲线C 上,满足22202202b a y a x b =-矛盾,故直线l 与双曲线的渐近线不平行;又当00=y 时,双曲线C 的切线方程为0x x =,也满足方程(*),从而知方程(*)为双曲线C 的切线方程.(3)当0),(=y x f 表示抛物线时,只要断定直线l 与抛物线的对称轴不平行,就能证明直线l 就是切线,方程(*)为其切线方程.设抛物线C 的方程:)0(22>=p px y ,则方程(*):00200=-+-px y y y px .当00≠y 时,其斜率00≠=y pk ,故直线l 与抛物线C 的对称轴不平行;又当00=y 时,抛物线C 的切线方程为0x x =,也满足方程(*),从而知方程(*)为抛物线C 的切线方程.综上所述,方程(*)为圆锥曲线C 上过P 点的切线方程. 下面用此命题给出的方法解决本文一开始提出的问题.解:椭圆13422=+y x 关于点)23,1(P 对称的椭圆方程为13)3(4)2(22=-+-y x , 将这两个椭圆方程相减:-+3422y x 03)3(4)2(22=---y x , 整理得042=-+y x ,即为所求的切线方程.更为一般的情况,过曲线外一点的曲线的切线如何画出呢?我们就从圆锥曲线的切线与过切点的弦来看。
曲线如果在某一点处可导,那么该点处的导数的几何意义是该点处切线的斜率。
以椭圆型函数为例,设)()000,,,y a b x a P x y =>>≤为其图象上异于长轴端点的任意一点,利用复合函数求导法则,2020x x b x y a y ='==-;对于)0,y a b x a =>>≤,也有202x x b x y a y ='=-。
如果利用复合函数求导法则,对222222220,220b x a y a b b x a y y '+-=+⋅=有,当()00,P x y 为其上一点,()0200200x x b x y y a y ='=-≠。
这样在()00,P x y 处的切线方程为222200b x x a y y a b +=。
当00y =时,切线为x a =±,也适合上式。
故椭圆曲线上任意一点处的切线方程为222200b x x a y y a b +=。
()00,P x y 处切线方程的纵、横截距分别为200,b E y ⎛⎫' ⎪⎝⎭、20,0a D x ⎛⎫' ⎪⎝⎭,具有对称性。
当()00,P x y 在椭圆外,即22222200b x a y a b +>时,过()00,P x y 的切线有两条。
设切点为()11,R x y 、()22,S x y ,则切线PR 、PS 方程分别为222211b x x a y y a b +=和222222b x x a y y a b +=,()00,p x y Q 在切线上,故有22221010b x x a y y a b +=和22222020b x x a y y a b +=,此两式又表明()11,R x y 、()22,S x y 满足222200b x x a y y a b +=,故对应于点()00,P x y 的切点弦RS 所在直线方程为222200b x x a y y a b +=,切点弦的纵、横截距也为200,b E y ⎛⎫' ⎪⎝⎭、20,0a D x ⎛⎫' ⎪⎝⎭,切点弦的纵、横截距的对称性,为我们寻找切点的位置,统一圆锥曲线的尺规作法提供了思路。
(1)椭圆的切线设椭圆C 的方程为()222210x y a b a b+=>>,点()00,P x y 为椭圆外一点,切线PR 、PS 分别与椭圆相切于R 、S 点,则切点弦RS 所在的直线方程为222200b x x a y y a b +=。
利用平面几何中直角三角形的比例中项定理,结合对称找点法,可以利用直尺和圆规确定两个切点的位置。
作法:⑴分别在两坐标轴上截得()0,0M x 、(),0B b 和()00,N y 、()0,A a 四点; ⑵作DA AM ⊥,,DA x D EB BN ⊥与轴交于,EB 与y 轴交于E ;⑶作D 、E 关于原点对称点D '、E ',作直线D E ''与椭圆相交于R 、S ; ⑷连结PR 、PS ,则PR 、PS 为椭圆过点P 的切线。
证明:如图⑴所示,由作法,,DA DM AO AM ⊥⊥Q 又,由比例中项定理得20D a x x =⋅,必有0D x x 与异号,2,D a x x ∴=-D D 'Q 与关于原点对称,20D a x x '∴=有,同理2E b y y '=,D E ''∴直线方程为00221x x y ya b+=,故切点弦所在直线方程为222200b x x a y y a b +=,相应地,直线PR 、PS 与椭圆相切于R 、S 点。
证毕。
特别地,当()00,P x y 在椭圆上时,如图⑵所示,切点弦退化为切线。
只须找到切线之横截距20,0a D x ⎛⎫' ⎪⎝⎭。
作PM x ⊥轴于()0,0M x ,()0,A a ,作DA AM ⊥,DA 交ox 于D 点,D 关于原点的对称点为D ',连PD ',即椭圆C 在点P 处的切线。
(2)双曲线的切线设双曲线C 的方程为()222210,0x y a b a b-=>>,()00,P x y 为双曲线C 外(不图(1))00,x y含焦点区域),且不在渐近线上的任意一点,PR 、PS 是过点P 的双曲线C 的两条切线,则切点弦所在直线方程为222200b x x a y y a b -=。
直线RS 的纵横截距分别为200,b y ⎛⎫- ⎪⎝⎭、20,0a x ⎛⎫ ⎪⎝⎭。
作法:⑴分别在x 、y 轴上截得()0,0M x 、(),0B b 和()00,N y 、()0,A a 四点; ⑵作DA AM ⊥,,DA x D EB BN ⊥交轴交于,EB 与y 轴交于E ;⑶仅作D 关于原点对称点D ',连结DE '与双曲线C 交于R 、S 两点;⑷连结PR 、PS ,则PR 、PS为双曲线C 的过点P 的两条切线。
证明:如图⑶所示,由作法,()0,0M x 、()0,A a ,DA AM AO DM ⊥⊥Q ,∴有20D a x x =⋅,Q 0D x x 与异号,2,D a x x ∴=-D D '又与关于原点对称,20D a x x '∴=,即20,0a D x ⎛⎫' ⎪⎝⎭,同理200,b E y ⎛⎫- ⎪⎝⎭,∴直线D E '方程为222200b x x a y y a b -=,即切点弦RS所在直线方程,故PR 、PS 为双曲线C 过点P 的两条切线。
证毕。
特别地,当()00,P x y 在双曲线上时,且异于顶点时,如图⑷所示,作法简化。
只须作PM ox ⊥,点()0,A a ,作DA AM ⊥,DA 交x 轴于D ,D 关于原点的对称点为D ',连PD ',则PD '与双曲线C 相切于P 点。
(证略) (3)设抛物线的切线设抛物线C 的方程为()220y px p =>,()00,P x y 为抛物线C 外(不含焦点区域,且不在对称轴上)的任意一点,PR 、PS 为抛物线C 的过P 点的两条切线,R 、S 为切点。
则切点弦方程为()00y y p x x =+,利用对称法作切线步骤如下:作法:⑴作PD ox ⊥于D ,作D 点关于原点的对称点()0,0D x '-;⑵作直线//PQ ox ,与抛物线C 交于Q ,作P 关于Q 的对称点M ; ⑶连MD ',交抛物线于R 、S 两点;⑷作直线PR 、PS ,即为抛物线的过点P 的两条切线。
