自动控制原理(第2版)(余成波)-第5章习题解答--

合集下载

自控原理习题答案(第2版)

第1章习题答案1-1 解：自动控制系统：被控对象和控制装置的总体；被控对象：要求实现自动控制的机器、设备和生产过程；扰动：除给定值之外，引起被控制量变化的各种外界因素；给定值：作用于控制系统输入端，并作为控制依据的物理量；反馈：将输出量直接或间接的送到输入端，并与之相比较，使系统按其差值进行调节，使偏差减小或消除。

1-2 解：开环控制有洗衣机的洗衣过程，闭环控制有抽水马桶的蓄水控制、电冰箱制冷系统等。

1-3 解：1-4 解：a与d相连，b与c相连即可；系统原理框图如下所示：1-5 解：系统原理框图如下所示：1-6 解：对控制系统的基本要求是稳定性、准确性和快速性：稳定性是系统正常工作的前提条件；准确性反映控制系统的控制精度，要求过渡过程结束后，系统的稳态误差越小越好；快速性是要求系统的响应速度快，过渡过程时间短，超调量小。

1-7 解：该系统的任务是使工作机械（被控对象）的转角θc（被控量）自动跟踪手柄给定角度θr（给定量）的变化。

该系统的工作原理是：检测电位计与给定电位计的电气特性相同，工作机械的转角θc经检测电位计转换成电压u c，手柄给定角度θr经给定电位计转换成给定电压u r，u c与u r接入放大器前端的电桥。

当工作机械转角θc没有跟踪手柄给定角度θr时，u c与u r两者不相等而产生偏差Δu=u r-u c，Δu经过放大器放大，使电动机转动，通过减速器使得负载产生减小偏差的转动。

当检测电位计检测并转换的u c与u r相等，此时Δu=u r-u c=0,电动机不转，工作机械停在当前位置。

其原理框图如下图所示。

1-8 解：谷物湿度控制系统原理框图如下。

该系统的被控量是谷物湿度，给定量是希望的谷物湿度。

谷物加湿后的实时湿度经湿度检测后送到调节器，若与希望的湿度产生偏差，则通过调节器控制给水阀门的开大或关小，以减小两者的偏差。

谷物在入口端的湿度由前馈通道输入到调节器。

这样若入口处谷物湿度较大，则会使得偏差减小，从而减小阀门的开度；若谷物干燥，会增大偏差，从而加大阀门的开度。

自动控制原理课后习题答案(2020年7月整理).pdf

第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统，说明它们的工作原理并比较开环控制和闭环控制的优缺点。

解：开环控制——半自动、全自动洗衣机的洗衣过程。

工作原理：被控制量为衣服的干净度。

洗衣人先观察衣服的脏污程度，根据自己的经验，设定洗涤、漂洗时间，洗衣机按照设定程序完成洗涤漂洗任务。

系统输出量（即衣服的干净度）的信息没有通过任何装置反馈到输入端，对系统的控制不起作用，因此为开环控制。

闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。

工作原理：以卫生间蓄水箱蓄水量控制为例，系统的被控制量（输出量）为蓄水箱水位（反应蓄水量）。

水位由浮子测量，并通过杠杆作用于供水阀门（即反馈至输入端），控制供水量，形成闭环控制。

当水位达到蓄水量上限高度时，阀门全关（按要求事先设计好杠杆比例），系统处于平衡状态。

一旦用水，水位降低，浮子随之下沉，通过杠杆打开供水阀门，下沉越深，阀门开度越大，供水量越大，直到水位升至蓄水量上限高度，阀门全关，系统再次处于平衡状态。

开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成？各个环节分别的作用是什么？解：自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。

各个基本单元的功能如下：（1）被控对象—又称受控对象或对象，指在控制过程中受到操纵控制的机器设备或过程。

（2）给定元件—可以设置系统控制指令的装置，可用于给出与期望输出量相对应的系统输入量。

（3）检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量，再反馈到系统输入端作比较，一般为各类传感器。

（4）比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较，分析计算并产生反应两者差值的偏差信号。

常用的比较元件有差动放大器、机械差动装置和电桥等。

（5）放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时，可通过放大元件将微弱信号作线性放大。

自动控制原理第二版课后答案

自动控制原理第二版课后答案1. 介绍。

自动控制原理是现代自动化领域中的重要基础课程，它涉及到控制系统的设计、分析和应用，对于工程技术人员来说具有重要的意义。

本文档将针对自动控制原理第二版课后习题进行详细解答，帮助学习者更好地掌握课程内容。

2. 第一章。

2.1 课后习题1。

答，根据控制系统的基本结构，可以将其分为开环控制系统和闭环控制系统。

开环控制系统中，控制器的输出不受到被控对象的影响，而闭环控制系统中，控制器的输出受到被控对象的影响。

闭环控制系统具有更好的稳定性和鲁棒性，但也更加复杂。

2.2 课后习题2。

答，传递函数是描述控制系统输入和输出之间关系的数学模型，其形式为输出变量的拉普拉斯变换除以输入变量的拉普拉斯变换。

传递函数可以帮助我们分析控制系统的性能和稳定性，并进行控制器的设计。

3. 第二章。

3.1 课后习题1。

答，稳定性是控制系统设计中需要考虑的重要因素，它决定了系统在受到干扰或参数变化时的表现。

稳定性分析可以通过判据、根轨迹和频域等方法进行，其中判据法是最为直观和简单的方法，通过对系统的特征方程进行判别来判断系统的稳定性。

3.2 课后习题2。

答，根轨迹是一种描述控制系统特征方程根在复平面上运动规律的方法，它可以直观地反映系统的稳定性、过渡过程和静态误差等性能指标。

通过对根轨迹的分析，可以帮助我们设计合适的控制器来满足系统性能指标的要求。

4. 第三章。

4.1 课后习题1。

答，比例控制器是一种简单的控制器，它的输出与系统的误差成正比。

比例控制器可以改善系统的静态误差性能，但无法消除系统的稳定性问题和过渡过程中的振荡。

4.2 课后习题2。

答，积分控制器是一种消除系统静态误差的控制器，它的输出与系统的误差积分成正比。

积分控制器可以有效地消除系统的静态误差，但在实际应用中可能会导致系统的过度调节和振荡。

5. 总结。

通过对自动控制原理第二版课后习题的详细解答，我们可以更好地理解控制系统的基本原理和设计方法。

自动控制原理第五章课后答案

五频域分析法2-5-1 系统单位阶跃输入下的输出)0(8.08.11)(94≥+-=--t e e t c tt ,求系统的频率特性表达式。

【解】： 98.048.11)]([L )(1+++-==-s s s t c s C 闭环传递函数)9)(4(36198.048.11)()()(++=+++-==s s ss s s s R s C s G )9tg 4(tg 2211811636)9)(4(36)(ωωωωωωω--+-+⨯+=++=j ej j j G2-5-2系统时，系统的稳态输出（1）)30sin()(0+=t t r ；（2）)452cos(2)(0+=t t r ；（3）)452cos(2)30sin()(00--+=t t t r 。

【解】：求系统闭环传递函数5tg 21254)5(4)(54)(1)()()()(14)(ωωωω--+=+=+=+==+=j B K K B K ej j G s s G s G s R s C s G s s G根据频率特性的定义，以及线性系统的迭加性求解如下：（1）︒===30,1,11θωr A︒--====-3.1151tg )1(178.0264)1()(1j j j B e eeA j G θωω[])7.18sin(78.0)1(sin )1()sin()(12︒+=++=+=t t A A t A t c r c s θθθ（2）︒===45,2,21θωr A︒--==+=-8.2152tg 274.02544)(1j j B e ej G ωω)2.232cos(48.1)(︒+=t t c s（3）)8.662cos(48.1)7.18sin(78.0)(︒--︒+=t t t c s2-5-3 试求图2-5-3所示网络的频率特性，并绘制其幅相频率特性曲线。

【解】：（1）网络的频率特性1)(111)(212212+++=+++=ωωωωωC R R j C jR C j R R C j R j G（2）绘制频率特性曲线)tg (tg 22212121111)(1)(11)(ωωωωωωωT T j eT T jT jT j G ---++=++= 其中1221221,)(,T T C R R T C R T >+==。

自动控制原理第五章课后习题答案(免费)[1]

自动控制原理第五章课后习题答案（免费）5－１设单位反馈系统的开环传递函数为对系统进行串联校正，满足开环增益及解:① 首先确定开环增益K,00()12lim v s K SG S k →===② 未校正系统开环传函为:012()(1)G s s s =+M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramGm = 70.5 dB (at 200 rad/sec) , P m = 16.5 deg (at 3.39 rad/sec)Frequency (rad/sec)③ 绘制未校正系统的开环对数频率特性,得到幅穿频率 3.4c ω=,对应相位角'0()164,16c G j ωγ∠=-∴=,采用超前校正装置,最大相角 0(180())4016630m c G j ϕγωγ=-+∠+=-+=④ 11sin ,31m αϕαα--=∴=+ 0()(1)KG s s s =+40γ=︒112K s -=⑤ 在已绘图上找出10lg 10lg3 4.77α-=-=-的频率 4.4m ω=弧度/秒令c m ωω=⑥0.128/,0.385/m T s T s ωα=⇒==∴=校正装置的传函为:110.385()110.128Ts s G s Ts s α++==++校正后的开环传函为:012(10.39)()()()(1)(10.13)c s G s G s G s s s s +==++ 校正后1801374340γ=-=>,满足指标要求.-100-50050100M a g n i t u d e (d B )101010101010P h a s e (d e g )Bode DiagramGm = 99.2 dB (at 1.82e+003 rad/sec) , P m = 42.4 deg (at 4.53 rad/sec)Frequency (rad/sec)5－２设单位反馈系统的开环传递函数为要求设计串联迟后校正装置。

自动控制原理课后答案余成波

自动控制原理课后答案余成波【篇一：自动控制原理课程实习报告】t>matlab应用及实现》自动控制原理课程实习报告专业：电气工程及其自动化班级：电气一班姓名：指导教师：二○一五年十二月十五日目录1实验目的 (1)2实习内容 (2)3 实习总结.....................................................................14 4 参考文献 (14)1.实习目的（1）熟悉掌握matlab应用软件（2）能用其绘制出相应所需的图形（3）增强对课程的理解及其应用，增加重点知识的掌握（4）能熟悉运用matlab进行程序编写及绘制2.实习内容s2?3s?6m2.5将传递函数g?s??3分解为部分分式。

s?5s2?6snum=[1 3 6]; den=[1 5 6 0]; x=roots(den)x =0-3.0000-2.0000[r,p,k]=residue(num,den)r = 2.0000-2.00001.0000p = -3.0000-2.0000k = [ ]tf(num,den)transfer function:s^2 + 3 s + 6-----------------s^3 + 5 s^2 + 6 sm2.6 系统传递函数为g?s??100?s?5?ss?0.5s?352，求其传递函数模型的实现。

z=[-5]; p=[0 -0.5 -35 -35]; k=[100];sys=zpk(z,p,k)zero/pole/gain:100 (s+5)------------------s (s+0.5) (s+35)^2[num,den]=zp2tf(z,p,k)num = 0 0 0100500den = 1.0e+003 *0.0010 0.0705 1.26000.6125 0sys=tf(num,den)transfer function:100 s + 500-----------------------------------s^4 + 70.5 s^3 + 1260 s^2 + 612.5 ss2?3s?2m2.7 系统传递函数为g?s??4，求其零、极点模型的实现。

自动控制原理第五章习题集与答案解析

第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。

u rR1u cR2CR2R1u r u c(a) (b)题5-1图 R-C网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图：⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++==5-2某系统结构图如题5-2图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(tcs和稳态误差)(tes（1）ttr2sin)(=（2）)452cos(2)30sin()(︒--︒+=tttr题5-2图反馈控制系统结构图解系统闭环传递函数为: 21)(+=Φs s 频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则)2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时,2=ω，r m =1则,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2( -=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2( +=-Φ=t t j r e e e m ss ϕ （2）当)452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ= )902cos(7.0)4.3sin(4.0 --+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0 --+=t t5-3若系统单位阶跃响应h t e e t t t()..=-+≥--11808049试求系统频率特性。

自动控制原理(第2版)(余成波_张莲_胡晓倩)习题全解及MATLAB实验_____第1、2章习题解答

第1章控制系统的基本概念本章介绍了自动控制的定义，自动控制系统的组成、工作原理和相关的常用术语。

比较了开环控制系统和闭环控制系统，并进一步说明了其优缺点和适用范围，介绍了典型闭环系统的功能框图。

需要重点掌握负反馈在自动控制系统中的作用，闭环系统（或反馈系统）的特征是：采用负反馈，系统的被控变量对控制作用有直接影响，即被控变量对自身有控制作用。

在分析系统的工作原理时，确定控制系统的被控对象、控制量和被控制量，根据控制系统的工作原理及各元件信号的传送方向，可画出控制系统的职能方框图。

方框图是分析控制系统的基础。

本章的难点在于由系统的物理结构图或工作原理示意图绘出系统元件框图。

按照不同的分类方法可以将自动控制系统分成不同的类型，实际系统可能是几种方式的组合。

对自动控制系统的基本要求包括：系统首先必须是稳定的；系统的稳态控制精度要高，即稳态误差要小；系统的动态性能要好，即系统的响应过程要平稳，响应过程要快。

这些要求可归纳成稳、准、快三个字。

教材习题同步解析1.1 试列举几个日常生活中的开环控制和闭环控制系统的例子，并简述其工作原理。

解：1）开环控制最普通的热得快，加热到一定程度提醒断电，但不会自主断电，需要人为去断电。

电风扇，人工转换电扇档位实现转速的控制，但不能根据环境温度自动调节。

洗衣机，洗衣人根据经验，预先设定洗涤、漂洗等洗衣程序，则洗衣机根据设定的程序完成洗衣过程。

系统的被控制量（输出量）没有通过任何装置反馈回输入端，对系统的控制不起作用。

2）闭环系统饮水机或电水壶，自动断电保温，加温到一定温度停止加温，进入保温状态；温度降低进入加温状态，如此循环。

自动调温空调，当环境温度高于或低于设定温度时，空调制冷系统自动开启，调定室温到设定值。

全自动洗衣机的水位控制，红外传感器扫描水位高低，当水位合适时，洗衣机自动停止加水。

走道路灯的声光控制系统，基本工作原理如下：白天或夜晚光线较亮时，光控部分将开关自动关断，声控部分不起作用。

自动控制原理课后习题答案第五章

第五章5-2 若系统单位阶跃响应为49()1 1.80.8tth t ee--=-+试确定系统的频率特性。

分析先求出系统传递函数，用j ω替换s 即可得到频率特性。

解：从()h t 中可求得：(0)0,(0)0h h '==在零初始条件下，系统输出的拉普拉斯变换()H s 与系统输出的拉普拉斯变换()R s 之间的关系为()()()H s s R s =Φ⋅即()()()H s s R s Φ=其中()s Φ为系统的传递函数，又1 1.80.836()[()]49(4)(9)H s L h t s s s s s s ==-+=++++1()[()]R s L r t s ==则()36()()(4)(9)H s s R s s s Φ==++令s j ω=，则系统的频率特性为()36()()(4)(9)H j j R j j j ωωωωωΦ==++5-7 已知系统开环传递函数为)1s T (s )1s T (K )s (G 12++-=;（Ｋ、Ｔ1、Ｔ2＞０）当取ω＝１时， o180)j (G -=ω∠,|Ｇ(ｊω)|＝０.５。

当输入为单位速度信号时，系统的稳态误差为0.1，试写出系统开环频率特性表达式G(ｊω)。

分析：根据系统幅频和相频特性的表达式，代入已知条件，即可确定相应参数。

解：由题意知：()G j ω=21()90arctan arctan G j T T ωωω∠=---因为该系统为Ⅰ型系统，且输入为单位速度信号时，系统的稳态误差为0.1，即1()lim ()0.1ss s e E s K→∞===所以：10K =当1ω=时，(1)0.5G j ==21(1)90arctan arctan 180G j T T ∠=---=-由上两式可求得1220,0.05T T ==，因此10(0.051)()(201)j G j j j ωωωω-+=+5-14 已知下列系统开环传递函数(参数K 、T 、T ｉ＞０，ｉ＝１，2，…，６)(1))1s T )(1s T )(1s T (K)s (G 321+++=(2))1s T )(1s T (s K)s (G 21++=(3))1Ts (s K )s (G 2+=(4))1s T (s )1s T (K )s (G 221++=(5)3s K )s (G =(6)321s)1s T )(1s T (K )s (G ++=(7))1s T )(1s T )(1s T )(1s T (s )1s T )(1s T (K )s (G 432165++++++=(8)1Ts K)s (G -=(9)1Ts K )s (G +--=(10))1Ts (s K)s (G -=其系统开环幅相曲线分别如图5-6(1)～(10)所示，试根据奈氏判据判定各系统的闭环稳定性，若系统闭环不稳定，确定其s 右半平面的闭环极点数。

《自动控制原理》第二版课后习题答案

ui uo ， ue 经放大后驱动电动机转动，在驱动导弹发射架转动的同时，通过输出轴带
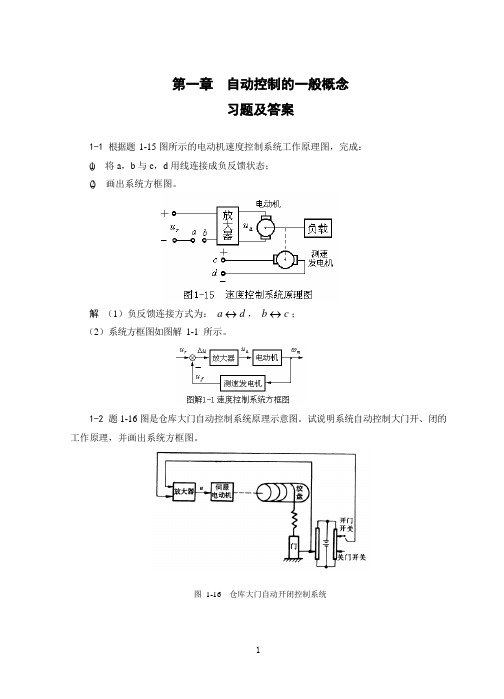
动电位器 P2 的滑臂转过一定的角度 o ，直至 o i 时， ui uo ，偏差电压ue 0 ，电动机停止转动。这时，导弹发射架停留在相应的方位角上。只要 i o ，偏差就会产生调节作
3
用，控制的结果是消除偏差 e ，使输出量 o 严格地跟随输入量 i 的变化而变化。系统中，导弹发射架是被控对象，发射架方位角 o 是被控量，通过手轮输入的角度 i 是
大，提高发电机的端电压，使发电机 G 的端电压回升，偏差电压减小，但不可能等于零，因
为当偏差电压为 0 时， i f =0，发电机就不能工作。即图(b)所示系统的稳态电压会低于 110
伏。 1-8 图 1-22 为水温控制系统示意图。冷水在热交换器中由通入的蒸汽加热，从而得到一
定温度的热水。冷水流量变化用流量计测量。试绘制系统方块图，并说明为了保持热水温度为期望值，系统是如何工作的？系统的被控对象和控制装置各是什么？
图 1-16 仓库大门自动开闭控制系统
1
解当合上开门开关时，电桥会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。与此同时，和大门连在一起的电刷也向上移动，直到桥式测量电路达到平衡，电动机停止转动，大门达到开启位置。反之，当合上关门开关时，电动机带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。系统方框图如图解 1-2 所示。
征炉温的希望值）。系统方框图见图解 1-3。
1-4 图 1-18 是控制导弹发射架方位的电位器式随动系统原理图。图中电位器 P1 、 P2 并联后跨接到同一电源 E0 的两端，其滑臂分别与输入轴和输出轴相联结，组成方位角的给定元件

自动控制原理习题解答(余成波,张莲,胡晓倩)

第1章控制系统的基本概念1.5 图1.1所示的转速闭环控制系统中，若测速发电机的正负极性接反了，试问系统能否正常工作？为什么？图1.1 直流电动机转速闭环控制系统电压放大器功率放大器M c负载nM电动机+ _+a u_+ _ g u + E电位器测速发电机+_f u+ e u _解：若测速发电机的正负极性接反，偏差电压则为e g fu u u =+系统将由负反馈变为正反馈，而正反馈不能进行系统控制，会使系统的偏差越来越大。

因此，系统不能正常工作。

1.9 仓库大门自动控制系统原理如图1.8所示。

试说明仓库大门开启、关闭的工作原理。

如果大门不能全开或全关，应该怎样进行调整？解当给定电位器和测量电位器输出相等时，放大器无输出，门的位置不变。

假设门的原始位置在“关”状态，当门需要打开时，“开门”开关打开，“关门”开关闭合，给定电位器和测量电位器输出不相等。

电位器组会测量出开门位置与大门实际位置间对应的偏差电压，偏差电压经放大器放大后，驱动伺服电动机带动绞盘转动，将大门向上提起。

与此同时，和大门连在一起的电刷也向上移动，直图1.8仓库大门自动控制系统图1.9 仓库大门自动控制系统方框图给定电位器到电位器组达到平衡，即测量电位器输出与给定电位器输出相等，则电动机停止转动，大门达到开启位置。

反之，当合上关门开关时，电动机带动绞盘使大门关闭，从而可以实现大门远距离开闭自动控制。

系统方框图如图1.9所示。

如果大门不能全开或者全闭，说明电位器组给定的参考电压与期望的开门位置或关门位置不一致，应该调整电位器组的滑臂位置，即调整“开门”或“关门”位置对应的参考电压。

第2章自动控制系统的数学模型2.1 求图2.1中RC 电路和运算放大器的传递函数o ()()i U s U s 。

解：（a ）令Z 1=111R Cs +为电容和电阻的复数阻抗之和；Z 2=2R 为电阻的复数阻抗。

由此可求得传递函数为：22121211221()()1()1o i U s Z R R R G s U s Z Z R Cs R R Cs R R ====+++++(c) 该电路由运算放大器组成，属于有源网络。

自动控制原理（第2版）（余成波）-第5章习题解答--

自动控制原理（第2版）（余成波）-第5章习题解答--108第5章频率特性法教材习题同步解析5.1 一放大器的传递函数为：G (s )=1+Ts K 测得其频率响应，当ω=1rad/s 时，稳态输出与输入信号的幅值比为12/2，稳态输出与输入信号的相位差为－π/4。

求放大系数K 及时间常数T 。

解：系统稳态输出与输入信号的幅值比为A == 222172K T ω=+ 稳态输出与输入信号的相位差arctan 45T ?ω=-=-?，即1T ω=当ω=1rad/s 时，联立以上方程得T =1，K =12放大器的传递函数为：G (s )=121s +5.2 已知单位负反馈系统的开环传递函数为 5()1K G s s =+ 根据频率特性的物理意义，求闭环输入信号分别为以下信号时闭环系统的稳态输出。

（1）r （t ）=sin （t +30°）；（2）r （t ）=2cos （2t －45°）；（3）r （t ）= sin （t +15°）－2cos （2t －45°）；解：该系统的闭环传递函数为65)(+=Φs s 闭环系统的幅频特性为109 365)(2+=ωωA闭环系统的相频特性为 6arctan )(ωω?-= （1）输入信号的频率为1ω=，因此有37375)(=ωA ，()9.46?ω?=- 系统的稳态输出()20.54)37ss c t t ?=+ （2）输入信号的频率为2ω=，因此有()A ω=，()18.43?ω?=- 系统的稳态输出()cos(263.43)2ss c t t ?=- （3）由题（1）和题（2）有对于输入分量1：sin （t +15°），系统的稳态输出如下1() 5.54)37ss c t t ?=+ 对于输入分量2：－2cos （2t －45°），系统的稳态输出为2()63.43)ss c t t ?=- 根据线性系统的叠加定理，系统总的稳态输出为)4363.632cos(210)537.5sin(37375)(??--+=t t t c ss5.3 绘出下列各传递函数对应的幅相频率特性与对数频率特性。

自动控制原理答案完全版_第二版

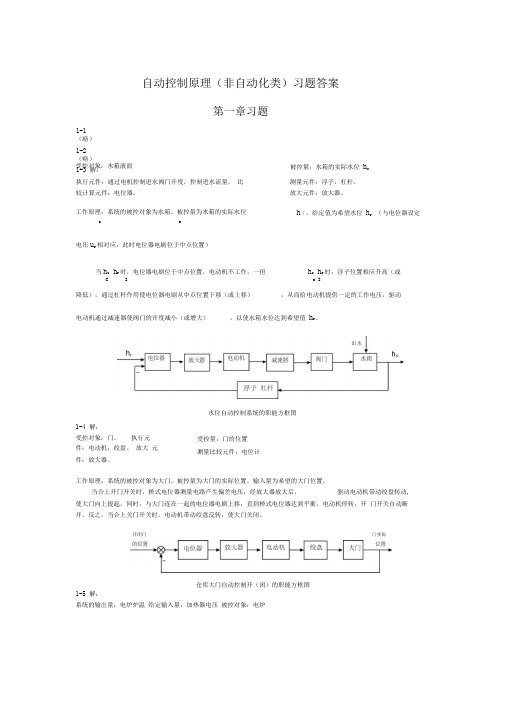
自动控制原理（非自动化类）习题答案第一章习题被控量：水箱的实际水位 h c执行元件：通过电机控制进水阀门开度，控制进水流量。

比较计算元件：电位器。

h 「。

给定值为希望水位 h r （与电位器设定cr电压u r 相对应，此时电位器电刷位于中点位置）当h c h r 时，电位器电刷位于中点位置，电动机不工作。

一但h c h r 时，浮子位置相应升高（或CIc I降低），通过杠杆作用使电位器电刷从中点位置下移（或上移），从而给电动机提供一定的工作电压，驱动电动机通过减速器使阀门的开度减小（或增大），以使水箱水位达到希望值 h r 。

水位自动控制系统的职能方框图受控量：门的位置测量比较元件：电位计工作原理：系统的被控对象为大门。

被控量为大门的实际位置。

输入量为希望的大门位置。

当合上开门开关时，桥式电位器测量电路产生偏差电压，经放大器放大后，驱动电动机带动绞盘转动,使大门向上提起。

同时，与大门连在一起的电位器电刷上移，直到桥式电位器达到平衡，电动机停转，开门开关自动断开。

反之，当合上关门开关时，电动机带动绞盘反转，使大门关闭。

1-5 解：系统的输岀量：电炉炉温给定输入量：加热器电压被控对象：电炉1-1 （略） 1-2（略）1-3 解：受控对象：水箱液面测量元件：浮子，杠杆。

放大元件：放大器。

工作原理：系统的被控对象为水箱。

被控量为水箱的实际水位1-4 解：受控对象：门。

执行元件：电动机，绞盘。

放大元件：放大器。

开闭门门实际仓库大门自动控制开（闭）的职能方框图放大元件：电压放大器，功率放大器，减速器比较元件：电位计测量元件：热电偶职能方框图:KK3 2 Ts (T 1)s s K1K 3电位器电压放大炉温热电偶第二章习题2-1解：对微分方程做拉氏变换：X,(s) R(s) C(s) N,(s)X 2 (s) Q X/s)X 3 (s) X2 (s) X5(s TsX4 (s) X 3 (s)X5 (s) X4 (s) K2 N2(s k 3 X5 (s) s2C (s) sC(s) C(s) / R(s) 功率放大加热器'电机电炉R(s)绘制上式各子方程的方块图如下图所示:C(s) / N i (s) C(s) / R(s),K 2K 3TSTs 3~~T 1)s 2s K 1K 32-2解：对微分方程做拉氏变换X i (s) K[R(s) C (s)] X 2 (s)sR(s)(s 1) X 3(s) X i (s) X 2 (s) (Ts 1)X 4 (s)X 3 (s) X 5 (s)C(s) X 4 (s) N (s) X 5 (s) (Ts 1) N(s)(b) C (s)字红R(s) 1 G 1G 3 G G 4 G 2 G 3 G 2G 4X3(s) 绘制上式各子方程的方块如下图:将方块图连接得出系统的动态结构图:..R(s)1(s 1)：Ts 1)C(s)N (s) 02-3解：（过程略）K____________C(s) (s 1)<Js 1) (s 1XTs 1) K ____________ Ts 2(T s1)s (K 1)C(s) / N 2 (s)R(s) ms fs K(c)誤 R(s) G 2 G 1G 2 1 G-i G 2G-I (d 普 R(s)G 1 G 2 1 G 2G 3(e)R^ R(s)G 1G 2G 3G 4 1 G<|G 2 G 2G 3 G 3G 4 G 1G 2G 3G 4 2-4 解：（1）求 C/R ，令 N=0 KK K 3s(Ts 1) C (s) / R(s) G(s)1 G(s) 求C/N ，令R=0，向后移动单位反馈的比较点 K C(s) / N (s) (K n G n K 1 0 ) — J s 1 亠 K 1G(s)K 1K 2 K 3 Ts 2K i K 2 K 3K n K 3s K 1K 2 K 3G K 2 n2 一Ts 2s K 1K 2 K 3 Ts 1 s （2）要消除干扰对系统的影响C(s) / N (s) K n K3s K1K2 K3GnTs 2 s K 1K 2 K 3G n (s) KnsK 1K 22-5 解：（a ）（1 ）系统的反馈回路有三个，所以有3L a L 1 L 2 L 3 a 1G 1G 2G 5 G 2G 3G 4 G 4G 2G 5三个回路两两接触，可得 1 L a 1 GG 2G 5 G 2G 3G 4 G 4G 2G 5(2) 有两条前向通道，且与两条回路均有接触，所以P P 2 G 1G 2G 3,11, 2 1(3) 闭环传递函数C/R 为GGG 3 11 G 1G 2G 5 G 2G 3G 4 G 4G 2G 5(b)(1) 系统的反馈回路有三个，所以有3L aa 1L 1L 3 G 1G 2 G 1 G 1三个回路均接触，可得 1 L a 1 G-i G 2 2G-)(2 )有四条前向通道，且与三条回路均有接触，所以R G 1G 2 , 11P 2G, 21PG2,3 1P 4G 1,41(3)闭环传递函数C/R 为C G 1G 2 G 1 G 2 GG-i G 2 G 2 R 1 G 1G 22G 1 1 G-|G 2 2G.2-6解：用梅逊公式求，有两个回路，且接触，可得1L a 1 GG 2G 3 G 2，可得第三章习题采用K 0 , K H 负反馈方法的闭环传递函数为1OK o要使过渡时间减小到原来的 0.1倍，要保证总的放大系数不变，则：(原放大系数为10,时间常数为0.2)3-2解：系统为欠阻尼二阶系统(书上改为“单位负反馈……”，“已知系统开环传递函数”)% e / 1 $100%100% 1C(s) G-|G 2G 3 G 2G 3 R(s) 1 G 1G 2G 3 G 2 C (s)(1 G 2 )G 3N 2 (s) 1 GG 2G 3 G 2 E(s) 1 G 2 G 2G 3 R(s) 1 G-|G 2G ：3 G 2 E(s) C(s) (1 G 2 G N 2 (s)N 2 (s)1 G 1G 2G 3 G 2C (s) NQC(s) / R(s)C(s) 1 (1 GG 2G 3 G 2 ) 1N 3 (s) 1 G 1G 2G 3 G 2 E(s) C(s) G 2G 3 G 1G 2G 3 N 1 (s) N 1(s) 1 G 1G 2G 3 G 2E(s)C(s) 1N 3 (s)N 3 (s)3-1解：(原书改为G(s) 100.2s 1)(s)C(s) K G(s) R(s) 01 G(S )K H1 10K H 0.2s1 10K10K 。

自动控制原理简明教程第二版课后答案第五章习题答案

作用下，系统的稳态误差 ess (t) 。解：系统的闭环传递函数为：
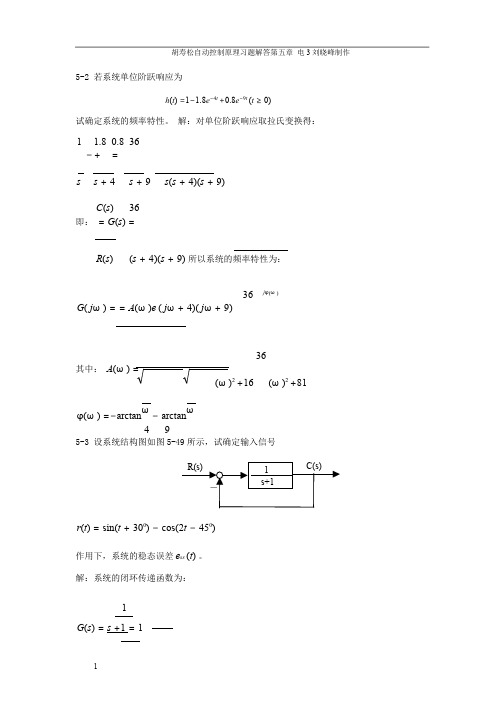
1 G(s) = s +1 = 1
1
胡寿松自动控制原理习题解答第五章电 3 刘晓峰制作
1 1+ s +1
s+2
根据公式（5-16）和公式（5-17）得到：css (t) =
AG( jω )sin(ω t = A1 G( jω 1)sin(ω 1t
胡寿松自动控制原理习题解答第五章电 3 刘晓峰制作
5-2 若系统单位阶跃响应为
h(t) =1−1.8e−4t +0.8e−9t (t ≥ 0)
试确定系统的频率特性。解：对单位阶跃响应取拉氏变换得：
1
1.8 0.8 36 −+ = s+4 s+9 s(s + 4)(s + 9)
s
C(s) 36 即： = G(s) = (s + 4)(s + 9) 所以系统的频率特性为： 36 G( jω ) = = A(ω )e ( jω + 4)( jω + 9)
-40 66
L(ω) -60
6 0.1 1 -80
ω
（3）系统的交接频率为 0.1 1 2，低频段渐近线的斜率为-20，且过（0.1,38dB）点，
截止频率为 ω c = 5.43。
对数幅频渐进特性曲线如下：
10
胡寿松自动控制原理习题解答第五章电 3 刘晓峰制作
（4）系统的交接频率为 0.1 1 20，低频段渐近线的斜率为-20，且过（0.1,40dB）点，
8
胡寿松自动控制原理习题解答第五章电 3 刘晓峰制作
L（ω ）（dB）
60 40 20

自动控制原理第五章课后答案2

① 0=ν② )1)(12()12()(32222211221+++++=s T s T s T s T s T K s G k ξξ③32.0116.340lg 10lg 201111==⇒=⇒=-ωωωT032.016.314010lg lg 202222==⇒=⇒=-ωωωT025.040013==T 2.0821lg 2011≈⇒=ζζ 1621lg2022≈⇒-=ζζ④ 1.020lg 20=⇒-=K K)10025.0)(1064.0001.0()113.01.0(1.0)(22+++++=∴s s s s s s G k【解】：（1）504.12lg 2021===ωνK 其伯德图如解图（1）所示。

剪切频率204.121lg40≈⇒=c cωω相角裕量︒-≈⨯-︒⨯-︒=-8.2122.0tg 9021801γ 系统不稳定（特征方程漏项），相角裕量为负数。

（2）系统传递函数为)12.0()1(4)(2++=s s s s G其伯德图如解图（2）所示。

剪切频率(1)(2) 题2-5-12解图404.121lg20≈⇒=c cωω相角裕量︒≈⨯-=-︒⨯-+︒=----3.3742.0tg 4tg 2.0tg 902tg 1801111c c ωωγ系统稳定。

（3）一阶微分环节的介入，增加了剪切频率附近的相位，即增加了相位裕量，提高了系统的稳定性。

（4）希望中频段折线斜率为-20db/十倍频程，且该斜线的频宽越大越好。

【解】：方法一[])1()1()1()1()1)(1()1)(1(1)1)(1()1(1)(31231212321311+++-+=-+-++-++=+=s T K s T s T s T K K s T s T s T s T K s T s T s T K K GH G K s G k二阶系统，有一个右半平面的开环极点，0,1==v p 。

由开环幅相曲线可知21,1==b a 。

自动控制原理第二版课后习题参考答案

自动控制原理第二版课后习题参考答案2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+=(b) ()()141112+⋅-=Cs R R R s U s U (c)()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i 2-8 (a)()()()()3113211G H G G G G s R s C +++=(b)()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。

图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。

图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b)()()()1221211222112++++=s C R C R C R s C R C R R s R s C 2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()⎪⎭⎫ ⎝⎛++-=-=-t e t t c s n t n n nn 21222,1ωωωωω()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 32220220222001200=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t(2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t (3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件（1）~（4）确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。