行列式的性质及展开计算讲解
§3 行列式的展开定理

§1 行列式的定义 §2 行列式的性质与计算 §3 行列式展开定理、克拉默法则
一、余子式、代数余子式 二、行列式按一行(列)展开法则 三、克拉默法则
§3 行列式展开定理、克拉默法则
引例
a11 a12 a13 a21 a22 a23 a11a22a33 a12a23a31 a13a21a32 a31 a32 a33 a11a23a32 a12a21a33 a13a22a31,
3.推论
行列式任一行(列)的元素与另一行(列)的 对应元素的代数余子式乘积之和等于零,即
ai1 Aj1 ai2 Aj2 ain Ajn 0, i j a1i A1 j a2i A2 j ani Anj 0, i j
a11 A21 a12 A22 a1n A2n 0
§3 行列式的展开定理
( xn xn1 )
( x2 x1 ) ( x3 x1 )( x3 x2 ) ( xn x1 )( xn x2 ) ( xn xn1 )
§3 行列式的展开定理
先证明3阶范德蒙行列式
111
D3 x1 x2 x3
( xi x j )
x12 x22 x32 1 ji3
( x2 x1 )( x3 x1 )( x3 x2 ).
ai1 , n ai1 ,n
an1
an, j1 an , j1
ann
称之为元素 aij 的余子式,记作 Mij .
§3 行列式的展开定理
令
Aij (1)i j Mij
称 Aij之为元素 aij 的代数余子式.
注:
① 行列式中每一个元素分别对应着一个余子式
和一个代数余子式.
② 元素 aij 的余子式和代数余子式与 aij 的大小 无关,只与该元素所在行列式中的位置有关.
第二讲 行列式的性质 行列式按行(列)展开

第二讲Ⅰ 授课题目(章节):§1.3 行列式的性质;§1.4 行列式按行(列)展开Ⅱ 教学目的与要求:了解行列式的性质,会将行列式按一行(一列)展开,会用行列式的性质计算一些较简单的行列式以及某些n 阶行列式Ⅲ 教学重点与难点:重点:行列式的性质,将行列式化为上三角行列式,行列式按行列展开 难点:行列式的计算Ⅳ 讲授内容:§1.3 行列式的性质定义1.8 行列式D 中的行与列对换后得到的行列式称为D 的转置行列式,记作T D即:若=D nnn n n n a a a a a a a a a ... (2)12222111211,则有=T D nnnnn n a a a a a a a a a ... (212221212111)注1 行列式的转置可以看作将行列式以主对角线为对称轴做对称变换;注2 D 中位于第i 行第j 列的元素ij a ,在T D 中位于第j 行第i 列;D 与T D 中同位于第i 行第j 列的元素,D 中是ij a ,而T D 中是ji a 性质1 D =T D证 D 中的项是取自不同行不同列的元素的乘积,可以表示为:n n nj j j j j j N a a a ...)1(212121)...(- 它的符号为) (21)1(n j j j N -而由于D 与T D 中的元素行列互换,这些元素在T D 中位于相应的不同列不同行, 因而它们的乘积nnj j j a a a (2)121也是T D 中的一项。
又由定理1.3知,作为T D 中的一项,它的符号可由行标排列n j j j ...21的逆序数与列标排列n...12的逆序数确定,因而在T D 中,其符号为)...()...12() (2121)1()1(n n j j j N n N j j j N -=-+综上所述,D 中的任一项都是T D 中的一项,且符号相同。
反之也成立 从而得证D =T D注 由本性质可知,行列式的行具有的性质,列同样也有。
第2讲 1.3行列式的性质 1.4行列式按行(列)展开

7 15 6 6 2. 5 38
记 交换 i、j 两行: ri rj ;交换i、j两列: ci c j
推论1 如果行列式有两行(列)完全相同,则此行
列式为零
证明 把相同的两行互换,有D=-D,所以 D=0
性质3 用数 k 乘行列式的某一行(列)中所有元素,等
于用数 k 乘此行列式
a11
a12
a1n
a11 a12
a1n
即 kas1 kas2
kasn k as1 as 2
asn
an1
an2
ann
an1 an2
ann
记 第 i 行乘以 k:kri;第j列乘以 k: kcj 推论1 若行列式D中某一行(列)的所有元素均为零,
则D=0.
推论2 行列式的某一行(列)中所有元素的公 因子 可以提到行列式符号的外面.
a 3a b 6a 3b c
d abcd 4a 3b 2c d 10a 6b 3c d
解 从第 4 行开始,后行减前行得,
r4 r3 a b
c
d
r3 r2 0 a a b a b c
r2 r1
D
0
a
2a b
3a 2b c
0 a 3a b 6a 3b c
r4 r3 a b c
a11 a12 a1n
s ai1 ai2 ain
s ai1 ai2 ain
t
k
kai1 kai2 kain
ai1 ai2 ain
0.
t
an1 an2 ann
an1 an2 ann
例1 设
a11 a12 a13
6a11 2a12 10a13
a21 a22 a23 1, 求 3a21 a22
§1.2 行列式的性质与计算
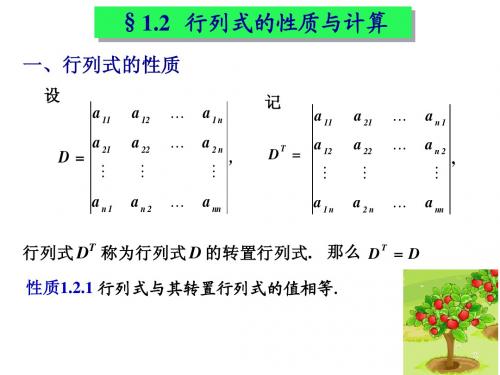
上节例4 0 例1 上节例 中 计算四阶行列式 1 1 1
用性质计算行列式
1 0 1 1 解: 0 2 5 1 ( 1)r1 + r3 D= 1 x 2 3 0 3 0 1
1
1 1 0 2 5 1 0
0 0
x 3
3 2 0 1
2 5 1 3 5 5 1 3c3 + c1 1+ 1 x 6 3 2 3 2 +6 x 展开1( 1) 0 0 1 0 3 0 1 3
… … …
→1 →i → j
i、 j行互换,行列式变号 行互换, 、 行互换 行列式变号.
2 4 2 2 1 1 1
ai 1 D= ain
2 4
… … →i →j
= D
D= 0
性质1.2.4 把行列式的某一行(列)中的各元素都乘以同一常 性质 把行列式的某一行( 乘此行列式的值. 数 k , 等于用数 k 乘此行列式的值 推论1.2.2 符号外面. 符号外面. 推论1.2.3 若行列式中有两行(列)元素对应成比例,则此行列 若行列式中有两行( 元素对应成比例, 推论 式值为零. 式值为零. 行列式中某一行( 行列式中某一行(列)的公因子可以提到行列式
D=
a a
b a+b
c a+b+c
d a+b+c+d
r3 + r4 = r2 + r3
a b c d 0 a a+b a+b+c 0 0 0 0 a a 2a + b 3a + b
r3 + r4 =
a b
c
d
0 a a+b a+b+c 0 0 a 2a + b 0 0 算 例2 解:1
高考数学中的行列式解析技巧

高考数学中的行列式解析技巧在高考数学中,行列式是一个比较重要的概念。
它不仅在数学上有极大的用处,同时也广泛应用于物理、工程等领域。
在高考中,行列式的解析技巧是非常关键的。
本文将从理论与实践两方面来介绍高考数学中的行列式解析技巧。
一、行列式的定义与性质在数学中,一个n阶行列式是由n行n列的矩阵构成的,其中每一个元素都是实数或者复数。
通过对这些元素的排列和相乘,得到一个标量值。
行列式的定义可以用以下方式表达:左乘右减法则一个n阶行列式可以表示为:$$\begin{vmatrix}a_{11} & a_{12} & ... &a_{1n}\\a_{21} & a_{22} & ... &a_{2n}\\... & ... & ... & ... \\a_{n1} & a_{n2} & ...&a_{nn}\end{vmatrix}=\sum\limits_{j_1,j_2,...j_n}(-1)^TA_{1j1}A_{2j2}...A_{njn}$$其中,$A_{ij}$表示将第i行第j列元素去掉后所剩的(n-1)阶行列式。
而上述式子中的$\sum\limits_{j_1,j_2,...j_n}$则表示对所有有序排列$j_1,j_2,...j_n$进行求和。
行列式还具有以下性质:(1)交换两行或列,行列式相反;(2)行列式中的一列(行)乘以k,等于在原行列式中的值乘以k;(3)行列式的某一列(行)可分解为两列(行)相加或相减。
以上仅仅是行列式定义与性质的基本介绍。
下面,我们将详细介绍高考数学中常用的行列式解析技巧。
二、数学上的行列式解析技巧(1)三阶行列式的计算对于3阶行列式A:$$A=\begin{vmatrix}a_{11} & a_{12} & a_{13}\\a_{21} & a_{22} & a_{23}\\a_{31} & a_{32} & a_{33}\end{vmatrix}$$其中的元素$a_{ij}$可以按任意一行(列)展开,得到:$$A=a_{11}\begin{vmatrix}a_{22} & a_{23}\\a_{32} &a_{33}\end{vmatrix}-a_{12}\begin{vmatrix}a_{21} & a_{23}\\a_{31} & a_{33}\end{vmatrix}+a_{13}\begin{vmatrix}a_{21} &a_{22}\\a_{31} & a_{32}\end{vmatrix}$$这一结论显然是成立的。
线性代数行列式的性质与计算

下页
2 1 3 1
例1. 计算行列式 D = 3 1 0 7 1 2 4 2 1 0 1 5
解:
1 0 1 5 r2 3r1 1 0 1 5
r3 +r1
r1r4 3 1 0 7 0 1 r4 2r1 3 8
D =
=
1 2 4 2
02 3 3
2 1 3 1
0 1 1 11
令Aij=(1)i+jMij, Aij称为元素aij的代数余子式.
例如,求4阶行列式中a32的代数余子式
a11 a12 a13 a14 a21 a22 a23 a24 a31 a32 a33 a34 a41 a42 a43 a44
M32=
A32= (1)3+2M32 = M32
a11 a13 a14 a21 a23 a24 a41 a43 a44
下页
范得蒙(Vandermonde)行列式
1
a1 a12 Dn = a1n3 a1n2 a1n1
下页
1
1
0
Dn
=
0
0
0
a2 a1 a22 a1a2
a2n2 a1a2n3
a2n1 a1a2n2
1
a3 a1 a32 a1a3
a3n2 a1a3n3 a3n1 a1a3n2
1
an a1
an2 a1an
ann2 a1ann3
ann1 a1ann2
a2 a1 a22 a1a2
按第二列展开
D=a12A12 +a22A22 +a32A32
=0 (1)1+2 1 3 +1 (1)2+2 1 2 +3 (1)3+2 1 2
行列式的性质及求解方法

行列式的性质及求解方法行列式是线性代数中的一个重要概念,具有广泛的应用领域,例如矩阵求逆、线性方程组的解法、空间向量的叉积等。
在本文中,我们将探讨行列式的性质及其求解方法。
一、行列式的定义及性质1.1 行列式的定义对于一个$n$阶方阵$A=[a_{ij}]$,定义它的行列式为:$$\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn}\\\end{vmatrix}=\sum_{\sigma \in S_n}(-1)^{\mathrm{sgn}(\sigma)}a_{1\sigma(1)}a_{2\sigma(2)}\cdotsa_{n\sigma(n)}$$其中,$\sigma$是$n$个元素的全排列,$S_n$表示$n$个元素的置换群,$\mathrm{sgn}(\sigma)$表示$\sigma$的符号,即$(-1)^k$,其中$k$为$\sigma$的逆序数。
1.2 行列式的性质- 行列式的值不变性行列式的值只与矩阵的元素有关,而与矩阵的行列变换或线性组合无关。
- 互换矩阵的两行或两列,行列式变号将矩阵的两行(列)互换,则该行列式的值取相反数。
- 矩阵的某一行(列)乘以一个数$k$,行列式的值乘以$k$将矩阵的某一行(列)乘以一个数$k$,则该行列式的值乘以$k$。
- 矩阵的某一行(列)加上另一行(列)的k倍,行列式不变将矩阵的某一行(列)加上另一行(列)的k倍,行列式的值不变。
- 方阵的行列式等于其转置矩阵的行列式$$\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn}\\\end{vmatrix}=\begin{vmatrix}a_{11} & a_{21} & \cdots & a_{n1} \\a_{12} & a_{22} & \cdots & a_{n2} \\\vdots & \vdots & \ddots & \vdots \\a_{1n} & a_{2n} & \cdots & a_{nn}\\\end{vmatrix}$$二、行列式的求解方法2.1 按定义计算法按照上述定义,计算行列式涉及到全排列的遍历与逆序数的计算,这种方法虽然理论上可行,但计算量较大,不适用于较大的矩阵。
2.2 行列式的性质与计算

a n1
an 2 ann
a n1
an 2 ann
10
a11
a12 an 2 a12 a1n bi 2
a1n
性质5 bi 1 ci 1
an1 a11 bi 1 an1
bi 2 ci 2 bin cin a11 an1 ann a12 a1n ci 2 cin
例9 证明范德蒙行列式(n≥2).
1 x1
2 Vn x1
1 x2
2 x2
1 x3
2 x3
1 xn
2 xn ( xi x j ),
n x1 1
n x 2 1
1 j i n
n n x 3 1 x n 1
证 n = 2:
1 x1
1 x2
x2 x1 , 结论成立.
2r1 r2 r1 r3
1
2
3
0 2 3 0 1 2
1 r2 r3 2
1
2
3 3 1 1 2
0 2 0 0
21
x
y x y
y y x
y x y
y y x
例7 计算 Dn
y y
.
x ( n 1) y
y y x
9
性质4 行列式中如果有两行(列)元素成比例,
则此行列式为零.
a11 ai 1
a12 a1n ai 2 ain
a11 ai 1
a12 a1 n ai 2 ain
k 0 ai 1 ai 2 ain kai 1 kai 2 kain
行列式的展开定理

Dn (a b) Dn 1 abDn 2 Dn aDn 1 b( Dn 1 aDn 2 ) b 2 ( Dn2 aDn3 )
b n2 ( D2 aD1 ) b n2 ((a b) 2 ab a(a b)) Dn aDn1 b n Dn bDn1 a n
行列式的展开定理
n阶行列式的性质
性质1.1 行列式与它的转置行列式相等. 性质1.2 交换行列式的两行(或两列)的位置, 则行列式的绝对值 不变而符号改变. 推论1.1 如果一个行列式的两行(或两列)完全相同, 则这个行列 式等于零. 性质1.3. 把一个行列式的某一行(列)的所有元素乘以同一个数 k, 等于用k乘这个行列式. 推论 一个行列式中某一行(列)中所有元素的公因子可以提到 行列式符号的外边. 推论1.2 如果一个行列式有两行(列)的对应元素成比例, 那么这 个行列式等于零.
在计算数字行列式时,直接应用行列式展开公式并不一定 简化计算,因为把一个n阶行列式换成n个(n-1)阶行列 式的计算并不减少计算量,只是在行列式中某一行或某一 列含有较多的零时,应用展开定理才有意义。但展开定理 在理论上是重要的。
利用行列式按行按列展开定理,并结先用行列式的性质将某
3 5 3
例1 计算行列式
D 0 7
1 0 7 2
解
按第一行展开,得
D 3 1 0 7 2 5 0 0 7 2 3 0 1 7 7
27.
例2.计算 x 0 D y y x 0 y x 0 y x 0 0 y x
0
解:按第一列展开,得 D
0
行列式有两行 相同,值为0
综上,得公式
ai1 Aj1 ai 2 Aj 2 ain Ajn
行列式计算法则

行列式计算法则行列式是线性代数中一个重要的概念,它在矩阵和向量运算中起着重要的作用。
在本文中,我们将讨论行列式的计算法则,包括展开定理、性质和应用。
1. 展开定理行列式的展开定理是计算行列式的重要方法之一。
对于一个n 阶行列式A,可以通过展开定理将其转化为n-1阶行列式的和的形式。
展开定理的具体形式如下:\[|A| = \sum_{i=1}^{n}(-1)^{i+j}a_{ij}M_{ij}\]其中,\(a_{ij}\)表示矩阵A的第i行第j列的元素,\(M_{ij}\)表示剩余元素构成的n-1阶行列式,\(i\)和\(j\)分别表示所选取的行和列。
通过展开定理,可以将一个n阶行列式转化为n-1阶行列式的和的形式,从而简化行列式的计算过程。
2. 性质行列式具有许多重要的性质,这些性质对于行列式的计算和应用都具有重要的意义。
其中一些重要的性质包括:- 交换性质:行列式中交换两行(列)的位置,行列式的值相反。
- 线性性质:如果行列式的某一行(列)可以表示为两个向量的线性组合,那么该行列式可以表示为两个行列式的和。
- 数乘性质:如果行列式的某一行(列)所有元素都乘以一个数k,那么行列式的值也乘以k。
这些性质为行列式的计算提供了重要的理论基础,同时也为行列式的应用提供了便利。
3. 应用行列式在线性代数和相关领域中有着广泛的应用。
其中一些重要的应用包括:- 线性方程组的求解:通过行列式的方法可以求解线性方程组的解,特别是对于n阶线性方程组,行列式的方法是一种重要的求解手段。
- 矩阵的求逆:矩阵的逆可以通过行列式的方法求解,行列式为0的矩阵没有逆矩阵,而非零行列式的矩阵存在逆矩阵。
- 线性变换的性质:行列式可以用来判断线性变换是否保持了面积或体积的性质,从而对线性变换的性质进行分析。
通过行列式的计算和应用,我们可以更好地理解线性代数中的重要概念,同时也可以解决实际问题中的相关计算和分析。
总结行列式是线性代数中的重要概念,它通过展开定理、性质和应用为线性代数和相关领域的计算和分析提供了重要的方法和工具。
§2 行列式的性质与计算

j (1) ( j j j ) a1 j (aij j j
1 2 n 1 1 2 n
i
biji ) anjn
a11 a12 a1n a11 a12 a1n ( 1) ( j j j ) a1 j aij anj j j j ai 1 ai 2 ain bi 1 bi 2 bin ( j j j ) ( 1) a1 j bij anj j j j an1 an 2 ann an1 an 2 ann
a1 p1 aip j a jpi anpn
p p (1) p p
( p1 p j pi pn )
D
§2 行列式的性质与计算
推论1 如果行列式中有两行(列)相同,那么
该行列式为零. 比如:
1 2 3 1 2 3 4 5 6
r1 r2
1 2 3 1 2 3 4 ห้องสมุดไป่ตู้ 6
3、再用同样的方法处理除去第一行和第一列后余下 的低一阶行列式; 4、如此继续下去,直至使它成为上三角形行列式, 这时主对角线上元素的乘积就是所求行列式的值.
§2 行列式的性质与计算
二、应用举例
例1. 计算行列式
0 1 D 1 2 2 2 0 0
1 1 2 1
1 0 1 1
2 2 0 0 1 1 1 3 0 1 1 1 2 2 2 4
§2 行列式的性质与计算
a b c d a ab abc abcd r3 r2 ( 1) 0 a 2a b 3a 2b c 0 a 3a b 6a 3b c
a 0 r2 r1 ( 1) 0 0
a r4 r3 ( 1) 0 0 0
第二讲行列式的性质与行列式按行按列展开

§1.4行列式的性质1、转置行列式:记 22212221212111212222111211,a a a a a a a a a D a a a a a a a a a D n n n n T nnn n n n ⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅⋅⋅= 行列式T D 称为行列式D 的转置行列式。
2、性质1 :行列式与它的转置行列式相等 利用定义即可证明3、性质2: 互换行列式的两行(列),行列式反号nk i n k i nnj kj ij j j j j j j j j nnn n kn k k ini i n a a a a a a a a a a a a a a a a11211)(21212111211)1(τ∑-=将第i 行与第k 行交换,则ni k n i k nnj ij kj j j j j j j j j nnn n ini i kn k k na a a a a a a a a a a a a a a a11211)(21212111211)1(τ∑-=其中列标进行了一次对换,所以添加了一个负号,即可证明 推论:如果行列式有两行(列)完全相同,则此行列式等于零 证 把这两行互换,有D D -=,故0=D4、性质3 :行列式的某一行(列)中所有元素都乘以同一数k ,等于用数k 乘此行列式。
可用定义证明推论1:行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面。
推论2: 行列式中如果有两行(列)元素成比例,则此行列式等于零。
5、性质4: 若行列式中某一行(列)的元素ij a 都可以分解为两个数ij b 和ij c 之和,即)2,1,(n j i c b a ij ij ij ⋅⋅⋅=+=,则此行列式也可以分解为两个行列式的和 利用定义证明6、性质5: 把行列式的某一行(列)的个元素乘以同一数然后加到另一行(列)对应的元素上去,行列式不变。
可由性质4与性质3的推论证得例1: 计算3331110243152113-----=D解:4072160648011202131721601120648021313315112043512131321412215=-----==------==-------==↔+-↔r r r r r r c c D§1.5 行列式按行(列)展开先引进余子式和代数余子式的概念1、定义: 在n 阶行列式中,把元素ij a 所在的第i 行和第j 列划去后,剩下的元素按原来顺序不变构成的1-n 阶行列式叫做元素ij a 的余子式,记作ij M ;记ij ij j i ij A M A ,)1(+-=为元素ij a 的代数余子式。
行列式的性质与计算
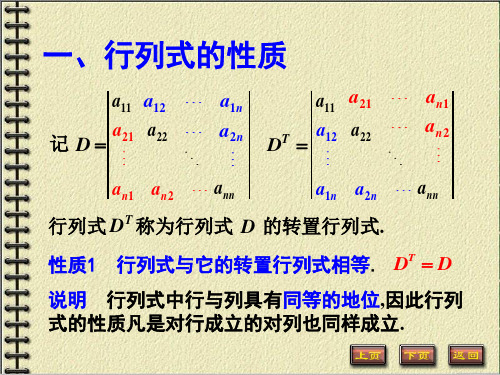
1b bb
a (n 1)b
ab
ab 0
0 ab
a (n 1)b(a b)n1.
a0 1 1
1
1 a1 0
0
例 求行列式的值 D 1 0 a2
0
100
an
解
D
c1
(
1 a1
)c2
(
1 an
)cn1
a0
1 a1
0
0
0
1 an
1 a1 0
0
1 0 a2
0
1 0 0
an
(a0
3
2 2
0 0 0 1 0 0 0 2 2 2
1 1 2 3 1
0 2 1 5 3 r5 2r3 0 0 1 1 2
0 0 0 1 0 4
0 0 0 4 6
1 1 2 3 1
0 2 1 5 3
r5 4r4 0 0 1 1 2 2 1 6 12.
0 0 0 1 0
0 0 0 0 6
ni j1
x1n1 x2n1 xnn1
证 用数学归纳法
1 D2 x1
1
x2
x2 x1
( xi x j ),
2i j1
当 n 2 时(1)式成立.
假设(1)对于 n 1 阶范德蒙德行列式成立,
11
1
x1 x2
xn
Dn x12
x22
xn2
x x n1
n1
1
2
x n1 n
rn ( x1 )rn1 1 rn1 ( x1 )rn2 0
1 16 81 256 625
解 D5 是 5 阶范德蒙行列式
D5
(xi xj )
行列式性质,按行展开

a11 L = bi 1 L an1
a12 L a1n L L L
a11
a12 L a1n L ci 2 L an 2 L L L L L cin L ann
L bi 2 L bin + ci 1 L L L L an1 an 2 L ann
性质5 将行列式的某一行 列)的所有元素乘以数 后 将行列式的某一行(列 的所有元素乘以数 的所有元素乘以数k后
1
2 0
3 1
4 2 .
【例1】 计算 D = 】
1
3 −1 −1 0 1 2 0 −5
【解】 D = a14 A14 + a24 A24 + a34 A34 + a44 A44
1 2 3 1 0 1 1+ 4 + 2 × ( −1) 2 + 4 3 − 1 − 1 = 4 × ( −1) 3 − 1 − 1 1 2 0 1 2 0 1 2 3 + ( −5) × ( −1)4 + 4 1 0 1 3 −1 −1
【解】
1 −1 0
2
1
1
0
(1) + (3) 0 −1 −1 2 0 −1 −1 2 − D=− − 2×(1) + (4) 0 1 −1 2 −1 2 −1 0 0 3 1 −4
2 1 1 0
1 0
0 0
2
1
−1
0
2
( 2) + ( 3 ) 3 × ( 2) + ( 4) −
−1 −1
0 0
0 −1
加到另一行( 加到另一行(列)的相应元素上,行列式的值不变. 的相应元素上,行列式的值不变
1 a 1
行列式的性质和计算

i+ j
4 0 0 1 4 0 0 2 1 3 1 = 22 1 3 = 2×4 1 3 D= 4 3 0 0 0 2 7 4 3 7 4 3 2
= 2×4 ×(15)
例 计算 解
a11 a12 a1n a22 a2n Dn = 0 a1,n1 a2,n1 ann
Dn = ann
证
不可逆时: 当A不可逆时 设 不可逆时
初等行变换 A R(最后一行的元全为零) →
即存在初等矩阵 E1, E2, ..., Et, A = E1E2 Et R
det R = 0 det A = (det E1 )(det Et )(det R) = 0.
不可逆 又A不可逆 AT不可逆 不可逆 所以 det AT = 0.
2 A ≠ 2A
k An×n = k A ≠ k A .
n
初等矩阵与任一方阵A乘积的行列式: 初等矩阵与任一方阵 乘积的行列式: 乘积的行列式
det(Eij A) = det A = (det Eij )(det A), det(Ei (c) A) = c(det A) = (det Ei (c))(det A),
det(Eij (c) A) =det A = (det Eij (c))(det A).
对任一初等矩阵 E , det( EA ) = (det E )(det A )
设E1 , E2 ,, Et为初等矩阵,则 为初等矩阵, det( E1 E2 Et A) = (det E1 )(det Et )(det A)
1 7 5 r3 + ( 3 )r1 0 10 3 0 15 5 1 7 5 r3 + 3 r3 0 5 2 0 0 1
1 r2 r3 0
第二节 行列式的基本性质与计算

a j1
a j1 a jn
ai1
an1 ann
an1
注: 换行: ri rj; 换列: ci c j .
a1n a jn . ain ann
例如:
x1 y1 z1
z1
x2 y2 z2 c1 c3 z2
x3 y3 z3
z3
y1 x1 y2 x2 . y3 x3
4
返回
又如:
1 0 0 0 1
1 4 1 1 1 1 1
a i1 xi a x1 a x2 a x3 a x4 a
0
1000
a(x1 a)(x2 a)(x3 a)(x4 a) 0
0100
0
0010
028
0 0 0 1返回
1 4 1
a( x1
a)(x2
a)(x3
a)(x4
a)( a
i 1
j 1
n
n
(1)1 jb1 j M1 j (1)1 jc1 j M1 j
j 1
j 1
9
返回
b11 b12 b1n c11 c12 c1n
a21
a22
a2n a21
a22
a2n
an1 an2 ann an1 an2 ann
当i>1时,把第i行与第一行i 互换,再按上面的方法 把行列式拆成两个行列式之和,然后再把这两个行 列式的第i行与第一行互换即可.
bi 2
bin
ci1
ci 2
an1 an2 ann
an1 an2
8
a1n a2n cin ann
返回
证明:当 i=1时,由行列式的定义知
b11 c11 b12 c12 b1n c1n
高考数学知识点解析行列式的性质与计算

高考数学知识点解析行列式的性质与计算高考数学知识点解析:行列式的性质与计算在高考数学中,行列式是一个重要的知识点,它在解决线性方程组、向量的叉积等问题中发挥着关键作用。
接下来,咱们就一起深入探讨行列式的性质与计算方法,帮助同学们更好地掌握这一知识点。
一、行列式的定义首先,咱们来了解一下行列式的定义。
对于一个二阶行列式,它的形式是:\\begin{vmatrix}a_{11} & a_{12} \\a_{21} & a_{22}\end{vmatrix} = a_{11}a_{22} a_{12}a_{21}\对于一个三阶行列式,其形式为:\\begin{vmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{vmatrix} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} +a_{13}a_{21}a_{32} a_{13}a_{22}a_{31} a_{12}a_{21}a_{33}a_{11}a_{23}a_{32}\从二阶和三阶行列式的定义,我们可以推广到更高阶的行列式。
二、行列式的性质1、行列式与它的转置行列式相等。
所谓转置行列式,就是将原行列式的行与列互换得到的新行列式。
例如,二阶行列式:\\begin{vmatrix}a &b \\c & d\end{vmatrix}\它的转置行列式为:\\begin{vmatrix}a & c \\b & d\end{vmatrix}\这两个行列式的值是相等的。
2、互换行列式的两行(列),行列式的值变号。
比如对于二阶行列式:\\begin{vmatrix}a &b \\c & d\end{vmatrix}\如果将第一行和第二行互换,得到:\\begin{vmatrix}c &d \\a & b\end{vmatrix}\那么这个新行列式的值是原行列式值的相反数。
2.行列式的性质和展开

ain a jn ain ann
ain ain 0 ain ann
推论 如果行列式中两行(列)相同,则行列式值为0,即:
性质4 行列式的某一行(列)中所有的元素都乘 以同一数 k 等于用数k乘此行列式,即:
a12 ai 2 ai 2 an 2
ain ain a jn ann
ain ain ain ann
a11 a j1 ai1 an1
a11 ai1 ai1 an1
a12 a j2 ai 2 an 2
ai1 bi1 ai 2 bi 2 ain bin ai1 ai 2 ain bi1 bi 2 bin
性质3 互换行列式的两行(列) 则行列式变号即
a11 ai1 a j1 an1
a11 ai1 ai1 an1
a12 ai 2 a j2 an 2
a b 0 例3 a b满足什么条件时有 b a 0 0 ? 1 0 1 解 a b 0 b a 0 a2b2 1 0 1
若要a2b20 则a与b须同时等于零 因此当a0且b0时 给定的行列式等于零
r4r3 r3r2 解 D r2r1 a b c d abc 0 a ab 0 a 2ab 3a2bc 0 a 3ab 6a3bc r4r3 a b c d r3r2 0 a ab abc 0 0 a 2ab 0 0 a 3ab a b c d r4r3 0 a ab abc a4 0 0 a 2ab 0 0 0 a
性质4行列式的某一行列中所有的元素都乘以同一数推论如果行列式中有两行列成比例则行列式值为0性质5把行列式的某一行列的各元素乘以同一数然后加到另一行列对应的元素上去行列式不变a是任意的n阶矩阵对于n阶的初等阵e有deteadetedeta以及detaedetadete推论利用上述的性质和推论结合特殊类型的行列式的结果可以计算一般的行列式
行列式展开定理

行列式展开定理行列式展开定理是线性代数中的一个重要定理,它描述了一个n阶行列式可通过对其中一行(或一列)进行展开,用余子式乘以对应元素的代数余子式构成的和来表示。
这个定理的证明主要基于数学归纳法和代数性质的运用。
首先,我们来介绍一些必要的定义和概念。
行列式是一个有序数表,是一个正方形矩阵中对角线上元素相乘并按照一定规则相加得到的一个数。
例如,对于一个2阶行列式(2x2矩阵):$\begin{vmatrix}a &b \\c & d\\\end{vmatrix}$ = ad - bc行列式的计算可以通过对行或列的操作转化为三角形矩阵,从而简化计算。
对于n阶行列式,可以递归地进行以下展开运算:选择第i行(或第j列)进行展开,将此行的元素乘以对应的代数余子式,并进行符号调整后相加。
具体地,使用数学归纳法,我们可以证明行列式展开定理。
当n=2时,定理显然成立。
假设当n=k时,定理成立,即k阶行列式可以通过任选一行(或一列)展开为余子式乘以对应元素的代数余子式之和,即$\begin{vmatrix}a_{11} & a_{12} & \ldots & a_{1k} \\a_{21} & a_{22} & \ldots & a_{2k}\\\vdots & \vdots & \ldots & \vdots\\a_{k1} & a_{k2} & \ldots & a_{kk}\\\end{vmatrix}$=$a_{i1}\begin{vmatrix}a_{11} & \ldots & a_{1,i-1} & a_{1,i+1} & \ldots &a_{1k} \\\ldots & \ldots & \ldots & \ldots & \ldots & \ldots\\ a_{k1} & \ldots & a_{k,i-1} & a_{k,i+1} & \ldots &a_{kk}\\\end{vmatrix}$+(-1)^(i+1)$a_{i2}\begin{vmatrix}a_{11} & \ldots & a_{1,i-1} & a_{1,i+1} & \ldots &a_{1k} \\\ldots & \ldots & \ldots & \ldots & \ldots & \ldots\\ a_{k1} & \ldots & a_{k,i-1} & a_{k,i+1} & \ldots &a_{kk}\\\end{vmatrix}$+$\ldots$+(-1)^(i+k)$a_{ik}\begin{vmatrix}a_{11} & \ldots & a_{1,i-1} & a_{1,i+1} & \ldots &a_{1k} \\\ldots & \ldots & \ldots & \ldots & \ldots & \ldots\\ a_{k1} & \ldots & a_{k,i-1} & a_{k,i+1} & \ldots &a_{kk}\\\end{vmatrix}$。
《行列式展开定理》课件

行列式展开定理
总结词
外代数中的行列式展开定理是行列式理论的一个重要推广,它涉及到更广泛的代数结构 ,包括向量空间、线性变换和矩阵等。
详细描述
在外代数中,行列式展开定理表述为在任意维度的向量空间中,任意线性变换的行列式 值等于其各个特征值的乘积。这个定理在向量空间和线性变换的研究中具有重要意义,
因为它提供了一种计算行列式值的方法,并且有助于理解线性变换的性质和行为。
多线性代数中的行列式展开定理
总结词
多线性代数中的行列式展开定理是针对 高阶矩阵和多线性映射的行列式值的计 算。
VS
详细描述
在多线性代数中,行列式展开定理表述为 对于一个给定的n阶矩阵A,其行列式值 可以通过对A的每个元素进行求和得到。 这个定理在研究高阶矩阵和多线性映射时 非常有用,因为它提供了一种计算高阶矩 阵行列式值的方法。
《行列式展开定理》ppt课 件
目录
• 行列式展开定理的概述 • 行列式展开定理的证明 • 行列式展开定理的应用 • 行列式展开定理的推广 • 行列式展开定理的习题与解析
01 行列式展开定理 的概述
定义与性质
定义
行列式展开定理是线性代数中的基本 定理之一,它描述了行列式与矩阵元 素之间的关系。
性质
计算多元函数的偏导数
行列式展开定理可以用于计算多元函数的偏导数,通过偏导数的定 义和行列式展开定理,可以方便地计算出偏导数值。
求解多元函数的极值
通过行列式展开定理,可以求解多元函数的极值,利用极值的必要 条件和行列式展开定理,可以找到函数的极值点。
计算高阶导数
利用行列式展开定理,可以方便地计算高阶导数,从而求解一些复 杂的高阶微分方程。
非交换代数中的行列式展开定理
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 0
L a11a22 L ann .
an1 an2 L ann
特别的,
对角行列式
1 2
O
12 L n .
n
第二节 行列式的性质
一、行列式的性质 二、应用举例 三、小结
一、行列式的性质
改变书写方向
记
a11 a12 a1n
a11 a21 an1
D a21 a22
记作 D a21 a22 L a2n
MM
M
an1 an2 L ann 简记作 det(aij ). 数 aij 称为行列式det(aij ) 的元素.
上三角行列式
a11 a12 L a1n 0 a22 L a2n LLLLLLL
a11a22 L ann .
0 0 L ann
a11 0 L 下三角行列式 a21 a22 L
由行列式定义
DT
(1) b b b ( j1 j2 jn )
1 j1 2 j2
njn
j1 j2 jn
(1) ( j1 j2
a a jn ) j1 1 j2 2
a jnn
D
j1 j2 jn
说明:行列式中行与列地位相同,对行成立的性质
对列也成立,反之亦然。
性质2 互换行列式的两行(列),行列式变号.
奇偶性相反,所以项(1)与项(3)相差一符号,这就证明
了D的任一项的反号是 D1 中的项,同样可以证明 D1 中的
任一项的反号也是D中的项。
因此,D=-D1
记法 行列式的第s行: rs 行列式的第s列: c s
交换s、t两行: rs rt 交换s、t两列: cs ct
例如 1 7 5 1 7 5 6 6 2 3 5 8, 358 662
atn s行
as1 as2 asn t行
an1 an2 ann
由行列式定义可知,D中任一项可以写成
(1) a a a a ( j1 js jt jn ) 1 j1
sjs
tjt
njn (1)
因为
a1 j1 asjs atjt anjn a1 j1 atjt asjs an(jn 2)
an1 an2 L ann
an1 an2 L ann
a11 a12 a13
6a11
Ex.1设 a21 a22 a23 1, 求 3a21
a31 a32 a33
3a31
解 利用行列式性质, 有
2a12 a22 a32
10a13 5a23 . 5a33
6a11 3a21 3a31
a11 a12 L a1n LLLLLLL
kai1 kai2 L kain k ai1 ai 2 L ain
LLLLLLL
LLLLLLL
an1 an2 L ann
an1 an2 L ann
推论 行列式的某一行(列)中所有元素的公因 子可以提到行列式符号的外面.
性质4 行列式中如果有两行(列)元素成比 例,则此行列式为零.
1 b b b 1 a b b
a (n 1)b 1 b a b
1 b b a
1b b b
ab
a (n 1)b
0 a b
a (n 1)b(a b)n1.
0 ab
三、小结
行列式的性质 (行列式中行与列具有同 等的地位,行列式的性质凡是对行成立的对列也 同样成立).
1 15 1 2 5 0 3 7 0 2 7 .
2 11 2 2 1
性质6 把行列式的某一列(行)的各元素乘以 同一数然后加到另一列(行)对应的元素上去,行 列式不变.
例如
a11 a1i a1 j a1n
a21
a2i
k
a2 j
a2 j
an1 ani anj anj
显然这是 D1 中取自不同行、不同列的n个元素的乘积,而且
(2)式右端的n个元素是按它们在 D1 中所处的行标为自然顺序
排好的。因此
(1) a a a a ( j1 jt js jn )
1 j1
tjt
sjs
njn
是 D1 中的一项。
(3)
因为,排列 j1 js jt jn 与排列 j1 jt js jn 的
a13a22a31 a11a23a32 a12a21a33 .
证明:
a11 a12 a1n
D a21 a22 a2n
an1 an2 ann
b11 b12 b1n 设 DT b21 b22 b2n
bn1 bn2 bnn
则 bij a ji (i, j 1,2, , n)
a11 a12 a13 a11 a12 a13 a11 a12 D1 a31 a32 a33 a31 a32 a33 a31 a32
a21 a22 a23 a21 a22 a23 a21 a22
a11a32a23 a12a33a21 a13a31a22 a13a32a21 a11a33a22 a12a31a23
交换2,3行
a11 a12 a13
a11 a12 a13
D a21 a22 a23 D1 a31 a32 a33
a31 a32 a33
a21 a22 a23
a11 a12 a13
D a a a a11a22a33 a12a23a31 a13a21a32
21
22
23
a a a 31
a31 a32 a33
a13a22a31 a12a21a33 a11a23a32 .
a11 a21 a31 a11 a21 a31 a11 a21 DT a12 a22 a32 a12 a22 a32 a12 a22
a13 a23 a33 a13 a23 a33 a13 a23
a11a22a33 a13a21a32 a12a23a31
计算行列式常用方法:(1)利用定义;(2)利用 性质把行列式化为上三角形行列式,从而算得行 列式的值.
1234 Ex1.
1 2 3 4 1
3412 4123
0111
2 1 0 1 1
1101 1110
1234
12 3 4
1 2
3
4
1
1 10
3
4
1
3412
14 1 2
4123
11 23
D
性质2 互换行列式的两行(列),行列式变号.
证明:a11 a12 a1n
as1 as2 asn
设 D 交换s、t 两行,得
at1 at 2 atn
a11 a12 a1n
an1
an2
ann
at1 D1
at 2
1 r1 r2 r3 r4 1
6 3
6 1
6 1
1131
1131
1113
1113
1 1 1 1 r2 r1 1 1 1 1
r1 6 1 3 1 1 r3 r1 0 2 0 0
6
6
1 1 3 1 r4 r1 0 0 2 0
1113
0002
48.
例2 计算行列式
abbb babb D bbab bbba
32
33 a13a22a31 a12a21a33 a11a23a32 .
a11 a12 a13
D a a a a11a22a33 a12a23a31 a13a21a32
21
22
23
a a a 31
32
33 a13a22a31 a12a21a33 a11a23a32 .
例如
3 2 1
D 1 1 2 8
2 1 1
2c2 c1
7 2 1
1 1 2 8
0 1 1
二、应用举例
计算行列式常用方法:利用运算 ri krj把行列式 化为上三角形行列式,从而算得行列式的值.
3111
1311
例1
D
1131
1113
解
3 1 D
1 3
1 1
1
6
解 将第2,3,4列都加到第1列得
a 3b b b b
D a 3b a b b a 3b b a b
a 3b b b a
1bbb
1b b b
a 3b 1
1
a b
b a
b b
a
3b
0 0
ab 0
0 ab
0 0
1bba
0 0 0 ab
a 3b(a b)3.
1 2 (3 4) 7
例如
6 3 (5 2) 8
D 5
9
6 1
5
4 2 (4 8) 6
则D等于下列两个行列式之和:
1237 1247
6358 6328
D
5965 5915
4246 4286
性质5动画演示
例 1 1 2 5 1 1 2 5 0 3 2 7 0 3 (2) 7 2 1 2 1 2 1 ( 2) 1
证明 a11 a12 L a1n LLLLLLL ai1 ai 2 L ain LLLLLLL
a11 a12 L a1n LLLLLLL ai1 ai 2 L ain k L L L L L L L 0.
