三角形内外角平分线所成角的问题
【精选】八年级数学上册三角形解答题(篇)(Word版 含解析)

【精选】八年级数学上册三角形解答题(篇)(Word 版 含解析) 一、八年级数学三角形解答题压轴题(难)1.阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究一:如图1.在△ABC 中,已知O 是∠ABC 与∠ACB 的平分线BO 和CO 的交点,通过分析发现1902BOC A ︒∠=+∠.理由如下: ∵BO 和CO 分别是∠ABC 与∠ACB 的平分线,∴112ABC ∠=∠,122ACB ∠=∠; ∴()0011112()18090222ABC ACB A A ∠+∠=∠+∠=-∠=-∠, ∴11180(12)180909022BOC A A ︒︒︒︒⎛⎫∠=-∠+∠=--∠=+∠ ⎪⎝⎭(1)探究二:如图2中,已知O 是∠ABC 与外角∠ACD 的平分线BO 和CO 的交点,试分析∠BOC 与∠A 有怎样的关系?并说明理由.(2)探究二:如图3中,已知O 是外角∠DBC 与外角∠ECB 的平分线BO 和CO 的交点,试分析∠BOC 与∠A 有怎样的关系?【答案】(1)12BOC A ∠=∠,理由见解析;(2)1902BOC A ︒∠=-∠. 【解析】【分析】(1)根据角平分线的定义可得∠OBC =12∠ABC ,∠OCD =12∠ACD ,再根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义可得∠OCD =12∠ACD =12∠A +∠OBD ,∠BOC =∠OCD -∠OBC ,然后整理即可得解;(2)根据三角形的外角性质以及角平分线的定义表示出∠OBC 和∠OCB ,再根据三角形的内角和定理解答;【详解】(1)12BOC A ∠=∠,理由如下: ∵BO 和CO 分别是ABC ∠与ACD ∠的平分线,∴12OBD ABC ∠=∠,12OCD ACD ∠=∠, 又∵ACD ∠是ABC 的一个外角,∴1122OCD ACD A OBD ∠=∠=∠+∠, ∵OCD ∠是BOC 的一个外角, ∴1122BOC OCD OBD A OBD OBD A ∠=∠-∠=∠+∠-∠=∠ 即12BOC A ∠=∠ (2)∵BO 与CO 分别是∠CBD 与∠BCE 的平分线,∴∠OBC =12∠CBD ,∠OCB =12∠BCE 又∵∠CBD 与∠BCE 都是△ABC 的外角,∴∠CBD =∠A +∠ACB ,∠BCE =∠A +∠ABC ,∴∠OBC =12∠CBD =12(∠A +∠ACB ),∠OCB =12∠BCE =12(∠A +∠ABC ), ∴∠BOC =180°-(∠OBC +∠OCB )∴1902BOC A ︒∠=-∠ 【点睛】本题考查了三角形的外角性质,角平分线的定义,三角形的内角和定理,熟记性质并准确识图,整体思想的利用是解题的关键.2.如图①,在△ABC 中,CD 、CE 分别是△ABC 的高和角平分线,∠BAC =α,∠B =β(α>β).(1)若α=70°,β=40°,求∠DCE 的度数;(2)试用α、β的代数式表示∠DCE 的度数(直接写出结果);(3)如图②,若CE 是△ABC 外角∠ACF 的平分线,交BA 延长线于点E ,且α﹣β=30°,求∠DCE 的度数.【答案】(1)15°;(2)DCE 2αβ-∠=;(3)75°.【解析】 【分析】 (1)三角形的内角和是180°,已知∠BAC 与∠ABC 的度数,则可求出∠BAC 的度数,然后根据角平分线的性质求出∠BCE ,再利用三角形的一个外角等于和它不相邻的两个内角的和求出∠DEC 的度数,进而求出∠DCE 的度数;(2)∠DCE =2αβ- .(3)作∠ACB 的内角平分线CE′,根据角平分线的性质求出∠ECE′=∠ACE+∠ACE′=12∠ACB+12∠ACF=90°,进而求出∠DCE 的度数. 【详解】解:(1)因为∠ACB =180°﹣(∠BAC+∠B )=180°﹣(70°+40°)=70°,又因为CE 是∠ACB 的平分线, 所以1352ACE ACB ∠=∠=︒. 因为CD 是高线,所以∠ADC =90°,所以∠ACD =90°﹣∠BAC =20°, 所以∠DCE =∠ACE ﹣∠ACD =35°﹣20°=15°.(2)DCE 2αβ-∠=.(3)如图,作∠ACB 的内角平分线CE′,则152DCE αβ-'==︒∠.因为CE 是∠ACB 的外角平分线,所以∠ECE′=∠ACE+∠ACE′=11+22ACB ACF ∠∠=1(+)2ACB ACF ∠∠=90°, 所以∠DCE =90°﹣∠DCE′=90°﹣15°=75°.即∠DCE 的度数为75°.【点睛】本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.解决(3),作辅助线是关键.3.如图,四边形ABCD ,BE 、DF 分别平分四边形的外角∠MBC 和∠NDC ,若∠BAD=α,∠BCD=β(1)如图,若α+β=120°,求∠MBC+∠NDC的度数;(2)如图,若BE与DF相交于点G,∠BGD=30°,请写出α、β所满足的等量关系式;(3)如图,若α=β,判断BE、DF的位置关系,并说明理由.【答案】(1)120°;(2)β﹣α=60° 理由见解析;(3)平行,理由见解析.【解析】【分析】(1)利用四边形的内角和求出∠ABC与∠ADC的和,利用角平分线的定义以及α+β=120°推导即可;(2)由(1)得,∠MBC+∠NDC=α+β,利用角平分线的定义得∠CBG+∠CDG=12(α+β),在△BCD中利用三角形的内角和定理得∠BDC+∠CDB =180°﹣β,在△BDG中利用三角形的内角和定理得出关于α、β的等式整理即可得出结论;(3)延长BC交DF于H,由(1)得∠MBC+∠NDC=α+β,利用角平分线的定义得∠CBE+∠CDH=12(α+β),利用三角形的外角的性质得∠CDH=β﹣∠DHB,然后代入∠CBE+∠CDH=12(α+β)计算即可得出一组内错角相等.【详解】(1)解:(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,∴∠ABC+∠ADC=360°-(α+β),∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)=360°-[360°-(α+β)]=α+β,∵α+β=120°,∴∠MBC+∠NDC=120°;(2)β﹣α=60°理由:如图1,连接BD,由(1)得,∠MBC+∠NDC=α+β,∵BE、DF分别平分四边形的外角∠MBC和∠NDC,∴∠CBG=12∠MBC,∠CDG=12∠NDC,∴∠CBG+∠CDG=12∠MBC+12∠NDC=12(∠MBC+∠NDC)=12(α+β),在△BCD中,∠BDC+∠CDB=180°﹣∠BCD=180°﹣β,在△BDG中,∠GBD+∠GDB+∠BGD=180°,∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,∴12(α+β)+180°﹣β+30°=180°,∴β﹣α=60°,(3)平行,理由:如图2,延长BC交DF于H,由(1)有,∠MBC+∠NDC=α+β,∵BE、DF分别平分四边形的外角∠MBC和∠NDC,∴∠CBE=12∠MBC,∠CDH=12∠NDC,∴∠CBE+∠CDH=12∠MBC+12∠NDC=12(∠MBC+∠NDC)=12(α+β),∵∠BCD=∠CDH+∠DHB,∴∠CDH=∠BCD﹣∠DHB=β﹣∠DHB,∴∠CBE+β﹣∠DHB=12(α+β),∵α=β,∴∠CBE+β﹣∠DHB=12(β+β)=β,∴∠CBE=∠DHB,∴BE∥DF.【点睛】此题是三角形综合题,主要考查了平角的意义,四边形的内角和,三角形内角和,三角形的外角的性质,角平分线的意义,用整体代换的思想是解本题的关键,整体思想是初中阶段的一种重要思想,要多加强训练.4.如图1,在△ABC中,∠B=90°,分别作其内角∠ACB与外角∠DAC的平分线,且两条角平分线所在的直线交于点E.(1)∠E= °;(2)分别作∠EAB与∠ECB的平分线,且两条角平分线交于点F.①依题意在图1中补全图形;②求∠AFC的度数;(3)在(2)的条件下,射线FM在∠AFC的内部且∠AFM=∠AFC,设EC与AB的交点为H,射线HN在∠AHC的内部且∠AHN=∠AHC,射线HN与FM交于点P,若∠FAH,∠FPH和∠FCH满足的数量关系为∠FCH=m∠FAH+n∠FPH,请直接写出m,n的值.【答案】(1)45;(2)67.5°;(3)m=2,n=﹣3.【解析】【分析】(1)根据角平分线的定义可得∠CAF=12∠DAC,∠ACE=12∠ACB,设∠CAF=x,∠ACE=y,根据已知可推导得出x﹣y=45,再根据三角形外角的性质即可求得答案;(2)①根据角平分线的尺规作图的方法作出图形即可;②如图2,由CF平分∠ECB可得∠ECF=12y,再根据∠E+∠EAF=∠F+∠ECF以及∠E+∠EAB=∠B+∠ECB,可推导得出45°+452y+=∠F+12y,由此即可求得答案;(3)如图3,设∠FAH=α,根据AF平分∠EAB可得∠FAH=∠EAF=α,根据已知可推导得出∠FCH=α﹣22.5①,α+22.5=30+23∠FCH+∠FPH②,由此可得∠FPH=22.53α+,再根据∠FCH=m∠FAH+n∠FPH,即可求得答案.【详解】(1)如图1,∵EA平分∠DAC,EC平分∠ACB,∴∠CAF=12∠DAC,∠ACE=12∠ACB,设∠CAF=x,∠ACE=y,∵∠B=90°,∴∠ACB+∠BAC=90°,∴2y+180﹣2x=90,x﹣y=45,∵∠CAF=∠E+∠ACE,∴∠E=∠CAF﹣∠ACE=x﹣y=45°,故答案为:45;(2)①如图2所示,②如图2,∵CF平分∠ECB,∴∠ECF=12 y,∵∠E+∠EAF=∠F+∠ECF,∴45°+∠EAF=∠F+12y ①,同理可得:∠E+∠EAB=∠B+∠ECB,∴45°+2∠EAF=90°+y,∴∠EAF=452y+②,把②代入①得:45°+452y+=∠F+12y,∴∠F=67.5°,即∠AFC=67.5°;(3)如图3,设∠FAH=α,∵AF平分∠EAB,∴∠FAH=∠EAF=α,∵∠AFM=13∠AFC=13×67.5°=22.5°,∵∠E+∠EAF=∠AFC+∠FCH,∴45+α=67.5+∠FCH,∴∠FCH=α﹣22.5①,∵∠AHN=13∠AHC=13(∠B+∠BCH)=13(90+2∠FCH)=30+23∠FCH,∵∠FAH+∠AFM=∠AHN+∠FPH,∴α+22.5=30+23∠FCH+∠FPH,②把①代入②得:∠FPH=22.53α+,∵∠FCH=m∠FAH+n∠FPH,α﹣22.5=mα+n22.5·3α+,解得:m=2,n=﹣3.【点睛】本题考查了三角形内角和定理、三角形外角的性质、基本作图——角平分线等,熟练掌握三角形内角和定理以及三角形外角的性质、结合图形进行求解是关键.5.操作示例:如图1,在△ABC中,AD为BC边上的中线,△ABD的面积记为S1,△ADC的面积记为S2.则S1=S2.解决问题:在图2中,点D、E分别是边AB、BC的中点,若△BDE的面积为2,则四边形ADEC的面积为 .拓展延伸:(1)如图3,在△ABC中,点D在边BC上,且BD=2CD,△ABD的面积记为S1,△ADC的面积记为S2.则S1与S2之间的数量关系为.(2)如图4,在△ABC中,点D、E分别在边AB、AC上,连接BE、CD交于点O,且BO=2EO,CO=DO,若△BOC的面积为3,则四边形ADOE的面积为 .【答案】解决问题:6;拓展延伸:(1)S1=2S2(2)10.5【解析】试题分析:解决问题:连接AE,根据操作示例得到S△ADE=S△BDE,S△ABE=S△AEC,从而得到结论;拓展延伸:(1)作△ABD的中线AE,则有BE=ED=DC,从而得到△ABE的面积=△AED的面积=△ADC的面积,由此即可得到结论;(2)连接AO.则可得到△BOD的面积=△BOC的面积,△AOC的面积=△AOD的面积,△EOC的面积=△BOC的面积的一半,△AOB的面积=2△AOE的面积.设△AOD的面积=a,△AOE的面积=b,则a+3=2b,a=b+1.5,求出a、b的值,即可得到结论.试题解析:解:解决问题连接AE.∵点D、E分别是边AB、BC的中点,∴S△ADE=S△BDE,S△ABE=S△AEC.∵S△BDE=2,∴S△ADE =2,∴S△ABE=S△AEC=4,∴四边形ADEC的面积=2+4=6.拓展延伸:解:(1)作△ABD的中线AE,则有BE=ED=DC,∴△ABE的面积=△AED的面积=△ADC的面积= S2,∴S1=2S2.(2)连接AO .∵CO =DO ,∴△BOD 的面积=△BOC 的面积=3,△AOC 的面积=△AOD 的面积.∵BO =2EO ,∴△EOC 的面积=△BOC 的面积的一半=1.5, △AOB 的面积=2△AOE 的面积.设△AOD 的面积=a ,△AOE 的面积=b ,则a +3=2b ,a =b +1.5,解得:a =6,b =4.5,∴四边形ADOE 的面积为=a +b =6+4.5=10.5.6.已知,在ABC 中,∠A =60°,(1)如图①,∠ABC 和∠ACB 的角平分线交于点O ,则∠BOC= ;(2)如图②,∠ABC 和∠ACB 的三等分线分别对应交于点O 1,O 2,则2_________BO C ∠=;(3)如图③,∠ABC 和∠ACB 的n 等分线分别对应交于点O 1,O 2,……,1n O -(内部有1n -个点),则1-∠=n BO C ;(4)如图③,∠ABC 和∠ACB 的n 等分线分别对应交于点O 1,O 2,……,1n O -,若190-∠=︒n BO C ,求n 的值.【答案】(1)120°;(2)100°;(3)60120+⎛⎫︒⎪⎝⎭n n ;(4)n=4 【解析】【分析】 (1)根据三角形的内角和定理即可求出∠ABC +∠ABC ,然后根据角平分线的定义即可求出∠OBC +∠OCB ,再根据三角形的内角和定理即可求出结论;(2)根据三角形的内角和定理即可求出∠ABC +∠ABC ,然后根据三等分线的定义即可求出∠O 2BC +∠O 2CB ,再根据三角形的内角和定理即可求出结论;(3)根据三角形的内角和定理即可求出∠ABC +∠ABC ,然后根据n 等分线的定义即可求出∠O n -1BC +∠O n -1CB ,再根据三角形的内角和定理即可求出结论;(4)根据(3)的结论列出方程即可求出结论.【详解】解:(1)∵在ABC 中,∠A =60°,∴∠ABC +∠ABC=180°-∠A=120°∵∠ABC 和∠ACB 的角平分线交于点O ,∴∠OBC=12∠ABC ,∠OCB=12∠ACB ∴∠OBC +∠OCB=12∠ABC +12∠ACB =12(∠ABC +∠ACB ) =60°∴∠BOC=180°-(∠OBC +∠OCB )=120°故答案为:120°.(2)∵在ABC 中,∠A =60°,∴∠ABC +∠ABC=180°-∠A=120°∵∠ABC 和∠ACB 的三等分线分别对应交于点O 1,O 2,∴∠O 2BC=23∠ABC ,∠O 2CB=23∠ACB ∴∠O 2BC +∠O 2CB=23∠ABC +23∠ACB =23(∠ABC +∠ACB ) =80°∴2∠=BO C 180°-(∠O 2BC +∠O 2CB )=100°故答案为:100°.(3)∵在ABC 中,∠A =60°,∴∠ABC +∠ABC=180°-∠A=120°∵∠ABC 和∠ACB 的n 等分线分别对应交于点O 1,O 2,……,1n O -∴∠O n -1BC=1n n -∠ABC ,∠O n -1CB=1n n-∠ACB ∴∠O n -1BC +∠O n -1CB=1n n -∠ABC +1n n -∠ACB =1n n-(∠ABC +∠ACB ) =120120-⎛⎫ ⎪⎝⎭n n ° ∴1-∠=n BO C 180°-(∠O 2BC +∠O 2CB )=60120+⎛⎫︒ ⎪⎝⎭n n 故答案为:60120+⎛⎫︒ ⎪⎝⎭n n(4)由(3)知:1-∠=n BO C 60120+⎛⎫︒ ⎪⎝⎭n n ∴6012090+=n n解得:n=4 经检验:n=4是原方程的解.【点睛】本题考查了n 等分线的定义和三角形的内角和定理,掌握n 等分线的定义和三角形的内角和定理是解决此题的关键.7.(1)如图①∠1+∠2与∠B +∠C 有什么关系?为什么?(2)把图①△ABC 沿DE 折叠,得到图②,填空:∠1+∠2_______∠B +∠C(填“>”“<”“=”),当∠A =40°时,∠B +∠C +∠1+∠2=______.(3)如图③,是由图①的△ABC 沿DE 折叠得到的,如果∠A =30°,则x +y =360°-(∠B +∠C +∠1+∠2)=360°- = ,猜想∠BDA +∠CEA 与∠A 的关系为【答案】见解析.【解析】【分析】试题分析:(1)根据三角形内角是180度可得出,∠1+∠2=∠B+∠C ;(2)△ABC 沿DE 折叠,∠1+∠2=∠B+∠C ,从而求出当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°,(3)根据以上计算可归纳出一般规律:∠BDA+∠CEA=2∠A .试题解析:解:(1)∠1+∠2 = ∠B+∠C ,理由如下:在△ADE 中,∠1+∠2 = 180°- ∠A在△ABC 中,∠B+∠C = 180°- ∠A∴ ∠1+∠2 = ∠B+∠C(2)∵∠1+∠2+∠BDE+∠CED=∠B+∠C+∠BDE+∠CED=360°,∴∠1+∠2=∠B+∠C ,当∠A=40°时,∠B+∠C+∠1+∠2=140×2=280°(3)如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°-300°=60°,所以∠BDA+∠CEA 与∠A 的关系为:∠BDA+∠CEA=2∠A.考点:1.翻折变换(折叠问题);2. 三角形内角和.【详解】 请在此输入详解! 8.如图,90CDE CED ∠+∠=︒,EM 平分CED ∠,并与CD 边交于点M .DN 平分CDE ∠,并与EM 交于点N .(1)依题意补全图形,并猜想EDN NED ∠+∠的度数等于 ;(2)证明以上结论.证明:∵ DN 平分CDE ∠,EM 平分CED ∠,∴ 12EDN CDE ∠=∠, NED ∠= .(理由: )∵ 90CDE CED ∠+∠=︒,∴EDN NED ∠+∠= ×(∠ +∠ )= ×90°= °.【答案】(1)45度;(2)1,2CED ∠ 角平分线的定义, 12 ,CDE,CED, 12, 45. 【解析】 试题分析:(1)按要求画∠CDE 的角平分线交ME 于点N ,根据题意易得∠EDN+∠NED=45°; (2)根据已有的证明过程添上相应空缺的部分即可;试题解析:(1)补充画图如下:猜想:∠EDN+∠NED 的度数=45°;(2)将证明过程补充完整如下:证明:∵ DN 平分CDE ∠,EM 平分CED ∠,∴ 12EDN CDE ∠=∠,NED ∠=12∠CED .(理由:角平分线的定义) ∵ 90CDE CED ∠+∠=︒, ∴EDN NED ∠+∠=12×(∠CDE+∠CED )= 12×90°=45°.故原空格处依次应填上:12∠CED 、角平分线的定义、CDE 、CED 、12和45.9.如图,在△ABC 中,AD ⊥BC ,AE 平分∠BAC .(1)若∠B =72°,∠C =30°,①求∠BAE 的度数;②求∠DAE 的度数;(2)探究:如果只知道∠B =∠C +42°,也能求出∠DAE 的度数吗?若能,请你写出求解过程;若不能,请说明理由.【答案】(1)①39°;②21°;(2)21°.【解析】【分析】()1①先根据三角形内角和定理计算出BAC 78∠=,然后根据角平分线定义得到1BAE BAC 392∠∠==;②根据垂直定义得到ADB 90∠=,则利用互余可计算出BAD 90B 18∠∠=-=,然后利用DAE BAE BAD ∠∠∠=-进行计算即可; ()2由B C BAC 180∠∠∠++=,B C 42∠∠=+可消去C ∠得到BAC 2222B ∠∠=-,则根据角平分线定义得到BAE 111B ∠∠=-,接着在ABD 中利用互余得BAD 90B ∠∠=-,然后利用DAE BAE BAD ∠∠∠=-进行计算即可得到DAE 21∠=.【详解】解:()1B C BAC 180∠∠∠++=①,BAC 180723078∠∴=--=,AE 平分BAC ∠,1BAE BAC 392∠∠∴==; AD BC ⊥②,ADB 90∠∴=,BAD 90B 18∠∠∴=-=,DAE BAE BAD 391821∠∠∠∴=-=-=;()2能.B C BAC 180∠∠∠++=,B C 42∠∠=+,C B 42∠∠∴=-,2B BAC 222∠∠∴+=,BAC 2222B ∠∠∴=-,AE 平分BAC ∠,BAE 111B ∠∠∴=-,在ABD 中,BAD 90B ∠∠=-,()()DAE BAE BAD 111B 90B 21∠∠∠∠∠∴=-=---=.【点睛】本题考查三角形内角和定理:三角形内角和是180.掌握角平分线和高的定义,熟练进行角度的运算.10.已知:如图,等边三角形ABD 与等边三角形ACE 具有公共顶点A ,连接CD ,BE ,交于点P .(1)观察度量,BPC ∠的度数为____.(直接写出结果)(2)若绕点A 将△ACE 旋转,使得180BAC ∠=︒,请你画出变化后的图形.(示意图)(3)在(2)的条件下,求出BPC ∠的度数.【答案】(1)120°;(2)作图见解析;(3)∠BPC =120°.【解析】分析:(1)∠BPC 的度数为120°,理由为:由△ABD 与△ACE 都是等边三角形,利用等边三角形的性质得到∠DAB=∠ABD=∠CAE=60°,AD=AB ,AC=AE ,利用等式的性质得到夹角相等,利用SAS 得出三角形DAC 与三角形BAE 全等,由全等三角形的对应角相等得到∠ADC=∠ABE ,利用外角性质,等量代换即可得到所求;(2)作出相应的图形,如图所示;(3)解法同(1),求出∠BPC 的度数即可.本题解析:(1)∠BPC的度数为120°,理由为:证明:∵△ABD与△ACE都是等边三角形,∴∠DAB=∠ABD=∠CAE=60°,AD=AB,AC=AE,∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,在△DAC与△BA E中,{AD ABDAC BAE AC AE=∠=∠=,∴△DAC≌△BAE(SAS),∴∠ADC=∠ABE,∵∠ADC+∠CDB=60°,∴∠ABE+∠CDB=60°,∴∠BPC=∠DBP+∠PDB=∠ABE+∠CDB+∠ABC=120°;(2)作出相应的图形,如图所示;(3)∵△ABD与△ACE都是等边三角形,∴∠ADB=∠BAD=∠ABD=∠CAE=60°,AD=AB,AC=AE,∴∠DAB+∠DAE=∠CAE+∠DAE,即∠DAC=∠BAE,在△DAC与△BAE中,{AD ABDAC BAC AC AE=∠=∠=,∴△DAC≌△BAE(SAS),∴∠ADC=∠ABE,∵∠ABE+∠DBP=60°,∴∠ADC+∠DBP=60°,∴∠BPC=∠BDP+∠PBD=∠ADC+∠DBP+∠ADB=120°.点睛:本题考查了等边三角形的性质,外角性质,以及全等三角形的判定与性质,熟练掌握等边三角形的性质是解本题的关键.。
三角形角平分线定理

三角形角平分线定理三角形角平分线定理是指:三角形内一条角的角平分线把这条角分成两个相等角,并且这条角平分线所在的边与三角形外一边的两个对边的比等于被分角的两边的比。
三角形角平分线定理是一个重要且有用的几何定理,它可以帮助我们推导解决许多与三角形相关的问题。
本文将详细介绍三角形角平分线定理以及其应用。
一、三角形角平分线定理的定义与性质三角形角平分线定理可以描述为:设三角形ABC中,AD是角BAC的角平分线,则有以下两个性质成立:1. 角BAD与角DAC的度数相等,即∠BAD = ∠DAC。
2. AB/BC = BD/DC。
角平分线的定义是指一条线段或射线从一个角的顶点出发,将该角分成两个相等的角。
根据角平分线的定义,我们可以得出性质1。
性质2则是说明了角平分线所在边与三角形外一边的两个对边的比例关系。
这个比例关系在解决一些三角形相关问题时非常有用,比如计算未知边长或角度大小等。
二、三角形角平分线定理的证明现在我们来证明三角形角平分线定理中的性质2。
首先,我们假设角BAD = α,角CAD = β,角DAC = α,角BDA = β。
根据正弦定理,我们可以得到以下两个等式:sinα/BD = sinβ/AB (1)sinα/DC = sinβ/AC (2)将(1)除以(2),可以得到:(AB/BD)/(AC/DC) = sinα/sinα = 1由于左边等式的分数形式是BD/DC的比,因此我们可以得出:AB/BC = BD/DC这就证明了三角形角平分线定理中的性质2。
三、三角形角平分线定理的应用三角形角平分线定理有着广泛的应用,特别是在解决与三角形相关的题目时,可以通过应用该定理得到简洁而准确的答案。
以下是三个典型的应用案例:1. 求角平分线所分角的大小已知三角形ABC中,BD为角BAC的角平分线,要求角BAD的大小。
根据三角形角平分线定理的性质1,我们知道角BAD与角DAC的大小相等,即∠BAD = ∠DAC。
部编数学八年级上册专题08内外角平分线问题(解析版)含答案

专题08 内外角平分线问题类型一一内一外求角1.如图∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE,CE交于点E.(1)求∠E的度数;(2)请猜想∠A与∠E之间的数量关系,不用说明理由.【答案】(1)∠E=20°;(2)∠A=2∠E.【解析】【分析】(1)根据角平分线的定义,三角形内角和定理,三角形外角的性质进行解答即可;(2)根据(1)中的推导过程进行推论即可.【详解】(1)∵BE平分∠ABC,CE平分∠ACD,∴∠ABC=2∠CBE,∠ACD=2∠DCE,由三角形的外角性质得,∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,∴∠A+∠ABC=2(∠E+∠CBE),∴∠A =2∠E ,∵∠A =40°,∴∠E =20°.(2)∠A =2∠E .理由如下:∵BE 平分∠ABC ,CE 平分∠ACD ,∴∠ABC =2∠CBE ,∠ACD =2∠DCE ,由三角形的外角性质得,∠ACD =∠A +∠ABC ,∠DCE =∠E +∠CBE ,∴∠A +∠ABC =2(∠E +∠CBE ),∴∠A =2∠E ,【点睛】本题考查了角平分线的定义,三角形内角和定理,三角形外角的性质,熟练掌握以上知识点是解本题的关键.2.如图,在△ABC 中,∠A =30°,E 为BC 延长线上一点,∠ABC 与∠ACE 的平分线相交于点D ,则∠D 等于( )A .10°B .15°C .20°D .30°【答案】B【解析】【分析】先根据角平分线的定义得到12Ð=Ð,34Ð=Ð,再根据三角形外角性质得1234A Ð+Ð=Ð+Ð+Ð,13D Ð=Ð+Ð,则2123A Ð=Ð+Ð,利用等式的性质得到12D A Ð=Ð,然后把A Ð的度数代入计算即可.【详解】解答:解:∵ABC Ð的平分线与ACE Ð的平分线交于点D ,∴12Ð=Ð,34Ð=Ð,∵ACE A ABCÐ=Ð+Ð,即1234A Ð+Ð=Ð+Ð+Ð,∴2123AÐ=Ð+Ð,∵13DÐ=Ð+Ð,∴11301522D AÐ=Ð=´°=°.故选:B.【点睛】本题考查了三角形内角和定理和三角形外角性质、角平分线的性质等,根据三角形内角和是180°和三角形外角性质进行分析是解题关键.3.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠BAC的度数是____________.【答案】80°.【解析】【详解】试题分析:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠PCD=∠P+∠PCB,根据角平分线的定义可得∠PCD=12∠ACD,∠PBC=12∠ABC,然后整理得到∠PCD=12∠A,再代入数据计算即可得解.在△ABC中,∠ACD=∠A+∠ABC,在△PBC中,∠PCD=∠P+∠PCB,∵PB、PC分别是∠ABC和∠ACD的平分线,∴∠PCD=12∠ACD,∠PBC=12∠ABC,∴∠P+∠PCB=12(∠A+∠ABC)=12∠A+12∠ABC=12∠A+∠PCB,∴∠PCD=12∠A,∴∠BPC=40°,∴∠A=2×40°=80°,即∠BAC=80°.考点:三角形内角和定理.4.如图△ABC,BD平分∠ABC且与△ABC的外角∠ACE的角平分线交于点D,若∠ABC=m°,∠ACB=n°,求∠D 的度数为()A.90°+12m°-12n°B.90°-12m°+12n°C.90°-12m°-12n°D.不能确定【答案】C【解析】【分析】由角平分线分别求出∠DBC和∠ACD,然后在△BCD中利用三角形内角和定理可求出∠D.【详解】∵BD平分∠ABC∴∠DBC=12∠ABC=12m°∵∠ACB=n°∴∠ACE=180°-n°又∵CD平分∠ACE∴∠ACD=12∠ACE=()111809022-=-o o o on n在△BCD中,∠DBC=12m°,∠BCD=∠ACB+∠ACD=1902+o o n,∴∠D=1111180DBC BCD=180********æö-Ð-Ð--+=--ç÷èøo o o o o o o o m n m n 故选C.【点睛】本题考查三角形中的角度计算,熟练运用三角形内角和定理是关键.5.如图,在ABC V 中,点D 在边BA 的延长线上,∠ABC 的平分线和∠DAC 的平分线相交于点M ,若∠BAC =80°,∠AB C =40°,则∠M 的大小为( )A .20°B .25°C .30°D .35°【答案】C【解析】【分析】先由80,BAC Ð=° 结合角平分线求解,,MAC MAB ÐÐ 再利用角平分线与40,ABC Ð=°求解ABM Ð,利用三角形的内角和定理可得答案.【详解】解:∵∠BAC=80°,∴100,DAC Ð=°AM Q 平分,DAC Ð150,2MAC DAC \Ð=Ð=° 130,BAM BAC MAC \Ð=Ð+Ð=°Q ∠ABC=40°,BM 平分ABC Ð,∴∠ABM=20°,∴∠M=1802013030,°-°-°=°故选:C .【点睛】本题考查了角平分线的性质,三角形的内角和定理,邻补角的定义,熟记定理和概念是解题的关键.6.如图,已知BD 为ABC V 中ABC Ð的平分线,CD 为ABC V 的外角ACE Ð的平分线,与BD 交于点D .若∠ABD =20°,50ACD Ð=°,则A D Ð+Ð=( )A .70°B .90°C .80°D .100°【答案】B【解析】【分析】根据角平分线定义求出∠DCE 、∠ACE 、∠DBC ,根据三角形外角性质求出∠A 、∠D ,即可求出答案.【详解】解:∵∠ABC 的平分线与∠ACB 的外角平分线交于D ,∠ABD =20°,∠ACD =55°,∴∠ABD =∠DBC =12∠ABC =20°,∠ACD =∠DCE =12∠ACE =50°,∴∠ABC =40°,∠ACE =100°,∴∠A =∠ACE -∠ABC =60°,∠D =∠DCE -∠DBC =50°-20°=30°,∴∠A +∠D =90°,故选:B .【点睛】本题考查了三角形的外角的性质,角平分线的性质,熟练掌握性质定理是解题的关键.7.如图所示,在Rt ABC △中,∠ACB=90°,∠CAB=60°,∠ACB 的角平分线与∠ABC 的外角平分线交于E 点,则∠AEB=( )A .50°B .45°C .40°D .35°【答案】B【解析】【分析】过点E 作ED BC ^,EH AB ^,EF AC ^,利用角平分线性质结合三角形内角和即可得出答案.【详解】解:如图所示,过点E 作ED BC ^,EH AB ^,EF AC ^,∴BE ,CE 是角平分线,∴ED EH =,ED EF =.∴EH EF =.∵EH AB ^,EF AC ^,∴AE 是BAF Ð的角平分线.∵60CAB Ð=°,∴30CBA Ð=°,60=°∠BAE ,∴75ABE Ð=°,由三角形内角和可得:45AEB Ð=°.故答案为:45.【点评】本题考查的知识点是角平分线性质,综合利用角平分线的性质是解此题的关键.8.如图,在△ABC 中,∠A =80°,∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1,∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得∠A 2,⋯,∠A 3BC 与∠A 3CD 的平分线相交于点A 4,得∠A 4,则∠A 4的度数为( )A .5°B .10°C .15°D .20°【答案】A【解析】【分析】根据角平分线的定义,三角形的外角性质及三角形的内角和定理可知11118022A A Ð=Ð=´°,212118022A A Ð=Ð=´°,¼,依此类推可知4A Ð的度数【详解】解:ABC ÐQ 与ACD Ð的平分线交于点1A ,11118022A ACD ACB ABC \Ð=°-Ð-Ð-Ð,11180()(180)22ABC A A ABC ABC =°-Ð+Ð-°-Ð-Ð-Ð,11804022A =Ð=´°=°,同理可得,21211802022A A Ð=Ð=´°=°,¼4480521A \Ð=´°=°.故选:A .【点睛】本题是找规律的题目,主要考查了三角形的外角性质及三角形的内角和定理,同时考查了角平分线的定义.解答的关键是掌握外角和内角的关系.类型二 内外角分线进阶9.如图,在四边形ABCD 中,∠DAB 的角平分线与∠ABC 的邻补角的平分线相交于点P ,且∠D +∠C =210°,则∠P =( )A .10°B .15°C .30°D .40°【答案】B【解析】【分析】利用四边形内角和是360°可以求得150DAB ABC Ð+Ð=°.然后由角平分线的性质,邻补角的定义求得 PAB ABP Ð+Ð的度数,所以根据ABP D 的内角和定理求得P Ð的度数即可.【详解】解:210D C Ð+Ð=°Q ,360DAB ABC C D Ð+Ð+Ð+Ð=°,150DAB ABC \Ð+Ð=°.又DAB ÐQ 的角平分线与ABC Ð的外角平分线相交于点P ,111(180)90()165222PAB ABP DAB ABC ABC DAB ABC \Ð+Ð=Ð+Ð+°-Ð=°+Ð+Ð=°,180()15P PAB ABP \Ð=°-Ð+Ð=°.故选:B .【点睛】本题考查了三角形内角和定理、多边形的内角与外角.熟知“四边形的内角和是360°”是解题的关键.10.如图,在V ABC 中,∠ABC 和∠ACB 的角平分线交于点O ,延长BO 与∠ACB 的外角平分线交于点D ,若∠DOC =48°,则∠D =_____°.【答案】42【解析】【分析】根据角平分线的定义和三角形的内角和定理即可得到结论.【详解】解:∵∠ABC 和∠ACB 的角平分线交于点O ,∴∠ACO =12∠ACB ,∵CD 平分∠ACE ,∴∠ACD =12∠ACE ,∵∠ACB +∠ACE =180°,∴∠OCD =∠ACO +∠ACD =12(∠ACB +∠ACE )=12×180°=90°,∵∠DOC =48°,∴∠D =90°﹣48°=42°,故答案为:42.【点睛】本题考查了角平分线和三角形内角和,解题关键是熟练运用相关性质进行计算求角.11.如图,等腰ABC V 中,顶角42A Ð=°,点E ,F 是内角ABC Ð与外角ACD Ð三等分线的交点,连接EF ,则BFC Ð=_________°.【答案】14【解析】【分析】根据等腰三角形的性质和三角形的内角和定理可求∠ABC 和∠ACB ,再根据三角形外角的性质可求∠ACD ,再根据三等分线的定义与和差关系可求∠FBC 和∠BCF ,再根据三角形的内角和定理可求∠BFC .【详解】解:∵等腰△ABC 中,顶角∠A=42°,∴∠ABC=∠ACB=12×(180°-42°)=69°,∴∠ACD=111°,∵点E,F是内角∠ABC与外角∠ACD三等分线的交点,∴∠FBC=13×69°=23°,∠FCA=23×111°=74°,∴∠BCF=143°,∴∠BFC=180°-23°-143°=14°.故答案为:14.【点睛】本题考查了等腰三角形的性质,三角形内角和定理以及三角形外角的性质,解答此题的关键是找到角与角之间的关系.12.如图,在△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,则∠A1=__,若∠A1BC 与∠A1CD的平分线相交于点A2,则∠A2=__,…,以此类推,则∠An﹣1BC与∠An﹣1CD的平分线相交于点An,则∠An的度数为__.【答案】 48°, 24°, 96°×1 (2n【解析】【分析】利用角平分线的定义和三角形内角与外角的性质计算.【详解】解:∵A1B、A1C分别平分∠ABC和∠ACD,∴∠ACD=2∠A1CD,∠ABC=2∠A1BC,而∠A1CD=∠A1+∠A1BC,∠ACD=∠ABC+∠A,∴∠A=2∠A1=96°,∴∠A1=48°,同理可得∠A1=2∠A2,即∠A=2×2∠A2=96°,∴∠A2=24°,∴∠A=2n n AÐ,∴1962nnAæöÐ=°´ç÷èø.故答案为48°,24°,96°×1 ()2n.【点睛】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图然后求出后一个角是前一个角的一半是解题的关键.13.如图,在五边形ABCDE中,∠A+∠B+∠E=310°,CF平分∠DCB,FC的延长线与五边形ABCDE外角平分线相交于点P,求∠P的度数【答案】∠P=25°.【解析】【分析】延长ED,BC相交于点G.由四边形内角和可求∠G=50°,由三角形外角性质可求∠P度数.【详解】解:延长ED,BC相交于点G.在四边形ABGE中,∵∠G=360°-(∠A+∠B+∠E)=50°,∴∠P=∠FCD-∠CDP=12(∠DCB-∠CDG)=1 2∠G=12×50°=25°.【点睛】本题考查了三角形内角和定理,三角形角平分线性质,外角的性质,熟练运用外角的性质是本题的关键.类型三综合解答14.如图,∠XOY=90°,点A,B分别在射线OX,OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化,如果不变,求出∠C的度数.【答案】不变,45°【解析】【分析】根据角平分线的定义、三角形的内角和、外角性质求解.【详解】解:∵∠ABY=90°+∠OAB,AC平分∠OAB,BE平分∠ABY,∴∠4=12∠ABY=12(90°+∠OAB)=45°+12∠OAB,即∠4=45°+∠1,又∵∠4=∠C+∠1,∴∠C=45°.【点睛】本题考查的是三角形内角与外角的关系,解答此题目要注意:①求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;②三角形的外角通常情况下是转化为内角来解决.15.如图,∠CBF, ∠ACG是△ABC的外角, ∠ACG的平分线所在的直线分别与∠ABC,∠CBF的平分线BD,DE交于点D,E.(1)∠DBE 的度数;(2)若∠A=70,求∠D 的度数;(3)若∠A=a ,求∠E 的度数(用含a 的式子表示).【答案】(1)90DBE Ð=°;(2)35D Ð=°;(3)1902E a Ð=°-【解析】【分析】(1)根据角平分线的定义可得11,,22DBC ABC EBC FBC Ð=ÐÐ=Ð 再根据平角的定义可得出结论;(2)根据角平分线的定义可得11,,22DCG ACG DBC ABC Ð=ÐÐ=Ð 再根据三角形外角的性质可推出2A D Ð=Ð则可求出∠D 的度数;(3)由第(2)问的结论可知1122D A a Ð=Ð=,再加上第(1)问的结论90DBE Ð=°,则可表示出∠E 的度数.【详解】(1)∵BD 平分ABC Ð,BE 平分,FBC Ð∴11,,22DBC ABC EBC FBC Ð=ÐÐ=Ð∵180ABF Ð=°∴1()902DBE DBC EBC ABC FBC Ð=Ð+Ð=Ð+Ð=°(2)∵CD 平分ACG Ð, BD 平分ABCÐ∴11,,22DCG ACG DBC ABC Ð=ÐÐ=Ð∵ACG A ABC Ð=Ð+Ð∴22DCG A DBCÐ=Ð+Ð∵DCG D DBCÐ=Ð+Ð∴222DCG D DBCÐ=Ð+Ð∴2A DÐ=Ð∴11703522D A Ð=Ð=´°=°(3)由(2)知1122D A a Ð=Ð=∵90DBE Ð=°∴1902E a Ð=°-【点睛】本题主要考查角平分线的定义及三角形外角的性质,掌握角平分线的定义及三角形外角的性质是解题的关键.16.已知,在四边形ABCD 中,∠F 为四边形ABCD 的∠ABC 的平分线及外角∠DCE 的平分线所在的直线构成的锐角,若∠A =α,∠D =β,(1)如图①,当α+β>180°时,∠F =____(用含α,β的式子表示);(2)如图②,当α+β<180°时,请在图②中,画出∠F ,且∠F =___(用含α,β的式子表示);(3)当α,β满足条件___时,不存在∠F .【答案】(1)12(α+β)﹣90°;(2)90°﹣12(α+β);(3)α+β=180°.【解析】【分析】(1)根据四边形的内角和定理表示出∠BCD,再表示出∠DCE,然后根据角平分线的定义可得∠FBC=12∠ABC,∠FCE=12∠DCE,三角形的一个外角等于与它不相邻的两个内角的和可得∠F+∠FBC=∠FCE,然后整理即可得解;(2)与(1)的思路相同,得到∠FBC=12∠ABC,∠FCE=12∠DCE,由外角性质,得到∠F+∠FBC=∠FCE,通过等量代换,求解即可;(3)根据∠F的表示,∠F为0时,不存在.【详解】解:(1)如图:由四边形内角和定理得,∠BCD=360°﹣∠A﹣∠D﹣∠ABC,∴∠DCE=180°﹣(360°﹣∠A﹣∠D﹣∠ABC)=∠A+∠D+∠ABC﹣180°,由三角形的外角性质得,∠FCE=∠F+∠FBC,∵BF、CF分别是∠ABC和∠DCE的平分线,∴∠FBC=12∠ABC,∠FCE=12∠DCE,∴∠F+∠FBC=12(∠A+∠D+∠ABC﹣180°)=12(∠A+∠D)+12∠ABC﹣90°,∴∠F=12(∠A+∠D)﹣90°,∵∠A=α,∠D=β,∴∠F=12(α+β)﹣90°;(2)如图3,由(1)可知,∠BCD =360°﹣∠A ﹣∠D ﹣∠ABC ,∴∠DCE =180°﹣(360°﹣∠A ﹣∠D ﹣∠ABC )=∠A+∠D+∠ABC ﹣180°,∴∠FCE =∠F+∠FBC ,∵∠FBC =12(360°﹣∠ABC ),∠FCE =180°﹣12∠DCE ,∴∠F=∠FCE ﹣∠FBC=180°﹣12(∠A+∠D+∠ABC ﹣180°)﹣12(360°﹣∠ABC ),∴∠F=90°﹣12(∠A+∠D )∴∠F =90°﹣12(α+β);(3)当α+β=180°时,∴∠F =90°﹣118002´°=,此时∠F 不存在.【点睛】本题考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.17.如图,90MON Ð=°,点A 、B 分别在OM 、ON 上运动(不与点O 重合).(1)如图1,BC 是ABN Ð的平分线,BC 的反方向延长线与BAO Ð的平分线交于点D .①若60BAO Ð=°,则D Ð为多少度?请说明理由.②猜想:D Ð的度数是否随A 、B 的移动发生变化?请说明理由.(2)如图2,若13ABC ABN Ð=Ð,13BAD BAO Ð=Ð,则D Ð的大小为 度(直接写出结果);(3)若将“90MON Ð=°”改为“MON a Ð=(0180a °<<°)”,且1ABC ABN n Ð=Ð,1BAD BAO n Ð=Ð,其余条件不变,则D Ð的大小为 度(用含a 、n 的代数式直接表示出米).【答案】(1)①45°,理由见解析;②∠D 的度数不变;理由见解析(2)30 ;(3)a n【解析】【分析】(1)①先求出∠ABN=150°,再根据角平分线得出∠CBA=12∠ABN=75°、∠BAD=12∠BAO=30°,最后由外角性质可得∠D 度数;②设∠BAD=α,利用外角性质和角平分线性质求得∠ABC=45°+α,利用∠D=∠ABC-∠BAD 可得答案;(2)设∠BAD=α,得∠BAO=3α,继而求得∠ABN=90°+3α、∠ABC=30°+α,根据∠D=∠ABC-∠BAD 可得答案;(3)设∠BAD=β,分别求得∠BAO=nβ、∠ABN=∠AOB+∠BAO=α+nβ、∠ABC=n a +β,由∠D=∠ABC-∠BAD 得出答案.【详解】解:(1)①45°∵∠BAO=60°,∠MON=90°,∴∠ABN=150°,∵BC 平分∠ABN 、AD 平分∠BAO ,∴∠CBA=12∠ABN=75°,∠BAD=12∠BAO=30°∴∠D=∠CBA-∠BAD=45°,②∠D 的度数不变.理由是:设∠BAD=α,∵AD 平分∠BAO ,∴∠BAO=2α,∵∠AOB=90°,∴∠ABN=∠AOB+∠BAO=90°+2α,∵BC 平分∠ABN ,∴∠ABC=45°+α,∴∠D=∠ABC-∠BAD=45°+α-α=45°;(2)设∠BAD=α,∵∠BAD=13∠BAO,∴∠BAO=3α,∵∠AOB=90°,∴∠ABN=∠AOB+∠BAO=90°+3α,∵∠ABC=13∠ABN,∴∠ABC=30°+α,∴∠D=∠ABC-∠BAD=30°+α-α=30°;(3)设∠BAD=β,∵∠BAD=1n∠BAO,∴∠BAO=nβ,∵∠AOB=α°,∴∠ABN=∠AOB+∠BAO=α+nβ,∵∠ABC=1n∠ABN,∴∠ABC=an+β,∴∠D=∠ABC-∠BAD=an+β-β=an.【点睛】本题主要考查角平分线和外角的性质,熟练掌握三角形的外角性质和角平分线的性质是解题的关键.。
七下第5讲三角形内外角平分线夹角模型归纳与内外角和计算方法总结

七下第5讲三⾓形内外⾓平分线夹⾓模型归纳与内外⾓和计算⽅法总结写在前⾯在前四讲中,我们对本章的重点内容作了归纳,剩下的知识点仅剩⼀个重要模型和内外⾓的相关题型变式,就以本讲作为本章的收尾,更多的难题,留⾄期中复习吧.⼀、三⾓形内外⾓平分线夹⾓模型模型呈现:如图,已知,在△ABC中,BD平分∠ABC,CD平分∠ACB,CH平分∠ACI,BG平分∠EBC,CG平分∠BCF.试探究∠BDC,∠BHC,∠BGC与∠A的关系.分析:这是本章的最后⼀个重要模型,要结合整体思想,外⾓定理综合运⽤.解答:补充结论:其实这个模型中,还能有许多发现,⽐如,∠GBD=90°,∠DCH=90°,理由是邻补⾓的⾓平分线互相垂直.∠BGC和∠BHC互余,∠BGC和∠BDC互补,在△DCH中,∠BDC作为外⾓,∠BDC=90°+∠BHC.例1:如图,O是三⾓形三条⾓平分线的交点,∠1=15°,则∠2=_____°.分析:本题的关键是,发现∠2的作⽤,∠2可以作为△AOB的外⾓,即∠OAB和∠OBA的和,⼜是∠AOB的邻补⾓,∠AOB是三⾓形两内⾓平分线的夹⾓,因此本题既可以⽤⼀步⼀步完成,也可⽤结论模型⼝算.解答:例2:如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=_______.分析:本题是⼀道将三个模型结合在⼀起的题⽬,我们要关注哪些⾓可以求,∠BDC是两内⾓平分线的夹⾓,则知道∠A即可求,∠E是两外⾓,∠MBC,∠NCB的⾓平分线的夹⾓,则知道∠BDC即可求,∠F是△EBC的内⾓∠EBC和外⾓∠ECQ的⾓平分线夹⾓,则知道∠E即可求.解答:例3:分析:解答:综上所述,结论正确的是①②③⑤共4个.⼆、多边形内外⾓计算例1:⼀个学⽣计算多边形的内⾓和,少算了⼀个内⾓,得到答案是1400°,求少算的内⾓的度数及多边形边数.分析:显然,根据多边形内⾓和公式(n-2)·180°,可知内⾓和⼀定是180度的倍数,我们可以⽤1400除以180,算出其余数,那么⾃然可得,少算的那个内⾓与余数的和⼀定是180度的倍数,⽽根据多边形每个内⾓必然⼩于180°,则这个内⾓度数就是⽤180°减去这个余数即可.解答:1400°÷180°=7······140°,180°–140°=40°,设多边形边数为n,(n–2)·180=1400+40,n=10答:少算的内⾓度数为40°,边数为10.例2:⼀个学⽣计算多边形的内⾓和,多算了⼀个外⾓,得到答案是1400°,求多算的外⾓的度数及多边形边数.分析:显然,本题是上⼀题的变式,⽅法还是⽤1400除以180,算出其余数,那么多算的外⾓度数,就是这个余数.解答:1400°÷180°=7······140°,设多边形边数为n,(n–2)·180=1400-140,n=9答:多算的外⾓度数为140°,边数为9.例3:⼀个多边形每个内⾓都等于150°,求这个多边形的边数.分析:本题不难,但我们要学会多种思路解题,可以从多边形内⾓和公式⼊⼿,也可以逆向思维,求出每个外⾓的度数,⽤外⾓和除以每个外⾓的度数.解答:法1:设多边形边数为n,(n–2)·180=150n,n=12法2:180°-150°=30°,360°÷30°=12答:多边形边数为12.三、作图探究例:在△ABC中,∠ACB=90°,BD是△ABC的⾓平分线,P是射线AC上任意⼀点(不与A、D、C三点重合),过点P作PQ⊥AB,垂⾜为Q,交直线BD于E.(1)探索∠PDE与∠PED的关系,画出图形并说明理由.(2)作∠CPQ的⾓平分线交直线AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.分析:本题中,点P的位置不确定,在射线AC上,就有多种可能,线段AD上,线段DC上,线段DC延长线上,在延长线上时,⼜要考虑垂⾜Q的位置,可能在线段AB上,也可能在线段AB的延长线上.因此,分四种情况讨论.碍于篇幅,我们将两⼩题的图汇总在⼀起.解答:①点P在线段AD上(1)∵PQ⊥AB,∴∠EQB=∠C=90°,∴∠PED+∠EBQ=90°,∠CBD+∠CDB=90°,∵∠PDE=∠CDB,∴∠CBD+∠PDE=90°,∵BD为∠ABC的平分线,∴∠CBD=∠EBQ,∴∠PDE=∠PED;(2)在四边形PQBC中,∠CPQ+∠CBA=360°-2×90°=180°∵PF平分∠CPQ,BD平分∠CBA∴∠1+∠2=90°∵∠1+∠3=90°∴∠2=∠3,PF∥BD②点P在线段DC上(1)∵PQ⊥AB,∴∠EQB=∠C=90°,∴∠BEQ+∠EBQ=90°,∠CBD+∠PDE=90°,∵∠PED=∠BEQ,∴∠PED +∠EBQ=90°,∵BD为∠ABC的平分线,∴∠CBD=∠EBQ,∴∠PDE=∠PED;(2)在四边形PQBC中,∠CPQ+∠CBA=360°-2×90°=180°∵PF平分∠CPQ,BD平分∠CBA∴∠1+∠2=90°∵∠1+∠3=90°∴∠2=∠3,PF∥BD③点P在线段DC延长线上,点Q在线段AB上(1)∵PQ⊥AB,∴∠EQB=∠ACB=90°,∴∠BEQ+∠EBQ=90°,∠CBD+∠PDE=90°,∵∠PED=∠BEQ,∴∠PED +∠EBQ=90°,∵BD为∠ABC的平分线,∴∠CBD=∠EBQ,∴∠PDE=∠PED;(2)∵∠CPQ+∠A=90°∠CBA+∠A=90°∴∠CPQ=∠CBA∵PF平分∠CPQ,BD平分∠CBA∴∠1=∠2∵∠1+∠3=90°∴∠2+∠3=90°,PF⊥BD④点P在线段DC延长线上,点Q在线段AB延长线上(1)∵PQ⊥AB,∴∠EQB=∠ACB=90°,∴∠PED+∠EBQ=90°,∠CBD+∠PDE=90°,∵∠ABD=∠EBQ,∴∠PED +∠ABD=90°,∵BD为∠ABC的平分线,∴∠CBD=∠ABD,∴∠PDE=∠PED;(2)∵∠CPQ+∠A=90°∠CBA+∠A=90°∴∠CPQ=∠CBA∵PF平分∠CPQ,BD平分∠CBA∴∠1=∠2∵∠1+∠3=90°∴∠2+∠3=90°,PF⊥BD上讲思考题答案。
证明命题三角形的两条内角平分线所夹的锐角

证明命题三角形的两条内角平分线所夹的锐角【证明命题:三角形的两条内角平分线所夹的锐角】命题:在三角形ABC中,D为AB上一点,E为AC上一点,且满足AD=AE,则∠BDC=∠CDE。
引言:在初中阶段学习数学时,我们经常遇到各种各样的几何命题。
其中命题三角形内的角平分线所形成的相关角是一个常见而重要的几何知识点。
如何证明在一个三角形中,两条内角平分线所夹的角是锐角呢?在本文中,我们将从多个角度来证明这个命题,让我们一起深入探讨。
1. 命题的几何图示让我们来看一下三角形ABC中,D为AB上一点,E为AC上一点的几何图示。
根据题目所给的条件,根据定义作出角平分线BD和CE,所形成的角度如何?通过图示我们可以更直观地认识到这个问题。
2. 证明方法一:角平分线的定义和性质接下来,我们将运用角平分线的定义和性质来证明这个命题。
首先我们回顾一下角平分线的定义,然后通过画图和几何推理来论证命题的成立。
我们将逐步展示证明过程,并用文字和图像来详细描述。
3. 证明方法二:三角形相似性的运用除了角平分线的性质,我们还可以运用三角形的相似性来证明这个命题。
通过建立三角形的对应边比例关系,我们可以得出两条内角平分线所夹的锐角的成立。
这样的证明方法在实际解题中也是非常常见的。
4. 总结与回顾:深刻理解命题的重要性通过以上的证明方法,我们得到了命题的成立。
但是更重要的是,我们应该从中总结和回顾出一些重要的几何知识,并且更深入地理解命题的原理和应用。
只有这样,我们才能真正掌握这个知识点,并且在实际生活中更加灵活地运用它。
5. 个人观点和理解:命题的启发我想共享一下我对这个命题的个人观点和理解。
在我看来,几何知识是一种美妙而深刻的数学语言,通过不断地探索和发现,我们可以发现其中的奥秘和乐趣。
命题三角形的两条内角平分线所夹的锐角,正是这样一种启发,它让我们更深入地理解了三角形的性质和几何相似的原理。
结语:在本文中,我们从多个角度对命题三角形的两条内角平分线所夹的锐角进行了全面探讨和论证。
初中数学-三角形内外角平分线有关命题的证明及应用

三角形内外角平分线一.命题的证明及应用在中考常有与三角形内外角平分线有关的题目,若平时不注意总结是很难一下子解决的.下面来一起学习一下.命题1 如图1,点D是△ABC两个内角平分线的交点,则∠D=90°+∠A.证明:如图1:∵∠1=∠,∠2=∠,∴2∠1+2∠2+∠A=180°①∠1+∠2+∠D=180°②①-②得:∠1+∠2+∠A=∠D③由②得:∠1+∠2=180°-∠D④把③代入④得:∴180°-∠D+∠A=∠D∠D=90°+∠A.点评利用角平分线的定义和三角形的内角和等于180°,不难证明.命题2 如图2,点D是△ABC两个内角平分线的交点,则∠D=90°-∠A.证明:如图2:∵DB和DC是△ABC的两条外角平分线,∴∠D=180°-∠1-∠2=180°-(∠DBE+∠DCF)=180°-(∠A+∠4+∠A+∠3)=180°-(∠A+180°)=180°-∠A-90°=90°-∠A;点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和以及三角形的内角和等于180°,可以证明.命题3 如图3,点E是△ABC一个内角平分线与一个外角平分线的交点,则∠E=∠A.证明:如图3:∵∠1=∠2,∠3=∠4,∠A+2∠1=2∠4①∠1+∠E=∠4②①×代入②得:∠E=∠A.点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和,很容易证明.命题4如图4,点E是△ABC一个内角平分线BE与一个外角平分线CE 的交点,证明:AE是△ABC的外角平分线.证明:如图3:∵BE是∠ABC的平分线,可得:EH=EFCE是∠ACD的平分线, 可得:EG=EF∴过点E分别向AB、AC、BC所在的直线引垂线,所得的垂线段相等.即EF=EG=EH∵EG=EH∴AE是△ABC的外角平分线.点评利用角平分线的性质和判定能够证明.应用上面的结论能轻松地解答一些相关的比较复杂的问题,下面来一起看.例1如图5,PB和PC是△ABC的两条外角平分线.①已知∠A=60°,请直接写出∠P的度数.②三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?解析:①由命题2的结论直接得:∠P=90°-∠A=90°-×60°=60°②根据命题2的结论∠P=90°-∠A,知三角形的三条外角平分线所在的直线形成的三角形的三个角都是锐角,则该三角形是锐角三角形.点评此题直接运用命题2的结论很简单.同时要知道三角形按角分为锐角三角形、直角三角形和钝角三角形.例2如图6,在△ABC中,延长BC到D,∠ABC与∠ACD的角平分线相较于点,∠BC与∠CD 的平分线交与点,以此类推,…,若∠A=96°,则∠= 度.解析:由命题③的结论不难发现规律∠∠A .可以直接得:∠=×96°=3°.点评 此题是要找出规律的但对要有命题③的结论作为基础知识.例3(203陕西第一大题填空题第八小题,此题3分)如图7,△ABC 的外角∠ACD 的平分线CP 的内角∠ABC 平分线BP 交于点P ,若∠BPC=40°,则∠CAP=_______________.解析:此题直接运用命题4的结论可以知道AP是△ABC 的一个外角平分线,结合命题3的结论知道∠BAC=2∠BPC, CAP=(180°-∠BAC )= (180°-2∠BPC )=50°.点评 对命题3、4研究过的读者此题不难,否则将是一道在考试的时候花时间也不一定做的出来的题目. 例4 (2003年山东省)如图,在Rt △ABC 中,∠ACB=90°,∠BAC=30°,∠ACB 的平分线与∠ABC 的外角平分线交与E 点,连接AE ,则∠AEB= 度.解析:有题目和命题4的结论可以知道AE 是△ABC 的一个外角平分线, 结合命题2的结论知道∠AEB=∠ACB -∠ACB=90°-×90°=45°点评 从上面的做题过程来看题目中给出的“∠A=30°”这个条件是可以不用的.二.角平分线定理使用中的几种辅助线作法一、已知角平分线,构造三角形例题、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。
三角形中的特殊模型-双角平分线模型(解析版)

三角形中的特殊模型-双角平分线模型模型1、双角平分线模型1)两内角平分线的夹角模型条件:如图1,在△ABC 中,∠ABC 和∠ACB 的平分线BE ,CF 交于点G ;结论:∠BGC =90°+12∠A .图1图2图32)两外角平分线的夹角模型条件:如图2,在△ABC 中,BO ,CO 是△ABC 的外角平分线;结论:∠O =90°-12∠A .3)一个内角一个外角平分线的夹角模型条件:如图3,在△ABC 中,BP 平分∠ABC ,CP 平分∠ACB 的外角,两条角平分线相交于点P ;结论:∠P =12∠A .图4图5图64)凸多边形双内角平分线的夹角模型条件:如图4,BP 、CP 平分∠ABC 、∠DCB ,两条角平分线相交于点P ;结论:2∠P =∠A +∠D 5)两内角平分线的夹角模型条件:如图5,BP 、DP 平分∠BCD 、∠CDE ,两条角平分线相交于点P ;结论:2∠P =∠A +∠B +∠E -180°6)一个内角一个外角平分线的夹角模型(累计平分线)条件:如图6,∠A =α,∠ABC ,∠ACD 的平分线相交于点P 1,∠P 1BC ,∠P 1CD 的平分线相交于点P 2,∠P 2BC,∠P2CD的平分线相交于点P3⋯⋯以此类推;结论:∠P n的度数是α2n.7)旁心模型旁心:三角形的一条内角平分线与其他两个角的外角平分线交于一点条件:如图,BD平分∠ABC,CD平分∠ACB的外角,两条角平分线相交于点D;结论:AD平分∠CAD 1(2023·绵阳市八年级课时练习)如图,在ΔABC中,∠ABC=80°,∠ACB=50°,BP平分∠ABC,CP平分∠ACB,则∠BPC=.【答案】115°【分析】先根据角平分线的性质求出∠PBC+∠PCB的度数,再利用三角形内角和定理即可求解.【详解】解:∵BP平分∠ABC,CP平分∠ACB,∴∠PBC+∠PCB=12(80°+50°)=65°,∴∠BPC=180°-65°=115°.【点睛】本题考查了角平分线的性质及三角形内角和定理.熟练掌握三角形内角和定理是解题的关键.2(2023·河南周口·八年级统考期末)如图,在四边形ABCD中,∠A+∠D=∂,∠ABC的平分线与∠BCD 的平分线交于点P,则∠P=()A.90°+12∂ B.90°-12∂ C.12∂ D.180°-12∂【答案】C【分析】根据四边形的内角和求得∠ABC+∠BCD=360°-∂,再根据角平分线的定义求得∠PBC+∠PCB,再根据三角形内角和即可求解.【详解】解:在四边形ABCD中,∠A+∠D=∂,∴∠ABC+∠BCD=360°-∂,由题意可得:BP平分∠ABC,CP平分∠BCD,∴∠PBC=12∠ABC,∠PCB=12∠BCD,∴∠PBC+∠PCB=12∠ABC+∠BCD=180°-∂2,∴∠BPC=180°-∠PBC+∠PCB=12∂故选:C.【点睛】此题考查了多边形内角和的性质、三角形内角和的性质以及角平分线的性质,解题的关键是掌握并灵活运用相关性质进行求解.3(2023秋·山西太原·八年级校考期末)已知:如图,P是△ABC内一点,连接PB,PC.(1)猜想:∠BPC与∠ABP、∠ACP、∠A存在怎样的等量关系?证明你的猜想.(2)若∠A=69°,PB、PC分别是∠ABC、∠ACB的三等分线,直接利用(1)中结论,可得∠BPC的度数为.【答案】(1)∠BPC=∠A+∠ABP+∠ACP,证明见解析(2)106°【分析】(1)根据三角形内角和定理得到∠A+∠ABC+∠ACB=180°,∠BPC+∠CBP+∠BCP=180°,再结合∠CBP=∠ABC-∠ABP,∠BCP=∠ACB-∠ACP即可得到结论;(2)先根据三角形内角和定理和角三等分线的定义得到∠ABC+∠ACB=111°,∠ABP=13∠ABC,∠ACP=13∠ACB,再代入(1)中结论求解即可.【详解】(1)解:猜想:∠BPC=∠A+∠ABP+∠ACP,证明:由题意得:∠A+∠ABC+∠ACB=180°,∠BPC+∠CBP+∠BCP=180°,∵∠CBP=∠ABC-∠ABP,∠BCP=∠ACB-∠ACP,∴∠BPC+∠ABC-∠ABP+∠ACB-∠ACP=180°,∴∠BPC+∠ABC+∠ACB-∠ABP+∠ACP=180°,∴∠BPC+180°-∠A-∠ABP+∠ACP=180°,∴∠BPC=∠A+∠ABP+∠ACP;(2)解:∵∠A=69°,PB、PC分别是∠ABC、∠ACB的三等分线,∴∠ABC+∠ACB=180°-∠A=111°,∠ABP=13∠ABC,∠ACP=13∠ACB,∴∠BPC=∠A+13∠ABC+∠ACB=69°+37°=106°.故答案为:106°.【点睛】本题主要考查了三角形内角和定理,角三等分线的定义,熟知三角形内角和为180度是解题的关键.4(2023秋·成都市·八年级专题练习)如图,在△ABC中,∠B=58°,三角形两外角的角平分线交于点E,则∠AEC=.【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数,再根据角平分线的定义求得∠EAC+∠ECA的度数,即可解答.【详解】解:∵∠B+∠BAC+∠BCA=180°,∠B=58°,∴∠BAC+∠BCA=180°-∠B=180°-58°= 122°,∵∠BAC+∠DAC=180°,∠BCA+∠ACF=180°,∴∠DAC+∠ACF=360°-(∠BAC+∠BCA)=360°-122°=238°,∵AE平分∠DAC,CE平分∠ACF,∴∠EAC=12∠DAC,∠ECA=12∠ACF,∴∠EAC+∠ECA=12(∠DAC+∠ACF)=119°,∵∠EAC+∠ECA+∠AEC=180°,∴∠AEC=180°-(∠EAC+∠ECA)=180°-119°=61°,故答案为:61°.【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义,熟练掌握三角形的内角和定理和角平分线的定义是解答的关键.5(2023·绵阳市·八年级专题练习)如图,已知在ΔABC中,∠B、∠C的外角平分线相交于点G,若∠ABC =m°,∠ACB=n°,求∠BGC的度数.【答案】∠BGC=12m°+n°【分析】运用角平分线的知识列出等式求解即可.解答过程中要注意代入与之有关的等量关系.【详解】解:∠B、∠C的外角平分线相交于点G,在ΔBCG中,∠BGC=180°-12∠EBC+12∠BCF=180°-12(∠EBC+∠BCF)=180°-12(180°-∠ABC+180°-∠ACB)=180°-12(180°-m°+180°-n°);=12m°+n°【点睛】本题考查的是三角形内角和定理以及角平分线的知识.此类题的关键是找出与之相关的等量关系简化计算得出.6(2023春·广西·七年级专题练习)如图,在△ABD中,∠ABD的平分线与∠ACD的外角平分线交于点E,∠A=80°,求∠E的度数【答案】40°【分析】由题意:设∠ABE =∠EBC =x ,∠ACE =∠ECD =y ,利用三角形的外角的性质构建方程组解决问题即可.【详解】由题意:设∠ABE =∠EBC =x ,∠ACE =∠ECD =y ,则有2y =2x +∠A ①y =x +∠E ②,①-2×②可得∠A =2∠E ,∴∠E =12∠A =40°.【点睛】本题考查三角形的外角的性质,角平分线的定义等知识,解题的关键是学会利用参数构建方程组解决问题.7(2023春·山东泰安·七年级校考阶段练习)如图,在△ABC 中,∠A =α,∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得A 2;⋯;∠A 2019BC 与∠A 2019CD 的平分线相交于点A 2020,得∠A 2020,则∠A 2020=.【答案】α22020【分析】结合题意,根据角平分线、三角形外角、三角形内角和的性质,得∠A 1=12∠A ,同理得∠A 2=12∠A 1=α22;再根据数字规律的性质分析,即可得到答案.【详解】根据题意,∠A =α,∠ABC 与∠ACD 的平分线交于点A 1∴∠A 1=180°-12∠ABC -∠ACB -12∠ACD ∵∠ACD =∠A +∠ABC ∴∠A 1=180°-∠ABC -∠ACB -12∠A∵∠A +∠ABC +∠ACB =180°∴∠A 1=12∠A 同理,得∠A 2=12∠A 1=12×12∠A =α22;∠A 3=12∠A 2=12×12×12∠A =α23;∠A 4=12∠A 3=12×12×12×12∠A =α24;⋯∠A n =12∠A n -1=α2n ∴∠A 2020=α22020故答案为:α22020.【点睛】本题考查了三角形和数字规律的知识;解题的关键是熟练掌握三角形内角和、三角形外角、角平分线、数字规律的性质,从而完成求解.8(2023·河北·九年级专题练习)问题情境:如图1,点D 是△ABC 外的一点,点E 在BC 边的延长线上,BD 平分∠ABC ,CD 平分∠ACE .试探究∠D 与∠A 的数量关系.(1)特例探究:如图2,若△ABC是等边三角形,其余条件不变,则∠D=;如图3,若△ABC是等腰三角形,顶角∠A=100°,其余条件不变,则∠D=;这两个图中,与∠A度数的比是 ;(2)猜想证明:如图1,△ABC为一般三角形,在(1)中获得的∠D与∠A的关系是否还成立?若成立,利用图1证明你的结论;若不成立,说明理由.【答案】(1)30°;50°;1:2(2)成立,见解析【分析】(1)根据三角形的一个外角等于和它不相邻的两个内角的和用∠A和∠D表示出∠ACE,再根据角平分线的定义得到∠ACE=2∠DCE,∠ABC=2∠DBC,然后整理即可.(2)根据三角形的一个外角等于和它不相邻的两个内角的和用∠A和∠D表示出∠ACE,再根据角平分线的定义得到∠ACE=2∠DCE,∠ABC=2∠DBC,然后整理即可.【详解】(1)解:如图2,∵ΔABC是等边三角形,∴∠ABC=60°,∠ACE=120°,∵BD平分∠ABC,CD平分∠ACE.∴∠DBC=30°,∠DCE=60°,∵∠DCE=∠D+∠DBC,∴∠D=30°;如图3,∵ΔABC是等腰三角形,∠A=100°,∴∠ABC=∠ACB=40°,∠ACE=140°,∵BD平分∠ABC,CD平分∠ACE.∴∠DBC=20°,∠DCE=70°,∵∠DCE=∠D+∠DBC,∴∠D=50°;故答案为30°,50°,1:2;(2)解:成立,如图1,在ΔABC中,∠ACE=∠A+∠ABC,在ΔDBC中,∠DCE=∠D+∠DBC,⋯(1)∵CD平分∠ACE,BD平分∠ABC,∴∠ACE=2∠DCE,∠ABC=2∠DBC,又∵∠ACE=∠A+∠ABC,∴2∠DCE=∠A+2∠DBC,⋯(2)由(1)×2-(2),∴2∠D+2∠DBC-(∠A+2∠DBC)=0,∴∠A=2∠D.【点睛】本题考查了等边三角形的性质、等腰三角形的性质、利用三角形的外角性质和角平分线的定义解答是关键.9(2023·重庆·七年级专题练习)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,分析发现∠BOC=90°∠A,理由如下:∵BO和CO分别是∠ABC、∠ACB的角平分线+12∴∠1=12∠ABC,∠2=12∠ACB∴∠1+∠2=12(∠ABC+∠ACB)=12(180°-∠A)=90°-12∠A∴∠BOC=180°-(∠1+∠2)=180°-90°-12∠A=90°+12∠A(1)探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.(2)探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)(4)运用:如图5,五边形ABCDE中,∠BCD、∠EDC的外角分别是∠FCD、∠GDC,CP、DP分别平分∠FCD和∠GDC且相交于点P,若∠A=140°,∠B=120°,∠E=90°,则∠CPD=度.【答案】(1)∠BOC=12∠A;(2)∠BOC=90°-12∠A;(3)∠BOC=12(∠BAD+∠CDA);(4)95【分析】(1)根据角平分线的性质及三角形外角的性质求解即可;(2)根据角平分线的性质、三角形内角和及三角形外角的性质求解即可;(3)由角平分线的性质、四边形内角和及三角形内角和定理即可求得两者的关系;(4)由角平分线的性质、五边形内角和及三角形内角和定理即可求得结果.【详解】(1)探究2结论:∠BOC=12∠A理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线∴∠1=12∠ABC,∠2=12∠ACD∵∠ACD是△ABC的一个外角∴∠ACD=∠A+∠ABC∴∠2=12∠ACD=12(∠A+∠ABC)=12∠A+∠1∵∠2是△BOC的一个外角∴∠BOC=∠2-∠1=12∠A+∠1-∠1=12∠A(2)探究3结论:∠BOC=90°-12∠A∵BO和CO分别是∠DBC和∠ECB的角平分线∴∠OBC=12∠DBC,∠OCB=12∠ECB∵∠DBC=2∠OBC=∠ABC+∠A,∠ECB=2∠OCB=∠ACB+∠A 两式相加得:2∠OBC+2∠OCB=∠ABC+∠ACB+2∠A即∠OBC+∠OCB=12(∠ABC+∠ACB)+∠A∴180°-∠BOC=12(180°-∠A)+∠A整理得:∠BOC=90°-12∠A(3)拓展结论:∠BOC =12(∠A +∠D )∵BO 和CO 分别是∠ABC 和∠BCD 的角平分线∴∠OBC =12∠ABC ,∠OCB =12∠BCD ∴∠OBC +∠OCB =12(∠ABC +∠BCD )=12(360°-∠A -∠D )=180°-12(∠A +∠D )在△BOC 中,180°-∠BOC =∠OBC +∠OCB∴180°-∠BOC =180°-12(∠A +∠D )∴∠BOC =12(∠BAD +∠CDA )(4)运用:∵CP 和DP 分别是∠DCF 和∠GDC 的角平分线∴∠PCD =12∠DCF ,∠PDC =12∠GDC∴∠PCD =12(180°-∠DCB ),∠PDC =12(180°-∠EDC )∴∠PCD +∠PDC =12(360°-∠DCB -∠EDC )∵∠DCB +∠EDC =540°-∠A -∠B -∠E =190°∴∠PCD +∠PDC =12(360°-190°)=85°在△CPD 中,∠CPD =180°-(∠PCD +∠PDC )=180°-85°=95°故答案为:95【点睛】本题考查了角平分线的性质,多边形内角和定理与三角形外角的性质,难度不大,掌握角平分线的性质及多边形内角和定理是关键.课后专项训练1(2023·浙江·八年级假期作业)如图,OG 平分∠MON ,点A ,B 是射线OM ,ON 上的点,连接AB .按以下步骤作图:①以点B 为圆心,任意长为半径作弧,交AB 于点C ,交BN 于点D ;②分别以点C 和点D 为圆心,大于12CD 长为半径作弧,两弧相交于点E ;③作射线BE ,交OG 于点P .若∠ABN =140°,∠MON =50°,则∠OPB 的度数为()A.35°B.45°C.55°D.65°【答案】B【分析】根据条件可知BP 平分∠ABN ,则可求出∠PBN ,根据OG 平分∠MON 求出∠BOG ,进而利用∠PBN =∠POB +∠OPB 即可求出答案.【详解】由作法得BP 平分∠ABN ,∴∠PBN =12∠ABN =12×140°=70°,∵OG 平分∠MON ,∴∠BOP =12∠NOM =12×50°=25°,∵∠PBN =∠POB +∠OPB ,∴∠OPB =∠PBN -∠POB =70°-25°=45°.故选B .【点睛】本题主要考查角平分线的定义及作法,三角形的外角的性质,根据题目条件发现角平分线是解题的关键.2(2023·江苏·八年级月考)ΔABC中,点O是ΔABC内一点,且点O到ΔABC三边的距离相等;∠A= 40°,则∠BOC=()A.110°B.120°C.130°D.140°【解答】解:∵O到三角形三边距离相等,∴O是内心,即三条角平分线交点,AO,BO,CO都是角平分线,∴∠CBO=∠ABO=12∠ABC,∠BCO=∠ACO=12∠ACB,∴∠ABC+∠ACB=180°-40°=140°,∴∠OBC+∠OCB=70°,∴∠BOC=180°-70°=110°.故选:A.3(2023·成都·八年级月考)如图,ΔABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=()A.40°B.45°C.50°D.60°【解答】解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,设∠PCD=x°,∵CP平分∠ACD,∴∠ACP=∠PCD=x°,PM=PN,∵BP平分∠ABC,∴∠ABP=∠PBC,PF=PN,∴PF=PM,∵∠BPC=40°,∴∠ABP=∠PBC=∠PCD-∠BPC=(x-40)°,∴∠BAC=∠ACD-∠ABC=2x°-(x°-40°)-(x°-40°)=80°,∴∠CAF=100°,在RtΔPFA和RtΔPMA中,PA=PA PM=PF,∴RtΔPFA≅RtΔPMA(HL),∴∠FAP=∠PAC=50°.故选:C.4(2023·重庆·八年级专题练习)已知,如图,△ABC中,∠ABC=48°,∠ACB=84°,点D、E分别在BA、BC延长线上,BP平分∠ABC,CP平分∠ACE,连接AP,则∠PAC的度数为()A.45°B.48°C.60°D.66°【答案】D【分析】根据角平分线的性质定理证得PF=PH,PF=PG,进而得出PH=PG,从而判定AP平分∠CAD,再利用外角的性质求出∠CAD即可.【详解】解:作PF⊥BE于点F,PH⊥BD于点H,PG⊥AC于点G,∵BP平分∠ABC,CP平分∠ACE,∴PF=PH,PF=PG,∴PH=PG,∵PH⊥BD,PG⊥AC,∴AP平分∠CAD,∵∠ABC=48°,∠ACB=84°,∴∠CAD=∠ABC+∠ACB=48°+84°=132°,∴∠PAC=12∠CAD=66°.故选:D.【点睛】本题考查了角平分线的判定和性质定理,解题的关键是根据已知添加适当的辅助线.5(2023秋·绵阳市·八年级专题练习)如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,下列结论中不正确的是()A.∠BAC=70°B.∠DOC=90°C.∠BDC=35°D.∠DAC=55°【答案】B【分析】根据三角形的内角和定理列式计算即可求出∠BAC,即可判断A选项;根据角平分线的定义求出∠ABO,再利用三角形的内角和定理求出∠AOB,然后利用对顶角,即可判断B选项;根据邻补角的定义和角平分线的定义求出∠DCO,再利用三角形的内角和定理求出∠BDC,即可判断C选项;利用角平分线的性质,推出AD为△ABC的外角平分线,然后列式计算求出∠DAC,即可判断D选项.【详解】解:∵∠ABC=50°,∠ACB=60°,∴∠BAC=180°-∠ABC-∠ACB=180°-50°-60°=70°,故A选项正确,不符合题意;∵BD平分∠ABC,∴∠ABO=12∠ABC=12×50°=25°,在△ABO中,∠AOB=180°-∠BAC-∠ABO=180°-70°-25°=85°,∴∠DOC=∠AOB=85°,故B选项错误,符合题意;∵CD平分∠ACE,∴∠ACD=12∠ACE=12180°-∠ACB=12180°-60°=60°,在△COD中,∠BDC=180°-∠COD-∠ACD=180°-85°-60°=35°,故C选项正确,不符合题意;∵BD、CD分别是∠ABC和∠ACE的平分线,∴D到AB、AC、BC的距离相等,∴AD是△ABC的外角平分线,∴∠DAC=12180°-∠BAC=12180°-70°=55°,故D选项正确,不符合题意.故选:B.【点睛】本题考查角平分线的性质,三角形的内角和定理,角平分线的定义,熟记定理和概念是解题关键.6(2022春·重庆黔江·七年级统考期末)如图,已知AB∥CD,点E在两平行线之间,连接BE,CE,∠ABE的平分线与∠BEC的平分线的反向延长线交于点F,若∠BFE=50°,则∠C等于( ).A.70°B.80°C.85°D.90°【答案】B【分析】延长BE交DC的延长线于G,根据三角形内角和定理,可得∠EBF+∠BEF=130°,根据∠ABE的平分线与∠BEC的平分线的反向延长线交于点F可得∠ABE+∠BEF+∠FEC=260°,根据平行线的性质可得∠ECG=100°,进而可求解.【详解】解:延长BE交DC延长线于点G,∵∠BFE=50°,∠EBF+∠FEB+∠BFE=180°,∴∠EBF+∠BEF=180°-50°=130°,∵∠ABE的平分线与∠BEC的平分线的反向延长线交于点F,∴∠ABE+∠BEF+∠FEC=260°,∵AB∥CD,∴∠ABE=∠BGC,∴∠BGC+∠BEF+∠FEC=260°,∵∠BEF+∠FEG=180°,∴∠BGC+∠CEG=80°,∴∠ECG=100°,∴∠ECD=180°-100°=80°.故选:B【点睛】本题主要考查有关角平分线的计算,平行线的性质,三角形内角和定理,熟练掌握平行线的性质是解题的关键.7(2022春·北京海淀·七年级校考期中)如图,在平面直角坐标系中,直线AB与y轴在正半轴、x轴正半轴分别交A 、B 两点,点C 在BA 的延长线上,AD 平分∠CAO ,BD 平分∠ABO ,则∠D 的度数是()A.30°B.45°C.55°D.60°【答案】B 【分析】由OA ⊥OB 即可得出∠OAB +∠ABO =90°、∠AOB =90°,再根据角平分线的定义以及三角形内角和定理即可求出∠D 的度数.【详解】解:∵OA ⊥OB ,∴∠OAB +∠ABO =90°,∠AOB =90°.∵DA 平分∠CAO ,∴∠DAO =12∠OAC =12(180°-∠OAB ).∵DB 平分∠ABO ,∴∠ABD =12∠ABO ,∴∠D =180°-∠DAO -∠OAB -∠ABD =180°-12(180°-∠OAB )-∠OAB -12∠ABO =90°-12(∠OAB +∠ABO )=45°.故选:B .【点睛】本题考查了三角形内角和定理,解题的关键是找出∠D =90°-12(∠OAB +∠ABO ).本题属于基础题,难度不大,解决该题型题目时,熟练运用三角形内角和定理解决问题是关键.8(2023·江苏·八年级月考)如图,ΔABC 的外角∠ACD 的平分线CP 与内角∠ABC 平分线BP 交于点P ,若∠BPC =40°,则∠BAC 的度数是.【解答】解:在ΔABC 中,∠ACD =∠A +∠ABC ,在ΔPBC 中,∠PCD =∠P +∠PBC ,∵PB 、PC 分别是∠ABC 和∠ACD 的平分线,∴∠PCD =12∠ACD ,∠PBC =12∠ABC ,∴∠P +∠PCB =12(∠A +∠ABC )=12∠A +12∠ABC =12∠A +∠PCB ,∴∠PCD =12∠A ,∴∠BPC =40°,∴∠A =2×40°=80°,即∠BAC =80°.故答案为:80°.9(2023春·河北·七年级专题练习)如图,在△ABC 中,∠ABC 和∠ACB 的角平分线交于点O ,延长BO 与∠ACB 的外角平分线交于点D ,若∠BOC =130°,则∠D =【答案】40°【分析】根据角平分线的定义结合三角形外角的性质即可得到结论.【详解】解:∵∠ABC和∠ACB的角平分线交于点O,∴∠ACO=12∠ACB,∵CD平分∠ACE,∴∠ACD=12∠ACE,∵∠ACB+∠ACE=180°,∴∠OCD=∠ACO+∠ACD=12(∠ACB+∠ACE)=12×180°=90°,∵∠BOC=130°,∴∠D=∠BOC-∠OCD=130°-90°=40°,故答案为:40°.【点睛】本题考查了三角形的外角性质,角平分线的定义,熟练掌握相关性质和概念正确推理计算是解题的关键.10(2022秋·浙江八年级课时练习)(2018育才单元考)如图,在△ABC中,∠ABC和∠ACD的角平分线交于点A1,得∠A1,∠A1BC和∠A1CD的角平分线交于点A2,得∠A2,⋯⋯,∠A n-1BC和∠A n-1CD的角平分线交于点A n,得∠A n(1)若∠A=80°,则∠A1=,∠A2=,∠A3=(2)若∠A=m°,则∠A2015=.【答案】40°20°10°m 22015 °【分析】(1)利用角平分线的定义和三角形外角性质,易证∠A1=12∠A,进而可求∠A1,同理易证∠A2=1 2∠A1,∠A3=12∠A2,进而可求∠A2和∠A3;(2)利用角平分线的定义和三角形外角性质,易证∠A1=12∠A,进而可求∠A1,同理易证∠A2=12∠A1,∠A3=12∠A2,⋯,以此类推可知∠A2015即可求得.【详解】解:(1)∵∠A=∠ACD-∠ABC,∠A1=∠A1CD-∠A1BC∵∠ABC和∠ACD的角平分线交于点A1,∠A=80°∴∠A1CD=12∠ACD,∠A1BC=12∠ABC∴∠A1=∠A1CD-∠A1BC=12∠ACD-12∠ABC=12(∠ACD-∠ABC)=12∠A=40°同理可证:∠A2=12∠A1=20°,∠A3=12∠A2=10°故答案为:40°;20°;10°.(2)∵∠A=∠ACD-∠ABC,∠A1=∠A1CD-∠A1BC∵∠ABC 和∠ACD 的角平分线交于点A 1,∠A =m °∴∠A 1CD =12∠ACD ,∠A 1BC =12∠ABC ∴∠A 1=∠A 1CD -∠A 1BC =12∠ACD -12∠ABC =12(∠ACD -∠ABC )=12∠A =m 2°同理可证:∠A 2=12∠A 1=m 22 °,∠A 3=12∠A 2=m 23 °∴∠A 2015=m 22015 °故答案为:m 22015°.【点睛】本题考查了角平分线定义和三角形外角性质,解题的关键是推导出∠A 1=12∠A ,并依此找出规律.11(2023·浙江杭州·八年级期末)如图,在四边形ABCD 中,∠A +∠D =m °,∠ABC 的平分线与∠BCD 的平分线交于点P ,则∠P =.(用含字母m 的代数式表示)【答案】12m o 【分析】根据四边形的内角和是360°,求出∠ABC +∠BCD 的度数,然后根据角平分线的定义及三角形的内角和定理求出∠P 的度数即可.【详解】解:∵∠A +∠D =m °,且四边形内角和为360°,∴∠ABC +∠BCD =360°-m °,∵PB 、PC 是∠ABC 、∠BCD 的角平分线,∴∠PBC =12∠ABC ,∠BCP =12∠BCD ,∴∠PBC +∠BCP =12∠ABC +12∠BCD =12∠ABC +∠BCD =12360°-m o ∴∠P =180°-(∠PBC +∠BCP )=180°-12360°-m o 故答案为:12m o .【点睛】本题考查了四边形的内角和及三角形的内角和与角平分线相关的角度计算问题,解题的关键是表达出∠PBC +∠BCP 的度数.12(2023春·河南·七年级专题练习)如图,点M 是△ABC 两个内角平分线的交点,点N 是△ABC 两外角平分线的交点,如果∠CMB :∠CNB =3:2,那么∠CAB =.【答案】36°【分析】由角平分线的定义得∠NCM =∠MBN =12×180°=90°,再比的关系可求得∠CMB =108°,再由内角平分线及三角形内角和即可求得结果.【详解】由题意得:∠NCM =∠MBN =12×180°=90°,∴∠CMB +∠CNB =180°,又∠CMB :∠CNB =3:2,∴∠CMB =108°,∴12(∠ACB +∠ABC )=180°-∠CMB =72°,∴∠ACB+∠ABC=144°,∴∠CAB=180°-(∠ACB+∠ABC)=36°.【点睛】本题考查了三角形内角和定理、三角形角平分线的定义等知识,由条件得到∠NCM=∠MBN=90°是关键.13(2023·甘肃陇南·统考一模)在△ABC中,AB=AC,∠A=100°.点M在BC的延长线上,∠ABC 的平分线交AC于点D.∠MCA的平分线与射线BD交于点E.(1)依题意补全图形;用尺规作图法作∠MCA的平分线;(2)求∠BEC的度数.【答案】(1)见解析(2)50°【分析】(1)根据尺规作图法可作∠MCA的平分线;(2)根据角平分线的定义可得∠ABD=∠CBD=20°,∠MCE=∠DCE=70°,再根据三角形内角和定理即可求解.【详解】(1)解:如图,CE即为所求;(2)解:∵AB=AC,∠A=100°,∴∠ACB=∠ABC=40°,∵BD是∠ABC的平分线,∴∠ABD=∠CBD=20°,∵∠ACM=180°-40°=140°,CE是∠MCA的平分线,∴∠MCE=∠DCE=70°,∴∠BEC=∠MCE-∠CBD=70°-20°=50°.【点睛】本题考查尺规作图-角平分线、角平分线的定义、三角形内角和定理,熟练掌握尺规作图的方法和相关知识是解题的关键.14(2023·山东八年级期中)如图,在ΔABC中,角平分线AD、BE、CF相交于点O,过点B作BG⊥CF于点G,∠OBG=12∠BAC成立吗?说明理由.【答案】∠OBG=12∠BAC 成立,见解析.【分析】根据三角形内角平分线的交角的基本图形和结论和三角形外角的性质定理即可得出答案【详解】解:∠OBG=12∠BAC成立.理由如下:∵在ΔABC中,角平分线AD、BE、CF相交于点O,由三角形内角平分线的交角的基本图形和结论得,∠BOC=90°+12∠BAC.由三角形的外角性质得,∠BOC=∠G+∠OBG=90°+∠OBG,∴90°+12∠BAC=90°+∠OBG,∴∠OBG=12∠BAC【点睛】本题考查三角形的内角和定理,及三角形的角平分线的性质,熟练掌握相关的知识点是解题关键.15(2023·黑龙江八年级课时练习)(1)如图(1)所示,已知在△ABC中,O为∠ABC和∠ACB的平分线BO,CO的交点.试猜想∠BOC和∠A的关系,并说明理由.(2)如图(2)所示,若O为∠ABC的平分线BO和∠ACE的平分线CO的交点,则∠BOC与∠A的关系又该怎样?为什么?【答案】(1)∠BOC=12∠A+90°;理由见解析;(2)∠BOC=12∠A;理由见解析【分析】(1)根据三角形内角和定理得出∠A+∠ABC+∠ACB=180°,∠BOC+∠OBC+∠OCB=180°,根据角平分线的性质得出∠ABC=2∠OBC,∠ACB=2∠OCB,然后得出∠BOC+12∠ABC+12∠ACB=180°,最后得出结论;(2)根据外角的性质得出∠A+∠ABC=∠ACE,∠OBC+∠BOC=∠OCE,然后根据角平分线的性质得出∠ABC=2∠OBC,∠ACE=2∠OCE,最后根据∠BOC=∠OCE-∠OBC得出答案.【详解】(1)∠BOC=12∠A+90°.在△ABC中,∠A+∠ABC+∠ACB=180°,在△BOC中,∠BOC+∠OBC+∠OCB=180°,又∵BO,CO分别是∠ABC,∠ACB的平分线,∴∠ABC=2∠OBC,∠ACB=2∠OCB.∴∠BOC+12∠ABC+12∠ACB=180°.∴∠BOC=180°-12(∠ABC+∠ACB)=180°-12(180°-∠A)=90°+12∠A.(2)∠BOC=12∠A.∵∠A+∠ABC=∠ACE,∠OBC+∠BOC=∠OCE,∴∠A=∠ACE-∠ABC,∠BOC=∠OCE-∠OBC又∵BO,CO分别是∠ABC和∠ACE的平分线,∴∠ABC=2∠OBC,∠ACE=2∠OCE.∴∠BOC=∠OCE-∠OBC=12∠ACE-12∠ABC=12(∠ACE-∠ABC)=12∠A.【点睛】本题考查了角平分线的性质和三角形外角的性质,熟练掌握外角性质并能正确计算是解题关键.16(2023春·八年级单元测试)如图,∠CBF,∠ACG是△ABC的外角,∠ACG的平分线所在的直线分别与∠ABC,∠CBF的平分线BD,BE交于点D,E.(1)若∠A=70°,求∠D的度数;(2)若∠A=a,求∠E;(3)连接AD,若∠ACB=β,则∠ADB=.【答案】(1)35°;(2)90°-12α;(3)12β【分析】(1)由角平分线的定义得到∠DCG=12∠ACG,∠DBC=12∠ABC,然后根据三角形外角的性质即可得到结论;(2))根据角平分线的定义得到∠DBC=12∠ABC,∠CBE=12∠CBF,于是得到∠DBE=90°,由(1)知∠D=12∠A,根据三角形的内角和得到∠E=90°-12α;(3)根据角平分线的定义可得,∠ABD=12∠ABC,∠DAM=12∠MAC,再利用三角形外角的性质可求解.【详解】解:(1)∵CD平分∠ACG,BD平分∠ABC,∴∠DCG=12∠ACG,∠DBC=12∠ABC,∵∠ACG=∠A+∠ABC,∴2∠DCG=∠ACG=∠A+∠ABC=∠A+2∠DBC,∵∠DCG=∠D+∠DBC,∴2∠DCG=2∠D+2∠DBC,∴∠A+2∠DBC=2∠D+2∠DBC,∴∠D=12∠A=35°;(2)∵BD平分∠ABC,BE平分∠CBF,∴∠DBC=12∠ABC,∠CBE=12∠CBF,∴∠DBC+∠CBE=12(∠ABC+∠CBF)=90°,∴∠DBE=90°,∵∠D=12∠A,∠A=α,∴∠D=12α,∵∠DBE=90°,∴∠E=90°-12α;(3)如图,∵BD平分∠ABC,CD平分∠ACG,∴AD平分∠MAC,∠ABD=12∠ABC,∴∠DAM=12∠MAC,∵∠DAM=∠ABD+∠ADB,∠MAC=∠ABC+∠ACB,∠ACB=β,∴∠ADB=12∠ACB=12β.故答案为:12β.【点睛】本题主要考查三角形的角平分线,三角形外角的性质,灵活运用三角形外角的性质是解题的关键.17(2023·福建泉州·七年级阶段练习)在ΔABC 中,已知∠A =α.(1)如图1,∠ABC 、∠ACB 的平分线相交于点D .①当α=80°时,∠BDC 度数=度(直接写出结果);②∠BDC 的度数为(用含α的代数式表示);(2)如图2,若∠ABC 的平分线与∠ACE 角平分线交于点F ,求∠BFC 的度数(用含α的代数式表示).(3)在(2)的条件下,将ΔFBC 以直线BC 为对称轴翻折得到ΔGBC ,∠GBC 的角平分线与∠GCB 的角平分线交于点M (如图3),求∠BMC 的度数(用含α的代数式表示).【答案】(1)①130°;②90°+12α;(2)∠BFC =12α(3)∠BMC =90°+14α【详解】:(1)①130°;②90°+12α;(2)∵BF 和CF 分别平分∠ABC 和∠ACE ∴∠FBC =12∠ABC ,∠FCE =12∠ACE ∴∠BFC =∠FCE -∠FBC =12∠ACE -∠ABC =12∠A 即∠BFC =12α(3)由轴对称性质知:∠BGC =∠BFC =12α由(1)②可得∠BMC =90°+12∠BGC ∴∠BMC =90°+14α.18(2023·江苏盐城·七年级阶段练习)如图,△ABC 的角平分线相交于P ,∠A =m °,(1)若∠A =40°,求∠BPC 的度数;(2)设△ABC 的外角∠CBD 、∠BCE 的平分线相交于Q ,且∠A =m °,求∠BQC 的度数(3)设△ABC 的外角∠CBD 、∠BCE 的n 等分线相交于R ,且∠A =m °,∠CBR =1n ∠CBD ,∠BCR =1n ∠BCE ,求∠BRC 的度数【答案】(1)110°(2)90°+12m °(3)n -1n ×180°-m n(此结果形式可以不同,只要正确皆可)【详解】试题分析:(1)根据三角形内角和定理和角平分线的性质解答即可;(2)(3)根据三角形内角和定理和三角形外角的性质解答即可.试题解析:解:(1)∵∠A =40°,∴∠ABC +∠ACB =180°-40°=140°.∵BP 、CP 是角平分线,∴∠ABC=2∠PBC ,∠ACB =2∠PCB ,∴∠PBC +∠PCB =12(∠ABC +∠ACB )==12×140°=70°,∴∠P =180°-70°=110°.(2)∵∠DBC =∠A +∠ACB ,∠BCE =∠A +∠ABC ,∴∠DBC +∠BCD =2∠A +∠ABC +∠ACB =∠A +180°=m +180°.∵BQ ,CQ 是角平分线,∴∠DBC =2∠QBC ,∠BCE =2∠BCQ ,∴∠QBC +∠BCQ =12(∠DBC +∠ECB )=12(m +180°)=90°+12m .在△BCQ 中,∠Q =180°-(∠QBC +∠BCQ )=180°-90°+12m =90°-12m .(3)由(2)得:∠DBC +∠BCD =m +180°,∠RBC +∠BCR =1n (∠DBC +∠ECB )=1n (m +180°).在△BCR 中,∠R =180°-(∠RBC +∠BCR )=180°-1n (m +180°)=n -1n ×180-m n.点睛:本题主要考查了三角形内角和定理,角平分线的定义以及三角形外角性质的运用,解题时注意:三角形内角和等于180°.根据角的和差关系进行计算是解决问题的关键.19(2023·江西上饶·八年级校考阶段练习)(1)探究1:如图1,P 是△ABC 的内角∠ABC 与∠ACB 的平分线BP 和CP 的交点,若∠A =70∘,则∠BPC =度;(2)探究2:如图2,P 是△ABC 的外角∠DBC 与外角∠ECB 的平分线BP 和CP 的交点,求∠BPC 与∠A的数量关系?并说明理由.(3)拓展:如图3,P 是四边形ABCD 的外角∠EBC 与∠BCF 的平分线BP 和CP 的交点,设∠A +∠D =α.,直接写出∠BPC 与α的数量关系;【答案】(1)125°;(2)∠BPC =90°-12∠A ,理由见解析;(3)∠BPC =180°-12α【分析】(1)借助角平分线的性质即可得到∠PBC =12∠ABC 以及∠PCB =12∠ACB ,然后在△BPC 中进一步分析可找出∠BPC 与∠A 的关系,进而求出∠BPC 的度数;(2)根据三角形内角和定理可知∠BPC =180°-(∠PBC +∠PCB ),根据角平分线的定义可用12(∠DBC +∠ECB )表示∠PBC +∠PCB ,再利用三角形外角性质得到∠DBC +∠ECB =∠A +∠ACB +∠A +∠ABC ,即可求出∠BPC 与∠A 的关系;(3)延长BA 、CD 相交于点Q ,由(2)的分析可直接得出∠P 与∠Q 的关系,而∠BAD 与∠CDA 是△ADQ 的外角,再结合三角形外角性质即可解答.【详解】(1)解:∠BPC =180°-(∠PBC +∠PCB )=180°-12(∠ABC +∠ACB )=180°-12(180°-∠A )=90°+12∠A =90°+35°=125°故答案为125°(2)∠BPC =90°-12∠A 理由如下:∠BPC =180°-(∠PBC +∠PCB )=180°-12(∠DBC +∠ECB )=180°-12(∠A +∠ACB +∠A +∠ABC )=180°-12(∠A +180°)=90°-12∠A(3)延长BA 、CD 相交于点Q ,如图∠BPC =90°-12∠Q ∴∠Q =180°-2∠BPC ∴∠BAD +∠CDA =180°+∠Q =180°+180°-2∠BPC =360°-2∠BPC∴∠BPC =180°-12α故答案为∠BPC =180°-12α【点睛】本题考查的是三角形内角和与外角的知识,掌握三角形外角性质以及内角和定理是解题关键.20(2023·甘肃天水·七年级统考期末)已知在△ABC 中,图1,图2,图3中的△ABC 的内角平分线或外角平分线交于点O ,(1)如图1,点O 是△ABC 的两个内角平分线的交点,猜想∠O 与∠A 之间的数量关系,并加以证明.(2)请直接写出结果.如图2,若∠A =60°,△ABC 的内角平分线与外角平分线交于点O ,则∠O =;如图3,若∠A =60°,△ABC 的两个外角平分线交于点O ,则∠O =.【答案】(1)∠O =90°+12∠A ,证明见解析;(2)30°;60°.【分析】(1)根据角平分线的性质可以得到∠OBC =12∠ABC ,∠OCB =12∠ACB ,再根据三角形的内角和定理得到△ABC 和△OBC 的三个内角的和是180°,对角度进行等价代换即可;(2)图2中,根据角平分线的性质可以得到∠OBC =12∠ABC ,∠OCM =12∠ACM ,再根据三角形外角的性质得到∠O =∠OCM -∠OBC 和∠A =∠ACM -∠ABC ,最后对角度进行等价代换即可;图3中,根据角平分线的性质可以得到∠OBC =12∠PBC ,∠OCB =12∠QCB ,再根据三角形的内角和定理得到△ABC 和△OBC 的三个内角的和是180°,最后再结合平角的性质对角度进行等价代换即可.【详解】解:(1)∠O =90°+12∠A .证明:∵BO 平分∠ABC ,CO 平分∠ACB ,∴∠OBC =12∠ABC ,∠OCB =12∠ACB ,∴∠O =180°-(∠OBC +∠OCB )=180°-12∠ABC +12∠ACB =180°-12(∠ABC +∠ACB )=180°-12180°-∠A =90°+12∠A .即∠O =90°+12∠A .(2)30°;60°.如图2所示:∵BO平分∠ABC,CO平分∠ACM,∴∠OBC=12∠ABC,∠OCM=12∠ACM,∴∠O=∠OCM-∠OBC=12∠ACM-12∠ABC=12(∠ACM-∠ABC)=12∠A.∵∠A=60°∴∠O=12∠A=12×60°=30°.即∠O=30°.如图3所示:∵BO平分∠PBC,CO平分∠QCB,∴∠OBC=12∠PBC,∠OCB=12∠QCB,∴∠O=180°-(∠OBC+∠OCB)=180°-12∠PBC+12∠QCB=180°-12180°-∠ABC+12180°-∠ACB=12∠ABC+12∠ACB=12∠ABC+∠ACB=1 2180°-∠A.∵∠A=60°∴∠O=12180°-∠A=12×180°-60°=60°.即∠O=60°.故答案为:30°;60°.【点睛】本题考查了角平分线的性质,三角形的内角和定理和三角形外角的性质,熟练掌握这些知识点是解题关键,特别注意等价代换的使用.21。
巧借三角形的两条内(外)角平分线夹角的模型解决问题
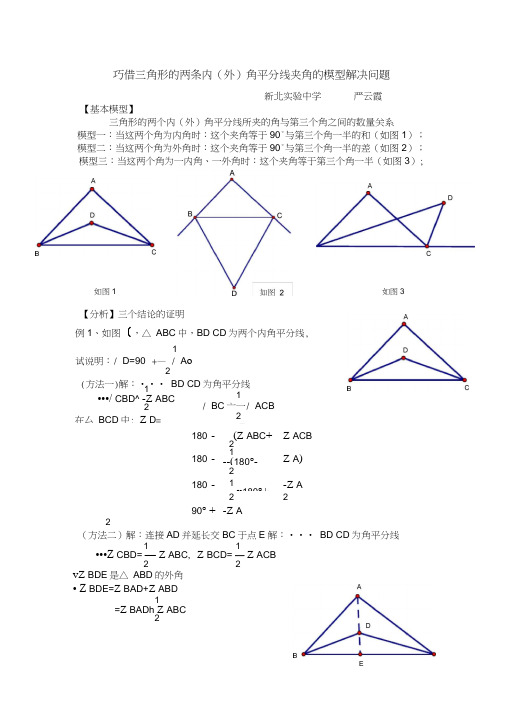
巧借三角形的两条内(外)角平分线夹角的模型解决问题新北实验中学严云霞【基本模型】三角形的两个内(外)角平分线所夹的角与第三个角之间的数量关系模型一:当这两个角为内角时:这个夹角等于90°与第三个角一半的和(如图1); 模型二:当这两个角为外角时:这个夹角等于90°与第三个角一半的差(如图2); 模型三:当这两个角为一内角、一外角时:这个夹角等于第三个角一半(如图3);180°-(Z ABC + 2Z ACB 180°- 1 --(180°-Z A )2180°-1x 180°+ -Z A22 90° + -Z A2(方法二)解:连接AD 并延长交BC 于点E 解:••• BD CD 为角平分线1 1•••Z CBD= — Z ABC, Z BCD= — Z ACB22vZ BDE 是△ ABD 的外角• Z BDE=Z BAD+Z ABD1=Z BADh Z ABC2如图1 【分析】三个结论的证明例1、如图〔,△ ABC 中,BD CD 为两个内角平分线,1试说明:/ D=90° +— / A o2(方法一)解:••• BD CD 为角平分线1/ BC 亠一/ ACB2(/ CBDb Z BCD1•••/ CBD^ -Z ABC2在厶 BCD 中: Z D =如图3E1 同理可得/ CDE ^Z CAD+1/ ACB2又•••/ BDO Z BDE 亡 CDE11•••/ BDO Z BAD+丄 / ABC+/ CAD+丄 / ACB2 21=/ BA 迭(/ ABC+ZACB1 =Z BACi (180°—/ BAC21 =90°+—/ BAC2 例2、如图,ED 、CD 为AABC 的两条外角平分线, 1 试说明:/ D=90°— - / A o 2 解:••• BD CD 为角平分线1•••/ CBD — / CBE21 / BCD= — / BCF 2又•••/ CBE / BCDABC 的外角 •••/ CBE=Z A +Z ACB / BC1 A +Z ABC•••/ CBE^Z Bd A +Z ACB+Z A +Z ABO / + 180°在厶BCD 中:(/ CBE ^Z BCFZ A + 180°)2 —1 Z A2【小结】通过对模型1、2的分析和证明,我们还能发现三角形两内角平分 线的夹角和两外角平分线的夹角互补,即和为 180。
三角形角平分线地结论及应用

浅议三角形角平分线的结论及应用摘要:一个角的平分线是一条射线,而三角形的角平分线是一条线段。
本文主要谈两点:关于三角形的、外角平分线的夹角的问题和关于三角形、外角平分线的交点问题。
关于三角形的、外角平分线的夹角问题:(1)三角形两角平分线的夹角等于90度与三角形第三个角的一半的和。
(2)三角形两外角平分线的夹角等于90度与三角形第三个角的一半的差。
(3)三角形一个角的平分线与一个外角平分线的夹角等于三角形第三个角的一半(4)三角形两角平分线的夹角与两外角平分线的夹角互补或相等。
关于三角形外角平分线的交点问题:(5)三角形的三条角平分线相交于一点,这点到三角形的三边的距离相等(6)三角形两外角平分线的交点到三角形三边所在的直线相等,并且这点在三角形第三个角的平分线上等关键词:三角形角平分线夹角交点变式练习一个三角形的角平分线不外乎就是角的平分线和外角的角平分线。
在学习过程中,教师要指导学生善于对三角形的角平分线的基本图形进行归纳,对角平分线的性质和结论做好总结,这样对以后知识的积累有很大的帮助,对解决复杂的几何证明题也更便捷。
下面就三角形角平分线的相关结论逐一探讨。
结论一:如图1、在△ABC中,∠ABC、∠ACB的角平分线的交与点D,1∠A。
试探究:∠D=90°+2解:∵BD、CD为角平分线1∠ABC,(图1)∴∠CBD=21∠ACB。
∠BCD=2在△BCD中:∠D=180°-(∠CBD+∠BCD)1(∠ABC+∠ACB)=180°-21(180°-∠A)=180°-21∠A=90°+2变式练习的题目有(1)如图2、在△ABC中,∠ABC、∠ACB的角平分线的交与点D,∠D=100°,则∠A的度数是度。
1∠A。
则∠A=2∠D―180°,解:由结论1得知,∠D=90°+2容易得出∠A=20°(图2)(2)如图3:在四边形ABCD中,∠D=120°,∠A=100°∠ABC、∠ACB的角平分线的交与点E,试求∠BEC的度数。
三角形角平分线的求角问题归纳

2∠M=180O-∠A
∠M=90O- 1 ∠A 2
B
C
αα ββ
F
E
M
八年级数学上册
人民教育出版社
二、两外角平分线求角
如图:在∆ABC中,M点是外角∠CBF和∠BCE的角平分线的交点,则∠M与∠A有什么
关系?
A
解:∵BM平分∠CBF CM平分∠BCE
∴∠MBC=∠MBF ∠MCB=∠MCE
设∠MBC=∠MBF=α ∠MCB=∠MCE=β ∵∠ABC+∠ACB=180O-∠A
关系?
A
∠A+∠ABC+∠ACB=180O ∠ABC+∠ACB=180O-∠A
α+β+∠M=180O α+β=180O-∠M
2α+∠ABC=180O ∠ABC=180O-2α
2β+∠ACB=180O ∠ACB=180O-2β
∠ABC+∠ACB=3216M800OO--22α(α-+α1218+β80β0O)-O∠-M 2β)
O
ββ C
α+β=90O- 1 ∠A 2
90O- 1 ∠A=180O-∠O 2
1 ∠O=180O-90O+ 2 ∠A
∠O=90O+1 ∠A
2
八年级数学上册
人民教育出版社
一、两内角平分线求角
已知:在∆ABC中,若O点是∠ABC和∠ACB的角平分线的交点,求证:∠O=90O+ 1 ∠A
证明:∵ BO平分∠ABC ,CO平分∠ACB
一、两内角平分线求角
已知:在∆ABC中,若O点是∠ABC和∠ACB的角平分线的交点,求证:∠O=90O+ 1∠A 2
巧借三角形的两条内外角平分线夹角的模型解决问题

三角形边长的求解 方法
三角形边长求解的 步骤
三角形边长求解的 实例
三角形内外角平分线夹角模型的应 用场景
三角形内切圆半径的几何意义
添加标题
添加标题
三角形内切圆半径的求解方法
添加标题
添加标题
三角形内切圆半径在解题中的应用
三角形内外角平分 线夹角模型的解题 思路
确定三角形内外角平分 线的位置是解题的关键 步骤,可以通过作图或 逻辑推理来确定。
三角形内外角平分线夹角与三角形其他角的关系 三角形内外角平分线夹角的定理和证明 三角形内外角平分线夹角的性质定理及其应用 三角形内外角平分线夹角与三角形面积的关系
确定三角形内外角平分线夹角 的位置和性质
利用三角形内外角平分线夹角 进行角度计算
利用三角形内外角平分线夹角 解决几何问题
三角形内外角平分线夹角的特 殊性质和定理
该模型的应用范围广泛,不仅适用于三角形,还可以拓展到多边形等领域。
掌握三角形内外角平分线夹角模型有助于提高学生的几何思维能力,为进一步学习其他几何知 识打下基础。
在实际生活中,三角形内外角平分线夹角模型的应用也十分广泛,涉及到建筑设计、工程测量 等多个领域。
感谢您的观看
汇报人:XX
在解题过程中,需要利 用三角形内外角平分线 的性质,如平行线性质、 角平分线性质等。
确定三角形内外角平分线 的位置有助于进一步推导 和证明其他相关结论,如 三角形内角和定理、外角 定理等。
在实际应用中,确定三角 形内外角平分线的位置可 以帮助解决一些实际问题, 如测量、几何作图等。
定义:三角形内外角平分线夹角为α,利用性质建立方程
三角形面积计算 案例:一个三角 形的三边长分别 为5cm、6cm和 7cm,求其面积
三角形中角平分线形成的角的三个小结论

三角形中角平分线形成的角的三个小结论湖北省黄石市下陆中学802班成昌力(14岁)指导教师:陈勇学习三角形角平分线的知识时,我发现了三个有趣的结论,让大家一起来看看吧!例1 如图1,已知△ABC的∠B和∠C的平分线BD、CE相交于点O,求证:∠BOC= 90°+∠A。
解:∵BD平分∠ABC∴∠ABC=2∠ABD=2∠DBC同理:∠ACB=2∠ACE=2∠ECB.在△BOC中,∠BOC+∠DBC+∠ECB= 180°,∴∠BOC=180°-(∠DBC+∠ECB)∵在△ABC中, ∠A+∠ABC+∠ACB= 180°,∴∠ABC+∠ACB =180°-∠A∴2∠DBC+2∠ECB =180°-∠A∴∠DBC+∠ECB =90°-∠A∴∠BOC=180°-(90°-∠A)即∠BOC= 90°+∠A。
结论1:在一个三角形中,任意两个内角的角平分线相交形成的钝角等于90°加上第三个角的一半。
例2 如图2,已知BO平分∠EBC,CO平分∠FCB,BO、CO相交于点O,探究∠BOC与∠A的关系。
解:∵BO平分∠EBC∴∠EBC=2∠CBO=2∠EBO同理:∠FCB=2∠BCO=2∠FCO又∵∠ABC+∠EBC=180°∴∠ABC=180°-∠EBC=180°-2∠CBO同理:∠ACB=180°-∠FCB=180°-2∠BCO∵∠A+∠ABC+∠ACB=180°∴∠A+180°-2∠CBO+180°-2∠BCO =180°∴∠CBO+∠BCO= 90°+∠A又∠BOC+∠CBO+∠BCO =180°∴∠BOC =180°-(∠CBO+∠BCO)=180°-(90°+∠A)=90°-∠A结论2:三角形两个外角的角平分线相交形成的角等于90°减去第三个外角对应的内角的一半。
初中数学_三角形内外角平分线有关命题的证明及应用

三角形内外角平分线一.命题的证明及应用在中考常有与三角形内外角平分线有关的题目,若平时不注意总结是很难一下子解决的.下面来一起学习一下.命题1 如图1,点D是△ABC两个内角平分线的交点,则∠D=90°+∠A.证明:如图1:∵∠1=∠,∠2=∠,∴2∠1+2∠2+∠A=180°①∠1+∠2+∠D=180°②①-②得:∠1+∠2+∠A=∠D③由②得:∠1+∠2=180°-∠D④把③代入④得:∴180°-∠D+∠A=∠D∠D=90°+∠A.点评利用角平分线的定义和三角形的内角和等于180°,不难证明.命题2 如图2,点D是△ABC两个内角平分线的交点,则∠D=90°-∠A.证明:如图2:∵DB和DC是△ABC的两条外角平分线,∴∠D=180°-∠1-∠2=180°-(∠DBE+∠DCF)=180°-(∠A+∠4+∠A+∠3)=180°-(∠A+180°)=180°-∠A-90°=90°-∠A;点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和以及三角形的内角和等于180°,可以证明.命题3 如图3,点E是△ABC一个内角平分线与一个外角平分线的交点,则∠E=∠A.证明:如图3:∵∠1=∠2,∠3=∠4,∠A+2∠1=2∠4①∠1+∠E=∠4②①×代入②得:∠E=∠A.点评利用角平分线的定义和三角形的一个外角等于与它不相邻两外角的和,很容易证明.命题4如图4,点E是△ABC一个内角平分线BE与一个外角平分线CE的交点,证明:AE是△ABC的外角平分线.证明:如图3:∵BE是∠ABC的平分线,可得:EH=EFCE是∠ACD的平分线, 可得:EG=EF∴过点E分别向AB、AC、BC所在的直线引垂线,所得的垂线段相等.即EF=EG=EH∵EG=EH∴AE是△ABC的外角平分线.点评利用角平分线的性质和判定能够证明.应用上面的结论能轻松地解答一些相关的比较复杂的问题,下面来一起看.例1如图5,PB和PC是△ABC的两条外角平分线.①已知∠A=60°,请直接写出∠P的度数.②三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?解析:①由命题2的结论直接得:∠P=90°-∠A=90°-×60°=60°②根据命题2的结论∠P=90°-∠A,知三角形的三条外角平分线所在的直线形成的三角形的三个角都是锐角,则该三角形是锐角三角形.点评此题直接运用命题2的结论很简单.同时要知道三角形按角分为锐角三角形、直角三角形和钝角三角形.例2如图6,在△ABC中,延长BC到D,∠ABC与∠ACD的角平分线相较于点,∠BC与∠CD的平分线交与点,以此类推,…,若∠A=96°,则∠= 度.解析:由命题③的结论不难发现规律∠∠A.可以直接得:∠=×96°=3°.点评此题是要找出规律的但对要有命题③的结论作为基础知识.例3(203陕西第一大题填空题第八小题,此题3分)如图7,△ABC的外角∠ACD 的平分线CP的内角∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP=_______________.解析:此题直接运用命题4的结论可以知道AP是△ABC的一个外角平分线,结合命题3的结论知道∠BAC=2∠BPC, CAP=(180°-∠BAC )= (180°-2∠BPC )=50°.点评对命题3、4研究过的读者此题不难,否则将是一道在考试的时候花时间也不一定做的出来的题目.例4(2003年山东省)如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,∠ACB的平分线与∠ABC的外角平分线交与E点,连接AE,则∠AEB= 度.解析:有题目和命题4的结论可以知道AE是△ABC的一个外角平分线, 结合命题2的结论知道∠AEB=∠ACB-∠ACB=90°-×90°=45°点评从上面的做题过程来看题目中给出的“∠A=30°”这个条件是可以不用的.二.角平分线定理使用中的几种辅助线作法一、已知角平分线,构造三角形例题、如图所示,在△ABC 中,∠ABC=3∠C ,AD 是∠BAC 的平分线,BE ⊥AD 于F 。
用三角形的角平分线解决问题

用三角形的角平分线解决问题三角形是几何学中一个基本的形状,它具有许多特性和性质。
在数学和几何学的研究中,我们经常会遇到需要解决三角形相关问题的情况。
其中一个非常有用的工具是三角形的角平分线。
本文将探讨如何利用三角形的角平分线来解决问题。
一、角平分线的定义和性质在一个三角形中,如果从一个角的顶点引一条线段,将该角平分成相等的两部分,这条线段就被称为角的平分线。
三角形的每个角都可以找到一个角平分线。
利用角平分线,我们可以得到许多有用的性质。
首先,角平分线将一个角分成两个相等的角。
其次,三角形的三条角平分线相交于一个点,该点被称为三角形的内心。
三角形的内心是一个重要的几何中心,它与三角形的其他特性和性质有密切的关联。
二、利用角平分线解决三角形问题的方法1. 证明两条边相等或相似当我们需要证明三角形的两条边相等或相似时,角平分线是一个有力的工具。
通过绘制角平分线并观察角的性质,我们可以得出两条边相等或相似的结论。
2. 求解角度和边长在一些情况下,我们需要求解三角形中的角度或边长。
利用角平分线可以帮助我们简化问题。
通过绘制角平分线,我们可以将复杂的三角形问题转化为简单的几何问题,比如使用正弦、余弦、正切等函数来计算角度或边长。
3. 构造新的图形三角形的角平分线还可以帮助我们构造新的图形。
例如,我们可以利用角平分线来构造出三角形的内切圆,这是一个与三角形密切相关的圆形。
内切圆的圆心即为三角形的内心,利用内切圆的性质可以推导出许多有趣的结果。
三、实例分析为了更好地理解如何利用角平分线解决问题,让我们通过一个实例进行分析。
假设我们有一个三角形ABC,需要证明角平分线AD和角平分线BE的交点O为三角形ABC的内心。
我们首先观察角平分线的性质,发现角平分线将每个角分成两个相等的部分。
设角BAD等于角CAD,角ABE等于角CBE。
由于角平分线AD和BE分别平分了角BAC和角ABC,根据角的性质可以得出以下结论:1. 角BAD等于角CAD,角ABE等于角CBE;2. 角BAC等于角ABC;3. 角A和角B各自等于它们的平分线所平分的两个部分之和。
三角形角平分线的结论及应用

浅议三角形角平分线的结论及应用摘要:一个角的平分线是一条射线,而三角形的角平分线是一条线段。
本文主要谈两点:关于三角形的内、外角平分线的夹角的问题和关于三角形内、外角平分线的交点问题。
关于三角形的内、外角平分线的夹角问题:(1)三角形两内角平分线的夹角等于90度与三角形第三个内角的一半的和。
(2)三角形两外角平分线的夹角等于90度与三角形第三个内角的一半的差。
(3)三角形一个内角的平分线与一个外角平分线的夹角等于三角形第三个内角的一半(4)三角形两内角平分线的夹角与两外角平分线的夹角互补或相等。
关于三角形内外角平分线的交点问题:(5)三角形的三条内角平分线相交于一点,这点到三角形的三边的距离相等(6)三角形两外角平分线的交点到三角形三边所在的直线相等,并且这点在三角形第三个内角的平分线上等关键词:三角形角平分线夹角交点变式练习一个三角形的角平分线不外乎就是内角的平分线和外角的角平分线。
在学习过程中,教师要指导学生善于对三角形的角平分线的基本图形进行归纳,对角平分线的性质和结论做好总结,这样对以后知识的积累有很大的帮助,对解决复杂的几何证明题也更便捷。
下面就三角形角平分线的相关结论逐一探讨。
结论一:如图1、在△ABC中,∠ABC、∠ACB的角平分线的交与点D,试探究:∠D=90°+1∠A。
2解:∵BD、CD为角平分线∴∠CBD=1∠ABC,(图1)2∠BCD=1∠ACB。
2在△BCD中:∠D=180°-(∠CBD+∠BCD)=180°-1(∠ABC+∠ACB)2=180°-1(180°-∠A)2=90°+1∠A2变式练习的题目有(1)如图△2、在ABC中,∠ABC、∠ACB的角平分线的交与点D,∠D=100°,则∠A的度数是度。
解:由结论1得知,∠D=90°+1∠A。
则∠A=2∠D―180°,2容易得出∠A=20°(图2)(2)如图3:在四边形ABCD中,∠D=120°,∠A=100°∠ABC、∠ACB的角平分线的交与点E,试求∠BEC的度数。
三角形角平分线性质的引申及应用

-
1 2
( 180°
-
∠A)
=
90°
+
1 2
∠A.
性质 2 由三角形两条外角平分线所组
成的角等于 90° 与第三角一半的差.
如图 2,在 ABC 中,∠ABC、∠ACB 的外
角平分线交于点 P,则 ∠P
=
90° -
1 2
∠A.
%
A
B 1
D
C 2
E
P
图2
证明 因 为 BP、CP 分 别 平 分 ∠DBC,
∠ECB,
所以 ∠1
=
1 2
∠DBC,∠2
=
1 2
∠ECB.
在 PBC 中,
∠P = 180° - ( ∠1 + ∠2)
=
180° -
1 2
(
∠DBC
+
∠ECB)
= 180°
-
1 2
(
180°
- ∠ABC + 180°
-
∠ACB)
=
180°
-
1 2
[360°
- ( ∠ABC
+ ∠ACB) ]
=
1 2
( 180° - 2∠BPC)
= 50°.
例 3 如图 11,已知线段 AB、CD 相交于
点 O,连结 AD、CB,我们把形如图 11 的图形称
之为“8 字 形”. 如 图 12,在 图 11 的 条 件 下,
∠DAB 和 ∠BCD 的平分线 AP 和 CP 相交于点
P,并且与 CD、AB 分别相交于点 M、N.
叫做“规形图”. 观察如图 7 的“规形图”,若
∠ABC、∠ADC 的 平 分 线 相 交 于 点 O,则
三角形内外角平分线定理

三角形内外角平分线定理【三角形内外角平分线定理】是指在一个三角形中,如果一条直线既是一内角的角平分线,又是另外一个外角的角平分线,那么它将平分这个三角形的第三个内角。
这个定理在解决一些与三角形相关的几何问题时非常有用。
通过运用该定理,我们能够更深入地理解三角形的内外角关系,拓展我们对三角形性质的认识。
让我们来详细解释一下三角形内外角平分线定理的几何意义。
假设我们有一个三角形ABC,其中角A是一个内角,角D是一个外角,线段DE是角A的内角平分线,同时也是角D的外角平分线。
根据这个定理,我们可以得出结论:线段DE将平分角B的度数。
这意味着角BED和角CEA的度数相等。
那么,如何证明三角形内外角平分线定理呢?我们可以运用一些基本的几何知识和性质来推导。
我们知道在三角形ABC中,三个内角的和为180度。
假设角A的度数为x,角BED和角CEA的度数都设为y。
根据内角的性质,我们可以得到以下等式:x + y + (180 - x) = 180x + y = x + 180 - xy = 180从上述推导中可以看出,我们无法得出具体的角度度数。
在具体问题中,我们可以将该定理与其他定理、关系和性质结合使用,以解决更复杂的问题。
三角形内外角平分线定理不仅具有几何意义,还深刻影响着我们对数学抽象概念的理解。
这个定理揭示了三角形内外角的平分线之间的关系,通过思考和探索,我们可以发现更多有趣且深入的现象。
通过应用这个定理,我们能够更好地解决与三角形相关的问题。
总结来说,三角形内外角平分线定理是一个重要的几何性质。
它揭示了三角形内外角平分线之间的关系,并为我们解决与三角形相关的问题提供了有力的工具。
在解决问题时,我们可以从简单的情况出发,逐步深入,灵活运用不同的原理和方法。
通过不断学习和思考,我们能够提高对三角形性质的理解和运用能力。
对于我个人而言,三角形内外角平分线定理是几何学中一条重要的定理。
它不仅仅是数学知识的一部分,更是一种思维方式和解决问题的工具。
