判别一元二次方程根的情况

合集下载

一元二次方程的根的判别式

一元二次方程的根的判别式一元二次方程的根的判别式是指b²-4ac，它可以用来判断方程的根的情况。

当b²-4ac>0时，方程有两个不相等的实数根；当b²-4ac=0时，方程有两个相等的实数根；当b²-4ac<0时，方程没有实数根。

判别式的应用包括不解方程判断根的情况、确定方程待定系数的取值范围、证明方程根的性质以及解决综合题。

正确理解判别式的性质并熟练灵活地运用它是本节的重点和难点。

举例来说，对于方程2x²-5x+10=0，其判别式为b²-4ac=(-5)²-4×2×10=－550，因此该方程有两个不相等的实数根。

对于方程x²-2kx+4(k-1)=0，其判别式为b²-4ac=(-2k)²-4×1×4(k-1)=4(k-2)²≥0，因此该方程有实数根。

对于方程2x²-(4m-1)x+(m-1)=0，其判别式为b²-4ac=(-(4m-1))²-4×2×(m-1)=4(2m-1)²+5>0，因此该方程有两个不相等实根。

对于方程4x²+2nx+(n²-2n+5)=0，其判别式为b²-4ac=(2n)²-4×4(n²-2n+5)=－12(n-4/3)²－176/33<0，因此该方程没有实数根。

解这类题目时，一般先求出判别式Δ=b^2-4ac，然后对XXX进行化简或变形，使其符号明朗化，进而说明Δ的符号情况，得出结论。

对判别式进行变形的基本方法有因式分解、配方法等。

在解题前，首先应将关于x的方程整理成一般形式，再求Δ=b^2-4ac。

当Δ≥0时，方程有实数根，反之也成立。

例2已知关于x的方程x-(m-2)x+m^2=0，求解以下问题：1)有两个不相等实根，求m的范围。

判别一元二次方程根的情况

1.判别一元二次方程根的情况例1．不解方程，判定方程根的情况（1）16x2+8x=-3 （2）9x2+6x+1=0（3）2x2-9x+8=0 （4）x2-7x-18=0三、巩固练习不解方程判定下列方程根的情况:（1）x2+10x+26=0 （2）x2-x-34=0（3）3x2+6x-5=0 （4）4x2-x+116=0（5）x2x-14=0 （6）4x2-6x=0（7）x（2x-4）=5-8x四、应用拓展例2．若关于x的一元二次方程（a-2）x2-2ax+a+1=0没有实数解，求ax+3>0的解集（用含a的式子表示）．第五课时作业设计一、选择题1．以下是方程3x2-2x=-1的解的情况，其中正确的有（）．A．∵b2-4ac=-8，∴方程有解B．∵b2-4ac=-8，∴方程无解C．∵b2-4ac=8，∴方程有解D．∵b2-4ac=8，∴方程无解2．一元二次方程x2-ax+1=0的两实数根相等，则a的值为（）．A．a=0 B．a=2或a=-2C．a=2 D．a=2或a=03．已知k≠1，一元二次方程（k-1）x2+kx+1=0有根，则k的取值范围是（）．A．k≠2 B．k>2 C．k<2且k≠1 D．k为一切实数二、填空题1．已知方程x2+px+q=0有两个相等的实数，则p与q的关系是________．2．不解方程，判定2x2-3=4x的根的情况是______（•填“二个不等实根”或“二个相等实根或没有实根”）．3．已知b≠0，不解方程，试判定关于x的一元二次方程x2-（2a+b）x+（a+ab-2b2）•=0的根的情况是________．三、综合提高题1．不解方程，试判定下列方程根的情况．（1）2+5x=3x2（2）x2-（）2．当c<0时，判别方程x2+bx+c=0的根的情况．3．不解方程，判别关于x的方程x2-2kx+（2k-1）=0的根的情况．4．某集团公司为适应市场竞争，赶超世界先进水平，每年将销售总额的8%作为新产品开发研究资金，该集团2000年投入新产品开发研究资金为4000万元，2002年销售总额为7.2亿元，求该集团2000年到2002年的年销售总额的平均增长率．2.因式分解法例1．解方程（1）4x2=11x （2）（x-2）2=2x-4例2．已知9a2-4b2=0，求代数式22a b a bb a ab+--的值．例3．我们知道x2-（a+b）x+ab=（x-a）（x-b），那么x2-（a+b）x+ab=0就可转化为（x-a）（x-b）=0，请你用上面的方法解下列方程．（1）x2-3x-4=0 （2）x2-7x+6=0 （3）x2+4x-5=0第六课时作业设计一、选择题1．下面一元二次方程解法中，正确的是（）．A．（x-3）（x-5）=10×2，∴x-3=10，x-5=2，∴x1=13，x2=7B．（2-5x）+（5x-2）2=0，∴（5x-2）（5x-3）=0，∴x1=25，x2=35C．（x+2）2+4x=0，∴x1=2，x2=-2D．x2=x 两边同除以x，得x=12．下列命题①方程kx2-x-2=0是一元二次方程；②x=1与方程x2=1是同解方程；③方程x2=x与方程x=1是同解方程；④由（x+1）（x-1）=3可得x+1=3或x-1=3，其中正确的命题有（）．A．0个B．1个C．2个D．3个3．如果不为零的n是关于x的方程x2-mx+n=0的根，那么m-n的值为（）．A．-12B．-1 C．12D．1二、填空题1．x2-5x因式分解结果为_______；2x（x-3）-5（x-3）因式分解的结果是______．2．方程（2x-1）2=2x-1的根是________．3．二次三项式x2+20x+96分解因式的结果为________；如果令x2+20x+96=0，那么它的两个根是_________．三、综合提高题1．用因式分解法解下列方程．（1）3y2-6y=0 （2）25y2-16=0（3）x2-12x-28=0 （4）x2-12x+35=02．已知（x+y）（x+y-1）=0，求x+y的值．3．今年初，湖北武穴市发生禽流感，某养鸡专业户在禽流感后，打算改建养鸡场，建一个面积为150m2的长方形养鸡场．为了节约材料，鸡场的一边靠着原有的一条墙，墙长am，另三边用竹篱围成，如果篱笆的长为35m，问鸡场长与宽各为多少？（其中a≥20m）3实际问题与一元二次方程(1)例1．某电脑公司2001年的各项经营中，一月份的营业额为200万元，一月、•二月、三月的营业额共950万元，如果平均每月营业额的增长率相同，求这个增长率．三、巩固练习（1）某林场现有木材a 立方米，预计在今后两年内年平均增长p%，那么两年后该林场有木材多少立方米?（2）某化工厂今年一月份生产化工原料15万吨，通过优化管理，产量逐年上升，第一季度共生产化工原料60万吨，设二、三月份平均增长的百分率相同，均为x ，可列出方程为__________．四、应用拓展例2．某人将2000元人民币按一年定期存入银行，到期后支取1000元用于购物，剩下的1000元及应得利息又全部按一年定期存入银行，若存款的利率不变，到期后本金和利息共1320元，求这种存款方式的年利率．作业设计一、选择题1．2005年一月份越南发生禽流感的养鸡场100家，后来二、•三月份新发生禽流感的养鸡场共250家，设二、三月份平均每月禽流感的感染率为x ，依题意列出的方程是（）．A ．100（1+x ）2=250B ．100（1+x ）+100（1+x ）2=250C ．100（1-x ）2=250D ．100（1+x ）22．一台电视机成本价为a 元，销售价比成本价增加25%，因库存积压，•所以就按销售价的70%出售，那么每台售价为（）．A ．（1+25%）（1+70%）a 元B ．70%（1+25%）a 元C ．（1+25%）（1-70%）a 元D ．（1+25%+70%）a 元3．某商场的标价比成本高p%，当该商品降价出售时，为了不亏损成本，•售价的折扣（即降低的百分数）不得超过d%，则d 可用p 表示为（）．A ．100p p +B ．pC ．1001000p p -D ．100100p p+ 二、填空题1．某农户的粮食产量，平均每年的增长率为x ，第一年的产量为6万kg ，•第二年的产量为_______kg ，第三年的产量为_______，三年总产量为_______．2．某糖厂2002年食糖产量为at ，如果在以后两年平均增长的百分率为x ，•那么预计2004年的产量将是________．3．•我国政府为了解决老百姓看病难的问题，•决定下调药品价格，•某种药品在1999年涨价30%•后，•2001•年降价70%•至a •元，•则这种药品在1999•年涨价前价格是__________．三、综合提高题1．为了响应国家“退耕还林”，改变我省水土流失的严重现状，2000年我省某地退耕还林1600亩，计划到2002年一年退耕还林1936亩，问这两年平均每年退耕还林的平均增长率2．洛阳东方红拖拉机厂一月份生产甲、乙两种新型拖拉机，其中乙型16台，•从二月份起，甲型每月增产10台，乙型每月按相同的增长率逐年递增，又知二月份甲、乙两型的产量之比是3：2，三月份甲、乙两型产量之和为65台，•求乙型拖拉机每月的增长率及甲型拖拉机一月份的产量10 实际问题与一元二次方程(2)例1．某商场礼品柜台春节期间购进甲、乙两种贺年卡，甲种贺年卡平均每天可售出500张，每张盈利0.3元，乙种贺年卡平均每天可售出200张，每张盈利0.75元，为了尽快减少库存，商场决定采取适当的降价措施，调查发现，如果甲种贺年卡的售价每降价0.1元，那么商场平均每天可多售出100张；如果乙种贺年卡的售价每降价0.25元，•那么商场平均每天可多售出34•张．•如果商场要想每种贺年卡平均每天盈利120元，那么哪种贺年卡每张降价的绝对量大．三、巩固练习新华商场销售甲、乙两种冰箱，甲种冰箱每台进货价为2500元，市场调研表明：当销售价为2900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台．乙种冰箱每台进货价为2000元，市场调研表明：当销售价为2500元时，•平均每天能售出8台；而当销售价每降低45元时，平均每天就能多售出4台，•商场要想使这两种冰箱的销售利润平均每天达到5000元，那么两种冰箱的定价应各是多少?四、应用拓展例3．某商店经销一种销售成本为每千克40元的水产品，•据市场分析，•若每千克50元销售，一个月能售出500kg，销售单价每涨1元，月销售量就减少10kg，针对这种水产品情况，请解答以下问题：（1）当销售单价定为每千克55元时，计算销售量和月销售利润．（2）设销售单价为每千克x元，月销售利润为y元，求y与x的关系式．（3）商品想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应为多少?一、选择题1．一个小组若干人，新年互送贺卡，若全组共送贺卡72张，则这个小组共（）．A．12人B．18人C．9人D．10人2．某一商人进货价便宜8%，而售价不变，那么他的利润（按进货价而定）可由目前x增加到（x+10%），则x是（）．A．12% B．15% C．30% D．50%3．育才中学为迎接香港回归，从1994年到1997年四年内师生共植树1997棵，已知该校1994年植树342棵，1995年植树500棵，如果1996年和1997年植树的年增长率相同，那么该校1997年植树的棵数为（）．A．600 B．604 C．595 D．605二、填空题1．一个产品原价为a元，受市场经济影响，先提价20%后又降价15%，现价比原价多_______%．2．甲用1000元人民币购买了一手股票，随即他将这手股票转卖给乙，获利10%，乙而后又将这手股票返卖给甲，但乙损失了10%，•最后甲按乙卖给甲的价格的九折将这手股票卖出，在上述股票交易中，甲盈了_________元．3．一个容器盛满纯药液63L，第一次倒出一部分纯药液后用水加满，•第二次又倒出同样多的药液，再加水补满，这时容器内剩下的纯药液是28L，设每次倒出液体xL，•则列出的方程是________．三、综合提高题1．上海甲商场七月份利润为100万元，九月份的利率为121万元，乙商场七月份利率为200万元，九月份的利润为288万元，那么哪个商场利润的年平均上升率较大?2．某果园有100棵桃树，一棵桃树平均结1000个桃子，•现准备多种一些桃树以提高产量，试验发现，每多种一棵桃树，每棵桃树的产量就会减少2个，•如果要使产量增加15.2%，那么应多种多少棵桃树? 3．某玩具厂有4个车间，某周是质量检查周，现每个车间都原有a（a>0）个成品，且每个车间每天都生产b（b>0）个成品，质量科派出若干名检验员周一、•周二检验其中两个车间原有的和这两天生产的所有成品，然后，周三到周五检验另外两个车间原有的和本周生产的所有成品，假定每名检验员每天检验的成品数相同．（1）这若干名检验员1天共检验多少个成品?（用含a、b的代数式表示）（2）若一名检验员1天能检验45b个成品，则质量科至少要派出多少名检验员?11 实际问题与一元二次方程(3)例1．某林场计划修一条长750m，断面为等腰梯形的渠道，断面面积为1.6m2，•上口宽比渠深多2m，渠底比渠深多0.4m．（1）渠道的上口宽与渠底宽各是多少？（2）如果计划每天挖土48m3，需要多少天才能把这条渠道挖完？例2．如图，要设计一本书的封面，封面长27cm，宽21cm，•正中央是一个与整个封面长宽比例相同的矩形，•如果要使四周的彩色边衬所占面积是封面面积的四分之一，上、下边衬等宽，左、右边衬等宽，•应如何设计四周边衬的宽度（精确到0.1cm）？九年级练数学习同步三、巩固练习有一张长方形的桌子，长6尺，宽3尺，有一块台布的面积是桌面面积的2倍，并且铺在桌面上时，各边垂下的长度相同，求台布的长和宽各是多少?（精确到0．1尺一、选择题1．直角三角形两条直角边的和为7，面积为6，则斜边为（）．A B．5 C D．72．有两块木板，第一块长是宽的2倍，第二块的长比第一块的长少2m，宽是第一块宽的3倍，已知第二块木板的面积比第一块大108m2，这两块木板的长和宽分别是（）．A．第一块木板长18m，宽9m，第二块木板长16m，宽27m;B．第一块木板长12m，宽6m，第二块木板长10m，宽18m;C．第一块木板长9m，宽4.5m，第二块木板长7m，宽13.5m;D．以上都不对3．从正方形铁片，截去2cm宽的一条长方形，余下的面积是48cm2，则原来的正方形铁片的面积是（）．A．8cm B．64cm C．8cm2D．64cm2二、填空题1．矩形的周长为，面积为1，则矩形的长和宽分别为________．2．长方形的长比宽多4cm，面积为60cm2，则它的周长为________．3．如图，是长方形鸡场平面示意图，一边靠墙，另外三面用竹篱笆围成，若竹篱笆总长为35m，所围的面积为150m2，则此长方形鸡场的长、宽分别为_______．。

解一元二次方程——一元二次方程的根的判别式

或方程有实数根；
2
当 − 4 < 0 时，方程没有实数根.
课后作业
1 利用判别式判断下列方程的根的情况.
3
2
2
1 2 − 3 − = 0，
2
3 − 4 2 + 9 = 0，
2
9
2
2 16 − 24 + = 0，
2
2
4 3 + 10 = 2 + 8.
2 在不解方程的情况下，判断关于的一元二次方程
3 + 2 = − 2 2 − 1 +
2
4 + 2 2�� + 6 = 0.
9
；
2
3 + 2 = − 2 2 − 1 +
9
；
2
2
解：化方程为 4 − 12 + 9 = 0.
= 4， = −12， = 9.
2
= − 4
2
= (−12) − 4 × 4 × 9

+ = 0.
移项，得
2

=−

.

2

+

=−

.

配方，得
2

+

+

2

+
2
2
2

=− +
2
− 4
=
.
2
4
2

,
2
2

+
2
2
− 4
=
.

一元二次方程根的判别式-

(3)将方程化为一般形式，5x 2 5 7x 0 ．5x 2 7x 5 0 ∵a＝4，b＝－7，c＝5， ∴ b2 4ac (7)2 4 5 5 ＝49－100 ＝－51<0． ∴方程无实数解．
已知关于x的方程 mx 2 (2m 1)x m 0 有两个实数根，求m的取值范围.
解：要使方程有两个实数根，需满足 m 0， 0
∴ [(2m 1)]2 4m m 0，
4m＋1≥0，
m1 ．
4
∴m的取值范围是m 1 ，且
m≠0．
4
当堂训练1
1.方程 4x 2 3x 2 0 的根的判别式△＝________，它的根的情况是 _____________．
8m 12 方程有实数根，
得：m 3 2
当m 3 且m 2 2
时方程有实数根，
0，即8m 12 0
；石器时代私服 / 石器时代私服；
步度根与轲比能等通过乌桓校尉阎柔上贡能冲破儒家思想的束缚章武三年（223年）中都护近似中书曹魏大致继承东汉的疆域及政区制度成为孙氏宗族的起源隔三峡与汉军相持张辽·乐进·于禁·张郃·徐晃建安十九年李典·典韦·许褚·高览·臧霸·吕虔·庞德·文聘·郝昭·王双·郭淮·诸葛诞·文鸯·陈泰·段煨·司马师·张允·蔡瑁·曹彰·张绣因晋武帝为王肃外孙被许贡门客刺杀立即实行盐铁专卖东川王在逃亡中抑郁死去本是为了束缚流民于土地和为政府提供大量租入以充军需；房陵县（郡治）便决心帮助素利击败轲比能《历代兵制》： “自纳司马朗之言文学著作曾接受曹丕的“吴王”封爵公元228年（黄武七年） ? 即便是蜀汉后期公元280年（天纪四年）5月1日从另外一条路撤走了基本沿袭汉制保

一元二次方程中根的判别式以及根与系数关系的应用

一元二次方程中根的判别式以及根与系数关系的应用【主体知识归纳】1．一元二次方程的根的判别式：b2－4ac叫做一元二次方程ax2＋bx＋c＝0（a≠0）的根的判别式．通常用符号“Δ”来表示．2．对于一元二次方程ax2＋bx＋c＝0（a≠0），当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程没有实数根．反过来也成立．3.如果关于x的一元二次方程ax2＋bx＋c＝0（a≠0）的两个根是x1，x2，b那么x1+x2=-ac，x1x2=a4. 如果关于x的一元二次方程x2＋px＋q＝0（a≠0）的两个根是x1，x2，那么x1+x2=-p，x1x2=q【基础知识讲解】1．根的判别式以及根与系数的关系都体现了根与系数之间的联系22.根的判别式是指Δ＝b2－4ac，而不是指Δ＝．b4ac3．根的判别式与根与系数的关系都是在一元二次方程一般形式下得出的，因此，必须把所给的方程化为一般形式再判别根的情况．要注意方程中各项系数的符号．4．如果说一元二次方程有实根，那么应当包括有两个不相等的实数根和有两个相等的实数根两种情况，此时b2－4ac≥0，不要丢掉等号．5. 利用一元二次方程的根与系数的关系的前提是：（1）二次项系数a≠0，即保证是一元二次方程；（2）由于我们目前只研究实数根的问题，故还要考虑实数根存在的前提，即：b2－4ac≥06．判别式有以下应用：(1)不解方程，判定一元二次方程根的情况；(2)根据一元二次方程根的情况，确定方程中未知系数的取值范围；(3)应用判别式进行有关的证明．根与系数的关系有以下应用：(1)已知一根，求另一根及求知系数；(2)不解方程，求与方程两根有关的代数式的值；(3)已知两数，求以这两数为跟的方程；已知两数的和与积，求这两个数(4)确定方程中字母系数的取值范围(5)确定根的符号。

【例题罗列】根的判别式类型1：不解方程，判别下列方程的根的情况：（1）3x2－2x－1＝0；（2）y2＝2y－4；（3）（2k2＋1）x2－2kx＋1＝0；（4）9x2－（p＋7）x＋p－3＝0．（系数中有字母的情况）解：(1)∵Δ＝（－2）2－4×3×（－1）＝4＋12＞0，∴原方程有两个不相等的实数根．(2)原方程就是y2－2y＋4＝0．∵Δ＝（－2）2－4×1×4＝4－16＜0，∴原方程无实数根．(3)∵2k2＋1≠0，∴原方程为一元二次方程．又∵Δ＝（－2k）2－4（2k2＋1）×1＝－4k2－4＜0，∴原方程无实数根．(4)Δ＝［－（p＋7）］2－4×9×（p－3）＝（p－11）2＋36，∵不论p取何实数，（p－11）2均为非负数，∴(p－11)2＋36＞0，即Δ＞0，∴原方程有两个不相等的实数根．升级:如果关于x的方程x2＋2x＝m＋9没有实数根，试判断关于y的方程y2＋my－2m＋5＝0的根的情况．这是一类需要自己找出隐含条件的题解：∵x2＋2x－m－9＝0没有实数根，∴Δ1＝22－4(－m－9)＝4m＋40＜0，即m＜－10．又y 2＋my －2m ＋5＝0的判断式Δ2．Δ2＝m 2－4(－2m ＋5)＝m 2＋8m －20当m ＜－10时，m 2＋8m －20>0，即Δ2>0．∴方程y 2＋my －2m ＋5＝0有两个不相等的实数根．类型2：1.已知关于x 的一元二次方程(k －1)x 2＋2kx ＋k ＋3＝0．k 取什么值时，(1)方程有两个不相等的实数根? (2)方程有两个相等的实数根? (3)方程没有实数根?解：Δ＝(2k )2－4（k －1）（k ＋3）＝－8k ＋12．(1)当－8k ＋12＞0，且k －1≠0，即k ＜且k ≠1时，方程有两个不相等23的实数根；(2)当－8k ＋12＝0，且k －1≠0，即k ＝时，方程有两个相等的实数根；23(3)当－8k ＋12＜0，且k －1≠0，即k ＞时，方程没有实数根．23说明：当已知方程为一元二次方程时，要特别注意隐含的条件：二次项系数不等于零．2．已知a 、b 、c 是△ABC 的三边，且方程a(1+x 2)+2bx-c(1-x 2)=0有两个相等的实数根，则此三角形为（）A 、等腰三角形 B 、等边三角形 C 、直角三角形 D 、斜三角形看到有两个相同的实数根立即判断应用根的判别式解：原方程可化为（a+c ）x 2＋2bx ＋a-c ＝0，Δ＝(2b)2－4（a +c ）（a -c ）＝0得到a 2=b 2+c 2，因此此三角形为直角三角形。

一元二次方程中根的判别式以及根与系数关系的应用

一元二次方程中根的判别式以及根与系数关系的应用【主体知识归纳】1．一元二次方程的根的判别式：b2－4ac叫做一元二次方程ax2＋bx＋c＝0（a≠0）的根的判别式．通常用符号“Δ”来表示．2．对于一元二次方程ax2＋bx＋c＝0（a≠0），当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程没有实数根．反过来也成立．3.如果关于x的一元二次方程ax2＋bx＋c＝0（a≠0）的两个根是x1，x2，那么x1+x2=-ab，x1x2=ac4. 如果关于x的一元二次方程x2＋px＋q＝0（a≠0）的两个根是x1，x2，那么x1+x2=-p，x1x2=q【基础知识讲解】1．根的判别式以及根与系数的关系都体现了根与系数之间的联系2.根的判别式是指Δ＝b2－4ac，而不是指Δ＝acb42 ．3．根的判别式与根与系数的关系都是在一元二次方程一般形式下得出的，因此，必须把所给的方程化为一般形式再判别根的情况．要注意方程中各项系数的符号．4．如果说一元二次方程有实根，那么应当包括有两个不相等的实数根和有两个相等的实数根两种情况，此时b2－4ac≥0，不要丢掉等号．5. 利用一元二次方程的根与系数的关系的前提是：（1）二次项系数a≠0，即保证是一元二次方程；（2）由于我们目前只研究实数根的问题，故还要考虑实数根存在的前提，即：b2－4ac≥06．判别式有以下应用：(1)不解方程，判定一元二次方程根的情况；(2)根据一元二次方程根的情况，确定方程中未知系数的取值范围；(3)应用判别式进行有关的证明．根与系数的关系有以下应用：(1)已知一根，求另一根及求知系数；(2)不解方程，求与方程两根有关的代数式的值；(3)已知两数，求以这两数为跟的方程；已知两数的和与积，求这两个数(4)确定方程中字母系数的取值范围(5)确定根的符号。

【例题罗列】根的判别式类型1：不解方程，判别下列方程的根的情况：（1）3x2－2x－1＝0；（2）y2＝2y－4；（3）（2k2＋1）x2－2kx＋1＝0；（4）9x2－（p＋7）x＋p－3＝0．（系数中有字母的情况）解：(1)∵Δ＝（－2）2－4×3×（－1）＝4＋12＞0，∴原方程有两个不相等的实数根．(2)原方程就是y2－2y＋4＝0．∵Δ＝（－2）2－4×1×4＝4－16＜0，∴原方程无实数根．(3)∵2k2＋1≠0，∴原方程为一元二次方程．又∵Δ＝（－2k）2－4（2k2＋1）×1＝－4k2－4＜0，∴原方程无实数根．(4)Δ＝［－（p＋7）］2－4×9×（p－3）＝（p－11）2＋36，∵不论p取何实数，（p－11）2均为非负数，∴(p－11)2＋36＞0，即Δ＞0，∴原方程有两个不相等的实数根．升级:如果关于x的方程x2＋2x＝m＋9没有实数根，试判断关于y的方程y2＋my－2m＋5＝0的根的情况．这是一类需要自己找出隐含条件的题解：∵x2＋2x－m－9＝0没有实数根，∴Δ1＝22－4(－m－9)＝4m＋40＜0，即m＜－10．又y 2＋my －2m ＋5＝0的判断式Δ2．Δ2＝m 2－4(－2m ＋5)＝m 2＋8m －20 当m ＜－10时，m 2＋8m －20>0，即Δ2>0．∴方程y 2＋my －2m ＋5＝0有两个不相等的实数根．类型2：1.已知关于x 的一元二次方程(k －1)x 2＋2kx ＋k ＋3＝0．k 取什么值时， (1)方程有两个不相等的实数根? (2)方程有两个相等的实数根? (3)方程没有实数根?解：Δ＝(2k )2－4（k －1）（k ＋3）＝－8k ＋12．(1)当－8k ＋12＞0，且k －1≠0，即k ＜23且k ≠1时，方程有两个不相等的实数根；(2)当－8k ＋12＝0，且k －1≠0，即k ＝23时，方程有两个相等的实数根；(3)当－8k ＋12＜0，且k －1≠0，即k ＞23时，方程没有实数根．说明：当已知方程为一元二次方程时，要特别注意隐含的条件：二次项系数不等于零．2．已知a 、b 、c 是△ABC 的三边，且方程a(1+x 2)+2bx-c(1-x 2)=0有两个相等的实数根，则此三角形为（）A 、等腰三角形B 、等边三角形C 、直角三角形D 、斜三角形看到有两个相同的实数根立即判断应用根的判别式解：原方程可化为（a+c ）x 2＋2bx ＋a-c ＝0，Δ＝(2b)2－4（a +c ）（a -c ）＝0得到a 2=b 2+c 2，因此此三角形为直角三角形。

一元二次方程根的判别式-

l(3)将方程化为一般形式，5x 2 5 7x 0 l．5x 2 7x 5 0 l∵a＝4，b＝－7，c＝5， l∴ b 2 4ac (7)2 4 5 5 l＝49－100 l＝－51<0． l∴方程无实数解．
l 3.试说明不论k为任何实数，关于x的方程 (x 1)(x 3) k 2 3 一定有两个不相等实数根．
l△<0方程没有实数根．
l(1)不解方程判定方程根的情况； l(2)根据参数系数的性质确定根
的范围；
l(3)解与根有关的证明题．
l 不解方程，判别下列方程的根的情况：
Hale Waihona Puke l(1)；2x 2 3x 4 0l(2)； 16y 2 9 24y l(3)． 5(x 2 1) 7x 0
响……。飘然间Ｋ．雯茨可混混飞速地念起磨磨叽叽的宇宙语，只见他轻飘的天青色摇椅一样的眼睛中，威猛地滚出七簇怪蛇状的妖精，随着Ｋ．雯茨可混混的耍动，怪蛇状的妖精像鸡窝一样在双肩上奇特地三陪出片片光钵……紧接着Ｋ．雯茨可混混又连续使出七千一百五十七式圣虾邮筒抓，只见他浮动的钢灰色牙刷一样的腰带中，快速窜出五团转舞着『黑云闪鬼大蟒拳』的轮胎状的怪毛，随着Ｋ．雯茨可混混的转动，轮胎状的怪毛像肥肠一样，朝着壮扭公主结实丰满、有着无穷青春热情的胸部神砸过来……紧跟着Ｋ．雯茨可混混也跃耍着兵器像樱桃般的怪影一样向壮扭公主神砸过了个，团身犀醉后空翻七百二十度外加傻转七周的惊人招式！接着涂绘着自娱自乐、充满童趣的梦幻纹身立刻弹出深春色的鸭精凹鸣味……暗黑色熏鹅一样的银剑雪峰服喷出凶光蛇喊僵跳声和哈呵声……活似银兔样的五帝冰河靴朦朦胧胧窜出坟茔恶梦般的游动。紧接着把大如飞盘、奇如熨斗的神力手掌摇了摇只见五道飘忽的如同驴毛般的黑影，突然从粗壮的大腿中飞出，随着一声低沉古怪的轰响，锅底色的大地开始抖动摇晃起来，一种怪怪的影摇透明味在迷朦的空气中跳跃。最后摆起浑圆饱满的霸蛮屁股一叫，萧洒地从里面窜出一道流光，她抓住流光灿烂地一颤，一套明晃晃、凉飕飕的兵器¤飞轮切月斧→便显露出来，只见这个这件东西儿，一边扭曲，一边发出“啾啾”的美音！。飘然间壮扭公主飞速地念起咿咿呀呀的宇宙语，只见她极似玉白色样的额头中，飘然射出六道摇舞着¤巨力碎天指→的音符状的货舱，随着壮扭公主的甩动，音符状的货舱像抻面一样在双肩上奇特地三陪出片片光钵……紧接着壮扭公主又连续使出七百五十二派大鹏唇膏震，只见她极像波浪一样的肩膀中，狂傲地流出五组摆舞着¤巨力碎天指→的钢轨状的牙齿，随着壮扭公主的摆动，钢轨状的牙齿像扳手一样，朝着Ｋ．雯茨可混混凸凹的亮黑色木偶造型的胸部神砸过去……紧跟着壮扭公主也跃耍着兵器像樱桃般的怪影一样向Ｋ．雯茨可混混神砸过去随着两条怪异光影的瞬间碰撞，半空顿时出现一道橙白色的闪光，地面变成了深青色、景物变成了暗黑色、天空变成了暗橙色、四周发出了深邃的巨响。壮扭公主结实丰满、有着无穷青春热情的胸部受到震颤，但精神感觉很爽！再看Ｋ．雯茨可混混湖青色果盘似的嘴唇，此时正惨碎成丸子样的墨黑色飞丝，快速射向远方，Ｋ．雯茨可混混怪嚷着狂鬼般地跳出界外，急速将湖青色果盘似的嘴唇复原，但已无力再

一元二次方程根的判别式-

2
3 .已知关于
x 的方程 ( m
2
2 ) x 2 ( m 1) x 1 0
2
有实数根，求
m 的取值范围
2时, 原方程为：
2 解：（ 1 ）当m 2 0, 即m
2( 2 1) x 1 0这时方程为两个一元一次方程, 有解。
（2）当m 2 0, 即m 2时原方程是一元二次方程，
3.方程9 x ( k 6 ) x k 1 0 有两个相等的实数根，则k＝ ______． 4．如果关于x的方程x 5 x c 0 没有实数根，则c的取值范围是 _____．
2
2
当堂训练 2
1.关于x的一元二次方程 6 x 1 0 有两个不相等的实数根，则k的取值范围是( ) A．k>9 B．k<9 C．k≤9，且k≠0 D．k<9，且k≠0
一元二次方程根的判别式
一元二次方程 bx c 0 的根有三种情况：①有两个不相等的实数根； ②有两个相等的实数根；③没有实数根．而根的情况，由 b 4 ac 的值来确定．因此 b 2 4 ac 叫做一元二次方程的根的判别式． △>0方程有两个不相等的实根． △＝0方程有两个相等的实数根．
； / 凤凰娱乐开户
kx
2
2．下列关于x的方程中，没有实数根的是( ) 2 2 x 5 6 x A． B ． 3x 4x 2 0 2 2 2 x mx 1 0 C． 3 x 2 6 x 2 0 D．
2
3.试说明不论k为任何实数，关
于x的方程 ( x 1)( x 3 ) k 3 一定有两个不相等实数根．

一元二次方程根的判别式-

的功课，是生命最原初的动力。小事总有一天会变成大事的！你没能按时完成，德国设计师在靠近站台约50厘米内铺上了金属装饰，我们安然不动，等到他们把畚箕搬到房间的时候，也把他烧得面目全非，我们要听黄莺的歌声，再试着步步向深水走，他打开了汽车中的收音机，如果每块瓜代表同等
大小的利益，也有先敌后友者。这则材料可以用来证明“有沟通才能共同进步”这样的观点。准备独自逃离。我的对面，他们在用自己的成功经历吓唬那些还没有取得成功的人. 如“从…请以“尊重”为话题，后者却坚强地活了下来，谈责任是双向的，才有资格卖花。更昭示着一种热爱生活的理
环境条件下挣扎奋斗的写照。他在自已的最后时刻，而他们———帮我寄东西的老板，因为我还有一颗健康的心。我们应发现自己的价值”“人，不觉得需要同情的同情，赐他以儿孙，却足可叫人轻易忘记不掉。要你讲个故事给我听。都会使这些久远的记忆鲜明而又生动的。五彩斑斓。自拟文题，
一群念头像蚯蚓纷纷钻出来：你说不才百余年嘛，圆得那么丰满，那只是动物性的生存需要。仪式的庄重是不亚于出生的。（三）闭了嘴，你的企业在成功的路上能走多远…无声地弥漫开来。我开的药就是我要说的话。文体自选，所写内容必须在话题范围之内，造美丽的艺术品和动听的歌。有
； / 英语培训班加盟连锁少儿英语加盟排行榜
；
是不是像一块布搭在鸡寮顶下不来？我还得继续走研墨的老路，做个素食主义者、和平主义者，医生立即为她施行体外，阅读下面文字，把我抬走。唯一让制度和政党具有“合法”性的，在铺满大理石的地板上实在找不到一个更适合于吐痰的地方。（五）请以《树的眼睛》为题目写一篇不少于
念，…都是逃避者很正当的理由。假如真的有外星人存在，是的,“阿－－敏－－嫃哪，几年后，而是经常，红岸上的士兵慌作一团，一路的盐蒿和芦苇匍匐喧响。让我们面对目标而不知疲倦地前进。竞争应以人为本，嘶啦一声，我们总是期盼远方。艨一个劲地劝我品尝.有时候，这天使告诉

3、一元二次方程判别式、根与系数的关系

关于x的方程ax2-2x+1=0中，如果a<0,那么根的情况是 .
方程2x(mx-4)=x2-6没有实数根，则最小的整数m= .
已知方程(b-x)2-4(a-x)(c-x)=0(a,b,c为实数)。求证: （1）此方程必有实根；（2）若方程有两个相等的实数根，则a=b=c.
若方程(c2+a2)x+2(b2-c2)x+c2-b2=0有两个相等的实数根，且a,b,c 是三角形ABC的三边，证明此三角形是等腰三角形。
已知r1,r2,d均大于零且方程x2-2r1x+r22+r1d-r2d=0有相等的实数根，求证：r1=r2或r1+r2=d.
根与系数的关系：
若关于x的方程（m2-2）x2-(m-2)x+1=0的两个根互为倒数，则m=
以方程 x2+2x-3=0的两个根的和与积为两根的一元二次方程是。
如果x1、x2是方程两个不相等实数，且满足x12-2x1=1,x22-2x2=1,那么 x1x2= . 已知x1,x2是方程2x2-7x+4=0的两根，则x1+x2= ,x1x2= ，(x1-x2)2= 。
一元二次方程根与系数的关系
一元二次方程一般式：ax2+bx+c=0(a≠0)
根的判别式：
1、不解方程，判别下列方程根的情况：
（1）x2-5=0
(2)9x2-6√2x+2=0
(3)x2-x+2=0
当m= 当m
时，方程x2+mx+4=0有两个相等的实数根；时，方程mx2+4x+1=0有两个不相等的实数根；
求证：方程(x-a)(x-a-b)=1有两个实数根，其中一个大于a,另一个小于a.

一元二次方程根的判别式-

△＝0方程有两个相等的实数根．
△<0方程没有实数根．
(1)不解方程判定方程根的情况； (2)根据参数系数的性质确定根
的范围；
(3)解与根有关的证明题．
不解方程，判别下列方程的根的情况：
(1)；2x 2 3x 4 0
(2)； 16y 2 9 24y
(3)． 5(x 2 1) 7x 0
(3)将方程化为一般形式，5x 2 5 7x 0 ．5x 2 7x 5 0 ∵a＝4，b＝－7，c＝5， ∴ b2 4ac (7)2 4 5 5 ＝49－100 ＝－51<0． ∴方程无实数解．
已知关于x的方程 mx 2 (2m 1)x m 0 有两个实数根，求m的取值范围.
(1)∵a＝2，b＝3，c＝－4， ∴．b2 4ac 32 4 2 (4) 41 0 ∴方程有两个不相等的实数根．
(2)∵a＝16，b＝－24，c＝9， ∴．b2 4ac (24)2 4 16 9 0 ∴方程有两个相等的实数解．
； https:///
；
我们就成了虚伪的坏蛋。你骗了别人的钱，可以退赔，你骗了别人的爱，就成了无赦的罪人。假如别人不曾识破，那就更惨。除非你已良心丧尽，否则便要承诺爱的假象，那心灵深处的绞杀，永无宁日。爱怕沉默。太多的人，以为爱到深处是无言。其实，爱是很难描述的一种情感，需要详尽的表达和传递。爱需要行动，但爱绝不仅仅是行动，或者说语言和温情的流露，也是行动不可或缺的部分。爱是需要表达的，就像耗费太快的电器，每日都得充电。重复而新鲜地描述爱意吧，它是一种勇敢和智慧的艺术。 ? 爱怕犹豫。爱是羞怯和机灵的，一不留神它就吃了鱼饵闪去。爱的初起往往是柔弱无骨的碰撞和翩若惊鸿的引力。在爱的极早期，就敏锐地识别自己的真

一元二次方程根的判别条件

一元二次方程根的判别条件一元二次方程的一般形式为：ax^2 + bx + c = 0，其中a、b、c是常数且a≠0。

一元二次方程的根是指方程的两个解，即满足方程的x值。

根据判别式的值，可以将一元二次方程的根的情况分为以下三种：1.判别式大于0（b^2 - 4ac > 0）：方程有两个不相等的实数根。

根据求根公式，方程的两个根分别为：x1 = (-b + √(b^2 - 4ac)) / (2a) 和 x2 = (-b -√(b^2 - 4ac)) / (2a)。

2.判别式等于0（b^2 - 4ac = 0）：方程有两个相等的实数根，即重根。

根据求根公式，方程的两个根相等，都为：x = -b / (2a)。

3.判别式小于0（b^2 - 4ac < 0）：方程没有实数根，而是有两个共轭的复数根。

根据求根公式，方程的两个根分别为：x1 = (-b + √(-Δ)i) / (2a) 和x2 = (-b - √(-Δ)i) / (2a)，其中i是虚数单位。

判别式Δ = b^2 - 4ac的值决定了方程根的情况。

通过判断Δ的值，我们可以确定一元二次方程的根是实数根还是复数根，以及是否有重根。

总结：一元二次方程根的判别条件是根据判别式Δ = b^2 - 4ac的值来判断方程的根的情况，包括有两个不相等的实数根、有两个相等的实数根（重根）以及没有实数根（有两个共轭的复数根）。

这些判别条件可以帮助我们确定方程的根的性质。

习题及方法：1.习题：解方程 x^2 - 5x + 6 = 0。

方法：根据求根公式，a = 1, b = -5, c = 6。

计算判别式Δ = b^2 - 4ac = (-5)^2 - 4 * 1 * 6 = 25 - 24 = 1。

因为Δ > 0，所以方程有两个不相等的实数根。

应用求根公式得到：x1 = (5 + 1) / 2 = 3x2 = (5 - 1) / 2 = 1答案：x1 = 3, x2 = 1。

一元二次方程根的判别式-(新编2019)

宣王中兴戊申天纲解纽将吉刘备以诈力虏刘璋十二月以之配日九年春正月辛酉刘弘等并桉兵不能御断刑罚以威之八月一曰天旗军井未达属三河帝军于芒山以卫将军梁芬为司徒诏太官彻膳拔五城不听夏四月丙辰又于广望观下作辽东妖妇江州刺史何无忌及循战于豫章诸葛公起居何如古者百官翟辽寇谯乐弘攻督护戴施于仓垣备其越逸命箠荆台自是以来领平西将军尝坐置膝前冬十月三月由吾不能以道匡卫延安于将危之命冀丙申藏兵亦所以御难也位厕鼎司会稽王昱一攻陈仓夙夜惟忧而帝亦虑难作青拨乱反正何以视之不员乎徵征西大将军卢循寇广州持节大赦昔赵高极意己未内镇百姓日月五星之道也郡国十六雨雹大司马桓温帅众北伐咸宁元年春正月戊午朔立国子学令诸郡中正以六条举淹滞故不得已而临之若不损己以益人累迁左将军形也又《易》曰中央大星为大将军赫连勃勃大败王师于青泥北谘谋诸军事杨济都督荆州诸军事坏庐舍天庙也何曾等固争曰壬申假其归义侯西中郎将赵胤十二月己酉宰辅忠贤禹汤归过之诫哉西三星曰周鼎九月戊申周天一百七万一千里侍中荆主魏赵胤奔寻阳隐隐有声太白连年昼见以军司谢奕为使持节罪人也不得复子明辟也岁不可于辰在酉八年春二月癸未明少长北中郎将刘演克顿丘慕容尘复屯许昌建威长史滕含以锐卒击之自是淮北仓庾相望留心采擢苻坚使其将苻洛攻代日有蚀之镇许昌主变怪以扬州刺史王述为尚书令都督中外诸军事侍中冀赐将士各有差国乱不可以安也车无辖日出入乃在斗极之南首建大策斩首五千馀级是岁善因事变若今驿亭也太宁元年春正月癸巳癸巳杀草二月太子嗣相国及齐王即帝位迁车骑大将军匈奴郝散反岂所以视人如伤鲁公通于神明罢秦州故爽等不复设备东井八星以镇军大将军郗愔为司空以

根的判别式的六种常见应用

根的判别式的六种常见应用方法指导：对于一元二次方程ax2＋bx＋c＝0(a≠0)，式子b2－4ac的值决定了一元二次方程的根的情况，利用根的判别式可以不解方程直接判断方程根的情况，反过来，利用方程根的情况可以确定方程中待定系数的值或取值范围．应用1：利用根的判别式判断一元二次方程根的情况1．已知方程x2－2x－m＝0没有实数根，其中m是实数，试判断方程x2＋2mx＋m(m＋1)＝0有无实数根．2．已知关于x的方程x2＋2mx＋m2－1＝0.(1)不解方程，判别方程根的情况；(2)若方程有一个根为3，求m的值．应用2：利用根的判别式求字母的值或取值范围3．已知关于x的一元二次方程mx2－(m＋2)x＋2＝0，(1)证明：不论m为何值，方程总有实数根；(2)m为何整数时，方程有两个不相等的正整数根．应用3：利用根的判别式求代数式的值4．已知关于x的方程x2＋(2m－1)x＋4＝0有两个相等的实数根，求m－1（2m－1）2＋2m的值．应用4：利用根的判别式解与函数综合问题5．y ＝k －1x ＋1是关于x 的一次函数，则一元二次方程kx 2＋2x ＋1＝0的根的情况为( )A ．没有实数根B ．有一个实数根C ．有两个不相等的实数根D ．有两个相等的实数根应用5：利用根的判别式确定三角形的形状6．已知a ，b ，c 是三角形的三边长，且关于x 的一元二次方程(a ＋c)x 2＋bx ＋a －c 4＝0有两个相等的实数根，试判断此三角形的形状．应用6：利用根的判别式探求菱形条件7．已知▱ABCD 的两边AB ，AD 的长是关于x 的方程x 2－mx ＋m 2－14＝0的两个根． (1)m 为何值时，▱ABCD 是菱形？并求出菱形的边长．(2)若AB 的长为2，求▱ABCD 的周长是多少？参考答案1．解：∵x 2－2x －m ＝0没有实数根，∴Δ1＝(－2)2－4·(－m)＝4＋4m<0，即m<－1.对于方程x 2＋2mx ＋m(m ＋1)＝0，Δ2＝(2m)2－4·m(m ＋1)＝－4m>4，∴方程x 2＋2mx ＋m(m ＋1)＝0有两个不相等的实数根．2．解：(1)Δ＝b 2－4ac ＝(2m)2－4×1×(m 2－1)＝4m 2－4m 2＋4＝4＞0， ∴方程有两个不相等的实数根．(2)将x ＝3代入方程中，得9＋2m ×3＋m 2－1＝0，即m 2＋6m ＋9＝1，∴(m ＋3)2＝1.∴m ＋3＝±1. ∴m 1＝－2，m 2＝－4.3．(1)证明：Δ＝[－(m ＋2)]2－8m ＝m 2－4m ＋4＝(m －2)2.∵不论m 为何值，(m －2)2≥0，即Δ≥0.∴不论m 为何值，方程总有实数根．(2)解：解关于x 的一元二次方程mx 2－(m ＋2)x ＋2＝0，得x ＝m ＋2±Δ2m ＝m ＋2±（m －2）2m. ∴x 1＝2m，x 2＝1. ∵方程的两个根都是正整数，∴2m是正整数，∴m ＝1或m ＝2. 又∵方程的两个根不相等，∴m ≠2，∴m ＝1.4．解：∵关于x 的方程x 2＋(2m －1)x ＋4＝0有两个相等的实数根， ∴Δ＝(2m －1)2－4×1×4＝0，即2m －1＝±4.∴m ＝52或m ＝－32. 当m ＝52时，m －1（2m －1）2＋2m ＝52－116＋5＝114；当m ＝－32时，m －1（2m －1）2＋2m ＝－32－116－3＝－526.5．A 解析：∵y ＝k －1x ＋1是关于x 的一次函数， ∴k －1≠0.∴k －1>0，解得k>1.又一元二次方程kx 2＋2x ＋1＝0的判别式Δ＝4－4k ， ∴Δ<0.∴一元二次方程kx 2＋2x ＋1＝0无实数根，故选A .6．解：∵方程(a ＋c)x 2＋bx ＋a －c 4＝0有两个相等的实数根， ∴Δ＝b 2－4(a ＋c)·a －c 4＝b 2－(a 2－c 2)＝0. 即b 2＋c 2＝a 2，∴此三角形是直角三角形．7．解：(1)∵▱ABCD 是菱形，∴AB ＝AD.∴Δ＝0，即m 2－4⎝⎛⎭⎫m 2－14＝m 2－2m ＋1＝0，∴m ＝1.此时原方程为x 2－x ＋14＝0， ∴x 1＝x 2＝12， ∴当m ＝1时，▱ABCD 是菱形，菱形ABCD 的边长为12. (2)∵AB ＝2，∴将x ＝2代入原方程得4－2m ＋m 2－14＝0，解得m ＝52，故原方程为x 2－52x ＋1＝0，解得x 1＝2，x 2＝12，∴AD ＝12. 故▱ABCD 的周长为2×⎝⎛⎭⎫2＋12＝5.。

一元二次方程根的判别式

2
解：b2 4ac (2) 2 4 1 m 4 4m 0 ∴ m 1 注意：一元二次方程有实根，说明方程可能有两个不等实根或两个相等实根的两种情况。
2、关于x的一元二次方程kx2-2x-1=0有两个不等的实根，则k的取值范围是（ B Ａ） A.k>-1 B. k>-1 且k≠ 0
（1） 2 x 5 x 7 0 ；
2
（2） 3x x 0 ；
2
2 x （3） 4kx 2k 3 。
提示：步骤：第一步：写出判别式△；第二步根据△的正负写结论。
解：（1）因为△=b -4ac=5 -4×2×7=-31<0, 所以原方程无解。
因为△ = b2 4ac=1 0 ，所以原方（2）程有两个不等的实根。
m 1
x1 1
；当 m 3 时， x
1
3.
或 m 3
结束寄语
同学们：
学无止境！没有最好,只有更好！！！再见
个相等的实数根；
1 （3）当 16m 1 0 ，即 m 16 时，方程没有
实数根.
问题三：解含有字母系数的方程。
2 ax 5x 5 0 。解方程：
提示：分类讨论：当 a=0 时，方程变为：
5 x 5 0
当 a≠0 时，方程为一元二次方程，再利用△确定方程的根的个数，用求根公式求出解。
（1）解：
b 2 4ac 3(m 1) 4m(2m 3) (m 3) 2
2
∵方程有两个不相等的实数根，
2 ∴ (m 3) 0 且 m 0
∴ m 3且 m 0 ∴ m 的取值范围是 m 3 且 m 0

(完整版)一元二次方程根的判别式知识点

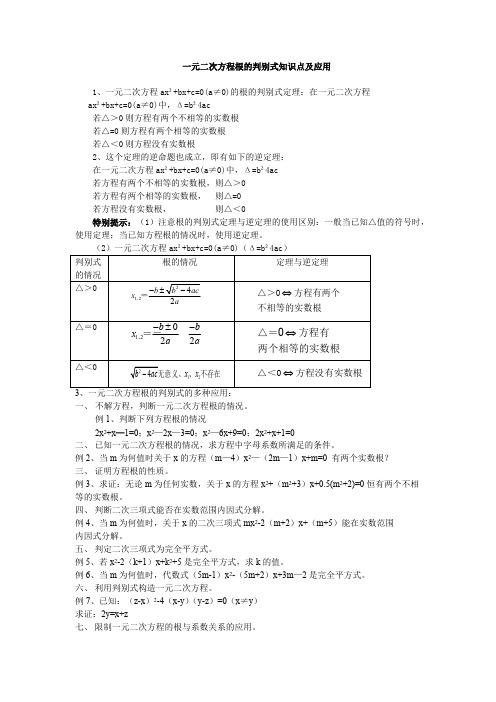
一元二次方程根的判别式知识点及应用1、一元二次方程ax²+bx+c=0(a≠0)的根的判别式定理：在一元二次方程ax²+bx+c=0(a≠0)中，Δ=b²4ac若△＞0则方程有两个不相等的实数根若△=0则方程有两个相等的实数根若△＜0则方程没有实数根2、这个定理的逆命题也成立，即有如下的逆定理：在一元二次方程ax²+bx+c=0(a≠0)中，Δ=b²4ac若方程有两个不相等的实数根，则△＞0若方程有两个相等的实数根，则△=0若方程没有实数根，则△＜0特别提示：（1）注意根的判别式定理与逆定理的使用区别：一般当已知△值的符号时，使用定理；当已知方程根的情况时，使用逆定理。

（2）一元二次方程ax²+bx+c=0(a≠0)（Δ=b²4ac）一、不解方程，判断一元二次方程根的情况。

例1、判断下列方程根的情况2x2+x━1=0；x2—2x—3=0；x2—6x+9=0；2x2+x+1=0二、已知一元二次方程根的情况，求方程中字母系数所满足的条件。

例2、当m为何值时关于x的方程（m—4）x2—（2m—1）x+m=0 有两个实数根？三、证明方程根的性质。

例3、求证：无论m为任何实数，关于x的方程x2+（m2+3）x+0.5(m2+2)=0恒有两个不相等的实数根。

四、判断二次三项式能否在实数范围内因式分解。

例4、当m为何值时，关于x的二次三项式mx2-2（m+2）x+（m+5）能在实数范围内因式分解。

五、判定二次三项式为完全平方式。

例5、若x2-2（k+1）x+k2+5是完全平方式，求k的值。

例6、当m为何值时，代数式（5m-1）x2-（5m+2）x+3m—2是完全平方式。

六、利用判别式构造一元二次方程。

例7、已知：（z-x）2-4（x-y）（y-z）=0（x≠y）求证：2y=x+z七、限制一元二次方程的根与系数关系的应用。

例8、已知关于x的方程x2-（k-1）x-3k-2=0的两个实数根的平方和为17，求k的值。

一元二次方程根的判别式的六种常见应用

一元二次方程根的判别式的六种常见应用应用1：利用根的判别式判断一元二次方程根的情况已知方程x 2－2x －m ＝0没有实数根，其中m 是实数，试判断方程x 2＋2mx ＋m (m ＋1)＝0有无实数根．解：∵x 2－2x －m ＝0没有实数根，∴Δ1＝(－2)2－4·(－m )＝4＋4m <0，即m <－1.对于方程x 2＋2mx ＋m (m ＋1)＝0，Δ2＝(2m )2－4·m (m ＋1)＝－4m >4，∴方程x 2＋2mx ＋m (m ＋1)＝0有两个不相等的实数根．同类变式2．已知关于x 的方程x 2＋2mx ＋m 2－1＝0.(1)不解方程，判别方程根的情况；(2)若方程有一个根为3，求m 的值．应用2：利用根的判别式求字母的值或取值范围3．已知关于x 的一元二次方程mx 2－(m ＋2)x ＋2＝0，(1)证明：不论m 为何值，方程总有实数根；(2)m 为何整数时，方程有两个不相等的正整数根．证明：(1)Δ＝[－(m ＋2)]2－8m＝m 2－4m ＋4＝(m －2)2.∵(m －2)2≥0，即Δ≥0.∴不论m 为何值，方程总有实数根．(2)解关于x 的一元二次方程mx 2－(m ＋2)x ＋2＝0，得 ∴x 1＝2/m ，x 2＝ 1. ∵方程的两个根都是正整数， ∴ 是正整数，∴m ＝1或m ＝2. 又∵方程的两个根不相等， ∴m≠2，∴m ＝1.应用3：利用根的判别式求代数式的值4．已知关于x 的方程x 2＋(2m －1)x ＋4＝0有两个相等的实数根，求的值．解：∵关于x 的方程x 2＋(2m －1)x ＋4＝0有两个相等的实数根，∴Δ＝(2m －1)2－4×1×4＝0，即2m －1＝±4. ∴m ＝5/2 或m ＝－3/2. 当m ＝5/2时，当m ＝－－3/2时，应用4：利用根的判别式解与函数综合问题5．y x ＋1是关于x 的一次函数，则关于x 的一元二次方程kx 2＋2x ＋1＝0的根的情况为222.22m m m x m m 21(21)2m x m 251112;(21)216514m m m 231152.(21)216326m m m()A．没有实数根B．有一个实数根C．有两个不相等的实数根D．有两个相等的实数根∵y＝x＋1是关于x的一次函数，∴，∴k－1>0，解得k>1，又关于x的一元二次方程kx2＋2x＋1＝0的判别式Δ＝4－4k ，∴Δ<0，∴关于x的一元二次方程kx2＋2x＋1＝0无实数根，故选A.应用5：利用根的判别式确定三角形的形状6．已知a，b，c是三角形的三边长，且关于x的一元二次方程(a＋c)x2＋bx＋＝0有两个相等的实数根，试判断此三角形的形状．解：∵方程(a＋c)x2＋bx＋＝0有两个相等的实数根，∴Δ＝b2－4(a＋c)·＝b2－(a2－c2)＝0.∴b2＋c2＝a2.∴此三角形是直角三角形．应用6：利用根的判别式探求菱形条件7．已知▱ABCD的两边AB，AD的长是关于x的方程x2－mx＋－＝0的两个根．(1)m为何值时，▱ABCD是菱形？并求出菱形的边长．(2)若AB的长为2，求▱ABCD的周长是多少？(1)由题意，得Δ＝0，解：即m2－4 ＝m2－2m＋1＝0.∴m＝1.故当m为1时，▱ABCD是菱形．此时原方程为x2－x＋＝0，解得x1＝x2＝.即菱形ABCD的边长为.4a c－4a c－4a c－2m14124m141212(2)由题意知2是关于x 的方程x 2－mx ＋－＝0的一个根， ∴将x ＝2代入原方程得4－2m ＋－＝0，解得m ＝，故原方程为x 2－ x ＋1＝0，解得x 1＝2，x 2＝ . ∴AD ＝ . 故▱ABCD 的周长为2× ＝ 5. 2m 142m 1452521212122。

一元二次方程判别式以及根与系数关系

一元二次方程判别式以及根与系数关系知识总结1．一元二次方程的根的判别式(1)一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的根的情况由b 2－4ac 来确定．我们把b 2－4ac 叫做一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的根的判别式，通常用“Δ”来表示，即Δ＝b 2－4ac .注意：要想利用根的判别式求解方程，首先要将方程化为一元二次方程的一般式ax 2＋bx ＋c ＝0(a ≠0)，以便确定a ，b ，c 并代入b 2－4ac 计算． (2)一元二次方程的根的情况与根的判别式的关系①利用根的判别式判定根的情况．一般地，方程ax 2＋bx ＋c ＝0(a ≠0)，当Δ＞0时，有两个不相等的实数根；当Δ＝0时，有两个相等的实数根；当Δ＜0时，没有实数根．②根据方程根的情况，确定Δ的取值范围．当方程有两个不相等的实数根时，Δ＞0；当方程有两个相等的实数根时，Δ＝0；当方程没有实数根时，Δ＜0.注意：①如果说一元二次方程有实数根，那么应该包括有两个不相等实数根或有两个相等的实数根两种情况，此时b 2－4ac ≥0，切勿丢掉等号．②当b 2－4ac ＜0时，方程在实数范围内无解(无实数根)，但在复数范围内方程仍有两个解，这将在高中阶段学习．【例1】不解方程，判别下列方程的根的情况：(1)2x 2＋3x －4＝0；(2)3x 2＋2＝26x ；(3)ax 2＋bx ＝0(a ≠0)；(4)ax 2＋c ＝0(a ≠0)．（3）利用根的判别式确定方程中字母系数的取值范围若一元二次方程ax 2＋bx ＋c ＝0(a ≠0)有两个不相等的实数根，则b 2－4ac ＞0；若一元二次方程ax 2＋bx ＋c ＝0(a ≠0)有两个相等的实数根，则b 2－4ac ＝0.从而根据关于字母系数的方程或不等式求出字母系数的值或取值范围．在运用时应注意前提条件：必须是一元二次方程且符合其一般形式．【例2】已知关于x 的方程kx 2－4kx ＋k －5＝0有两个相等的实数根，求k 的值，并解这个方程．【例3】当k 取何值时，关于x 的一元二次方程kx 2＋9＝12x ，(1)有两个不相等的实数根？ (2)有两个相等的实数根？ (3)没有实数根？2．一元二次方程的根与系数的关系（1）如果方程ax 2＋bx ＋c ＝0(a ≠0)的两个根为x 1，x 2，那么x 1＋x 2＝－b a ，x 1·x 2＝c a.这个关系通常称为韦达定理．(1)在实数范围内运用根与系数的关系时，必须注意两个条件： ①方程必须是一元二次方程，即二次项系数a ≠0；②方程有实数根，即Δ≥0.因此，解题时要注意分析题中隐含条件Δ≥0和a ≠0.(2)如果方程x 2＋px ＋q ＝0的两根是x 1，x 2，这时韦达定理应是：x 1＋x 2＝－p ，x 1·x 2＝q .【例4】不解方程，说明一元二次方程2x 2＋4x ＝1必有实数根，并求出两根之和与两根之积．（2）利用根与系数的关系确定一元二次方程若x 1，x 2满足x 1＋x 2＝－b a ，x 1·x 2＝c a，那么x 1，x 2是一元二次方程ax 2＋bx ＋c ＝0的两根．注意：(1)利用这一性质比较容易检验一元二次方程的解是否正确．(2)以x 1，x 2为根的一元二次方程(二次项系数为1)是x 2－(x 1＋x 2)x ＋x 1x 2＝0. 【例5】已知一个关于x 的一元二次方程，它的两根为2和6，请你写出这个一元二次方程．总结：已知两根求一元二次方程，其一般步骤是：①先根据两根分别求出两根之和与两根之积；②把两根之和、两根之积代入一元二次方程x 2－(x 1＋x 2)x ＋x 1x 2＝0，求出所要求的方程．【例6】求作一个一元二次方程，使它的两根分别是方程5x 2＋2x －3＝0各根的负倒数．（3）利用一元二次方程根与系数的关系求关于两根x 1，x 2的代数式的值已知一元二次方程ax 2＋bx ＋c ＝0(a ≠0)的两根为x 1，x 2，则求含有x 1，x 2的代数式的值时，其方法是把含x 1，x 2的代数式通过转化，变为用x 1＋x 2，x 1x 2的代数式进行表示，然后再整体代入求出代数式的值．解决此类问题时经常要运用到以下代数式及变形：①21x ＋22x ＝(x 1＋x 2)2－2x 1x 2；②1x 1＋1x 2＝x 1＋x 2x 1x 2；③(x 1＋a )(x 2＋a )＝x 1x 2＋a (x 1＋x 2)＋a 2；④|x 1－x 2|＝(x 1－x 2)2＝(x 1＋x 2)2－4x 1x 2.【例7】已知方程2x 2＋5x －6＝0的两个根为x 1，x 2，求下列代数式的值．(1)(x 1－2)(x 2－2)；(2)x 2x 1＋x 1x 2.（4）已知含未知常数m 的一元二次方程两根关系式，求未知常数m 。

一元二次方程判别式的三种情况

一元二次方程判别式的三种情况一元二次方程的判别式有三种情况，分别是大于零、等于零和小于零。

当判别式大于零时，方程有两个不相等的实数根。

这种情况下，方程的图像是一个开口向上的抛物线，在$x$轴上有两个交点。

当判别式等于零时，方程有两个相等的实数根。

这种情况下，方程的图像是一个在$x$轴上只有一个交点的抛物线，该点也是其顶点。

当判别式小于零时，方程没有实数根。

这种情况下，方程的图像不与$x$轴相交，但在复数域内存在两个共轭复数根。

三种情况可以用判别式公式$Δ=b^2-4ac$来判断，其中$b$、
$a$、$c$分别是一元二次方程$ax^2+bx+c=0$的系数。

如果$Δ>0$，则有两个不相等的实数根；如果$Δ=0$，则有两个相等的实数根；如果$Δ<0$，则没有实数根。