力偶和力偶矩
哈工大建筑力学第3章(第2 3节) 力偶 力偶矩(2学时)

第三章力系简化的基础知识林国昌§3-2 力对点的矩A o o4力对物体具有转动效果,转动效果与三个因素有关:(1)力F 的大小;(2)转动中心O 到力F 作用线的距离d ;(3)力F 使扳手转动的方向。
注意:距离d 是转动中心O 到力F 作用线的垂直距离。
5力对点的矩:力对点的矩是力使物体绕点转动效果的度量,它是一个代数量,其绝对值等于力的大小与力臂之积。
正负规定:力使物体绕矩心逆时针转动时取正号,反之取负号。
符号表示:)(F M O Fd=±力矩的单位:牛顿•米(N •m)1.在门位置上施力,门很容易转动2.从门位置依序至位置施力,转动越不易ABC转轴OO 'OO’C B A 3-2 力对点的矩转动效果与三个因素有关:(1)力F 的大小;(2)转动中心O 到力F 作用线的距离d ;(3)力F 使扳手转动的方向。
7M O (F ) = ±2ΔOAB 面积=±Fd力对点的矩还可以用矩心为顶点,以力矢量为底边所构成的三角形的面积的2倍来表示,即:三角形ΔOAB 底边:力矢量F 三角形ΔOAB 的高:力臂d 力矩的单位:牛顿•米(N •m)注意:距离d 是转动中心O 到力F 作用线的垂直距离。
§3-3 力偶· 力偶矩林国昌103-3 力偶· 力偶矩一、力偶(F ,F ′)FF ′力偶实例由物理学可知:作用在物体上同一点的两个力,可以合成为作用在该点的合力。
合力:是作用在同一点上的各力的矢量和。
13a)力偶没有合力;b)力偶不能与一个力等效,也不能用一个力来平衡;c)力偶只能与力偶等效,也只能与力偶平衡。
力偶的性质1:力偶与力同属于机械作用的范畴,但又不同于力。
力与力偶分别是力学中的两个基本参量!3-3-1力偶•力偶的第一个性质143-3-1力偶•力偶的第二个性质力对物体具有转动效果,力使物体绕点转动的效果用力对点的矩来度量。
力偶对物体也有转动效果,力偶使物体转动的效果用力偶矩来度量。
力系的简化和平衡-2.2力矩和力偶

定理叙述:平面汇交力系的合力对平面内任一点的矩等
于各分力对同一点力矩的代数和
n
M o FR
M o Fi
i 1
定理证明:
FR
F1
r
A
O
Fn
F2 Fi
若 n 个力汇交于A点,则其合力为:
n
FR F1 F2 Fn Fi
i 1
r 用 同时矢积上式两端
r FR
r F1
zFx
xFz
j
xFy yFx k
由此可得:
M x
F
yFz zFy
M y
F
zFx xFz
M z F xFy yFx
Fz Fx Fy
18
力矩的单位: N m 或 kN m
B
Mo(F)
r
O
h
F
A
③力对点之矩矢的性质: a) 当力沿其作用线移动时,
M O F 保持不变。
12
①力对点之矩矢的概念 力对刚体产生的绕点转动效应取决于三要素: a.强度:力与力偶臂乘积 b.方位:转动轴的方位 c.方向:转动方向
13
力矩矢量的方向
MO
r
F
按右手定则
MO r F
14
②力对点之矩矢的矢量积和解析表达式
B
Mo(F)
r
O
h
F
A
力矢: F Fx , Fy , Fz
求: 光滑螺柱AB所受水平力。
解:由力偶只能由力偶平衡的 性质,其受力图为:
M 0
FAl M1 M 2 M 3 0
解得
FA
FB
M1
M2 l
M3
200N
理论力学13力偶与力偶矩

习题: P.29 1-15、1-16
2020/4/30
19
谢谢大家!
2020/4/30
20
理论力学
主讲
广东海洋大学寸金学院
庞雪飞
2020/4/30
1
1.3 力偶与力偶矩
F =-F′
F' F
2020/4/30
2
F =-F′
■力偶的定义
F
两个大小相等、
作用线不重合的反
向平行力组成的力
系称为力偶
F′
(couple)。
2020/4/30
3
力偶中两个力的作
用线所确定的平面称 为力偶的作用面
(acting plane of a couple),二力作用线 之间的垂直距离d称 为力偶臂(couple arm)。
x
黑版手书计算上例。
2020/4/30
17
练习
如图汽缸盖上4个相同的 孔,每个孔的切削力偶矩大 小为M1=M2=M3=M4=15 N.m。
求工件的总切削力偶矩
解:根据 M Mi 可得
M2
M1
M4
M3
M M 1 M 2 M 3 M 4
415 60N .m 负号表示合力偶矩的转向为顺时针方向
2020/4/30
8
d1 M=F0×d1=F×d
平面问题
由于力偶的作用面总是与力系所在的平面 重合,力偶矩由矢量变成代数量
M = Fd
正负号用来区别 转向,通常规定: 逆时针为正 顺时针为负
+–
这里的逆时针或顺时针转向是指物体在力偶的作用下转
动202的0/4/方30 向。
10
■力偶是最简单的力系之一
第2章 平面力系-平面力对点之矩及平面力偶

即
MO(F) F d
O点为力矩的中心,称为矩心; d 为O点到力F 作用线的垂直
距离,称为力臂。 力矩的正负号:力使物体绕逆时针方向转动时为正,反
之为负。
应注意: 在平面问题中,力对点之矩只取决于力矩的大小及其旋 转方向(力矩的正负),因此它是一个代数量。
力矩的单位: 国际制 N·m,kN·m 工程制 公斤力米(kgf·m)
偶矩的代数和等于零,即 ∑Mi=0
利用这个平衡条件,可以求解一个未知量。
例题
两力偶作用在板上,尺寸如图,已知 F1 = F2=1.5 kN , F3
=F4 = 1 kN, 求作用在板上的合力偶矩。
F 1 180mm
解:由式
F2
M = M1 + M2
F4
则
M =-F1 ·0.18 –F3 ·0.08
FBA
B
A
FAB
M1
FO
O
M2 D
FD
M1 - FABrcosq 0 - M 2 2FBArcosq 0
因为 FAB FBA
所以求得 M 2 2M1
思考题1 一力偶(F1,F1′)作用在Oxy平面内,另一力偶(F2 ,F2′)作用在
Oyz平面内,它们的力偶矩大小相等(如图)。试问此两力偶是否 等效,为什么?
F1
d1
F2 d2
F1′
=
F2′
M1 F1 d1 , M 2 -F2 d2
F22 d F11
F11′
=
F22′
d
FR
FR′
M1 F11 d , M 2 -F22 d
FR F11 - F22 , FR F11 - F22
力偶的概念

力偶的概念
力偶是指数值相等但方向相反的两平行力,产生的力矩为力偶矩。
力偶就是作用在同一物体上的等值、反向、不共线的一对力。
力偶对物体产生转动效应,它的度量以力偶矩表示,即其中任一个力的大小与两个力作用线之间的垂直距离的乘积。
力偶就是受到大小相等,方向相反,互相平行的两个力的作用。
它对物体产生的是纯转动效应(力偶可以在其作用面内任意移动,而不影响它对刚体的作用效应。
力偶最简单的例子包含两个大小相同、反向相反的力。
力矩平面力偶

30◦
B RB
∑ mi = 0
R A ⋅ L sin 30o = M 2M 方向如图所示 R A = RB = L
15
16
NB =
60 = 300N 0.2
N A = N B = 300 N
14
平衡时, 处和 处的反力 处和B处的反力? [例2] 已知M 和 L,图示梁AB平衡时,A处和 处的反力? 解: BC 杆为二力杆
C M A L M RA
RB 沿BC 杆方向
由力偶只能与力偶平衡的性质, 由力偶只能与力偶平衡的性质, 与力R 组成一力偶。 力RA与力 B组成一力偶。 根据平面力偶系平衡方程有: 根据平面力偶系平衡方程有:
1
第三章 平面汇交力系 §3–1 力对点之矩 §3–2 力偶与力偶矩 §3–3 力偶的等效 §3–4 平面力偶系的合成与平衡
2
§3-1 力对点之矩
一、平面上力对点之矩 力对物体可以 产生运动效应 移动效应——取决于力的大小、方向 取决于力的大小、 移动效应 取决于力的大小
转动效应——取决于力矩的大小、转向 取决于力矩的大小、 转动效应 取决于力矩的大小 r 点的矩, 力F 对O 点的矩,简称力矩 M O F = ± F ⋅ d + O 点称为力矩中心(简称矩心) 点称为力矩中心(简称矩心)
(
)
现沿力偶臂AB方向 现沿力偶臂 方向 r r 加一对平衡力 Q, Q′ r r r r r r 将Q, F合成R, 将Q′, F ′合成R′, r r 得到新力偶 R, R′ r r r r r r 将R和R′移到 A′, B′点, 则 R , R′ 取代了原力偶 F , F ′ ,
(
)
(
( )
( )
工程力学(人民交通出版社)第3章 第2节力偶系

Fy
F
C
B D
b
Fx x
a
MA( F ) MA( Fx ) MA( Fy ) Fx b Fy a F cos b F sin a Fa sin Fb cos
F Fx Fy
Fx F cos Fy F sin
Mo (F , F ' ) Mo (F ) Mo (F ' ) F (d x ) F ' x F d
⑦正负规定:逆时针为正 ⑧单位量纲:N m 或 kN m
二、力偶与力偶矩
2、力偶的特点 ⑨力偶的三要素: 力偶矩的大小、力偶的转向、力偶的作用面 ⑩力偶矩矢 用一个矢量表达三要素:力偶矩矢。
§3-2
力矩与力偶理论
一、力对点之矩 二、力偶与力偶矩 三、力偶系的合成与平衡
一、力对点之矩
1、平面中力矩的概念
力对物体可产生运动效应,在一般情况下,既可能产生移动(平动)效应, 也可能产生转动效应,或者同时产生这两种运动效应。力的移动效应取决于 力的大小和方向,而力使物体绕某点的转动效应,则用力对该点的矩来度量, 简称力矩。
2)合力矩定理 将力Fn分解为切由合力矩定理得:
M o (Fn ) M o (Ft ) M o (Fr ) Fn r cos 0 Fn r cos
小结力偶和力偶矩
1. 力矩是力学中的一个基本概念。度量力对物体的转动 效应:
即有: Mx mx My my Mz mz 同理: M Mx 2 My 2 Mz 2
( Mx ) ( My ) ( Mz )
2 2 2
z
MZ
力矩力偶

力偶系的合成和平衡
空间力偶系的合成:
M Mi
M x M xi M y M yi M z M zi
合力偶矩的大小:
M ( M x )2 ( M y )2 ( M z )2
合力偶矩矢的方向:
cos(M , i )
M x
cos(M ,
MO (F) = MO (F cos)+MO(F sin )
例题 1
如 图 所 示 圆 柱 直 齿 轮 , 受 到 啮 合 力 Fn 的 作 用 。 设 Fn=1400N。压力角α=20o ,齿轮的节圆(啮合圆)的半径 r = 60
mm,试计算力 Fn 对于轴心O的力矩。
解: 计算力Fn对轴心O的矩,按力矩的定义得
其力偶矩矢为:
解得
FA
M1 r sin 30
再取摇杆BC为研究对象:
∑M = 0:
M 2 FA
r
sin
0
其中 FA FA
解得 M2 4M1 8 kN m
FO
FB
FA
M1 r sin 30
8
kN
例题 4
图示三角柱刚体是正方体的一半,其上作用着三个力偶。已知力 偶(F1,F1)的矩 M1= 20 N·m;力偶(F2, F2)的矩 M2= 20 N·m;力偶(F3,F3)的矩 M3= 20 N·m,试求合力偶矩矢 M。 又问若要使这个刚体平衡,还需要施加怎样一个力偶?
0
0l
3
力偶及其性质
力偶及其性质
1. 力偶与力偶矩 2. 力偶等效定理 3. 力偶系的合成和平衡
力偶的实例
力矩力偶力偶矩滑轮差动轮

力矩力偶力偶矩滑轮差动轮【力矩】又叫转矩,是表示力对物体作用时,使物体发生转动或改变转动状态的物理量.力矩是矢量.力矩的大小等于力与从转轴到力的作用线的垂直距离之乘积.如果物体所受的力不在垂直于转轴O的平面内,就必须把力分解成两个分力:一个分力与转轴平行;另一个分力是在转动的平面内.只有转动平面内的分力才可能改变物体的转动状态.因此,在力矩等于力跟力臂乘积的计算中,应理解力是在它的作用点的转动平面内的分力.如这一点在力的作用线上,则力矩为零.如果若干个力同时作用在一个物体上,则合力矩是所有分力矩的代数和.一个处于平衡的物体,顺时针方向力矩的和等于逆时针方向力矩的和,在国际单位制中,力矩的单位是米.牛顿.其方向用右手螺旋法则决定.在中学阶段,因为只研究有固定转轴的物体的平衡,力矩就只有两种转向.规定物体逆时针转动的力矩为正,使物体顺时针转动的力矩为负.力矩愈大,使物体转动状态发生改变的效果就愈明显.用大小相同的力推门时,力的作用点离转轴愈远,且方向垂直于门,力臂愈大,则推门愈省力.【力偶】大小相等、方向相反,但作用线不在同一直线上的两个力叫作力偶.用双手攻螺纹或用手旋钥匙、水龙头时,所施加的作用常是力偶.它能使物体发生转动,或改变其转动状态.汽车驾驶员双手转动转向盘时所施加的一对力就是一个力偶.力偶的转动效果决定于力偶矩的大小.力偶矩等于其中任何一个力的大小和两力作用线之间的垂直距离(力偶臂)的乘积.如图1-24所示.如果作用力F的方向跟AB垂直,AB的长度等于d,那么这个力偶的力偶矩(M)为:M=/-Fd.式中Fd为力偶矩的大小,符号用来表示力偶的转向.规定力偶逆时针转向取,反之取-(也可规定,力偶顺时针转向取,那么力偶逆时针转向就取-).应注意:力偶中力的方向不跟AB垂直时,应像力矩那样分解成垂直分量,再进行计算.力偶的转矩(即力偶矩)和所绕着转动的点无关.由于力偶的合力为零,它不能使物体产生位移,只能使物体发生转动或改变物体的转动状态.【力偶矩】简称为力偶的力矩,亦称力偶的转矩.力偶是两个相等的平行力,它们的合力矩等于平行力中的一个力与平行力之间距离(称力偶臂)的乘积,称作力偶矩,力偶矩与转动轴的位置无关.力偶矩是矢量,其方向和组成力偶的两个力的方向间的关系,遵从右手螺旋法则.对于有固定轴的物体,在力偶的作用下,物体将绕固定轴转动;没有固定轴的物体,在力偶的作用下物体将绕通过质心的轴转动.【力偶臂】力偶之两个力之间的垂直距离.见力偶条图1-24所示.【轮轴】是固定在同一根轴上的两个半径不同的轮子构成的杠杆类简单机械.半径较大者是轮,半径较小的是轴.从形式上看是圆盘,但从实质上看起来只有它们的直径或半径起力学作用.用R表示轮半径,也就是动力臂;r表示轴半径,也就是阻力臂;O表示支点.当轮轴在作匀速转动时,动力t轮半径=阻力t轴半径,所以轮和轴的半径相差越大则越省力.上式动力用F表示,阻力用W表示,则可写成FR=Wr.即利用轮轴可以省力.若将重物挂在轮上则变成费力的轮轴,但它可省距离.轮轴的原理也可用机械功的原理来分析.轮轴每转一周,动力功等于Ft2pR,阻力功等于Wt2pr.在不计无用阻力时,机械的日常生活中常见的辘轳、绞盘、石磨、汽车的驾驶盘、手摇卷扬机等都是轮轴类机械.【滑轮】滑轮是属于杠杆变形的一种简单机械,是可以绕中心轴转动的,周围有槽的轮子.使用时,根据需要选择.滑轮可分为定滑轮、动滑轮、滑轮组、差动滑轮等.有的省力,有的可以改变作用力的方向,但是都不能省功.【定滑轮】滑轮的轴固定不动,它实质上是一个等臂杠杆.动力臂和阻力臂都是滑轮的半径r,根据杠杆原理Fr1=Wr2.它的机械利益为变了动力的方向,如要把物体提到高处,本应用向上的力,如利用定滑轮,就可以改用向下的力,优惠打折,因而便于工作.【动滑轮】滑轮的轴和重物一起移动的滑轮.它实质上是一个动力臂二倍于阻力臂的杠杆.根据杠杆平衡的原理Wr=F.2r,它的机械利改变用力的方向.其方向是与物体移动的方向一致.【滑轮组】动滑轮和定滑轮组合在一起叫滑轮组.因为动滑轮能够省力,定滑轮能改变力的方向,若将几个动滑轮和定滑轮搭配合并而成滑轮组,既可以改变力的大小,又能改变力的方向.普通的滑轮组是由数目相等的定滑轮和动滑轮组成的.而这些滑轮或者是上下相间地坐落在同一个轮架(或叫轮辕),优惠打折,或者是左右相邻地装在同一根轴心上.绳子的一端固定在上轮架上,即相当于系在一个固定的吊挂设备上,然后依次将绳子绕过每一个下面的动滑轮和上面的定滑轮.在绳子不受拘束的一端以F力拉之,被拉重物挂在活动的轮架上.对所有各段绳子可视为是互相平行的,当拉力与重物平衡时,则重物W必平均由每段绳子所承担.若有n个定滑轮和n个动滑轮时,且为匀速运动时,淘宝客,则所需之F力的大小仍和上面一样.因此,在提升重物时才能省力.其传动比乃为F∶W=1∶2n.注意,在使用滑轮组时,不能省功,只能省力,但省力是以多耗距离(即行程)为前题的.前边所分析的定滑轮、动滑轮以及滑轮组,都是在不计滑轮重力,滑轮与轴之间的摩擦阻力的情况下得出的结论.但在使用时,实际存在轮重和摩擦阻力,所以实际用的力要大些.【差动滑轮】即链式升降机,是一种用于起重的滑轮组.上面是由两个直径不同装在同一个轴上的圆盘A、B组成的定滑轮.下面是一个动滑轮,用铁索与上面的定滑轮联结起来而成滑轮组.若大轮A的半径是R,小轮B的半径是r,如图1-25所示.当动力F拉链条使大轮转一周,动力F拉链条向下移动了2pR,大轮卷起链条2pR,此时小轮也转动一周,并放下链条长2pr于是动滑轮和重物W上升的高度为由于2R大于(R-r),差动滑轮的机械利益大于1,若提高机械利益,可加大两轮的半径同时缩小两轮间的半径差.这种机械,亦称葫芦,有手动,也有用电来驱动的.链条是闭合的,为防止滑轮和链条间的滑动,滑轮上有齿牙与链条配合运动.。
力矩和平面力偶系

所以两个力偶等效,必须是该两个力偶旳力偶矩 大小相同,转向相同,作用面相同。(对刚体, 可作用面平行。)
例题:
F
1.习题3-2
a
b
Fx F cosa
a
Fy f sin a
M A (F ) -Fx b Fy 0 -Fb cosa
M B (F ) -Fx b Fy a F (a sin a - b cosa )
2.习题3-7
正三角形ABC
B F2
F1 F2 F3 F
X F1 cos 60 F2 cos 60 - F3 0
F1
Y F1 sin 60 - F2 sin 60 0
A
即合力FR=0
F1x
F
cos 60
第三章: 力矩与平面力偶系
本章研究力矩和力偶旳概念、力偶旳 性质、平面力偶系旳合成与平衡。本 章与第二章旳理论是研究平面一般力 系旳基础。
§3-1 力矩旳概念和计算
一般情况下,力对物体作用时能够产 生移动和转动两种外效应。力旳移动 效应取决于力旳大小和方向。为了度 量力旳转动效应,需要引入力矩旳概 念。
设物体上作用有一 力偶臂为d旳力偶 (F,F‘)
该力偶对作用面内任 一点O之矩为:
O x
F
F’ d
Mo(F)+Mo(F’)=F(x+d)-Fx=Fd
力偶对作用面内任一点旳矩之大小恒等于力偶中 一力旳大小和力偶臂旳乘积,而与矩心旳位置无关。
力偶对物体旳转动效应可用力与力偶臂旳乘积Fd 及转向来度量,该物理量称为力偶矩。
互成平衡旳二力对同一点旳力矩之和为 零
虽然力矩概念由力对物体上固定点旳 作用引出。实际上,作用于物体上旳力 能够对任意点取矩,即矩心可是空间中 旳任意点。
工程力学5 力偶及平面力偶系的合成
M 60° 30°
0.25m
数值为正,M使物体顺时针转动,计算时数值为负。
M1=P1d1=200 ×1=200(N·M) M2=P结2d果2=为60正0 数×,0.2代5/表si最n3后0°合=成300(N·M)
M3=-M的=合-1力00偶(N为·M逆) 时针,即:物
P2
P1
则合力体偶最M后合为将:逆时针转动。
即: M i 0
平面力偶系的平衡条件有何作用呢?
例题2:如图所示,梁AB受荷载作用。M=10kN·m,P=P’=5kN,
不计梁自重,求支座A、B的反力。
解:取AB为研究对象。作用在梁
P
M 上的力有:M、P和P’形成的力
A
B
偶,以及支座A和B的反力形成的
P'
力偶。由于梁处于平衡状态,因
此,整个体系力偶矩之和为零。
力偶三要素:力偶矩的大小、力偶的转向和力偶的作用面。
10KN 2m
5KN
20KN
1m
M=20KN ·m
10KN
5KN
20KN
3.平面力偶系的合成
10KN 5KN
2m
20KN
10KN
5KN
1m 20KN
在物体的某一平面内同时作用有两个或两个以上的力偶时, 这些力偶就称为平面力偶系。
(1)平面力偶系的合成
1m
M合=M1+M2+M3
=200+300-100=400(N·M)
3.平面力偶系的合成
(2)平面力偶系的平衡条件
平面力偶系可以合成为一个合力偶,当合力偶矩等于零时,则 力偶系中各力偶对物体的转动效应相互抵消,物体处于平衡状态; 反之,当合力偶不等于零时,物体必有转动效应而不平衡。平面力 偶系平衡的充要条件是:力偶系中所有各力偶矩的代数和等于零。
平面力偶系

总切削力偶矩和A 、B端水平反力?
解: 各力偶的合力偶矩为
M m m m m 1 2 3 4 4 ( 15 ) 60 N m
由力偶只能与力偶平衡的性质, 力NA与力NB组成一力偶。
根据平面力偶系平衡方程有:
60 N 300 N B 0 .2
N 0 . 2 m m m m 0 B 1 2 3 4
2.4 平面力偶
2.4.1力偶与力偶矩
由两个大小相等、方向相反且不共线的平行力组成的力系, 称为力偶,记为(F, F')。力偶的两力之间的垂直距离d称为力臂, 力偶所在的平面称为力偶作用面。 力偶不能合成为一个力,也不能用一个力来平衡。力和力 偶是静力学的两个基本要素。
2.4.1 力偶与力偶矩
M ( F ) M ( F R i) O O
i 1
n
y
(2) 力矩的解析表达式
Fy
A
O x y
F
q
M ( F ) x F s i n q y F c o s q O x F y F y x
Fx x
已知F=1400 N, r=60 mm, a=20°,求力Fn对O点的矩。
例1
Ft Fn Fn
R C
m 2 m N R AD B 0 l sin 45 l
[例6]不计自重的杆AB与DC在C处为光滑接触,它们分别受力
偶矩为M1与M2的力偶作用 ,转向如图。问M1与M2的比值为多 大,结构才能平衡?
B
C
M1
A 60o 60o
M2
D
B
解: 取杆AB为研究对象画受力图。 杆A B只受力偶的作用而平衡且C处为光 A 60o 滑面约束,则A处约束反力的方位可定。
力矩和力偶系

§3-1 力矩(* 重点)
一、力对点之矩
• 点•例力O力同规力右转物生力连如矩矩,一定矩手动d理力臂线用的心个:为向力中逆学矩是和板表,计负上臂心(时过,转力手示算。表F,称针力),力动作拧方单什示产为转矩用矩中用螺法位么方生矩动单板=例受柄的为心线栓要是便:力力心M,位手零力 端受,到垂 统 顺AO力矩×(,:转,板F部力,力F直一、矩的力3常)N动力矩F手沿,作=。逆,为·力臂4力用±螺矩心或,卡手用时正m,臂一F±栓为为线力板口柄d针;;?字,正,零A垂臂手外轴?顺k不母其;或施直均手的线因时N垂表中拧负·加距逆针直示M螺号m在离力时转,矩栓,板等力,矩针动F心B手。臂若,用,,,①钟和所把针上?转转垂指力把中的动向足钟想矩心力中想点像心,必心须像位为想②到要为置推像把作产指动为,力用针指时③臂
6
二、合力矩定理
定理:平面汇交力系的合力对平面内任一点(轴)的矩,等于
所有各分力对同一点(轴)的矩的代数和。
MO(FR ) MO(F1) MO(F2 ) MO(Fn ) MO(F )
[证因]为由物合理力已投知影,定合理力有和:分力等od效=,o所b+以o,合c 力力矩等于各分
例矩,心力为F1B拧紧螺栓A,连线和力线不垂直, MA(F1)=-
F1d1;力F2拧松,垂直, MA(F2)=+F2d2 怎样判定转动方向是顺时针或逆时针?──想像法!
特例:力作用线通过矩心,力矩等于零。
2020/2/2
4
力矩是计算力对矩心的力矩,同一力不同矩心力矩不同,
矩心是一个点,所以又称为力对点的力矩,以符号Mo(F)
§3-5 平面力偶系的合成与平衡
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系 设有两个力偶
2.2 力矩和力偶
∑Fx=0 ∑Fy=0 ∑MO(F)=0
上述三组方程是平面一般力系平 衡方程的三种表达形式,实际计算时 应根据问题的具体条件来选择其中的 一组方程。但不论采用哪种形式,都 只有写出三个独立的平衡方程才可以 求解三个未知量。
建筑力学与结构基础
第二章 平面力系
例1-8
已知F=15kN,M=3kN.m,求A、B处支座反力 解:
y
Fx
F
(二)合力矩定理
合力对平面内任意一点之矩, F 等于所有分力对同一点之矩的代数 和。
o
r
d
x
A
y
Fy
x
M O F M O F1 M O F2 M O Fn
即:
Mo (FR ) Mo (F )
利用合力矩定理可以简化力矩的计算
建筑力学与结构基础
第二章 平面力系
• 【例2.1】如图所示每1m长挡土墙
• 所受的压力的合力为F,它的大小为 • 160kN,方向如图所示。求土压力F
• 使墙倾覆的力矩。
• 【解】土压力F 可使墙绕点A倾覆, • 故求F 对点A的力矩。 • 采用合力矩定理进行计算比较方便。 • MA(F) =MA(F1)+MA(F2)=F1×h/3-F2b
§2-2 力矩和力偶
一、 力矩
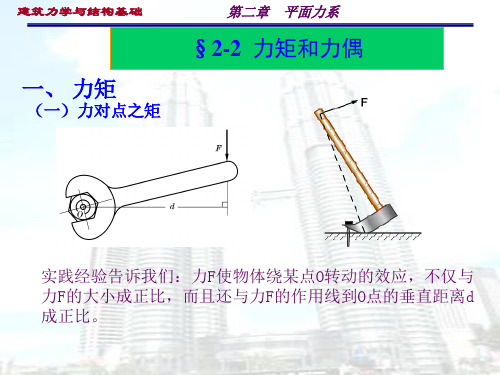
(一)力对点之矩
实践经验告诉我们:力F使物体绕某点O转动的效应,不仅与 力F的大小成正比,而且还与力F的作用线到O点的垂直距离d 成正比。
建筑力学与结构基础
第二章 平面力系
§2-2 力矩和力偶
一、 力矩
(一)力对点之矩
l
d
A
o
将力F与O点到力F作用线的垂直距离d的乘积Fd并加上 正负号称为力F对O点的力矩,用MO(F)表示,即
工程力学第三章力矩力偶系

M ( F ) r F sin O
定理:如果力系存在合力,则合力对某一点的矩等于力 系中各分力对同一点的矩的矢量和。
即:若作用在刚体上 { F , F , , F } { F } 1 2 n R
则:
M ( F ) M ( F O R O i)
i 1
n
例 水平梁 AB 受按三角形分布的载荷作用。载荷的最 大值为 q ,梁长为 l 。试求合力作用线的位置。
0
将 Q 和 q(x) 的数值代入可得
xC
2 l 3
§3-2 力偶理论
一.力偶和力偶矩
1、力偶 · 力偶的作用 效果 ·力偶的第一性质
力偶的定义:由大小相等,方 向相反且不共线的两个平行力 所组成的力系,称为力偶。记 之为: ( F, F ' )
F
hபைடு நூலகம்
F
'
h——力偶臂
力与力偶的作用效果比较:
FA
第三章 力矩 力偶系理论
§3-1 力对点之矩(力矩) 力对刚体的移动效应用力矢量来度量 力对刚体的转动效应用力矩来度量 一、力对点之矩
B F O
定义:
r
h
A
M r F oF
矢量积形式
M r F oF
二、 合力矩定理
大小: r F F h 2 OAB 方向: 由右手定则判定
25 N 0.4 m
M=10 Nm
25 N
§3-3 力偶系的合成与平衡
力偶系合成的结果为一合力偶
{ M , M , , M } { M } 1 2 n R
n
即:
M R Mi
i 1
力偶平衡的充分必要条件:
同济版_理论力学_王斌耀(同济理力最好老师)_第3章 力矩理论与 力偶理论

z
Fz B β
y=180mm
F Fy
A
Fx α Fxy
y
z=200mm
0 x x=0, =0, y=180mm, =180mm, z=200mm. =200mm.
§3-2力偶的概念
一、力偶与力偶矩
大小相等、方向相反、作用线相互平行的两个力所 大小相等、方向相反、 组成的力系称为力偶。 组成的力系称为力偶。
M O ( FR ) = M O ( F1 ) + M O( F2 ) = ∑ M O ( Fi )
合力对点(或轴) 合力对点(或轴)之矩等于各分力对 同点(或同轴)之矩的矢量和(代数和) 同点(或同轴)之矩的矢量和(代数和)。
z A
F1 F2
y
FR
r × FR = ∑ r × Fi
i =1
O
n
r
x
1、平面力偶
F
F’
1、平面力偶
F’ F
F’ F
F
A
d
rBA
B
F′
+ _
M=±Fd (Nm) ±
力偶作用平面
d:力偶臂
2、空间力偶 力偶的矢量表示
M A = rBA × F = M B = rAB × F
'
M
右手法 则为正
B
F
rBA
A
F’
力偶矩矢量垂直于力偶所在平面,其大小和方向与取矩点无关 力偶矩矢量垂直于力偶所在平面 其大小和方向与取矩点无关. 其大小和方向与取矩点无关
P力作用点的矢径 力作用点的矢径
r = xi + yj + zk ,
x = 5cm, y = 6cm, z = 0
1.5力偶与力偶矩
力偶的三要素
1.力偶矩的大小 2.力偶在作用平面内的转向 3.力偶的作用面
力偶的特性
1、力偶没有合力,不能与一个力平衡,只能用力偶来平衡。 2、力偶对物体的转动效果可用力偶矩来度量。 3、凡是三要素相同的力偶都是等效力偶,可以相互代替。
§3.2 力偶与力偶矩
三、力偶与力偶矩的性质
相同点
使物体转动状态பைடு நூலகம்变。
力偶矩是矢量,逆时针为正,顺时针为正。
力偶的三要素和特性
力偶在作用面内可以任意移动和转动, 而不改变它对物体的作用。
力偶的转动作用 取决于力偶矩, 在同一平面内凡 是力偶矩相同的 力偶,一定是等 效力偶。
不改变力偶矩的大小和转动条件下同时改 变力偶中力的大小和力偶臂,不改变它对 物体的转动作用效果。
力矩 不同点 不同点 力偶
转动效应与矩心有关
对作用面内任一点矩 为常数,即等于力偶 矩。
小结
• • • • • • 力偶 力偶臂 力偶矩 力偶矩公式 力偶三要素 力偶三特性
§3.2 力偶与力偶矩
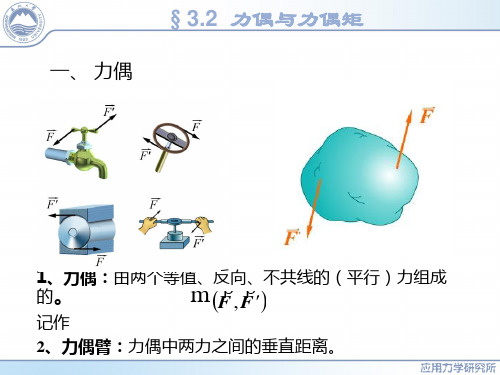
一、 力偶
1、力偶:由两个等值、反向、不共线的(平行)力组成 的。 m F , F 记作 2、力偶臂:力偶中两力之间的垂直距离。
§3.2 力偶与力偶矩
二、力偶矩
M F , F F d
力偶矩记作 mF , F 或m
d ——力偶臂,m F——力的大小,N m——力偶矩,N . m
力偶与力偶矩
一、 力偶
由两个等值、反向、不共线的(平行)力组成的 力系称为力偶,记作
No Image
§3.2 力偶与力偶矩
二、力偶矩
力偶中两力所在平面称为力偶作用面 力偶两力之间的垂直距离称为力偶臂 两个要素 a.大小:力与力偶臂乘积 b.方向:转动方向
力偶矩
No Image
§3.2 力偶与力偶矩
三、力与力偶矩的性质
(1).力偶在任意坐标轴上的投影等于零.
(2).力偶没有合力,力偶只能由力偶来平衡. (3) .力偶对任意点取矩都等于力偶矩, 不因矩心的改变而改变.
§3.2 力偶与力偶矩
No Image
No Image
No Image
力矩的符号
No Image
力偶矩的符号 M
力偶与力偶矩

力偶无合力,即在任何情况下,一个力 偶都不能与一个力等效。
力偶对物体只产生转动效应。
二、力偶矩
—— 度量力偶对物体转动效应的物理量 用力偶的两个力对其作用面内任一点之矩 的代数和来度量。
m o ( F ) m o ( F ) F ( d x ) F x Fd
力偶的两个力对其作用面内任 一点之矩的代数和,其大小恒 等于一力的大小与力偶臂的乘 积,而与矩心的位置无关;其 正、负号与力偶的转向有关。 定义力偶矩为
m Fd
可见,平面力偶的力偶矩也是一个代数量。
返回
力偶的两个力在同一坐标轴上的投影之一力偶大小相等方向相反作用线相互平行而不重力偶无合力即在任何情况下一个力偶都不能与一个作用线相互平行而不重 合的两个力 ( F , F ) 。 力偶作用面、力偶臂d(两力作用线之间 的垂直距离) 力偶的两个力不是平衡力系。 力偶的两个力在同一坐标轴上的投影之 和为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8. 力偶的等效定理 定理:在同平面内的两个力偶,如果力偶矩相等,则 两力偶彼此等效。
二、力的平移定理
1.定理:可以把作用在刚体上点 A的力F平行移到 一点B,但同时必须附加一个力偶,这个附加力偶的 矩等于原来的力 F对新作用点B的矩。
F'
F'
F
F
B
d
= A
B
d
= BM
A
A
(a)Biblioteka F(" b)(c)
一、力偶 1.定义:由两个大小相等方向相反的平行力组成 的二力,称为力偶。 2.记作:(F,F′)。 3.力偶臂:力偶两力之间的垂直距离 d。
显然力偶不能合成一个 力,也不能用一个力来平衡, 或用一个力来等效替换。力 偶可使物体转动或改变物体 的转动的状态。
力偶对物体的转动效果与力矩对物体的转动效果 相同,力偶对物体的作用效应可用力偶矩来度量。 5.力偶矩:
课堂小结
定义:等值、反向、共线的一对平行力。
表达式: ( F, F ') 力偶 影响因素: ①力的大小;②力偶臂的长短
正负规定:逆正顺负 单位: 国际单位制中,牛顿米,记作N·M。
第五节 力偶 力偶矩
考纲要求
1.力、力矩、力偶的概念与基本特性; 2.力的三要素; 3.静力学四公理; 4.约束力与约束反力的分类与概念;
本节课学习目标 1.掌握力偶的定义; 2.掌握力偶的性质; 3.正确应用力的平移定理解决实际问题。 4.区分力偶与平衡二力的不同点。
在实际生活中,我们常见到汽车司机用双手转动 方向盘,钳工用手动铰刀铰孔等。
力与力偶臂的乘积称为力偶矩,记作 M。
MO(F,F′) = MO(F) + MO(F′)= F・d
6.方向规定: 逆时针转向为正,顺时针转向为负,于是力偶矩可 记作 M= F・d。 7.单位:N・m。
7.性质: (1)力偶在任何坐标轴上的投影为零,力偶无合 力。 (2)力偶可以在其作用面内任意移转,而不改变 它对刚体的作用。 (3)只要保持力偶矩大小和力偶的转动方向不变, 可以同时改变力偶中力的大小和力偶臂的长短, 而不改变力偶对刚体的作用。
