第04章分子的对称性资料
合集下载
分子的对称性
本章提要： 本章提要：
1. 2. 3. 4. 对称操作和对称元素。 对称操作和对称元素。 对称操作群。 对称操作群。 分子的点群。 分子的点群。 分子的对称性与性质之间的关系。 分子的对称性与性质之间的关系。
4.1
对称操作和对称元素
对称：是指一个物体包含若干等同部分，这些部分相对（对等、 对称：是指一个物体包含若干等同部分，这些部分相对（对等、 对应）而又相称（适合、相当）。 ）。这些部分能经过不改变其内 对应）而又相称（适合、相当）。这些部分能经过不改变其内 部任何两点间距离的对称操作所复原。 部任何两点间距离的对称操作所复原。 复原: 对称物体经过某一操作后， 复原 对称物体经过某一操作后，物体中每一点都被放在周围 环境与原先相似的相当点上， 环境与原先相似的相当点上，无法区别是操作前的还是操作 后的物体。 后的物体。 操作： 操作：是指将图形中每一点按一定规则从一位置移动到另一 位置。 位置。 对称操作是指不改变物体内部任何两点间的距离而使物体复 对称操作是指不改变物体内部任何两点间的距离而使物体复 原的操作。例如：旋转、反映、反演。 原的操作。例如：旋转、反映、反演。 不对称操作：改变了图形中任意两点之间的距离的操作。 不对称操作：改变了图形中任意两点之间的距离的操作。
C 2 =C1C1 n n n
C 3 =C1C1C1 n n n n
，…
恒等操作(主操作 恒等操作 主操作)E: 不改变图形中任意一点位置的操作 主操作
Cn = E n
1 对于分子等有限物体, 对于分子等有限物体 Cn ,
C1 = E
的轴次n不受限制 可为任意整数 的轴次 不受限制, n可为任意整数 不受限制 可为任意整数.
通过主轴C 平分副轴（ σd：σ通过主轴 n ，平分副轴（C2轴）的夹角
第四章分子对称性
S1 h ; S2 i ;
S3 C3 h ; S4独立，包含C2 ;
S5 C5 h ; S6 ቤተ መጻሕፍቲ ባይዱC3 i
S1 C1 ; S 2 Cˆ 1 ; S 3 C1ˆ ; S 4 Cˆ 2 ; S 5 C1 ; S 6 Eˆ
6
6
6
3
6
3
6
h---与主轴垂直的对称面
12
试找出分子中的镜面
13
四 旋转反演和反轴
映轴与旋转反映操作 旋转反映或旋转反演都是复合操作，相应的对称元素
分别称为映轴Sn和反轴In . 这两种复合操作都包含虚操作. 相应地,Sn和In都是虚
轴.
对于Sn，若n等于奇数，则Cn和与之垂直的σ都独立存 在；
若n等于偶数，则有Cn/2与Sn共轴，但Cn和与之垂 直的σ并不一定独立存在.
4
分子对称操作的特点：
分子在对称操作过程中至少保持一点不动—点操作。 分子中每一类原子经操作后环境---化学组成、各原子的 方向、原子间的距离不变。
对称元素
一、对称元素的要素
1、简单几何元素：点(i)、 线(Cn)、面(σ)
名称：
对称中心 旋转轴 镜面
2、几何元素的组合：Cn& σ( 线与面) Sn 映轴
3
6
6
6
17
Sn 产生对称操作的个数 当n为奇数时，Sn：{Sn1,Sn2,…,Sn2n} 2n个对称操作 n 个Cn，n个hCn，—— Cn＋ h
当n为偶数时，Sn：{Sn1,Sn2,…,Snn} n个对称操作 n为4倍数： Sn，（ Cn/2 ）独立操作 n为非4倍数：Cn/2 + i
分子的对称性
第四章 分子的对称性§4.1 对称性操作和对称元素§ <1>分子对称性概念原子组成分子构成有限的图形，具有对称性。
与晶体的对称性不同。
晶体的主要对称性是点阵结构，而分子的对称性主要是指分子骨架在空间的对称性以及分子轨道（波函数）的对称性。
○1分子对称性：指分子的几何图形（原子骨架和原子、分子轨道空间形状）中有相互等同的部分，而这些等同部分互相交换以后，与原来的状态相比，不发生可辨别的变化，即交换前后图形复原。
○2对称操作：不改变物体内部任何两点间的距离，使图形完全复原的一次或连续几次的操作。
（借助于一定几何实体）○3对称元素：对图形进行对称操作，所依赖的几何要素，如：点，线，面及其组合。
<2>对称元素及相应的对称操作○1恒等元素和恒等操作，（E ） ΛE 所有分子图形都具有。
○2旋转轴（对称轴）和旋转操作，Λn n C C ,；对称轴是一条特定的直线。
绕该线按一定方向（逆时针方向为正方面）进行一个角度θ旋转，nπθ2=如：H 2O ： πθ21==n 。
分子中可能有 n 个对称轴，其中n 最大的称为主轴，其它称为非主轴，如：BF 3 ，主轴C 3 ，三个C 2垂直于C 3 与分子平面平行。
n C 将产生n 个旋转操作：E =-nn n n n n C C C C ,,,,12逆时旋转为正操作，k n C ；顺时旋转为逆操作，k n C -。
)(k n nk n C C --= 分子图形完全复原的最少次数称操作周期，旋转操作的周期为 n ；分子中，nC的轴次不受限制，n 为任意整数。
如： E =→332333,,C C C C○3对称和反映操作。
Λσσ, ：对称面是一个特定的镜面，把分子图形分成两个完全相等的对称部分，两部分之间互为镜中映像，对称操作是镜面的一个反映。
图形中相等的部分互相交换位置，其反映的周期为2。
E =Λ2σ。
对称面可分为：v σ面：包含主轴； h σ面：垂直于主轴；d σ面：包含主轴且平分相邻'2C 轴的夹角（或两个v σ之间的夹角）。
结构化学分子的对称性ppt课件
一个h阶有限群的乘法表由h行和h列组成，共h2个乘积； 设行坐标为x，列坐标为y，则交叉点yx,先操作x，再操作y；对 称操作的乘法一般是不可交换的，故应注意次序。
在群的乘法表中，每个元素在每一行和每一列中被列入一 次而且只被列入一次，不可能有两行或两列是全同的。每一行 或每一列都是群元素的重新排列，这就是群的重排定理。
作时分子中至少有一点不动；(2) 分子的全部对称元
素至少通过一个公共点。
19
以H2O为例来说明： H2O分子的对称操作的完全集合为
G Eˆ,Cˆ2 ,σˆV ,σˆV
20
Cˆ 2
σv
C2
σˆ v σ v
σˆ v
σ v
21
(a)满足封闭性：如：Cˆ2σˆv σˆv
(b)有恒等元素：恒等操作 Eˆ
(c)满足缔合性： Cˆ2σˆvσˆv Cˆ2σˆv σˆv σˆvσˆv Eˆ
Cˆ2σˆvσˆv Cˆ2 σˆvσˆv Cˆ2Cˆ2 Eˆ
(d)有逆元素： Cˆ21 Cˆ2 ,σˆv1 σˆv ,
22
(2) 群的乘法表
假若有一个有限群的h个元素的完全而不重复的名单，并 且知道所有可能的乘积(有h2个乘积)是什么，那么这个群就完全 而唯一地被定义了——至少在抽象地意义上是如此。上述概念 可以方便地呈现在群的乘法表的形式中。
第二节 对称操作群与对称元素的组合
(1) 群的定义： 设元素A，B，C，属于集合G，在G中定义
有称之为“乘法”的某种组合运算。如果满足以 下四个条件，则称集合G构成群：
(a) 封闭性：设A和B为集合G中的任意两个元素， 且AB＝C，则C也必是集合G中的一个元素；
(b) 恒等元素：在集合G中必有一个恒等元素E，满 足RE＝ER＝R，R是集合G中任意一个元素。
在群的乘法表中，每个元素在每一行和每一列中被列入一 次而且只被列入一次，不可能有两行或两列是全同的。每一行 或每一列都是群元素的重新排列，这就是群的重排定理。
作时分子中至少有一点不动；(2) 分子的全部对称元
素至少通过一个公共点。
19
以H2O为例来说明： H2O分子的对称操作的完全集合为
G Eˆ,Cˆ2 ,σˆV ,σˆV
20
Cˆ 2
σv
C2
σˆ v σ v
σˆ v
σ v
21
(a)满足封闭性：如：Cˆ2σˆv σˆv
(b)有恒等元素：恒等操作 Eˆ
(c)满足缔合性： Cˆ2σˆvσˆv Cˆ2σˆv σˆv σˆvσˆv Eˆ
Cˆ2σˆvσˆv Cˆ2 σˆvσˆv Cˆ2Cˆ2 Eˆ
(d)有逆元素： Cˆ21 Cˆ2 ,σˆv1 σˆv ,
22
(2) 群的乘法表
假若有一个有限群的h个元素的完全而不重复的名单，并 且知道所有可能的乘积(有h2个乘积)是什么，那么这个群就完全 而唯一地被定义了——至少在抽象地意义上是如此。上述概念 可以方便地呈现在群的乘法表的形式中。
第二节 对称操作群与对称元素的组合
(1) 群的定义： 设元素A，B，C，属于集合G，在G中定义
有称之为“乘法”的某种组合运算。如果满足以 下四个条件，则称集合G构成群：
(a) 封闭性：设A和B为集合G中的任意两个元素， 且AB＝C，则C也必是集合G中的一个元素；
(b) 恒等元素：在集合G中必有一个恒等元素E，满 足RE＝ER＝R，R是集合G中任意一个元素。
结构化学分子的对称性课件.ppt
(c)满足缔合性： Cˆ2σˆvσˆv Cˆ2σˆv σˆv σˆvσˆv Eˆ
Cˆ2σˆvσˆv Cˆ2 σˆvσˆv Cˆ2Cˆ2 Eˆ
(d)有逆元素： Cˆ21 Cˆ2 ,σˆv1 σˆv ,
0.0
22
(2) 群的乘法表
假若有一个有限群的h个元素的完全而不重复的名单，并
作时分子中至少有一点不动；(2) 分子的全部对称元
素至少通过一个公共点。 0.0
19
以H2O为例来说明： H2O分子的对称操作的完全集合为
G Eˆ,Cˆ2 ,σˆV ,σˆV
0.0
20
Cˆ 2
σv
C2
σˆ v σ v
σˆ v
σ v
0.0
21
(a)满足封闭性：如：Cˆ2σˆv σˆv
(b)有恒等元素：恒等操作 Eˆ
的夹角的对称面；
0.0
9
(2) 对称面和反映
H2O
σv
C2
0.0
σv
10
C2轴
主轴C4轴 σd σh
C2轴
0.0
11
C2(z)
d'
d
C2(x)
C2(y)
0.0
12
(3) 对称中心和反演
分子中若存在一点,将每个原子通过这一点引连线 并延长到反方向等距离处而使分子复原,这一点就是对 称中心 i ,这种操作就是反演.
一个偶数次的旋转轴C2n可以产生2n个对称操作：
Cˆ2n ,Cˆ22n ,Cˆ23n ,,Cˆ2nn ,,Cˆ22nn1 ,Cˆ22nn E
而
Cˆ
n 2n
n 0.220πn
2π 2
Cˆ 2
29
x, y, z
Cˆ2σˆvσˆv Cˆ2 σˆvσˆv Cˆ2Cˆ2 Eˆ
(d)有逆元素： Cˆ21 Cˆ2 ,σˆv1 σˆv ,
0.0
22
(2) 群的乘法表
假若有一个有限群的h个元素的完全而不重复的名单，并
作时分子中至少有一点不动；(2) 分子的全部对称元
素至少通过一个公共点。 0.0
19
以H2O为例来说明： H2O分子的对称操作的完全集合为
G Eˆ,Cˆ2 ,σˆV ,σˆV
0.0
20
Cˆ 2
σv
C2
σˆ v σ v
σˆ v
σ v
0.0
21
(a)满足封闭性：如：Cˆ2σˆv σˆv
(b)有恒等元素：恒等操作 Eˆ
的夹角的对称面；
0.0
9
(2) 对称面和反映
H2O
σv
C2
0.0
σv
10
C2轴
主轴C4轴 σd σh
C2轴
0.0
11
C2(z)
d'
d
C2(x)
C2(y)
0.0
12
(3) 对称中心和反演
分子中若存在一点,将每个原子通过这一点引连线 并延长到反方向等距离处而使分子复原,这一点就是对 称中心 i ,这种操作就是反演.
一个偶数次的旋转轴C2n可以产生2n个对称操作：
Cˆ2n ,Cˆ22n ,Cˆ23n ,,Cˆ2nn ,,Cˆ22nn1 ,Cˆ22nn E
而
Cˆ
n 2n
n 0.220πn
2π 2
Cˆ 2
29
x, y, z
04章分子的对称和群
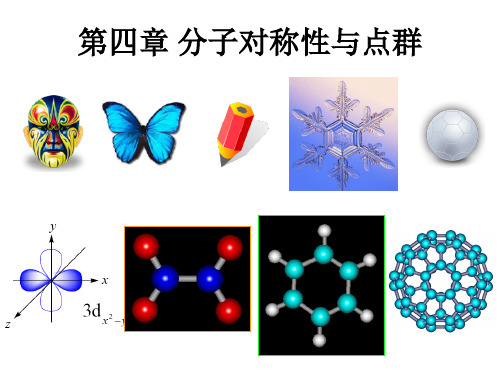
Cnv 是 S2n
是 Ci
否 S2n?
否 i?
否 C1
否 Cn
一些化学中重要的点群
点群 对 称 元 素(未包括恒等元素)
举例
Cs 仅有一个对称面 C1 无对称性 Cn 仅有一根n－重旋转轴 Cnv n－重旋转轴和通过该轴的镜面 Cnh n－重旋转轴和一个水平镜面 C∞v 无对称中心的线性分子 Dn n－重旋转轴和垂直该轴的n根C2轴 Dnh Dn的对称元素、再加一个水平镜面 D∞h 有对称中心的线性分子
ONCl, HOCl
SiFClBrI
H2O2, PPh3 H2O, NH3 反－N2F2 CO，HCN Cr(C2O4)33－ BF3，PtCl42－ H2, Cl2
Dnd Dn的对称元素、再加一套平分每一C2轴的垂直镜面 Sn 有唯一对称元素(Sn映轴) Td 正四面体分子或离子，4C3、3C2、3S4和6d
B2Cl4,交错C2H6
S4N4F4 CH4, ClO4－
Oh 正八面体分子或离子，3C4、4C3、6C2、6d、3h、i SF6
Ih 正二十面体，6C5、10C3、15C2及15σ
B12H122－
分子点群的分类：5 类 1. 无轴群—无Cn轴或Sn轴的群
如 C1，
H
C
F
Br
Cl
Ci，
H
Cl
F
F
Cl
第四章 分子对称性与点群
本章重点
掌握分子轨道理论及其应用； 掌握对称操作与对称元素的概念； 了解常见无机分子（离子）所属的点群； 掌握运用对称性知识判断分子的偶极矩和旋光性的 方法
2.1 对称元素与对称操作
如果分子各部分能够进行互换，而分子的取向没有产生可 以辨认的改变，这种分子就被说成是具有对称性。
结构化学第四章分子对称性
X射线晶体学需要制备晶体样品，通过X射线照射晶 体并记录衍射数据，再通过计算机软件分析衍射数 据，最终得到分子的晶体结构。
X射线晶体学对于理解分子结构和性质具有重要意义 ，尤其在化学、生物学和材料科学等领域中广泛应 用。
分子光谱方法
分子光谱方法是研究分子对称 性的另一种实验方法。通过分 析光谱数据，可以确定分子的 振动、转动和电子等运动状态 ，从而推断出分子的对称性。
04
分子的点群
点群的分类
80%
按照对称元素类型分类
分子点群可按照对称元素类型进 行分类，如旋转轴、对称面、对 称中心等。
100%
按照对称元素组合分类
分子点群可按照对称元素的组合 进行分类，如Cn、Dn、Sn等。
80%
按照分子形状分类
分子点群可按照分子的形状进行 分类，如线性、平面、立体等。
点群的判断方法
分子没有对称元素，如 NH3。
分子有一个对称元素， 如H2O。
分子有两个对称元素， 如CO2。
分子有多个对称元素， 如立方烷。
02
分子的对称性
对称面和对称轴
对称面
将分子分成左右两部分的面。
对称轴
将分子旋转一定角度后与原分子重合的轴。
对称中心
• 对称中心：通过分子中心点，将分子分成互为镜像的两部分。
具有高对称性的分子往往表现出较弱的磁性，因为它们具有较低的轨道和自旋分 裂能。相反，对称性较低的分子可能表现出较强的磁性，因为它们的轨道和自旋 分裂能较高。
对称性与化学反应活性
总结词
分子对称性对化学反应活性也有重要影响，可以通过对称性 分析来预测和解释分子的化学反应行为。
详细描述
具有高对称性的分子往往具有较低的反应活性，因为它们的 电子云分布较为均匀，难以发生化学反应。相反，对称性较 低的分子可能具有较高的反应活性，因为它们的电子云分布 较为不均匀，容易发生化学反应。
X射线晶体学对于理解分子结构和性质具有重要意义 ，尤其在化学、生物学和材料科学等领域中广泛应 用。
分子光谱方法
分子光谱方法是研究分子对称 性的另一种实验方法。通过分 析光谱数据，可以确定分子的 振动、转动和电子等运动状态 ，从而推断出分子的对称性。
04
分子的点群
点群的分类
80%
按照对称元素类型分类
分子点群可按照对称元素类型进 行分类，如旋转轴、对称面、对 称中心等。
100%
按照对称元素组合分类
分子点群可按照对称元素的组合 进行分类，如Cn、Dn、Sn等。
80%
按照分子形状分类
分子点群可按照分子的形状进行 分类，如线性、平面、立体等。
点群的判断方法
分子没有对称元素，如 NH3。
分子有一个对称元素， 如H2O。
分子有两个对称元素， 如CO2。
分子有多个对称元素， 如立方烷。
02
分子的对称性
对称面和对称轴
对称面
将分子分成左右两部分的面。
对称轴
将分子旋转一定角度后与原分子重合的轴。
对称中心
• 对称中心：通过分子中心点，将分子分成互为镜像的两部分。
具有高对称性的分子往往表现出较弱的磁性，因为它们具有较低的轨道和自旋分 裂能。相反，对称性较低的分子可能表现出较强的磁性，因为它们的轨道和自旋 分裂能较高。
对称性与化学反应活性
总结词
分子对称性对化学反应活性也有重要影响，可以通过对称性 分析来预测和解释分子的化学反应行为。
详细描述
具有高对称性的分子往往具有较低的反应活性，因为它们的 电子云分布较为均匀，难以发生化学反应。相反，对称性较 低的分子可能具有较高的反应活性，因为它们的电子云分布 较为不均匀，容易发生化学反应。
04 分子的对称性
时， n 为奇数时， 包含 2n 个对称动作， 个对称动作，可由 Cn +i I 组成； 组成； 当 n为偶数时， 为偶数时， 不是4的倍数时， 组成， (1) n 不是4的倍数时，In 可由 Cn/ 2 +σh组成，包 个对称动作。 含 n 个对称动作。 (2) n是4的倍数，为独立的对称元素(n个动作)。 的倍数，为独立的对称元素(n个动作) (n个动作
ˆ 共有两个独立动作。 σ共有两个独立动作。
反映操作是一种虚动作。
20112011-1-28 16
第四章 分子的对称性
4. 镜面的分类 设主轴位于z轴 设主轴位于z 水平的）； σ ⊥Cn ，记为 σ（horizontal水平的）； h horizontal水平的
σ // Cn ，记为 σ（Vertical 垂直的 ）； v
y (x', y') (x, y)
α
x' x cosα −sinα 0x ' ˆ y = C(α) y = sinα cosα 0y ' z z 0 0 1z
x
20112011-1-28 12
20112011-1-28
13
第四章 分子的对称性
2. 对称中心 对称中心(
i)
反演操作依据的是一个几何点称为对称中心。 反演操作依据的是一个几何点称为对称中心。 3. 反演操作的独立动作
ˆ i n = i , n = 奇 数 ˆ n ˆ ˆ i = E, n = 偶 数
i 共有两个独立动作 。
转900
ˆ C4
ˆ i
20112011-1-28
19
第四章 分子的对称性
分子中的反轴有： 分子中的反轴有： I1, I2, I3, I4, I5, I6, I7, I8 。
ˆ 共有两个独立动作。 σ共有两个独立动作。
反映操作是一种虚动作。
20112011-1-28 16
第四章 分子的对称性
4. 镜面的分类 设主轴位于z轴 设主轴位于z 水平的）； σ ⊥Cn ，记为 σ（horizontal水平的）； h horizontal水平的
σ // Cn ，记为 σ（Vertical 垂直的 ）； v
y (x', y') (x, y)
α
x' x cosα −sinα 0x ' ˆ y = C(α) y = sinα cosα 0y ' z z 0 0 1z
x
20112011-1-28 12
20112011-1-28
13
第四章 分子的对称性
2. 对称中心 对称中心(
i)
反演操作依据的是一个几何点称为对称中心。 反演操作依据的是一个几何点称为对称中心。 3. 反演操作的独立动作
ˆ i n = i , n = 奇 数 ˆ n ˆ ˆ i = E, n = 偶 数
i 共有两个独立动作 。
转900
ˆ C4
ˆ i
20112011-1-28
19
第四章 分子的对称性
分子中的反轴有： 分子中的反轴有： I1, I2, I3, I4, I5, I6, I7, I8 。
结构化学：分子的对称性
对称元素：对称操作所依据的几何元素（点、线、面） 分子中的对称元素有：
1. 恒等元素E 和恒等操作
ˆ E
恒等元素E是所有分子几何图形都有的，其相应的操作是恒等操 作 E。对分子施行这种操作后，分子保持完全不动，即分子中各原子 的位置及其轨道方位完全不变。
恒等操作对向量（x, y, z）不产生任何影响。
6. 映轴 Sn 和旋转反映
ˆ S n
对应的操作为
ˆ ˆ ˆ hC S n n
当对分子施行 轴的 S k次操作
n
时 Sn
k
k ˆk ˆk ˆ S n n Cn
k k ˆ ˆ ˆ S C n n k ˆ C ˆk S n n
当k为奇数时
当k为偶数时 当n为奇数时 当n为偶数时
4. 对称中心 i 和反演(倒反)操作
iˆ
5. 反轴 In 和旋转反演
ˆ I n
若将分子绕某轴旋转2/n角度后，再经对称中心反演产生分 子的等价图形，该对称操作称为反演，表示为 ，相应的 对称元素称反轴，用In表示。
ˆ I n
旋转反演是一种复合操作，且先反演后旋转( 转后反演(
)，和先旋
ˆi ˆ C n
4.1.1 分子的对称性
对称性是物质内部分子结构对称性的反映。在
分子中，原子可以看做是固定在其平衡位置上的， 分子的结构参数，如键长、键角等决定了分子的几 何构型和分子的对称性。许多分子的几何构型具有 一定的对称性。
分子的对称性
对称操作和相应的对称元素
4.1.2 对称操作和相应的对称元素
对称操作：指不改变物体内部任何 两点间的距离而使物体复原的操作。
例: CH4 (放在正方体中)
ˆ I n
第04章分子的对称性资料
对称在科学界开始产生重要的影响始于19世纪.发展到近代，
我们已经知道这个观念是晶体学、分子学、原子学、原子核物 理学、化学、粒子物理学等现代科学的中心观念。 近年来，对
称更变成了决定物质间相互作用的中心思想（所谓相互作用，
是物理学的一个术语，意思就是力量，质点跟质点之间之力
量）。
——杨振宁
分子对称性
4.1.3 对称中心（i）和反演操作（ i）
分子中若存在一点,将每个原子通过这一点引连线并延i
长到反方向等距离处而使分子复原,这一点就是对称中心i,
这种操作就是反演操作。
z
y
分子对称性
x
n
i
E
(n为偶数）
i （n为奇数） 21
y
i n 为奇数
i
in
x
E n 为偶数
连续进行两次反演操作等于不动操作，即
分子对称性
6
分子对称性
7
对称性特点：物体上存在若干个相等的部分，或可以划 分为若干个相等的部分。如果把这些相等部分对换一下， 就好象没有动过一样（即物体复原）。
分子对称性
8
分子对称性：分子的几何图形中有相互等同的部分，交换以 后，与原来的状态相比，不发生可辨别的变化。
对称性是通过对称元素和对称操作来描述的。
第四章 分子的对称性
Molecular Symmetry
分子对称性
1
对称性概念－物体相同部分有规律的重复
对称是自然界中普遍存在的一种性质,因而常常被认为是最 平凡、最简单的现象。然而, 对称又具有最深刻的意义。
判天地之美,析万物之理。
—— 庄 子
在所有智慧的追求中，很难找到其他例子能够在深刻的普
04分子对称性精品PPT课件
对称元素
符号
名称
E
单位元
Cn
旋转轴
s
镜面
i
对称中心
Sn
映轴
In
反轴
符号
Eˆ Cˆ n sˆ iˆ Sˆ n σˆ Cˆ n Iˆ n iˆCˆ n
对称操作
操作 恒等操作（不动操作） 绕轴逆时针旋转 2n 通过镜面的反映 按质心进行的反演 旋转反映 旋转反演
一个 n 重对称轴包含 n 个对称操作，可表示为：
C n (C ˆn 1 ,C ˆn 2 , ,C ˆn i, ,C ˆn n E )
逆时针方向转动记为“ + ” 。
Cˆ
1 3
逆时针方向转动记为“ + ” ；反之，记为“ - ” 。
Cˆ
3
1
Cˆ
1 3
逆时针方向转动记为“ + ” ；反之，记为“ - ” 。
trans-CHClBr—CHClBr
除质心外，中心对称性要求分子中的其它原子均成对出 现。因此，包含奇数个原子的种类多于 1 的分子，不会有对 称中心（如 BF3）。
SF6
C2H4
4.2.5 映轴与旋转反映操作
旋转反映是一个复合操作，可以想象为按照二个步骤发 生：首先是一个真转动，然后通过垂直于转动轴的平面反映。 记为：
我们在谈论生活中的对称性时，更多的是定性的，和 出于美感的。然而，当我们开始讨论分子的对称性时，必 须对分子对称性的含义具有明确的概念。
使对称概念严格、系统化，是从引进，并明确“对称 操作”的基本概念开始的。
对称操作：在不改变物体任意两 点间距离的前提下，能使物体的 初始位置和最终位置，客观上不 能区别的动作。
s S ˆ 3 1 C ˆ 3 ˆ
《分子对称性》课件
05
分子对称性的实例分析
烷烃的分子对称性
烷烃的分子结构：由碳原子和氢原子组成，碳原子之间以单键相连
烷烃的对称性：烷烃分子具有对称性，可以划分为对称中心和旋转 对称轴 烷烃的对称性分类：根据对称性的不同，可以分为Cn、Dn、Cnv、 Dnh等类型
烷烃的对称性应用：在化学合成、药物设计等领域具有重要应用
添加 标题
杂环化合物的分子对称性：指杂环化合物 分子中存在的对称性关系
添加 标题
实例分析：苯环、吡啶环、嘧啶环等杂环 化合物的分子对称性
添加 标题
分子对称性的应用：在药物设计、材料科 学等领域具有重要应用
添加 标题
分子对称性的研究进展：近年来，杂环化 合物的分子对称性研究取得了重要进展， 为相关领域的发展提供了新的思路和方法。
对称操作和对称元素
对称操作：在空间中保持分子 不变的操作，如旋转、反射等
对称元素：在分子中保持不变 的元素，如原子、键等
对称性：分子在空间中的对称 性，如旋转对称、反射对称等
对称操作和对称元素的关系： 对称操作保持对称元素不变， 对称元素在空间中保持对称性
对称性的分类
对称性分为旋转对称性和反射 对称性
官能团
拉曼光谱（Raman）：通 过拉曼光谱实验测定分子结
构中的振动模式
电子显微镜（EM）：通过 电子显微镜实验测定分子结
构中的精细结构
对称性分析的方法
化学键对称性：研究分子中 化学键的对称性，如单键、 双键、三键等
空间对称性：研究分子在空 间中的对称性，如旋转对称、 反射对称等
电子对称性：研究分子中电 子的分布和对称性，如电子
对称性在化学反应中的应用主要体现在化学反应的预测、反应机理的解析、反应产物的 预测等方面。 对称性在化学反应中的应用还可以帮助科学家更好地理解化学反应的本质，为化学反应 的设计和优化提供指导。
结构化学基础课件 第四章 分子的对称性
②第二步，进行右上角的乘法， 分子进行 反映，N和H1保持不变，H2与H3互换位置，
再绕 轴旋转120度，则N还是不变，H2到H1 位置，H1到H2位置，H3回到原位置，两个操 作的净结果，相当于一个 镜面反映……可
写出右上角的九个结果。
③同理也可写出左下角的九个结果。旋转操 作和反映操作相乘，得到的是反映操作；两 个旋转操作相乘和两个反映操作相乘得到的 是旋转操作。
学时安排 学时----- 4学时
第四章.分子的对称性
对称 是一种很常见的现象。在自然界
我们可观察到五瓣对称的梅花、桃花，六瓣 的水仙花、雪花、松树叶沿枝干两侧对称， 槐树叶、榕树叶又是另一种对称……在人工 建筑中，北京的古皇城是中轴线对称。在化 学中，我们研究的分子、晶体等也有各种对 称性，有时会感觉这个分子对称性比那个分 子高，如何表达、衡量各种对称？数学中定 义了对称元素来描述这些对称。
I1 S2 i
S1
I
2
I2 S1
S2 I1 i
I3
S
6
C3
i
S3
I
6
C3
I4 S4
S4
I
4
I5 S10 C5 i
S5 I10 C5
I6 S3 C3 S6 I3 C3 i
负号代表逆操作，即沿原来的操作退回去的操作。
S4 S6
对称元 素符号
E Cn
I1n=iC1n 4.1.5.映轴和旋转反映操作
映轴S1n的基本操作为绕轴转3600/n， 接着按垂直于轴的平面进行反映，是C1n和 σ相继进行的联合操作：
S1n=σC1n
如果绕一根轴旋转2/n角度后立即对垂直于这根轴的一 平面进行反映，产生一个不可分辨的构型，那么这个轴就
第04章 分子的对称性(定稿)
S4 h C4 , S C2 , S h C , S E
2 4 3 4 4 4 3 4
旋转90°
反映
图4-3 CH4的四重象转轴S4及旋转反映操作
4.1.6 反轴(In )和旋转反演操作( Î n)
这也是一个复合对称操作：先绕轴旋转 3600/n( 并未进 入等价图形)，接着按对称中心(在轴上)进行反演(图形才进 入等价图形)。对应的操作为:
2
C2
1
σh
4
I2=S1 示意图
I3
包括 6 个对称操作
1 1 I3 iC3 ,
3 I3 i,
5 2 I3 iC3 ,
2 2 I3 C3 ,
4 1 I3 C3 ,
6 I3 E
I3 轴除包括 C3 和 i 的全部对称操作外，还包括 C3 和 i 的 组合操作 合得到的:
1 1 5 2 I3 iC3 ， I3 iC3 . 所以 I3 轴可看作是 C3 和 i 组
6 6
对称操作的积相当于连续行施两次对称操作
对应两个矩阵相乘，即矩阵的积。
矩阵可乘的条件：
只有第一矩阵的列数与第二矩阵的行数相等 时才可相乘，否则不可乘。
4.1.3 镜面（m 或 ）和反映操作（ m, , M ）
镜面（或对称面），是平分
分子的平面，它把分子图形分成 两个完全相等的两个部分，两部 分之间互为镜中关系。与对称面 相对应的操作是反映，它把分子 中的任一点都反映到镜面的另一 侧垂直延长线的等距离处。
H2O2中的C2 n 重旋转可衍生出 n-1 旋转操作， 记为Cni(i=1,2,…,n-1 ),Ĉnn = Ê ( n 为任意正整数 )；
旋转操作是实动作，可以真实操作实现。
2 4 3 4 4 4 3 4
旋转90°
反映
图4-3 CH4的四重象转轴S4及旋转反映操作
4.1.6 反轴(In )和旋转反演操作( Î n)
这也是一个复合对称操作：先绕轴旋转 3600/n( 并未进 入等价图形)，接着按对称中心(在轴上)进行反演(图形才进 入等价图形)。对应的操作为:
2
C2
1
σh
4
I2=S1 示意图
I3
包括 6 个对称操作
1 1 I3 iC3 ,
3 I3 i,
5 2 I3 iC3 ,
2 2 I3 C3 ,
4 1 I3 C3 ,
6 I3 E
I3 轴除包括 C3 和 i 的全部对称操作外，还包括 C3 和 i 的 组合操作 合得到的:
1 1 5 2 I3 iC3 ， I3 iC3 . 所以 I3 轴可看作是 C3 和 i 组
6 6
对称操作的积相当于连续行施两次对称操作
对应两个矩阵相乘，即矩阵的积。
矩阵可乘的条件：
只有第一矩阵的列数与第二矩阵的行数相等 时才可相乘，否则不可乘。
4.1.3 镜面（m 或 ）和反映操作（ m, , M ）
镜面（或对称面），是平分
分子的平面，它把分子图形分成 两个完全相等的两个部分，两部 分之间互为镜中关系。与对称面 相对应的操作是反映，它把分子 中的任一点都反映到镜面的另一 侧垂直延长线的等距离处。
H2O2中的C2 n 重旋转可衍生出 n-1 旋转操作， 记为Cni(i=1,2,…,n-1 ),Ĉnn = Ê ( n 为任意正整数 )；
旋转操作是实动作，可以真实操作实现。
《分子的对称性》课件
分子点群的应用
化学反应机理
了解分子的对称性有助于理解化 学反应的机理，因为某些对称元 素可能影响反应的活性和选择性
。
晶体结构预测
分子点群可以用来预测分子的晶 体结构，因为相同点群的分子往
往具有相似的晶体结构。
药物设计
在药物设计中，了解分子的对称 性有助于预测分子的药理活性，
从而优化药物设计。
BIG DATA EMPOWERS TO CREATE A NEW ERA
05
分子的对称性与物理化学性质
对称性与分子光谱的关系
总结词
分子对称性与光谱性质密切相关，可以通过对称性分析预测光谱特征和变化规律 。
详细描述
分子的对称性决定了其电子云分布和分子振动模式，进而影响分子吸收和发射光 谱的性质。通过对称性分析，可以预测分子的光谱峰位、强度和形状等信息，有 助于理解分子与光相互作用的机制。
02
分子的对称元素
BIG DATA EMPOWERS TO CREATE A NEW
ERA
镜面对称元素
总结词
镜面对称元素是分子中存在的对称元素之一，它使得分子在镜像方向上对称。
详细描述
镜面对称元素通常由平面或轴构成，使得分子在镜像方向上呈现对称性。例如 ，二氧化碳分子中的碳氧双键就是一种镜面对称元素，使得分子在垂直于双键 轴线的平面上对称。
平移对称
分子沿某轴平移一定距离 后，形状和方向保持不变 。
对称性在化学中的重要性
01
对称性是化学中重要的 概念之一，它有助于理 解分子的结构和性质。
02
对称性可以帮助我们预 测分子的某些性质，例 如光学活性、反应活性 等。
03
对称性在化学反应中也 有重要作用，例如对称 催化、对称合成等。
分子的对称性习题解答
3
乐山师范学院 化学学院
本章习题解答
【4.1】HCN 和 CS2 都是直线型分子，写出该分子的对称元素。 解：HCN：直线型分子，左右不对称，分子所在的直线为 C∞ ，包含 对称轴的平面为对称面： ∞σv ;
CS2：直线型分子，左右对称，分子所在的直线为 C∞ ，包含对称 轴的平面为对称面： ∞σv ;C 原子为对称中心 i ，经过 C 原子垂直于对 称轴的面为σv 。
面，也没有包含主轴且平分垂直于主轴二重轴的对称面，故为： D2
【4.15】由下列分子的偶极矩数据，推测分子立体构型及其点群。 （a） C3O2 （ µ = 0 ） 解：由于偶极矩为 0，因此具有较高的对称性，若三个 C 原子等价， 则为正三角形，两个氧原子必须对称地分布于正三角形中心的垂直线
上，即为三角双锥形，但这种结果不符合 C 四价，氧二价。
（c） 用矩阵的方法证明：
⎛ −1 0 0⎞
⎛1 0 0⎞
⎛ −1 0 0⎞
σ yz
=
⎜ ⎜
0
1
0
⎟ ⎟
，
σ
xz
=
⎜ ⎜
0
−1
0
⎟ ⎟
， C1 2(z)
=
⎜ ⎜
0
−1
0
⎟ ⎟
⎜⎝ 0 0 1 ⎟⎠
⎜⎝ 0 0 1 ⎟⎠
⎜⎝ 0 0 1 ⎟⎠
⎛ −1 0 0⎞⎛ 1 0 0⎞ ⎛ −1 0 0⎞
∵⎜⎜ 0 ⎜⎝ 0
用作用的结果证明：
⎡x⎤
⎡ x ⎤ ⎡−x⎤
C21(z)σ xy
⎢ ⎢
y ⎥⎥
=
C21( z )
⎢ ⎢
y
⎥ ⎥
=
⎢⎢− y⎥⎥
乐山师范学院 化学学院
本章习题解答
【4.1】HCN 和 CS2 都是直线型分子，写出该分子的对称元素。 解：HCN：直线型分子，左右不对称，分子所在的直线为 C∞ ，包含 对称轴的平面为对称面： ∞σv ;
CS2：直线型分子，左右对称，分子所在的直线为 C∞ ，包含对称 轴的平面为对称面： ∞σv ;C 原子为对称中心 i ，经过 C 原子垂直于对 称轴的面为σv 。
面，也没有包含主轴且平分垂直于主轴二重轴的对称面，故为： D2
【4.15】由下列分子的偶极矩数据，推测分子立体构型及其点群。 （a） C3O2 （ µ = 0 ） 解：由于偶极矩为 0，因此具有较高的对称性，若三个 C 原子等价， 则为正三角形，两个氧原子必须对称地分布于正三角形中心的垂直线
上，即为三角双锥形，但这种结果不符合 C 四价，氧二价。
（c） 用矩阵的方法证明：
⎛ −1 0 0⎞
⎛1 0 0⎞
⎛ −1 0 0⎞
σ yz
=
⎜ ⎜
0
1
0
⎟ ⎟
，
σ
xz
=
⎜ ⎜
0
−1
0
⎟ ⎟
， C1 2(z)
=
⎜ ⎜
0
−1
0
⎟ ⎟
⎜⎝ 0 0 1 ⎟⎠
⎜⎝ 0 0 1 ⎟⎠
⎜⎝ 0 0 1 ⎟⎠
⎛ −1 0 0⎞⎛ 1 0 0⎞ ⎛ −1 0 0⎞
∵⎜⎜ 0 ⎜⎝ 0
用作用的结果证明：
⎡x⎤
⎡ x ⎤ ⎡−x⎤
C21(z)σ xy
⎢ ⎢
y ⎥⎥
=
C21( z )
⎢ ⎢
y
⎥ ⎥
=
⎢⎢− y⎥⎥
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
结合律：A(BC)=(AB)C; 2+(3+4)=(2+3)+4
单位元素： 0;
0+3=3+0=3
逆元素： A-1=-A ; 3-1=-3 3+(-3)=(-3)+3=0
群的例子
除零外，全体非零实数对乘法构成群
（群的乘法即为代数乘法）
封闭性： 实数相乘仍为实数 结合律： 乘积与次序无关 单位元素： 1 逆元素： A-1=1/A
H
C H
H C
H
Cl
Cl 2-
Pt
Cl Cl
H
H
H
H
H
H
-
Dnh点群的分子实例
D2h 群 ：N2O4
D2h群：乙烯
D3h 群 ： 乙烷重叠型
D4h群：XeF4
Dh群： I3-
D6h群：苯
Dnd群
在 Dn 群的基础上加上n个通过主轴且又平分C2 副轴夹角
的镜面 d ，属于此类点群的分子也较少。
D3d : 乙烷交错型
从正四面体的每两条相对的棱中点有一条S4穿过, 6
条棱对应着3条S4. 每个S4可作出S41 、S42 、S43 三个
② Cnh群
在Cn的基础上加上与垂直Cn的h。Cnh群为2n阶群，对
称操作为：
Cnh
E,
Cn ,
Cn2 , , Cnn1,
h,
hCn,
hCn2，
，
C n1
hn
C2h群: 反式二氯乙烯
C2h群: N2F2
Cnh群分子实例
C3h群
③ Cnv群
在 Cn 的基础上加上n个通过主轴的v，Cnv群为2n阶
4.1.4 对称中心（i）和反演操作（ i）
与对称中心 i 对应的对称操作叫反演或倒反 。 若将i 坐标原点放在对称中心处，则反演操作将空间 任意一点（x, y, z）变为其负值（-x, -y, -z），反演操 作的矩阵表示为：
y
i x
y
i n 为奇数
i
in
x
E n 为偶数
连续进行两次反演操作等于不动操作，即
群。对称操作：
Cnv
{E
,
Cn
,
Cn2
,
Cnn1
,
(1) v
,
( v
2)
,
( v
n
)}
分子中常见的Cnv点群有：
C2v：H2O, H2S, HCHO, 顺1,2-乙烯等。 C3v：NH3, CH3Cl等三角锥分子。 C4v：BrF5（四方锥结构） Cv：HCl, CO, NO, HCN等直线型异核分子。
C2v
臭氧
菲
H2O中的C2和两个σv
C3v
NF3
CHCl3
Cv CO2 , HCl 等直线分子
4.3.3 双轴群(双面群)
Dn群
在Cn群的基础上，加上n个垂直Cn的C2轴，Cn群 为2n阶。对称操作为：
Dn
E
,Cn
,
Cn2
,
,
C பைடு நூலகம்1 n
,
C (1) 2
,C2(2)
,
C(n) n
低 月 半
落 花 余
苏锦 轼图
阁城梧碧 回
空暮桐草 。，。，
文
4.1 对称元素与对称操作
对称操作（symmetry operation）
4.1.2 旋转轴 Cn(n) 和旋转操作Ĉn
4.1.3
镜面（
）和反映操作
（
）
镜面（或对称面），是平分 分子的平面，它把分子图形分成 两个完全相等的两个部分，两部 分之间互为镜中关系。与对称面 相对应的操作是反映，它把分子 中的任一点都反映到镜面的另一 侧垂直延长线的等距离处。
Td群(四面体群)
对称元素有：4个C3轴，3个C2轴，6个d ，3个S4 （与3
个C2重合）；为24阶群。对称操作为：
Td {E, 8C3, 3C2, 6S4, 6 d }
正四面体构型分子都属于此点群。 如：CH4，PO43-，SO42-
在Td群中, 你可以找到一个四面体结构. 打开P4分子，对照以下讲解自己进行操作：
对称性的概念：
对称性普遍存在于自然界。 例如五瓣对称的梅花、桃花， 六瓣对称的水仙花、雪花（轴 对称或中心对称）；建筑物和 动物的镜面对称；美术与文学 中也存在很多对称的概念。
草桐暮空 碧梧城阁 余半边绣 花月远帘 落低雁疏 晚凉随映 春夜人雨 。，。，
雨人夜春 题
映随凉晚 织
疏 帘 绣
雁 远 边
i2
E
，
最小周期为2；反演操作和它的逆操作相等，即
iˆ iˆ1
反演操作是虚动作，不可能具体真实操作， 只能在想象中实现。
4.1.5 象转轴(或映轴 Sn )和旋转反映操作(Ŝn )
这是一个复合动作：先绕轴旋3600/n（并未进入等价图形），
接着按垂直于轴的平面 h 进行反映（图形才进入等价图形）。
D4d ：单质硫
俯视图
D5d : 交错型二茂铁
4.3.4 立方群
特点是有多个高次轴（n≥3 的轴称为高次轴）。 含有多个高次轴的对称元素组合所得的对称元素 系和正多面体的对称性相对应。
立方群：包括Td 、Th 、Oh 、Ih 等.
Td 群：属于该群的分子，对称性与正四面体完全相同。
CH4
P4 （白磷）
Sn h Cn
CH4 的
四
旋转90°
重
象
转
轴
S4
相互等价
及
旋
转
反映
反
映
操
作
仍代表 H
4.2 群的基础知识
4.2.1 群的定义
4.2.2 群的乘法表
群的例子
立正（ ），向右转（ ），向左转 （ ），向后转（ ）构成对称操作群
-1 =
-1 =
-1 =
全体整数对加法构成群，称为整数加群
封闭性： 所有整数（包括零）相加仍为整数
D2 群
D3：这种分子比较少见，其对称元素也不易看出. [Co(NH2CH2CH2NH2)3]3+是一实例
何其相似！
唯一的C3旋转轴从xyz轴连
成的正三角形中心穿过, C2
通向Co;
三条C2旋转轴分别从每个N–N
x
键中心穿过通向Co.
C2 z
y
C2
Dnh群
在Dn群的基础上，加上一个垂直主轴的h。
4.3.2 单轴群(轴向群)
① Cn群
对称元素只有一个n次轴，对称操作共有n个，即 Cn1， Cn2，Cn3，···，Cnn = E，其阶次为n。 对称操作为：
Cn
Cn1
,Cn2,, Cnn
E
n 阶群
分子中常见的 Cn点群有：C1, C2, C3 。
C2 群
R2
R1
R2
R1
C2 群
C3群
Cn群分子实例
此群为无限群
4.2.3 对称元素的组合规律
4.3 分子点群
4.3.1 点群
分子点群
分子中全部对称操作的集合构成分子点群(point groups ). 分子点群可以归为四类:
(1) 单轴群: 包括Cn 、Cnh 、Cnv ; (2) 双面群：包括Dn、Dnh、Dnd ; (3) 立方群：包括Td 、Th 、Oh 、Ih 等; (4) 非真旋轴群：包括Cs 、Ci 、S4等.