线面角练习题(三个角之间的关系)

合集下载

线面角的求法总结

线面角的三种求法1.直接法：平面的斜线与斜线在平面内的射影所成的角即为直线与平面所成的角。

通常是解由斜线段，垂线段，斜线在平面内的射影所组成的直角三角形，垂线段是其中最重要的元素，它可以起到联系各线段的作用。

例1 （如图1 ）四面体 ABCS中，SA,SB,SC 两两垂直，/ SBA=45 , / SBC=60 , M 为 AB的中点，求（1）BC与平面SAB所成的角。

（2） SC与平面ABC所成的角。

解：（1）•/ SC± SB,SC丄 SA,••• SC丄平面SAB 故SB是斜线BC在平面SAB上的射影，•••/ SBC是直线BC与平面SAB所成的角为60°。

（2）连结 SM,CM，贝U SM 丄 AB,又••• SC± AB, • AB 丄平面 SCM,•••面ABC丄面SCM过S作SH丄CM于H, 则SH丄平面 ABC•CH即为SC在面ABC内的射影。

/ SCH为SC与平面ABC所成的角。

sin / SCH=SH /SC•SC与平面ABC所成的角的正弦值为V 7/7（“垂线”是相对的， SC是面SAB的垂线，又是面 ABC的斜线.作面的垂线常根据面面垂直的性质定理，其思路是：先找出与已知平面垂直的平面，然后一面内找出或作出交线的垂线，则得面的垂线。

）2.利用公式sin 0 =h/ i其中0是斜线与平面所成的角， h是垂线段的长，i是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可用三棱锥的体积自等来求垂线段的长。

例2 （如图 2）长方体 ABCD-A 1B1C1D1 , AB=3 ,BC=2, A 1A= 4 ，求 AB 与面 AB1C1D解：设点 B 到AB i C i D 的距离为h,T V B - ABC =V A -BBC.'. 1 / 3 S ^ ABC h= 1/3 SM BC AB ，易得 h=12/ 5 设AB 与面A B 1C 1D 所成的角为0 ,则sin 0 =h/AB=4 /5图2 3. 利用公式 cos 0 =cos 0 i cos 0 2已知，如图，AO 是平面〉的斜线，A 是斜足，0B 垂直于平面直线AB 是斜线在平面a 内的射影。

空间角

即B1O MA ， B1O MC。又MA MC C 所以B1O 平面MAC
② 由①知 B1O 平面MAC 所以B1O是平面MAC的一个法向量 z 且B1O (1， 1， 2) C1 设平面B1MA的一个法向量为n ( x，y，z ) D1 由A(2，0) M (0，1) B1 (2， 2)得 0，， 0，， 2， A1 B1 M MA (2， 1)， 1 (2，1) 0， MB 2，所以n MA 0，n MB1 0
质疑：空间向量的夹角与异面直线的夹角有什么
区别？
例1、如图，正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为 2a 求AC1和CB1的夹角，分析：求异面直线的夹角解法步骤：1、写出异面直线的方向向量的坐标。 2、利用空间两个向量的夹角公式求出夹角。
Z
A1
C1
B1
3 1 3 1 AC1 ( a, a, 2a) CB1 ( a, a, 2a) 2 2 2 2
C1
B1
D1
A1
C
所以： 1 ( 1 , 0,1), BD1 ( 1 , 1 ,1) AF A 2 2 2 1 x 1 AF1 BD1 30 4 cos AF1 , BD1 10 | AF1 || BD1 | 5 3 4 2 30 所以 BD1与 AF1 所成角的余弦值为 10
①证明：以 DA、、 1 DC DD为正交基底， A1 建立空间直角坐标系如图。则可得所以MA (2， 1)， (0， 1)， 0， MC 2， B1O ( 1， 1， 2)
M
B1
C1
D O B

初一数学点线面角试题

初一数学点线面角试题1.下列图形中，由AB//CD能得到∠1=∠2的是【答案】B．【解析】A、∵AB∥CD，∴∠1+∠2=180°，故A选项错误；B、∵AB∥CD，∴∠1=∠3，∵∠2=∠3，∴∠1=∠2，故B选项正确；C、∵AB∥CD，∴∠BAD=∠CDA，若AC∥BD，可得∠1=∠2；故C选项错误；D、若梯形ABCD是等腰梯形，可得∠1=∠2，故D选项错误．故选B．【考点】平行线的判定与性质．2.把命题“平行于同一直线的两直线平行”写成“如果…，那么…”的形式：．【答案】如果两条直线都与第三条直线平行，那么这两条直线互相平行．【解析】命题可以改写为：“如果两条直线都与第三条直线平行，那么这两条直线互相平行”．故答案是如果两条直线都与第三条直线平行，那么这两条直线互相平行．【考点】命题与定理．3.命题“相等的角是对顶角”的逆命题是．【答案】对顶角相等.【解析】根据“原命题的题设是逆命题的结论，原命题的结论是逆命题的题设”即可写出一个命题的逆命题.试题解析：命题“相等的角是对顶角”的逆命题是“对顶角相等”.【考点】命题.4.如图，AB∥ED，则∠A＋∠C＋∠D＝( )A．180°B．270°C．360°D．540°【答案】C．【解析】过点C作CF∥AB，∵AB∥ED，∴CF∥AB∥DE，∴∠1+∠A=180°，∠2+∠D=180°，∴∠A+∠ACD+∠D=∠A+∠1+∠2+∠D=360°．故选C．【考点】平行线的性质．5.已知如图：E、F分别在DC、AB延长线上.,,.（1）求证：DC//AB.（2）求的大小.【答案】（1）证明见解析，（2）60°【解析】（1）由知，而，所以得，从而DC∥AB.（2）由（1）知：，而，从而可求的大小.试题解析：（1）∵∴又∵∴∴DC∥AB.（2）由（1）知：，∵∴∴.【考点】平行线的判定与性质.6.如图，点O在直线AB上，射线OC平分∠AOD，若∠AOC=35°，则∠BOD等于（）A．145°B．110°C．70°D．35°【答案】B．【解析】∵射线OC平分∠DOA．∴∠AOD=2∠AOC，∵∠COA=35°，∴∠DOA=70°，∴∠BOD=180°﹣70°=110°，故选：B．【考点】角平分线的定义．7.如图，按各组角的位置判断错误的是（）A．∠1与∠A是同旁内角B．∠3与∠4是内错角C．∠5与∠6是同旁内角D．∠2与∠5是同位角【答案】C．【解析】A、∠1和∠A是同旁内角，说法正确；B、∠3和∠4是内错角，说法正确；C、∠5和∠6不是两条直线被第三条直线截成的角，说法错误；D、∠2和∠5是同位角，说法正确．故选C．【考点】1.同位角2.内错角3.同旁内角．8.如图，属于同位角是（）A．∠1和∠2B．∠1和∠3C．∠1和∠4D．∠2和∠3【答案】C．【解析】同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角．因此，根据同位角的定义可知∠1和∠4是同位角．故选C．【考点】同位角、内错角、同旁内角．9.如图，将三角尺的直角顶点放在直尺的一边上，,,则的度数等于（）A．B．C．D．【答案】A【解析】如图：∠4=∠1+∠3=30°+20°=50°，∵AB∥CD，∴∠2=∠4=50°．故选A．【考点】1．平行线的性质2．三角形的外角性质．10.已知线段则线段的长度是（）A．5B．1C．5或1D．以上都不对【答案】D【解析】如图，线段但线段的长度既不是1也不是5，故选D.11.如图，平分平分若则 __.【答案】90°【解析】因为平分，平分，所以因为所以即.所以.12.以下四个命题：①在同一平面内，过一点有且只有一条直线与已知直线垂直；②若a>b，则-2a>-2b；③如果三条直线a、b、c满足：a∥b，b∥c，那么直线a与直线c必定平行；④对顶角相等，其中真命题有（）个.A．1B．2C．3D．4【答案】C【解析】根据基本的数学概念依次分析各小题即可作出判断.解：①在同一平面内，过一点有且只有一条直线与已知直线垂直，③如果三条直线a、b、c满足：a∥b，b∥c，那么直线a与直线c必定平行，④对顶角相等，均正确；②若，则，错误；故选C.【考点】真假命题点评：本题属于基础应用题，只需学生熟练掌握基本的数学概念，即可完成.13.如图，点E在直线DF上，点B在直线AC上，若∠1＝∠2，∠3＝∠4，则∠A＝∠F，请说明理由．解：∵∠1＝∠2（已知）∠2＝∠DGF（）∴∠1＝∠DGF∴BD∥CE（）∴∠3＋∠C＝180º（）又∵∠3＝∠4（已知）∴∠4＋∠C＝180º∴∥（同旁内角互补，两直线平行）∴∠A＝∠F（）【答案】对顶角相等；同位角相等，两直线平行；两直线平行，同旁内角互补；AC，DF；两直线平行，内错角相等.【解析】依题意知，由图知∠2＝∠DGF（对顶角相等）∴∠1＝∠DGF∴BD∥CE（同位角相等，两直线平行）∴∠3＋∠C＝180º（两直线平行，同旁内角互补）；又∵∠3＝∠4（已知）∴∠4＋∠C＝180º∴ AC∥DF∴∠A＝∠F（两直线平行，内错角相等.）【考点】平行线性质及判定点评：本题难度较低，主要考查学生对平行线性质及判定知识点的掌握。

第8章立体几何专题7 线面角的求解常考题型专题练习——【含答案】

线面角的求解【方法总结】1、线面角的范围：[0°,90°]2、线面角求法（一）：先确定斜线与平面，找到线面的交点A为斜足；找线在面外的一点B，过点B向平面α做垂线，确定垂足O；连结斜足与垂足为斜线AB在面α上的投影；投影AO与斜线AB之间的夹角为线面角；把投影AO与斜线AB归到一个三角形中进行求解（可能利用余弦定理或者直角三角形）。

注意：以上第二步过面外一点向平面做垂线的方法有一下几种：1）线在面外的一点B与平面上某点的连线正垂直于面α，无需再做辅助线；2）题中已知有与面α垂直的直线，过线在面外的一点B直接做此垂线的平行线；3）过线在面外的一点B做两垂直平面交线的垂线，利用面面垂直的性质证明OB⊥面α（这两个垂直平面一个是面α，另一个是过点B且与α垂直的平面）。

3、线面角求法（二）用等体积法，求出斜线PA在面外的一点P到面的距离，利用三角形的正弦公式进行求解。

114、线面角求法（三）利用空间向量进行求解，高二再学。

高中数学线面角与线线角例题、习题-学生

线面角与线线角专练（小练习一）【知识网络】1、异面直线所成的角：（1）范围：(0,]2πθ∈；（2）求法；2、直线和平面所成的角：（1）定义：（2）范围：[0,90]；（3）求法；【典型例题】例1：（1）在正方体1111ABCD A BC D -中，下列几种说法正确的是（）A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1BC 成60角（2）在正方体AC 1中，过它的任意两条棱作平面，则能作得与A 1B 成300角的平面的个数为（）A 、2个B 、4个C 、6个D 、8个（3）正六棱柱ABCDEF －A 1B 1C 1D 1E 1F 1底面边长是1，2则这个棱柱的侧面对角线E 1D 与BC 1所成的角是（）A ．90ºB ．60ºC ．45ºD ．30º（4）在空间四边形ABCD 中，AB ⊥CD ，BC ⊥DA ，那么对角线AC 与BD 的位置关系是。

（5）点AB 到平面α距离距离分别为12，20，若斜线AB 与α成030的角，则AB 的长等于__ ___.例2：．如图：已知直三棱柱ABC —A 1B 1C 1，AB ＝AC ，F 为棱BB 1上一点，BF ∶FB 1＝2∶1，BF ＝BC ＝2a 。

（I ）若D 为BC 的中点，E 为AD 上不同于A 、D 的任意一点，证明EF ⊥FC 1；（II ）试问：若AB ＝2a ，在线段AD 上的E点能否使EF 与平面BB 1C 1C 成60°角，为什么？证明你的结论。

例3：如图, 四棱锥P-ABCD 的底面是AB=2, BC =2的矩形, 侧面PAB 是等边三角形, 且侧面PAB ⊥底面ABCD.(Ⅰ)证明:BC ⊥侧面PAB;(Ⅱ)证明: 侧面PAD ⊥侧面PAB;(Ⅲ)求侧棱PC 与底面ABCD 所成角的大小; A B C DPA B C H S M 线面角与线线角专练（小练习二）例4：设△ABC 内接于⊙O ，其中AB 为⊙O 的直径，PA ⊥平面ABC 。

空间三大角(向量法)

空间三大角一、线线角1．（2021年全国高考乙卷数学（文）试题）在正方体1111ABCD A B C D -中，P 为11B D 的中点，则直线PB 与1AD 所成的角为（）A ．π2B ．π3C ．π4D ．π62.（2018年全国普通高等学校招生统一考试理数（全国卷II ））在长方体1111ABCD A B C D -中，1AB BC ==，13AA =，则异面直线1AD 与1DB 所成角的余弦值为（）A ．15B ．56C ．55D ．223.（2015年全国普通高等学校招生统一考试理科数学（新课标Ⅰ））如图，四边形ABCD 为菱形，ⅠABC =120°，E ，F 是平面ABCD 同一侧的两点，BE Ⅰ平面ABCD ，DF Ⅰ平面ABCD ，BE =2DF ，AE ⅠEC ．（1）证明：平面AEC Ⅰ平面AFC ；（2）求直线AE 与直线CF 所成角的余弦值．二、线面角1.（2018年全国普通高等学校招生统一考试理科数学（新课标I 卷））如图，四边形ABCD 为正方形，,E F 分别为,AD BC 的中点，以DF 为折痕把DFC △折起，使点C 到达点P 的位置，且PF BF ⊥. （1）证明：平面PEF ⊥平面ABFD ；（2）求DP 与平面ABFD 所成角的正弦值.2. （2018年全国普通高等学校招生统一考试理数（全国卷II ））如图，在三棱锥P ABC -中，22AB BC ==，4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且二面角M PA C --为30，求PC 与平面PAM 所成角的正弦值．3.（2016年全国普通高等学校招生统一考试理科数学（新课标3卷））如图，四棱锥P−ABCD 中，PAⅠ底面ABCD ，ADⅠBC ，AB=AD=AC=3，PA=BC=4，M 为线段AD 上一点，AM=2MD ，N 为PC 的中点. （Ⅰ）证明MNⅠ平面PAB;（Ⅰ）求直线AN 与平面PMN 所成角的正弦值.三、二面角1（2021年全国高考乙卷数学（理）试题）如图，四棱锥P ABCD -的底面是矩形，PD ⊥底面ABCD ，1PD DC ==，M 为BC 的中点，且PB AM ⊥．（1）求BC ；（2）求二面角A PM B --的正弦值．2.（2020年全国统一高考数学试卷（理科）（新课标Ⅰ））如图，在长方体1111ABCD A B C D -中，点,E F 分别在棱11,DD BB 上，且12DE ED =，12BF FB =．（1）证明：点1C 在平面AEF 内；（2）若2AB =，1AD =，13AA =，求二面角1A EF A --的正弦值．3.（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，ⅠBAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MNⅠ平面C1DE；（2）求二面角A-MA1-N的正弦值．4.（2019年全国统一高考数学试卷（理科）（新课标Ⅰ））如图，长方体ABCD–A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BEⅠEC1.（1）证明：BEⅠ平面EB1C1；（2）若AE=A1E，求二面角B–EC–C1的正弦值.5. （2018年全国卷Ⅰ理数高考试题）如图，边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点．（1）证明：平面AMD ⊥平面BMC ；（2）当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．6.（2017年全国普通高等学校招生统一考试理科数学（新课标1卷））如图，在四棱锥P−ABCD 中，AB//CD ，且90BAP CDP ∠=∠=.（1）证明：平面P AB Ⅰ平面P AD ；（2）若P A =PD =AB =DC ，90APD ∠=，求二面角A −PB −C 的余弦值.7.（2017年全国普通高等学校招生统一考试理科数学（新课标3））（2017新课标全国Ⅰ理科）如图，四面体ABCD 中，ⅠABC 是正三角形，ⅠACD 是直角三角形，ⅠABD =ⅠCBD ，AB =BD ．（1）证明：平面ACD Ⅰ平面ABC ；（2）过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D –AE –C 的余弦值.8.（2016年全国普通高等学校招生统一考试）试题）如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，四边形ABEF 为正方形，2AF FD =，90AFD ∠=︒，且二面角D AF E --与二面角C BE F --都是60︒.（1）证明：平面ABEF ⊥平面EFDC ；（2）求二面角E BC A --的余弦值.9.（2016年全国普通高等学校招生统一考试数学）如图，菱形ABCD 的对角线AC 与BD 交于点,5,6O AB AC ==，点,E F 分别在,AD CD 上，5,4AE CF EF ==交BD 于点H ，将DEF ∆沿EF 折到D EF '∆位置，10OD '=.（1）证明：D H '⊥平面ABCD ；（2）求二面角B D A C '--的正弦值.答案一、线线角1【答案】D如图，连接11,,BC PC PB ，因为1AD Ⅰ1BC ，所以1PBC ∠或其补角为直线PB 与1AD 所成的角，因为1BB ⊥平面1111D C B A ，所以11BB PC ⊥，又111PC B D ⊥，1111BB B D B ⋂=，所以1PC ⊥平面1PBB ，所以1PC PB ⊥，设正方体棱长为2，则1111122,22BC PC D B === 1111sin 2PC PBC BC ∠==，所以16PBC π∠=. 2.【答案】C 【详解】：以D 为坐标原点，DA,DC,DD 1为x,y,z 轴建立空间直角坐标系，则11(0,0,0),(1,0,0),(1,13),3)D A B D ,所以11(1,0,3),(1,13)AD DB =-=, 因为11111115cos ,25AD DB AD DB AD DB ⋅-===⨯，所以异面直线1AD 与1DB 5 3.【解析】：（Ⅰ）连接BD ，设BD∩AC=G ，连接EG ，FG ，EF ，在菱形ABCD 中，不妨设GB=1易证EGⅠAC ，通过计算可证EGⅠFG ，根据线面垂直判定定理可知EGⅠ平面AFC ，由面面垂直判定定理知平面AFCⅠ平面AEC ；（Ⅰ）以G 为坐标原点，分别以,GB GC 的方向为x 轴，y 轴正方向，||GB 为单位长度，建立空间直角坐标系G -xyz ，利用向量法可求出异面直线AE 与CF 所成角的余弦值.试题解析：（Ⅰ）连接BD ，设BD∩AC=G ，连接EG ，FG ，EF ，在菱形ABCD 中，不妨设GB=1，由ⅠABC=120°，可得3由BEⅠ平面ABCD ，AB=BC 可知，AE=EC ，又ⅠAEⅠEC ，3，EGⅠAC ，在RtⅠEBG 中，可得2，故DF=22.在RtⅠFDG 中，可得6 在直角梯形BDFE 中，由BD=2，2，2可得32，Ⅰ222EG FG EF +=，ⅠEGⅠFG ， ⅠAC∩FG=G ，ⅠEGⅠ平面AFC ，ⅠEG ⊂面AEC ，Ⅰ平面AFCⅠ平面AEC.（Ⅰ）如图，以G 为坐标原点，分别以,GB GC 的方向为x 轴，y 轴正方向，||GB 为单位长度，建立空间直角坐标系G -xyz ，由（Ⅰ）可得A （030），E （1,0, 2，F （－1,02，C （030），ⅠAE =（1，3，2），CF =（-1，-3，22）.…10分故3cos ,3AE CFAE CF AE CF ⋅==-. 所以直线AE 与CF 所成的角的余弦值为33. 二、线面角1.【分析】（1）由已知可得，BF PF ⊥，BF EF ⊥，又PFEF F =，所以BF ⊥平面PEF . 又BF ⊂平面ABFD ，所以平面PEF ⊥平面ABFD ；（2）作PH EF ⊥，垂足为H .由（1）得，PH ⊥平面ABFD .以H 为坐标原点，HF 的方向为y 轴正方向，BF 为单位长，建立如图所示的空间直角坐标系H xyz -. 由（1）可得，DE PE ⊥.又2DP =，1DE =，所以3PE =.又1PF =，2EF =，故PE PF ⊥.可得33,22PH EH ==.则()33330,0,0,0,0,,1,,0,1,,,2222H P D DP ⎛⎫⎛⎫⎛⎫--= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭30,0,2HP ⎛⎫= ⎪ ⎪⎝⎭为平面ABFD 的法向量. 设DP 与平面ABFD 所成角为θ，则334sin 43HP DP HP DPθ⋅===⋅. 所以DP 与平面ABFD 所成角的正弦值为34. 2.【分析】（1）因为4AP CP AC ===，O 为AC 的中点，所以OP AC ⊥，且23OP =．连结OB ．因为22AB BC AC ==，所以ABC 为等腰直角三角形，且1,22OB AC OB AC ⊥== 由222OP OB PB +=知PO OB ⊥．由,OP OB OP AC ⊥⊥知PO ⊥平面ABC ．（2）如图，以O 为坐标原点，OB 的方向为x 轴正方向，建立空间直角坐标系O xyz -由已知得(0,0,0),(2,0,0),(0,2,0),(0,2,0),(0,0,23),(0,2,23)O B A C P AP -= 取平面PAC 的法向量(2,0,0)OB =．设(,2,0)(02)M a a a -<≤，则(,4,0)AM a a =-．设平面PAM 的法向量为(,,)n x y z =．由0,0AP n AM n ⋅=⋅=得2230(4)0y z ax a y ⎧+=⎪⎨+-=⎪⎩，可取2(3(4),3,)n a a a =--所以22223(4)cos 23(4)3a OB n a a a -〈⋅〉=-++ ．由已知得3cos 2OB n 〈⋅〉= ．所以22223|4|3223(4)3a a a a -=-++ ．解得4a =-(舍去)，43a = ．所以83434,,333n ⎛⎫=-- ⎪ ⎪⎝⎭ ．又(0,2,23)PC =- ，所以3cos ,4PC n 〈〉=．所以PC 与平面PAM 所成角的正弦值为34． 3.【详解】（Ⅰ）由已知得. 取的中点T ，连接，由为中点知，. 又，故=TN AM ∥，四边形AMNT 为平行四边形，于是MN AT ∥. 因为平面，平面，所以平面. （Ⅰ）取的中点，连结.由得，从而，且 . 以A 为坐标原点， AE 的方向为轴正方向，建立如图所示的空间直角坐标系.由题意知，，，，， (0,2,4)PM =-， 5(,1,2)2PN =-，5(,1,2)2AN =.设(,,)x y z =n 为平面 PMN 的一个法向量，则0,{0,n PM n PN ⋅=⋅=即 240,520,2y z x y z -=+-= 可取(0,2,1)n =.于是85cos ,25n AN n AN n AN⋅〈〉==. 三、二面角1【分析】（1）PD ⊥平面ABCD ，四边形ABCD 为矩形，不妨以点D 为坐标原点，DA 、DC 、DP所在直线分别为x 、y 、z 轴建立如上图所示的空间直角坐标系D xyz -，设2BC a =，则()0,0,0D 、()0,0,1P 、()2,1,0B a 、(),1,0M a 、()2,0,0A a ，则()2,1,1PB a =-，(),1,0AM a =-，PB AM ⊥，则2210PB AM a ⋅=-+=，解得22a =，故22BC a ==；（2）设平面PAM 的法向量为()111,,m x y z =，则22AM ⎛⎫=-⎪ ⎪⎝⎭，()2,0,1AP =-，由111120220m AM x y m AP x z ⎧⋅=-+=⎪⎨⎪⋅=-+=⎩，取12x =，可得()2,1,2m =，设平面PBM 的法向量为()222,,n x y z =，2,0,02BM ⎛⎫=- ⎪ ⎪⎝⎭，()2,1,1BP =--，由222220220n BM x n BP x y z ⎧⋅=-=⎪⎨⎪⋅=--+=⎩，取21y =，可得()0,1,1n =，3314cos ,1472m n m n m n⋅<>===⨯⋅，所以，270sin ,1cos ,14m n m n <>=-<>=，因此，二面角A PM B --的正弦值为7014. 2.【分析】（1）在棱1CC 上取点G ，使得112C G CG =，连接DG 、FG 、1C E 、1C F ，在长方体1111ABCD A B C D -中，//AD BC 且AD BC =，11//BB CC 且11BB CC =，112C G CG =，12BF FB =，112233CG CC BB BF ∴===且CG BF =，所以，四边形BCGF 为平行四边形，则//AF DG 且AF DG =，同理可证四边形1DEC G 为平行四边形，1//C E DG ∴且1C E DG =，1//C E AF ∴且1C E AF =，则四边形1AEC F 为平行四边形，因此，点1C 在平面AEF 内；（2）以点1C 为坐标原点，11C D 、11C B 、1C C 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系1C xyz -，则()2,1,3A 、()12,1,0A 、()2,0,2E 、()0,1,1F ， ()0,1,1AE =--，()2,0,2AF =--，()10,1,2A E =-，()12,0,1A F =-，设平面AEF 的法向量为()111,,m x y z =，由0m AE m AF ⎧⋅=⎪⎨⋅=⎪⎩，得11110220y z x z --=⎧⎨--=⎩取11z =-，得111x y ==，则()1,1,1m =-，设平面1A EF 的法向量为()222,,n x y z =，由1100n A E n A F ⎧⋅=⎪⎨⋅=⎪⎩，得22222020y z x z -+=⎧⎨-+=⎩，取22z =，得21x =，24y =，则()1,4,2n =，37cos ,7321m n m n m n⋅<>===⨯⋅，设二面角1A EF A --的平面角为θ，则7cos 7θ=，242sin 1cos 7θθ∴=-=. 因此，二面角1A EF A --的正弦值为427. 3【分析】（1）连接ME ，1B CM ，E 分别为1BB ，BC 中点 ME ∴为1B BC ∆的中位线 1//ME B C ∴且112ME B C =又N 为1A D 中点，且11//A D B C 1//ND B C ∴且112ND B C =//ME ND ∴ ∴四边形MNDE 为平行四边形//MN DE ∴，又MN ⊄平面1C DE ，DE ⊂平面1C DE //MN ∴平面1C DE（2）设AC BD O ⋂=，11111A C B D O ⋂= 由直四棱柱性质可知：1OO ⊥平面ABCD 四边形ABCD 为菱形 AC BD ∴⊥则以O 为原点，可建立如下图所示的空间直角坐标系：则：()3,0,0A，()0,1,2M ，()13,0,4A ，D （0，-1,0）31,,222N ⎛⎫- ⎪ ⎪⎝⎭取AB 中点F ，连接DF ，则31,,022F ⎛⎫⎪⎪⎝⎭四边形ABCD 为菱形且60BAD ∠= BAD ∴∆为等边三角形 DF AB ∴⊥ 又1AA ⊥平面ABCD ，DF ⊂平面ABCD 1DF AA ∴⊥DF ∴⊥平面11ABB A ，即DF ⊥平面1AMADF ∴为平面1AMA 的一个法向量，且33,,022DF ⎛⎫= ⎪ ⎪⎝⎭设平面1MA N 的法向量(),,n x y z =，又()13,1,2MA =-，33,,022MN ⎛⎫=- ⎪ ⎪⎝⎭132033022n MA x y z n MN x y ⎧⋅=-+=⎪∴⎨⋅=-=⎪⎩，令3x =，则1y =，1z =- ()3,1,1n ∴=-315cos ,515DF n DF n DF n⋅∴===⋅ 10sin ,5DF n ∴=∴二面角1A MA N --的正弦值为：1054.【分析】证明（1）因为1111ABCD A B C D -是长方体，所以11B C ⊥侧面11A B BA ，而BE ⊂平面11A B BA ，所以11BE B C ⊥又1BE EC ⊥，1111B C EC C ⋂=，111,B C EC ⊂平面11EB C ，因此BE ⊥平面11EB C ；（2）以点B 坐标原点，以1,,BC BA BB 分别为,,x y z 轴，建立如下图所示的空间直角坐标系，1(0,0,0),(,0,0),(,0,),(0,,)2b B C a C a b E a ，因为1BE EC ⊥，所以2210(0,,)(,,)002224b b b BE EC a a a a b a ⋅=⇒⋅-=⇒-+=⇒=，所以(0,,)E a a ，1(,,),(0,0,2),(0,,)EC a a a CC a BE a a =--==，设111(,,)m x y z =是平面BEC 的法向量，所以111110,0,(0,1,1)0.0.ay az m BE m ax ay az m EC +=⎧⎧⋅=⇒⇒=-⎨⎨--=⋅=⎩⎩，设222(,,)n x y z =是平面1ECC 的法向量，所以2122220,0,(1,1,0)0.0.az n CC n ax ay az n EC =⎧⎧⋅=⇒⇒=⎨⎨--=⋅=⎩⎩，二面角1B EC C --的余弦值的绝对值为11222m n m n ⋅==⨯⋅，所以二面角1B EC C --的正弦值为2131()22-=. 5.【分析】解：（1）由题设知,平面CMD Ⅰ平面ABCD ,交线为CD .因为BC ⅠCD ,BC ⊂平面ABCD ,所以BC Ⅰ平面CMD ,故BC ⅠDM .因为M 为CD 上异于C ，D 的点,且DC 为直径，所以 DM ⅠCM . 又 BC CM =C ,所以DM Ⅰ平面BMC . 而DM ⊂平面AMD ,故平面AMD Ⅰ平面BMC .（2）以D 为坐标原点,DA 的方向为x 轴正方向,建立如图所示的空间直角坐标系D −xyz . 当三棱锥M −ABC 体积最大时，M 为CD 的中点.由题设得()()()()()0,0,0,2,0,0,2,2,0,0,2,0,0,1,1D A B C M ，()()()2,1,1,0,2,0,2,0,0AM AB DA =-==设(),,n x y z =是平面MAB 的法向量,则0,0.n AM n AB ⎧⋅=⎨⋅=⎩即20,20.x y z y -++=⎧⎨=⎩ 可取()1,0,2n =.DA 是平面MCD 的法向量, 因此5cos ,5n DA n DA n DA⋅==，25sin ,5n DA =，所以面MAB 与面MCD 所成二面角的正弦值是255. 6.【详解】（1）由已知90BAP CDP ∠=∠=︒，得AB ⅠAP ，CD ⅠPD ．由于AB//CD ，故AB ⅠPD ，从而AB Ⅰ平面P AD ．又AB ⊂平面P AB ，所以平面P AB Ⅰ平面P AD ．（2）在平面PAD 内作PF AD ⊥，垂足为F ，由（1）可知，AB ⊥平面PAD ，故AB PF ⊥，可得PF ⊥平面ABCD .以F 为坐标原点，FA 的方向为x 轴正方向，AB 为单位长，建立如图所示的空间直角坐标系F xyz -. 由（1）及已知可得2,0,02A ⎛⎫ ⎪⎪⎝⎭，20,0,2P ⎛⎫ ⎪ ⎪⎝⎭，2,1,02B ⎛⎫ ⎪ ⎪⎝⎭，2,1,02C ⎛⎫- ⎪ ⎪⎝⎭. 所以22,1,22PC ⎛⎫=-- ⎪ ⎪⎝⎭，()2,0,0CB =，22,0,22PA ⎛⎫=- ⎪ ⎪⎝⎭，()0,1,0AB =.设(),,n x y z =是平面PCB 的法向量，则0,0,n PC n CB ⎧⋅=⎨⋅=⎩即220,2220,x y z x ⎧-+-=⎪⎨⎪=⎩可取()0,1,2n =--. 设(),,m x y z =是平面PAB 的法向量，则0,0,m PA m AB ⎧⋅=⎨⋅=⎩即220,220.x z y ⎧-=⎪⎨⎪=⎩可取()1,0,1m =. 则3cos ,3n m n m n m ⋅==-，所以二面角A PB C --的余弦值为33-. 7.【解析】：（1）由题设可得，ABD CBD ≌△△，从而AD DC =. 又ACD △是直角三角形，所以=90ADC ∠︒. 取AC 的中点O ，连接DO ,BO ,则DO ⅠAC ,DO =AO . 又由于ABC 是正三角形，故BO AC ⊥. 所以DOB ∠为二面角D AC B --的平面角. 在Rt AOB 中，222BO AO AB +=.又AB BD =，所以222222BO DO BO AO AB BD +=+==，故90DOB ∠=. 所以平面ACD Ⅰ平面ABC .（2）由题设及（1）知，,,OA OB OD 两两垂直，以O 为坐标原点，OA 的方向为x 轴正方向，OA 为单位长，建立如图所示的空间直角坐标系O xyz -.则()()()()1,0,0,0,3,0,1,0,0,0,0,1A B C D -.由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得310,,22E ⎛⎫ ⎪ ⎪⎝⎭. 故()()311,0,1,2,0,0,1,,22AD AC AE ⎛⎫=-=-=- ⎪ ⎪⎝⎭.设(),,n x y z =是平面DAE 的法向量，则00n AD n AE ⎧⋅=⎨⋅=⎩，，即0,310.22x z x y z -+=⎧⎪⎨-++=⎪⎩可取31,,13⎛⎫= ⎪ ⎪⎝⎭n . 设m 是平面AEC 的法向量，则00m AC m AE ⎧⋅=⎨⋅=⎩，，同理可取()0,1,3=-m .则7cos ,7⋅==n m n m n m . 所以二面角D -AE -C 的余弦值为77.8.【分析】（Ⅰ）因为四边形ABEF 为正方形，所以AF FE ⊥，又AF DF ⊥，DF FE F ⋂=，所以AF ⊥平面EFDC ．又AF ⊂平面ABEF ，故平面ABEF ⊥平面EFDC ．（Ⅰ）过D 作DG EF ⊥，垂足为G ，因为平面ABEF ⊥平面EFDC ，平面ABEF平面EFDCEF ，DG ⊂平面EFDC ，故DG ⊥平面ABEF ．以G 为坐标原点，GF 的方向为x 轴正方向，GD 的方向为z 轴正向，建立如图所示的空间直角坐标系G xyz -．由（Ⅰ）知DFE ∠为二面角D AF E --的平面角，故60DFE ∠=︒，设()20DF a a =>，则3DG a =，FG a =，所以(),4,0A a a ，()3,4,0B a a -，()3,0,0E a -，()0,0,3D a ．由已知，//AB EF ，而AB ⊄平面EFDC ，EF ⊂平面EFDC ，所以//AB 平面EFDC ，又平面ABCD 平面EFDC DC =，AB ⊂平面ABCD ，故//AB CD ，所以//CD EF ．由//BE AF ，可得BE ⊥平面EFDC ，同理CEF ∠为二面角C BE F --的平面角，所以60CEF ∠=︒，从而可得()2,0,3C a a -．所以(),0,3EC a a =，()0,4,0EB a =，()3,4,3AC a a a =--，()4,0,0AB a =-．设(),,n x y z =是平面BCE 的法向量，则00n EC n EB ⎧⋅=⎨⋅=⎩，即3040ax az ay ⎧+=⎪⎨=⎪⎩，取3x =，则0,3y z ==-，可取()3,0,3n =-．设m 是平面ABCD 的法向量，则00m AC m AB ⎧⋅=⎨⋅=⎩，同理可取()0,3,4m =，则43219cos ,192319n m n m n m⋅〈〉==-=-⨯．因为二面角E BC A --的平面角为钝角，故二面角E BC A --的余弦值为21919-．9.【详解】：(1)由已知得AC BD ⊥，AD CD =,又由AE CF =得AE CFAD CD=，故AC ⅠEF ，因此 EF HD ⊥，从而EF ⅠD H '.由56AB AC ==，得224DO BO AB AO ==-=.由AC ⅠEF 得14OH AE DO AD ==.所以1OH =,3D H DH '==. 于是222223110D H OH D O +=+='=',故D H OH '⊥.又D H EF '⊥,而OH EF H =,所以D H'⊥平面ABCD .如图，以H 为坐标原点，HF 的方向为x 轴的正方向，建立空间直角坐标系H xyz -，则()0,0,0H ，()3,1,0A --，()0,6,0B -，()3,1,0C -，()0,0,3D '，()3,4,0AB =-，()6,0,0AC =，()3,1,3AD '=.设()111,,m x y z =是平面ABD '的法向量，则0{m AB m AD '⋅=⋅=，即11111340{330x y x y z -=++=，可取()4,3,5m =-.设()222,,n x y z =是平面ACD '的法向量，则0{n AC n AD '⋅=⋅=，即222260{330x x y z =++=，可取()0,3,1n =-于是1475cos ,255010m n m n m n ⋅-===-⨯，设二面角的大小为θ，295sin 25θ=.因此二面角B D A C '--的正弦值是29525.。

线面夹角练习题

线面夹角练习题一、选择题1. 线面夹角是指：A. 直线与平面的交角B. 直线与平面的夹角C. 平面与平面的夹角D. 直线与直线的夹角2. 在空间几何中，线面夹角的取值范围是：A. [0°, 90°]B. [0°, 180°]C. [90°, 180°]D. [0°, 360°]3. 如果直线l与平面α的夹角为θ，那么直线l在平面α上的投影与平面α的夹角是：A. θB. 90° - θC. 180° - θD. 无法确定4. 直线l与平面α垂直，则线面夹角为：A. 0°B. 90°C. 180°D. 无法确定5. 直线l与平面α平行，则线面夹角为：A. 0°B. 90°C. 180°D. 无法确定二、填空题6. 若直线l与平面α的夹角为45°，则直线l在平面α上的投影与平面α的夹角为________。

7. 若直线l与平面α的夹角为30°，则直线l在平面α上的投影与平面α的夹角为________。

8. 当直线l与平面α相交时，线面夹角的计算公式为________。

9. 当直线l与平面α垂直时，直线l在平面α上的投影长度为________。

10. 当直线l与平面α平行时，直线l在平面α上的投影长度为________。

三、判断题11. 线面夹角总是小于90°。

（）12. 线面夹角的计算可以通过直线上的一点到平面的距离来确定。

（）13. 当直线l与平面α的夹角为锐角时，直线l在平面α上的投影长度小于直线l的实际长度。

（）14. 直线l与平面α平行时，线面夹角为0°。

（）15. 直线l与平面α垂直时，线面夹角为90°。

（）四、简答题16. 简述如何确定直线与平面的夹角。

17. 描述直线l在平面α上的投影长度与线面夹角之间的关系。

线面角、面面角强化训练(含答案)

线面角、面面角强化训练一．解答题（共24小题）1．（2012•浙江）如图，在侧棱垂直底面的四棱柱ABCD﹣A1B1C1D1中，AD∥BC，AD⊥AB，AB=．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值．2．（2010•湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．3．（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．4．（2008•上海）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．5．（2005•黑龙江）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．（1）求证：EF⊥面PAB；（2）若，求AC与面AEF所成的角．6．如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．7．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．8．（2008•安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．9．（2005•北京）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D为AB的中点．（Ⅰ）求证AC⊥BC1；（Ⅱ）求证AC1∥平面CDB1；（Ⅲ）求异面直线AC1与B1C所成角的余弦值．10．（2009•江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．11．（2008•海南）如图，已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上，∠PDA=60°．（Ⅰ）求DP与CC′所成角的大小；（Ⅱ）求DP与平面AA′D′D所成角的大小．12．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．13．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点．（Ⅰ）求异面直线CC1和AB的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣B1的平面角的余弦值．14．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点（Ⅰ）求点C到平面A1ABB1的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．15．（2012•浙江）如图，在四棱锥P﹣ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．（1）证明：MN∥平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A﹣MN﹣Q的平面角的余弦值．16．（2012•四川）如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，点P在平面ABC内的射影O在AB上．（Ⅰ）求直线PC与平面ABC所成的角的大小；（Ⅱ）求二面角B﹣AP﹣C的大小．17．（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．18．（2011•辽宁）如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．（I）证明：平面PQC⊥平面DCQ（II）求二面角Q﹣BP﹣C的余弦值．19．如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．20．如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E分别是AC、A1C1的中点；（Ⅰ）求证：直线AE∥平面BDC1；（Ⅱ）求证：直线A1D⊥平面BDC1；（Ⅲ）求直线A1C1与平面BDC1所成的角．21．已知斜三棱柱ABC﹣A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求C1到平面A1AB的距离；（Ⅲ）求二面角A﹣A1B﹣C的余弦值．22．已知在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD 的中点．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求PC与平面ABCD所成角的大小；（Ⅲ）求二面角P一EC一D的大小．23．如图，ABCD﹣A1B1C1D1是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．（1）求证：A1F⊥C1E；（2）当A1、E、F、C1共面时，求：①D1到直线C1E的距离；②面A1DE与面C1DF所成二面角的余弦值．24．如图，在直三棱柱ABC﹣A1B1C1中，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．（Ⅰ）求证：AC1∥平面CDB1；（Ⅱ）求点B到平面CDB1的距离；（Ⅲ）求二面角B﹣B1C﹣D的大小．线面角、面面角强化训练参考答案与试题解析一．解答题（共24小题）1．（2012•浙江）如图，在侧棱垂直底面的四棱柱ABCD﹣A1B1C1D1中，AD∥BC，AD⊥AB，AB=．AD=2，BC=4，AA1=2，E是DD1的中点，F是平面B1C1E与直线AA1的交点．（1）证明：（i）EF∥A1D1；（ii）BA1⊥平面B1C1EF；（2）求BC1与平面B1C1EF所成的角的正弦值．B=B=，即∠，BH=，H=，2．（2010•湖南）如图所示，在正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点．（Ⅰ）求直线BE与平面ABB1A1所成的角的正弦值；（Ⅱ）在棱C1D1上是否存在一点F，使B1F∥平面A1BE？证明你的结论．BE=中，所成的角的正弦值为3．（2009•湖南）如图，在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=，点D是BC的中点，点E在AC上，且DE⊥A1E．（1）证明：平面A1DE⊥平面ACC1A1；（2）求直线AD和平面A1DE所成角的正弦值．），，﹣，，﹣所成角的正弦值为4．（2008•上海）如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，E是BC1的中点．求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）．EF=（5．（2005•黑龙江）如图，四棱锥P﹣ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E，F分别为CD，PB的中点．（1）求证：EF⊥面PAB；（2）若，求AC与面AEF所成的角．EF DGa所成角的正弦值为所成角为，∴）解：由，得，∴所成的角为所成的角为．6．如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．（Ⅰ）证明：SD⊥平面SAB；（Ⅱ）求AB与平面SBC所成的角的大小．的法向量为锐角时，所求的角即为它的余角；当=MD=SM=（，y==，，＞==，＞arcsin7．（2011•北京）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．（Ⅰ）求证：BD⊥平面PAC；（Ⅱ）若PA=AB，求PB与AC所成角的余弦值；（Ⅲ）当平面PBC与平面PDC垂直时，求PA的长．，则，代入公式可求的法向量的法向量，，﹣，，，=|）知，设的法向量令的法向量所以的法向量=0t=PA=8．（2008•安徽）如图，在四棱锥O﹣ABCD中，底面ABCD四边长为1的菱形，∠ABC=，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．（Ⅰ）证明：直线MN∥平面OCD；（Ⅱ）求异面直线AB与MD所成角的大小；（Ⅲ）求点B到平面OCD的距离．ADC=DP=利用勾股定理求得等于，，的坐标表示．设平面的法向量为，，表示出和在向量的距离为，∴，所成角的大小为．的距离为．，，•=0•=0•（，﹣，．在向量=）上的投影的绝对值，的距离为9．（2005•北京）如图，在直三棱柱ABC﹣A1B1C1中，AC=3，BC=4，AB=5，AA1=4，点D为AB的中点．（Ⅰ）求证AC⊥BC1；（Ⅱ）求证AC1∥平面CDB1；（Ⅲ）求异面直线AC1与B1C所成角的余弦值．=λ，与AC，AB=，CE=CBCED==所成角的余弦值（（Ⅰ）∵=0⊥，，=∥（Ⅲ）∵=，＞所成角的余弦值为10．（2009•江西）在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=4，AB=2．以AC的中点O为球心、AC为直径的球面交PD于点M，交PC于点N（1）求证：平面ABM⊥平面PCD；（2）求直线CD与平面ACM所成的角的大小；（3）求点N到平面ACM的距离．距离的的一个法向量，结合然后求出距离的，再利用向量的射影公式直接求点的中点可得即，则，，由PN=（．）可知所求距离为．的一个法向量，由可得：，所以所求角的大小为，所以，则距离的，设点．11．（2008•海南）如图，已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上，∠PDA=60°．（Ⅰ）求DP与CC′所成角的大小；（Ⅱ）求DP与平面AA′D′D所成角的大小．（Ⅰ）利用，求出．即可．．通过，得到．求出，，由已知，．解得，所以（Ⅰ）因为．即．，所以．．则，）则，则，由已知，，解得，∴（Ⅰ）因为，．即．，所以12．如图，四棱锥P﹣ABCD中，底面ABCD为菱形，PA⊥底面ABCD，，PA=2，E是PC上的一点，PE=2EC．（Ⅰ）证明：PC⊥平面BED；（Ⅱ）设二面角A﹣PB﹣C为90°，求PD与平面PBC所成角的大小．，（2），﹣=，（）•==0•=0），（的法向量为，则，=，则，﹣），∴•﹣，（﹣，﹣，＞==13．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点．（Ⅰ）求异面直线CC1和AB的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣B1的平面角的余弦值．=．=，得D=，D=2=．=，﹣得=0，2，）=，=，则⊥，⊥取=（=，则⊥，，即取得，＞==．14．（2012•重庆）如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点（Ⅰ）求点C到平面A1ABB1的距离；（Ⅱ）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．=，从而D=．所以=，，，从而，，﹣，故，2，，=，则有⊥，⊥•且•，即，取=，=，则⊥，⊥，即且=0，＞=，所以二面角的平面角的余弦值15．（2012•浙江）如图，在四棱锥P﹣ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=，M，N分别为PB，PD的中点．（1）证明：MN∥平面ABCD；（2）过点A作AQ⊥PC，垂足为点Q，求二面角A﹣MN﹣Q的平面角的余弦值．的法向量，AQ=2AC=AB=中，（﹣，（），的平面角的余弦值为BD=AM=PB=AE=AQ=2BPC=MQ=．QE=，∴AEQ=的平面角的余弦值为16．（2012•四川）如图，在三棱锥P﹣ABC中，∠APB=90°，∠PAB=60°，AB=BC=CA，点P在平面ABC内的射影O在AB上．（Ⅰ）求直线PC与平面ABC所成的角的大小；（Ⅱ）求二面角B﹣AP﹣C的大小．OP=与平面OP=，，OC====．为原点，建立空间直角坐标系．则）=2=，则由得出，取﹣，所以（﹣===．OP=，，，所以=2 =）为平面==arcsin（Ⅱ）由（Ⅰ）知，，，=，则由得出，，则，所以=，的一个法向量为==arccos17．（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．（Ⅰ）求证：BD⊥平面AED；（Ⅱ）求二面角F﹣BD﹣C的余弦值．，﹣，，因此（，﹣==，则•，•y=z，则==，＞=，所以二面角CB=CGFGC=的余弦值为18．（2011•辽宁）如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．（I）证明：平面PQC⊥平面DCQ（II）求二面角Q﹣BP﹣C的余弦值．求出则、、由向量积的运算易得•，•、、的坐标，的法向量法向量，==••=即因此可取，=，＞﹣的余弦值为﹣19．如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．（Ⅰ）证明：PA⊥BD；（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．的坐标，求出向量，和平面BD=，，，，=的法向量为，则因此可取（，=，==﹣的余弦值为：﹣20．如图，已知正三棱柱ABC﹣A1B1C1的，底面边长是侧棱长2倍，D、E分别是AC、A1C1的中点；（Ⅰ）求证：直线AE∥平面BDC1；（Ⅱ）求证：直线A1D⊥平面BDC1；（Ⅲ）求直线A1C1与平面BDC1所成的角．D=21．已知斜三棱柱ABC﹣A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．（Ⅰ）求证：AC1⊥平面A1BC；（Ⅱ）求C1到平面A1AB的距离；（Ⅲ）求二面角A﹣A1B﹣C的余弦值．，求，））=的法向量=，则，）∴的距离为的法向量（，的法向量，的余弦值为22．已知在四棱锥P﹣ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=1，AB=2，E、F分别是AB、PD 的中点．（Ⅰ）求证：AF∥平面PEC；（Ⅱ）求PC与平面ABCD所成角的大小；（Ⅲ）求二面角P一EC一D的大小．FO=中，中，所成的角大小为，可得的大小为23．如图，ABCD﹣A1B1C1D1是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．（1）求证：A1F⊥C1E；（2）当A1、E、F、C1共面时，求：①D1到直线C1E的距离；②面A1DE与面C1DF所成二面角的余弦值．坐标，代入向量数量积公式，易得满足，的一个法向量为，的一个法向量为24．如图，在直三棱柱ABC﹣A1B1C1中，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．（Ⅰ）求证：AC1∥平面CDB1；（Ⅱ）求点B到平面CDB1的距离；（Ⅲ）求二面角B﹣B1C﹣D的大小．（Ⅰ）求出通过，相关向量，计算，求二面角，∴，的距离是，．的大小是。

线面夹角知识点及试题与答案(整理)

新疆源头学子小屋特级教师王新敞新疆源头学子小屋特级教师王新敞新疆源头学子小屋特级教师王新敞
h t w : /p w .x jk t y g .c o m /w /x c h t w : /p w .x jk t y g .c o m /w /x c h t w : /p w .x jk t y g .c o m /w /x c w x @ c k t 1 2 .c o 6 m w x @ c k t 1 2 .c o 6 m w x @ c k t 1 2 .c o 6 m

∴ a ⊥平面 POA
(1)三垂线定理描述的是 PA(斜线),AO(射影), a (直线)之间的垂直关系. (2) a 与 PA 可以相交,也可以异面.
1
(3)三垂线定理的实质是空间内的一条斜线和平面内的一条直线垂直的判定定理. 关于三垂线定理的应用,关键是找出平面(基准面)的垂线. 至于射影则是由垂足,斜足来确定的,因而是第二位的. 从三垂线定理的证明得到证明 a⊥b 的一个程序:一垂, 二射,三证.即第一,找平面(基准面)及平面垂线，定理中四条线均针对同一平面而言第二,找射影线,这时 a,b 便成平面上的一条直线与一条斜线. 第三,证明射影线与直线 a 垂直,从而得出 a 与 b 垂直. 总结：一面四线三垂直（2）三垂线定理的逆定理:在平面内的一条直线，如果它和这个平面的一条斜线垂直，那么它也和这条斜线在平面内的射影垂直. 【如图即：若 AB⊥BD，DC⊥BC，得 AB⊥BC（三垂线定理的逆定理）】 6. 求线面夹角的步骤如下： ①找出或作出线面夹角； ②证明其确实是所求的线面夹角； ③计算角的值，一般均在三角形中进行。
例 4：已知棱长为 1 的正方体 ABCD－A1B1C1D1 中，E 是 A1B1 的中点，求直线 AE 与平面 ABC1D1 所成的角的正弦值。解：如图建立空间直角坐标系， A1

线面角练习题

线面角练习题在数学中，线面角是一种常见的概念，用于描述线与面之间的相对关系。

本文将为你提供一系列线面角练习题，帮助你加深对线面角概念的理解并提高解题能力。

练习题一：线与平面的关系1. 建立直角坐标系，并画出平面P：4x - 2y + z = 6。

a) 在该平面上选择一点A(x1, y1, z1)，其中x1, y1, z1为任意实数。

画出该平面与点A的关系示意图。

b) 选择另一点B(x2, y2, z2)，其中x2, y2, z2为任意实数。

画出该平面、点A和点B之间的关系示意图。

练习题二：线与平面上的点的关系2. 平面P：2x + 3y - 4z = 12与直线L：x = 2 + t, y = 3 - t, z = -1 + 2t相交于点A。

求出点A的坐标。

练习题三：线面角的计算3. 已知平面P：2x - y + 3z = 1和直线L：x = 3 - t, y = 2 + 2t, z = -1 + t。

求出直线L与平面P的线面角。

练习题四：垂直线面角的判断4. 平面P1：2x - y + 2z = 5与平面P2：4x - 2y + 4z = 9之间的夹角为α。

判断平面P1与平面P2是否垂直。

练习题五：平行线面角的计算5. 平面P：3x - 2y + 4z = 7和直线L：x = 1 + 2t, y = -2 + 3t, z = 3 - t 之间的夹角为β。

判断直线L与平面P是否平行。

练习题六：点到平面的距离计算6. 平面P：2x - y + z = 5上有一点A(1, -3, 2)。

求出点A到平面P的距离。

练习题七：平行平面之间的距离计算7. 已知平面P1：2x - 3y + z = 4和平面P2：4x - 6y + 2z = 8平行。

求出平面P1与平面P2之间的距离。

练习题八：垂直线面之间的距离计算8. 平面P：2x - y + 3z = 5与直线L：x = 1 + t, y = 2 - t, z = 3t之间的距离为d。

第8章立体几何专题7 线面角的求解常考题型专题练习——【含答案】

3、线面角求法（二）用等体积法，求出斜线PA在面外的一点P到面的距离，利用三角形的正弦公式进行求解。

114、线面角求法（三）利用空间向量进行求解，高二再学。

【巩固练习】1、已知正方体1111ABCD A B C D -的体积为162，点P 在正方形1111D C B A 上，且1,A C 到P 的距离分别为2,23，则直线CP 与平面11BDD B 所成角的正切值为( )A.2 B.3 C.12D.13【答案】A【解析】易知22AB =；连接1C P ，在直角1CC P ∆中，可计算22112C P CP CC =-=；又1112,4A P A C ==，所以点P 是11A C 的中点；连接AC 与BD 交于点O ，易证AC ⊥平面11BDD B ，直线CP 在平面11BDD B 内的射影是OP ，所以CPO ∠就是直线CP 与平面11BDD B 所成的角，在直角CPO ∆中，2tan 2CO CPO PO ∠== .2、把正方形沿对角线折起,当以四点为顶点的三棱锥体积最大时，直线和平面所成的角的大小为A．B．C．D．[来源网ZXXK]【答案】C【解析】如图所示，当平面平面时，三棱锥的体积最大，取的中点，则平面，故直线和平面所成的角为，则，所以，故选C.3、如图，在三棱锥P-ABC中，,PA AB⊥PC BC⊥，,AB BC⊥22,AB BC==5PC=，则PA与平面ABC所成角的大小为_______.【答案】45︒【解析】如图，作平行四边形ABCD，连接PD，由AB BC⊥，则平行四边形ABCD是矩形．由BC CD⊥，BC PC⊥，PC CD C=，∴BC⊥平面PCD，而PD⊂平面PCD，∴BC PD⊥，同理可得AB PD⊥，又AB BC B⋂=，∴PD⊥平面11ABCD ．,PD CD PD AD ⊥⊥，PAD ∠是PA 与平面ABC 所成角．由2,5CD AB PC ===得1PD =，又1AD BC ==，∴45PAD ∠=︒．∴PA 与平面ABC 所成角是45︒．4、已知三棱柱ABC －A 1B 1C 1的侧棱与底面边长都相等，A 1在底面ABC 内的射影为△ABC 的中心O ，则AB 1与底面ABC 所成角的正弦值为（）A ．23B ．13C ．33D ．23【答案】A【解析】作1A H ⊥面ABC 于点H ,延长11B A 到D ,延长BA 到E 使得111B A A D =，,BA AE =如图则有11A EAB ，又因为1A O ⊥面ABC ，故1A EO ∠为所求角，且111sin AO A EO A E∠=已知底面为正三角形，且O为底面中点，解三角形可知：111336,333AO AB AA A O AA==∴=又在AEO∆中运用余弦定理，150EAO∠=︒则()()22212cos3EO EA AO EA AO EAO AB=+-⋅∠=故由勾股定理可得22113A E AO EO AB=+=则1623sin33A EO∠==故选A5、如图所示，已知AB为圆O的直径，且AB＝4，点D为线段AB上一点，且13AD DB=，点C为圆O上一点，且3BC AC=.点P在圆O所在平面上的正投影为点D，PD＝DB.(1)求证：CD⊥平面PAB；(2)求直线PC与平面PAB所成的角．【答案】（1）见解析；（2）301旗开得胜1【解析】(1)证明：连接CO ，由3AD ＝DB 知，点D 为AO 的中点．又因为AB 为圆O 的直径，所以AC ⊥CB. 由3AC ＝BC 知，∠CAB ＝60°，所以△ACO 为等边三角形．故CD ⊥AO. 因为点P 在圆O 所在平面上的正投影为点D ，所以PD ⊥平面ABC ，又CD ⊂平面ABC ，所以PD ⊥CD ，由PD ⊂平面PAB ，AO ⊂平面PAB ，且PD ∩AO ＝D ，得CD ⊥平面PAB.(2)由(1)知∠CPD 是直线PC 与平面PAB 所成的角，又△AOC 是边长为2的正三角形，所以CD ＝3. 在Rt △PCD 中，PD ＝DB ＝3，CD ＝3，所以3tan 3CD CPD PD ∠==，∠CPD ＝30°，即直线PC 与平面PAB 所成的角为30°.16、如图，在四棱锥P -ABCD 中，AP ⊥平面PCD ，//AD BC ，AB BC ⊥，12AP AB BC AD ===，E 为AD 的中点，AC 与BE 相交于点O .（1）证明：PO ⊥平面ABCD .（2）求直线BC 与平面PBD 所成角的正弦值.【答案】（1）证明见解析（2）2211【解析】（1）证明：AP ⊥平面PCD ，CD ⊂平面PCD ，AP CD ∴⊥，//,AD BC 12BC AD =，E 为AD 的中点，则//BC DE 且BC DE =. ∴四边形BCDE 为平行四边形，//BE CD ∴，AP BE ∴⊥.1又,AB BC⊥12AB BC AD ==，且E 为AD 的中点，∴四边形ABCE 为正方形，BE AC ∴⊥，又,AP AC A =BE ∴⊥平面APC ，PO ⊂平面APC ，则BE PO ⊥.AP ⊥平面,PCD PC ⊂平面PCD ，AP PC ∴⊥，又22AC AB AP ==，PAC ∴∆为等腰直角三角形，O 为斜边AC 上的中点，PO AC ∴⊥且,ACBE O =PO ∴⊥平面ABCD .（2）高一学生可以用等体积法求解。

线线角、线面角、二面角知识点及练习

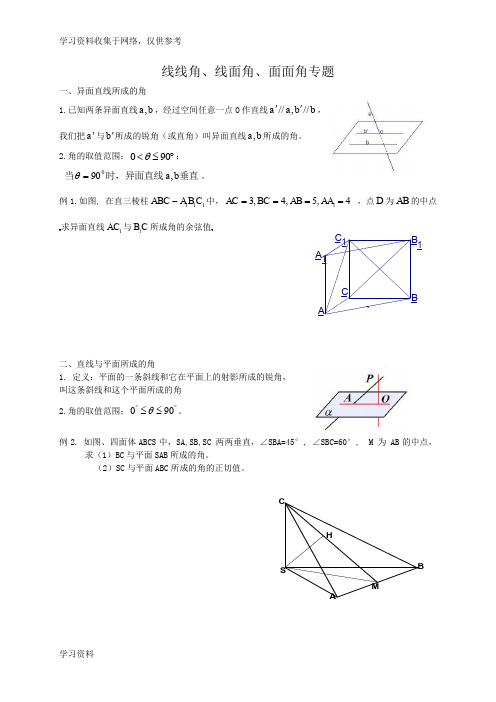
线线角、线面角、面面角专题一、异面直线所成的角1.已知两条异面直线,a b ，经过空间任意一点O 作直线//,//a a b b ''，我们把a '与b '所成的锐角（或直角）叫异面直线,a b 所成的角。

2.角的取值范围：090θ<≤︒；垂直时，异面直线当b a ,900=θ。

例1.如图, 在直三棱柱111ABC A B C -中，13,4,5,4AC BC AB AA ==== ，点D 为AB 的中点求异面直线1AC 与1B C 所成角的余弦值二、直线与平面所成的角1. 定义：平面的一条斜线和它在平面上的射影所成的锐角，叫这条斜线和这个平面所成的角2.角的取值范围：︒︒≤≤900θ。

例2. 如图、四面体ABCS 中，SA,SB,SC 两两垂直，∠SBA=45°, ∠SBC=60°, M 为 AB 的中点，求（1）BC 与平面SAB 所成的角。

（2）SC 与平面ABC 所成的角的正切值。

BMH S CA_1_A一、二面角：1. 从一条直线出发的两个半平面所组成的图形叫做二面角。

这条直线叫做二面角的棱，这两个半平面叫做二面角的面。

2. 二面角的取值范围：︒︒≤≤1800θ 两个平面垂直：直二面角。

3.作二面角的平面角的常用方法有六种：1.定义法：在棱上取一点O ，然后在两个平面内分别作过棱上O 点的垂线。

2.三垂线定理法：先找到一个平面的垂线，再过垂足作棱的垂线，连结两个垂足即得二面角的平面角。

3.向量法：分别作出两个半平面的法向量，由向量夹角公式求得。

二面角就是该夹角或其补角。

二面角一般都是在两个平面的相交线上，取恰当的点，经常是端点和中点。

例3.如图，E 为正方体ABCD －A 1B 1C 1D 1的棱CC 1的中点，求 (1)二面角111D C A D --所成的角的余弦值 (2)平面AB 1E 和底面C C BB 11所成锐角的正切值. A 1D 1B 1C 1 EDBCA巩固练习1.若直线a 不平行于平面α，则下列结论成立的是（）A.α内所有的直线都与a 异面；B.α内不存在与a 平行的直线；C.α内所有的直线都与a 相交；D.直线a 与平面α有公共点.2.空间四边形ABCD 中，若AB AD AC CB CD BD =====，则AD 与BC 所成角为（）A.030B.045C.060D.090 3．正方体ABCD-A 1B 1C 1D 1中，与对角线AC 1异面的棱有（）条A.3B.4C.6D.84.如图长方体中，AB=AD=23，CC 1=2，则二面角C 1—BD —C 的大小为（）A.300B.450C.600D.9005．如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ，点E 、F 分别是AB 、BD 的中点．求证：(1)直线EF ∥面ACD .(2)平面EFC ⊥平面BCD .6．如图，DC ⊥平面ABC ，EB ∥DC ，AC ＝BC ＝EB ＝2DC ＝2，∠ACB ＝120°，P ，Q 分别为AE ，AB 的中点．(1)证明：PQ ∥平面ACD ；(2)求AD 与平面ABE 所成角的正弦值． ABC D A 1B 1C 1D 17.如图，已知四棱锥S－ABCD的底面ABCD是正方形，SA⊥底面ABCD，设SA＝4，AB＝2，求点A到平面SBD的距离；。

人教A版必修二立体几何中的三类角的求解基础练

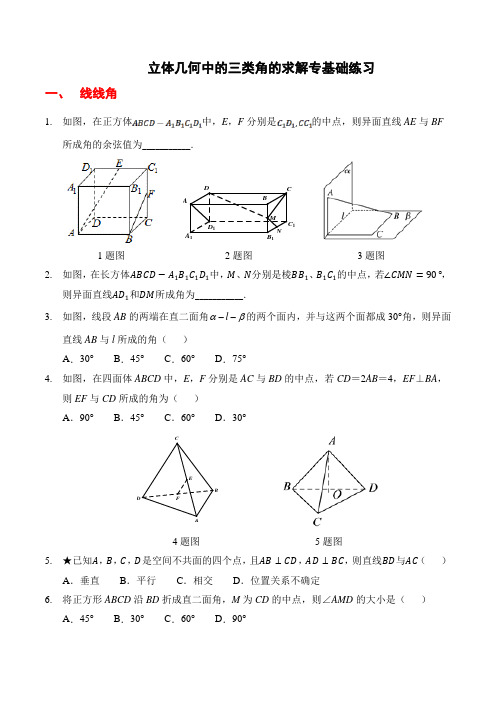
立体几何中的三类角的求解专基础练习一、线线角1. 如图，在正方体中，E ，F 分别是的中点，则异面直线AE 与BF所成角的余弦值为___________．1题图 2题图 3题图2. 如图，在长方体中，、分别是棱、的中点，若，则异面直线和所成角为___________．3. 如图，线段AB 的两端在直二面角l αβ--的两个面内，并与这两个面都成30°角，则异面直线AB 与l 所成的角（）A ．30°B ．45°C ．60°D ．75°4. 如图，在四面体ABCD 中，E ，F 分别是AC 与BD 的中点，若CD ＝2AB ＝4，EF ⊥BA ，则EF 与CD 所成的角为（）A ．90°B ．45°C ．60°D ．30°4题图 5题图5. ★已知，，，是空间不共面的四个点，且，，则直线与（）A ．垂直B ．平行C ．相交D ．位置关系不确定6. 将正方形ABCD 沿BD 折成直二面角，M 为CD 的中点，则∠AMD 的大小是（）A ．45°B ．30°C ．60°D ．90°NMDCB C 11A 1D 1AFECDB7. 已知三棱柱ABC -A 1B 1C 1的侧棱与底面垂直，体积为94的正三角形．若P 为底面A 1B 1C 1的中心，则P A 与平面ABC 所成角的大小为___________．7题图 8题图 10题图8. 如图，在底面为正方形的四棱锥中，侧面底面ABCD ，，，则异面直线PB 与AC 所成的角为___________． 9. 已知直三棱柱中，，，，则异面直线与所成角的余弦值为___________． 10. 如图，在直三棱柱中，，1AC BC ==，则异面直线与AC 所成角的余弦值是______．二、线面角11. 在正方体中，直线与所成角大小为___________． 12. 已知长方体中，，，则直线和平面所成角的正弦值为___________．13. 在长方体中，，，则直线与平面所成角的余弦值等于______．14. 如图，在三棱柱中，各棱长相等，侧棱垂直于底面，点是侧面的中心，则与平面所成角的大小是___________．14题图 15题图 16题图15. 如图，在三棱锥中，侧面底面BCD ，，，，，直线AC 与底面BCD 所成角的大小为___________． 16. 如图，在矩形ABCD 中，，将沿折起，使得D 折起的位置为，且在平面ABC 的射影恰好落在AB 上，则直线与平面ABC 所成角的正弦值为___________．17. 如图，在三棱锥中，底面ABC 为等边三角形，，，平面平面ABC ，则S C 与平面ABC 所成角的大小是______ ．17题图 18题图 19题图18. 如图，二面角的大小是，线段，AB 与l 所成的角为则AB与平面所成的角的正弦值是______．19. ★在三棱锥中，平面，，，则直线与平面所成角的大小为__________．三、面面角20. 如图，锐二面角的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于已知，，，则锐二面角的平面角的余弦值是___________．20题图 21题图CB21.在三棱锥中，平面，已知，则二面角的平面角是___________．22.正四棱锥(顶点在底面的射影是底面正方形的中心)的体积为12，底面对角线的长为，则侧面与底面所成的二面角为___________．23.在等腰Rt△ABC中，AB＝BC＝1，M为AC的中点，沿BM把它折成二面角，折后A与C的距离为1，则二面角C－BM－A的大小为___________．24.如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体A-BCD,则在四面体A-BCD中,下列说法正确的是（）A．平面ABD⊥平面ABC B．平面ADC⊥平面BDCC．平面ABC⊥平面BDC D．平面ADC⊥平面ABD25.等腰直角△ABC中，AB=BC=1，M为AC的中点，沿BM把△ABC折成二面角，折后A与C的距离为1，则二面角C—BM—A的大小为_____________．26.如图，正三棱柱中，各棱长都相等，则二面角的平面角的正切值为___________．26题图27题图27.三棱锥的两侧面PAB、PBC都是边长为2的正三角形，，则二面角的大小为___________．立体几何中的各类角的求解专练（答案）一、线线角1. 如图，在正方体中，E ，F 分别是的中点，则异面直线AE 与BF 所成角的余弦值为 DA ．B ．C ．D ．2. 如图，在长方体中，、分别是棱、的中点，若，则异面直线和所成角为( D )A ．B ．C ．D ．【解析】∵M 、N 分别是棱BB 1、B 1C 1的中点，∴MN ∥AD 1， ∵∠CMN =90∘，∴CM ⊥MN ，∴CM ⊥AD 1，由长方体的几何特征,我们可得CD ⊥AD 1， ∴AD 1⊥平面CDM ，故AD 1⊥DM 即异面直线AD 1与DM 所成的角为90∘3. 线段AB 的两端在直二面角l αβ--的两个面内，并与这两个面都成30°角，则异面直线AB 与l 所成的角是( B )A ．30°B ．45°C ．60°D ．75° 【解析】设AB=a ，在平面α内，作AA′⊥l 于A′，则AA′⊥β，连A′B ，则∠ABA′=30°．在Rt △AA′B 中，AB=a ，所以AA′=a ．同理作BB′⊥l 于B′，连AB′，则∠BAB′=30°，所以BB′=a ，AB′=a ，所以A′B′= ′ ′ =a ，过B 作BCA′B′．连接A′C ，则A′CBB′，连接AC ，在Rt △AA′C 中，AC= ′′=a ．由BC ⊥平面AA′C ，所以△ABC 为直角三角形，且AC=BC ，所以∠ABC=45°，为l 与AB 所成角．4. 如图，在四面体ABCD 中，E ，F 分别是AC 与BD 的中点，若CD ＝2AB ＝4，EF ⊥BA ，111A则EF 与CD 所成的角为( D )A ．90°B ．45°C ．60°D ．30°【解析】设G 为AD 的中点，连接GF GE ，，则GF GE ，分别为ABD ，三角形ACD 的中位线．则GF AB ，且112GF AB GE CD ==，，且122GE CD ==，则EF 与CD 所成角的度数等于EF 与GE 所成角的度数又EF AB GF AB EF GF ⊥∴⊥，，则GEF 为直角三角形，1290GF GE GFE ==∠=︒，，则在直角GEF 中，1302sin GEF GEF ∠=∴∠=︒．5. ★已知，，，是空间不共面的四个点，且，，则直线与（ A ）．A ．垂直B ．平行C ．相交D ．位置关系不确定【解析】过点作平面，垂足为．∵ ，由三垂线定理可得．同理，，所以．6. 已知三棱柱ABC -A 1B 1C 1的侧棱与底面垂直，体积为94，正三角形．若P 为底面A 1B 1C 1的中心，则P A 与平面ABC 所成角的大小为( B )A ．75°B ．60°C ．45°D ．30°【解析】如图所示，P 为正三角形A 1B 1C 1的中心，设O 为△ABC 的中心，由题意知：PO ⊥平面ABC ，连接OA ，则∠P AO 即为P A 与平面ABC 所成的角．在正三角形ABC 中，AB ＝BC ＝AC则S＝3×(3)2＝33，V ABC -A 1B 1C 1＝S ×PO ＝，∴PO ＝．又AO ＝31，∴tan ∠P AO ＝0PO A =P AO ＝60°． 7. 将正方形ABCD 沿BD 折成直二面角，M 为CD 的中点，则∠AMD 的大小是( D )A ．45°B ．30°C ．60°D ．90° 8. 如图，在底面为正方形的四棱锥中，侧面底面ABCD ，，，则异面直线PB 与AC 所成的角为 C A ．B ．C ．D ．【解析】由题意：底面ABCD 为正方形，平面ABCD ，分别过P ，D 点作AD ，AP 的平行线交于M ，连接CM ，AM ，，，，．是平行四边形，，所以MCA ∠就是异面直线PB 与AC 所成的角．设，在三角形ACM 中，，，三角形ACM 是等边三角形．所以MCA ∠等于，即异面直线PB 与AC 所成的角为．9. 已知直三棱柱中，，，，则异面直线与所成角的余弦值为 CA ．B ．C ．D ．10. 如图，在直三棱柱中，，1AC BC ==，则异面直线与AC 所成角的余弦值是______．【答案】二、线面角11. 如图，在正方体中，直线与所成角大小为_____【答案】12.已知长方体中，，，则直线和平面所成角的正弦值为CA．B．C．D．13.在长方体中，，，则直线与平面所成角的余弦值等于______．【答案】14.如图，在三棱柱中，各棱长相等，侧棱垂直于底面，点是侧面的中心，则与平面所成角的大小是（ A ）A．B．C．D．15.如图，在三棱锥中，侧面底面BCD，，，，，直线AC与底面BCD所成角的大小为AA．B．C．D．【解析】解：面底面BCD，，取DB中点O，则面BCD，就是直线AC与底面BCD所成角．，，，，在中，，在中，．直线AC与底面BCD所成角的大小为．16.如图，在矩形ABCD中，，将沿折起，使得D折起的位置为，且在平面ABC的射影恰好落在AB上，则直线与平面ABC所成角的正弦值为BA．B．C．D．【解析】设在平面ABC的射影为O，则又因为，所以平面，，即，，，，即，在直角三角形中由等面积可得：，，直线与平面ABC所成角的正弦值为．17.如图，在三棱锥中，底面ABC为等边三角形，，，平面平面ABC，则S C与平面ABC所成角的大小是______ ．【答案】【解析】取AB的中点O，连接SO，CO，底面ABC为等边三角形，，，，面平面ABC，平面ABC，即是SC与平面ABC所成的角，，，，，，则直角三角形SOC中，，则，故答案为：．18.如图，二面角的大小是，线段，AB与l所成的角为则AB与平面所成的角的正弦值是______．【答案】【解析】过点A作平面的垂线，垂足为C，在内过C作l的垂线垂足为D∠为二面角的平面角，为连接AD，有三垂线定理可知AD BD⊥，故ADC又由已知，∠为AB与平面所成的角连接CB，则ABC设，则，；故答案为．19.★在三棱锥中，平面，，，则直线与平面所成角的大小为__________．【答案】【解析】作AD⊥PC，连接BD，∵P A⊥平面ABC，BC⊂平面ABC，∴P A⊥BC，∵AC⊥BC，P A∩AC＝A，∴BC⊥平面P AC，∵AD⊂平面P AC，∴BC⊥AD，∵AD⊥PC，BC∩PC＝C，∴AD⊥平面PBC，∴∠ABD为AB与平面PBC所成角，在直角△P AC中，由等面积可得AD＝＝，在直角△ADB中，sin∠ABD＝＝=，∠ABD=∴AB与平面PBC所成的角为，故答案为：．三、面面角20.如图，锐二面角的棱上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于已知，，，则锐二面角的平面角的余弦值是BA．B．C．D．【解析】过B点作，且．，．，，是二面角的平面角，且面DBE，，．，，，．21.在三棱锥中，平面，已知，则二面角的平面角是（ D ）A．B．C．D．【解析】因为平面⊂平面，∠即为二面角的平面角，又，所以，故为直角三角形，∠，二面角的平面角是．22.正四棱锥(顶点在底面的射影是底面正方形的中心)的体积为12，底面对角线的长为，则侧面与底面所成的二面角为(C)A．30°B．45°C．60°D．90°23.在等腰Rt△ABC中，AB＝BC＝1，M为AC的中点，沿BM把它折成二面角，折后A与C的距离为1，则二面角C－BM－A的大小为(C)A．30°B．60°C．90°D．120°【解析】如图，由A ′B ＝BC ＝1，∠A ′BC ＝90°知A ′C ．∵M 为A ′C 的中点，∴MC ＝AM ＝2，且CM ⊥BM ，AM ⊥BM ， ∴∠CMA 为二面角C －BM －A 的平面角．∵AC ＝1，MC ＝MA ＝2，∴MC 2＋MA 2＝AC 2，∴∠CMA ＝90°． 24. 如图所示,四边形ABCD 中,AD ∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD 沿BD 折起,使平面ABD ⊥平面BCD,构成四面体A-BCD,则在四面体A-BCD 中,下列说法正确的是( D )A ．平面ABD ⊥平面ABCB ．平面ADC ⊥平面BDCC ．平面ABC ⊥平面BDCD ．平面ADC ⊥平面ABD【解析】因为,,45,90AD BC AD AB BCD BAD =∠=︒∠=︒，所以45ABD ADB ∠=∠=︒，所以90BDC ∠=︒，所以BD CD ⊥，又平面ABD ⊥平面BCD ，平面ABD ∩平面BCD BD =, CD ⊂平面BCD ，所以CD ⊥平面ABD ，又CD ⊂平面ADC ，所以平面ADC ⊥平面ABD ．25. 等腰直角△ABC 中，AB =BC =1，M 为AC 的中点，沿BM 把△ABC 折成二面角，折后A与C 的距离为1，则二面角C —BM —A 的大小为_____________．【答案】【解析】结合题意可知 ,∠∠ ∠ ∠所以 ,而发现所以∠ ,结合二面角的找法:如果两平面内两直线分别垂直两平面交线,则该两直线的夹角即为所求二面角,故∠为所求的二面角,为26.如图，正三棱柱中，各棱长都相等，则二面角的平面角的正切值为DA．B．C．1 D．27.三棱锥的两侧面PAB、PBC都是边长为2的正三角形，，则二面角的大小为AA．B．C．D．【解析】取PB中点M，连接AM，CM，∆PAB、∆PBC都是边长为2的正三角形，，，则∠AMC为二面角的平面角．在中，由，可得，同理可得，在中，由，得．二面角的大小为．。

高三立体几何大题线面角练习

高三立体几何大题线面角练习介绍:立体几何是数学中的一个重要分支，主要研究物体的形状和空间位置关系。

高三学生在准备高考时，需要熟练掌握立体几何的相关知识和解题方法。

本文档为高三学生提供一个包含线面角练题的大题集，旨在帮助学生加深对立体几何的理解并提升解题能力。

大题一: 平面与立体的关系题目: 已知一个平面与一个立方体的三个面相交，求证该平面与立方体的其他三个面也相交。

解析:考虑立方体的性质，每个顶点都是三个面的交点。

假设已知的平面与立方体的三个面相交，将其中的三个交点标记为$A$，$B$和$C$。

由于平面与立方体的其他三个面都经过$A$，$B$和$C$，所以可以得出结论：该平面与立方体的其他三个面也相交。

大题二: 线面角的计算题目: 在一个正方体中，一个角所在的三条边分别与三个不同的面平行，已知其中两个面的夹角为$60^\circ$，求该角的大小。

解析:设该角所在的三条边分别为$AB$，$AC$和$AD$，与三个面分别平行。

已知$AC$与$AD$所在的两个面的夹角为$60^\circ$，即$∠CAD=60^\circ$。

由于正方体的每个内角都是$90^\circ$，所以可知$∠BAD=180^\circ - ∠CAD - ∠ACD = 180^\circ - 60^\circ -90^\circ =30^\circ$。

因此，该角的大小为$30^\circ$。

大题三: 空间几何的应用题目: 已知一个球塔高$10\sqrt{3}$，上底半径为$10$，下底半径为$8$，求球与塔的交线的长度。

解析:根据题意，球与塔的交线可以看作是球与一个圆台的交线，而圆台的上下底半径分别为$10$和$8$，高为$10\sqrt{3}$。

通过计算，可以得到圆台的斜高为$2\sqrt{3}$。

根据球和圆台的交线特性，可以计算出交线的长度为$\sqrt{3}$倍的圆台底面周长。

因此，球与塔的交线的长度为$2\sqrt{3}$倍的$\pi \times 10 = 20\pi\sqrt{3}$。

空间角(空间线线、线面、面面成角问题)练习题(答案)

空间角练习题1．二面角是指（ D ）A 两个平面相交所组成的图形B 一个平面绕这个平面内一条直线旋转所组成的图形C 从一个平面内的一条直线出发的一个半平面与这个平面所组成的图形D 从一条直线出发的两个半平面所组成的图形2．平面α与平面β、γ都相交，则这三个平面可能有（ D ）A 1条或2条交线B 2条或3条交线C 仅2条交线D 1条或2条或3条交线3．在300的二面角的一个面内有一个点，若它到另一个面的距离是10，则它到棱的距离是( B )A 5B 20 CD4．在直二面角α-l-β中，RtΔABC在平面α内，斜边BC在棱l上，若AB 与面β所成的角为600，则AC与平面β所成的角为（ A ）A 300B 450 C600 D 12005．如图，射线BD、BA、BC两两互相垂直，AB=BC=1，BD=，则弧度数为的二面角是（ A ）A D-AC-B B A-CD-BC A-BC-D D A-BD-C6．△ABC在平面α的射影是△A1B1C1，如果△ABC所在平面和平面α成θ角，有（B）A S△A1B1C1=S△ABC·sinθB S△A1B1C1=S△ABC·cosθC S△ABC =S△A1B1C1·sinθD S△ABC=S△A1B1C1·cosθ7．如图，若P为二面角M-l-N的面N内一点，PB⊥l，B为垂足，A为l上一点，且∠PAB=α，PA与平面M所成角为β，二面角M-l-N的大小为γ，则有（ B ）A sinα=sinβsinγB sinβ=sinαsinγC sinγ=sinαsinβD 以上都不对8．在600的二面角的棱上有两点A、B，AC、BD分别是在这个二面角的两个面内垂直于AB的线段，已知：AB=6，AC=3，BD=4，则CD= 7cm 。

9．已知△ABC和平面α，∠A=300，∠B=600，AB=2，ABα，且平面ABC与α所成角为300，则点C到平面α的距离为。

线面角、二面角练习(含答案)

(D) 证明 , 4B L PD; G)若 P4 = PD = AB, /APD = 90“, 设 Q 为 PB 中点 , 求直线 4Q 与平面 PBC 所成角的余弦值
.(10分 ) 如图 , 在四楂锥 P 一 4BC 丁中 , 底面 4BC是D矩形 ,M7 是 P4 的中点 ,PD 平 _ 面 4L BCD,
心的 M L DN, 即异面直线 4M 与 DN 所成角大小为 90., 故选 D.
2. ( AP4D 为直角三角形 , 且 P4 = 4D, …LP4D 二 90., 即 P4 L 4D, 四边形 4B8为C正 D方形 , - DA L BA, N PANBA= 4, P4 c 面 P4B,PB C 面 P4B,
A. 307
B. 45°
二、解答题 ( 共 14 小题 , 每小题 10 分 , 共 140分 )
C. 60°
D. 90°
2.(分1) 0如图 , 平面 P4D L 平面 4BCD,4B为 C正D方形 ,AP 是 4 直角D 三角形 , 且 P4 = 4D 二 2, E
、友、G 分别是线段 P4、PD、CD 的中点。
(D) 证明 , PB平 |面 4BC ) 设二面角 D - 4F - C 为 60“,=4P 1,4一Dv, 求三棒锥丁一 4CD 的体积 .
三、填空题 ( 共 1 小题 ,每小题 5 分 , 共 5 分 )
16.(5 分 ) 已知长方体 A4BCD 一 4 BCLD 中 ,4B 万 2,4D = AA; 三 1, 则的线 BDu 与平面