第六章——简单的超静定问题
材料力学 简单的超静定问题
FN 3 l 3 E 3 A3
FN1
FN3
a a A
A1 FN2
l3
FN 3l3 E 3 A3
(3)
(4)补充方程：由几何方程和物理方程得：
F N 1l1 E1 A1
2
cos a
(5)联解（1）、（2）、（3）式，得:
FN 1 FN 2 E1 A1 F cos a 2 E1 A1 cos a E 3 A3
第六章
简单的超静定问题
1
第六章
§6-1
§6-2
简单的超静定问题
超静定问题及其解法
拉压超静定问题
§6-3 §6-4
扭转超静定问题 简单超静定梁
2
§6-1
超静定问题及其解法
1.单纯依靠静力平衡方程能够确定全部未知力（支反 力、内力）的问题，称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力（支反 力、内力）的问题，称为超静定问题。 相应的结构称为超静定结构。
3
F N3 A3 9F 14 A [ ]
F
[F ]
14 9
14 9
[ ] A
[ ] A
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢 加固，角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa，弹性模量分别为E1=200GPa 和 E2 =10GPa；求许可载荷P。 解：（1）以压头为研究对象, 设每 个角钢受力为FN1，木柱受力为FN2.
14
B
1
D
C
3 2
(2) 几何方程
l1 ( l 3 ) cos a
7第六章简单的超静定问题
E3 A3
FN 1
FN 2
2COS
F E3 A3
EACOS
2
解超静定问题的步骤
（1）列 静力平衡方程 确定超静定次数； （2）根椐变形相容条件建立变形几何方程。变形几何方程的
个数与超静定次数相等； （3）将 物理方程 （胡克定律）代入变形几何方程得补充方程； （4）联立补充方程与静力平衡方程求解。
第六章
简单的超静定问题
• 超静定问题及其解法 • 拉压超静定问题 • 扭转超静定问题 • 简单超静定梁
§6—1 超静定问题及其解法
1，静定问题 约束反力或杆件的内力可以用静力平衡方程求出，这种情 况称作静定问题。
2，超静定问题
只凭静力平衡方程已不能解出全部未知力，这种情况称做超 静定问题。
F
A
C
2
3
1
A
B
C
P 40
80
FN1
FN2
80
FN3
P
几何方程
2 l2 l1 l3
物理方程
l1
F N1l1 EA
l 2
F N2l2 EA
l3
F N3l3 EA
2
3
1
A
B
C
l1
P l2
l3
4080807575补充方程
2 F N 2 l2 F N1l1 F N 3 l3 EA EA EA
2
3
1
A
B
2
A
F
B
D
C
3 1
2
A
FN1
FN3
FN2
αα
A
F
F
解：列静力平衡方程
F N1 F N2
材料力学(I)第六章(配孙训方版)
4. 将补充方程与平衡方程联立求解得：
FN1 FN2
eEA l
1
1 2
EA
，
E3 A3
FN3
eE3 A3 l
1
1 E3 A3
2EA
所得结果为正，说明原先假定杆1,2的装配内力为拉
力和杆3的装配内力为压力是正确的。
载Me和“多余”未知力偶矩MB，如图b；它应满足的位移 相容条件为
BMe
BM B
注：这里指的是两个扭转角的绝对值相等。
33
材料力学Ⅰ电子教案
第六章 简单的超静定问题
3. 根据位移相容条件利用物理关系得补充方程：
Mea M Bl GI p GI p
由此求得“多余”未知力，亦即约束力偶矩MB为
材料力学Ⅰ电子教案
第六章 简单的超静定问题
在基本静定系上加
B
C
D
上原有荷载及“多
1
2
余”未知力
FN3
并使“多余”约束
A
A
处满足变形(位移)
ΔA'
相容条件
A'
ΔA
A
F
FN3
相当系统 (equivalent system)
6
材料力学Ⅰ电子教案
第六章 简单的超静定问题
B 1
C 2
FN3
第六章 简单的超静定问题
求算FN3需利用位移(变形)相容条件 (图a)
AA AA e
列出补充方程
FN3l3 E3 A3
FN3l1
2 E1 A1cos2
6-简单超静定问题
FN 1l FN 3l cos EA cos EA FN 1 FN 3 cos 2
5、求解方程组得
FN 1 FN 2
F cos 2 1 2 cos 3
FN 3
F 1 2 cos 3
目 录
二、装配应力
构件的加工误差是难以避免的。对静定结构，加工误 差只是引起结构几何形状的微小变化，而不会在构件内引 起应力。但对静不定结构，加工误差就要在构件内引起应 力。这种由于装配而引起的应力称为装配应力。 装配应力是结构构件在载荷作用之前已具有的应力， 因而是一种初应力。
超静定结构中才有温度应力。
目 录
解题思路： 平衡方程:RA = RB 变形几何关系: 物理关系:
(t 时)
lT lF
lT l t
RB L
RB l lF EA
EA Lt
补充方程:
联立求解: RA RB EAt
EAt t Et A
目 录
一静定问题及超静定问题三基本静定系或相当系统是一个静定结构该结构上作用有荷载和多余约束力61超静定问题及其解法61超静定问题及其解法二多余约束及多余约束力在静定结构的基础上增加的约束
第六章
简单的超静定问题
§6–1 概述
§6–2 §6–3 §6–4 拉压超静定问题 扭转超静定问题 简单超静定梁
目的与要求：
M
max
WZ
32 M
d
max 3
76.4MPa
目 录
例题
结构如图示,设梁AB和CD的弯曲刚度EIz相同. 拉杆BC的拉压刚度EA为已知,求拉杆BC的轴力.
a
C
将杆CB移除，则AB,CD均为静定结构， 杆CB的未知轴力FN作用在AB,CD梁上。为1 D 次超静定。
第六章简单的超静定问题
第六章简单的超静定问题知识要点1．超静定问题的概念（1）静定问题结构或结构的约束反力或内力均能通过静力学平衡方程求解的问题。
（2）超静定问题结构或构件的约束反力或内力不能仅凭静力学平衡方程全部求解的问题。
（3）超静定次数未知力(约束反力或内力)数超过独立的静力平衡方程书的数目。
（4）多余约束力超静定问题中，多余维持静力平衡所必需的约束（支座或杆件）。
（5）多余未知力与多余（支座或杆件）相应的支座反力或内力。
（6）基本静定系在求解静定结构时，解除多余约束，并代之以多余未知力，从而得到一个作用有荷载和多余未知力的静定结构，称之为原超静定结构的基本体静定系。
2．静不定问题的解题步骤（1） 静力平衡条件——利用静力学平衡条件，列出平衡方程。
（2） 变形相容条件——根据结构或杆间变形后应保持连续的变形相容条件，作出位移图，由位移图的几何关系列出变形间的关系方程。
（3） 物理关系——应用胡克定律列出力与变形间的关系方程。
（4） 将物理关系代入变形相容条件，得补充方程 。
补充方程和静力平衡方程，二者方程数之和正好等于未知数的个数，联立平衡方程和补充方程，求解全部未知数。
习题详解6-1 试作题6-1图（a ）所示等直杆的轴力图。
解 解除题6-1图（a ）所示等直杆的约束，代之以约束反力，作受力图，如题6-1图（b ）所示。
由静力学平衡条件,03,0=-+=∑F F F FB A Y和变形协调条件0=∆+∆+∆DB CD AC 并将()EAa F EA a F F EA a F B DB A CD A AC -=∆-=∆=∆,22,代入式②，可得 联立式①，③，解得45,47F F F F B A == 轴力如图6-1图（c ）所示6-2 题6-2图（a ）所示支架承受荷载F=10 kN,1,2,3各杆由同一材料制成，其横截面面积分别为232221200,150,100mm A mm A mm A ===。
试求各杆的轴力。
《材料力学》第6章 简单超静定问题 习题解
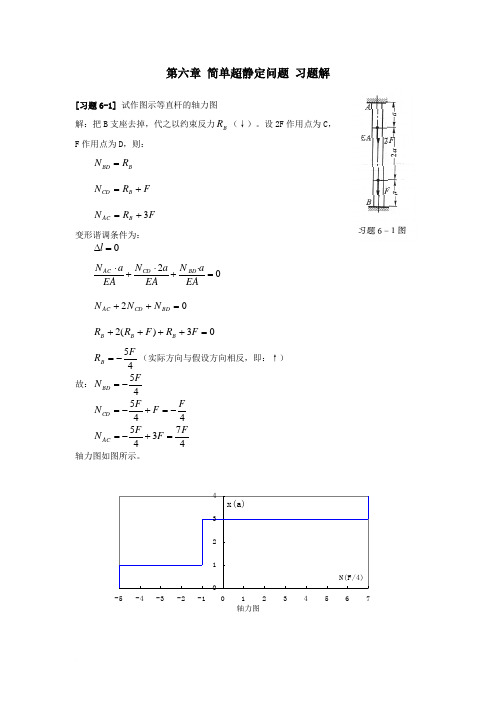
第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解：把B 支座去掉，代之以约束反力B R （↓）。
设2F 作用点为C ， F 作用点为D ，则：B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为：0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=（实际方向与假设方向相反，即：↑） 故：45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=，1，2，3各杆由同一种材料制成，其横截面面积分别为21100mm A =，22150mm A =，23200mm A =。
试求各杆的轴力。
解：以节点A 为研究对象，其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件：设A 节点的水平位移为x δ，竖向位移为y δ，则由变形协调图（b ）可知：00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31，则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得：kN N 45.81=；kN N 68.22=；kN N 54.111=（方向如图所示，为压力，故应写作：kN N 54.111-=）。
第六章简单的超静定问题
2 . 1 F 2 8 F 1 2 4 0 1 . 5 1 2 . 5 4 6 . 2 1 2 N 0
L1
F138.52kN
F 2 1.1 2k9 6N
计算1，2杆的正应力
L2
1
F1 A1
33188.0.550M 2m01mP023Na
1 F1
F
2m
列静力平衡方程 MA0
F12F2F
变形协调方程2 m F F L1 1 24 mm F 2 L24m
2m A
L2 2L1
4m
F2
1m 2
L1
F1L1 E1A!
gTL1
F2L2 E2A2
L2tTEFL222LA222(EFt11LA1T! L2gTL1)
B 变形协调方程
a
aF
FN1
FN 2
A
B
C L1
L2
a
aF
2L1L2
2 FN1L FN2L E1A1 E2A2
FN1
2F
14E2A2
E1A1
FN2
4F 4E1A1 E2A2
L
1.8L LDB
2.拉压超静定问题 图示刚性梁AB受均布载荷作用，梁在A端铰支，在B点和C
例题
6.2
作折杆的剪力和弯矩图
14.14
14.14
A
1
14.14
2
14.14
14.14kN
14.14kN
F
14.14
F s ( kN )
M ( kNm )
例题
求图示简单钢架自由端C的水平位移和垂直位移，设EI为 常数
材料力学(I)第六章
(2) 几何方程
L2
( L3 ) cos L1
材料力学(Ⅰ)电子教案
简单的超静定问题
15
(3)、物理方程及补充方程：
FN 1L1 FN 3 L3 ( ) cos E1 A1 E3 A3
(4) 、解平衡方程和补充方程，得:
FN1 FN 2
E1 A1 cos2 L3 1 2 cos3 E1 A1 / E3 A3
FN 1L FN 3 L 得: cos E1 A1 cos E3 A3
5）联立①、④求解：
FN ! F
④
E 3 A3 2 co s E1 A1 co s2
FN 3
F E1 A1 1 2 co s3 E A
材料力学(Ⅰ)电子教案
简单的超静定问题
[例2-19]刚性梁AD由1、2、3杆悬挂，已知三杆材料 相同，许用应力为[σ ]，材料的弹性模量为 E，杆长 均为l，横截面面积均为A，试求各杆内力。
5
1.比较变形法 把超静定问题转化为静定问题解，但 必须满足原结构的变形约束条件。
[例2-16] 杆上段为铜,下段为钢杆，
E1 A1
A
1
上段长 1 , 截面积A1 , 弹性模量E1 下段长 2 , 截面积A2 , 弹性模量E2
杆的两端为固支,求两段的轴力。
C
E 2 A2
F
FB
B
2
（1）选取基本静定结构（静定基如图），B 解： 端解除多余约束，代之以约束反力RB
2E1 A1 cos3 FN 3 3 L3 1 2 cos E1 A1 / E3 A3
例2-22
材料力学(Ⅰ)电子教案
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
未知力个数与平衡方程数之差,称为超静定次数或静不定次数。
求解超静定问题,需要综合考察结构的平衡,变形协调和物理等三个方面。
§6—2 拉压超静定问题
一、静定与超静定问题
章 节
名 称
学时
备注
第六章
简单的超静定问题
1 教学目标：
2 教学内容：
3 重点、难点分析及解决策略
4教学方法：
5 教学进程：
§6—1 超静定问题及其解法
未知力个数等于独立的平衡方程数目,则仅由平衡方程即可解出全部未知力,这类问题称为静定问题,相应的结构称为静定结构。
未知力个数多于独立的平衡方程数目,则仅由平衡方程无法确定全部未知力,这类问题称为超静定问题或静不定问题,相应的结构称为超静定结构或静不定结构。
1、静定问题
杆件的轴力可以用静力平衡条件求出,这种情况称作静定问题。
2、超静定问题
只凭静力平衡方程已不能解出全部未知力，这种情况称做超静定问题。
二、超静定问题求解方法
1、超静定的次数
未知力数超过独立平衡方程数的数目,称作超静定的次数.
n=未知力的个数-独立平衡பைடு நூலகம்程的数目
2、求解超静定问题的步骤
(1)确定静不定次数；列静力平衡方程
(2)根据变形协调条件列变形几何方程
(3)将变形与力之间的关系（胡克定律）代入变形几何方程得补充方程
(4)联立补充方程与静力平衡方程求解