人教版八上数学整式的乘除及因式分解专题培优
人教版八年级数学上册 整式的乘法与因式分解单元培优测试卷

人教版八年级数学上册 整式的乘法与因式分解单元培优测试卷一、八年级数学整式的乘法与因式分解选择题压轴题(难)1.将多项式24x +加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( ) A .4-B .±4xC .4116xD .2116x 【答案】D【解析】【分析】分x 2是平方项与乘积二倍项,以及单项式的平方三种情况,根据完全平方公式讨论求解.【详解】解:①当x 2是平方项时,4士4x+x ²=(2士x )2,则可添加的项是4x 或一4x ; ②当x 2是乘积二倍项时,4+ x 2+4116x =(2+214x )2,则可添加的项是4116x ; ③若为单项式,则可加上-4.故选:D.【点睛】本题考查了完全平方式,比较复杂,需要我们全面考虑问题,首先考虑三个项分别充当中间项的情况,就有三种情况,还有就是第四种情况加上一个数,得到一个单独的单项式,也是可以成为一个完全平方式,这种情况比较容易忽略,要注意.2.已知a=2012x+2011,b=2012x+2012,c=2012x+2013,那么a 2+b 2+c 2—ab -bc -ca 的值等于( )A .0B .1C .2D .3【答案】D【解析】【分析】首先把a 2+b 2+c 2﹣ab ﹣bc ﹣ac 两两结合为a 2﹣ab +b 2﹣bc +c 2﹣ac ,利用提取公因式法因式分解,再把a 、b 、c 代入求值即可.【详解】a 2+b 2+c 2﹣ab ﹣bc ﹣ac=a 2﹣ab +b 2﹣bc +c 2﹣ac=a (a ﹣b )+b (b ﹣c )+c (c ﹣a )当a =2012x +2011,b =2012x +2012,c =2012x +2013时,a -b =-1,b -c =-1,c -a =2,原式=(2012x +2011)×(﹣1)+(2012x +2012)×(﹣1)+(2012x +2013)×2=﹣2012x ﹣2011﹣2012x ﹣2012+2012x ×2+2013×2=3.故选D .【点睛】本题利用因式分解求代数式求值,注意代数之中字母之间的联系,正确运用因式分解,巧妙解答题目.3.若999999a =,990119b =,则下列结论正确是( ) A .a <bB .a b =C .a >bD .1ab =【答案】B【解析】 ()9999999909990909119991111===99999a b +⨯⨯==⨯, 故选B.【点睛】本题考查了有关幂的运算、幂的大小比较的方法,一般说来,比较几个幂的大小,或者把它们的底数变得相同,或者把它们的指数变得相同,再分别比较它们的指数或底数.4.若3x y -=,则226x y y --=( )A .3B .6C .9D .12 【答案】C【解析】【分析】由3x y -=得x=3+y ,然后,代入所求代数式,即可完成解答.【详解】解:由3x y -=得x=3+y代入()2222369669y y y y y y y +--=++--=故答案为C.【点睛】本题主要考查了完全平方公式的应用,灵活对代数式进行变形是解答本题的关键.5.已知三角形三边长为a 、b 、c ,且满足247a b -=, 246b c -=-, 2618c a -=-,则此三角形的形状是( )A .等腰三角形B .等边三角形C .直角三角形D .无法确定【答案】A【解析】解:∵a 2﹣4b =7,b 2﹣4c =﹣6,c 2﹣6a =﹣18,∴a 2﹣4b +b 2﹣4c +c 2﹣6a =7﹣6﹣18,整理得:a 2﹣6a +9+b 2﹣4b +4+c 2﹣4c +4=0,即(a ﹣3)2+(b ﹣2)2+(c ﹣2)2=0,∴a =3,b =2,c =2,∴此三角形为等腰三角形.故选A .点睛:本题考查了因式分解的应用,解题的关键是正确的进行因式分解.6.计算,得( ) A . B .C .D .【答案】C【解析】【分析】 直接提取公因式(-3)m-1,进而分解因式即可.【详解】(-3)m +2×(-3)m-1=(-3)m-1(-3+2)=-(-3)m-1.故选C .【点睛】此题主要考查了提取公因式法分解因式,正确分解因式是解题关键.7.规定一种运算:a*b=ab+a+b ,则a*(﹣b )+a*b 的计算结果为( )A .0B .2aC .2bD .2ab【答案】B【解析】【分析】【详解】解:∵a*b=ab+a+b∴a*(﹣b )+a*b=a (﹣b )+a -b+ab+a+b=﹣ab+a -b+ab+a+b=2a故选B .考点:整式的混合运算.8.若(x 2-x +m )(x -8)中不含x 的一次项,则m 的值为( )A .8B .-8C .0D .8或-8【答案】B【解析】(x 2-x +m )(x -8)=322328889(8)8x x mx x x m x x m x m -+-+-=-++-由于不含一次项,m+8=0,得m=-8.9.下列等式由左边向右边的变形中,属于因式分解的是 ( )A .x 2+5x -1=x(x+5)-1B .x 2-4+3x=(x+2)(x -2)+3xC .(x+2)(x -2)=x 2-4D .x 2-9=(x+3)(x -3)【答案】D【解析】【分析】根据因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,判断求解.【详解】解:A 、右边不是积的形式,故A 错误;B 、右边不是积的形式,故B 错误;C 、是整式的乘法,故C 错误;D 、x 2-9=(x+3)(x -3),属于因式分解.故选D .【点睛】此题主要考查因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.10.将多项式241x +加上一个单项式后,使它能成为另一个整式的完全平方,下列添加单项式错误的是( )A .4xB .4x -4C .4x 4D .4x -【答案】B【解析】【分析】完全平方公式:()222=2a b a ab b +++,此题为开放性题目.【详解】设这个单项式为Q ,如果这里首末两项是2x 和1这两个数的平方,那么中间一项为加上或减去2x 和1积的2倍,故Q=±4x ;如果这里首末两项是Q 和1,则乘积项是22422x x =⋅,所以Q=44x ;如果该式只有24x 项,它也是完全平方式,所以Q=−1;如果加上单项式44x -,它不是完全平方式故选B.【点睛】此题考查完全平方式,解题关键在于掌握完全平方式的基本形式.二、八年级数学整式的乘法与因式分解填空题压轴题(难)11.若4x 2+20x + a 2是一个完全平方式,则a 的值是 __ .【答案】±5【解析】225,5a a ==±12.计算(-3x 2y)•(13xy 2)=_____________. 【答案】33x y -【解析】【分析】 根据单项式乘以单项式的法则计算即可.【详解】原式=(-3)×13x 2+1y 1+2= -x 3y 3 故答案为-x 3y 3【点睛】 本题主要考查单项式乘以单项式的法则.要准确把握法则是解答此题的关键.13.已知a m =3,a n =2,则a 2m ﹣n 的值为_____.【答案】4.5【解析】分析:首先根据幂的乘方的运算方法,求出a 2m 的值;然后根据同底数幂的除法的运算方法,求出a 2m-n 的值为多少即可.详解:∵a m =3,∴a 2m =32=9,∴a 2m-n =292m n a a ==4.5. 故答案为:4.5. 点睛:此题主要考查了同底数幂的除法法则,以及幂的乘方与积的乘方,同底数幂相除,底数不变,指数相减,要熟练掌握,解答此题的关键是要明确:①底数a≠0,因为0不能做除数;②单独的一个字母,其指数是1,而不是0;③应用同底数幂除法的法则时,底数a 可是单项式,也可以是多项式,但必须明确底数是什么,指数是什么.14.分解因式6xy 2-9x 2y -y 3 = _____________.【答案】-y(3x -y)2【解析】【分析】先提公因式-y ,然后再利用完全平方公式进行分解即可得.【详解】6xy 2-9x 2y -y 3=-y(9x 2-6xy+y 2)=-y(3x-y)2,故答案为:-y(3x-y)2.【点睛】本题考查了利用提公因式法与公式法分解因式,熟练掌握因式分解的方法及步骤是解题的关键.因式分解的一般步骤:一提(公因式),二套(套用公式),注意一定要分解到不能再分解为止.15.请看杨辉三角(1),并观察下列等式(2):根据前面各式的规律,则(a+b)6= .【答案】a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.【解析】【分析】通过观察可以看出(a+b)6的展开式为6次7项式,a的次数按降幂排列,b的次数按升幂排列,各项系数分别为1、6、15、20、15、6、1.【详解】通过观察可以看出(a+b)6的展开式为6次7项式,a的次数按降幂排列,b的次数按升幂排列,各项系数分别为1、6、15、20、15、6、1.所以(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.16.分解因式:4ax2-ay2=________________.【答案】a(2x+y)(2x-y)【解析】【分析】首先提取公因式a,再利用平方差进行分解即可.【详解】原式=a(4x2-y2)=a(2x+y)(2x-y),故答案为a(2x+y)(2x-y).【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.17.分解因式:x2﹣1=____.【答案】(x+1)(x﹣1).【解析】试题解析:x 2﹣1=(x+1)(x ﹣1).考点:因式分解﹣运用公式法.18.若2x+5y ﹣3=0,则4x •32y 的值为________.【答案】8【解析】∵2x+5y ﹣3=0,∴2x+5y=3,∴4x •32y =(22)x ·(25)y =22x ·25y =22x+5y =23=8, 故答案为:8.【点睛】本题主要考查了幂的乘方的性质,同底数幂的乘法,转化为以2为底数的幂是解题的关键,整体思想的运用使求解更加简便.19.分解因式:3x 2-6x+3=__.【答案】3(x-1)2【解析】【分析】先提取公因式3,再对余下的多项式利用完全平方公式继续分解.【详解】 ()()22236332131x x x x x -+=-+=-.故答案是:3(x-1)2.【点睛】考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.20.已知8a b +=,224a b =,则222a b ab +-=_____________. 【答案】28或36.【解析】【分析】【详解】解:∵224a b =,∴ab=±2.①当a+b=8,ab=2时,222a b ab +-=2()22a b ab +-=642﹣2×2=28; ②当a+b=8,ab=﹣2时,222a b ab +-=2()22a b ab +-=642﹣2×(﹣2)=36; 故答案为28或36.【点睛】本题考查完全平方公式;分类讨论.。
2020年人教版八年级数学上册 章节专项提高练习《整式的乘除与因式分解》(含答案)

2020年人教版八年级数学上册 章节专项提高练习《整式的乘除与因式分解》1.若(x ﹣2)(x 2+ax+b)的积中不含x 的二次项和一次项,求(2a+b+1)(2a ﹣b ﹣1)﹣(a+2b)(﹣2b+a)+2b 的值.2.(1)如图是用4个全等的长方形拼成的一个“回形”正方形,图中阴影部分面积用2种方法表示可得一个等式,这个等式为 .(2)若(4x ﹣y)2=9,(4x+y)2=169,求xy 的值.3.比较下列四个算式结果的大小(在横线上填“>”“<”或“=”).(1)42+52_______2×4×5;(2)(-1)2+22_______2×(-1)×2;(3)(-3)2+312______2×(-3)×31; (4)32+32_______2×3×3;(5)请通过观察归纳,写出反映这种规律的一般结论.4.观察下列各式的规律:(a﹣b)(a+b)=a2﹣b2(a﹣b)(a2+ab+b2)=a3﹣b3(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…可得到(a﹣b)(a2016+a2015b+…+ab2015+b2016)= .5.在日历上,我们发现某些数会满足一定的規律,比如2016年1月份的日历,我们设计这样的算法:任意选择其中的2×2方框,将方框中4个位置上的数先平方,然后交叉求和,再相减请你按照这个算法完成下列计算,并回答以下问题[2016年1月份的日历](1)计算:(12+92)﹣(22+82)= ,﹣= ,自己任选一个有4个数的方框进行计算 (2)通过计算你发现什么规律,并说明理由.6.阅读:已知x2y=3,求2xy(x5y2-3x3y-4x)的值.分析:考虑到x,y的可能值较多,不能逐一代入求解,故考虑整体思想,将x2y=3整体代入.解:2xy(x5y2-3x3y-4x)=2x6y3-6x4y2-8x2y=2(x2y)3-6(x2y)2-8x2y=2×33-6×32-8×3=-24.你能用上述方法解决以下问题吗?试一试!已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值.7.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数.(1)28和2012这两个数是神秘数吗?为什么?(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?8.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)图1中阴影部分面积为 ,图2中阴影部分面积为 ,对照两个图形的面积可以验证 公式(填公式名称)请写出这个乘法公式 .(2)应用(1)中的公式,完成下列各题:①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.9.在形如a b=N的式子中,我们已经研究过两种情况:已知a和b求N,这是乘方运算:已知b 和N求a,这是开方运算,现在我们研究第三种情况:已知a和N求b,我们称这种运算为对数运算.定义:如果23=8,所以log28=3:因为32=9,所以log39=2,根据以上信息回答下列问题:(1)计算:log381= ,log33= ,log636= ,log x16=4,则x= .(2)设a x=M,a y=N(a>0,且a≠1,M>0,N>0),猜想log a MN和log a的结果,并证明.(3)计算:①log2(2×4×8×16×32×64);②log3;③log93+log927.10.阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.根据你的观察,探究下面的问题:(1)已知a2+6ab+10b2+2b+1=0,求a﹣b的值;(2)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣6b+11=0,求△ABC的周长;(3)已知x+y=2,xy﹣z2﹣4z=5,求xyz的值.参考答案1.解:(x ﹣2)(x 2+ax+b)=x 3+ax 2+bx ﹣2x 2﹣2ax ﹣2b=x 3+(a ﹣2)x 2+(b ﹣2a)x ﹣2b ,∵(x ﹣2)(x 2+ax+b)的积中不含x 的二次项和一次项,∴a ﹣2=0且b ﹣2a=0,解得:a=2、b=4,(2a+b+1)(2a ﹣b ﹣1)﹣(a+2b)(﹣2b+a)+2b=(2a)2﹣(b+1)2﹣(a 2﹣4b 2)+2b=4a 2﹣b 2﹣2b ﹣1﹣a 2+4b 2+2b=3a 2+3b 2﹣1,当a=2、b=4时,原式=3×22+3×42﹣1=12+48﹣1=59.2.解:(1)(b+a )2﹣(b ﹣a )2=4ab(2)(4x+y )2﹣(4x ﹣y )2=16xy=160,∴xy=10.3.解:(1)>.(2)>.(3)>.(4)=.(5)结论:对于任意有理数a ,b ,都有a 2+b 2≥2ab.当a ≠b 时,a 2+b 2>2ab ;当a=b 时,a 2+b 2=2ab.4.解:(a ﹣b )(a+b )=a 2﹣b 2;(a ﹣b )(a 2+ab+b 2)=a 3﹣b 3;(a ﹣b )(a 3+a 2b+ab 2+b 3)=a 4﹣b 4;…可得到(a ﹣b )(a 2016+a 2015b+…+ab 2015+b 2016)=a 2017﹣b 2017,故答案为:a 2017﹣b 20175.解:(1)(12+92)﹣(22+82)=1+81﹣4﹣64=14﹣=100+324﹣121﹣289=14,(32+112)﹣(42+102)=9+121﹣16﹣100=14,故答案为:14;(2)计算结果等于14,理由是:设最小的数字为n ,则其余三个分别为n+8,n+1,n+7,所以[n 2+(n+8)2]﹣[(n+1)2+(n+7)2]=n 2+n 2+16n+64﹣n 2﹣2n ﹣1﹣n 2﹣14n ﹣49=14.6.原式=-4a 3b 3+6a 2b 2-8ab=-4(ab)3+6(ab)2-8ab,当ab=3时,原式=-4×33+6×32-8×3=-108+54-24=-78.7.解:(1)找规律:2244120=⨯=-, 22124342=⨯=-, 22204564=⨯=-, 22284786=⨯=-, ……2220124503504502=⨯=-,所以28和2012都是神秘数.(2)()()()22222421k k k +-=+,因此由这两个连续偶数22k +和2k 构造的神秘数是4的倍数.(3)由(2)知,神秘数可以表示成()421k +,因为21k +是奇数,因此神秘数是4的倍数,但一定不是8的倍数.另一方面,设两个连续奇数为21n +和21n -,则()()2221218n n n +--=,即两个连续奇数的平方差是8的倍数. 因此,两个连续奇数的平方差不是神秘数.8.解:(1)图1中阴影部分面积为a 2﹣b 2,图2中阴影部分面积为(a+b)(a ﹣b),对照两个图形的面积可以验证平方差公式:a 2﹣b 2=(a+b)(a ﹣b).故答案为:a 2﹣b 2,(a+b)(a ﹣b),平方差,a 2﹣b 2=(a+b)(a ﹣b).(2)①∵x 2﹣4y 2=(x+2y)(x ﹣2y),∴15=3(x ﹣2y),∴x ﹣2y=5;②(2+1)(22+1)(24+1)(28+1)……(264+1)+1=(2﹣1)(2+1)(22+1)(24+1)(28+1)……(264+1)+1=(22﹣1)(22+1)(24+1)(28+1)……(264+1)+1=(24﹣1)(24+1)(28+1)……(264+1)+1=(28﹣1)(28+1)……(264+1)+1=(264﹣1)(264+1)+1=2128﹣1+1=2128.9.解:(1)log 381=log 334=4,log 33=1,log 636=log 662=2,log x 16=4,则x=2;答案为:4;1;2;2;(2)log a MN=log a M+log a N ;log a =log a M ﹣log a N ;证明:log a MN=log a a x •a y =log a a x+y =x+y ;log a M+log a N=x+y ,则log a MN=log a M+log a N ;log a =log a =log a a x ﹣y =x ﹣y ;log a M ﹣log a N=x ﹣y ,则log a =log a M ﹣log a N ;(3)①原式=log 22+log 24+log 28+log 216+log 232+log 264=1+2+3+4+5+6=21;②原式=log 3243﹣log 381=5﹣4=1;③原式=log 93×27=log 981=2.一、综合题10.解:(1)∵a2+6ab+10b2+2b+1=0,∴a2+6ab+9b2+b2+2b+1=0,∴(a+3b)2+(b+1)2=0,∴a+3b=0,b+1=0,解得b=﹣1,a=3,则a﹣b=4;(2)∵2a2+b2﹣4a﹣6b+11=0,∴2a2﹣4a++2+b2﹣6b+9=0,∴2(a﹣1)2+(b﹣3)2=0,则a﹣1=0,b﹣3=0,解得,a=1,b=3,由三角形三边关系可知,三角形三边分别为1、3、3,∴△ABC的周长为1+3+3=7;(2)∵x+y=2,∴y=2﹣x,则x(2﹣x)﹣z2﹣4z=5,∴x2﹣2x+1+z2+4z+4=0,∴(x﹣1)2+(z+2)2=0,则x﹣1=0,z+2=0,解得x=1,y=1,z=﹣2,∴xyz=2.。
人教版八年级数学上册 整式的乘法与因式分解(培优篇)(Word版 含解析)

一、八年级数学整式的乘法与因式分解解答题压轴题(难)1.如图1是一个长为4a 、宽为b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)(1)观察图2请你写出2()a b +、2()a b -、ab 之间的等量关系是______;(2)根据(1)中的结论,若5x y +=,94x y ⋅=,则x y -=______; (3)拓展应用:若22(2019)(2020)7m m -+-=,求(2019)(2020)m m --的值.【答案】(1)22()()4a b a b ab +=-+;(2)4,-4:(3)-3【解析】【分析】(1)观察图2,大正方形由4个矩形和一个小正方形组成,根据面积即可得到他们之间的关系.(2)由(1)的结论可得(x-y) ²=16,然后利用平方根的定义求解即可.(3)从已知等式的左边看,左边配成两数和的平方来求解.【详解】解:(1)由题可得,大正方形的面积2()a b =+,大正方形的面积2()4a b ab =-+,∴22()()4a b a b ab +=-+,(2)∵22()()4x y x y xy +=-+, ∴229()()4254164x y x y xy -=+-=-⨯=, ∴4x y -=或-4, (3)∵22(2019)(2020)7m m -+-=,又2(20192020)m m -+-22(2019)(2020)2(2019)(2020)m m m m =-+-+-- ∴172(2019)(2020)m m =+--∴(2019)(2020)3m m --=-故答案为:(1)22()()4a b a b ab +=-+;(2) 4,-4:(3)-3【点睛】本题通过观察图形发现规律,并运用规律求值,使问题简单化是解题关键.2.我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到()()22322a ab b a b a b ++=++.请回答下列问题:(1)写出图2中所表示的数学等式是 ;(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有x ,y 的式子表示) ; (3)通过上述的等量关系,我们可知: 当两个正数的和一定时,它们的差的绝对值越小,则积越 (填“ 大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越 (填“ 大”或“小”).【答案】(1)22(2)(2)225a b a b a b ab ++=++;(2)22()()4x y x y xy +=-+;(3)大 小【解析】【分析】(1)图2面积有两种求法,可以由长为2a+b ,宽为a+2b 的矩形面积求出,也可以由两个边长为a 与边长为b 的两正方形,及4个长为a ,宽为b 的矩形面积之和求出,表示即可; (2)阴影部分的面积可以由边长为x+y 的大正方形的面积减去边长为x-y 的小正方形面积求出,也可以由4个长为x ,宽为y 的矩形面积之和求出,表示出即可;(3)两正数和一定,则和的平方一定,根据等式224()()xy x y x y =+--,得到被减数一定,差的绝对值越小,即为减数越小,得到差越大,即积越大;当两正数积一定时,即差一定,差的绝对值越小,得到减数越小,可得出被减数越小;【详解】(1)看图可知,22(2)(2)225a b a b a b ab ++=++(2)22()()4x y x y xy +=-+(3)当两个正数的和一定时,它们的差的绝对值越小则积越大;当两个正数的积一定时,它们的差的绝对值越小则和越小.【点睛】本题考点:整式的混合运算,此题考查了整式的混合运算的应用,弄清题意是解本题的关键. 3.(1)填空:()()a b a b -+= ;22()()a b a ab b -++= ;3223()()a b a a b ab b -+++= .(2)猜想:1221()(...)n n n n a b a a b ab b -----++++= (其中n 为正整数,且2n ≥).(3)利用(2)猜想的结论计算:98732222...222-+-+-+.【答案】(1)22a b -,33a b -,44a b -;(2)n n a b -;(3)342.【解析】试题分析:(1)根据平方差公式与多项式乘以多项式的运算法则运算即可;(2)根据(1)的规律可得结果;(3)原式变形后,利用(2)得出的规律计算即可得到结果.试题解析:(1)()()a b a b -+=22a b -;3223()()a b a a b ab b -+++=33a b -;3223()()a b a a b ab b -+++=44a b -;故答案为22a b -,33a b -,44a b -;(2)由(1)的规律可得:原式=n n a b -,故答案为n n a b -;(3)令98732222...222S =-+-+-+,∴987321222...2221S -=-+-+-+-=98732[2(1)](222...2221)3---+-+-+-÷=10(21)3(10241)3341-÷=-÷=,∴S=342.考点:1.平方差公式;2.规律型.4.阅读材料小明遇到这样一个问题:求计算()()()22334x x x +++所得多项式的一次项系数.小明想通过计算()()()22334x x x +++所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.他决定从简单情况开始,先找()()223x x ++所得多项式中的一次项系数,通过观察发现:也就是说,只需用2x +中的一次项系数1乘以23x +中的常数项3,再用2x +中的常数项2乘以23x +中的一次项系数2,两个积相加13227⨯+⨯=,即可得到一次项系数. 延续上面的方法,求计算()()()22334x x x +++所得多项式的一次项系数,可以先用2x +的一次项系数1,23x +的常数项3,34+x 的常数项4,相乘得到12;再用23x +的一次项系数2,2x +的常数项2,34+x 的常数项4,相乘得到16;然后用34+x 的一次项系数3,2x +的常数项223x +的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.参考小明思考问题的方法,解决下列问题:(1)计算()()443x x ++所得多项式的一次项系数为____________________.(2)计算()()()13225x x x +-+所得多项式的一次项系数为_____________.(3)若231x x -+是422x ax bx +++的一个因式,求a 、b 的值.【答案】(1)19;(2)1;(3) a= -6,b= -3.【解析】【分析】(1)根据两多项式常数项与一次项系数乘积的和即为所得多项式一次项系数可得;(2)根据三个多项式中两个多项式的常数项与另一个多项式一次项系数的乘积即为所求可得;(3)由x 4+ax 2+bx+2中4次项系数为1、常数项为2可设另一个因式为x 2+mx+2,根据三次项系数为0、二次项系数为a 、一次项系数为b 列出方程组求出a 、b 的值,可得答案.【详解】解:(1)(x+4)(4x+3)所得多项式的一次项系数为1×3+4×4=19,故答案为:19;(2)()()()13225x x x +-+所得多项式的一次项系数为1×(-2)×5+1×3×5+1×(-2)×2=1, 故答案为:1;(3)由x 4+ax 2+bx+2中4次项系数为1、常数项为2可设另一个因式为x 2+mx+2,则(x 2-3x+1)(x 2+mx+2)=x 4+ax 2+bx+2,13101211(3)321m m a m b ⨯-⨯=⎧⎪∴⨯+⨯+-⨯=⎨⎪-⨯+⨯=⎩解得: 363m a b =⎧⎪=-⎨⎪=-⎩故答案为:a= -6,b= -3.【点睛】本题考查多项式乘多项式,解题关键是熟练掌握多项式乘多项式的运算法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.5.阅读理解:把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.(1)请写出一个六位连接数 ,它 (填“能”或“不能”)被13整除.(2)是否任意六位连接数,都能被13整除,请说明理由.(3)若一个四位连接数记为M ,它的各位数字之和的3倍记为N ,M ﹣N 的结果能被13整除,这样的四位连接数有几个?【答案】(1)证明见解析(2)abcabc 能被13整除(3)这样的四位连接数有1919,2525,3131,一共3个【解析】分析:(1)根据六位连接数的定义可知123123为六位连接数,再将123123进行因数分解,判断得出它能被13整除;(2)设abcabc 为六位连接数,将abcabc 进行因数分解,判断得出它能被13整除; (3)设xyxy 为四位连接数,用含x 、y 的代数式表示M 与N ,再计算M ﹣N ,然后将13M N -表示为77x +7y +3413x y +,根据M ﹣N 的结果能被13整除以及M 与N 都是1~9之间的整数,求得x 与y 的值,即可求解.详解:(1)123123为六位连接数;∵123123=123×1001=123×13×77,∴123123能被13整除;(2)任意六位连接数都能被13整除,理由如下:设abcabc 为六位连接数.∵abcabc =abc ×1001=abc ×13×77,∴abcabc 能被13整除;(3)设xyxy 为四位连接数,则M =1000x +100y +10x +y =1010x +101y ,N =3(x +y +x +y )=6x +6y ,∴M ﹣N =(1010x +101y )﹣(6x +6y )=1004x +95y ,∴13M N -=10049513x y +=77x +7y +3413x y +.∵M ﹣N 的结果能被13整除,∴3413x y +是整数.∵3x +4y 取值范围大于3小于63,所以能被13整除的数有13,26,39,52,∴x =1,y =9;x =2,y =5;x =3,y =1;x =8,y =7;x =9,y =3;x =5,y =6;x =6,y =2;满足条件的四位连接数的3131,2525,6262,9393,8787,5656,1919共7个. 点睛:本题考查了因式分解的应用,整式的运算,理解“连接数”的定义是解题的关键.6.阅读以下文字并解决问题:对于形如222x ax a ++这样的二次三项式,我们可以直接用公式法把它分解成()2x a +的形式,但对于二次三项式2627x x +-,就不能直接用公式法分解了。
人教版数学八上第22讲整式的乘除与因式分解全章复习与巩固(提高)知识讲解

整式的乘除与因式分解全章复习与巩固(提高)【学习目标】1. 掌握正整数幂的运算性质,并能运用它们熟练地进行运算;掌握单项式乘(或除以)单项式、多项式乘(或除以)单项式以及多项式乘多项式的法则,并运用它们进行运算;2. 会推导乘法公式(平方差公式和完全平方公式),了解公式的几何意义,能利用公式进行乘法运算;3. 掌握整式的加、减、乘、除、乘方的较简单的混合运算,并能灵活地运用运算律与乘法公式简化运算;4. 理解因式分解的意义,并感受分解因式与整式乘法是相反方向的运算,掌握提公因式法和公式法(直接运用公式不超过两次)这两种分解因式的基本方法,了解因式分解的一般步骤;能够熟练地运用这些方法进行多项式的因式分解. 【知识网络】【要点梳理】要点一、幂的运算 1.同底数幂的乘法:(m n ,为正整数);同底数幂相乘,底数不变,指数相加.2.幂的乘方: (mn ,为正整数);幂的乘方,底数不变,指数相乘. 3.积的乘方: (n 为正整数);积的乘方,等于各因数乘方的积.4.同底数幂的除法:(a ≠0, mn ,为正整数,并且m n >). 同底数幂相除,底数不变,指数相减.5.零指数幂:()010.a a =≠即任何不等于零的数的零次方等于1.要点诠释:公式中的字母可以表示数,也可以表示单项式,还可以表示多项式;灵活地双向应用运算性质,使运算更加方便、简洁. 要点二、整式的乘法和除法 1.单项式乘以单项式单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. 2.单项式乘以多项式单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.即mc mb ma c b a m ++=++)((c b a m ,,,都是单项式).3.多项式乘以多项式多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即()()a b m n am an bm bn ++=+++.要点诠释:运算时,要注意积的符号,多项式中的每一项前面的“+”“-”号是性质符号,单项式乘以多项式各项的结果,要用“+”连结,最后写成省略加号的代数和的形式.根据多项式的乘法,能得出一个应用比较广泛的公式:()()()2x a x b x a b x ab ++=+++.4.单项式相除把系数、相同字母的幂分别相除作为商的因式,对于只在被除式里出现的字母,则连同它的指数一起作为商的一个因式. 5.多项式除以单项式先把这个多项式的每一项分别除以单项式,再把所得的商相加. 即:()am bm cm m am m bm m cm m a b c ++÷=÷+÷+÷=++ 要点三、乘法公式1.平方差公式:22()()a b a b a b +-=-两个数的和与这两个数的差的积,等于这两个数的平方差.要点诠释:在这里,a b ,既可以是具体数字,也可以是单项式或多项式.平方差公式的典型特征:既有相同项,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方.2. 完全平方公式:()2222a b a ab b +=++;2222)(b ab a b a +-=-两数和 (差)的平方等于这两数的平方和加上(减去)这两数乘积的两倍.要点诠释:公式特点:左边是两数的和(或差)的平方,右边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍. 要点四、因式分解把一个多项式化成几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.因式分解的方法主要有: 提公因式法, 公式法, 分组分解法, 十字相乘法, 添、拆项法等.要点诠释:落实好方法的综合运用:首先提取公因式,然后考虑用公式;两项平方或立方,三项完全或十字; 四项以上想分组,分组分得要合适; 几种方法反复试,最后须是连乘式; 因式分解要彻底,一次一次又一次.【典型例题】类型一、幂的运算1、已知25mx=,求6155m x -的值.【思路点拨】由于已知2mx 的值,所以逆用幂的乘方把6mx变为23()m x ,再代入计算.【答案与解析】 解:∵25mx=,∴62331115()55520555m m x x -=-=⨯-=. 【总结升华】本题培养了学生的整体思想和逆向思维能力.举一反三:【变式】(1)已知246122,9,5===a b c ,比较,,a b c 的大小.(2)比较3020103,9,27大小。
《整式的乘除与因式分解》培优训练及答案

整式的乘除与因式分解一、选择题:1.下列计算正确的是( )A .105532a a a =+B .632a a a =⋅C .532)(a a =D . 8210a a a =÷2.下列计算结果正确的是( )A .4332222y x xy y x -=⋅-B .2253xy y x -=y x 22-C .xy y x y x 4728324=÷D .49)23)(23(2-=---a a a3.两个三次多项式相加,结果一定是 ( )A .三次多项式B .六次多项式C .零次多项式D .不超过三次的多项式4.把多项式()()()111---+x x x 提取公因式()1-x 后,余下的部分是( )A .()1+xB .()1+-xC .xD .()2+-x5.计算24(1)(1)(1)(1)x x x x -++--的结果是 ( )A 、2B 、0C 、-2D 、-56.已知代数式12x a -1y 3与-3x -b y 2a+b 是同类项,那么a 、b 的值分别是( )A .2,1a b =-⎧⎨=-⎩B .2,1a b =⎧⎨=⎩C .2,1a b =⎧⎨=-⎩D .2,1a b =-⎧⎨=⎩7.已知2239494b b a b a n m =÷,则( )A .3,4==n mB .1,4==n mC .3,1==n mD .3,2==n m8.如图,是一个正方形与一个直角三角形所拼成的图形,则该图形的面积为()A .m 2+12mnB .22mn n -C .22m mn+ D .222m n +9.若2()9a b +=,2()4a b -=,则ab 的值是( )A 、54B 、-54C 、1D 、-1 二、填空题: 1.分解因式2233ax ay -= .2.分解因式ab b a 8)2(2+- =_______.3.分解因式221218x x -+= .4.若22210a b b -+-+=,则a = ,b = .5.代数式4x 2+3mx +9是完全平方式,则m =___________.6. 已知a+b=5,ab=3,求下列各式的值:(1)a 2+b 2= ;(2)-3a 2+ab-3b 2= .7. 已知522=+b a ,()()223232a b a b --+=-48,则a b +=________. 8. 已知正方形的面积是2269y xy x ++ (x >0,y >0),利用分解因式,写出表示该正方形的边长的代数式 .9.观察下列等式: 第一行 3=4-1第二行 5=9-4第三行 7=16-9第四行 9=25-16… …按照上述规律,第n 行的等式为____________ .三、解答题:1.计算题(1)(-3xy 2)3·(61x 3y )2 (2)4a 2x 2·(-52a 4x 3y 3)÷(-21a 5xy 2)(3)222)(4)(2)x y x y x y --+( (4)221(2)(2))x x x x x-+-+-(2.因式分解(1)3123x x - (2)2222)1(2ax x a -+(3)xy y x 2122--+ (4))()3()3)((22a b b a b a b a -+++-3.解方程:41)8)(12()52)(3(=-+--+x x x x4.已知x 2+x -1=0,求x 3+2x 2+3的值5.若(x 2+px +q )(x 2-2x -3)展开后不含x 2,x 3项,求p 、q 的值.四.综合拓展:1.已知c b a 、、是△ABC 的三边的长,且满足0)(22222=+-++c a b c b a ,试判断此三角形的形状.2.已知2006x+2006y=1,x+3y=2006,试求2x 2+8xy+6y 2的值五.巩固练习:1.若n221623=÷,则n 等于( )A .10B .5C .3D .62.计算:xy xy y x y x 2)232(2223÷+--的结果是( ) A .xy y x 232- B .22322+-xy y x C .1232+--xy y x D .12322+--xy y x3.下列计算正确的是( )A .x y x y x 221222223=⋅÷ B .57222257919n m n m m n n m =÷⋅ C .mn mn n m n m =⋅÷24322)(2 D .22242231043)3012(y x y x y x y x +=÷+4.已知一个多项式与单项式457y x -的积为2234775)2(72821y x y y x y x +-,则这个多项式为___5.若(a+b )2=13(a-b )2=7求a 2+b 2和ab 的值。
八年级数学上册 整式的乘法与因式分解(培优篇)(Word版 含解析)

八年级数学上册 整式的乘法与因式分解(培优篇)(Word 版 含解析)一、八年级数学整式的乘法与因式分解选择题压轴题(难)1.将多项式24x +加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( ) A .4-B .±4xC .4116xD .2116x 【答案】D【解析】【分析】分x 2是平方项与乘积二倍项,以及单项式的平方三种情况,根据完全平方公式讨论求解.【详解】解:①当x 2是平方项时,4士4x+x ²=(2士x )2,则可添加的项是4x 或一4x ; ②当x 2是乘积二倍项时,4+ x 2+4116x =(2+214x )2,则可添加的项是4116x ; ③若为单项式,则可加上-4.故选:D.【点睛】本题考查了完全平方式,比较复杂,需要我们全面考虑问题,首先考虑三个项分别充当中间项的情况,就有三种情况,还有就是第四种情况加上一个数,得到一个单独的单项式,也是可以成为一个完全平方式,这种情况比较容易忽略,要注意.2.已知a =2018x +2018,b =2018x +2019,c =2018x +2020,则a 2+b 2+c 2-ab -ac -bc 的值是( )A .0B .1C .2D .3 【答案】D【解析】【分析】 把已知的式子化成12[(a-b )2+(a-c )2+(b-c )2]的形式,然后代入求解即可. 【详解】原式=12(2a 2+2b 2+2c 2-2ab-2ac-2bc ) =12[(a 2-2ab+b 2)+(a 2-2ac+c 2)+(b 2-2bc+c 2)] =12[(a-b )2+(a-c )2+(b-c )2] =12×(1+4+1) =3,故选D.【点睛】本题考查了因式分解的应用,代数式的求值,正确利用因式分解的方法把所求的式子进行变形是关键.3.若()(1)x m x +-的计算结果中不含x 的一次项,则m 的值是( )A .1B .-1C .2D .-2.【答案】A【解析】【分析】根据多项式相乘展开可计算出结果.【详解】 ()()1x m x +-=x 2+(m-1)x-m ,而计算结果不含x 项,则m-1=0,得m=1.【点睛】本题考查多项式相乘展开系数问题.4.已知实数a 、b 满足a+b=2,ab=34,则a ﹣b=( ) A .1B .﹣52C .±1D .±52 【答案】C【解析】分析:利用完全平方公式解答即可.详解:∵a+b=2,ab=34, ∴(a+b )2=4=a 2+2ab+b 2,∴a 2+b 2=52, ∴(a-b )2=a 2-2ab+b 2=1,∴a-b=±1,故选C .点睛:本题考查了完全平方公式的运用,熟记公式结构是解题的关键.5.下列多项式中,能运用公式法进行因式分解的是( )A .a 2+b 2B .x 2+9C .m 2﹣n 2D .x 2+2xy+4y 2【答案】C【解析】试题分析:直接利用公式法分解因式进而判断得出答案.解:A 、a 2+b 2,无法分解因式,故此选项错误;B 、x 2+9,无法分解因式,故此选项错误;C 、m 2﹣n 2=(m+n )(m ﹣n ),故此选项正确;D 、x 2+2xy+4y 2,无法分解因式,故此选项错误;故选C .6.我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图①可以用来解释(a +b)2-(a -b)2=4ab.那么通过图②中阴影部分面积的计算验证了一个恒等式,此等式是( )A .a 2-b 2=(a +b)(a -b)B .(a -b)2=a 2-2ab +b 2C .(a +b)2=a 2+2ab +b 2D .(a -b)(a +2b)=a 2+ab -b 2【答案】B【解析】图(4)中,∵S 正方形=a 2-2b (a-b )-b 2=a 2-2ab+b 2=(a-b )2,∴(a-b )2=a 2-2ab+b 2.故选B7.下列分解因式正确的是( )A .24(4)x x x x -+=-+B .2()x xy x x x y ++=+C .2()()()x x y y y x x y -+-=-D .244(2)(2)x x x x -+=+-【答案】C【解析】【分析】根据因式分解的步骤:先提公因式,再用公式法分解即可求得答案.注意分解要彻底.【详解】A. ()244x x x x -+=-- ,故A 选项错误; B. ()21x xy x x x y ++=++,故B 选项错误; C. ()()()2x x y y y x x y -+-=- ,故C 选项正确;D. 244x x -+=(x-2)2,故D 选项错误,故选C.【点睛】本题考查了提公因式法,公式法分解因式.注意因式分解的步骤:先提公因式,再用公式法分解.注意分解要彻底.8.观察下列两个多项式相乘的运算过程:根据你发现的规律,若(x +a )(x +b )=x 2-7x +12,则a ,b 的值可能分别是( ) A .3-,4-B .3-,4C .3,4-D .3,4 【答案】A【解析】【分析】根据题意可得规律为712a b ab +=-⎧⎨=⎩,再逐一判断即可. 【详解】 根据题意得,a ,b 的值只要满足712a b ab +=-⎧⎨=⎩即可, A.-3+(-4)=-7,-3×(-4)=12,符合题意;B.-3+4=1,-3×4=-12,不符合题意;C.3+(-4)=-1,3×(-4)=-12,不符合题意;D.3+4=7,3×4=12,不符合题意.故答案选A.【点睛】本题考查了多项式乘多项式,解题的关键是根据题意找出规律.9.将多项式241x +加上一个单项式后,使它能成为另一个整式的完全平方,下列添加单项式错误的是( )A .4xB .4x -4C .4x 4D .4x -【答案】B【解析】【分析】完全平方公式:()222=2a b a ab b +++,此题为开放性题目.【详解】设这个单项式为Q ,如果这里首末两项是2x 和1这两个数的平方,那么中间一项为加上或减去2x 和1积的2倍,故Q=±4x ;如果这里首末两项是Q 和1,则乘积项是22422x x =⋅,所以Q=44x ;如果该式只有24x 项,它也是完全平方式,所以Q=−1;如果加上单项式44x -,它不是完全平方式故选B.【点睛】此题考查完全平方式,解题关键在于掌握完全平方式的基本形式.10.已知a =96,b =314,c =275,则a 、b 、c 的大小关系是( )A .a >b >cB .a >c >bC .c >b >aD .b >c >a【答案】C【解析】【分析】根据幂的乘方可得:a =69=312,c =527=315,易得答案. 【详解】因为a =69=312,b =143,c =527=315, 所以,c>b>a故选C【点睛】本题考核知识点:幂的乘方. 解题关键点:熟记幂的乘方公式.二、八年级数学整式的乘法与因式分解填空题压轴题(难)11.若a-b=1,则222a b b --的值为____________.【答案】1【解析】【分析】先局部因式分解,然后再将a-b=1代入,最后在进行计算即可.【详解】解:222a b b --=(a+b )(a-b )-2b=a+b-2b=a-b=1【点睛】本题考查了因式分解的应用,弄清题意、并根据灵活进行局部因式分解是解答本题的关键.12.在边长为a 的正方形中剪掉一个边长为b 的小正方形()a b >,再沿虚线剪开,如图①,然后拼成一个梯形,如图②.根据这两个图形的面积关系,用等式表示是____________.【答案】a 2-b 2=(a+b)(a-b)【解析】【分析】根据正方形的面积公式和梯形的面积公式,即可求出答案.【详解】∵第一个图形的面积是a 2-b 2, 第二个图形的面积是12(b +b +a +a )(a -b )=(a +b )(a -b ), ∴根据两个图形的阴影部分的面积相等得:a 2-b 2=(a+b)(a-b).故答案为a 2-b 2=(a+b)(a-b).【点睛】 本题考查了平方差公式得几何背景,熟练掌握平方差公式的定义是本题解题的关键.13.(a-b )2(x-y )-(b-a )(y-x )2=(a-b )(x-y )×________.【答案】(a-b+x-y )【解析】运用公因式的概念,把多项式(a-b )2(x-y )-(b-a )(y-x )2运用提取公因式法因式分解(a-b )2(x-y )-(b-a )(y-x )2=(a-b )(x-y )×(a-b+x-y ). 故答案为:(a-b+x-y ).点睛:此题主要考查了提公因式法分解因式,关键是根据找公因式的方法,确定公因式,注意符号的变化.14.若22(3)16x m x +-+是关于x 的完全平方式,则m =__________. 【答案】7或-1【解析】【分析】直接利用完全平方公式的定义得出2(m-3)=±8,进而求出答案.详解:∵x 2+2(m-3)x+16是关于x 的完全平方式,∴2(m-3)=±8,解得:m=-1或7,故答案为-1或7.点睛:此题主要考查了完全平方公式,正确掌握完全平方公式的基本形式是解题关键.15.因式分解:x 3﹣4x=_____.【答案】x (x+2)(x ﹣2)【解析】试题分析:首先提取公因式x ,进而利用平方差公式分解因式.即x 3﹣4x=x (x 2﹣4)=x (x+2)(x ﹣2).故答案为x (x+2)(x ﹣2).考点:提公因式法与公式法的综合运用.16.分解因式:4ax 2-ay 2=________________.【答案】a (2x+y )(2x-y )【解析】【分析】首先提取公因式a ,再利用平方差进行分解即可.【详解】原式=a (4x 2-y 2)=a (2x+y )(2x-y ),故答案为a (2x+y )(2x-y ).【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.17.因式分解:223ax 12ay -=______.【答案】()()3a x 2y x 2y +-【解析】【分析】先提公因式3a ,然后再利用平方差公式进行分解即可得.【详解】原式()223a x 4y =-()()3a x 2y x 2y =+-,故答案为:()()3a x 2y x 2y +-.【点睛】本题考查了综合提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.18.因式分解:=______. 【答案】2(x +3)(x ﹣3).【解析】试题分析:先提公因式2后,再利用平方差公式分解即可,即=2(x 2-9)=2(x+3)(x-3).考点:因式分解.19.已知:7a b +=,13ab =,那么 22a ab b -+= ________________.【答案】10【解析】∵(a+b ) 2 =7 2 =49,∴a 2 -ab+b 2 =(a+b ) 2 -3ab=49-39=10,故答案为10.20.因式分解34x x -= .【答案】()()x x 2x 2-+-【解析】试题分析:要将一个多项式分解因式的一般步骤是首先看各项有没有公因式,若有公因式,则把它提取出来,之后再观察是否是完全平方公式或平方差公式,若是就考虑用公式法继续分解因式.因此,先提取公因式x -后继续应用平方差公式分解即可:()()()324x x x x 4x x 2x 2-=--=-+-.。
人教版数学八年级上册 整式的乘法与因式分解(培优篇)(Word版 含解析)

一、八年级数学整式的乘法与因式分解解答题压轴题(难)1.阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m2﹣2mn+n2)+(n2﹣8n+16)=0∴(m﹣n)2+(n﹣4)2=0,∴(m﹣n)2=0,(n﹣4)2=0,∴n=4,m=4.根据你的观察,探究下面的问题:(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC 的最大边c的值;(3)已知a﹣b=8,ab+c2﹣16c+80=0,求a+b+c的值.【答案】(1)9;(2)△ABC的最大边c的值可能是6、7、8、9、10;(3)8.【解析】试题分析:(1)直接利用配方法得出关于x,y的值即可求出答案;(2)直接利用配方法得出关于a,b的值即可求出答案;(3)利用已知将原式变形,进而配方得出答案.试题解析:(1)∵x2﹣2xy+2y2+6y+9=0,∴(x2﹣2xy+y2)+(y2+6y+9)=0,∴(x﹣y)2+(y+3)2=0,∴x﹣y=0,y+3=0,∴x=﹣3,y=﹣3,∴xy=(﹣3)×(﹣3)=9,即xy的值是9.(2)∵a2+b2﹣10a﹣12b+61=0,∴(a2﹣10a+25)+(b2﹣12b+36)=0,∴(a﹣5)2+(b﹣6)2=0,∴a﹣5=0,b﹣6=0,∴a=5,b=6,∵6﹣5<c<6+5,c≥6,∴6≤c<11,∴△ABC的最大边c的值可能是6、7、8、9、10.(3)∵a﹣b=8,ab+c2﹣16c+80=0,∴a(a﹣8)+16+(c﹣8)2=0,∴(a﹣4)2+(c﹣8)2=0,∴a﹣4=0,c﹣8=0,∴a=4,c=8,b=a﹣8=4﹣8=﹣4,∴a+b+c=4﹣4+8=8,即a+b+c的值是8.2.先阅读下列材料,然后解后面的问题.材料:一个三位自然数abc (百位数字为a ,十位数字为b ,个位数字为c ),若满足a+c=b ,则称这个三位数为“欢喜数”,并规定F (abc )=ac .如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F (374)=3×4=12. (1)对于“欢喜数abc ”,若满足b 能被9整除,求证:“欢喜数abc ”能被99整除; (2)已知有两个十位数字相同的“欢喜数”m ,n (m >n ),若F (m )﹣F (n )=3,求m ﹣n 的值.【答案】(1)详见解析;(2)99或297.【解析】【分析】(1)首先由题意可得a +c =b ,将欢喜数展开,因为要证明“欢喜数abc ”能被99整除,所以将展开式中100a 拆成99a +a ,这样展开式中出现了a +c ,将a +c 用b 替代,整理出最终结果即可;(2)首先设出两个欢喜数m 、n ,表示出F (m )、F (n )代入F (m )﹣F (n )=3中,将式子变形分析得出最终结果即可.【详解】(1)证明:∵abc 为欢喜数,∴a +c =b . ∵abc =100a +10b +c =99a +10b +a +c =99a +11b ,b 能被9整除,∴11b 能被99整除,99a 能被99整除,∴“欢喜数abc ”能被99整除;(2)设m =11a bc ,n =22a bc (且a 1>a 2),∵F (m )﹣F (n )=a 1•c 1﹣a 2•c 2=a 1•(b ﹣a 1)﹣a 2(b ﹣a 2)=(a 1﹣a 2)(b ﹣a 1﹣a 2)=3,a 1、a 2、b 均为整数,∴a 1﹣a 2=1或a 1﹣a 2=3.∵m ﹣n =100(a 1﹣a 2)﹣(a 1﹣a 2)=99(a 1﹣a 2),∴m ﹣n =99或m ﹣n =297.∴若F (m )﹣F (n )=3,则m ﹣n 的值为99或297.【点睛】做此类阅读理解类题目首先要充分理解题目,会运用因式分解将式子变形.3.若一个整数能表示成22a b +(a ,b 是整数)的形式,则称这个数为“完美数”.例如,5是“完美数”,因为22521=+.再如,()222222M x xy y x y y =++=++(x ,y 是整数),所以M 也是“完美数”. (1)请你再写一个小于10的“完美数”,并判断29是否为“完美数”;(2)已知224412S x y x y k =++-+(x ,y 是整数,是常数),要使S 为“完美数”,试求出符合条件的一个2200-0=值,并说明理由.(3)如果数m ,n 都是“完美数”,试说明mn 也是“完美数”..【答案】(1)8、29是完美数(2)S 是完美数(3)mn 是完美数【解析】【分析】(1)利用“完美数”的定义可得;(2)利用配方法,将S 配成完美数,可求k 的值(3)根据完全平方公式,可证明mn 是“完美数”;【详解】(1) 22228,8+=∴是完美数;222925,29=+∴是完美数 (2) ()222)2313S x y k =++-+-( 13.k S ∴=当时,是完美数(3) 2222,m a b n c d 设=+=+,则()()()()222222mn a bc d ac bd ad bc =++=++- 即mn 也是完美数.【点睛】本题考查了因式分解的应用,完全平方公式的运用,阅读理解题目表述的意思是本题的关键.4.阅读材料小明遇到这样一个问题:求计算()()()22334x x x +++所得多项式的一次项系数.小明想通过计算()()()22334x x x +++所得的多项式解决上面的问题,但感觉有些繁琐,他想探寻一下,是否有相对简洁的方法.他决定从简单情况开始,先找()()223x x ++所得多项式中的一次项系数,通过观察发现:也就是说,只需用2x +中的一次项系数1乘以23x +中的常数项3,再用2x +中的常数项2乘以23x +中的一次项系数2,两个积相加13227⨯+⨯=,即可得到一次项系数. 延续上面的方法,求计算()()()22334x x x +++所得多项式的一次项系数,可以先用2x +的一次项系数1,23x +的常数项3,34+x 的常数项4,相乘得到12;再用23x +的一次项系数2,2x +的常数项2,34+x 的常数项4,相乘得到16;然后用34+x 的一次项系数3,2x +的常数项223x +的常数项3,相乘得到18.最后将12,16,18相加,得到的一次项系数为46.参考小明思考问题的方法,解决下列问题:(1)计算()()443x x ++所得多项式的一次项系数为____________________.(2)计算()()()13225x x x +-+所得多项式的一次项系数为_____________.(3)若231x x -+是422x ax bx +++的一个因式,求a 、b 的值.【答案】(1)19;(2)1;(3) a= -6,b= -3.【解析】【分析】(1)根据两多项式常数项与一次项系数乘积的和即为所得多项式一次项系数可得;(2)根据三个多项式中两个多项式的常数项与另一个多项式一次项系数的乘积即为所求可得;(3)由x4+ax2+bx+2中4次项系数为1、常数项为2可设另一个因式为x2+mx+2,根据三次项系数为0、二次项系数为a、一次项系数为b列出方程组求出a、b的值,可得答案.【详解】解:(1)(x+4)(4x+3)所得多项式的一次项系数为1×3+4×4=19,故答案为:19;(2)()()()13225x x x+-+所得多项式的一次项系数为1×(-2)×5+1×3×5+1×(-2)×2=1,故答案为:1;(3)由x4+ax2+bx+2中4次项系数为1、常数项为2可设另一个因式为x2+mx+2,则(x2-3x+1)(x2+mx+2)=x4+ax2+bx+2,13101211(3)321mm am b⨯-⨯=⎧⎪∴⨯+⨯+-⨯=⎨⎪-⨯+⨯=⎩解得:363mab=⎧⎪=-⎨⎪=-⎩故答案为:a= -6,b= -3.【点睛】本题考查多项式乘多项式,解题关键是熟练掌握多项式乘多项式的运算法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.5.图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积:方法1:方法2:(2)观察图②请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系.;(3)根据(2)题中的等量关系,解决:已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;【答案】(1)(m-n)2;(m+n)2-4mn;(2)(m-n)2=(m+n)2-4mn;(3)1.【解析】【分析】(1)方法1:表示出阴影部分的边长,然后利用正方形的面积公式列式;方法2:利用大正方形的面积减去四周四个矩形的面积列式;(2)根据不同方法表示的阴影部分的面积相同解答;(3)根据(2)的结论整体代入进行计算即可得解.【详解】解:(1)方法1:∵阴影部分的四条边长都是m-n,是正方形,∴阴影部分的面积=(m-n)2方法2:∵阴影部分的面积=大正方形的面积减去四周四个矩形的面积∴阴影部分的面积=(m+n)2-4mn;(2)根据(1)中两种计算阴影部分的面积方法可知(m-n)2=(m+n)2-4mn;(3)由(2)可知(a+b)2=(a-b)2+4ab,∵a-b=5,ab=-6,∴(a+b)2=(a-b)2+4ab=52+4×(-6)=25-24=1.【点睛】本题考查几何图形与完全平方公式,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.6.阅读下列因式分解的过程,再回答所提出的问题:1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]=(1+x)2(1+x)=(1+x)3(1)上述分解因式的方法是,共应用了次.(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,则需应用上述方法次,结果是 .(3)分解因式:1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n为正整数).【答案】(1)提公因式,两次;(2)2004次,(x+1)2005;(3) (x+1)1n+【解析】【分析】(1)根据已知材料直接回答即可;(2)利用已知材料进而提取公因式(1+x),进而得出答案;(3)利用已知材料提取公因式进而得出答案.【详解】(1)上述分解因式的方法是:提公因式法,共应用了2次.故答案为提公因式法,2次;(2)1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,=(1+x)[1+x+x(1+x)+…+ x(x+1)2003]⋯=22003(1) (1)(1)(1)(1)xx x x x+++++个=(1+x)2005,故分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,,则需应用上述方法2004次,结果是:(x+1)2005.(3)分解因式:1+x+x(x+1)+x(x+1)2…+x(x+1)n(n为正整数)的结果是:(x+1)n+1.故答案为(x+1)n+1.【点睛】此题主要考查了提取公因式法分解因式,正确提取公因式是解题关键.7.阅读材料后解决问题:小明遇到下面一个问题:计算(2+1)(22+1)(24+1)(28+1).经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)=(2+1)(2﹣1)(22+1)(24+1)(28+1)=(22﹣1)(22+1)(24+1)(28+1)=(24﹣1)(24+1)(28+1)=(28﹣1)(28+1)=216﹣1请你根据小明解决问题的方法,试着解决以下的问题:(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).【答案】232﹣13231 2-;【解析】【分析】(1)原式变形后,利用题中的规律计算即可得到结果;(2)原式变形后,利用题中的规律计算即可得到结果;(3)分m=n与m≠n两种情况,化简得到结果即可.【详解】(1)原式=(2-1)(2+1)(22+1)(24+1)(28+1)(216+1)=232-1;(2)原式=12(3-1)(3+1)(32+1)(34+1)(38+1)(316+1)=32312-;(3)(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).当m≠n时,原式=1m n-(m-n)(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16)=3232m nm n--;当m=n时,原式=2m•2m2…2m16=32m31.【点睛】此题考查了平方差公式,弄清题中的规律是解本题的关键.8.阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式(x2﹣4x+1)(x2﹣4x+7)+9进行因式分解的过程.解:设x2﹣4x=y原式=(y+1)(y+7)+9(第一步)=y2+8y+16(第二步)=(y+4)2(第三步)=(x2﹣4x+4)2(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的;A.提取公因式法B.平方差公式法C.完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:;(3)请你用换元法对多项式(x2+2x)(x2+2x+2)+1进行因式分解.【答案】(1)C;(2)(x﹣2)4;(3)(x+1)4.【解析】【分析】(1)根据完全平方公式进行分解因式;(2)最后再利用完全平方公式将结果分解到不能分解为止;(3)根据材料,用换元法进行分解因式.【详解】(1)故选C;(2)(x2﹣4x+1)(x2﹣4x+7)+9,设x2﹣4x=y,则:原式=(y+1)(y+7)+9=y2+8y+16=(y+4)2=(x2﹣4x+4)2=(x﹣2)4.故答案为:(x﹣2)4;(3)设x2+2x=y,原式=y(y+2)+1=y2+2y+1=(y+1)2=(x2+2x+1)2=(x+1)4.【点睛】本题考查了因式分解﹣换元法,公式法,也是阅读材料问题,熟练掌握利用公式法分解因式是解题的关键.9.由多项式的乘法:(x+a)(x+b)=x2+(a+b)x+ab,将该式从右到左使用,即可得到用“十字相乘法”进行因式分解的公式:x2+(a+b)x+ab=(x+a)(x+b).实例分解因式:x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3).(1)尝试 分解因式:x 2+6x +8;(2)应用 请用上述方法解方程:x 2-3x -4=0.【答案】(1) (x+2)(x +4);(2) x =4或x =-1.【解析】【分析】(1)类比题干因式分解方法求解可得;(2)利用十字相乘法将左边因式分解后求解可得.【详解】(1)原式=(x+2)(x +4);(2)x 2-3x -4=(x -4)(x +1)=0,所以x -4=0或x +1=0,即x =4或x =-1.【点睛】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.10.(探究)如图①,从边长为a 的大正方形中剪掉一个边长为b 的小正方形,有阴影部分沿虚线剪开,拼成图②的长方形(1)请你分别表示出这两个图形中阴影部分的面积(2)比较两图的阴影部分面积,可以得到乘法公式 (用字母表示)(应用)请应用这个公式完成下列各题①已知22412m n -=,24m n +=,则2m n -的值为②计算:(2)(2)a b c a b c +--+(拓展)①()()()()24832(21)21212121+1+++++结果的个位数字为 ②计算:222222221009998974321-+-++-+-【答案】[探究](1)a 2﹣b 2;(a +b )(a ﹣b );(2)(a +b )(a ﹣b )=a 2﹣b 2;[应用]①3;②4a 2﹣b 2+2bc ﹣c 2;[拓展]①6;②5050.【解析】【分析】[探究](1)由面积公式可得答案;(2)公式由(1)直接可得;[应用]①用平方差公式分解4m 2﹣n 2,将已知值代入可求解;②将三项恰当组分成两组,先用平方差,再用完全平方公式展开后合并同类项即可;[拓展]①将原式乘以(2﹣1),就可以反复运用平方差公式化简,最后按照循环规律可得解;②将原式从左向右依次两项一组,运用平方差公式分解,化为100+99+98+…+4+3+2+1,从而可得答案.【详解】(1)图①按照正方形面积公式可得:a2﹣b2;图②按照长方形面积公式可得:(a+b)(a﹣b).故答案为:a2﹣b2;(a+b)(a﹣b).(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2故答案为:(a+b)(a﹣b)=a2﹣b2.【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n),∴(2m﹣n)=12÷4=3.故答案为:3.②(2a+b﹣c)(2a﹣b+c)=[2a+(b﹣c)][2a﹣(b﹣c)]=4a2﹣(b﹣c)2=4a2﹣b2+2bc﹣c2【拓展】①原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1=(24﹣1)(24+1)(28+1)…(232+1)+1=(28﹣1)(28+1)…(232+1)+1=(216﹣1)…(232+1)+1=264﹣1+1=264.∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16.故答案为:6.②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)=100+99+98+97+…+4+3+2+1=5050.【点睛】本题考查了平方差公式的几何背景及其应用与拓展,计算具有一定的难度,属于中档题.。
新人教版八年级上数学第十四章整式乘除培优经典题型

整式乘除培优经典题型第一类:平方差公式应用1.平方差公式:22))((b a b a b a -=-+222222222249))(32(94))(32())(())(())((1xy y x y x y x m n n m m n n m n m n m -=---=---=--=+-=+例2、()()()()()()()12121212121212643216842+++++++计算:3、(1-221)(1-231)(1-241)…(1-291)(1-2011)的值.4、()()()()()()2222222222299100...8767452312-++-+-+-+-+-第二类:完全平方公式变形及其应用1、已知19992000a x =+,19992001b x =+,19992002c x =+,则多项式222a b c ab bc ca ++---的值为( )A.0B.1C.2D.32、已知2()4x y -=,2()64x y +=;求代数式值:(1)22x y +; (2)xy3、 已知x +x 1=2,求x 2+21x ,x 4+41x的值.第三类:整体带入法1、已知a+2b=0,则式子a 3+2ab (a+b )+4b 3的值是___________. 2..若133=-x x ,则199973129234+--+x x x x 的值等于( ) A .1997 B .1999 C .2001 D .2003 3、 已知3x 2-x-1=0,求6x 3十7x 2一5x+1999的值第四类:幂的个位数1、20154的个位是_______201527的个位是:______ 2005200423125⨯积的个位数字是:________2、. 若3a =-,25b =,则20072006ab +的个位数字是( )A.3B.5C.8D.9第五类 :不含某一项1、多项式875223-+-x x x 与多项式112++bx ax 的乘积中,没有含4x 的项,也没有含3x 的项,则b a +2= .第六类:待定系数法1、))(2(67222B y x A y x y x y xy x +++-=-----.求A 、B 的值.2、 已知)3)(32(1437622c y x b y x a y x y xy x +++-=+++--试确定c b a 、、 值.3、若多项式7432+-x x 能表示成c x b x a ++++)1()1(2的形式,则a = .第七类:走进竞赛1.已知,,a b c 均不为0,且0a b c ++=,那么111111()()()a b c b c c a a b+++++的值为 .2、设1abc =.试求111a b cab a bc b ca c ++++++++的值.3.把(x 2一x+1)6展开后得012211111212a x a x a x a x a +++++ ,则024681012a a a a a a a ++++++ .4.. 已知200025=x,200080=y,则yx 11+等于( ). A .2 B .1 C .21D .235.设d c b a 、、、都是自然数,且17,,2345=-==c a d c b a ,求d 一b 的值6..已知102222=⋅=⋅dcba,求证:(a 一1)(d —1)=(b 一1)(c 一1).。
八年级上册整式的乘法与因式分解(培优篇)(Word版 含解析)

八年级上册整式的乘法与因式分解(培优篇)(Word 版 含解析)一、八年级数学整式的乘法与因式分解选择题压轴题(难)1.对二次三项式4x 2﹣6xy ﹣3y 2分解因式正确的是( )A .3213214()()x y x y +-++B .2132134()()x y x y +---C .(321)(321)x y y x y y ---+D .321213(2)(2)x y x y -+-- 【答案】D【解析】【分析】 【详解】解:4x 2﹣6xy ﹣3y 2=4[x 2﹣32xy +(34y )2]﹣3y 2﹣94y 2 =4(x ﹣34y )2﹣214y 2 =(2x ﹣32y ﹣212y )(2x ﹣32y +212y ) =(2x 321+y )(2x 321- 故选D .【点睛】本题主要是用配方法来分解因式,但本题的计算,分数,根式多,所以学生还是很容易出错的,注意计算时要细心.2.(2017重庆市兼善中学八年级上学期联考)在日常生活中如取款、上网等都需要密码.有一种用“因式分解法”产生的密码方便记忆,如:对于多项式44x y -,因式分解的结果是()()()22x y x y x y -++,若取9x =, 9y =时,则各个因式的值为()0x y -=, ()18x y +=, ()22162x y +=,于是就可以把“018162”作为一个六位数的密码.对于多项式32x xy -,取20x, 10y =时,用上述方法产生的密码不可能...是( ) A .201030B .201010C .301020D .203010【答案】B【解析】【分析】【详解】解:x 3-xy 2=x (x 2-y 2)=x (x+y )(x-y ),当x=20,y=10时,x=20,x+y=30,x-y=10,组成密码的数字应包括20,30,10,所以组成的密码不可能是201010.故选B .3.已知n 16221++是一个有理数的平方,则n 不能取以下各数中的哪一个( ) A .30B .32C .18-D .9 【答案】B【解析】【分析】分多项式的三项分别是乘积二倍项时,利用完全平方公式分别求出n 的值,然后选择答案即可.【详解】2n 是乘积二倍项时,2n +216+1=216+2×28+1=(28+1)2,此时n=8+1=9,216是乘积二倍项时,2n +216+1=2n +2×215+1=(215+1)2,此时n=2×15=30,1是乘积二倍项时,2n +216+1=(28)2+2×28×2-9+(2-9)2=(28+2-9)2,此时n=-18,综上所述,n 可以取到的数是9、30、-18,不能取到的数是32.故选B .【点睛】本题考查了完全平方式,难点在于要分情况讨论,熟记完全平方公式结构是解题的关键.4.若999999a =,990119b =,则下列结论正确是( ) A .a <bB .a b =C .a >bD .1ab =【答案】B【解析】 ()9999999909990909119991111===99999a b +⨯⨯==⨯, 故选B.【点睛】本题考查了有关幂的运算、幂的大小比较的方法,一般说来,比较几个幂的大小,或者把它们的底数变得相同,或者把它们的指数变得相同,再分别比较它们的指数或底数.5.化简()22x 的结果是( )A.x4B.2x2C.4x2D.4x【答案】C【解析】【分析】利用积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘即可.【详解】(2x)²=2²·x²=4x²,故选C.【点睛】本题考查了积的乘方,解题的关键是掌握积的乘方的运算法则.6.计算,得()A.B.C.D.【答案】C【解析】【分析】直接提取公因式(-3)m-1,进而分解因式即可.【详解】(-3)m+2×(-3)m-1=(-3)m-1(-3+2)=-(-3)m-1.故选C.【点睛】此题主要考查了提取公因式法分解因式,正确分解因式是解题关键.7.已知a,b,c是△ABC的三条边的长度,且满足a2-b2=c(a-b),则△ABC是()A.锐角三角形B.钝角三角形C.等腰三角形D.等边三角形【答案】C【解析】【分析】已知等式左边分解因式后,利用两数相乘积为0两因式中至少有一个为0得到a=b,即可确定出三角形形状.【详解】已知等式变形得:(a+b)(a-b)-c(a-b)=0,即(a-b)(a+b-c)=0,∵a+b-c≠0,∴a-b=0,即a=b,则△ABC为等腰三角形.故选C .【点睛】此题考查了因式分解的应用,熟练掌握因式分解的方法是解本题的关键.8.如图,矩形的长、宽分别为a 、b ,周长为10,面积为6,则a 2b +ab 2的值为( )A .60B .30C .15D .16 【答案】B【解析】【分析】直接利用矩形周长和面积公式得出a+b ,ab ,进而利用提取公因式法分解因式得出答案.【详解】∵边长分别为a 、b 的长方形的周长为10,面积6,∴2(a+b )=10,ab=6,则a+b=5,故ab 2+a 2b=ab (b+a )=6×5=30.故选:B .【点睛】此题主要考查了提取公因式法以及矩形的性质应用,正确分解因式是解题关键.9.下列从左到右的变形,是因式分解的是( )A .()()23x 3x 9x -+=-B .()()()()y 1y 33y y 1+-=-+C .()24yz 2y z z 2y 2z zy z -+=-+ D .228x 8x 22(2x 1)-+-=-- 【答案】D【解析】【分析】把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,结合选项进行判断即可.【详解】根据因式分解的定义得:从左边到右边的变形,是因式分解的是228x 8x 22(2x 1)-+-=--.其他不是因式分解:A,C 右边不是积的形式,B 左边不是多项式.故选D.【点睛】本题考查了因式分解的意义,注意因式分解后左边和右边是相等的,不能凭空想象右边的式子.10.有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示.右边场地为长方形,长为()2a b+,则宽为()A.12B.1 C.()12a b+D.+a b【答案】C【解析】【分析】用长方形的面积除以长可得.【详解】宽为:()()()()22222a ab ab b a b a b a b+++÷+=+÷+=()12a b+故选:C【点睛】考核知识点:整式除法与面积.掌握整式除法法则是关键.二、八年级数学整式的乘法与因式分解填空题压轴题(难)11.已知222246140x y z x y z++-+-+=,则()2002x y z--=_______.【答案】0【解析】【分析】利用完全平方式的特点把原条件变形为222(1)(2)(3)0x y z-+++-=,再利用几个非负数之和为0,则每一个非负数都为0的结论可得答案.【详解】解:因为:222246140x y z x y z++-+-+=所以222(21)(44)(69)0x x y y z z-+++++-+=所以222(1)(2)(3)0x y z-+++-=所以102030xyz-=⎧⎪+=⎨⎪-=⎩,解得123xyz=⎧⎪=-⎨⎪=⎩所以()2002x y z --=[]221(2)3(33)0---=-= 故答案为0.【点睛】 本题考查完全平方式的特点,非负数之和为0的性质,掌握该知识点是关键.12.因式分解:225101a a -+=______________【答案】()251a -【解析】根据完全平方公式()2222a ab b a b ±+=±进行因式分解为:225101a a -+=()251a -. 故答案为:()251a -.13.(1)已知32m a =,33nb =,则()()332243m n m n m a b a b a +-⋅⋅=______. (2)对于一切实数x ,等式()()212x px q x x -+=+-均成立,则24p q -的值为______.(3)已知多项式2223286x xy y x y +--+-可以分解为()()22x y m x y n ++-+的形式,则3211m n +-的值是______. (4)如果2310x x x +++=,则232016x x x x +++⋅⋅⋅+=______.【答案】(1)5-; (2)9; (3)78-; (4)0. 【解析】【分析】(1)根据积的乘方和幂的乘方,将32m a =整体代入即可;(2)将等式后面部分展开,即可求出p 、q 的值,代入即可;(3)根据多项式乘法法则求出()()22x y m x y n ++-+,即可得到关于m 、n 的方程组,解之即可求得m 、n 、的值,代入计算即可;(4)4个一组提取公因式,整体代入即可.【详解】(1)32m a =,33n a =,()()()()332222343333m n m n m m n m n a b a b a a b a b ∴+-⋅⋅=+-22232343125=+-⨯=+-=-(2)222x px q x x -+=--对一切实数x 均成立,1p ∴=,2q =-249p q ∴-=(3)()()222223286x y m x y n x xy y x y ++-+=+--+-,()()22222322223286x xy y m n x n m y mn x xy y x y ∴+-+++-+=+--+- 21,28,6,m n n m mn +=-⎧⎪∴-=⎨⎪=-⎩解得2,3.m n =-⎧⎨=⎩321718m n +∴=-- (4)2310x x x +++=,232016x x x x ∴+++⋅⋅⋅+()()2320132311x x x x x x x x =++++⋅⋅⋅++++000=+⋅⋅⋅+=故答案为: −5;9;78-;0. 【点睛】本题主要考察幂的运算及整式的乘法,掌握其运算法则是关键.14.计算:=_____. 【答案】1【解析】【分析】根据平方差公式可以使本题解答比较简便.【详解】解:====1.【点睛】本题应根据数字特点,灵活运用运算定律会或运算技巧,灵活简算.15.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了n(a b)(n +为非负整数)展开式的项数及各项系数的有关规律.例如:0(a b)1+=,它只有一项,系数为1;系数和为1; 1(a b)a b +=+,它有两项,系数分别为1,1,系数和为2;222(a b)a 2ab b +=++,它有三项,系数分别为1,2,1,系数和为4;33223(a b)a 3a b 3ab b +=+++,它有四项,系数分别为1,3,3,1,系数和为8;⋯,则n (a b)+的展开式共有______项,系数和为______.【答案】n 1+ n 2【解析】【分析】本题通过阅读理解寻找规律,观察可得(a+b )n (n 为非负整数)展开式的各项系数的规律:首尾两项系数都是1,中间各项系数等于(a+b )n-1相邻两项的系数和.因此根据项数以及各项系数的和的变化规律,得出(a+b )n 的项数以及各项系数的和即可.【详解】根据规律可得,(a+b )n 共有(n+1)项,∵1=201+1=211+2+1=221+3+3+1=23∴(a+b )n 各项系数的和等于2n故答案为n+1,2n【点睛】本题主要考查了完全平方式的应用,能根据杨辉三角得出规律是解此题的关键.在应用完全平方公式时,要注意:①公式中的a ,b 可是单项式,也可以是多项式;②对形如两数和(或差)的平方的计算,都可以用这个公式.16.222---x xy y =__________【答案】()2x y -+【解析】根据因式分解的方法,先提公因式“﹣”,再根据完全平方公式分解因式为:()()2222222x xy y x xy y x y ---=-++=-+. 故答案为()2x y -+.点睛:此题主要考查了因式分解,因式分解是把一个多项式化为几个因式积的形式.根据因式分解的一般步骤:一提(公因式)、二套(平方差公式()()22a b a b a b -=+-,完全平方公式()2222a ab b a b ±+=±)、三检查(彻底分解),注意符号的变化.17.4x(m -n)+8y(n -m)2中各项的公因式是________.【答案】4(m -n)【解析】根据题意,先变形为4x(m -n)+8y(m -n)2,把m-n 看做一个整体,即可找到公因式4(m-n ).故答案为:4(m-n ).点睛:此题主要考查了提公因式法因式分解,根据公因式的特点,利用整体法确定公因式即可,关键是要把n-m 与m-n 变形为统一的式子.18.若x ﹣1x=2,则x 2+21x 的值是______. 【答案】6【解析】 根据完全平方公式,可知(x ﹣1x )2= x 2-2+21x =4,移项整理可得x 2+21x=6. 故答案为6.点睛:此题主要考查了整式的乘法,解题关键是利用完全平方公式进行变形,然后化简整理即可求解,注意整体思想的应用,比较简单,是常考题.19.因式分解:2()4()a a b a b ---=___.【答案】()()()22a b a a -+-【解析】分析:先提公因式,再利用平方差公式因式分解即可.详解:a 2(a-b )-4(a-b )=(a-b )(a 2-4)=(a-b )(a-2)(a+2),故答案为:(a-b )(a-2)(a+2).点睛:本题考查的是因式分解,掌握提公因式法、平方差公式进行因式分解是解题的关键.20.若2x+5y ﹣3=0,则4x •32y 的值为________.【答案】8【解析】∵2x+5y ﹣3=0,∴2x+5y=3,∴4x •32y =(22)x ·(25)y =22x ·25y =22x+5y =23=8, 故答案为:8.【点睛】本题主要考查了幂的乘方的性质,同底数幂的乘法,转化为以2为底数的幂是解题的关键,整体思想的运用使求解更加简便.。
八年级数学上册 整式的乘法与因式分解(培优篇)(Word版 含解析)

八年级数学上册整式的乘法与因式分解(培优篇)(Word版含解析)一、八年级数学整式的乘法与因式分解选择题压轴题(难)1.有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为()A.6 B.7 C.8 D.9【答案】C【解析】【分析】设2为a,3为b,则根据5张边长为2的正方形纸片的面积是5a2,4张边长分别为2、3的矩形纸片的面积是4ab,6张边长为3的正方形纸片的面积是6a2,得出a2+4ab+4b2=(a+2b)2,再根据正方形的面积公式将a、b代入,即可得出答案.【详解】解:设2为a,3为b,则根据5张边长为2的正方形纸片的面积是5a2,4张边长分别为2、3的矩形纸片的面积是4ab,6张边长为3的正方形纸片的面积是6b2,∵a2+4ab+4b2=(a+2b)2,(b>a)∴拼成的正方形的边长最长可以为a+2b=2+6=8,故选C.【点睛】此题考查了完全平方公式的几何背景,关键是根据题意得出a2+4ab+4b2=(a+2b)2,用到的知识点是完全平方公式.2.已知a=2018x+2018,b=2018x+2019,c=2018x+2020,则a2+b2+c2-ab-ac-bc 的值是( )A.0B.1C.2D.3【答案】D【解析】【分析】把已知的式子化成12[(a-b)2+(a-c)2+(b-c)2]的形式,然后代入求解即可.【详解】原式=12(2a 2+2b 2+2c 2-2ab-2ac-2bc ) =12[(a 2-2ab+b 2)+(a 2-2ac+c 2)+(b 2-2bc+c 2)] =12[(a-b )2+(a-c )2+(b-c )2] =12×(1+4+1) =3,故选D.【点睛】本题考查了因式分解的应用,代数式的求值,正确利用因式分解的方法把所求的式子进行变形是关键.3.已知20192019a x =+,20192020b x =+,20192021c x =+,则222a b c ab ac bc ++---的值为( )A .0B .1C .2D .3【答案】D【解析】【分析】根据20192019a x =+,20192020b x =+,20192021c x =+分别求出a-b 、a-c 、b-c 的值,然后利用完全平方公式将题目中的式子变形,即可完成.【详解】∵20192019a x =+,20192020b x =+,20192021c x =+, 20192019201920201a b x x -=+--=-20192019201920212a c x x -=+--=-20192020201920211b c x x -=+--=-∴222a b c ab ac bc ++---2221(222222)2a b c ab ac bc =++--- 2222221(222)2a ab b a ac c b bc c =-++-++-+ 222111()()()222a b a c b c =-+-+- 222111(1)(2)(1)222=⨯-+⨯-+⨯- 11222=++ 3=故选D【点睛】本题考查完全平方公式的应用,熟练掌握完全平方公式是解题关键.4.如果多项式29x kx -+能用公式法分解因式,那么k 的值是( )A .3B .6C .3±D .6±【答案】D【解析】由于可以利用公式法分解因式,所以它是一个完全平方式222a ab b ±+,所以236k =±⨯=±.故选D.5.已知实数a 、b 满足a+b=2,ab=34,则a ﹣b=( ) A .1B .﹣52C .±1D .±52 【答案】C【解析】分析:利用完全平方公式解答即可.详解:∵a+b=2,ab=34, ∴(a+b )2=4=a 2+2ab+b 2,∴a 2+b 2=52, ∴(a-b )2=a 2-2ab+b 2=1,∴a-b=±1,故选C .点睛:本题考查了完全平方公式的运用,熟记公式结构是解题的关键.6.下列运算正确的是A .532b b b ÷=B .527()b b =C .248·b b b =D .2·22a a b a ab -=+() 【答案】A【解析】选项A , 532b b b ÷=,正确;选项B , ()25b =10b ,错误;选项C , 24·b b =6b ,错误;选项D , 2·22a a b a ab -=-,错误.故选A.7.下列各式从左边到右边的变形是因式分解的是( )A .(a +1)(a -1)=a 2-1B .a 2-6a +9=(a -3)2C .x 2+2x +1=x (x +2x )+1D .-18x 4y 3=-6x 2y 2·3x 2y【答案】B【解析】【分析】 分解因式就是把一个多项式化为几个整式的积的形式.因此,要确定从左到右的变形中是否为分解因式,只需根据定义来确定.【详解】A 、是多项式乘法,不是因式分解,错误;B 、是因式分解,正确.C 、右边不是积的形式,错误;D 、左边是单项式,不是因式分解,错误.故选B .【点睛】本题的关键是理解因式分解的定义:把一个多项式化为几个最简整式的积的形式,这种变形叫做把这个多项式因式分解,然后进行正确的因式分解.8.若2149x kx ++是完全平方式,则实数k 的值为( ) A .43 B .13 C .43± D .13± 【答案】C【解析】【分析】本题是已知平方项求乘积项,根据完全平方式的形式可得出k 的值.【详解】由完全平方式的形式(a±b )2=a 2±2ab+b 2可得: kx=±2•2x•13, 解得k=±43. 故选:C【点睛】本题关键是有平方项求乘积项,掌握完全平方式的形式(a±b )2=a 2±2ab+b 2是关键.9.观察下列两个多项式相乘的运算过程:根据你发现的规律,若(x +a )(x +b )=x 2-7x +12,则a ,b 的值可能分别是( ) A .3-,4-B .3-,4C .3,4-D .3,4 【答案】A【解析】【分析】根据题意可得规律为712a b ab +=-⎧⎨=⎩,再逐一判断即可. 【详解】 根据题意得,a ,b 的值只要满足712a b ab +=-⎧⎨=⎩即可, A.-3+(-4)=-7,-3×(-4)=12,符合题意;B.-3+4=1,-3×4=-12,不符合题意;C.3+(-4)=-1,3×(-4)=-12,不符合题意;D.3+4=7,3×4=12,不符合题意.故答案选A.【点睛】本题考查了多项式乘多项式,解题的关键是根据题意找出规律.10.将多项式241x +加上一个单项式后,使它能成为另一个整式的完全平方,下列添加单项式错误的是( )A .4xB .4x -4C .4x 4D .4x -【答案】B【解析】【分析】完全平方公式:()222=2a b a ab b +++,此题为开放性题目.【详解】设这个单项式为Q ,如果这里首末两项是2x 和1这两个数的平方,那么中间一项为加上或减去2x 和1积的2倍,故Q=±4x ;如果这里首末两项是Q 和1,则乘积项是22422x x =⋅,所以Q=44x ;如果该式只有24x 项,它也是完全平方式,所以Q=−1;如果加上单项式44x -,它不是完全平方式故选B.【点睛】此题考查完全平方式,解题关键在于掌握完全平方式的基本形式.二、八年级数学整式的乘法与因式分解填空题压轴题(难)11.如果关于x 的二次三项式24x x m -+在实数范围内不能因式分解,那么m 的值可以是_________.(填出符合条件的一个值) 【答案】5【解析】【分析】根据前两项,此多项式如用十字相乘方法分解,m 应是3或-5;若用完全平方公式分解,m 应是4,若用提公因式法分解,m 的值应是0,排除3、-5、4、0的数即可.【详解】当m=5时,原式为245x x -+,不能因式分解,故答案为:5.【点睛】此题考查多项式的因式分解方法,熟记每种分解的因式的特点及所用因式分解的方法,掌握技巧才能熟练运用解题.12.计算:=_____. 【答案】1【解析】【分析】根据平方差公式可以使本题解答比较简便.【详解】解:====1.【点睛】本题应根据数字特点,灵活运用运算定律会或运算技巧,灵活简算.13.(m+n+p+q) (m-n-p-q)=(__________) 2-(__________) 2.【答案】m n+p+q【解析】(m+n+p+q)(m-n-p-q)=[m+(n+p+q)][m-(n+p+q)]=()22m n p q -++,故答案为(1)m ,(2)n+p+q. 点睛:本题主要考查了平方差公式,平方差公式是两个数的和与这两个数的差的积,等于这两个数的平方差,多项式与多项相乘时,要注意观察能否将其中符号相同的项结合成为一项后,再运用平方差公式运算.14.分解因式212x 123y xy y -+-=___________【答案】()232x 1y --【解析】根据因式分解的方法,先提公因式-3y ,再根据完全平方公式分解因式为:()()22212x 12334x 41321y xy y y x y x -+-=--+=--. 故答案为()232x 1y --.15.把多项式(x -2)2-4x +8分解因式,哪一步开始出现了错误( )解:原式=(x -2)2-(4x -8)…A=(x -2)2-4(x -2)…B=(x -2)(x -2+4)…C=(x -2)(x +2)…D【答案】C【解析】根据题意,第一步应是添括号(注意符号变化),解法正确,第二步先对后面因式提公因式4,再提取公因式(x-2)这时出现符号错误,所以从C 步出现错误.故选C.16.计算:532862a a a -÷=()___________.【答案】343a a -【解析】根据整式的除法—多项式除以单项式,可知:532862a a a -÷=()8a 5÷2a 2-6a 3÷2a 2=343a a -.故答案为:343a a -.17.若a ,b 互为相反数,则a 2﹣b 2=_____.【答案】0【解析】【分析】直接利用平方差公式分解因式进而结合相反数的定义分析得出答案.【详解】∵a ,b 互为相反数,∴a+b=0,∴a 2﹣b 2=(a+b )(a ﹣b )=0,故答案为0.【点睛】本题考查了公式法分解因式以及相反数的定义,正确分解因式是解题关键.18.已知a m =3,a n =2,则a 2m ﹣n 的值为_____.【答案】4.5【解析】分析:首先根据幂的乘方的运算方法,求出a 2m 的值;然后根据同底数幂的除法的运算方法,求出a 2m-n 的值为多少即可.详解:∵a m =3,∴a 2m =32=9,∴a 2m-n =292m n a a ==4.5. 故答案为:4.5. 点睛:此题主要考查了同底数幂的除法法则,以及幂的乘方与积的乘方,同底数幂相除,底数不变,指数相减,要熟练掌握,解答此题的关键是要明确:①底数a≠0,因为0不能做除数;②单独的一个字母,其指数是1,而不是0;③应用同底数幂除法的法则时,底数a 可是单项式,也可以是多项式,但必须明确底数是什么,指数是什么.19.若3a b +=,则226a b b -+的值为__________.【答案】9【解析】分析:先将226a b b -+化为()()6a b a b b +-+,再将3a b +=代入所化式子计算即可. 详解:∵3a b +=,∴226a b b -+=()()6a b a b b +-+=3()6a b b -+=336a b b -+=3()a b +=9.故答案为:9.点睛:“能够把226a b b -+化为()()6a b a b b +-+”是解答本题的关键.20.已知:7a b +=,13ab =,那么 22a ab b -+= ________________.【答案】10【解析】∵(a+b)2 =7 2 =49,∴a 2 -ab+b 2 =(a+b)2 -3ab=49-39=10,故答案为10.。
人教版八年级数学上整式的乘除及因式分解培优

综合题训练
11.若 ,且 ,求 值.
26
预习归纳
1.单项式与单项式相乘,把它们、分别相乘,对于只在一个单项式里含有的字母,则连同它的作为积的一个.
例题讲解
[例]计算
① ② ③
基础题训练
1.(2013·绍兴)计算 的结果是( )
A.3abB.6aC.6abD.5ab
第十四章整式的乘除及因式分解
23.同底数幂的乘法
预习归纳
1.同底数幂相乘,底数_______,指数________,用式子表示为:am·an=am+n(m,n都是正整数)
例题讲解
[例]计算
①-x5·x2·x10②(-2)9·(-2)8·(-2)3③a6·a2+a5·a3-2a·a7
基础题训练
1.(2014•安徽)x2·x3=()
10.已知2·8n·16n=222,则n=_____.
11.已知a3m=3,b3n=2,求(a2m)3+(bn)3-a2m·bn·a4m·b2n的值.
综合题训练
12.阅读下列解题过程.
试比较2100与375的大小.
解:∵2100=(24)25=1625,375=(33)25=2725而∴2100<375.
2.(2014·扬州)若 ,则内应填的单项式是( )
A.xyB.3xyC.xD.3x
3.(2014·扬州) ( )
A. B. C. D.
4.计算:① ﹦;② .
5.一种电子计算机每秒可以做 次运算,它工作 秒可做次运算.
6.计算
① ② ③
中档题训练
7.若 ,则 ﹦.
8.魏明家新购一套结构如图的住房,正准备装修.
5.①(-m)·m·(-m)2=_______;②-22×(-2)2=_______;③(- )5·(- )8=______.
(家教培优专用)人教版数学八年级上册--《整式的乘除与因式分解》全章复习与巩固(提高)知识讲解
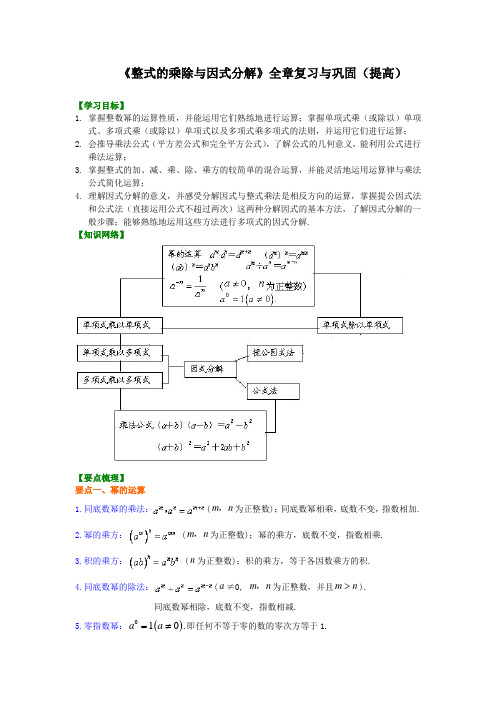
《整式的乘除与因式分解》全章复习与巩固(提高)【学习目标】1. 掌握整数幂的运算性质,并能运用它们熟练地进行运算;掌握单项式乘(或除以)单项式、多项式乘(或除以)单项式以及多项式乘多项式的法则,并运用它们进行运算;2. 会推导乘法公式(平方差公式和完全平方公式),了解公式的几何意义,能利用公式进行乘法运算;3. 掌握整式的加、减、乘、除、乘方的较简单的混合运算,并能灵活地运用运算律与乘法公式简化运算;4. 理解因式分解的意义,并感受分解因式与整式乘法是相反方向的运算,掌握提公因式法和公式法(直接运用公式不超过两次)这两种分解因式的基本方法,了解因式分解的一般步骤;能够熟练地运用这些方法进行多项式的因式分解.【知识网络】【要点梳理】要点一、幂的运算1.同底数幂的乘法:(m n ,为正整数);同底数幂相乘,底数不变,指数相加. 2.幂的乘方:(m n ,为正整数);幂的乘方,底数不变,指数相乘. 3.积的乘方:(n 为正整数);积的乘方,等于各因数乘方的积. 4.同底数幂的除法:(a ≠0, m n ,为正整数,并且m n >).同底数幂相除,底数不变,指数相减.5.零指数幂:()010.a a =≠即任何不等于零的数的零次方等于1.6.负指数幂:1n n a a-=(0a ≠,n 为正整数).任何不等于0的数的-n 次幂,等于这个数的n 次幂的倒数.要点诠释:公式中的字母可以表示数,也可以表示单项式,还可以表示多项式;灵活地双向应用运算性质,使运算更加方便、简洁.要点二、整式的乘法1.单项式乘以单项式单项式与单项式相乘,把他们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.2.单项式乘以多项式单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.即mc mb ma c b a m ++=++)((c b a m ,,,都是单项式).3.多项式乘以多项式多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即()()a b m n am an bm bn ++=+++.要点诠释:运算时,要注意积的符号,多项式中的每一项前面的“+”“-”号是性质符号,单项式乘以多项式各项的结果,要用“+”连结,最后写成省略加号的代数和的形式.根据多项式的乘法,能得出一个应用比较广泛的公式:()()()2x a x b x a b x ab ++=+++. 要点三、乘法公式1.平方差公式:22()()a b a b a b +-=-两个数的和与这两个数的差的积,等于这两个数的平方差.要点诠释:在这里,a b ,既可以是具体数字,也可以是单项式或多项式.平方差公式的典型特征:既有相同项,又有“相反项”,而结果是“相同项”的平方减去“相反项”的平方.2. 完全平方公式:()2222a b a ab b +=++;2222)(b ab a b a +-=-两数和 (差)的平方等于这两数的平方和加上(减去)这两数乘积的两倍.要点诠释:公式特点:左边是两数的和(或差)的平方,右边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍.要点四、因式分解把一个多项式化成几个整式的积的形式,像这样的式子变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式.因式分解的方法主要有: 提公因式法, 公式法, 分组分解法, 十字相乘法, 添、拆项法等.要点诠释:落实好方法的综合运用:首先提取公因式,然后考虑用公式;两项平方或立方,三项完全或十字;四项以上想分组,分组分得要合适;几种方法反复试,最后须是连乘式;因式分解要彻底,一次一次又一次.【典型例题】类型一、幂的运算 1、已知25m x =,求6155m x -的值. 【思路点拨】由于已知2m x的值,所以逆用幂的乘方把6m x 变为23()m x ,再代入计算. 【答案与解析】解:∵25m x=, ∴62331115()55520555m m x x -=-=⨯-=. 【总结升华】本题培养了学生的整体思想和逆向思维能力.举一反三:【高清课堂 整式的乘除与因式分解单元复习 例1】【变式】(1)已知246122,9,5===a b c ,比较,,a b c 的大小.(2)比较3020103,9,27大小。
【精选】人教版八年级数学上册 整式的乘法与因式分解(培优篇)(Word版 含解析)

一、八年级数学整式的乘法与因式分解解答题压轴题(难)1.材料:数学兴趣一小组的同学对完全平方公式进行研究:因()20a b -≥,将左边展开得到2220a ab b -+≥,移项可得:222a b ab +≥.数学兴趣二小组受兴趣一小组的启示,继续研究发现:对于任意两个非负数m 、n ,都存在m n +≥m 、n 的和一定存在着一个最小值. 根据材料,解答下列问题:(1)()()2225x y +≥__________(0x >,0y >);221x x ⎛⎫+≥ ⎪⎝⎭___________(0x >);(2)求()5602x x x+>的最小值; (3)已知3x >,当x 为何值时,代数式92200726x x ++-有最小值,并求出这个最小值.【答案】(1)20xy ,2;(2)3)当92x =时,代数式92200726x x ++-的最小值为2019.【解析】【分析】(1)根据阅读材料即可得出结论;(2)根据阅读材料介绍的方法即可得出结论;(3)把已知代数式变为926201326x x -++-,再利用阅读材料介绍的方法,即可得到结论.【详解】(1)∵0x >,0y >,∴()()222522520x y x y xy +≥⨯⋅=,∵0x >, ∴221122x x x x ⎛⎫+≥⋅= ⎪⎝⎭; (2)当x 0>时,2x ,52x 均为正数,∴562x x +≥=所以,562x x +的最小值为(3)当x 3>时,2x ,926x -,2x-6均为正数, ∴92200726x x ++- 92x 6201326x =-++-20132013≥= 2019= 由()20a b -≥可知,当且仅当a b =时,22a b +取最小值, ∴当92626x x -=-,即92x =时,有最小值.∵x 3> 故当92x =时,代数式92200726x x ++-的最小值为2019. 【点睛】 本题考查了完全平方公式的变形应用,解答本题的关键是理解阅读材料所介绍的方法.2.阅读下列材料,然后解答问题:问题:分解因式:3245x x +-.解答:把1x =带入多项式3245x x +-,发现此多项式的值为0,由此确定多项式3245x x +-中有因式()1x -,于是可设()()322451x x x x mx n +-=-++,分别求出m ,n 的值.再代入()()322451x x x x mx n +-=-++,就容易分解多项式3245x x +-,这种分解因式的方法叫做“试根法”.(1)求上述式子中m ,n 的值;(2)请你用“试根法”分解因式:3299x x x +--.【答案】(1)5m =,5n =;(2)()()()133x x x ++-【解析】【分析】(1)先找出一个x 的值,进而找出一个因式,再将多项式设成分解因式的形式,即可得出结论;(2)先找出x=-1时,得出多项式的值,进而找出一个因式,再将多项式设成分解因式的形式,即可得出结论.【详解】解:(1)把1x =带入多项式3245x x +-,发现此多项式的值为0,∴多项式3245x x +-中有因式()1x -,于是可设322451xx x x mx n , 得出:3232451x x x m x n m x n ,∴14m ,0n m,∴5m =,5n =, (2)把1x =-代入3299x x x +--,多项式的值为0,∴多项式3299x x x +--中有因式()1x +,于是可设322329911x x x x x mx n x m x n m x n ,∴11m +=,9n m,9n =- ∴0m =,9n =-,∴3229133991x x x x x x x x【点睛】此题是分解因式,主要考查了试根法分解因式的理解和掌握,解本题的关键是理解试根法分解因式.3.把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.例如,由图1,可得等式:(a+2b )(a+b )=a 2+3ab+2b 2(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c 的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c =11,ab+bc+ac =38,求a 2+b 2+c 2的值.(3)如图3,将两个边长分别为a 和b 的正方形拼在一起,B ,C ,G 三点在同一直线上,连接BD 和BF .若这两个正方形的边长满足a+b =10,ab =20,请求出阴影部分的面积.【答案】(1)(a+b+c )2=a 2+b 2+c 2+2ab+2bc+2ac ;(2)45;(3)20.【解析】【分析】(1)此题根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积,种是大正方形的面积,可得等式(a+b+c )2=a 2+b 2+c 2+2ab+2bc+2ac ;(2)利用(1)中的等式直接代入求得答案即可;(3)利用S 阴影=正方形ABCD 的面积+正方形ECGF 的面积-三角形BGF 的面积-三角形ABD 的面积求解.【详解】(1)(a+b+c )2=a 2+b 2+c 2+2ab+2bc+2ac ;(2)∵a+b+c=11,ab+bc+ac=38,∴a 2+b 2+c 2 =(a+b+c )2﹣2(ab+ac+bc )=121﹣76=45;(3)∵a+b=10,ab=20,∴S 阴影=a 2+b 2﹣12(a+b )•b ﹣12a 2 =12a 2+12b 2﹣12ab =12(a+b )2﹣32ab =12×102﹣32×20 =50﹣30=20.【点睛】 本题考查了完全平方公式几何意义,解题的关键是注意图形的分割与拼合,会用不同的方法表示同一图形的面积.4.若一个整数能表示成22a b +(a ,b 是整数)的形式,则称这个数为“完美数”.例如,5是“完美数”,因为22521=+.再如,()222222M x xy y x y y =++=++(x ,y 是整数),所以M 也是“完美数”. (1)请你再写一个小于10的“完美数”,并判断29是否为“完美数”;(2)已知224412S x y x y k =++-+(x ,y 是整数,是常数),要使S 为“完美数”,试求出符合条件的一个2200-0=值,并说明理由.(3)如果数m ,n 都是“完美数”,试说明mn 也是“完美数”..【答案】(1)8、29是完美数(2)S 是完美数(3)mn 是完美数【解析】【分析】(1)利用“完美数”的定义可得;(2)利用配方法,将S 配成完美数,可求k 的值(3)根据完全平方公式,可证明mn 是“完美数”;【详解】(1) 22228,8+=∴是完美数;222925,29=+∴是完美数(2) ()222)2313S x y k =++-+-( 13.k S ∴=当时,是完美数(3) 2222,m a b n c d 设=+=+,则()()()()222222mn a bc d ac bd ad bc =++=++- 即mn 也是完美数.【点睛】本题考查了因式分解的应用,完全平方公式的运用,阅读理解题目表述的意思是本题的关键.5.观察下列等式:22()()a b a b a b -=-+3322()()a b a b a ab b -=-++443223()()a b a b a a b ab b -=-+++55432234()()a b a b a a b a b ab b -=-++++完成下列问题:(1)n n a b -=___________(2)636261322222221+++⋯⋯++++= (结果用幂表示).(3)已知4,1a b ab -==,求33a b -.【答案】(1)(a-b )(a n-1+a n-2b+…+ab n-2+b n-1);(2)264-1;(3)76.【解析】【分析】(1)根据规律可得结果(a-b )(a n-1+a n-2b+…+a b n-2+b n-1);(2)利用(1)得出的规律先计算(2-1)63626132(2222221+++⋯⋯++++)即可得出结果;(3)利用(1)得出的规律变形,再用完全平方公式进行变形,变成只含a-b 及ab 的形式,整体代入计算即可得到结果.【详解】解:(1)()()22a b a b a b -=-+,()()3322a b a b a ab b -=-++,()()443223a b a b a a b ab b -=-+++, ()()55432234a b a b a a b a b ab b -=-++++, 由此规律可得:a n -b n =(a-b )(a n-1+a n-2b+…+ab n-2+b n-1),故答案是:(a-b )(a n-1+a n-2b+…+ab n-2+b n-1);(2)由(1)的规律可得(2-1)()636261322222221+++⋯⋯++++=264-1,∴636261322222221+++⋯⋯++++=264-1.故答案是:264-1.(3)已知4,1a b ab -==,求33a b -.()()3322a b a b a ab b -=-++=()() [a b a b --2+3 a b ]∴33a b -=24431⨯+⨯()=76. 故答案是:76.【点睛】此题考查了多项式乘以多项式,弄清题中的规律是解本题的关键.6.(1)填空:()()a b a b -+= ;22()()a b a ab b -++= ;3223()()a b a a b ab b -+++= .(2)猜想:1221()(...)n n n n a b a a b ab b -----++++= (其中n 为正整数,且2n ≥).(3)利用(2)猜想的结论计算:98732222...222-+-+-+.【答案】(1)22a b -,33a b -,44a b -;(2)n n a b -;(3)342.【解析】试题分析:(1)根据平方差公式与多项式乘以多项式的运算法则运算即可;(2)根据(1)的规律可得结果;(3)原式变形后,利用(2)得出的规律计算即可得到结果.试题解析:(1)()()a b a b -+=22a b -;3223()()a b a a b ab b -+++=33a b -;3223()()a b a a b ab b -+++=44a b -;故答案为22a b -,33a b -,44a b -;(2)由(1)的规律可得:原式=n n a b -,故答案为n n a b -;(3)令98732222...222S =-+-+-+,∴987321222...2221S -=-+-+-+-=98732[2(1)](222...2221)3---+-+-+-÷=10(21)3(10241)3341-÷=-÷=,∴S=342.考点:1.平方差公式;2.规律型.7.阅读下列因式分解的过程,再回答所提出的问题:1+x +x (x +1)+x (x +1)2=(1+x )[1+x +x (x +1)]=(1+x )2(1+x )=(1+x )3(1)上述分解因式的方法是,共应用了次.(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,则需应用上述方法次,结果是 .(3)分解因式:1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n为正整数).【答案】(1)提公因式,两次;(2)2004次,(x+1)2005;(3) (x+1)1n+【解析】【分析】(1)根据已知材料直接回答即可;(2)利用已知材料进而提取公因式(1+x),进而得出答案;(3)利用已知材料提取公因式进而得出答案.【详解】(1)上述分解因式的方法是:提公因式法,共应用了2次.故答案为提公因式法,2次;(2)1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,=(1+x)[1+x+x(1+x)+…+ x(x+1)2003]⋯=22003(1) (1)(1)(1)(1)xx x x x+++++个=(1+x)2005,故分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,,则需应用上述方法2004次,结果是:(x+1)2005.(3)分解因式:1+x+x(x+1)+x(x+1)2…+x(x+1)n(n为正整数)的结果是:(x+1)n+1.故答案为(x+1)n+1.【点睛】此题主要考查了提取公因式法分解因式,正确提取公因式是解题关键.8.阅读理解:把两个相同的数连接在一起就得到一个新数,我们把它称为“连接数”,例如:234234,3939…等,都是连接数,其中,234234称为六位连接数,3939称为四位连接数.(1)请写出一个六位连接数,它(填“能”或“不能”)被13整除.(2)是否任意六位连接数,都能被13整除,请说明理由.(3)若一个四位连接数记为M,它的各位数字之和的3倍记为N,M﹣N的结果能被13整除,这样的四位连接数有几个?【答案】(1)证明见解析(2)abcabc能被13整除(3)这样的四位连接数有1919,2525,3131,一共3个【解析】分析:(1)根据六位连接数的定义可知123123为六位连接数,再将123123进行因数分解,判断得出它能被13整除;(2)设abcabc为六位连接数,将abcabc进行因数分解,判断得出它能被13整除;(3)设xyxy 为四位连接数,用含x 、y 的代数式表示M 与N ,再计算M ﹣N ,然后将13M N -表示为77x +7y +3413x y +,根据M ﹣N 的结果能被13整除以及M 与N 都是1~9之间的整数,求得x 与y 的值,即可求解.详解:(1)123123为六位连接数;∵123123=123×1001=123×13×77,∴123123能被13整除;(2)任意六位连接数都能被13整除,理由如下:设abcabc 为六位连接数.∵abcabc =abc ×1001=abc ×13×77,∴abcabc 能被13整除;(3)设xyxy 为四位连接数,则M =1000x +100y +10x +y =1010x +101y ,N =3(x +y +x +y )=6x +6y ,∴M ﹣N =(1010x +101y )﹣(6x +6y )=1004x +95y ,∴13M N -=10049513x y +=77x +7y +3413x y +.∵M ﹣N 的结果能被13整除,∴3413x y +是整数.∵3x +4y 取值范围大于3小于63,所以能被13整除的数有13,26,39,52,∴x =1,y =9;x =2,y =5;x =3,y =1;x =8,y =7;x =9,y =3;x =5,y =6;x =6,y =2;满足条件的四位连接数的3131,2525,6262,9393,8787,5656,1919共7个. 点睛:本题考查了因式分解的应用,整式的运算,理解“连接数”的定义是解题的关键.9.(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b )2=a 2+2ab+b 2,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式: .(2)利用(1)中得到的结论,解决下面的问题:若a+b+c =10,ab+ac+bc =35,则a 2+b 2+c 2= .(3)小明同学用图3中x 张边长为a 的正方形,y 张边长为b 的正方形,z 张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z=.(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:.【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)30;(3)9;(4)x3﹣x=(x+1)(x﹣1)x【解析】【分析】(1)依据正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,可得等式;(2)依据a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,进行计算即可;(3)依据所拼图形的面积为:xa2+yb2+zab,而(2a+b)(a+2b)=2a2+4ab+ab+2b2=2a2+5b2+2ab,即可得到x,y,z的值.(4)根据原几何体的体积=新几何体的体积,列式可得结论.【详解】(1)由图2得:正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,∵a+b+c=10,ab+ac+bc=35,∴102=a2+b2+c2+2×35,∴a2+b2+c2=100﹣70=30,故答案为:30;(3)由题意得:(2a+b)(a+2b)=xa2+yb2+zab,∴2a2+5ab+2b2=xa2+yb2+zab,∴225xyz=⎧⎪=⎨⎪=⎩,∴x+y+z=9,故答案为:9;(4)∵原几何体的体积=x3﹣1×1•x=x3﹣x,新几何体的体积=(x+1)(x﹣1)x,∴x3﹣x=(x+1)(x﹣1)x.故答案为:x3﹣x=(x+1)(x﹣1)x.【点睛】本题主要考查的是整式的混合运算,利用直接法和间接法分别求得几何图形的体积或面积,然后根据它们的体积或面积相等列出等式是解题的关键.10.(探究)如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,有阴影部分沿虚线剪开,拼成图②的长方形(1)请你分别表示出这两个图形中阴影部分的面积(2)比较两图的阴影部分面积,可以得到乘法公式 (用字母表示)(应用)请应用这个公式完成下列各题①已知22412m n -=,24m n +=,则2m n -的值为②计算:(2)(2)a b c a b c +--+(拓展)①()()()()24832(21)21212121+1+++++结果的个位数字为 ②计算:222222221009998974321-+-++-+-【答案】[探究](1)a 2﹣b 2;(a +b )(a ﹣b );(2)(a +b )(a ﹣b )=a 2﹣b 2;[应用]①3;②4a 2﹣b 2+2bc ﹣c 2;[拓展]①6;②5050.【解析】【分析】[探究](1)由面积公式可得答案;(2)公式由(1)直接可得;[应用]①用平方差公式分解4m 2﹣n 2,将已知值代入可求解;②将三项恰当组分成两组,先用平方差,再用完全平方公式展开后合并同类项即可;[拓展]①将原式乘以(2﹣1),就可以反复运用平方差公式化简,最后按照循环规律可得解;②将原式从左向右依次两项一组,运用平方差公式分解,化为100+99+98+…+4+3+2+1,从而可得答案.【详解】(1)图①按照正方形面积公式可得:a 2﹣b 2;图②按照长方形面积公式可得:(a +b )(a ﹣b ).故答案为:a 2﹣b 2;(a +b )(a ﹣b ).(2)令(1)中两式相等可得:(a +b )(a ﹣b )=a 2﹣b 2故答案为:(a +b )(a ﹣b )=a 2﹣b 2.【应用】①∵4m 2﹣n 2=12,2m +n =4,4m 2﹣n 2=(2m +n )(2m ﹣n ),∴(2m ﹣n )=12÷4=3. 故答案为:3.②(2a +b ﹣c )(2a ﹣b +c )=[2a +(b ﹣c )][2a ﹣(b ﹣c )]=4a 2﹣(b ﹣c )2=4a 2﹣b 2+2bc ﹣c 2【拓展】①原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1=(24﹣1)(24+1)(28+1)…(232+1)+1=(28﹣1)(28+1)…(232+1)+1=(216﹣1)…(232+1)+1=264﹣1+1=264.∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16.故答案为:6.②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)=100+99+98+97+…+4+3+2+1=5050.【点睛】本题考查了平方差公式的几何背景及其应用与拓展,计算具有一定的难度,属于中档题.。
人教版数学八年级上册 整式的乘法与因式分解(培优篇)(Word版 含解析)

人教版数学八年级上册 整式的乘法与因式分解(培优篇)(Word版 含解析)一、八年级数学整式的乘法与因式分解选择题压轴题(难)1.多项式x 2﹣4xy ﹣2y +x +4y 2分解因式后有一个因式是x ﹣2y ,另一个因式是( ) A .x +2y +1B .x +2y ﹣1C .x ﹣2y +1D .x ﹣2y ﹣1【答案】C【解析】【分析】首先将原式重新分组,进而利用完全平方公式以及提取公因式法分解因式得出答案.【详解】解:x 2﹣4xy ﹣2y +x +4y 2=(x 2﹣4xy +4y 2)+(x ﹣2y )=(x ﹣2y )2+(x ﹣2y )=(x ﹣2y )(x ﹣2y +1).故选:C .【点睛】此题考察多项式的因式分解,项数多需用分组分解法,在分组后得到两项中含有公因式(x-2y ),将其当成整体提出,进而得到答案.2.若()(1)x m x +-的计算结果中不含x 的一次项,则m 的值是( )A .1B .-1C .2D .-2.【答案】A【解析】【分析】根据多项式相乘展开可计算出结果.【详解】 ()()1x m x +-=x 2+(m-1)x-m ,而计算结果不含x 项,则m-1=0,得m=1.【点睛】本题考查多项式相乘展开系数问题.3.如果多项式29x kx -+能用公式法分解因式,那么k 的值是( )A .3B .6C .3±D .6±【答案】D【解析】由于可以利用公式法分解因式,所以它是一个完全平方式222a ab b ±+,所以236k =±⨯=±.故选D.4.已知4821可以被在0~10之间的两个整数整除,则这两个数是()A.1、3 B.3、5 C.6、8 D.7、9【答案】D【解析】248-1=(224+1)(224-1)= (224+1)(212+1)(212-1)= (224+1)(212+1)(26+1)(26-1)= (224+1)(212+1)(26+1)(23+1) (23-1) , 23+1=9, 23-1=7,所以这两个数是7、9.故选D.点睛:平方差公式:a2-b2=(a+b)(a-b).5.已知实数a、b满足a+b=2,ab=34,则a﹣b=()A.1 B.﹣52C.±1 D.±52【答案】C【解析】分析:利用完全平方公式解答即可.详解:∵a+b=2,ab=34,∴(a+b)2=4=a2+2ab+b2,∴a2+b2=52,∴(a-b)2=a2-2ab+b2=1,∴a-b=±1,故选C.点睛:本题考查了完全平方公式的运用,熟记公式结构是解题的关键.6.已知4y2+my+9是完全平方式,则m为()A.6 B.±6 C.±12 D.12【答案】C【解析】【分析】原式利用完全平方公式的结构特征求出m的值即可.【详解】∵4y2+my+9是完全平方式,∴m=±2×2×3=±12.故选:C.【点睛】此题考查完全平方式,熟练掌握完全平方公式是解题的关键.7.通过计算几何图形的面积可表示代数恒等式,图中可表示的代数恒等式是( )A .22()()a b a b a b +-=-B .222()2a b a ab b +=++C .22()22a a b a ab +=+D .222()2a b a ab b -=-+【答案】A【解析】【分析】 根据阴影部分面积的两种表示方法,即可解答.【详解】图1中阴影部分的面积为:22a b -,图2中的面积为:()()a b a b +-,则22()()a b a b a b +-=-故选:A.【点睛】本题考查了平方差公式的几何背景,解决本题的关键是表示阴影部分的面积.8.下面计算正确的是( )A .33645x x x +=B .236a a a ⋅=C .()4312216x x -=D .()()22222x y x y x y +-=- 【答案】C【解析】【分析】A.合并同类项得到结果;B.利用同底数幂的乘法法则计算得到结果;C.利用幂的乘方与积的乘方运算法则计算得到结果;D.利用平方差公式计算得到结果,即可作出判断.【详解】A.原式=35x ,错误;B.原式=5a ,错误;C.原式=1216x ,正确;D.原式=224x y -,错误.故选C.【点睛】本题主要考查同底数幂的乘法,合并同类项,幂的乘方与积的乘方,平方差公式运算,熟知其运算法则是解题的关键.9.下列由左到右的变形,属于因式分解的是( )A .2(2)(2)4x x x +-=-B .242(4)2x x x x +-=+-C .24(2)(2)x x x -=+-D .243(2)(2)3x x x x x -+=+-+ 【答案】C【解析】【分析】根据因式分解的意义,可得答案.【详解】A. 是整式的乘法,故A 错误;B. 没把一个多项式转化成几个整式积的形式,故B 错误;C. 把一个多项式转化成几个整式积的形式,故C 正确;D 没把一个多项式转化成几个整式积的形式,故D 错误.故答案选:C.【点睛】本题考查的知识点是因式分解的意义,解题的关键是熟练的掌握因式分解的意义.10.下列等式由左边向右边的变形中,属于因式分解的是 ( )A .x 2+5x -1=x(x+5)-1B .x 2-4+3x=(x+2)(x -2)+3xC .(x+2)(x -2)=x 2-4D .x 2-9=(x+3)(x -3)【答案】D【解析】【分析】根据因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,判断求解.【详解】解:A 、右边不是积的形式,故A 错误;B 、右边不是积的形式,故B 错误;C 、是整式的乘法,故C 错误;D 、x 2-9=(x+3)(x -3),属于因式分解.故选D .【点睛】此题主要考查因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.二、八年级数学整式的乘法与因式分解填空题压轴题(难)11.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了n(a b)(n +为非负整数)展开式的项数及各项系数的有关规律.例如:0(a b)1+=,它只有一项,系数为1;系数和为1;1(a b)a b +=+,它有两项,系数分别为1,1,系数和为2;222(a b)a 2ab b +=++,它有三项,系数分别为1,2,1,系数和为4;33223(a b)a 3a b 3ab b +=+++,它有四项,系数分别为1,3,3,1,系数和为8;⋯,则n (a b)+的展开式共有______项,系数和为______.【答案】n 1+ n 2【解析】【分析】本题通过阅读理解寻找规律,观察可得(a+b )n (n 为非负整数)展开式的各项系数的规律:首尾两项系数都是1,中间各项系数等于(a+b )n-1相邻两项的系数和.因此根据项数以及各项系数的和的变化规律,得出(a+b )n 的项数以及各项系数的和即可.【详解】根据规律可得,(a+b )n 共有(n+1)项,∵1=201+1=211+2+1=221+3+3+1=23∴(a+b )n 各项系数的和等于2n故答案为n+1,2n【点睛】本题主要考查了完全平方式的应用,能根据杨辉三角得出规律是解此题的关键.在应用完全平方公式时,要注意:①公式中的a ,b 可是单项式,也可以是多项式;②对形如两数和(或差)的平方的计算,都可以用这个公式.12.分解因式212x 123y xy y -+-=___________【答案】()232x 1y --【解析】根据因式分解的方法,先提公因式-3y ,再根据完全平方公式分解因式为:()()22212x 12334x 41321y xy y y x y x -+-=--+=--. 故答案为()232x 1y --.13.因式分解:214y y ++=______ 【答案】212y ⎛⎫+ ⎪⎝⎭ 【解析】根据完全平方公式()2222a ab b a b ±+=±进行因式分解为:2222111124222y y y y y ⎛⎫⎛⎫++=+⨯+=+ ⎪ ⎪⎝⎭⎝⎭. 故答案为:212y ⎛⎫+ ⎪⎝⎭ .14.4x(m -n)+8y(n -m)2中各项的公因式是________.【答案】4(m -n)【解析】根据题意,先变形为4x(m -n)+8y(m -n)2,把m-n 看做一个整体,即可找到公因式4(m-n ).故答案为:4(m-n ).点睛:此题主要考查了提公因式法因式分解,根据公因式的特点,利用整体法确定公因式即可,关键是要把n-m 与m-n 变形为统一的式子.15.若m+1m =3,则m 2+21m =_____. 【答案】7【解析】分析:把已知等式两边平方,利用完全平方公式化简,即可求出答案.详解:把m+1m =3两边平方得:(m+1m )2=m 2+21m +2=9, 则m 2+21m =7, 故答案为:7点睛:此题考查了分式的混合运算,以及完全平方公式,熟练掌握运算法则及公式是解本题的关键.16.分解因式:x 3y ﹣2x 2y+xy=______.【答案】xy (x ﹣1)2【解析】【分析】原式提取公因式,再利用完全平方公式分解即可.【详解】解:原式=xy (x 2-2x+1)=xy (x-1)2.故答案为:xy (x-1)2【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.17.若(x+p)与(x+5)的乘积中不含x的一次项,则p=_____.【答案】-5【解析】【分析】根据多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn计算,再根据乘积中不含x的一次项,得出它的系数为0,即可求出p的值.【详解】解:(x+p)(x+5)=x2+5x+px+5p=x2+(5+p)x+5p,∵乘积中不含x的一次项,∴5+p=0,解得p=﹣5,故答案为:﹣5.18.因式分解:3x3﹣12x=_____.【答案】3x(x+2)(x﹣2)【解析】【分析】先提公因式3x,然后利用平方差公式进行分解即可.【详解】3x3﹣12x=3x(x2﹣4)=3x(x+2)(x﹣2),故答案为3x(x+2)(x﹣2).【点睛】本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.19.分解因式:2x2﹣8=_____________【答案】2(x+2)(x﹣2)【解析】【分析】先提公因式,再运用平方差公式.【详解】2x2﹣8,=2(x2﹣4),=2(x+2)(x﹣2).【点睛】考核知识点:因式分解.掌握基本方法是关键.20.已知(2x 21)(3x 7)(3x 7)(x 13)-----可分解因式为(3x a)(x b)++,其中a 、b 均为整数,则a 3b +=_____.【答案】31-.【解析】首先提取公因式3x ﹣7,再合并同类项即可根据代数式恒等的条件得到a 、b 的值,从而可算出a+3b 的值:∵()()()()(2x 21)(3x 7)(3x 7)(x 13)3x 72x 21x 133x 7x 8-----=---+=--, ∴a=-7,b=-8.∴a 3b 72431+=--=-.。
人教版八年级数学上册 整式的乘法与因式分解(培优篇)(Word版 含解析)

人教版八年级数学上册 整式的乘法与因式分解(培优篇)(Word 版 含解析)一、八年级数学整式的乘法与因式分解选择题压轴题(难)1.已知226a b ab +=,且a>b>0,则a b a b+-的值为( ) A .2B .±2C .2D .±2 【答案】A【解析】【分析】已知a 2+b 2=6ab ,变形可得(a+b )2=8ab ,(a-b )2=4ab ,可以得出(a+b )和(a-b )的值,即可得出答案.【详解】∵a 2+b 2=6ab ,∴(a+b )2=8ab ,(a-b )2=4ab ,∵a >b >0,∴a+b=8ab ,a-b=4ab ,∴a b a b +-=824ab ab=, 故选A.【点睛】本题考查了分式的化简求值问题,观察式子可以得出应该运用完全平方式来求解,要注意a 、b 的大小关系以及本身的正负关系.2.有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为 ( )A .6B .7C .8D .9【答案】C【解析】【分析】设2为a ,3为b ,则根据5张边长为2的正方形纸片的面积是5a 2,4张边长分别为2、3的矩形纸片的面积是4ab ,6张边长为3的正方形纸片的面积是6a 2,得出a 2+4ab+4b 2=(a+2b )2,再根据正方形的面积公式将a 、b 代入,即可得出答案.【详解】解:设2为a ,3为b ,则根据5张边长为2的正方形纸片的面积是5a 2,4张边长分别为2、3的矩形纸片的面积是4ab,6张边长为3的正方形纸片的面积是6b2,∵a2+4ab+4b2=(a+2b)2,(b>a)∴拼成的正方形的边长最长可以为a+2b=2+6=8,故选C.【点睛】此题考查了完全平方公式的几何背景,关键是根据题意得出a2+4ab+4b2=(a+2b)2,用到的知识点是完全平方公式.3.因式分解x2+mx﹣12=(x+p)(x+q),其中m、p、q都为整数,则这样的m的最大值是()A.1 B.4 C.11 D.12【答案】C【解析】分析:根据整式的乘法和因式分解的逆运算关系,按多项式乘以多项式法则把式子变形,然后根据p、q的关系判断即可.详解:∵(x+p)(x+q)= x2+(p+q)x+pq= x2+mx-12∴p+q=m,pq=-12.∴pq=1×(-12)=(-1)×12=(-2)×6=2×(-6)=(-3)×4=3×(-4)=-12∴m=-11或11或4或-4或1或-1.∴m的最大值为11.故选C.点睛:此题主要考查了整式乘法和因式分解的逆运算的关系,关键是根据整式的乘法还原因式分解的关系式,注意分类讨论的作用.4.已知x-y=3,12x z-=,则()()22554y z y z-+-+的值等于()A.0 B.52C.52-D.25【答案】A【解析】【分析】此题应先把已知条件化简,然后求出y-z的值,代入所求代数式求值即可.【详解】由x-y=3,12x z-=得:()()x z x y y z---=-15322 =-=-;把52-代入原式,可得255252525255=0224424⎛⎫⎛⎫-+-+-+= ⎪ ⎪⎝⎭⎝⎭. 故选:A .【点睛】此题考查的是学生对代数式变形方法的理解,这一方法在求代数式值时是常用办法.5.若x 2+2(m+1)x+25是一个完全平方式,那么m 的值( )A .4 或-6B .4C .6 或4D .-6【答案】A【解析】【详解】解:∵x 2+2(m+1)x+25是一个完全平方式,∴△=b 2-4ac=0,即:[2(m+1)]2-4×25=0整理得,m 2+2m-24=0,解得m 1=4,m 2=-6,所以m 的值为4或-6.故选A.6.下列变形,是因式分解的是( )A .2(1)x x x x -=-B .21(1)1x x x x -+=-+C .2(1)x x x x -=-D .2()22a b c ab ac +=+【答案】C【解析】分析:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解. 详解:A 、右边不是整式积的形式,不是因式分解,故本选项错误;B 、右边不是整式积的形式,不是因式分解,故本选项错误;C 、是符合因式分解的定义,故本选项正确;D 、右边不是整式积的形式,不是因式分解,故本选项错误;故选:C .点睛:本题考查了因式分解的知识,理解因式分解的定义是解题关键.7.下列分解因式正确的是( )A .24(4)x x x x -+=-+B .2()x xy x x x y ++=+C .2()()()x x y y y x x y -+-=-D .244(2)(2)x x x x -+=+- 【答案】C【解析】【分析】根据因式分解的步骤:先提公因式,再用公式法分解即可求得答案.注意分解要彻底.【详解】A. ()244x x x x -+=-- ,故A 选项错误; B. ()21x xy x x x y ++=++,故B 选项错误; C. ()()()2x x y y y x x y -+-=- ,故C 选项正确;D. 244x x -+=(x-2)2,故D 选项错误,故选C.【点睛】本题考查了提公因式法,公式法分解因式.注意因式分解的步骤:先提公因式,再用公式法分解.注意分解要彻底.8.下面四个代数式中,不能表示图中阴影部分面积的是( )A .()()322x x x ++-B .25x x +C .()232x x ++D .()36x x ++【答案】B【解析】【分析】依题意可得S S S =-阴影大矩形小矩形、S S S =+阴影正方形小矩形、S S S =+阴影小矩形小矩形,分别可列式,列出可得答案.【详解】解:依图可得,阴影部分的面积可以有三种表示方式:()()322S S x x x -=++-大矩形小矩形;()232S S x x +=++正方形小矩形;()36S S x x +=++小矩形小矩形.故选:B.【点睛】本题考查多项式乘以多项式及整式的加减,关键是熟练掌握图形面积的求法,还有本题中利用割补法来求阴影部分的面积,这是一种在初中阶段求面积常用的方法,需要熟练掌握.9.已知31416181279a b c ===,,,则a b c 、、的大小关系是( )A .a b c >>B .a c b >>C .a b c <<D .b c a >> 【答案】A【解析】【分析】先把a ,b ,c 化成以3为底数的幂的形式,再比较大小.【详解】解:3112412361122a 813b 3c 93a b c.,,,=====>>故选A.【点睛】此题重点考察学生对幂的大小比较,掌握同底数幂的大小比较方法是解题的关键.10.下列从左到右的变形中,属于因式分解的是( )A .()()2224x x x +-=-B .2222()a ab b a b -+=-C .()11am bm m a b +-=+-D .()21(1)1111x x x x ⎛⎫--=--- ⎪-⎝⎭ 【答案】B【解析】【分析】 把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,根据因式分解的定义,即可得到本题的答案.【详解】A .属于整式的乘法运算,不合题意;B .符合因式分解的定义,符合题意;C .右边不是乘积的形式,不合题意;D .右边不是几个整式的积的形式,不合题意;故选:B .【点睛】本题考查了因式分解的定义,即将多项式写成几个因式的乘积的形式,掌握定义是解题的关键.二、八年级数学整式的乘法与因式分解填空题压轴题(难)11.已知a-b=4,ab=6,则22a b += _________.【答案】28【解析】【分析】对完全平方公式进行变形即可解答.【详解】解:∵222()216a b a ab b -=-+=∴22a b +=2()a b -+2ab=16+2×6=28故答案为28.【点睛】本题考查了完全平方公式的应用,掌握完全平方公式并能够进行灵活变形是解答本题的关键.12.因式分解:225101a a -+=______________【答案】()251a -【解析】根据完全平方公式()2222a ab b a b ±+=±进行因式分解为:225101a a -+=()251a -. 故答案为:()251a -.13.将4个数a ,b ,c ,d 排列成2行、2列,两边各加一条竖直线记成a b c d ,定义a bad bc c d =-,上述记号就叫做2阶行列式.若11611x x x x --=-+,则x=_________.【答案】4【解析】【分析】根据题目中所给的新定义运算方法可得方程 (x-1)(x+1)- (x-1)2=6,解方程求得x 即可.【详解】由题意可得,(x-1)(x+1)- (x-1)2=6,解得x=4.故答案为:4.【点睛】本题考查了新定义运算,根据新定义运算的运算方法列出方程是解本题的关键.14.在实数范围内因式分解:22967x y xy --=__________.【答案】11933xy xy ⎛⎫+--- ⎪ ⎪⎝⎭⎝⎭【解析】【分析】将原多项式提取9,然后拆项分组为222189399x y xy ⎛⎫-+- ⎪⎝⎭,利用完全平方公式将前一组分解后,再利用平方差公式继续在实数范围内分解.【详解】解:22967x y xy -- 2227=939x y xy ⎛⎫-- ⎪⎝⎭ 222117=9+3999x y xy ⎛⎫--- ⎪⎝⎭ 218=939xy ⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦11=933xy xy ⎛---+ ⎝⎭⎝⎭=9xy xy ⎛ ⎝⎭⎝⎭故答案为:11933xy xy ⎛+--- ⎝⎭⎝⎭【点睛】本题考查在实数范围内因式分解,利用分组分解法将原多项式“三一”分组后采用公式法因式分解,注意在实数范围内因式分解是指系数可以是根式.15.若a 2+a-1=0,则a 3+2a 2+2014的值是___________.【答案】2015【解析】【分析】根据a 2+a-1=0可得a 2+a=1,对a 3+2a 2+2014进行变形,整体代入即可.【详解】∵a 2+a-1=0∴a 2+a=1a 3+2a 2+2014=a (a 2+a )+a 2+2014=a+a 2+2014=2015故答案为2015【点睛】本题考查的是多项式的乘法,整体代入法是解答的关键.16.(1)已知32m a =,33n b =,则()()332243m n m n m ab a b a +-⋅⋅=______. (2)对于一切实数x ,等式()()212x px q x x -+=+-均成立,则24p q -的值为______.(3)已知多项式2223286x xy y x y +--+-可以分解为()()22x y m x y n ++-+的形式,则3211m n +-的值是______. (4)如果2310x x x +++=,则232016x x x x +++⋅⋅⋅+=______.【答案】(1)5-; (2)9; (3)78-; (4)0. 【解析】【分析】(1)根据积的乘方和幂的乘方,将32m a =整体代入即可;(2)将等式后面部分展开,即可求出p 、q 的值,代入即可;(3)根据多项式乘法法则求出()()22x y m x y n ++-+,即可得到关于m 、n 的方程组,解之即可求得m 、n 、的值,代入计算即可;(4)4个一组提取公因式,整体代入即可.【详解】(1)32m a =,33n a =,()()()()332222343333m n m n m m n m n a b a b a a b a b ∴+-⋅⋅=+-22232343125=+-⨯=+-=-(2)222x px q x x -+=--对一切实数x 均成立,1p ∴=,2q =-249p q ∴-=(3)()()222223286x y m x y n x xy y x y ++-+=+--+-,()()22222322223286x xy y m n x n m y mn x xy y x y ∴+-+++-+=+--+- 21,28,6,m n n m mn +=-⎧⎪∴-=⎨⎪=-⎩解得2,3.m n =-⎧⎨=⎩ 321718m n +∴=-- (4)2310x x x +++=,232016x x x x ∴+++⋅⋅⋅+()()2320132311x x x x x x x x =++++⋅⋅⋅++++000=+⋅⋅⋅+=故答案为: −5;9;78-;0. 【点睛】 本题主要考察幂的运算及整式的乘法,掌握其运算法则是关键.17.(m+n+p+q) (m-n-p-q)=(__________) 2-(__________) 2.【答案】m n+p+q【解析】(m+n+p+q)(m-n-p-q)=[m+(n+p+q)][m-(n+p+q)]=()22m n p q -++,故答案为(1)m ,(2)n+p+q. 点睛:本题主要考查了平方差公式,平方差公式是两个数的和与这两个数的差的积,等于这两个数的平方差,多项式与多项相乘时,要注意观察能否将其中符号相同的项结合成为一项后,再运用平方差公式运算.18.222---x xy y =__________【答案】()2x y -+【解析】根据因式分解的方法,先提公因式“﹣”,再根据完全平方公式分解因式为:()()2222222x xy y x xy y x y ---=-++=-+. 故答案为()2x y -+.点睛:此题主要考查了因式分解,因式分解是把一个多项式化为几个因式积的形式.根据因式分解的一般步骤:一提(公因式)、二套(平方差公式()()22a b a b a b -=+-,完全平方公式()2222a ab b a b ±+=±)、三检查(彻底分解),注意符号的变化.19.分解因式:x 3y ﹣2x 2y+xy=______.【答案】xy (x ﹣1)2【解析】【分析】原式提取公因式,再利用完全平方公式分解即可.【详解】解:原式=xy (x 2-2x+1)=xy (x-1)2.故答案为:xy (x-1)2【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.20.已知x 2+2x =3,则代数式(x +1)2﹣(x +2)(x ﹣2)+x 2的值为_____.【答案】8【解析】【分析】利用完全平方公式及平方差公式把原式第一项和第二项展开,去括号合并同类项得到最简结果,把x2+2x=3代入即可得答案.【详解】原式=x2+2x+1-(x2-4)+x2=x2+2x+1-x2+4+x2=x2+2x+5.∵x2+2x=3,∴原式=3+5=8.故答案为8【点睛】此题考查了整式的混合运算-化简求值,涉及的知识有:完全平方公式,平方差公式,去括号法则,以及合并同类项法则,熟练掌握公式及法则是解本题的关键.。
人教版八年级数学上册 整式的乘法与因式分解(培优篇)(Word版 含解析)

人教版八年级数学上册 整式的乘法与因式分解(培优篇)(Word版 含解析)一、八年级数学整式的乘法与因式分解选择题压轴题(难)1.将多项式24x +加上一个整式,使它成为完全平方式,则下列不满足条件的整式是( ) A .4-B .±4xC .4116xD .2116x 【答案】D【解析】【分析】分x 2是平方项与乘积二倍项,以及单项式的平方三种情况,根据完全平方公式讨论求解.【详解】解:①当x 2是平方项时,4士4x+x ²=(2士x )2,则可添加的项是4x 或一4x ;②当x 2是乘积二倍项时,4+ x 2+4116x =(2+214x )2,则可添加的项是4116x ; ③若为单项式,则可加上-4.故选:D.【点睛】本题考查了完全平方式,比较复杂,需要我们全面考虑问题,首先考虑三个项分别充当中间项的情况,就有三种情况,还有就是第四种情况加上一个数,得到一个单独的单项式,也是可以成为一个完全平方式,这种情况比较容易忽略,要注意.2.已知243m -m-10m -m -m 2=+,则计算:的结果为( ).A .3B .-3C .5D .-5【答案】A【解析】【分析】观察已知m 2-m-1=0可转化为m 2-m=1,再对m 4-m 3-m+2提取公因式因式分解的过程中将m 2-m 作为一个整体代入,逐次降低m 的次数,使问题得以解决.【详解】∵m 2-m-1=0,∴m 2-m=1,∴m 4-m 3-m+2=m 2 (m 2-m)-m+2=m 2-m+2=1+2=3,故选A .【点睛】本题考查了因式分解的应用,解决本题的关键是将m 2-m 作为一个整体出现,逐次降低m 的次数.3.若代数式x 2+ax +64是一个完全平方式,则a 的值是( )A.-16 B.16 C.8 D.±16【答案】D【解析】试题分析:根据完全平方式的意义,首平方,尾平方,中间加减积的2倍,可知a=±2×8=16.故选:D点睛:此题主要考查了完全平方式的意义,解题关键是明确公式的特点,即:完全平方式分两种,一种是完全平方和公式,就是两个整式的和括号外的平方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十四章整式的乘除及因式分解23.同底数幂的乘法 基础题训练 1、计算 的结果是( B ) A 、B 、C 、D 、2、下列计算正确的是( D ) A 、B 、C 、D 、3、下面计算不正确的是( D ) A 、B 、C 、D 、4、①834a a a a =⋅⋅ ②()()953)-(x x x x -=-⋅-⋅ ③14122++=⋅m m m x xx 5、①963)()()(b a b a b a -=-⋅- ② 16)2(222-=-•- ③1385313131-=⎪⎭⎫⎝⎛-⋅⎪⎭⎫⎝⎛-6、计算①1025-x x x ⋅⋅ ② ()()()389222-⋅-⋅- ③735262a a a a a a ⋅+⋅+⋅【解】: 17-x 【解】:202 【解】:0④()()632a ⋅-⋅-a a ⑤)1()1()123-⋅-⋅-a a a ( ⑥()()()32b ac a c b c b a +--+-- 【解】:11-a 【解】:()61-a 【解】:()6c b a ---7、在等式()112a a a =⋅⋅中,括号里的代数式为8a .8、若20091000510101010=⋅⋅n ,则1004=n . 9、若()()()262x y y x p -=--(p 为大于3的整数),则括号里应为()62--p y x .10、若n b a n m、(m .2,2==为正整数),则ab mn =2.11、若y x 、是正整数,且5333=⋅yx,则y x 、的值有4对.12、计算:13553213520062007=⎪⎭⎫ ⎝⎛⋅⎪⎭⎫⎝⎛. 13、①若,3222=+x 则;3=x ②若,81312=+x 则23=x 14、计算:()()2009200833-⋅-.【解】:看不清15、已知,302,52,32===cb a 求c b a 、、之间的关系. 【解】: c b a c b a baba=++∴=∴=⋅⋅∴=⋅++1,22,30222,1522124.幂的乘方 基础题训练 1、①()824x x = ②()1234y y -=- ③()m ma a 44= ④()824y y =-.2、①()[]();22933b a b a -=- ②()();276253a a a -=-⋅-③()()[]();11332y x y x y x -=--3、()()()861246848a a a a ===4、下列计算错误的是( B )A 、43a a a =⋅ B 、1234a a a =⋅ C 、()632a a = D 、5552a a a =+5、下列各式正确的是( B ) A 、()832m m= B 、()632m m= C 、()[]6222m m= D 、()422m m =--6、若(),32ab M -=那么2M -的正确结果是( C ) A 、126b a B 、85b a C 、126b a - D 、63b a - 7、计算 ①()()()322332a a a -⋅-⋅ ②()()52332y y y y ⋅-+ ③()()422332a a a a ⋅--+-【解】:18a - 【解】:6y 【解】:6a - ④()[]()[]4232b a b a +⋅+ ⑤()()a a a a a a a⋅⋅-+⋅⋅-233435635【解】:()14b a + 【解】:12a中档题训练 8、 若,32=na则()2723=na .1、 若n 是正整数,当1-=a 时,().1122=--+n n a2、 已知 ,2168222=⋅⋅nn 则3=n .3、 若,610,510==ba则54001032=+b a . 4、 已知,2,333==n mb a求()()n m n m n mb a b a b a 242332⋅⋅-+的值.【解】: 7-5、 若,0352=-+y x 求yx324⋅的值. 【解】:原式=.8222235252===⋅+y x y x综合题训练6、 阅读下列解题过程. 试比较1002与753的大小. 【解】:()()25253752525410027331622====,7510032 ∴请根据上述解答过程,比较334455432、、的大小. 【解】:()()().34264448133,3222443355111133311114441111555 ∴======,,25.积的乘方基础题训练1、①()222n m mn = ②()363282y x yx -=-③93338121n m mn =⎪⎭⎫⎝⎛ ④()623104102⨯=⨯-2、若(),682b a b a n m =则3,4==n m .3、①()[]184332ba ab-=- ②()81-81820072006=⎪⎭⎫ ⎝⎛-⋅-.4、下列计算正确的是( D )A 、()33xy xy = B 、()33322y x xy = C 、()93362x x -=- D 、()8442y x xy =-5、若m 正整数时,在①()m ma a 22=②()m ma a 22=③()m ma a 22=-④()m ma a 22=-⑤()()m mm a a a 2=-⋅-中,等式成立的个数是( C )A 、2个B 、3个C 、4个D 、5个 6、计算 ①()()3222222-b a ba -⋅ ②()()()()32223282-y x x y x --⋅+【解】:81032b a - 【解】:3616y x -③()()()337232354.3a a a a a -⋅-+- 【解】:9100a -7、先化简,再求值:()3223321⎪⎭⎫⎝⎛-+-ab b a ,其中.4,41==b a【解】:568763=b a . 中档题训练8、若,3,2==xxb a 则()14422=xba . 9、计算:()()[].15-04.0220092009=⨯10、若a28233=⨯,则()1112009-=-a . 11、当n 满足 n 是奇数时,().nnx x --12、若,452=+n m 求nm324⨯的值. 【解】:16 13、若()()()()n n nm n mn m y x y x y x y x x y y x 求,且,)()(9555-=--+++-+的值.【解】:216.综合题训练 14、若,1089312=+-n n 求()nn 22-的值.【解】:.4223)31(3,3122333231223212==⨯=+=-⨯=+--原式n n n n n26.单项式乘以单项式基础题训练1、下列计算正确的是( D )A 、632623a a a =⋅ B 、2221243x x x =⋅ C 、1553842a a a =⋅ D 、5321553a a a =⋅ 2、式子14+m x可以写成( B )A 、()41+m x B 、mx x 4⋅ C 、()mm x 13+ D 、x xm+43、式子()()32345.2-m m -⋅的计算结果是( D )A 、9100m B 、9100m - C 、9400m D 、9400m4、计算:①()()c b a c ab b a 3322623-=-⋅;②()()z y x yx z y x m n nn n 1562231+++-=-;5、一种电子计算机每秒可以做8106⨯次运算,它的工作2108⨯秒可以做11108.4⨯次运算.6、计算:①()();2232ab ab a -⨯-⨯ ②();22123332z xy xy ⋅⎪⎭⎫⎝⎛-【解】:464b a 【解】:2156z y x -中档题训练 7、若()15105y x xy y x mn =⋅,则9)1(3=+m m ,8、当0 a 时,()0122+⋅--n na a 成立,则n 为( B )A 、奇数B 、偶数C 、自然数D 、以上都不对 9、魏明家新购一套结构如图的住房,正准备装修, ⑴用代数式表示这套住房的面积;⑵若m y m x 3,5.2==,装修客厅和卧室至少需要准备多少面积的木地板? 【解】:⑴ xy 15 ⑵ 9010、已知n 为正整数,且,73=nx 求()()nnx x 323243-的值.【解】:1127 11、已知3,2==n ma a,求①n m a +3,②n m a 32+的值.【解】:①24 ②108 12、若n m y x2132-+与m n y x ---364的积与y x 44-是同类项,求n m 、的值.【解】:.3,2==m n综合题训练13、已知199837323=⋅⋅cba,其中c b a 、、味整数,求()1998c b a --的值.【解】: 3732373233*⨯=⋅⋅c ba,1,1,1===∴c b a原式1)111(1998=--=27.多项式乘以多项式基础题训练1、计算:()()1523-2--⋅x x x 的结果是( B )A 、x x x 315622---B 、x x x 315623++- 2、计算:)132(42-+-a a a 的结果是( C ) A 、a a a 412823-+- B 、112823+--a a 3、计算)1()1(a a a a --+的结果为( B ) A 、a 2 B 、22a C 、0 D 、a a 22+-4、一个三角形的底为m 2,高为n m 2+,它的面积是( B ) A 、mn m 422+ B 、mn m 22+ C 、mn m 42+ D 、mn m 222+ 5、计算:ab b a b a ab b a ab 262)13(2-333322+--=-+. 6、①()333222)(2xy y x xy y x -=-. 7、①xy xy y x y x xy +-=+-22)1(. 8、计算:①)12(3-a a ②322))(2xy y x -( ③⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛22226.02334-b ab a b a 【解】:a a 362- 【解】:73852y x y x - 【解】:42332454342b a b a b a +--④⎥⎦⎤⎢⎣⎡+--b b a a ab 32)(43212 ⑤)5217(4)2()(3452323--⋅--⋅-ab b a ab ab a 【解】:221715ab b a + 【解】:2526620220ab b a b a ++- 9、先化简,再求值①)1()13(522a a a a a --+-,其中2=a , 【解】:6516623-=+-a a a②[],)(2)2()31(22y xy x y x xy xy ----其中,2,211-=-=y x 【解】:69143-=y x .中档题训练10、要使())6(132x ax x -++的展开式中吧含4x ,则a 的值应为 0 . 11、若,012=-+x x 则6222-+x x 的值为 -4 .12、若,63)4(31-=++n n xx x 则21-=x . 13、已知n327322=⋅,求)142(-n n 的值. 【解】:1614、已知,12-=ab 求))((352b ab b a ab ---的值.【解】: 115、长方形的长、宽、高分别是x x 243、-和x ,它们的表面积是多少? 【解】:x x 24222-16、已知,032=-a 求代数式9)5()(22--+-a a a a a 的值. 【解】: 017、已知,65=+b a 求b ab a 3052++的值.36)5(630630)5(=+=+=++=b a b a bb a a 解:原式18、先阅读下列解题过程,再解答问题已知,012=-+x x 求3223++x x 的值.【解】:3223++x x =3223+++-+x x x x x 41)1(22+-++-+=x x x x x 400++= 4=如果0132=+++x x x ,求8765432x x x x x x x x +++++++的值. 【解】:原式=)()(8765432x x x x x x x x +++++++ )1()1(32532x x x x x x x x +++++++= 0=28. 多项式乘以多项式基础题训练01.下列各式计算正确的是( ) A .(x +5)(x -5)=x 2-10x +25 B .(2x +3)(x -3)=2x 2-9 C .(3x +2)(3x -1)=9x 2+3x -2 D .(x -1)(x +7)=x 2-6x -7【解答】:C02.下列计算错误的是( ) A .(x +1)(x +4)=x 2+5x +4 B .(a +3)(a -4)=a 2+7a -12 C .(n -2)(n +3)=n 2+n -6 D .(m -2)(m -3)=m 2-5m +6【解答】:B03.计算(x +3)(x -2)+(x -3)(x +2)得( ) A .2x 2+12 B .2x 2-12 C .2x 2+x +12 D .2x 2-x -12【解答】:B04.计算① (x +2)(x -4)=_________; ② (x +2)(x -2)= _________;【解答】:x 2-2x -8; x 2-4;05.计算(a -b )(a 2+ab +b 2)= _________;【解答】:a 3-b 3;06.计算:① (2a +b )(a -2b ) ② (a +b )2【解答】:2a 2-3ab -2b 2; a 2+2ab +b 2; 07.计算:① (a +b )(a -2b )-(a +2b )(a -b ) ② 5x (x 2+2x +1)-(2x +3)(x -5)【解答】:-2ab ; 5x 3+8x 2+12x +15 08.① 解方程(x +7)(x +5)-(x +1)(x +5)=42 ② 解不等式(3x +4)(3x -4)>9(x -2)(x +3)【解答】:① 2;② 389x <09.小张永买了一部电视机,电视机的长为xcm,宽为ycm,屏幕外边缘长的方向厚度为8cm,宽的方向厚度为4cm.如图,试求屏幕的面积(用含x,y的式子表示)【解答】:xy-8x-16y+128中档题训练10.已知(x+3)(x-2)=x2+ax+b,则a、b的值分别是()A.a=-1,b=-6 B.a=1,b=-6 C.a=-1,b=6 D.a=1,b=6【解答】:B11.一个长方体的长、宽、高分别是3x-4,2x-1和x,则它的体积是()A.6x3-5x2+4x B.6x3-11x2+4x C.6x3-4x2D.6x3-4x2+x+4【解答】:B12.计算:① (a-b)(a-2b-1) ② (x-y+1)(x-y-3)【解答】:a2-3ab+2b2-a+b x2-2xy+y2-2x+2y-313.若规定1=.4 a b x xad bcc d x x--+,求【解答】:3x-414.已知(x2+px+8)(x2-3x+q)展开后不含x2与x3项,求p,q.【解答】:p=3 q=115.已知(x+my)(x+ny)=x2+2xy-8y2,求m2n+mn2的值.【解答】:-16综合训练16.观察下列等式:(x-1)(x+1)=x2-1(x-1)(x2+x+1)=x3-1(x-1)(x3+x2+x+1)=x4-1(x-1)(x4+x3+x2+x+1)=x5-1……运用上述规律,试求26+25+24+23+22+2+1的值.【解答】:设26+25+24+23+22+2+1=S,则(2-1)S=(2-1)( 26+25+24+23+22+2+1)=27-1 ∴S=27-1专题 整式乘法01.计算: ⑴a ·a 2·a 3=_________; ⑵(-3ab 2c 3)2=_________; ⑶a 3b 2·(-ab 3)3=_________; ⑷(-x 3y 3)(7xy 2-9x 2y )= _________; ⑸-3x ·(_________)=-12x 3+5x 2-2xy ; ⑹(x -3)(x +4)= _________.【解答】:⑴a 6; ⑵9a 2b 4c 6; ⑶-a 6b 11; ⑷-7x 4y 5+9x 5y 4;⑸ 252433x x y -+; ⑹x 2+x -12. 02.若3m =81,3n =9,则m +n =_________.【解答】:6 03.若a 5·(a m )3=a 4m ,则m =_________.【解答】:504.若x 2+kx -15= (x +3)(x +b ),则k =_________.【解答】:-2 05.计算:⑴(a 2)3·a 3-(3a 3)3+(5a 7)·a 2;⑵ ()232315?()253a b bc ac --⋅ ⑶a (a -b )-(a +b )(-2b ); ⑷2(x +3)(x -4)-(2x -3)(x +2)【解答】:⑴-21a 9; ⑵-a 7b 3c 4; ⑶a 2+ab +2b 2; ⑷-3x -18; 06.化简求值:(3x +2y )(4x -5y )-11(x +y +(x -y )+5xy ,其中113,222x y ==-. 【解答】:x 2-2xy +y 2= (x -y )2=3607.化简求值:()()2321[()]2122,=1=.213xy x x y x y x yx x y ---+-+其中,【解答】:2x 3y =-6.08.解方程:(x -3)(x -2)= (x +9)(x +1)+4 【解答】:715x =-09.已知x 2-8x -3=0,求(x -1)(x -3)(x -5)(x -7)的值. 【解答】:18029. 同底数幂相除 单项式除以单项式基础题训练01.下面的计算正确的是() A .b 10÷b 5=b 2 B .b 6÷b 3=b 2 C .b 2÷b 2=b D . b 6÷b 4=b 2【解答】:D02.下列计算真,计算结果正确的是( ) A .x ·x 3=2x 3 B .x 3÷x =x 2 C .(x 3)2=x 5 D .x 3+x 3=2x 6【解答】:B03.下列计算正确的是( ) A .4x 3÷2x 2y =2x B .-12x 4y 3÷2x 2yz =-6x 2y 2zC .22211644x y z x y z -÷=-D .222211()224x y x y x y -÷= 【解答】:A04.若8x 6y 4z ÷( )=4x 2y 2,则括号里应填( ) A .32x 8y 4z B .2x 3y 2 C .2x 4y 2z D .2x 3y 2z【解答】:C 05.① (-a )6÷a 2=_________;② (x 2)3÷(x 2)2=_________;③ (a -2b )7(a -2b )2÷(2b -a )6=_______;④2323321()()32a b c a b -÷-=_______; 【解答】:a 4;x 2;(a -2b )3;3289ab c - 06.计算: ① x 3÷x② (b 4)2÷(b 2)3 ③ (-xy )3÷(-xy ) ④ (-x )5÷(-x )2·x 2 ⑤[(a 3)2·(a 2)3]÷(-a 3)2 ⑥(2a )3b 3÷12a 3b 2 ⑦(6x 6y 6z 5)÷(-3x 2y 4z )÷(-2x 4yz 4) 【解答】:x 2;b 2;x 2y 2;-x 5;a 6;23b ; y ; 07.化简求值:(x +y )(x -y )-(x -y )2-6x 2y ÷2y +(2xy )2÷(-4xy ),其中x =-2,y =13【解答】:-3x 2+xy -2y 2=8129- 中档题题训练08.若a =-0.32,b =-32,291133c d ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,,则( )A .a <b <c <dB .b <a <c <dC .b <a <d <cD .a <b <d <c【解答】:B09.计算:[(-y 5)2]3÷[(-y )3]5=_________; 【解答】:-y 1810.若4x =m ,4y =n ,则43x -2y =_________;【解答】:32m n11.已知A 2×(-3x 2y 3)=-12x 6y 5,求单项式A . 【解答】:±2x 2y 12.若3a m -n ÷4a =34,且2m +n =2,求3m -4n . 【解答】:313.已知x m =2,x n =3,求x 3m -2n 的值.【解答】:8914.已知a m ·a n =a 7,a m ÷a n =a 5,求mn 的值. 【解答】:615.已知9x +1-32x =72,求x .【解答】:32x +2-32x =23·32 32x ·23=32·23x =1综合题训练16.已知:(a -2)2+(b +2)2≤-(c -3)2. ⑴求a +b +c 的值. ⑵求代数式()()22234222343316a b c ab c a b c ÷【解答】:⑴(a -2)2+(b +2)2+(c -3)2⑵112b =-30. 多项式除以单项式 01.计算:(xm +ym +zm )÷m =_________; (16x 3-24x 2)÷(-4x 2)= _________. 【解答】:x +y +z ; -4x +6 02.若(4xy )·M =12x 2y 3-16x 3y 2+42y 2,则多项式M =_________; 【解答】:3xy 2-4x 2y +xy03.计算:(16a 2b 4+8a 4b 2-4a 2b 2)÷(-4a 2b 2)= _________; 【解答】:-4b 2-2a 2+104.一个长方形的面积为(6ab 2+4a 2b ) cm 2,一边长为2ab cm ,则它的另一边长为_________cm . 【解答】:3b +2a05.计算(14a 3b 2-21ab 2)÷7ab 2等于( ) A .2a 2-3 B .2a -3 C .2a 2-3b D .2a 2b -3 【解答】:A06.计算(-4a 3+12a 2b -8a 3b 2)÷(-4a 2)的结果为( ) A .a +2ab 2 B .a -3b +2ab 2 C .a 2-3b +2ab 2 D .a -3b +0.5a 【解答】:B07.下列计算正确的是( ) A .(-x )3÷(-x )2=x B .(2a +b )3÷(2a +b )= (2a +b )2 C .a 2n ·(a 2n )e ÷a 4n =a 2D . 63343523635()24554a x a x ax a a x -+÷=-+ 【解答】:D08.长方形的长是(2m +4),面积是2(m +2)(m +5),求它的周长. 【解答】:6m +18 09.计算: ① (6xy +5x )÷x ② (8xy -6x 2y )÷2xy ③ (15x 2y -10xy 2)÷5xy ④ (8a 2-4ab )÷(-4a ) ⑤ (25x 3+15x 2-20x )÷(-5x ) ⑥(12x 3-8x 2+16x )÷(-4x )⑦ [(x +y ) (x -y )-(x -y )2]÷2y ⑧ [(a +b )2-b (2a +b )-8a ]÷2a【解答】:①6y +5; ②4-3x ; ③3x -2y ; ④-2a +b ; ⑤-5x 2-3x +4;⑥-3x 2+2x -4;⑦x -2y ;⑧142a - 中档题训练10.如果x 2+x -6除以(x -a )(x +a )的商为1,那么a =_________; 【解答】:311.已知被除式等于x 3+2x -1,商式是x ,于是等于-1,则除式是_________; 【解答】:x 2+212 )A .nB .n 2C .2nD .1 【解答】:D13.计算:[4a n b n -1·(-6a 3b 4)+(-3a n b n )(-2ab )3]÷3ab =( )A .-48z n +3b n +3B .-a n +2b n +2 C .0 D .以上均不对 【解答】:C14.先化简,后求值. [2x (x 2y -xy 2)+xy (xy -x 2)]÷x 2y ,其中x =2013,y =2012. 【解答】:原式=x -y =115.已知多项式M 除以3x 2-2x +4得商式2x +6,余式为3x -1,求多项式M . 【解答】:M =6x 3+14x 2-x +23 16. 已知2x -y =10,求代数式[(x 2+y 2)-(x -y )2+2y (x -y )]÷4y 的值. 【解答】:1(2)52x y -= 综合题训练17.计算:(x 2-x -6)÷(x -3). 【解答】:设(x 2-x -6)÷(x -3)=x +m , ∴(x +m )(x -3)=x 2-x -6. ∴x 2+(m -3)x -3m = x 2-x -6, ∴m =2,∴原式=x +2.专题 整式除法01.计算: ⑴a 5÷a 3=_________; ⑵(-x 4)÷(-x 3)= _________;⑶(8x 8)÷(2x 3)= _________; ⑷(12m 2)÷(3m )= _________; ⑸20x 3y 5÷(-5x 2y 3)= _________; ⑹(2ab )5÷(2ab )3=_________; (7)(6m 3-4m 2)÷(2m )= _________; (8)3222(72)()33y y y y -+÷-= _________. 【解答】:⑴a 2; ⑵x ;⑶4x 5; ⑷4m ;⑸-4xy 2z ; ⑹4a 2b 2;(7)3m 2-2m ; (8) 22132y y -+-02.①y8÷(y6÷_________)=y4;②6m2·(-n3)2÷(_________)2=2 3③M·(1-3a)=1-9a2,则M=_________.【解答】:①y2;② ±3mn3;③ 1+3a.03.计算:⑴(x4)2÷(x2)2÷x2-x2⑵28x3y4÷(-4x2y2) ③ (12m6n6p)÷(-3m2n4p)÷(-2m3n2p4)【解答】:⑴0;⑵-7xy2;⑶2m;⑷11353m mn-+;⑸21444y x--+.04.化简求值:[(3m+4n)2-3m(3m+4n)]÷(-6m),其中m=1,n=3.【解答】:282303nnm--=-05.已知:m-2n=3.求[(3m+2n)(3m-2n)-(m+2n)(5m-2n)]÷13m的值.【解答】:12m-24n=36.06.已知:2a-b=5.求[(a2+b2)+2b(a-b)-(a-b)2]÷4b的值.【解答】:1522 a-=07.已知:x2+x+1=0,求x3-x2-x+7的值.【解答】:931.平方差公式基础题训练01.①(x+2)(x-2)=_________;②(x+2)(2-x)=_________.【解答】:①x2-4;②4-x2.02.①(2a+b)(2a-b)=_________;②102×98=_________.【解答】:①4a2-b2;②9996.03.①(3x-y)( _________)=9x2-y2;②(_________)(x-1)=1-x2.【解答】:①3x+y;②-1-x.04.若x-y=2,x2-y2=6,则x+y=_________.【解答】:305.下列计算正确的是()A.(a-4)(a+b)=a2-4 B.(2x-3)(2x+3)=2x2-9C.(4xy+1)(4xy-1)=16x2y2-1 D.(a+3)(a-3)=a-9【解答】:C06.计算(x-y)(-y-x)的结果正确的是()A.-x2+y2B.-x2-y2C.x2-y2D.x2+y2【解答】:A07.利用平方差公式计算(2x-5)(-2x-5)的结果是()A.4x2-5 B.4x2-25 C.25-4x2D.4x2+25【解答】:C08.计算结果等于a2-b2的式子是()A .(a -b )2B .(a -b )(-a -b )C .(-a -b )(b -a )D .(a +b )(-a +b )【解答】:C09.下列多项式中不能用平方差公式计算的是( ) A .(-a -b )(-b +a ) B .(xy +a )(xy -a ) C .(-2a -b )(2a +b )D .11()()22x y y x ---【解答】:C10.运用平方差公式计算. ① (3a +b )(3a -b ) ② (-x +2y )(-x -2y ) ③ 11()()22a b a b --- ④ 59.8×60.2⑤ (2x -3y )(3y +2x )-(4y -3x )(3x +4y )【解答】:① 9a 2-b 2;② x 2-4y 2; ③2214b a -;④ 3599.96; ⑤ 13x 2-25y 2. 11.已知(-4x +3y )(-3y -4x )与多项式M 的差是36y 2+5xy ,求M . 【解答】:16x 2-5xy -45y 2中档题训练12.若M ·(3x -y 2)=y 4-9x 2,则多项式M 为( ) A .-(3x +y 2) B .-y 2 C .3x +y 2 D .3x -y 2 【解答】:A13.若x 2-y 2=6,x +y =3,则2 (x -y )= _________. 【解答】:-4 14.4111()()2216A x x x +-+=-,则多项式A 为_________. 【解答】:214x +15.计算:① a 4+(1-a )(1+a )(1+a 2) ② (2x -1)2-(2x +1)2 【解答】:① 1; ② -8x .16.已知x 2-y 2=24,x +y =6,求代数式5x +3y 的值. 【解答】:2817.对于任意正整数n ,求证:(3n +1)(3n -1)-(3-n )(3+n )的值是10的倍数. 【解答】:原式= (10n 2-10n )=10(n +1)(n -1) 18.计算:248163221(21)(21)(21)(21)(21()1)+⨯+⨯+⨯+⨯+⨯++【解答】:264.综合题训练19.探究题: ⑴计算下列各题:① (x -1)(x +1)= _________; ② (x -1)(x 2+x +1)= _________; ③ (x -1)(x 3+x 2+x +1)= _________.⑵猜想:(x -1)(x n +x n -1+x n -2+…+x +1)的结果是_________. ⑶证明你的猜想:【解答】:⑴ ① x 2-1; ② x 3-1; ③ x 4-1. ⑵x n +1-1;⑶ 原式= (x n +1+1+x n +x n -1+…+x )-(x n +x n -1+x n -2+…+x +1)=x n +1-132. 完全平方公式基础题训练01.① (x -2)2= _________; ② (2m +n )2= _________;③1()2a b +=_________; ④ (-2m -1)2= _________;【解答】:① x 2-4x +4; ② 4m 2+4mn +n 2;③2214a ab b ++;④ 4m 2+4m +1. 02.a 2+b 2 = (a +b )2-_________ = (a -b )2+_________; 【解答】:2ab ; 2a b .03.计算(a +b )(-a -b )的结果是( ) A .a 2-b 2 B .-a 2-b 2 C .a 2-2ab +b 2 D .-a 2-2ab -b 2 【解答】:D04.用完全平方公式计算正确的是() A .(a +bx )(-bx +a )=a 2-b 2x B .(-3x +y )2=3x 2-6xy +y 2 C .(-a -b )(a +b )=-a 2-2ab -b 2D .22211()24m n m n -=- 【解答】:C05.下列各式可以写成完全平方公式的有( ) ① x 2+xy +y 2②2214x xy y -+③ x 2+2xy +4y 2 ④442114x y x y -+ A .1个 B .2个 C .3个 D .4个 【解答】:A06.如图①,在边长为a 的正方形中挖掉一个边长为b 的小正方形(a >b ),把余下的部分剪拼成一个矩形(如图②).通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )A .a 2-b 2 = (a +b ) (a -b )B .(a +b )2 = a 2+2ab +b 2C .(a -b )2= a 2-2ab +b 2D .a 2-ab = a ( a -b ) 07.运用完全平方公式计算 ① (-xy +5)2 ② (-x -y )2 ③ (x +3)(x -3)(x 2-9)④ 2012 ⑤ 99.82⑥ (3a -4b )2-(3a +4b )2 ⑦ (2x -3y )2-(4y -3x )(4y +3x ) 【解答】:① x 2y 2-10xy +25; ② x 2+2xy +y 2; ③ x 4-18x 2+81;④ 40401; ⑤ 9960.04; ⑥ -48ab ; ⑦ 13x 2-12xy -7y 2;08.① 若x 2+kx +4是完全平方式,则k =_________. ② 若x 2-18xy +m 是完全平方式,则m =_________.③ 若x 2-14x +m 2是完全平方式,则m =_________. ④ 若9x 2+6xy +m 是完全平方式,则m =_________. 【解答】:① ±4; ② 81y 2; ③ ±7; ④ y 2. 09.已知a +b =5,ab =3,求:① a 2+b 2;② a -b ;③ a 2-b 2;④a bb a+;⑤a 2-ab +b 2;【解答】:① 19;②③±④193;⑤16. 10.已知13x x +=,求:①221x x +;②441x x+.【解答】:① 7;② 47.11.已知m 3+n 2-6m +10n +34=0,求m +n . 【解答】:-2.12.求证:a (a +1)(a +2)(a +3)+1是完全平方式. 【解答】:原式= (a 2+3a )·[(a 2+3a )+2]+1= (a 2+3a )2+2(a 2+3a )+1= (a 2+3a +1)2.综合题训练13.已知实数a 、b 、x 、y 满足ax +by =3,ay -bx =5,求(a 2+b 2)(x 2+y 2 )的值. 【解答】: (ax +by )2 = 9 ①;(ay -bx )2 = 25 ②; ①+②:a 2x 2+b 2y 2+a 2y 2+b 2x 2=34 ∴原式=34.33. 乘法公式运用基础题训练01.在括号里填上适当的项.① a -2b -c =a -(_________); ② a -2b +c =a -(_________); ③ a +b -c =a +(_________); ④ a -b +c -d = (a -d )+( _________). 【解答】:① 2b +c ; ② 2b -c ; ③ b -c ; ④ b -c . 02.计算:① (2x -1)2= _________; ②21()2x +=_________.【解答】:①4x 2-4x +1;②214x x ++; 03.若a +b =4,则a 2+2ab +b 2的值为_________. 【解答】:1604.x 2+y 2= (x +y )2- _________= (x +y )2+ _________. 【解答】:2xy ; 2xy .05.(x -y +z )(-x +y +z )=[z +( _________)] [z -( _________)]=z 2-( _________)2. 【解答】:x -y ; x -y ; x -y .06下列等式成立的是( ) A .(x -y )2= (y -x )2 B .(x +6)(x -6)=x 2-6 C .(x +y )2=x 2+y 2 D .6(x -2)+x (2-x )= (x -2)(x -6) 【解答】:A07.为了运用平方差公式公式计算(a -b +c )(a +b -c ),必须先适当变形,下列变形中正确的是( )A .[(a +c )-b ] [(a -c )+b ]B .[(a -b )+c ] [(a +b )-c ]C .[(b +c )-a ] [(b -c )+a ]D .[a -(b -c )] [a +(b -c )] 【解答】:D08.设(3m +2n )2= (3m -2n )2+P ,则P 的值是( ) A .12mn B .24mn C .6mn D .48mn 【解答】:B09.若x 2-kxy +9y 2是一个完全平方式,则k 值为( ) A .3 B .6 C .±6 D .±81 10.已知a 2+b 2=25,且ab =12,则a +b 的值是( )AB .C .7D .±711.计算: ① (2x +3y )(2x -3y ) ② (-x -2y )(x -2y )③2211()()22x x -+ ④(2a +3)2⑤ (a +2b -c )(a -2b -c )⑥ (a 2+2b -c )2 【解答】:① 4x 2-9y 2;② 4y 2-x 2;③414x -; ④ 4a 2+12a +9⑤ a 2-2ac +c 2-4b 2; ⑥ a 4+4b 2+c 2+4a 2b -2a 2c -4b c .12.多项式4x 2+1加上一个单项式后能成为一个整式的完全平方,请你写出符合条件的这个单项式是_________. 【解答】:4x 4 或4x 或-4x13.若(x -y )2=18,(x +y )2=12,则xy =_________. 【解答】:32-14.若x =1时,代数式ax 2+bx +1的值是3,则(a +b -a )(1-a -b )= _________. 【解答】:-115.若a 2+b 2+2c 2+2ac -2bc =0,则a +b =( ) A .0 B .1 C .-1 D .不确定 【解答】:A16.已知:a +b =10,ab =20,求下列式子的值:① a 2+b 2;② (a -b )2. 【解答】:① 60; ② 20.17.若a 2+b 2+4a -6b +13=0,试求a b 的值. 【解答】:-8 18.已知x 2-3x -1=0,求:①221x x +; ② 221x x -.【解答】:① 11;②±综合题训练19.已知:如图,现有a ×a 、b ×b 的正方形纸片和a ×b 的矩形纸片各若干张,是选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),视频出的矩形面积为2a 2+5ab +2b 2,并标出此矩形的长和宽.【解答】:专题 整式乘法1.计算:⑴ (x -3y )(x +3y ) = _________ ; ⑵ (x +y )(-x +y ) = _________ ; ⑶(x +1)(x -1)(x 2+1) = _________ ; ⑷ (x +y )2 = _________ ; ⑸ 21()2x y --= _________ ;⑹ (2m -n )2= _________.【解答】: ⑴ x 2-9y 2;⑵ y 2-x 2;⑶ x 4-1;⑷ x 2+2xy +y 2;⑸2214x xy y ++; ⑹ 4m 2 -4mn +n 2;2.若x 2-y 2=6,x +y =3,则4(x -y )= _________ . 【解答】:-83.若9x 2+4y 2= (3x +2y )2+M ,则M = _________ . 【解答】:-12xy 4.a 2+ _________ +214b = ( _________)2. 【解答】:±ab5.(a +b -c ) (a -b +c ) = a 2-( _________)2.【解答】:b -c 6.计算:⑴ (-3ab -2b ) ( 3a -2b ) ⑵ 21()2m -⑶ (a +2b ) (a -2b ) (a 2+4b 2)⑷ (x +3)2-(x -3)2⑸ (a -b +c )2⑹ (a -2b +c ) (a +2b -c ) 【解答】:⑴ 4b 2-9a 2;⑵ 214m m -+;⑶ a 4-16b 4;⑷ 12x ;⑸ a 2+b 2+c 2-2ab +2ac -2bc⑹ a 2-4b 2+4bc-c 27.已知x +y =1,求221122x xy y ++的值. 【解答】:128.已知:x 2+y 2=25,x +y = 7,求x -y . 【解答】:±19.已知 ( x +y )2=12,(x -y )2 = 8,求xy 的值. 【解答】:1 10.已知13x x -=,求21()x x +的值. 【解答】:13 11.已知13x x +=,求441x x+的值. 【解答】:4734.运用提取公因式法分解因式基础题训练1、①6m 2n 与2mn 的公因式是 ;②2a (m -n )与3b (n -m )的公因式是【解答】①、2mn ②、m -n2、分解因式:①ma +mb +mc = ②6x 3y 2-4x 2y 3=③(m +1)(m -1)+(m -1)=【解答】:①、m (a +b +c ) ②、2x 2y 2(3x -2y ) ③、(m -1)(m +2) 3、下列从左到右的变形属于分解因式的是( ) A 、(x +1)(x -1)=x 2-1 B 、m 2-2m -3=m (m -2)-3 C 、x 2-5x +6=(x -2)(x -3) D 、(a -b )(x -y )=(b -a )(y -x )【解答】:C4、多项式-6x 3y 2-3x 2y +12x 2y 2 分解因式时,应先提公因式的是( )A 、3xyB 、-3x 2yC 、3xy 2D 、-3x 2y 2【解答】:B5、下列分解因式正确的是( )A 、3(x -2)-2x (2-x )=(x -2)(3-2x )B 、3(x -2)-2x (2-x )=(x -2)- (3-2x )C 、3(x -2)-2x (2-x )=x (x -2)D 、3(x -2)-2x (x -2)=(x -2)(3-2x )【解答】:D6、下列各组中,没有公因式的一组是( )A 、ax -bx 与by -ayB 、6xy +8x 2y 与-4x -3C 、ab -ac 与ab -bcD 、(a -b )3x 与(b -a )2y【解答】:C7、把 2(a -3)+a (3-a ) 提取公因式(a -3) 后,另一个因式是( )A 、a -2B 、a +2C 、2-aD 、-2-a【解答】:C8、化简:(-2)2008+(-2)2009的结果为( )A 、-22008B 、22008C 、-22009D 、22009【解答】:A9、若x 2(x +1)+y (xy +y )=(x +1)*A ,则A =( )【解答】:x 2+y 210、分解因式①、21xy -14xz +35x 2 ②、15xy +10x 2-5x③、(2a +b )(3a -2b )-4a (2a +b ) ④、(x -2)2-x +2⑤、a 2(x -2a )2-a (2a -x )2 ⑥、 15b (2a -b )2+25(b -2a )3【解答】:①、7x (3y -2z +5x ) ②、5x (3y +2x -1) ③、-(2a +b )(a +2b )④、(x -2)(x -3) ⑤、a (x -2a )2(a -1) ⑥、10(2a -b )2(4b -5a )中档题训练11、填空:①(1-a )mn +a -1=( )(mn -1)②m (m -n )2-(n -m )2=(m -n )2( )【解答】:1-a , m -112、若2x 2+ax -b 能分解为(2x +1)(x -1),则a = ,b =【解答】:-1,113、已知方程组{13623=-=-y x y x 用简便方法求7x (x -3y )2-2(3y -x )3的值 【解答】:1814、分解因式⑴(x +2y )2-x 2-2xy ⑵(a -b )2(m +n )-(-m -n )(b -a )【解答】:⑴2y (x +2y ) ⑵(a -b )(m +n )(a -b -1)15、已知 x +y =-5,xy =7,求x 2y +xy 2-x -y 的值【解答】:-3016、观察下面的分解因式过程,说说你发现了什么?把多项式am +an +bm +bn 分解因式解法1:am +an +bm +bn =(am +an )+(bm +bn )=a (m +n )(a +b )=(m +n )(a +b ) 解法2:am +an +bm +bn =(am +bm )+(an +bn )=m (a +b )+n (a +b )= (a +b )(m +n ) 根据你的发现,把下面的多项式分解因式:⑴mx-my+nx-ny; ⑵2a+4b-3ma-6mb【解答】:⑴(x-y)(m+n) ⑵(a+2b)(2-3m)综合训练17、已知a,b,x,y满足a+b=x+y=3,ax+by=7.求(a2+b2)xy+ab(x2+y2)的值【解答】:∵(a+b)(x+y)=9∴(ax+by)+(ay+bx)=9∴ay+bx=2∴原式=(ax+by) (ay+bx)=1435、运用平方差公式分解因式基础题训练1、分解因式:①x2-4=②4x2-9=③-m2+1=④2m2-8n2=【解答】:①(x+2)(x-2) ②(2x+3)(2x-3)③(1+m)(1-m) ④2(m+2n)(m-2n)2、一个长方形面积是a2-b2(a>0),其中一边长为a+b,则另一边长为【解答】:a-b3、①25a2-( )=(5a+3b)(5a-3b) ②( )+b2=(-2a+b)(b+2a) 【解答】:9b2,-4a24、分解因式x2(a+b)-y2(a+b)=【解答】:(a+b)(x+y)(x-y)5、下列二项式中,能用平方差公式分解因式的是( )A、x2+4y2B、-4y2+x2C、-x2-4y2D、x-4y2【解答】:B6、下列各式能用平方差公式分解因式的有( )①x2+y2②x2-y2③-x2+y2④-x2-y2⑤1-a2b2⑥x2+4A、2个B、3个C、4个D、5个【解答】:B7、下列各式分解因式正确的是( )A、16-4x2=(4+2x)(2x-4)B、m2-16m=m(m+4)(m-4)C、x2-9b2=(x+9b)(x-9b)D、1-25a2=(1+5a)(1-5a)【解答】:D8、分解因式①16x2y2-1②-25x2+49y2③a5-9a3④3(a+b)2-27c2⑤-x4+x2y2⑥a2-b2⑦m2(x-y)+n2(y-x)⑧16(x+y)2-25(x-y)2【解答】:①(4xy +1)(4xy -1) ②-(5x +7y )(5x -7y ) ③a 3(a +3)(a -3)④3(a +b +3c )(a +b -3c ) ⑤-x 2(x +y )(x -y ) ⑥(a +b )(a -b )⑦(x -y )(m +n )(m -n ) ⑧-(x -9y )(9x -y )9、如图一个圆环,外圆的半径为R ,内圆的半径为r⑴写出圆环的面积计算公式⑵当R =15.25cm ,r =5.25cm 时,求圆环面积,(结果保留π)【解答】:⑴S =π(R 2-r 2) ⑵S =205π中档题训练10、若{346423=-=+y x y x ,则9x 2-4y 2= 【解答】:611、分解因式:①-4x 2+(2x -3y )2 ②16(a +b )2-9(a -b )2③9m 2(a -b )3+49(b -a )3 ④(x +y -z )2-(x -y +z )2⑤(a 2-b 2)+(3a -3b ) ⑥x 4-1【解答】:①-3y (4x -3y ) ②(7a +b )(a +7b ) ③(a -b )3(3m +7)(3m -7)④4x (y -z ) ⑤(a -b )(a +b +3) ⑥(x 2+1)(x +1)(x -1)12、已知:∣a -b -3∣+(a +b -2)2=0,求a 2-b 2的值【解答】:613、证明:无论m 为何整数时,多项式(4m +5)2-9能被8整除.【解答】:8(m +2)(2m +1)综合题训练14、观察下列等式,解答问题.①9-1=8 ②16-4=12 ③25-9=16 ④36-16=20⑴写出第10个等式:⑵写出第n (n ≧1)个式子:验证第⑵的结论【解答】:⑴122-102=44⑵(n +2)2-n 2=4(n +1)⑶略36、运用完全平方公式分解因式基础题训练1、分解因式:①x 2+6x +9= ②1-4y +4y 2= ;③-a 2+2a -1=【解答】:①(x +3)2 ②(1-2y )2 ③-(a -1)22、分解因式①ab 2-2ab +a = ②(a +b )2-6(a +b )+9 =【解答】:①a (b -1)2 ②(a +b -3)23、若m 2+km +4是完全平方式,则k =【解答】:±44、9a 2+( )+25b 2=(3a -5b )2【解答】:-30ab5、下列多项式能用平方差公式分解因式的有( )①x 2+2x +1 ②4a 2-4a -1 ③m 2+m +41 ④4m 2+2mn +n2 ⑤1+16y 2 A 、2个 B 、3个 C 、4个 D 、5个【解答】:A6、下列因式分解正确的是( )A 、1+4x 2=(1+2x )2B 、6a -9-a 2=-(a -3)2C 、1+4m -4m 2=(1-2m )2D 、x 2+xy +y 2=(x +y )2【解答】:B7、下列因式分解错误的是( )A 、a 2-b 2=(a +b )(a -b )B 、x 2+4xy +4y 2=(x +2y )2C 、x 2+y 2=(x +y )2D 、a 2+ab =a (a +b )【解答】:C8、下列因式分解正确的是( )A 、a 4-8a 2+64=(a 2-8)2B 、a (x -y )-b (x -y )=(x -y )(a +b )C 、a 4-b 4=(a 2+b 2)(a 2-b 2)D 、-a 2+a -41=- (2a -1)2 【解答】:D9、分解因式:①a 2+2a +1 ②x 2+36+12x ③4x 2-20x +25④ax 2-4ax +4a ⑤xy 3-2x 2y 2+x 3y ⑥(x +y )2+(x +y )+9【解答】:①(a +1)2 ②(x +6)2 ③(2x +5)2④a (x -2)2 ⑤xy (x -y )2 ⑥(x +y +3)210、已知 a +b =21,ab =81 求-2a 2b 2+ab 3+a 3b 的值 .(提示:先分解因式) 【解答】:321中档题训练11、-4x 2+4xy +( )=-( )2【解答】:-y 2 2x -y12、已知x 是有理数,则多项式x -1- 41 x2 的值 A 、一定为负数 B 、不可能为正数C 、一定为正数D 、可能是正数或负数或零【解答】:B13、分解因式:①(x 2+y 2)2-4x 2y 2 ②(x +y )2-4(x +y -1)③(a 2+b 2)2-4ab (a 2+b 2)+4a 2b 2 ④x 4+x 2+1【解答】:①(x +y )2(x -y )2 ②(x +y -2)2③(a -b )4 ④(x 2+x +1)(x 2-x +1)14、实数范围内分解因式:⑴5x 2-3 ⑵a 4-9【解答】:⑴(5x +3)(5x -3) ⑵(a 2+3)(a +3)(a -3)15、若 a ,b ,c 是△ABC 三边,判断(a 2+b 2-c 2)2-4a 2b 2 的正负符号.【解答】:负16、若一个三角形的三边a ,b ,c ,满足a 2+2b 2+c 2-2ab -2bc =0 ,试说明该三角形的形状.【解答】:a =b =c 等边三角形综合题训练17、已知(a 2+b 2-4)(a 2+b 2)+4=0,求a 2+b 2【解答】:∵(a 2+b 2-4)(a 2+b 2)+4=0 ∴(a 2+b 2-2)2=0 ∴a 2+b 2=2专题 分解因式1、十字相乘法分解因式:⑴x 2+3x +2 ⑵x 2-3x +2 ⑶x 2+2x -3⑷x2-2x-3⑸x2+5x+6⑹x2-5x-6(7)x2+x-6 (8)x2-x-6 (9)x2-5x-36(10)x2+3x-18 (11)2x2-3x+1 (12)6x2+5x-6【解答】:⑴(x+1)(x+2) ⑵(x-1)(x-2) ⑶(x+3)(x+1)⑷(x-3)(x+1) ⑸(x+3)(x+2) ⑹(x-6)(x+1)(7)(x+3)(x-2) (8)(x-3)(x+2) (9)(x-9)(x+4)(10)(x+6)(x-3) (11)(2x-1)(x-1) (12)(2x+3)(3x-2)2、分解因式⑴2a+2a2+4a3⑵5x3y-5xy3⑶a2+b2+2ab-16⑷4x3-8x2+4x⑸(x+y)2-2x-2y+1⑹(m2-2m)2n+2n(m2-2m)+n(7)(x2+y2-1)2-4x2y2 (8)a(2a-b)+2a(b-2a)2-a(b-2a)3【解答】:⑴2a(1+a+2a2) ⑵5xy(x+y)(x-y)⑶(a+b+4)(a+b-4) ⑷4x(x-1)2⑸(x+y-1)2⑹n(m-1)2(7)(x+y+1)(x+y-1)(x-y+1)(x-y-1) (8)a(2a-b)(2a-b+1)23、解答题⑴已知x2+y2-2x+4y=-5,求x,y⑵a,b满足a(a+1)-(a2+2b)=1,求a2-4ab+4b2-2a+4b的值⑶已知a2+b2=5,a+b=3,求(a-b)2⑷已知x2-y2=20,求〔(x-y)2+4xy〕〔(x+y)2-4xy〕的值【解答】:⑴x=1,y=-2⑵-1⑶1⑷400。
