圆-阴影部分面积(含答案).

合集下载

2024河南中考数学复习与圆有关的计算(含阴影部分面积) 强化精练 (含答案)

2024河南中考数学复习与圆有关的计算(含阴影部分面积)强化精练基础题1.(2023兰州)如图①是一段弯管，弯管的部分外轮廓线如图②所示是一条圆弧AB ︵，圆弧的半径OA ＝20cm ，圆心角∠AOB ＝90°，则AB ︵＝()第1题图A.20πcmB.10πcmC.5πcmD.2πcm2.(2023新疆维吾尔自治区)如图，在⊙O 中，若∠ACB ＝30°，OA ＝6，则扇形OAB (阴影部分)的面积是()第2题图A.12πB.6πC.4πD.2π3.(2023鄂州)如图，在△ABC 中，∠ABC ＝90°，∠ACB ＝30°，AB ＝4，点O 为BC 的中点，以O 为圆心，OB 长为半径作半圆，交AC 于点D ，则图中阴影部分的面积是()第3题图A.53－33πB.53－4πC.53－2πD.103－2π4.(2023连云港)如图，矩形ABCD 内接于⊙O ，分别以AB 、BC 、CD 、AD 为直径向外作半圆．若AB ＝4，BC ＝5，则阴影部分的面积是()第4题图A.414π－20B.412π－20C.20πD.205.(2023金华)如图，在△ABC 中，AB ＝AC ＝6cm ，∠BAC ＝50°，以AB 为直径作半圆，交BC 于点D ，交AC 于点E ，则弧DE 的长为________cm.第5题图6.如图，在2×3的网格图中，每个小正方形的边长均为1，点A ，B ，C ，D 都在格点上，线段CD 与AC ︵交于点E ，则图中AE ︵的长度为________．第6题图7.(2023重庆A 卷)如图，⊙O 是矩形ABCD 的外接圆，若AB ＝4，AD ＝3，则图中阴影部分的面积为________．(结果保留π)第7题图8.(2023包头)如图，正方形ABCD的边长为2，对角线AC，BD相交于点O，以点B为圆心，对角线BD的长为半径画弧，交BC的延长线于点E，则图中阴影部分的面积为________．第8题图9.(万唯原创)如图，在Rt△ABC中，∠BAC＝90°，∠B＝30°，AC＝2，以点A为圆心，AC 长为半径作弧，分别交AB，BC于点D，E，则图中阴影部分的周长为________．第9题图10.(2023新乡一模)如图，△ABC中，∠C＝90°，AC＝BC＝2.将△ABC绕着点A顺时针旋转90度到△AB1C1的位置，则边BC扫过区域的面积为________．第10题图11.(2023驻马店二模)如图，将扇形OAB沿OA方向平移得到对应扇形CDE，线段CE交AB︵于点F，当OC＝CF时平移停止．若∠O＝60°，OB＝3，则阴影部分的面积为________．第11题图拔高题12.(2023通辽)如图，在扇形AOB中，∠AOB＝60°，OD平分∠AOB交AB︵于点D，点C是半径OB 上一动点，若OA ＝1，则阴影部分周长的最小值为()A.2＋π6B.2＋π3C.22＋π6 D.22＋π3第12题图13.如图，两个半径长均为2的直角扇形的圆心分别在对方的圆弧上，扇形CFD 的圆心C 是AB ︵的中点，且扇形CFD 绕着点C 旋转，半径AE ，CF 交于点G ，半径BE ，CD 交于点H ，则图中阴影部分面积等于()第13题图A.π2－1B.π2－2C.π－1D.π－214.如图，AB 为⊙O 的直径，将BC ︵沿BC 翻折，翻折后的弧交AB 于点D.若BC ＝45，sin ∠ABC ＝55，则图中阴影部分的面积为()第14题图A.25πB.25πC.8D.1015.如图，在矩形ABCD中，AD＝2，AB＝22，对角线AC，BD交于点O，以A为圆心，AB的长为半径画弧，交CD于点F，连接FO并延长交AB于点M，连接AF，则图中阴影部分的面积是______．(结果保留π)第15题图参考答案与解析1.B 【解析】∵圆弧的半径OA ＝20cm ，圆心角∠AOB ＝90°，∴ AB 的长＝90π×20180＝10π(cm).2.B 【解析】∵∠ACB ＝30°，∴∠AOB ＝2∠ACB ＝60°，∴S 扇形AOB ＝60×π×62360＝6π.3.C【解析】如解图，连接OD ，BD ，在Rt △ABC 中，tan 30°＝AB BC ，∴BC ＝AB tan 30°＝43，∵OC ＝OD ，∴∠OCD ＝∠ODC ＝30°，∴∠BOD ＝60°，∵BO ＝DO ，∴△BOD 是等边三角形，∴BD ＝BO ＝12BC ＝23，∠BDO ＝60°，∴∠BDC ＝90°，AD ＝BD ·tan 30°＝2.∴S 阴影部分＝S △ABD ＋S △BOD －S 扇形BOD ＝12×23×2＋34×(23)2－60π×（23）2360＝53－2π.第3题解图4.D 【解析】如解图，连接AC ，∵矩形ABCD 内接于⊙O ，AB ＝4，BC ＝5，∴AC 2＝AB 2＋BC 2，∴阴影部分的面积为S矩形ABCD ＋π×(AB 2)2＋π×(BC 2)2－π×(AC 2)2＝S 矩形ABCD ＋π×14(AB 2＋BC 2－AC 2)＝S 矩形ABCD ＝4×5＝20.第4题解图5.56π【解析】如解图，连接OE ，OD ，∵OD ＝OB ，∴∠B ＝∠ODB ，∵AB ＝AC ，∴∠B ＝∠C ，∴∠C ＝∠ODB ，∴OD ∥AC ，∴∠EOD ＝∠AEO ，∵OE ＝OA ，∴∠OEA ＝∠BAC ＝50°，∴∠EOD ＝∠BAC ＝50°，∵OD ＝12AB ＝12×6＝3(cm)，∴ DE 的长为50π×3180＝56π(cm).6.54π【解析】如解图，连接AC ，AD ，设AC 交网格线于点O ，连接OE .∵AD 2＝22＋12＝5，AC 2＝22＋12＝5，CD 2＝12＋32＝10，∴AD ＝AC ，AD 2＋AC 2＝CD 2，∴△ACD 是等腰直角三角形，∴∠ACD ＝45°，∵∠ABC 是直角，∴AC 是⊙O 的直径，∴∠AOE ＝90°.∵AC ＝5，∴OE ＝OA ＝12AC ＝52，∴ AE 的长为90π×52180＝54π.第6题解图7.254π－12【解析】如解图，连接BD ，由题知∠BAD ＝90°，∴BD 是⊙O 的直径，∵AB ＝4，AD ＝3，∴BD ＝AD 2＋AB 2＝32＋42＝5，∴S 阴影＝S ⊙O －S 矩形ABCD ＝π×(52)2－3×4＝254π－12.第7题解图8.π【解析】∵正方形ABCD 对角线相交于点O ，∴AO ＝BO ，CO ＝DO ，∠AOD ＝∠BOC ，∴△AOD ≌△BOC ，∴阴影部分的面积＝扇形DBE 的面积，∵正方形的边长为2，∴由勾股定理得BD ＝22，∠DBC ＝45°，∴阴影部分的面积＝45360×π·(22)2＝π.9.π3＋23【解析】如解图，连接AE ，∵在Rt △ABC 中，∠B ＝30°，∴BC ＝2AC ＝4，AB ＝23.∵ DE 是以点A 为圆心，AC 长为半径的弧，∴AD ＝AE ＝AC ＝2，∴BD ＝AB －AD＝23－2，∠AEC ＝∠C ＝60°，∴△AEC 为等边三角形，∴AE ＝EC ＝2.，∴BE ＝2，∠BAE＝∠B ＝30°，∴ DE 的长为30π×2180＝π3，∴阴影部分的周长为2＋π3＋23－2＝π3＋23.10.π【解析】在△ABC 中，∠ACB ＝90°，AC ＝BC ＝2，由勾股定理得，AB ＝22＋22＝22，∵将△ABC 绕着点A 顺时针旋转90度到△AB 1C 1的位置，∴∠CAC 1＝90°，∴阴影部分的面积S ＝S 扇形BAB 1＋S △B 1AC 1－S △ACB －S 扇形CAC 1＝S 扇形BAB 1－S 扇形CAC 1＝90π×（22）2360－90π×22360＝π.11.3π4－334【解析】如解图，连接OF ，过点C 作CH ⊥OF 于点H ，由平移性质知，CE ∥OB ，∴∠CFO ＝∠BOF ，∵CO ＝CF ，∴∠COF ＝∠CFO ，∴∠COF ＝∠BOF ＝12∠BOC ＝30°，在等腰△OCF 中，OH ＝12OF ＝12OB ＝32，∴CH ＝OH ·tan 30°＝32×33＝32，∴S 阴影＝S 扇形AOF －S △COF ＝30·π×32360－12×3×32＝3π4－334.第11题解图12.A 【解析】如解图，作D 点关于直线OB 的对称点E ，连接AE ，OE ，DE ，CE ，AE 与OB 的交点为C 点，则CD ＝CE ，OD ＝OE ，∠DOB ＝∠EOB ，∴AC ＋CD ＝AC ＋CE ≥AE ，当A ，C ，E 三点共线时，AC ＋CD 取得最小值，此时阴影部分周长最小，在扇形AOB 中，∠AOB ＝60°，OD 平分∠AOB 交 AB 于点D ，∴∠AOD ＝∠BOD ＝30°，由轴对称的性质，∠EOB ＝∠BOD ＝30°，OE ＝OD ，∴∠AOE ＝90°，∴△AOE 是等腰直角三角形，∵OA ＝1，∴AE ＝2， AD 的长＝30π×1180＝π6，∴阴影部分周长的最小值为2＋π6.第12题解图13.D 【解析】两扇形的面积和为180π·（2）2360＝π，如解图，过点C 作CM ⊥AE 于点M ，CN ⊥BE 于点N ，连接CE ，则四边形EMCN 是矩形，∵点C 是 AB 的中点，∴EC 平分∠AEB ，∴CM ＝CN ，∴矩形EMCN 是正方形，∵∠MCG ＋∠FCN ＝90°，∠NCH ＋∠FCN ＝90°，∴∠MCG ＝∠NCH ，在△CMG 与△CNH 中，MCG ＝∠NCH ，＝CN ，CMG ＝∠CNH ，∴△CMG ≌△CNH (ASA)，∴中间空白区域面积相当于对角线是2的正方形面积，∴空白区域的面积为12×2×2＝1，∴图中阴影部分的面积＝π－2.第13题解图14.C 【解析】如解图，连接AC ，CD ，过点C 作CH ⊥AB 于点H ，∵∠ABC ＝∠DBC ，∴ AC ＝ CD，∴AC ＝CD ，∵CH ⊥AD ，∴AH ＝HD ，∵BC ＝45，sin ∠ABC ＝55，∴CH ＝BC ·sin ∠ABC ＝4，∵AB 为⊙O 的直径，∴∠ACB ＝90°，∵sin ∠ABC ＝AC AB ＝55，∴设AC ＝5m ，AB ＝5m ，根据勾股定理，AC 2＋BC 2＝AB 2，∴5m 2＋80＝25m 2，∴m ＝2(负值已舍去)，∴AC ＝CD ＝25，∴AH ＝AC 2－CH 2＝（25）2－42＝2，∴AD ＝2AH ＝4，∴S 阴影＝S △ACD ＝12AD ·CH ＝12×4×4＝8.第14题解图15.π－22＋2【解析】在矩形ABCD 中，AD ＝2，AB ＝22，∴∠ADC ＝90°，AB ∥CD ，OB ＝OD ，∴∠ABD ＝∠CDB ，∵AF ＝AB ＝22，AF 2＝AD 2＋DF 2，∴(22)2＝22＋DF 2，∴DF ＝2，∴AD ＝DF ，∴∠DAF ＝∠DFA ＝45°，∴∠BAF ＝45°，在△BOM 和△DOF 中，MBO ＝∠FDO＝ODBOM ＝∠DOF ，∴△BOM ≌△DOF (ASA)，∴BM ＝DF ＝2，∴AM ＝22－2，∴图中45π×（22）2360－12×(22－2)×2＝π－22＋2.阴影部分的面积为：。

圆-阴影部分面积(附答案)

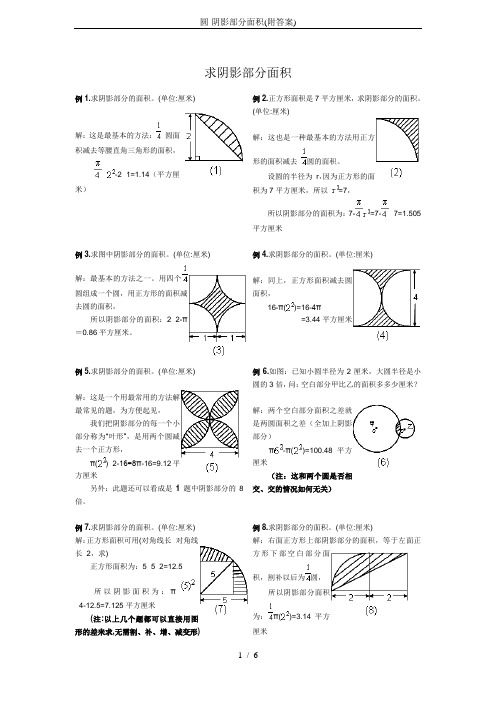
求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米) 解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

专题8 巧求圆中阴影部分的面积（含答案）

专题8 巧求圆中阴影部分的面积【知识解读】求与圆有关的阴影部分的面积，能考查同学们的观察能力、随机应变能力和综合运用数学知识的能力，解答此类问题要注意观察和分析图形的形成，学会分解和组合图形，消除思路中的“阴影”，明确要计算图形的面积，可以通过哪些图形的和或差得到，就能给解决问题带来一片光明，切勿盲目计算；下面介绍几种常用的解法．培优学案【典例示范】等积变换法：是在不改变图形面积的前提下，利用“等底、等高的两个三角形的面积相等”，将不规则图形转化为规则图形的面积来求解的方法．例1 如图1－8－1，点P 是半径为1的⊙O 外一点，OP ＝2，P A 切⊙O 于点A ，弦AB ∥OP ，连接PB ，则图中阴影部分的面积是．图181AB OP图182ABCDEMNO【跟踪训练】如图1－8－2，AB 是⊙O 的直径，MN 是⊙O 的切线，C 为切点，过点A 作AD ⊥MN 于点D ，交⊙O 于点E ．已知AB ＝6，BC ＝3，求图中阴影部分的面积．【解答】和差法：是指将阴影部分看作两个规则图形的和或差．例2 如图1－8－3，扇形OAB 中，∠AOB ＝60°，扇形半径为4，点C 在BC 上，CD ⊥OA ，垂足为点D ，当CD ＝OD 时，图中阴影部分的面积为．图183BCD图184CEF【跟踪训练】如图1－8－4，在等腰直角三角形ABC 中，∠C ＝90°，点D 为AB 的中点，已知扇形EAD 和扇形FBD 的圆心分别为点A 、点B ，且AC ＝2，则图中阴影部分的面积为（结果不取近似值）．割补法：是在不改变图形面积的前提下，通过割补，将发散的图形面积集中在一起，把不规则的图形凑合成规则图形的方法．例3 如图1－8－5，半径为2cm ，圆心角为90°的扇形OAB 中，分别以OA ，OB 为直径作半圆，则图中阴影部分的面积为cm 2．图185ABO图186A 'O 'O ABC【跟踪训练】如图1－8－6，将半圆O 绕直径AB 的端点B 逆时针旋转30°，得到半圆O ′，A ′B 交直径AB 于点C ，若BC ＝23，则图中阴影部分的面积为．【提示】连接O ′C ，A ′C ，将阴影部分的面积通过割补，转化为△BO ′C 的面积加上扇形O ′AC 的面积．特殊位置法：是在不改变题意的前提下，通过取特殊位置，将图形特殊化，以方便求解．例4 如图1－8－7，一个半径为r 的圆形纸片在边长为a （a ＞3r ）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“接触不到的部分”的面积是()A ．23r πB 233π- C ．()233r πD ．2r π【提示】解答本题的关键是搞清楚圆形纸片“不能接触到的部分”的面积，即圆形纸片与正三角形的相邻两边都相切时，两切点与正三角形的一个顶点形成的曲边三角形的面积．图187图188【跟踪训练】如图1－8－8，一张半径为1的圆形纸片在边长为a （a ≥3）的正方形内任意移动，则该正方形内，这张圆形纸片“不能接触到的部分”的面积是（） A ．2a π-B ．()24a π-C ．πD ．4π-整体代换法：是指在解答过程中，可将某些不易求的且不发生变化的量看作整体处理．例5 如图1－8－9，在Rt △ABC 中，∠C ＝90°，CA ＝CB ＝4，分别以A ，B ，C 为圆心，以12AC 为半径画弧，三条弧与边AB 所围成的阴影部分的面积是．图189CBA【提示】直接求阴影部分的面积是不可能的，根据题意结合图形，知阴影部分的面积等于直角三角形的面积减去三个扇形的面积，其中A ，B 两个扇形的面积无法直接求出，但若把它们看作一个“整体”，则问题易求．【跟踪训练】1.如图1-8-10，正方形的边长a ，以各边为直径在正方形内画半圆，则图中阴影部分的面积为 . 【提示】图中阴影部分的面积可以看作四个半圆的面积之和与正方形的面积之差.CBAOFEDCBA2.如图1-8-11，⊙A ，⊙B ，⊙C 两两不相交，且半径都是2cm ，则图中三个扇形（即阴影部分）面积之和是 cm 2.【提示】图中3个扇形正好拼成一个圆心角为180°的大扇形。

小学六年级数学之圆_阴影部分面积(含答案)

求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分面积。

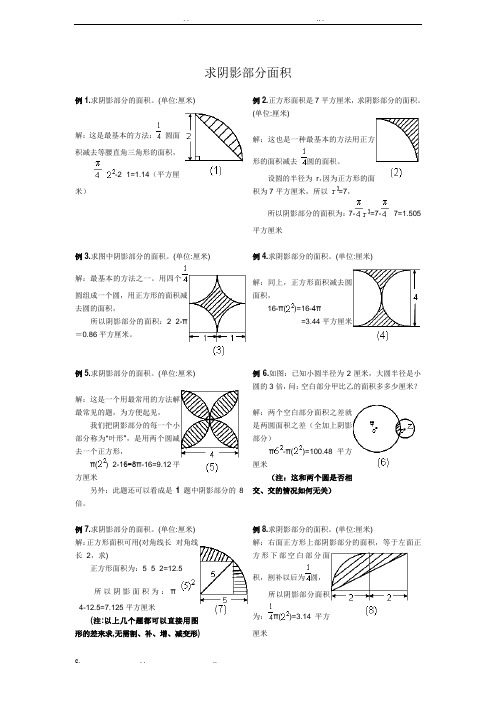
小学六年级圆_阴影部分面积(含答案)

求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米) 解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

小学六年级圆_阴影部分面积(含答案)

求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米) 解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米) 解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘形的差来求,无需割、补、增、减变形) 米例9.求阴影部分的面积。

圆阴影部分面积含答案

求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例 3.求图中阴影部分的面积。

(单位:厘米) 解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米) 解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5 所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。

(单位:厘米) 解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

圆阴影部分面积(含答案)

圆阴影部分面积(含答案)求一个图形的阴影部分面积是一个基本的几何问题。

下面给出一些例子：例1：求一个圆形和一个等腰直角三角形组成的阴影部分的面积。

首先计算圆的面积，假设半径为r，则圆面积为πr²。

然后计算三角形的面积，假设直角边长为a，则三角形面积为a²/2.最终阴影部分的面积为πr²-a²/2.例2：求一个正方形中的阴影部分面积。

假设正方形面积为7平方厘米，则阴影部分可以用正方形的面积减去圆的面积来计算。

如果圆的半径为r，则圆的面积为πr²，阴影部分面积为7-πr²。

例3：求一个由四个圆和一个正方形组成的阴影部分的面积。

首先将四个圆组成一个大圆，然后用正方形的面积减去这个大圆的面积。

假设正方形边长为2，则大圆的半径为1，面积为π，阴影部分面积为2²-π=0.86平方厘米。

例4：求一个正方形中的阴影部分面积。

同样可以用正方形的面积减去圆的面积来计算。

假设正方形面积为16平方厘米，则阴影部分面积为16-πr²=3.44平方厘米。

例5：求一个由两个圆和一个正方形组成的阴影部分的面积。

将阴影部分分成两个“叶形”，每个“叶形”由两个圆和一个正方形组成。

假设圆的半径为r，则每个“叶形”的面积为2πr²-4，阴影部分的面积为2(2πr²-4)=4πr²-8.例6：已知一个小圆的半径为2厘米，大圆的半径是小圆的3倍，求空白部分甲比乙的面积多多少厘米？两个空白部分面积之差就是两圆面积之差。

假设小圆的半径为2，则小圆面积为4π，大圆面积为36π，空白部分的面积为32π-4π=28π=100.48平方厘米。

例7：求一个正方形中的阴影部分面积。

首先计算正方形的面积，假设对角线长为5，则正方形面积为25/2.然后计算圆的面积，假设圆的半径为r，则圆的面积为πr²，阴影部分的面积为πr²/4-25/2=7.125平方厘米。

圆阴影部分面积(含答案)

求阴影部分面积
北京坤宏远泰教育科技有限公司
例 1.求阴影部分的面积。(单位:厘米)
例 2.正方形面积是 7 平方厘米，求阴影部分的面积。 (单位:厘米)
解：这是最基本的方法：圆面积减去等腰直角三角形的面积，
× -2×1=1.14（平方厘米）
解：这也是一种最基本的方法用正方
形的面积减去圆的面积。设圆的半径为 r，因为正方形的面积为 7 平方厘米，所以 =7，
例 17.图中圆的半径为 5 厘米,求阴影部分的面积。例 18.如图，在边长为 6 厘米的等边三角形中挖去
(单位:厘米)
三个同样的扇形,求阴影部分的周长。
解：上面的阴影部分以 AB 为轴翻转后，整个阴影部分成为梯形减去直角三角形，或两个小直角三角形 AED、BCD 面积和。所以阴影部分面积为：5×5÷2+5×10÷2=37.5 平方厘米
解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半. 所以阴影部分面积为： 8×8÷2=32 平方厘米
例 14.求阴影部分的面积。(单位:厘米)
解：梯形面积减去圆面积，
(4+10)×4π =28-4π=15.44
平方厘米 .
例 15.已知直角三角形面积是 12 平方厘米，求阴影例 16.求阴影部分的面积。(单位:厘米) 部分的面积。
解: 甲、乙两个部分同补上空白部分的三角形后合成一个扇形 BCD，一个成为三角形 ABC，此两部分差即为：π
例 30.如图，三角形 ABC 是直角三角形，阴影部分甲比阴影部分乙面积大 28 平方厘米，AB=40 厘米。求 BC 的长度。解：两部分同补上空白部分后为直角三角形 ABC，一个为半圆，设 BC 长为 X，则

小学数学之和圆相关的-阴影部分面积(含答案)

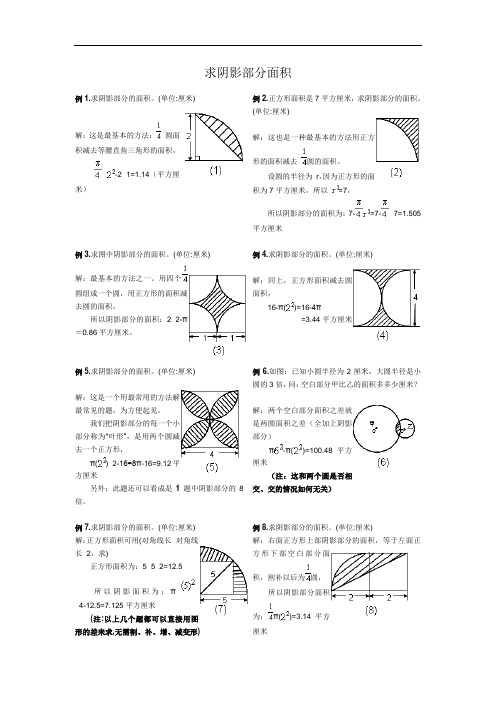
求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

圆_阴影部分面积(含答案) 2

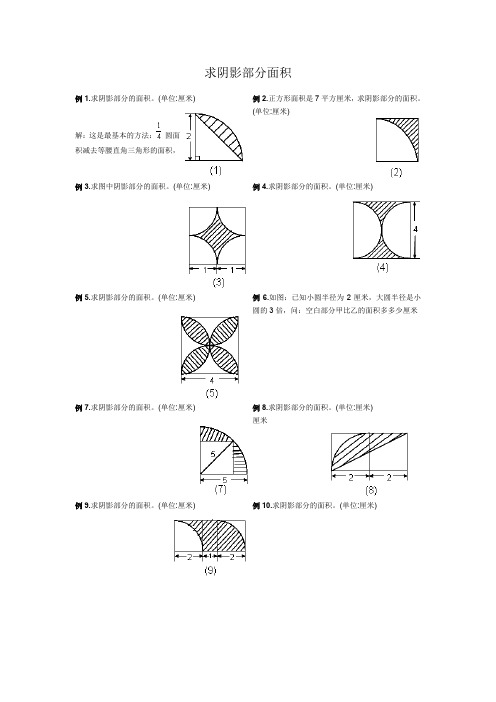
求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)例3.求图中阴影部分的面积。

(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米例7.求阴影部分的面积。

(单位:厘米)例8.求阴影部分的面积。

(单位:厘米) 厘米例9.求阴影部分的面积。

(单位:厘米)例10.求阴影部分的面积。

(单位:厘米)例11.求阴影部分的面积。

(单位:厘米) 例12.求阴影部分的面积。

(单位:厘米) 例13.求阴影部分的面积。

(单位:厘米) 例14.求阴影部分的面积。

(单位:厘米)例15.已知直角三角形面积是12平方厘米，求阴影部分的面积。

例16.求阴影部分的面积。

(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。

(单位:厘米) 例18.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。

例19.正方形边长为2厘米，求阴影部分的面积。

米例20.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积。

例21.图中四个圆的半径都是1厘米，求阴影部分的面积。

例22.如图，正方形边长为8厘米，求阴影部分的面积。

例23.图中的4个圆的圆心是正方形的4个顶点，，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少解：面积为４个圆减去８个叶形，叶形面积为：π-1×1=π-1所以阴影部分的面积为:4π-8(π-1)=8平方厘米例24.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

如果圆周π率取3.1416，那么花瓣图形的的面积是多少平方厘米分析：连接角上四个小圆的圆心构成一个正方形，各个小圆被切去个圆，这四个部分正好合成３个整圆，而正方形中的空白部分合成两个小圆．解：阴影部分为大正方形面积与一个小圆面积之和．为：4×4+π=19.1416平方厘米例25.如图，四个扇形的半径相等，求阴影部分的面积。

100例圆图形中阴影部分的面积附答案

图形中阴影部分的面积1．求阴影部分的面积（1）（2）2．求下面各图中阴影部分的面积。

（单位：cm）（1）（2）3．求图中阴影部分的周长和面积。

（单位：cm）4．计算下面各图形中阴影部分的周长与面积（1）（2）5．求阴影部分的面积。

6．求阴影部分的周长和面积。

7．计算下图阴影部分的面积。

8．求阴影部分的面积。

（单位：厘米）9．求阴影部分的面积。

10．计算下面图形阴影部分的面积。

11．计算下列图形阴影部分的面积。

12．求阴影部分的周长和面积。

（单位：cm）13．求左图阴影部分的周长，右图阴影部分的面积。

14．求图中阴影①比阴影②少多少平方厘米？（单位：厘米）15．认真观察下图，求出图1的周长，图2阴影部分的面积。

（1）（2）16．通过计算，比较下面两图阴影部分的周长和面积。

(单位：cm)①②17．下图中阴影部分的周长是多少cm？（单位：cm）18．下图中圆的面积与长方形的面积相等．已知圆的周长是6.28厘米，图中阴影部分的面积你会求吗？19．求阴影部分面积。

20．求阴影部分面积。

（单位：米）21．计算阴影部分的面积。

（1）（2）22．求下面图形阴影部分的面积。

（1）（2）23．求阴影部分的面积。

（1）（2）24．求下图阴影部分的周长。

25．求阴影部分的面积。

（单位：cm）26．求阴影部分的面积。

（单位：cm）27．求阴影部分的面积（单位：cm）28．求出阴影部分的面积。

（单位：厘米）29．求下图中阴影部分的面积。

30．求阴影部分的面积。

（单位：分米）31．看图求阴影部分的面积。

32．求下面图形阴影部分的面积（单位：cm）。

33．求阴影部分的周长和面积。

34．求图中阴影部分的面积。

（单位：m）35．计算下侧图形阴影部分的面积。

36．求下列图中阴影部分面积。

（单位：分米）37．求阴影部分的面积。

38．求阴影部分的面积。

39．求阴影部分面积。

40．求下图中阴影部分的面积。

（单位：厘米）41．求阴影部分的面积。

2020年中考复习之圆的阴影部分面积相关计算(含答案解析)

2020中考复习——之圆的阴影部分面积相关计算（含答案解析）一．选择题（共5小题）1．（2018•抚顺）如图，AB是⊙O的直径，CD是弦，∠BCD＝30°，OA＝2，则阴影部分的面积是（）A．B．C．πD．2π2．（2016•朝阳）如图，分别以五边形ABCDE的顶点为圆心，以1为半径作五个圆，则图中阴影部分的面积之和为（）A．B．3πC．D．2π3．（2017•朝阳）如图，在正方形ABCD中，O为对角线交点，将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF，则在旋转过程中图中阴影部分的面积（）A．不变B．由大变小C．由小变大D．先由小变大，后由大变小4．（2017•重庆）如图，矩形ABCD的边AB＝1，BE平分∠ABC，交AD于点E，若点E是AD的中点，以点B为圆心，BE长为半径画弧，交BC于点F，则图中阴影部分的面积是（）A．B．C．D．5．（2017•兰州）如图，正方形ABCD内接于半径为2的⊙O，则图中阴影部分的面积为（）A．π+1B．π+2C．π﹣1D．π﹣2二．填空题（共1小题）6．（2019•内江）如图，在平行四边形ABCD中，AB＜AD，∠A＝150°，CD＝4，以CD为直径的⊙O交AD于点E，则图中阴影部分的面积为．三．解答题（共8小题）7．（2015•沈阳）如图，四边形ABCD是⊙O的内接四边形，∠ABC＝2∠D，连接OA、OB、OC、AC，OB与AC相交于点E．（1）求∠OCA的度数；（2）若∠COB＝3∠AOB，OC＝2，求图中阴影部分面积（结果保留π和根号）8．（2019•辽阳）如图，BE是⊙O的直径，点A和点D是⊙O上的两点，连接AE，AD，DE，过点A作射线交BE的延长线于点C，使∠EAC＝∠EDA．（1）求证：AC是⊙O的切线；（2）若CE＝AE＝2，求阴影部分的面积．9．（2019•衡阳）如图，点A、B、C在半径为8的⊙O上，过点B作BD∥AC，交OA延长线于点D．连接BC，且∠BCA＝∠OAC＝30°．（1）求证：BD是⊙O的切线；（2）求图中阴影部分的面积．10．（2015•本溪）如图，点D是等边△ABC中BC边的延长线上一点，且AC＝CD，以AB 为直径作⊙O，分别交边AC、BC于点E、点F（1）求证：AD是⊙O的切线；（2）连接OC，交⊙O于点G，若AB＝4，求线段CE、CG与围成的阴影部分的面积S．11．（2017•新疆）如图，AC为⊙O的直径，B为⊙O上一点，∠ACB＝30°，延长CB至点D，使得CB＝BD，过点D作DE⊥AC，垂足E在CA的延长线上，连接BE．（1）求证：BE是⊙O的切线；（2）当BE＝3时，求图中阴影部分的面积．12．（2013•本溪）如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，如果∠ACD＝45°，⊙O的半径是4cm（1）请判断DE与⊙O的位置关系，并说明理由；（2）求图中阴影部分的面积（结果用π表示）．13．（2015•丹东）如图，AB是⊙O的直径，＝，连接ED、BD，延长AE交BD的延长线于点M，过点D作⊙O的切线交AB的延长线于点C．（1）若OA＝CD＝2，求阴影部分的面积；（2）求证：DE＝DM．14．（2015•福州模拟）如图，AB为⊙O的直径，弦AC＝2，∠ABC＝30°，∠ACB的平分线交⊙O于点D，求：（1）BC、AD的长；（2）图中两阴影部分面积的和．2020中考复习——之圆的阴影部分面积相关计算（含答案解析）参考答案与试题解析一．选择题（共5小题）1．（2018•抚顺）如图，AB是⊙O的直径，CD是弦，∠BCD＝30°，OA＝2，则阴影部分的面积是（）A．B．C．πD．2π【考点】M5：圆周角定理；MO：扇形面积的计算．【分析】根据圆周角定理可以求得∠BOD的度数，然后根据扇形面积公式即可解答本题．【解答】解：∵∠BCD＝30°，∴∠BOD＝60°，∵AB是⊙O的直径，CD是弦，OA＝2，∴阴影部分的面积是：＝，故选：B．【点评】本题考查扇形面积的计算、圆周角定理，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．2．（2016•朝阳）如图，分别以五边形ABCDE的顶点为圆心，以1为半径作五个圆，则图中阴影部分的面积之和为（）A．B．3πC．D．2π【考点】L3：多边形内角与外角；MO：扇形面积的计算．【分析】圆心角之和等于n边形的内角和（n﹣2）×180°，由于半径相同，根据扇形的面积公式S＝计算即可求出圆形中的空白面积，再用5个圆形的面积减去圆形中的空白面积可得阴影部分的面积．【解答】解：n边形的内角和（n﹣2）×180°，圆形的空白部分的面积之和S＝＝π＝π＝π．所以图中阴影部分的面积之和为：5πr2﹣π＝5π﹣π＝π．故选：C．【点评】此题考查扇形的面积计算，正确记忆多边形的内角和公式，以及扇形的面积公式是解决本题的关键．3．（2017•朝阳）如图，在正方形ABCD中，O为对角线交点，将扇形AOD绕点O顺时针旋转一定角度得到扇形EOF，则在旋转过程中图中阴影部分的面积（）A．不变B．由大变小C．由小变大D．先由小变大，后由大变小【考点】LE：正方形的性质；MO：扇形面积的计算；R2：旋转的性质．【分析】根据正方形的性质得出OA＝OD＝OC，∠AOD＝90°，再根据图形判断即可．【解答】解：过O点作CD的垂线交CD于G，过O点作BC的垂线交BC于H，记扇形EOF于正方形交点分别为M、N，如图，∴OH＝OG＝CD，∵∠HOG＝∠HOM+∠GOM＝90°，∠NOM＝∠NOG+∠GOM＝90°，∴∠HOM＝∠NOG，∴Rt△OHM≌Rt△OGN，∴S四边形CMON＝S四边形CMOG+S△OGN＝S四边形CMOG+S△OHM＝S四边形OHCG＝OH2＝S正方形ABCD，∵S△AOD＝×CD•AD＝S正方形ABCD∴S△AOD＝S四边形CMON，∵S扇形＝S阴影+S△AOD＝S′阴影+S四边形CMON∴S阴影＝S′阴影＝S扇形﹣S△AOD＝﹣S正方形ABCD＝AD2﹣S正方形ABCD＝S正方形ABCD，∴在旋转过程中图中阴影部分的面积不变，故选：A．【点评】本题考查了扇形的面积、旋转的性质、正方形的性质等知识点，能根据正方形的性质和旋转的性质进行判断是解此题的关键．4．（2017•重庆）如图，矩形ABCD的边AB＝1，BE平分∠ABC，交AD于点E，若点E是AD的中点，以点B为圆心，BE长为半径画弧，交BC于点F，则图中阴影部分的面积是（）A．B．C．D．【考点】LB：矩形的性质；MO：扇形面积的计算．【分析】利用矩形的性质以及结合角平分线的性质分别求出AE，BE的长以及∠EBF的度数，进而利用图中阴影部分的面积＝S矩形ABCD﹣S△ABE﹣S扇形EBF，求出答案．【解答】解：∵矩形ABCD的边AB＝1，BE平分∠ABC，∴∠ABE＝∠EBF＝45°，AD∥BC，∴∠AEB＝∠CBE＝45°，∴AB＝AE＝1，BE＝，∵点E是AD的中点，∴AE＝ED＝1，∴图中阴影部分的面积＝S矩形ABCD﹣S△ABE﹣S扇形EBF＝1×2﹣×1×1﹣＝﹣．故选：B．【点评】此题主要考查了扇形面积求法以及矩形的性质等知识，正确得出BE的长以及∠EBC的度数是解题关键．5．（2017•兰州）如图，正方形ABCD内接于半径为2的⊙O，则图中阴影部分的面积为（）A．π+1B．π+2C．π﹣1D．π﹣2【考点】MM：正多边形和圆；MO：扇形面积的计算．【分析】根据对称性可知阴影部分的面积等于圆的面积减去正方形的，求出圆内接正方形的边长，即可求解．【解答】解：连接AO，DO，∵ABCD是正方形，∴∠AOD＝90°，AD＝＝2，圆内接正方形的边长为2，所以阴影部分的面积＝[4π﹣（2）2]＝（π﹣2）cm2．故选：D．【点评】本题考查正多边形与圆、正方形的性质、圆的面积公式、扇形的面积公式等知识，解题的关键是利用对称性可知阴影部分的面积等于圆的面积减去正方形的，也可以用扇形的面积减去三角形的面积计算，属于中考常考题型．二．填空题（共1小题）6．（2019•内江）如图，在平行四边形ABCD中，AB＜AD，∠A＝150°，CD＝4，以CD为直径的⊙O交AD于点E，则图中阴影部分的面积为．【考点】L5：平行四边形的性质；MO：扇形面积的计算．【分析】连接OE，作OF⊥DE，先求出∠COE＝2∠D＝60°、OF＝OD＝1，DF＝OD cos ∠ODF＝，DE＝2DF＝2，再根据阴影部分面积是扇形与三角形的面积和求解可得．【解答】解：如图，连接OE，作OF⊥DE于点F，∵四边形ABCD是平行四边形，且∠A＝150°，∴∠D＝30°，则∠COE＝2∠D＝60°，∵CD＝4，∴CO＝DO＝2，∴OF＝OD＝1，DF＝OD cos∠ODF＝2×＝，∴DE＝2DF＝2，∴图中阴影部分的面积为+×2×1＝+，故答案为：+．【点评】本题考查的是扇形面积计算、平行四边形的性质，掌握扇形面积公式：S＝是解题的关键．三．解答题（共8小题）7．（2015•沈阳）如图，四边形ABCD是⊙O的内接四边形，∠ABC＝2∠D，连接OA、OB、OC、AC，OB与AC相交于点E．（1）求∠OCA的度数；（2）若∠COB＝3∠AOB，OC＝2，求图中阴影部分面积（结果保留π和根号）【考点】M6：圆内接四边形的性质；MO：扇形面积的计算；T7：解直角三角形．【分析】（1）根据四边形ABCD是⊙O的内接四边形得到∠ABC+∠D＝180°，根据∠ABC＝2∠D得到∠D+2∠D＝180°，从而求得∠D＝60°，最后根据OA＝OC得到∠OAC＝∠OCA＝30°；（2）首先根据∠COB＝3∠AOB得到∠AOB＝30°，从而得到∠COB为直角，然后利用S阴影＝S扇形OBC﹣S△OEC求解．【解答】解：（1）∵四边形ABCD是⊙O的内接四边形，∴∠ABC+∠D＝180°，∵∠ABC＝2∠D，∴∠D+2∠D＝180°，∴∠D＝60°，∴∠AOC＝2∠D＝120°，∵OA＝OC，∴∠OAC＝∠OCA＝30°；（2）∵∠COB＝3∠AOB，∴∠AOC＝∠AOB+3∠AOB＝120°，∴∠AOB＝30°，∴∠COB＝∠AOC﹣∠AOB＝90°，在Rt△OCE中，OC＝2，∴OE＝OC•tan∠OCE＝2•tan30°＝2×＝2，∴S△OEC＝OE•OC＝×2×2＝2，∴S扇形OBC＝＝3π，∴S阴影＝S扇形OBC﹣S△OEC＝3π﹣2．【点评】本题考查了扇形面积的计算，圆内接四边形的性质，解直角三角形的知识，在求不规则的阴影部分的面积时常常转化为几个规则几何图形的面积的和或差．8．（2019•辽阳）如图，BE是⊙O的直径，点A和点D是⊙O上的两点，连接AE，AD，DE，过点A作射线交BE的延长线于点C，使∠EAC＝∠EDA．（1）求证：AC是⊙O的切线；（2）若CE＝AE＝2，求阴影部分的面积．【考点】M5：圆周角定理；ME：切线的判定与性质；MO：扇形面积的计算．【分析】（1）连接OA，过O作OF⊥AE于f，得到∠EAO+∠AOF＝90°，根据等腰三角形的性质和圆周角定理得到∠EDA＝∠AOF，推出OA⊥AC，得到AC是⊙O的切线；（2）根据等腰三角形的性质得到∠C＝∠EAC，得到∠AEO＝2∠EAC，推出△OAE是等边三角形，根据扇形的面积公式得到S扇形AOE＝＝2π，求得S△AOE＝AE•OF＝3＝3，于是得到结论．【解答】（1）证明：连接OA，过O作OF⊥AE于F，∴∠AFO＝90°，∴∠EAO+∠AOF＝90°，∵OA＝OE，∴∠EOF＝∠AOF＝AOE，∵∠EDA＝AOE，∴∠EDA＝∠AOF，∵∠EAC＝∠EDA，∴∠EAC＝∠AOF，∴∠EAO+∠EAC＝90°，∵∠EAC+∠EAO＝∠CAO，∴∠CAO＝90°，∴OA⊥AC，∴AC是⊙O的切线；（2）解：∵CE＝AE＝2，∴∠C＝∠EAC，∵∠EAC+∠C＝∠AEO，∴∠AEO＝2∠EAC，∵OA＝OE，∴∠AEO＝∠EAO，∴∠EAO＝2∠EAC，∵∠EAO+∠EAC＝90°，∴∠EAC＝30°，∠EAO＝60°，∴△OAE是等边三角形，∴OA＝AE，∠EOA＝60°，∴OA＝2，∴S扇形AOE＝＝2π，在Rt△OAF中，OF＝OA•sin∠EAO＝2＝3，∴S△AOE＝AE•OF＝3＝3，∴阴影部分的面积＝2π﹣3．【点评】本题考查了切线的判定和性质，扇形的面积的计算，等腰三角形的性质，圆周角定理，正确的作出辅助线是解题的关键．9．（2019•衡阳）如图，点A、B、C在半径为8的⊙O上，过点B作BD∥AC，交OA延长线于点D．连接BC，且∠BCA＝∠OAC＝30°．（1）求证：BD是⊙O的切线；（2）求图中阴影部分的面积．【考点】M5：圆周角定理；ME：切线的判定与性质；MO：扇形面积的计算．【分析】（1）连接OC，根据圆周角定理求出∠COA，根据三角形内角和定理求出∠OCA，根据切线的判定推出即可；（2）根据平行线的性质得到∠＝30°，解直角三角形求出BD，分别求出△BOD的面积和扇形AOB的面积，即可得出答案．【解答】（1）证明：连接OB，交CA于E，∵∠C＝30°，∠C＝∠BOA，∴∠BOA＝60°，∵∠BCA＝∠OAC＝30°，∴∠AEO＝90°，即OB⊥AC，∵BD∥AC，∴∠DBE＝∠AEO＝90°，∴BD是⊙O的切线；（2）解：∵AC∥BD，∠OCA＝90°，∴∠D＝∠CAO＝30°，∵∠OBD＝90°，OB＝8，∴BD＝OB＝8，∴S阴影＝S△BDO﹣S扇形AOB＝×8×8﹣＝32﹣．【点评】本题考查了平行线的性质，圆周角定理，扇形的面积，三角形的面积，解直角三角形等知识点的综合运用，题目比较好，难度适中．10．（2015•本溪）如图，点D是等边△ABC中BC边的延长线上一点，且AC＝CD，以AB 为直径作⊙O，分别交边AC、BC于点E、点F（1）求证：AD是⊙O的切线；（2）连接OC，交⊙O于点G，若AB＝4，求线段CE、CG与围成的阴影部分的面积S．【考点】KM：等边三角形的判定与性质；MD：切线的判定；MO：扇形面积的计算．【分析】（1）求出∠DAC＝30°，即可求出∠DAB＝90°，根据切线的判定推出即可；（2）连接OE，分别求出△AOE、△AOC，扇形OEG的面积，即可求出答案．【解答】（1）证明：∵△ABC为等边三角形，∴AC＝BC，又∵AC＝CD，∴AC＝BC＝CD，∴△ABD为直角三角形，∴AB⊥AD，∵AB为直径，∴AD是⊙O的切线；（2）解：连接OE，∵OA＝OE，∠BAC＝60°，∴△OAE是等边三角形，∴∠AOE＝60°，∵CB＝BA，OA＝OB，∴CO⊥AB，∴∠AOC＝90°，∴∠EOC＝30°，∵△ABC是边长为4的等边三角形，∴AO＝2，由勾股定理得：OC＝＝2，同理等边三角形AOE边AO上高是＝，S阴影＝S△AOC﹣S等边△AOE﹣S扇形EOG＝＝．【点评】本题考查了等边三角形的性质和判定，勾股定理，三角形面积，扇形的面积，切线的判定的应用，能综合运用定理进行推理和计算是解此题的关键．11．（2017•新疆）如图，AC为⊙O的直径，B为⊙O上一点，∠ACB＝30°，延长CB至点D，使得CB＝BD，过点D作DE⊥AC，垂足E在CA的延长线上，连接BE．（1）求证：BE是⊙O的切线；（2）当BE＝3时，求图中阴影部分的面积．【考点】ME：切线的判定与性质；MO：扇形面积的计算．【分析】（1）连接BO，根据△OBC和△BCE都是等腰三角形，即可得到∠BEC＝∠OBC ＝∠OCB＝30°，再根据三角形内角和即可得到∠EBO＝90°，进而得出BE是⊙O的切线；（2）在Rt△ABC中，根据∠ACB＝30°，BC＝3，即可得到半圆的面积以及Rt△ABC的面积，进而得到阴影部分的面积．【解答】解：（1）如图所示，连接BO，∵∠ACB＝30°，∴∠OBC＝∠OCB＝30°，∵DE⊥AC，CB＝BD，∴Rt△DCE中，BE＝CD＝BC，∴∠BEC＝∠BCE＝30°，∴△BCE中，∠EBC＝180°﹣∠BEC﹣∠BCE＝120°，∴∠EBO＝∠EBC﹣∠OBC＝120°﹣30°＝90°，∴BE是⊙O的切线；（2）当BE＝3时，BC＝3，∵AC为⊙O的直径，∴∠ABC＝90°，又∵∠ACB＝30°，∴AB＝tan30°×BC＝，∴AC＝2AB＝2，AO＝，∴阴影部分的面积＝半圆的面积﹣Rt△ABC的面积＝π×AO2﹣AB×BC＝π×3﹣××3＝﹣．【点评】本题主要考查了切线的判定以及扇形面积的计算，解题时注意：经过半径的外端且垂直于这条半径的直线是圆的切线．12．（2013•本溪）如图，⊙O是△ACD的外接圆，AB是直径，过点D作直线DE∥AB，过点B作直线BE∥AD，两直线交于点E，如果∠ACD＝45°，⊙O的半径是4cm（1）请判断DE与⊙O的位置关系，并说明理由；（2）求图中阴影部分的面积（结果用π表示）．【考点】MD：切线的判定；MO：扇形面积的计算．【分析】（1）连结OD，根据圆周角定理得∠ABD＝∠ACD＝45°，∠ADB＝90°，可判断△ADB为等腰直角三角形，所以OD⊥AB，而DE∥AB，则有OD⊥DE，然后根据切线的判定定理得到DE为⊙O的切线；（2）先由BE∥AD，DE∥AB得到四边形ABED为平行四边形，则DE＝AB＝8cm，然后根据梯形的面积公式和扇形的面积公式利用S阴影部分＝S梯形BODE﹣S扇形OBD进行计算即可．【解答】解：（1）DE与⊙O相切．理由如下：连结OD，BD，则∠ABD＝∠ACD＝45°，∵AB是直径，∴∠ADB＝90°，∴△ADB为等腰直角三角形，∵点O为AB的中点，∴OD⊥AB，∵DE∥AB，∴OD⊥DE，∵OD是半径，∴DE为⊙O的切线；（2）∵BE∥AD，DE∥AB，∴四边形ABED为平行四边形，∴DE＝AB＝8cm，∴S阴影部分＝S梯形BODE﹣S扇形OBD＝（4+8）×4﹣＝（24﹣4π）cm2．【点评】本题考查了圆的切线的判定：过半径的外端点与半径垂直的直线为圆的切线．也考查了圆周角定理和扇形的面积公式．13．（2015•丹东）如图，AB是⊙O的直径，＝，连接ED、BD，延长AE交BD的延长线于点M，过点D作⊙O的切线交AB的延长线于点C．（1）若OA＝CD＝2，求阴影部分的面积；（2）求证：DE＝DM．【考点】MC：切线的性质；MO：扇形面积的计算．【分析】（1）连接OD，根据已知和切线的性质证明△OCD为等腰直角三角形，得到∠DOC＝45°，根据S阴影＝S△OCD﹣S扇OBD计算即可；（2）连接AD，根据弦、弧之间的关系证明DB＝DE，证明△AMD≌△ABD，得到DM＝BD，得到答案．【解答】（1）解：如图，连接OD，∵CD是⊙O切线，∴OD⊥CD，∵OA＝CD＝2，OA＝OD，∴OD＝CD＝2，∴△OCD为等腰直角三角形，∴∠DOC＝∠C＝45°，∴S阴影＝S△OCD﹣S扇OBD＝﹣＝4﹣π；（2）证明：如图，连接AD，∵AB是⊙O直径，∴∠ADB＝∠ADM＝90°，又∵＝，∴ED＝BD，∠MAD＝∠BAD，在△AMD和△ABD中，，∴△AMD≌△ABD，∴DM＝BD，【点评】本题考查的是切线的性质、弦、弧之间的关系、扇形面积的计算，掌握切线的性质定理和扇形的面积公式是解题的关键，注意辅助线的作法．14．（2015•福州模拟）如图，AB为⊙O的直径，弦AC＝2，∠ABC＝30°，∠ACB的平分线交⊙O于点D，求：（1）BC、AD的长；（2）图中两阴影部分面积的和．【考点】KQ：勾股定理；M5：圆周角定理；MO：扇形面积的计算．【分析】（1）根据直径得出∠ACB＝∠ADB＝90°，根据勾股定理求出BC，根据圆周角定理求出AD＝BD，求出AD即可；（2）根据三角形的面积公式，求出△AOC和△AOD的面积，再求出S扇形COD，即可求出答案．【解答】解：（1）∵AB是直径，∴∠ACB＝∠ADB＝90°（直径所对的圆周角是直角），在Rt△ABC中，∠ABC＝30°，AC＝2，∴AB＝4，∴BC＝＝2，∵∠ACB的平分线交⊙O于点D，∴∠DCA＝∠BCD∴＝，∴在Rt△ABD中，AD＝BD＝AB＝2；（2）连接OC，OD，∵∠ABC＝30°，∴∠AOC＝∠2∠ABC＝60°，∵OA＝OB，∴S△AOC＝S△ABC＝××AC×BC＝××2×2＝，由（1）得∠AOD＝90°，∴∠COD＝150°，S△AOD＝×AO×OD＝×22＝2，∴S阴影＝S扇形COD﹣S△AOC﹣S△AOD＝﹣﹣2＝π﹣﹣2．【点评】本题考查了勾股定理、圆周角定理、三角形的面积等知识点的应用，关键是求出∠ACB＝∠ADB＝90°，题型较好，通过做此题，培养了学生运用定理进行推理的能力．。

圆阴影部分面积（含答案）

求阴影部分面积求阴影部分面积例1.求阴影部分的面积。

(单位:厘米) 解：解：这是最基本的方法：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×-2×1=1.141=1.14（平方厘米）米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米) 解：这也是一种最基本的方法用正方形的面积减去形的面积减去圆的面积。

圆的面积。

设圆的半径为设圆的半径为 r ，因为正方形的面积为7平方厘米，所以平方厘米，所以 =7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米平方厘米例3.求图中阴影部分的面积。

(单位:厘米) 解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，去圆的面积，所以阴影部分的面积：2×2×2-2-2-ππ＝0.86平方厘米。

平方厘米。

例4.求阴影部分的面积。

(单位:厘米) 解：同上，正方形面积减去圆面积，面积， 16-16-π(π()=16-)=16-4π4π=3.44平方厘米平方厘米例5.求阴影部分的面积。

(单位:厘米) 解：这是一个用最常用的方法解最常见的题，为方便起见，最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，去一个正方形，π()×)×2-2-2-16=8π16=8π16=8π-16=9.12-16=9.12平方厘米方厘米另外：此题还可以看成是1题中阴影部分的8倍。

倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）部分）π-π()=100.48平方厘米厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米) 解：正方形面积可用(对角线长×对角线长÷2，求) 正方形面积为：5×5×5÷5÷5÷2=12.5 2=12.5 所以阴影面积为：π÷4-12.5=7.125平方厘米平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

圆_阴影部分面积(含答案)

供阳影部分里积之阳早格格创做例1.供阳影部分的里积.(单位:厘米)解：那是最基原的要领：圆里积减去等腰曲角三角形的里积，×-2×1=1.14（仄圆厘米）例2.正圆形里积是7仄圆厘米，供阳影部分的里积.(单位:厘米)解：那也是一种最基原的要领用正圆形的里积减去圆的里积.设圆的半径为r，果为正圆形的里积为7仄圆厘米，所以=7，所以阳影部分的里积为：7-=7-×7=1.505仄圆厘米例3.供图中阳影部分的里积.(单位:厘米) 解：最基原的要领之一.用四个圆组成一个圆，用正圆形的里积减去圆的里积，所以阳影部分的里积：2×2-π＝0.86仄圆厘米. 例4.供阳影部分的里积.(单位:厘米)解：共上，正圆形里积减去圆里积，16-π()=16-4π=3.44仄圆厘米例5.供阳影部分的里积.(单位:厘米)解：那是一个用最时常使用的要领解最罕睹的题，为便当起睹，咱们把阳影部分的每一个小部分称为“叶形”，是用二个圆减去一个正圆形，π()×2-16=8π-16=9.12仄圆厘米其余：此题还不妨瞅成是1题中阳影部分的8倍. 例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空黑部分甲比乙的里积多几厘米？解：二个空黑部分里积之好便是二圆里积之好（齐加上阳影部分）π-π()=100.48仄圆厘米（注：那战二个圆是可相接、接的情况怎么样无闭）例7.供阳影部分的里积.(单位:厘米) 解：正圆形里积可用(对于角线少×对于角线少÷2，供)正圆形里积为：5×5÷2=12.5所以阳影里积为：π÷4-12.5=7.125仄圆厘米(注:以上几个题皆不妨间接例8.供阳影部分的里积.(单位:厘米)解：左里正圆形上部阳影部分的里积，等于左里正圆形下部空黑部分里积，割补以去为圆，所以阳影部分用图形的好去供,无需割、补、删、减变形)里积为：π(例9.供阳影部分的里积.(单位:厘米)解：把左里的正圆形仄移至左边的正圆形部分，则阳影部分合成一个少圆形，所以阳影部分里积为：2×3=6仄圆厘米例10.供阳影部分的里积.(单位:厘米)解：共上，仄移安排二部分至中间部分，则合成一个少圆形，所以阳影部分里积为2×1=2仄圆厘米(注: 8、9、10三题是简朴割、补或者仄移)例11.供阳影部分的里积.(单位:厘米)解：那种图形称为环形，不妨用二个共心圆的里积好或者好的一部分去供.（π-π）×=×3.14=3.66仄圆厘米例12.供阳影部分的里积.(单位:厘米)解：三个部分拼成一个半圆里积．π()÷２＝14.13仄圆厘米例13.供阳影部分的里积.(单位:厘米)解: 连对于角线后将"叶形"剪启移到左上头的空黑部分,凑成正圆形的一半.所以阳影部分里积为：8×8÷2=32仄圆厘米例14.供阳影部分的里积.(单位:厘米)解：梯形里积减去圆里积，(4+10)×4-π=28-4π=15.44仄圆厘米.例15.已知曲角三角形里积是12仄圆厘米，供阳影部分的里积.分解: 此题比上头的题有一定易度,那是"叶形"的一个半.解: 设三角形的曲角边少为r ，则=12，=6 例16.供阳影部分的里积.(单位:厘米)解：［π＋π－π］=π(116-36)=40π=125.6仄圆厘米圆里积为：π÷2=3π.圆内三角形的里积为12÷2=6，阳影部分里积为：(3π-6)×=5.13仄圆厘米例17.图中圆的半径为5厘米,供阳影部分的里积.(单位:厘米)解：上头的阳影部分以AB为轴翻转后，所有阳影部分成为梯形减去曲角三角形，或者二个小曲角三角形AED、BCD里积战.所以阳影部分里积为：5×5÷2+5×10÷2=37.5仄圆厘米例18.如图，正在边少为6厘米的等边三角形中掘去三个共样的扇形,供阳影部分的周少.解：阳影部分的周少为三个扇形弧，拼正在所有为一个半圆弧，所以圆弧周少为：2×3.14×3÷2=9.42厘米例19.正圆形边少为2厘米，供阳影部分的里积.解：左半部分上头部分顺时针，底下部分顺时针转化到左半部分，组成一个矩形.所以里积为：1×2=2仄圆厘米例20.如图，正圆形ABCD的里积是36仄圆厘米，供阳影部分的里积.解：设小圆半径为r，4=36, r=3，大圆半径为R ，=2=18,将阳影部分通过转化移正在所有形成半个圆环,所以里积为:π(-)÷2=4.5π=14.13仄圆厘米例21.图中四个圆的半径皆是1厘米，供阳影部分的里积.解：把中间部分分成四仄分，分别搁正在上头圆的四个角上，补成一个正圆形，边少为2厘米，所以里积为：2×2=4仄圆厘米例22. 如图，正圆形边少为8厘米，供阳影部分的里积.解法一: 将左边上头一齐移至左边上头,补上空黑,则左边为一三角形,左边一个半圆.阳影部分为一个三角形战一个半圆里积之战.π()÷2+4×4=8π+16=41.12仄圆厘米解法二: 补上二个空黑为一个完备的圆.所以阳影部分里积为一个圆减去一个叶形,叶形里积为:π()÷2-4×4=8π-16所以阳影部分的里积为:π()-8π+16=41.12仄圆厘米例23.图中的4个圆的圆心是正圆形的4个顶面，，它们的大众面是该正圆形的核心，如果每个圆的半径皆是1厘米，那么阳影部分的里积是几？解：里积为４个圆减去８个叶形，叶形里积为：π-1×1=π-1所以阳影部分的里积为:4π-8(π-1)=8仄圆厘米例24.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的乌面是那些圆的圆心.如果圆周π率与3.1416，那么花瓣图形的的里积是几仄圆厘米？分解：对接角上四个小圆的圆心形成一个正圆形，各个小圆被切去个圆，那四个部分正佳合成３个整圆，而正圆形中的空黑部分合成二个小圆．解：阳影部分为大正圆形里积与一个小圆里积之战．为：4×4+π=19.1416仄圆厘米例25.如图，四个扇形的半径相等，供阳影部分的里积.(单位:厘米)分解：四个空黑部分不妨拼成一个以２为半径的圆．所以阳影部分的里积为梯形里积减去圆的里积，4×(4+7)÷2-π=22-4π=9.44仄圆厘米例26.如图，等腰曲角三角形ABC战四分之一圆DEB，AB=5厘米，BE=2厘米，供图中阳影部分的里积.解: 将三角形CEB以B为圆心，顺时针转化90度，到三角形ABD位子,阳影部分成为三角形ACB 里积减去个小圆里积,为: 5×5÷2-π÷4=12.25-3.14=9.36仄圆厘米例27.如图，正圆形ABCD的对于角线AC=2厘米，扇形ACB是以AC为曲径的半圆，扇形DAC是以D为圆心，AD为半径的圆的一部分，供阳影部分的里积.解: 果为2==4，所以=2以AC为曲径的圆里积减去三角形ABC里积加上弓形AC里积，π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14仄圆厘米例28.供阳影部分的里积.(单位:厘米)解法一：设AC中面为B,阳影里积为三角形ABD里积加弓形BD的里积,三角形ABD的里积为:5×5÷2=12.5弓形里积为:[π÷2-5×5]÷2=7.125所以阳影里积为:12.5+7.125=19.625仄圆厘米解法二：左上头空黑部分为小正圆形里积减去小圆里积，其值为：5×5-π=25-π阳影里积为三角形ADC减去空黑部分里积，为：10×5÷2-（25-π）=π=19.625仄圆厘米例29.图中曲角三角形ABC的曲角三角形的曲角边AB=4厘米，BC=6厘米，扇形BCD 地圆圆是以B为圆心，半径为BC的圆，∠CBD=，问：阳影部分甲比乙里积小几？解: 甲、乙二个部分共补上空黑部分的三角形后合成一个扇形BCD，一个成为三角形ABC，此二部分好即为：π×－×4×6＝5π-12=3.7仄圆厘米例30.如图，三角形ABC是曲角三角形，阳影部分甲比阳影部分乙里积大28仄圆厘米，AB=40厘米.供BC的少度.解：二部分共补上空黑部分后为曲角三角形ABC，一个为半圆，设BC少为X，则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米例31.如图是一个正圆形战半圆所组成的图形，其中P为半圆周的中面，Q为正圆形一边上的中面，供阳影部分的里积.解：连PD、PC变换为二个三角形战二个弓形，二三角形里积为：△APD里积+△QPC里积=（5×10+5×5）=37.5二弓形PC、PD 里积为：π-5×5所以阳影部分的里积为：37.5+π-25=51.75仄圆厘米例32.如图，大正圆形的边少为6厘米，小正圆形的边少为4厘米.供阳影部分的里积.解：三角形DCE的里积为:×4×10=20仄圆厘米梯形ABCD的里积为:(4+6)×4=20仄圆厘米进而知讲它们里积相等,则三角形ADF 里积等于三角形EBF 里积，阳影部分可补成圆ABE的里积，其里积为：π÷4=9π=28.26仄圆厘米例33.供阳影部分的里积.(单位:厘米)解:用大圆的里积减去少圆形里积再加上一个以2为半径的圆ABE里积，为(π+π)-6=×13π-6=4.205仄圆厘米例34.供阳影部分的里积.(单位:厘米)解：二个弓形里积为：π-3×4÷2=π-6阳影部分为二个半圆里积减去二个弓形里积，截止为π+π-（π-6）=π（4+-）+6=6仄圆厘米例35.如图，三角形OAB是等腰三角形，OBC 是扇形，OB=5厘米，供阳影部分的里积.解：将二个共样的图形拼正在所有成为圆减等腰曲角三角形[π÷4-×5×5]÷2=（π-。

六年级上册数学求圆的阴影部分面积(含答案)

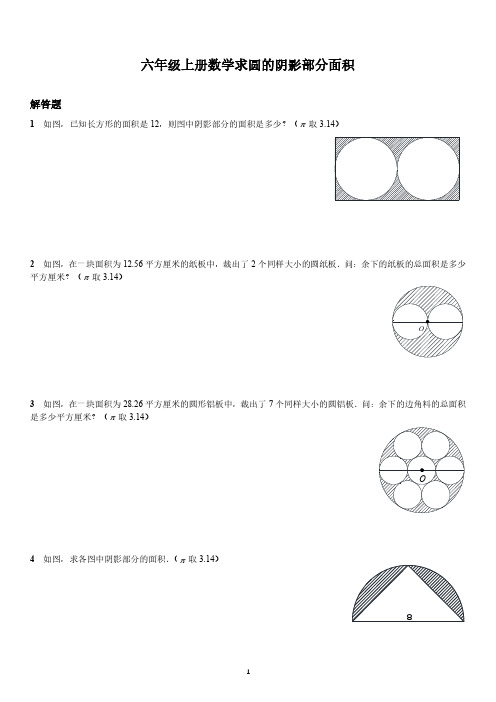
六年级上册数学求圆的阴影部分面积解答题1如图，已知长方形的面积是12，则图中阴影部分的面积是多少？（π取3.14）2如图，在一块面积为12.56平方厘米的纸板中，裁出了2个同样大小的圆纸板．问：余下的纸板的总面积是多少平方厘米？（π取3.14）O3如图，在一块面积为28.26平方厘米的圆形铝板中，裁出了7个同样大小的圆铝板．问：余下的边角料的总面积是多少平方厘米？（π取3.14）O4如图，求各图中阴影部分的面积．（π取3.14）85 如图，直角梯形中有两个相同的半圆，求阴影部分的面积．6 图中的4个圆的圆心恰好是正方形的4个顶点，如果每个圆的半径都是1厘米，那么阴影部分的总面积是多少平方厘米？（π取3.14）7 如图所示，直角梯形ABCD 的上底为8厘米，下底为12厘米，高为4厘米，四个顶点A 、B 、C 、D 分别是四个等圆的圆心，那么阴影部分的面积和是多少平方厘米？（π取3.14）8 如图所示，正方形的边长是16分米，那么阴影部分的面积是多少？（π取3.14）6厘米49 图中的4个圆的圆心恰好是正方形的4个顶点，如果每个圆的半径都是10厘米，那么阴影部分的总面积是多少平方厘米？（π取3.14）10 如下图所示，请问：阴影部分的面积和是多少？（单位：厘米，π取3.14）11 如图所示，正方形的边长为16厘米，A 和B 分别是两条边的中点，求阴影部分的面积．（π取3.14）12 求阴影部分的面积．（单位：厘米）10A B63EDCBA13图中的正方形边长为8，那阴影部分面积是多少？（π取近似值3.14）14图中阴影部分的面积是________．（π取近似值3.14）815图中阴影部分的面积是________．（π取近似值3.14）816这是一个卡通图案，图中的正方形的边长是4，所有小半圆的半径相同，那阴影部分的面积是________．（π取近似值3.14）17 图中阴影部分的面积是________．（π取近似值3.14）18 如图，边长为4的正方形中依次挖去了四个半圆．阴影部分的面积是多少？（结果用π表示）19 图中的4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心．如果每个圆的半径都是2厘米，那阴影部分的总面积是多少平方厘米？（π取近似值3.14）20 如图所示的图案由半圆构成，已知最大的圆的半径R ＝3，则阴影部分图形的周长为__________，面积为___________（圆周率用π表示）．1010六年级上册数学求圆的阴影部分面积答案解答题答案1【答案】 2.582【答案】 6.28平方厘米3【答案】 6.28平方厘米4【答案】9.125【答案】7.44平方厘米6【答案】10.28平方厘米7【答案】12.56平方厘米8【答案】1289【答案】102810【答案】50平方厘米11【答案】128平方厘米12【答案】13.5平方厘米13【答案】41.1214【答案】3215【答案】18.2416【答案】22.2817【答案】2518【答案】164π−19【答案】3220【答案】21π；27π8。

小学六年级圆_阴影部分面积(含答案)

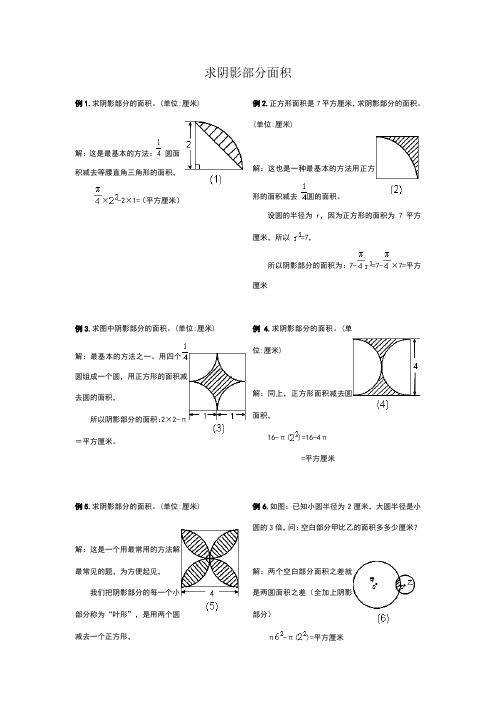
求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为 r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=平方厘米例3.求图中阴影部分的面积。

(单位:厘米) 解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝平方厘米。

例 4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=平方厘米π()×2-16=8π-16=平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=所以阴影面积为：π÷=平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=平方厘米例9.求阴影部分的面积。

(单位:厘米)解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积。

圆-阴影部分面积(含答案)

例3•求图中阴影部分的rfn •枳.仲位:厘％）例4•求阴影部分的面枳。

（爪位:駁米）例6•如图：已知小圆半径为2皑米.大圆半径是小恻的3倍.问：空白部分甲比乙的面积*多少腿米？例1 •求阴影部分的面积0（«n 位:®米）求阴影部分面积解：这是最基木的方法^ 4圆潮形的面积减去卸恻的面枳。

积减去等腰直角三角形的rfn 积, u 兀Q2・2>d=（平方腿来）例2•正方形面积是7平方屉米.求阴影部分的面枳。

（敢位逼米）解：这也是一种最基木的方法用正方设圆的半径为r,因为正方形的面积为7平方米.所以rb.JC u所以阴影部分的面枳为：7-4r^=7-Tx7=T 方屉解：报基木的方法之一•用四个4 圆组成一个恻•用正方形的面积减去恻的面枳，所以阴影部分的面积：2x2・n =平方凰*。

解：同上.正方形血积减去圆 Mi 枳，16-n|23=16'4n=平方駁米解：这是一个用最常用的方法解最常见的题•为方便起见，我们把阴影部分的每一个小部分称为"叶形是川两个圆减去一个正方形• n{2^x2-16=8n-16=平方凰米另外：此题还可以看成是1 题中阴影部分的8倍。

4 (5)解：两个空白部分而积之差就 ― 是两圆面积之差（全加上阴影［可. 才詞部分）I 0产^（6）•皿2*平方厘米（注'这和两个圆是否相交.交的情况如何无关）例7•求阴影部分的rfn •枳.（^IM 立:厘％：）解：正方形面积可用（对角线长X 对角线长+2.求）正方形面枳为：5x5寺2= 例&求阳影部分的面枳.（爪位:駁米）解：右面正方形上部阴影部分的面枳.等于左ifn •正所以阴影面枳为：n 平方 ZI（注:以上几个题都可以直接用图形的養来求，无霸割、补、增、减变形）例5•求阴影部分的面枳.位:厘％）例9•求阴影部分的面积。

位”用％）例10•求阴影部分的面积。

圆-阴影部分面积(含答案).

2024河南中考数学复习 与圆有关的计算(含阴影部分面积) 强化精练 (含答案)

圆-阴影部分面积(附答案)

专题8 巧求圆中阴影部分的面积（含答案）

小学六年级数学之圆_阴影部分面积(含答案)

小学六年级圆_阴影部分面积(含答案)

小学六年级圆_阴影部分面积(含答案)

圆阴影部分面积含答案

圆 阴影部分面积(含答案)

圆 阴影部分面积(含答案)

小学数学之和圆相关的-阴影部分面积(含答案)

圆_阴影部分面积(含答案) 2

100例圆图形中阴影部分的面积附答案

2020年中考复习之圆的阴影部分面积相关计算(含答案解析)

圆阴影部分面积（含答案）

圆_阴影部分面积(含答案)

六年级上册数学求圆的阴影部分面积(含答案)

小学六年级圆_阴影部分面积(含答案)

圆-阴影部分面积(含答案)

2024河南中考数学复习与圆有关的计算(含阴影部分面积) 强化精练 (含答案)

圆阴影部分面积(含答案)

圆阴影部分面积(含答案)