斯托克斯公式环流量与旋度
合集下载
9-7 斯托克斯公式 环流量与旋度.
上侧的单位法向量为
(cos , cos , cos ) ( 1 , 1 , 1 ) 3 3 3 cos cos cos dS I x y z 2 y x2 z 2 x2 x2 y 2
4 4 3 9 ( x y z)dS dS 2 3 3dxdy 2 3 32 D
按斯托克斯公式 有
dydz dzdx dxdy zdx xdy ydz x y z z x y
dydz dzdx dxdy dydz dzdx dxdy 3 2
D yz Dzx Dxy D yz Dzx Dxy
§9.7 斯托克斯公式
一、斯托克斯公式
首页
上页
返回
下页
结束
铃
一、斯托克斯公式
定理 设为分段光滑的空间有向闭曲线 是以为边界的分 片光滑的有向曲面 的正向与的侧符合右手规则 函数 P(xyz)、Q(xyz)、R(xyz)在曲面(连同边界)上具有一阶连 续偏导数则有 R Q )dydz ( P R )dzdx ( Q P )dxdy ( y z z x x y
Pdx Qdy Rdz
首页
上页
返回
下页
结束
铃
n
z
o x
Dx y
y C
首页
上页
返回
下页Βιβλιοθήκη 结束铃例 1 利用斯托克斯公式计算曲线积分 zdx xdy ydz 其中
其中为平面xyz1被三个坐标面所截成的三角形的整个边 界 它的正向与这个三角形上侧的法向量之间符合右手规则 解 设为平面xyz1被三个坐标面所截成的三角形
8_2_4 斯托克斯公式 环流量与旋度 高等数学 微积分 考研数学
轴正向看为顺时针, 计算 I y2 d x xy d y xz d z .
解: 设为平面 z = y 上被 所围椭圆域 , 且取下侧,
则其法线方向余弦
cos 0 , cos
1, 2
cos
1 2
z
利用斯托克斯公式得
cos cos cos
o x
2y
I
x y
y2 xy
z
dS 1 (y z)dS 0 2
内容小结
1. 斯托克斯公式
d yd z
P d x Q d y R d z
x
P
dzdx
y
Q
dxd y
z
R
cos
x
P
cos
y
Q
cos
z
dS
R
Page 10
2. 场论中的三个重要概念
设 u u (x, y, z),
A
(P,
Q,
R),
x
,
y
,
z
,
则
梯度:
grad u
u x
d ydz dzdx P d x Q d y R d z
R
或用第一类曲面积分表示:
cos cos cos
x
y
z
d S P d x Q d y R d z
PQR
Page 3
例1. 利用斯托克斯公式计算积分
zdx xd y ydz
其中为平面 x+ y+ z = 1 被三坐标面所截三角形的整个
出了著名的粘性流体运动方程 ( 后称之 为纳维 – 斯托克斯方程 ), 1847年先于
柯西提出了一致收敛的概念. 他提出的斯托克斯公式
10-7斯托克斯公式,环流量与旋度
其中
(rA o )n trA o n t
( R Q )c o (s P R )c o (s Q P )cos
y z
z x
x y
A t A n P c Q c o R o c so s
环 流 r A o d S 量 t A tds
Stokes公式的物理解释:
五 、 求 向 量 场 A ( x z )i ( x 3 yz ) j 3 xy 2 k 沿 闭 曲 线 为圆 周 z 2 x 2 y 2 , z 0 ( 从 z 轴 正 向 看 依逆 时 针 方 向 ) 的 环 流 量 .
六 、设 u u ( x , y , z ) 具 有 二 阶 连 续 偏 导 数 , 求 rot ( gradu ) .
则沿A场中某一封闭的有C向 上曲 的线 曲线积分
CAds CPdxQdyRokes公式, 有
i jk
环流 量 C A dsx
y
dS z
P QR
2. 旋度的定义: i jk
称向 量 为向量场 (ro的 A )t. 旋度 x y z
向 量场A沿有向闭曲线 的环流量等于向量场 A的旋度场通过所张的曲面的通量.( 的正 向与的侧符合右手法则)
四、小结
斯托克斯公式
cos cos cos
dydz dzdx dxdy
x
y
z
dS
x
y
z
PQR
PQ R
PdQ x d R y d zrA o n d t S A tds
斯托克斯公式成立的条件
由于 的法向量的三弦 个都 方为 向正 余， 再由对称性知：
dyddzzdxdxdy3 d
D xy
y
Dxy如图
10-7斯托克斯公式 环流量和旋度
P P P[ x , y , f ( x , y )] fy y y z
P P dzdx dxdy y z P[ x , y , f ( x , y )]dxdy , D y
xy
1
D 由分段光滑的曲线 L 围 设闭区域
D 上具有一阶连 成,函数 P ( x , y )及 Q ( x , y ) 在
3 其中 是平面 x y z 截立方体:0 x 1 , 2 0 y 1 ,0 z 1 的表面所得的截痕,若从 ox
轴的正向看去,取逆时针方向.
3 解 取Σ 为平面 x y z 2 的上侧被 所围成的部分. 1 则 n {1,1,1} 3
z
n
R Q P R Q P ( )dydz ( )dzdx ( )dxdy y z z x x y
Pdx Qdy Rdz
斯托克斯公式
n
右手法则
正向边界曲线
z
是有向曲面 的
n
证明
如图
z 轴的直线 设 Σ 与平行于
续偏导数, 则有
Q P ( )dxdy L Pdx Qdy x y D 其中 L 是D 的取正向的边界曲线,
公式(1)叫做格林公式.
(1)
根椐格林公式
Dxy
P[ x , y , f ( x , y )]dxdy P[ x , y , f ( x , y )]dx c y
相交不多于一点 , 并Σ 取 上侧,有向曲线 C 为Σ 的正 向边界曲线 在 xoy 的投 影.且所围区域D xy .
x
:z
f ( x, y )
P P dzdx dxdy y z P[ x , y , f ( x , y )]dxdy , D y
xy
1
D 由分段光滑的曲线 L 围 设闭区域
D 上具有一阶连 成,函数 P ( x , y )及 Q ( x , y ) 在
3 其中 是平面 x y z 截立方体:0 x 1 , 2 0 y 1 ,0 z 1 的表面所得的截痕,若从 ox
轴的正向看去,取逆时针方向.
3 解 取Σ 为平面 x y z 2 的上侧被 所围成的部分. 1 则 n {1,1,1} 3
z
n
R Q P R Q P ( )dydz ( )dzdx ( )dxdy y z z x x y
Pdx Qdy Rdz
斯托克斯公式
n
右手法则
正向边界曲线
z
是有向曲面 的
n
证明
如图
z 轴的直线 设 Σ 与平行于
续偏导数, 则有
Q P ( )dxdy L Pdx Qdy x y D 其中 L 是D 的取正向的边界曲线,
公式(1)叫做格林公式.
(1)
根椐格林公式
Dxy
P[ x , y , f ( x , y )]dxdy P[ x , y , f ( x , y )]dx c y
相交不多于一点 , 并Σ 取 上侧,有向曲线 C 为Σ 的正 向边界曲线 在 xoy 的投 影.且所围区域D xy .
x
:z
f ( x, y )
斯托克斯公式 环流量与旋度
向前进 , 在左手边.
表达了有向曲面上的曲面积分与其边界曲线 上的曲线积分之间的关系.
(当Σ 是 xoy 面的平面闭区域时)
斯托克斯公式
特殊情形
格林公式
为便于记忆, 斯托克斯公式还可写作:
d yd z d zd x d xd y Pd x Qd y Rd z x y z P Q R
, , x y z
,
则
grad u u , u , u 梯度: x y z
散度:
u
P Q R div A x y z A
i
旋度: rot A
x
j
y
k
z
A
P
Q
R
o
1
1 y
d yd z d zd x d xd y
x y z
x
Dx y
z
x
y
利用对称性
3 d y d z d z d x d x d y 3 d x d y Dx y 2
例2. 为柱面
轴正向看为顺时针, 计算
与平面 y = z 的交线,从 z
曲线 的单位切向量为
则斯托克斯公式可写为
n (cos , cos , cos ) (cos , cos , cos )
( P cos Q cos R cos ) d s
令 A ( P, Q, R) , 引进一个向量
记作
rot A
x y z P Q R
P d x Q d y R d z
d yd z d zd x d xd y
第七节 斯托克斯公式与旋度
第七节 斯托克斯公式与旋度
一、斯托克斯(stokes)公式 二、物理意义 -- 环流量与旋度 三、空间定向曲线积分与路径无关条件
一、斯托克斯(stokes)公式
1、定向曲面∑的正向边界曲线： 设定向曲面∑ 的边界曲线为，规定 的正向 如下：当人站立于定向曲面的一侧上，并沿 行走时，邻近处的 始终位于他的左方. 带有正向的边界曲线 称作定向曲面 的正向边界 曲线，记作 + .
Stokes公式的实质: 表达了有向曲面上的曲面积分与其边界曲线 上的曲线积分之间的关系.
(当Σ是xoy面的平面闭区域,且R(x,y,z)=0
斯托克斯公式
特殊情形
格林公式
z
例 1 计算 zdx xdy ydz , 其中 是平面 x y z 1 被 三坐标面所截成的三角形的 整个边界,取逆时针方向.
称为向量场 F 沿曲线 按所取方向的环流量 .
环流量
F dr Pdx Qdy Rdz
F dr
i x P
j y Q
k dS z R
P ( x , y , z ) i Q ( x , y , z ) j R( x , y , z ) k i j k 称向量 x y z P Q R R Q P R Q P ( )i ( ) j ( )k . y z z x x y 为F在点( x , y, z )处的旋度(rotation), 记为rotF .
设空间区域G, 如果G内任一闭曲面所围成 的区域全属于G, 则称G是空间二维单连通域;
如果G内任一闭曲线总可以张一片完全属于 G的曲面, 则称G为空间一维单连通区域.
一、斯托克斯(stokes)公式 二、物理意义 -- 环流量与旋度 三、空间定向曲线积分与路径无关条件
一、斯托克斯(stokes)公式
1、定向曲面∑的正向边界曲线： 设定向曲面∑ 的边界曲线为，规定 的正向 如下：当人站立于定向曲面的一侧上，并沿 行走时，邻近处的 始终位于他的左方. 带有正向的边界曲线 称作定向曲面 的正向边界 曲线，记作 + .
Stokes公式的实质: 表达了有向曲面上的曲面积分与其边界曲线 上的曲线积分之间的关系.
(当Σ是xoy面的平面闭区域,且R(x,y,z)=0
斯托克斯公式
特殊情形
格林公式
z
例 1 计算 zdx xdy ydz , 其中 是平面 x y z 1 被 三坐标面所截成的三角形的 整个边界,取逆时针方向.
称为向量场 F 沿曲线 按所取方向的环流量 .
环流量
F dr Pdx Qdy Rdz
F dr
i x P
j y Q
k dS z R
P ( x , y , z ) i Q ( x , y , z ) j R( x , y , z ) k i j k 称向量 x y z P Q R R Q P R Q P ( )i ( ) j ( )k . y z z x x y 为F在点( x , y, z )处的旋度(rotation), 记为rotF .
设空间区域G, 如果G内任一闭曲面所围成 的区域全属于G, 则称G是空间二维单连通域;
如果G内任一闭曲线总可以张一片完全属于 G的曲面, 则称G为空间一维单连通区域.
10.7_斯托克斯公式__环流量与旋度
W ydx zdy xdz
x
y
1 3
y
1 3
dS z
x
1 3
A x
O
y
1
C
y
z
1 n D xy (1 , 1 , 1) 3
x y yz 1 x 1
x 3d1xdy
d OS
1 (3)dS 3
3
D xy
3 3 dxdy . 2
ydx zdy xdz
B
z
O
n
C
y
dydz dzdx dxdy
Σ
3 dxdy
Σ
A x
一投
二代
三定号
化 为 ( 3) dxdy 二 Dxy 重 1 3 积 分 3 .
2
y 1
x y1
D xy
1
x
O
2
19
10.7 斯托克斯公式 环流量与旋度
斯托克斯公式是微积分基本公式在曲面
积分情形下的推广, 也是格林公式在空间的
推广, 它将定向曲面上的面积分与曲面的定向
边界曲线上的线积分联系了起来.
2
10.7 斯托克斯公式 环流量与旋度
一、斯托克斯(Stokes)公式
定理10.11 设Γ为分段光滑的空间有向闭曲线,
Σ是以Γ为边界的分片光滑的有向闭曲面, Γ的正向 与Σ的正侧符合右手法则, 若向量函数 F ( x , y , z )
3
Pdx Qdy Rdz
10.7 斯托克斯公式 环流量与旋度
即有
Pdx Qdy Rdz
9.5 斯托克斯公式 环流量 旋度
i jk
解
rot A
x
y
z
(0, 0 , 1)
2y 3x z2
n 为
I cos d S
8
18
*三、汉密尔顿算子
定义向量微分算子:
x
i
y
j
z
k
它又称为▽(Nabla)算子, 或汉密尔顿(Hamilton)算子.
(1) 设 u u( x, y, z), 则
P
Q
R
或用第一类曲面积分表示:
cos cos cos
x
y
z
d S P d x Q d y R d z
PQR
4
例1 利用斯托克斯公式计算积分
其中为平面 x+ y+ z = 1 被三坐标面所截三角形的整
个 边界, 方向如图所示.
z
解 记三角形域为, 取上侧, 则
xyz
rrr
23
于是得斯托克斯公式的向量形式 :
i jk
x
y
z
PQR
rot A n d S A d s
或
(rot A)n d S A d s ①
定义 P d x Q d y R d z A d s 称为向量场A
沿有向闭曲线 的环流量。向量 rotA称为向量场A的
,
u y
,
u z
u
散度:
div A
P x
Q y
R z
A
i jk
旋度:
高数之斯托克斯公式、环流量、旋度
Dxy
= − ∫∫
∂ {P[ x, y, f ( x, y )]}dxdy y ∂ Dxy
C
Γ
Green v ∫ P[ x, y, f ( x, y)]dx = v ∫ P( x, y, z )dx ．
其余部分证明，自己看书．
5
v ∫
或
Γ
Pdx + Qdy + Rdz = ∫∫
Σ
dydz dzdx dxdy ∂ ∂ ∂ ∂x ∂y ∂z P Q R cos α ∂ ∂x P cos β ∂ ∂y Q cos γ ∂ dS ∂z R
（ 1′ ）
v ∫
G
Γ
Pdx + Qdy + Rdz = ∫∫
Σ
（ 1′′ ）
其中 n = (cos α , cos β , cos γ ) 为有向曲面 Σ 在点 ( x, y, z ) 处的单位法向量． 2、若 Σ 是 xOy 面上的一块平面闭区域，则 Stokes 公式就变为 Green 公式，即 Green 公式为 Stokes 公式的特例．
§11.7 斯托克斯(Stokes)公式
*
环流量与旋度
教学目的：理解和掌握斯托克斯公式，了解环流量和旋度的概念及其求法 教学重点：斯托克斯公式 教学难点：斯托克斯公式的应用 教学内容：
一、Stokes 公式
斯托克斯(Stokes)公式是 Green 公式的推广．Green 公式表达了平 面闭区域上的二重积分与其边界曲线上的曲线积分间的关系， 而 Stokes 公式则把曲面 Σ 上的曲面积分与沿着 Σ 的边界曲线的曲线积分联系起 来．这个联系可陈述如下：
1 1 ． , cos γ = − 2 2
O x
1
= − ∫∫
∂ {P[ x, y, f ( x, y )]}dxdy y ∂ Dxy
C
Γ
Green v ∫ P[ x, y, f ( x, y)]dx = v ∫ P( x, y, z )dx ．
其余部分证明，自己看书．
5
v ∫
或
Γ
Pdx + Qdy + Rdz = ∫∫
Σ
dydz dzdx dxdy ∂ ∂ ∂ ∂x ∂y ∂z P Q R cos α ∂ ∂x P cos β ∂ ∂y Q cos γ ∂ dS ∂z R
（ 1′ ）
v ∫
G
Γ
Pdx + Qdy + Rdz = ∫∫
Σ
（ 1′′ ）
其中 n = (cos α , cos β , cos γ ) 为有向曲面 Σ 在点 ( x, y, z ) 处的单位法向量． 2、若 Σ 是 xOy 面上的一块平面闭区域，则 Stokes 公式就变为 Green 公式，即 Green 公式为 Stokes 公式的特例．
§11.7 斯托克斯(Stokes)公式
*
环流量与旋度
教学目的：理解和掌握斯托克斯公式，了解环流量和旋度的概念及其求法 教学重点：斯托克斯公式 教学难点：斯托克斯公式的应用 教学内容：
一、Stokes 公式
斯托克斯(Stokes)公式是 Green 公式的推广．Green 公式表达了平 面闭区域上的二重积分与其边界曲线上的曲线积分间的关系， 而 Stokes 公式则把曲面 Σ 上的曲面积分与沿着 Σ 的边界曲线的曲线积分联系起 来．这个联系可陈述如下：
1 1 ． , cos γ = − 2 2
O x
1
11-9 斯托克斯公式 环流量与旋度
第九讲 斯托克斯公式 环流量与旋度
➢对弧长的空间曲线积分
空间曲线弧的质量 M f ( x, y, z)ds
n
f (x,
y, z)ds
lim
0
i 1
f (i ,i , i )si
Γ：x (t), y (t), z (t), ( t )
f (x, y, z)ds f (t), (t),(t) 2(t) 2(t) 2(t)dt
r
r
r
A(x, y, z) P(x, y, z)i Q(x, y, z) j R(x, y, z)k ,
z
r
P,Q,R均连续,Γ是一分段光滑有向闭曲线,
r
是Γ在点(x,y,z)处的单位切向量,
A
o
y
积分
Ads
A
d
r
Pdx
Qdy
Rdz
x
称为向量场 A沿有向闭曲线Γ的环流量.
➢物理意义
Ads
A
1y
所得的截痕,若从ox轴的正向看去,
x
取逆时针方向.
斯托克斯公式 环流量和旋度
一 、斯托克斯公式 二 、环流量与旋度
斯托克斯公式 环流量和旋度
一 、斯托克斯公式 二 、环流量与旋度
二 环流量与旋度
(一) 环流量 (二) 旋度
二 环流量与旋度
(一) 环流量 (二) 旋度
➢定义 设有向量场
r
➢对坐标的空间曲线积分
变力沿空间曲线弧作功
W
r F
drr
Pdx
Qdy
Rdz
Γ：x (t), y (t), z (t), (t : )
P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz
➢对弧长的空间曲线积分
空间曲线弧的质量 M f ( x, y, z)ds
n
f (x,
y, z)ds
lim
0
i 1
f (i ,i , i )si
Γ：x (t), y (t), z (t), ( t )
f (x, y, z)ds f (t), (t),(t) 2(t) 2(t) 2(t)dt
r
r
r
A(x, y, z) P(x, y, z)i Q(x, y, z) j R(x, y, z)k ,
z
r
P,Q,R均连续,Γ是一分段光滑有向闭曲线,
r
是Γ在点(x,y,z)处的单位切向量,
A
o
y
积分
Ads
A
d
r
Pdx
Qdy
Rdz
x
称为向量场 A沿有向闭曲线Γ的环流量.
➢物理意义
Ads
A
1y
所得的截痕,若从ox轴的正向看去,
x
取逆时针方向.
斯托克斯公式 环流量和旋度
一 、斯托克斯公式 二 、环流量与旋度
斯托克斯公式 环流量和旋度
一 、斯托克斯公式 二 、环流量与旋度
二 环流量与旋度
(一) 环流量 (二) 旋度
二 环流量与旋度
(一) 环流量 (二) 旋度
➢定义 设有向量场
r
➢对坐标的空间曲线积分
变力沿空间曲线弧作功
W
r F
drr
Pdx
Qdy
Rdz
Γ：x (t), y (t), z (t), (t : )
P(x, y, z)dx Q(x, y, z)dy R(x, y, z)dz
10-7 斯托克斯公式环流量与旋度要点
一、斯托克斯( Stokes )公式定理1. 右手法则(斯托克斯公式)证:情形1(利用格林公式) ∂P∂P=-⎰⎰[+fy]cosγdS∑∂y∂z情形2 证毕注意:⎰⎰∑dydzdzdxdxdy∂∂∂∂x∂y∂zPQRcosαcosβcosλ∂∂∂dS⎰⎰∂x∂y∂z∑PQR例1.解:利用对称性=3⎰⎰dxdyDxy 例2.解:*二、空间曲线积分与路径无关的条件定理2. ⎰ΓPdx+Qdy+Rdz=0Γ⎰Pdx+Qdy+Rdzdu=Pdx+Qdy+Rdz证:(4)⇒(1)(1)⇒(2)(2)⇒(3)(x,y,z)Pdx+Qdy+Rdz(x0,y0,z0)u(x,y,z)=⎰∂u∂x=P(x,y,z)du=Pdx+Qdy+Rdz(3)⇒(4)证毕例3.解:P=y+z,Q=z+x,R=x+y三、环流量与旋度n=(cosα,cosβ,cosγ)τ=(cosλ,cosμ,cosν)记作rotA⎰⎰∑(rotA)ndS=⎰ΓAτds定义: 环流量旋度旋度的力学意义:=2ω(此即“旋度”一词的来源)斯托克斯公式①的物理意义:注意∑与Γ的方向形成右手系!例4.解:例5.解:*四、向量微分算子=gradu=divA=rotA内容小结1. 斯托克斯公式2. 空间曲线积分与路径无关的充要条件∂Q∂R∂R∂P∂P∂Q==,=,∂y∂x∂z∂y∂x∂zrot(P,Q,R)==03. 场论中的三个重要概念梯度:散度:旋度:2r0提示:思考与练习作业。
第七节%20%20斯托克斯(stokes)公式%20%20环流量与旋度ppt
解 1 2 3 4 其中1：z 0, 2：x 0, 3：y 0, 4：z 1 x y
ds 1 则 dxdy 2 2 1(1+x+y) Dxy (1+x+y) 1 1 x 1 1 dx dy ln 2 2 0 0 (1+x+y) 2
j y Q
k z R
x P
因此，stokes公式可以写成向量形式 rot A nds A ds(3) 或 (rot A ） n ds A ds 公式（3）可叙述为：向量场 A沿有向闭曲线的环流量等于 向量场 A的旋度场通过所张的曲面的通量。
设向量常 A( x, y, z ) P( x, y, z )i Q( x, y, z ) j R( x, y, z )k , 则
i R Q P R Q P 1)rot A { , , } y z z x x y 称为向量场 A的旋度。 2) ( P cos Q cos R cos )ds 称为向量场 A沿闭曲线的环流量。
第七节 斯托克斯（stokes）公式 环流量与旋度
一 斯托克斯公式
stokes公式是Green公式的推广，它将曲面上的曲面 积分与沿的边界曲线积分联系起来。 定理1
设为分段光滑的空间有向闭曲线， 是以为边界的分片光滑的有向曲 面，正向与的侧符合右手规则。 P(x,y,z)、Q(x,y,z)、R(x,y,z)在 曲面(连同边界)上具有一阶连续 偏导数，则
例4 求面密度为0的均匀半球壳x 2 y 2 z 2 a 2 ( z 0) 对于z轴的转动惯量。
11.7斯托克斯公式
o x
2
沿有向闭曲线 所作的 例4. 求力 功, 其中 为平面 x + y + z = 1 被三个坐标面所截成三 角形的整个边界, 从 z 轴正向看去沿顺时针方向. 设三角形区域为 , 方向向上, 则 解：
z
C y
cos cos cos
何来?
3 3
B
o
A x
BNAl
0 0
l
0
Ａ. Ｍ
Ｎ
( y)dx 2 xydy
2x y
4
． B
BMAl
两式相减得,
BNA AMB
BNAMB
所以在右半平面内线积分与路径无关.即… (2) …
1 3 x
1 3 y
1 3 z
dS
y
1 3
z
x
3 (3) d S 3 d S 3S 3( ( 2) 2 ) 4
二、 环流量与旋度
令 A ( P, Q, R) , 引进一个向量
记作
rot A
x y z P Q R
i
j
k
定义:
x
Q cos
y z
R cos dS R
P
Q
场论中的三个重要概念
设 u u ( x, y, z ) , A ( P , Q , R) ,
, , x y z
,
则
grad u u , u , u 梯度:
(常向量)
则 L cos( T , a )d S T a 0 d S L
斯托克斯公式环流量与旋度
环流量与旋度的关系式
斯托克斯公式
∮F·dr=∫(curlF)·dS，其中∮表示线积分符 号，∫表示面积分符号，dS表示微分面积。
VS
解释
斯托克斯公式表明，矢量场中封闭曲线上 的线积分等于该曲线所围成的面积上旋度 的面积分。即，矢量场穿过封闭曲线的线 段数等于矢量场在围成该曲线的各点处的 旋转程度在面积上的积分。
证明过程
利用数学归纳法证明斯托克斯公式的正确性，通过逐 步推导和归纳，最终得出结论。
结论
斯托克斯公式可以通过数学归纳法证明，证明了其在 数学上的严谨性和正确性。
05 斯托克斯公式的扩展与推 广
适用于非牛顿流体的推广
总结词
斯托克斯公式在非牛顿流体中的推广主要考虑了流体的非线性性质，包括剪切稀化和弹 性等特性。
基于电动力学公式的推导
电动力学公式
01
描述电磁场对带电粒子的作用电动力学公式分析流体微团在
磁场中受到的作用力，从而推导出斯托克斯公式。
结论
03
斯托克斯公式可以通过电动力学公式推导得出，适用于分析粘
性流体在磁场中的运动。
基于数学归纳法的证明
数学归纳法
一种证明数学命题的方法，通过递推关系证明无限序 列的结论。
物理意义
斯托克斯公式揭示了流体的动量守恒和角动量守恒两个基本物理规律，是流体力学中的基本方程之一 。
解释
通过斯托克斯公式，我们可以理解流体在粘性力作用下的运动行为，包括旋涡的形成、流体绕过障碍 物的流动以及流体内部的剪切力等。
02 环流量与旋度的关系
环流量的定义与计算
环流量定义
环流量是矢量场中封闭曲线上的线积 分，表示矢量场中穿过封闭曲线的矢 量线段数。
详细描述
斯托克斯公式
解:按斯托克斯公式：
Γ
zdx xdy ydz dydz dzdx dxdy
由于 的 法向量的三个方向余弦都为正, 又由于对称性，上式右端为: 3 d 其中Dxy为xOy面上由直线x y 1及
Dxy
两条坐标轴围成的三角形闭区域.
故
3 zdx xdy ydz 2 Γ
( P cos Q cos R cos )dS .
Γ
设有向量场 A( x,y,z ) P( x,y,z )i Q( x,y,z ) j R( x,y,z )k 在坐标轴上的投影分别为
R Q P R Q P , , y z z x x y
曲面Σ的通量，这里Γ的正向与曲面Σ的侧应 符合右手规则.
rot A 的表达式可利用行列式记号形式地表示为
i rot A x P j y Q k . z R
P P 即 : dzdx dxdy P( x, y, z )dx 成立 y Γ z (此时, Px, y, f ( x, y )在C上点( x, y )处的值与P( x, y, z ) 在Γ上对应点( x, y, z )处的值是一样的，且两曲线上的 对应小弧段在x轴上的投影也一样.)
第七节 斯托克斯公式
一、斯托克斯公式 二、环流量与旋度
一、斯托克斯公式
定理1 设Γ为分段光滑的空间有向闭曲线， 是以Γ为
边界的分片光滑的有向曲面，Γ的正向与 的侧符合 右手规则，函数P( x, y, z )、Q( x, y, z )、R( x, y, z )在曲面
(连同边界Γ )上具有在一阶连续偏导数，则有：
注意：
斯托克斯公式 若 是xoy面上的一平面闭区域，
斯托克斯公式 环流量与旋度
斯托克斯公式 环流量与旋度一、斯托克斯公式斯托克斯公式是格林公式的推广。
格林公式表达了平面闭区域上的二重积分与其边界曲线上的曲线积分之间的关系，而斯托克斯公式则把曲面∑上的曲面积与沿着∑的边界曲线Γ的曲线积分联系起来。
我们首先介绍有向曲面∑的边界曲线Γ的正向的规定，然后陈述并证明斯托克斯公式。
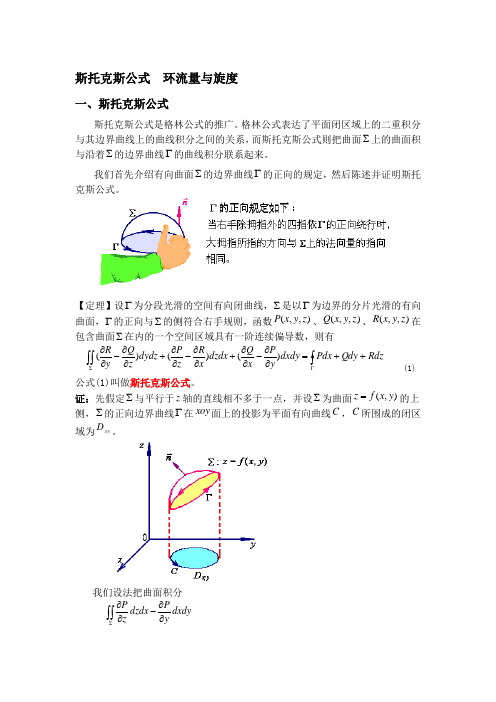
【定理】设Γ为分段光滑的空间有向闭曲线，∑是以Γ为边界的分片光滑的有向曲面，Γ的正向与∑的侧符合右手规则，函数),,(z y x P 、),,(z y x Q 、),,(z y x R 在包含曲面∑在内的一个空间区域具有一阶连续偏导数，则有⎰⎰⎰Γ∑++=∂∂-∂∂+∂∂-∂∂+∂∂-∂∂Rdz Qdy Pdx dxdy y P x Q dzdx x R z P dydz z Q y R )()()( (1) 公式(1)叫做斯托克斯公式。
证：先假定∑与平行于z 轴的直线相不多于一点，并设∑为曲面),(y x f z =的上侧，∑的正向边界曲线Γ在xoy 面上的投影为平面有向曲线C ，C 所围成的闭区域为xy D。
我们设法把曲面积分⎰⎰∑∂∂-∂∂dxdy y P dzdx z P化为闭区域xy D上的二重积分，然后通过格林公式使它与曲线积分联系。
根据对面积的和对坐标的曲面积分间的关系，有⎰⎰⎰⎰∑∑γ∂∂-β∂∂=∂∂-∂∂dS y P z P dxdy y P dzdx z P )cos cos ( (2)由第8.6节知道，有向曲面∑的法向量的方向余弦为221cos y x x f f f ++-=α，221cos y x y f f f ++-=β，2211cos y x f f ++=γ因此γβcos cos y f -=，把它代入(2)式得⎰⎰⎰⎰∑∑γ⎪⎪⎭⎫ ⎝⎛∂∂-⋅∂∂-=∂∂-∂∂dS y P f z P dxdy y P dzdx z P y cos 即⎰⎰⎰⎰∑∑γ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-=∂∂-∂∂dS y P f z P dxdy y P dzdx z P y cos (3)上式右端的曲面积分化为二重积分时，应把),,(z y x P 中的z 用),(y x f 来代替，因为由复合函数的微分法，有y f z P y P y x f y x P y ⋅∂∂+∂∂=∂∂)],(,,[所以，(3)式可写成⎰⎰⎰⎰∑∂∂-=∂∂-∂∂xy D dxdy y x f y x P y dxdy y P dzdx z P )],(,,[ 根据格林公式，上式右端的二重积分可化为沿闭区域xyD 的边界C 的曲线积分⎰⎰⎰=∂∂-xy D c dxy x f y x P dxdy y x f y x P y )],(,,[)],(,,[于是⎰⎰⎰∑=∂∂-∂∂c dx y x f y x P dxdy y P dzdx z P )],(,,[因为函数)],(,,[y x f y x P 在曲线C 上点),(y x 处的值与函数),,(z y x P 在曲线Γ上对应点),,(z y x 处的值是一样的，并且两曲线上的对应小弧段在x 轴上的投影也是一样，根据曲线积分的定义，上式右端的曲线积分等于曲线Γ上的曲线积分⎰Γdxz y x P ),,(,因此，我们证得 ⎰⎰⎰∑Γ=∂∂-∂∂dx z y x p dxdy y P dzdx z P ),,( (4)如果∑取下侧，Γ也相应地改成相反的方向，那末(4)式两端同时改变符号，因此(4)式仍成立。
斯托克斯公式
2
∂Q ∂ R ∂ R ∂ P = , = ∂z ∂ y ∂x ∂z
证毕
例3. 验证曲线积分∫Γ ( y + z ) d x + ( z + x) d y + ( x + y )dz
与路径无关, 并求函数
u ( x, y , z ) = ∫
( x, y , z ) (0,0,0)
( y + z )d x + ( z + x) d y + ( x + y ) d z
rot v =
−ω y ω x 0
∂ ∂x
i
∂ ∂y
j
∂ ∂z
k
= (0, 0, 2ω ) = 2 ω
(此即“旋度”一词的来源)
斯托克斯公式①的物理意义 斯托克斯公式①的物理意义:
∫∫Σ (rot A) n d S = ∫Γ Aτ d s
向量场 A 产生的旋度场 穿过 Σ 的通量 注意 Σ 与 Γ 的方向形成右手系! q 例4. 求电场强度 E = 3 r 的旋度 . r i j k 解:
例2. Γ 为柱面
轴正向看为顺时针, 计算
与平面 y = z 的交线,从 z
解: 设∑为平面 z = y 上被 Γ 所围椭圆域 , 且取下侧, z 则其法线方向余弦 Γ
利用斯托克斯公式得
Σ
cos α cos β cos γ
I = ∫∫
∑ ∂ ∂x 2 ∂ ∂y ∂ ∂z
o x
dS
2
=0
y
y
xy
xz
∂ rot (grad r ) = ∂ x x r ∂ ∂y y r ∂ ∂z z r
思考与练习
= ( 0 , 0 , 0)
∂Q ∂ R ∂ R ∂ P = , = ∂z ∂ y ∂x ∂z
证毕
例3. 验证曲线积分∫Γ ( y + z ) d x + ( z + x) d y + ( x + y )dz
与路径无关, 并求函数
u ( x, y , z ) = ∫
( x, y , z ) (0,0,0)
( y + z )d x + ( z + x) d y + ( x + y ) d z
rot v =
−ω y ω x 0
∂ ∂x
i
∂ ∂y
j
∂ ∂z
k
= (0, 0, 2ω ) = 2 ω
(此即“旋度”一词的来源)
斯托克斯公式①的物理意义 斯托克斯公式①的物理意义:
∫∫Σ (rot A) n d S = ∫Γ Aτ d s
向量场 A 产生的旋度场 穿过 Σ 的通量 注意 Σ 与 Γ 的方向形成右手系! q 例4. 求电场强度 E = 3 r 的旋度 . r i j k 解:
例2. Γ 为柱面
轴正向看为顺时针, 计算
与平面 y = z 的交线,从 z
解: 设∑为平面 z = y 上被 Γ 所围椭圆域 , 且取下侧, z 则其法线方向余弦 Γ
利用斯托克斯公式得
Σ
cos α cos β cos γ
I = ∫∫
∑ ∂ ∂x 2 ∂ ∂y ∂ ∂z
o x
dS
2
=0
y
y
xy
xz
∂ rot (grad r ) = ∂ x x r ∂ ∂y y r ∂ ∂z z r
思考与练习
= ( 0 , 0 , 0)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第七节
第十一章
斯托克斯公式
*环流量与旋度
一、斯托克斯公式 *二、空间曲线积分与路径无关的条件 *三、环流量与旋度
1
一、 斯托克斯(Stokes)公式
双侧曲面的侧与其边界曲线的方向
设 为双侧曲面, 为其边界曲线,
则 在
的取侧定和的侧的,取方一向代之表间法满向足量右n,手法则n .
若右手大拇指指向n 的方向,
具有连续一阶偏导数, 则下列四个条件相互等价:
(1) 对G内任一分段光滑闭曲线 , 有
P d x Q d y R d z 0
(2)
对G内任一分段光滑曲线 ,
PdxQd y Rdz
与路径无关
(3) 在G内存在某一函数 u, 使 d u P d x Q d y R d z
一点, 设其方程为
: z f (x, y), (x, y) Dx y
O
为确定起见, 不妨设 取上侧 (如图).
x
有向曲线C是在xOy平面上的 投影.
n
Dxy C y
3
分析 :
只证
P z
dzdx P dxdy y
Pdx
P z
cos
dS
C P( x, y, z( x, y))dx
则四指所指的方向就是 的
S
方向.
2
简介
定理1. 设分片光滑曲面 的边界 是分段光滑闭曲线, 的
侧与 的正向符合右手法则,
在曲面 (包括边界)
上具有连续一阶偏导数, 则有
P d x Q d y R d z (斯托克斯公式)
证: 情形1. 与平行 z 轴的直线只交于 z
为便于记忆, 斯托克斯公式还可写作:
d ydz dzdx dxd y
x
y
z P d x Q d y R d z
PQ R
或用第一类曲面积分表示:
cos
x
P
cos
y Q
cos
z
d S P d x Q d y R d z
轴的正向看去,取逆时针方向.
解 取 S 为平面 x y z 3 2
z
n
S
的上侧被 所围成的部分.Βιβλιοθήκη 则 n 1 {1,1,1}
o
y
x
3
12
即 cos cos cos 1 ,
3
1
1
1
x y3
Dxy
2
3
I
S
x
y2 z2
3
y z2 x2
通过作辅助线把 分成与z 轴只交于一点的几部分,
在每一部分上应用斯托克斯公式, 然后相加, 由于沿辅助
曲线方向相反的两个曲线积分相加刚好抵消, 所以对这
类曲面斯托克斯公式仍成立.
同理可证
Qd
y
Q x
d
xd
y
Q z
d
yd
z
Rd
x
R d y
yd
z
Rd zd x
x
三式相加, 即得斯托克斯公式. 7 定理1
注意: 如果 是 xOy 面上的一块平面区域, 则斯托克斯
公式就是格林公式, 故格林公式是斯托克斯公式的特例.
P d x Q d y R d z
Stokes 公式 表达了有向曲面上的曲面积分 与其边界曲线上的曲线积分之间的关系.
8
定理1
3
x y1
2
dS
z
x2 y2
4 3
S
(
x
y z)dS
(在S上x y z 3) 2
4 3
3 2
S
dS
2
3
Dxy
3dxdy 9 . 2
13
*二、空间曲线积分与路径无关的条件
定理2. 设 G 是空间一维单连通域, 函数 P,Q, R 在G内
P( x(t ),
y(t), z(x(t),
y(t)))xt
dt
C P(x, y, z(x, y))d x
z
Dx
y
P(x, y
y,
z(
x,
y))
d
(利用格林公式)
xd y
O
Dx y
P P z y z y
d x d y
x
(
P y
P y
dxdy
cos
1,
1
f
2 x
f
2 y
cos
fy ,
1
f
2 x
f
2 y
fy
cos cos
P P y z
fy
d x dy
6
因此
P
P
P d x z d z d x y d x d y
情形2 曲面 与平行 z 轴的直线交点多于一个, 则可
P z
f y )dxdy
定理1
n
Dxy C y
5
而
P z
dzdx
P y
dxdy
P z
cos
dS
P y
dxdy
P z
cos cos
cos
dS
P y
dxdy
P cos
z
cos
dxdy
y2 xy xz
O x
2y
0
11
公式其他形式
例 3 计算曲线积分
( y2 z2 )dx (z2 x2 )dy ( x2 y2 )dz
其中是平面 x y z 3截立方体:0 x 1, 2
0 y 1,0 z 1的表面所得的截痕,若从 ox
dxd y 3
利用对称性Dx y
2
10
例2. 为柱面
轴正向看为顺时针, 计算
与平面 y = z 的交线, 从 z
解: 设 为平面 z = y 上被 所围椭圆域 , 且取下侧,
则其法线方向余弦
z
Γ
利用斯托克斯公式得
cos cos cos
I
x y z dS
P z
cos cos
cos
dS
P[ x, y, z( x, y)]dxdy
Dxy y
(
P y
P z
z y
)dxdy
4
设 C 的参数方程为: x x(t), y y(t), t .
则
P x, y, zd x
P(x, y, z(x, y))dx
R
9
定理1
例1. 利用斯托克斯公式计算积分
其中 为平面 x+ y+ z = 1 被三坐标面所截三角形的整
个边界, 方向如图所示.
z 1
解: 记三角形域为 , 取上侧,则
d ydz dzdx dxd y
x
y
z
z
x
y
O
1
1y
x
Dxy
d y d z d z d x d x d y 3
第十一章
斯托克斯公式
*环流量与旋度
一、斯托克斯公式 *二、空间曲线积分与路径无关的条件 *三、环流量与旋度
1
一、 斯托克斯(Stokes)公式
双侧曲面的侧与其边界曲线的方向
设 为双侧曲面, 为其边界曲线,
则 在
的取侧定和的侧的,取方一向代之表间法满向足量右n,手法则n .
若右手大拇指指向n 的方向,
具有连续一阶偏导数, 则下列四个条件相互等价:
(1) 对G内任一分段光滑闭曲线 , 有
P d x Q d y R d z 0
(2)
对G内任一分段光滑曲线 ,
PdxQd y Rdz
与路径无关
(3) 在G内存在某一函数 u, 使 d u P d x Q d y R d z
一点, 设其方程为
: z f (x, y), (x, y) Dx y
O
为确定起见, 不妨设 取上侧 (如图).
x
有向曲线C是在xOy平面上的 投影.
n
Dxy C y
3
分析 :
只证
P z
dzdx P dxdy y
Pdx
P z
cos
dS
C P( x, y, z( x, y))dx
则四指所指的方向就是 的
S
方向.
2
简介
定理1. 设分片光滑曲面 的边界 是分段光滑闭曲线, 的
侧与 的正向符合右手法则,
在曲面 (包括边界)
上具有连续一阶偏导数, 则有
P d x Q d y R d z (斯托克斯公式)
证: 情形1. 与平行 z 轴的直线只交于 z
为便于记忆, 斯托克斯公式还可写作:
d ydz dzdx dxd y
x
y
z P d x Q d y R d z
PQ R
或用第一类曲面积分表示:
cos
x
P
cos
y Q
cos
z
d S P d x Q d y R d z
轴的正向看去,取逆时针方向.
解 取 S 为平面 x y z 3 2
z
n
S
的上侧被 所围成的部分.Βιβλιοθήκη 则 n 1 {1,1,1}
o
y
x
3
12
即 cos cos cos 1 ,
3
1
1
1
x y3
Dxy
2
3
I
S
x
y2 z2
3
y z2 x2
通过作辅助线把 分成与z 轴只交于一点的几部分,
在每一部分上应用斯托克斯公式, 然后相加, 由于沿辅助
曲线方向相反的两个曲线积分相加刚好抵消, 所以对这
类曲面斯托克斯公式仍成立.
同理可证
Qd
y
Q x
d
xd
y
Q z
d
yd
z
Rd
x
R d y
yd
z
Rd zd x
x
三式相加, 即得斯托克斯公式. 7 定理1
注意: 如果 是 xOy 面上的一块平面区域, 则斯托克斯
公式就是格林公式, 故格林公式是斯托克斯公式的特例.
P d x Q d y R d z
Stokes 公式 表达了有向曲面上的曲面积分 与其边界曲线上的曲线积分之间的关系.
8
定理1
3
x y1
2
dS
z
x2 y2
4 3
S
(
x
y z)dS
(在S上x y z 3) 2
4 3
3 2
S
dS
2
3
Dxy
3dxdy 9 . 2
13
*二、空间曲线积分与路径无关的条件
定理2. 设 G 是空间一维单连通域, 函数 P,Q, R 在G内
P( x(t ),
y(t), z(x(t),
y(t)))xt
dt
C P(x, y, z(x, y))d x
z
Dx
y
P(x, y
y,
z(
x,
y))
d
(利用格林公式)
xd y
O
Dx y
P P z y z y
d x d y
x
(
P y
P y
dxdy
cos
1,
1
f
2 x
f
2 y
cos
fy ,
1
f
2 x
f
2 y
fy
cos cos
P P y z
fy
d x dy
6
因此
P
P
P d x z d z d x y d x d y
情形2 曲面 与平行 z 轴的直线交点多于一个, 则可
P z
f y )dxdy
定理1
n
Dxy C y
5
而
P z
dzdx
P y
dxdy
P z
cos
dS
P y
dxdy
P z
cos cos
cos
dS
P y
dxdy
P cos
z
cos
dxdy
y2 xy xz
O x
2y
0
11
公式其他形式
例 3 计算曲线积分
( y2 z2 )dx (z2 x2 )dy ( x2 y2 )dz
其中是平面 x y z 3截立方体:0 x 1, 2
0 y 1,0 z 1的表面所得的截痕,若从 ox
dxd y 3
利用对称性Dx y
2
10
例2. 为柱面
轴正向看为顺时针, 计算
与平面 y = z 的交线, 从 z
解: 设 为平面 z = y 上被 所围椭圆域 , 且取下侧,
则其法线方向余弦
z
Γ
利用斯托克斯公式得
cos cos cos
I
x y z dS
P z
cos cos
cos
dS
P[ x, y, z( x, y)]dxdy
Dxy y
(
P y
P z
z y
)dxdy
4
设 C 的参数方程为: x x(t), y y(t), t .
则
P x, y, zd x
P(x, y, z(x, y))dx
R
9
定理1
例1. 利用斯托克斯公式计算积分
其中 为平面 x+ y+ z = 1 被三坐标面所截三角形的整
个边界, 方向如图所示.
z 1
解: 记三角形域为 , 取上侧,则
d ydz dzdx dxd y
x
y
z
z
x
y
O
1
1y
x
Dxy
d y d z d z d x d x d y 3