特殊角三角函数值课件
合集下载
24.特殊角的三角函数值PPT课件(华师大版)
第24章 解直角三角形
24.3 锐角三角函数
第2课时 特殊角的三角函数值
1．cos60°的值等于( A )
1 A.2
C.
3 2
2 B. 2
D.
3 3
2．M(－sin60°，cos60°)关于 x 轴对称的点的坐标是( B )
A．( 23，12) B．(－ 23，－12)
C．(－ 23，12)
D．(－12，－
15．如图，在 Rt△ABC 中，∠BAC＝90°，点 D 在 BC 边上，且△ABD 是等边三角形．若 BA＝2，求△ABC 的周长和面积．(结果保留根号)
解：周长＝6＋2 3 面积＝2 3
16．(2015·襄阳)如图，AD 是△ABC 的中线，tanB＝13，cosC＝ 22， AC＝ 2.求：
7．下列各式中不正确的是( B)
A．sin260°＋cos260°＝1 B．sin30°＋cos30°＝1
C．sin60°＝cos30° D．tan45°＞sin45°
8．已知在△ABC中，∠C＝90°，且△ABC不是等腰直角三角形，
设sinB＝n，当∠B是最小内角时，n的取值范围是
0＜n＜
．2 2
易错提示：
注意：(1) （sinα－1）2＝1－sinα. (2) （sinα－cosα）2＝|sinα－cosα|.
(3)tan230°＝( 33)2≠(30°)2. (4)cos50 °＜cos40°.
3 2)
3．计算 6tan45°－2cos60°的结果是( D )
A．4 3 B．4 C．5 3 D．5
4设．s已inB知＝在n△，A当B∠CB中是，最∠小C＝内9角0°时，，且n△的A取B值C 不范是围等是腰0直＜角n＜三角22形， ．
24.3 锐角三角函数
第2课时 特殊角的三角函数值
1．cos60°的值等于( A )
1 A.2
C.
3 2
2 B. 2
D.
3 3
2．M(－sin60°，cos60°)关于 x 轴对称的点的坐标是( B )
A．( 23，12) B．(－ 23，－12)
C．(－ 23，12)
D．(－12，－
15．如图，在 Rt△ABC 中，∠BAC＝90°，点 D 在 BC 边上，且△ABD 是等边三角形．若 BA＝2，求△ABC 的周长和面积．(结果保留根号)
解：周长＝6＋2 3 面积＝2 3
16．(2015·襄阳)如图，AD 是△ABC 的中线，tanB＝13，cosC＝ 22， AC＝ 2.求：
7．下列各式中不正确的是( B)
A．sin260°＋cos260°＝1 B．sin30°＋cos30°＝1
C．sin60°＝cos30° D．tan45°＞sin45°
8．已知在△ABC中，∠C＝90°，且△ABC不是等腰直角三角形，
设sinB＝n，当∠B是最小内角时，n的取值范围是
0＜n＜
．2 2
易错提示：
注意：(1) （sinα－1）2＝1－sinα. (2) （sinα－cosα）2＝|sinα－cosα|.
(3)tan230°＝( 33)2≠(30°)2. (4)cos50 °＜cos40°.
3 2)
3．计算 6tan45°－2cos60°的结果是( D )
A．4 3 B．4 C．5 3 D．5
4设．s已inB知＝在n△，A当B∠CB中是，最∠小C＝内9角0°时，，且n△的A取B值C 不范是围等是腰0直＜角n＜三角22形， ．
特殊角的三角函数值优秀课件
（6）tan 45°，tan 60°等于多少？
老师期望： 你可以对伴随你九个学年的这副三角尺所具有的功能来 个重新认识和评价.
第六页，共十八页。
做一做
B
2
1
45°
A1C
sin 45 ° = 2
2
cos 45°= 2
2
tan 45°= 1
第七页，共十八页。
做一做
B
2
3
60°
A
C
1
sin 60 ° = 3
30°，45°，60°角的三角函数值
第一页，共十八页。
脑中有“图”，心中有“式”
直角三角形中边与角的关系：锐角三角函数. 如图，在直角三角形中，若一个锐角确定，则这个角的 对边，邻边和斜边之间的比值也随之确定.
sin A a , c
sin B b , c
tan A= a b
cos A b , c
w互余两角之间的三角函数关系. w同角之间的三角函数关系.
B
c
a
┌
A
b
C
30°
45°
45° ┌
60° ┌
第十五页，共十八页。
习题
1. 计算： （1）tan 45°-sin 30°； （2）cos 60°+ sin 45°-tan 30°； （3）6tan 30°- si3n 60°- 2cos 45°.
45°
（3）tan 30°等于多少？ 45° ┌
请与同伴交流你是怎么想的又是怎么做的.
30°
60° ┌
第四页，共十八页。
做一做
B
2
1
30°
A
C
3
sin 30°=
1 2
老师期望： 你可以对伴随你九个学年的这副三角尺所具有的功能来 个重新认识和评价.
第六页，共十八页。
做一做
B
2
1
45°
A1C
sin 45 ° = 2
2
cos 45°= 2
2
tan 45°= 1
第七页，共十八页。
做一做
B
2
3
60°
A
C
1
sin 60 ° = 3
30°，45°，60°角的三角函数值
第一页，共十八页。
脑中有“图”，心中有“式”
直角三角形中边与角的关系：锐角三角函数. 如图，在直角三角形中，若一个锐角确定，则这个角的 对边，邻边和斜边之间的比值也随之确定.
sin A a , c
sin B b , c
tan A= a b
cos A b , c
w互余两角之间的三角函数关系. w同角之间的三角函数关系.
B
c
a
┌
A
b
C
30°
45°
45° ┌
60° ┌
第十五页，共十八页。
习题
1. 计算： （1）tan 45°-sin 30°； （2）cos 60°+ sin 45°-tan 30°； （3）6tan 30°- si3n 60°- 2cos 45°.
45°
（3）tan 30°等于多少？ 45° ┌
请与同伴交流你是怎么想的又是怎么做的.
30°
60° ┌
第四页，共十八页。
做一做
B
2
1
30°
A
C
3
sin 30°=
1 2
【数学课件】九年级下28.1.3特殊角的三角函数值(人教版)
(2)cos²45°+tan60°·cos60°
(3)
cos 60 1 sin 60
1 tan 30
(4)tan450·sin450-4sin300·cos450+cos2300
巩固
2、在△ABC中，∠C=90°，sinA= 3 ,
则tanAcosA的值是( A )
5
A. 3 5
C. 9 25
学会使用计算器
小结 :
我们学习了30°, 45°, 60°这 几类特殊角的三角函数值．
小结 :
我们学习了30°, 45°, 60°这几类特殊角
的三角函数值．
α
30° 45° 60°
sinα
1
23
2
cosα
3
22
2
1
2
2
2
tanα
3
3
1
3
1、做老师的只要有一次向学生撒谎撒漏了底，就可能使他的全部教育成果从此为之毁灭。——卢梭
B
7
A
C
21
巩固
2、若( 3 tan A - 3)2 + 2cos B -
则△ABC是( A )
A.直角三角形 B.等边三角形 C.含有60°角的任意三角形 D.顶角为钝角的等腰三角形
3 =0
巩固 3、如图，已知圆锥的高AO等于圆锥 的底面半径OB的 3 倍，求α。
A
O αB
范例 例4、在Rt△ABC中，∠C=90°，已 知AC=21，AB=29，求∠A的度数(精 确到′)。
特殊角的三角函数值
复习： 1.锐角三角函数的定义
B
c
在 RtABC中，C 90
a
九年级数学PPT特殊角的三角函数值课件
2 1
2
tan 300 3 3
cot 300 3
tan 600 3
cot 600 3 3
300
2
3
1
如图，求
角的四个
sin 450 4三520 角函数值，
2
cos 450 2450 2
450
tan 450 1
2
1
cot 450 1
1
请记住：
30的0 三450角6函00 数值
22
2 6 2
6
6 cot2 600 tan 600
4.
3 tan 300
6 ( 3 )2 3
解：原式
3
(2 3) 3 3 3
3
3 3
2 33 3
2 3 3
练习：计算
1.sin 30 cos2 45 0
3
2.2cos45 2 3
2.在ABC中，A 300, tan B 3, BC 2 3
则AB ________ .
如图，在△ABC中，∠C=90°，
AC=8cm，AB的垂直平分线MN交AC
于D，连结BD，若cos∠BDC=3 ，
求BC的长
5
B
N
5x 4x
C
3x
M
D
5x
A
如图，△ABC中，AB＝AC，∠A ＝30度，AC的垂直平分线分别交
3 3 22
0
例：计算下列各值：
2.sin2 60 cos2 60
解：原式 ( 3 )2 ( 1 )2 22
3 1 sin 2 600 (sin 600)2
44
1
特殊角的三角函数值 课件
3
2
（3） 1 3 2 2 （4）
2 1 2 3 1 8 4 8 4
2.某商场有一自动扶梯,其倾斜角为 30°,高为7m,扶梯的长度是多少?
B 【解析】如图所示,BC=7，
∠A=30°
sinA=
BC 7 1 AB AB 2
C
A
∴AB=14
即扶梯长度为14m.
1.计算: (1)sin60°-cos45°; (2)cos60°+tan60°;
300
1 2
2 2
3 2
2 2
3 3
450 600
1
3
3 2
1 2
考考你的记性
例1 计算: (1)sin300+cos450;(2) sin2600+cos2600+tan450.
解（１） 解 （２）
sin 30 cos 45
0
0
sin 60 cos 60 tan45
2 0 2 0
45°
45°
┌
60°
┌
(4)sin45°,sin60°等于多少? (5)cos45°,cos60°等于多少?
45°
30°
(6)tan45°,tan60°等于多
少? 老师期望:
45°
┌
60°
┌
根据上面的计算,完成下表:<特殊角的三角函 数值表>
特殊角的三角函数值表
三角函数 正弦sinα 余弦cosα 正切tanα
锐角α
0
1 2 2 2
3 1 1 2 2
2
2
1 2 2
怎样计算？ 提示
3 1 1 4 4 2
沪科版初中数学九年级上册2锐角的三角函数特殊角的三角函数值课件
tanB 3 , AC 2 3, 2
C
D
B
2、已知：α为锐角，且满 足 3tan 2 -4tan + 3 =0 ，求α的度数。
3、在Rt△ABC中，∠C=90°，化简
1-2sinAcosA
23.1 锐角三角函数（3）
——特殊角的三角函数值
*根据三角尺各边的长度关系，探索sin30°、 cos30°、tan3o°、sin45°、cos45°、 tan45°、sin60°、cos600、tan600这些特 殊角的三角函数值
*请你视察特殊角的三角函数值探索锐角 三角函数的增减性
探索:30°、60°角的三角函数值
sin30°=A斜的边对边
1 2
cos30°=A的
邻
边
3
斜边
2
1 60°
2
30°
3
tan30°=AA的 的邻 对边 边
3 3
sin60°=A斜的边对边
3 2
A的邻边
cos60°= 斜边
1 2
tan60°=AA的 的邻 对边 边 3
新知探索:45°角的三角函数值
2
45°
1
sin45°= A的对边 2
斜边
2
1
cos45°= A的邻边 2
斜边
2
tan45°= A的对边 1 A的邻边
填表
30°、45°、60°角的正弦值、余弦值和正切值如下表：
锐角a
三角函数 sin a
30°
45°6Βιβλιοθήκη °cos atan a
对于sinα与tanα，角度越大，函数值也越大； 对于cosα，角度越大，函数值越小。
例1 求下列各式的值：
特殊角的三角函数值表ppt课件
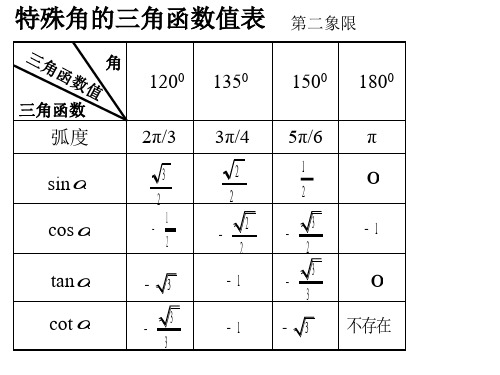
0
1
0 不存在
特殊角的三角函数值表 认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
第三象限
角
三角函数
弧度
2100 7π/6
sin
1 2
cos
3
2
tan
3
3
cot
3
2250
5π/4
2 2
2 2 1
1
2400 2700
4π/3 3π/2
3
1
2
1 2
0
3 不存在
3
0
3
特殊角的三角函数值表 认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
第四象限
角
三角函数
弧度
3000 5π/3
sin
3
2
cos
1
2
tan
3
cot
3
3
3150
7π/4
2 2 2 2
1
1
3300 3600
11π/6 2π
1
0
2
3
1
2
3
0
3
3 不存在
特殊角的三角函数值总表 认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
认识到了贫困户贫困的根本原因，才 能开始 对症下 药，然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视， 已经展 开了“ 精准扶 贫”项 目
特殊角的三角函数值表 认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
1
0 不存在
特殊角的三角函数值表 认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
第三象限
角
三角函数
弧度
2100 7π/6
sin
1 2
cos
3
2
tan
3
3
cot
3
2250
5π/4
2 2
2 2 1
1
2400 2700
4π/3 3π/2
3
1
2
1 2
0
3 不存在
3
0
3
特殊角的三角函数值表 认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
第四象限
角
三角函数
弧度
3000 5π/3
sin
3
2
cos
1
2
tan
3
cot
3
3
3150
7π/4
2 2 2 2
1
1
3300 3600
11π/6 2π
1
0
2
3
1
2
3
0
3
3 不存在
特殊角的三角函数值总表 认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
认识到了贫困户贫困的根本原因，才 能开始 对症下 药，然 后药到 病除。 近年来 国家对 扶贫工 作高度 重视， 已经展 开了“ 精准扶 贫”项 目
特殊角的三角函数值表 认识到了贫困户贫困的根本原因，才能开始对症下药，然后药到病除。近年来国家对扶贫工作高度重视，已经展开了“精准扶贫”项目
人教版九年级数学下册课件：28.1.2特殊角的三角函数值(共30张PPT)
sin A BC 3 2 , AB 6 2
A 45.
B
6
3
A
C
在直角三角形中，根据边的比值反推出角的大小
（2）如图，已知圆锥的高AO等于圆锥的 底面半径OB的 3 倍，求α ．
解：在Rt△ABO中
tan AO 3OB 3,
OB OB
60.
A OB
3、计算
二、逆向应用 ：通过直角三角形边长求出角的度数。
一、直接应用 ：根据特殊角的三角函数值，直接代 入计算即可。
☆ 应用练习
求下列各式的值
1.已知角，求值
1. 2sin30°+3tan30°+tan45°
=2 + d3
2. cos245°+ tan60°cos30°
=2
☆ 应用练习
1.已知角，求值 2.已知值，求角
于 3 时，∠A（ D ）
(A)0°＜∠A＜30° (B)30°＜∠A＜90° (C)0 °＜∠A＜60° (D)60°＜∠A＜90
1、如图，在△ABC中，已知BC=1+ 3 ， ∠B=60°，∠C=45°，求AB的长.
A
B
D
C
2 （1）如图，在Rt△ABC中，∠C＝90°， AB 6, BC 3 ，求∠A的度数．
解：延长BC与AD交于点E。
tan 60 BE BE 2 3 2 3 AB
B
B A
90 60
E
30
C 2
又CDA 90 在RtCDE中
60°
1
A
D
E
tan E CD DE CD 3
24.特殊角的三角函数值课件九年级数学上册(华东师大版)
2
解：过点 C 作 CD⊥AB 于点 D， ∠A = 30°，
∵sin A = CD = 1， AC 2
∵cos A AD 3 ， AC 2
∵ tan B CD 3 ， BD 2
C
A
D
B
第24章 解直角三角形
锐角a
三角
30° 45° 60°
函数
sin a
1
2
3
2
2
2
cos a
3
2
1
2
2
2
tan a
3 1
3
3
第24章 解直角三角形
60° 30°
45°
45°
课堂练习
1. cos45°的值等于（ B ）
A. 1 2
B. 2 2
C. 3 2
D. 3
1
2..如果∠α是等边三角形的一个内角，则cosα=____2.
.在△ABC中，∠C=90°，若∠B=2∠A,
3
tanA=____.3
第24章 解直角三角形
3.求下列各式的值： （1）1－2 sin30°cos30° 解：1－2 sin30°cos30°
（2）3tan30°－tan45°+2sin60° 3tan30°－tan45°+2sin60°
第24章 解直角三角形
活动一 设 30° 所对的直角边长为 a，那么斜边长为 2a，
另一条直角边长 = 2a2 a2 3a.
∴ sin 30o a 1， 2a 2
∴ sin 60o 3a 3 ，
2a 2
60°
cos 30o 3a 3 ，cos 60o a 1， Nhomakorabea2a 2
解：过点 C 作 CD⊥AB 于点 D， ∠A = 30°，
∵sin A = CD = 1， AC 2
∵cos A AD 3 ， AC 2
∵ tan B CD 3 ， BD 2
C
A
D
B
第24章 解直角三角形
锐角a
三角
30° 45° 60°
函数
sin a
1
2
3
2
2
2
cos a
3
2
1
2
2
2
tan a
3 1
3
3
第24章 解直角三角形
60° 30°
45°
45°
课堂练习
1. cos45°的值等于（ B ）
A. 1 2
B. 2 2
C. 3 2
D. 3
1
2..如果∠α是等边三角形的一个内角，则cosα=____2.
.在△ABC中，∠C=90°，若∠B=2∠A,
3
tanA=____.3
第24章 解直角三角形
3.求下列各式的值： （1）1－2 sin30°cos30° 解：1－2 sin30°cos30°
（2）3tan30°－tan45°+2sin60° 3tan30°－tan45°+2sin60°
第24章 解直角三角形
活动一 设 30° 所对的直角边长为 a，那么斜边长为 2a，
另一条直角边长 = 2a2 a2 3a.
∴ sin 30o a 1， 2a 2
∴ sin 60o 3a 3 ，
2a 2
60°
cos 30o 3a 3 ，cos 60o a 1， Nhomakorabea2a 2
《特殊角的三角函数值》PPT课件
）
D．1
3
2
【详解】sin60°＝ ，tan45°＝1，所以sin60°+tan45°＝
2．如果α是锐角， =
1
A．2
B．
2
2
3
，那么cosα的值是（
2
C．
3
2
D．
3
2
【详解】∵α是锐角，sinα＝ ，
∴α＝60°，
1
∴cosα＝cos60°＝2．
故选：A．
3
3
）
3+2
.故选B.
2
3．已知∠A是锐角，且满足3tanA﹣ 3＝0，则∠A的大小为（
4、会由一个特殊角的三角函数值说出这个角的度数。
C O N T E N T S
计算含有特殊角的三角函数值的式子。
推导30°、45°、60°角的三角函数值。
LEARNING OBJECTIVES
1、推导30°、45°、60°角的三角函数值。
2、熟记30°、45°、60°角的各个三角函数值。
3、计算含有特殊角的三角函数值的式子。
第二十八章
锐角三角函数
TOPIC 28.1 ACUTE TRIANGLE (SINE, COSINE, TANGENT VALUE OF SPECIAL ANGLE)
- .
目录
1、推导30°、45°、60°角的三角函数值。
2、熟记30°、45°、60°角的各个三角函数值。
3、计算含有特殊角的三角函数值的式子。
1.对于sinα与tanα，角度越大，函数值越越大；
对于cosα，角度越大，函数值越越小.
2. 互余的两角之间的三角函数关系：
若∠A+∠B=90°，则sinA = cosB，cosA = sinB，tanA · tanB =1 .
24.3.2 特殊角的三角函数值 华师大版数学九年级上册课件
解：原式= 1 23 31 236 32 3233.
例2 在Rt△ABC中，若sinA= .则cos 的值是多少？
解：
巩固练习
答案:1.sin60°，cos45; sin45°，cos45°; tan45°，tan60°. 2.（1）1.（2）6.（3）
3.45°.
应用拓展
1.如图，在Rt△ABC中，∠C=90°，∠BAC=30°，延 长CA到D，使DA=AB，连结BD．利用这些条件，你 能否求出tan15°的值？
第24章 解直角三角形
24.3.2 特殊角的三角函数值
复习导入
探索新知
1.在Rt△ABC中，∠A=30°，∠C=90°，如 图，试求∠A的三个三角函数值。
解：设∠A所对的直角边为1，即BC=1，则 AB=2，由勾股定理得： sin30°= B C 1
AB 2 cos30°=A C 3
AB 2
只要一门科学分支能提出大量的 问题，它就充满着生命力，而问 题缺乏则预示着独立发展的终止 或衰亡。
——希尔伯特
谢谢大家！
Байду номын сангаас
tan30°= B C 3
AC 3
探索新知
2.在Rt△ABC中，∠C=90°，∠A=∠B=45°， 如图，试求45°角的三个三角函数值。
2 解：若设AC=BC=1，则AB= ，
易得， sin45°= 2 2 cos45°= 2
2
tan45°=1.
例1 求值： sin30°∙tan30°+cos30°∙tan60°.
例2 在Rt△ABC中，若sinA= .则cos 的值是多少？
解：
巩固练习
答案:1.sin60°，cos45; sin45°，cos45°; tan45°，tan60°. 2.（1）1.（2）6.（3）
3.45°.
应用拓展
1.如图，在Rt△ABC中，∠C=90°，∠BAC=30°，延 长CA到D，使DA=AB，连结BD．利用这些条件，你 能否求出tan15°的值？
第24章 解直角三角形
24.3.2 特殊角的三角函数值
复习导入
探索新知
1.在Rt△ABC中，∠A=30°，∠C=90°，如 图，试求∠A的三个三角函数值。
解：设∠A所对的直角边为1，即BC=1，则 AB=2，由勾股定理得： sin30°= B C 1
AB 2 cos30°=A C 3
AB 2
只要一门科学分支能提出大量的 问题，它就充满着生命力，而问 题缺乏则预示着独立发展的终止 或衰亡。
——希尔伯特
谢谢大家！
Байду номын сангаас
tan30°= B C 3
AC 3
探索新知
2.在Rt△ABC中，∠C=90°，∠A=∠B=45°， 如图，试求45°角的三个三角函数值。
2 解：若设AC=BC=1，则AB= ，
易得， sin45°= 2 2 cos45°= 2
2
tan45°=1.
例1 求值： sin30°∙tan30°+cos30°∙tan60°.
九年级数学锐角三角函数《特殊角的三角函数值》课件
归纳
知1－导
30°，45°，60°角的正弦值、余弦值和正 切值如下表：
锐角 三角函数
锐角A
sin A
cos A
tan A
30°
1 2 3 2 3 3
45°
2 2 2 2
1
60°
3 2 1 2
3
例1 求下列各式的值：
知1－讲
（1）cos260°+sin260°；
（2） cos 45 tan 45. sin 45
第二十八章 锐角三角函数
28.1 锐角三角函数
第3课时
特殊角的三角函数值
复习回答问题
在Rt△ABC中，∠C=90°，cosA= 3 ，BC=10， 53
则AB=___1_2_；__，AC=___7_；___，sinB=____5___，
5
5
△ABC的周长是___3_0__。
知识点 1 特殊角的三角函数值
；
知3－讲
解：∵sin A＝ 1 ，sin2 A＋cos2 A＝1，
∴
1 3
∴cos2
23 ＋cos2
A＝1－
A＝1, 18
,
99
∴cos A＝ 8 2 2 (负值舍去)； 93 1
∴ tan A sin A 3 1 2 . cos A 2 2 2 2 4
3
（来自《点拨》）
知3－练
（来自《典中点》）
；
知识点 3 锐角三角函数间的关系
知3－讲
（1）求特殊锐角的三角函数值的关键是先把它 转化为实数的运算，再根据实数的运算法 则计算；
（2）求锐角的度数的关键是先求其正弦值或余 弦值或正切值，然后对应特殊锐角的三角 函数值求角的度数；
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
sin45° ＝
BC AB
＝
a
2a＝
2 2
cos45° ＝
AC AB
＝
a 2a
＝
2 2
tan45° ＝
BC AC
＝
a a
＝
1
B
2a
a
45°
┌
A aC
预习检测
特殊角的三角函数值表
三角函数值 三角函数 sinα
角α
30°
1
2
45°
2
2
60°
3
2
cosα
3 2
2 2
1 2
tanα
3 3
1
3
课堂探究一：特殊三角函数值的计算：
O
30° 2
B
C D
A
解:如图,根据题意可知,
1
∠AOD＝2 ×60°＝30°,OD＝2m,
∴OC＝OD• COS30°＝2×23 = 3 ∴AC＝2－3≈0.27 （m）
所以,最高位置与最低位置的
高度差约为0.27m.
B
O C
D
A
课堂小结：
特殊角的三角函数值表
三角函数值 三角函数 sinα
角α
4、计算：sin2 60°+cos2 60°-tan45° 5、计算：2 sin45°+sin60°-2cos45 °
2
课堂探究二：运用特殊角的三角函数值解决实际问题
一个小孩荡秋千,秋千链子的长度为2m,当秋千向两边摆 动时,摆角恰为60°,且两边的摆动角度相同,求它摆至最 高位置时与其摆至最低位置时的高度之差（结果精确到 0.01m）。
预习检测：
1、如图所示: (1)sin300等于多少? (2)cos300等于多少? (3)tan300等于多少?
A 300
B
┌C
如下图所示,假设BC＝a,则
AB＝2,AC＝ 3a a
sin30°＝
BC AB
＝
a 2a
＝
1 2
cos30°＝
AC AB
＝
＝ 3a
2a
3 2
tan30°＝
BC AC
3
1、在Rt△ABC中，∠A=30°，则tanA=_____3_____。
2、在△ABC中，∠C=90°，∠B=2 ∠A,
3
则cosA=___2_____。
3、在△ABC中，若cosA= 2 ，tanB= 3 ,那么这个
2
三角形一定是（ A ）
A、锐角三角形
B、直角三角形
C、钝角三角形
D、等腰三角形
特殊角三角函数值
复习回顾:
B
c a
A sinA＝ac ,
b
┌C
cosA＝bc
, tanA＝ba
sinB
=
b c
,
cosB =
ac, tanB =
b a
1.2 30°，45°，60°角 的三角函数值
学习目标：
⒈经历探索30°,45°,60°角的三角函数值的过 程，进一步体会三角函数的意义。
⒉能够进行含有30°,45°,60°角的三角函数值 的计算. ⒊能够根据30°,45°,60°角的三角函数值,说出 相应的锐角的大小.
4、计算： cos2 30°-2sin60°• cos45°
0
5、计算： （1+tan45°） -
1 tan 60o +
1
1
2
30°
1
2
45°
2
2
60°
3
2
cosα
3 2
2 2
1 2
tanα
3 3
1
3
当堂检测
1、已知
为锐角，cos
=
1Hale Waihona Puke 2，则tan =___3____。
2、已知 为锐角，sin =cos30 °,那么∠ =__6_0_°_。
3、在△ABC中，若
sin A 1 2
2
+（1-tanB）
=0，
则∠C=__1_0_5_°___。
＝
a 3a
＝
3 3
A
30°
2a
3a
60° ┌
B aC
预习检测
A
2、60°角的三角函数值分别是多少?
30°
你是怎样得到的?
2a
3a
sin60° ＝
AC AB
＝
3a 2a
＝
3 2
cos60°
＝
B A
C B
＝
a 2a
＝
1 2
B C 60° ┌ a
tan60° ＝
A B
C C
＝
3a a
＝
3
预习检测
3、45°角的三角函数值分别是多少? 你是怎样得到的?