中考数学之平面几何总结经典习题
中考数学平面几何经典题
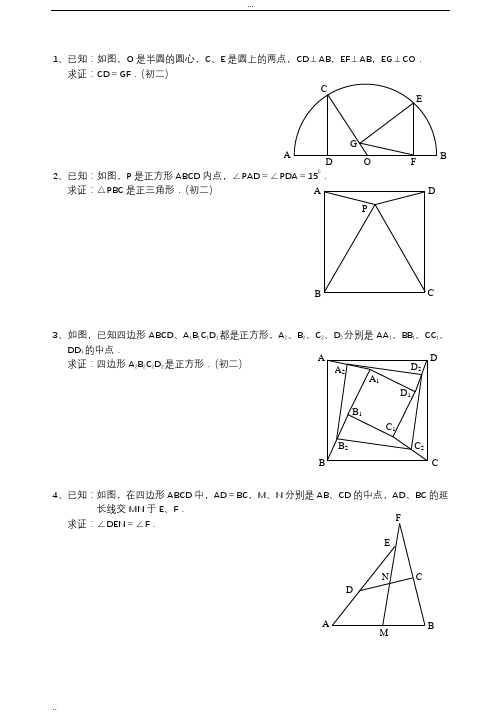
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F GC EBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABCP 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)E1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)D1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 200,求∠BED 的度数.1.如下图做GH ⊥AB,连接EO 。
中考数学之平面几何最全总结+经典习题

平面几何知识要点(一)【线段、角、直线】1.过两点有且只有一条直线。
2.两点之间线段最短。
3.过一点有且只有一条直线和已知直线垂直。
4.直线外一点与直线上各点连接的所有线段中,垂直线段最短。
垂直平分线,简称“中垂线”。
定义:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线)。
线段的垂直平分线可看作和线段两端点距离相等的所有点的集合。
中垂线性质:垂直平分线垂直且平分其所在线段。
垂直平分线定理:垂直平分线上任意一点,到线段两端点的距离相等。
逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
.三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等。
角1.同角或等角的余角相等。
2.同角或等角的补角相等。
3.对顶角相等。
角的平分线性质角的平分线是到角的两边距离相等的所有点的集合定理1:角的平分线上的点到这个角的两边的距离相等。
定理2:到一个角的两边距离相等的点,在这个角的平分线上。
三角形各内角平分线的交点,该点叫内心,它到三角形三边距离相等。
【平行线】平行线性质1:两直线平行,同位角相等。
平行线性质2:两直线平行,内错角相等。
平行线性质3:两直线平行,同旁内角互补。
平行线判定1:同位角相等,两直线平行。
平行线判定2:内错角相等,两直线平行。
平行线判定3:同旁内角互补,两直线平行。
平行线判定4:如果两条直线都和第三条直线平行,这两条直线也互相平行。
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
平面几何知识要点(二)【三角形】面积公式:1. 已知三角形底a ,高h ,12S ah =2. 正三角形面积 S=24(a 为边长正三角形)3.已知三角形三边a,b,c ,则S (海伦公式) 其中:()2a b c p ++= (周长的一半) 4.已知三角形两边a ,b 及这两边夹角C ,则1sin 2S ab C =。
[必刷题]2024九年级数学上册平面几何专项专题训练(含答案)
![[必刷题]2024九年级数学上册平面几何专项专题训练(含答案)](https://img.taocdn.com/s3/m/c98a8998ba4cf7ec4afe04a1b0717fd5370cb244.png)
[必刷题]2024九年级数学上册平面几何专项专题训练(含答案)试题部分一、选择题:1. 在平行四边形ABCD中,若AB=6cm,BC=8cm,则平行四边形ABCD的周长是()cm。
A. 14cmB. 28cmC. 48cmD. 56cm2. 已知等边三角形ABC的边长为3cm,点D是边AB上的一点,且AD=1cm,则CD的长度为()cm。
A. 2cmB. 4cmC. 5cmD. 6cm3. 下列哪个图形是轴对称图形?()A. 等腰梯形B. 长方形C. 正方形D. 所有选项都是4. 在直角坐标系中,点A(2,3)关于原点对称的点是()。
A. (2,3)B. (2,3)C. (2,3)D. (3,2)5. 若一个等腰三角形的底边长为10cm,腰长为13cm,则这个三角形的周长为()cm。
A. 26cmB. 32cmC. 42cmD. 46cm6. 下列哪个角是钝角?()A. 30°B. 45°C. 120°D. 90°7. 在三角形ABC中,若AB=AC,∠BAC=40°,则∠ABC的度数是()。
A. 40°B. 70°C.80°D. 100°8. 下列哪个图形既是中心对称图形,又是轴对称图形?()A. 正三角形B. 矩形C. 正方形D. 平行四边形9. 若一个圆的半径为5cm,则其直径的长度为()cm。
A. 5cmB. 10cmC. 15cmD. 20cm10. 在直角三角形ABC中,若∠C=90°,BC=3cm,AC=4cm,则AB 的长度为()cm。
A. 5cmB. 6cmC. 7cmD. 8cm二、判断题:1. 平行四边形的对角线互相平分。
()2. 任意两个等边三角形的面积相等。
()3. 两条平行线的距离处处相等。
()4. 在直角三角形中,斜边上的中线等于斜边的一半。
()5. 对角线互相垂直的四边形一定是矩形。
中招数学经典例题

中招数学经典例题中考数学经典例题在中考数学考试中占据重要地位,考生们应该掌握这些例题,才能够顺利应对中考数学考试。
下面我们来介绍一些经典例题。
一、平面向量1. 有两个平面向量 $\vec{a}=3\vec{i}-\vec{j}$,$\vec{b}=2\vec{i}+\vec{j}$,求它们的数量积。
2. 已知两个平面向量 $\vec{a}=2\vec{i}-\vec{j}+3\vec{k}$,$\vec{b}=-\vec{i}+5\vec{j}+2\vec{k}$,求它们的叉积。
3. 已知两个平面向量 $\vec{a}=3\vec{i}+4\vec{j}$,$\vec{b}=2\vec{i}-\vec{j}$,试求它们的夹角 $cos\alpha$。
二、三角函数1. 求证:$cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}$。
2. 已知 $\frac{sinx}{cosx}+tanx=1$,求 $x$ 的值。
3. 已知正弦函数 $y=a\sin\omega x$,求 $y$ 的最大值和最小值。
三、平面几何1. 已知四边形 $ABCD$,$E$、$F$ 分别为 $AB$、$BC$ 上的点,$EF$ 与 $AD$、$CD$ 的延长线交于 $P$、$Q$,试证明:四边形$APBQ$ 与 $EPFQ$ 的面积相等。
2. 在 $\triangle ABC$ 中,点 $E$、$F$ 分别在 $AC$、$AB$ 上,$BE$ 与 $CF$ 交于点 $O$,若 $\frac{AE}{EC}=\frac{BF}{FA}$,则证明 $AO$ 是 $\triangle ABC$ 中的角平分线。
3. 已知圆 $O$ 的半径为 $r$,圆上分别取两点 $A$、$B$,则弦$AB$ 的中垂线长为多少?四、解析几何1. 已知点 $A$、$B$ 的坐标分别为 $A(-2,-1)$,$B(4,3)$,求点 $M$ 到$AB$ 的距离。
初中数学解平面几何题练习题及答案

初中数学解平面几何题练习题及答案解题方法1:平面几何的基本概念初中数学中的平面几何题目有很多,解答这些题目的方法也有很多种。
在解答平面几何题目之前,我们首先需要了解一些基本概念。
1. 点、直线和射线:点是没有大小和形状的,用大写字母表示,如:A、B、C;直线是由有无数个点组成的,用小写字母表示,如:a、b、c;射线是由一个起点和无限延伸方向的线段组成的,用字母和一个箭头表示,如:AB→。
2. 线段和向量:线段是由两个点确定的,用两个字母表示,如:AB;向量是有大小和方向的,用一个字母和上面加一箭头表示,如:→AB。
3. 角度和角:角度是由两个射线或线段确定的,用一个小写字母表示,如:∠a;角是由三个点确定的,其中一个点是顶点,用大写字母表示,如:∠ABC。
解题方法2:平面几何的定理和公式在解答平面几何题目时,我们还需要运用一些定理和公式。
1. 相关定理:- 同位角定理:若两条直线被一条截线所交,则两条直线上的同位角互等。
- 垂直角定理:如果两条直线相交,且相交的四个角中有两个相互垂直,则这两个角是垂直角,垂直角互等。
2. 相关公式:- 两点之间的距离公式:设两点A(X₁, Y₁)和B(X₂, Y₂),则AB 的距离为√[(X₂-X₁)²+(Y₂-Y₁)²]。
- 斜率公式:设点A(X₁, Y₁)和点B(X₂, Y₂),则AB的斜率为k=ΔY/ΔX=(Y₂-Y₁)/(X₂-X₁)。
练习题1:已知点A(-3,4),B(1,6),C(5,2),D(-1,0),连接AD和BC,求证:AD与BC平行。
解答过程:首先,我们需要求出线段AD和BC的斜率,然后判断斜率是否相等,若相等,则可以证明AD与BC平行。
斜率公式:k=ΔY/ΔX=(Y₂-Y₁)/(X₂-X₁)线段AD的斜率:k₁=(0-4)/(-1+3)=-2/2=-1线段BC的斜率:k₂=(2-6)/(5-1)=-4/4=-1由上述计算可知,线段AD和BC的斜率相等,因此AD与BC平行。
中考数学分类解析平面几何的综合

平面几何的综合一、选择题1. (2012湖北鄂州3分)如图,四边形OABC 为菱形,点A 、B 在以O 为圆心的弧上,若OA=2,∠1=∠2,则扇形ODE 的面积为【 】A.π34B.π35C.π2D.π3【答案】A 。
【考点】菱形的性质,等边三角形的判定和性质,扇形面积的计算。
【分析】如图,连接OB .∵OA=OB=OC=AB=BC,∴∠AOB+∠BOC=120°。
又∵∠1=∠2,∴∠DOE=120°。
又∵OA=2,∴扇形ODE 的面积为21202 43603ππ⋅⋅=。
故选A 。
2. (2012湖南岳阳3分)如图,AB 为半圆O 的直径,AD 、BC 分别切⊙O 于A 、B 两点,CD 切⊙O 于点E ,AD 与CD 相交于D ,BC 与CD 相交于C ,连接OD 、OC ,对于下列结论:①OD 2=DE•CD; ②AD+BC=CD;③OD=OC;④S 梯形ABCD =CD•OA;⑤∠DOC=90°,其中正确的是【 】A .①②⑤ B.②③④ C.③④⑤ D.①④⑤ 【答案】A 。
【考点】切线的性质,切线长定理,相似三角形的判定与性质。
1052629【分析】如图,连接OE ,∵AD 与圆O 相切,DC 与圆O 相切,BC 与圆O 相切, ∴∠DAO=∠DEO=∠OBC=90°, ∴DA=DE,CE=CB ,AD∥BC。
∴CD=DE+EC=AD+BC。
结论②正确。
在Rt△ADO 和Rt△EDO 中,OD=OD ,DA=DE ,∴Rt△ADO≌Rt△EDO(HL ) ∴∠AOD=∠EOD。
同理Rt△CEO≌Rt△CBO,∴∠EOC=∠BOC。
又∠AOD+∠DOE+∠EOC+∠COB=180°,∴2(∠DOE+∠EOC)=180°,即∠DOC=90°。
结论⑤正确。
∴∠DOC=∠DEO=90°。
又∠EDO=∠ODC,∴△EDO∽△O DC 。
初中平面几何经典题集锦

平面几何是初中数学至关重要的部分,无论是平时学习还是中考,对学生来讲都是难点。
平面几何的不在于知识,几何知识常常是一句话,一个公式,所有同学都可以看懂;然而,几何题目却是千变万化的,特别是辅助线相关的题型,对很多同学来讲非常头痛。
当然,若能快速提升的话同学们也就不会心痛了,几何能力提升并不如代数那样简单,更不是多做题可以达到效果的,常常题目做了很多,但效果并不明显。
很多同学确实找不到方法,题目也做了,也非常努力了,但就是提升不了。
其实,最好的方法在于做经典题,经典题不仅包含了各类辅助线的题型,还包含了各种几何知识,如三角形全等,相似,正方形的性质,平行的性质,比例,共圆,射影定理等;同时常常这类题方法不唯一,通过对不同方法的思考,可以加深对几何知识的理解。
所以对经典题进行反复训练,对学生的能力会有较大的提升。
中考· 平面几何复习压轴题(1)

原创精编试题集(难题、思考题)——增集——期末考试解答题压轴题型专项练习(上)1、图形的变换1、小华用两块不全等的等腰直角三角形的三角板摆放图形.(1)如图①所示△ABC,△DBE,两直角边交于点F,过点F作FG∥BC交AB于点G,连接BF、AD,则线段BF与线段AD的数量关系是______;直线BF与直线AD的位置关系是______,并求证:FG+DC=AC;(2)如果小华将两块三角板△ABC,△DBE如图②所示摆放,使D、B、C三点在一条直线上,AC、DE的延长线相交于点F,过点F作FG∥BC,交直线AE于点G,连接AD,FB,则FG、DC、AC之间满足的数量关系式是____________;(3)在(2)的条件下,若AG=27,DC=5,将一个45°角的顶点与点B重合,并绕点B旋转,这个角的两边分别交线段FG于P、Q两点(如图③),线段DF分别与线段BQ、BP相交于M、N两点,若PG=2,求线段MN的长.2、如图,操作:把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M.探究:线段MD、MF的关系,并加以证明.说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程后,可以从下列①、②、③中选取一个补充或更换已知条件,完成你的证明.注意:选取①完成证明得满分;选取②完成证明得多半分;选取③完成证明得半分.①:DM的延长线交CE于点N,且AD=NE;②:将正方形CGEF绕点C逆时针旋转45°(如图),其他条件不变;③:在②的条件下,且CF=2AD.附加题:将正方形CGEF绕点C旋转任意角度后(如图),其他条件不变.探究:线段MD、MF的关系,并加以证明.3、如图1,在Rt△ABC中,∠ACB=90°,点O是BC的中点,D为AB上一动点,延长DO到E,且OE=OD,连接CE.(1)如图2,若D为AB的中点,请判断四边形EDAC的形状,并说明理由;(2)如图3,若∠A=60°,∠BOD=30°,四边形EDAC是等腰梯形吗?请说明理由;(3)若AC=15,AB=25,请在图4中作出点D的位置使四边形的EDAC周长最小,请补全图形并求出四边形的EDAC的最小周长.4、(1)如图1,已知矩形ABCD中,点E是BC上的一动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H,试证明CH=EF+EG;(2)若点E在BC的延长线上,如图2,过点E作EF⊥BD于点F,EG⊥AC的延长线于点G,CH⊥BD于点H,,则EF、EG、CH三者之间具有怎样的数量关系,直接写出你的猜想;(3)如图3,BD是正方形ABCD的对角线,L在BD上,且BL=BC,连接CL,点E是CL上任一点,EF ⊥BD于点F,EG⊥BC于点G,猜想EF、EG、BD之间具有怎样的数量关系,直接写出你的猜想;(4)观察图1、图2、图3的特性,请你根据这一特性构造一个图形,使它仍然具有EF、EG、CH这样的线段,并满足(1)或(2)的结论,写出相关题设的条件和结论.5、【2010·临沂市】如图1,将三角板放在正方形ABCD 上,使三角板的直角顶点E 与正方形ABCD 的顶点A 重合,三角扳的一边交CD 于点F .另一边交CB 的延长线于点G .(1)求证:EF=EG ;(2)如图2,移动三角板,使顶点E 始终在正方形ABCD 的对角线AC 上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:(3)如图3,将(2)中的“正方形ABCD ”改为“矩形ABCD ”,且使三角板的一边经过点B ,其他条件不变,若AB=a ,BC=b ,求EGEF 的值.6、(1)如图1,以等腰直角△ABC 的直角边AB 、AC 为直角边向外作等腰直角△ABE 和△ACD ,M 是BC 的中点,则DE 与AM 之间的数量关系为_________,位置关系为_________ ;(2)如图2,以任意直角△ABC 的直角边AB 、AC 为直角边向外作等腰直角△ABE 和△ACD ,M 是BC 的中点,则DE 与AM 之间的数量关系为_________,位置关系为_________ ;(3)如图3,以任意非直角△ABC 的边AB 、AC 为直角边向外作等腰直角△ABE 和△ACD ,M 是BC 的中点,试判断DE 与AM 之间的数量关系与位置关系,并说明理由;(4)如图4,若以△ABC 的边AB 、AC 为直角边,向内作等腰直角△ABE 和△ACD ,其它条件不变,请直接写出线段DE 与AM 之间的数量关系与位置关系.7、已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC 与BE,G、F分别是DC与BE的中点.(1)如图1,若∠DAB=60°,则∠AFG=________ ;如图2,若∠DAB=90°,则∠AFG=________ ;(2)如图3,若∠DAB=α,试探究∠AFG与α的数量关系,并给予证明;(3)如果∠ACB为锐角,AB≠AC,∠BAC≠90°,点M在线段BC上运动,连接AM,以AM为一边以点A为直角顶点,且在AM的右侧作等腰直角△AMN,连接NC;试探究:若NC⊥BC(点C、M重合除外),则∠ACB等于多少度?画出相应图形,并说明理由.(画图不写作法)8、已知:△ABC中,以AC、BC为边分别向形外作等边三角形ACD和BCE,M为CD中点,N为CE中点,P为AB中点.(1)如图1,当∠ACB=120°时,∠MPN的度数为________ ;(2)如图2,当∠ACB=α(0°<α<180°)时,∠MPN的度数是否变化?给出你的证明.9、如图1,四边形ABCD ,将顶点为A 的角绕着顶点A 顺时针旋转,角的一条边与DC 的延长线交于点F ,角的另一边与CB 的延长线交于点E ,连接EF .(1)如果四边形ABCD 为正方形,当∠EAF =45°时,有EF=DF-BE .请你思考如何证明这个结论(只需思考,不必写出证明过程);(2)如图2,如果在四边形ABCD 中,AB=AD ,∠ABC=∠ADC =90°,当∠EAF =21∠BAD 时,EF 、DF 、BE 之间有怎样的数量关系?请写出它们之间的关系式(只需写出结论);(3)如图3,如果在四边形ABCD 中,AB=AD ,∠ABC 与∠ADC 互补,当∠EAF =21 ∠BAD 时,EF 、DF 、BE 之间有怎样的数学关系?请写出它们之间的关系式并给予证明;(4)在(3)中,若BC=4,DC=7,CF=2,求△CEF 的周长(直接写出结果即可).10、已知:四边形ABCD 中,AD ∥BC ,AB=AD=DC ,∠BAD=∠ADC ,点E 在CD 边上运动(点E 与点C 、D 两点不重合),△AEP 为直角三角形,∠AEP =90°,∠P =30°,过点E 作EM ∥BC 交AF 于点M .(1)若∠BAD =120°(如图1),求证:BF+DE=EM ;(2)若∠BAD =90°(如图2),则线段BF 、DE 、EM 的数量关系为________ ;(3)在(1)的条件下,若AD :BF=3:2,EM=7,求CE 的长.11、如图所示,△ABC是正三角形,△A1B1 C1的三条边A1B1、B l C1、C1A1交△ABC各边分别于C2、C3,A2、A3,B2、B3.已知A2C3=C2B3=B2A3,且C2C32+B2B32=A2A32.请你证明:A l B1⊥C1A1.12、已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是__________ .线段AM、BN、MN之间的数量关系是__________ ;(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是__________ .试证明你的猜想;(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是__________ .(不要求证明)13、如图,G、H分别是两个有公共顶点B的等腰直角三角形斜边的中点,P是两直角顶点连线CE的中点.(1)如图1,当A、B、D在同一条直线上,探究PG、PH的关系,并说明理由;(2)如图2,当A、B、D不在同一条直线上,(1)中的结论还成立吗?若成立,请加以证明;若不成立,说明理由.14、【2010·遵义市】如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.(1)求证:CF=CH;(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.15、已知等腰Rt△ABC和等腰Rt△EDF,其中D、G分别为斜边AB、EF的中点,连CE,又M为BC中点,N为CE的中点,连MN、MG。
初三数学平面专题经典 (含答案)

初三数学平面专题经典 (含答案)
标题:初三数学平面专题经典(含答案)
本文档包含初三数学平面几何专题题目,涵盖了三角形、圆、相似等多个方面。
每个专题都配有详细的解题思路和答案解析,旨在帮助初三学生夯实数学基础,做好中考准备。
一、三角形专题
1. 已知三角形三边长度,求三角形周长和面积
2. 已知三角形的三个内角,判断其形状,并证明结论
3. 在三角形中,若两边之和大于第三边,则这两边所对的角的大小关系是什么?
4. 已知等腰三角形的底边和高,求面积
5. 已知等边三角形的高,求面积
二、圆专题
1. 已知圆的直径长度,求圆的周长和面积
2. 如何画出一个圆的内切正方形?
3. 如何用圆锥曲线画出一个正五边形?
4. 如何用圆锥曲线画出一个正三角形?
5. 已知圆的半径和圆心角的大小,求扇形面积
三、相似专题
1. 什么是相似三角形?
2. 如何判断两个三角形是否相似?
3. 如何求出两个相似三角形之间的边长比和面积比?
4. 如何利用相似三角形求解实际问题?。
平面几何经典测试题(含答案)

平面几何经典测试题(含答案)1. 题目:已知正方形ABCD,边长为a,点O是正方形中线的中点,连接AO、BO、CO、DO,求角AOB的大小。
解答:首先,我们知道正方形的中线与边的交点是该边的中点。
因此,点O是正方形ABCD的中心点,且AO、BO、CO、DO都是正方形的对角线。
由于正方形的对角线互相垂直且平分对方角,所以角AOB的大小是90度。
2. 题目:在平面直角坐标系中,点A(1, 3)和点B(4, -2)确定了一条直线L,求直线L的斜率和截距。
解答:直线的斜率可以用两点的坐标来计算。
斜率表示了直线的倾斜程度。
设两点的坐标分别为A(x1, y1)和B(x2, y2),则直线的斜率k可以计算为:k = (y2 - y1) / (x2 - x1)在这个题目中,点A的坐标为A(1, 3),点B的坐标为B(4, -2)。
将这些值代入斜率公式,可以计算出直线L的斜率。
斜率 k = (-2 - 3) / (4 - 1) = -5/3直线的截距表示了直线与y轴的交点的纵坐标。
设与y轴的交点坐标为(0, b),则直线的截距b可以计算为:b = y - kx将点A或B的坐标代入,就可以计算出直线L的截距。
以点A(1, 3)为例,截距 b = 3 - (-5/3) * 1 = 8/3所以,直线L的斜率为-5/3,截距为8/3。
3. 题目:已知三角形ABC,边长分别为a、b、c,其中a=4,b=5,c=6,判断三角形ABC的类型(锐角三角形、直角三角形、钝角三角形)。
解答:根据三角形的边长关系,如果三边满足任意两边之和大于第三边,那么这个三角形是一个合法的三角形。
在这个题目中,三角形的边长分别为a=4,b=5,c=6。
我们可以验证一下是否符合三角形的边长关系:4 +5 > 65 +6 > 46 + 4 > 5由于以上的不等式都成立,所以这个三角形是一个合法的三角形。
接下来,判断三角形的类型。
根据三角形的内角和,我们可以知道:如果三角形的所有内角都小于90度,则这个三角形是一个锐角三角形。
初三数学 几何综合-中考必做题(详解版)

中,点 是 边的中点,延长 至点 ,使
,连接
, .将
绕点 按顺时针方向旋转.当点 恰好落在 上的点 处时,连接 、
、 ,则 的长是
.
答案
解析 如图,过 作
于 ,过 作
于 ,过 作
.
∵
,
,
∵四边形
是正方形,
∴
,
∴
,
由勾股定理得:
,
∵
,
,
∴
,
∴
,
∴
,
∴
,
∴
,
由旋转得
,
∵
,
∴
,
∴
,
∴
,
∴
,
∴
,
∴
,
,交 于 ,交 于
和
,连接 、 , 与 的延长线交于点 ,下列结论:①
;②
;③
是
的中线;④
,其中,正确结论的个数是 ( ).
A.
B.
答案 A
解析 在正方形
和
中,
C.
,
,
D. ,
∴
,
即
,
∵在
和
中,
,
∴
≌
,
∴
,(故①正确);
设 、 相交于点 ,
∵
≌
,
∴
,
∵
,
∴
,
∴
,(故②正确);
过点 作
的延长线于 ,过点 作
于,
∵
,
∴
圆 圆的基础知识 圆心角、弧、弦的关系
, 不一定成立,因此④不正确.
10
如图,已知 是⊙ 的直径,点 在 上,过点 的直线与 的延长线交于点 ,
2023年中考数学---《尺规作图》知识总结与专项练习题(含答案解析)精选全文完整版

2023年中考数学---《尺规作图》知识总结与专项练习题(含答案解析)知识总结1.尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.2.基本要求它使用的直尺和圆规带有想像性质,跟现实中的并非完全相同.①直尺必须没有刻度,无限长,且只能使用直尺的固定一侧.只可以用它来将两个点连在一起,不可以在上画刻度.②圆规可以开至无限宽,但上面亦不能有刻度.它只可以拉开成你之前构造过的长度3.基本作图有:(1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)作已知线段的垂直平分线.具体步骤:①以线段两个端点为圆心,大于线段长度的一半为半径画圆弧,两圆弧在线段的两侧别分交于M、N。
如图①②连接MN,过MN的直线即为线段的垂直平分线。
如图②(4)作已知角的角平分线.具体步骤:①以角的顶点O为圆心,一定长度为半径画圆弧,圆弧与角的两边分别交于两点M、N。
如图①。
②分别以点M与点N为圆心,大于MN长度的一半为半径画圆弧,两圆弧交于点P。
如图②。
③连接OP,OP即为角的平分线。
(5)过一点作已知直线的垂线.4.复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作。
5.设计作图:应用与设计作图主要把简单作图放入实际问题中.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图。
专项练习题1.尺规作图(保留作图痕迹,不要求写出作法):如图,已知线段m,n.求作△ABC,使∠A=90°,AB=m,BC=n.【分析】先在直线l上取点A,过A点作AD⊥l,再在直线l上截取AB=m,然后以B点为圆心,n为半径画弧交AD于C,则△ABC满足条件.【解答】解:如图,△ABC为所作.2.如图,在△ABC中,AB=AC,BD是△ABC的角平分线.(1)作∠ACB的角平分线,交AB于点E(尺规作图,不写作法,保留作图痕迹);(2)求证:AD=AE.【分析】(1)按照角平分线的作图步骤作图即可.(2)证明△ACE≌△ABD,即可得出AD=AE.【解答】(1)解:如图所示.(2)证明:∵AB=AC,∴∠ABC=∠ACB,∵BD是∠ABC的角平分线,CE是∠ABC的角平分线,∴∠ABD=∠ACE,∵AB=AC,∠A=∠A,∴△ACE≌△ABD(ASA),∴AD=AE.3.如图,已知线段AC和线段a.(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,不写作法)①作线段AC的垂直平分线l,交线段AC于点O;②以线段AC为对角线,作矩形ABCD,使得AB=a,并且点B在线段AC的上方.(2)当AC=4,a=2时,求(1)中所作矩形ABCD的面积.【分析】(1)①按照线段垂直平分线的作图步骤作图即可.②以点O为圆心,OA的长为半径画弧,再以点A为圆心,线段a的长为半径画弧,两弧在线段AC上方交于点B,同理,以点O为圆心,OC的长为半径画弧,再以点C为圆心,线段a的长为半径画弧,两弧在线段AC下方交于点D,连接AD,CD,AB,BC,即可得矩形ABCD.(2)利用勾股定理求出BC,再利用矩形的面积公式求解即可.【解答】解:(1)①如图,直线l即为所求.②如图,矩形ABCD即为所求.(2)∵四边形ABCD为矩形,∴∠ABC=90°,∵a=2,∴AB=CD=2,∴BC=AD===,∴矩形ABCD的面积为AB•BC=2×=.4.如图,四边形ABCD中,AB∥DC,AB=BC,AD⊥DC于点D.(1)用尺规作∠ABC的角平分线,交CD于点E;(不写作法,保留作图痕迹)(2)连接AE.求证:四边形ABCE是菱形.【分析】(1)根据角平分线的作图步骤作图即可.(2)由角平分线的定义和平行四边形的判定定理,可得四边形ABCE为平行四边形,再结合AB=BC,可证得四边形ABCE为菱形.【解答】(1)解:如图所示.(2)证明:∵BE是∠ABC的角平分线,∴∠ABE=∠CBE,∵AB∥CD,∴∠ABE=∠BEC,∴∠CBE=∠BEC,∴BC=EC,∵AB=BC,∴AB=EC,∴四边形ABCE为平行四边形,∵AB=BC,∴四边形ABCE为菱形.5.如图,在4×4的方格纸中,点A,B在格点上.请按要求画出格点线段(线段的端点在格点上),并写出结论.(1)在图1中画一条线段垂直AB.(2)在图2中画一条线段平分AB.【分析】(1)利用数形结合的思想作出图形即可;(2)利用矩形的对角线互相平分解决问题即可.【解答】解:(1)如图1中,线段EF即为所求(答案不唯一);(2)如图2中,线段EF即为所求(答案不唯一).6.“水城河畔,樱花绽放,凉都宫中,书画成风”的风景,引来市民和游客争相“打卡”留念.已知水城河与南环路之间的某路段平行宽度为200米,为避免交通拥堵,请在水城河与南环路之间设计一条停车带,使得每个停车位到水城河与到凉都宫点F的距离相等.(1)利用尺规作出凉都宫到水城河的距离(保留作图痕迹,不写作法);(2)在图中格点处标出三个符合条件的停车位P1,P2,P3;(3)建立平面直角坐标系,设M(0,2),N(2,0),停车位P(x,y),请写出y与x之间的关系式,在图中画出停车带,并判断点P(4,﹣4)是否在停车带上.【分析】(1)利用过直线外一点作垂线的方法作图即可;(2)根据停车位到水城河与到凉都宫点F的距离相等,可得点P1,P2,P3;(3)根据停车位P(x,y)到点F(0,﹣1)和直线y=1的距离相等,得1﹣y=,从而解决问题.【解答】解:(1)如图,线段F A的长即为所求;(2)如图,点P1,P2,P3即为所求;(3)∵停车位P(x,y)到点F(0,﹣1)和直线y=1的距离相等,∴1﹣y=,化简得y=﹣,当x=4时,y=﹣4,∴点P(4,﹣4)在停车带上.7.图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.(1)网格中△ABC的形状是;(2)在图①中确定一点D,连结DB、DC,使△DBC与△ABC全等;(3)在图②中△ABC的边BC上确定一点E,连结AE,使△ABE∽△CBA;(4)在图③中△ABC的边AB上确定一点P,在边BC上确定一点Q,连结PQ,使△PBQ∽△ABC,且相似比为1:2.【分析】(1)利用勾股定理的逆定理证明即可;(2)根据全等三角形的判定,作出图形即可;(3)根据相似三角形的判定作出图形即可;(4)作出AB,BC的中点P,Q即可.【解答】解:(1)∵AC==,AB==2,BC=5,∴AC2+AB2=BC2,∴∠BAC=90°,∴△ABC是直角三角形;故答案为:直角三角形;(2)如图①中,点D,点D′,点D″即为所求;(3)如图②中,点E即为所求;(4)如图③,点P,点Q即为所求.8.如图,⊙O是△ABC的外接圆,∠ABC=45°.(1)请用尺规作出⊙O的切线AD(保留作图痕迹,不写作法);(2)在(1)的条件下,若AB与切线AD所夹的锐角为75°,⊙O的半径为2,求BC的长.【分析】(1)过点A作AD⊥AO即可;(2)连接OB,OC.证明∠ACB=75°,利用三角形内角和定理求出∠CAB,推出∠BOC=120°,求出CH可得结论.【解答】解:(1)如图,切线AD 即为所求;(2)过点O 作OH ⊥BC 于H ,连接OB ,OC .∵AD 是切线,∴OA ⊥AD ,∴∠OAD =90°,∵∠DAB =75°,∴∠OAB =15°,∵OA =OB ,∴∠OAB =∠OBA =15°,∴∠BOA =150°,∴∠BCA =∠AOB =75°,∵∠ABC =45°,∴∠BAC =180°﹣45°﹣75°=60°,∴∠BOC =2∠BAC =120°,∵OB =OC =2,∴∠BCO =∠CBO =30°,∵OH ⊥BC ,∴CH =BH =OC •cos30°=,∴BC =2. 9.如图,在△ABC 中,AD 是△ABC 的角平分线,分别以点A ,D 为圆心,大于21AD 的长为半径作弧,两弧交于点M ,N ,作直线MN ,分别交AB ,AD ,AC 于点E ,O ,F ,连接DE ,DF .(1)由作图可知,直线MN 是线段AD 的 .(2)求证:四边形AEDF是菱形.【分析】(1)根据作法得到MN是线段AD的垂直平分线;(2)根据垂直平分线的性质则AF=DF,AE=DE,进而得出DF∥AB,同理DE∥AF,于是可判断四边形AEDF是平行四边形,加上F A=FD,则可判断四边形AEDF为菱形.【解答】(1)解:根据作法可知:MN是线段AD的垂直平分线;故答案为:垂直平分线;(2)证明:∵MN是AD的垂直平分线,∴AF=DF,AE=DE,∴∠F AD=∠FDA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠FDA=∠BAD,∴DF∥AB,同理DE∥AF,∴四边形AEDF是平行四边形,∵F A=FD,∴四边形AEDF为菱形.10.如图,已知Rt△ABC中,∠ACB=90°,AB=8,BC=5.(1)作BC的垂直平分线,分别交AB、BC于点D、H;(要求:尺规作图,不写作法,保留作图痕迹)(2)在(1)的条件下,连接CD,求△BCD的周长.【分析】(1)利用基本作图,作BC的垂直平分线即可;(2)根据线段垂直平分线的性质得到DC=DB,则利用等角的余角相等得到∠A=∠DCA,则DC=DA,然后利用等线段代换得到△BCD的周长=AB+BC.【解答】解:(1)如图,DH为所作;(2)∵DH垂直平分BC,∴DC=DB,∴∠B=∠DCB,∵∠B+∠A=90°,∠DCB+∠DCA=90°,∴∠A=∠DCA,∴DC=DA,∴△BCD的周长=DC+DB+BC=DA+DB+BC=AB+BC=8+5=13.11.已知:△ABC.(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.【分析】(1)作∠ABC,∠ACB的角平分线交于点O,点O即为所求;(2)△ABC的面积=(a+b+c)•r计算即可.【解答】解:(1)如图,点O即为所求;(2)由题意,△ABC的面积=×14×1.3=9.1(cm2).12.已知四边形ABCD为矩形,点E是边AD的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.(1)在图1中作出矩形ABCD的对称轴m,使m∥AB;(2)在图2中作出矩形ABCD的对称轴n,使n∥AD.【分析】(1)如图1中,连接AC,BD交于点O,作直线OE即可;(2)如图2中,同法作出点O,连接BE交AC于点T,连接DT,延长TD交AB于点R,作直线OR即可.【解答】解:(1)如图1中,直线m即为所求;(2)如图2中,直线n即为所求;13.如图,在10×10的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中△ABC为格点三角形.请按要求作图,不需证明.(1)在图1中,作出与△ABC全等的所有格点三角形,要求所作格点三角形与△ABC有一条公共边,且不与△ABC重叠;(2)在图2中,作出以BC为对角线的所有格点菱形.【分析】(1)根据全等三角形的判定画出图形即可;(2)根据菱形的定义画出图形即可.【解答】解:(1)如图1中,△ABD1,△ABD2,△ACD3,△ACD4,△CBD5即为所求;(2)如图2中,菱形ABDC,菱形BECF即为所求.14.【问题提出】如何用圆规和无刻度的直尺作一条直线或圆弧平分已知扇形的面积?【初步尝试】如图1,已知扇形OAB,请你用圆规和无刻度的直尺过圆心O作一条直线,使扇形的面积被这条直线平分;【问题联想】如图2,已知线段MN,请你用圆规和无刻度的直尺作一个以MN为斜边的等腰直角三角形MNP;【问题再解】如图3,已知扇形OAB,请你用圆规和无刻度的直尺作一条以点O为圆心的圆弧,使扇形的面积被这条圆弧平分.(友情提醒:以上作图均不写作法,但需保留作图痕迹)【分析】【初步尝试】如图1,作∠AOB的角平分线OP即可;【问题联想】如图2,作线段MN的垂直平分线RT,垂足为R,在射线RT上截取RP=RM,连接MP,NP,三角形MNP即为所求;【问题再解】方法一:构造等腰直角三角形OBE,作BC⊥OE,以O为圆心,OC为半径画弧交OB于点D,交OA于点F,弧DF即为所求.方法二:作OB的中垂线交OB于点C,然后以C为圆心,CB长为半径画弧交OB中垂线于点D,再以O为圆心,OD长为半径画弧分别交OA、OB于点E、F.则弧EF即为所求.【解答】解:【初步尝试】如图1,直线OP即为所求;【问题联想】如图2,三角形MNP即为所求;【问题再解】如图3中,即为所求.15.如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形.(1)如图1,作一条线段,使它是AB向右平移一格后的图形;(2)如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)如图3,作一个与△ABC相似的三角形,相似比不等于1.【分析】(1)把点B、A向右作平移1个单位得到CD;(2)作A点关于BC的对称点D即可;(3)延长CB到D使CD=2CB,延长CA到E点使CE=2CA,则△EDC满足条件.【解答】解:(1)如图1,CD为所作;(2)如图2,(3)如图3,△EDC为所作.。
平面几何:有关三角形五心的经典考题及证明-(中考提分助力)

平面几何:有关三角形五心的经典试题三角形的外心、重心、垂心、内心及旁心,统称为三角形的五心. 一、外心.三角形外接圆的圆心,简称外心。
与外心关系密切的有圆心角定理和圆周角定理。
例1.过等腰△ABC 底边BC 上一点P 引PM ∥CA 交AB 于M ;引PN ∥BA 交AC 于N 。
作点P 关于MN 的对称点P ′.试证:P ′点在△ABC 外接圆上。
(杭州大学《中学数学竞赛习题》)分析:由已知可得MP ′=MP =MB ,NP ′=NP=NC ,故点M 是△P ′BP 的外心,点N 是△P ′PC 的外心.有∠BP ′P =21∠BMP =21∠BAC , ∠PP ′C =21∠PNC =21∠BAC .∴∠BP ′C =∠BP ′P +∠P ′PC =∠BAC 。
从而,P ′点与A ,B ,C 共圆、即P ′在△ABC 外接圆上. 由于P ′P 平分∠BP ′C ,显然还有 P ′B :P ′C =BP :PC .例2.在△ABC 的边AB ,BC ,CA 上分别取点P ,Q ,S .证明以△APS ,△BQP ,△CSQ 的外心为顶点的三角形与△ABC 相似。
(B ·波拉索洛夫《中学数学奥林匹克》)分析:设O 1,O 2,O 3是△APS ,△BQP ,△CSQ 的外心,作出六边形 O 1PO 2QO 3S 后再由外心性质可知 ∠PO 1S =2∠A , ∠QO 2P =2∠B , ∠SO 3Q =2∠C 。
∴∠PO 1S +∠QO 2P +∠SO 3Q =360°.从而又知∠O 1PO 2+∠O 2QO 3+∠O 3SO 1=360°将△O 2QO 3绕着O 3点旋转到△KSO 3,易判断△KSO 1≌△O 2PO 1,同时可得△O 1O 2O 3≌△O 1KO 3。
∴∠O 2O 1O 3=∠KO 1O 3=21∠O 2O 1K=21(∠O 2O 1S +∠SO 1K )=21(∠O 2O 1S +∠PO 1O 2)=21∠PO 1S =∠A ;同理有∠O 1O 2O 3=∠B .故△O 1O 2O 3∽△ABC .A B C P P MN 'A B C K P O O O ....S 123二、重心三角形三条中线的交点,叫做三角形的重心.掌握重心将每 条中线都分成定比2:1及中线长度公式,便于解题. 例3.AD ,BE ,CF 是△ABC 的三条中线,P 是任意一点.证明:在△PAD ,△PBE ,△PCF 中,其中一个面积等于另外两个面积的和. (第26届莫斯科数学奥林匹克)分析:设G 为△ABC 重心,直线PG 与AB,BC 相交.从A ,C ,D ,E ,F 分别 作该直线的垂线,垂足为A ′,C ′, D ′,E ′,F ′。
九年级数学中考典型及竞赛训练专题25 平面几何的最值问题2(附答案解析)

第2题图 第3题图 第4题图 第5题图
3.如图⊙O的半径为2,⊙O内的一点P到圆心的距离为1,过点P的弦与劣弧 组成一个弓形,则此弓形面积的最小值为.
4.如图,△ABC的面积为1,点D,G,E和F分别在边AB,AC,BC上,BD<DA,DG∥BC,DE∥AC,GF∥AB,则梯形DEFG面积的最大可能值为.(上海市竞赛试题)
所以,应选择路线2.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1分米,高AB为5分米”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:l12=AC2=25+π2;
路线2:l22=(AB+BC)2=49.∵l12l22,∴l1<l2(填“>”或“<”),所以应选择路线1
8.(1)连结ME,过N作NF⊥AB于F,可证明Rt△EB A≌Rt△MNF,得MF=AE=x.∵ME2=AE2+AM2,故MB2=x2+AM2,即(2-AM)2=x2+AM2,AM=1- x2,∴S= ×AD= ×2=AM+AM+MF=2AM+AE=2(1- x2)+x=- x2+x+2.
(2)S=- (x2-2x+1)+ =- (x-1)2+ .故当AE=x=1时,四边形ADNM的面积最大,此时最大值为 .
(1)当MN为何值时,点P恰好落在BC上?
(2)设MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式,当x为何值时,y的值最大,最大值是多少?(宁夏省中考试题)
B级
1.已知凸四边形ABCD中,AB+AC+CD= 16,且S四边彤ABCD=32,那么当AC=,BD=时,四边形ABCD面积最大,最大值是.(“华杯赛”试题)
平面几何习题大全

平面几何习题大全(总39页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--平面几何习题大全下面的平面几何习题均是我两年来收集的,属竞赛范围。
共分为五种类型,1,几何计算;2,几何证明;3,共点线与共线点;4,几何不等式;5,经典几何。
几何计算-1命题设点D是Rt△ABC斜边AB上的一点,DE⊥BC于点E,DF⊥AC于点F。
若AF=15,BE=10,则四边形DECF的面积是多少解:设DF=CE=x,DE=CF=y. ∵Rt△BED∽Rt△DFA, ∴BE/DE=DF/AF<==> 10/y=x/15 <==> xy=150.所以,矩形DECF的面积150.几何证明-1命题在圆内接四边形ABCD中,O为圆心,己知∠AOB+∠COD=180.求证:由O向四边形ABCD所作的垂线段之和等于四边形ABCD的周长的一半。
证明(一) 连OA,OB,OC,OD,过圆心O点分别作AB,BC,CD,DA的垂线,垂足依次为P,Q,R,S。
易证ΔAPO≌ΔORD,所以 DR=OP,AP=OR,故 OP+OR=DR+AP=(CD+AB)/2。
同理可得:OQ+OS=(DA+BC)/2。
因此有 OP+OQ+OR+OS=(AB+BC+CD+DA)/2。
证明(二) 连OA,OB,OC,OD,因为∠AOB+∠COD=180°,OA=OD,所以易证RtΔAPO≌RtΔORD,故得 DR=OP,AP=OR,即 OP+OR=DR+AP=(CD+AB)/2。
同理可得:OQ+OS=(DA+BC)/2。
因此有 OP+OQ+OR+OS=(AB+BC+CD+DA)/2。
几何不等式-1命题设P是正△ABC内任意一点,△DEF是P点关于正△ABC的内接三角形[AP,BP,CP延长分别交BC,CA,AB于D,E,F],记面积为S1;△KNM是P点关于正△ABC的垂足三角形[过P点分别作BC,CA,AB垂线交于K,N,M],记面积为S2。
中考数学20道经典几何题

中考数学20道经典几何题1.已知三角形ABC,AB=AC,∠A=36°,求BC与AB的比值。
2.直角三角形ABC中,∠C=90°,AC=3,BC=4,求斜边AB上的高。
3.四边形ABCD是平行四边形,对角线AC、BD相交于点O,若AB=5,AC=8,BD=6,求平行四边形ABCD的面积。
4.三角形ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且DE⊥DF,求证:BE²+CF²=EF²。
5.圆O的半径为5,弦AB=8,求圆心O到弦AB的距离。
6.等腰梯形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=3,BC=7,求梯形ABCD的周长。
7.三角形ABC中,∠C=90°,∠A=30°,BC=3,求三角形ABC的外接圆半径。
8.正方形ABCD的边长为4,E是BC中点,F是CD上一点,且CF=1,求∠AEF的度数。
9.三角形ABC是等边三角形,D是AC中点,E在BC延长线上,CE=CD,求证:BD=DE。
10.矩形ABCD中,AB=6,BC=8,点P在AD上,且AP=2,求点P到对角线BD的距离。
11.三角形ABC中,AB=AC,D是BC中点,DE⊥AB于E,DF⊥AC于F,若AB=5,DE=3,求DF的值。
12.菱形ABCD的对角线AC=6,BD=8,求菱形ABCD的边长。
13.三角形ABC中,∠B=90°,AB=3,BC=4,以BC为直径作圆O,交AC于D,求AD的长。
14.等腰三角形ABC中,AB=AC,∠A=120°,AB=4,求三角形ABC的面积。
15.三角形ABC中,∠C=90°,AC=4,BC=3,以AC为一边向三角形外作等腰直角三角形ACD,∠ACD=90°,求BD的长。
16.圆O的直径AB=10,弦AC=6,∠BAC的平分线交圆O于D,求CD的长。
历年中考平面几何基础题精选欣赏

历年中考平面几何基础题精选欣赏历年中考平面几何基础题精选欣赏历年中考平面几何基础题精选一、选择题1.(河北省2分)如图,2等于A、60B、90C、110D、180【答案】B。
【考点】平角的定义。
【分析】根据平角的定义得到1+902=180,即由2=90。
故选B。
2.(河北省3分)已知三角形三边长分别为2,,13,若为正整数则这样的三角形个数为A、2B、3C、5D、13【答案】B。
【考点】一元一次方程组的应用,三角形三边关系。
【分析】根据三角形的三边关系:三角形两边之和大于第三边,两边差小于第三边,得,解得,1115,所以,为12、13、14。
故选B。
3.(山西省2分)如图所示,AOB的两边.OA、OB均为平面反光镜,AOB=35,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则DEB的度数是A.35B.70C.110D.120【答案】B。
【考点】平行线的性质,入射角与反射角的关系,三角形内角和定理,等腰三角形的性质。
【分析】过点D作DFAO交OB于点F,则DF是法线,根据入射角等于反射角的关系,得3,∵CD∥OB,2(两直线平行,内错角相等)。
3(等量代换);在Rt△DOF中,ODF=90,AOB=35,2=55在△DEF中,DEB=1802=70。
故选B。
4.(山西省2分)一个正多边形,它的每一个外角都等于45,则该正多边形是A.正六边形B.正七边形C.正八边形D.正九边形【答案】C。
【考点】多边形内角与外角。
【分析】多边形的外角和是360度,因为是正多边形,所以每一个外角都是45,即可得到外角的个数,从而确定多边形的边数:∵36045=8,这个正多边形是正八边形。
故选C。
5.(内蒙古巴彦淖尔、赤峰3分)下列图形中,1一定大于2的是A、【答案】C。
【考点】对顶角的性质,内错角的性质,三角形外角定理,圆周角定理。
【分析】根据对顶角的性质,内错角的性质,三角形外角定理,圆周角定理逐一作出判断:A.1和2是对顶角,根据对顶角相等的性质,2,选项错误;B.1和2是内错角,当两条直线平行时2,选项错误;C. 根据三角形的外角等于和它不相邻的两内角之和的性质,得2,选项正确;D.根据同弧所对圆周角相等的'性质,2,选项错误。
中考数学中的平面几何与垂直线性质应用实例总结

中考数学中的平面几何与垂直线性质应用实例总结一、直线与垂直线性质在中考数学中,研究直线与垂直线性质是非常重要的内容。
下面将结合一些实例,总结平面几何中直线与垂直线的应用。
实例一:垂直线分割等腰三角形在等腰三角形ABC中,AC = BC,垂直于底边AC的直线AD将三角形分成两个等面积的小三角形ACE和BCD。
这个问题涉及到垂直线性质的应用,我们可以利用垂直线分割等腰三角形,使得两个小三角形的面积相等。
实例二:判断两条直线是否垂直在解决一些几何问题时,我们常需要判断两条直线是否垂直。
根据中考数学的知识,我们可以利用直线斜率的乘积来判断两条直线是否垂直。
如果两条直线的斜率之积为-1,则可以判定它们垂直。
二、平面几何中的线段垂直分割问题在中考数学中,线段垂直分割也是一个重要的内容。
下面将通过实例来总结线段垂直分割的应用。
实例三:垂直平分线段的存在性在平面几何中,给定一条线段AB,我们需要寻找一条二分线段AB 的直线,同时这条直线还要垂直于线段AB。
在证明中考数学中存在垂直平分线段的问题时,我们可以通过构造垂直平分线的等分点来解决问题。
实例四:证明线段垂直分割的唯一性在中考数学中,证明线段垂直分割的唯一性也是一个常见的问题。
假设直线l同时垂直分割线段AB和线段CD,我们需要证明线段AB 与线段CD垂直分割的直线是唯一的。
在证明该问题时,我们可以利用垂直线性质和反证法来解决。
三、直线与平面垂直线性质的应用在中考数学中,直线与平面垂直线性质也是一个重要内容。
下面将通过实例来总结直线与平面垂直线性质的应用。
实例五:垂直平分线段与平面垂直在空间几何中,给定一条线段AB和一个平面P,如果直线l同时垂直平分线段AB和平面P,我们需要证明垂直平分线段与平面垂直。
在证明中考数学中垂直平分线段与平面垂直的问题时,我们可以证明l 与平面P上的两条线段互相垂直,并利用垂直线性质解决。
实例六:平面垂直分割等腰三棱锥在空间几何中,如果一个平面与一个等腰三棱锥的底面垂直分割,我们需要证明垂直平分等腰三棱锥的平面通过顶点垂直于底面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【线段、角、直线】1.过两点有且只有一条直线。
2.两点之间线段最短。
3.过一点有且只有一条直线和已知直线垂直。
4.直线外一点与直线上各点连接的所有线段中,垂直线段最短。
垂直平分线,简称“中垂线”。
定义:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线)。
线段的垂直平分线可看作和线段两端点距离相等的所有点的集合。
中垂线性质:垂直平分线垂直且平分其所在线段。
垂直平分线定理:垂直平分线上任意一点,到线段两端点的距离相等。
逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
.三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等。
角1.同角或等角的余角相等。
2.同角或等角的补角相等。
3.对顶角相等。
角的平分线性质角的平分线是到角的两边距离相等的所有点的集合定理1:角的平分线上的点到这个角的两边的距离相等。
定理2:到一个角的两边距离相等的点,在这个角的平分线上。
三角形各内角平分线的交点,该点叫内心,它到三角形三边距离相等。
【平行线】平行线性质1:两直线平行,同位角相等。
平行线性质2:两直线平行,内错角相等。
平行线性质3:两直线平行,同旁内角互补。
平行线判定1:同位角相等,两直线平行。
平行线判定2:内错角相等,两直线平行。
平行线判定3:同旁内角互补,两直线平行。
平行线判定4:如果两条直线都和第三条直线平行,这两条直线也互相平行。
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
【三角形】面积公式:1. 已知三角形底a ,高h ,12S ah =2. 正三角形面积 S=24(a 为边长正三角形)3.已知三角形三边a,b,c ,则S (海伦公式) 其中:()2a b c p ++= (周长的一半) 4.已知三角形两边a ,b 及这两边夹角C ,则1sin 2S ab C =。
5.设三角形三边分别为a 、b 、c ,内切圆半径为r ,则()2a b c r S ++= 6.设三角形三边分别为a 、b 、c ,外接圆半径为R ,则4abc S R =记住★:已知正三角形边长为a ,其外接圆半径为R ,内切圆半径为r ,则有:R = ,r = , 2R r = 内角和定理:三角形三个内角的和等于180°推论1 :直角三角形的两个锐角互余推论2 :三角形的一个外角等于和它不相邻的两个内角的和推论3 :三角形的一个外角大于任何一个和它不相邻的内角全等三角形性质:如果两三角形全等,那么其对应边,对应角相等。
其中对应边除了三角形的边长外,还包括对应高,对应中线,对角平分线。
全等三角形判定定理:边边边公理:有三边对应相等的两个三角形全等。
(SSS )边角边公理:有两边和它们的夹角对应相等的两个三角形全等。
(SAS )角边角公理:有两角和它们的夹边对应相等的两个三角形全等。
(ASA )推论:有两角和其中一角的对边对应相等的两个三角形全等。
斜边、直角边公理:有斜边和一条直角边对应相等的两个直角三角形全等。
相似三角形性质定理性质定理1:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比。
性质定理2:相似三角形周长的比等于相似比。
性质定理3:相似三角形面积的比等于相似比的平方。
相似三角形判定定理判定定理1:两角对应相等,两三角形相似(ASA )判定定理2:两边对应成比例且夹角相等,两三角形相似(SAS )判定定理3 三边对应成比例,两三角形相似(SSS )定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。
定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
梯形中位线定理: 梯形的中位线平行于两底,并且等于两底和的一半 。
平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等推论1:经过梯形一腰的中点与底平行的直线,必平分另一腰 。
推论2:经过三角形一边的中点与另一边平行的直线,必平分第三边。
定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边等腰三角形的性质定理:等腰三角形的两个底角相等。
推论1:等腰三角形顶角的平分线平分底边并且垂直于底边 。
推论2:等腰三角形的顶角平分线、底边上的中线和高互相重合。
(三线合一)推论3:等边三角形的各角都相等,并且每一个角都等于60°等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)推论1:三个角都相等的三角形是等边三角形推论2:有一个角等于60°的等腰三角形是等边三角形直角三角形1.勾股定理:直角三角形两直角边a 、b 的平方和、等于斜边c 的平方(222a b c +=) 逆命题:如果三角形的三边长有关系222a b c +=,那么这个三角形是直角三角形。
勾股定理的逆定理可以判断一个三角形为锐角或钝角的一个简单的方法,其中c 为最长边: 如果:222a b c +=,则△ABC 是直角三角形;如果222a b c +>,则△ABC 是锐角三角形;如果222a b c +<,则△ABC 是钝角三角形。
2.直角三角形斜边中线定理:直角三角形斜边上的中线等于斜边长的一半。
逆命题:如果一个三角形一条边的中线等于这条边的一半,那么这个三角形是直角三角形,且这条边为直角三角形的斜边。
3.在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半,由此性质可推出:含30°的直角三角形三边之比为12。
4.直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
5.直角三角形的内切圆半径等于两直角边之和减去斜边的差的一半, 即2a b c r +-=也等于 ab r a b c =++6. 射影定理:①如果△ABC 是直角三角形,∠C=90°,CD ⊥AB ,则 2.AC AD AB =2.BC DB AB =2.CD AD DB = 22AC AD BC DB= ②如果△ABC ,CD ⊥AB ,2.CD AD DB =,则:△ADC ∽△CDB③对一般三角形的拓展:如图,如果△ADC ∽△ACB ,则: 2.AC ADAB =7.如果∠ADE=∠B 或 ∠AED=∠C ,或 ∠C+∠DEB=180°,或 ∠B+∠CDE=180°那么有:AD ·AC=AE ·AB8.如果DE ∥BC , 那么有::::AD AC AE AB DE BC ==9.在△ABC 中,AD 是∠A 的平分线,那么:AB BD AC DC=A B CD a bc ha A BC D A B CD A A10.内、外角角平分线:DO 平分∠AOB ,EO 平分∠COB ,可以推出:∠DOE=90°,∠AOD+∠COE=90° 平面几何知识要点(三) 【四边形及多边形】面积公式:平行四边形面积=底×高 矩形面积=长×宽菱形面积=对角线乘积的一半 或 菱形面积=底×高梯形面积=()2+⨯上底下底高=中位线×高 对角线相互垂直四边形面积=对角线乘积的一半。
平行四边形:性质定理1:平行四边形两组对边分别平行性质定理2:平行四边形两组对角分别相等。
性质定理3:平行四边形两组对边分别相等。
推论:夹在两条平行线间的平行线段相等;平行线间的距离处处相等。
性质定理4:平行四边形的对角线互相平分。
是中心对称图形判定定理1:两组对边分别平行的四边形是平行四边形判定定理2:两组对角分别相等的四边形是平行四边形。
判定定理3:两组对边分别相等的四边形是平行四边形。
判定定理4:一组对边平行且相等的四边形是平行四边形。
判定定理5:对角线互相平分的四边形是平行四边形。
矩形性质定理1:矩形对边分别平行且相等;性质定理2:矩形的四个角都是直角。
性质定理3:矩形对角线互相平分且相等性质定理4:矩形既是中心对称图形,也是轴对称图形。
判定定理1:有三个角是直角的四边形是矩形判定定理2:有一个直角的平行四边形;判定定理3:对角线相等的平行四边形是矩形菱形性质定理1:菱形对边平行,四条边都相等。
性质定理2:菱形的对角线互相垂直,并且每一条对角线平分一组对角。
性质定理3:菱形既是中心对称图形也是轴对称图形。
判定定理1:四边都相等的四边形是菱形。
判定定理2:一组邻边相等的平行四边形是菱形;判定定理3:对角线互相垂直的平行四边形是菱形。
正方形性质定理1:正方形对边平行,四边相等;性质定理2:正方形的四个角都是直角;A性质定理3:正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角。
性质定理3:正方形既是中心对称图形也是轴对称图形。
判定定理1:有一个直角一组邻边相等的平行四边形是正方形;判定定理2:一组邻边相等的矩形是正方形;判定定理3:一个角为直角的菱形是正方形。
等腰梯形性质定理1:等腰梯形两底互相平行,两腰相等;性质定理2:等腰梯形在同一底上的两个底角相等。
性质定理3:等腰梯形的两条对角线相等。
性质定理4:等腰梯形是轴对称图形。
判定定理1:腰相等的梯形是等腰梯形;判定定理2:在同一底上的两个底角相等的梯形是等腰梯形。
判定定理3:对角线相等的梯形是等腰梯形。
如果等腰梯形对角线相互垂直,则高与中位线相等。
四边形四边中点连成的四边形图形:1.如果原四边形对角线相等且垂直,那么四边形中点连成的新四边形为正方形;2.如果原四边形对角线只相等不垂直,那么四边形中点连成的新四边形为菱形;3.如果原四边形对角线垂直但不相等,那么四边形中点连成的新四边形为矩形;4.如果原四边形对角线既不相等又非垂直,那么四边形中点连成的新四边形为平行四边形。
5.四边形中点连接的图形的面积是原四边形面积的一半.其它定理和公式1.定理:四边形的内角和等于360°,四边形的外角和等于360°。
2.多边形内角和定理: n边形的内角的和等于(n-2)×180°推论:任意多边的外角和等于360°3.n边形从一个顶点出发的对角线,共有(n-3)条,将n边形分成了(n-2)个三角形;n边形一共有n2(n-3)条对角线。
4.正n边形的每个内角都等于:(2)180 nn-⨯常用辅助线平面几何知识要点(四)【圆、弧、弦】圆及圆的相关量的定义圆的定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆。
