附有限制条件的间接平差9概括模型
第八章 附有限制条件的间接平差

⎡ w1 ⎤
⎢⎢v
2
⎥ ⎥
⎢ ⎢
0
0
1
⎢⎢⎢vv43
⎥ ⎥ ⎥
=
⎢−1 ⎢⎢− 1
1 0
0 1
⎢ ⎢
v5
⎥ ⎥
⎢ 0 −1 1 ⎢
⎢v6 ⎥ ⎢ 0 −1 0
0 0 0 0 1
⎥
⎥ ⎥ ⎥ ⎥ ⎥ ⎥
⎡ ⎢ ⎢ ⎢ ⎢ ⎣
xˆ1 xˆ 2 xˆ3 xˆ 4
⎤ ⎥ ⎥ ⎥ ⎥ ⎦
⎥
−
⎢ ⎢
w2
⎢ ⎢ ⎢
⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦
∧
σ0 = ±
V T PV = ± r
19.75 = 2.2mm 4
⎢⎢⎢⎡σσXX∧∧12
⎤ ⎥ ⎥ ⎥
=
⎡ ⎢ ⎢ ⎢
∧
σ0
∧
σ0
∧
0.5320= ±1.6mm⎥⎤ 0.7739= ±1.9m⎥ ⎦
⎢⎢⎣σ0 1.1432= ±2.35mm⎥⎥⎦
+ W
CT x=
K 0
s
−
BT
Pl
=0
矩阵表示:
⎡ ⎢ ⎣
N bb C
CT 0
⎤ ⎡ xˆ ⎤
⎥ ⎦
⎢ ⎣
K
s
⎥ ⎦
−
⎡ B T Pl
⎢ ⎣
Wx
⎤ ⎥ ⎦
=
0
⎡ ⎢
∧
x
⎢⎣ K s
⎤ ⎥ ⎥⎦
=
⎡ ⎢ ⎣
N bb C
C T ⎤ − 1 ⎡ B T Pl ⎤
0
⎥ ⎦
⎢
⎥
⎣ Wx ⎦
N cc
第八章 附有限制条件的间接平差

第八章 附有限制条件的间接平差知识点1、附有限制条件的间接平差法的概念依据几何模型,针对具体的平差问题,确定观测值个数n ,必要观测数t ,则多余观测数r=n-t 。
如果又选了u 个量为参数(而u>t 且包含t 个独立量)参加平差计算,则u 中存在s 个限制条件式,则根据几何模型中的几何关系,将n 个观测值的平差值利用所选u 个参数表示出来,列出s 个函数式,共可列出n+s 个函数式,即为附有参数的条件平差的函数模型。
然后转换为误差方程的形式⎭⎬⎫=+-=0ˆˆx W x C l xB V ,然后按求自由极值的方法,解出使V T PV=min 的V 、xˆ,最后计算出X ˆ,L ˆ; 2、公式汇编函数模型和随机模型⎪⎭⎪⎬⎫=Φ+=0)ˆ(ˆˆX d X B L ,转化后⎭⎬⎫=+-=0ˆˆx W xC l x B V ,12020-==P Q D σσ其中 )(0X F L l -=,)(0X W x Φ= 。
法方程⎭⎬⎫=+=-+0ˆ0ˆx s T BB W x C W K C xN式中PB B N T BB =,Pl B W T= 。
其解x CC T BB X X x CC T BB BB CC T BB BB W N C N W Q W N C N W CN N C N N x 11ˆˆ111111)(ˆ---------=--=)(11x BB CC s W W CN N K +=--式中TBB CC C CN N 1-= 。
观测值和参数的平差值x X Xˆˆ0+=,V L L +=ˆ单位权方差的估值su n PVV T +-=20ˆσPV V T 的计算:(1)PV l PV B x PV V T T T -=ˆ;(2)x PB l Pl l PV V TT T ˆ-=;参数平差值函数)ˆ(ˆX Φ=ϕ平差值函数的权函数式 x F X d F d T T ˆˆˆ==ϕ协因数: F Q F Q X XT ˆˆˆˆ=ϕϕ;方差:ϕϕϕϕσˆˆ20ˆˆQ D =; 3、按附有限制条件按的间接平差求平差值的计算步骤:(1)确定n 、t ,选u (u>t 且包含t 个独立量)个量为参数参与平差;得出s 个参数是相关的(2)列出n+s 个方程,即先将n 个观测值的平差值利用所选参数表示出来,再列出s 个函数式:即先列出平差值形式,再转化为误差方程形式,最后矩阵形式⎭⎬⎫=+-=0ˆˆx W xC l xB V ;(3)确定权阵P ;(4)依据以下公式计算,PB B N T BB =,Pl B W T=,TBB CC C CN N 1-=,x CC T BB BB CC T BB BB W N C N W CN N C N N x 111111)(ˆ--------=,x X Xˆˆ0+=,V L L +=ˆ;(5)检核;(6)精度评定。
平差知识点总结

平差知识点总结(总10页) -CAL-FENGHAI.-(YICAI)-CompanY One 1-CAL-本页仅作为文档封面,使甬请直接删除测量平差知识点观测误差包括:粗差、系统误差、偶然误差。
粗差:即粗大误差,或者说是一种大量级的误观测差,是由观测过程中的差错造成的。
发现粗差的方法:进行必要的重复测量或多余观测,采用必要而又严格的检核、验算等,发现后舍弃或重测。
系统误差:在相同条件下进行一系列观测,如果误差在大小、符号表现出一致性,或者在观测过程中按一定的规律变化,或者为一常数,这种误差称为系统误差。
消除或削弱的方法:采取合理的操作程序(正、倒镜,中间法,对向观测等);用公式改正,即加改正裁(如钢尺量距时的尺长误差等)。
偶然误差:在相同条件下进行一系列观测,如果误差在大小、符号上表现出偶然性,即就单个误差而言,该误差的大小和符号没有规律性,但就大量误差的总体而言,具有一定的统计规律,这种误差称为偶然误差,或者随机误差。
采臥措施:处理带仔偶然误差的观测值,就是木课程的内容,也叫做测量平差。
偶然谋差又称随机误差,有以I、•四个特性:1)一定观测条件下,误差绝对值有一泄限值(有限性);2)绝对•值较小的课差比绝对值较人的课差出现概率人(渐降性):3)绝对值相等的正负误差出现概率相同(对称性);4)偶然谋差的数学期望为零(抵偿性)。
衡量精度的指标有五个,分别眉中矗、平均矗、或然i灵差、极限i灵差以及相对中谋差。
其中中矗和极限误差以及相对中保差是工程測量中常用的指标。
5、相对谋差颠差、屮促差、极限促差等指标,对于菜些观测结果,有时还•侮全表达观测结果的好坏,例如,分别丈1000m及500⑴的两段距离,它们的中课差均为±2cn】,虽然两者■的中误差相同,但就M位长度而言,两者精度并彳、相同。
显然询耆的郴对蒂度比后者耍高。
一般:而言,一些与长度有关的观测俺或其函数值,单纯用中误苣还不能区分出蒂度的高低,所以常用相对课差。
第九章 概括平差函数模型

附有限制条件的条件平差
U=0 条件平差
U=t 间接平差
u<t 附有参数的条件平差
ut 附有限制条件的间接平差
函数模型
B 0,C 0 ˆ AL A0 0
函数模型
函数模型
C 0 ˆ ˆ AL BX A0 0
函数模型
A I ˆ ˆ L BX d ˆ CX A0 0
P1
P3 A
P4
P2
1)t=3,n=5,r=2, 2)如选P1,P2点高程为参数,u=2, 3)应列立C=2+2=4个条件式; 4)其中一个限制条件方程,3个一般条件方 程。
取:
X 10 H A L1 119.990m
0 X 2 H A L4 L5 39.984m
由此可断:
函数模型的个数总是等于多余观测数与所选参 数个数之和!C=r+U
思考: 如果所选的参数不一定要求独立,函数模 型的个数以及函数模型的类型又会怎样?
6 1
5
4 2 3
如果:当U=4(不独立)时,则仍应列2+4个条 件式,包括一般条件式和限制条件式。 其函数模型为:
F L,X) 0 (ˆ ˆ (X) 0
精度评定:
V T PV 7.527 V T PV ˆ ˆ 02 3.76(mm) 2 , 0 1.94mm r Qˆ 1.550 ˆ 2ˆ ˆ ˆ H 02Qˆ 5.83(mm) 2 , H 2.41(mm)
3 3
也就是说,概括模型可以概括其它各种平差的函数模型。
例:设有工程施工放样时的水准网,如图,已知 HA=125.850m,P1、P2两点间的已知高差为-80.00m, 观测高差为: L=[-5.860 -35.531 -44.470 50.783 35.083]T(m) 观测值的方差阵为:DL=diag(4 6 6 8 8) • 试以附有限制条件的条件平差求P1、P2点高程的 平差值、以及中误差。
09概括平差函数模型

试按附有限制条件的条件平差列出条件方程和参数的限制
条件。
B
24
A
3
7
1
P1 5
8 11
9 10
P3
6
12
P2
§9-2 附有限制条件的条件平差原理
解:n 12 , t 2 3 1=5 , r 12 5 7 , u 2 , s 1 c r u s 7 2 1=8
Lˆ1 Lˆ5 Lˆ8 Lˆ11 360 0 圆周条件
P1A P1B P1P2 P1P3 1 0 极条件 P1B P1P2 P1P3 P1 A
Xˆ1 Xˆ 2 (BA ˆBP2 ) 0 限制条件
B
24
A3 7
1 5P1 8 11
一般条件式, 9 10
若选∠AOB, ∠BOC和∠AOC的平差值为参数,试按附有限制条件
的条件平差列出条件方程和参数的限制条件。
解:n 6 , t 3 , r 6 3 3 , u 3 , s 1
A
crus 5
Lˆ1 Xˆ1 0 Lˆ2 Xˆ 2 0
O
14 2
B
一、条件方程的形式
F (Lˆ) 0 F (Lˆ, Xˆ ) 0
Lˆ F ( Xˆ )
( Xˆ ) 0
一般条件方程式,
用 c 表示个数
限制条件式
§9-1 基本平差方法的概括函数模型
二、参数与平差方法
1.条件平差法
u 0, c n t r
2.附有参数的条件平差法
附有条件的间接平差)ppt课件

平差对象
地理数据,如经纬度、高程等
案例描述
在GIS中,为了确保地图的准确性,需要使用附有 条件的间接平差对地理数据进行处理,如对全球定 位系统(GPS)数据进行平差处理,以提高其定位 精度。
案例二:气象数据平差
• 应用领域:气象预报
• 平差对象:气象观测数据,如温度、湿度、风速、气压等 • 平差方法:利用已知的气象数据和气象站的位置信息,通过平差计算,对未知的气象数据进行修正,提高其准确性 • 案例描述:在气象预报中,需要对大量的气象观测数据进行平差处理,以获取更准确的气象信息。例如,通过附有条件的间接平差方法,可以修正气象观测数据的误差,提高气象预报的准确率。
附有条件的间接平差的应用场景
附有条件的间接平差广泛应用于大地 测量、工程测量、航空摄影测量等领 域。
在工程测量中,附有条件的间接平差 可以用于桥梁、隧道、建筑物等工程 的施工测量和监测,提高工程质量和 安全性。
在大地测量中,附有条件的间接平差 可以用于处理地球重力场模型的数据, 提高模型精度和可靠性。
解算参数
通过计算或软件解算,得 出未知点的坐标和其它相 关参数的估计值。
参数精度评估
对解算出的参数进行精度 评估,了解其可靠性和误 差范围。
结果检验
残差分析
对解算出的结果进行残差 分析,检查是否符合预期 的误差分布。
精度验证
通过实地测量或其它方式, 验证解算结果的精度和可 靠性。
模型适用性评估
评估所建立的数学模型是 否适用于实际测量情况, 并根据评估结果进行必要 的调整或改进。
常用的计算方法包括最小二乘法、梯度下降法等,选择合 适的计算方法可以提高求解效率和结果的准确性。
03
附有条件的间接平差的 实现步骤
误差理论与测量平差基础第八章 附有限制条件的间接平差
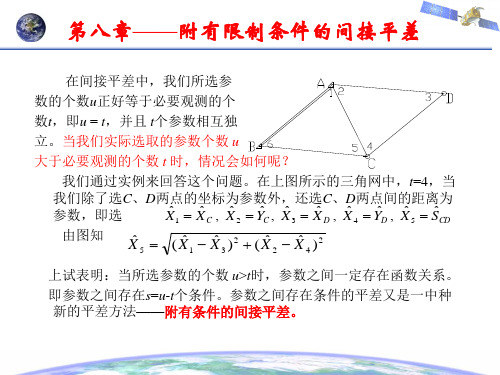
Q XX Q XL B T ˆˆ ˆ QLL BQXX B T ( B E ) ˆˆ Q ˆ Q E LX LL
(1)根据具体问题,按(1)式列出误差方程和条件方 程。
(2)由误差方程和条件方程列出法方程(3)式。
(3)按(4)式计算参数的改正数 x 。 ˆ
(4)按(5)式计算观测值的平差值和参数的平差值。
教材:8-1
第八章——附有限制条件的间接平差
4、举例
水准网如图所示,同 精度观测值为: L1 0.008m
观测值的平差值(略)
习题:8.1.10,8.1.11
第八章——附有限制条件的间接平差 §8-2 精度评定
(1)、单位权中误差 在附有条件的间接平差中,单位权中误差的估值仍为
V T PV ˆ2 0 r
(2)、基本向量的协因数矩阵 在附有条件的间接平差中,基本向量为:
ˆ ˆ L, W , X , K s , V , L
求解法方程,得
ˆ xC 1.8505 , yC 0.6653 cm ˆ cm ˆ x D 0.1399 , y D 2.4593 cm ˆ cm k S 28.9655
第八章——附有限制条件的间接平差
改正数为:
V 2.4 5.7 5.7 8.0 0.0 0.0
第八章——附有限制条件的间接平差
误差方程和条件方程如下:
1.786 1.031 1.786 1.031 2.24 ˆ 0 2.063 xC 4.62 1.786 1.032 0 y 6.62 2.063 1.786 1.032 ˆ C V x 0.38 0 2.063 ˆ D 1.786 1.032 0 y 1.38 2.063 1.786 1.032 ˆ D 1.786 1.032 1.786 1.032 6.24 ˆ ˆ 0.500x D 0.866y D 2.20 0
第2讲附有条的间接平差

5.2 附有限制条件的间接平差
如果在某平差问题中,选取 u>t 个参数, 其中包含t个独立参数 ,则多选的 s=u-t 个参 数必定是 t个独立参数的函数,即在 u个参数 之间存在着 s 个函数关系式。
方程的总数 r+u=r+t+s=n+s 个,建立模 型时,除了列立 n个观测方程 外,还要增加 参 数之间满足的s个条件方程 。
x?T C T ? (Cx?)T
二、精度评定
2. 协因数阵
基本思想是把其它变量表示为已知协因数阵的量的线性函数。
L ? L,
W ? BT Pl ? BT PL ? W 0 ,
X?
?
X0
?
x? ?
X0
?
(
N
?1 bb
?
N
C ?1
bb
T
N
c?c1CN
?1 bb
)W
?
N
C ? 1
bb
T
N
W ?1
cc x
,
Ks
?
N
c?c1CN
W ? 1
bb
?
N
W ? 1
cc
x
,
V ? Bx? ? l,
L? ? L ? V .
QLL ? Q QWW ? BT PQPB ? BT PB ? N bb
二、精度评定
2. 协因数阵
X?
?
X0
?
x? ?
X0
?
(
N
?1 bb
?
N
C ? 1
bb
T
N
c?c1CN
?1 bb
)W
6.5 第二十讲 附有条件的间接平差资料
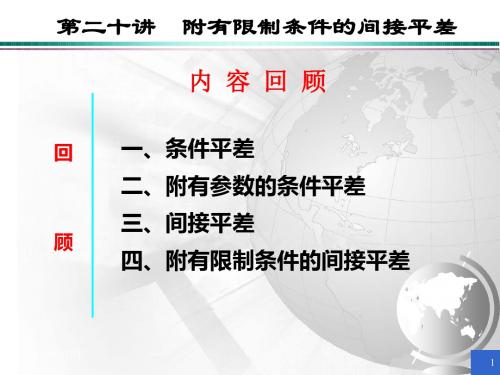
QWW BT PQPB BT PB N bb ,
1 1 T 1 1 1 1 T 1 1 T QX ( N N C N CN ) Q ( N N C N CN ˆX ˆ bb bb cc bb WW bb bb cc bb )
1 1 T 1 1 1 1 T 1 1 ( N bb N bb C N cc CN bb ) N bb ( N bb N bb C N cc CN bb )
T
Av W 0 W ( AL A0 )
2018/11/1
v B~ x l l L ( BX 0 d )
2
第二十讲
附有限制条件的间接平差
附有限制条件的间接平差: 看成是特殊的间接平差; 特殊在所选参数个数要比 间接平差时个数多; 参数个数u:u>t 函数模型的个数: c=n+(u-t)=n+s 函数模型的类型: 1.按间接平差的观测方程、 2.未知数之间的条件方程(限 ~ ~ 制条件式)。 L F(X ) ~ 函数模型可表示为: ( X )0
u ,1 u ,s s ,1
ˆ Wx 0. C x
s ,u u ,1 s ,1
2018/11/1 12
第二十讲
附有限制条件的间接平差
u ,u
法方程解法一(显性形式): 用
1 CN bb
ˆ CT Ks W 0 N bb x
u ,1 u ,s s ,1 u ,1
左乘(1)-(2)得:
s ,u u ,1 s ,1
B PB x C T K s B T Pl 0,
T
u,n
B
T
n , n n ,1
P V C Ks O.
近代测量数据处理进展

在
V T PV min ˆ TX ˆ min X II II
部分参数最小范数条件下
高德曼(Goldman)蔡勒(Zelen)(1964年)(奇异 权逆阵的最小二乘) Q,P满秩 Q,P奇异阵
V T Q V min
劳(C.R.Rao)(1971年)提出广义G-M模型
ˆ l V BX
最小二乘配置(拟合推估): L AX BY 既包含最小二乘中的非随机未知数,又包含随机未知参数(信 号) 广义LS准则:
V T PV VYT PYVY min
拟合推估
Bayes准则:
进行随机参数向量估计
Bayes估计
L AX BY
③
4
随机模型的验后估计
经典平差研究:平差函数模型的建立——研究平差方法,方程 式的建立; 近代平差研究:随机模型——观测值的权(观测值之间的精度 比例) 近代: 不同类多种观测值,不同精度的观测值;
① L随机独立 → 随机相关,P—对称方阵(相关平差)。
② A列满秩→A秩亏,秩亏自由网平差;
③ X非随机参数具有各态经历性的平稳随机函数(拟合推估) 最小二乘配置; ④ 仅考虑研究函数模型(各种平差方法)→考虑研究随机 模型(方差分量估计); ⑤ 不考虑模型误差(系统误差,粗差)→顾及模型误差 (附加系统参数的平差,可靠靠性理论,数据探测,稳 健估计)
成果的精度与可靠性
6
有偏估计
经典平差——最小二乘原理——最优无偏估计。 ˆ X E X
ˆ X X ˆ X T X E min
ˆ X) 0 lim( E X
T r
当平差中含有较多未知参数的大型线性模型,往往会出现模型线 性近似或参数近似相关,法方程性态不好(病态)——接近奇异,按 最小二乘平差将导致虽满足最小二乘最优条件。方差最小,但值都很 大,精度差,相当不稳定。 有偏估计: 偏差: 有偏估计:
第八章概括平差函数模型

第八章 概括平差函数模型§8.1概述在已经介绍过的条件平差,间接平差,附有参数的条件平差以及附有限制条件的间接平差等四种基本平差方法,其差别就在于函数模型不同。
若将误差方程也视为参数形式的条件方程,以未知参数为纽带,可以对4种平差方法概括如下:(1)、条件平差:0)ˆ(=L F ,不选择未知参数,方程数等于多余观测数:c=t n r -= (2)、间接平差:)ˆ(ˆX F L=,选函数独立未知数t u =,方程数n t r u r c =+=+= (3)、附有参数的条件平差:0)ˆ,ˆ(=X LF ,选择t u <个函数独立参数,除应列出r 个条件方程外,还要附加u 个对未知参数的约束条件方程,所以必须列出u r c +=个条件方程。
(4)、附有限制条件的间接平差:)ˆ(ˆX F L =,0)ˆ(=ΦX 。
选择t u >个参数,参数间存在t u s -=个函数关系。
所以除列出n 个误差方程)ˆ(ˆX F L=(也可视为特殊形式的条件方程-参数方程形式的条件方程),还要列出s 个限制条件方程0)ˆ(=ΦX。
方程数c=n +s 。
由此可见,是否选择参数及如何选择参数决定着平差方法,即参数是联系各种平差方法的纽带。
另外可以看到,前三种函数模型中都含有观测量,或者同时包含观测量和未知参数,而后一种只含有未知参数而无观测量。
为了便于区别,将前三种统称为一般条件方程,而后者称为限制条件方程,并统称为条件方程。
在任何几何模型中,函数独立参数个数总是介于下列范围之内: t u ≤≤0。
也就是说,在任一平差问题中,最多只能列出t u =个函数独立的参数。
在不选择参数时,一般条件方程数c 等于多余观测数t n r -=,若又选用了u 个函数独立参数,则总共应当列出u r c +=个一般条件方程。
由于t u ≤,因此一般条件方程的个数总是介于n c r ≤≤范围,即一般条件方程总数不超过n 个。
08附有条件的间接平差

n1
s1
ˆ C x Wx 0
2 2 D 0 Q 0 p 1 nn
s1
随机模型为: 平差原则:
V PV min
T
组成新函数
ˆ V T PV 2 K sT (Cx Wx ) ˆ
对取偏导数并令其为零
解联系数和参数:
1 1 K s NCC (CN BBW Wx ) 1 1 1 1 1 1 ˆ x ( N BB N BB C T NCC CN BB )W N BBC T N CCWx 1 ( N BB BT PB,W BT Pl , N CC CN BBC T )
求参数和观测值的平差值:
ˆ L L V ˆ ˆ X X0 x
平差计算步骤:
1)选个数大于必要观测数的参数(包含t个独 立); 2)列出误差方程和限制条件方程;
3)组法方程,解
ˆ x
、
Ks
;
、
4)求改正数V,最后求
ˆ L
ˆ X
;
8-2 精度评定
一、单位权方差的估值公式
T T
V PV V PV ˆ r n (u s)
得到的法方程以及基本向量的自(互)协因 数阵公式有所不同!
8-1 附有限制条件的间接平差原理
若选P1,P2点高程以及第四段高差的平差值为参数 进行最小二乘平差,该如何作?
在作间接平差时多选了未知数(例1)、或者有 时为了列立误差方程方便而多选了未知数(例 2);
这样,未知数之间会存在条件式,这种情况下所 作的平差方法就是附有限制条件的间接平差。
T V 2VP 2 K sT C 2V T PB 2 K sT C 0 ˆ ˆ x x
经典平差中各种模型的关系

图1
现选 3 个观测值为参数 , 即 X^ T = ( ^x 1 ^x 2 ^x 3) = L^ T = ( ^l1 ^l2 ^l 3) 。因为 u = n > t , s = u - t = n - t = r = 3 - 2 = 1 ,所以 3 个参数之间存在一个条 件 。于是 ,由图知附有条件的间接平差模型为
将此附有条件的间接平差模型的第 1 式代入第
2 式 ,消去参数 L^ ,得
1 1 1 v1
0
0
1 0 0 v2 + - 0. 542 0. 773
0 - 1 0 v3
- 1. 324 0. 288
δx c δyc -
5″ - 0. 1″ = 0 0. 1″
(8)
式 (8) 就是附有未知数的条件平差的条件方程 。
收稿日期 : 2003206209 基金项目 :国家高新技术研究发展计划 (863 计划) 资助项目 (2001AA135081) 作者简介 :王新洲 (19542) ,男 ,博士 ,教授 ,博士生导师 ,主要从事测量数据处理理论研究 。
© 1995-2005 Tsinghua Tongfang Optical Disc Co., Ltd. All rights reserved.
的个数 ,且选择观测值的真值为前 n 个参数 ,而后 q
= u - n 个参数相互独立时的附有条件的间接平差
在消去前 n 个参数以后的中间形式 。所以附有参数
的条件平差模型是附有条件的间接平差模型的特例 。
例 2. 对于例 1 中的单三角形 , 现选 3 个观测值 和 C 点 的 两 个 坐 标 改 正 数 为 参 数 , 即 X^ T
^l 1 + ^l 2 + ^l 3 - 180°= 0 αAB + ^l 1 +α^ A C = 0 αBA - ^l 2 - α^ B C = 0 式中 ,αij为 i 点到 j 点的方位角 。上面的两个方位 角条件是非线性条件 ,应先线性化 。线性化后 ,得附 有条件的间接平差模型为
第8章 附有限制条件的间接平差

ˆ l PV x ˆ TB T PV l T PV 2. V T PV Bx
T
ˆ TCTK S l T PBx ˆ l x
顾及 B PV = C K
T T S
ˆ TCTK S l T PB x ˆ l T Pl x
ˆ l T Pl WxT K S W T x
10
转置得
B T PV C T K S 0
上式与误差方程和限制条件方程联立得附有限制条件 的间接平差法的基础方程:
u ,n
B P V C KS 0
n , n n ,1 u ,s s ,1
T
T
u ,1
ˆ l VBx
n ,1 n ,u u ,1
n ,1
ˆ Wx 0 Cx
s ,u u ,1 s ,1
s ,1
8 /17
方程的个数与未知数的个数相同,方程有唯一解。
主页
附有限制条件的间接平差
三、基础方程的解
误差理论与测量平差
1 2 3 4 5 6 7 8 9
10
将基础方程的第二式代入第一式与第三式联立,得 ˆ CT KS W 0 N BB x -法方程 ˆ Cx Wx 0 1 将法方程第一式左乘 CN BB 与第二式相减,得
S
Q LX ˆ QWX ˆ QK
SX
QLV QW V Q K SV QX ˆV QVV QL ˆV
ˆ
QX ˆX ˆ QVX ˆ QL ˆX ˆ
13 /17
QVK S
S
Q LL ˆ QWL ˆ QK L ˆ S QX ˆL ˆ QVL ˆ QL ˆL ˆ
主页
附有限制条件的间接平差
误差理论与平差基础-第9章 概括平差函数模型

BT K + C T K S = 0
æ N B 0 öæ ç aa ÷ç T T ç B 0 C ÷ç ç 0 C 0 ÷è è ø K ˆ x KS ö æ W ö ÷+ç 0 ÷ = 0 ÷ ÷ ç ø è WX ø
ˆ AQAT K + Bx +W = 0 BT K + CT KS =0 ˆ Cx +WX = 0
ö ÷ ÷ ÷ ÷ -1 ÷ ø
n=6 t =4 r =2
C= 1 1 1 0
(
)
u=4
s =1
三、精度评定
计算单位权中误差
V T PV ˆ0 = ± s r
-1 BB
参数精度 QX ˆX ˆ =N
- N C N CN
T T Qjˆjˆ = FQX F ˆX ˆ
-1 BB
-1 CC
-1 BB
ˆ W 0 AV B x
cu u1 s1 c1 s1
c1
ˆ Wx 0 C x
当参数个数u = 0时,有B = 0,C = 0,变为条件平差 AV W 0
当参数个数u < t,且彼此独立时,有C = 0。变为附有参数的
ˆ W 0 , c r u 条件平差 A V B x
ˆ -l V = Bx
必要观测数:t
多余观测数:r 参数个数: u 限制条件数:s u u
ˆ, X ˆ) = 0 Fi ( L
ˆ +W = 0 AV + Bx
ìV = Bx ˆ-l í ˆ + WX = 0 îCx
u
限制条件方程
u
t n
r
一、基本平差方法的概括函数模型
四种经典平差模型的分析与设计

3.四中经典平差模型的分析与设计在生产实践中观测的数据可以通过以最小二乘原理为基本原理进行平差提高测量精度,但由于所设参数个数与观测个数和非必要观测个数的关系不同,可以分为条件平差、附有参数的条件平差、间接平差、附有限制条件的间接平差四种。
通过对它们的分析,可以很好地解决生产实践中的实际问题,亦可为以后的某些理论推导作必要的准备。
3.1条件平差模型条件平差的函数模型:A V+W=0其中A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n n n r r r b b b a a a 212121,W=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡r b a w w w ,V=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n v v v 21 随机模型:D=Q 20δ法方程:0=+W K N aa其中:T aa AQA N =解之得 K=W N aa 1--误差方程 : V=K QA T观测量平差值: V L L +=平差值函数:)(21n L L L f+++=ϕ 其权函数式为⎪⎪⎭⎫ ⎝⎛∂∂+++=i i n n Lff L d f L d f L d f d ,***2211ϕ 单位权方差的估值:rPVV r PV V T T ==020,δδ 平差值函数ϕ的协因数阵:AQf N AQf Qf f Q aaT T 1)(--=ϕϕ 条件平差的基本向量的协因数和互协因数3.2附有限制参数的条件平差模型在一个平差问题中,如果观测值个数为n ,必要观测数为t ,则多余观测数r=n-t 。
若不增选参数,只需列出r 个条件方程,这就是条件平差方法。
如果又选了u 个独立量为参数(0<u<t )参加平差计算,这就可建立含有参数的条件平差作为平差的函数模型,这就是附有参数的条件平差方法。
0**1,1,,1,,=++c u uc n nc W x B V A②式中,V 为观测值L 的改正数,1,u x为参数近似值0X 的改正值,即x X X V L L +=+=0,随机模型:D=12020-=P Q δδ为了求出能使min =PV V T的一组解,按求函数条件极值的方法,组成函数)(2W x B AV K PV V T T ++-=Φ式中,K 是对应于条件方程②的XXX 数向量,为求Φ的极小值,将其分别对V 和x求一阶导数并令其等于零,则有02022=-=∂Φ∂=-=∂Φ∂B K xA K P V VT T T由两式转置之后第一式左乘1-P ,再加②式得其基础方程解算此基础方程,通常是将其中的改正数方程代入条件方程,得到一组包含K 和1,,u x的对称线性方程组,即⎪⎭⎪⎬⎫==++00K B w x B K AQA T T令Ta a AQA N =,,上式也可写成:⎪⎭⎪⎬⎫==++00,K B W x B K N T a a③ 上式称为附有参数的的条件平差的法方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-1 附有限制条件的间接平差原理 8-2 精度评定 8-3 综合练习题
§8-1 附有限制条件的间接平差原理
一 函数模型
平差问题中,观测值
ห้องสมุดไป่ตู้
L ,权阵
n ,1
P
n,n
,选u个参数
X
u ,1
u> t,且包含t个独立参数,则有s=u-t个未知数之
间的条件。附有限制条件的间接平差的线性或线性
xˆ
u1
wx
s1
0
条件方程式形式
F (Lˆ) 0
F
(Lˆ,
Xˆ
)
0
Lˆ F ( Xˆ )
( Xˆ ) 0
一般条件方程式,用c表示 个数
限制条件式
由于引入参数的不同,出现不同的平差模型
u个独立参数
u 0 条件平差 0 u t 附有参数的条件平差
数c=r+u个。
F (Lˆ, Xˆ ) 0 A V B xˆ W 0 cn n1 cu u1 c1
(3)间接平差法
观测数为n,必要观测数为t,多余观测数r=n-t,
设t个相互独立的未知参数,则条件个数c=n+t-t=n,即
n个误差方程:
Lˆ F ( Xˆ )
V B xˆ l
3 在图中的大地四边形中,A、B为
已知点,C 、D为为待定点,现选取
L3、L4、L5、L6、L8的平差值为参数,
记为
Xˆ1, Xˆ 2, ,,Xˆ列5 出误差方程
和条件方程。
4 附有限制条件的间接平差法中,参数选择有什么特点?
4 如图水准网中,A为已知点,高程为HA=10.000m,观测高
差及路线长度为:
条件平差
u t crus s 0 rt n
A I
C
0
间接平差
ut crus s 0 ru
C0
附有参数的条件平差
ut
s0
c r u s ns
A I
附有限制条件的间接平差
思考题 1 何谓一般条件方程?何谓限制条件方程?它们之间有什
么区别? 2 什么是概括平差函数模型?指出此模型的主要作用是什么。 3 某平差问题有15个同精度观测值,必要观测数等于8,现
u t 间接平差
u个非独立参数
u t且包含t个独立参数,附有限制条件的间接平差
u
0,独立参数为u
s,附有限制条件的条件平差
二 附有限制条件的条件平差
观测数为n,必要观测数为t,多余观测数r=n-t,现有 u个参数(独立参数的个数u-s),则条件个数r+u,其中, u个参数中其中可以形成s个限制条件,一般条件个数为: c=r+u-s:
一、计算单位权中误差
ˆ
2 0
V T PV r
二、协因数阵
三、参数函数的协因数
平差中所求任一量都能表达成所选参数的函数。设某
个量的平差值为: ˆ Φ( Xˆ ).
对其全微分,得权函数式为
dˆ
dΦ dXˆ
dXˆ
FT
1u
dXˆ
u1
式中F为
FT
Φ Xˆ 1
Φ Xˆ 2
Φ Xˆ u
.
用代入各偏导数中,即得各偏导数值,然 后按下式计算其协因数:
Qˆˆ F T QXˆXˆ F.
函数的中误差为
ˆ ˆ 0 Qˆˆ .
思考题
1 附有限制条件的间接平差中的限制条件与条件平差中的条 件方程有何异同?
2 附有限制条件的间接平差法适用于什么样的情况?
化后的函数模型为:
V B xˆ l
n1 nu u1 n1
C
su
xˆ
u1
wx
s1
0
二、 基础方程和它的解
最小二乘解:
V B xˆ l
n1
C
su
nu u1
xˆ
u1
wx
s1
n1
0
V T PV 最小
按求函数极值的拉格朗日乘数法,构造新的函数:
取8个参数,且参数之间一个限制条件。若按附有限制条 件的的条件平差法进行平差,应列出多少个条件方程和限 制条件方程?其法方程有几个? 4 概括平差函数模型的方程数是否和附有参数的条件平差的 方程数一样?其中r、u、c和s各表示什么量? 5 写出概括平差函数模型的一般表达式。与其他平差方法的 关系
F (Lˆ, Xˆ ) 0
(
Xˆ
)
0
cAn
V
n1
B
cu
xˆ W
u1 c1
0
C
su
xˆ
u1
wx
s1
0
概括平差函数模型
cAn
V
n1
B
cu
xˆ W
u1 c1
0
C
su
xˆ
u1
wx
s1
0
u0 cr
B 0 C 0
一、平差模型的回顾
(1)条件平差法 观测数为n,必要观测数为t,多余观测数r=n-t,
条件方程个数c=r。
F (Lˆ) 0
A V W 0
cn n1 c1
(2) 附有参数的条件平差法
观测值个数为n,t为必要观测数,则可列出r=n-t个
条件方程,现有u个独立量作为参数,而0<u<t,方程总
n1 nt t1 n1
(4)附有限制条件的间接平差法
观测数为n,必要观测数为t,多余观测数r=n-t,
现有u个参数u>t,包含t个独立参数,则条件个数r+u,
其中,有s个限制条件:
Lˆ F ( Xˆ )
(
Xˆ
)
0
Vn1
B
nu
xˆ
u1
l
n1
C
su
0
K
s
Wx
0
法方程的解:
xˆ
K
s
Nbb C
CT
1
BT
Pl
0
Wx
Ks xˆ
(CNbb1CT )1(Wx CNbb1BT
N 1 bb
(C
T
Ks
BT
Pl)
Pl
)
§8-2 精度评定
线路 1 2 3 4
h/m 2.563 -1.326 -3.885 -3.883
S / km 1 1 2 2
若设参数 Xˆ Xˆ1
Xˆ 2
Xˆ
3
T
Hˆ B
Hˆ C
hˆ4
T
,定权时C=
2km,试列出误差方程和限制条件
第九章 概括平差函数模型
附有限制条件的条件平差
9-1 基本平差方法和概括函数模型 9-2 附有限制条件的条件平差原理 9-3 精度评定 9-4 各种平差方法的共性与特性 9-5 平差结果的统计性质
G
V
T
PV
2K
T s
(Cxˆ
Wx
)
K T [ka kb ks ]T
求其一阶偏导数,并令其为0:
G xˆ
2V T PB
2
K
T
s
C
0
BT PV CT Ks 0
法方程式为
BT PBxˆ CT Cxˆ Wx 0
Ks
BT
Pl
0
Nbb C
CT xˆ BT Pl
