计算方法引论-第六章

合集下载

南开大学算法导论第六章课件

23
带权的区间调度

预处理：算法实现的过程中先对开始时间和结束时间排序，便于后面的处理一些编程语言，如Lisp，就可以自动实现备忘录的功能(built-in support for memorization)，因而有好的执行效率；但是在其他的一些语言中，比如Java，就没有实现这一功能。
7
带权的区间调度
不同区间的影响是不一样的
a b c d e f g h
0 1 2 3 4 5 6 7 8 9 10 11
Time
8
带权的区间调度

贪心算法情形下，区间的权重可以看成都是1 对于区间权重不同的情形，贪心算法就失效了
weight = 999
b
weight = 1
a Time
解决之道：更加灵活的调度策略

对于带权区间调度问题，我们可以不使用备忘录式的递归方法，而通过迭代算法直接计算M[]中的项。
,
Input: n, s1,…,sn
f1,…,fn
,
v1,…,vn
Sort jobs by finish times so that f1 ≤ f2 ≤ ... ≤ fn. Compute p(1), p(2), …, p(n) Iterative-Compute-Opt { M[0] = 0 for j = 1 to n M[j] = max(vj + M[p(j)], M[j-1]) } 自底向上
19
带权的区间调度

递归的备忘录形式为了避免上面的重复计算，我们把中间计算的结果存储起来，需要的时候先查找是否计算过下面将用到一个数组M[0…n]保存中间计算结果
20

计算方法

1 3 1 2 ≈ n + n − n. 3 3
►高斯消元法(Gauss)：运算量(乘除)
取 n = 20,
Gauss: 3060次；
Cramer: ( 20+ 1) ≈ 5. × 1019 ≈ 16200年(108 次 / 秒) ! 1
2011-2-25 5
本课程的任务：本课程的任务：
● 建立各种数学问题的数值计算算法的方法和理论。通俗地讲，就是为各种实际问题提供有效的数值近似解方法。 ● 提供在计算机上实际可行的、理论可靠的、计算复杂性好的各种常用算法。
绝对误差限不超过该近似数末位的半个单位。
2011-2-25
13
相对误差
先看两种产品的不合格率： 8/1000=0.8% ； 12/2000=0.6% （相对误差的值）定义：设 x* 为精确值，x 为近似值，相对误差为
e x * −x er = = . x* x*
当绝对误差 e 较小时，相对误差可写为
一、防止相近的两数相减
(会耗失许多有效数字,可以用数学公式化简后再做).
例1: 各有五位有效数字的23.034与22.993相减. 23.034-22.993=0.041 0.041只有两位有效数字,有效数字的耗失,说明准确度减小,因此, 在计算时需要加工计算公式,以免这种情况发生. 例2:当较大时,计算 x +1 − x
2011-2-25
11
误差的概念
(绝对)误差设 x* 为精确值（或准确值），x 为 x* 的近似值，称 e = x*－ x 为近似值x的(绝对)误差。 (绝对)误差限（ ε ）如果精确值 x* 与近似值 x 的误差的绝对值不超过某个正数 ε，即 | e |= | x*－ x |≤ ε。于是，精确值也可表示为 x* = x ± ε，或

计算方法的课后答案解析

《计算方法》习题答案第一章数值计算中的误差1．什么是计算方法？（狭义解释）答：计算方法就是将所求的的数学问题简化为一系列的算术运算和逻辑运算，以便在计算机上编程上机，求出问题的数值解，并对算法的收敛性、稳定性和误差进行分析、计算。

2．一个实际问题利用计算机解决所采取的五个步骤是什么？答：一个实际问题当利用计算机来解决时，应采取以下五个步骤：实际问题→建立数学模型→构造数值算法→编程上机→获得近似结果4．利用秦九韶算法计算多项式4)(53-+-=x x x x P 在3-=x 处的值，并编程获得解。

解：400)(2345-+⋅+-⋅+=x x x x x x P ，从而所以，多项式4)(53-+-=x x x x P 在3-=x 处的值223)3(-=-P 。

5．叙述误差的种类及来源。

答：误差的种类及来源有如下四个方面：（1）模型误差：数学模型是对实际问题进行抽象，忽略一些次要因素简化得到的，它是原始问题的近似，即使数学模型能求出准确解，也与实际问题的真解不同，我们把数学模型与实际问题之间存在的误差称为模型误差。

（2）观测误差：在建模和具体运算过程中所用的一些原始数据往往都是通过观测、实验得来的，由于仪器的精密性，实验手段的局限性，周围环境的变化以及人们的工作态度和能力等因素，而使数据必然带有误差，这种误差称为观测误差。

（3）截断误差：理论上的精确值往往要求用无限次的运算才能得到，而实际运算时只能用有限次运算的结果来近似，这样引起的误差称为截断误差（或方法误差）。

（4）舍入误差：在数值计算过程中还会用到一些无穷小数，而计算机受机器字长的限制，它所能表示的数据只能是一定的有限数位，需要把数据按四舍五入成一定位数的近似的有理数来代替。

这样引起的误差称为舍入误差。

6．掌握绝对误差（限）和相对误差（限）的定义公式。

答：设*x 是某个量的精确值，x 是其近似值，则称差x x e -=*为近似值x 的绝对误差（简称误差）。

计算方法各章小结

计算方法各章小结第一篇：计算方法各章小结计算方法各章小结第一章计算方法与误差小结误差在数值计算中是不可避免的，误差的传播和积累直接影响到计算结果的精度。

在研究算法的同时，必须注重误差分析，使建立起来的算法科学有效。

绝大多数情况下不存在绝对的严格和精确，在考虑数值算法时要能将误差限制在许可的范围之内，这种算法就是数值稳定的。

本章介绍了计算方法和误差理论的基本概念，并且对误差的产生与防止进行了分析；同时介绍了绝对误差(限)、相对误差(限)、有效数字的概念和三者的联系及计算的方法；最后介绍了误差在近似值运算中的传播、估算方法和数值稳定性的概念以及减少运算误差的原则。

按照误差产生的来源可分为模型误差、观测误差、截断误差和舍入误差等。

误差的表示法有绝对误差和相对误差两种。

在表示一个近似数时，要用到有效数字的概念，这在数值计算中非常有用，有效数字是由绝对误差决定的。

通常用函数的泰勒展开对误差进行估计。

第二章一元非线性方程数值解法小结非线性方程厂f(x)=o的解通常叫做方程的根，也叫做函数，f(x)的零点，本章讨论了求解非线性方程近似根常用的一些数值方法。

先要确定有根区间，且对于收敛的迭代格式，这个区间要足够小。

针对各种求根的数值方法的特点，要考虑其收敛性、收敛速度和计算量。

二分法是逐步将含根区间分半，主要用来求实根，特别适合于为收敛的迭代公式提供好的初值。

迭代法是一种逐次逼近的方法，这种方法是建章在已知方程根的大致位置的基础上，迭代法只是起着把根的精确值一步一步算出来的作用，即通过迭代公式反复校正根的近似值，使之逐步精确化，直到求出满足精度要求的结果。

一通过选代牧敛的理论可知，迭代法具有线性收敛速度。

迭代法不仅可用于含一个未知元的一个方程，也可用于含多个未知元的方程组。

牛顿法具有较快的收敛速度，但对初值选取要求较高。

扩大初值的选取范围，可采用牛顿下山法。

若改用差商替换牛顿公式中的导数后得到的迭代公式便是弦截法，它避开了导数的计算，具有超线性的收敛速度，每计算一步，要用到前面两步的信息。

计算方法引论课后答案

计算方法引论课后答案第一章误差1.什么是模型误差，什么是方法误差？例如，将地球近似看为一个标准球体，利用公式 $A=4\pi r$ 计算其表面积，这个近似看为球体的过程产生的误差即为模型误差。

在计算过程中，要用到 $\pi$，我们利用无穷乘积公式计算 $\pi$ 的值：pi=2\cdot\frac{2}{1}\cdot\frac{2}{3}\cdot\frac{4}{3}\cdot\f rac{4}{5}\cdot\frac{6}{5}\cdot\frac{6}{7}\cdot\frac{8}{7}\cdot\ frac{8}{9}\cdot\cdots我们取前9项的乘积作为 $\pi$ 的近似值，得$\pi\approx3.xxxxxxxx5$。

这个去掉 $\pi$ 的无穷乘积公式中第9项后的部分产生的误差就是方法误差，也称为截断误差。

2.按照四舍五入的原则，将下列各数舍成五位有效数字：816.956，76.000，.322，501.235，.182，130.015，236.23.解：816.96，76.000，.501.24，.130.02，236.23.3.下列各数是按照四舍五入原则得到的近似数，它们各有几位有效数字？81.897，0.008，136.320，050.180.解：五位，三位，六位，四位。

4.若 $1/4$ 用 0.25 表示，问有多少位有效数字？解：两位。

5.若 $a=1.1062$，$b=0.947$，是经过舍入后得到的近似值，问：$a+b$，$a\times b$ 各有几位有效数字？已知 $da<\frac{1}{2}\cdot10^{-4}$，$db<\frac{1}{2}\cdot10^{-3}$，又 $a+b=0.\times10$。

begin{aligned}d(a+b)&=da+db\leq da+db=\frac{1}{2}\cdot10^{-4}+\frac{1}{2}\cdot10^{-3}=0.55\times10^{-3}<\frac{1}{2}\cdot10^{-2}end{aligned}所以 $a+b$ 有三位有效数字；因为 $a\timesb=0.xxxxxxxx\times10$。

计算方法_第六章

设方程组系数矩阵 A (aij ) n ，其顺序主子式
a11 Am a m1
a Am
(1) 11

a1m 0
（m =1,2,…，n）
a mm
a a
(1) 12 ( 2) 22
经变换得到的上三角形方程组的顺序主子式
a a
(1) 1m ( 2) 2m
(1 (2 (m a11) a 22) a mm) 0
(1) 1n ( 2) 2n (1) 1 ( 2) 2
即
(1 (1 ( a11) x1 a12) x 2 a11) x n b1(1) n (2 ( ( a 22) x 2 a 22 ) x n b2 2 ) n (n) (n) a nn x n bn
(4) Gauss消去法计算量 ≈
1 3 n 3
① 消元计算: aij(k+1)= aij(k)- mik akj(k) (i,j=k+1,k+2, … , n)
第一步计算乘数mik, mik=ai1/a11 (i=2,3,…,n)
需要n-1次除法运算,
计算 aij(2）(i,j=2,3,…,n)
其中
( (1 ( a ij2 ) a ij ) mi1 a11) j ( 2) ( bi bi(1) mi1b1 1) i, j 2,3 , n
第k步（k=2,3,…,n-1）继续上述消元过程，设第k-1次消元已经完成，得到与原方程组等价的方程组
(1 a11)
(1 )
简记为 Ax=b，其中
a11a12 ...a1n x1 b1 a21a22 ...a2 n x2 b2 A ,X ,B ...... ... ... xn bn an1an 2 ...ann

西安交通大学《计算方法》课件-第六章

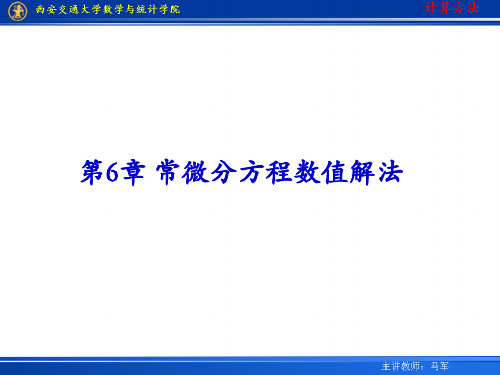
当f (t , y)在区域a t b c y d 中连续 ,且对变量y
满足Lipschitz条件 :对t [a, b] , y1 , y2 [c, d ] , 都有
f (t , y1 ) f (t , y2 ) L y1 y2 (6-2)
其中L为常数则初值问题(6-1)的解存在且唯一
y(t ) f (t , y (t ))确定了函数y (t )在平面上的方向场
yi 1 yi hf (ti , yi )是y(ti 1 )的一个近似,即由(ti , yi )到(ti 1 , yi 1 )的直线段局部近似代替了由(ti , y(ti ))到(ti 1 , y(ti 1 ))的曲线
( 3)可以看出后退Euler方法比Euler方法的结果更好一些
显式方法:由yi直接计算yi 1的算法隐式方法:不能直接由yi直接计算yi 1,而需要从方程中求解yi 1的算法
第6章常微分方程数值解法 6.1 常微分方程初值问题的数值方法 6.1.2 多步法
对于微分方程 y f ( t , y( t ))
条件下是
h h2 (b a) y( ) O(h), a b y (i ) 2 i 1 2
N
若初值问题(6-1)通过某一种数值方法得到yN ,则最终误差 E ( y(b), h) y(b) - yN
称为总体截断误差简记为 EN
第6章常微分方程数值解法 6.1 常微分方程初值问题的数值方法 6.1.1 Euler方法及其变形
令t0 0, y0 1 yi 1 yi h( yi 2sin ti )进行计算,得到数值解.
程序演示
第6章常微分方程数值解法
例.用Euler法求解初值问题

计算方法引论课后答案

第一章误差1. 试举例,说明什么是模型误差,什么是方法误差.解: 例如,把地球近似看为一个标准球体,利用公式24A r π=计算其表面积,这个近似看为球体的过程产生的误差即为模型误差.在计算过程中,要用到π,我们利用无穷乘积公式计算π的值: 其中我们取前9项的乘积作为π的近似值,得这个去掉π的无穷乘积公式中第9项后的部分产生的误差就是方法误差,也成为截断误差.2. 按照四舍五入的原则,将下列各数舍成五位有效数字:816.956 7 6.000 015 17.322 50 1.235 651 93.182 13 0.015 236 23 解: 816.96 6.000 0 17.323 1.235 7 93.182 0.015 2363. 下列各数是按照四舍五入原则得到的近似数,它们各有几位有效数字? 81.897 0.008 13 6.320 05 0.180 0 解: 五位三位六位四位4. 若1/4用0.25表示,问有多少位有效数字? 解: 两位5. 若 1.1062,0.947a b ==,是经过舍入后得到的近似值,问:,a b a b +⨯各有几位有效数字?解: 已知4311d 10,d 1022a b --<⨯<⨯, 又0.2053210a b +=⨯,()433211110100.551010222d a b da db da db ----+=+≤+=⨯+⨯=⨯<⨯,所以a b +有三位有效数字;因为0.1047571410a b ⨯=⨯,所以a b ⨯有三位有效数字.6. 设120.9863,0.0062y y ==,是经过舍入后作为12,x x 的近似值.求1211,y y 的计算值与真值的相对误差限及12y y ⋅与真值的相对误差限.解: 已知-4-41112221211d ,d ,d =10,d 1022x y x x y x x x =+=+⨯=⨯, ()44111111110d d 12dr dr 0.50100.9863x xx x x y --⨯⎛⎫==≈=≈⨯ ⎪⎝⎭;()42222222110d d 12dr dr 0.81100.0062x xx x x y --⨯⎛⎫==≈=≈⨯ ⎪⎝⎭;()()()4221212dr dr dr 0.50100.81100.8210x x x x ---⋅=+≈⨯+⨯≈⨯.7. 正方形的边长约为100cm,应该怎样测量,才能使其面积的误差不超过1cm 2. 解: 设正方形面积为S,边长为a,则S=a 2.所以要使:2d d 2d 1s a a a ==≤,则要求211d 0.5102200a a -≤==⨯.所以边长的误差不能超过20.510-⨯cm.8. 用观测恒星的方法求得某地维度为4502'''(读到秒),试问:计算sin ϕ将有多大误差?解: ()()1d sin cos d cos 45022ϕϕϕ*''⎛⎫'''== ⎪⎝⎭.9 . 真空中自由落体运动距离s 与时间的关系由公式212s gt =确定,g 是重力加速度.现在假设g 是准确的,而对t 的测量有0.1s ±的误差,证明t 增加时,距离的绝对误差增加而相对误差却减小. 证明: 因为:221d d d d d d d ;2.122s gt t gt t t s gt gt t s s t gt ⎛⎫=====⎪⎝⎭ d s 与t成正比,d s s与t 成反比,所以当d t 固定的时候, t增加时,距离的绝对误差增加而相对误差却减小.10. 设0x >,x 的相对误差为δ,求ln x 的绝对误差. 解: 已知d x x δ=,所以ln x 的绝对误差()d d ln x x xδ==. 11. 设x 的相对误差为%α,求nx 的相对误差.解: 1d d d %n n n nx nx x n xn x x xα-===. 12. 计算球的体积,为了使相对误差限为1%,问度量半径R 时允许的相对误差限如何? 解: 已知343V R π=,设()d dr R R a R ==,则要使得 ()()3d dr dln d ln 3d ln 3d ln 3dr 31%V V V R R R R a V ========,则11%3a =⋅. 第二章插值法与数值微分1.设y =在100,121,144x =三处的值是很容易求得的,试以这三个点建立y =的二次插值多项式,并用,且给出误差估计.用其中的任意两点,构造线性插值函数,用得到的三个线性插值函数,,并分析其结果不同的原因.解: 已知012012100,121,144;10,11,12x x x y y y ======,建立二次Lagrange 插值函数可得:()211510.7228L ≈=.误差()()()()()()2012012,,,,3!f R x x x x x x x x x x ξξξ'''=---∈,所以利用前两个节点建立线性插值函数可得:()111510.7143L ≈=.利用后两个节点建立线性插值可得:()111510.7391L ≈=.利用前后两个节点建立线性插值可得:()111510.6818L ≈=.与,二次插值比线性插值效果好,利用前两个节点的线性插值比其他两个线性插值效果好.此说明,二次插值比线性插值效果好,内插比外插效果好.2. 利用(2.9)式证明证明: 由(2.9)式当01x x x <<时,()()01max x x x f f x ξ≤≤''''≤,()()()01201101max 4x x x x x x x x x ≤≤--≤- 所以3. 若()0,1,...,j x n 为互异节点,且有证明证明: 由于且()0nk j j j x l x =∑和kx都为k 次多项式,而且在k+1个不同的节点处的函数值都相同0,1,...,k n =, 所以马上有()0,0,1,...,nk kj j j x l x xk n =≡=∑.4. 设给出sin x 在[],ππ-上的数值表,用二次插值进行计算,若希望截断误差小于510-,问函数表的步长最大能取多少?解: 记插值函数为p(x),则所以()()()()11cos max sin 3!i i i x x p x x x x x x ππξ-+-≤≤--=---()cos 1ξ-≤;令()()()()11i i i g x x x x x x x -+=---,设1i x x th -=+,得又()()()[]12,0,2t t t t t ϕ=--∈的最大值为10.3849ϕ⎛= ⎝⎭,所以有所以0.0538h ≤.5. 用拉格朗日插值和牛顿插值找经过点()()()()3,1,0,2,3,2,6,10---的三次插值公式. 解: Lagrange 插值函数:牛顿插值: 首先计算差商也可以利用等距节点构造,首先计算差分可得前插公式和后插公式6. 确定一次数不高于4的多项式()x ϕ,使()()()()()00,00,111,21ϕϕϕϕϕ''=====. 解: 利用重节点计算差商则可构造Hermite 插值函数满足题设条件:7. 寻找过1n +个点01,,...,n x x x 的21n +次多项式()21n H x +,满足条件: 解: 和Lagrange 插值函数的构造类似,可将插值函数写成其中,基函数满足条件 (1)()()(),,,21n i n i h x h x P n ∈+;(2)()()()(),,,,,0;,0n i n i n ij ij n i j j ijj h x h x h x h x δδ''====则可由已知条件,可得()()()()2,,,12n i n i i i n i h x l x x x l x '⎡⎤=--⎣⎦;()()()2,,n i i n i h x x x l x '=-.所以可得8. 过0,1两点构造一个三次Hermite 插值多项式,满足条件: 解: 计算重节点的差商马上可得9. 过给定数组(1) 作一分段线性插值函数.(2) 取第二类边界条件,作三次样条插值多项式.(3) 用两种插值函数分别计算75.5,78.3x x ==的函数值. 解: (1)做分段线性插值函数可得:其中, ()[][]076 75,76;0 75,76.x x l x x ⎧-∈⎪=⎨∉⎪⎩()[][][]175 75,7677 76,77;0 75,77.x x l x x x x ⎧-∈⎪=-∈⎨⎪∉⎩ (2)把已知节点值带入M 关系式可得: 由边界条件可得050M M ==,所以上面方程组变为可求解方程组解得12340.0058,0.0067,0.0036,0.0071M M M M ====.所以可得在每个区间上的三次样条函数的表达式: (3)当75.5x =时,()()()50175.5 2.76875.5 2.83375.5 2.8005I l l =+=;()()()()()30.00580.005875.575.576 2.7687675.5 2.83375.575 2.79966s ⎛⎫=-+-+--= ⎪⎝⎭当78.3x =时,()()()53475.5 2.97978.3 3.06278.3 3.0039I ll =+=;10. 若给出sin ,cos ,tan x x x 的函数表:用表上的数据和任一插值公式求: (1) 用tan x 表格直接计算tan1.5695.(2) 用sin1.5695和cos1.5695来计算tan1.5695.并讨论这两个结果中误差变化的原因. 解: 利用Lagrange 插值直接用tan 表计算得tan1.5695819.0342874999274≈;利用Lagrange 插值计算sin 得sin1.56950.99999917500000≈;利用Lagrange 插值计算cos 得cos1.56950.00129630000000≈;最后利用sin/cos 计算tan 得tan1.5695771.4257309264500≈.出现小除数,误差被放大.11. 求三次样条函数()s x ,已知和边界条件解: 把表中数据带入M 关系式可得由边界条件还可得到两个方程: 联立两个方程组可解得:带入M 表达式便可得所求三次样条函数.12. 称n 阶方阵()ij A a =具有严格对角优势,若 (1) 试证明:具有严格对角优势的方阵必可逆. (2) 证明:方程组(2.62)解存在唯一.证明: (1)设矩阵A 按行严格对角占优,如果A 奇异,则存在非零向量x 使得Ax=0,写成分量形式为令指标0i 使得00i x x∞=≠,则因此0000010n i i i i j j j i x a a =≠⎛⎫⎪-≤ ⎪ ⎪⎝⎭∑ 即000010ni i i j j j i a a =≠-≤∑上式与矩阵按行严格对角占优矛盾,因此矩阵非奇异. (2)方程组(2.62)由于该方程组系数矩阵为严格对角占优的方阵,所以由克拉默法则可知方程组存在唯一解.。

计算机科学引论课件06

13
多媒体处理
理解声音
第一步：把声音信号变换到频域
FFT： Fast Fourier transform DFT： Discrete Fourier transform ……
第二步：把频率信息变换成特征
倒谱(cepstrum)：把频域信息再次进行频率变换
MFCC LPCC
就成为一个数学问题
把特征矢量转换成语义的数学算法：分类
2020年1月6日
Machine Structure
15
多媒体处理
理解声音
分类(classification)
把特征矢量转换成语义的数学算法
例：语音识别
把MFCC所组成的高维空间分解成不同的部分，每部分
p
代表一个读音。如某个特征矢量落在某部分，则可知道该矢量代表的读音。
文本的内容，即特征矢量
在某些应用获得成功：如主题分类目标具有统计性质
如何实现提取时间、地点、人物、事件等细节特征？目标是一个个体，不具有统计性质 WEB分析：如果有很多文档，则这些个体内容很可能被多次重复，从而具有了统计性e
语义：不同的应用有不同的含义
声音、图像、视频：文字（关键字：keyword)即被认为是语义的最佳表示
当前研究致力于提取可以表示声音、图像、视频等的文字
文本：文字的真实含义才是语义
信息提取(IR: Information Retrieval)：时间、地点、人物、事件
主题分类(Topic Classification)
5
人工智能
理解人类的感知
理解听觉理解视觉理解自然语言(NL: Natural Language)

计算方法课程教学大纲汇总

《计算方法》课程教学大纲课程编号：学时：54 学分：3适用对象：教育技术学专业先修课程：高等数学、线性代数考核方式：本课程考试以笔试为主70%，兼顾学生的平时成绩30%。

使用教材及主要参考书：使用教材：李庆扬.《数值分析(第四版)》, 清华大学出版,2014年。

主要参考书：1.朱建新,李有法.《高等学校教材:数值计算方法(第3版)》,高等教育出版社,2012。

2.徐萃薇,孙绳武.《计算方法引论(第4版)》,高等教育出版社,2015。

一课程的性质和任务计算方法是教育技术学专业学生的一门专业选修课。

作为计算数学的一个重要分支，它是数学科学与计算机技术结合的一门应用性很强的学科，本课程重点介绍计算机上常用的基本计算方法的原理和使用；同时对计算方法作适当的分析。

教学任务：通过本课程的学习，要使学生具有现代数学的观点和方法，并初步掌握处理计算机常用数值分析的构造思想和计算方法。

同时，也要培养学生抽象思维和慎密概括的能力，使学生具有良好的开拓专业理论的素质和使用所学知识分析和解决实际问题的能力。

二教学目的与要求教学目的：通过学习使学生了解数值计算方法的基本原理。

了解计算机与数学结合的作用及课程的应用性。

为今后使用计算机解决实际问题中的数值计算问题打下基础。

通过理论教学达到如下基本要求。

1．了解误差的概念2．掌握常用的解非线性方程根的方法3．熟练掌握线性代数方法组的解法4．熟练掌握插值与拟合的常用方法5．掌握数值积分方法6．了解常微分方程初值问题的数值方法三学时分配四教学中应注意的问题本课程是一门理论性较强、内容较抽象的综合课程，因此面授辅导或自学，将是不可缺少的辅助教学手段，教师在教学的过程中一定要注意理论结合实际，课堂教学并辅助上机实验，必须通过做练习题和上机实践来加深对概念的理解和掌握，熟悉公式的运用，从而达到消化、掌握所学知识的目的。

同时应注重面授辅导或答疑，及时解答学生的疑难问题。

五教学内容第一章绪论（误差）基本内容:第一节数值分析研究的对象和特点第二节数值计算的误差1.误差的来源与分类2.误差与有效数字3.数值运算的误差估计第三节误差的定性分析与避免误差的危害1.病态问题与条件数2.算法的数值稳定性3.避免误差危害的若干原则教学重点难点:重点：数值运算的误差估计。

计算引论6 推理与计算

置换满足结合律
(θ · λ) · µ= θ ·(λ · µ) (
置换不满足交换律
θ · λ ≠ λ · θ ε ·θ = θ ·ε = θ
合一置合一置换：给定表达式E1,…,Ek，若存在置换θ ，使若存在置换θ 给定表达式则称θ 得E1θ=…=Ekθ ，则称θ是E1,…,Ek的一个合一置合一置换。
最一般合一置换求法：最一般合一置换求法：
设有公式：设有公式：E1=P(x,y,z); E2= P(x,f(a),g(b)) 从左至右查找不同的项，构成了不一致集：从左至右查找不同的项，构成了不一致集： D1={y,f(a)} 继续向右比较又得到一个不一致集：继续向右比较又得到一个不一致集： D2={z,g(b)} 置换为θ 置换为θ = {f(a)/y, g(b)/z}
对公式P的化的步骤如下：对公式的SKOLEM化的步骤如下：化的步骤如下（1）将P化为前束范式）化为前束范式（Q1x1）…（Qnxn）H(x1.... xn) （是存在量词或者全称量词，为合其中 Q1…Qn是存在量词或者全称量词，H为合取范式的形式,不含取范式的形式不含→, ↔ ；不含
计算引论
第四章推理与计算
主要内容
逻辑与推理 Horn逻辑程序逻辑程序命题Horn逻辑中的自动推理逻辑中的自动推理命题谓词Horn逻辑中的自动推理逻辑中的自动推理谓词 Prolog逻辑程序设计逻辑
4.1 逻辑基础知识
符号表示：符号表示：
常量：常量：小写字母 a, b, c,...。。函数：函数：小写字母 f, g, h,... 。变量：变量：小写字母 x, y, z,...。。逻辑算子(或连结词：逻辑算子或连结词)：¬, ∧, ∨, →, ↔ 。或连结词量词：量词：∀ , ∃. 谓词：谓词：大写字母 P, Q, R,... 。

计算方法引论课后答案.

计算⽅法引论课后答案.第⼀章误差1. 试举例,说明什么是模型误差,什么是⽅法误差.解: 例如,把地球近似看为⼀个标准球体,利⽤公式24A r π=计算其表⾯积,这个近似看为球体的过程产⽣的误差即为模型误差.在计算过程中,要⽤到π,我们利⽤⽆穷乘积公式计算π的值:12222...q q π=?其中112,3,...n q q n +?=??==?? 我们取前9项的乘积作为π的近似值,得3.141587725...π≈这个去掉π的⽆穷乘积公式中第9项后的部分产⽣的误差就是⽅法误差,也成为截断误差.2. 按照四舍五⼊的原则,将下列各数舍成五位有效数字:816.956 7 6.000 015 17.322 50 1.235 651 93.182 13 0.015 236 23 解: 816.96 6.000 0 17.323 1.235 7 93.182 0.015 236 3. 下列各数是按照四舍五⼊原则得到的近似数,它们各有⼏位有效数字? 81.897 0.008 13 6.320 05 0.180 0 解: 五位三位六位四位4. 若1/4⽤0.25表⽰,问有多少位有效数字? 解: 两位5. 若 1.1062,0.947a b ==,是经过舍⼊后得到的近似值,问:,a b a b +?各有⼏位有效数字?解: 已知4311d 10,d 1022a b --()433211110100.551010222d a b da db da db ----+=+≤+=?+?=?所以a b +有三位有效数字;因为0.1047571410a b ?=?,()43321110.94710 1.1062100.600451010222所以a b ?有三位有效数字.6. 设120.9863,0.0062y y ==,是经过舍⼊后作为12,x x 的近似值.求1211,y y 的计算值与真值的相对误差限及12y y ?与真值的相对误差限. 解: 已知-4-41112221211d ,d ,d =10,d 1022x y x x y x x x =+=+?=?, ()44111111110d d 12dr dr 0.50100.9863x xx x x y --==≈=≈? ???;()42222222110d d 12dr dr 0.81100.0062x xx x x y --==≈=≈? ???;()()()4221212dr dr dr 0.50100.81100.8210x x x x ---?=+≈?+?≈?.7. 正⽅形的边长约为100cm,应该怎样测量,才能使其⾯积的误差不超过1cm 2.解: 设正⽅形⾯积为S,边长为a,则S=a 2.所以要使:2d d 2d 1s a a a ==≤,则要求211d 0.5102200a a -≤==?.所以边长的误差不能超过20.510-?cm.8. ⽤观测恒星的⽅法求得某地维度为4502'''o(读到秒),试问:计算sin ?将有多⼤误差?解: ()()1d sin cos d cos 45022*''?'''==o.9 . 真空中⾃由落体运动距离s 与时间的关系由公式212s gt =确定,g 是重⼒加速度.现在假设g 是准确的,⽽对t 的测量有0.1s ±的误差,证明t 增加时,距离的绝对误差增加⽽相对误差却减⼩.证明: 因为:221d d d d d d d ;2.122s gt t gt t t s gt gt t s s t gt ??d s 与t 成正⽐,d s s与t 成反⽐,所以当d t 固定的时候, t 增加时,距离的绝对误差增加⽽相对误差却减⼩.10. 设0x >,x 的相对误差为δ,求ln x 的绝对误差. 解: 已知d x x δ=,所以ln x 的绝对误差()d d ln x x x δ==.11. 设x 的相对误差为%α,求nx 的相对误差.解: 1d d d %n n n n x nx x n xn x x xα-===.12. 计算球的体积,为了使相对误差限为1%,问度量半径R 时允许的相对误差限如何? 解: 已知34 3V R π=,设()d dr R R a R ==,则要使得 ()()3d dr dln d ln 3d ln 3d ln 3dr 31%V V V R R R R a V ========,则11%3a =?.第⼆章插值法与数值微分1.设y =在100,121,144x =三处的值是很容易求得的,试以这三个点建⽴y =的⼆次插值多项式,,且给出误差估计.⽤其中的任意两点,构造线性插值函数,⽤得到的三个线性插值函数,,并分析其结果不同的原因.解: 已知012012100,121,144;10,11,12x x x y y y ======,建⽴⼆次Lagrange 插值函数可得:()()()()21211441001441011100121100144121100121144121100 12144121144100x x x x L x x x ----= +------+--()211510.7228L ≈=.误差()()()()()()2012012,,,,3!f R x x x x x x x x x x ξξξ'''=---∈,所以20.00065550.001631R <<利⽤前两个节点建⽴线性插值函数可得:()()()()()11211001011100121121100x x L x --=+--()111510.7143L ≈=.利⽤后两个节点建⽴线性插值可得:()()()()()11441211112121144144121x x L x --=+--()111510.7391L ≈=.利⽤前后两个节点建⽴线性插值可得:()()()()()21441001012100144144100x x L x --=+()111510.6818L ≈=.,⼆次插值⽐线性插值效果好,利⽤前两个节点的线性插值⽐其他两个线性插值效果好.此说明,⼆次插值⽐线性插值效果好,插⽐外插效果好.2. 利⽤(2.9)式证明()()()0121001max ,8x x x x x R x f x x x x ≤≤-''≤≤≤证明: 由(2.9)式()()()()0101,2!f R x x x x x x x ξξ''=--<<当01x x x <<时,()()01max x x x f f x ξ≤≤''''≤,()()()01201101max 4x x x x x x x x x ≤≤--≤- 所以()()()0121001max ,8x x x x x R x f x x x x ≤≤-''≤≤≤3. 若()0,1,...,j x n 为互异节点,且有()()()()()()()()()011011............j j n j jj j j j j n x x x x x x x x l x xx x x x x x x -+-+----=证明()0,0,1,...,nk kj j j x l x xk n =≡=∑证明: 由于() 1 ;0 .j i ij i j l x i j δ=?==?≠? 且()0nk j j j x l x =∑和kx都为k 次多项式,⽽且在k+1个不同的节点处的函数值都相同0,1,...,k n =, 所以马上有()0,0,1,...,nk kj j j x l x xk n =≡=∑.4. 设给出sin x 在[],ππ-上的数值表,⽤⼆次插值进⾏计算,若希望截断误差⼩于5 10-,问函数表的步长最⼤能取多少? 解: 记插值函数为p(x),则()()()()()11sin sin 3!i i i x p x x x x x x x ξ-+'''-=--- 所以()()()()11cos max sin 3!i i i x x p x x x x x x ππξ-+-≤≤--=---()()()[]3112,0,2i g x th h t t t t -+=--∈⼜()()()[]12,0,2t t t t t ?=--∈的最⼤值为10.3849??= ?,所以有 350.3849max sin 106x x p h ππ--≤≤-≤< 所以 0.0538h ≤.5. ⽤拉格朗⽇插值和⽜顿插值找经过点()()()()3,1,0,2,3,2,6,10---的三次插值公式. 解: Lagrange 插值函数:()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()12302330101020310121301301223202123303132 31033101622731033 .2781/5x x x x x x x x x x x x L x y y x x x x x x x x x x x x x x x x x x x x x x x x y y x x x x x x x x x x x x x x x x x x x x x x x x ------= +------------++--------+--=++-+-++⽜顿插值: ⾸先计算差商3 10 2 13 2 1.333 0.38896 104 0.8889 0.1420-----()()()()()3130.38893 1.142033.N x x x x x x x =-++-+++-也可以利⽤等距节点构造,⾸先计算差分。

计算方法-第1章

13
一．自然语言法
1. 输入数据a, b, c 2.如果a=0, 转3，否则转4
c 3.如果 b 0，则 x1 ，转7；否则，无解停机 b 2 ， b 4 ac 4. 设 D SD SQRT (| D |)
0 ,x ( b iSD ) / 2 a , 如果 D 1 x ( b iSD ) / 2 a ，转7 2 否则， 5. 如果b>0不成立， S 1 b SD ，转7 x S 1 / 2 a , x 2 c / S 1 1 2 S 2 / 2 a , x 2 c / S 2 2 b SD 6. S ，x 1 2 7. 输出x1和x2
x1， x2，……， x100 取为
数值方法
0.1, 0.2, 0.3, ……,10=a
2-1
★ 计算公式不一定都是数值方法。如求
类似地，求根公式
2 b b 4 ac x 1 ,2 2 a
3 。
不能在计算机上直接运行
◆ 研究数值方法的任务有三条：
1）将计算机不能直接计算的运算化成计算机上可执行的运算；利用等价或近似等价的方法转化； 7
1）数学的发展极大地促进了计算机科学的发展：
★ Leibniz发现二进制编码； ★ Von Neumann提出现代计算机建构理论； ★ Bohm和Jacopini为结构化程序设计奠定了基础。
2）计算机科学为数学提供先进手段，并对数学发展产生了重大影响。
★ 为利用数学解决实际问题提供了工具； ★ 解决了一些数学难题，并提出了新的研究课题；
x 2 ( b iS D ) / 2 a
输出 x1, x 2
15
▲ 结构化框图法：N-S图示法

计算方法word教案第六章常微分方程的数值解法word资料23页

第六章常微分方程的数值解法§6.0 引言§6.1 算法构造的主要途径§6.2 Runge-Kutta Method算法§6.3 线性多步法§6.4 线性多步法的一般形式§6.5 算法的稳定性、收敛性§6.6 小结§6.0 引言1．主要考虑如下的一阶常微分方程初值问题的求解:微分方程的解就是求一个函数()y y x =，使得该函数满足微分方程并且符合初值条件。

2.例如微分方程:'-24(1)-3 xy y x y =⎧⎨=⎩初始条件. 可得一阶常微分方程的初始问题显然函数y(x)=x 2-4x 满足以上条件,因而是该初始问题的微分方程的解。

3. 但是,只有一些特殊类型的微分方程问题能够得到用解析表达式表示的函数解，而大量的微分方程问题很难得到其解析解，有的甚至无法用解析表达式来表示。

因此，只能依赖于数值方法去获得微分方程的数值解。

4．微分方程的数值解：设微分方程问题的解y(x)的存在区间是[a,b ]，初始点x 0=a ，将[a,b ]进行划分得一系列节点x 0 , x 1 ,...,x n ，其中a= x 0< x 1<…< x n =b 。

y(x)的解析表达式不容易得到或根本无法得到，我们用数值方法求得y(x)在每个节点x k 的近似值y(x k )，即这样y 0 , y 1 ,...,y n 称为微分方程的数值解。

如图所示:abx 0 x 1 x 2 ... x n-1 x n§6.1 算法构造的主要途径1 欧拉公式 1.1 构造的思想：微分方程初值问题: ()()00,dyf x y dx y x y ⎧=⎪⎨⎪=⎩利用差商代替一阶导数，即则于是，可求出y(x 1)的近似值y 1，同样地，可利用x 1处的微分方程可得：一般地，利用在x n 处的微分方程可得：此式称为欧拉公式。

《徐翠微计算方法引论》

第二章插值法知识点：拉格朗日插值法，牛顿插值法，余项，分段插值。

实际问题中，时常不能给出f （x ）的解析表达式或f （x ）解析表达式过于复杂而难于计算，能采集的只是一些f （x ）的离散点值{xi,f(xi)}(i=0,1,2,…n )。

因之，考虑近似方法成为自然之选。

定义：设f （x ）为定义在区间[a ，b]上的函数，x0,x1,…,xn 为[a ，b]上的互异点，yi=f （xi ）。

若存在一个简单函数ϕ（x ），满足（插值条件）ϕ（xi ）=f （xi ），i=0，1，…，n 。

则称 ϕ（x ）为f （x ）插值函数，f （x ）为被插函数,点x0,x1,…,xn 为插值节点,点{xi,f(xi)},i=0,1,2,…n 为插值点。

于是计算f （x ）的问题就转换为计算 ϕ（x ）。

构造插值函数需要解决：插值函数是否存在唯一；插值函数如何构造(L 插值)；插值函数与被插函数的误差估计和收敛性。

对插值函数 ϕ（x ）类型有多种不同的选择，代数多项式常被选作插值函数。

P23(2.18)和(2.19)指出，存在唯一的满足插值条件的n 次插值多项式p n (x )。

但是需要计算范德蒙行列式，构造插值多项式工作量过大，简单表达式不易得到，实际中不采用这类方法。

插值法是一种古老的数学方法，拉格朗日（Lagrange ）、牛顿（Newton ）等分别给出了不同的解决方法。

拉格朗日插值拉格朗日（Lagrange ）插值的基本思想：把插值多项式p n (x )的构造问题转化为n+1个插值基函数l i (x)(i=0,1,…,n)的构造。

(1)线性插值 ①构造插值函数已知函数y =f (x )的两个插值点(x 0,y 0)，(x 1,y 1)，构造多项式y =p 1(x )，使p 1(x 0)=y 0,p 1(x 1)=y 1。

p n (x )≈f (x )由直线两点式可知，通过A ，B 的直线方程为变形为记则p 1(x )=l 0(x )y 0+l 1(x )y 1插值完毕！注意性质：l 0(x 0)=l 1(x 1)=1，l 0(x 1)=l 1(x 0)=0，p 1(x 0)=y 0，p 1(x 1)=y 1。

计算方法引论-第六章

南开大学算法导论第六章课件

计算方法

计算方法的课后答案解析

计算方法各章小结

计算方法引论课后答案

计算方法_第六章

西安交通大学《计算方法》课件-第六章

计算方法引论课后答案

计算机科学引论课件06

计算方法课程教学大纲汇总

计算引论6 推理与计算

计算方法引论课后答案.

计算方法-第1章

计算方法word教案第六章 常微分方程的数值解法word资料23页

《徐翠微计算方法引论》

计算方法word教案第六章常微分方程的数值解法word资料23页